PCA Weight Determination-Based InSAR Baseline Optimization Method: A Case Study of the HaiKou Phosphate Mining Area in Kunming, Yunnan Province, China
Abstract
1. Introduction
2. Study Area and Data Sources
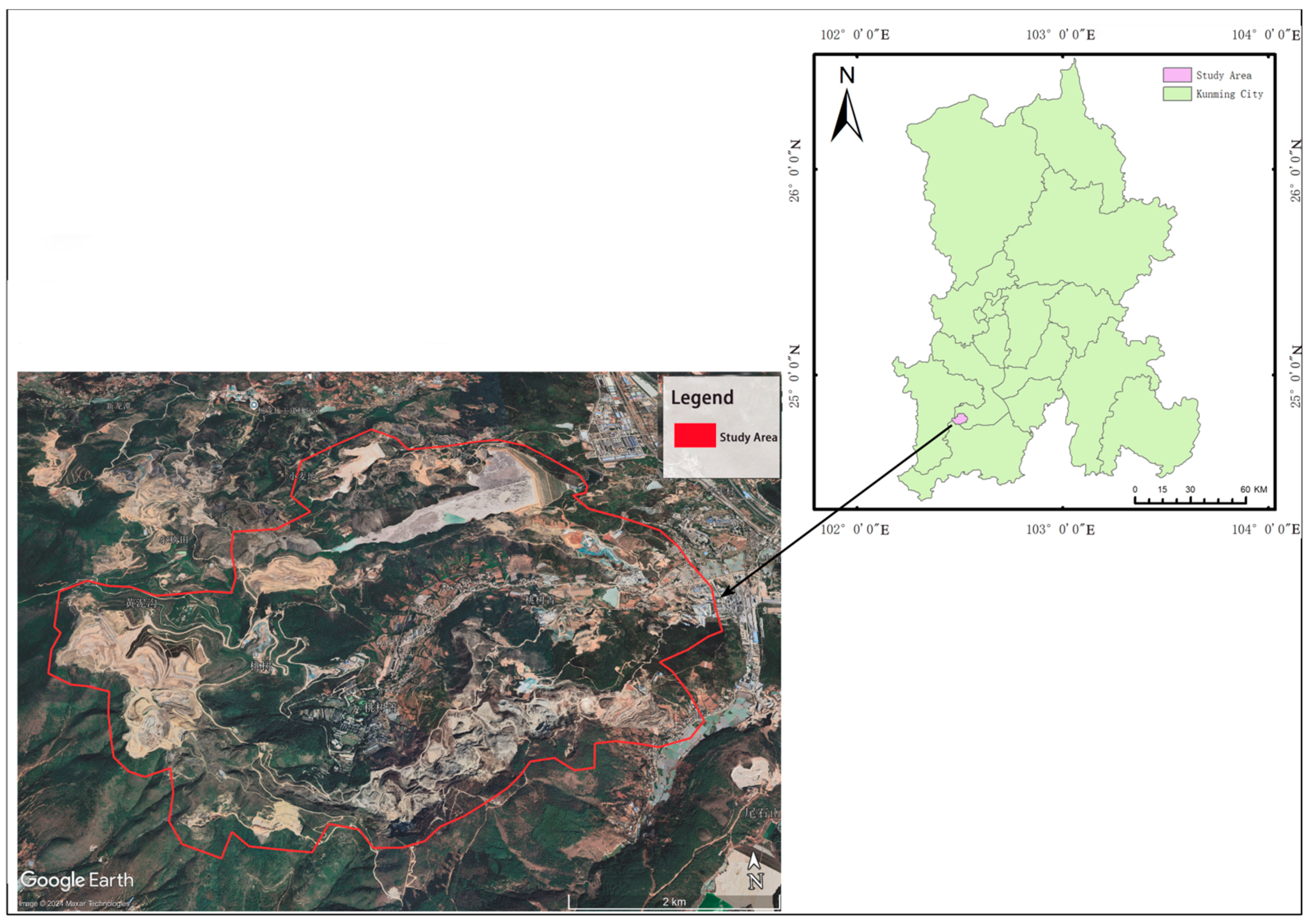
2.1. Study Area Description
2.2. Data Sources
- Landsat-8 optical imagery (30 m spatial resolution);
- Precise orbit determination (POD) ephemeris data from the Copernicus Sentinel missions;
- ALOS World 3D-30m digital elevation model (DEM);
- Generic Atmospheric Correction Online Service (GACOS) atmospheric delay products;
- The data sources and applications are summarized in Table 1.
3. Method
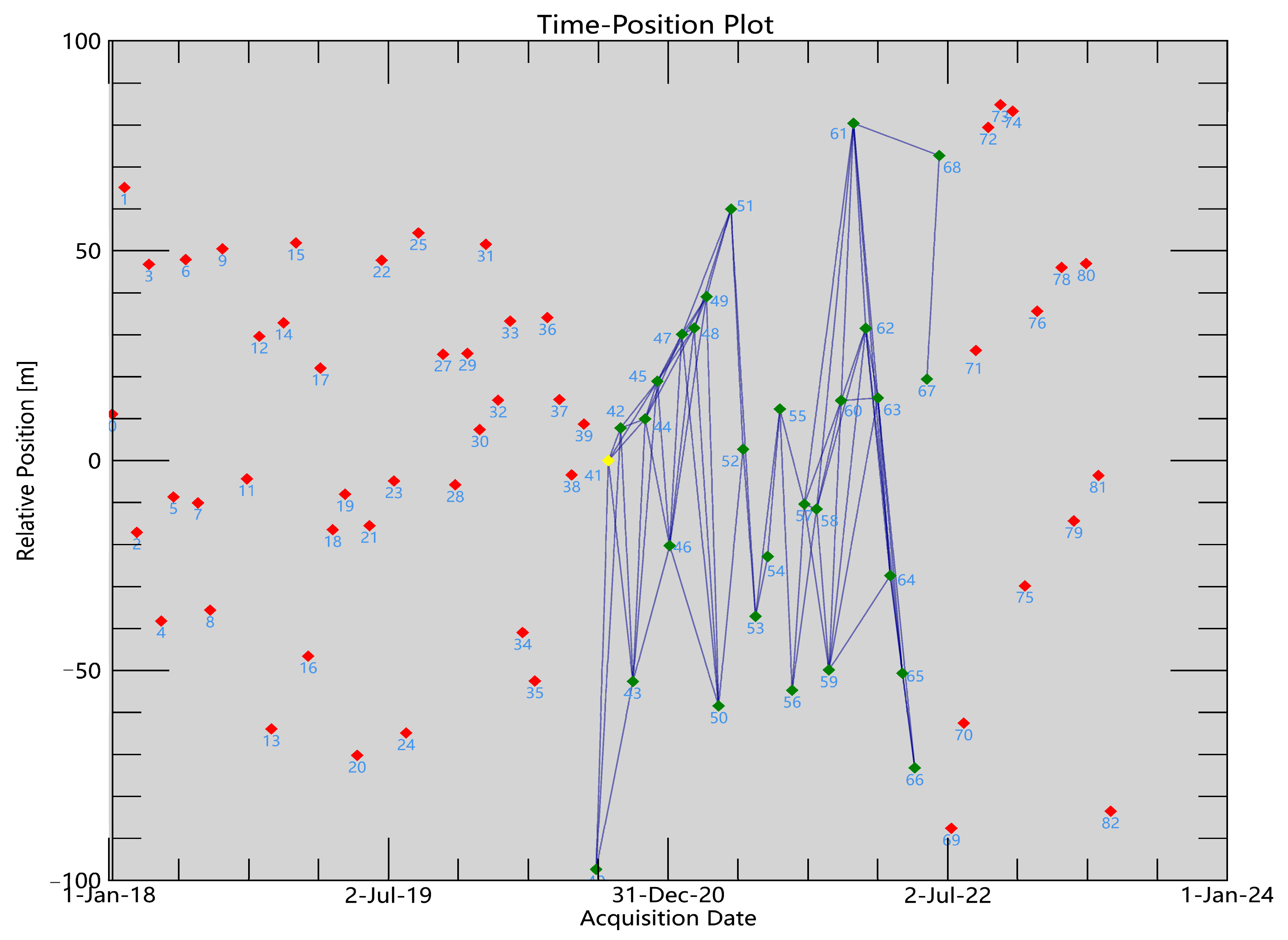
3.1. Interferometric Pair Stacking with Sentinel-1A Data and GACOS Atmospheric Correction
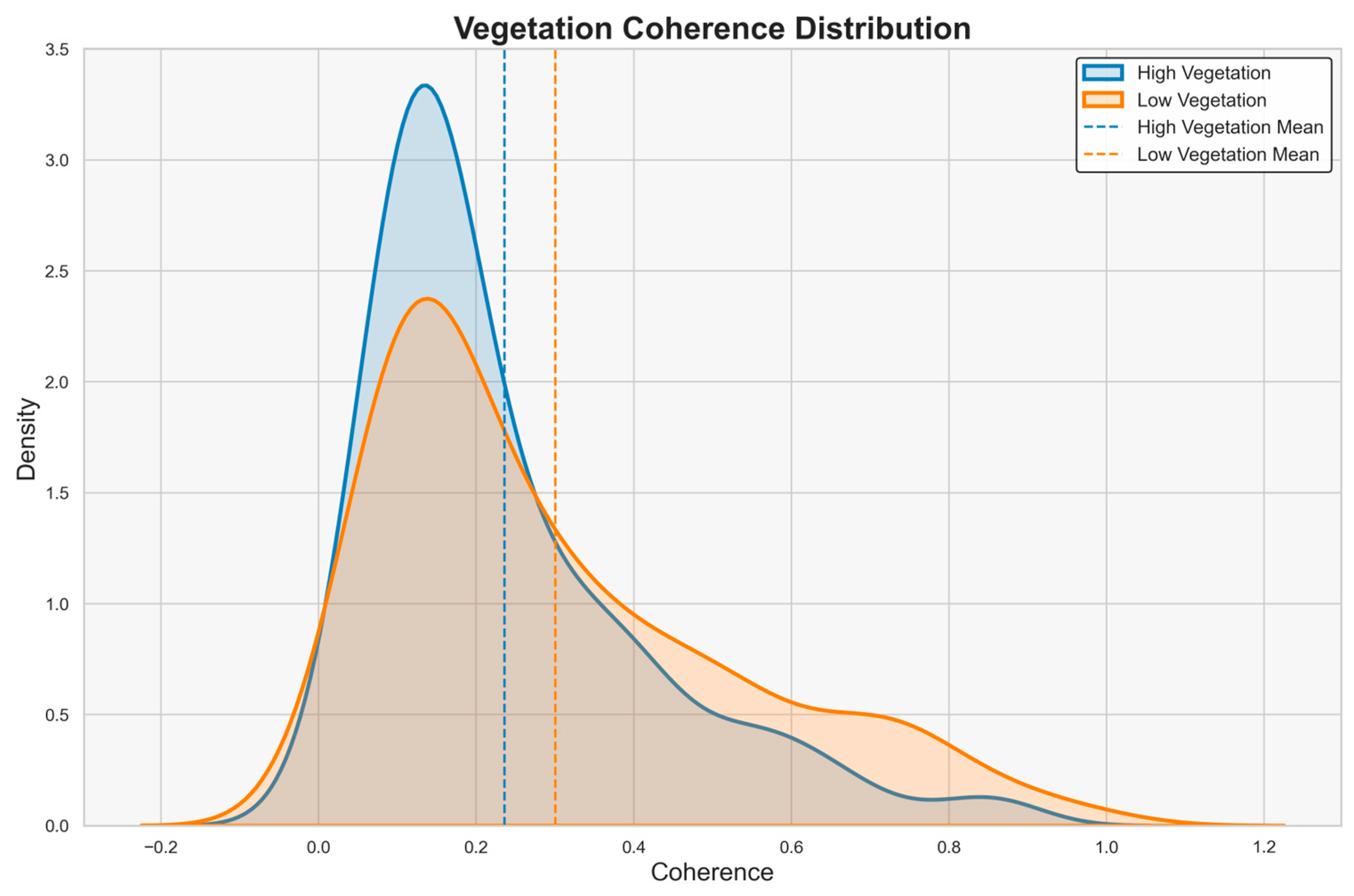
3.2. Spatiotemporal Baselines, Coherence, and NDVI Difference Calculations
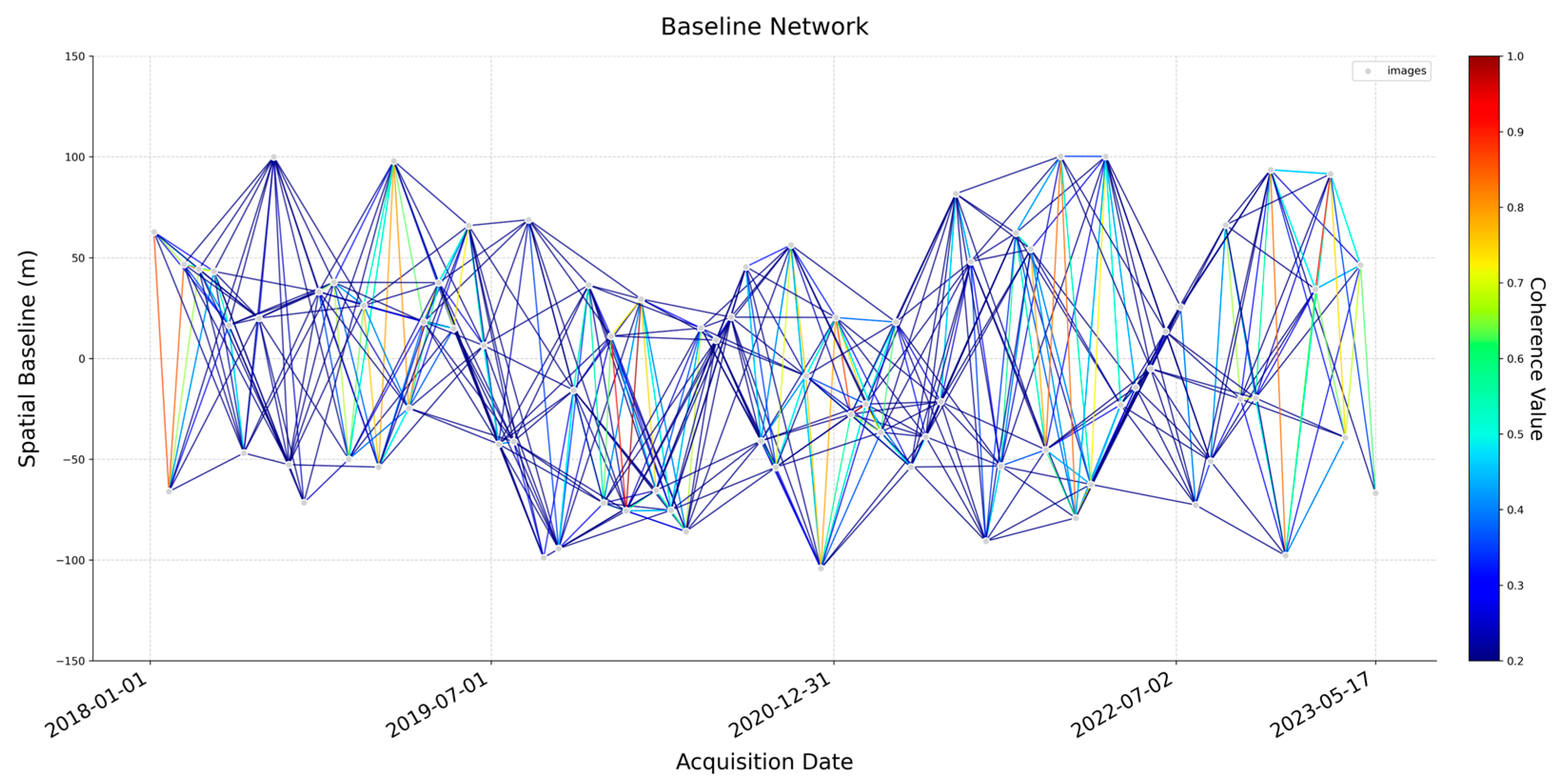
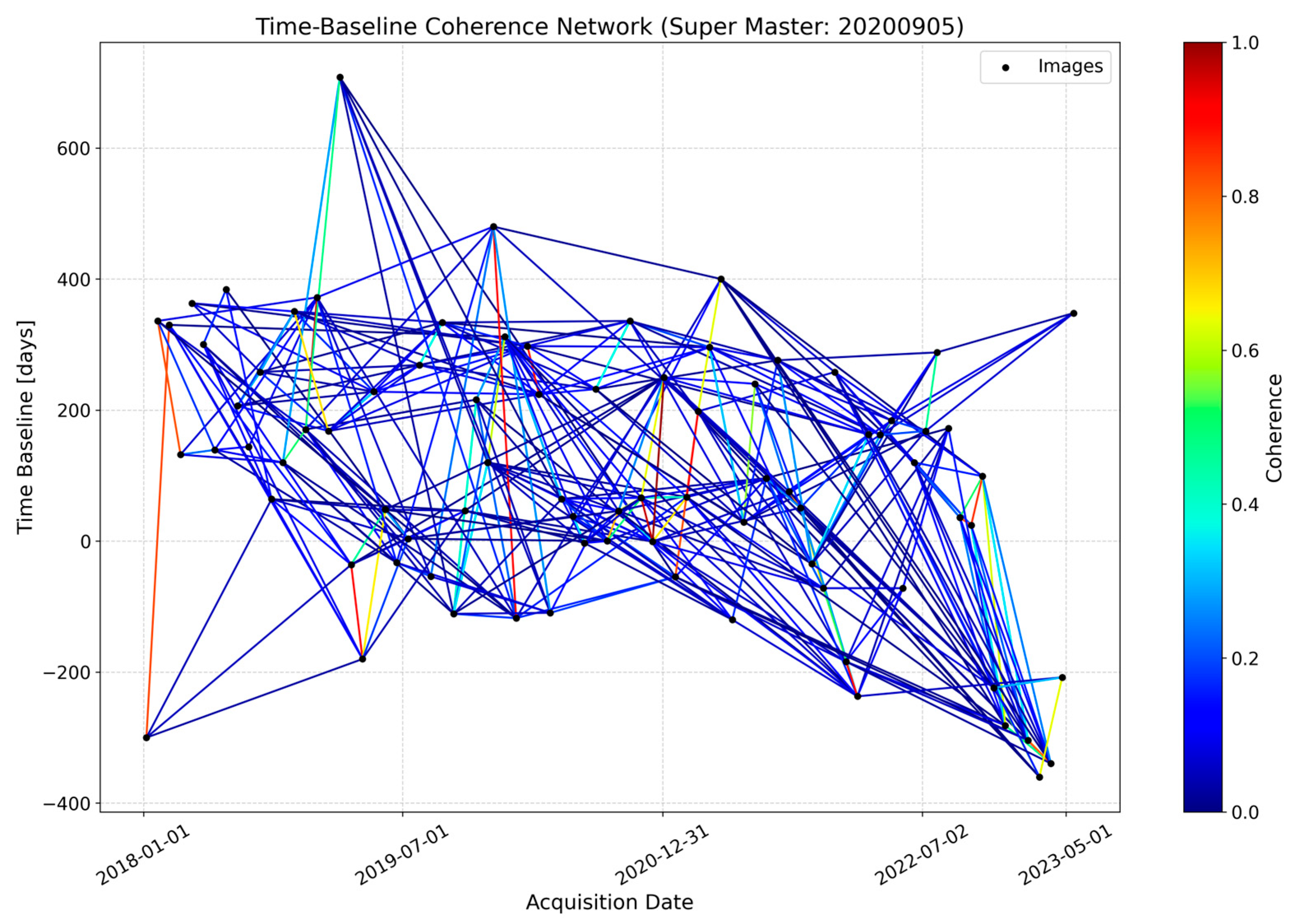
3.2.1. Spatiotemporal Baselines and Coherence Calculation
3.2.2. NDVI Difference Calculation
3.3. PCA-Based Baseline Optimization
3.3.1. Data Preprocessing and PCA Calculation
- 1.
- Data Preparation and Standardization
- Temporal Baseline (D): The time difference (days) between the master and slave images;
- Spatial Baseline (S): The geometric distance (meters) between the master and slave images;
- NDVI Difference (ΔNDVI): The difference in NDVI between the master and slave images, representing vegetation change;
- Coherence (C): The average coherence of each interferometric pair, indicating image quality.
- 2.
- Calculation of Covariance Matrix
- 3.
- Eigenvalue and Eigenvector Decomposition
- 4.
- Calculation of Explained Variance Ratio
3.3.2. Principal Component Analysis and Weight Calculation
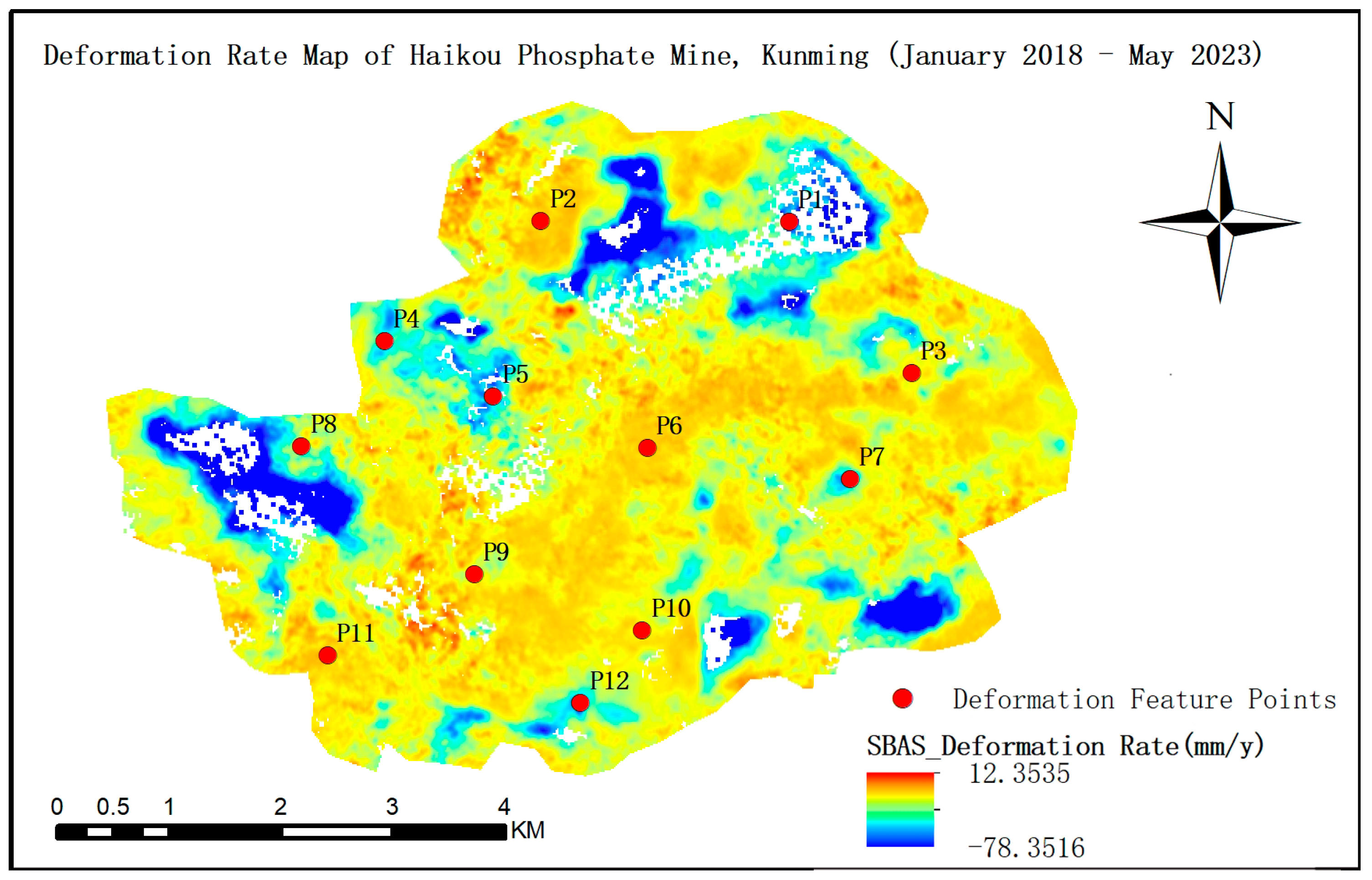
3.4. SBAS-InSAR Surface Deformation Monitoring Results
3.5. Comparative Experiment Design
- Spatiotemporal threshold selection method: All interferometric pairs generated under temporal (180 days) and spatial baseline (2%) thresholds without further screening, followed by SBAS-InSAR processing (Method 1);
- Average coherence-based screening: Based on the spatiotemporal threshold selection method, all image pairs are ranked in descending order of their average coherence. A 30% threshold (consistent with the PCA method) is set, and the image pairs with lower coherence are removed, followed by SBAS-InSAR processing (Method 2);
- Coherence-replaced temporal thresholding: Keeping other parameters unchanged from the non-optimized settings, coherence is used instead of the time threshold. By calculating the average coherence of all image pairs and sorting them in descending order, the top 347 pairs (consistent with the number of pairs after PCA optimization) are selected, followed by SBAS-InSAR processing (Method 3);
- Vegetation-adjusted optimization: Based on the spatiotemporal threshold selection method, the study area is divided into high and low vegetation coverage zones using the fractional vegetation coverage (FVC). Within each zone, image pairs are filtered based on the average coherence of that zone, retaining only those with coherence higher than the average to obtain the final set of pairs, followed by SBAS-InSAR processing (Method 4).
4. Result
4.1. RMSE Results
4.2. Analysis of Other Indicators
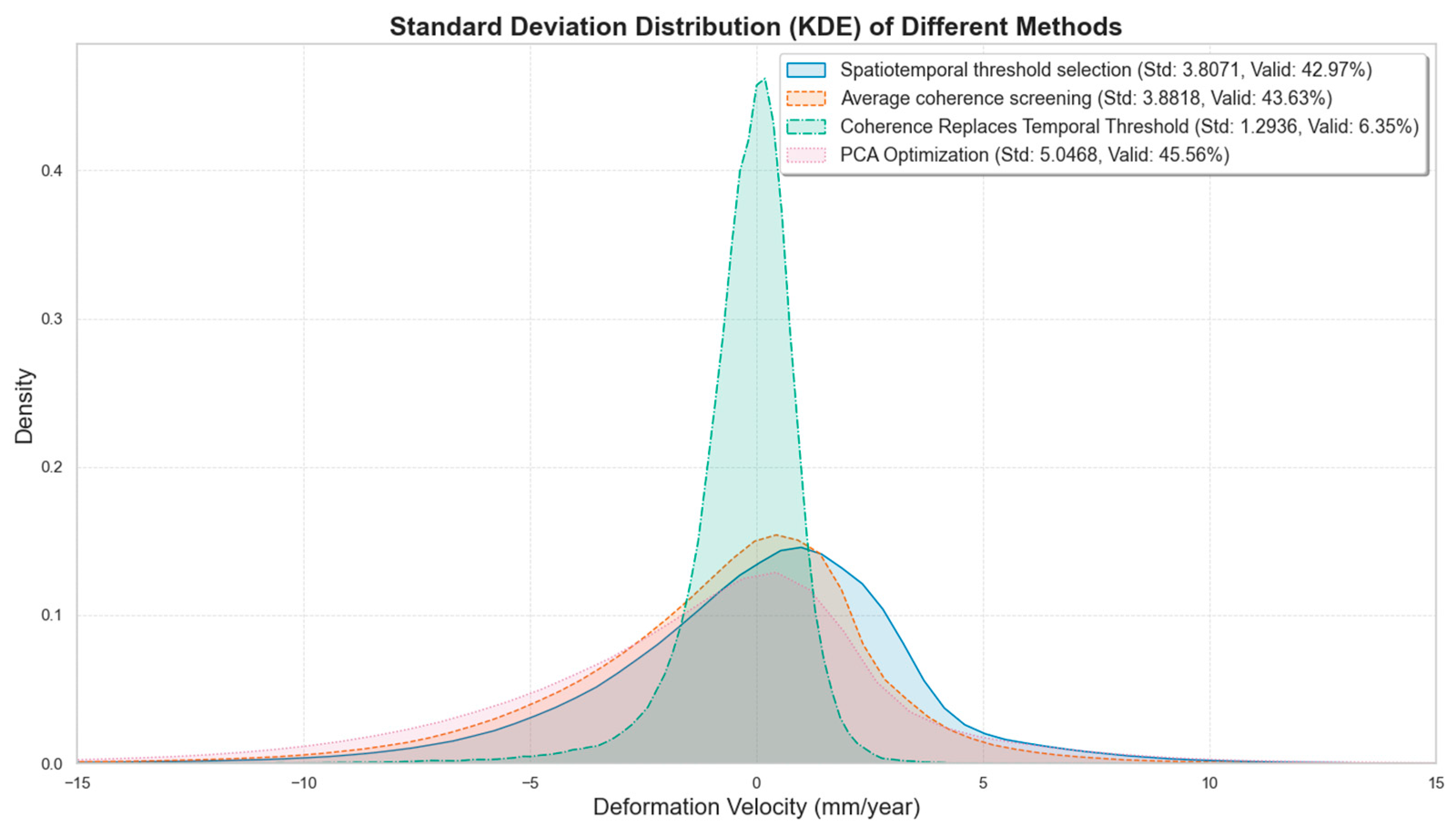
4.3. Comparative Experiment Analysis
4.4. Analysis of Deformation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Erban, L.E.; Gorelick, S.M.; Zebker, H.A. Groundwater extraction, land subsidence, and sea-level rise in the Mekong Delta, Vietnam. Environ. Res. Lett. 2014, 9, 084010. [Google Scholar] [CrossRef]
- Hu, B.; Wang, H.S.; Sun, Y.L.; Hou, J.G.; Liang, J. Long-term land subsidence monitoring of Beijing (China) using the small baseline subset (SBAS) technique. Remote Sens. 2014, 6, 3648–3661. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer: Dordrecht, The Netherlands, 2001. [Google Scholar] [CrossRef]
- Smittarello, D.; d’Oreye, N.; Jaspard, M.; Derauw, D.; Samsonov, S. Pair selection optimization for InSAR time series processing. J. Geophys. Res. Solid Earth 2022, 127, e2021JB022825. [Google Scholar] [CrossRef]
- Lin, F.; Dong, W.M.; Huang, J.; Zhang, H.Z. Application of deformation monitoring in dam area of Xinjiang Plain Reservoir based on SBAS-InSAR method. Geomat. Sci. Technol. 2024, 12, 150–158. [Google Scholar] [CrossRef]
- Pan, G.Y.; Tao, Q.X.; Chen, Y.; Wang, K. Subsidence monitoring and analysis of Jiyang mining area in Shandong Province based on SBAS-InSAR. Chin. J. Geol. Hazard Control. 2020, 31, 100–106. [Google Scholar]
- Duan, M.; Xu, B.; Li, Z.W.; Wu, W.H.; Wei, J.C.; Cao, Y.M.; Liu, J.H. Adaptively selecting interferograms for SBAS-InSAR based on graph theory and turbulence atmosphere. IEEE Access 2020, 8, 112898–112909. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, G.; Chen, Z.; Cui, H.; Zheng, Y.; Xu, Z.; Li, Q. Surface deformation extraction from small baseline subset synthetic aperture radar interferometry (SBAS-InSAR) using coherence-optimized baseline combinations. GISci. Remote Sens. 2022, 59, 295–309. [Google Scholar] [CrossRef]
- Falabella, F.; Serio, C.; Zeni, G.; Pepe, A. On the use of weighted least-squares approaches for differential InSAR analyses: The weighted adaptive variable-lEngth (WAVE) technique. Sensors 2020, 20, 1103. [Google Scholar] [CrossRef]
- Guo, J.; Xi, W.; Yang, Z.; Huang, G.; Xiao, B.; Jin, T.; Hong, W.; Gui, F.; Ma, Y. Study on optimization method for InSAR baseline considering changes in vegetation coverage. Sensors 2024, 24, 4783. [Google Scholar] [CrossRef]
- Lee, J.C.; Shirzaei, M. Novel algorithms for pair and pixel selection and atmospheric error correction in multitemporal InSAR. Remote Sens. Environ. 2023, 286, 113447. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, Q.; Hu, J. Quantitatively estimating of InSAR decorrelation based on Landsat-derived NDVI. Remote Sens. 2021, 13, 2440. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Ruiz, J.J.; Cohen, J.; Haapamaa, J.; Kontu, A.; Pulliainen, J.; Praks, J. Attenuation of radar signal by a boreal forest canopy in winter. IEEE Geosci. Remote Sens. Lett. 2022, 19, 2505905. [Google Scholar] [CrossRef]
- HZebker, A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Jolivet, R.; Agram, P.S.; Lin, N.Y.; Simons, M.; Doin, M.P.; Peltzer, G.; Li, Z. Improving InSAR geodesy using global atmospheric models. J. Geophys. Res. Solid Earth 2014, 119, 2324–2341. [Google Scholar] [CrossRef]
- De Zan, F.; Guarnieri, A.M. TOPSAR: Terrain observation by progressive scans. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Morishita, Y.; Hanssen, R.F. Temporal decorrelation in L-, C-, and X-band satellite radar interferometry for pasture on drained peat soils. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1096–1104. [Google Scholar] [CrossRef]
- Pepe, A.; Lanari, R. On the extension of the minimum cost flow algorithm for phase unwrapping of multitemporal differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2374–2383. [Google Scholar] [CrossRef]
- Morishita, Y. Nationwide urban ground deformation monitoring in Japan using Sentinel-1 LiCSAR products and LiCSBAS. Prog. Earth Planet. Sci. 2021, 8, 6. [Google Scholar] [CrossRef]
- Xiao, R.; Yu, C.; Li, Z.; He, X. Statistical assessment metrics for InSAR atmospheric correction: Applications to generic atmospheric correction online service for InSAR (GACOS) in Eastern China. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102289. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, W.; Xu, B.; Wei, G. Assessing the use of GACOS products for SBAS-INSAR deformation monitoring: A case in Southern California. Sensors 2019, 19, 3894. [Google Scholar] [CrossRef] [PubMed]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. WIREs Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Ansari, H.; De Zan, F.; Bamler, R. Efficient phase estimation for interferogram stacks. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4109–4125. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Lanari, R.; Lundgren, P.; Manzo, M.; Casu, F. Satellite radar interferometry time series analysis of surface deformation for Los Angeles, California. Geophys. Res. Lett. 2004, 31, L23613. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Perissin, D.; Wang, T. Time-series InSAR applications over urban areas in China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 4, 92–100. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, L23611. [Google Scholar] [CrossRef]
- Zhao, R.; Li, Z.; Feng, G.; Wang, Q.J.; Hu, J. Monitoring surface deformation over permafrost with an improved SBAS-InSAR algorithm: With emphasis on climatic factors modeling. Remote Sens. Environ. 2016, 184, 276–287. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Cigna, F.; Osmanoğlu, B.; Cabral-Cano, E.; Dixon, T.H.; Ávila-Olivera, J.A.; Garduño-Monroy, V.H.; DeMets, C.; Wdowinski, S. Monitoring land subsidence and its induced geological hazard with Synthetic Aperture Radar Interferometry: A case study in Morelia, Mexico. Remote Sens. Environ. 2012, 117, 146–161. [Google Scholar] [CrossRef]
- FRaspini; Bianchini, S.; Ciampalini, A.; Del Soldato, M.; Solari, L.; Novali, F.; Del Conte, S.; Rucci, A.; Ferretti, A.; Casagli, N. Continuous, semi-automatic monitoring of ground deformation using Sentinel-1 satellites. Sci. Rep. 2018, 8, 7253. [Google Scholar] [CrossRef]
- Li, D.; Deng, K.; Gao, X.; Niu, H. Monitoring and analysis of surface subsidence in mining area based on SBAS-InSAR. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 1531–1537. [Google Scholar] [CrossRef]






| Dataset | Time Span | Resolution | Source | Application |
|---|---|---|---|---|
| Sentinel-1A SAR | May 2018–May 2023 | 5 × 20 m (range × azimuth) | ESA Copernicus Programme | Primary dataset for SBAS-InSAR baseline optimization and deformation inversion |
| Landsat-8 | May 2018–May 2023 | 30 m | USGS/NASA | NDVI difference calculation |
| Precise Orbit Determination (POD) | May 2018–May 2023 | N/A | ESA Copernicus Sentinel | Orbital error correction |
| ALOS World 3D-30 m DEM | May 2018–May 2023 | 30 m | Japan Aerospace Exploration Agency (JAXA) | Topographic phase removal |
| GACOS atmospheric products | May 2018–May 2023 | 90 m | University of Newcastle, UK | Atmospheric delay mitigation |
| Principal Component | Explained Variance Ratio | Temporal Baseline (Days) | Spatial Baseline (m) | ΔNDVI | Coherence |
|---|---|---|---|---|---|
| PC1 | 0.5103 | −0.6295 | −0.4000 | −0.4559 | 0.6279 |
| PC2 | 0.2497 | −0.0404 | 0.9989 | −0.0218 | 0.0073 |
| PC3 | 0.1817 | −0.3150 | 0.0043 | 0.8897 | 0.3304 |
| PC4 | 0.0583 | 0.7091 | 0.0233 | −0.0107 | 0.7046 |
| Factor | Weight |
|---|---|
| Temporal Baseline (days) | −0.3472 |
| Spatial Baseline (m) | 0.2311 |
| ΔNDVI | −0.0770 |
| Coherence | 0.4234 |
| Method | Min | Max | Mean | Std |
|---|---|---|---|---|
| Spatiotemporal threshold selection method | 0.578 | 7.669 | 2.098 | 0.842 |
| Average coherence screening | 0.335 | 8.080 | 1.795 | 0.859 |
| Coherence-replaced temporal thresholding | 0.287 | 7.841 | 2.324 | 0.932 |
| Vegetation-adjusted method | N/A | N/A | N/A | N/A |
| PCA-optimized method | 0.248 | 7.600 | 1.589 | 0.797 |
| Methods | Moran’s I |
|---|---|
| Spatiotemporal threshold selection method | 3.7510 |
| Average coherence screening | 3.7289 |
| Coherence Replaces Temporal Threshold | 3.6110 |
| PCA Optimization | 3.7221 |
| Method Pair | Pearson | Spearman |
|---|---|---|
| Spatiotemporal threshold selection method vs. Average Coherence Screening | 0.8811 | 0.8232 |
| Spatiotemporal threshold selection method vs. Coherence Replaces Temporal Threshold | 0.6698 | 0.4627 |
| Spatiotemporal threshold selection method vs. PCA Optimization | 0.8013 | 0.7199 |
| Average Coherence Screening vs. Coherence Replaces Temporal Threshold | 0.6495 | 0.4466 |
| Average Coherence Screening vs. PCA Optimization | 0.8104 | 0.7272 |
| Coherence Replaces Temporal Threshold vs. PCA Optimization | 0.6637 | 0.5280 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Zhou, J.; Wang, J.; Mei, H.; Ou, X.; Li, B. PCA Weight Determination-Based InSAR Baseline Optimization Method: A Case Study of the HaiKou Phosphate Mining Area in Kunming, Yunnan Province, China. Remote Sens. 2025, 17, 2163. https://doi.org/10.3390/rs17132163
Xu W, Zhou J, Wang J, Mei H, Ou X, Li B. PCA Weight Determination-Based InSAR Baseline Optimization Method: A Case Study of the HaiKou Phosphate Mining Area in Kunming, Yunnan Province, China. Remote Sensing. 2025; 17(13):2163. https://doi.org/10.3390/rs17132163
Chicago/Turabian StyleXu, Weimeng, Jingchun Zhou, Jinliang Wang, Huihui Mei, Xianjun Ou, and Baixuan Li. 2025. "PCA Weight Determination-Based InSAR Baseline Optimization Method: A Case Study of the HaiKou Phosphate Mining Area in Kunming, Yunnan Province, China" Remote Sensing 17, no. 13: 2163. https://doi.org/10.3390/rs17132163
APA StyleXu, W., Zhou, J., Wang, J., Mei, H., Ou, X., & Li, B. (2025). PCA Weight Determination-Based InSAR Baseline Optimization Method: A Case Study of the HaiKou Phosphate Mining Area in Kunming, Yunnan Province, China. Remote Sensing, 17(13), 2163. https://doi.org/10.3390/rs17132163








