A Cooperative GNSS Vector-DLL (CoVDLL) Method for Multiple UAVs Positioning
Abstract
1. Introduction
- (1)
- In view of the VT technology utilizing the navigation data to predict signal tracking parameters, full usage of the mutual navigation information from the UAV swarm has great potential to improve the positioning accuracy. This study explores the application of VT technology in UAV GNSS positioning and proposes a CoVDLL framework to improve the positioning accuracy of UAV swarms. Additionally, an inter-ranging-based cooperative positioning model for UAVs is developed and thoroughly investigated.
- (2)
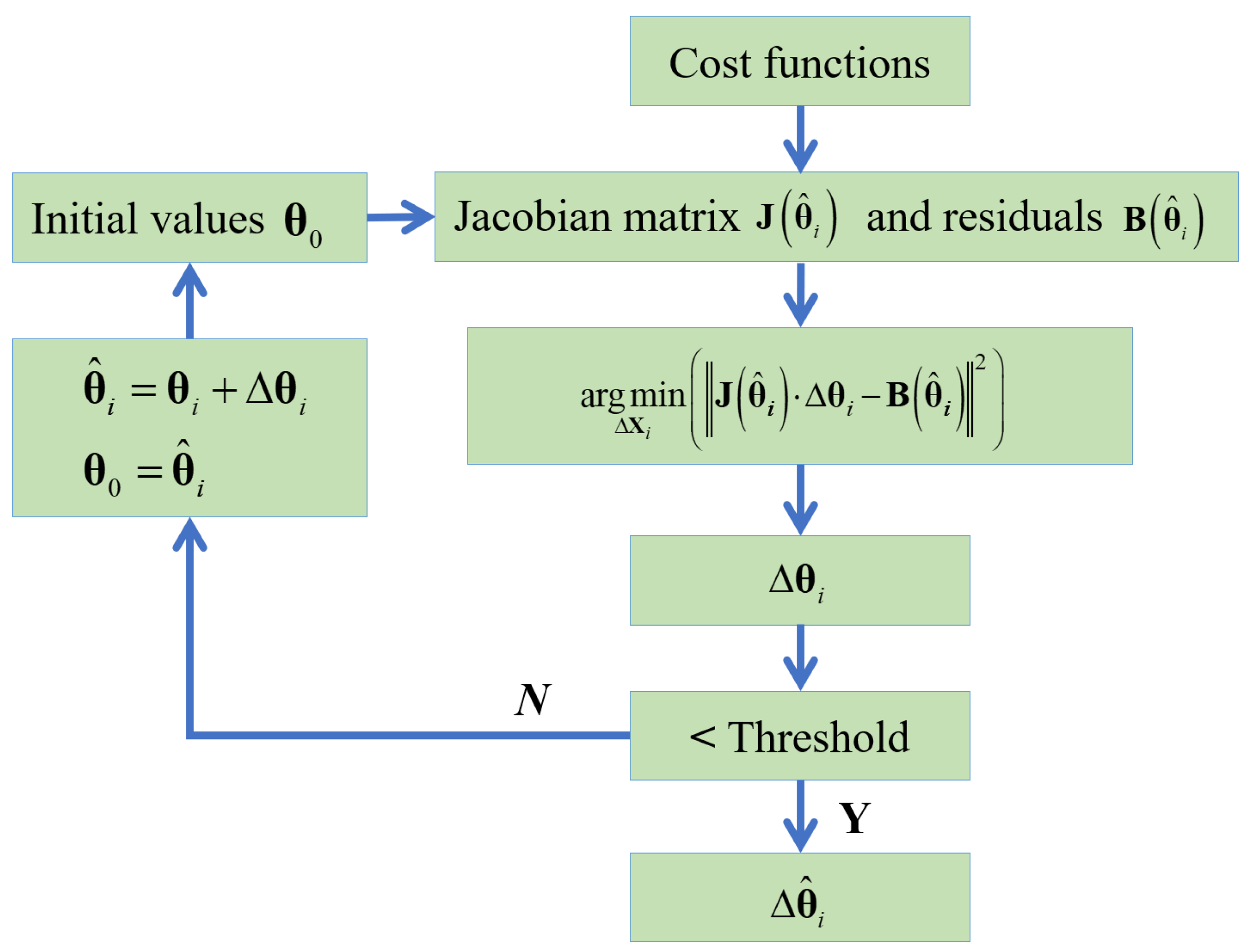
- Based on the inter-ranging information, the state vector of the CoVDLL is constructed. A Factor Graph Optimization (FGO) method is incorporated with the CoVDLL to realize the optimal estimation of the UAV swarms’ position. A cost function is defined, including the VDLL measurement factor, state transformation factor, and the inter-ranging factor. A nonlinear solver is employed to solve for the state estimation with the cost function.
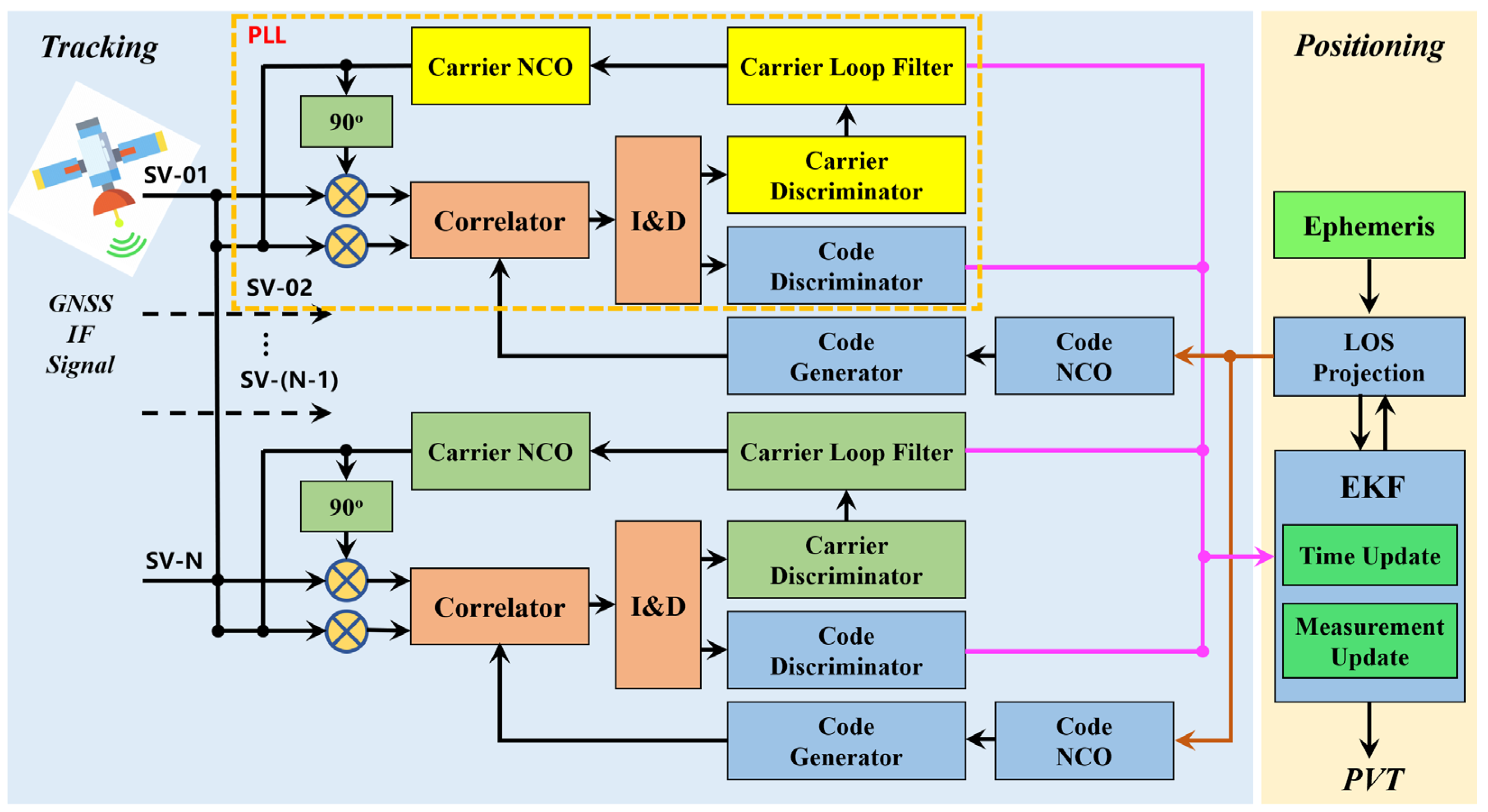
2. Phase Lock Loop Assisted Vector Delay Lock Loop (PLL-A-DLL)
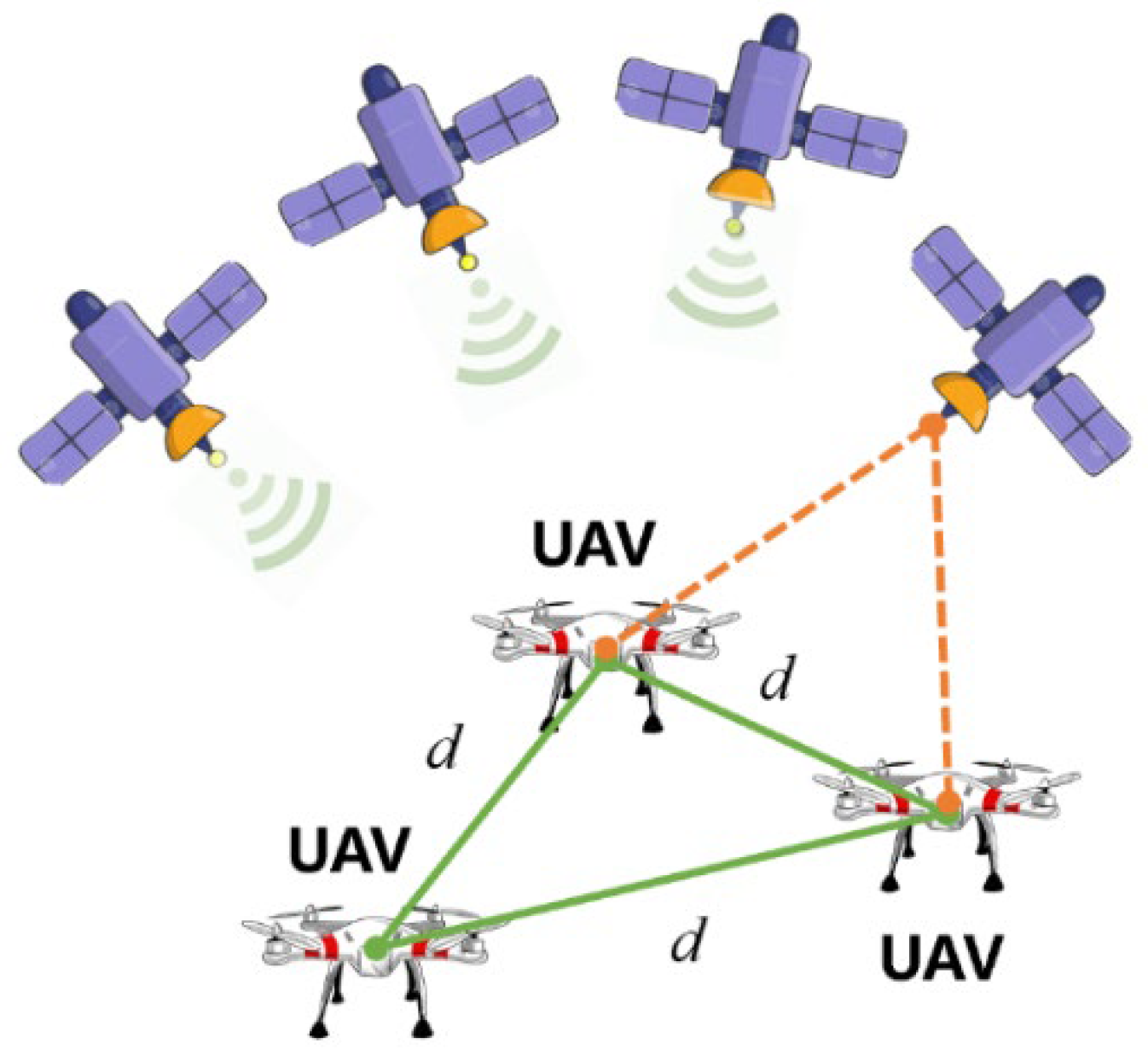
3. Cooperative Vector Delay Lock Loop
3.1. Factor Graph Optimization
3.2. CoVDLL
- (1)
- State transformation factor
- (2)
- Measurement Factor
- (3)
- Cooperative Ranging Factor
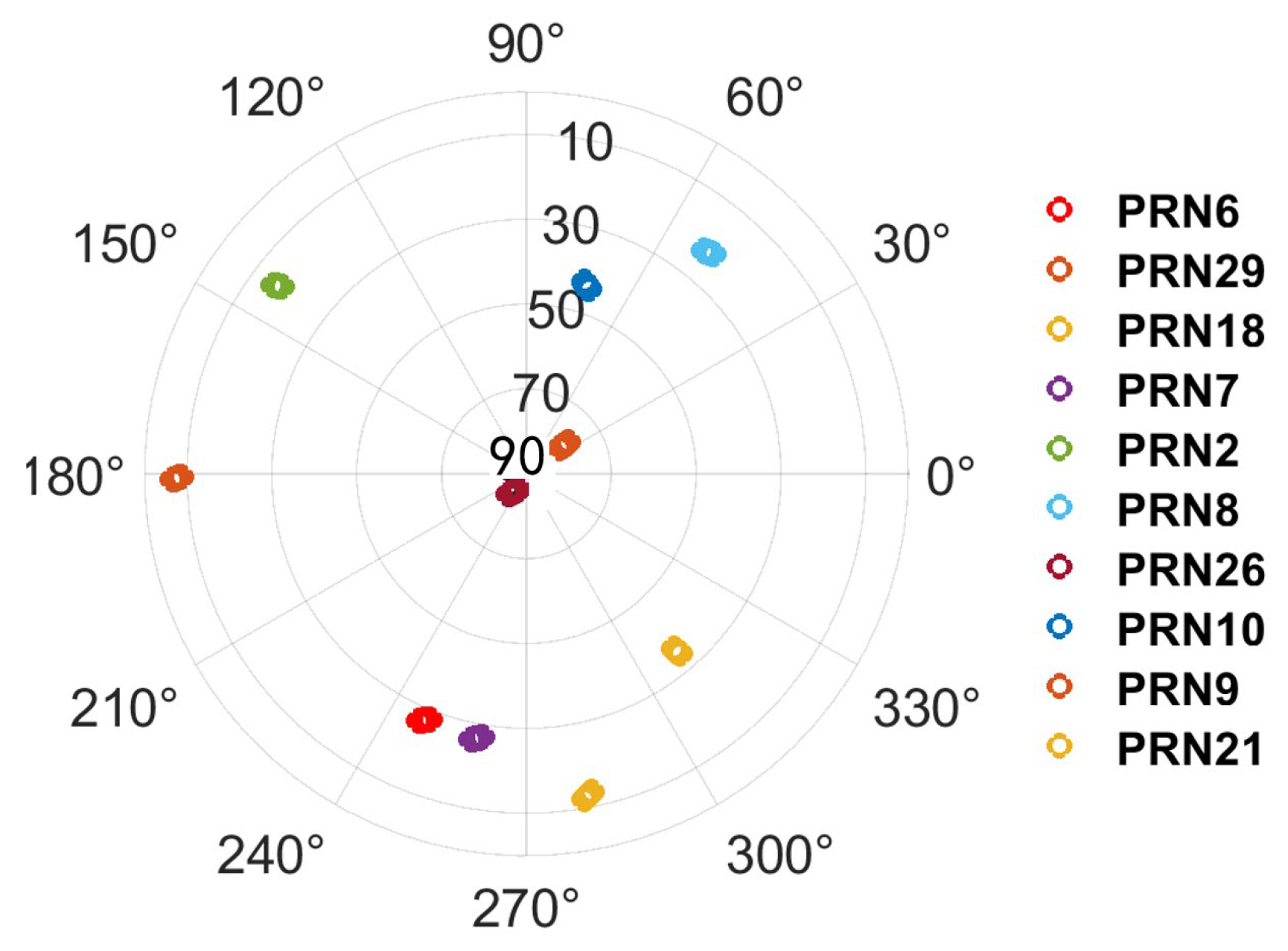
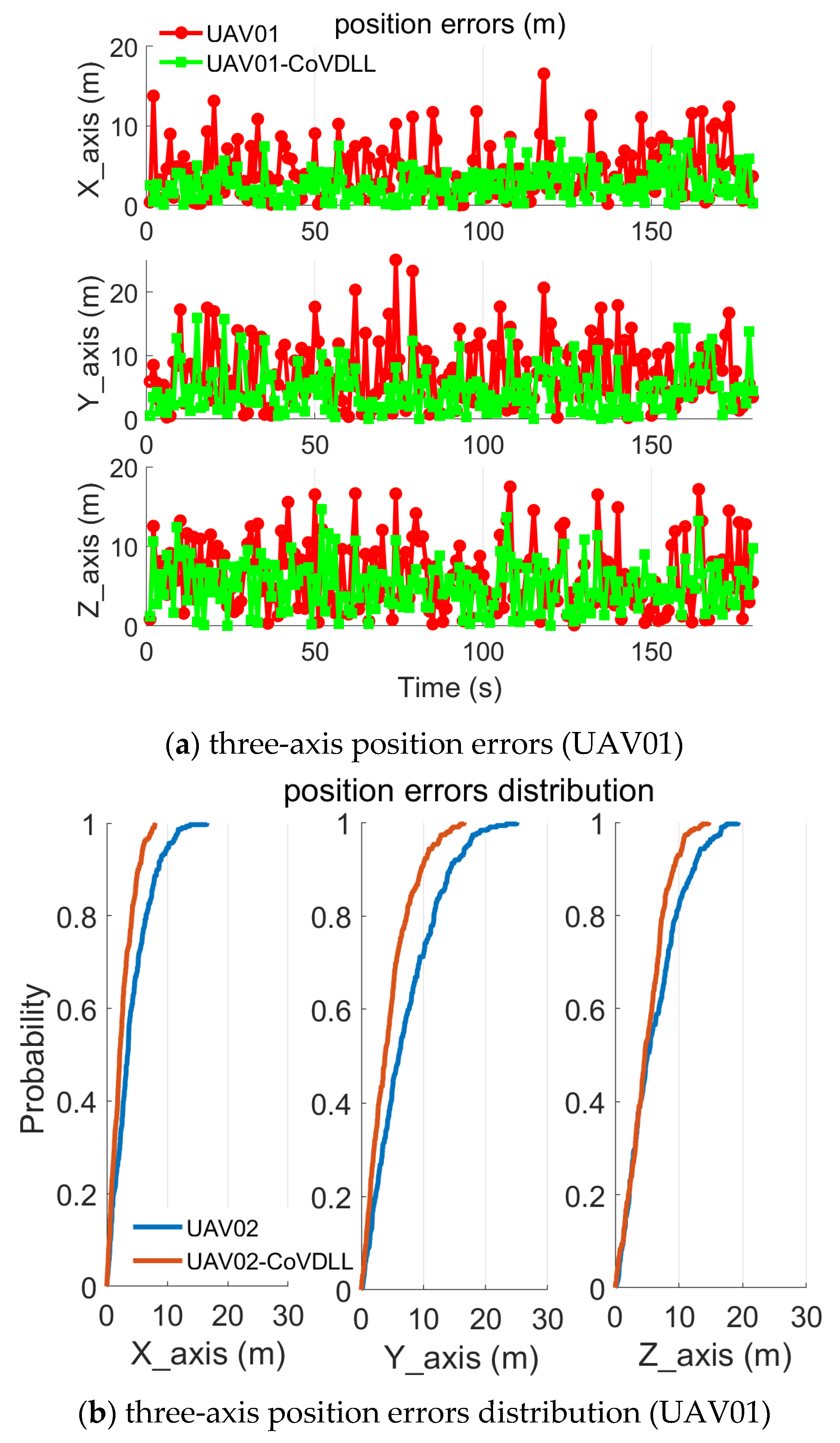
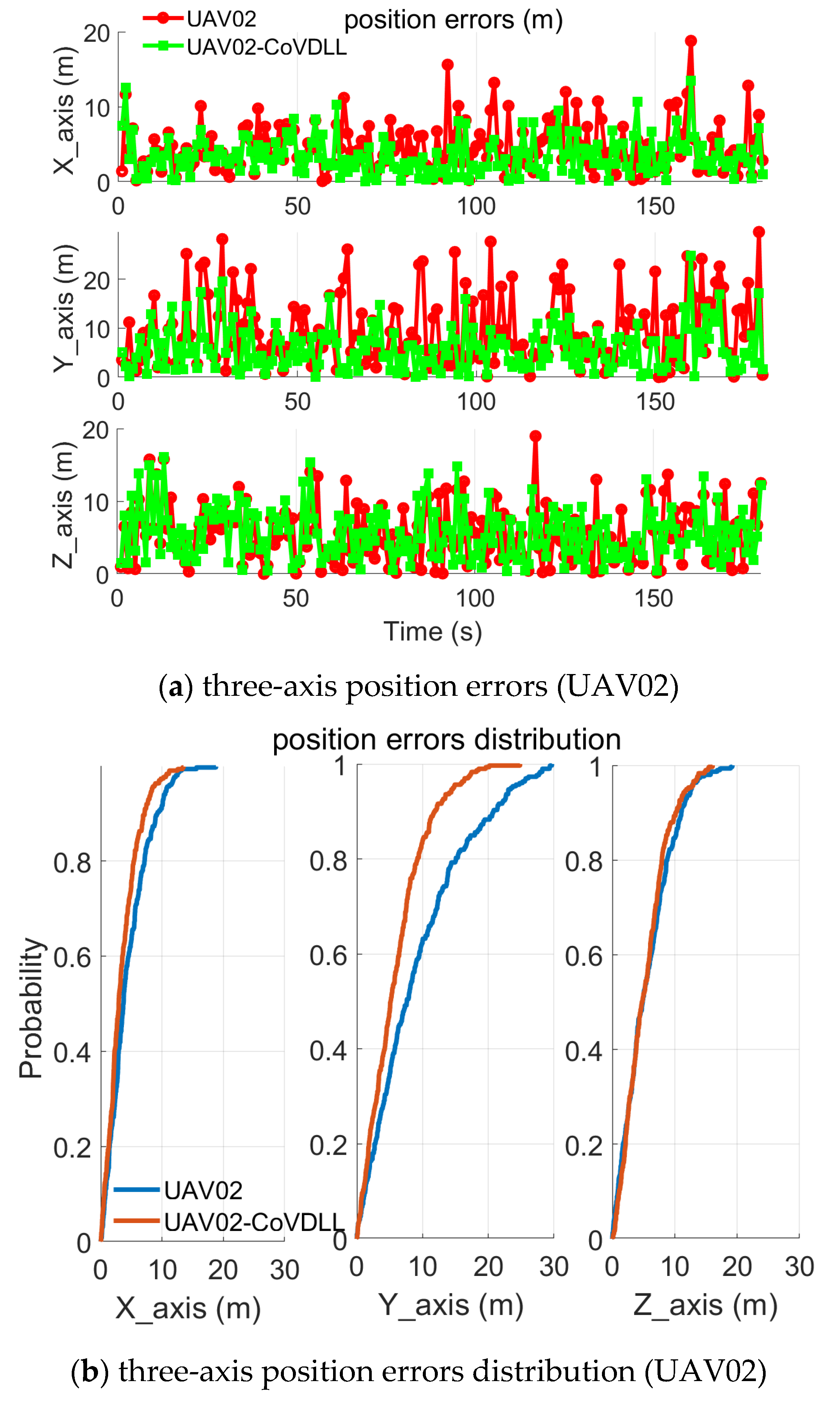
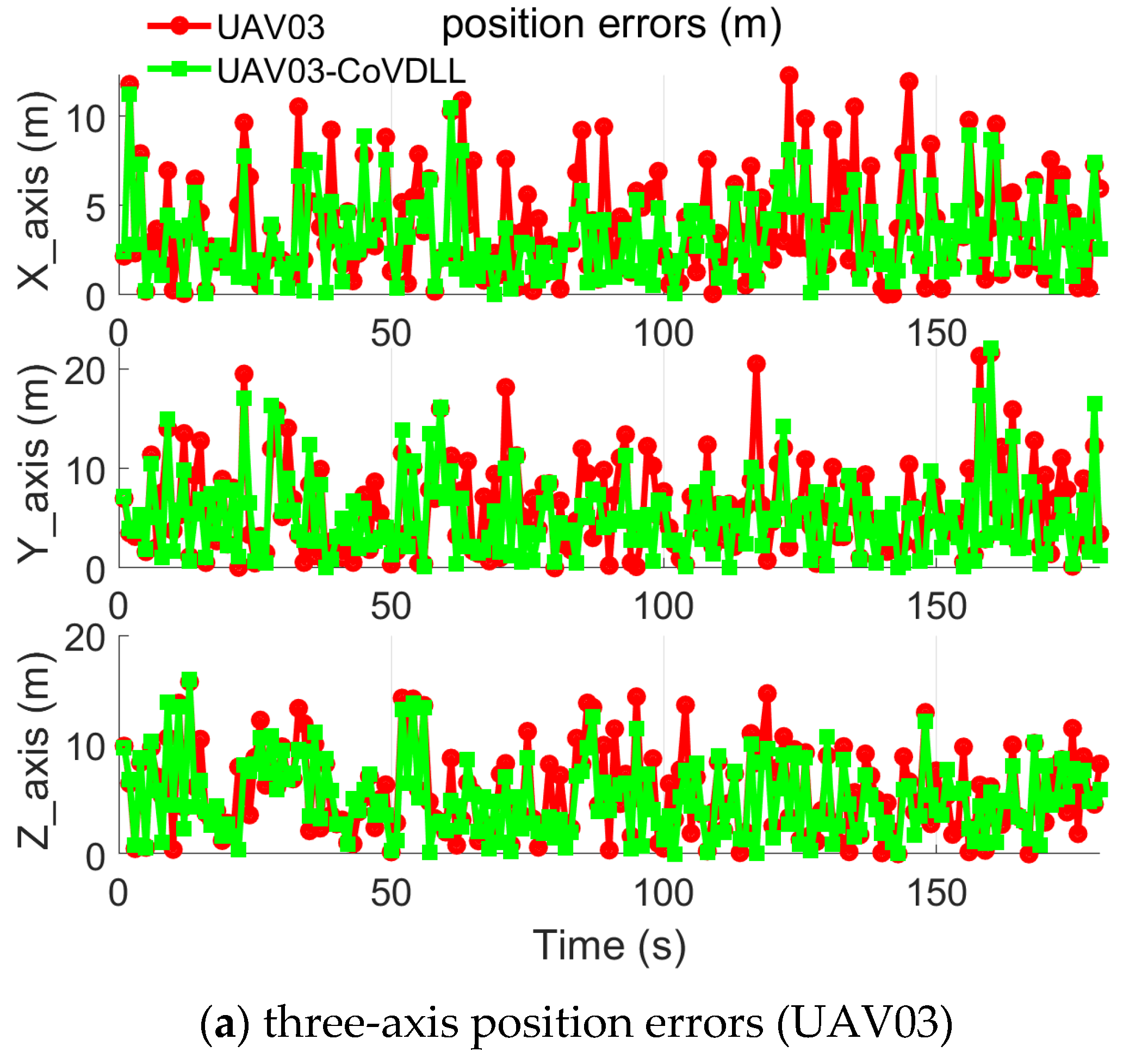
4. Experimental Results and Analysis
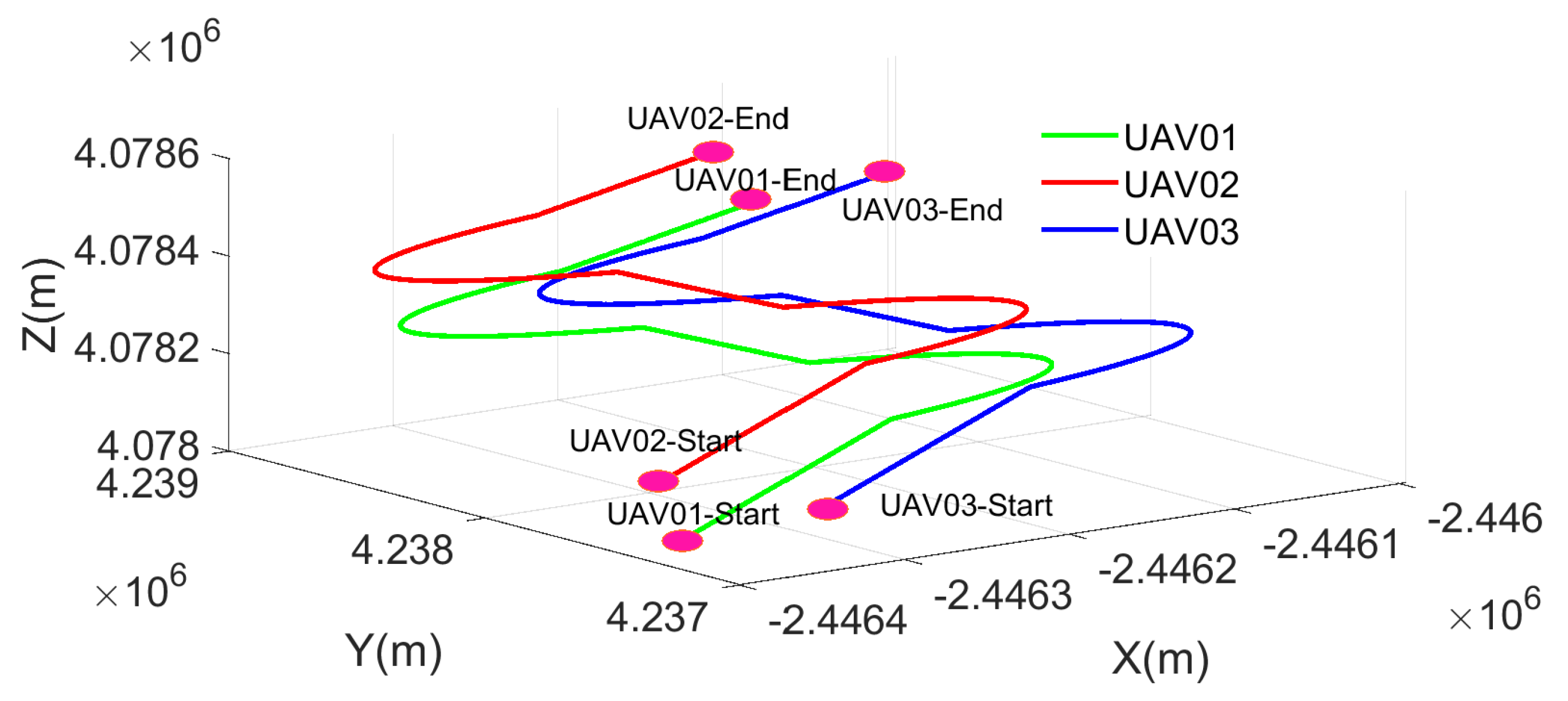
4.1. Experiment with Fixed Inter-Ranging Measurements
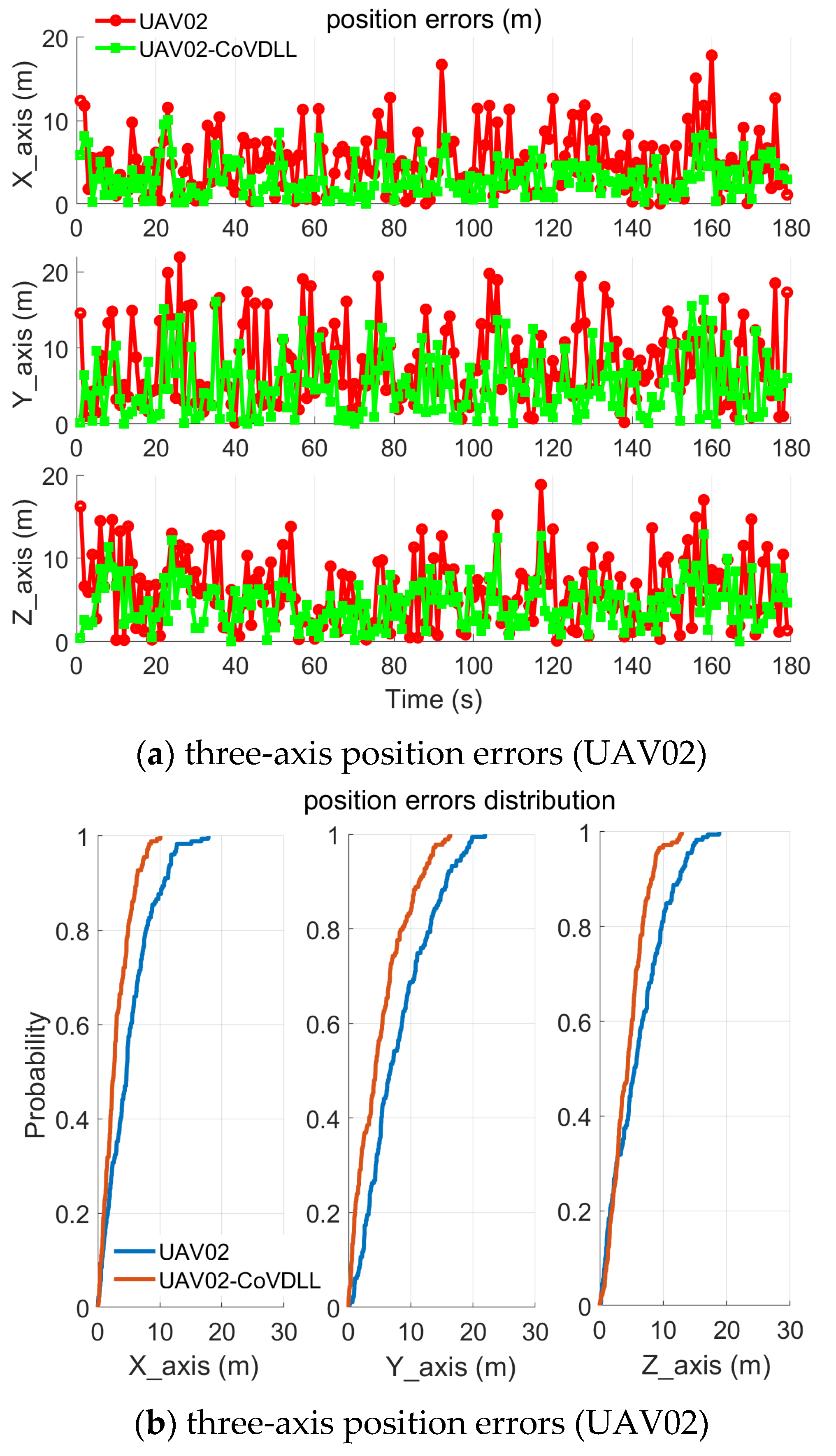
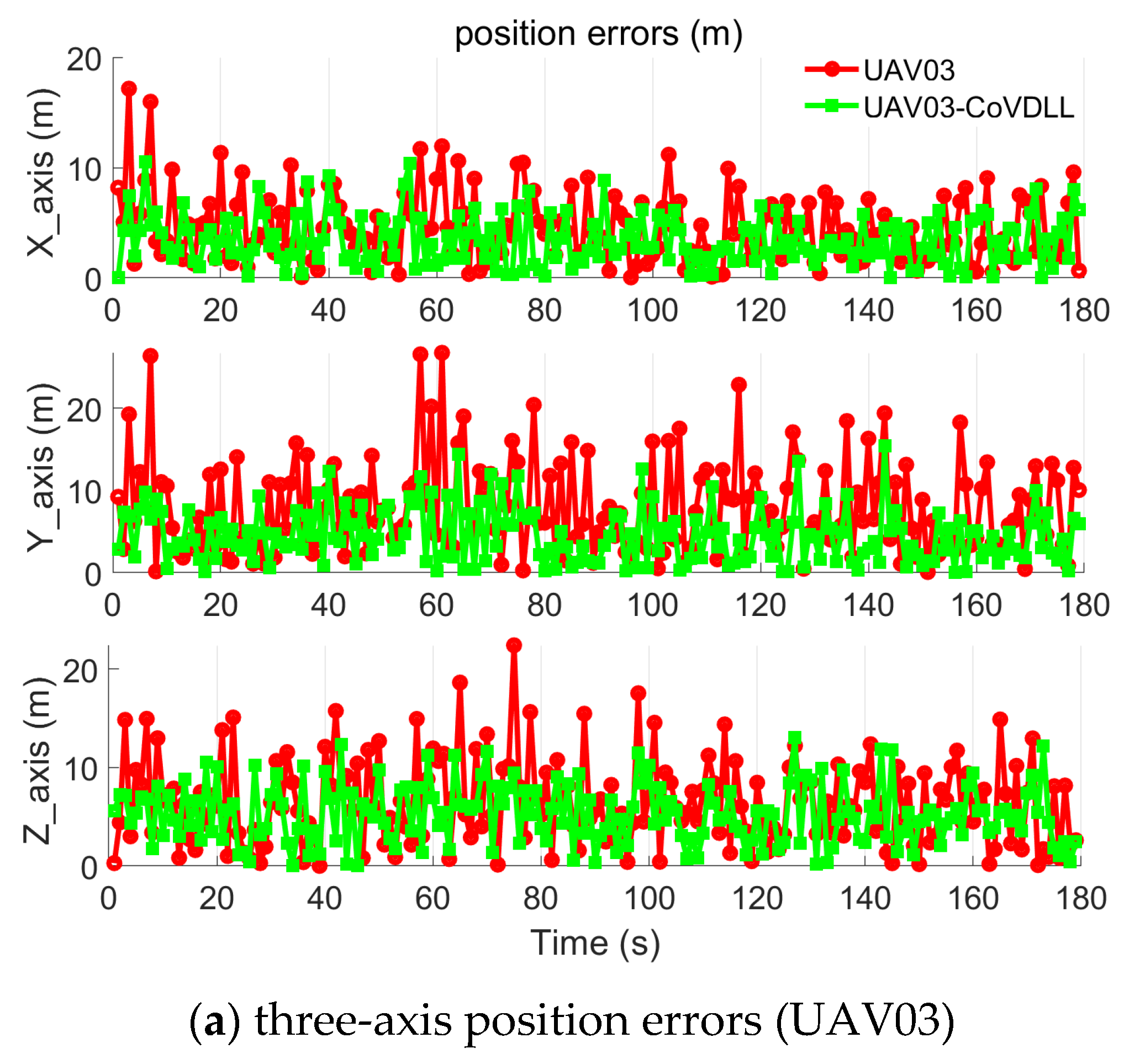
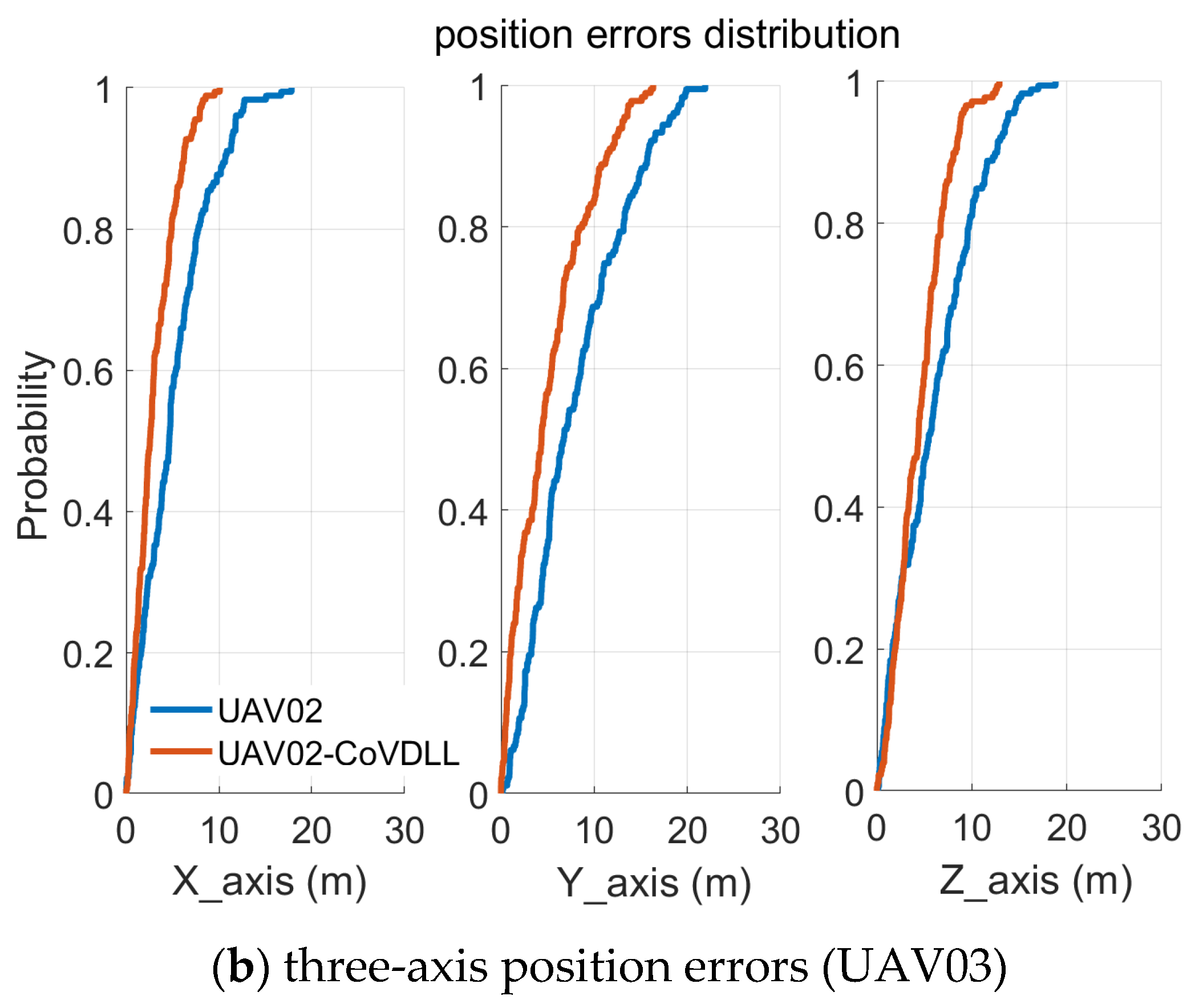
4.2. Experiment with Time-Varying Inter-Ranging Measurements
5. Limitations and Future Works
- (1)
- Due to hardware computational limitations, the proposed method was validated only through a three-UAV simulation. In addition, limited by the hardware equipment, we did not have enough equipment to collect real-world flying datasets to evaluate the CoVDLL. Future work should include field tests with real-world UAVs and GNSS signals to thoroughly evaluate the algorithm’s performance. Additionally, expanding the experiments to include more UAVs would provide a more comprehensive assessment. Furthermore, since the computational load of FGO is significantly higher than that of the Kalman Filter, optimizing the moving-window size is essential to reduce computational demands while maintaining performance.
- (2)
- Limited by the simulation settings and software, UAVs are typically equipped with various onboard sensors, such as Inertial Measurement Units (IMUs), LiDAR, and visual cameras. Software including the GNSS IF signal simulation, IMU measurements simulation, and other sensor simulations has the potential to help to evaluate the proposed method. These sensors can capture UAV motion and environmental data, which can be leveraged to estimate position and other dynamic information. In our experiments, we observed only marginal improvements in z-axis position errors (Figure 15). Integrating VDLL with other sensors to utilize dynamic information—such as velocity and observation angles—could lead to the development of a multi-sensor fusion system; potentially enhancing both positioning accuracy and system reliability.
- (3)
- GNSS IF signal simulation software here has limited function, i.e., no spoofing simulation function and no signal blockage or signal degradation simulation function. Therefore, in the simulation, we did not carry out the assessment of the CoVDLL under a signal-challenging environment. This study assumes ideal GNSS signal conditions to achieve satisfactory positioning results. It would be valuable to test the proposed method in challenging GNSS environments to evaluate how the cooperative scheme can improve positioning accuracy under adverse signal conditions, i.e., signal spoofing and weak signal.
6. Conclusions
- (1)
- The CoVDLL method effectively reduces position errors compared to individual VDLL methods, and including inter-ranging measurements significantly enhances the construction of the CoVDLL.
- (2)
- The nonlinear optimization technique proves to be effective in achieving optimal position estimations by utilizing the correlated ranging information.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, B.; Hu, G.; Zhong, Y.; Zhu, X. Cubature Kalman filter with both adaptability and robustness for tightly-coupled GNSS/INS integration. IEEE Sens. J. 2021, 21, 14997–15011. [Google Scholar] [CrossRef]
- Gao, G.; Gao, B.; Gao, S.; Hu, G.; Zhong, Y. A hypothesis test-constrained robust Kalman filter for INS/GNSS integration with abnormal measurement. IEEE Trans. Veh. Technol. 2022, 72, 1662–1673. [Google Scholar] [CrossRef]
- Ruan, L.; Li, G.; Dai, W.; Tian, S.; Fan, G.; Wang, J.; Dai, X. Cooperative relative localization for UAV swarm in GNSS-denied environment: A coalition formation game approach. IEEE Internet Things J. 2021, 9, 11560–11577. [Google Scholar] [CrossRef]
- Ng, Y.; Gao, G.X. GNSS multi-receiver vector tracking. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2583–2593. [Google Scholar] [CrossRef]
- Xu, B.; Jia, Q.; Hsu, L.T. Vector tracking loop-based GNSS NLOS detection and correction: Algorithm design and performance analysis. IEEE Trans. Instrum. Meas. 2019, 69, 4604–4619. [Google Scholar] [CrossRef]
- Zhao, S.; Akos, D. An open-source GPS/GNSS vector tracking loop-implementation, filter tuning, and results. In Proceedings of the 2011 International Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 24–26 January 2011; pp. 1293–1305. [Google Scholar]
- Shen, J.; Wang, S.; Zhai, Y.; Zhan, X. Cooperative relative navigation for multi-UAV systems by exploiting GNSS and peer-to-peer ranging measurements. IET Radar Sonar Navig. 2021, 15, 21–36. [Google Scholar] [CrossRef]
- Vetrella, A.R.; Fasano, G.; Accardo, D.; Moccia, A. Differential GNSS and vision-based tracking to improve navigation performance in cooperative multi-UAV systems. Sensors 2016, 16, 2164. [Google Scholar] [CrossRef]
- Causa, F.; Fasano, G.; Grassi, M. Improving autonomy in GNSS-challenging environments by multi-UAV cooperation. In Proceedings of the 2019 IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 8–12 September 2019; IEEE: Piscataway, NJ, USA; pp. 1–10. [Google Scholar]
- Sivaneri, V.O.; Gross, J.N. Flight-testing of a cooperative UGV-to-UAV strategy for improved positioning in challenging GNSS environments. Aerosp. Sci. Technol. 2018, 82, 575–582. [Google Scholar] [CrossRef]
- Goel, S.; Kealy, A.; Gikas, V.; Retscher, G.; Toth, C.; Brzezinska, D.G.; Lohani, B. Cooperative localization of unmanned aerial vehicles using GNSS, MEMS inertial, and UWB sensors. J. Surv. Eng. 2017, 143, 04017007. [Google Scholar] [CrossRef]
- Marçal, J.; Nunes, F. Robust vector tracking for GNSS carrier phase signals. In Proceedings of the 2016 International Conference on Localization and GNSS (ICL-GNSS), Barcelona, Spain, 28–30 June 2016; IEEE: Piscataway, NJ, USA; pp. 1–6. [Google Scholar]
- Jiang, C.; Chen, S.; Chen, Y.; Liu, D.; Bo, Y. GNSS vector tracking method using graph optimization. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 1313–1317. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Y.; Wu, S.; Wang, P. Multipath effects on vector tracking algorithm for GNSS signal. Sci. China Inf. Sci. 2014, 57, 1–13. [Google Scholar] [CrossRef]
- Ren, T.; Petovello, M.; Basnayake, C. Improving GNSS bit synchronization and decoding using vector tracking. In Proceedings of the 26th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013; pp. 121–134. [Google Scholar]
- Yang, H.; Zhou, B.; Wang, L.; Wei, Q.; Ji, F.; Zhang, R. Performance and evaluation of GNSS receiver vector tracking loop based on adaptive cascade filter. Remote Sens. 2021, 13, 1477. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Xu, B.; Jia, J.; Sun, H.; Chen, C.; Duan, Z.; Bo, Y.; Hyyppä, J. Vector tracking based on factor graph optimization for GNSS NLOS bias estimation and correction. IEEE Internet Things J. 2022, 9, 16209–16221. [Google Scholar] [CrossRef]
- Abedi, A.A.; Mosavi, M.R. Low computational-complexity vector tracking for low-cost GNSS receivers. Measurement 2022, 195, 111171. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, S.; Chen, Y.; Bo, Y.; Wang, C.; Tao, W. Performance analysis of GNSS vector tracking loop based GNSS/CSAC integrated navigation system. J. Aeronaut. Astronaut. Aviat. 2017, 49, 289–297. [Google Scholar]
- Bhattacharyya, S.; Gebre-Egziabher, D. Integrity monitoring with vector GNSS receivers. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2779–2793. [Google Scholar] [CrossRef]
- Xu, B.; Hsu, L.T. Open-source MATLAB code for GPS vector tracking on a software-defined receiver. GPS Solut. 2019, 23, 46. [Google Scholar] [CrossRef]
- Lashley, M.; Bevly, D.M.; Hung, J.Y. Performance analysis of vector tracking algorithms for weak GPS signals in high dynamics. IEEE J. Sel. Top. Signal Process. 2009, 3, 661–673. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Chen, C.; Hyyppa, J. Walking Gait Assisted Vector Tracking GNSS for Pedestrian Position. IEEE Trans. Instrum. Meas. 2023, 72, 8506711. [Google Scholar] [CrossRef]
- Chan, B.; Petovello, M.G. Collaborative vector tracking of GNSS signals with ultra-wideband augmentation in degraded signal environments. In Proceedings of the 2011 International Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 24–26 January 2011; pp. 404–413. [Google Scholar]
- Gao, W.; Yang, R.; Huang, J.; Zhan, X. Quasi-deep integration for DPE/INS in GNSS navigation domain: Framework design and optimization. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 6774–6793. [Google Scholar] [CrossRef]
- Yang, R.; Ling, K.V.; Poh, E.K.; Morton, Y. Generalized GNSS signal carrier tracking: Part I—Modeling and analysis. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1781–1797. [Google Scholar] [CrossRef]
- Yan, Z.; Chen, X.; Tang, X.; Zhu, X. The implementation and comparison between Kalman filter-based and vector tracking loops. In Proceedings of the IEEE International Conference on Sensing, Measurement & Data Analytics in the Era of Artificial Intelligence (ICSMD), Xi’an, China, 15–17 October 2020; pp. 45–50. [Google Scholar]
- Burchfield, S.; Givhan, C.; Martin, S. A Beam Steering Vector Tracking GNSS Software-Defined Receiver for Robust Positioning. Sensors 2025, 25, 1951. [Google Scholar] [CrossRef] [PubMed]
- Goel, S.; Kealy, A.; Lohani, B. Development and experimental evaluation of a low-cost cooperative UAV localization network prototype. J. Sens. Actuator Netw. 2018, 7, 42. [Google Scholar] [CrossRef]
- Jin, R.; Zhang, G.; Hsu, L.T.; Hu, Y. A Survey on Cooperative Positioning Using GNSS Measurements. IEEE Transactions on Intelligent Vehicles 2024, 1–20. [Google Scholar] [CrossRef]
- Chen, M.; Xiong, Z.; Xiong, J.; Wang, R. A hybrid cooperative navigation method for UAV swarm based on factor graph and Kalman filter. Int. J. Distrib. Sens. Netw. 2022, 18, 15501477211064758. [Google Scholar] [CrossRef]
- Ding, X.; Li, K.; Yang, Y. A navigation-data-tolerated EKF carrier loop for GNSS signals. IEICE Trans. Commun. March 2025. [Google Scholar] [CrossRef]
- Jiang, C.; Xu, B.; Hsu, L.T. Probabilistic approach to detect and correct GNSS NLOS signals using an augmented state vector in the extended Kalman filter. GPS Solut. 2021, 25, 72. [Google Scholar] [CrossRef]
- Gleason, S. A real-time on-orbit signal tracking algorithm for GNSS surface observations. Remote Sens. 2019, 11, 1858. [Google Scholar] [CrossRef]



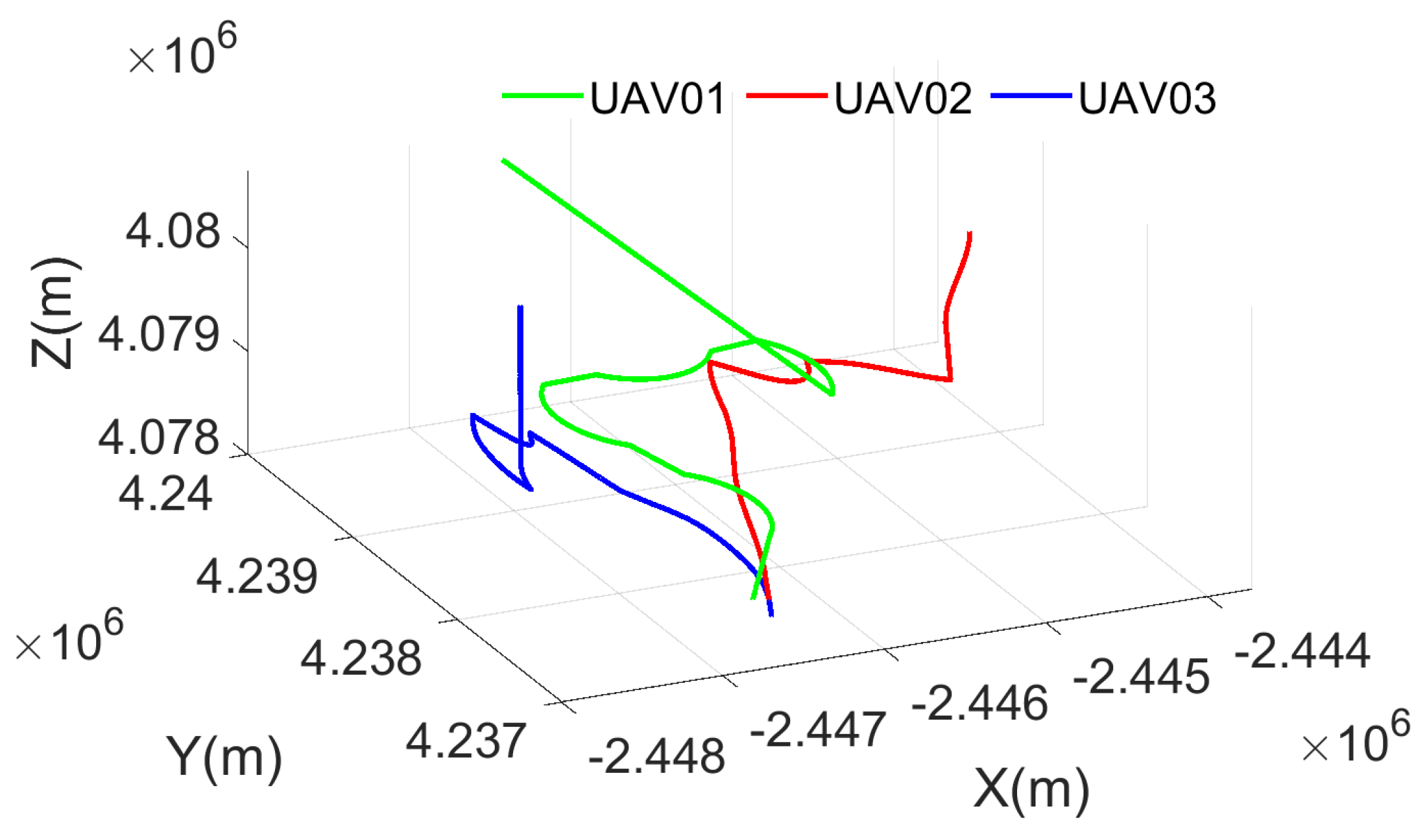
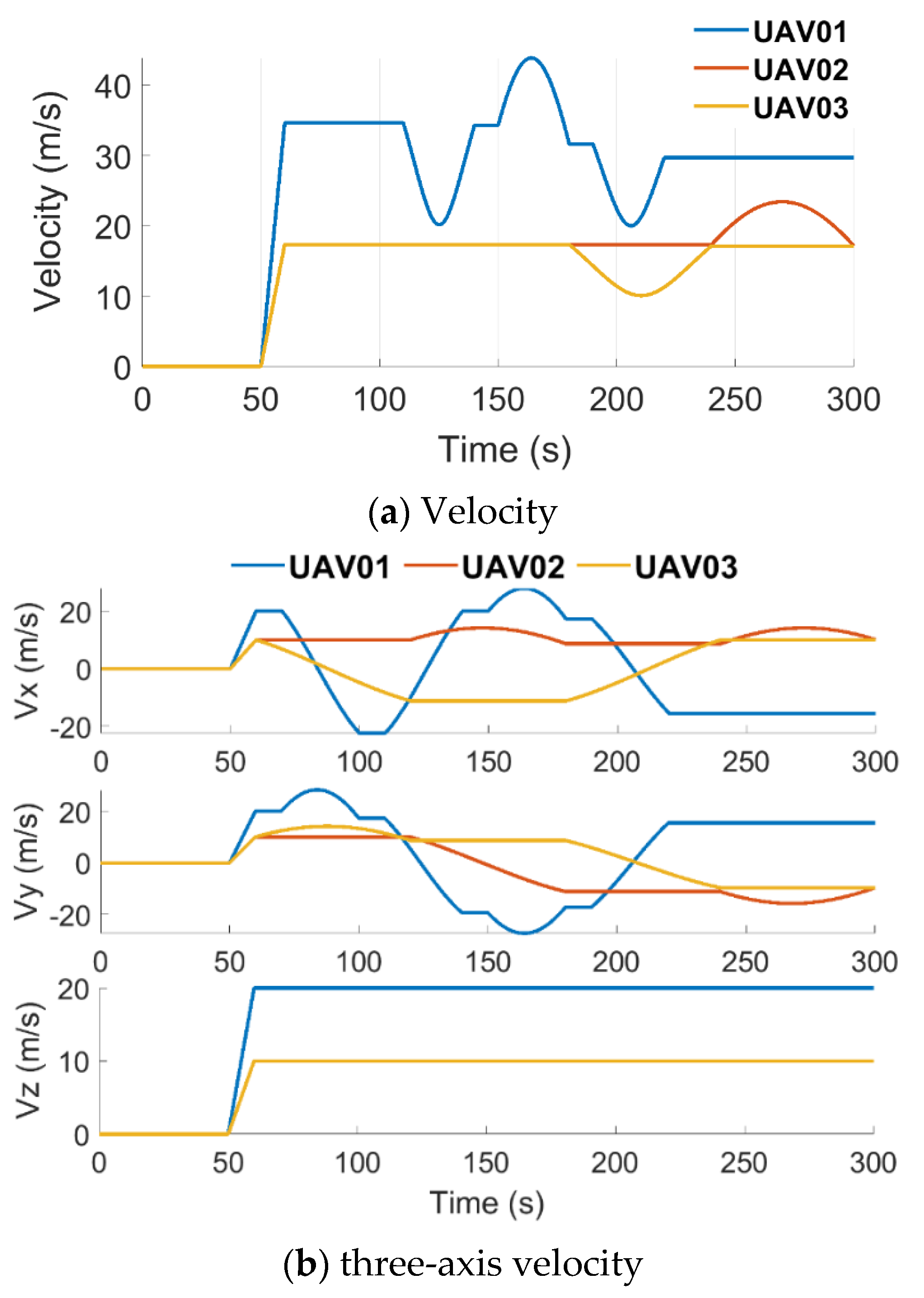

| Time | Action |
|---|---|
| 0 ~ 50 s | static |
| 50 s ~ 60 s | uniform acceleration |
| 60 s ~ 90 s | circular motion |
| 90 s ~ 100 s | uniform motion |
| 100 s ~ 130 s | circular motion |
| 130 s ~ 180 s | uniform motion |
| Mean Values | STD Values | ||||
|---|---|---|---|---|---|
| VDLL (m) | CoVDLL (m) | VDLL (m) | CoVDLL (m) | ||
| UAV01 | X-Axis | 5.33 | 2.97 | 3.86 | 2.30 |
| Y-Axis | 6.98 | 3.90 | 5.34 | 2.95 | |
| Z-Axis | 5.22 | 3.00 | 3.49 | 2.28 | |
| UAV02 | X-Axis | 5.04 | 3.03 | 3.67 | 2.21 |
| Y-Axis | 7.94 | 5.08 | 5.20 | 4.10 | |
| Z-Axis | 6.04 | 4.49 | 4.30 | 2.74 | |
| UAV03 | X-Axis | 4.51 | 3.35 | 3.15 | 2.29 |
| Y-Axis | 7.89 | 4.48 | 5.63 | 3.32 | |
| Z-Axis | 6.49 | 5.26 | 4.45 | 3.07 | |
| Mean Values | STD Values | ||||
|---|---|---|---|---|---|
| VDLL (m) | CoVDLL (m) | VDLL (m) | CoVDLL (m) | ||
| UAV01 | X-Axis | 4.06 | 2.53 | 3.08 | 1.87 |
| Y-Axis | 7.10 | 4.54 | 5.17 | 3.53 | |
| Z-Axis | 6.07 | 5.00 | 4.23 | 3.05 | |
| UAV02 | X-Axis | 4.46 | 3.50 | 3.29 | 2.61 |
| Y-Axis | 9.28 | 5.94 | 7.28 | 4.44 | |
| Z-Axis | 5.56 | 5.30 | 3.96 | 3.49 | |
| UAV03 | X-Axis | 4.19 | 3.39 | 3.17 | 2.42 |
| Y-Axis | 6.55 | 5.22 | 5.02 | 4.03 | |
| Z-Axis | 5.51 | 4.96 | 4.02 | 3.40 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Wang, X.; Jiang, C.; Su, Z.; Chen, S.; Chen, Y. A Cooperative GNSS Vector-DLL (CoVDLL) Method for Multiple UAVs Positioning. Remote Sens. 2025, 17, 2156. https://doi.org/10.3390/rs17132156
Li C, Wang X, Jiang C, Su Z, Chen S, Chen Y. A Cooperative GNSS Vector-DLL (CoVDLL) Method for Multiple UAVs Positioning. Remote Sensing. 2025; 17(13):2156. https://doi.org/10.3390/rs17132156
Chicago/Turabian StyleLi, Chuntao, Xinru Wang, Changhui Jiang, Zikang Su, Shoubin Chen, and Yuwei Chen. 2025. "A Cooperative GNSS Vector-DLL (CoVDLL) Method for Multiple UAVs Positioning" Remote Sensing 17, no. 13: 2156. https://doi.org/10.3390/rs17132156
APA StyleLi, C., Wang, X., Jiang, C., Su, Z., Chen, S., & Chen, Y. (2025). A Cooperative GNSS Vector-DLL (CoVDLL) Method for Multiple UAVs Positioning. Remote Sensing, 17(13), 2156. https://doi.org/10.3390/rs17132156









