Abstract
High-Resolution Range Profile (HRRP) radar recognition suffers from data scarcity challenges in real-world applications. We present HRRPGraphNet++, a framework combining dynamic graph neural networks with meta-learning for few-shot HRRP recognition. Our approach generates graph representations dynamically through multi-head self attention (MSA) mechanisms that adapt to target-specific scattering characteristics, integrated with a specialized meta-learning framework employing layer-wise learning rates. Experiments demonstrate state-of-the-art performance in 1-shot (82.3%), 5-shot (91.8%), and 20-shot (94.7%) settings, with enhanced noise robustness (68.7% accuracy at 0 dB SNR). Our hybrid graph mechanism combines physical priors with learned relationships, significantly outperforming conventional methods in challenging scenarios.
1. Introduction
High-Resolution Range Profile (HRRP)-based radar automatic target recognition (RATR) plays a critical role in modern remote sensing systems [1,2,3,4], enabling the identification of aerial targets through their unique electromagnetic scattering signatures [5,6,7,8]. As shown in Figure 1, HRRPs encode target structural information as a one-dimensional projection of scattering centers along the radar line-of-sight (LOS) [9,10,11]. This representation offers advantages in all-weather applications [12,13,14,15], while maintaining a compact data structure that facilitates efficient processing [16,17,18]. Hence, RATR based on HRRPs has long been a heated research field in the remote sensing community [19,20,21,22,23,24,25].
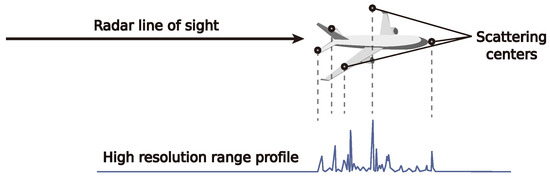
Figure 1.
Illustration of HRRP formation through projection of 3D scattering centers onto LOS.
Traditional approaches to HRRP recognition have primarily relied on pattern recognition techniques such as template matching [26], PCA-SVM [27], and statistical modeling [1,2], which perform poorly when confronting the intrinsic sensitivity of HRRP signatures to aspect angles, amplitude fluctuations, and range migration [28,29]. Deep learning methods, including CNNs [30,31], RNNs [32], and LSTM networks [4,33], have emerged as the dominant paradigm for HRRP classification, demonstrating superior feature representation capabilities by automatically extracting hierarchical features from raw profiles without manual feature engineering [13,28]. Advanced architectures incorporating attention mechanisms [32], quantum computing elements [34], and variational frameworks [29] have further improved performance on large-scale datasets. However, these models frequently overfit when training samples are limited—a common scenario in RATR where collecting comprehensive datasets for new target classes is impractical [35,36]. Transfer learning approaches [37] offer partial mitigation but struggle with domain shifts between source and target distributions. More recently, graph-based deep learning approaches have been introduced to better incorporate physical priors of electromagnetic scattering by modeling range cells as nodes with meaningful connections [5]. Despite this advancement, current graph models employ static graph topologies that inadequately capture the dynamic scattering characteristics that vary significantly with aspect angle. This fundamental limitation, compounded by few-shot learning challenges, results in poor generalization performance in practical deployment scenarios where both target variety and viewing conditions exhibit substantial variation [11,38,39,40].
Recent advances in few-shot learning offer potential solutions to data scarcity challenges in RATR systems. Meta-learning approaches such as Model-Agnostic Meta-Learning (MAML) [41,42] and its variants [43,44] have demonstrated impressive performance by learning to rapidly adapt to new tasks with minimal examples. These techniques have been adapted for HRRP recognition through various strategies including Gramian angular field transformations [45], task-specific meta-learning with mixed training [17], and prior information-assisted frameworks [46]. Prototypical networks [47] and contrastive learning methods [40] have also shown promise in addressing aspect sensitivity and missing data scenarios. However, their direct application to HRRP recognition is often hindered by the unique properties of radar data—specifically, the need for architectures that can dynamically model aspect-dependent electromagnetic scattering phenomena [20] while efficiently adapting parameters across different target distributions.
In this paper, we introduce HRRPGraphNet++, a novel framework that synergistically combines dynamic graph modeling with meta-optimization for few-shot HRRP recognition. Our approach models the HRRP signal as a graph where nodes represent range cells and edges encode their relationships. Unlike previous work [5], we generate these graph structures dynamically through MSA mechanisms that adapt to target-specific scattering characteristics, effectively addressing aspect sensitivity and range migration challenges. This representation is integrated with a specialized meta-learning framework that employs layer-wise learning rates tailored to the hierarchical nature of HRRP features, enabling efficient adaptation with as few as one example per target class.
Our main contributions are:
- A dynamic graph generation mechanism that adaptively models HRRP data by combining physics-informed static priors with attention-based dynamic relationships, effectively capturing the non-stationary scattering phenomena in radar signatures.
- A meta-learning optimization strategy for HRRP recognition that employs layer-specific adaptation rates and multi-step loss weighting, enabling rapid convergence on novel target classes with minimal labeled examples.
- Comprehensive experiments on simulated HRRP datasets demonstrating that HRRPGraphNet++ achieving state-of-the-art performance in 1-shot (82.3%) to 20-shot (94.7%) settings. Superior resilience maintaining 68.7% accuracy at 0 dB SNR with only 22.6% accuracy reduction from 20 dB to −5 dB. Codes are available at https://github.com/MountainChenCad/HRRPGNplus (accessed on 18 June 2025).
The remainder of this paper is organized as follows. Section 2 reviews related work in HRRP-based target recognition, graph neural networks, and few-shot learning. Section 3 describes our proposed HRRPGraphNet++ framework in detail, including dynamic graph modeling, network architecture, and meta-learning optimization. Section 4 presents experimental results and comprehensive comparisons with state-of-the-art methods. Finally, Section 5 concludes the paper and discusses future research directions.
2. Related Work
2.1. HRRP-Based Target Recognition
Traditional HRRP recognition approaches primarily rely on statistical pattern recognition techniques. Early works employed template matching [48], where test profiles are compared against reference templates using various distance metrics. Statistical models including Gaussian mixture models [49], hidden Markov models [50], and SVMs [27,51] have been applied to capture the statistical distributions of HRRP features. Signal processing methods such as time–frequency analysis [52,53,54] and wavelet transforms [55,56] have been utilized to extract robust features from HRRP data. These conventional approaches, while providing theoretical interpretability, struggle with aspect sensitivity and require extensive preprocessing to achieve acceptable performance [11,19,57,58].
In recent years, researchers have explored various deep neural architectures for HRRP recognition. Song et al. [30] pioneered the application of CNNs to extract shift-invariant features from range profiles. Recurrent networks, including LSTM [4,33] and Gated Recurrent Unit (GRU) variants [21,23], have been employed to model sequential dependencies in HRRP signals. More sophisticated architectures combining CNNs with attention mechanisms [8,24] and residual connections [59,60] have further improved performance on large-scale datasets. However, these approaches treat HRRPs as sequential data, failing to explicitly model the complex non-Euclidean relationships between range cells that arise from target geometry and electromagnetic scattering physics.
2.2. Graph Neural Networks for Signal Processing
Graph neural networks (GNNs) have emerged as powerful tools for processing data with inherent graph structures. Bruna et al. [61] and Defferrard et al. [62] extended convolutional operations to non-Euclidean domains through spectral graph theory. Kipf and Welling [63] introduced Graph Convolutional Networks (GCNs) with simplified spectral filters, while Veličković et al. [64] proposed Graph Attention Networks (GATs) that learn edge weights through self-attention.
In radar applications specifically, Chen et al. [5] first proposed representing HRRPs as graph structures in HRRPGraphNet, demonstrating improved performance over sequential models. Zhang et al. [65] explored similar graph-based approaches for SAR image classification. However, existing graph-based radar recognition methods employ static graph structures that cannot adapt to the dynamic nature of radar returns across different aspect angles and operating conditions. Our work addresses this limitation by introducing a dynamic graph generation mechanism that adaptively models the relationships between range cells based on their electromagnetic scattering characteristics.
2.3. Dynamic Graph Generation
Dynamic graph construction has gained attention for its ability to capture evolving relationships in data. Approaches can be broadly categorized into similarity-based methods that construct graphs from feature affinity [66,67], attention-based methods that learn edge weights through parameterized functions [68,69], and physics-informed methods that incorporate domain knowledge [70,71,72]. Recent works have explored the integration of Transformer architectures [73,74] with graph learning, using self-attention to capture long-range dependencies.
Most closely related to our approach, Wang et al. [72] proposed dynamic graph CNNs for point cloud processing, while Xu et al. [71] developed adaptive graph generation for traffic image recognition. However, these methods are not directly applicable to HRRP data, which exhibit unique challenges (i.e., aspect sensitivity, amplitude fluctuations, and range migration effects). Our proposed dynamic graph generation mechanism specifically addresses these radar-specific challenges by combining physics-informed priors with data-driven attention mechanisms, enabling more effective modeling of electromagnetic scattering phenomena.
2.4. Few-Shot Learning and Meta-Learning
Few-shot learning aims to recognize novel classes from limited examples [75,76]. Early approaches include metric-based methods like Matching Networks [77] and Prototypical Networks [78], which learn embeddings where similarity corresponds to class membership. Optimization-based methods, exemplified by MAML [41], instead learn initialization parameters that facilitate rapid adaptation. MAML++ [43] introduced multi-step loss optimization and per-layer learning rates, while Reptile [79] simplified the algorithm with first-order approximations. Other variations include Meta-SGD [80], which learns adaptive learning rates, and Almost No Inner Loop (ANIL) [81], which restricts adaptation to the classifier. Despite these advances, meta-learning approaches have been primarily developed for CV and NLP, with limited exploration in radar recognition domains. The meta-learning paradigm offers several key advantages for HRRP recognition: (1) it learns transferable feature representations that generalize across different aircraft types, (2) it optimizes the learning algorithm itself rather than just model parameters, enabling rapid adaptation with minimal examples, and (3) it addresses the fundamental challenge of distribution shifts between training and testing scenarios common in radar applications.
In the radar domain specifically, few-shot learning has been applied to SAR image classification [82,83] and micro-Doppler recognition [84], but with limited investigation for HRRP data [4,45,46]. The specialized challenges of aspect sensitivity and electromagnetic scattering variation in HRRP recognition necessitate tailored meta-learning strategies that can efficiently adapt across different target classes and radar conditions. Our work addresses this gap by developing a customized meta-learning framework specifically designed for the hierarchical feature structure of HRRP data.
3. Methods
3.1. Problem Setup
Formally, we define an N-way K-shot classification task, wherein we aim to classify query samples into one of N classes, using only K labeled examples per class (for our experiments, this means using only 1, 5, or 20 samples per class during the meta-testing phase to adapt the model to new, unseen aircraft types). Let represent our meta-training set, comprising M distinct few-shot learning tasks. Each task consists of a support set, , containing labeled examples and a query set, , with examples for evaluation. For each task, i, we denote the support set as , where represents an HRRP signal with L range cells, and denotes its corresponding class label. Similarly, the query set is defined as . Following previous HRRPGraphNet [5], the central insight of our work is to redefine the HRRP recognition problem through a graph-theoretic lens. We propose modeling each HRRP signal as a graph, , where the vertex set corresponds to individual range cells, and the edge set encodes meaningful relationships between them. This representation allows us to leverage the expressive power of GNNs to capture both local and global structural patterns within HRRP data [5].
HRRPGraphNet++ advances HRRP modeling through: (a) dynamic graph generation with MSA to model dynamic scattering relationships, and (b) meta-learning optimization with a bi-level structure. Figure 2 shows this framework where hybrid graph representation and efficient parameter adaptation enable few-shot RATR with minimal labeled examples.
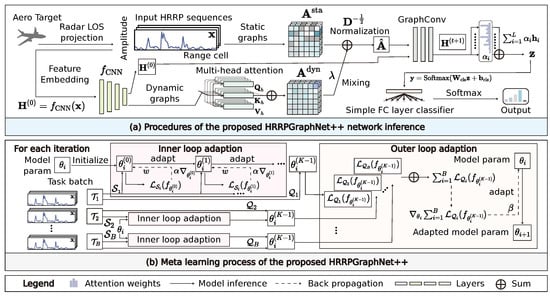
Figure 2.
Overview of our proposed dynamic graph-based meta-learning framework for few-shot HRRP radar target recognition. The architecture integrates (a) procedures of the proposed HRRPGraphNet++ network inference and (b) meta-learning process of the proposed HRRPGraphNet++. Our approach uniquely combines prior distance knowledge with learned dynamic relationships to enhance few-shot learning performance on radar target recognition tasks.
3.2. Dynamic Graph Modeling of HRRP
This section details our methodology for constructing meaningful graph structures from HRRP signals, specifically addressing the unique characteristics of HRRPs.
- Static Graph Construction with HRRP Priors. HRRPs exhibit distinctive scattering characteristics where electromagnetic reflections from different parts of targets create complex dependencies between range cells. To model these inherent relationships, we establish a static adjacency matrix, , based on radar scattering physics. For any two range cells at positions i and j, we define:where is a mixing coefficient ( = 0.5), represents the distance between range cells, and denotes the indicator function. The parameter defines a local neighborhood window set to 5, corresponding to the typical extent of coherent scattering centers in aircraft HRRP signatures. This formulation incorporates two radar-specific inductive biases:
- A distance decay term reflecting the diminishing electromagnetic interaction between separated range cells.
- A local connectivity term modeling the phenomenon where adjacent range cells often capture reflections from the same structural component of the target.
Static graphs, however, cannot address three critical HRRP characteristics: aspect angle sensitivity, amplitude variation, and range migration. These factors create complex, non-adjacent relationships between range cells that vary with each observation.
- Dynamic Graph Generation via MSA. To create a sample-specific graph representation, we employ a MSA mechanism that dynamically computes the relationships between range cells based on their features [73,85,86]. Given an input HRRP signal , we first apply a feature enhancement to obtain a richer representation:where includes convolutional (Conv1D) layers followed by batch-normalization (BN) and LeakyReLU activation and massage-passing operations (see Section 3.3 for details), and d represents the hidden dimension. The enhanced feature matrix, , is then processed through a MSA mechanism to generate a dynamic adjacency matrix. For each attention head , we compute query, key, and value projections:where are learnable projection matrices, and is the dimension per head. The attention scores for head h are then computed as:The division by serves as a scaling factor to prevent the dot products from growing too large in magnitude, which would push the softmax function into regions with extremely small gradients [85]. The operation ensures that the attention weights for each range cell add up to 1, effectively normalizing the importance of all other cells in the context of each individual cell. To obtain the final attention-based adjacency matrix, we average the contributions from all heads:Hybrid Graph Representation. To leverage the complementary strengths of both the static prior-based approach and the dynamic attention-driven method, we propose a hybrid graph representation that combines these two adjacency matrices:where is a learnable or predefined mixing coefficient that balances the contribution of static prior knowledge and dynamic content-based relationships (See Section 4.5 for more details). The theoretical superiority of our dynamic graph approach over static graph representations for aspect-variant HRRP data is formally established in Appendix A.1.
- Graph Normalization. To stabilize training and facilitate information propagation in subsequent graph convolutional layers, we apply a symmetric normalization to the hybrid adjacency matrix:where is the degree matrix of , with diagonal elements . This normalization prevents the scale of features from vanishing during message passing, ensuring nodes with many connections do not dominate the representation [87,88].
Through this comprehensive graph-modeling approach, we transform each HRRP signal into a rich graph representation that captures both physical priors and data-driven relationships, providing a solid foundation for subsequent GNN processing.
3.3. Graph Neural Network Architecture
Our GNN architecture comprises three key components following the style of Chen et al. [5]: (a) a feature extraction module, (b) multiple graph convolutional layers, and (c) a global attention pooling layer. Together, these components transform the raw HRRP signals into discriminative feature representations for target classification.
- Feature Extraction Module. The feature extraction module serves as the initial processing stage for the raw HRRP signals, enhancing local patterns before graph-based operations. Given an input HRRP signal , we apply a series of 1D convolutional layers to extract hierarchical features:contains three convolutional blocks, each of which consists of a Conv1D layer, a BN layer, and a LeakyReLU (), where the numbers of filters of these blocks are {16; 32; 64} (as shown in Figure 3). The first convolutional block employs a kernel size of 5 and padding of 2 to preserve the input sequence length, the second block utilizes a kernel size of 3 with padding of 1, and the final block applies a kernel size of 3 and padding of 1, maintaining the profile length L, where d is set to 64 in our implementation. Formally, each convolutional block can be expressed as:where represents the feature map at layer l, and and are the learnable weight and bias parameters of the convolution, optimized jointly with the rest of the network.
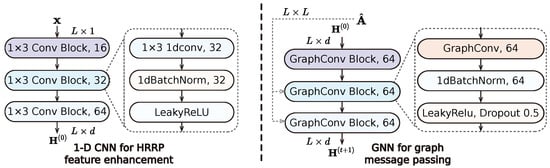 Figure 3. The network structure of layers in HRRPGraphNet++. Left panel: network structure of 1D CNN for HRRP feature enhancement. Right panel: network structure of GNN for message passing.
Figure 3. The network structure of layers in HRRPGraphNet++. Left panel: network structure of 1D CNN for HRRP feature enhancement. Right panel: network structure of GNN for message passing.
- Graph Convolutional Layers. Following feature extraction, a series of graph convolutional layers propagate and transform features according to the normalized adjacency matrix, . For each layer , the graph convolution operation is defined as:where represents the node features at layer t, is a learnable weight matrix, and denotes the LeakyReLU activation function. Subsequently, batch normalization and dropout are incorporated after each graph convolution. Dropout rates , and is the LeakyReLU (). In our architecture, we stack graph convolutional layers, which allows for the integration of information from 2-hop neighborhoods in the graph (see Section 4.5 for details). This design choice is motivated by the observation that radar targets typically exhibit scattering phenomena that span multiple adjacent range cells, yet maintain a relatively localized influence [89,90].
- Global Attention Pooling. After processing the HRRP through multiple graph convolutional layers (as shown in Figure 3), we obtain rich node-level features . To derive a graph-level representation for classification, we employ a global attention pooling mechanism that adaptively weights the contribution of each range cell:
The attention weights, , are computed through a two-layer neural network:
where , , , and are learnable parameters, and represents the LeakyReLU activation function. The resulting graph-level representation encapsulates the essential structural information of the HRRP, serving as the input to the final classification layer:
where and are the weight and bias parameters of the classification layer, and N is the number of target classes.
3.4. Meta-Learning Optimization Framework
To address the challenging few-shot scenario in HRRP RATR, we adopt a meta-learning approach centered around MAML [41]. The convergence advantages of our meta-learning approach compared with conventional fine tuning for HRRP recognition tasks are mathematically proven in Appendix A.2. This section elucidates the fundamental principles of MAML and its application to our specific context, before introducing our proposed enhancements in Section 3.5.
- MAML Fundamentals. The core insight of MAML is to train a model that can rapidly adapt to new tasks with minimal data through gradient-based optimization [41,75,76]. Rather than learning a fixed set of parameters that perform well on a specific task, MAML learns a set of meta-parameters that serve as an optimal initialization for fine tuning across a distribution of related tasks.
Formally, given a distribution of tasks , MAML aims to find parameters that minimize the expected loss after adaptation:
here, denotes the loss function for task , represents our model parameterized by , and is the inner loop learning rate. The adapted parameters, , are obtained by performing one or more gradient descent steps on the task-specific loss.
- MAML for HRRP Few-Shot Learning. In the context of HRRP few-shot learning, each task, , consists of a support set, , and a query set, , as defined in Section 3.1. The meta-learning process involves two nested optimization loops.
1. Inner Loop (Task Adaptation): For each task, , we adapt the model parameters using the support set, . Starting from the meta-parameters , we perform K gradient steps:
for , where is the cross-entropy loss computed on the support set:
here, denotes the predicted probability for class c, and is the indicator function that equals 1 when and 0 otherwise.
2. Outer Loop (Meta-Update): After adapting the model to each task, we evaluate the performance on the corresponding query set, , and update the meta-parameters to improve adaptation across tasks:
where B is the batch size of tasks, is the outer loop learning rate, and is the cross-entropy loss computed on the query set:
Computing the gradient for the meta-update involves calculating second derivatives, as we need to differentiate through the inner loop optimization process. Specifically, the gradient of the query loss with respect to the meta-parameters can be expressed as:
The computation of requires unrolling the recursive relation defined by the inner loop updates, which introduces higher-order derivatives and can be computationally expensive. Hence, the above mentioned Finn MAML [41] faces several challenges when applied to HRRP recognition: training instability due to second-order derivatives, inefficient adaptation from uniform learning rates, limited utilization of intermediate adaptation states, and high computational complexity.
3.5. Adoption of MAML for Efficient Meta-Learning
To address HRRP recognition challenges, we customize MAML with domain-specific adaptations integrating previous progress [43,91,92,93]. Firstly, we employ multi-step loss optimization to leverage intermediate adaptation information:
In addition, we implement layer-wise learning rates, giving graph layers (0.004–0.006) higher adaptability than feature extraction layers (0.002–0.004) to better model HRRP scattering patterns:
For stable optimization, we use cosine learning rate scheduling and compute task-specific batch normalization statistics:
These enhancements enable our graph model to efficiently adapt to varying HRRP distributions across different target classes and radar conditions with minimal labeled examples—critical for practical RATR applications. To formalize our approach, we present the complete meta-training and meta-testing procedures in Algorithms 1 and 2, respectively.
| Algorithm 1 HRRPGraphNet++ Meta-Training Stage |
|
| Algorithm 2 HRRPGraphNet++ Meta-Testing Stage |
|
4. Experiments
In this section, we present a comprehensive evaluation of the proposed HRRPGraphNet++ framework. We first describe the experimental setup and datasets used for evaluation. Then, we compare our method with various state-of-the-art approaches for HRRP-based radar target recognition. Finally, we conduct extensive ablation studies to analyze the contribution of each component in our framework.
4.1. Implementation Details
- Platform. All experiments were conducted on a 64-bit Linux system with 2 Intel Xeon Bronze 3204 CPU @1.9 GHz and 64 GB of RAM. The GPUs are 3 NVIDIA RTX A4000 with 16 GB of video memory (48 GB in total). The codes are implemented with PyTorch 2.2.0, CUDA 12.5, and Python 3.8.
- Training settings. We trained our model using Adam optimizer with an initial learning rate of and weight decay of . Meta-training employs a task batch size of four, with a maximum of 300 epochs and early stopping with a patience of 100 epochs. The inner loop adaptation performs five gradient steps with decreasing layer-specific learning rates (ranging from for graph convolution layers to for classification layers in later steps), which we found crucial for balancing adaptation speed across different components. Multi-step loss weights follow a progressive scheme [0.1, 0.2, 0.3, 0.4, 1.0], emphasizing later adaptation steps while still providing supervision throughout the adaptation process to ensure stable learning. To improve training stability, second-order derivative computation is enabled only after 50 epochs of training.
4.2. Experimental Dataset
We conducted all our experiments on a widely used aircraft electromagnetic simulation dataset [4,5,11,19,94]. We simulated twelve classes of aircraft and obtained their radar echo signals with four polarization modes (HH, HV, VH, VV) based on the 3D aircraft model simulation software. The types of aircraft in the aircraft electromagnetic simulation dataset are EA-18G, EP-3E, F2, F15, F16, F18, F22, F35, global hawk, mirage-2000, predator drone, and IDF. We selected six types as the training set and six types as the testing set. The radar of the simulation system works in X band and the frequency range is 9.5 GHz~10.5 GHz with a step length of 10 MHz. The pitch angle is 75~105 with a step length of 3 and the azimuth angle is 0~60 with a step length of 0.05 (While this dense sampling is common for creating simulation datasets for evaluation, our method is specifically designed to perform well in few-shot scenarios, making it suitable for practical applications where only sparse aspect angle data are available.). Based on the above settings, for each type of aircraft, we obtained a sub-dataset, D, as a few-shot dataset with size of , where 1 means the dataset is formed by the HH polarization mode 1st pitch angle, 1201 is the number of azimuth angles, and 1000 means each HRRP sample contains 1000 range cells. The HRRPs of 12 types of targets in the 1st pitch angle are shown in Figure 4.
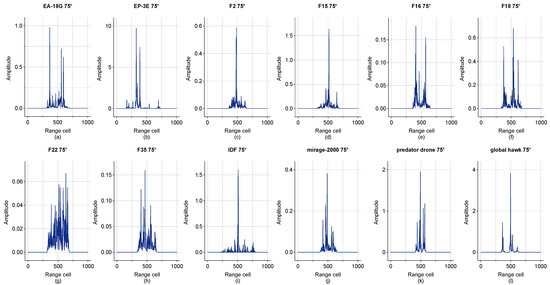
Figure 4.
Visualization of simulated HRRP samples from the 12-class aircraft dataset. The figure HRRPs of 12 different aircraft types captured at a pitch angle of 90 and azimuth angle of 0.15. (a–l) contains the HRRP sample of one included class. These profiles were generated using electromagnetic simulation software based on 3D models of aircraft.
4.3. Evaluation Metrics
- Baseline Methods. We compare HRRPGraphNet++ against a diverse set of baseline methods, including (1) traditional approaches such as PCA-SVM [27] and template matching [48]; (2) deep learning methods including CNN [30], LSTM [4], GCN [63], and GAT [64]; (3) meta-learning approaches including MAML [41], MAML++ [43], ANIL [81], and Meta-SGD [80]; and (4) the original HRRPGraphNet [5] (static graph only).
- Classification Accuracy. The primary evaluation metric is the average classification accuracy across multiple randomly sampled test episodes. For each N-way K-shot test episode , we first adapt our model parameters to using the support set, , following Algorithm 2. We then compute the accuracy on the query set, , as:where denotes the predicted class for input x with adapted parameters , and is the indicator function that equals 1 when the prediction matches the ground truth label y and 0 otherwise. To account for the variability in randomly sampled tasks, we generate 600 distinct test episodes and report the mean 3-way accuracy along with 95% confidence intervals:where is the standard deviation of accuracies across test episodes. This rigorous evaluation protocol ensures statistical reliability of our reported results, particularly important for few-shot learning where individual episodes can exhibit high variance.
4.4. Comparative Experiments
- Few-shot Learning Performance. Table 1 presents the performance comparison of different methods on HRRP target recognition under 3-way 1-shot, 5-shot, and 20-shot settings. Several key observations can be made. First, HRRPGraphNet++ consistently outperforms all baseline methods across all shot settings, achieving 82.3%, 91.8%, and 94.7% accuracy in 1-shot, 5-shot, and 20-shot settings, respectively. This represents a substantial improvement of 2.7%, 2.3%, and 0.9% over the next best method (MAML++) in the respective shot settings, demonstrating the superior few-shot learning capability of our approach. Second, we observe that meta-learning approaches (MAML++, MAML, ANIL, Meta-SGD) generally outperform traditional deep learning methods (CNN, LSTM, GCN, GAT), highlighting the importance of meta-learning for few-shot HRRP recognition. Among the meta-learning methods, MAML++ and Meta-SGD show the strongest performance, likely due to their adaptive learning rate mechanisms, which align with our findings on the importance of per-layer and per-step learning rates in our ablation study. Third, graph-based methods (GAT, GCN, HRRPGraphNet) demonstrate superior performance compared with sequence-based models (CNN, LSTM), confirming our hypothesis that graph representations better capture the spatial relationships between range cells in HRRP data. This advantage becomes more pronounced in extremely low-shot scenarios (1-shot), where HRRPGraphNet++ achieves a remarkable 15.1% improvement over CNN and 16.6% over LSTM. Fourth, traditional approaches (PCA-SVM, TemplateMatcher) exhibit the weakest performance, especially in the challenging 1-shot setting, indicating that these methods lack the representational capacity to effectively model complex HRRP data patterns when very few examples are available. Finally, the significant performance gap between HRRPGraphNet (static graph only) and HRRPGraphNet++ (hybrid graph with ) underscores the critical role of dynamic graph learning in capturing adaptive relationships among range cells. Our hybrid graph approach achieves an 8.8% accuracy improvement in the 1-shot setting, demonstrating that combining static structural information with dynamically learned relationships substantially enhances model performance.
 Table 1. Performance comparison of different methods on HRRP RATR across few-shot settings. The best results are marked in bold.
Table 1. Performance comparison of different methods on HRRP RATR across few-shot settings. The best results are marked in bold.
- Noise Robustness Analysis. Radar systems invariably operate in noisy environments, making noise robustness a critical factor for practical applications. To evaluate noise robustness, we added Additive White Gaussian Noise (AWGN) to the test samples to achieve the desired SNR. Figure 5 illustrates the performance of HRRPGraphNet++ under varying SNR levels, ranging from 20 dB (minimal noise) to −5 dB (severe noise). The results demonstrate that HRRPGraphNet++ maintains robust performance even under challenging noise conditions. At high SNR levels (20 dB), the model achieves 82.0% accuracy and an 81.2% F1 score, which gradually decreases to 59.4% accuracy and a 57.8% F1 score at −5 dB SNR. This represents a remarkably graceful degradation, with only a 22.6% accuracy reduction despite a 25 dB decrease in SNR. Compared with baseline methods, HRRPGraphNet++ consistently demonstrates superior noise robustness. For instance, at 0 dB SNR, our method maintains 68.7% accuracy, outperforming MAML++ (64.2%), GCN (58.3%), and CNN (53.1%) by substantial margins. This enhanced robustness can be attributed to two key aspects of our approach: (1) the graph-based representation effectively captures structural relationships that remain relatively stable under noise, and (2) the meta-learning framework allows the model to rapidly adapt to noisy conditions with minimal examples.
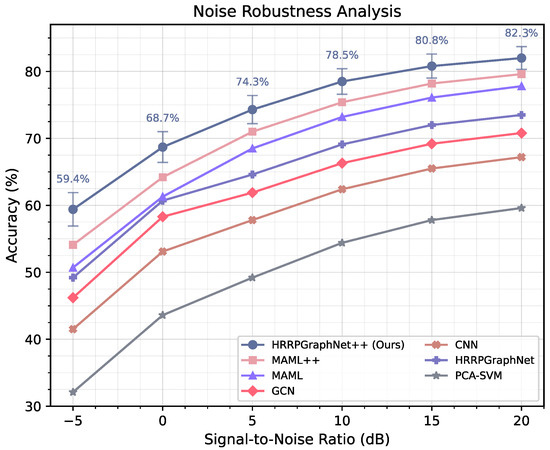 Figure 5. Noise robustness analysis of different HRRP recognition methods across varying SNR levels. The figure illustrates the performance degradation of seven representative methods under increasing noise conditions, with SNR ranging from 20 dB to −5 dB. Our proposed HRRPGraphNet++ demonstrates superior robustness.
Figure 5. Noise robustness analysis of different HRRP recognition methods across varying SNR levels. The figure illustrates the performance degradation of seven representative methods under increasing noise conditions, with SNR ranging from 20 dB to −5 dB. Our proposed HRRPGraphNet++ demonstrates superior robustness.
4.5. Ablation Study
To thoroughly understand the contribution of each component in HRRPGraphNet++, we conduct comprehensive ablation studies examining network architecture design, graph construction mechanisms, and hyperparameter sensitivity.
- Network Architecture. Figure 6 presents the performance impact of three key architectural components: (a) number of graph convolutional layers, (b) number of attention heads, and (c) pooling strategy. For graph convolutional layers (Figure 6a), we observe that performance improves significantly as we increase from one layer to three layers, followed by a slight decrease with four layers. This pattern suggests that stacking multiple GCN layers enables more effective hierarchical feature learning, but excessive depth may lead to over-smoothing of node features—a well-documented challenge in GNN architectures. Based on these results, we adopt three graph convolutional layers in our final model. Regarding attention heads (Figure 6b), our experiments show that four attention heads provides optimal performance compared with two heads and eight heads. This finding indicates that a moderate number of attention heads strikes the best balance between capturing diverse relationship patterns and maintaining computational efficiency. Too few heads limits the model’s ability to attend to different aspects of the data, while too many heads may cause focus diffusion and introduce unnecessary complexity. For pooling strategies (Figure 6c), attention-based pooling substantially outperforms mean pooling and max pooling, with improvements of 4.2% and 5.4%, respectively. This demonstrates that adaptive weighting of node features through attention mechanisms enables more effective information aggregation compared with simpler pooling operations. Attention pooling selectively emphasizes discriminative range cells while suppressing less informative ones, which is particularly beneficial for HRRP data where target-specific information may be concentrated in specific range cells.
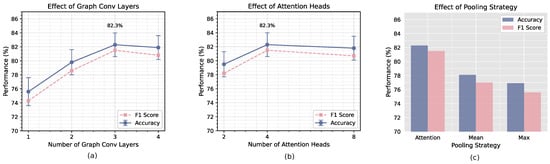 Figure 6. Ablation study on the architecture components of HRRPGraphNet++. (a): Effect of graph convolutional layers: model performance improves significantly from 1 to 3 layers. (b): Effect of attention heads: performance peaks at 4 attention heads compared with 2 heads and 8 heads. (c): Effect of pooling strategy: attention-based pooling substantially outperforms mean pooling and max pooling. Error bars indicate 95% confidence intervals across 600 few-shot tasks.
Figure 6. Ablation study on the architecture components of HRRPGraphNet++. (a): Effect of graph convolutional layers: model performance improves significantly from 1 to 3 layers. (b): Effect of attention heads: performance peaks at 4 attention heads compared with 2 heads and 8 heads. (c): Effect of pooling strategy: attention-based pooling substantially outperforms mean pooling and max pooling. Error bars indicate 95% confidence intervals across 600 few-shot tasks.
- Graph Construction Mechanisms (i.e., Hyperparameter Sensitivity). The mixing coefficient, , controls the balance between static and dynamic components in our hybrid graph construction. Figure 7 illustrates model performance across different values of , ranging from 0 (pure dynamic graph) to 1.0 (pure static graph). We observe that performance follows an inverted U-shape pattern, peaking at and gradually decreasing toward either extreme. This pattern confirms that neither purely static nor purely dynamic graphs are optimal for HRRP recognition. The optimal value of indicates that, while both components contribute to model performance, the dynamic component should be weighted more heavily than the static component. This finding aligns with our understanding of HRRP data: while physical constraints between range cells provide useful structural priors, the complex scattering mechanisms of radar targets create non-Euclidean relationships that cannot be fully captured by static distance-based graphs.
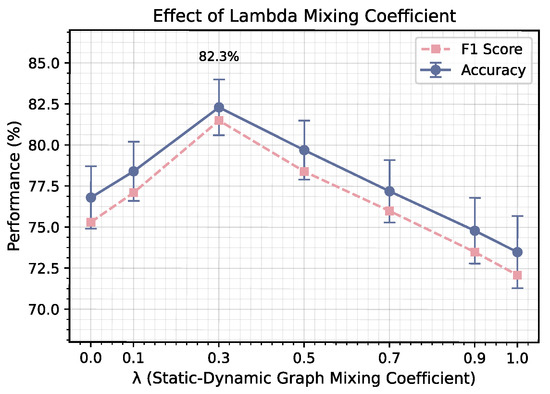 Figure 7. Sensitivity analysis of the lambda mixing coefficient (). The figure indicates that neither purely static nor purely dynamic graphs are optimal for HRRP recognition. Error bars represent 95% confidence intervals calculated over 600 randomly sampled few-shot tasks. This finding validates our hybrid graph approach, which combines physical structural priors with learned relationships to create a more effective representation for HRRP data.
Figure 7. Sensitivity analysis of the lambda mixing coefficient (). The figure indicates that neither purely static nor purely dynamic graphs are optimal for HRRP recognition. Error bars represent 95% confidence intervals calculated over 600 randomly sampled few-shot tasks. This finding validates our hybrid graph approach, which combines physical structural priors with learned relationships to create a more effective representation for HRRP data.
5. Conclusions
HRRPGraphNet++ addresses few-shot HRRP recognition through dynamic graph modeling and meta-learning optimization. Our approach significantly outperforms existing methods, especially in extreme 1-shot scenarios. The hybrid graph mechanism effectively captures aspect-dependent characteristics, while layer-wise adaptation rates enable rapid adaptation with minimal examples. Limitations include suboptimal performance at extremely low SNR (−5 dB) and computational complexity concerns for real-time deployment. Future work should explore noise-resistant features, model compression, and multi-modal fusion. HRRPGraphNet++ establishes a solid foundation for adaptive radar recognition systems in dynamic threat environments.
Author Contributions
Conceptualization, L.C.; methodology, L.C.; software, L.C.; validation, L.C.; formal analysis, L.C.; investigation, L.C.; resources, P.H.; data curation, Q.L., Z.P. and P.H.; writing—original draft preparation, L.C.; writing—review and editing, Z.P., Q.L. and P.H.; visualization, L.C.; supervision, P.H.; project administration, L.C. and P.H.; funding acquisition, L.C. and P.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by National Natural Science Foundation of China under Grant 62201588, in part by Natural Science Foundation of Hunan under Grant 2024JJ10007.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Theoretical Analysis
Appendix A.1. Optimality of Dynamic Graph Representation for HRRP Data
This section provides theoretical justification for the superiority of dynamic graph representations over static graph structures in HRRP-based target recognition.
Appendix A.1.1. Theoretical Framework
Let denote an HRRP signal with L range cells, and represent the aspect angle. The HRRP signature of a target can be modeled as:
where M is the number of dominant scattering centers, is the amplitude of the i-th scattering center at aspect angle , is the corresponding basis vector (indicating the position of the scattering center), and represents noise. This formulation follows the electromagnetic scattering model established by Rihaczek and Hershkowitz [95,96] and extended by Chen et al. [5] for HRRP graph representation.
For a static graph with adjacency matrix , as defined in Equation (1), the message-passing operation in a GNN layer can be expressed as:
For a dynamic graph with aspect-dependent adjacency matrix , as computed in Equation (5), the message passing becomes:
Appendix A.1.2. Representation Power Theorem
Theorem A1
(Representational Capacity). For any static graph adjacency matrix, , there exists an aspect angle difference, , such that the approximation error for HRRP signals across this aspect difference exceeds a constant bound, ϵ, while a properly designed dynamic graph can maintain an approximation error below ϵ.
Proof of Theorem A1.
Consider two aspect angles, and . The corresponding HRRP signals are and . Define the optimal static adjacency matrix that minimizes the expected representation error across all aspect angles:
where is a loss function and is the graph neural network with adjacency matrix .
Let us define the representation gap as:
For HRRP data, we can show that, as increases, the scattering centers’ positions shift significantly [11,38,39,40]:
for some constant C depending on target geometry.
For any fixed , as increases, the representation gap grows:
Conversely, for a dynamic graph with parameterized by H attention heads, as in Equation (5), we can construct aspect-specific adjacency matrices such that:
Therefore, for the dynamic graph, while this cannot be guaranteed for any static graph when is sufficiently large. □
Appendix A.2. Convergence Analysis of Meta-Learning for HRRP Recognition
This section demonstrates the theoretical advantages of meta-learning over conventional fine tuning for few-shot HRRP recognition.
Appendix A.2.1. Meta-Learning Framework
Let be a set of tasks, where each task consists of a support set, , and a query set, . Define the inner loop adaptation operator as:
where ⊙ represents element-wise multiplication and are the layer-specific learning rates defined in Equation (11).
For conventional transfer learning with fine tuning, the expected error on a new task, , is:
where represents parameters after K adaptation steps from pre-trained parameters.
For meta-learning, the objective is to find:
This formulation builds on the meta-learning framework of Finn et al. [41] and the theoretical analysis by Baxter [97].
Appendix A.2.2. Sample Efficiency Theorem
Theorem A2
(Sample Efficiency). For a K-shot learning task on HRRP data, the expected error of meta-learning with optimal initialization decreases at rate , where M is the number of meta-training tasks, while conventional fine tuning decreases at rate .
Proof of Theorem A2.
Consider the class of functions , representable by our graph neural network within K gradient steps from initialization. For conventional fine tuning from a pre-trained model with parameters , the expected error on a new task is bounded by [98,99]:
where is the set of functions reachable within K gradient steps from , and C is a constant.
For meta-learning, following the analysis of Tripuraneni et al. [100] and Rajeswaran et al. [101], we can show:
where is the space of meta-parameters and is a constant.
The first term in both bounds represents the approximation error. For the second term (estimation error), meta-learning decreases at rate while fine tuning decreases at rate .
Furthermore, for HRRP data specifically, we can demonstrate that the task distribution has shared structure across aspect angles and target types, which meta-learning can leverage [102]. Let:
be the optimal parameters for task . For HRRP data, we can establish the following bound on the parameter distance between optimal solutions for different tasks:
where is a measure of task similarity and D is a constant. To prove this, we make the standard assumption that task-specific loss functions are -strongly convex [97]. Following Achille et al. [103] and Du et al. [104], we define the task similarity metric based on gradient information:
For optimal parameters, and by definition. Applying the mean value theorem, there exists between and such that:
where is the Hessian matrix of at . Due to -strong convexity, all eigenvalues of are at least , leading to:
Since , we have:
By definition of task similarity:
Combining these inequalities and setting :
For HRRPs, this mathematical relationship has a clear physical interpretation: targets observed from similar aspect angles produce similar electromagnetic scattering patterns, resulting in optimal model parameters that lie close to each other in parameter space.
In practice, even though deep neural network loss landscapes may not be globally strongly convex, they can be locally approximated as such near optima, making this analysis relevant for practical HRRP recognition scenarios. □
References
- Jian, C.; Lan, D.U.; Leiyao, L. Survey of Radar HRRP Target Recognition Based on Parametric Statistical Model. J. Radars 2022, 11, 1020–1047. [Google Scholar]
- Liu, H.; Du, L.; Wang, P.; Pan, M.; Bao, Z. Radar HRRP automatic target recognition: Algorithms and applications. In Proceedings of the 2011 IEEE CIE International Conference on Radar, Chengdu, China, 24–27 October 2011; pp. 14–17. [Google Scholar]
- Xia, Z.; Wang, P.; Liu, H. Radar HRRP Open Set Target Recognition Based on Closed Classification Boundary. Remote Sens. 2023, 15, 468. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, X.; Liu, Y.; Huo, K.; Jiang, W.; Li, X. Multi-Polarization Fusion Few-Shot HRRP Target Recognition Based on Meta-Learning Framework. IEEE Sens. J. 2021, 21, 18085–18100. [Google Scholar] [CrossRef]
- Chen, L.; Sun, X.; Pan, Z.; Liu, Q.; Wang, Z.; Su, X.; Liu, Z.; Hu, P. HRRPGraphNet: Make HRRPs to be graphs for efficient target recognition. Electron. Lett. 2024, 60, e70088. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Y.; Li, X.; Bi, G. Bayesian High Resolution Range Profile Reconstruction of High-Speed Moving Target From Under-Sampled Data. IEEE Trans. Image Process. 2020, 29, 5110–5120. [Google Scholar] [CrossRef]
- Dong, H.; Dai, F.; Zhang, J. High-Speed Target HRRP Reconstruction Based on Fast Mean-Field Sparse Bayesian Unrolled Network. Remote Sens. 2025, 17, 8. [Google Scholar] [CrossRef]
- Liu, X.; Wang, L.; Bai, X. End-to-End Radar HRRP Target Recognition Based on Integrated Denoising and Recognition Network. Remote Sens. 2022, 14, 5254. [Google Scholar] [CrossRef]
- Winters, D.W. Target Motion and High Range Resolution Profile Generation. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2140–2153. [Google Scholar] [CrossRef]
- Guo, C.; Wang, H.; Jian, T.; Xu, C.; Sun, S. Method for denoising and reconstructing radar HRRP using modified sparse auto-encoder. Chin. J. Aeronaut. 2020, 33, 1026–1036. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, X.; Liu, Y. SCNet: Scattering center neural network for radar target recognition with incomplete target-aspects. Signal Process. 2024, 219, 109409. [Google Scholar] [CrossRef]
- Yang, L.; Feng, W.; Wu, Y.; Huang, L.; Quan, Y. Radar-Infrared Sensor Fusion Based on Hierarchical Features Mining. IEEE Signal Process. Lett. 2024, 31, 66–70. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, Y.; Wang, W. Patch-Wise Autoencoder Based on Transformer for Radar High-Resolution Range Profile Target Recognition. IEEE Sens. J. 2023, 23, 29406–29414. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Huang, P.; Zheng, M.; Tian, B.; Xu, S. MTBC: Masked Vision Transformer and Brown Distance Covariance Classifier for Cross-domain Few-shot HRRP Recognition. IEEE Sens. J. 2025, 25, 16440–16454. [Google Scholar] [CrossRef]
- Ye, Y.; Deng, Z.; Pan, P.; He, W. Range-Spread Target Detection Networks Using HRRPs. Remote Sens. 2024, 16, 1667. [Google Scholar] [CrossRef]
- Du, L.; He, H.; Zhao, L.; Wang, P. Noise Robust Radar HRRP Target Recognition Based on Scatterer Matching Algorithm. IEEE Sens. J. 2016, 16, 1743–1753. [Google Scholar] [CrossRef]
- Kong, Y.; Zhang, Y.; Peng, X.; Leung, H. Few-Shot High-Resolution Range Profile Ship Target Recognition Based on Task-Specific Meta-Learning with Mixed Training and Meta Embedding. Remote Sens. 2023, 15, 5301. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, L.; Wang, Y. Limited Sample Radar HRRP Recognition Using FWA-GAN. Remote Sens. 2024, 16, 2963. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, X.; Liu, Y. A Prior-Knowledge-Guided Neural Network Based on Supervised Contrastive Learning for Radar HRRP Recognition. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 2854–2873. [Google Scholar] [CrossRef]
- Gao, F.; Ren, D.; Yin, J.; Yang, J. Polarimetric HRRP Recognition Using Vision Transformer with Polarimetric Preprocessing and Attention Loss. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 10838–10842. [Google Scholar]
- Zeng, Z.; Sun, J.; Han, Z.; Hong, W. Radar HRRP Target Recognition Method Based on Multi-Input Convolutional Gated Recurrent Unit With Cascaded Feature Fusion. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4026005. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, P.; Dong, G.; Liu, H. Radar HRRP Open Set Recognition Based on Extreme Value Distribution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5102416. [Google Scholar] [CrossRef]
- Yang, W.; Chen, T.; Lei, S.; Zhao, Z.; Hu, H.; Hu, J. Radar HRRP Feature Fusion Recognition Method Based on ConvLSTM Network with Multi-Input Gate Recurrent Unit. Remote Sens. 2024, 16, 4533. [Google Scholar] [CrossRef]
- Gao, F.; Lang, P.; Yeh, C.; Li, Z.; Ren, D.; Yang, J. An Interpretable Target-Aware Vision Transformer for Polarimetric HRRP Target Recognition with a Novel Attention Loss. Remote Sens. 2024, 16, 3135. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, P.; Fang, M.; Guo, Y.; Cao, L.; Yan, J.; Liu, H. Radar High-Resolution Range Profile Rejection Based on Deep Multi-Modal Support Vector Data Description. Remote Sens. 2024, 16, 649. [Google Scholar] [CrossRef]
- Wu, H.; Li, G.; Zhou, J. High-resolution Range Profiles Recognition Based on SAR/ISAR Images. In Proceedings of the 2019 IEEE 3rd Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 11–13 October 2019; pp. 1514–1518. [Google Scholar]
- Liu, Z.; Zhang, X.; Huo, K.; Liu, Y.; Li, X. Experimental study on HRRP-based airborne target recognition using neural networks. In Proceedings of the IET International Radar Conference (IET IRC 2020), Online, 4–6 November 2020; pp. 283–286. [Google Scholar]
- Tu, J.; Huang, T.; Liu, X.; Gao, F.; Yang, E. A Novel HRRP Target Recognition Method Based on LSTM and HMM Decision-making. In Proceedings of the 2019 25th International Conference on Automation and Computing (ICAC), Lancaster, UK, 5–7 September 2019; pp. 1–6. [Google Scholar]
- Zhai, Y.; Chen, B.; Zhang, H.; Wang, Z. Robust Variational Auto-Encoder for Radar HRRP Target Recognition. In Proceedings of the Intelligence Science and Big Data Engineering, Dalian, China, 22–23 September 2017; pp. 356–367. [Google Scholar]
- Song, J.; Wang, Y.; Chen, W.; Li, Y.; Wang, J. Radar HRRP recognition based on CNN. J. Eng. 2019, 2019, 7766–7769. [Google Scholar] [CrossRef]
- Chen, J.; Du, L.; Guo, G.; Yin, L.; Wei, D. Target-attentional CNN for Radar Automatic Target Recognition with HRRP. Signal Process. 2022, 196, 108497. [Google Scholar] [CrossRef]
- Pan, M.; Liu, A.; Yu, Y.; Wang, P.; Li, J.; Liu, Y.; Lv, S.; Zhu, H. Radar HRRP Target Recognition Model Based on a Stacked CNN–Bi-RNN With Attention Mechanism. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5100814. [Google Scholar] [CrossRef]
- Jithesh, V.; Sagayaraj, M.J.; Srinivasa, K.G. LSTM recurrent neural networks for high resolution range profile based radar target classification. In Proceedings of the 2017 3rd International Conference on Computational Intelligence & Communication Technology (CICT), Ghaziabad, India, 9–10 February 2017; pp. 1–6. [Google Scholar]
- Liu, X.; Zhou, D.; Huang, Q. Radar HRRP Target Recognition Based on Hybrid Quantum Neural Networks. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 6173–6188. [Google Scholar] [CrossRef]
- Xu, Y.; Shi, L.; Lin, C.; Huang, Y.; Ding, X. Effective HRRP data augmentation by contrastive adversarial training. IET Conf. Proc. 2024, 2023, 1380–1385. [Google Scholar] [CrossRef]
- Thanapol, P.; Lavangnananda, K.; Bouvry, P.; Pinel, F.; Leprévost, F. Reducing Overfitting and Improving Generalization in Training Convolutional Neural Network (CNN) under Limited Sample Sizes in Image Recognition. In Proceedings of the 2020 5th International Conference on Information Technology (InCIT), Chonburi, Thailand, 21–22 October 2020; pp. 300–305. [Google Scholar]
- Wen, Y.; Shi, L.; Yu, X.; Huang, Y.; Ding, X. HRRP Target Recognition With Deep Transfer Learning. IEEE Access 2020, 8, 57859–57867. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Z.; Gao, X. Contrastive learning-based prototype calibration method for few-shot HRRP recognition. In Proceedings of the IET International Radar Conference (IRC 2023), Chongqing, China, 3–5 December 2023; pp. 920–923. [Google Scholar]
- Li, J.; Li, D.; Jiang, Y.; Yu, W. Few-Shot Radar HRRP Recognition Based on Improved Prototypical Network. In Proceedings of the IGARSS 2023—2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 5277–5280. [Google Scholar]
- Zhong, Y.; Lin, W.; Xu, Y.; Huang, L.; Huang, Y.; Ding, X. Contrastive Learning for Radar HRRP Recognition With Missing Aspects. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3504605. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; Volume 70, pp. 1126–1135. [Google Scholar]
- Yao, X.; Zhu, J.; Huo, G.; Xu, N.; Liu, X.; Zhang, C. Model-agnostic multi-stage loss optimization meta learning. Int. J. Mach. Learn. Cybern. 2021, 12, 2349–2363. [Google Scholar] [CrossRef]
- Antoniou, A.; Edwards, H.; Storkey, A. How to train your MAML. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yang, X.; Xu, J. Few-shot Classification with First-order Task Agnostic Meta-learning. In Proceedings of the 2022 3rd International Conference on Computer Vision, Image and Deep Learning & International Conference on Computer Engineering and Applications (CVIDL & ICCEA), Changchun, China, 20–22 May 2022; pp. 217–220. [Google Scholar]
- Liu, Q.; Zhang, X.; Liu, Y.; Huo, K.; Jiang, W.; Li, X. Few-Shot HRRP Target Recognition Based on Gramian Angular Field and Model-Agnostic Meta-Learning. In Proceedings of the 2021 IEEE 6th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 9–11 July 2021; pp. 6–10. [Google Scholar]
- Li, J.; Guo, W.; Wei, F.; Zhang, T.; Yu, W. Prior Information-Assisted Few-Shot HRRP Recognition Based on Task-Wise Shrinkage Quadratic Discriminant Analysis. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 9354–9368. [Google Scholar] [CrossRef]
- Tian, L.; Chen, B.; Guo, Z.; Du, C.; Peng, Y.; Liu, H. Open set HRRP recognition with few samples based on multi-modality prototypical networks. Signal Process. 2022, 193, 108391. [Google Scholar] [CrossRef]
- Cui, H.; Su, M.; Liu, J.; Liu, L. Template Construction of Radar Target Recognition based on Maximum Information Profile. J. Phys. Conf. Ser. 2022, 2284, 012021. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.-Y.; Zhao, F. Radar HRRP target recognition in amplitude spectrum subspace based on direct LDA. Syst. Eng. Electron. 2008, 30, 1815–1818. [Google Scholar]
- Du, L.; Wang, P.; Liu, H.; Pan, M.; Bao, Z. Radar HRRP target recognition based on dynamic multi-task hidden Markov model. In Proceedings of the 2011 IEEE RadarCon (RADAR), Kansas City, MO, USA, 23–27 May 2011; pp. 253–255. [Google Scholar]
- Pan, M.; Du, L.; Wang, P.; Liu, H.; Bao, Z. Noise-Robust Modification Method for Gaussian-Based Models With Application to Radar HRRP Recognition. IEEE Geosci. Remote Sens. Lett. 2013, 10, 558–562. [Google Scholar] [CrossRef]
- Huang, Z.; Wei, D.; Huang, Z.; Mao, H.; Li, X.; Huang, R.; Xu, P. Parameterized Local Maximum Synchrosqueezing Transform and its Application in Engineering Vibration Signal Processing. IEEE Access 2021, 9, 7732–7742. [Google Scholar] [CrossRef]
- Yu, G.; Wang, Z.; Zhao, P.; Li, Z. Local maximum synchrosqueezing transform: An energy-concentrated time-frequency analysis tool. Mech. Syst. Signal Process. 2019, 117, 537–552. [Google Scholar] [CrossRef]
- Chithra, K.R.; Sinith, M.S. A Comprehensive Study of Time-Frequency Analysis of Musical Signals. In Proceedings of the 2023 International Conference on Signal Processing, Computation, Electronics, Power and Telecommunication (IConSCEPT), Karaikal, India, 25–26 May 2023; pp. 1–5. [Google Scholar]
- Nabout, A.; Tibken, B. Object recognition using contour polygons and wavelet descriptors. In Proceedings of the 2004 International Conference on Information and Communication Technologies: From Theory to Applications, Damascus, Syria, 23 April 2004; pp. 473–474. [Google Scholar]
- Antony, L.T.; Kumar, S.N. Demystifying the Applications of Wavelet Transform in Bio Signal and Medical Data Processing. In Smart Trends in Computing and Communications; Senjyu, T., So-In, C., Joshi, A., Eds.; Springer Nature: Singapore, 2024; pp. 183–196. [Google Scholar]
- Rajput, G.K.; Murugan, R.; Tyagi, R.K. Wavelet Transformation Algorithm for Low Energy Data Aggregation. In Proceedings of the 2024 International Conference on Optimization Computing and Wireless Communication (ICOCWC), Debre Tabor, Ethiopia, 29–30 January 2024; pp. 1–7. [Google Scholar]
- Tang, Y. Mobile Communication De-noising Method Based on Wavelet Transform. In Big Data Analytics for Cyber-Physical System in Smart City; Atiquzzaman, M., Yen, N., Xu, Z., Eds.; Springer: Singapore, 2020; pp. 351–358. [Google Scholar]
- Huang, P.; Li, S.; Zheng, M.; Xie, J.; Tian, B.; Xu, S. Noise-robust HRRP target recognition based on residual scattering network. In Proceedings of the 2024 9th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 12–14 July 2024; pp. 37–41. [Google Scholar]
- Guo, C.; He, Y.; Wang, H.; Jian, T.; Sun, S. Radar HRRP target recognition based on deep one-dimensional residual-inception network. IEEE Access 2019, 7, 9191–9204. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3844–3852. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph attention networks. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Zhang, B.; Kannan, R.; Prasanna, V.; Busart, C. Accelerating GNN-based SAR automatic target recognition on HBM-enabled FPGA. In Proceedings of the 2023 IEEE High Performance Extreme Computing Conference (HPEC), Virtual, 25–29 September 2023; pp. 1–7. [Google Scholar]
- Dornaika, F.; Dahbi, R.; Bosaghzadeh, A.; Ruichek, Y. Efficient dynamic graph construction for inductive semi-supervised learning. Neural Netw. 2017, 94, 192–203. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, L.; Shi, D.; Cui, H.; Lu, X. Robust Unsupervised Multi-View Feature Learning With Dynamic Graph. IEEE Access 2019, 7, 72197–72209. [Google Scholar] [CrossRef]
- Yang, Y.; Yin, H.; Cao, J.; Chen, T.; Nguyen, Q.V.H.; Zhou, X.; Chen, L. Time-Aware Dynamic Graph Embedding for Asynchronous Structural Evolution. IEEE Trans. Knowl. Data Eng. 2023, 35, 9656–9670. [Google Scholar] [CrossRef]
- Li, Q.; Shang, Y.; Qiao, X.; Dai, W. Heterogeneous dynamic graph attention network. In Proceedings of the 2020 IEEE International Conference on Knowledge Graph (ICKG), Online, 9–11 August 2020; pp. 404–411. [Google Scholar]
- Bao, T.; Jia, X.; Zwart, J.; Sadler, J.; Appling, A.; Oliver, S.; Johnson, T.T. Partial differential equation driven dynamic graph networks for predicting stream water temperature. In Proceedings of the 2021 IEEE International Conference on Data Mining (ICDM), Auckland, New Zealand, 7–10 December 2021; pp. 11–20. [Google Scholar]
- Xu, X.; Xu, Y.; Zhang, Z.; Gong, K.; Dong, L.; Ma, L. Traffic control gesture recognition based on masked decoupling adaptive graph convolution network. In Proceedings of the American Society of Civil Engineers, Chicago, IL, USA, 18–21 October 2023; pp. 87–96. [Google Scholar]
- Wang, J.; Xiong, H.; Gong, Y.; Wu, X.; Wang, S.; Jia, Q.; Lai, Z. Attention-based dynamic graph CNN for point cloud classification. In Artificial Intelligence and Robotics; Yang, S., Lu, H., Eds.; Springer Nature: Singapore, 2022; pp. 357–365. [Google Scholar]
- Wu, Y.; Fang, Y.; Liao, L. On the feasibility of simple transformer for dynamic graph modeling. In Proceedings of the ACM Web Conference 2024, Virtual, 13–17 May 2024; pp. 870–880. [Google Scholar]
- Hoang, T.-L.; Ta, V.-C. Dynamic-GTN: Learning an node efficient embedding in dynamic graph with transformer. In PRICAI 2022: Trends in Artificial Intelligence; Khanna, S., Cao, J., Bai, Q., Xu, G., Eds.; Springer Nature: Cham, Switzerland, 2022; pp. 430–443. [Google Scholar]
- Wang, D.; Cheng, Y.; Yu, M.; Guo, X.; Zhang, T. A hybrid approach with optimization-based and metric-based meta-learner for few-shot learning. Neurocomputing 2019, 349, 202–211. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Yang, X.; Dong, C.; Tian, P.; Qin, T.; Huo, J.; Shi, Y.; Wang, L.; Gao, Y.; et al. LibFewShot: A Comprehensive Library for Few-Shot Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 14938–14955. [Google Scholar] [CrossRef]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Kavukcuoglu, K.; Wierstra, D. Matching networks for one shot learning. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Changsha, China, 20–23 November 2016; pp. 3637–3645. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4080–4090. [Google Scholar]
- Nichol, A.; Schulman, J. Reptile: A Scalable Metalearning Algorithm. arXiv 2018, arXiv:1803.02999. [Google Scholar]
- Li, Z.; Zhou, F.; Chen, F.; Li, H. Meta-SGD: Learning to learn quickly for few shot learning. arXiv 2017, arXiv:1707.09835. [Google Scholar]
- Raghu, A.; Raghu, M.; Bengio, S.; Vinyals, O. Rapid learning or feature reuse? Towards understanding the effectiveness of MAML. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Luo, H.; Li, Y.; Yang, Z.; Huang, J.; Han, T.; Xia, J. Few-shot SAR target classification via instance-level awareness contrastive learning. In Proceedings of the 2024 IEEE 2nd International Conference on Electrical, Automation and Computer Engineering (ICEACE), Changchun, China, 29–31 December 2024; pp. 159–164. [Google Scholar]
- Tai, Y.; Tan, Y.; Xiong, S.; Sun, Z.; Tian, J. Few-shot transfer learning for SAR image classification without extra SAR samples. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2240–2253. [Google Scholar] [CrossRef]
- Gurbuz, S.; Erol, B.; Amin, M.; Seyfioğlu, M. Data-driven cepstral and neural learning of features for robust micro-doppler classification. In Proceedings of the Radar Sensor Technology XXII, Orlando, FL, USA, 16–18 April 2018; p. 18. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All you Need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Lagergren, J.; Flores, K.; Gilman, M.; Tsynkov, S. Deep learning approach to the detection of scattering delay in radar images. J. Stat. Theory Pract. 2020, 15, 14. [Google Scholar] [CrossRef]
- Cai, T.; Luo, S.; Xu, K.; He, D.; Liu, T.-Y.; Wang, L. GraphNorm: A principled approach to accelerating graph neural network training. In Proceedings of the 38th International Conference on Machine Learning, Online, 18–24 July 2021; pp. 1204–1215. [Google Scholar]
- Skryagin, A.; Divo, F.; Ali, M.A.; Dhami, D.S.; Kersting, K. Graph neural networks need cluster-normalize-activate modules. Adv. Neural Inf. Process. Syst. 2024, 37, 79819–79842. [Google Scholar]
- Shui, P.-L.; Liu, H.-W.; Bao, Z. Range-spread target detection based on cross time-frequency distribution features of two adjacent received signals. IEEE Trans. Signal Process. 2009, 57, 3733–3745. [Google Scholar] [CrossRef]
- Guo, K.-Y.; Sheng, X.-Q.; Shen, R.-H.; Jing, C.-J. Influence of migratory scattering phenomenon on micro-motion characteristics contained in radar signals. IET Radar Sonar Navig. 2013, 7, 579–589. [Google Scholar] [CrossRef]
- Chen, J.; Yuan, W.; Chen, S.; Hu, Z.; Li, P. Evo-MAML: Meta-learning with evolving gradient. Electronics 2023, 12, 3865. [Google Scholar] [CrossRef]
- Li, S.; Wang, Z.; Narayan, A.; Kirby, R.; Zhe, S. Meta-learning with adjoint methods. In Proceedings of the 26th International Conference on Artificial Intelligence and Statistics, Valencia, Spain, 25–27 April 2023; pp. 7239–7251. [Google Scholar]
- Yu, L.; Li, X.; Zhang, P.; Zhang, Z.; Dunkin, F. Enabling few-shot learning with PID control: A layer adaptive optimizer. In Proceedings of the 41st International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024; pp. 57544–57558. [Google Scholar]
- Liu, Q.; Zhang, X.; Liu, Y. Attribute-informed and similarity-enhanced zero-shot radar target recognition. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 7337–7354. [Google Scholar] [CrossRef]
- Rihaczek, A.W.; Hershkowitz, S.J. Man-made target backscattering behavior: Applicability of conventional radar resolution theory. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 809–824. [Google Scholar] [CrossRef]
- Rihaczek, A.W.; Hershkowitz, S.J. Theory and Practice of Radar Target Identification; Artech House: Boston, MA, USA, 2000. [Google Scholar]
- Baxter, J. A model of inductive bias learning. J. Artif. Intell. Res. 2000, 12, 149–198. [Google Scholar] [CrossRef]
- Bousquet, O.; Elisseeff, A. Stability and generalization. J. Mach. Learn. Res. 2002, 2, 499–526. [Google Scholar]
- Maurer, A.; Pontil, M.; Romera-Paredes, B. The benefit of multitask representation learning. J. Mach. Learn. Res. 2016, 17, 2853–2884. [Google Scholar]
- Tripuraneni, N.; Jin, C.; Jordan, M. Provable meta-learning of linear representations. In Proceedings of the 38th International Conference on Machine Learning, Online, 18–24 July 2021; pp. 10434–10443. [Google Scholar]
- Rajeswaran, A.; Finn, C.; Kakade, S.M.; Levine, S. Meta-learning with implicit gradients. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 113–124. [Google Scholar]
- Li, D.; Zhang, J.; Yang, Y.; Liu, C.; Song, Y.-Z.; Hospedales, T. Episodic training for domain generalization. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1446–1455. [Google Scholar]
- Achille, A.; Lam, M.; Tewari, R.; Ravichandran, A.; Maji, S.; Fowlkes, C.; Soatto, S.; Perona, P. Task2Vec: Task embedding for meta-learning. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6429–6438. [Google Scholar]
- Du, S.S.; Hu, W.; Kakade, S.M.; Lee, J.D.; Lei, Q. Few-shot learning via learning the representation, provably. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).