MissPred: A Robust Two-Stage Radar Echo Extrapolation Algorithm for Incomplete Sequences
Abstract
1. Introduction
- A two-stage training strategy is proposed that allows for reliable extrapolation without introducing cumulative errors in the model cascade when the input sequence contains missing frames.
- In order to recover the missing spatiotemporal information of the input sequence, this paper proposes a parallel structure consisting of a raw sequence encoder and a differential encoder. The raw sequence encoder extracts the spatiotemporal characteristics of the sequence, while the differential encoder extracts the echo variation characteristics between frames.
- This paper presents a novel dual-path adaptive fusion module that has been specifically designed for missing data scenarios. The module features branch-specific channel attention, which enables the dynamic reweighting of complementary features from both encoders. These features are then concatenated and integrated through dual-pooling, with the aim of achieving robust spatial fusion.
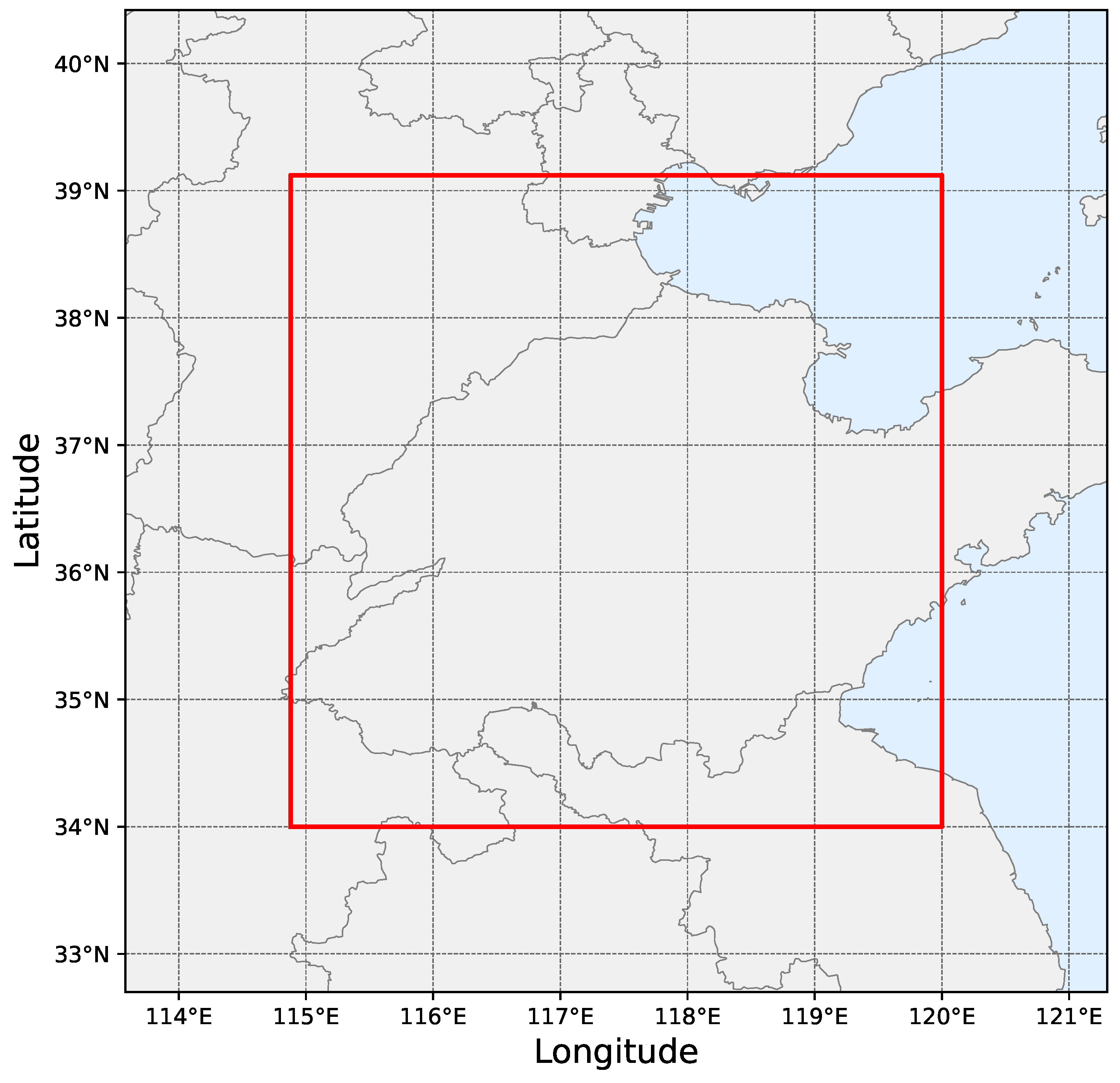
2. Data
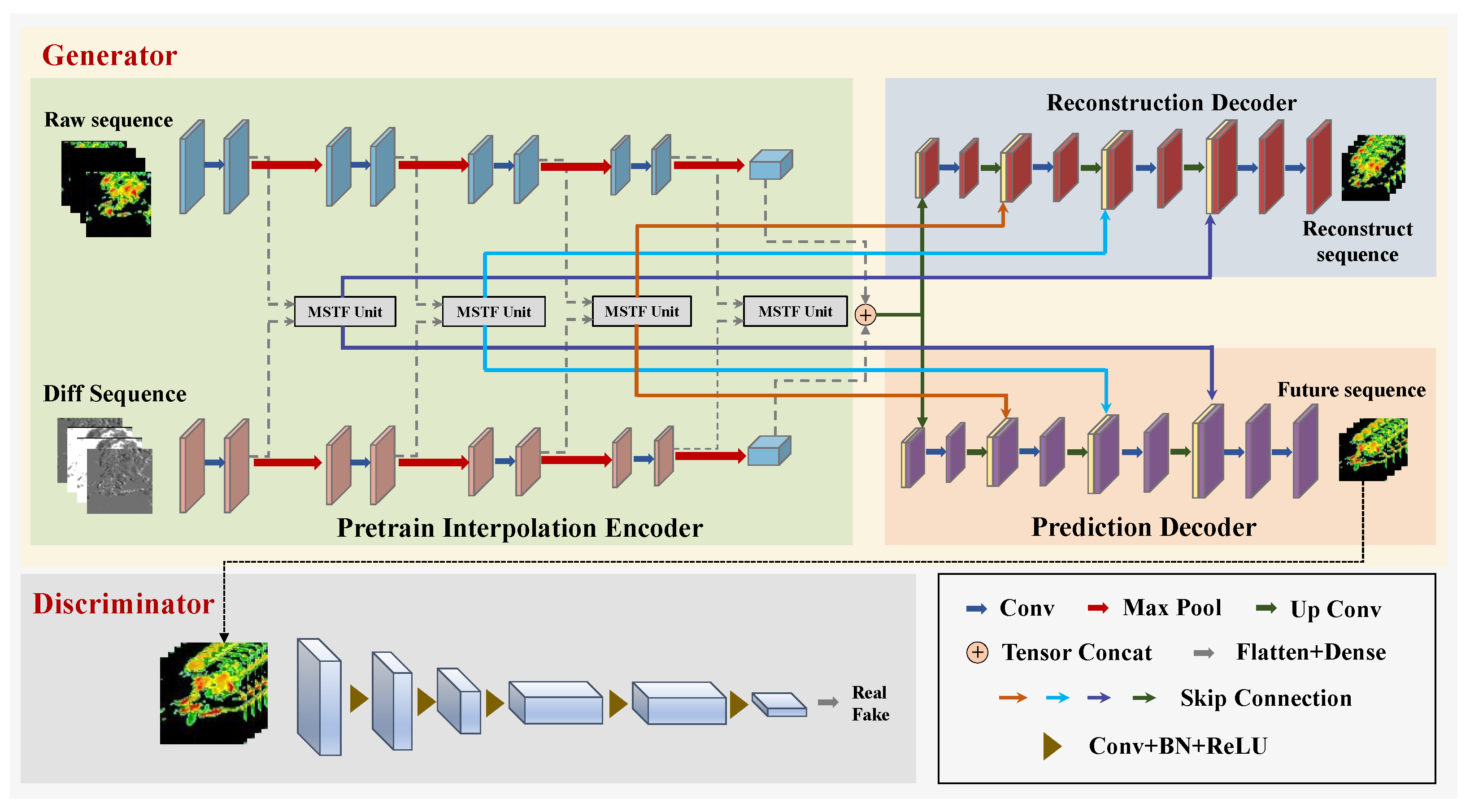
3. Method
3.1. Description of Tasks
3.2. Pretrain Interpolation Encoder
3.3. Dual-Branch Decoder
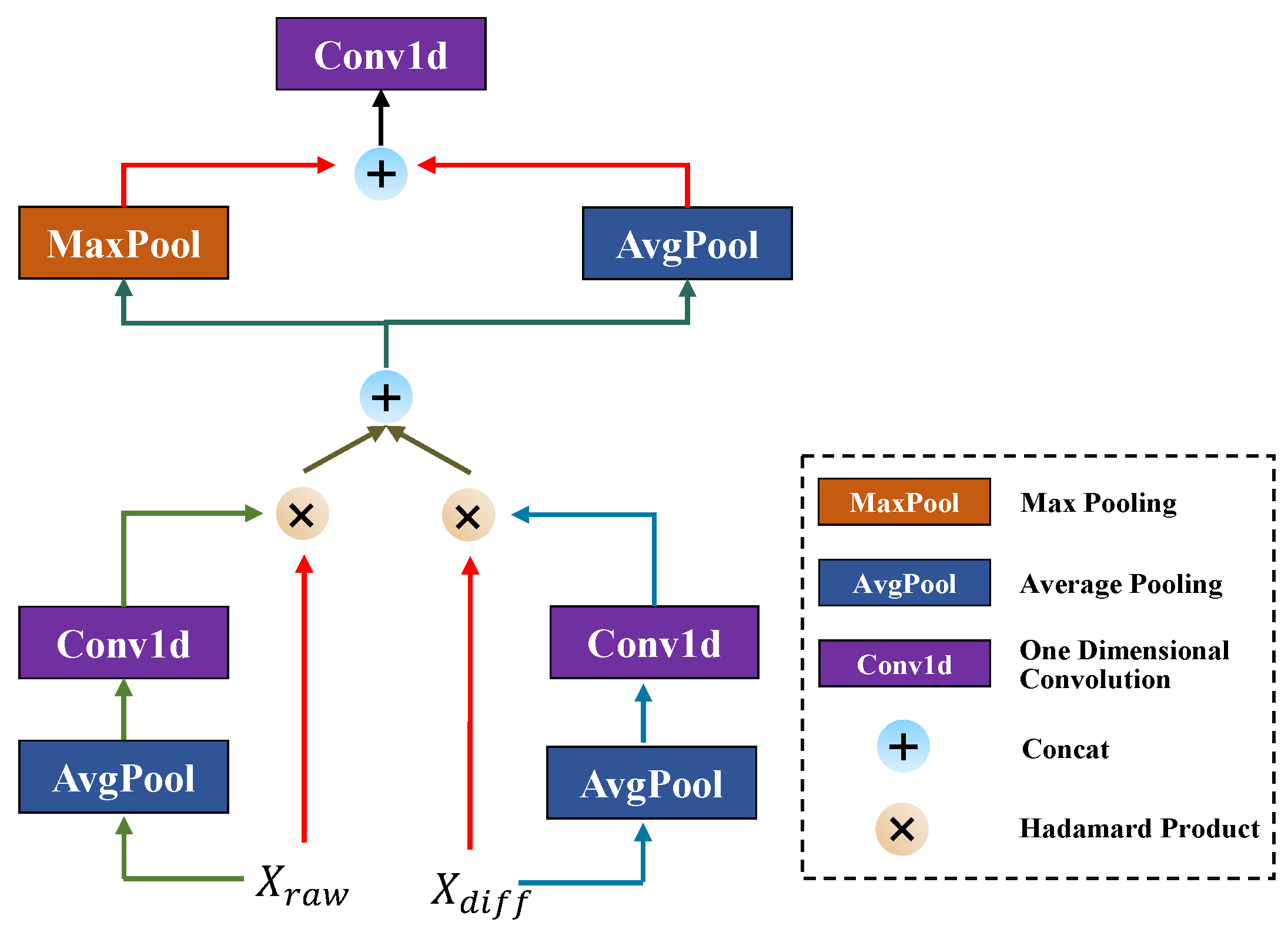
3.4. Missing Spatiotemporal Fusion Block
3.5. Adversarial Training
3.6. Training Strategy
| Algorithm 1 Training scheme. |
Input: Missing radar sequence , differential radar sequence Output: Predicted future sequences 1: Initialize the encoder parameters and decoder parameter of the pretrained model 2: for to Epoch do 3: for to Iteration do 4: 5: 6: Update the 7: end for 8: end for 9: Freeze parameter , initialize the decoder parameters and discriminator parameters 10: for to Epoch do 11: for to Iteration do 12: 13: Calculate the discriminator loss 14: Update the 15: if then 16: Calculate the generator loss 17: Update the 18: end if 19: end for 20: end for 21: return G |
3.7. Evaluation Metrics
- (1)
- MSE
- (2)
- PSNR
- (3)
- SSIM
- (4)
- CSI
- (5)
- POD
4. Experiments and Analysis
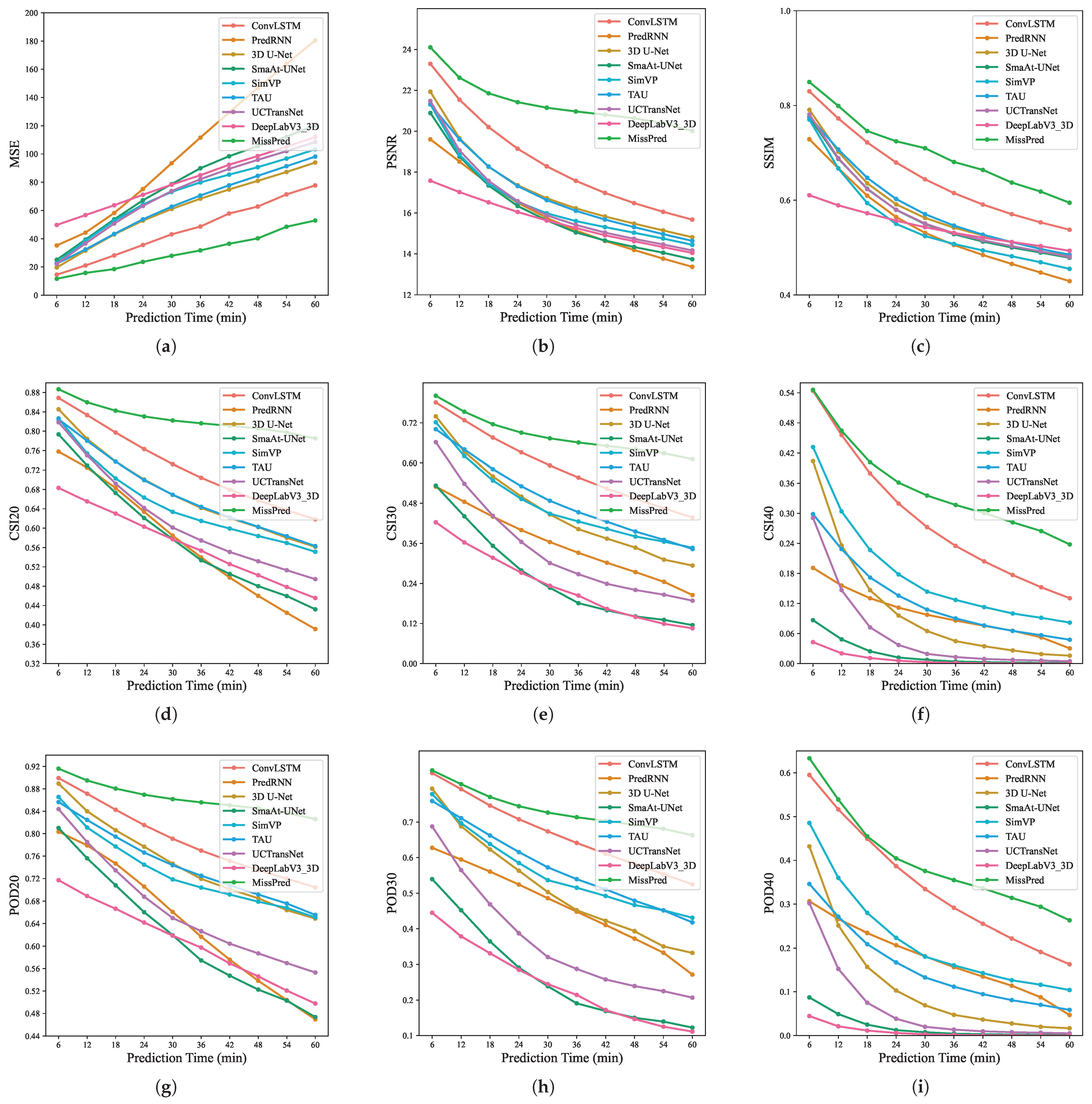
4.1. Quantitative Comparison
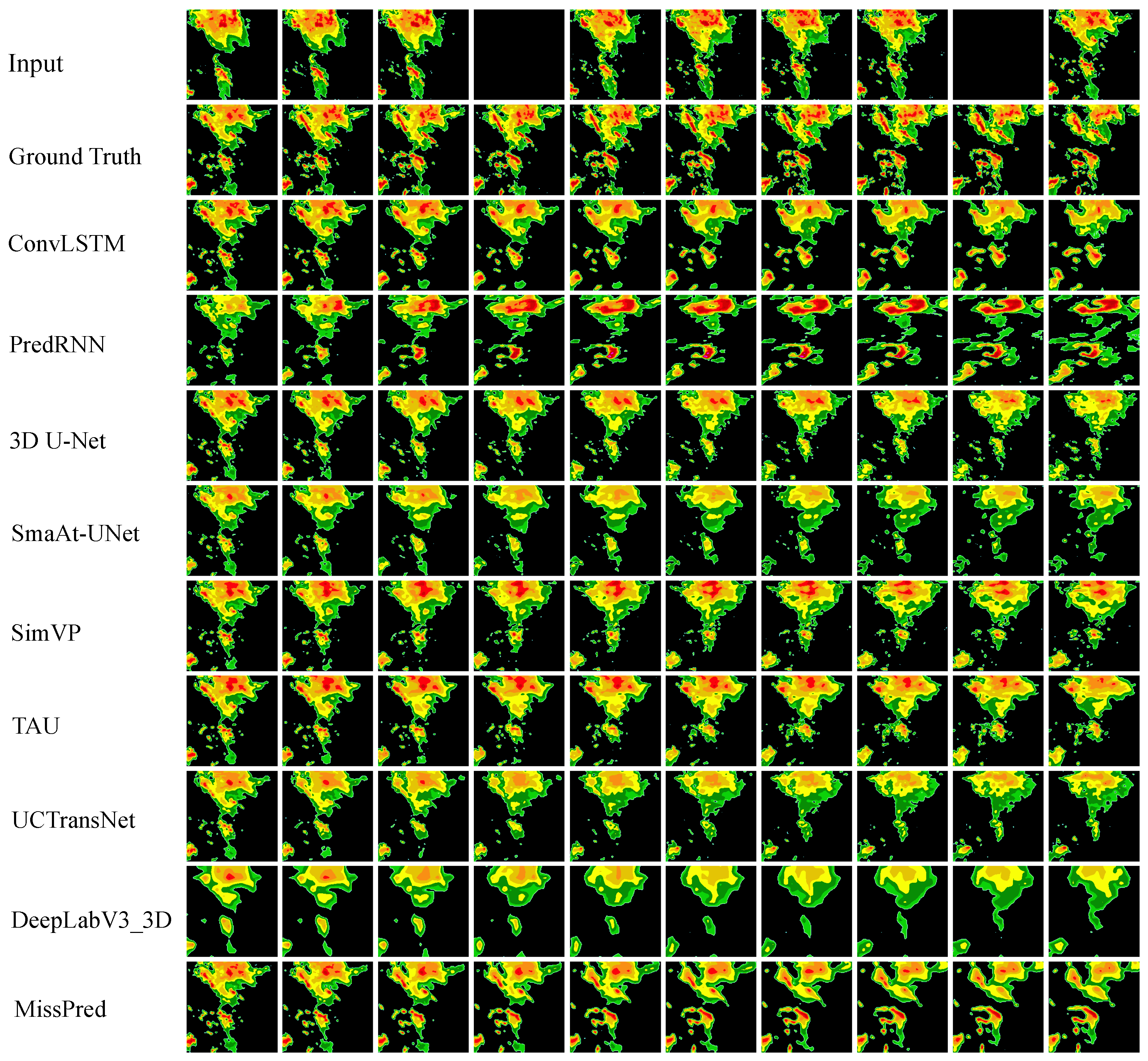
4.2. Visual Comparison
- (1)
- MR = 0.2
- (2)
- MR = 0.5
- (3)
- MR from 0.1 to 0.5.
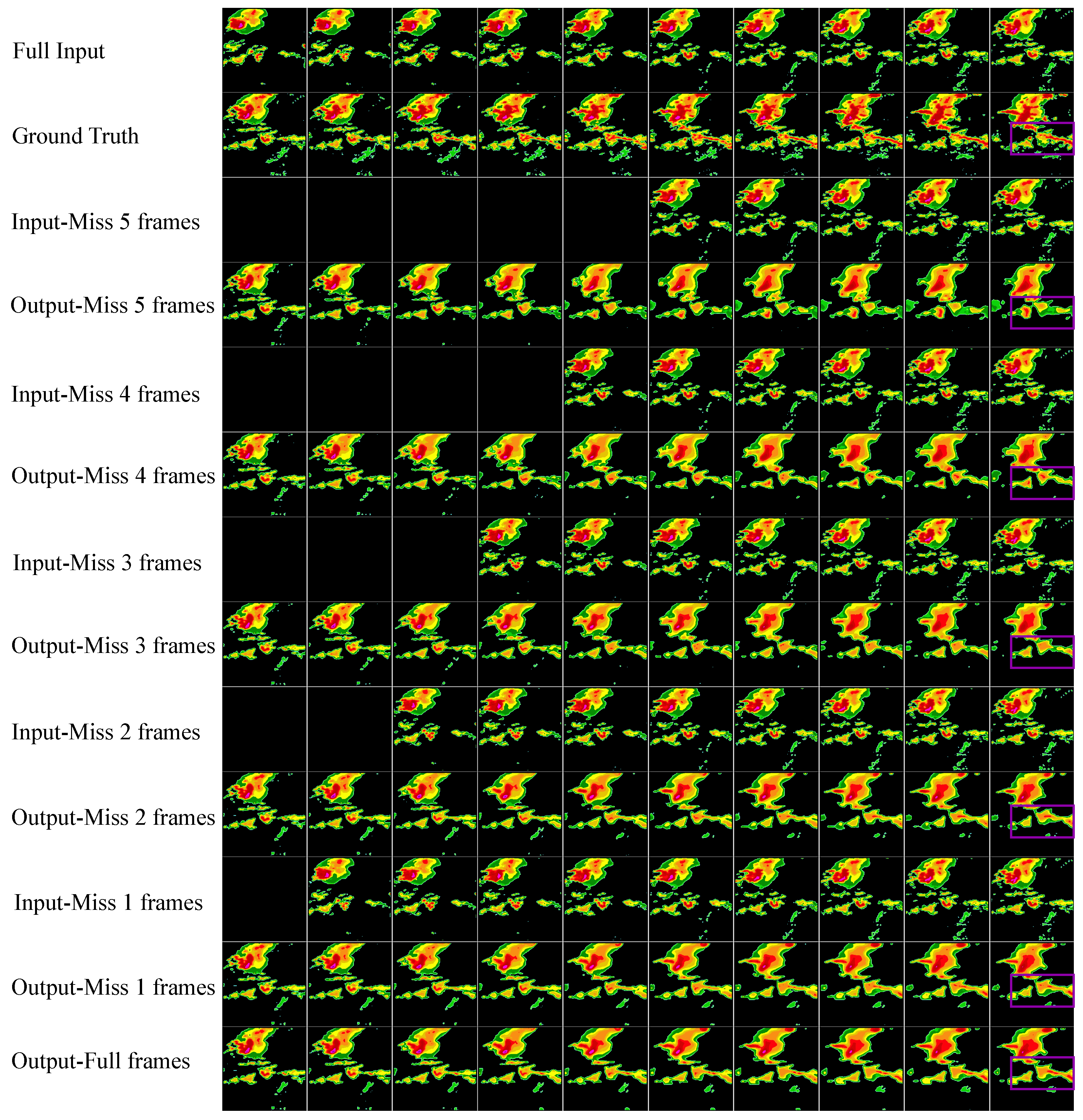
4.3. Robustness Verification
4.4. Ablation Study
5. Conclusions
- The two-stage training strategy can avoid the cumulative error of the cascade structure and improve the prediction accuracy of the radar echoes by sharing the encoder parameters.
- The difference sequence can reconstruct the missing information from coarse grains. Difference-based sequences can recover image details from a fine-grained level by reconstructing the echo evolution between frames. The two-branch feature fusion structure can effectively improve the encoder’s ability to complement information.
- The proposed MSTF module can effectively integrate the spatiotemporal features of the original and differential sequences to enhance the feature extraction capability of the model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, W.; Pang, L.; Sheng, V.S.; Wang, Q. STUNNER: Radar echo extrapolation model based on spatiotemporal fusion neural network. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5103714. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Song, Y.; Liang, S.; Xia, M.; Zhang, Q. Lightning nowcasting based on high-density area and extrapolation utilizing long-range lightning location data. Atmos. Res. 2025, 321, 108070. [Google Scholar] [CrossRef]
- Pei, Y.; Li, Q.; Zhang, L.; Sun, N.; Jing, J.; Ding, Y. MPFNet: Multi-product Fusion Network for Radar Echo Extrapolation. IEEE Trans. Geosci. Remote Sens. 2024, 62. [Google Scholar] [CrossRef]
- Sokol, Z. Assimilation of extrapolated radar reflectivity into a NWP model and its impact on a precipitation forecast at high resolution. Atmos. Res. 2011, 100, 201–212. [Google Scholar] [CrossRef]
- Wang, G.; Wong, W.-K.; Hong, Y.; Liu, L.; Dong, J.; Xue, M. Improvement of forecast skill for severe weather by merging radar-based extrapolation and storm-scale NWP corrected forecast. Atmos. Res. 2015, 154, 14–24. [Google Scholar] [CrossRef]
- Ridal, M.; Lindskog, M.; Gustafsson, N.; Haase, G. Optimized advection of radar reflectivities. Atmos. Res. 2011, 100, 213–225. [Google Scholar] [CrossRef]
- Gao, Z.; Tan, C.; Wu, L.; Li, S.Z. Simvp: Simpler yet better video prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 3170–3180. [Google Scholar]
- Geng, H.; Zhao, H.; Shi, Z.; Wu, F.; Geng, L.; Ma, K. MBFE-UNet: A Multi-Branch Feature Extraction UNet with Temporal Cross Attention for Radar Echo Extrapolation. Remote Sens. 2024, 16, 3956. [Google Scholar] [CrossRef]
- Li, J.; Li, L.; Zhang, T.; Xing, H.; Shi, Y.; Li, Z.; Wang, C.; Liu, J. Flood forecasting based on radar precipitation nowcasting using U-net and its improved models. J. Hydrol. 2024, 632, 130871. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015; Volume 28. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Yang, Z.; Wu, H.; Liu, Q.; Liu, X.; Zhang, Y.; Cao, X. A self-attention integrated spatiotemporal LSTM approach to edge-radar echo extrapolation in the Internet of Radars. ISA Trans. 2023, 132, 155–166. [Google Scholar] [CrossRef]
- Chen, S.; Shu, T.; Zhao, H.; Zhong, G.; Chen, X. TempEE: Temporal-Spatial Parallel Transformer for Radar Echo Extrapolation Beyond Autoregression. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5108914. [Google Scholar] [CrossRef]
- Xu, L.; Lu, W.; Yu, H.; Yao, F.; Sun, X.; Fu, K. SFTformer: A Spatial-Frequency-Temporal Correlation-Decoupling Transformer for Radar Echo Extrapolation. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4102415. [Google Scholar] [CrossRef]
- Guo, S.; Sun, N.; Pei, Y.; Li, Q. 3D-UNet-LSTM: A Deep Learning-Based Radar Echo Extrapolation Model for Convective Nowcasting. Remote Sens. 2023, 15, 1529. [Google Scholar] [CrossRef]
- Li, Q.; Jing, J.; Ma, L.; Chen, L.; Guo, S.; Chen, H. A Deep Contrastive Model for Radar Echo Extrapolation. IEEE Geosci. Remote Sens. Lett. 2024, 22, 3500705. [Google Scholar] [CrossRef]
- He, G.; Qu, H.; Luo, J.; Cheng, Y.; Wang, J.; Zhang, P. An Long Short-Term Memory Model with Multi-Scale Context Fusion and Attention for Radar Echo Extrapolation. Remote Sens. 2024, 16, 376. [Google Scholar] [CrossRef]
- Zheng, C.; Tao, Y.; Zhang, J.; Xun, L.; Li, T.; Yan, Q. TISE-LSTM: A LSTM model for precipitation nowcasting with temporal interactions and spatial extract blocks. Neurocomputing 2024, 590, 127700. [Google Scholar] [CrossRef]
- Tan, Y.; Zhang, T.; Li, L.; Li, J. Radar-Based Precipitation Nowcasting Based on Improved U-Net Model. Remote Sens. 2024, 16, 1681. [Google Scholar] [CrossRef]
- Liu, J.; Qian, X.; Peng, L.; Lou, D.; Li, Y. TEDR: A spatiotemporal attention radar extrapolation network constrained by optical flow and distribution correction. Atmos. Res. 2024, 311, 107702. [Google Scholar] [CrossRef]
- Niu, D.; Li, Y.; Wang, H.; Zang, Z.; Jiang, M.; Chen, X. FsrGAN: A satellite and radar-based fusion prediction network for precipitation nowcasting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 7002–7013. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Hu, W.; Bai, C. RainHCNet: Hybrid High-Low Frequency and Cross-Scale Network for Precipitation Nowcasting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 8923–8937. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, H.; Liu, T.; Yao, L.; Zhou, C. A Patch-wise Mechanism for Enhancing Sparse Radar Echo Extrapolation in Precipitation Nowcasting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 8138–8150. [Google Scholar] [CrossRef]
- Wang, C.; Wang, P.; Wang, P.; Xue, B.; Wang, D. Using Conditional Generative Adversarial 3-D Convolutional Neural Network for Precise Radar Extrapolation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5735–5749. [Google Scholar] [CrossRef]
- Vandal, T.J.; Nemani, R.R. Temporal Interpolation of Geostationary Satellite Imagery With Optical Flow. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 3245–3254. [Google Scholar] [CrossRef]
- Miller, L.; Pelletier, C.; Webb, G.I. Deep learning for satellite image time-series analysis: A review. IEEE Geosci. Remote Sens. Mag. 2024, 12, 81–124. [Google Scholar] [CrossRef]
- Tuheti, A.; Dong, Z.; Li, G.; Deng, S.; Li, Z.; Li, L. Spatiotemporal imputation of missing aerosol optical depth using hybrid machine learning with downscaling. Atmos. Environ. 2025, 343, 120989. [Google Scholar] [CrossRef]
- Si, J.; Chen, H.; Han, L. Enhancing Weather Radar Reflectivity Emulation From Geostationary Satellite Data Using Dynamic Residual Convolutional Network. IEEE Trans. Geosci. Remote Sens. 2025, 63, 4201711. [Google Scholar] [CrossRef]
- Yu, X.; Lou, X.; Yan, Y.; Yan, Z.; Cheng, W.; Wang, Z.; Zhao, D.; Xia, J. Radar Echo Reconstruction in Oceanic Area via Deep Learning of Satellite Data. Remote Sens. 2023, 15, 3065. [Google Scholar] [CrossRef]
- Gong, A.; Chen, H.; Ni, G. Improving the Completion of Weather Radar Missing Data with Deep Learning. Remote Sens. 2023, 15, 4568. [Google Scholar] [CrossRef]
- Wen, L.; Gao, L.; Li, X. A New Deep Transfer Learning Based on Sparse Auto-Encoder for Fault Diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 136–144. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2019, 63, 139–144. [Google Scholar] [CrossRef]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2016, Athens, Greece, 17–21 October 2016; Springer: Cham, Switzerland, 2016; pp. 424–432. [Google Scholar]
- Trebing, K.; Staṅczyk, T.; Mehrkanoon, S. SmaAt-UNet: Precipitation nowcasting using a small attention-UNet architecture. Pattern Recogn. Lett. 2021, 145, 178–186. [Google Scholar] [CrossRef]
- Tan, C.; Gao, Z.; Wu, L.; Xu, Y.; Xia, J.; Li, S.; Li, S.Z. Temporal attention unit: Towards efficient spatiotemporal predictive learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 18770–18782. [Google Scholar]
- Wang, H.; Cao, P.; Wang, J.; Zaiane, O.R. Uctransnet: Rethinking the skip connections in u-net from a channel-wise perspective with transformer. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022; pp. 2441–2449. [Google Scholar]
- Yurtkulu, S.C.; Şahin, Y.H.; Unal, G. Semantic segmentation with extended DeepLabv3 architecture. In Proceedings of the 27th Signal Processing and Communications Applications Conference (SIU), Sivas, Turkey, 24–26 April 2019; pp. 1–4. [Google Scholar]



| Model | MSE ↓ | SSIM ↑ | PSNR ↑ | CSI ↑ | POD ↑ | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 20 dBZ | 30 dBZ | 40 dBZ | 20 dBZ | 30 dBZ | 40 dBZ | |||||
| ConvLSTM | 37.0038 | 0.6981 | 22.7454 | 0.8028 | 0.6152 | 0.3015 | 0.8123 | 0.6847 | 0.3597 | |
| PredRNN | 31.3015 | 0.6858 | 23.5585 | 0.7918 | 0.6415 | 0.3118 | 0.8248 | 0.6948 | 0.3699 | |
| 3D U-Net | 26.0024 | 0.7088 | 24.3152 | 0.8157 | 0.6582 | 0.3122 | 0.8328 | 0.7092 | 0.3742 | |
| SmaAt-UNet | 27.2027 | 0.7061 | 24.1228 | 0.8045 | 0.6248 | 0.3082 | 0.8294 | 0.6882 | 0.3648 | |
| SimVP | 24.5026 | 0.7195 | 24.5851 | 0.8029 | 0.6681 | 0.3157 | 0.8311 | 0.7218 | 0.3790 | |
| TAU | 27.1768 | 0.7124 | 24.1241 | 0.8048 | 0.6658 | 0.3098 | 0.8324 | 0.7133 | 0.3672 | |
| UCTransNet | 23.5015 | 0.7328 | 24.7520 | 0.8158 | 0.6702 | 0.3492 | 0.8510 | 0.7305 | 0.3825 | |
| DeepLabV3_3D | 29.5032 | 0.7018 | 23.8285 | 0.7745 | 0.6328 | 0.2983 | 0.8105 | 0.6910 | 0.3548 | |
| MissPred | 21.2227 | 0.7414 | 25.3985 | 0.8257 | 0.6829 | 0.3510 | 0.8637 | 0.7348 | 0.3904 | |
| Model | MSE ↓ | SSIM ↑ | PSNR ↑ | CSI ↑ | POD ↑ | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 20 dBZ | 30 dBZ | 40 dBZ | 20 dBZ | 30 dBZ | 40 dBZ | |||||
| ConvLSTM | 46.4901 | 0.6516 | 21.6184 | 0.7291 | 0.5886 | 0.2870 | 0.7900 | 0.6672 | 0.3471 | |
| PredRNN | 103.8467 | 0.5434 | 18.3258 | 0.5698 | 0.3576 | 0.0997 | 0.6401 | 0.4628 | 0.1734 | |
| 3D U-Net | 61.3635 | 0.5844 | 20.4058 | 0.6742 | 0.4609 | 0.1088 | 0.7477 | 0.5123 | 0.1161 | |
| SmaAt-UNet | 79.0693 | 0.5726 | 19.4782 | 0.5805 | 0.2561 | 0.0192 | 0.6175 | 0.2658 | 0.0194 | |
| SimVP | 70.7463 | 0.5514 | 19.8457 | 0.6498 | 0.4754 | 0.1798 | 0.7310 | 0.5592 | 0.2179 | |
| TAU | 63.7063 | 0.5872 | 20.2200 | 0.6726 | 0.4929 | 0.1278 | 0.7441 | 0.5719 | 0.1543 | |
| UCTransNet | 72.4601 | 0.5746 | 19.7851 | 0.6168 | 0.3431 | 0.0608 | 0.6642 | 0.3646 | 0.0631 | |
| DeepLabV3_3D | 81.2753 | 0.5433 | 19.3582 | 0.5665 | 0.2340 | 0.0086 | 0.6064 | 0.2454 | 0.0089 | |
| MissPred | 21.2227 | 0.7414 | 25.3985 | 0.8257 | 0.6829 | 0.3510 | 0.8637 | 0.7348 | 0.3904 | |
| Pretrain | Diff-Branch | MSTF | Discriminator | MSE | SSIM | PSNR | CSI | POD |
|---|---|---|---|---|---|---|---|---|
| × | ✓ | ✓ | ✓ | 53.8457 | 0.6183 | 21.0854 | 0.4872 | 0.5275 |
| ✓ | × | ✓ | ✓ | 41.3586 | 0.6482 | 22.1687 | 0.5296 | 0.5984 |
| ✓ | ✓ | × | ✓ | 33.4896 | 0.6648 | 22.9870 | 0.5358 | 0.6158 |
| ✓ | ✓ | ✓ | × | 24.6859 | 0.7259 | 24.3841 | 0.5782 | 0.6570 |
| Full | ✓ | ✓ | ✓ | 21.2227 | 0.7414 | 25.3985 | 0.6199 | 0.6630 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Duan, C.; Song, L.; Zhang, Q.; Zhu, W.; Liu, Y. MissPred: A Robust Two-Stage Radar Echo Extrapolation Algorithm for Incomplete Sequences. Remote Sens. 2025, 17, 2066. https://doi.org/10.3390/rs17122066
Zhao Z, Duan C, Song L, Zhang Q, Zhu W, Liu Y. MissPred: A Robust Two-Stage Radar Echo Extrapolation Algorithm for Incomplete Sequences. Remote Sensing. 2025; 17(12):2066. https://doi.org/10.3390/rs17122066
Chicago/Turabian StyleZhao, Ziqi, Chunxu Duan, Lin Song, Qilin Zhang, Wenda Zhu, and Yi Liu. 2025. "MissPred: A Robust Two-Stage Radar Echo Extrapolation Algorithm for Incomplete Sequences" Remote Sensing 17, no. 12: 2066. https://doi.org/10.3390/rs17122066
APA StyleZhao, Z., Duan, C., Song, L., Zhang, Q., Zhu, W., & Liu, Y. (2025). MissPred: A Robust Two-Stage Radar Echo Extrapolation Algorithm for Incomplete Sequences. Remote Sensing, 17(12), 2066. https://doi.org/10.3390/rs17122066







