Comparison and Evaluation of Rain Gauge, CMORPH, TRMM PR and GPM DPR KuPR Precipitation Products over South China
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
3. Results
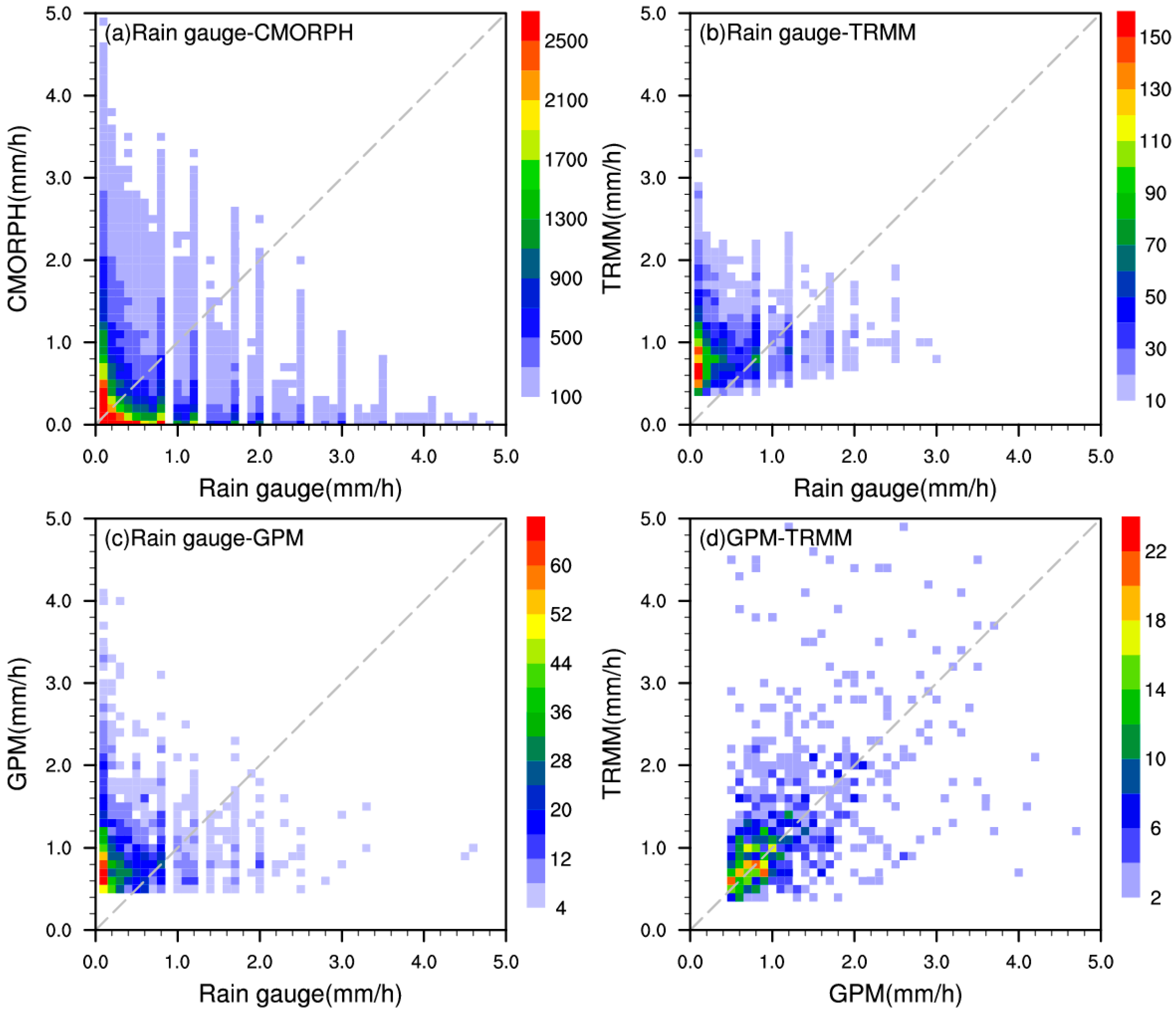
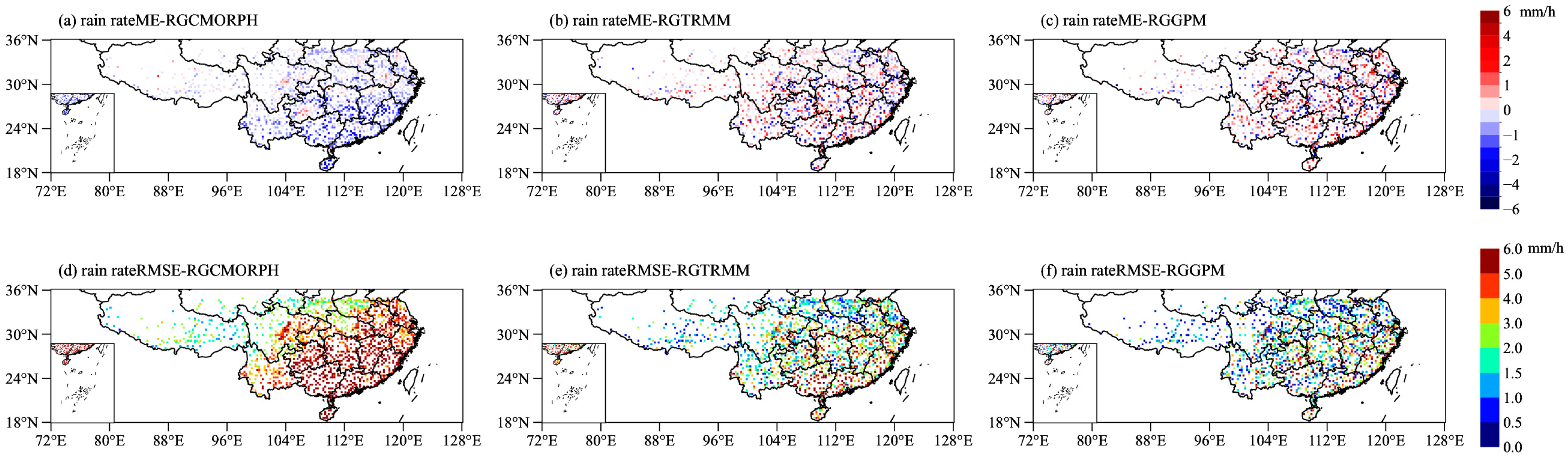
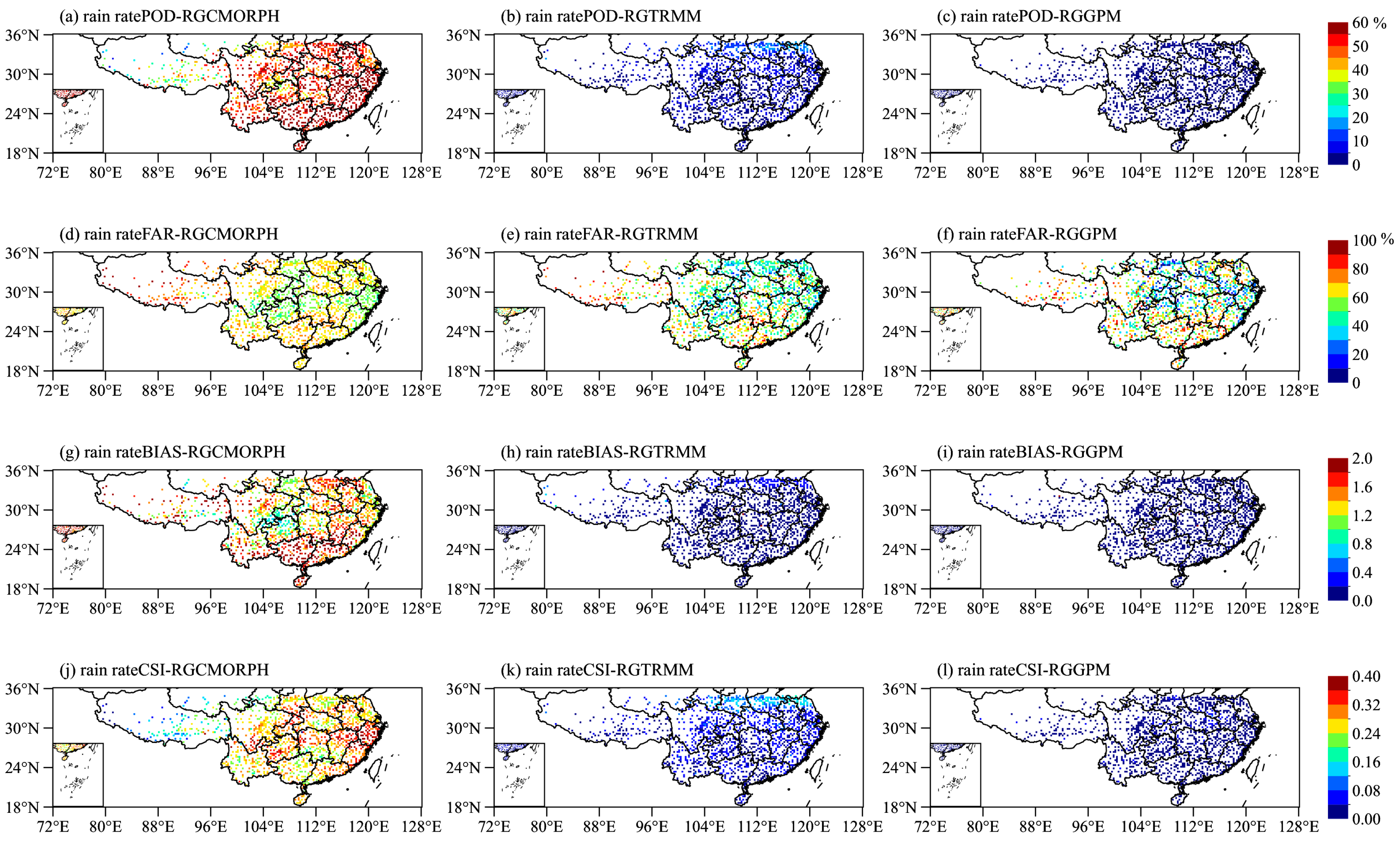
3.1. Spatial Distribution Characteristics of Precipitation from Rain Gauge, CMORPH, TRMM PR and GPM KuPR
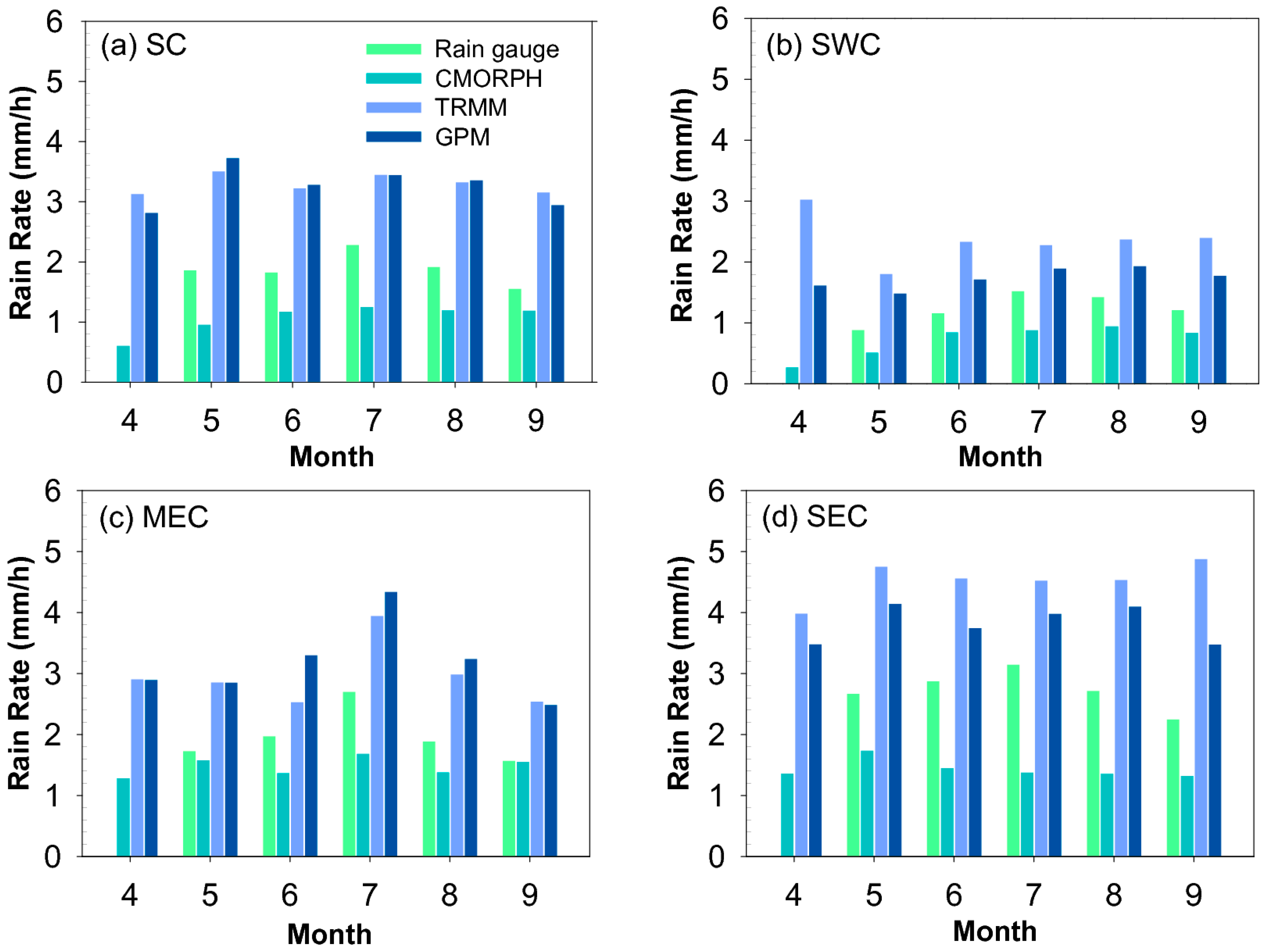
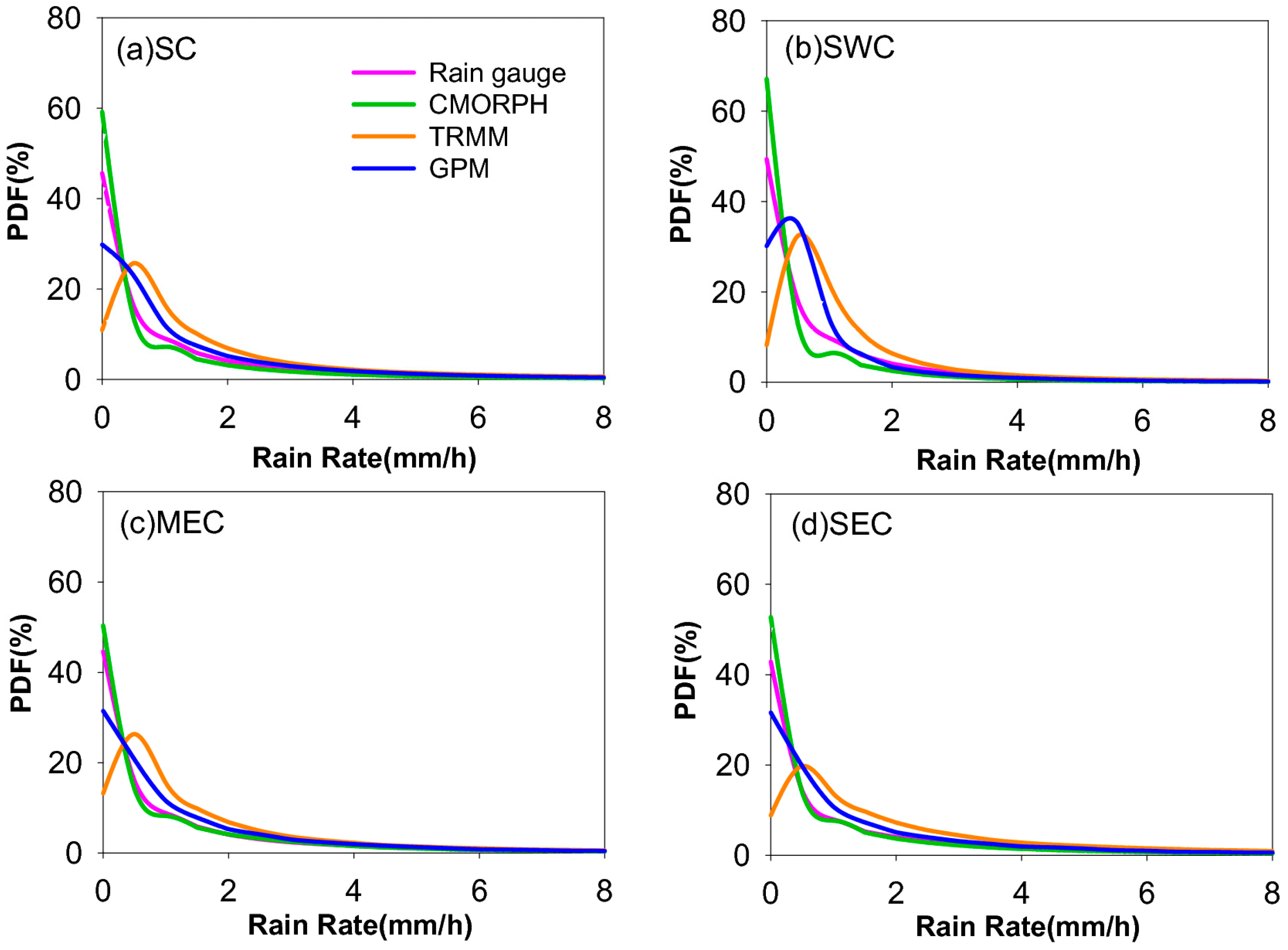
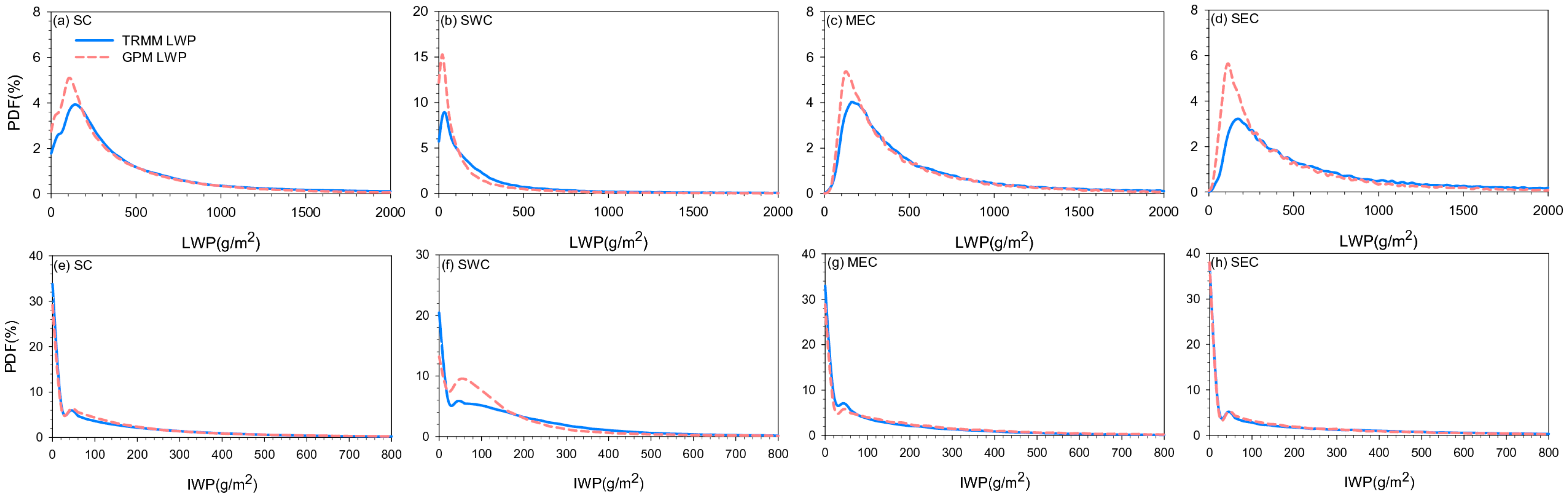
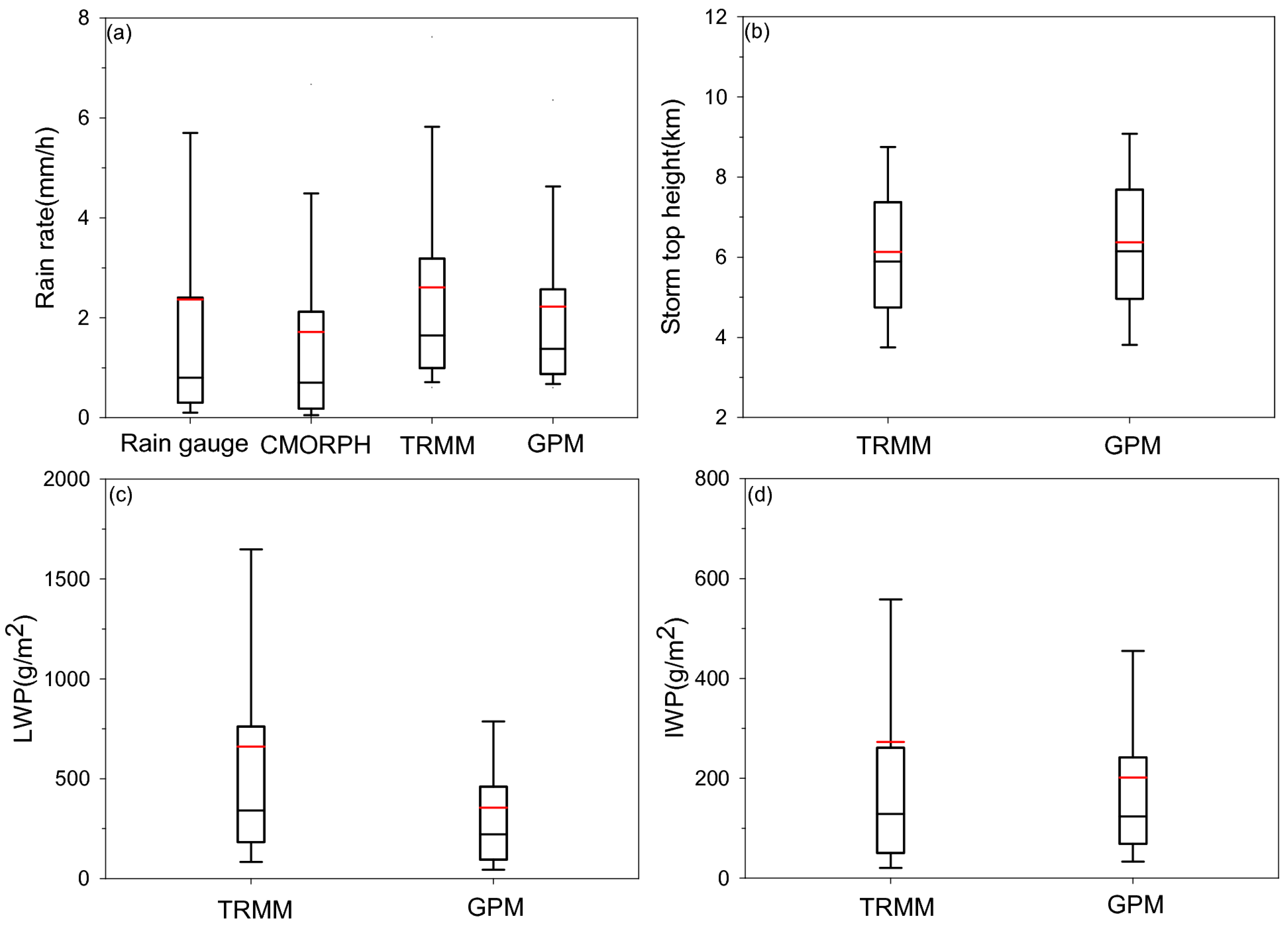
3.2. Monthly Average Rain Rate, Probability Density Function (PDF) and Vertical Structure of Precipitation from Rain Gauge, CMORPH, TRMM PR and GPM KuPR
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dai, A.; Rasmussen, R.M.; Liu, C.; Ikeda, K.; Prein, A.F. A new mechanism for warm-season precipitation response to global warming based on convection-permitting simulations. Clim. Dyn. 2020, 55, 343–368. [Google Scholar] [CrossRef]
- Hardwick Jones, R.; Westra, S.; Sharma, A. Observed relationships between extreme sub-daily precipitation, surface temperature, and relative humidity. Geophys. Res. Lett. 2010, 37, L22805. [Google Scholar] [CrossRef]
- Fu, Y.F.; Pan, X.; Xian, T.; Liu, G.S.; Zhong, L.; Liu, Q.; Li, R.; Wang, Y.; Ma, M. Precipitation characteristics over the steep slope of the Himalayas in rainy season observed by TRMM PR and VIRS. Clim. Dyn. 2018, 51, 1971–1989. [Google Scholar] [CrossRef]
- Zhou, T.J.; Ren, L.W.; Zhang, W.X. Anthropogenic influence on extreme Meiyu rainfall in 2020 and its future risk. Sci. China Earth Sci. 2021, 64, 1633–1644. [Google Scholar] [CrossRef]
- Espeholt, L.; Agrawal, S.; Sønderby, C.; Kumar, M.; Heek, J.; Bromberg, C.; Gazen, C.; Carver, R.; Andrychowicz, M.; Hickey, J.; et al. Deep learning for twelve hour precipitation forecasts. Nat. Commun. 2022, 13, 1–10. [Google Scholar] [CrossRef]
- Ding, Z.M.; Zhai, P.M.; Wu, R.G. Recent change in summer rainfall over the Tibetan Plateau: Roles of anthropogenic forcing and internal variability. Clim. Dyn. 2023, 61, 1887–1902. [Google Scholar] [CrossRef]
- Yu, R.C.; Xu, Y.P.; Zhou, T.J.; Li, J. Relation between rainfall duration and diurnal variation in the warm season precipitation over central eastern China. Geophys. Res. Lett. 2007, 34, L13703. [Google Scholar] [CrossRef]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J.J. A high spatiotemporal gauge-satellite merged precipitation analysis over China. J. Geophys. Res. Atmos. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
- Wu, G.C.; Li, Y.; Qin, S.; Mao, Y.N.; Wang, K.C. Precipitation unevenness in gauge observations and eight reanalyses from 1979 to 2018 over China. J. Clim. 2021, 34, 9797–9810. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Ren, Y.Y.; Ren, G.Y.; Wang, G.F. Precipitation trends over mainland China from 1961–2016 after removal of measurement biases. J. Geophys. Res. Atmos. 2020, 125, e2019JD031728. [Google Scholar] [CrossRef]
- Fu, Y.F.; Chen, F.J.; Liu, G.S.; Yang, Y.J.; Yuan, R.M.; Li, R.; Liu, Q.; Wang, Y.; Zhong, L.; Sun, L. Recent trends of summer convective and stratiform precipitation in mid-eastern China. Sci. Rep. 2016, 6, 33044. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.P.; Nelson, K.; Mohr, K.I.; Huffman, G.J.; Levy, R.; Grecu, M. A spatial-temporal extreme precipitation database from GPM IMERG. J. Geophys. Res. Atmos. 2019, 124, 10344–10363. [Google Scholar] [CrossRef]
- Gu, S.Y.; Zhang, P.; Chen, L.; Shang, J.; Zhang, H.W.; Lin, M.Y.; Zhu, A.J.; Jia, S.Z.; Yin, H.G.; Sun, F.L.; et al. Overview and prospect of the detection capability of China’s first precipitation measurement satellite FY-3G. Torrential Rain Disasters 2023, 42, 489–498. (In Chinese) [Google Scholar]
- Wu, Y.; Li, P.; Chen, H. The characteristic and seasonal variation of mesoscale convective systems’ precipitation over North China. Q. J. R. Meteorol. Soc. 2023, 149, 2348–2366. [Google Scholar] [CrossRef]
- Schumacher, C.; Houze, R.A. The TRMM precipitation radar’s view of shallow, isolated rain. J. Appl. Meteorol. Climatol. 2003, 42, 1519–1524. [Google Scholar] [CrossRef]
- Hamada, A.; Takayabu, Y.N. Improvements in detection of light precipitation with the Global Precipitation Measurement dual-frequency precipitation radar (GPM DPR). J. Atmos. Ocean. Technol. 2016, 33, 653–667. [Google Scholar] [CrossRef]
- Behrangi, A.; Song, Y.; Huffman, G.J.; Adler, R.F. Comparative analysis of the latest global oceanic precipitation estimates from GPM V07 and GPCP V3. 2 products. J. Hydrometeorol. 2024, 25, 293–309. [Google Scholar] [CrossRef]
- Li, Z.; Chen, H.N.; Cifelli, R.; Xie, P.P.; Chen, X.D. Characterizing the uncertainty of CMORPH products for estimating orographic precipitation over Northern California. J. Hydrol. 2024, 643, 131921. [Google Scholar] [CrossRef]
- Peng, F.C.; Zhao, S.H.; Chen, C.; Cong, D.M.; Wang, Y.M.; Ouyang, H.D. Evaluation and comparison of the precipitation detection ability of multiple satellite products in a typical agriculture area of China. Atmos. Res. 2020, 236, 104814. [Google Scholar] [CrossRef]
- Sohn, B.J.; Han, H.J.; Seo, E.K. Validation of satellite-based high-resolution rainfall products over the Korean Peninsula using data from a dense rain gauge network. J. Appl. Meteorol. Climatol. 2010, 49, 701–714. [Google Scholar] [CrossRef]
- Gao, Y.C.; Liu, M.F. Evaluation of high-resolution satellite precipitation products using rain gauge observations over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2013, 17, 837–849. [Google Scholar] [CrossRef]
- Liu, P.; Fu, Y.F.; Feng, S.; Cao, A.Q.; Yang, Y.J.; Li, T.Y.; Zi, Y. A comparison of the precipitation from rain gauge observations with from TRMM PR measurements in the southern China. Acta Meteorol. Sin. 2010, 68, 822–835. (In Chinese) [Google Scholar]
- Chen, H.Q.; Yong, B.; Qi, W.Q.; Wu, H. Investigating the evaluation uncertainty for satellite precipitation estimates based on two different ground precipitation observation products. J. Hydrometeorol. 2020, 21, 2595–2606. [Google Scholar] [CrossRef]
- Nesbitt, S.W.; Zipser, E.J. The diurnal cycle of rainfall and convective intensity according to three years of TRMM measurements. J. Clim. 2003, 16, 1456–1475. [Google Scholar] [CrossRef]
- Fu, Y.F.; Yang, L.; Wu, Z.H.; Zhang, P.; Gu, S.Y.; Chen, L.; Nan, S. A New Algorithm of Rain Type Classification for GPM Dual-Frequency Precipitation Radar in Summer Tibetan Plateau. Adv. Atmos. Sci. 2024, 41, 2093–2111. [Google Scholar] [CrossRef]
- Zhou, T.J.; Yu, R.C.; Chen, H.M.; Dai, A.G.; Pan, Y. Summer precipitation frequency, intensity, and diurnal cycle over China: A comparison of satellite data with rain gauge observations. J. Clim. 2008, 21, 3997–4010. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Q.W.; Duan, Z.; Zhang, J.Y.; Mo, K.L.; Li, Z.; Tang, G.Q. Multiscale comparative evaluation of the GPM IMERG v5 and TRMM 3B42 v7 precipitation products from 2015 to 2017 over a climate transition area of China. Remote Sens. 2018, 10, 944. [Google Scholar] [CrossRef]
- Xu, F.L.; Guo, B.; Ye, B.; Ye, Q.; Chen, H.N.; Ju, X.H.; Guo, J.Y.; Wang, Z.L. Systematical evaluation of GPM IMERG and TRMM 3B42V7 precipitation products in the Huang-Huai-Hai Plain, China. Remote Sens. 2019, 11, 697. [Google Scholar] [CrossRef]
- Deo, A.; Munchak, S.J.; Walsh, K.J.E. Cross Validation of Rainfall Characteristics Estimated from the TRMM PR, a Combined PR–TMI Algorithm, and a C-POL Ground Radar during the Passage of Tropical Cyclone and Nontropical Cyclone Events over Darwin, Australia. J. Atmos. Ocean. Technol. 2018, 35, 2339–2358. [Google Scholar] [CrossRef]
- Chen, H.N.; Chandrasekar, V.; Tan, H.M.; Cifelli, R. Rainfall estimation from ground radar and TRMM precipitation radar using hybrid deep neural networks. Geophys. Res. Lett. 2019, 46, 10669–10678. [Google Scholar] [CrossRef]
- Lasser, M.; O, S.; Foelsche, U. Evaluation of GPM-DPR precipitation estimates with WegenerNet gauge data. Atmos. Meas. Tech. 2019, 12, 5055–5070. [Google Scholar] [CrossRef]
- Deng, K.Q.; Yang, S.; Gu, D.J.; Lin, A.L.; Li, C.H. Record-breaking heat wave in southern China and delayed onset of South China Sea summer monsoon driven by the Pacific subtropical high. Clim. Dyn. 2020, 54, 3751–3764. [Google Scholar] [CrossRef]
- Zhang, W.X.; Zhou, T.J. Increasing impacts from extreme precipitation on population over China with global warming. Sci. Bull. 2020, 65, 243–252. [Google Scholar] [CrossRef]
- Chen, G.X.; Du, Y.; Wen, Z.P. Seasonal, interannual, and interdecadal variations of the East Asian summer monsoon: A diurnal-cycle perspective. J. Clim. 2021, 34, 4403–4421. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P.P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Habib, E.; Haile, A.T.; Tian, Y.D.; Joyce, R. Evaluation of the high-resolution CMORPH satellite rainfall product using dense rain gauge observations and radar-based estimates. J. Hydrometeorol. 2012, 13, 1784–1798. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J. The tropical rainfall measuring mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Liu, Z.; Ostrenga, D.; Teng, W.; Kempler, S.J. Tropical Rainfall Measuring Mission (TRMM) precipitation data and services for research and applications. Bull. Am. Meteorol. Soc. 2012, 93, 1317–1325. [Google Scholar] [CrossRef]
- Schumacher, C.; Houze, R.A., Jr.; Kraucunas, I. The tropical dynamical response to latent heating estimates derived from the TRMM precipitation radar. J. Atmos. Sci. 2004, 61, 1341–1358. [Google Scholar] [CrossRef]
- Kubota, T.; Yoshida, N.; Urita, S.; Iguchi, T.; Seto, S.; Meneghini, R. Evaluation of precipitation estimates by at-launch codes of GPM/DPR algorithms using synthetic data from TRMM/PR observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3931–3944. [Google Scholar] [CrossRef]
- Iguchi, T.; Seto, S.; Meneghini, R.; Yoshida, N.; Awaka, J.; Le, M.; Chandrasekar, V.; Brodzik, S.; Kubota, T. GPM/DPR Level-2 Algorithm Theoretical Basis Document; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2010.
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) mission for science and society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.H.; Yong, B.; Yi, L.; Wu, H.; Xu, H. From TRMM to GPM, how do improvements of post/near-real-time satellite precipitation estimates manifest? Atmos. Res. 2022, 268, 106029. [Google Scholar] [CrossRef]
- Wang, X.N.; Ding, Y.J.; Zhao, C.C.; Wang, J. Similarities and improvements of GPM IMERG upon TRMM 3B42 precipitation product under complex topographic and climatic conditions over Hexi region, Northeastern Tibetan Plateau. Atmos. Res. 2019, 218, 347–363. [Google Scholar] [CrossRef]
- Tang, G.Q.; Wen, Y.X.; Gao, J.Y.; Long, D.; Ma, Y.Z.; Wan, W.; Hong, Y. Similarities and differences between three coexisting spaceborne radars in global rainfall and snowfall estimation. Water Resour. Res. 2017, 53, 3835–3853. [Google Scholar] [CrossRef]
- Fu, Y.F.; Zhang, A.M.; Liu, Y.; Zheng, Y.Y.; Hu, Y.F.; Feng, S.; Cao, A.Q. Characteristics of seasonal scale convective and stratiform precipitation in Asia based on measurements by TRMM Precipitation Radar. Acta Meteorol. Sin. 2008, 66, 730–746. (In Chinese) [Google Scholar]
- Wang, R.; Tian, W.S.; Chen, F.J.; Wei, D.; Luo, J.L.; Tian, H.Y.; Zhang, J.K. Analysis of convective and stratiform precipitation characteristics in the summers of 2014–2019 over Northwest China based on GPM observations. Atmos. Res. 2021, 262, 105762. [Google Scholar] [CrossRef]
- Chen, F.J.; Wang, R.; Liu, P.; Yu, L.; Feng, Y.; Zheng, X.Y.; Gao, J.L. Evaluation of GPM IMERG and error sources for tropical cyclone precipitation over eastern China. J. Hydrol. 2023, 627, 130384. [Google Scholar] [CrossRef]
- Qie, X.S.; Wu, X.K.; Yuan, T.; Bian, J.C.; Lü, D. Comprehensive pattern of deep convective systems over the Tibetan Plateau–South Asian monsoon region based on TRMM data. J. Clim. 2014, 27, 6612–6626. [Google Scholar] [CrossRef]
- Liu, C.; Zipser, E.J. The global distribution of largest, deepest, and most intense precipitation systems. Geophys. Res. Lett. 2015, 42, 3591–3595. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Gourley, J.J.; Kirstetter, P.E.; Yong, B.; Tian, Y.; Zhang, Z.; Shen, Y.; Hu, J. Similarity and difference of the two successive V6 and V7 TRMM multisatellite precipitation analysis performance over China. J. Geophys. Res. Atmos. 2013, 118, 13060–13074. [Google Scholar] [CrossRef]
- Zeng, Q.L.; Wang, Y.Q.; Chen, L.F.; Wang, Z.F.; Zhu, H.; Li, B. Inter-comparison and evaluation of remote sensing precipitation products over China from 2005 to 2013. Remote Sens. 2018, 10, 168. [Google Scholar] [CrossRef]
- Wang, T.C.; Tang, G.Q. Spatial variability and linkage between extreme convections and extreme precipitation revealed by 22-year space-borne precipitation radar data. Geophys. Res. Lett. 2020, 47, e2020GL088437. [Google Scholar] [CrossRef]
- Gao, J.Y.; Tang, G.Q.; Hong, Y. Similarities and improvements of GPM dual-frequency precipitation radar (DPR) upon TRMM precipitation radar (PR) in global precipitation rate estimation, type classification and vertical profiling. Remote Sens. 2017, 9, 1142. [Google Scholar] [CrossRef]
- Wang, R.; Jiang, Z.S.; Chen, F.J.; Tian, W.S.; Li, L.L.; Tian, H.Y.; Luo, J.L. Comprehensive properties of non-penetrating and penetrating deep convection precipitation in summer over the Tibetan Plateau derived from GPM observations. Atmos. Res. 2023, 295, 107000. [Google Scholar] [CrossRef]
- Nakamura, K. Progress from TRMM to GPM. J. Meteorol. Soc. Japan. Ser. II 2021, 99, 697–729. [Google Scholar] [CrossRef]
- Iguchi, T.; Kozu, T.; Meneghini, R.; Awaka, J.; Okamoto, K. Rain-profiling algorithm for the TRMM precipitation radar. J. Appl. Meteorol. 2000, 39, 2038–2052. [Google Scholar] [CrossRef]
- Seto, S.; Iguchi, T.; Oki, T. The basic performance of a precipitation retrieval algorithm for the global precipitation measurement mission’s single/dual-frequency radar measurements. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5239–5251. [Google Scholar] [CrossRef]
- Haile, A.T.; Habib, E.; Rientjes, T. Evaluation of the climate prediction center (CPC) morphing technique (CMORPH) rainfall product on hourly time scales over the source of the Blue Nile River. Hydrol. Process. 2013, 27, 1829–1839. [Google Scholar] [CrossRef]
- Xie, P.P.; Joyce, R.; Wu, S.R.; Yoo, S.H.; Yarosh, Y.; Sun, F.Y.; Lin, R. Reprocessed, bias-corrected CMORPH global high-resolution precipitation estimates from 1998. J. Hydrometeorol. 2017, 18, 1617–1641. [Google Scholar] [CrossRef]
- Manual, I. Tropical Rainfall Measuring Mission (TRMM) Precipitation Radar Algorithm. 2005. Available online: https://www.eorc.jaxa.jp/TRMM/documents/PR_algorithm_product_information/pr_manual/PR_Instruction_Manual_V7_L1.pdf (accessed on 20 July 2011).
- Lau, K.M.; Wu, H.T. Climatology and changes in tropical oceanic rainfall characteristics inferred from Tropical Rainfall Measuring Mission (TRMM) data (1998–2009). J. Geophys. Res. Atmos. 2011, 116, D17111. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Tang, G.Q.; Long, D.; Yong, B.; Zhong, L.Z.; Wan, W.; Hong, Y. Similarity and error intercomparison of the GPM and its predecessor-TRMM multisatellite precipitation analysis using the best available hourly gauge network over the Tibetan Plateau. Remote Sens. 2016, 8, 569. [Google Scholar] [CrossRef]
- Xu, R.; Tian, F.Q.; Yang, L.; Hu, H.C.; Lu, H.; Hou, A.Z. Ground validation of GPM IMERG and TRMM 3B42V7 rainfall products over southern Tibetan Plateau based on a high-density rain gauge network. J. Geophys. Res. Atmos. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Tang, G.Q.; Long, D.; Hong, Y.; Gao, J.Y.; Wan, W. Documentation of multifactorial relationships between precipitation and topography of the Tibetan Plateau using spaceborne precipitation radars. Remote Sens. Environ. 2018, 208, 82–96. [Google Scholar] [CrossRef]
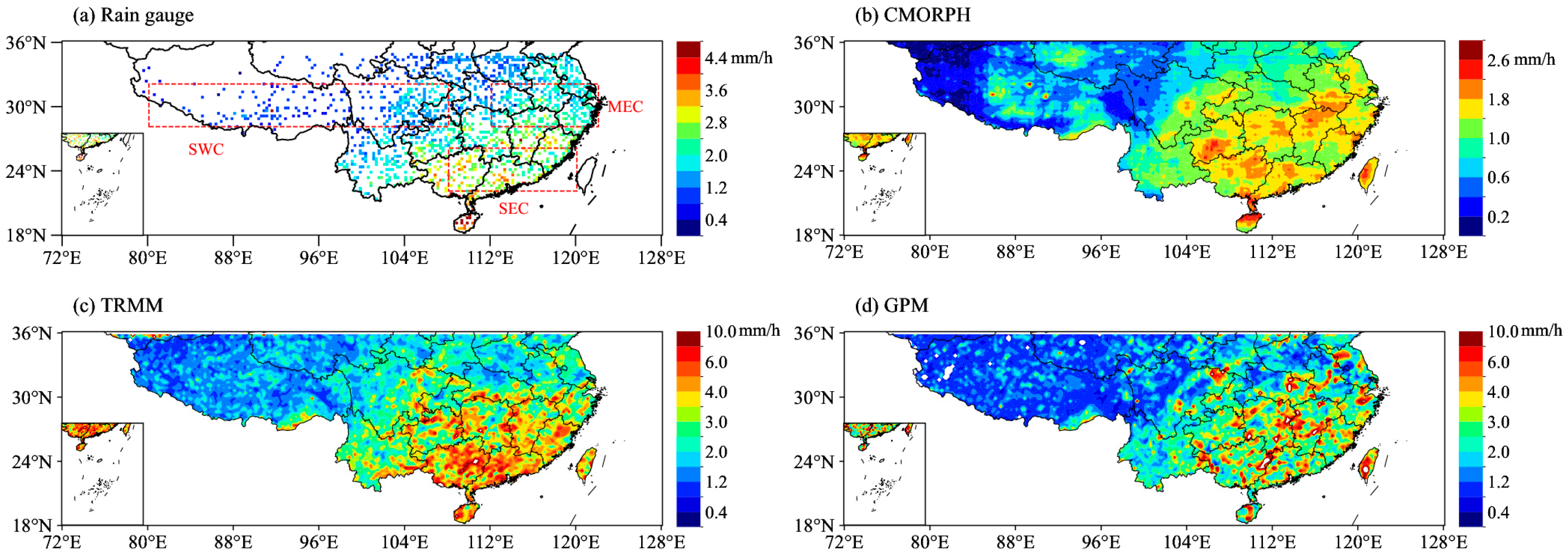
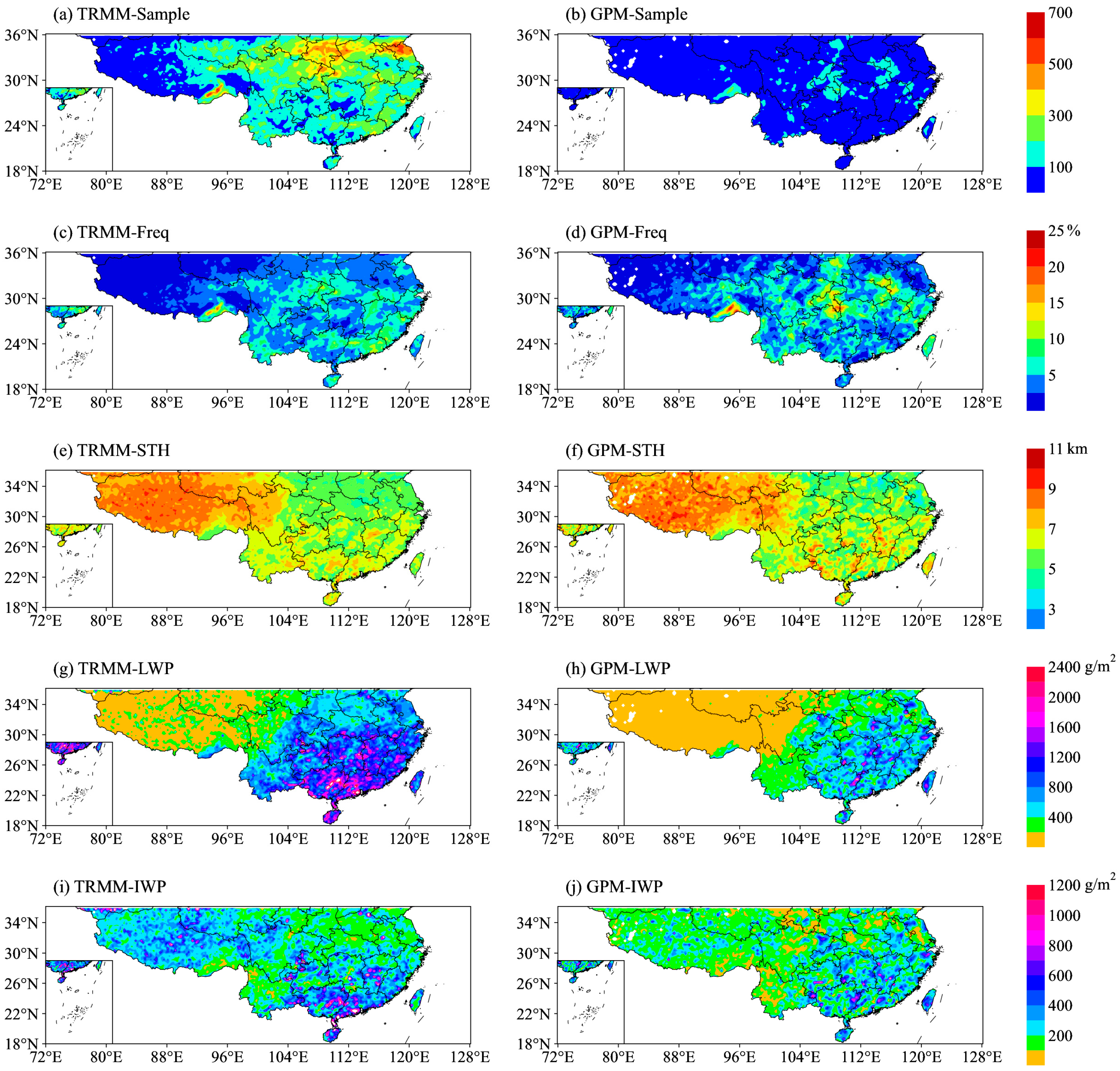

| Parameters | TRMM PR | GPM KuPR |
|---|---|---|
| Launch time | 27 November 1997 | 28 February 2014 |
| Swath width | 247 km | 245 km |
| Orbit inclination angle | 35° | 65° |
| Global coverage | 38°S~38°N | 68°S~68°N |
| Horizontal resolution | ~5 km | ~5 km |
| Vertical resolution | 250 m | 125 m |
| Maximum altitude | 20 km | 22 km |
| Band frequency | 13.8 GHz | 13.6 GHz |
| Detection threshold | 0.4 mm/h (17.0 dBZ) | 0.5 mm/h (18.0 dBZ) |
| Orbit data version | 2A25 V07 | 2A V06 |
| Statistical Metrics | Computational Formula | Perfect Value |
|---|---|---|
| Mean Error (ME) | 0 | |
| Root Mean Square Error (RMSE) | 0 | |
| Probability of Detection (POD) | 100% | |
| False Alert Ratio (FAR) | 0% | |
| Bias (BIAS) | 1 | |
| Critical Success Index (CSI) | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Li, H.; Huang, H.; Li, L. Comparison and Evaluation of Rain Gauge, CMORPH, TRMM PR and GPM DPR KuPR Precipitation Products over South China. Remote Sens. 2025, 17, 2040. https://doi.org/10.3390/rs17122040
Wang R, Li H, Huang H, Li L. Comparison and Evaluation of Rain Gauge, CMORPH, TRMM PR and GPM DPR KuPR Precipitation Products over South China. Remote Sensing. 2025; 17(12):2040. https://doi.org/10.3390/rs17122040
Chicago/Turabian StyleWang, Rui, Huiping Li, Hao Huang, and Liangliang Li. 2025. "Comparison and Evaluation of Rain Gauge, CMORPH, TRMM PR and GPM DPR KuPR Precipitation Products over South China" Remote Sensing 17, no. 12: 2040. https://doi.org/10.3390/rs17122040
APA StyleWang, R., Li, H., Huang, H., & Li, L. (2025). Comparison and Evaluation of Rain Gauge, CMORPH, TRMM PR and GPM DPR KuPR Precipitation Products over South China. Remote Sensing, 17(12), 2040. https://doi.org/10.3390/rs17122040





