Hyperspectral Image Denoising Based on Non-Convex Correlated Total Variation
Abstract
1. Introduction
- 1.
- Non-local self-similarity priors: Exploit the recurrence of structurally similar patches across spatial domains [4].
- 2.
- 3.
- 1.
- We propose the non-convex correlated total variation regularization term for simultaneously modeling the low-rank and local smoothness priors.
- 2.
- We propose a hyperspectral image denoising algorithm based on our non-convex correlated total variation, demonstrating excellent denoising performance in scenarios with severe mixed noise.
2. Background and Motivation
3. Method
3.1. Non-Convex Correlated Total Variation
3.2. Application of Non-Convex Correlation Total Variation in Hyperspectral Image Denoising
| Algorithm 1 ADMM Algorithm Process |
|
4. Experiments
- 1.
- NMoG (non-i.i.d. mixture of Gaussians) [69]: The NMoG method models the noise within each spectral band using a distinct MoG distribution and imposes hierarchical priors on the MoG parameters. The parameters were set as follows: target rank of the low-rank component = 5, initial rank of the low-rank component = 30, rank reduction per iteration = 7, Gaussian mixture components reduced per band = 1, maximum number of iterations = 30, and convergence tolerance = .
- 2.
- NGMeet (non-local meets global) [70]: NGMeet proposes a unified spatial–spectral denoising paradigm that jointly models the global spectral low-rank property (via an orthogonal basis and reduced image) and spatial non-local similarity (via low-rank regularization on the reduced image).
- 3.
- LRTV (low-rank total variation) [46]: LRTV integrates nuclear norm minimization for spectral low-rank property, total variation regularization for spatial smoothness, and -norm regularization for sparse noise separation within a unified framework. The parameters in this method were set as follows: when the number of bands exceeded 100, the parameter was set to , to , and the target rank to 10. When the number of bands did not exceed 100, the parameter was set to , to , and the target rank to 5.
- 4.
- CTV (correlated total variation) [54]: CTV regularization captures the joint low-rankness and local smoothness by applying the nuclear norm to the gradient maps of the data. The parameter was set to .
- 5.
- 3DTNN (three-directional tensor nuclear norm) [71]: 3DTNN employs a convex three-directional tensor nuclear norm as a regularizer to enforce low-rankness across all modes of the hyperspectral image tensor. The standard deviation of random noise was set to a uniform distribution between 0 and , while the parameter was set to , the parameter to , the parameter to 1, and the parameter to 100.
- 6.
- 3DLogTNN (three-directional log-based tensor nuclear norm) [71]: This model employs a non-convex logarithmic function to approximate the rank by penalizing singular values differently across three directional tensor nuclear norms. The standard deviation of random noise was set to a uniform distribution between 0 and . The parameter was set to , the parameter to , the parameter to , and the parameter to 10,000. Finally, the logarithmic tolerance was set to 80.
- 7.
- WNLRATV (weighted non-local low-rank model with adaptive total variation regularization) [72]: WNLRATV integrates a weighted term based on non-i.i.d. mixture-of-Gaussian noise modeling, a non-local low-rank tensor prior, and an adaptive edge-preserving total variation regularization for denoising. The parameters in this method were set as follows: the initial rank was set to 3, the target rank to 6, the parameter to 30, the parameter to 1, the parameter to , the maximum iteration to 15, the patch number to 200, and the parameter to .
- 8.
- BALMF (band-wise asymmetric Laplacian noise modeling matrix factorization) [63]: BALMF models the hyperspectral image noise per band using an asymmetric Laplacian distribution within a low-rank matrix factorization framework. The r parameter was set to 4.
4.1. Simulation Results and Analysis
4.1.1. Data Simulation
- 1.
- Gaussian noise with a standard deviation of is added following an independent and identically distributed (i.i.d.) pattern.
- 2.
- Non-i.i.d. Gaussian noise is added with a standard deviation randomly distributed between and .
- 3.
- On the basis of noise type 2, impulse noise is randomly added to of the bands, with the noise intensity randomly distributed between and .
- 4.
- On the basis of noise type 2, stripe noise is randomly added to of the bands, with the noise intensity randomly distributed between and .
- 5.
- On the basis of noise type 2, of the bands are randomly selected for added dead-line noise, with the noise intensity randomly distributed between and .
- 6.
- On the basis of noise type 2, of the bands are randomly selected for added mixed noise consisting of impulse noise, stripe noise, and dead-line noise, with the noise intensity randomly distributed between and for all types.
4.1.2. Results Analysis
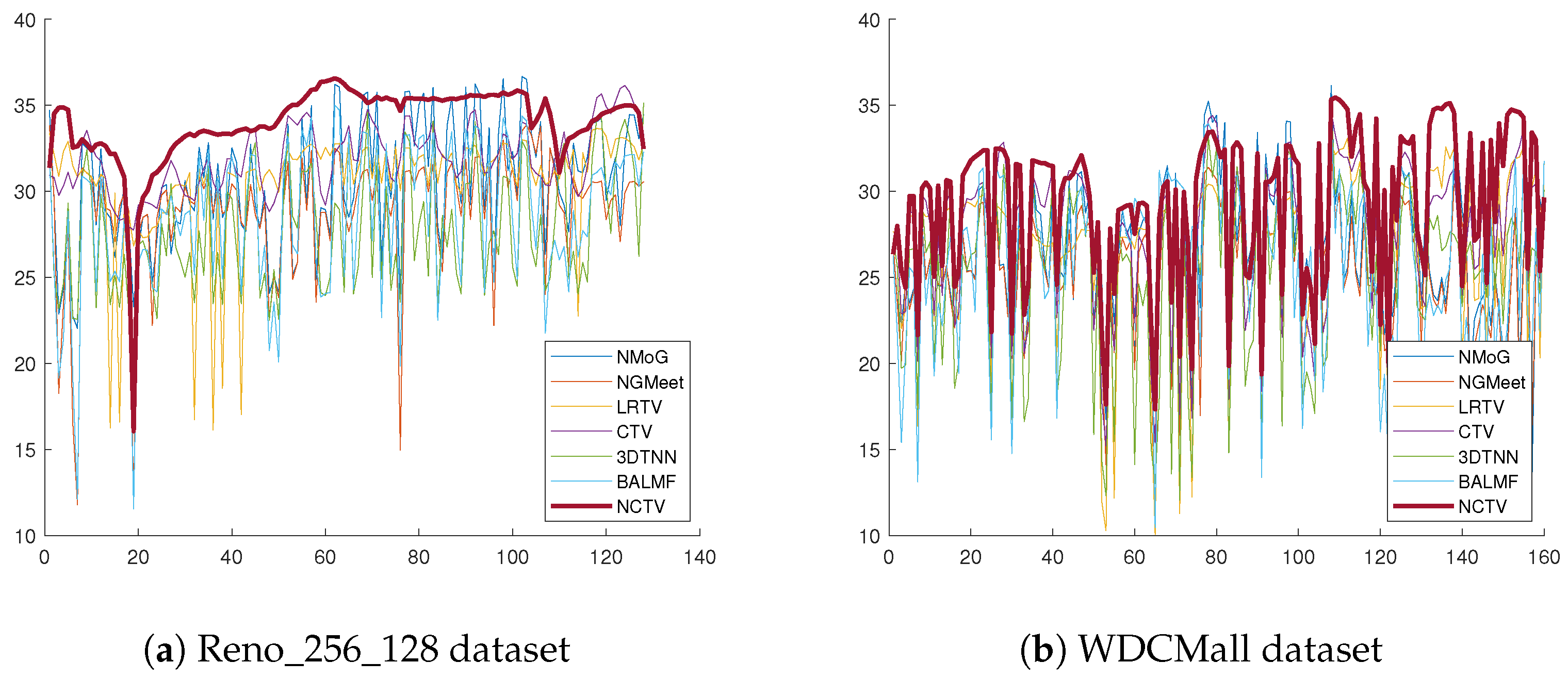
4.2. Experiments on Real-World Datasets
4.3. Model Analysis
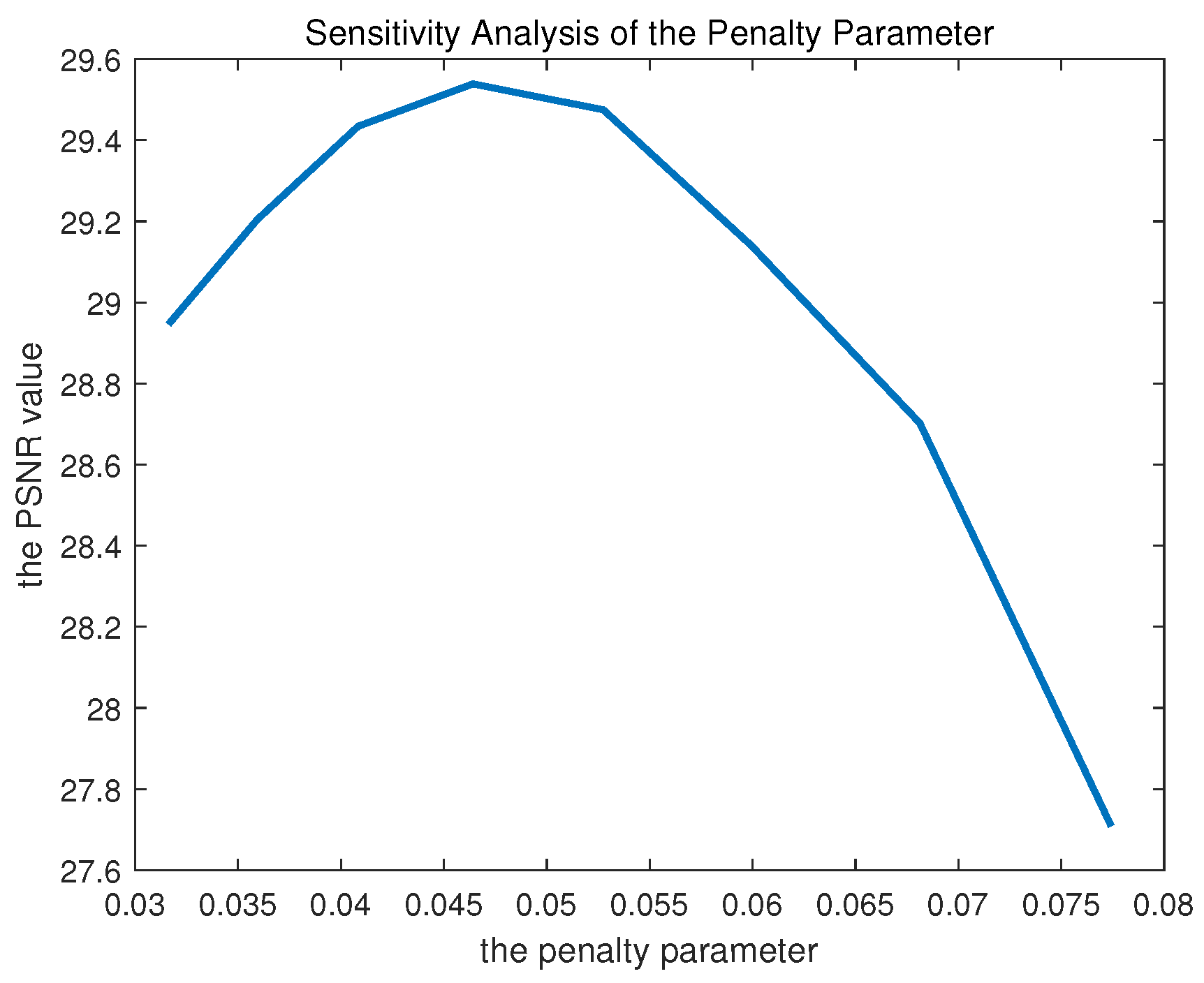
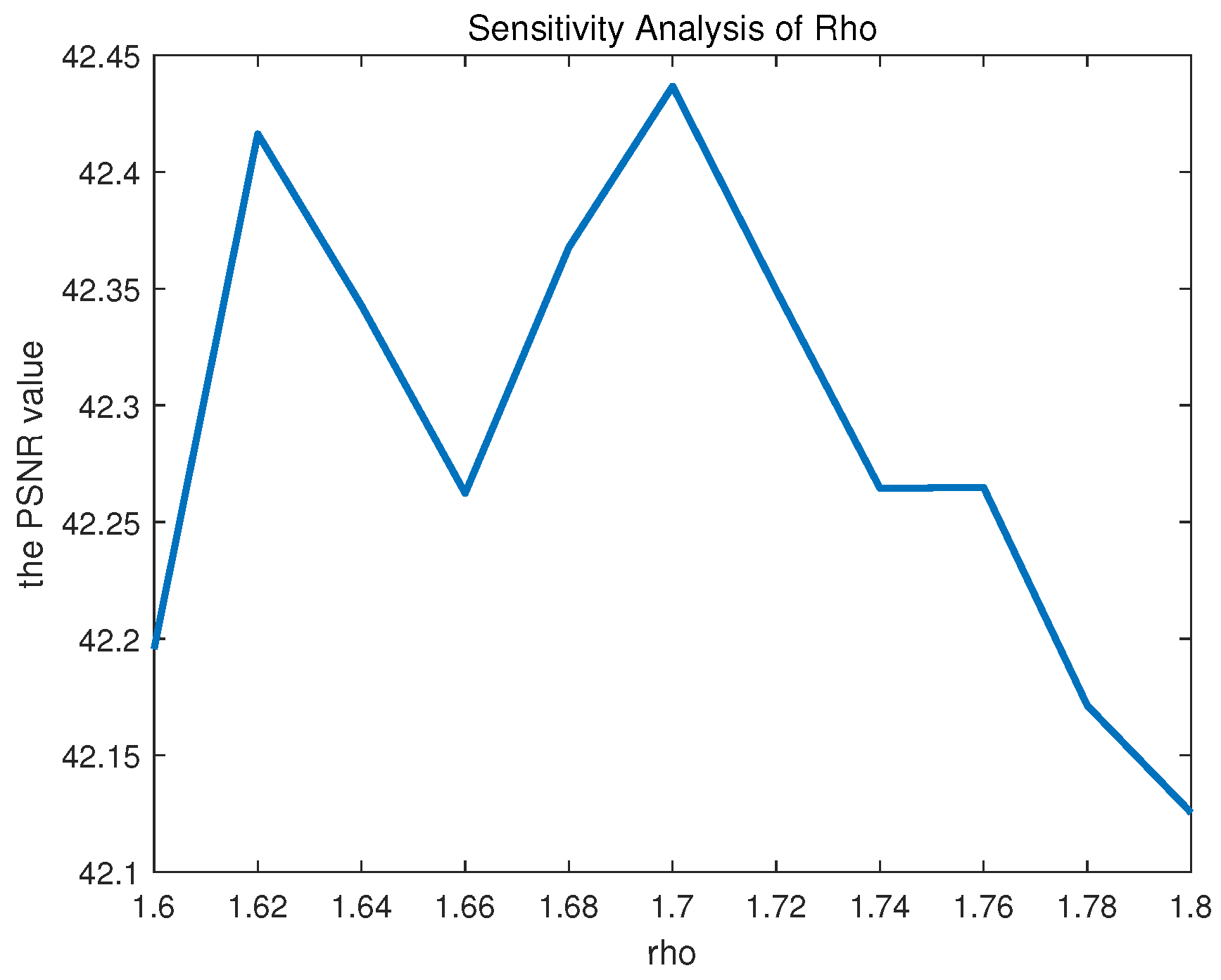
4.3.1. Parameter Sensitivity
4.3.2. Processing Time
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, G.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A.; et al. Recent advances in techniques for hyperspectral image processing. Remote Sens. Environ. 2009, 113, S110–S122, Imaging Spectroscopy Special Issue. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Hu, Y.; Li, X.; Gu, Y.; Jacob, M. Hyperspectral Image Recovery Using Nonconvex Sparsity and Low-Rank Regularizations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 532–545. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, Y.; Wang, Y.; Wang, D.; Peng, C.; He, G. Denoising of Hyperspectral Images Using Nonconvex Low Rank Matrix Approximation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5366–5380. [Google Scholar] [CrossRef]
- Lu, H.; Yang, Y.; Huang, S.; Tu, W.; Wan, W. A Unified Pansharpening Model Based on Band-Adaptive Gradient and Detail Correction. IEEE Trans. Image Process. 2022, 31, 918–933. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Tu, W.; Huang, S.; Lu, H.; Wan, W.; Gan, L. Dual-Stream Convolutional Neural Network With Residual Information Enhancement for Pansharpening. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 5402416. [Google Scholar] [CrossRef]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral Image Restoration Using Low-Rank Matrix Recovery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4729–4743. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, J.; Xu, S.; Zhao, Z.; Zhang, C.; Liu, J.; Hu, J. CACNN: Capsule Attention Convolutional Neural Networks for 3D Object Recognition. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 4091–4102. [Google Scholar] [CrossRef] [PubMed]
- Bai, H.; Zhao, Z.; Zhang, J.; Wu, Y.; Deng, L.; Cui, Y.; Jiang, B.; Xu, S. ReFusion: Learning Image Fusion from Reconstruction with Learnable Loss Via Meta-Learning. Int. J. Comput. Vis. 2025, 133, 2547–2567. [Google Scholar] [CrossRef]
- Bai, H.; Zhao, Z.; Zhang, J.; Jiang, B.; Deng, L.; Cui, Y.; Xu, S.; Zhang, C. Deep Unfolding Multi-Modal Image Fusion Network via Attribution Analysis. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 3498–3511. [Google Scholar] [CrossRef]
- Xu, S.; Amira, O.; Liu, J.; Zhang, C.; Zhang, J.; Li, G. HAM-MFN: Hyperspectral and Multispectral Image Multiscale Fusion Network With RAP Loss. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4618–4628. [Google Scholar] [CrossRef]
- Wang, C.; Pedrycz, W.; Li, Z.; Zhou, M. Residual-driven Fuzzy C-Means Clustering for Image Segmentation. IEEE CAA J. Autom. Sin. 2021, 8, 876–889. [Google Scholar] [CrossRef]
- Chen, Y.; Lai, W.; He, W.; Zhao, X.; Zeng, J. Hyperspectral Compressive Snapshot Reconstruction via Coupled Low-Rank Subspace Representation and Self-Supervised Deep Network. IEEE Trans. Image Process. 2024, 33, 926–941. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Chen, M.; He, W.; Zeng, J.; Huang, M.; Zheng, Y. Thick Cloud Removal in Multitemporal Remote Sensing Images via Low-Rank Regularized Self-Supervised Network. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5506613. [Google Scholar] [CrossRef]
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Sparse Unmixing of Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2014–2039. [Google Scholar] [CrossRef]
- Cerra, D.; Müller, R.; Reinartz, P. Noise Reduction in Hyperspectral Images Through Spectral Unmixing. IEEE Geosci. Remote Sens. Lett. 2014, 11, 109–113. [Google Scholar] [CrossRef]
- Xu, S.; Ke, Q.; Peng, J.; Cao, X.; Zhao, Z. Pan-Denoising: Guided Hyperspectral Image Denoising via Weighted Represent Coefficient Total Variation. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5528714. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, Y.; Yuan, Q.; Song, M.; Yu, H.; Xiao, Y. Hyperspectral Image Denoising: From Model-Driven, Data-Driven, to Model-Data-Driven. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 13143–13163. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Li, J.; Sun, F.; Zhang, L. Deep spatio-spectral Bayesian posterior for hyperspectral image non-i.i.d. noise removal. ISPRS J. Photogramm. Remote Sens. 2020, 164, 125–137. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Li, J.; Liu, X.; Shen, H.; Zhang, L. Hybrid Noise Removal in Hyperspectral Imagery With a Spatial–Spectral Gradient Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7317–7329. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral Image Denoising Employing a Spatial–Spectral Deep Residual Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1205–1218. [Google Scholar] [CrossRef]
- Liu, W.; Lee, J. A 3-D Atrous Convolution Neural Network for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5701–5715. [Google Scholar] [CrossRef]
- Chen, H.; Yang, G.; Zhang, H. Hider: A Hyperspectral Image Denoising Transformer With Spatial–Spectral Constraints for Hybrid Noise Removal. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 8797–8811. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Song, M.; Yu, H.; Zhang, L. Cooperated Spectral Low-Rankness Prior and Deep Spatial Prior for HSI Unsupervised Denoising. IEEE Trans. Image Process. 2022, 31, 6356–6368. [Google Scholar] [CrossRef] [PubMed]
- Shi, K.; Peng, J.; Gao, J.; Luo, Y.; Xu, S. Hyperspectral Image Denoising via Double Subspace Deep Prior. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5531015. [Google Scholar] [CrossRef]
- Lu, X.; Wang, Y.; Yuan, Y. Graph-regularized low-rank representation for destriping of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4009–4018. [Google Scholar] [CrossRef]
- Yuan, F.; Chen, Y.; He, W.; Zeng, J. Feature Fusion-Guided Network With Sparse Prior Constraints for Unsupervised Hyperspectral Image Quality Improvement. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5511912. [Google Scholar] [CrossRef]
- Liu, X.; Bourennane, S.; Fossati, C. Denoising of hyperspectral images using the PARAFAC model and statistical performance analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3717–3724. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Huang, J.; Mei, X.; Ma, J. Hyperspectral image denoising using the robust low-rank tensor recovery. J. Opt. Soc. Am. A 2015, 32, 1604–1612. [Google Scholar] [CrossRef]
- Renard, N.; Bourennane, S.; Blanc-Talon, J. Denoising and dimensionality reduction using multilinear tools for hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2008, 5, 138–142. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, S.; Cao, X.; Ke, Q.; Ji, T.; Zhu, X. Hyperspectral Denoising Using Asymmetric Noise Modeling Deep Image Prior. Remote Sens. 2023, 15, 1970. [Google Scholar] [CrossRef]
- Wu, J.M.; Yin, S.B.; Jiang, T.X.; Liu, G.S.; Zhao, X.L. PALADIN: A novel plug-and-play 3D CS-MRI reconstruction method. Inverse Probl. 2025, 41, 035014. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, J.; Wang, J.; Sun, K.; Zhang, C.; Liu, J.; Hu, J. A model-driven network for guided image denoising. Inf. Fusion 2022, 85, 60–71. [Google Scholar] [CrossRef]
- Xu, S.; Peng, J.; Ji, T.; Cao, X.; Sun, K.; Fei, R.; Meng, D. Stacked Tucker Decomposition With Multi-Nonlinear Products for Remote Sensing Imagery Inpainting. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5533413. [Google Scholar] [CrossRef]
- Letexier, D.; Bourennane, S. Noise removal from hyperspectral images by multidimensional filtering. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2061–2069. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image Denoising Via Sparse and Redundant Representations Over Learned Dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G.; Zisserman, A. Non-local sparse models for image restoration. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2272–2279. [Google Scholar] [CrossRef]
- Jiang, T.X.; Ng, M.K.; Pan, J.; Song, G.J. Nonnegative low rank tensor approximations with multidimensional image applications. Numer. Math. 2023, 153, 141–170. [Google Scholar] [CrossRef]
- Wright, J.; Ganesh, A.; Rao, S.; Peng, Y.; Ma, Y. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; pp. 2080–2088. [Google Scholar]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM (JACM) 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Song, H.; Wang, G.; Zhang, K. Hyperspectral image denoising via low-rank matrix recovery. Remote Sens. Lett. 2014, 5, 872–881. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Hyperspectral image denoising via noise-adjusted iterative low-rank matrix approximation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3050–3061. [Google Scholar] [CrossRef]
- Xie, Y.; Qu, Y.; Tao, D.; Wu, W.; Yuan, Q.; Zhang, W. Hyperspectral image restoration via iteratively regularized weighted schatten p-norm minimization. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4642–4659. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2015, 54, 178–188. [Google Scholar] [CrossRef]
- Ye, M.; Qian, Y.; Zhou, J. Multitask sparse nonnegative matrix factorization for joint spectral–spatial hyperspectral imagery denoising. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2621–2639. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, J.; Zhang, C. Hyperspectral image denoising by low-rank models with hyper-Laplacian total variation prior. Signal Process. 2022, 201, 108733. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Sun, J.; Xu, Z.; Shum, H.Y. Image super-resolution using gradient profile prior. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; IEEE: Piscataway, NJ, USA; pp. 1–8. [Google Scholar]
- Chambolle, A. An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 2004, 20, 89–97. [Google Scholar]
- Chambolle, A.; Caselles, V.; Cremers, D.; Novaga, M.; Pock, T. An introduction to total variation for image analysis. Theor. Found. Numer. Methods Sparse Recovery 2010, 9, 227. [Google Scholar]
- Li, S.Z. Markov random field models in computer vision. In Proceedings of the Computer Vision—ECCV’94: Third European Conference on Computer Vision, Stockholm, Sweden, 2–6 May 1994; Proceedings, Volume II. Springer: Berlin/Heidelberg, Germany, 1994; pp. 361–370. [Google Scholar]
- Peng, J.; Wang, Y.; Zhang, H.; Wang, J.; Meng, D. Exact Decomposition of Joint Low Rankness and Local Smoothness Plus Sparse Matrices. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 5766–5781. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zhang, C.H. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wang, Y.; Li, M.; He, G. Augmented Lagrangian alternating direction method for low-rank minimization via non-convex approximation. Signal Image Video Process. 2017, 11, 1271–1278. [Google Scholar] [CrossRef]
- Frank, L.E.; Friedman, J.H. A statistical view of some chemometrics regression tools. Technometrics 1993, 35, 109–135. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted ℓ1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Kang, Z.; Peng, C.; Cheng, Q. Robust PCA via nonconvex rank approximation. In Proceedings of the 2015 IEEE International Conference on Data Mining, Atlantic City, NJ, USA, 14–17 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 211–220. [Google Scholar]
- Lu, H.; Yang, Y.; Huang, S.; Chen, X.; Chi, B.; Liu, A.; Tu, W. AWFLN: An Adaptive Weighted Feature Learning Network for Pansharpening. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5400815. [Google Scholar] [CrossRef]
- Wang, C.; Lin, J.; Li, X. Structural-Equation-Modeling-Based Indicator Systems for Image Quality Assessment. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 1–14. [Google Scholar] [CrossRef]
- Xu, S.; Cao, X.; Peng, J.; Ke, Q.; Ma, C.; Meng, D. Hyperspectral Image Denoising by Asymmetric Noise Modeling. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5545214. [Google Scholar] [CrossRef]
- Peng, J.; Wang, H.; Cao, X.; Jia, X.; Zhang, H.; Meng, D. Stable Local-Smooth Principal Component Pursuit. SIAM J. Imaging Sci. 2024, 17, 1182–1205. [Google Scholar] [CrossRef]
- Lu, C.; Tang, J.; Yan, S.; Lin, Z. Nonconvex nonsmooth low rank minimization via iteratively reweighted nuclear norm. IEEE Trans. Image Process. 2015, 25, 829–839. [Google Scholar] [CrossRef]
- Bai, J.; Zhang, M.; Zhang, H. An inexact ADMM for separable nonconvex and nonsmotth optimization. Comput. Optim. Appl. 2025, 90, 445–479. [Google Scholar] [CrossRef]
- Bai, J.; Chen, Y.; Yu, X.; Zhang, H. Generalized Asymmetric Forward-Backward-Adjoint Algorithms for Convex-Concave Saddle-Point Problem. J. Sci. Comput. 2025, 102, 80. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Chen, Y.; Cao, X.; Zhao, Q.; Meng, D.; Xu, Z. Denoising Hyperspectral Image With Non-i.i.d. Noise Structure. IEEE Trans. Cybern. 2018, 48, 1054–1066. [Google Scholar] [CrossRef]
- He, W.; Yao, Q.; Li, C.; Yokoya, N.; Zhao, Q. Non-Local Meets Global: An Integrated Paradigm for Hyperspectral Denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, 16–20 June 2019; pp. 6868–6877. [Google Scholar]
- Zheng, Y.; Huang, T.; Zhao, X.; Jiang, T.; Ma, T.; Ji, T. Mixed Noise Removal in Hyperspectral Image via Low-Fibered-Rank Regularization. IEEE Trans. Geosci. Remote Sens. 2020, 58, 734–749. [Google Scholar] [CrossRef]
- Chen, Y.; Cao, W.; Pang, L.; Cao, X. Hyperspectral Image Denoising With Weighted Nonlocal Low-Rank Model and Adaptive Total Variation Regularization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5544115. [Google Scholar] [CrossRef]
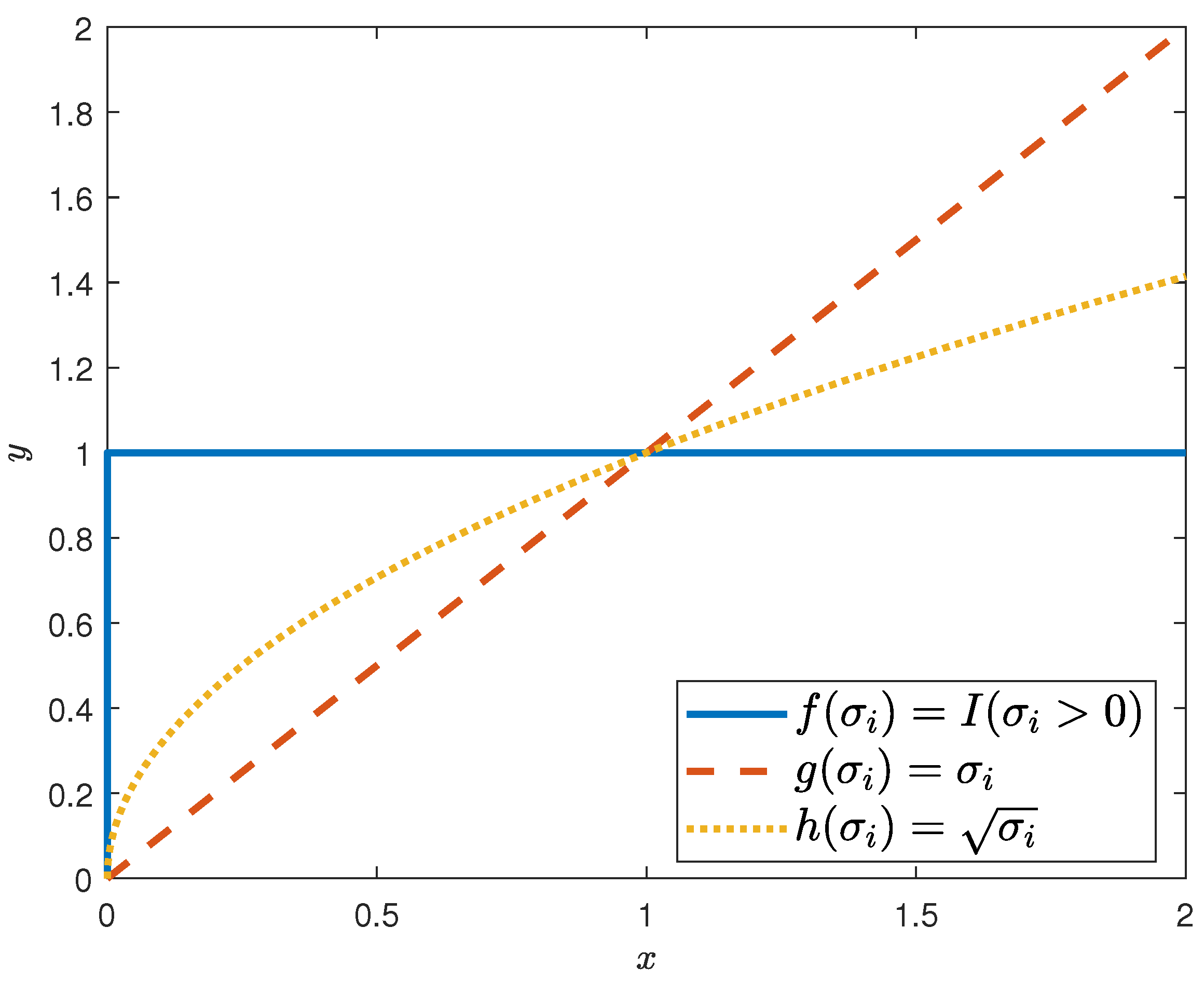




| Cases of the Noise | Metrics | Noisy | NMoG | NGMeet | LRTV | CTV | 3DTNN | 3DLogTNN | WNLRATV | BALMF | NCTV |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | PSNR | 20.17 | 35.23 | 39.24 | 32.81 | 34.03 | 34.45 | 36.02 | 36.57 | 33.22 | 35.58 |
| SSIM | 0.3747 | 0.9371 | 0.9758 | 0.8983 | 0.9136 | 0.9522 | 0.9572 | 0.9541 | 0.889 | 0.9436 | |
| ERGAS | 317.43 | 57.31 | 35.46 | 76.44 | 64.23 | 61.22 | 51.25 | 48.26 | 71.81 | 55.21 | |
| SAM | 23.95 | 3.73 | 2.04 | 4.26 | 4.5 | 3.03 | 2.82 | 2.89 | 4.99 | 3.33 | |
| 2 | PSNR | 16.87 | 34.59 | 31.67 | 30.85 | 31.78 | 32.27 | 33.87 | 33.01 | 31.85 | 33.96 |
| SSIM | 0.2696 | 0.9265 | 0.8683 | 0.8512 | 0.8629 | 0.9258 | 0.9186 | 0.915 | 0.8826 | 0.9198 | |
| ERGAS | 559.41 | 61.76 | 130.8 | 117.09 | 85.29 | 79.15 | 68.46 | 76.86 | 118.08 | 66.07 | |
| SAM | 37.13 | 4.06 | 9.85 | 7.6 | 6.09 | 3.74 | 4.22 | 4.65 | 9.45 | 3.88 | |
| 3 | PSNR | 15.86 | 31.67 | 29.81 | 30.12 | 32.05 | 31.99 | 34.07 | 33.92 | 30.24 | 34.12 |
| SSIM | 0.2418 | 0.8886 | 0.8378 | 0.8358 | 0.8682 | 0.9242 | 0.9283 | 0.9274 | 0.8693 | 0.921 | |
| ERGAS | 629.76 | 150.72 | 162.04 | 156.77 | 83.34 | 82.54 | 66.66 | 71.37 | 155.56 | 64.24 | |
| SAM | 38.31 | 10.16 | 10.84 | 11.4 | 5.98 | 3.81 | 3.95 | 4.23 | 11.33 | 3.71 | |
| 4 | PSNR | 16.35 | 33.03 | 31.49 | 30.38 | 31.17 | 30.72 | 30.81 | 31.58 | 31.31 | 33.56 |
| SSIM | 0.2509 | 0.9015 | 0.8694 | 0.8413 | 0.8463 | 0.8722 | 0.8377 | 0.8806 | 0.867 | 0.9106 | |
| ERGAS | 575.66 | 115.38 | 139.97 | 133.17 | 92.03 | 100.14 | 113.61 | 98.71 | 129.88 | 69 | |
| SAM | 37.91 | 8.55 | 10.2 | 9.5 | 6.62 | 6.26 | 8.41 | 5.86 | 9.77 | 4.04 | |
| 5 | PSNR | 16.01 | 30.06 | 28.84 | 27.33 | 27.48 | 27.08 | 26.46 | 29.26 | 28.15 | 29.63 |
| SSIM | 0.2375 | 0.8891 | 0.8396 | 0.7659 | 0.7559 | 0.7323 | 0.68 | 0.8541 | 0.7814 | 0.8695 | |
| ERGAS | 585.57 | 156.39 | 169.36 | 217.42 | 188.62 | 230.21 | 250.54 | 141.23 | 225.14 | 150.13 | |
| SAM | 39.9 | 10.56 | 11.61 | 14.91 | 13.85 | 15.96 | 18.4 | 7.42 | 15.54 | 10.19 | |
| 6 | PSNR | 14.36 | 27.77 | 27.3 | 27.15 | 26.97 | 25.94 | 25.7 | 28.78 | 26.54 | 29.24 |
| SSIM | 0.1911 | 0.8371 | 0.8222 | 0.7599 | 0.7409 | 0.7102 | 0.6721 | 0.8439 | 0.7484 | 0.8634 | |
| ERGAS | 690.46 | 202.48 | 189.33 | 225.61 | 195.79 | 243.66 | 257.79 | 146.98 | 259.12 | 154.53 | |
| SAM | 42.42 | 13.06 | 12.84 | 15.25 | 14.32 | 17.06 | 19.08 | 8.19 | 18.06 | 10.35 |
| Cases of the Noise | Metrics | Noisy | NMoG | NGMeet | LRTV | CTV | 3DTNN | 3DLogTNN | WNLRATV | BALMF | NCTV |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | PSNR | 20.17 | 35.53 | 38.01 | 32.05 | 33.57 | 33.64 | 35.22 | 34.72 | 33.74 | 35.36 |
| SSIM | 0.5223 | 0.9695 | 0.9829 | 0.9232 | 0.9496 | 0.9668 | 0.9714 | 0.9639 | 0.9523 | 0.9699 | |
| ERGAS | 368.76 | 60.9 | 45.26 | 91.87 | 76.59 | 75.3 | 63.04 | 65.8 | 75.4 | 64.27 | |
| SAM | 26.86 | 5.27 | 3.37 | 5.75 | 6.48 | 4.4 | 4.56 | 3.79 | 6.54 | 4.92 | |
| 2 | PSNR | 16.73 | 34.01 | 31.37 | 29.78 | 31.04 | 28.15 | 26.63 | 31.24 | 31.48 | 33.42 |
| SSIM | 0.3732 | 0.9566 | 0.9238 | 0.872 | 0.9106 | 0.823 | 0.7608 | 0.9176 | 0.9287 | 0.9536 | |
| ERGAS | 638.64 | 78.98 | 123.64 | 152.34 | 105.6 | 156.25 | 209.98 | 98.53 | 112.24 | 80.37 | |
| SAM | 38.9 | 7.29 | 11.15 | 11.63 | 8.76 | 12.42 | 17.52 | 5.17 | 10.19 | 5.95 | |
| 3 | PSNR | 15.74 | 31.17 | 28.86 | 29.92 | 31.62 | 28.33 | 27.28 | 32.08 | 30.35 | 33.84 |
| SSIM | 0.3448 | 0.9147 | 0.8675 | 0.8766 | 0.918 | 0.8202 | 0.7716 | 0.9278 | 0.8933 | 0.9591 | |
| ERGAS | 781.42 | 180.49 | 221.46 | 166.92 | 100.18 | 159.33 | 207.53 | 93.8 | 157.62 | 76.13 | |
| SAM | 40.38 | 11.2 | 13.67 | 12.06 | 7.88 | 11.93 | 16.15 | 5.63 | 9.92 | 5.24 | |
| 4 | PSNR | 16.44 | 34.16 | 30.97 | 29.54 | 30.8 | 28.87 | 28.16 | 31.54 | 31.57 | 33.37 |
| SSIM | 0.3646 | 0.9602 | 0.9115 | 0.8695 | 0.9074 | 0.8654 | 0.8292 | 0.9212 | 0.9225 | 0.954 | |
| ERGAS | 660.02 | 70.94 | 133.14 | 161.59 | 106.49 | 141.18 | 167.41 | 96.14 | 97.23 | 78.18 | |
| SAM | 39.79 | 6.05 | 11.18 | 12.78 | 8.89 | 10.56 | 13.97 | 5.52 | 8.55 | 5.91 | |
| 5 | PSNR | 16.3 | 31.12 | 28.86 | 27.15 | 27.95 | 26.8 | 27.14 | 29.15 | 29.13 | 29.88 |
| SSIM | 0.3568 | 0.9414 | 0.8989 | 0.8212 | 0.8454 | 0.8045 | 0.7979 | 0.8921 | 0.8703 | 0.9141 | |
| ERGAS | 679.36 | 141.75 | 171.92 | 231.82 | 189.1 | 246.81 | 252.03 | 149.13 | 199.12 | 153.49 | |
| SAM | 42.28 | 10.12 | 12.92 | 16.96 | 14.81 | 18.08 | 19.79 | 7.99 | 14.14 | 11.18 | |
| 6 | PSNR | 14.46 | 27.8 | 26.67 | 26.91 | 27.37 | 23.25 | 22.08 | 28.56 | 27.03 | 29.39 |
| SSIM | 0.2865 | 0.8819 | 0.8509 | 0.7992 | 0.8269 | 0.646 | 0.5961 | 0.8642 | 0.7992 | 0.9084 | |
| ERGAS | 826.68 | 210.11 | 230.92 | 244.93 | 196.95 | 313.68 | 360.36 | 182.72 | 260.23 | 156.2 | |
| SAM | 44.13 | 14.11 | 15.52 | 17.24 | 14.74 | 22.83 | 26.56 | 9.66 | 15.66 | 10.74 |
| Methods | Case1 | Case2 | Case3 | Case4 | Case5 | Case6 |
|---|---|---|---|---|---|---|
| NMoG | 88.46 | 127.22 | 115.96 | 108.67 | 104.06 | 138.45 |
| NGMeet | 143.90 | 125.23 | 128.43 | 118.65 | 123.90 | 174.14 |
| LRTV | 85.89 | 90.18 | 103.39 | 94.78 | 93.25 | 103.40 |
| CTV | 145.89 | 150.53 | 173.55 | 162.89 | 157.76 | 162.34 |
| 3DTNN | 215.74 | 301.84 | 279.58 | 265.59 | 260.54 | 349.90 |
| 3DLogTNN | 381.56 | 409.09 | 399.21 | 366.45 | 356.73 | 473.65 |
| WNLRATV | 948.94 | 811.66 | 967.99 | 911.02 | 915.61 | 1091.36 |
| BALMF | 215.75 | 153.76 | 208.99 | 208.10 | 209.64 | 225.33 |
| NCTV | 178.76 | 132.49 | 138.10 | 135.01 | 141.77 | 211.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Mao, C.; Yang, Y.; Wang, S.; Xu, S. Hyperspectral Image Denoising Based on Non-Convex Correlated Total Variation. Remote Sens. 2025, 17, 2024. https://doi.org/10.3390/rs17122024
Sun J, Mao C, Yang Y, Wang S, Xu S. Hyperspectral Image Denoising Based on Non-Convex Correlated Total Variation. Remote Sensing. 2025; 17(12):2024. https://doi.org/10.3390/rs17122024
Chicago/Turabian StyleSun, Junjie, Congwei Mao, Yan Yang, Shengkang Wang, and Shuang Xu. 2025. "Hyperspectral Image Denoising Based on Non-Convex Correlated Total Variation" Remote Sensing 17, no. 12: 2024. https://doi.org/10.3390/rs17122024
APA StyleSun, J., Mao, C., Yang, Y., Wang, S., & Xu, S. (2025). Hyperspectral Image Denoising Based on Non-Convex Correlated Total Variation. Remote Sensing, 17(12), 2024. https://doi.org/10.3390/rs17122024





