A Dual-Branch Network for Intra-Class Diversity Extraction in Panchromatic and Multispectral Classification
Abstract
1. Introduction
- (1)
- Existing solutions aimed at addressing intra-class diversity still suffer from issues such as inefficiency or excessively long training times. The forgetting network may result in feature loss, which weakens the discriminative power between different classes and may even introduce further classification confusion. Moreover, using GANs for sample augmentation significantly increases the training time and is not well suited for classification with limited sample numbers. Therefore, there is a strong need for a method that can effectively mitigate intra-class diversity without increasing the number of training samples, while preserving as much original sample information as possible.
- (2)
- In real-world scenarios, the number and distribution of land cover types are often inherently imbalanced. When constructing remote sensing datasets by sampling from large-scale scenes, the long-tailed problem is almost inevitable. Alleviating the model’s bias toward head classes remains a crucial challenge that warrants significant attention.
- (3)
- Samples in dual-source datasets represent different descriptions of the same scene; therefore, it is necessary to design an improved network to fuse dual-source features and perform classification.
- (1)
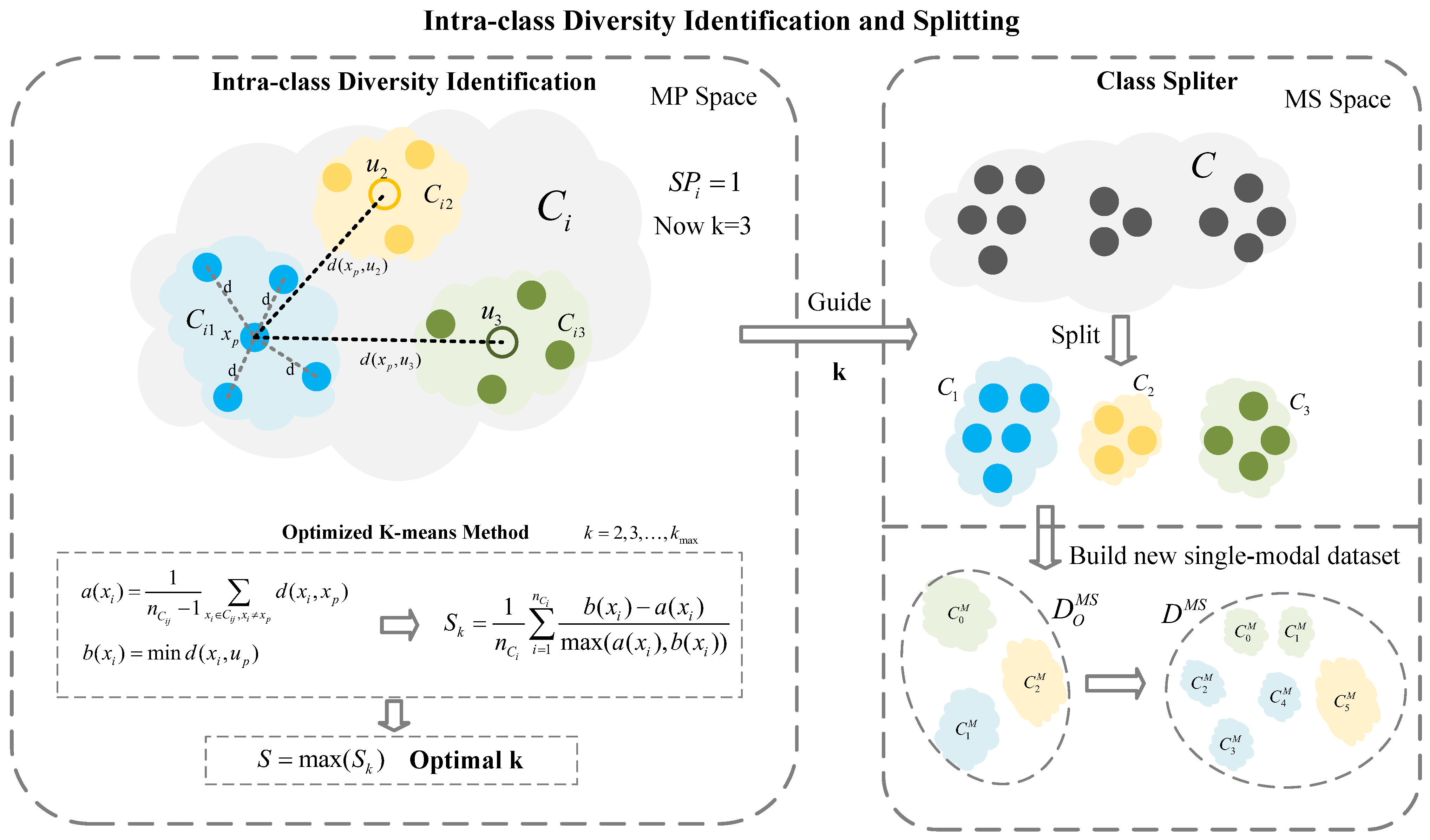
- We propose a novel modality-specific intra-class diversity modeling module, which independently estimates the intra-class diversity in MS and PAN modalities by computing the average intra-class variance. Classes exhibiting high diversity are automatically split using an optimized K-means algorithm, allowing fine-grained representation learning within each modality.
- (2)
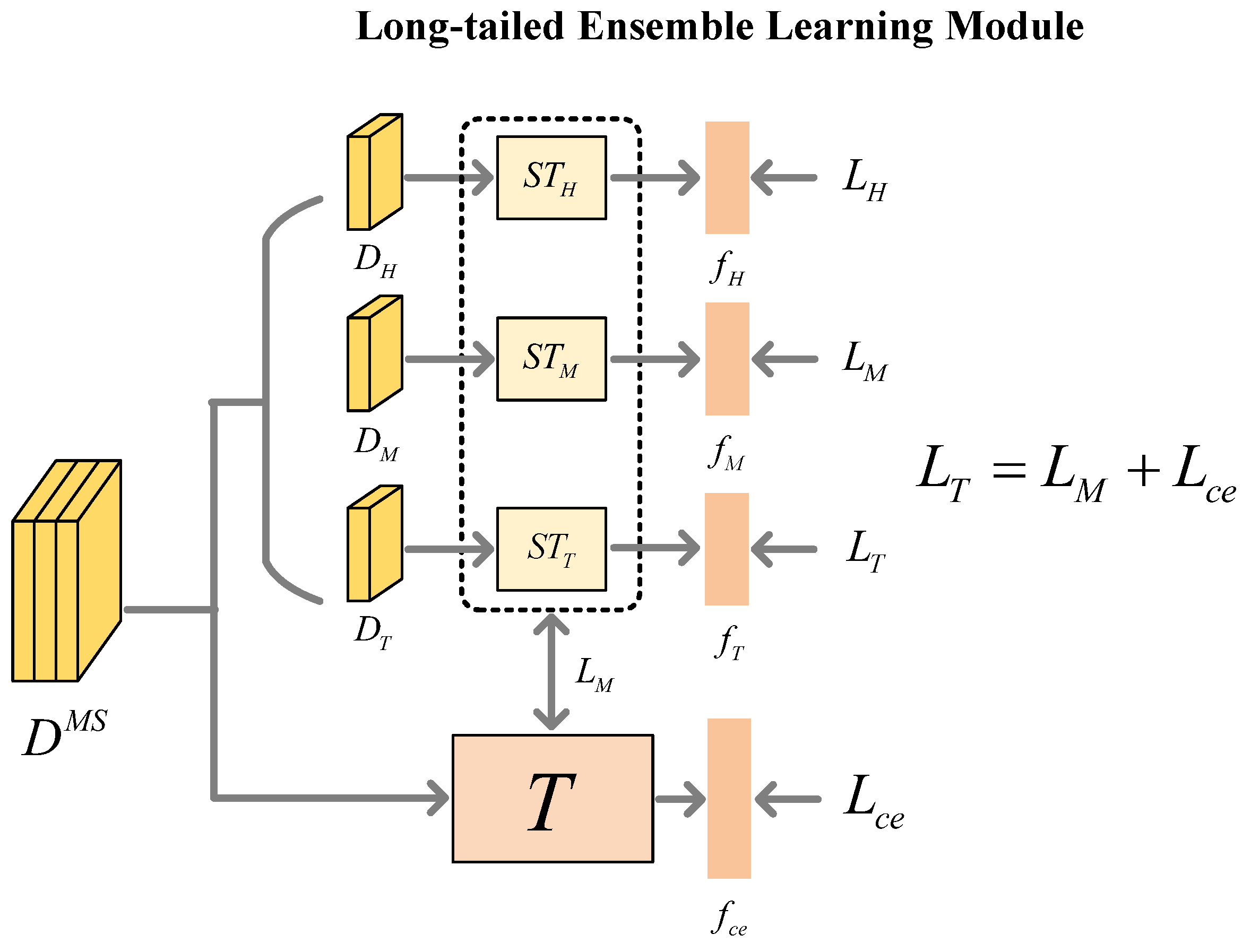
- To alleviate the long-tailed distribution problem commonly found in remote sensing data, we design a multi-expert-based long-tailed ensemble learning module (LELM), which independently extracts single-source features and reduces the dominance of head classes, thus improving the recognition of minority classes.
- (3)
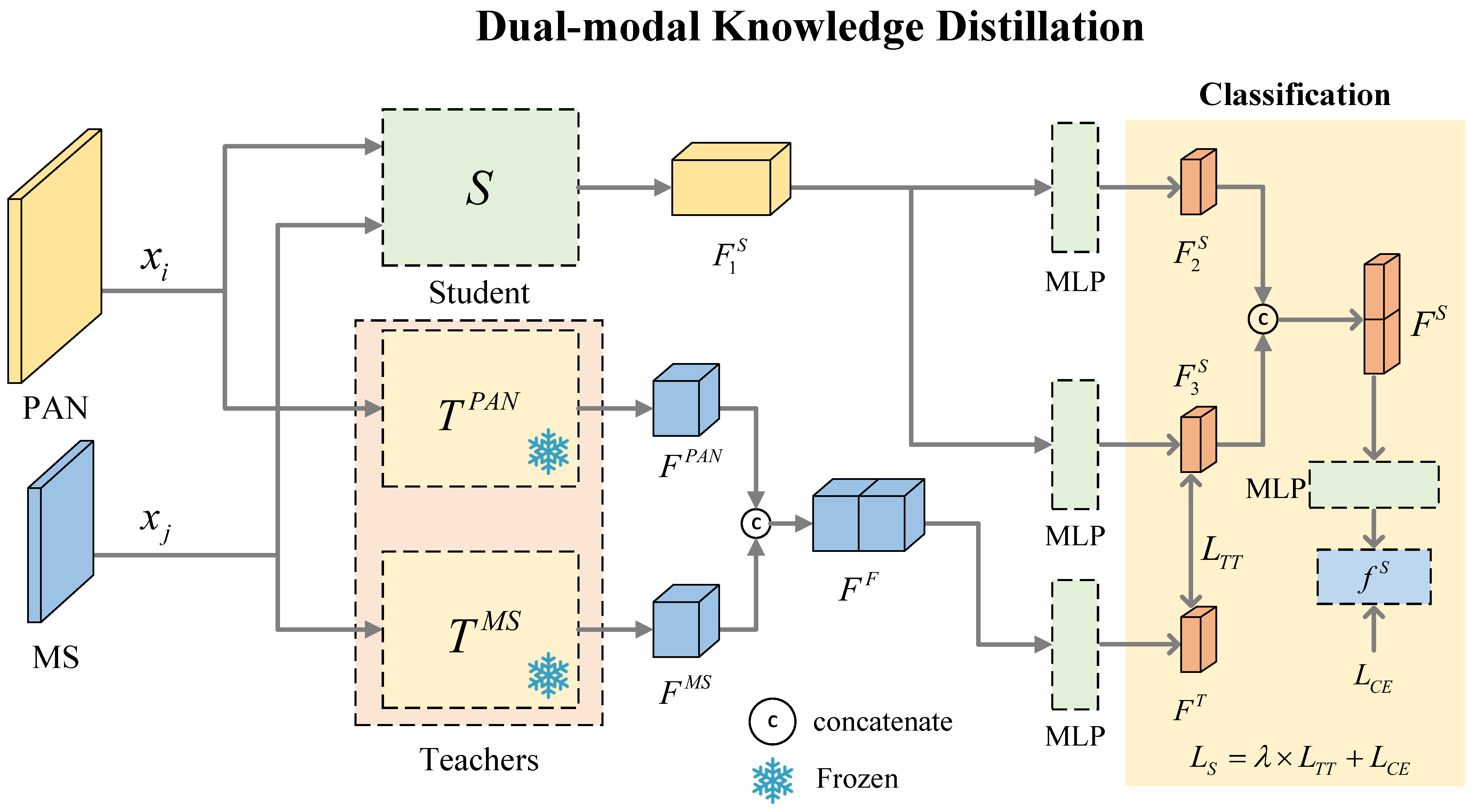
- We introduce a dual-modal knowledge distillation (DKD) framework to unify dual-source features while handling the class number inconsistency caused by modality-specific class splitting as shown in Figure 1. This framework facilitates effective feature fusion and enables compact student models to learn from teacher models with heterogeneous class structures.
2. Related Work
2.1. Intra-Class Diversity
2.2. Knowledge Distillation
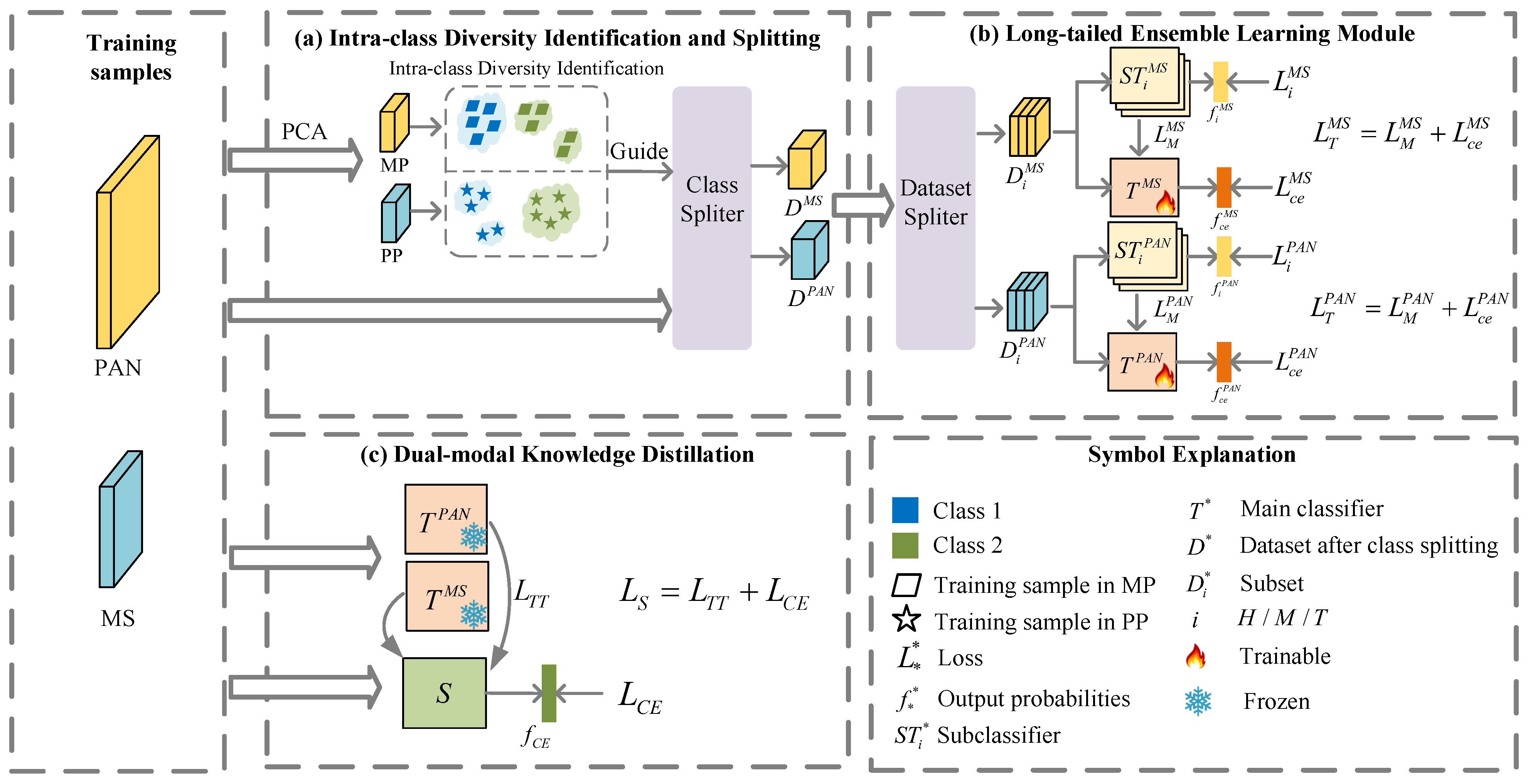
3. Method
3.1. Intra-Class Diversity Identification and Splitting
| Algorithm 1: Overall Pipeline of DEFC-Net |
Input: Original datasets , //
Step 1: Intra-Class Diversity Identification and Splitting (IDIS)
|
3.1.1. Intra-Class Diversity Identification
3.1.2. Optimized K-Means Method
3.2. Long-Tailed Ensemble Learning Module
3.2.1. Sub-Classifier Training Process
3.2.2. Main Classifier T Training Process
3.3. Dual-Modal Knowledge Distillation
4. Experimental Results
4.1. Dataset Description
4.1.1. Hohhot
4.1.2. Nanjing
4.1.3. Xi’an
4.2. Experimental Setup
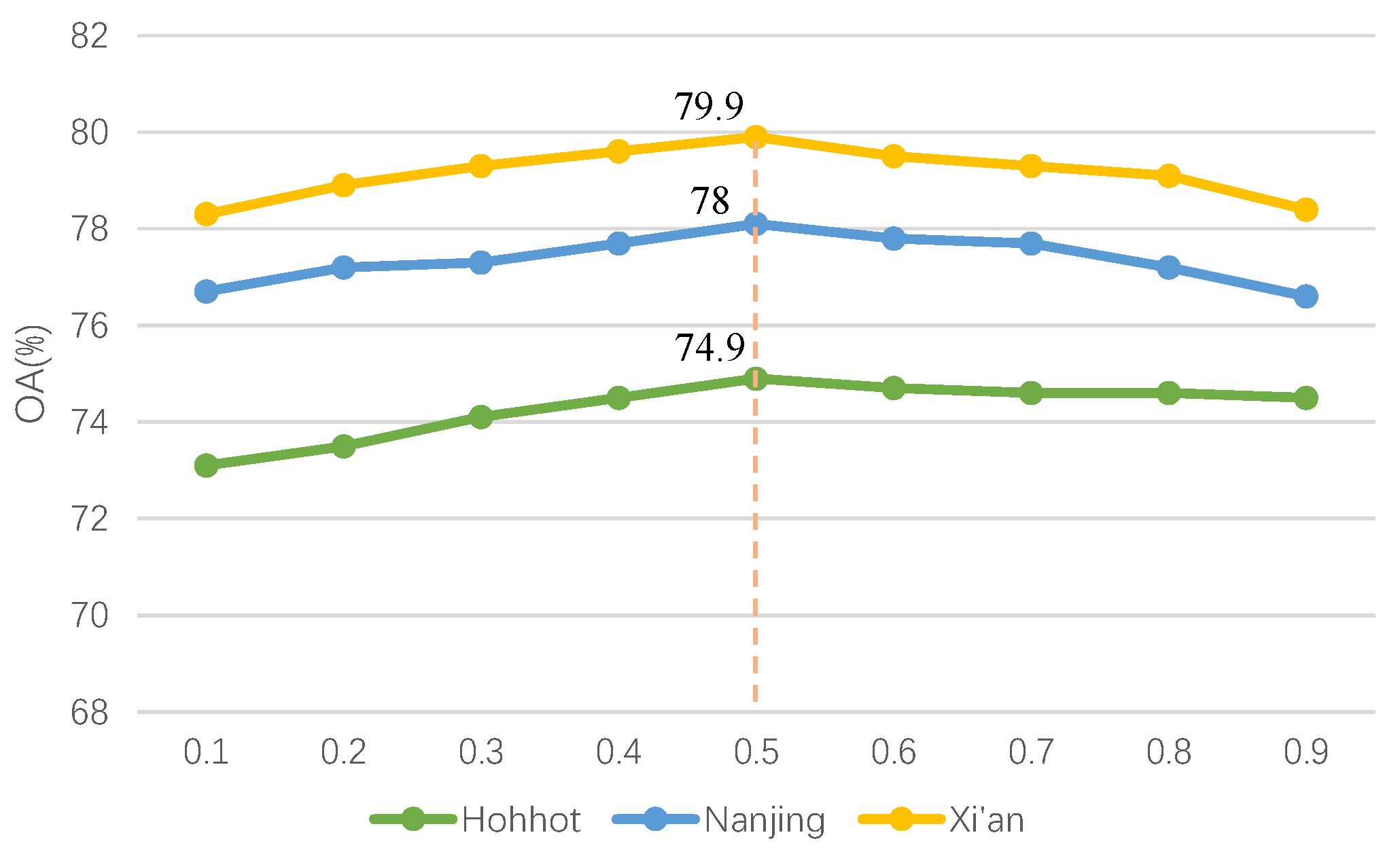
4.3. Hyperparameter Analysis
4.4. Experimental Results
4.4.1. Hohhot Dataset
4.4.2. Nanjing and Xi’an Datasets
4.5. Ablation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wady, S.; Bentoutou, Y.; Bengermikh, A.; Bounoua, A.; Taleb, N. A new IHS and wavelet based pansharpening algorithm for high spatial resolution satellite imagery. Adv. Space Res. 2020, 66, 1507–1521. [Google Scholar] [CrossRef]
- Zhang, X.; Dai, X.; Zhang, X.; Hu, Y.; Kang, Y.; Jin, G. Improved generalized IHS based on total variation for pansharpening. Remote Sens. 2023, 15, 2945. [Google Scholar] [CrossRef]
- Tu, T.M.; Lee, Y.C.; Chang, C.P.; Huang, P.S. Adjustable intensity-hue-saturation and Brovey transform fusion technique for IKONOS/QuickBird imagery. Opt. Eng. 2005, 44, 116201. [Google Scholar] [CrossRef]
- Chavez, P.; Sides, S.C.; Anderson, J.A. Comparison of three different methods to merge multiresolution and multispectral data- Landsat TM and SPOT panchromatic. Photogramm. Eng. Remote Sens. 1991, 57, 295–303. [Google Scholar]
- Yang, S.; Wang, M.; Jiao, L. Fusion of multispectral and panchromatic images based on support value transform and adaptive principal component analysis. Inf. Fusion 2012, 13, 177–184. [Google Scholar] [CrossRef]
- Singh, P.; Diwakar, M.; Cheng, X.; Shankar, A. A new wavelet-based multi-focus image fusion technique using method noise and anisotropic diffusion for real-time surveillance application. J. -Real-Time Image Process. 2021, 18, 1051–1068. [Google Scholar] [CrossRef]
- Wang, Z.; Cui, Z.; Zhu, Y. Multi-modal medical image fusion by Laplacian pyramid and adaptive sparse representation. Comput. Biol. Med. 2020, 123, 103823. [Google Scholar] [CrossRef]
- Luo, X.; Fu, G.; Yang, J.; Cao, Y.; Cao, Y. Multi-modal image fusion via deep Laplacian pyramid hybrid network. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 7354–7369. [Google Scholar] [CrossRef]
- Yao, J.; Zhao, Y.; Bu, Y.; Kong, S.G.; Chan, J.C.W. Laplacian pyramid fusion network with hierarchical guidance for infrared and visible image fusion. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 4630–4644. [Google Scholar] [CrossRef]
- Ma, J.; Yu, W.; Chen, C.; Liang, P.; Guo, X.; Jiang, J. Pan-GAN: An unsupervised pan-sharpening method for remote sensing image fusion. Inf. Fusion 2020, 62, 110–120. [Google Scholar] [CrossRef]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5449–5457. [Google Scholar]
- Liu, Q.; Zhou, H.; Xu, Q.; Liu, X.; Wang, Y. PSGAN: A generative adversarial network for remote sensing image pan-sharpening. IEEE Trans. Geosci. Remote Sens. 2020, 59, 10227–10242. [Google Scholar] [CrossRef]
- Zhu, H.; Yan, F.; Guo, P.; Li, X.; Hou, B.; Chen, K.; Wang, S.; Jiao, L. High-Low-Frequency Progressive-Guided Diffusion Model for PAN and MS Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–14. [Google Scholar] [CrossRef]
- Han, Y.; Zhu, H.; Jiao, L.; Yi, X.; Li, X.; Hou, B.; Ma, W.; Wang, S. SSMU-Net: A style separation and mode unification network for multimodal remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Zhu, H.; Sun, K.; Jiao, L.; Li, X.; Liu, F.; Hou, B.; Wang, S. Adaptive dual-path collaborative learning for PAN and MS classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Liao, Y.; Zhu, H.; Jiao, L.; Li, X.; Li, N.; Sun, K.; Tang, X.; Hou, B. A two-stage mutual fusion network for multispectral and panchromatic image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Ma, W.; Li, N.; Zhu, H.; Sun, K.; Ren, Z.; Tang, X.; Hou, B.; Jiao, L. A collaborative correlation-matching network for multimodality remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Zhao, G.; Ye, Q.; Sun, L.; Wu, Z.; Pan, C.; Jeon, B. Joint classification of hyperspectral and LiDAR data using a hierarchical CNN and transformer. IEEE Trans. Geosci. Remote Sens. 2022, 61, 1–16. [Google Scholar] [CrossRef]
- Han, H.; Zhang, Q.; Li, F.; Du, Y. Spatial oblivion channel attention targeting intra-class diversity feature learning. Neural Netw. 2023, 167, 10–21. [Google Scholar] [CrossRef]
- Li, W.; He, C.; Fang, J.; Zheng, J.; Fu, H.; Yu, L. Semantic segmentation-based building footprint extraction using very high-resolution satellite images and multi-source GIS data. Remote Sens. 2019, 11, 403. [Google Scholar] [CrossRef]
- Xie, H.; Chen, Y.; Ghamisi, P. Remote sensing image scene classification via label augmentation and intra-class constraint. Remote Sens. 2021, 13, 2566. [Google Scholar] [CrossRef]
- Sun, S.; Mu, L.; Wang, L.; Liu, P.; Liu, X.; Zhang, Y. Semantic segmentation for buildings of large intra-class variation in remote sensing images with O-GAN. Remote Sens. 2021, 13, 475. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Xu, K.; Rui, L.; Li, Y.; Gu, L. Feature normalized knowledge distillation for image classification. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer International Publishing: Zurich, Switwerland, 2020. [Google Scholar]
- Xu, C.; Gao, W.; Li, T.; Bai, N.; Li, G.; Zhang, Y. Teacher-student collaborative knowledge distillation for image classification. Appl. Intell. 2023, 53, 1997–2009. [Google Scholar] [CrossRef]
- Xu, M.; Zhao, Y.; Liang, Y.; Ma, X. Hyperspectral image classification based on class-incremental learning with knowledge distillation. Remote Sens. 2022, 14, 2556. [Google Scholar] [CrossRef]
- Chi, Q.; Lv, G.; Zhao, G.; Dong, X. A novel knowledge distillation method for self-supervised hyperspectral image classification. Remote Sens. 2022, 14, 4523. [Google Scholar] [CrossRef]
- Fu, H.; Zhou, S.; Yang, Q.; Tang, J.; Liu, G.; Liu, K.; Li, X. LRC-BERT: Latent-representation contrastive knowledge distillation for natural language understanding. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 12830–12838. [Google Scholar]
- Liu, X.; He, P.; Chen, W.; Gao, J. Improving multi-task deep neural networks via knowledge distillation for natural language understanding. arXiv 2019, arXiv:1904.09482. [Google Scholar]
- Liu, H.; Wang, Y.; Liu, H.; Sun, F.; Yao, A. Small scale data-free knowledge distillation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 6008–6016. [Google Scholar]
- Yang, C.; Zhu, Y.; Lu, W.; Wang, Y.; Chen, Q.; Gao, C.; Yan, B.; Chen, Y. Survey on knowledge distillation for large language models: Methods, evaluation, and application. ACM Trans. Intell. Syst. Technol. 2024. [Google Scholar] [CrossRef]
- Dinh, D.T.; Fujinami, T.; Huynh, V.N. Estimating the optimal number of clusters in categorical data clustering by silhouette coefficient. In Proceedings of the Knowledge and Systems Sciences: 20th International Symposium, KSS 2019, Da Nang, Vietnam, 29 November–1 December 2019; Proceedings 20. Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–17. [Google Scholar]
- Zhou, B.; Cui, Q.; Wei, X.S.; Chen, Z.M. Bbn: Bilateral-branch network with cumulative learning for long-tailed visual recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9719–9728. [Google Scholar]
- Sharma, S.; Yu, N.; Fritz, M.; Schiele, B. Long-tailed recognition using class-balanced experts. In Proceedings of the Pattern Recognition: 42nd DAGM German Conference, DAGM GCPR 2020, Tübingen, Germany, 28 September–1 October 2020; Proceedings 42. Springer: Berlin/Heidelberg, Germany, 2021; pp. 86–100. [Google Scholar]
- Li, T.; Cao, P.; Yuan, Y.; Fan, L.; Yang, Y.; Feris, R.S.; Indyk, P.; Katabi, D. Targeted supervised contrastive learning for long-tailed recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 6918–6928. [Google Scholar]
- Yang, Y.; Zha, K.; Chen, Y.; Wang, H.; Katabi, D. Delving into deep imbalanced regression. In Proceedings of the International Conference on Machine Learning, PMLR, Online, 18–24 July 2021; pp. 11842–11851. [Google Scholar]
- Zhao, H.; Liu, S.; Du, Q.; Bruzzone, L.; Zheng, Y.; Du, K.; Tong, X.; Xie, H.; Ma, X. GCFnet: Global Collaborative Fusion Network for Multispectral and Panchromatic Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Roy, S.K.; Deria, A.; Hong, D.; Rasti, B.; Plaza, A.; Chanussot, J. Multimodal Fusion Transformer for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–20. [Google Scholar] [CrossRef]
- Wang, M.; Gao, F.; Dong, J.; Li, H.C.; Du, Q. Nearest Neighbor-Based Contrastive Learning for Hyperspectral and LiDAR Data Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Shi, Y.; Lai, J.; Tan, X. AM3Net: Adaptive Mutual-Learning-Based Multimodal Data Fusion Network. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 5411–5426. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, H.; Ma, M.; Chen, C.; Hou, B. ISSP-Net: An interactive spatial-spectral perception network for multimodal classification. IEEE Trans. Geosci. Remote Sens. 2024. [CrossRef]

| Stage | Operation | MS_Branch | PAN_Branch | Output |
|---|---|---|---|---|
| Intra-Class Diversity Identification and Splitting | PCA | |||
| Variance | ||||
| Splitting | ||||
| Single-Modal Classification Enhancement Module | Training | |||
| T Training | ||||
| Dual-Modal Knowledge Distillation | - | |||
| - | ||||
| S | Class |
| Methods | IHS+ResNet | NNC-Net | MFT-Net | -Net | CRHFF-Net | GCF-Net | ISSP-Net | DEFC-Net |
|---|---|---|---|---|---|---|---|---|
| c1 | 84.60 | 87.55 | 96.18 | 92.02 | 95.80 | 86.70 | 92.45 | 89.20 |
| c2 | 69.14 | 75.40 | 76.46 | 76.39 | 81.48 | 62.20 | 82.82 | 85.39 |
| c3 | 90.13 | 84.76 | 81.99 | 84.44 | 88.48 | 68.84 | 84.01 | 84.79 |
| c4 | 79.20 | 85.24 | 69.03 | 84.38 | 87.85 | 76.07 | 79.24 | 84.12 |
| c5 | 66.45 | 67.63 | 54.23 | 56.88 | 59.57 | 58.99 | 63.79 | 67.57 |
| c6 | 59.90 | 60.41 | 60.83 | 65.17 | 60.56 | 61.91 | 64.18 | 63.74 |
| c7 | 78.01 | 73.94 | 67.83 | 86.66 | 69.98 | 70.10 | 71.92 | 79.36 |
| c8 | 90.10 | 91.94 | 91.36 | 92.59 | 93.53 | 89.51 | 95.12 | 89.98 |
| c9 | 63.1 | 52.93 | 58.79 | 55.63 | 55.16 | 54.46 | 62.65 | 61.51 |
| c10 | 53.75 | 57.38 | 82.46 | 74.00 | 78.50 | 32.37 | 72.32 | 71.74 |
| c11 | 77.81 | 59.86 | 75.04 | 67.77 | 77.11 | 32.03 | 78.13 | 69.12 |
| OA | 71.72 | 70.85 | 69.33 | 72.31 | 72.21 | 63.77 | 73.77 | 74.93 |
| AA | 73.84 | 72.46 | 74.02 | 75.91 | 77.09 | 63.01 | 76.97 | 77.96 |
| Kappa | 68.04 | 67.00 | 65.47 | 68.95 | 68.82 | 58.99 | 70.39 | 71.63 |
| Time | 131.39 | 83.42 | 15.62 | 81.62 | 150.86 | 265.81 | 145.18 | 173.24 |
| Method | IHS+ResNet | NNC-Net | MFT-Net | -Net | CRHFF-Net | GCF-Net | ISSP-Net | DEFC-Net |
|---|---|---|---|---|---|---|---|---|
| c1 | 91.74 | 94.77 | 94.23 | 88.44 | 94.86 | 93.45 | 94.24 | 95.96 |
| c2 | 25.47 | 67.25 | 64.21 | 40.62 | 72.96 | 37.36 | 59.47 | 70.27 |
| c3 | 86.26 | 88.19 | 91.84 | 54.10 | 94.24 | 84.98 | 94.50 | 92.97 |
| c4 | 85.94 | 75.83 | 76.58 | 71.55 | 84.85 | 78.65 | 80.80 | 84.53 |
| c5 | 63.92 | 77.94 | 75.54 | 67.85 | 77.61 | 24.98 | 78.04 | 84.98 |
| c6 | 94.53 | 93.03 | 91.60 | 93.66 | 95.59 | 44.95 | 95.33 | 97.27 |
| c7 | 72.55 | 75.72 | 64.48 | 74.96 | 59.08 | 64.42 | 69.34 | 66.53 |
| c8 | 81.61 | 84.37 | 75.73 | 90.98 | 81.76 | 64.74 | 58.44 | 82.13 |
| c9 | 35.96 | 47.68 | 38.92 | 80.99 | 53.61 | 45.62 | 52.80 | 51.54 |
| c10 | 58.88 | 53.03 | 34.21 | 91.86 | 43.07 | 13.58 | 33.90 | 48.30 |
| c11 | 85.38 | 66.78 | 63.27 | 43.96 | 62.74 | 47.84 | 59.09 | 58.43 |
| OA | 71.29 | 77.77 | 73.35 | 70.22 | 75.52 | 61.65 | 75.01 | 78.05 |
| AA | 71.11 | 74.96 | 70.06 | 72.63 | 74.58 | 54.60 | 70.54 | 75.72 |
| Kappa | 66.31 | 74.03 | 69.11 | 65.02 | 71.77 | 55.01 | 71.03 | 74.56 |
| Time | 158.73 | 142.89 | 28.57 | 140.97 | 206.27 | 198.96 | 286.71 | 241.34 |
| Method | IHS+ResNet | NNC-Net | MFT-Net | -Net | CRHFF-Net | GCF-Net | ISSP-Net | DEFC-Net |
|---|---|---|---|---|---|---|---|---|
| c1 | 92.19 | 93.15 | 97.35 | 95.61 | 95.89 | 96.75 | 95.89 | 97.52 |
| c2 | 9.72 | 34.16 | 16.82 | 1.72 | 18.35 | 17.46 | 26.29 | 32.32 |
| c3 | 61.09 | 62.14 | 50.69 | 11.61 | 62.01 | 55.38 | 68.75 | 58.70 |
| c4 | 65.03 | 69.01 | 64.58 | 67.74 | 66.45 | 66.46 | 72.70 | 74.35 |
| c5 | 36.50 | 55.10 | 46.68 | 18.81 | 55.51 | 36.06 | 54.81 | 40.00 |
| c6 | 63.91 | 68.41 | 51.69 | 76.35 | 69.74 | 64.31 | 71.42 | 80.29 |
| c7 | 93.52 | 77.92 | 91.78 | 37.73 | 84.84 | 89.12 | 86.47 | 76.60 |
| c8 | 94.97 | 74.62 | 62.85 | 72.44 | 77.59 | 72.65 | 74.57 | 84.01 |
| c9 | 62.26 | 77.48 | 75.73 | 80.85 | 77.18 | 76.40 | 77.17 | 75.61 |
| c10 | 94.26 | 96.81 | 91.90 | 99.81 | 95.51 | 97.81 | 95.47 | 96.56 |
| c11 | 88.42 | 94.23 | 94.52 | 75.48 | 95.39 | 90.71 | 92.03 | 93.78 |
| c12 | 62.48 | 76.02 | 72.87 | 45.00 | 75.33 | 66.36 | 67.29 | 74.92 |
| OA | 75.27 | 79.24 | 74.65 | 69.58 | 79.42 | 76.86 | 79.58 | 79.93 |
| AA | 68.70 | 73.25 | 68.12 | 56.93 | 72.81 | 69.05 | 73.64 | 73.72 |
| Kappa | 71.89 | 76.24 | 71.08 | 64.18 | 76.44 | 73.48 | 76.66 | 77.07 |
| Time | 423.34 | 756.16 | 140.23 | 1401.60 | 1159.40 | 2474.40 | 872.85 | 1867.91 |
| Baseline | IDIS | LELM | DKD | OA | AA | Kappa |
|---|---|---|---|---|---|---|
| 🗸 | 65.41 | 66.39 | 64.12 | |||
| 🗸 | 🗸 | 🗸 | 68.51 | 69.86 | 66.70 | |
| 🗸 | 🗸 | 🗸 | 71.34 | 73.35 | 69.07 | |
| 🗸 | 🗸 | 🗸 | 🗸 | 74.93 | 76.96 | 71.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Tian, P.; Zhu, H.; Guo, P.; Li, X. A Dual-Branch Network for Intra-Class Diversity Extraction in Panchromatic and Multispectral Classification. Remote Sens. 2025, 17, 1998. https://doi.org/10.3390/rs17121998
Huang Z, Tian P, Zhu H, Guo P, Li X. A Dual-Branch Network for Intra-Class Diversity Extraction in Panchromatic and Multispectral Classification. Remote Sensing. 2025; 17(12):1998. https://doi.org/10.3390/rs17121998
Chicago/Turabian StyleHuang, Zihan, Pengyu Tian, Hao Zhu, Pute Guo, and Xiaotong Li. 2025. "A Dual-Branch Network for Intra-Class Diversity Extraction in Panchromatic and Multispectral Classification" Remote Sensing 17, no. 12: 1998. https://doi.org/10.3390/rs17121998
APA StyleHuang, Z., Tian, P., Zhu, H., Guo, P., & Li, X. (2025). A Dual-Branch Network for Intra-Class Diversity Extraction in Panchromatic and Multispectral Classification. Remote Sensing, 17(12), 1998. https://doi.org/10.3390/rs17121998






