Sea Clutter Suppression for Shipborne DRM-Based Passive Radar via Carrier Domain STAP
Abstract
1. Introduction
2. Background
2.1. Signal Model
2.2. Traditional STAP Algorithm
3. Method
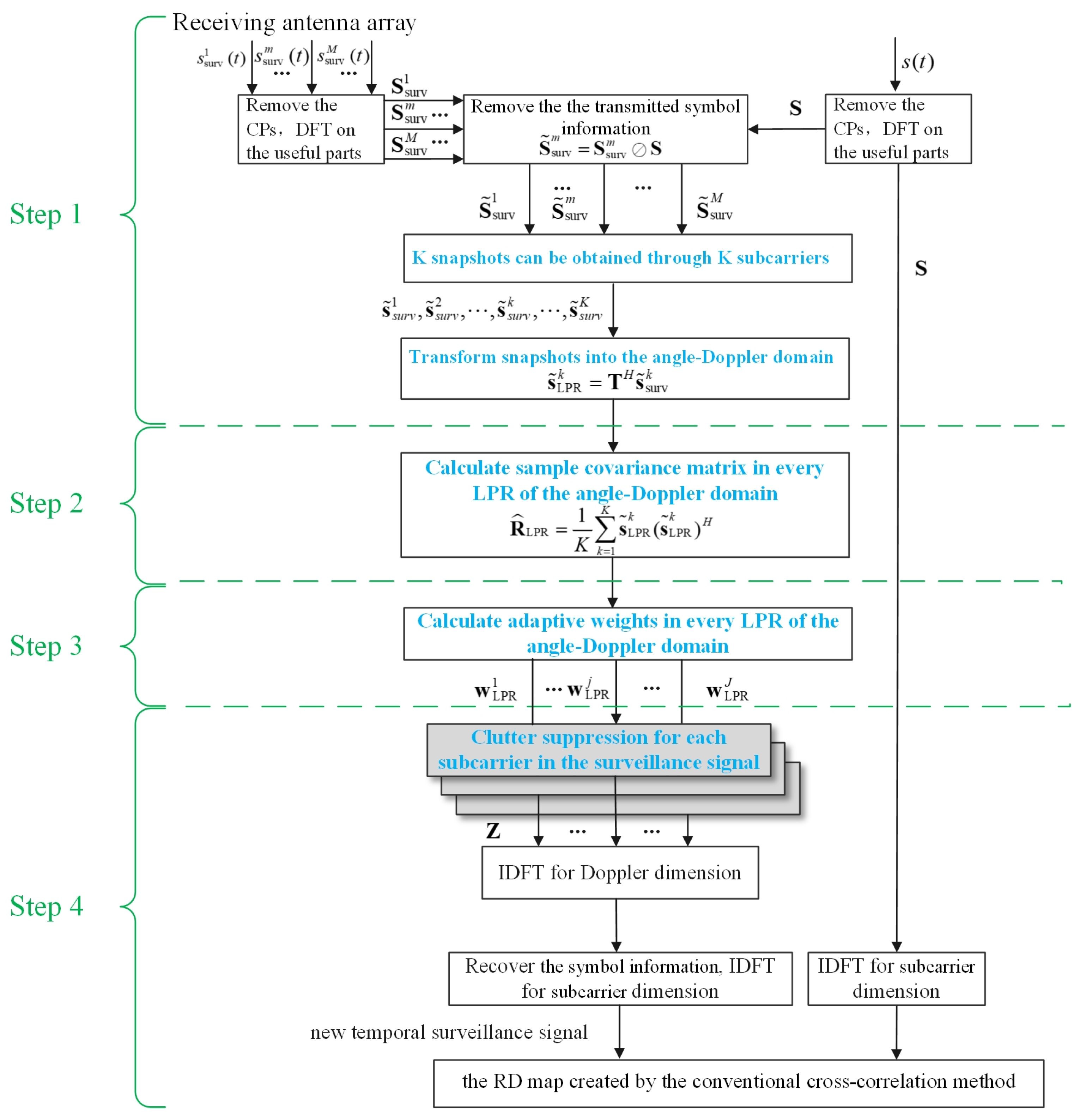
3.1. The Principle of the STAP-C
3.2. Dimensionality Reduction STAP
3.3. Computational Complexity
4. Results on Simulation Data
4.1. Improve Factor
4.2. The Results of Clutter Suppression
4.3. Computation Time
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Palmer, J.; Harms, H.; Searle, S.; Davis, L. DVB-T Passive Radar Signal Processing. IEEE Trans. Signal Process. 2013, 61, 2116–2126. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, J.; Zhang, Z.; Liu, H.; Zhou, S. Linear fusion for target detection in passive multistatic radar. Signal Process. 2017, 130, 175–182. [Google Scholar] [CrossRef]
- Mohammad, Z.; Abbas, S. Adaptive detection for passive radars using the structure of interference covariance matrix. Signal Process. 2021, 178, 107761. [Google Scholar]
- Filip, A.; Shutin, D. Ambiguity Function Analysis for OFDM-Based LDACS Passive Multistatic Radar. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1323–1340. [Google Scholar] [CrossRef]
- Zhao, Z.; Wan, X.; Zhang, D.; Cheng, F. An Experimental Study of HF Passive Bistatic Radar Via Hybrid Sky-Surface Wave Mode. IEEE Trans. Antennas Propag. 2013, 61, 415–424. [Google Scholar] [CrossRef]
- Kim, S.; Park, K.; Lee, K.; Choi, H. Detection method for digital radio mondiale plus in hybrid broadcasting mode. IEEE Trans. Consum. Electron. 2013, 59, 9–15. [Google Scholar] [CrossRef]
- Santi, F.; Pastina, D.; Bucciarelli, M. Experimental Demonstration of Ship Target Detection in GNSS-Based Passive Radar Combining Target Motion Compensation and Track-before-Detect Strategies. Sensors 2020, 20, 599. [Google Scholar] [CrossRef]
- Mazurek, G.; Kulpa, K.; Malanowski, M.; Droszcz, A. Experimental Seaborne Passive Radar. Sensors 2021, 21, 2171. [Google Scholar] [CrossRef]
- Liu, W.; Wu, Y.; Jiang, Q.; Liu, J.; Xu, S.; Gong, P. Eigenvalue-based distributed target detection in compound-Gaussian clutter. Sci. China Inf. Sci. 2025. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, W.; Liu, J.; Wu, Y.; Du, Q.; Hua, X. Bayesian Rao test for distributed target detection in interference and noise with limited training data. arXiv 2025, arXiv:2504.13235. [Google Scholar]
- Xu, Z.; Liu, W.; Wu, C.; Du, Q.; Liu, J. Statistical performance of Generalized direction detectors in the case of known spatial steering vector. arXiv 2025, arXiv:2505.03076. [Google Scholar]
- Ji, Y.; Zhang, J.; Wang, Y.; Yue, C.; Gong, W.; Liu, J.; Sun, H.; Yu, C.; Li, M. Coast–Ship Bistatic HF Surface Wave Radar: Simulation Analysis and Experimental Verification. Remote Sens. 2020, 12, 470. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Li, Y.; Wang, P.; Wu, L.; Liu, A. A Spread Sea Clutter Suppression Method Based on Prior Knowledge for HF Hybrid Sky-Surface Wave Radar. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; pp. 1905–1909. [Google Scholar]
- Guo, Y.; Geng, J.; Zhang, X.; Dong, H. Zero-Doppler clutter suppression for DRM-based passive radar under block fading channel via regularized ECA-C. Digit. Signal Process. 2025, 160, 105056. [Google Scholar] [CrossRef]
- Hu, S.; Yi, J.; Wan, X.; Cheng, F.; Tong, Y. Doppler Separation-Based Clutter Suppression Method for Passive Radar on Moving Platforms. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–14. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, H.; Zong, B.; Xie, J. A Fast Power Allocation Strategy for Multibeam Tracking Multiple Targets in Clutter. IEEE Syst. J. 2022, 16, 1249–1257. [Google Scholar] [CrossRef]
- Guan, X.; Hu, D.; Zhong, L.; Ding, C. Strong Echo Cancellation Based on Adaptive Block Notch Filter in Passive Radar. IEEE Geosci. Remote Sens. Lett. 2015, 12, 339–343. [Google Scholar] [CrossRef]
- Garry, J.; Baker, C.; Smith, G. Evaluation of Direct Signal Suppression for Passive Radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3786–3799. [Google Scholar] [CrossRef]
- Colone, F.; O’Hagan, D.; Lombardo, P.; Baker, C. A Multistage Processing Algorithm for Disturbance Removal and Target Detection in Passive Bistatic Radar. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 698–722. [Google Scholar] [CrossRef]
- Colone, F.; Palmarini, C.; Martelli, T.; Tilli, E. Sliding extensive cancellation algorithm for disturbance removal in passive radar. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1309–1326. [Google Scholar] [CrossRef]
- Searle, S.; Gustainis, D.; Hennessy, B.; Young, R. Cancelling strong Doppler shifted returns in OFDM based passive radar. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 0359–0354. [Google Scholar]
- Paolo Blasone, G.; Colone, F.; Lombardo, P.; Wojaczek, P.; Cristallini, D. Passive Radar DPCA Schemes with Adaptive Channel Calibration. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4014–4034. [Google Scholar] [CrossRef]
- Wojaczek, P.; Colone, F.; Cristallini, D.; Lombardo, P.; Kuschel, H. The application of the reciprocal filter and DPCA for GMTI in DVB-T - PCL. In Proceedings of the International Conference on Radar Systems (Radar 2017), Belfast, UK, 23–26 October 2017; pp. 1–5. [Google Scholar]
- Dawidowicz, B.; Kulpa, K.; Malanowski, M.; Misiurewicz, J.; Samczynski, P.; Smolarczyk, M. DPCA Detection of Moving Targets in Airborne Passive Radar. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1347–1357. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Z.; Xing, M.; Zhang, S.; Wang, Y. Research on Multi-Domain Dimensionality Reduction Joint Adaptive Processing Method for Range Ambiguous Clutter of FDA-Phase-MIMO Space-Based Early Warning Radar. Remote Sens. 2022, 14, 5536. [Google Scholar] [CrossRef]
- Xie, K.; Wang, C.; Liu, C.; Zhou, F. A novel non-convex penalty function-based STAP algorithm for airborne passive radar systems. Digit. Signal Process. 2024, 149, 104486. [Google Scholar] [CrossRef]
- Blasone, G.P.; Colone, F.; Lombardo, P.; Wojaczek, P.; Cristallini, D. Passive Radar STAP Detection and DoA Estimation Under Antenna Calibration Errors. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2725–2742. [Google Scholar] [CrossRef]
- Wang, B.; Cha, H.; Zhou, Z.; Tian, B. Clutter Cancellation and Long Time Integration for GNSS-Based Passive Bistatic Radar. Remote Sens. 2021, 13, 701. [Google Scholar] [CrossRef]
- Liu, Y.; Yi, J.; Wan, X.; Zhang, X.; Ke, H. Evaluation of Clutter Suppression in CP-OFDM-Based Passive Radar. IEEE Sens. J. 2019, 19, 5572–5586. [Google Scholar] [CrossRef]
- Yi, J.; Wan, X.; Li, D.; Leung, H. Robust Clutter Rejection in Passive Radar via Generalized Subband Cancellation. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1931–1946. [Google Scholar] [CrossRef]
- Li, Z.; Ka, F.; Dai, Y.; Nordholm, S. Distributed LCMV beamformer design by randomly permuted ADMM. Digit. Signal Process. 2020, 106, 102820. [Google Scholar] [CrossRef]
- Liang, J.; Wang, T.; Liu, W.; So, H.; Huang, Y.; Tang, B. Constant Modulus Waveform Estimation and Interference Suppression via Two-Stage Fractional Program-Based Beamforming. IEEE Trans. Signal Process. 2024, 72, 2348–2363. [Google Scholar] [CrossRef]
- Zhou, X.; Wei, Y.; Liu, Y. Broadened Sea Clutter Suppression Method for Shipborne HF Hybrid Sky-Surface Wave Radar. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar]
- Lan, L.; Liao, G.; Xu, J.; Xu, Y.; So, H. Beampattern Synthesis Based on Novel Receive Delay Array for Mainlobe Interference Mitigation. IEEE Trans. Antennas Propag. 2023, 71, 4470–4485. [Google Scholar] [CrossRef]
- Kawalec, A.; Ślesicka, A.; Ślesicki, B. A New Statistical Method for Determining the Clutter Covariance Matrix in Spatial–Temporal Adaptive Processing of a Radar Signal. Sensors 2023, 23, 4280. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Bai, Y.; Zhu, X.; Wu, X.; Hong, H.; Ding, C.; Zhao, H. Spreading Sea Clutter Suppression for High-Frequency Hybrid Sky-Surface Wave Radar Using Orthogonal Projection in Spatial–Temporal Domain. Remote Sens. 2024, 16, 2470. [Google Scholar] [CrossRef]
- Adve, R.; Hale, T.; Wicks, M. Practical joint domain localised adaptive processing in homogeneous and nonhomogeneous environments. Part 1: Homogeneous environments. IEEE Proc. Radar. Sonar Navig. 2000, 147, 57–65. [Google Scholar] [CrossRef]
- Ji, Z.; Yi, C.; Xie, J.; Li, Y. The Application of JDL to Suppress Sea Clutter for Shipborne HFSWR. Int. J. Antennas Propag. 2015, 2015, 825350. [Google Scholar] [CrossRef]
- Fan, X.; Yang, F. A robust space-time multiple-beam STAP algorithm. In Proceedings of the 2010 2nd International Conference on Signal Processing Systems, Dalian, China, 5–7 October 2010; Volume 1, pp. V1-44–V1-47. [Google Scholar]
- Mahfoudia, O.; Horlin, F.; Neyt, X. Performance analysis of the reference signal reconstruction for DVB-T passive radars. Signal Process. 2019, 158, 26–35. [Google Scholar] [CrossRef]
- Wan, X.; Wang, J.; Sheng, H.; Hui, T. Reconstruction of reference signal for DTMB-based passive radar systems. In Proceedings of the 2011 IEEE CIE International Conference on Radar, Chengdu, China, 24–27 October 2011; Volume 1, pp. 165–168. [Google Scholar]
- Zhang, H.; Liu, W.; Zhang, Q.; Liu, B. Joint Customer Assignment, Power Allocation, and Subchannel Allocation in a UAV-Based Joint Radar and Communication Network. IEEE Internet Things J. 2024, 11, 29643–29660. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, Q.; Fei, T. A robust joint frequency spectrum and power allocation strategy in a coexisting radar and communication system. Chin. J. Aeronaut. 2024, 37, 393–409. [Google Scholar] [CrossRef]
- Baczyk, M.; Malanowski, M. Decoding and reconstruction of reference DVB-T signal in passive radar systems. In Proceedings of the Eleventh International Radar Symposium (IRS), Vilnius, Lithuania, 16–18 June 2010; pp. 1–4. [Google Scholar]
- Skolnik, M.I. An Analysis of Bistatic Radar. Ire Trans. Aerosp. Navig. Electron. 1961, ANE-8, 19–27. [Google Scholar] [CrossRef]
- Nicholas, J. Bistatic Radar, 2nd ed.; SciTech Publishing: Raleigh, NC, USA, 2005; pp. 119–123. [Google Scholar]
- Mestre, X.; Lagunas, M. Finite sample size effect on minimum variance beamformers: Optimum diagonal loading factor for large arrays. IEEE Trans. Signal Process. 2006, 54, 69–82. [Google Scholar] [CrossRef]
- Bolvardi, H.; Derakhtian, M.; Sheikhi, A. Dynamic Clutter Suppression and Multitarget Detection in a DVB-T-Based Passive Radar. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1812–1825. [Google Scholar] [CrossRef]
- Huang, P.; Zou, Z.; Xia, X.; Liu, X.; Liao, G. A Novel Dimension-Reduced Space–Time Adaptive Processing Algorithm for Spaceborne Multichannel Surveillance Radar Systems Based on Spatial–Temporal 2-D Sliding Window. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–21. [Google Scholar] [CrossRef]
- European Telecommunication Standards Institute (ETSI). ETSI ES 201 980 V4.3.1-Digital radio mondiale (DRM). Syst. Specif. 2023, 113–115. Available online: https://standards.iteh.ai/catalog/standards/etsi/1b590410-bef5-4baf-973b-8e51115676b6/etsi-es-201-980-v4-3-1-2023-11?srsltid=AfmBOopuy6glxIl-TuZzaGS2IMf9MA_LdrgMxnTlr24p-6EpcRgwzl9R (accessed on 25 January 2025).
- Skolnik, M. Radar Handbook, 3rd ed.; McGraw-Hill Companies: New York, NY, USA, 2008; Chapter 2. [Google Scholar]







| Algorithm | Dimension Value | Overall Computation |
|---|---|---|
| , , | ||
| , , | ||
| traditional JDL-STAP | , | |
| traditional STMB-STAP | , | |
| JDL-STAP-C | ||
| , |
| Parameters | Value |
|---|---|
| Radar frequency | MHz |
| Signal Bandwidth | 10 kHz |
| Sampling rate | 48 kHz |
| Number of symbols L | 1536 |
| the duration of one symbol | ms |
| Number of spatial channels M | 8 |
| Number of clutter range cells | 64 |
| radar wavelength | m |
| array element spacing d | |
| receiver velocity | 5 m/s |
| Initial localization of the transmitter | km |
| Initial localization of the receiver | km |
| Items | Time Delay | Range | Range | Radial | Doppler | Doppler | Direction | CNR, SNR |
|---|---|---|---|---|---|---|---|---|
| (ms) | Bin | (km) | Velocity (m/s) | Frequency (Hz) | Bin | (deg) | (dB) | |
| Direct wave | 0 | 1 | 0 | 772 | 150 | 75 | ||
| Sea clutter | 0~0.66 | 1~64 | 0~196.88 | −18.24~18.28 | −0.32~0.32 | 755.8~782.2 | 0~180 | 70 |
| Target 1 | 17 | 50 | 814 | 60 | 30 | |||
| Target 2 | 33 | 100 | 60 | 22 | ||||
| Target 3 | 49 | 150 | 60 | 15 |
| Items | Traditional JDL-STAP | Traditional STMB-STAP | JDL-STAP-C |
|---|---|---|---|
| IF(dB) |
| Items | Traditional JDL-STAP | Traditional STMB-STAP | JDL-STAP-C |
|---|---|---|---|
| Time(s) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Geng, J.; Zhang, X.; Dong, H. Sea Clutter Suppression for Shipborne DRM-Based Passive Radar via Carrier Domain STAP. Remote Sens. 2025, 17, 1985. https://doi.org/10.3390/rs17121985
Guo Y, Geng J, Zhang X, Dong H. Sea Clutter Suppression for Shipborne DRM-Based Passive Radar via Carrier Domain STAP. Remote Sensing. 2025; 17(12):1985. https://doi.org/10.3390/rs17121985
Chicago/Turabian StyleGuo, Yijia, Jun Geng, Xun Zhang, and Haiyu Dong. 2025. "Sea Clutter Suppression for Shipborne DRM-Based Passive Radar via Carrier Domain STAP" Remote Sensing 17, no. 12: 1985. https://doi.org/10.3390/rs17121985
APA StyleGuo, Y., Geng, J., Zhang, X., & Dong, H. (2025). Sea Clutter Suppression for Shipborne DRM-Based Passive Radar via Carrier Domain STAP. Remote Sensing, 17(12), 1985. https://doi.org/10.3390/rs17121985






