A Comprehensive Benchmarking Framework for Sentinel-2 Sharpening: Methods, Dataset, and Evaluation Metrics
Abstract
1. Introduction
- a.
- The lack of high-resolution PAN prevents a direct application of standard pansharpening methods.
- b.
- Bands distributed on three spatial resolution levels: 10, 20, and 60 m GSD.
- c.
- Wide spectral range, from visible to SWIR (443–2280 nm).
- d.
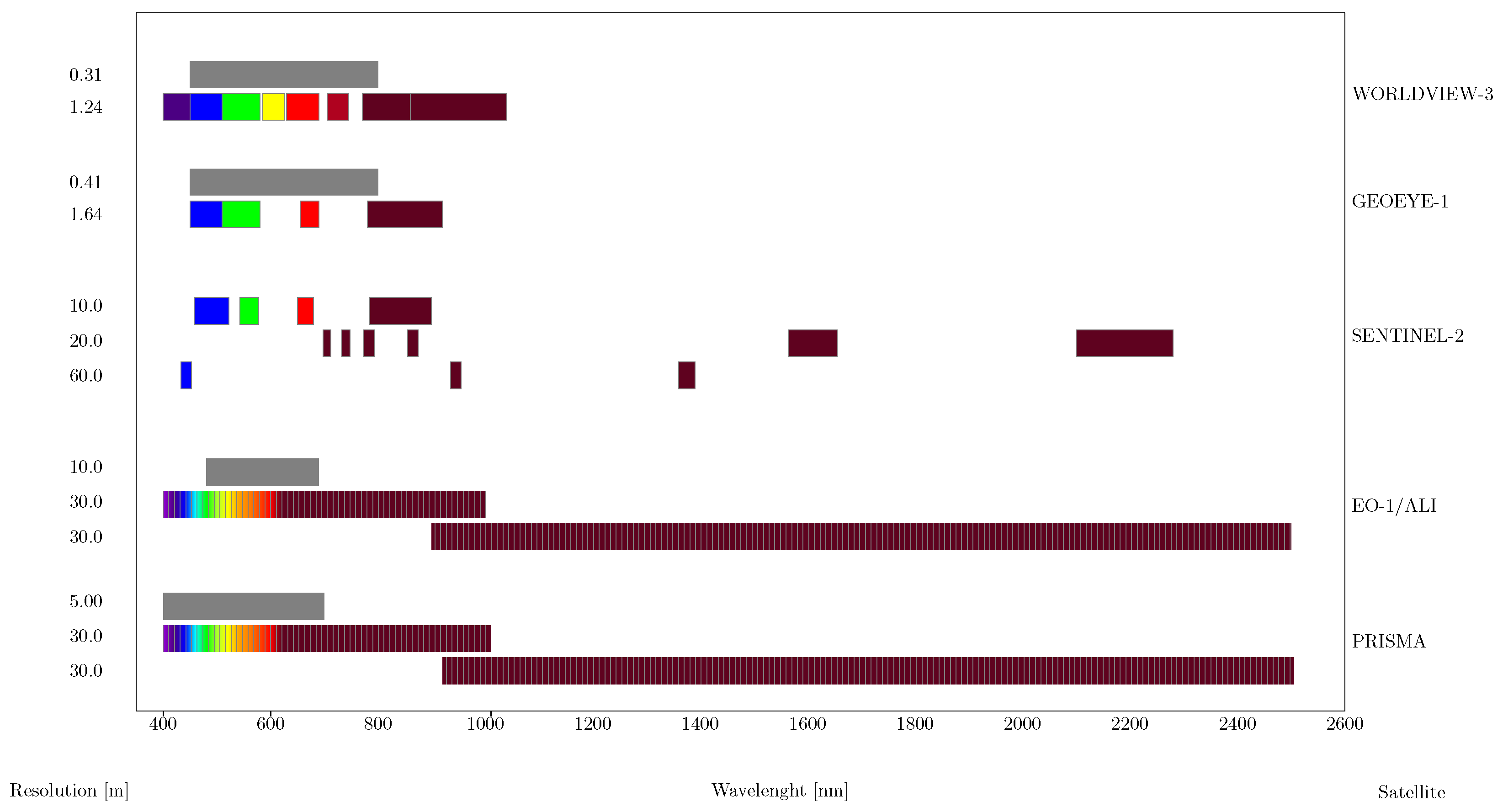
- Discontinuous spectral coverage with considerable gaps (see Figure 1) that induce significant correlation drops across certain “adjacent” bands.
2. Related Work
3. Selected Sentinel-2 Sharpening Methods
- a.
- Methodological uniqueness;
- b.
- High quality and/or computational efficiency;
- c.
- Availability of open-source code or sufficient documentation for reproducibility.
3.1. Adapting Pansharpening Methods
- Selective scheme: no bias terms and only one HR band selected for each target . Hence, and .
- Synthesis scheme: unlimited application of Equation (2).
3.2. Component Substitution (CS)
3.2.1. BDSD-PC
3.2.2. GSA
3.2.3. BT-H
3.2.4. PRACS
3.3. Multi-Resolution Analysis (MRA)
3.3.1. AWLP
3.3.2. Laplacian-Based Techniques: MTF-GLP-*
3.4. Model-Based Optimization/Adapted (MBO/A)
3.4.1. Total Variation (TV)
3.4.2. Area-to-Point Regression Kriging (ATPRK)
3.5. Model-Based Optimization (MBO)
3.5.1. Sen2Res
3.5.2. Super-Resolution for Multispectral Multi-Resolution Estimation (SupReMe)
3.5.3. Multi-Resolution Sharpening Approach (MuSA)
3.5.4. S2Sharp
3.5.5. Sentinel-2 Super-Resolution via Scene-Adapted Self-Similarity Method (SSSS)
3.6. Deep Learning
3.6.1. DSen2
3.6.2. FUSE
3.6.3. S2-SSC-CNN
3.6.4. U-FUSE
3.6.5. S2-UCNN
3.6.6. Beyond the Selected Methods
4. Quality Assessment
4.1. RR Assessment
4.1.1. ERGAS
4.1.2. SAM
4.1.3.
4.2. FR Assessment
4.2.1. Khan’s Spectral Distortion Index
4.2.2. Correlation Distortion Index
4.2.3. Local Correlation-Based QNR
5. Proposed Dataset
- Diversity: it includes images from various geographical regions, land cover types, and acquisition conditions, ensuring comprehensive applicability.
- Training and testing separation: training and test sets are derived from distinct acquisitions to prevent overfitting and ensure unbiased evaluations.
- Variability: training and test sets include multiple images, with the test set offering diverse scenarios to better reflect real-world conditions.
- Accessibility: the dataset is freely available to the research community, further fostering research collaborations.
6. Experimental Analysis
- (a)
- The capacity to generalize across diverse datasets;
- (b)
- Robustness across different scales (FR and RR);
- (c)
- The ability to perform consistently in sharpening both 20 m and 60 m data simultaneously;
- (d)
- The capability to preserve spectral features while enhancing spatial resolution;
- (e)
- The ability to produce visually perceptual results for an ideal observer;
- (f)
- Computational complexity.
6.1. Generalization Across Datasets
6.2. Generalization Across Scales
6.3. Spectral-Spatial Quality Balance
6.4. 20–60 m Cross-Band Quality
6.5. Visual Inspection
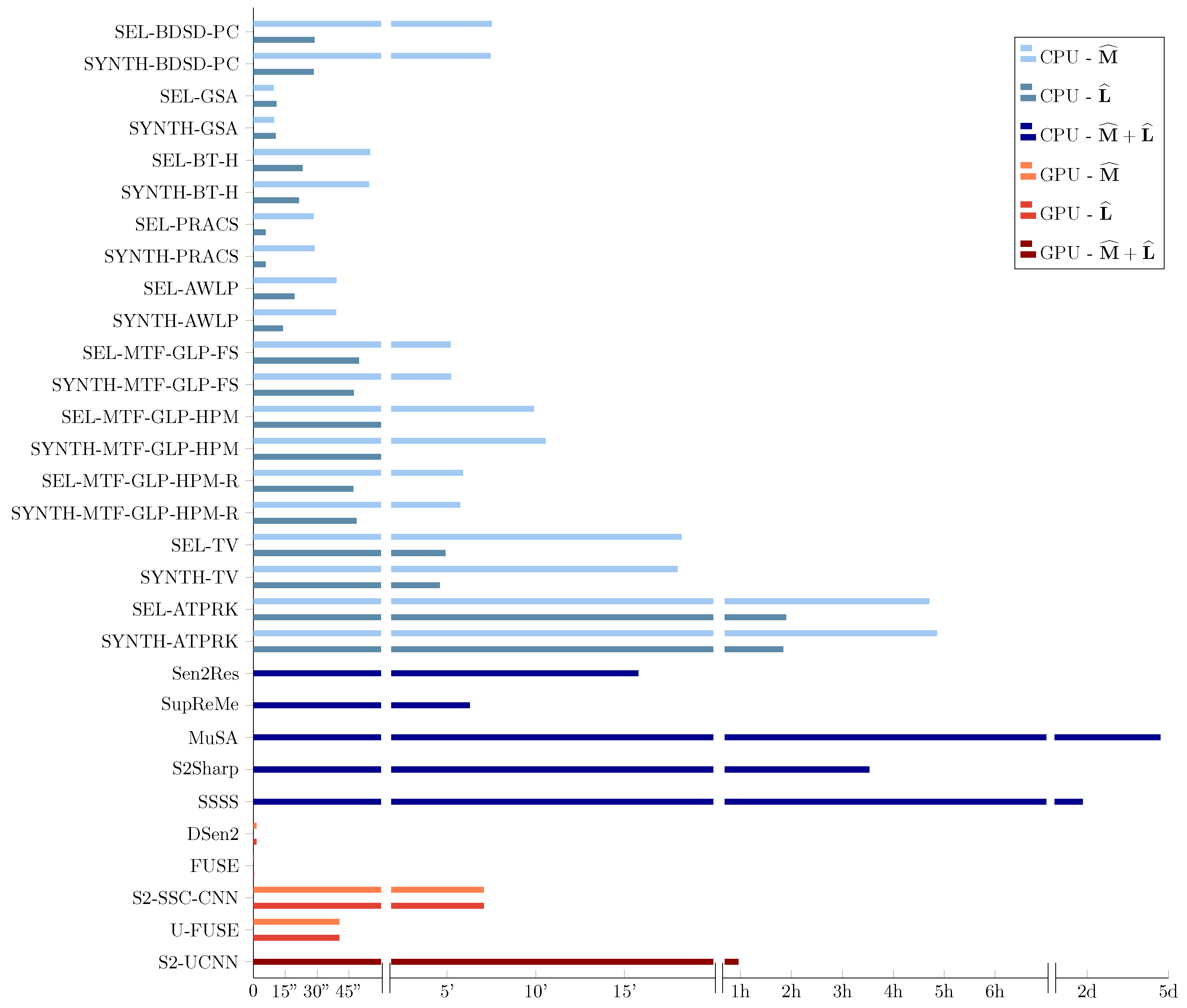
6.6. Computational Efficiency
6.7. Discussion
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ienco, D.; Interdonato, R.; Gaetano, R.; Ho Tong Minh, D. Combining Sentinel-1 and Sentinel-2 Satellite Image Time Series for land cover mapping via a multi-source deep learning architecture. ISPRS J. Photogramm. Remote Sens. 2019, 158, 11–22. [Google Scholar] [CrossRef]
- Phiri, D.; Simwanda, M.; Salekin, S.; Nyirenda, V.R.; Murayama, Y.; Ranagalage, M. Sentinel-2 Data for Land Cover/Use Mapping: A Review. Remote Sens. 2020, 12, 2291. [Google Scholar] [CrossRef]
- Karra, K.; Kontgis, C.; Statman-Weil, Z.; Mazzariello, J.C.; Mathis, M.; Brumby, S.P. Global land use/land cover with Sentinel 2 and deep learning. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 4704–4707. [Google Scholar] [CrossRef]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Khiali, L.; Ienco, D.; Teisseire, M. Object-oriented satellite image time series analysis using a graph-based representation. Ecol. Inform. 2018, 43, 52–64. [Google Scholar] [CrossRef]
- Baselice, F.; Ferraioli, G. Unsupervised coastal line extraction from SAR images. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1350–1354. [Google Scholar] [CrossRef]
- Razzano, F.; Stasio, P.D.; Mauro, F.; Meoni, G.; Esposito, M.; Schirinzi, G.; Ullo, S.L. AI Techniques for Near Real-Time Monitoring of Contaminants in Coastal Waters on Board Future Φsat-2 Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 16755–16766. [Google Scholar] [CrossRef]
- Roy, D.P.; Huang, H.; Boschetti, L.; Giglio, L.; Yan, L.; Zhang, H.H.; Li, Z. Landsat-8 and Sentinel-2 burned area mapping—A combined sensor multi-temporal change detection approach. Remote Sens. Environ. 2019, 231, 111254. [Google Scholar] [CrossRef]
- de Gélis, I.; Corpetti, T.; Lefèvre, S. Change Detection Needs Change Information: Improving Deep 3-D Point Cloud Change Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–10. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2565–2586. [Google Scholar] [CrossRef]
- Vivone, G.; Dalla Mura, M.; Garzelli, A.; Restaino, R.; Scarpa, G.; Ulfarsson, M.O.; Alparone, L.; Chanussot, J. A new benchmark based on recent advances in multispectral pansharpening: Revisiting pansharpening with classical and emerging pansharpening methods. IEEE Geosci. Remote Sens. Mag. 2020, 9, 53–81. [Google Scholar] [CrossRef]
- Deng, L.J.; Vivone, G.; Paoletti, M.E.; Scarpa, G.; He, J.; Zhang, Y.; Chanussot, J.; Plaza, A. Machine learning in pansharpening: A benchmark, from shallow to deep networks. IEEE Geosci. Remote Sens. Mag. 2022, 10, 279–315. [Google Scholar] [CrossRef]
- Scarpa, G.; Ciotola, M. Full-resolution quality assessment for pansharpening. Remote Sens. 2022, 14, 1808. [Google Scholar] [CrossRef]
- Wu, X.; Feng, J.; Shang, R.; Wu, J.; Zhang, X.; Jiao, L.; Gamba, P. Multi-task multi-objective evolutionary network for hyperspectral image classification and pansharpening. Inf. Fusion 2024, 108, 102383. [Google Scholar] [CrossRef]
- Lin, C.; Wu, C.C.; Tsogt, K.; Ouyang, Y.C.; Chang, C.I. Effects of atmospheric correction and pansharpening on LULC classification accuracy using WorldView-2 imagery. Inf. Process. Agric. 2015, 2, 25–36. [Google Scholar] [CrossRef]
- Zhao, J.; Zhong, Y.; Hu, X.; Wei, L.; Zhang, L. A robust spectral-spatial approach to identifying heterogeneous crops using remote sensing imagery with high spectral and spatial resolutions. Remote Sens. Environ. 2020, 239, 111605. [Google Scholar] [CrossRef]
- Mazza, A.; Guarino, G.; Scarpa, G.; Yuan, Q.; Vivone, G. PM2.5 Retrieval with Sentinel-5P Data over Europe Exploiting Deep Learning. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–17. [Google Scholar] [CrossRef]
- Ummerle, C.; Giganti, A.; Mandelli, S.; Bestagini, P.; Tubaro, S. Leveraging Land Cover Priors for Isoprene Emission Super-Resolution. Remote Sens. 2025, 17, 1715. [Google Scholar] [CrossRef]
- Goyens, C.; Lavigne, H.; Dille, A.; Vervaeren, H. Using hyperspectral remote sensing to monitor water quality in drinking water reservoirs. Remote Sens. 2022, 14, 5607. [Google Scholar] [CrossRef]
- Loncan, L.; De Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simoes, M.; et al. Hyperspectral pansharpening: A review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef]
- Borsoi, R.A.; Imbiriba, T.; Bermudez, J.C.M.; Richard, C.; Chanussot, J.; Drumetz, L.; Tourneret, J.Y.; Zare, A.; Jutten, C. Spectral Variability in Hyperspectral Data Unmixing: A comprehensive review. IEEE Geosci. Remote Sens. Mag. 2021, 9, 223–270. [Google Scholar] [CrossRef]
- Dobigeon, N.; Tourneret, J.Y.; Richard, C.; Bermudez, J.C.M.; McLaughlin, S.; Hero, A.O. Nonlinear Unmixing of Hyperspectral Images: Models and Algorithms. IEEE Signal Process. Mag. 2014, 31, 82–94. [Google Scholar] [CrossRef]
- Ciotola, M.; Guarino, G.; Vivone, G.; Poggi, G.; Chanussot, J.; Plaza, A.; Scarpa, G. Hyperspectral Pansharpening: Critical review, tools, and future perspectives. IEEE Geosci. Remote Sens. Mag. 2025, 13, 311–338. [Google Scholar] [CrossRef]
- Brodu, N. Super-resolving multiresolution images with band-independent geometry of multispectral pixels. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4610–4617. [Google Scholar] [CrossRef]
- Lanaras, C.; Bioucas-Dias, J.; Galliani, S.; Baltsavias, E.; Schindler, K. Super-resolution of Sentinel-2 images: Learning a globally applicable deep neural network. ISPRS J. Photogramm. Remote Sens. 2018, 146, 305–319. [Google Scholar] [CrossRef]
- Wu, J.; Lin, L.; Zhang, C.; Li, T.; Cheng, X.; Nan, F. Generating Sentinel-2 all-band 10-m data by sharpening 20/60-m bands: A hierarchical fusion network. ISPRS J. Photogramm. Remote Sens. 2023, 196, 16–31. [Google Scholar] [CrossRef]
- Selva, M.; Aiazzi, B.; Butera, F.; Chiarantini, L.; Baronti, S. Hyper-Sharpening: A First Approach on SIM-GA Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3008–3024. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Li, Z.; Atkinson, P.M. Fusion of Sentinel-2 images. Remote Sens. Environ. 2016, 187, 241–252. [Google Scholar] [CrossRef]
- Vaiopoulos, A.; Karantzalos, K. Pansharpening on the narrow VNIR and SWIR spectral bands of Sentinel-2. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 723–730. [Google Scholar] [CrossRef]
- Park, H.; Choi, J.; Park, N.; Choi, S. Sharpening the VNIR and SWIR bands of Sentinel-2A imagery through modified selected and synthesized band schemes. Remote Sens. 2017, 9, 1080. [Google Scholar] [CrossRef]
- Lanaras, C.; Bioucas-Dias, J.; Baltsavias, E.; Schindler, K. Super-resolution of multispectral multiresolution images from a single sensor. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 20–28. [Google Scholar]
- Paris, C.; Bioucas-Dias, J.; Bruzzone, L. A novel sharpening approach for superresolving multiresolution optical images. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1545–1560. [Google Scholar] [CrossRef]
- Lin, C.H.; Bioucas-Dias, J.M. An Explicit and Scene-Adapted Definition of Convex Self-Similarity Prior With Application to Unsupervised Sentinel-2 Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3352–3365. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1106–1114. [Google Scholar]
- Dong, C.; Loy, C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations, Virtual Event, Austria, 3–7 May 2021. [Google Scholar]
- Deudon, M.; Kalaitzis, A.; Goytom, I.; Arefin, M.R.; Lin, Z.; Sankaran, K.; Michalski, V.; Kahou, S.E.; Cornebise, J.; Bengio, Y. HighRes-net: Recursive Fusion for Multi-Frame Super-Resolution of Satellite Imagery. arXiv 2020, arXiv:2002.06460. [Google Scholar] [CrossRef]
- Capliez, E.; Ienco, D.; Gaetano, R.; Baghdadi, N.; Salah, A.H.; Le Goff, M.; Chouteau, F. Multisensor Temporal Unsupervised Domain Adaptation for Land Cover Mapping With Spatial Pseudo-Labeling and Adversarial Learning. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Schmitt, M.; Ahmadi, S.A.; Xu, Y.; Taşkin, G.; Verma, U.; Sica, F.; Hänsch, R. There Are No Data Like More Data: Datasets for deep learning in Earth observation. IEEE Geosci. Remote Sens. Mag. 2023, 11, 63–97. [Google Scholar] [CrossRef]
- Gargiulo, M.; Mazza, A.; Gaetano, R.; Ruello, G.; Scarpa, G. A CNN-Based Fusion Method for Super-Resolution of Sentinel-2 Data. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4713–4716. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. Sentinel-2 image fusion using a deep residual network. Remote Sens. 2018, 10, 1290. [Google Scholar] [CrossRef]
- Gargiulo, M.; Mazza, A.; Gaetano, R.; Ruello, G.; Scarpa, G. Fast super-resolution of 20 m Sentinel-2 bands using convolutional neural networks. Remote Sens. 2019, 11, 2635. [Google Scholar] [CrossRef]
- Wu, J.; He, Z.; Hu, J. Sentinel-2 sharpening via parallel residual network. Remote Sens. 2020, 12, 279. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Ulfarsson, M.O.; Sveinsson, J.R.; Sigurdsson, J. Zero-Shot Sentinel-2 Sharpening Using a Symmetric Skipped Connection Convolutional Neural Network. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 613–616. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Ulfarsson, M.O.; Sveinsson, J.R. Sharpening the 20 M Bands of SENTINEL-2 Image Using an Unsupervised Convolutional Neural Network. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2875–2878. [Google Scholar] [CrossRef]
- Ciotola, M.; Ragosta, M.; Poggi, G.; Scarpa, G. A Full-Resolution Training Framework for Sentinel-2 Image Fusion. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 1260–1263. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Ulfarsson, M.O.; Sveinsson, J.R.; Mura, M.D. Sentinel-2 Sharpening Using a Single Unsupervised Convolutional Neural Network With MTF-Based Degradation Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6882–6896. [Google Scholar] [CrossRef]
- Ciotola, M.; Martinelli, A.; Mazza, A.; Scarpa, G. An Adversarial Training Framework for Sentinel-2 Image Super-Resolution. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 3782–3785. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Ulfarsson, M.O.; Sveinsson, J.R.; Mura, M.D. Unsupervised Sentinel-2 Image Fusion Using a Deep Unrolling Method. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolution: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar] [CrossRef]
- Khan, M.M.; Alparone, L.; Chanussot, J. Pansharpening quality assessment using the modulation transfer functions of instruments. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3880–3891. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Carlà, R.; Garzelli, A.; Santurri, L. Full-scale assessment of pansharpening methods and data products. In Proceedings of the Image and Signal Processing for Remote Sensing XX, Amsterdam, The Netherlands, 22–25 September 2014; Bruzzone, L., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2014; Volume 9244, p. 924402. [Google Scholar] [CrossRef]
- Arienzo, A.; Vivone, G.; Garzelli, A.; Alparone, L.; Chanussot, J. Full-resolution quality assessment of pansharpening: Theoretical and hands-on approaches. IEEE Geosci. Remote Sens. Mag. 2022, 10, 168–201. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Color image denoising via sparse 3D collaborative filtering with grouping constraint in luminance-chrominance space. In Proceedings of the 2007 IEEE International Conference on Image Processing, San Antonio, TX, USA, 16 September–19 October 2007; IEEE: Piscataway, NJ, USA, 2007; Volume 1, pp. I-313–I-316. [Google Scholar]
- Danielyan, A.; Katkovnik, V.; Egiazarian, K. BM3D frames and variational image deblurring. IEEE Trans. Image Process. 2011, 21, 1715–1728. [Google Scholar] [CrossRef]
- Venkatakrishnan, S.V.; Bouman, C.A.; Wohlberg, B. Plug-and-play priors for model based reconstruction. In Proceedings of the 2013 IEEE Global Conference on Signal and Information Processing, Austin, TX, USA, 3–5 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 945–948. [Google Scholar]
- Ulfarsson, M.O.; Palsson, F.; Dalla Mura, M.; Sveinsson, J.R. Sentinel-2 sharpening using a reduced-rank method. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6408–6420. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Shocher, A.; Cohen, N.; Irani, M. “zero-shot” super-resolution using deep internal learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3118–3126. [Google Scholar]
- Luo, S.; Zhou, S.; Feng, Y.; Xie, J. Pansharpening via Unsupervised Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4295–4310. [Google Scholar] [CrossRef]
- Uezato, T.; Hong, D.; Yokoya, N.; He, W. Guided deep decoder: Unsupervised image pair fusion. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 87–102. [Google Scholar]
- Ciotola, M.; Poggi, G.; Scarpa, G. Unsupervised Deep Learning-Based Pansharpening With Jointly Enhanced Spectral and Spatial Fidelity. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar] [CrossRef]
- Ciotola, M.; Guarino, G.; Scarpa, G. An Unsupervised CNN-Based Pansharpening Framework with Spectral-Spatial Fidelity Balance. Remote Sens. 2024, 16, 3014. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Ulfarsson, M.O.; Sveinsson, J.R.; Dalla Mura, M. Deep SURE for Unsupervised Remote Sensing Image Fusion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Vivone, G. Robust Band-Dependent Spatial-Detail Approaches for Panchromatic Sharpening. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6421–6433. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS+Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Lolli, S.; Alparone, L.; Garzelli, A.; Vivone, G. Haze Correction for Contrast-Based Multispectral Pansharpening. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2255–2259. [Google Scholar] [CrossRef]
- Choi, J.; Yu, K.; Kim, Y. A New Adaptive Component-Substitution-Based Satellite Image Fusion by Using Partial Replacement. IEEE Trans. Geosci. Remote Sens. 2011, 49, 295–309. [Google Scholar] [CrossRef]
- Otazu, X.; González-Audícana, M.; Fors, O.; Núñez, J. Introduction of sensor spectral response into image fusion methods. Application to wavelet-based methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2376–2385. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. Full Scale Regression-Based Injection Coefficients for Panchromatic Sharpening. IEEE Trans. Image Process. 2018, 27, 3418–3431. [Google Scholar] [CrossRef]
- Alparone, L.; Garzelli, A.; Vivone, G. Intersensor Statistical Matching for Pansharpening: Theoretical Issues and Practical Solutions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4682–4695. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. A regression-based high-pass modulation pansharpening approach. IEEE Trans. Geosci. Remote Sens. 2017, 56, 984–996. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. A New Pansharpening Algorithm Based on Total Variation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 318–322. [Google Scholar] [CrossRef]
- Clerc, S.; M.P.C. Team. S2 MPC-Data Quality Report, S2-PDGS-MPC-DQR. Available online: https://sentiwiki.copernicus.eu/__attachments/1673423/S2-PDGS-MPC-DQR%20-%20S2%20MPC%20L1C%20DQR%20January%202015%20-%2001.pdf?inst-v=f9683405-accc-4a3f-a58f-01c9c5213fb1 (accessed on 25 May 2025).
- Tu, T.M.; Su, S.C.; Shyu, H.C.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fusion 2001, 2, 177–186. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal MMSE pan sharpening of very high resolution multispectral images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 228–236. [Google Scholar] [CrossRef]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent # 6,011,875, 4 January 2000. [Google Scholar]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images. II. Channel ratio and “chromaticity” transformation techniques. Remote Sens. Environ. 1987, 22, 343–365. [Google Scholar] [CrossRef]
- Baronti, S.; Aiazzi, B.; Selva, M.; Garzelli, A.; Alparone, L. A Theoretical Analysis of the Effects of Aliasing and Misregistration on Pansharpened Imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 446–453. [Google Scholar] [CrossRef]
- Thomas, C.; Ranchin, T.; Wald, L.; Chanussot, J. Synthesis of Multispectral Images to High Spatial Resolution: A Critical Review of Fusion Methods Based on Remote Sensing Physics. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1301–1312. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Dalla Mura, M.; Licciardi, G.; Chanussot, J. Contrast and error-based fusion schemes for multispectral image pansharpening. IEEE Geosci. Remote Sens. Lett. 2013, 11, 930–934. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Licciardi, G.; Dalla Mura, M.; Chanussot, J. MultiResolution Analysis and Component Substitution Techniques for Hyperspectral Pansharpening. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 2649–2652. [Google Scholar]
- Vicinanza, M.R.; Restaino, R.; Vivone, G.; Mura, M.D.; Chanussot, J. A Pansharpening Method Based on the Sparse Representation of Injected Details. IEEE Geosci. Remote Sens. Lett. 2015, 12, 180–184. [Google Scholar] [CrossRef]
- Wei, Q.; Dobigeon, N.; Tourneret, J.Y. Fast fusion of multi-band images based on solving a Sylvester equation. IEEE Trans. Image Process. 2015, 24, 4109–4121. [Google Scholar] [CrossRef]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J.Y. Hyperspectral and multispectral image fusion based on a sparse representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3658–3668. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Atkinson, P.M.; Zhao, Y. Downscaling MODIS images with area-to-point regression kriging. Remote Sens. Environ. 2015, 166, 191–204. [Google Scholar] [CrossRef]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Armannsson, S.E.; Ulfarsson, M.O.; Sigurdsson, J.; Nguyen, H.V.; Sveinsson, J.R. A comparison of optimized Sentinel-2 super-resolution methods using Wald’s protocol and Bayesian optimization. Remote Sens. 2021, 13, 2192. [Google Scholar] [CrossRef]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A. Fast image recovery using variable splitting and constrained optimization. IEEE Trans. Image Process. 2010, 19, 2345–2356. [Google Scholar] [CrossRef]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A. An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems. IEEE Trans. Image Process. 2010, 20, 681–695. [Google Scholar] [CrossRef] [PubMed]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by Convolutional Neural Networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A Deep Network Architecture for Pan-Sharpening. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar] [CrossRef]
- Scarpa, G.; Vitale, S.; Cozzolino, D. Target-Adaptive CNN-Based Pansharpening. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5443–5457. [Google Scholar] [CrossRef]
- Jiang, Y.; Ding, X.; Zeng, D.; Huang, Y.; Paisley, J. Pan-sharpening with a hyper-Laplacian penalty. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 540–548. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III. Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Ciotola, M.; Vitale, S.; Mazza, A.; Poggi, G.; Scarpa, G. Pansharpening by Convolutional Neural Networks in the Full Resolution Framework. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9446–9454. [Google Scholar]
- Heckel, R.; Hand, P. Deep decoder: Concise image representations from untrained non-convolutional networks. arXiv 2018, arXiv:1810.03982. [Google Scholar]
- Salgueiro, L.; Marcello, J.; Vilaplana, V. Single-Image Super-Resolution of Sentinel-2 Low Resolution Bands with Residual Dense Convolutional Neural Networks. Remote Sens. 2021, 13, 5007. [Google Scholar] [CrossRef]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Change Loy, C. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Stein, C.M. Estimation of the mean of a multivariate normal distribution. Ann. Stat. 1981, 9, 1135–1151. [Google Scholar] [CrossRef]
- Solo, V. A sure-fired way to choose smoothing parameters in ill-conditioned inverse problems. In Proceedings of the 3rd IEEE International Conference on Image Processing, Lausanne, Switzerland, 19 September 1996; IEEE: Piscataway, NJ, USA, 1996; Volume 3, pp. 89–92. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Vasilescu, V.; Datcu, M.; Faur, D. A CNN-Based Sentinel-2 Image Super-Resolution Method Using Multiobjective Training. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Armannsson, S.E.; Ulfarsson, M.O.; Sigurdsson, J. A Learned Reduced-Rank Sharpening Method for Multiresolution Satellite Imagery. Remote Sens. 2025, 17, 432. [Google Scholar] [CrossRef]
- Vivone, G.; Dalla Mura, M.; Garzelli, A.; Pacifici, F. A benchmarking protocol for pansharpening: Dataset, preprocessing, and quality assessment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6102–6118. [Google Scholar] [CrossRef]
- Vivone, G.; Garzelli, A.; Xu, Y.; Liao, W.; Chanussot, J. Panchromatic and Hyperspectral Image Fusion: Outcome of the 2022 WHISPERS Hyperspectral Pansharpening Challenge. IEEE J. Sel. Top. Appl. Earth Obs Remote Sens. 2023, 16, 166–179. [Google Scholar] [CrossRef]
- Wald, L. Data Fusion: Definitions and Architectures—Fusion of Images of Different Spatial Resolutions; Les Presses de l’École des Mines: Paris, France, 2002. [Google Scholar]
- Yuhas, R.H.; Goetz, A.F.H.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the Spectral Angle Mapper (SAM) algorithm. In Proceedings of the Summaries of the 3rd Annual JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 1–5 June 1992; pp. 147–149. [Google Scholar]
- Garzelli, A.; Nencini, F. Hypercomplex quality assessment of multi/hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2009, 6, 662–665. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Alparone, L.; Garzelli, A.; Vivone, G. Spatial Consistency for Full-Scale Assessment of Pansharpening. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 5132–5134. [Google Scholar] [CrossRef]





| Name | Ref | Summary |
|---|---|---|
| EXP | Approximation of the ideal interpolator | |
| Component Substitution (CS) | ||
| BDSD-PC | [67] | Band-dependent spatial detail injection with physical constraint |
| GSA | [68] | Gram–Schmidt adaptive component substitution |
| BT-H | [69] | Brovey transform with haze correction |
| PRACS | [70] | Partial replacement adaptive CS |
| Multi-resolution Analysis (MRA) | ||
| AWLP | [71] | Additive wavelet luminance proportional |
| MTF-GLP-FS | [72] | Modulation Transfer Function (MTF)-matched Generalized Laplacian Pyramid (MTF-GLP) with fusion rule at full scale |
| MTF-GLP-HPM | [73] | MTF-GLP with high pass modulation |
| MTF-GLP-HPM-R | [74] | MTF-GLP-HPM with regression-based spectral matching |
| Model-Based Optimization/Adapted (MBO/A) | ||
| TV | [75] | Total variation-based pansharpening |
| ATPRK | [28] | Area-to-Point Regression Kriging |
| Model-Based Optimization (MBO) | ||
| Sen2Res | [24] | Sentinel 2 super Resolution modeled as band-independent geometry convex optimization problem |
| SupReMe | [31] | SUPer-REsolution for multispectral Multi-resolution Estimation |
| MuSA | [32] | MUlti-resolution Sharpening Approach |
| S2Sharp | [59] | Sentinel-2 Shapening based on Bayesian theory and cross-validation |
| SSSS | [33] | Sentinel-2 Super-resolution via Scene-adapted Self-Similarity method |
| Deep Learning (DL) | ||
| DSen2 | [25] | CNN based on ResNet |
| FUSE | [42] | Light-weight network composed of 4 convolutional layers |
| S2-SSC-CNN | [44] | UNet-like architecture with zero-shot training procedure |
| U-FUSE (unsup.) | [46] | Unsupervised version of FUSE |
| S2-UCNN (unsup.) | [47] | Solution based on Deep Image Priors (DIPs) |
| Symbol | Dimensions | Meaning |
|---|---|---|
| Scalars | Width and height of the HR 10 m image | |
| Scalar | Resolution ratio, generic or referred to image ∗ | |
| Scalar | number of bands, generic or referred to image ∗ | |
| HR 10 m S2 image | ||
| MR 20 m S2 image | ||
| LR 60 m S2 image | ||
| Real or simulated PAN image | ||
| upsampling of and | ||
| Super-resolved or | ||
| Resolution-downgraded (Low-pass filtered and decimated) version of | ||
| Resolution-downgraded (Low-pass filtered and decimated) version of | ||
| Low-pass filtered version of any | ||
| High-pass filtered version of any |
| Method | Brisbane | New York | Tokyo | Tazoskij | Rome | Ulaanbaator | Brasilia | Alexandria | Paris | Berlin | Beijing | Cape Town | Niamey | Jakarta | Reynosa | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EXP | 0.806 | 0.836 | 0.911 | 0.911 | 0.898 | 0.943 | 0.940 | 0.902 | 0.903 | 0.925 | 0.826 | 0.933 | 0.926 | 0.896 | 0.924 | |
| SEL - | BDSD-PC | 0.733 | 0.890 | 0.944 | 0.944 | 0.895 | 0.963 | 0.961 | 0.941 | 0.932 | 0.951 | 0.899 | 0.959 | 0.954 | 0.939 | 0.956 |
| SYNTH - | BDSD-PC | 0.741 | 0.889 | 0.946 | 0.946 | 0.927 | 0.966 | 0.961 | 0.943 | 0.931 | 0.952 | 0.911 | 0.961 | 0.951 | 0.941 | 0.957 |
| SEL - | GSA | 0.732 | 0.902 | 0.954 | 0.954 | 0.904 | 0.970 | 0.967 | 0.956 | 0.948 | 0.956 | 0.919 | 0.966 | 0.961 | 0.951 | 0.969 |
| SYNTH - | GSA | 0.650 | 0.865 | 0.954 | 0.954 | 0.909 | 0.849 | 0.960 | 0.955 | 0.949 | 0.957 | 0.928 | 0.965 | 0.926 | 0.933 | 0.964 |
| SEL - | BT-H | 0.759 | 0.920 | 0.952 | 0.952 | 0.863 | 0.957 | 0.953 | 0.935 | 0.791 | 0.944 | 0.901 | 0.962 | 0.951 | 0.937 | 0.851 |
| SYNTH - | BT-H | 0.662 | 0.889 | 0.951 | 0.951 | 0.923 | 0.883 | 0.950 | 0.951 | 0.926 | 0.950 | 0.929 | 0.960 | 0.900 | 0.937 | 0.959 |
| SEL - | PRACS | 0.774 | 0.920 | 0.950 | 0.950 | 0.919 | 0.968 | 0.965 | 0.933 | 0.942 | 0.952 | 0.912 | 0.964 | 0.959 | 0.946 | 0.947 |
| SYNTH - | PRACS | 0.653 | 0.885 | 0.954 | 0.954 | 0.929 | 0.960 | 0.954 | 0.949 | 0.946 | 0.959 | 0.922 | 0.964 | 0.922 | 0.923 | 0.954 |
| SEL - | AWLP | 0.839 | 0.945 | 0.963 | 0.963 | 0.937 | 0.965 | 0.974 | 0.965 | 0.960 | 0.969 | 0.940 | 0.976 | 0.960 | 0.953 | 0.976 |
| SYNTH - | AWLP | 0.744 | 0.941 | 0.967 | 0.967 | 0.945 | 0.973 | 0.975 | 0.967 | 0.961 | 0.970 | 0.948 | 0.978 | 0.964 | 0.963 | 0.977 |
| SEL - | MTF-GLP-FS | 0.851 | 0.948 | 0.966 | 0.966 | 0.949 | 0.976 | 0.980 | 0.976 | 0.964 | 0.977 | 0.945 | 0.981 | 0.972 | 0.967 | 0.981 |
| SYNTH - | MTF-GLP-FS | 0.756 | 0.940 | 0.972 | 0.972 | 0.953 | 0.956 | 0.981 | 0.976 | 0.966 | 0.979 | 0.953 | 0.982 | 0.973 | 0.969 | 0.982 |
| SEL - | MTF-GLP-HPM | 0.851 | 0.951 | 0.966 | 0.966 | 0.955 | 0.914 | 0.980 | 0.975 | 0.965 | 0.977 | 0.946 | 0.982 | 0.970 | 0.961 | 0.981 |
| SYNTH - | MTF-GLP-HPM | 0.747 | 0.927 | 0.972 | 0.972 | 0.945 | 0.903 | 0.981 | 0.975 | 0.966 | 0.979 | 0.953 | 0.982 | 0.972 | 0.967 | 0.982 |
| SEL - | MTF-GLP-HPM-R | 0.856 | 0.952 | 0.967 | 0.967 | 0.958 | 0.977 | 0.980 | 0.974 | 0.964 | 0.977 | 0.947 | 0.982 | 0.972 | 0.967 | 0.981 |
| SYNTH - | MTF-GLP-HPM-R | 0.753 | 0.936 | 0.972 | 0.972 | 0.955 | 0.945 | 0.981 | 0.975 | 0.966 | 0.979 | 0.954 | 0.982 | 0.973 | 0.969 | 0.982 |
| SEL - | TV | 0.815 | 0.901 | 0.936 | 0.936 | 0.905 | 0.948 | 0.935 | 0.931 | 0.926 | 0.939 | 0.899 | 0.947 | 0.913 | 0.927 | 0.929 |
| SYNTH - | TV | 0.726 | 0.900 | 0.939 | 0.939 | 0.918 | 0.939 | 0.948 | 0.934 | 0.928 | 0.947 | 0.908 | 0.954 | 0.942 | 0.935 | 0.949 |
| SEL - | ATPRK | 0.789 | 0.883 | 0.908 | 0.908 | 0.897 | 0.930 | 0.940 | 0.918 | 0.914 | 0.937 | 0.876 | 0.943 | 0.929 | 0.913 | 0.941 |
| SYNTH - | ATPRK | 0.704 | 0.875 | 0.919 | 0.919 | 0.904 | 0.905 | 0.943 | 0.919 | 0.917 | 0.939 | 0.885 | 0.944 | 0.931 | 0.919 | 0.942 |
| Sen2Res | 0.812 | 0.865 | 0.906 | 0.915 | 0.903 | 0.931 | 0.940 | 0.911 | 0.911 | 0.935 | 0.857 | 0.939 | 0.936 | 0.909 | 0.935 | |
| SupReMe | 0.762 | 0.911 | 0.944 | 0.944 | 0.921 | 0.959 | 0.962 | 0.945 | 0.938 | 0.956 | 0.915 | 0.960 | 0.949 | 0.944 | 0.954 | |
| MuSA | 0.708 | 0.843 | 0.885 | 0.885 | 0.832 | 0.942 | 0.936 | 0.923 | 0.897 | 0.895 | 0.851 | 0.933 | 0.903 | 0.907 | 0.918 | |
| S2Sharp | 0.780 | 0.897 | 0.931 | 0.931 | 0.920 | 0.956 | 0.960 | 0.944 | 0.938 | 0.956 | 0.892 | 0.957 | 0.947 | 0.940 | 0.947 | |
| SSSS | 0.587 | 0.697 | 0.789 | 0.789 | 0.809 | 0.818 | 0.911 | 0.830 | 0.818 | 0.867 | 0.739 | 0.914 | 0.904 | 0.869 | 0.847 | |
| DSen2 | 0.858 | 0.964 | 0.977 | 0.973 | 0.955 | 0.967 | 0.977 | 0.970 | 0.966 | 0.974 | 0.959 | 0.982 | 0.972 | 0.968 | 0.984 | |
| FUSE | 0.897 | 0.972 | 0.985 | 0.989 | 0.976 | 0.988 | 0.990 | 0.986 | 0.984 | 0.990 | 0.976 | 0.992 | 0.987 | 0.985 | 0.990 | |
| S2-SSC-CNN | 0.880 | 0.972 | 0.986 | 0.989 | 0.975 | 0.991 | 0.990 | 0.989 | 0.981 | 0.988 | 0.979 | 0.990 | 0.989 | 0.984 | 0.990 | |
| U-FUSE | 0.816 | 0.923 | 0.936 | 0.954 | 0.954 | 0.949 | 0.977 | 0.970 | 0.964 | 0.979 | 0.925 | 0.971 | 0.962 | 0.960 | 0.958 | |
| S2-UCNN | 0.747 | 0.960 | 0.980 | 0.984 | 0.931 | 0.983 | 0.978 | 0.969 | 0.970 | 0.980 | 0.975 | 0.985 | 0.972 | 0.974 | 0.983 | |
| Method | Brisbane | New York | Tokyo | Tazoskij | Rome | Ulaanbaator | Brasilia | Alexandria | Paris | Berlin | Beijing | Cape Town | Niamey | Jakarta | Reynosa | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EXP | 0.513 | 0.532 | 0.567 | 0.516 | 0.542 | 0.679 | 0.645 | 0.488 | 0.597 | 0.656 | 0.395 | 0.646 | 0.673 | 0.540 | 0.621 | |
| SEL - | BDSD-PC | 0.890 | 0.967 | 0.964 | 0.980 | 0.947 | 0.986 | 0.977 | 0.975 | 0.974 | 0.971 | 0.968 | 0.984 | 0.978 | 0.964 | 0.985 |
| SYNTH - | BDSD-PC | 0.867 | 0.968 | 0.972 | 0.982 | 0.969 | 0.978 | 0.980 | 0.975 | 0.977 | 0.983 | 0.967 | 0.983 | 0.982 | 0.975 | 0.986 |
| SEL - | GSA | 0.856 | 0.967 | 0.963 | 0.980 | 0.948 | 0.984 | 0.978 | 0.975 | 0.972 | 0.979 | 0.966 | 0.982 | 0.975 | 0.961 | 0.985 |
| SYNTH - | GSA | 0.858 | 0.967 | 0.972 | 0.980 | 0.968 | 0.981 | 0.979 | 0.974 | 0.974 | 0.982 | 0.965 | 0.983 | 0.980 | 0.975 | 0.984 |
| SEL - | BT-H | 0.878 | 0.967 | 0.967 | 0.981 | 0.949 | 0.985 | 0.966 | 0.977 | 0.976 | 0.976 | 0.968 | 0.984 | 0.977 | 0.967 | 0.987 |
| SYNTH - | BT-H | 0.871 | 0.968 | 0.974 | 0.982 | 0.971 | 0.980 | 0.981 | 0.977 | 0.977 | 0.984 | 0.967 | 0.985 | 0.982 | 0.976 | 0.986 |
| SEL - | PRACS | 0.783 | 0.954 | 0.906 | 0.913 | 0.852 | 0.975 | 0.969 | 0.971 | 0.946 | 0.892 | 0.932 | 0.953 | 0.922 | 0.947 | 0.976 |
| SYNTH - | PRACS | 0.772 | 0.954 | 0.909 | 0.919 | 0.864 | 0.974 | 0.961 | 0.971 | 0.945 | 0.900 | 0.923 | 0.952 | 0.918 | 0.935 | 0.981 |
| SEL - | AWLP | 0.833 | 0.950 | 0.882 | 0.905 | 0.868 | 0.969 | 0.953 | 0.911 | 0.928 | 0.899 | 0.911 | 0.956 | 0.949 | 0.960 | 0.948 |
| SYNTH - | AWLP | 0.828 | 0.950 | 0.880 | 0.905 | 0.876 | 0.963 | 0.954 | 0.911 | 0.926 | 0.899 | 0.908 | 0.956 | 0.953 | 0.952 | 0.949 |
| SEL - | MTF-GLP-FS | 0.914 | 0.976 | 0.979 | 0.985 | 0.974 | 0.989 | 0.988 | 0.980 | 0.981 | 0.987 | 0.973 | 0.990 | 0.987 | 0.979 | 0.990 |
| SYNTH - | MTF-GLP-FS | 0.908 | 0.976 | 0.981 | 0.985 | 0.977 | 0.985 | 0.988 | 0.980 | 0.982 | 0.989 | 0.972 | 0.990 | 0.989 | 0.983 | 0.990 |
| SEL - | MTF-GLP-HPM | 0.914 | 0.976 | 0.979 | 0.984 | 0.967 | 0.988 | 0.988 | 0.980 | 0.982 | 0.988 | 0.973 | 0.990 | 0.987 | 0.977 | 0.990 |
| SYNTH - | MTF-GLP-HPM | 0.908 | 0.976 | 0.981 | 0.985 | 0.944 | 0.984 | 0.988 | 0.980 | 0.983 | 0.989 | 0.973 | 0.990 | 0.989 | 0.983 | 0.990 |
| SEL - | MTF-GLP-HPM-R | 0.914 | 0.976 | 0.980 | 0.985 | 0.966 | 0.988 | 0.988 | 0.980 | 0.982 | 0.988 | 0.973 | 0.990 | 0.986 | 0.979 | 0.990 |
| SYNTH - | MTF-GLP-HPM-R | 0.908 | 0.976 | 0.981 | 0.985 | 0.941 | 0.984 | 0.988 | 0.980 | 0.983 | 0.989 | 0.973 | 0.990 | 0.989 | 0.983 | 0.990 |
| SEL - | TV | 0.844 | 0.956 | 0.840 | 0.877 | 0.873 | 0.977 | 0.946 | 0.909 | 0.898 | 0.873 | 0.928 | 0.954 | 0.868 | 0.942 | 0.948 |
| SYNTH - | TV | 0.833 | 0.955 | 0.838 | 0.873 | 0.866 | 0.974 | 0.927 | 0.894 | 0.886 | 0.865 | 0.904 | 0.941 | 0.823 | 0.931 | 0.936 |
| SEL - | ATPRK | 0.896 | 0.967 | 0.971 | 0.978 | 0.964 | 0.985 | 0.979 | 0.974 | 0.973 | 0.978 | 0.966 | 0.982 | 0.975 | 0.970 | 0.983 |
| SYNTH - | ATPRK | 0.890 | 0.967 | 0.974 | 0.979 | 0.969 | 0.985 | 0.979 | 0.975 | 0.974 | 0.981 | 0.967 | 0.982 | 0.980 | 0.975 | 0.983 |
| Sen2Res | 0.801 | 0.838 | 0.860 | 0.813 | 0.845 | 0.901 | 0.886 | 0.811 | 0.856 | 0.880 | 0.813 | 0.916 | 0.909 | 0.875 | 0.912 | |
| SupReMe | 0.788 | 0.945 | 0.951 | 0.955 | 0.948 | 0.959 | 0.969 | 0.961 | 0.959 | 0.962 | 0.945 | 0.965 | 0.958 | 0.947 | 0.968 | |
| MuSA | 0.582 | 0.509 | 0.774 | 0.931 | 0.936 | 0.653 | 0.959 | 0.881 | 0.956 | 0.908 | 0.836 | 0.962 | 0.951 | 0.944 | 0.612 | |
| S2Sharp | 0.662 | 0.838 | 0.837 | 0.841 | 0.779 | 0.797 | 0.832 | 0.891 | 0.846 | 0.838 | 0.805 | 0.897 | 0.888 | 0.794 | 0.892 | |
| SSSS | 0.567 | 0.633 | 0.645 | 0.800 | 0.721 | 0.629 | 0.915 | 0.758 | 0.668 | 0.744 | 0.740 | 0.872 | 0.954 | 0.856 | 0.825 | |
| DSen2 | 0.872 | 0.973 | 0.956 | 0.972 | 0.969 | 0.994 | 0.973 | 0.973 | 0.968 | 0.978 | 0.975 | 0.986 | 0.945 | 0.976 | 0.989 | |
| FUSE | 0.905 | 0.971 | 0.980 | 0.980 | 0.975 | 0.987 | 0.986 | 0.984 | 0.977 | 0.979 | 0.973 | 0.986 | 0.978 | 0.978 | 0.989 | |
| S2-SSC-CNN | 0.790 | 0.909 | 0.907 | 0.948 | 0.938 | 0.984 | 0.942 | 0.955 | 0.942 | 0.947 | 0.667 | 0.933 | 0.922 | 0.612 | 0.971 | |
| U-FUSE | 0.785 | 0.933 | 0.957 | 0.941 | 0.926 | 0.956 | 0.956 | 0.955 | 0.946 | 0.950 | 0.945 | 0.954 | 0.960 | 0.957 | 0.957 | |
| S2-UCNN | 0.825 | 0.958 | 0.918 | 0.966 | 0.935 | 0.959 | 0.933 | 0.924 | 0.946 | 0.960 | 0.893 | 0.941 | 0.851 | 0.864 | 0.940 | |
| 20 m Sentinel-2 Bands Sharpening | 60 m Sentinel-2 Bands Sharpening | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RR | FR | RR | FR | |||||||||||||||
| ERGAS | SAM | QNR | ERGAS | SAM | QNR | |||||||||||||
| EXP | 4.444 | 1.890 | 0.899 | 0.041 | 0.431 | 0.590 | 3.469 | 2.530 | 0.574 | 0.079 | 0.703 | 0.597 | ||||||
| SEL- | BDSD-PC | 3.656 | 1.914 | 0.924 | 0.043 | 0.247 | 0.916 | 0.959 | 0.939 | 0.967 | 0.073 | 0.002 | 0.926 | |||||
| SYNTH- | BDSD-PC | 3.561 | 1.990 | 0.928 | 0.039 | 0.254 | 0.918 | 0.853 | 0.928 | 0.970 | 0.069 | 0.021 | 0.927 | |||||
| SEL- | GSA | 3.598 | 2.359 | 0.934 | 0.044 | 0.072 | 0.944 | 0.948 | 1.041 | 0.965 | 0.074 | 0.001 | 0.925 | |||||
| SYNTH- | GSA | 4.053 | 2.815 | 0.914 | 0.066 | 0.128 | 0.913 | 0.863 | 0.936 | 0.968 | 0.071 | 0.020 | 0.926 | |||||
| SEL- | BT-H | 5.372 | 2.570 | 0.909 | 0.047 | 0.061 | 0.943 | 0.933 | 0.959 | 0.967 | 0.074 | 0.002 | 0.926 | |||||
| SYNTH- | BT-H | 4.059 | 2.641 | 0.915 | 0.057 | 0.130 | 0.922 | 0.836 | 0.890 | 0.971 | 0.070 | 0.020 | 0.927 | |||||
| SEL- | PRACS | 3.510 | 1.956 | 0.933 | 0.031 | 0.155 | 0.943 | 1.841 | 1.697 | 0.926 | 0.071 | 0.019 | 0.926 | |||||
| SYNTH- | PRACS | 3.579 | 2.314 | 0.922 | 0.049 | 0.138 | 0.929 | 1.814 | 1.668 | 0.925 | 0.071 | 0.034 | 0.923 | |||||
| SEL- | AWLP | 3.308 | 2.054 | 0.952 | 0.027 | 0.082 | 0.960 | 1.985 | 1.777 | 0.921 | 0.073 | 0.053 | 0.919 | |||||
| SYNTH- | AWLP | 3.017 | 1.845 | 0.949 | 0.030 | 0.150 | 0.945 | 1.965 | 1.712 | 0.921 | 0.073 | 0.067 | 0.917 | |||||
| SEL- | MTF-GLP-FS | 2.724 | 1.577 | 0.960 | 0.026 | 0.103 | 0.957 | 0.763 | 0.726 | 0.978 | 0.072 | 0.010 | 0.927 | |||||
| SYNTH- | MTF-GLP-FS | 2.576 | 1.493 | 0.954 | 0.029 | 0.152 | 0.946 | 0.732 | 0.687 | 0.978 | 0.072 | 0.028 | 0.924 | |||||
| SEL- | MTF-GLP-HPM | 2.948 | 1.747 | 0.956 | 0.029 | 0.077 | 0.959 | 0.757 | 0.822 | 0.977 | 0.072 | 0.012 | 0.926 | |||||
| SYNTH- | MTF-GLP-HPM | 2.805 | 1.616 | 0.948 | 0.034 | 0.152 | 0.941 | 0.738 | 0.787 | 0.976 | 0.072 | 0.029 | 0.924 | |||||
| SEL- | MTF-GLP-HPM-R | 2.662 | 1.591 | 0.961 | 0.026 | 0.105 | 0.957 | 0.754 | 0.792 | 0.978 | 0.072 | 0.012 | 0.926 | |||||
| SYNTH- | MTF-GLP-HPM-R | 2.636 | 1.531 | 0.953 | 0.030 | 0.152 | 0.945 | 0.735 | 0.778 | 0.976 | 0.072 | 0.029 | 0.924 | |||||
| SEL- | TV | 4.986 | 3.008 | 0.919 | 0.021 | 0.147 | 0.954 | 2.912 | 2.733 | 0.909 | 0.081 | 0.081 | 0.906 | |||||
| SYNTH- | TV | 4.525 | 2.678 | 0.920 | 0.018 | 0.189 | 0.950 | 3.108 | 2.955 | 0.896 | 0.084 | 0.106 | 0.899 | |||||
| SEL- | ATPRK | 4.670 | 2.320 | 0.908 | 0.006 | 0.208 | 0.958 | 0.963 | 0.938 | 0.969 | 0.056 | 0.052 | 0.936 | |||||
| SYNTH- | ATPRK | 4.509 | 2.197 | 0.904 | 0.006 | 0.223 | 0.955 | 0.914 | 0.900 | 0.971 | 0.055 | 0.060 | 0.935 | |||||
| sen2res | 4.386 | 1.912 | 0.907 | 0.016 | 0.168 | 0.955 | 2.249 | 1.882 | 0.861 | 0.056 | 0.116 | 0.925 | ||||||
| SupReMe | 3.723 | 2.137 | 0.931 | 0.022 | 0.096 | 0.962 | 1.255 | 1.259 | 0.945 | 0.071 | 0.044 | 0.922 | ||||||
| MuSA | 4.546 | 2.594 | 0.884 | 0.051 | 0.305 | 0.898 | 2.172 | 1.620 | 0.826 | 0.078 | 0.269 | 0.879 | ||||||
| S2Sharp | 3.891 | 2.206 | 0.926 | 0.025 | 0.082 | 0.962 | 2.398 | 2.337 | 0.829 | 0.066 | 0.066 | 0.924 | ||||||
| SSSS | 6.696 | 3.428 | 0.812 | 0.057 | 0.230 | 0.906 | 3.039 | 2.584 | 0.755 | 0.074 | 0.213 | 0.892 | ||||||
| DSen2 | 2.652 | 1.577 | 0.963 | 0.027 | 0.178 | 0.944 | 1.045 | 1.038 | 0.967 | 0.072 | 0.049 | 0.920 | ||||||
| FUSE | 1.875 | 1.198 | 0.979 | 0.024 | 0.225 | 0.938 | 0.972 | 0.843 | 0.975 | 0.067 | 0.051 | 0.925 | ||||||
| S2-SSC-CNN | 1.730 | 1.107 | 0.978 | 0.041 | 0.220 | 0.922 | 1.706 | 1.638 | 0.891 | 0.118 | 0.077 | 0.871 | ||||||
| U-FUSE | 3.226 | 1.613 | 0.947 | 0.030 | 0.176 | 0.941 | 1.479 | 1.302 | 0.939 | 0.077 | 0.058 | 0.914 | ||||||
| S2-UCNN | 2.319 | 1.584 | 0.958 | 0.049 | 0.368 | 0.889 | 1.244 | 1.064 | 0.921 | 0.092 | 0.300 | 0.860 | ||||||
| Generalization Dataset | Generalization Scales | Sharpening | Spe. & Spa. Balance | Perceptive Quality | Computational Efficiency | ||
|---|---|---|---|---|---|---|---|
| SEL - | BDSD-PC | ★ | ★ | ||||
| SYNTH - | BDSD-PC | ★ | ★ | ||||
| SEL- | GSA | ||||||
| SYNTH - | GSA | ||||||
| SEL - | BT-H | ★ | |||||
| SYNTH - | BT-H | ||||||
| SEL - | PRACS | ||||||
| SYNTH - | PRACS | ||||||
| SEL - | AWLP | ||||||
| SYNTH - | AWLP | ||||||
| SEL - | MTF-GLP-FS | ||||||
| SYNTH - | MTF-GLP-FS | ||||||
| SEL - | MTF-GLP-HPM | ||||||
| SYNTH - | MTF-GLP-HPM | ||||||
| SEL- | MTF-GLP-HPM-R | ||||||
| SYNTH - | MTF-GLP-HPM-R | ||||||
| SEL - | TV | ★ | |||||
| SYNTH - | TV | ★ | |||||
| SEL - | ATPRK | ★ | |||||
| SYNTH - | ATPRK | ★ | |||||
| Sen2Res | ★ | ★ | |||||
| SupReMe | |||||||
| MuSA | ★ | ★ | ★ | ★ | ★ | ||
| S2Sharp | ★ | ★ | |||||
| SSSS | ★ | ★ | ★ | ★ | ★ | ★ | |
| DSen2 | |||||||
| FUSE | |||||||
| S2-SSC-CNN | ★ | ★ | |||||
| U-FUSE | |||||||
| S2-UCNN | ★ | ★ | ★ | ★ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciotola, M.; Guarino, G.; Mazza, A.; Poggi, G.; Scarpa, G. A Comprehensive Benchmarking Framework for Sentinel-2 Sharpening: Methods, Dataset, and Evaluation Metrics. Remote Sens. 2025, 17, 1983. https://doi.org/10.3390/rs17121983
Ciotola M, Guarino G, Mazza A, Poggi G, Scarpa G. A Comprehensive Benchmarking Framework for Sentinel-2 Sharpening: Methods, Dataset, and Evaluation Metrics. Remote Sensing. 2025; 17(12):1983. https://doi.org/10.3390/rs17121983
Chicago/Turabian StyleCiotola, Matteo, Giuseppe Guarino, Antonio Mazza, Giovanni Poggi, and Giuseppe Scarpa. 2025. "A Comprehensive Benchmarking Framework for Sentinel-2 Sharpening: Methods, Dataset, and Evaluation Metrics" Remote Sensing 17, no. 12: 1983. https://doi.org/10.3390/rs17121983
APA StyleCiotola, M., Guarino, G., Mazza, A., Poggi, G., & Scarpa, G. (2025). A Comprehensive Benchmarking Framework for Sentinel-2 Sharpening: Methods, Dataset, and Evaluation Metrics. Remote Sensing, 17(12), 1983. https://doi.org/10.3390/rs17121983











