Development of Laser Underwater Transmission Model from Maximum Water Depth Perspective
Abstract
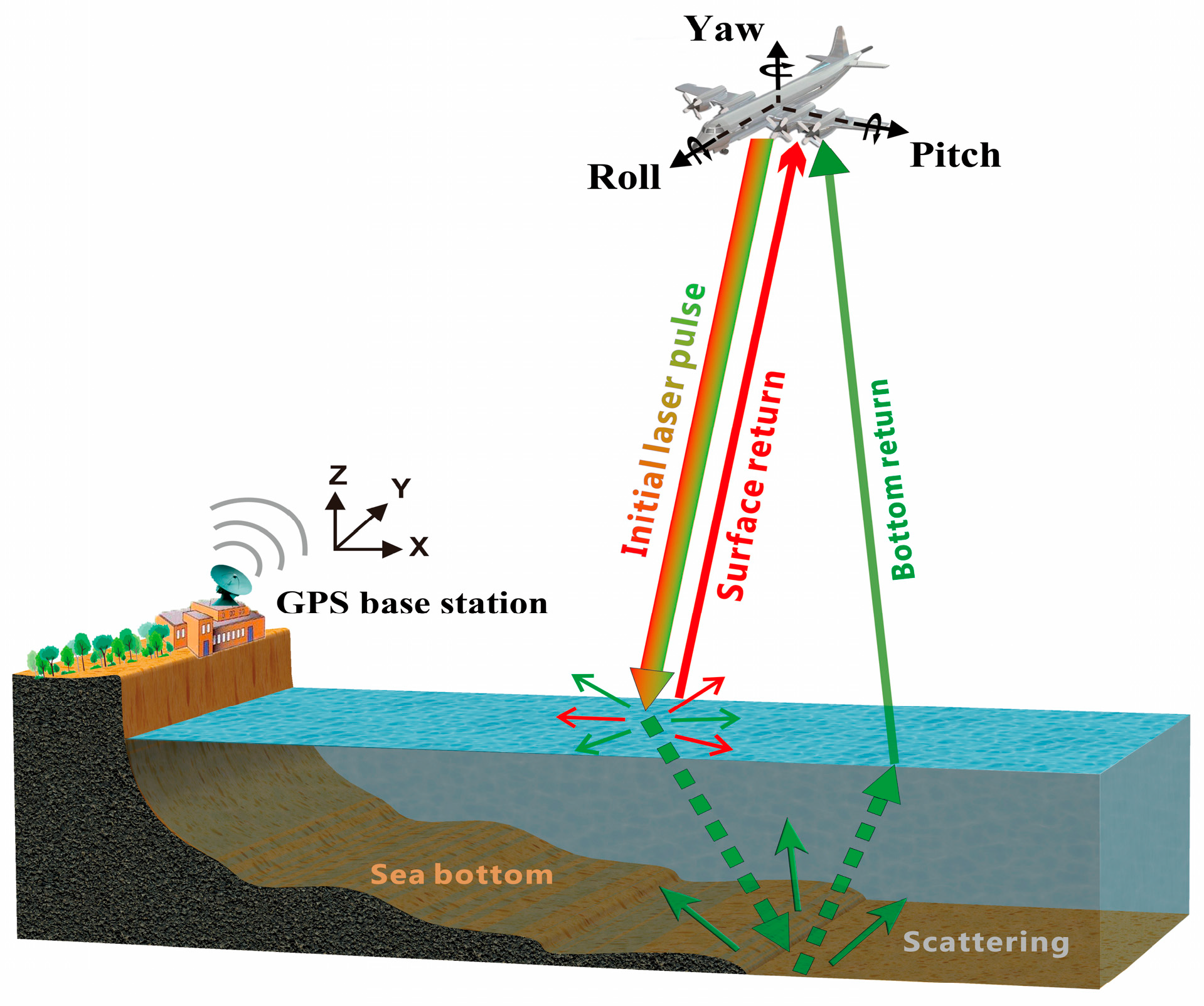
1. Introduction
2. Materials and Methods
2.1. Establishment of Green Light Transmission Models
2.1.1. Establishing New PB Model
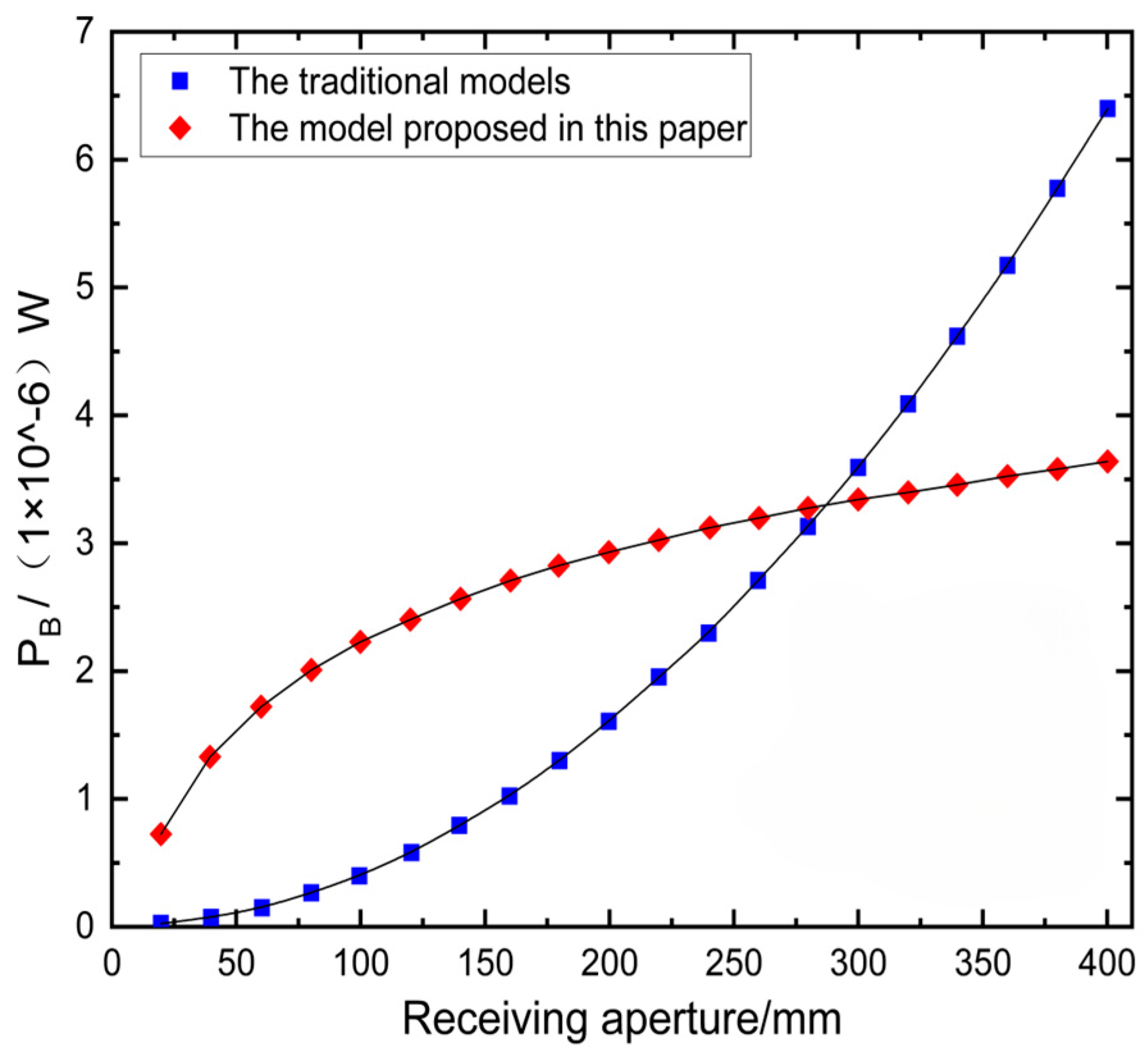
- The relationship between the size of the receiving aperture and the PB;
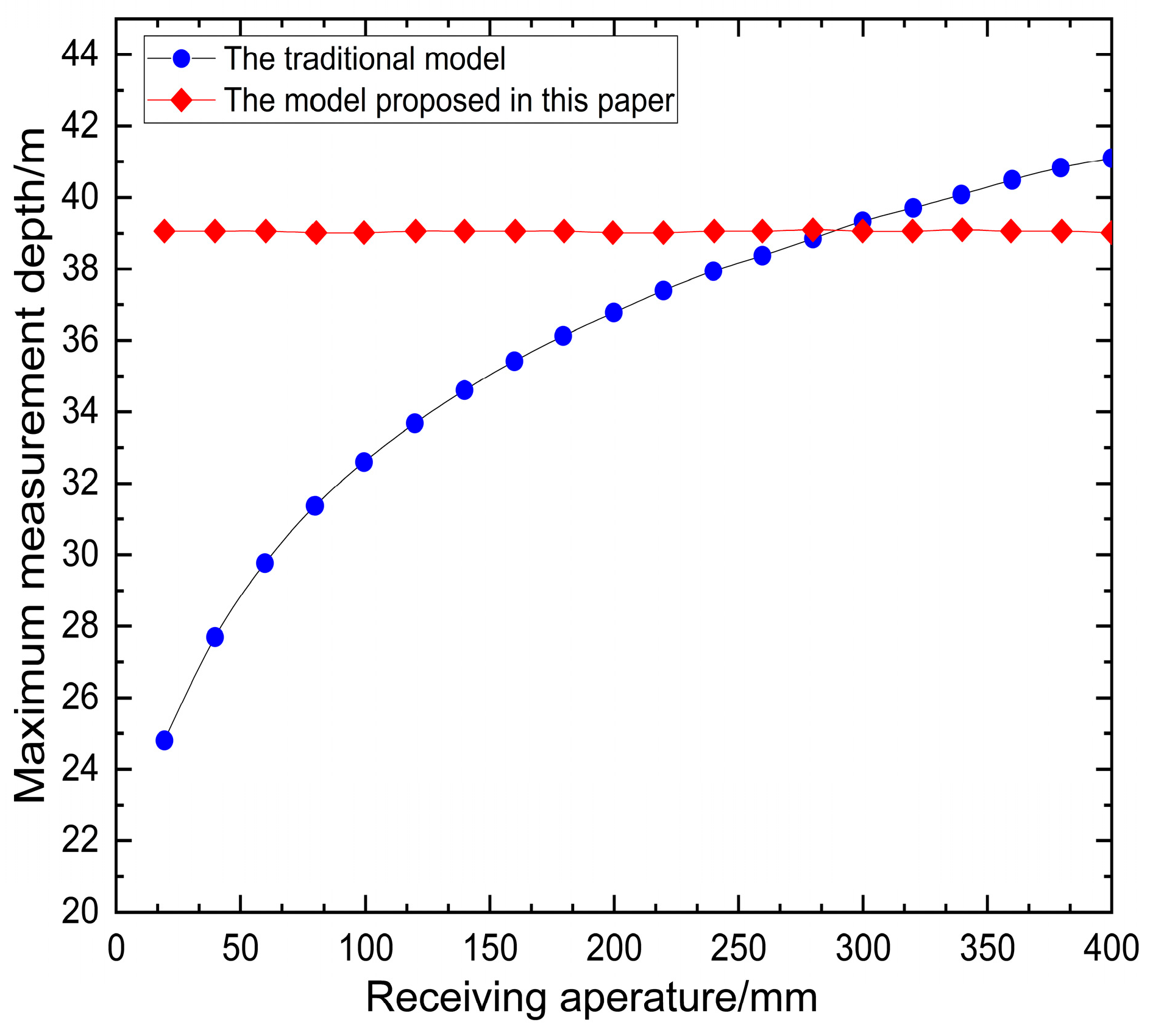
- The relationship between the PB and the measured water depth.
2.1.2. Estimating the Model of PA
- When the exponent of the parameter θ in Equation (7) is 2, the maximum measurement water depth does not change with increasing size of the receiving FOV from 2 mrad to 150 mrad. This means that the relationship between the PA and the receiving FOV is not a function of θ2, i.e., the PA/PB should not omit the influence of the receiving FOV.
- When the exponent of the parameter θ reaches 5/2, 3, and 4, the maximum measurement water depth increases with increasing the size of FOV from 2 mrad to 150 mrad. This understanding of the relationship between the received spot size and the sea surface spot provides further justification for the choice of θ5/2 in Equation (7). When the exponent is 5/2, the effective received power reflects this saturating behavior, i.e., the power continues to increase with increasing FOV until such time as further increases in FOV no longer affect the power. This behavior is consistent with the physical reality of energy capture, and therefore, θ5/2 is the most appropriate choice for modeling the PA-FOV relationship. This fact is in line with the actual situation. By carefully analyzing Figure 4, this paper finally chooses θ5/2. Firstly, θ5/2 obviously minimizes the change of the maximum measurement water depth. This result is consistent with the previous analysis, and also makes the overall change of PA more in line with the actual situation. Finally, this paper obtains an optimal solution for PA from the four parameters tested in the experiment, i.e.,
2.2. Coupling of Atmospheric Attenuation with Empirical Model
- The use of satellite remote sensing inversion;
- Direct measurement of a water body.
- The emission phase, i.e., before the laser enters the water surface;
- The reception phase, i.e., after the laser is out of the water surface.
2.3. Coupling of Water Surface Reflection Attenuation of Laser
2.4. Laser Transmission Model Considering Maximum Water Depth Measurable
3. Results
3.1. Experimental Verification
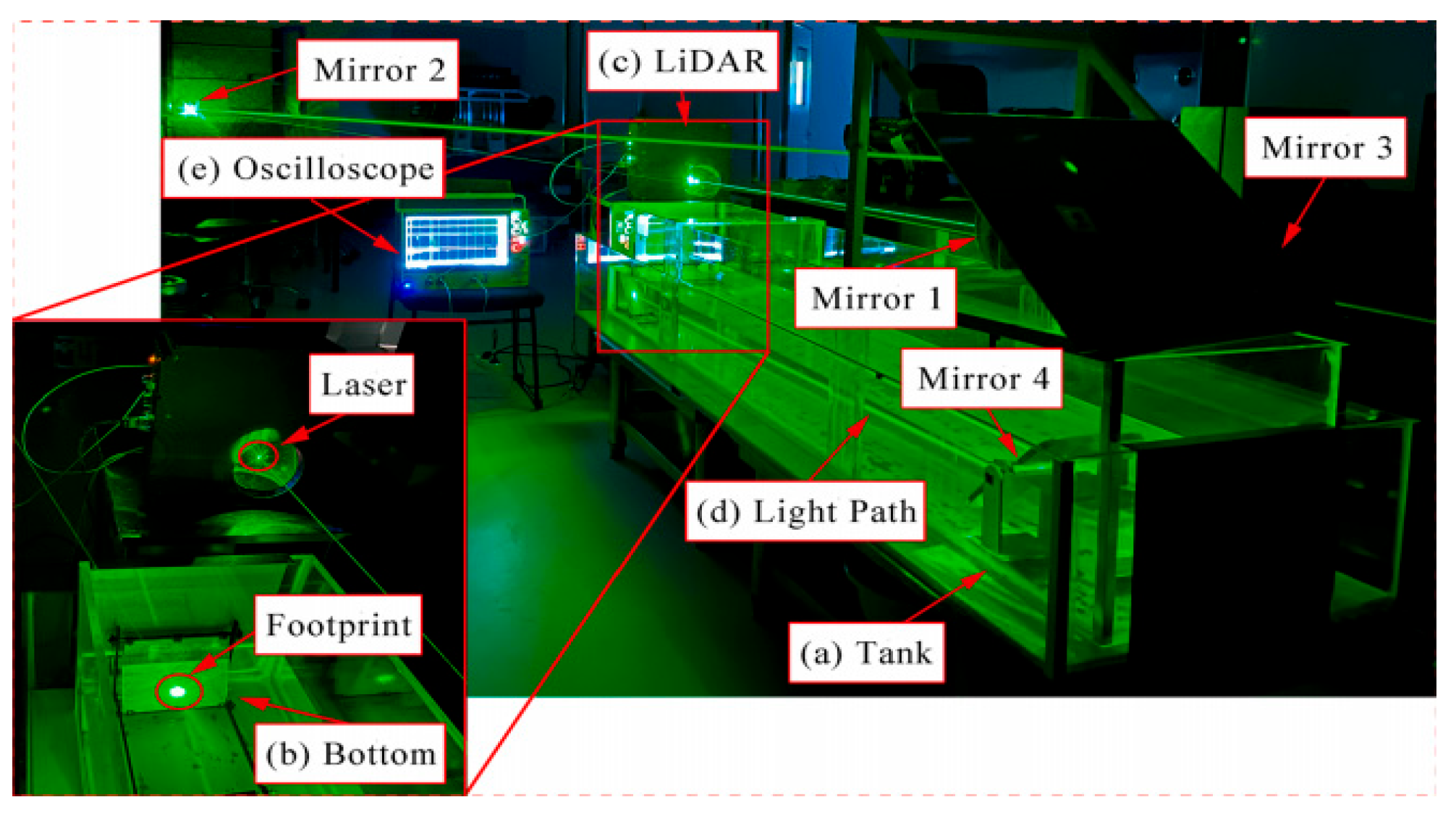
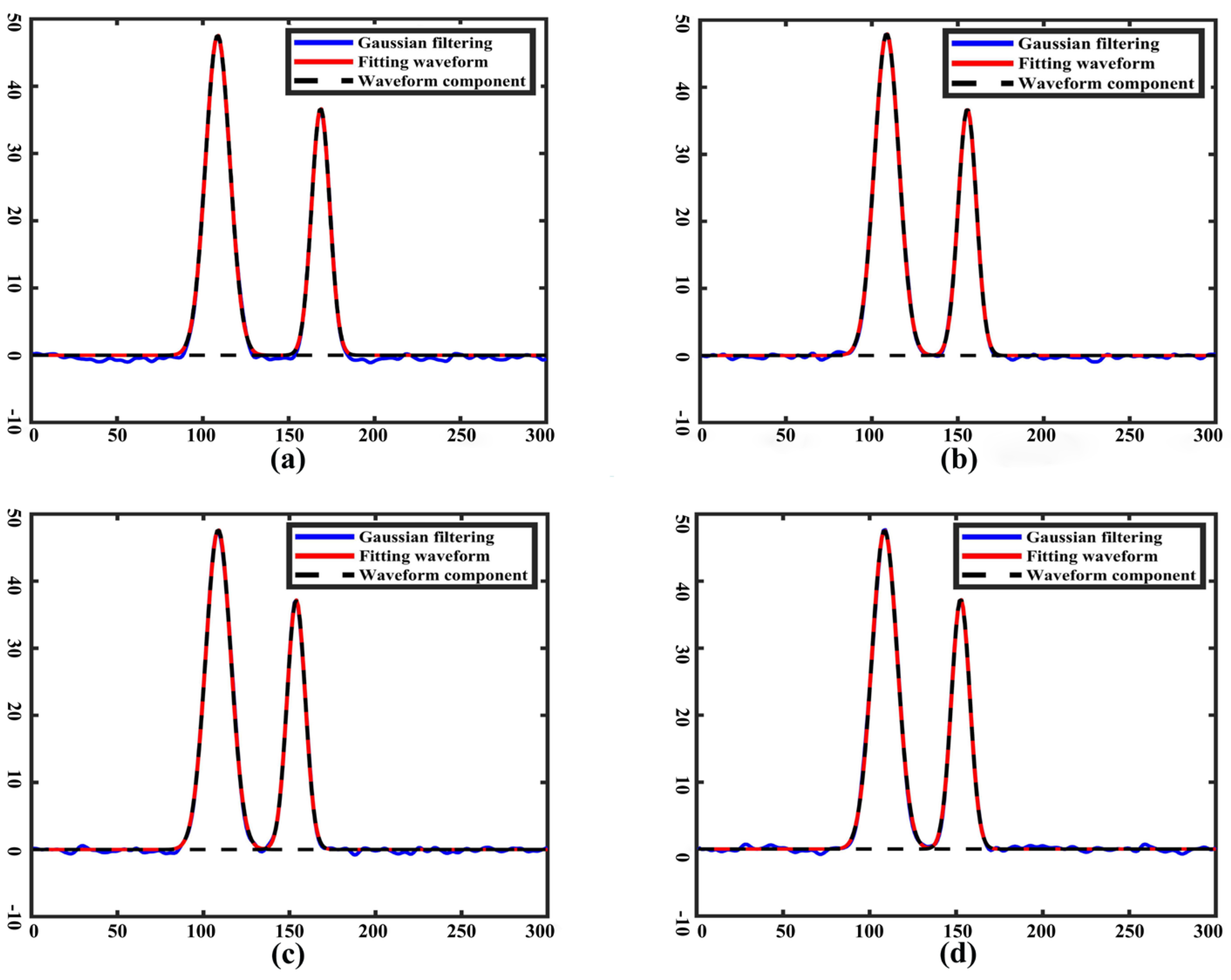
3.1.1. Verification in Indoor Water Tanks
- Step 1: Fill a certain amount of water into the indoor tank (see Figure 5a), and place a plane mirror at specific locations on the tank for reflection of the 532 nm laser into the water body.
- Step 2: Place another plane mirror at a specific location in the tank to reflect the laser light onto the tank wall. Meanwhile, a black baffle was fixed to the wall of the tank to simulate the bottom of the water source, and sediment was added to the water to simulate turbidity. By changing the position of the black baffle in the water tank to simulate the different water depths, multiple water depth data points are collected using a LiDAR device (GQ Eagle 18, Guilin University of Technology, China) (Figure 5c).
- Step 3: Place Reflectors #1, #2, and #3 at specific locations to increase the transmission distance of the optical path to 30 m, during which Reflector #3 reflects the laser beam onto Reflector #4. Finally, the laser light is reflected by Reflector #4 to hit the bottom of the simulated water bottom sediment.
- Step 4: Connect the oscilloscope (see Figure 5e) to the LiDAR device, and the oscilloscope data are automatically stored at each of the sampling operations conducted in Step 3.
- Step 5: Change the bottom of the simulated water bottom sediment, and repeat the same operation as Step 3 through Step 5.
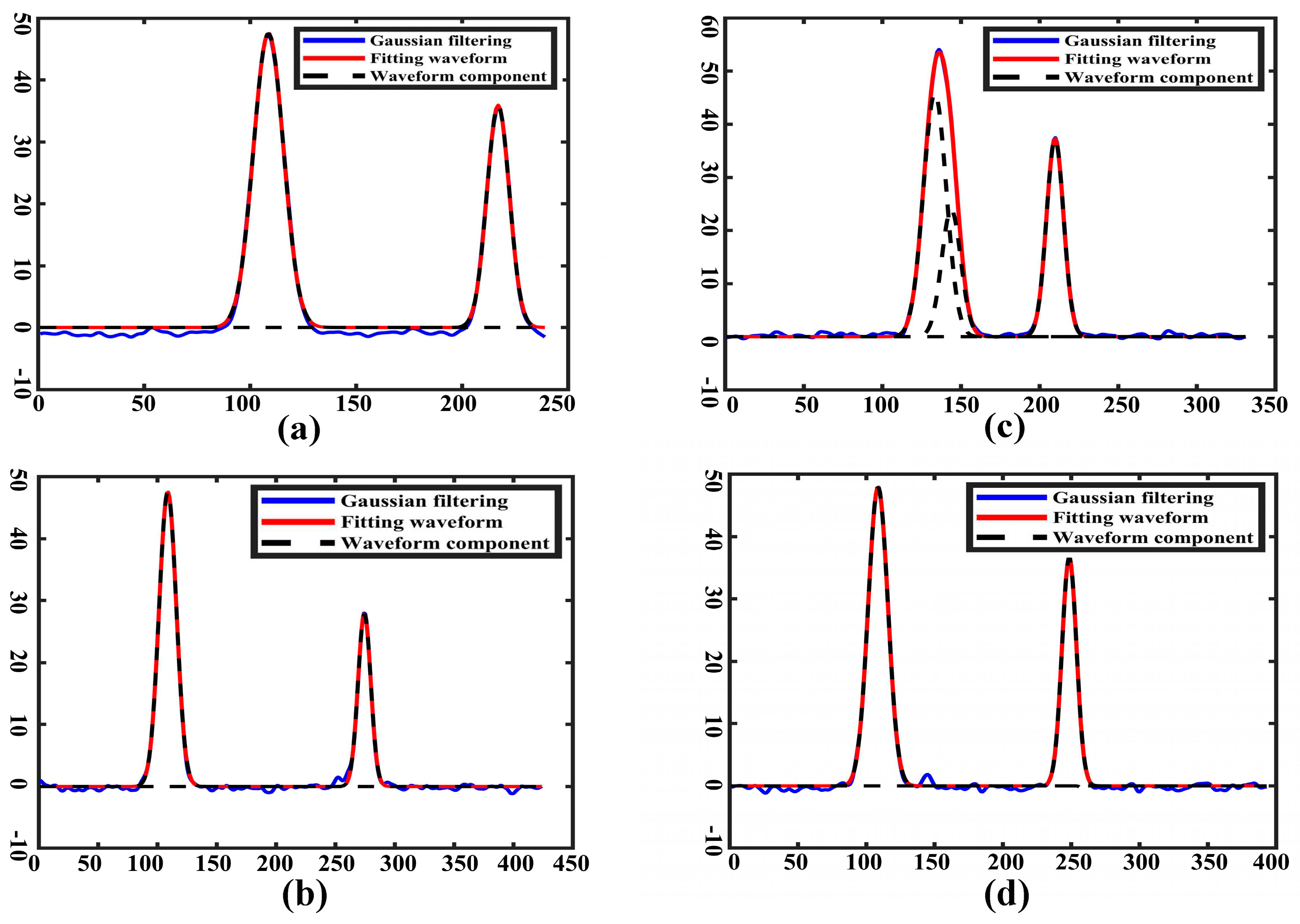
3.1.2. Validation in Indoor Swimming Pools
- Step 1: The LiDAR device is fixed on a stand 15 m high, and a laser transmitter is placed underwater to emit laser light.
- Step 2: The baffles underwater are set up as underwater targets, and the water depths are measured by changing the position of the baffles.
- Step 3: The oscilloscope is connected to the LiDAR device, and the LiDAR device is turned on. The position of the baffle in the pool is continuously changed four times, and the water depth data are recorded and stored.
3.1.3. Verification in Li River, Guilin, Guangxi
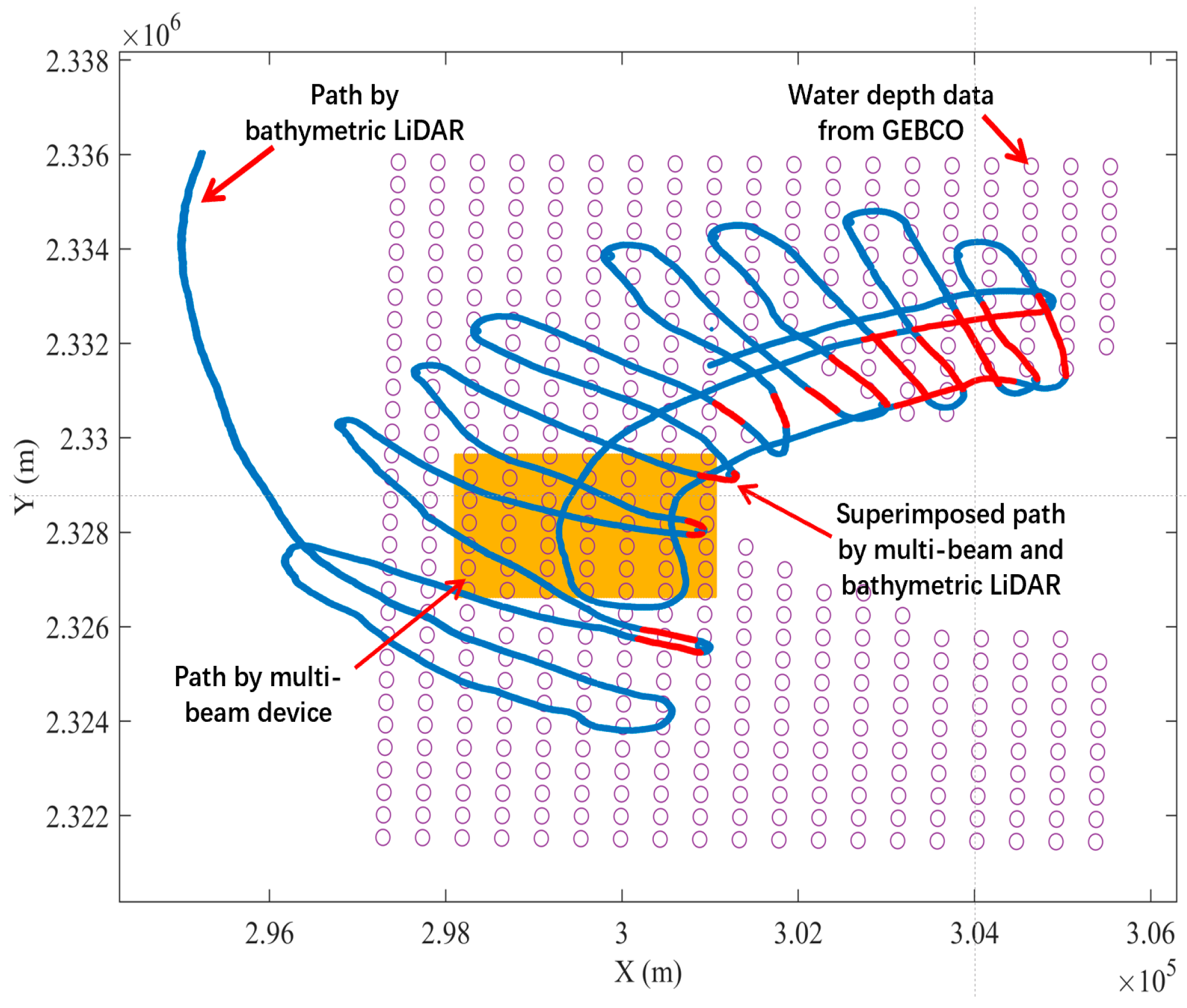
3.1.4. Verification in Beibu Gulf, Pacific Ocean
3.1.5. Experimental Analyses
3.2. Cross-Validation with Other Models
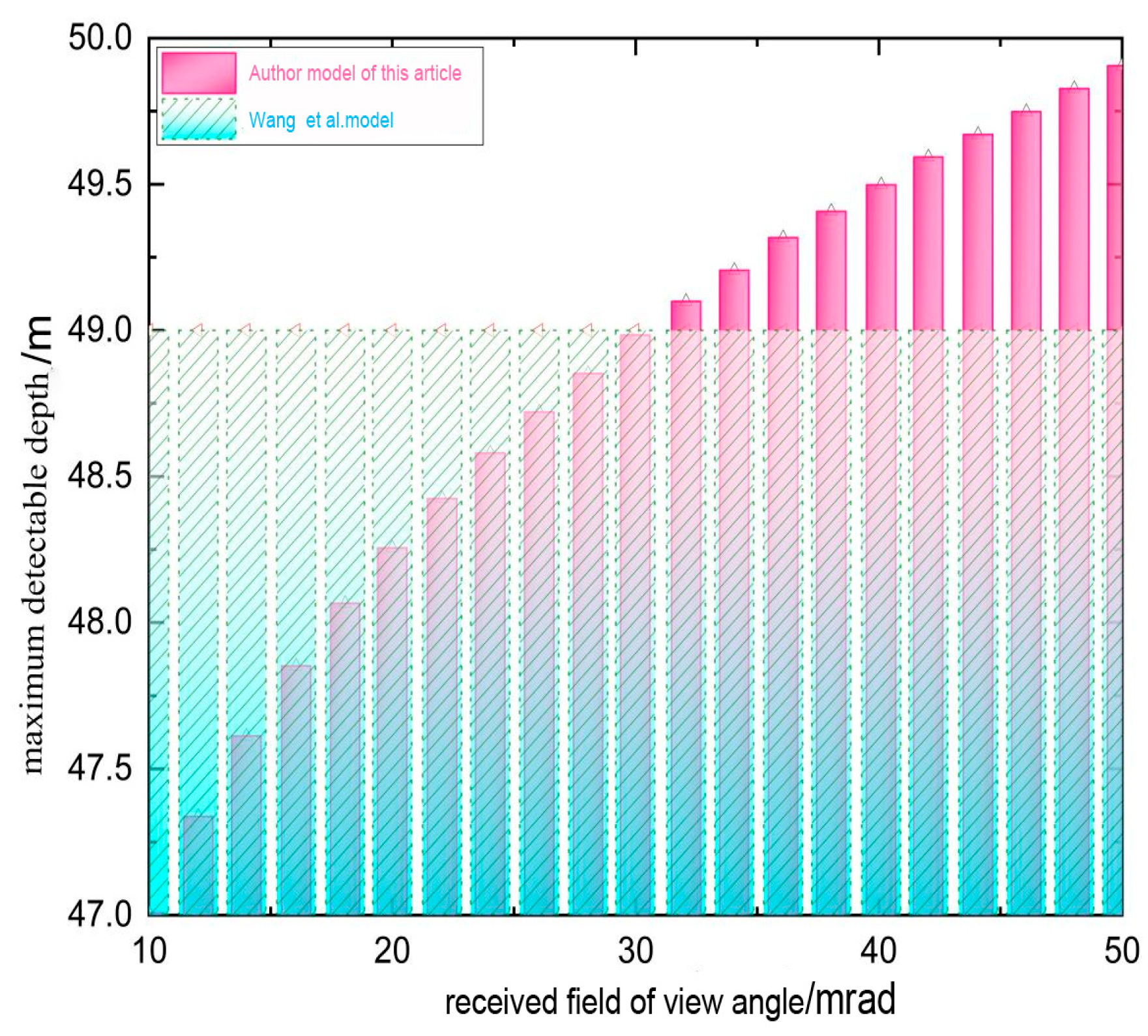
3.2.1. Cross-Validation with the Model from Wang et al. (2003) [18]
- The predicted maximum water depth by the model established by Wang et al. (2003) [18] is a constant, i.e., 49 m, for all FOVs from 10 to 50 mrad, while change from 47 m to 50 m by our model when the receiving FOV ranges from 10 mrad to 50 mrad. This result demonstrates that the model established in this paper is close to the real situation, and the difference between the two models is less than 1 m around.
- The model developed by Wang et al. (2003) [18] is based on signal-to-noise ratio prediction. In fact, the noises from the bathymetric LiDAR device can be pre-processed. So, the model developed by Wang et al. (2003) [18] is somewhat low accuracy, i.e., the model established in this paper is of higher accuracy than Wang et al. (2003) [18].
- If the parameters, including the ALB sensor, airborne platform flight parameters, transmission path parameters, transmission environment parameters and other parameters, are the same, the predicted maximum water depths are 49 m by Wang et al. (2003) [18] and 49.25 m by the model developed in this paper. This implies that their difference in maximum water depths reaches 0.25 m.
3.2.2. Cross-Validation with the Model from Ding et al. (2018) [22]
4. Discussion
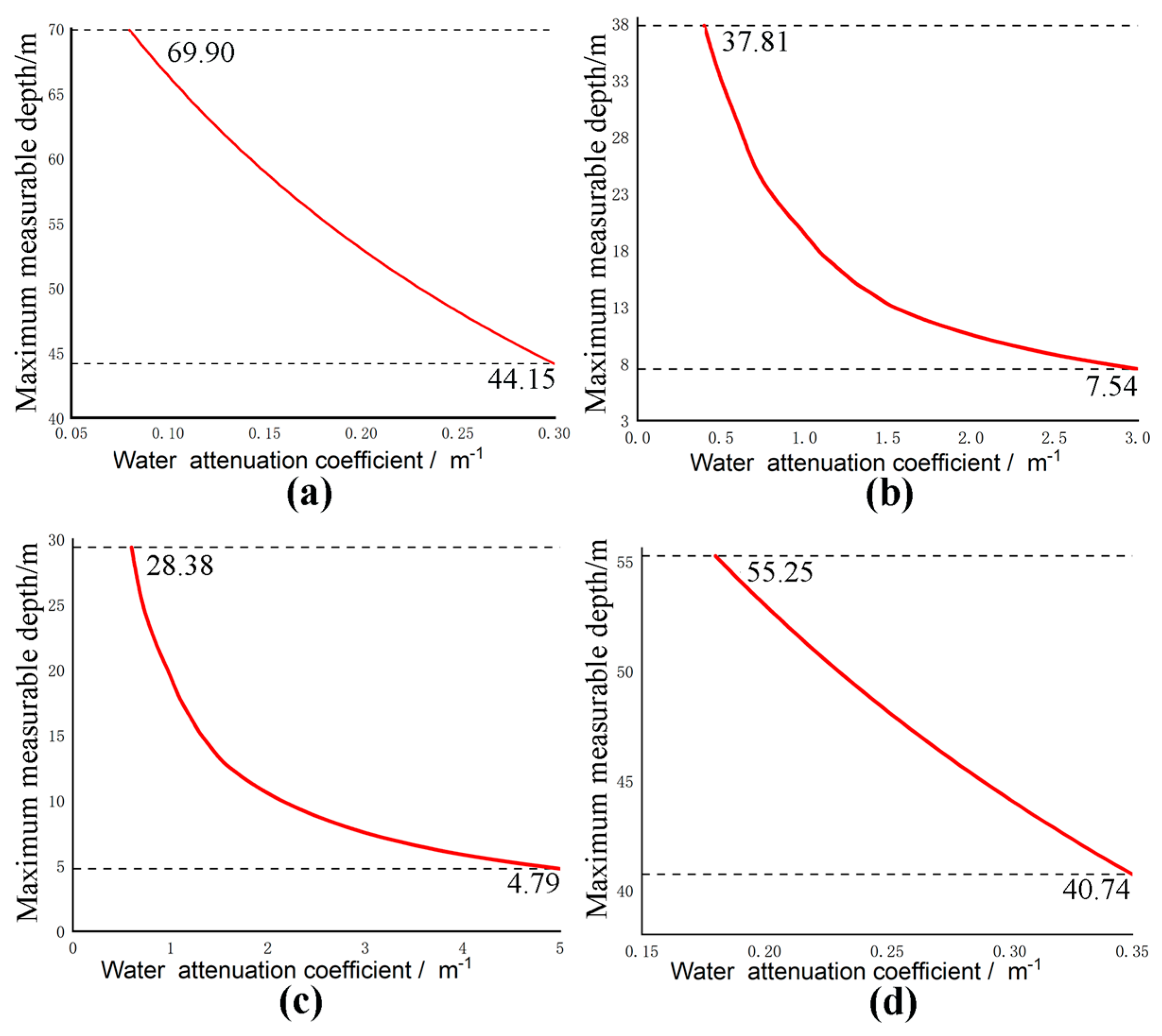
4.1. Maximum Water Depth Measurement vs. Water Quality
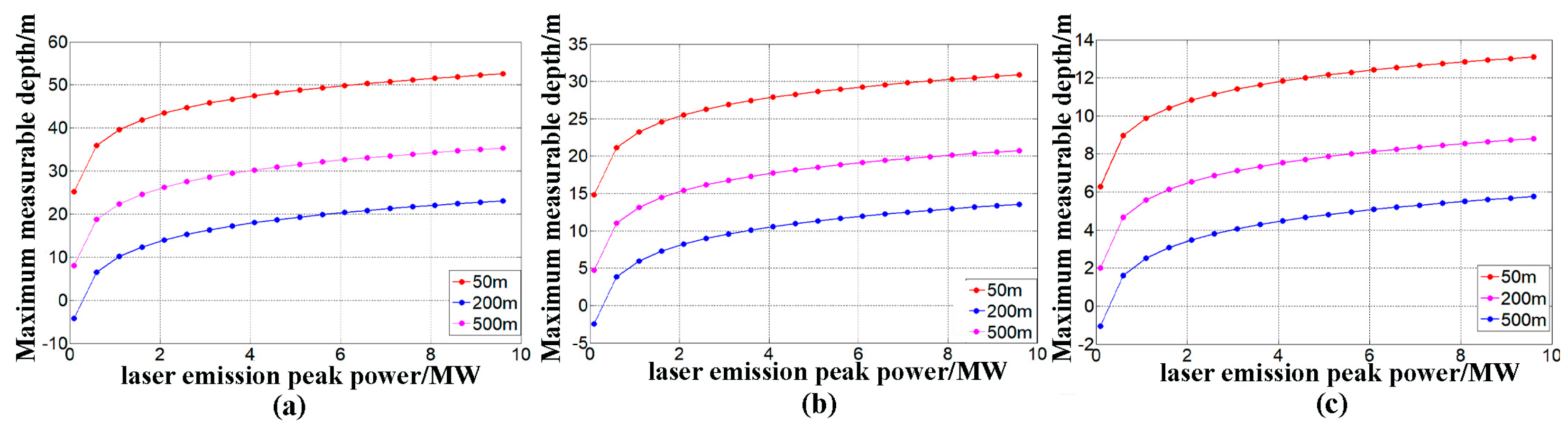
4.2. Maximum Water Depth Measurement vs. LiDAR Sensor Parameters
4.2.1. For the Variable of the Aircraft Flight Altitude
4.2.2. For the Variable of the Receiving FOV
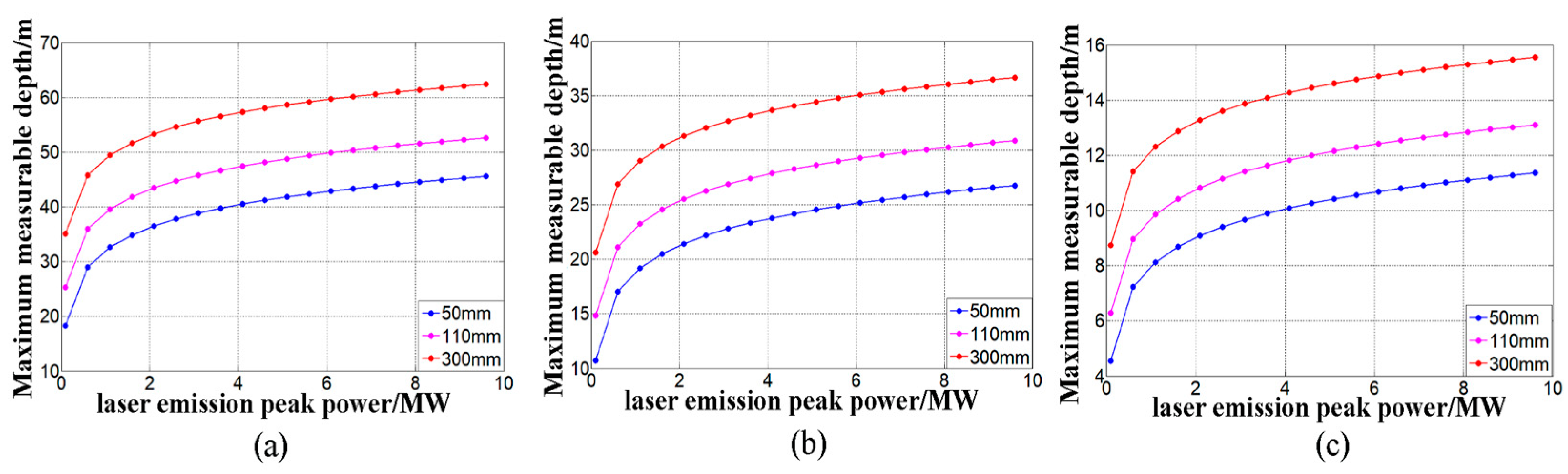
4.2.3. For the Variable of the Receiving Aperture
4.2.4. Synthesized Analysis
4.3. Extended Application of the Model
- ALB system design optimization: the laser power can be dynamically adjusted according to the predicted maximum water depth (e.g., power reduction in shallow water to extend the life of the equipment); by substituting the parameters of the designed ALB system into the model to determine in advance whether the design is reasonable under certain environmental parameters.
- Mission planning: combining real-time water quality data (e.g., satellite data, measured data, weather station data) to plan the optimal flight altitude and route to improve operational efficiency.
- Data processing: In shallow water bathymetry, the reflected signals on the surface of the water and the underwater signals are susceptible to aliasing [47,48], resulting in a significant increase in PB. The dynamic calibration algorithm of PA/PB is embedded in the echo signal preprocessing module, which can realize the noise adaptive filtering and further improve the dynamic optimization capability of PA/PB in shallow water.
5. Conclusions
- With the same other parameters, when the receiving FOV changes from 10 mrad to 50 mrad, the maximum water depth measurable from the model established in this paper reaches 0.86 m difference in comparison with the results from the model established by Wang et al. (2003) [18]. The maximum water depth measurable from the model established in this paper reaches 1.28 m, in comparison with the results from the model established by Ding et al. (2018) [22,23]. This fact demonstrates that the model constructed in this paper is correct.
- This model can predict the maximum water depth detectable by an airborne bathymetric LiDAR system, which can provide the operating route in practice and save costs. At the same time, it can be used as a basis for the design of the radar system parameters.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guenther, G.C. Airborne lidar bathymetry. Digit. Elev. Model. Technol. Appl. Dem. Users Man 2007, 2, 253–320. [Google Scholar]
- Shangguan, M.; Liao, Z.; Guo, Y.; Lee, Z. Seabed backscattered signal peak shift and broadening induced by multiple scattering in bathymetric lidar. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–14. [Google Scholar] [CrossRef]
- Zhou, G.; Zhou, X.; Li, W.; Zhao, D.; Song, B.; Xu, C.; Zhang, H.; Liu, Z.; Xu, J.; Lin, G.; et al. Development of a Lightweight Single-Band Bathymetric LiDAR. Remote Sens. 2022, 14, 5880. [Google Scholar] [CrossRef]
- Zhou, G.; Wu, J.; Gao, K.; Song, N.; Jia, G.; Zhou, X.; Xu, J.; Wang, X. Development of an Adaptive Fuzzy Integral-Derivative Line-of-Sight Method for Bathymetric LiDAR Onboard Unmanned Surface Vessel. Remote Sens. 2024, 16, 2657. [Google Scholar] [CrossRef]
- Luan, T.; Tao, B.; He, Y.; Li, J.; Fu, X.; Yu, J.; Wang, H. Range Bias Correction for Saturated Bottom Return from Bathymetry LiDAR Measurements. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–17. [Google Scholar] [CrossRef]
- Chen, P.; Jamet, C.; Zhang, Z.; He, Y.; Mao, Z.; Pan, D.; Wang, T.; Liu, D.; Yuan, D. Vertical distribution of subsurface phytoplankton layer in South China Sea using airborne Lidar. Remote Sens. Environ. 2021, 263, 112567. [Google Scholar] [CrossRef]
- Xu, W.; Guo, K.; Liu, Y.; Tian, Z.; Tang, Q.; Dong, Z.; Li, J. Refraction error correction of Airborne LiDAR Bathymetry data considering sea surface waves. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102402. [Google Scholar] [CrossRef]
- Zhou, G.; Xu, J.; Hu, H.; Liu, Z.; Zhang, H.; Xu, C.; Zhou, X.; Yang, J.; Nong, X.; Song, B.; et al. Off-Axis Four-Reflection Optical Structure for Lightweight Single-Band ALB. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar]
- Chen, P.; Jamet, C.; Liu, D. Lidar remote sensing for vertical distribution of seawater optical properties and chlorophyll-a from the East China Sea to the South China Sea. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–21. [Google Scholar] [CrossRef]
- Zhou, G.; Song, N.; Jia, G.; Wu, J.; Gao, K.; Huang, J.; Zhou, X.; Jiasheng, X.; Lin, T.; Zhang, L.; et al. Adaptive Adjustment for Laser Energy and PMT Gain Through Self-Feedback of Echo Data in Bathymetric LiDAR. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–22. [Google Scholar] [CrossRef]
- Arnush, D. Underwater light-beam propagation in the small-angle approximation. J. Opt. Soc. Am. 1972, 62, 1109–1111. [Google Scholar] [CrossRef]
- Steinvall, O.; Klevebrant, H.; Lexander, J.; Widen, A. Laser depth sounding in the Baltic Sea. Appl. Opt. 1981, 20, 3284–3286. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Zhou, G.; Li, C.; Zhang, D.; Liu, D.; Zhou, X.; Zhan, J. Overview of underwater transmission characteristics of oceanic LiDAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8144–8159. [Google Scholar] [CrossRef]
- Smith, R.C.; Baker, K.S. Optical Properties of the Clearest Natural Waters (200–800 Nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef]
- Lerner, R.M.; Summers, J.D. Monte Carlo description of time and space-resolved multiple forward scatter in natural water. Appl. Opt. 1982, 21, 861–869. [Google Scholar] [CrossRef] [PubMed]
- Caimi, F.M.; Bailey, B.C.; Blatt, J.H. Spatial Coherence Methods in Undersea Image Formation and Detection. In Proceeding of the OCEANS 96 MTS/IEEE Conference Proceedings. The Coastal Ocean-Prospects for the 21st Century, Fort Launderdale, FL, USA, 23–26 September 1996; pp. 40–46. [Google Scholar]
- Wang, Q.; Chen, W.; Lu, Y.; Chun, C. Analysis of Relationship Between Parameter Choice of Airborne Laser Bathymetry and Maximum Penetrability. Acta Opt. Sin. 2003, 10, 1255–1260. [Google Scholar]
- Cossio, T.; Slatton, K.C.; Carter, W.; Shrestha, K.; Harding, D. Predicting topographic and bathymetric measurement performance for low-SNR airborne lidar. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2298–2315. [Google Scholar] [CrossRef]
- Jamet, C.; Loisel, H.; Dessailly, D. Retrieval of the spectral diffuse attenuation coefficient Kd (λ) in open and coastal ocean waters using a neural network inversion: Retrieval of Diffuse Attenuation. J. Geophys. Res. Ocean. 2012, 117, C10023. [Google Scholar] [CrossRef]
- Austin, R.W. Spectral Dependence of the Diffuse Attenuation Coefficient of Light in Ocean Waters. Opt. Eng. 1986, 25, 253471. [Google Scholar] [CrossRef]
- Ding, K.; Li, Q.Q.; Zhu, J.S.; Wang, C.S.; Fan, X. Analysis of diffuse attenuation coefficient spectra of coastal waters of Hainan Island and performance estimation of airborne LiDAR bathymetry. Spectrosc. Spect. Anal. 2018, 38, 1582–1587. [Google Scholar]
- Ding, K.; Li, Q.; Zhu, J.; Wang, C.; Xu, T. Evaluation of Airborne LiDAR Bathymetric Parameters on the Northern South China Sea Based on MODIS Data. Acta Geod. Cartogr. Sin. 2018, 47, 180. [Google Scholar]
- Liu, Q.; Cui, X.; Jamet, C.; Zhu, X.; Mao, Z.; Chen, P.; Bai, J.; Liu, D. A semianalytic Monte Carlo simulator for spaceborne oceanic LiDAR: Framework and preliminary results. Remote Sens. 2020, 12, 2820. [Google Scholar] [CrossRef]
- Guo, S.; He, Y.; Chen, Y.; Chen, W.; Chen, Q.; Huang, Y. Monte Carlo Simulation with Experimental Research about Underwater Transmission and Imaging of Laser. Appl. Sci. 2022, 12, 8959. [Google Scholar] [CrossRef]
- He, Y.; Liu, Y.; Liu, C.; Li, D. Analysis of Transmission Depth and Photon Number in Monte Carlo Simulation for Underwater Laser Transmission. Remote Sens. 2022, 14, 2565. [Google Scholar] [CrossRef]
- Yang, F.; Qi, C.; Su, D.; Ma, Y.; He, Y.; Wang, X.H.; Liu, J. Modeling and analyzing water column forward scattering effect on airborne LiDAR bathymetry. IEEE J. Ocean. Eng. 2023, 48, 1373–1388. [Google Scholar] [CrossRef]
- Xie, C.; Chen, P.; Zhang, S.; Huang, H. Nearshore Bathymetry from ICESat-2 LiDAR and Sentinel-2 Imagery Datasets Using Physics-Informed CNN. Remote Sens. 2024, 16, 511. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, Y.; Stachlewska, I.S.; Hu, Y.; Lu, X.; Chen, W.; Liu, J.; Sun, W.; Yang, S.; Tao, Y.; et al. Spaceborne high-spectral-resolution lidar ACDL/DQ-1 measurements of the particulate backscatter coefficient in the global ocean. Remote Sens. Environ. 2024, 315, 114444. [Google Scholar] [CrossRef]
- Chen, S.; Chen, P.; Kong, W.; Shu, R.; Pan, D. A Semianalytical Method for Ocean LiDAR Radiative Transfer Considering Inelastic and Polarized Scattering. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–16. [Google Scholar] [CrossRef]
- Szafarczyk, A.; Toś, C. The Use of Green Laser in LiDAR Bathymetry: State of the Art and Recent Advancements. Sensors 2023, 23, 292. [Google Scholar] [CrossRef]
- Chen, W.; Chen, P.; Zhang, H.; He, Y.; Tang, J.; Wu, S. Review of airborne oceanic lidar remote sensing. Intell. Mar. Technol. Syst. 2023, 1, 10. [Google Scholar] [CrossRef]
- Hodara, H. Laser wave propagation through the atmosphere. Proc. IEEE 1966, 54, 368–375. [Google Scholar] [CrossRef]
- Guenther, G.; Thomas, R. System Design and Performance Factors for Airborne Laser Hydrography. In Proceedings of the Proceedings OCEANS’83, San Francisco, CA, USA, 29 August–1 September 1983; pp. 425–430. [Google Scholar]
- Chen, J.; Zhu, X.; Yang, K.W.; Li, Z.G. Environmental noise analysis of airborne laser barthymetry. Laser Technol. 1999, 23, 360–363. [Google Scholar]
- Ilisei, A.; Bruzzone, L. A model-based technique for the automatic detection of earth continental ice subsurface targets in radar sounder data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1911–1915. [Google Scholar] [CrossRef]
- Chen, W.G. The Effective Attenuation Coefficient of Airborne Oceanic Lidar System. Acta Electron. Sin. 1996, 6, 47–50. [Google Scholar]
- Wang, Y.J.; Fan, C.Y.; Wei, H.L. Laser Attenuation in the Atmosphere and Seawater; National Defense Industry Press: Beijing, China, 2015; Chapter 2; pp. 99–109. [Google Scholar]
- Mohlenhoff, B.; Romeo, M.; Diem, M.; Wood, B.R. Mie-Type Scattering and Non-Beer-Lambert Absorption Behavior of Human Cells in Infrared Microspectroscopy. Biophys. J. 2005, 88, 3635–3640. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne laser scanning—An introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Bufton, J.L.; Hoge, F.E.; Swift, R.N. Airborne Measurements of Laser Backscatter from the Ocean Surface. Appl. Opt. 1983, 22, 2603–2618. [Google Scholar] [CrossRef]
- Xie, Y.; Sengupta, M.; Habte, A.; Andreas, A. The “Fresnel equations” for diffuse radiation on inclined photovoltaic surfaces (FEDIS). Renew. Sustain. Energy Rev. 2022, 161, 112362. [Google Scholar] [CrossRef]
- Bass, M.; Van Stryland, E.W.; Williams, D.R.; Wolfe, W.L. Handbook of Optics; McGraw-Hill: New York, NY, USA, 1995; Volume 2. [Google Scholar]
- Cox, C.; Munk, W. Measurement of the Roughness of the Sea Surface from Photographs of the Suns Glitter. J. Opt. Soc. 1954, 44, 838–850. [Google Scholar] [CrossRef]
- Zhou, G.; Liu, J.; Gao, K.; Liu, R.; Tang, Y.; Cai, A.; Zhou, X.; Xu, J.; Xie, X. A Coupling Method for the Stability of Reflectors and Support Structure in an ALB Optical-Mechanical System. Remote Sens. 2025, 17, 60. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, N.; Ma, Y.; Yang, B.; Zhang, Z.; Wang, X.H.; Li, S. A Maximum Bathymetric Depth Model to Simulate Satellite Photon-Counting Lidar Performance. ISPRS J. Photogramm. Remote Sens. 2021, 174, 182–197. [Google Scholar] [CrossRef]
- Yang, F.; Qi, C.; Su, D.; Ding, S.; He, Y.; Ma, Y. An Airborne LiDAR Bathymetric Waveform Decomposition Method in Very Shallow Water: A Case Study around Yuanzhi Island in the South China Sea. Int. J. Appl. Earth Obs. Geoinf. 2022, 109, 102788. [Google Scholar] [CrossRef]
- Wang, D.; Xing, S.; He, Y.; Yu, J.; Xu, Q.; Li, P. Evaluation of a New Lightweight UAV-Borne Topo-Bathymetric LiDAR for Shallow Water Bathymetry and Object Detection. Sensors 2022, 22, 1379. [Google Scholar] [CrossRef]





| Light Intensity | Sunlight at Noon (No Filter) | Sunlight at Noon (with Filter) | Moonlight with Full Moon (No Filter) | Moonlight with Full Moon (with Filter) |
|---|---|---|---|---|
| PB/w | 5.45 × 10−4 | 4.3 × 10−8 | 6.67 × 10−1 | 3.46 × 10−16 |
| Parameter Category | Range of Values | Relevant Parameters of the Atmospheric Environment, etc. | Parameter Value (Description) |
|---|---|---|---|
| Peak laser power (MW) | 0.1–10 | Refractive index of water nwater | 1.33 (built-in) |
| Laser scanning zenith angle (°) | 5–30 | Atmospheric refractive index natmosphere | 1.000029 (built-in) |
| Receiving field of view (mrad) | 2–200 | Background irradiance/Mw∗cm−2∗sr−1∗nm−1 | 0.0147 (built-in) |
| Receiving caliber (mm) | 40–400 | atmospheric visibility | 6 |
| Spectral receiver bandwidth (nm) | 0.1–10 | Substrate reflectance | 0.1 |
| Receiving system efficiency | 0.1–0.5 | Water absorption coefficient/m−1 | 0.12 |
| Receiver sensitivity (nw) | 0.5–500 | Water scattering coefficient/m−1 | 0.06 |
| Inlet laser pulse wavelength (nm) | 532 | ||
| Aircraft altitude (m) | 40–1500 |
| Parameters of LiDAR Device | Parameters (Description) |
|---|---|
| Laser emission power PT/KW | 300 |
| Receiving field of view θ/mrad | 40 |
| Receiving caliber Dr/mm | 50 |
| Receiving system efficiency/η | 0.8 |
| Laser scanning zenith angle θ1/° | 10 |
| Spectral receiver bandwidth Ds/nm | 1.2 |
| Inlet laser pulse wavelength/nm | 532 (built-in) |
| Laser divergence angle/mrad | 1.5 |
| Weight/kg | 3.2 |
| Size/mm | 310 × 188 × 110 |
| Receiver sensitivity Pminimum sensitivity/W | 1 × 10−10 |
| Parameters | From LiDAR’s First Experiment | From LiDAR’s Second Experiment | From LiDAR’s Third Experiment | From the Model Predictions in This Paper |
|---|---|---|---|---|
| Maximum depth (m) | 7.02 | 7.41 | 7.26 | 7.85 |
| Marine, Atmospheric, and Other Relevant Parameters | Value |
|---|---|
| Refractive index of water nwater | 1.33 |
| Atmospheric refractive index natmospheric | 1.000029 |
| Background irradiance/mW*cm−2*sr−1*nm−1 | 0.0147 |
| atmospheric visibility | 6 |
| Substrate reflectance | 0.2 |
| Water attenuation coefficient/m−1 | 0.3 |
| Water absorption coefficient/m−1 | 0.0617 |
| Water scattering coefficient/m−1 | 0.24 |
| Parameters of LiDAR Device | Parameters (Description) |
|---|---|
| Laser emission power PT/MW | 1.5 |
| Receiving field of view θ/mrad | 33 |
| Receiving caliber Dr/mm | 200 |
| Receiving system efficiency/η | 0.8 |
| Laser scanning zenith angle θ1/° | 22.5 |
| Spectral receiver bandwidth Ds/nm | 0.5 |
| Inlet laser pulse wavelength/nm | 532 (built-in) |
| Receiver sensitivity Pminimum sensitivity/W | 1 × 10−10 |
| Parameters | From Multibeam Sonar | From Bathymetric LiDAR | From the Model in This Paper |
|---|---|---|---|
| Maximum depth (m) | 19.75 | 19.82 | 18.6173 |
| Experimental Location | Maximum Water Depth Measured by LiDAR | Maximum Water Depth Predicted by the Model in This Paper | Absolute Error | Relative Error |
|---|---|---|---|---|
| Indoor water tanks | 8.00 m | 7.62 m | 0.38 m | 4.7% |
| Indoor swimming pools | 28.20 m | 29.77 m | 1.57 m | 5.5% |
| Li River, Guilin, Guangxi | 7.41 m | 7.85 m | 0.44 m | 5.9% |
| Beibu Gulf, Pacific Ocean | 19.82 m | 18.61 m | 1.21 m | 6.1% |
| Parameter | Values |
|---|---|
| Aircraft altitude/m | 500 |
| Laser emission power/MW | 2 |
| Receiving field of view θ/mrad | 10~50 |
| Effective receiving area/m2 | 0.05 |
| Receiving system efficiency | 0.3 |
| Laser scanning zenith angle/° | 15 |
| Spectral receiver bandwidth Ds/nm | 0.5 |
| Inlet laser pulse wavelength/nm | 532 (built-in) |
| Background irradiance/mW*sr−1 cm−2 nm−1 | 0.014 |
| Refractive index of water | 1.34 |
| Water body attenuation factor/m−1 | 0.2 |
| Models | Beibu Gulf, Pacific Ocean, China | Northern Part of the South China Sea |
|---|---|---|
| Model established by Wang et al. (2003) [18] | 49.01 m | 70.53 m |
| Model established by Ding et al. (2018) [22] | 50.33 m | 71.18 m |
| Model established in this paper | 49.86 m | 69.90 m |
| Water Qualities | Water Column Attenuation Coefficient/m−1 | Water Column Absorption Coefficient/m−1 | Water Column Scattering Coefficient/m−1 |
|---|---|---|---|
| clear water | 0.2 | 0.06 | 0.14 |
| moderate water | 0.5 | 0.07 | 0.43 |
| turbid water | 1.5 | 0.10 | 1.40 |
| λ/nm | ap/m−1 | bp/m−1 | Kd/m−1 |
|---|---|---|---|
| 510 | 0.0357 | 0.0026 | 0.0370 |
| 520 | 0.0477 | 0.0024 | 0.0489 |
| 530 | 0.0507 | 0.0022 | 0.0519 |
| 540 | 0.0558 | 0.0021 | 0.0568 |
| Sea Area | Attenuation Coefficient/m−1 | Sea Area | Attenuation Coefficient/m−1 |
|---|---|---|---|
| Yellow Bohai Sea | 0.4~3 | Xisha Sea ranges | 0.18~0.35 |
| South Yellow Sea | 0.2~2 | Central South China Sea | 0.08~0.18 |
| Taiwan Strait | 0.6~5 | Nansha Sea | 0.08~0.3 |
| Northeastern South China Sea | 0.1~0.3 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, G.; Li, K.; Gao, J.; Ma, J.; Gao, E.; Lu, Y.; Xu, J.; Zhou, X. Development of Laser Underwater Transmission Model from Maximum Water Depth Perspective. Remote Sens. 2025, 17, 1982. https://doi.org/10.3390/rs17121982
Zhou G, Li K, Gao J, Ma J, Gao E, Lu Y, Xu J, Zhou X. Development of Laser Underwater Transmission Model from Maximum Water Depth Perspective. Remote Sensing. 2025; 17(12):1982. https://doi.org/10.3390/rs17121982
Chicago/Turabian StyleZhou, Guoqing, Kun Li, Jian Gao, Junyun Ma, Ertao Gao, Yanling Lu, Jiasheng Xu, and Xiao Zhou. 2025. "Development of Laser Underwater Transmission Model from Maximum Water Depth Perspective" Remote Sensing 17, no. 12: 1982. https://doi.org/10.3390/rs17121982
APA StyleZhou, G., Li, K., Gao, J., Ma, J., Gao, E., Lu, Y., Xu, J., & Zhou, X. (2025). Development of Laser Underwater Transmission Model from Maximum Water Depth Perspective. Remote Sensing, 17(12), 1982. https://doi.org/10.3390/rs17121982









