A Novel Supervoxel-Based NE-PC Model for Separating Wood and Leaf Components from Terrestrial Laser Scanning Data
Abstract
1. Introduction
2. Materials and Methods
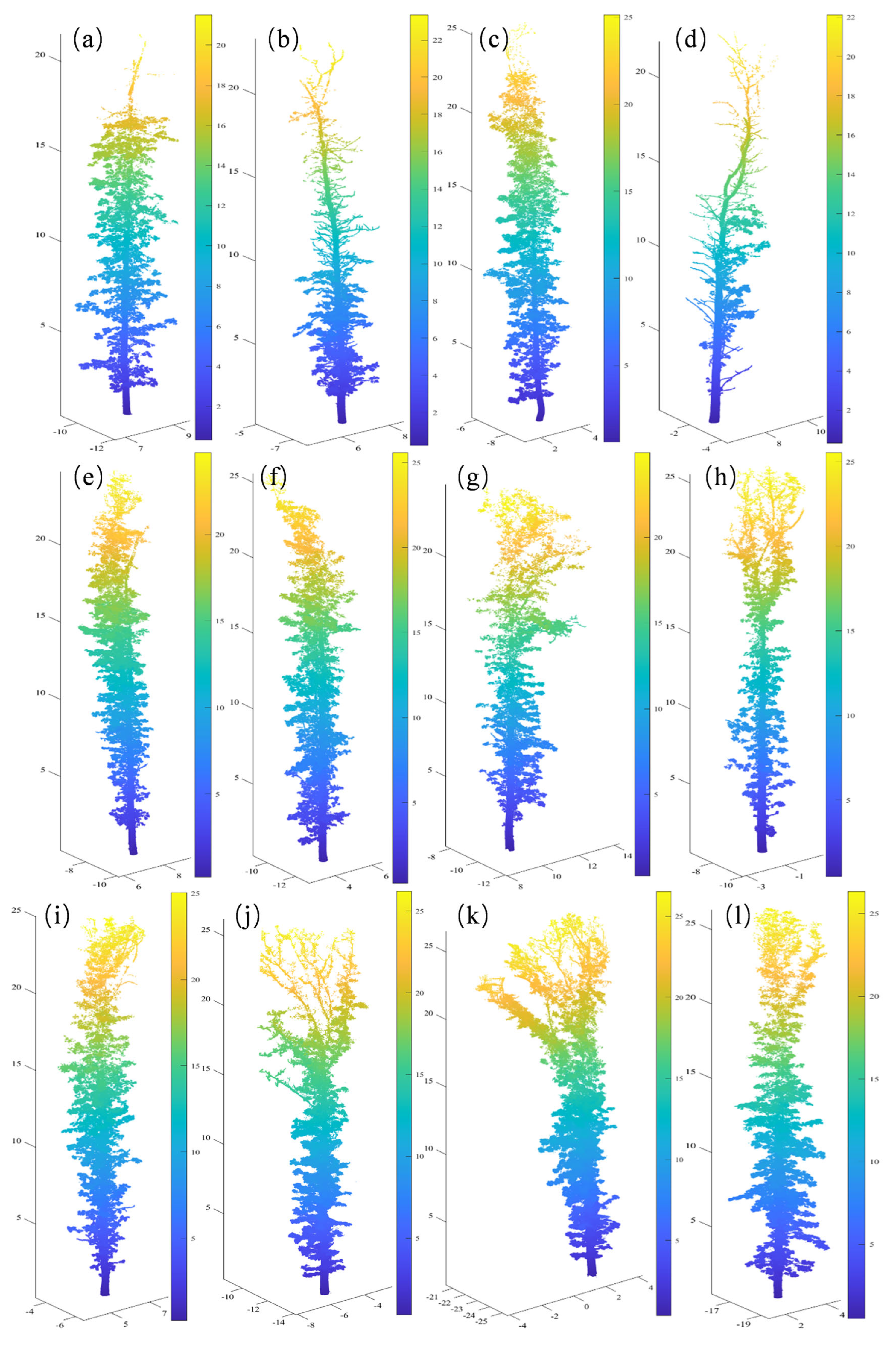
2.1. Study Data Acquisition and Preprocessing
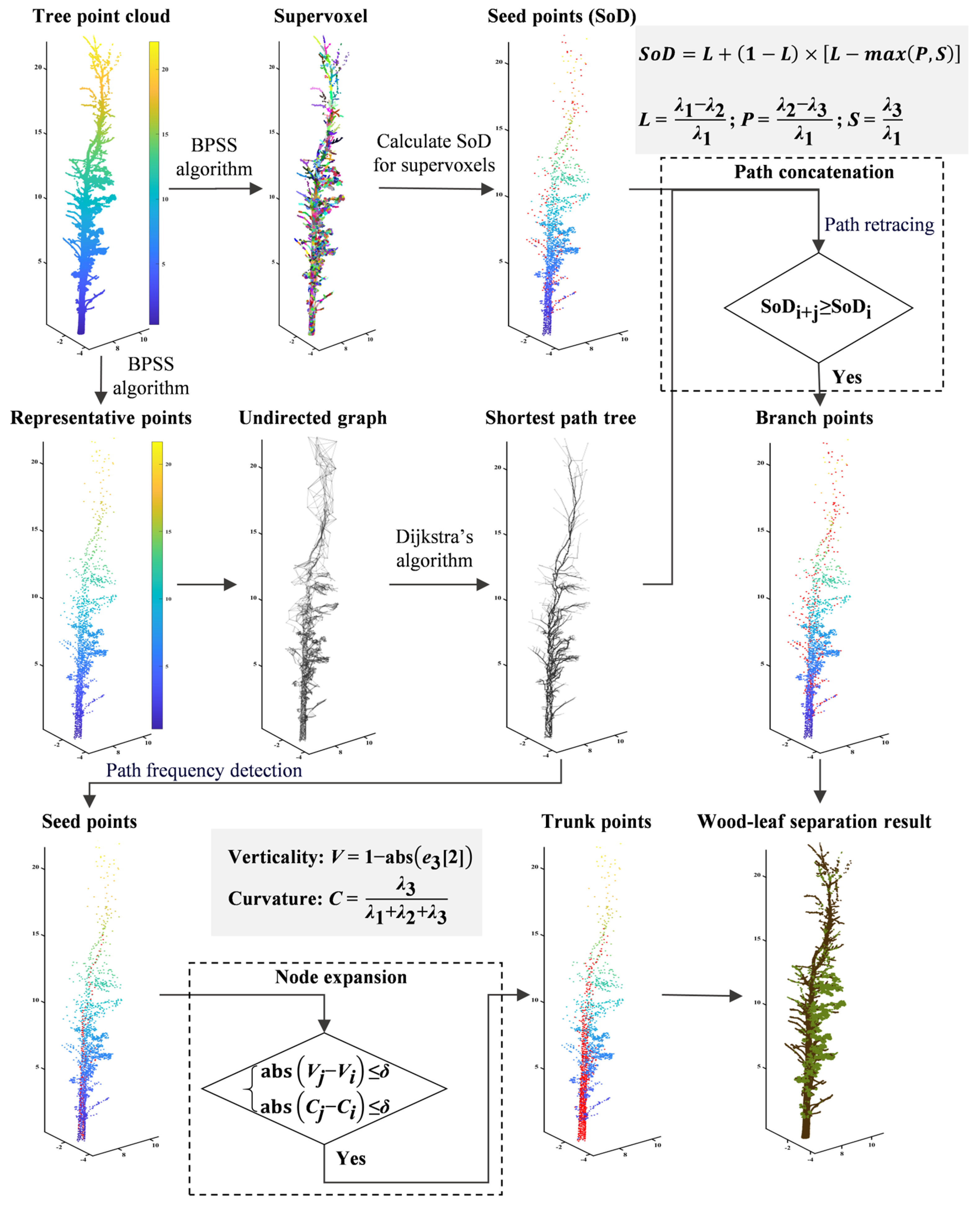
2.2. Wood–Leaf Separation
2.2.1. Constructing the Shortest-Path Tree for Single-Tree Point Clouds
- (1)
- Input the supervoxel representative points Q and the minimum elevation point d within all supervoxels.
- (2)
- Initialize an empty graph G.
- (3)
- Apply the k-nearest neighbors (KNN) algorithm to find n neighbors around each point in Q, recording their indices and distances r. Here, r is the Euclidean distance, with n set to 15.
- (4)
- Add all points in Q to graph G. Starting from d, use r as the weight and selectively add edges and their weights between each point in Q and the n neighbors found in step (3), following the constraint conditions.
- (5)
- Output the weighted topological network graph G.
2.2.2. Node Expansion for Trunk Detection
2.2.3. Path Concatenation for Branch Detection
2.2.4. Optimizing Wood–Leaf Separation Results Based on DBSCAN
2.3. Accuracy Assessment
3. Experimental Results and Analysis
3.1. Sensitivity Analysis of Parameters
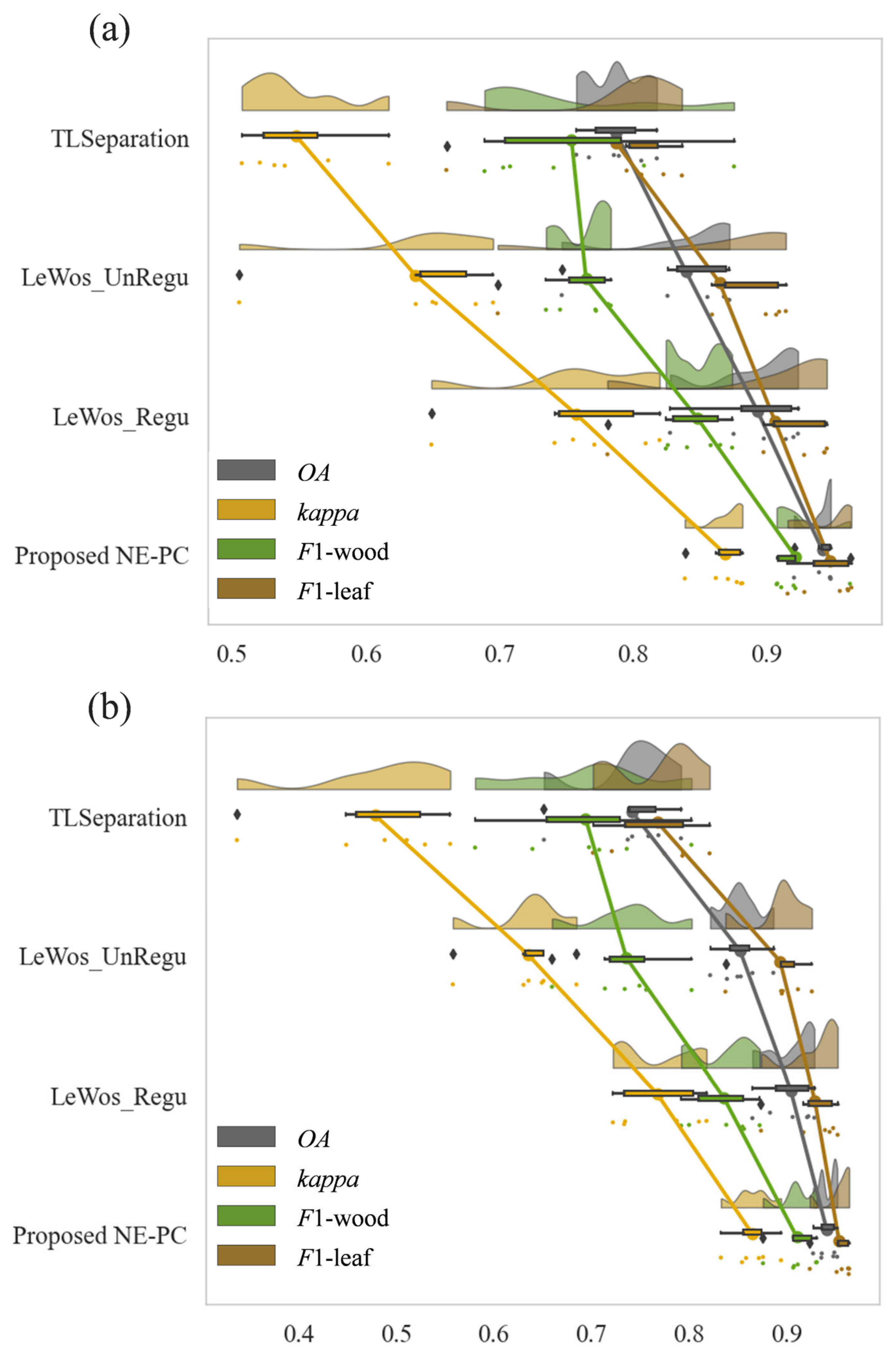
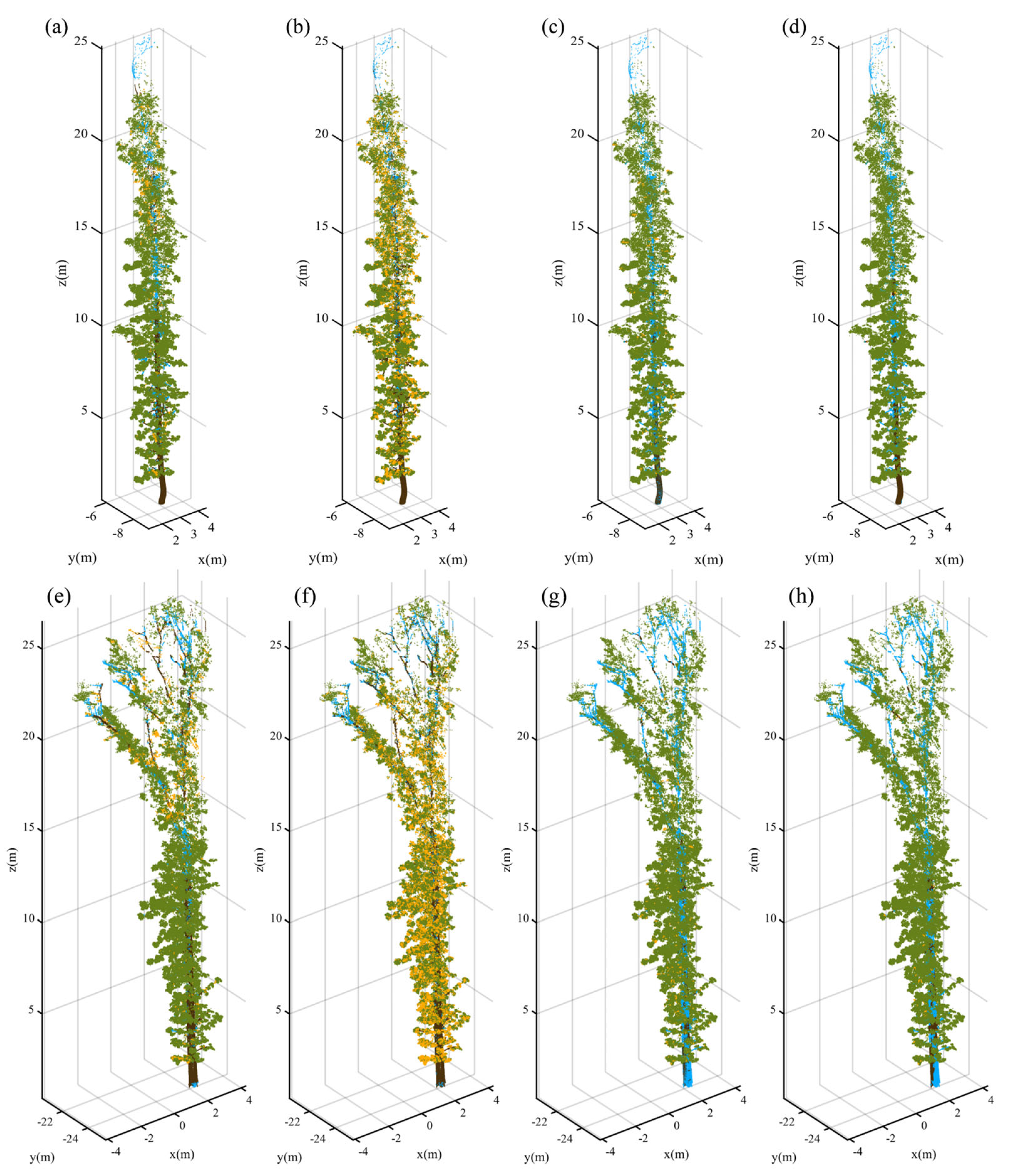
3.2. Point-Wise Classification
3.3. Validity of NE-PC
4. Discussion
4.1. Parameter Analysis
4.2. Point-Wise Classification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
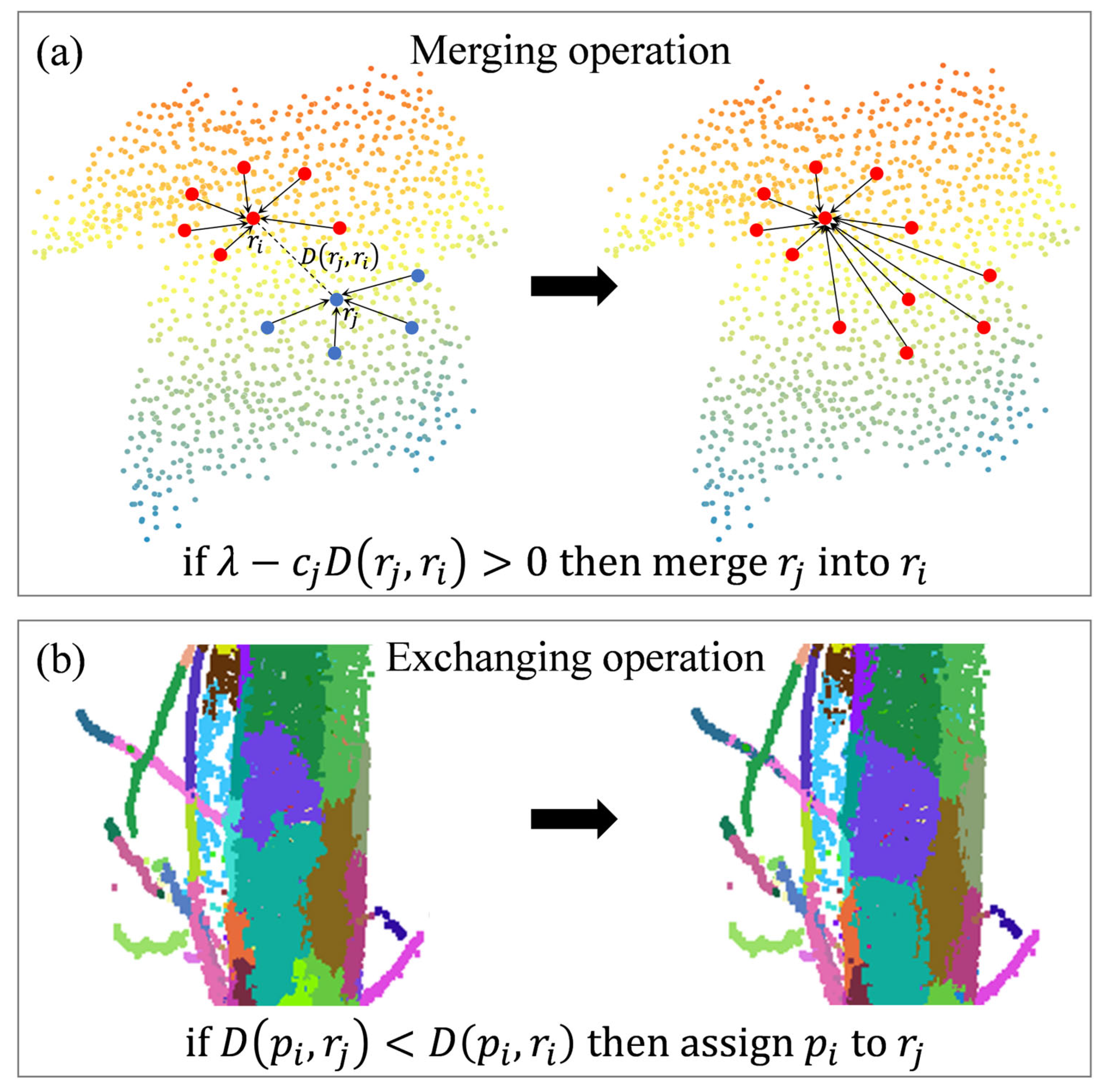
| Algorithm A1. BPSS |
| Input: point cloud, , neighborhood, , target resolution, R. Output: representative points, , labels L 1: Initialize 2: Merge operation: 3: while > K do 4: for each adjacent pair ( do 5: compute according Equation (4) 6: if > 0 then 7: 8: Update 9: 10: end while 11: Exchange operation: 12: for each boundary point do 13: find argmin_{} 14: If then 15: 16: end for |
Appendix C

Appendix D
| Plot | Tree ID | No. of Points | Height (m) | Processing Time (s) |
|---|---|---|---|---|
| Plot A | TreeA-1 | 597,399 | 21.5 | 90.95 |
| TreeA-2 | 632,257 | 23.4 | 31.59 | |
| TreeA-3 | 664,178 | 25.1 | 30.32 | |
| TreeA-4 | 717,921 | 22.1 | 60.05 | |
| TreeA-5 | 766,925 | 24.7 | 36.60 | |
| TreeA-6 | 952,533 | 25.6 | 45.30 | |
| TreeA-7 | 586,990 | 25 | 107.34 | |
| TreeA-8 | 723,175 | 25.6 | 35.47 | |
| TreeA-9 | 963,192 | 25.1 | 75.09 | |
| TreeA-10 | 1,495,627 | 26.2 | 107.49 | |
| TreeA-11 | 1,633,618 | 26.5 | 119.45 | |
| TreeA-12 | 1,911,356 | 26.3 | 94.47 | |
| Plot B | TreeB-1 | 1,166,361 | 18.7 | 64.00 |
| TreeB-2 | 900,975 | 17.2 | 53.83 | |
| TreeB-3 | 1,593,612 | 19.3 | 148.35 | |
| TreeB-4 | 1,326,197 | 18 | 87.93 | |
| TreeB-5 | 931,088 | 17.4 | 67.68 | |
| TreeB-6 | 836,643 | 16.5 | 47.99 | |
| Plot C | TreeC-1 | 3,243,740 | 12.2 | 245.96 |
| TreeC-2 | 3,421,306 | 11.8 | 233.73 | |
| TreeC-3 | 2,222,633 | 11.6 | 145.19 | |
| TreeC-4 | 2,085,081 | 10.5 | 125.89 | |
| TreeC-5 | 3,354,258 | 11.1 | 234.27 |
References
- Beland, M.; Parker, G.; Sparrow, B.; Harding, D.; Chasmer, L.; Phinn, S.; Antonarakis, A.; Strahler, A. On promoting the use of lidar systems in forest ecosystem research. For. Ecol. Manag. 2019, 450, 117484. [Google Scholar] [CrossRef]
- Disney, M.I.; Vicari, M.B.; Burt, A.; Calders, K.; Lewis, S.L.; Raumonen, P.; Wilkes, P. Weighing trees with lasers: Advances, challenges and opportunities. Interface Focus. 2018, 8, 20170048. [Google Scholar] [CrossRef] [PubMed]
- Ehbrecht, M.; Schall, P.; Ammer, C.; Seidel, D. Quantifying stand structural complexity and its relationship with forest management, tree species diversity and microclimate. Agric. For. Meteorol. 2017, 242, 1–9. [Google Scholar] [CrossRef]
- Terryn, L.; Calders, K.; Bartholomeus, H.; Bartolo, R.E.; Brede, B.; D’Hont, B.; Disney, M.; Herold, M.; Lau, A.; Shenkin, A.; et al. Quantifying tropical forest structure through terrestrial and UAV laser scanning fusion in Australian rainforests. Remote Sens. Environ. 2022, 271, 112912. [Google Scholar] [CrossRef]
- Wang, Y.; Lehtomäki, M.; Liang, X.; Pyörälä, J.; Kukko, A.; Jaakkola, A.; Liu, J.; Feng, Z.; Chen, R.; Hyyppä, J. Is field-measured tree height as reliable as believed—A comparison study of tree height estimates from field measurement, airborne laser scanning and terrestrial laser scanning in a boreal forest. Isprs-J. Photogramm. Remote Sens. 2019, 147, 132–145. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial laser scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Disney, M. Terrestrial LiDAR: A three-dimensional revolution in how we look at trees. New Phytol. 2019, 222, 1736–1741. [Google Scholar] [CrossRef]
- Yrttimaa, T.; Luoma, V.; Saarinen, N.; Kankare, V.; Junttila, S.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Structural Changes in Boreal Forests Can Be Quantified Using Terrestrial Laser Scanning. Remote Sens. 2020, 12, 2672. [Google Scholar] [CrossRef]
- Chianucci, F.; Puletti, N.; Grotti, M.; Ferrara, C.; Giorcelli, A.; Coaloa, D.; Tattoni, C. Nondestructive Tree Stem and Crown Volume Allometry in Hybrid Poplar Plantations Derived from Terrestrial Laser Scanning. For. Sci. 2020, 66, 737–746. [Google Scholar] [CrossRef]
- Li, Y.; Hess, C.; von Wehrden, H.; Hardtle, W.; von Oheimb, G. Assessing tree dendrometrics in young regenerating plantations using terrestrial laser scanning. Ann. For. Sci. 2014, 71, 453–462. [Google Scholar] [CrossRef]
- Demol, M.; Verbeeck, H.; Gielen, B.; Armston, J.; Burt, A.; Disney, M.; Duncanson, L.; Hackenberg, J.; Kukenbrink, D.; Lau, A.; et al. Estimating forest above-ground biomass with terrestrial laser scanning: Current status and future directions. Methods Ecol. Evol. 2022, 13, 1628–1639. [Google Scholar] [CrossRef]
- Kükenbrink, D.; Gardi, O.; Morsdorf, F.; Thürig, E.; Schellenberger, A.; Mathys, L. Above-ground biomass references for urban trees from terrestrial laser scanning data. Ann. Bot. 2021, 128, 709–724. [Google Scholar] [CrossRef] [PubMed]
- Disney, M.; Burt, A.; Calders, K.; Schaaf, C.; Stovall, A. Innovations in Ground and Airborne Technologies as Reference and for Training and Validation: Terrestrial Laser Scanning (TLS). Surv. Geophys. 2019, 40, 937–958. [Google Scholar] [CrossRef]
- Chen, Y.M.; Zhang, W.M.; Hu, R.H.; Qi, J.B.; Shao, J.; Li, D.; Wan, P.; Qiao, C.; Shen, A.J.; Yan, G.J. Estimation of forest leaf area index using terrestrial laser scanning data and path length distribution model in open-canopy forests. Agric. For. Meteorol. 2018, 263, 323–333. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Computational-Geometry-Based Retrieval of Effective Leaf Area Index Using Terrestrial Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3958–3969. [Google Scholar] [CrossRef]
- Liu, J.; Wang, T.J.; Skidmore, A.K.; Jones, S.; Heurich, M.; Beudert, B.; Premier, J. Comparison of terrestrial LiDAR and digital hemispherical photography for estimating leaf angle distribution in European broadleaf beech forests. ISPRS-J. Photogramm. Remote Sens. 2019, 158, 76–89. [Google Scholar] [CrossRef]
- Li, Y.; Guo, Q.; Tao, S.; Zheng, G.; Zhao, K.; Xue, B.; Su, Y. Derivation, Validation, and Sensitivity Analysis of Terrestrial Laser Scanning-Based Leaf Area Index. Can. J. Remote Sens. 2016, 42, 719–729. [Google Scholar] [CrossRef]
- Yan, G.; Hu, R.; Luo, J.; Mu, X.; Xie, D.; Zhang, W. Review of indirect methods for leaf area index measurement. J. Remote Sens. 2016, 20, 958–978. [Google Scholar]
- Zhu, X.; Skidmore, A.K.; Wang, T.; Liu, J.; Darvishzadeh, R.; Shi, Y.; Premier, J.; Heurich, M. Improving leaf area index (LAI) estimation by correcting for clumping and woody effects using terrestrial laser scanning. Agric. For. Meteorol. 2018, 263, 276–286. [Google Scholar] [CrossRef]
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual tree biomass estimation using terrestrial laser scanning. ISPRS-J. Photogramm. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Chen, S.; Verbeeck, H.; Terryn, L.; Van den Broeck, W.A.J.; Vicari, M.B.; Disney, M.; Origo, N.; Wang, D.; Xi, Z.; Hopkinson, C.; et al. The impact of leaf-wood separation algorithms on aboveground biomass estimation from terrestrial laser scanning. Remote Sens. Environ. 2025, 318, 114581. [Google Scholar] [CrossRef]
- Arseniou, G.; MacFarlane, D.W.; Calders, K.; Baker, M. Accuracy differences in aboveground woody biomass estimation with terrestrial laser scanning for trees in urban and rural forests and different leaf conditions. Trees-Struct. Funct. 2023, 37, 761–779. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS-J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS-J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Ma, L.; Zheng, G.; Eitel, J.U.H.; Moskal, L.M.; He, W.; Huang, H. Improved Salient Feature-Based Approach for Automatically Separating Photosynthetic and Nonphotosynthetic Components Within Terrestrial Lidar Point Cloud Data of Forest Canopies. IEEE Trans. Geosci. Remote Sens. 2016, 54, 679–696. [Google Scholar] [CrossRef]
- Wang, D.; Hollaus, M.; Pfeifer, N. Feasibility of machine learning methods for separating wood and leaf points from terrestrial laser scanning data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, IV-2/W4, 157–164. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L.; Fang, T.; Mathiopoulos, P.T.; Tong, X.; Qu, H.; Xiao, Z.; Li, F.; Chen, D. A multiscale and hierarchical feature extraction method for terrestrial laser scanning point cloud classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2409–2425. [Google Scholar] [CrossRef]
- Zhou, J.; Wei, H.; Zhou, G.; Song, L. Separating leaf and wood points in terrestrial laser scanning data using multiple optimal scales. Sensors 2019, 19, 1852. [Google Scholar] [CrossRef]
- Wan, P.; Shao, J.; Jin, S.; Wang, T.; Yang, S.; Yan, G.; Zhang, W. A novel and efficient method for wood-leaf separation from terrestrial laser scanning point clouds at the forest plot level. Methods Ecol. Evol. 2021, 12, 2473–2486. [Google Scholar] [CrossRef]
- Ferrara, R.; Virdis, S.G.P.; Ventura, A.; Ghisu, T.; Duce, P.; Pellizzaro, G. An automated approach for wood-leaf separation from terrestrial LIDAR point clouds using the density based clustering algorithm DBSCAN. Agric. For. Meteorol. 2018, 262, 434–444. [Google Scholar] [CrossRef]
- Wang, M.; Wong, M.S. A novel geometric feature-based wood-leaf separation method for large and crown-heavy tropical trees using handheld laser scanning point cloud. Int. J. Remote Sens. 2023, 44, 3227–3258. [Google Scholar] [CrossRef]
- Yun, T.; An, F.; Li, W.; Sun, Y.; Cao, L.; Xue, L. A Novel Approach for Retrieving Tree Leaf Area from Ground-Based LiDAR. Remote Sens. 2016, 8, 942. [Google Scholar] [CrossRef]
- Moorthy, S.M.K.; Calders, K.; Vicari, M.B.; Verbeeck, H. Improved Supervised Learning-Based Approach for Leaf and Wood Classification From LiDAR Point Clouds of Forests. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3057–3070. [Google Scholar] [CrossRef]
- Béland, M.; Baldocchi, D.D.; Widlowski, J.; Fournier, R.A.; Verstraete, M.M. On seeing the wood from the leaves and the role of voxel size in determining leaf area distribution of forests with terrestrial LiDAR. Agric. For. Meteorol. 2014, 184, 82–97. [Google Scholar] [CrossRef]
- Sun, Y.; Lin, X.; Xiong, J.; Ren, G. Separation of single wood branches and leaves based on corrected TLS intensity data. Chin. J. Lasers 2021, 48, 104001. [Google Scholar] [CrossRef]
- Sun, J.; Wang, P.; Gao, Z.; Liu, Z.; Li, Y.; Gan, X.; Liu, Z. Wood–leaf classification of tree point cloud based on intensity and geometric information. Remote Sens. 2021, 13, 4050. [Google Scholar] [CrossRef]
- Tan, K.; Zhang, W.; Dong, Z.; Cheng, X.; Cheng, X. Leaf and wood separation for individual trees using the intensity and density data of terrestrial laser scanners. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7038–7050. [Google Scholar] [CrossRef]
- Shao, J.Y.; Cheng, Y.T.; Koshan, Y.; Manish, R.; Habib, A.; Fei, S.L. Radiometric and geometric approach for major woody parts segmentation in forest lidar point clouds. In Proceedings of the IGARSS 2023-2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 6220–6223. [Google Scholar]
- Tao, S.; Guo, Q.; Su, Y.; Xu, S.; Li, Y.; Wu, F. A geometric method for wood-leaf separation using terrestrial and simulated lidar data. Photogramm. Eng. Remote Sens. 2015, 81, 767–776. [Google Scholar] [CrossRef]
- Wang, D.; Momo Takoudjou, S.; Casella, E. LeWoS: A universal leaf-wood classification method to facilitate the 3D modelling of large tropical trees using terrestrial LiDAR. Methods Ecol. Evol. 2020, 11, 376–389. [Google Scholar] [CrossRef]
- Vicari, M.B.; Disney, M.; Wilkes, P.; Burt, A.; Calders, K.; Woodgate, W. Leaf and wood classification framework for terrestrial LiDAR point clouds. Methods Ecol. Evol. 2019, 10, 680–694. [Google Scholar] [CrossRef]
- Tian, Z.; Li, S. Graph-Based Leaf–Wood Separation Method for Individual Trees Using Terrestrial Lidar Point Clouds. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5705111. [Google Scholar] [CrossRef]
- Lu, H.; Wu, J.; Zhang, Z. Tree branch and leaf separation using terrestrial laser point clouds. Chin. J. Lasers 2022, 49, 2310001. [Google Scholar]
- Hui, Z.; Jin, S.; Xia, Y.; Wang, L.; Yevenyo Ziggah, Y.; Cheng, P. Wood and leaf separation from terrestrial LiDAR point clouds based on mode points evolution. ISPRS-J. Photogramm. Remote Sens. 2021, 178, 219–239. [Google Scholar] [CrossRef]
- Wang, D. Unsupervised semantic and instance segmentation of forest point clouds. ISPRS-J. Photogramm. Remote Sens. 2020, 165, 86–97. [Google Scholar] [CrossRef]
- Fan, G.; Wang, R.; Wang, C.; Zhou, J.L.; Zhang, B.H.; Xin, Z.M.; Xiao, H.J. TLSLeaf: Unsupervised Instance Segmentation of Broadleaf Leaf Count and Area From TLS Point Clouds. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5700915. [Google Scholar] [CrossRef]
- Xi, Z.; Hopkinson, C.; Chasmer, L. Filtering Stems and Branches from Terrestrial Laser Scanning Point Clouds Using Deep 3-D Fully Convolutional Networks. Remote Sens. 2018, 10, 1215. [Google Scholar] [CrossRef]
- Xi, Z.; Chasmer, L.; Hopkinson, C. Delineating and Reconstructing 3D Forest Fuel Components and Volumes with Terrestrial Laser Scanning. Remote Sens. 2023, 15, 4778. [Google Scholar] [CrossRef]
- Wang, H.; Wang, D. 3D Semantic Understanding of Large-Scale Urban Scenes from LiDAR Point Clouds. In Proceedings of the 2023 9th International Conference on Virtual Reality (ICVR), Xianyang, China, 12–14 May 2023; pp. 86–92. [Google Scholar]
- Van den Broeck, W.A.J.; Terryn, L.; Cherlet, W.; Cooper, Z.T.; Calders, K. Three-dimensional deep learning for leaf-wood segmentation of tropical tree point clouds. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2023, XLVIII-1/W2-2023, 765–770. [Google Scholar] [CrossRef]
- Dai, W.; Jiang, Y.; Zeng, W.; Chen, R.; Xu, Y.; Zhu, N.; Xiao, W.; Dong, Z.; And Guan, Q. MDC-Net: A multi-directional constrained and prior assisted neural network for wood and leaf separation from terrestrial laser scanning. Int. J. Digit. Earth. 2023, 16, 1224–1245. [Google Scholar] [CrossRef]
- Wu, B.X.; Zheng, G.; Chen, Y. An Improved Convolution Neural Network-Based Model for Classifying Foliage and Woody Components from Terrestrial Laser Scanning Data. Remote Sens. 2020, 12, 1010. [Google Scholar] [CrossRef]
- Xi, Z.X.; Hopkinson, C.; Rood, S.B.; Peddle, D.R. See the forest and the trees: Effective machine and deep learning algorithms for wood filtering and tree species classification from terrestrial laser scanning. ISPRS-J. Photogramm. Remote Sens. 2020, 168, 1–16. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 5105–5114. [Google Scholar]
- Klokov, R.; Lempitsky, V. Escape from Cells: Deep Kd-Networks for the Recognition of 3D Point Cloud Models. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 863–872. [Google Scholar]
- Li, L.; Mu, X.; Soma, M.; Wan, P.; Qi, J.; Hu, R.; Zhang, W.; Tong, Y.; Yan, G. An iterative-mode scan design of terrestrial laser scanning in forests for minimizing occlusion effects. IEE E Trans. Geosci. Remote Sens. 2021, 59, 3547–3566. [Google Scholar] [CrossRef]
- Zande, D.V.D.; Jonckheere, I.; Stuckens, J.; Verstraeten, W.W.; Coppin, P. Sampling design of ground-based lidar measurements of forest canopy structure and its effect on shadowing. Can. J. Remote Sens. 2008, 34, 526–538. [Google Scholar] [CrossRef]
- Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; Gonzalez De Tanago, J.; Bartholomeus, H.; Brede, B.; Herold, M. Data acquisition considerations for terrestrial laser scanning of forest plots. Remote Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Tao, S.; Wu, F.; Guo, Q.; Wang, Y.; Li, W.; Xue, B.; Hu, X.; Li, P.; Tian, D.; Li, C.; et al. Segmenting tree crowns from terrestrial and mobile LiDAR data by exploring ecological theories. ISPRS-J. Photogramm. Remote Sens. 2015, 110, 66–76. [Google Scholar] [CrossRef]
- Shcherbcheva, A.; Campos, M.B.; Liang, X.; Puttonen, E.; Wang, Y. Unsupervised statistical approach for tree-level separation of foliage and non-leaf components from point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII-1/W2-2023, 1787–1794. [Google Scholar] [CrossRef]
- Wang, W.; Pang, Y.; Du, L.; Zhang, Z.; Liang, X. Individual tree segmentation for airborne LiDAR point cloud data using spectral clustering and supervoxel-based algorithm. Natl. Remote Sens. Bull. 2022, 26, 1650–1661. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.; Zhai, D.; Li, W.; Li, J. Toward better boundary preserved supervoxel segmentation for 3D point clouds. ISPRS-J. Photogramm. Remote Sens. 2018, 143, 39–47. [Google Scholar] [CrossRef]
- Elhamifar, E.; Sapiro, G.; Sastry, S.S. Dissimilarity-Based Sparse Subset Selection. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2182–2197. [Google Scholar] [CrossRef]
- Nguyen, R.M.H.; Brown, M.S. Fast and Effective L0 Gradient Minimization by Region Fusion. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 208–216. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Hackel, T.; Wegner, J.D.; Schindler, K. Contour detection in unstructured 3D point clouds. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1610–1618. [Google Scholar]
- Ester, M.; Kriegel, H.; Sander, J.O.R.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference On Knowledge Discovery and Data Mining (Kdd’ 96), Portland, OR, USA, 2–4 August 1996; AAAI Press: Washington, DC, USA, 1996; pp. 226–231. [Google Scholar]
- Li, H.; Wu, G.; Tao, S.; Yin, H.; Qi, K.; Zhang, S.; Guo, W.; Ninomiya, S.; Mu, Y. Automatic branch–leaf segmentation and leaf phenotypic parameter estimation of pear trees based on three-dimensional point clouds. Sensors 2023, 23, 4572. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.; Poggiali, D.; Whitaker, K.; Marshall, T.R.; van Langen, J.; Kievit, R.A. Raincloud plots: A multi-platform tool for robust data visualization. Wellcome Open Res. 2019, 4, 63. [Google Scholar] [CrossRef]
- Feng, Y.; Su, Y.; Wang, J.; Yan, J.; Qi, X.; Maeda, E.E.; Nunes, M.H.; Zhao, X.; Liu, X.; Wu, X.; et al. L1-Tree: A novel algorithm for constructing 3D tree models and estimating branch architectural traits using terrestrial laser scanning data. Remote Sens. Environ. 2024, 314, 114390. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L.; Fang, T.; Tong, X.; Mathiopoulos, P.T.; Zhang, L.; Mei, J. A local structure and direction-aware optimization approach for three-dimensional tree modeling. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4749–4757. [Google Scholar] [CrossRef]

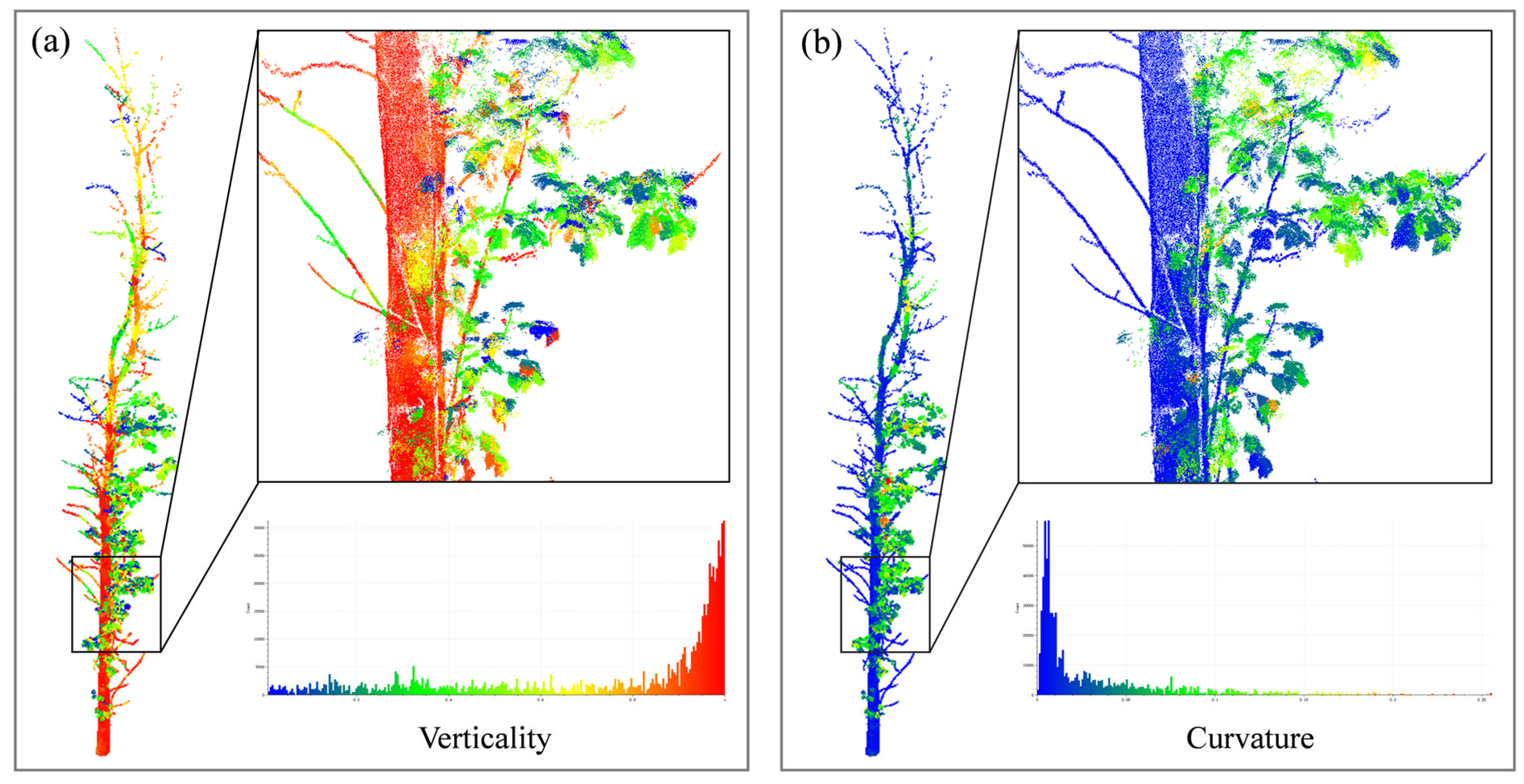
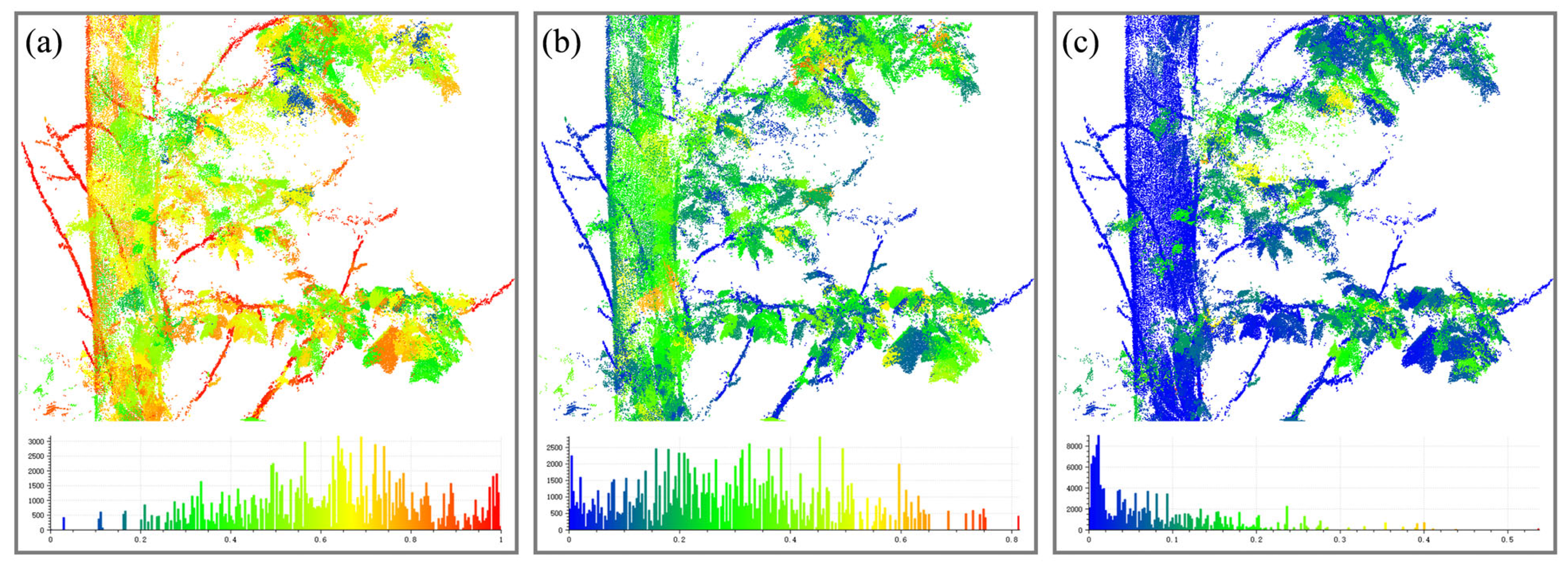




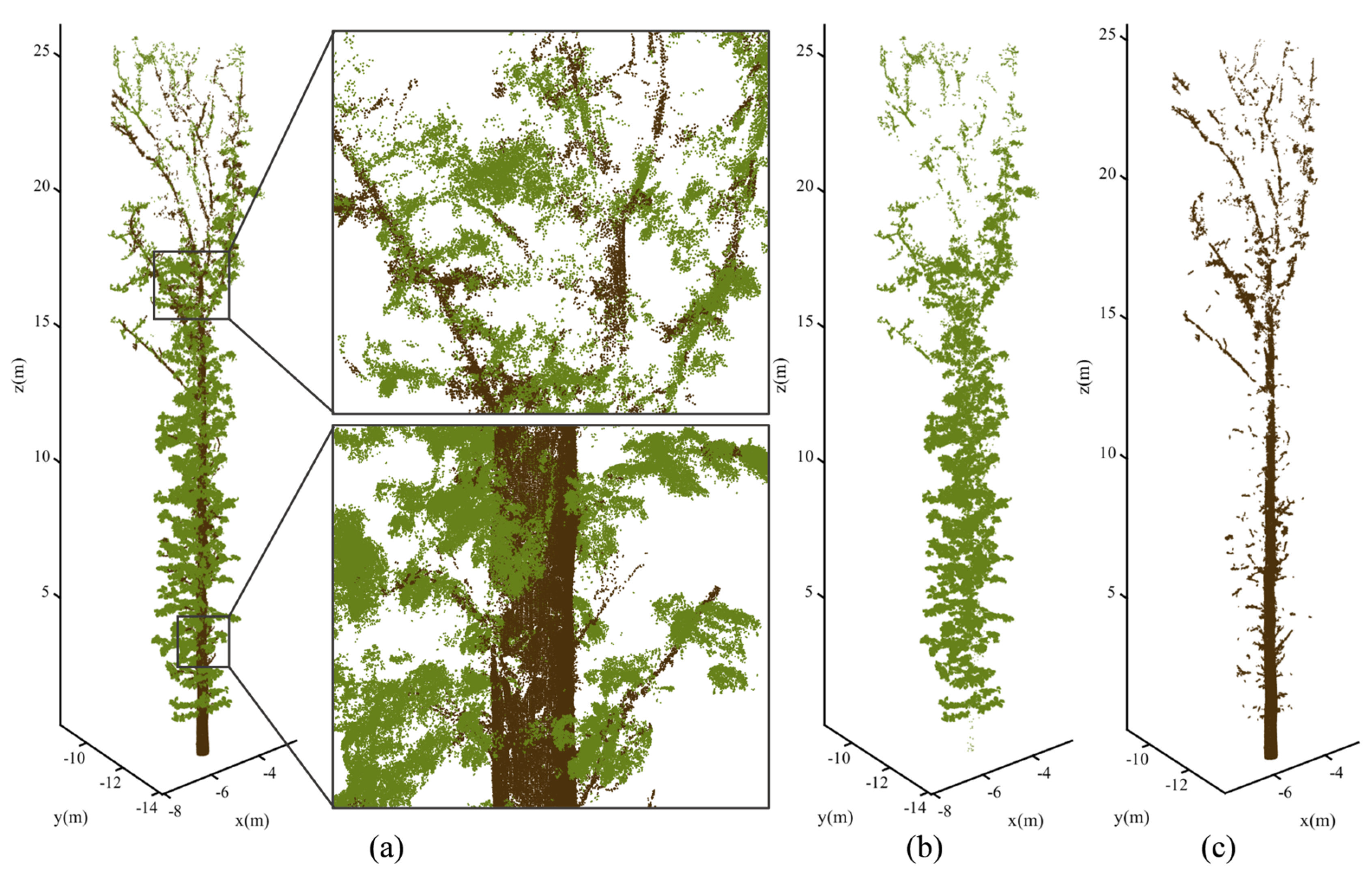
| Tree No. | Branch Type | Number of Points | Tree Height (m) | DBH (cm) | Average Point Spacing/m |
|---|---|---|---|---|---|
| Tree 1 | Linear | 597,399 | 21.5 | 17.8 | 0.0059 |
| Tree 2 | Linear | 632,257 | 23.4 | 20.8 | 0.0054 |
| Tree 3 | Linear | 664,178 | 25.1 | 25.5 | 0.0067 |
| Tree 4 | Linear | 717,921 | 22.1 | 32.1 | 0.0039 |
| Tree 5 | Linear | 766,925 | 24.7 | 27.4 | 0.0074 |
| Tree 6 | Linear | 952,533 | 25.6 | 26.7 | 0.0065 |
| Tree 7 | Complex | 586,990 | 25.0 | 34.6 | 0.0079 |
| Tree 8 | Complex | 723,175 | 25.6 | 33.4 | 0.006 |
| Tree 9 | Complex | 963,192 | 25.1 | 27.9 | 0.0066 |
| Tree 10 | Complex | 1,495,627 | 26.2 | 37.1 | 0.005 |
| Tree 11 | Complex | 1,633,618 | 26.5 | 32.6 | 0.0049 |
| Tree 12 | Complex | 1,911,356 | 26.3 | 30.7 | 0.0051 |
| Input: | wood nodes , threshold neighboring points k |
| Step 1: | For each wood node , calculate its k-nearest neighbors (KNN) nodes, . |
| Step 2: | For each node , calculate its verticality and curvature according to Equation (10). |
| Step 3: | Conditional constraints: &&. |
| Step 4: | If yes, {Wood} = {Wood}∪{}. |
| Output: | Wood nodes {Wood} |
| Input: | tree nodes , threshold wood nodes {Wood} = {} |
| Step 1: | For each node , calculate its SoD according to Equation (12). If >, {Wood} = {Wood}∪{}. |
| Step 2: | For each node , calculate its shortest path dictionary path_list SP[, , …, base}. |
| Step 3: | Conditional constraints: && |i − j| == 1 && |
| Step 4: | If yes, {Wood} = {Wood}∪{}. |
| Output: | Wood nodes {Wood} |
| Branch Style | OA (%) | F1-Wood (%) | F1-Leaf (%) | Kappa (%) |
|---|---|---|---|---|
| Linear | 94.14 | 92.15 | 94.70 | 86.84 |
| Complex | 94.15 | 91.07 | 95.40 | 86.47 |
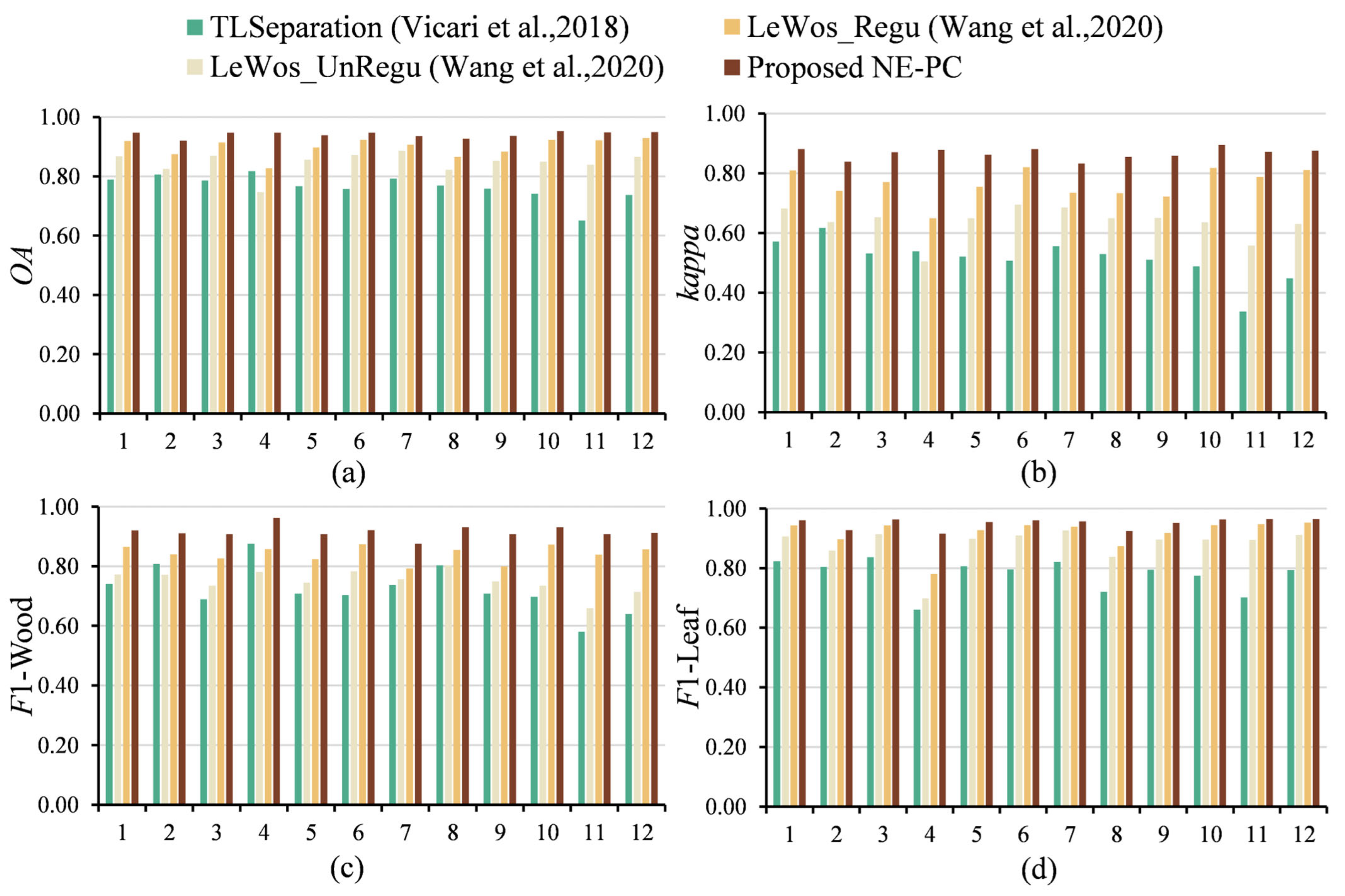
| Tree No. | TLSeparation | LeWos_UnRegu | LeWos_Regu | Proposed NE-PC | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OA (%) | F1-Wood (%) | F1-Leaf (%) | Kappa (%) | OA (%) | F1-Wood (%) | F1-Leaf (%) | Kappa (%) | OA (%) | F1-Wood (%) | F1-Leaf (%) | Kappa (%) | OA (%) | F1-Wood (%) | F1-Leaf (%) | Kappa (%) | |
| 1 | 78.9 | 74.0 | 82.3 | 57.2 | 86.8 | 77.2 | 90.7 | 68.2 | 92.0 | 86.5 | 94.3 | 80.9 | 94.7 | 92.0 | 96.1 | 88.1 |
| 2 | 80.6 | 80.8 | 80.4 | 61.7 | 82.6 | 77.2 | 85.9 | 63.7 | 87.5 | 84.0 | 89.7 | 74.1 | 92.0 | 91.1 | 92.8 | 83.9 |
| 3 | 78.6 | 68.9 | 83.6 | 53.2 | 87.0 | 73.5 | 91.4 | 65.2 | 91.4 | 82.6 | 94.3 | 77.1 | 94.7 | 90.8 | 96.3 | 87.1 |
| 4 | 81.8 | 87.5 | 66.0 | 53.9 | 74.7 | 78.1 | 69.9 | 50.5 | 82.8 | 85.8 | 78.1 | 64.9 | 94.8 | 96.2 | 91.5 | 87.7 |
| 5 | 76.7 | 70.8 | 80.6 | 52.1 | 85.6 | 74.5 | 89.9 | 65.0 | 89.8 | 82.4 | 92.8 | 75.5 | 93.9 | 90.7 | 95.4 | 86.2 |
| 6 | 75.7 | 70.3 | 79.5 | 50.7 | 87.2 | 78.3 | 90.9 | 69.5 | 92.3 | 87.4 | 94.5 | 82.0 | 94.7 | 92.1 | 96.0 | 88.2 |
| 7 | 79.2 | 73.6 | 82.1 | 55.5 | 88.7 | 75.6 | 92.6 | 68.5 | 90.6 | 79.2 | 94.0 | 73.5 | 93.6 | 87.6 | 95.7 | 83.3 |
| 8 | 76.9 | 80.3 | 72.1 | 52.9 | 82.2 | 80.3 | 83.8 | 64.9 | 86.5 | 85.5 | 87.4 | 73.4 | 92.7 | 93.1 | 92.4 | 85.5 |
| 9 | 75.9 | 70.8 | 79.4 | 51.1 | 85.3 | 74.9 | 89.6 | 65.1 | 88.3 | 80.0 | 91.8 | 72.2 | 93.6 | 90.7 | 95.2 | 85.9 |
| 10 | 74.2 | 69.8 | 77.5 | 48.8 | 85.0 | 73.4 | 89.5 | 63.6 | 92.3 | 87.3 | 94.4 | 81.8 | 95.2 | 93.1 | 96.3 | 89.5 |
| 11 | 65.1 | 58.1 | 70.2 | 33.7 | 83.9 | 66.0 | 89.5 | 55.8 | 92.1 | 83.8 | 94.8 | 78.8 | 94.8 | 90.8 | 96.4 | 87.2 |
| 12 | 73.7 | 64.0 | 79.3 | 44.9 | 86.5 | 71.4 | 91.2 | 63.1 | 92.9 | 85.7 | 95.3 | 81.0 | 94.9 | 91.2 | 96.4 | 87.6 |
| AVE | 76.4 | 72.4 | 77.8 | 51.5 | 84.6 | 75.0 | 87.9 | 63.6 | 89.9 | 84.2 | 91.8 | 76.3 | 94.1 | 91.6 | 95.1 | 86.7 |
| Tree No. | Type I Error | Type II Error | ||||||
|---|---|---|---|---|---|---|---|---|
| TLSeparation | LeWos_UnRegu | LeWos_Regu | Proposed NE-PC | TLSeparation | LeWos_UnRegu | LeWos_Regu | Proposed NE-PC | |
| 1 | 0.104 | 0.332 | 0.233 | 0.096 | 0.265 | 0.031 | 0.003 | 0.031 |
| 2 | 0.089 | 0.342 | 0.267 | 0.092 | 0.279 | 0.038 | 0.010 | 0.070 |
| 3 | 0.178 | 0.377 | 0.294 | 0.101 | 0.229 | 0.030 | 0.002 | 0.033 |
| 4 | 0.074 | 0.345 | 0.247 | 0.040 | 0.426 | 0.048 | 0.006 | 0.081 |
| 5 | 0.171 | 0.379 | 0.295 | 0.123 | 0.265 | 0.023 | 0.003 | 0.029 |
| 6 | 0.157 | 0.320 | 0.216 | 0.092 | 0.287 | 0.029 | 0.005 | 0.033 |
| 7 | 0.138 | 0.346 | 0.337 | 0.157 | 0.237 | 0.028 | 0.004 | 0.030 |
| 8 | 0.115 | 0.317 | 0.251 | 0.085 | 0.363 | 0.021 | 0.003 | 0.058 |
| 9 | 0.160 | 0.371 | 0.330 | 0.108 | 0.285 | 0.027 | 0.003 | 0.040 |
| 10 | 0.125 | 0.390 | 0.220 | 0.047 | 0.327 | 0.026 | 0.004 | 0.048 |
| 11 | 0.122 | 0.433 | 0.258 | 0.072 | 0.435 | 0.058 | 0.011 | 0.044 |
| 12 | 0.177 | 0.406 | 0.248 | 0.074 | 0.296 | 0.027 | 0.001 | 0.042 |
| AVE | 0.134 | 0.363 | 0.266 | 0.091 | 0.308 | 0.032 | 0.004 | 0.045 |
| Plot No. | Tree Count | OA (%) | F1-Wood (%) | F1-Leaf (%) | Kappa (%) | Type I Error (%) | Type II Error (%) |
|---|---|---|---|---|---|---|---|
| Plot A 1 | 12 | 94.1 (±2.1) | 91.6 (±4.6) | 95.0 (±3.5) | 86.7 (±3.4) | 9.1 (±6.7) | 4.5 (±3.6) |
| Plot B 2 | 6 | 92.8 (±2.3) | 86.9 (±6.7) | 94.4 (±4.5) | 81.3 (±4.2) | 18.3 (±9.5) | 3.0 (±1.9) |
| Plot C 3 | 5 | 94.4 (±0.7) | 85.3 (±3.9) | 96.5 (±0.8) | 81.8 (±3.2) | 17.4 (±3.5) | 2.7 (±0.7) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, S.; Shen, X.; Cao, L. A Novel Supervoxel-Based NE-PC Model for Separating Wood and Leaf Components from Terrestrial Laser Scanning Data. Remote Sens. 2025, 17, 1978. https://doi.org/10.3390/rs17121978
Gong S, Shen X, Cao L. A Novel Supervoxel-Based NE-PC Model for Separating Wood and Leaf Components from Terrestrial Laser Scanning Data. Remote Sensing. 2025; 17(12):1978. https://doi.org/10.3390/rs17121978
Chicago/Turabian StyleGong, Shengqin, Xin Shen, and Lin Cao. 2025. "A Novel Supervoxel-Based NE-PC Model for Separating Wood and Leaf Components from Terrestrial Laser Scanning Data" Remote Sensing 17, no. 12: 1978. https://doi.org/10.3390/rs17121978
APA StyleGong, S., Shen, X., & Cao, L. (2025). A Novel Supervoxel-Based NE-PC Model for Separating Wood and Leaf Components from Terrestrial Laser Scanning Data. Remote Sensing, 17(12), 1978. https://doi.org/10.3390/rs17121978







