Improved Performance of RT-PPP During Communication Outages Based on Position Constraints and Stochastic Model Optimization
Abstract
1. Introduction
2. Mathematical Model
- (1)
- -: Earth-Centered, Earth-Fixed (ECEF) coordinate system;
- (2)
- -: IMU Body Coordinate System, Right-Forward-Up;
- (3)
- -: Navigation Coordinate System, East-North-Up;
- (4)
- -: Inertial Coordinate System.
2.1. RT-PPP Mathematical Model
2.2. Traditional Stochastic Model
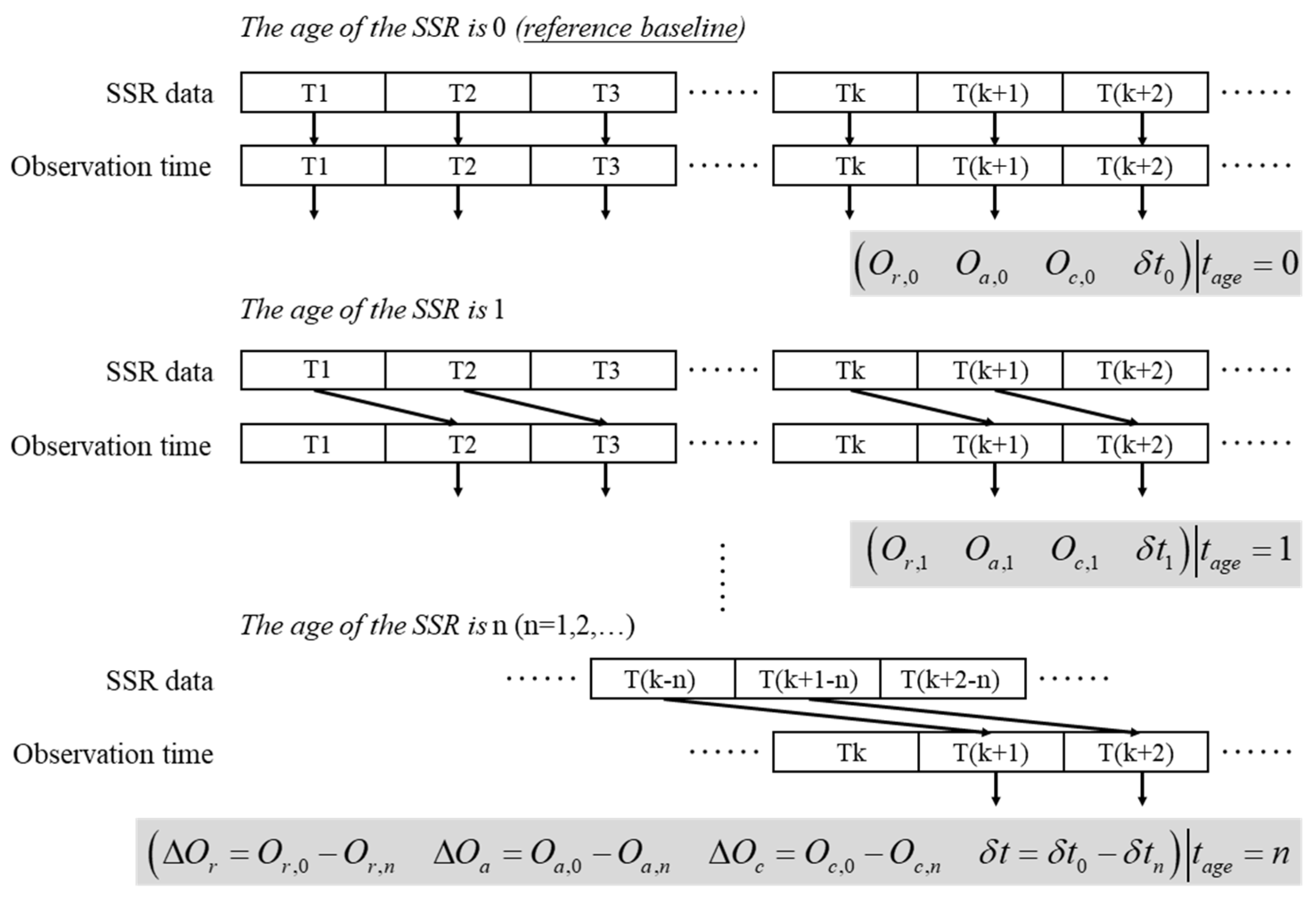
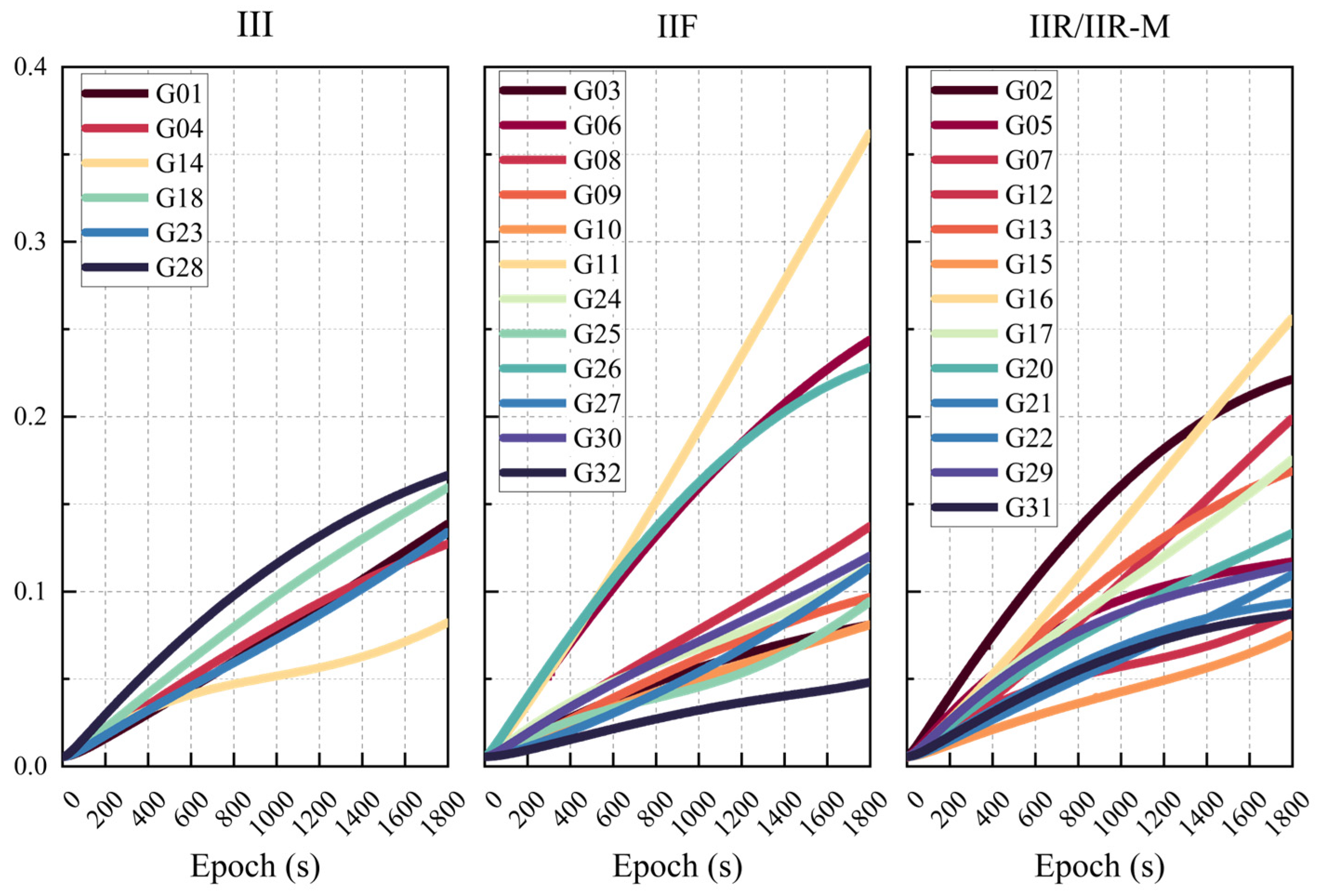
2.3. Optimized Stochastic Model Based on SSR Age and Clock–Orbit Degradation Parameters
- (1)
- Utilizing seven days of SSR data at a 1 Hz observation frequency, we collected 1800 continuous SISRE sequences for each GPS satellite;
- (2)
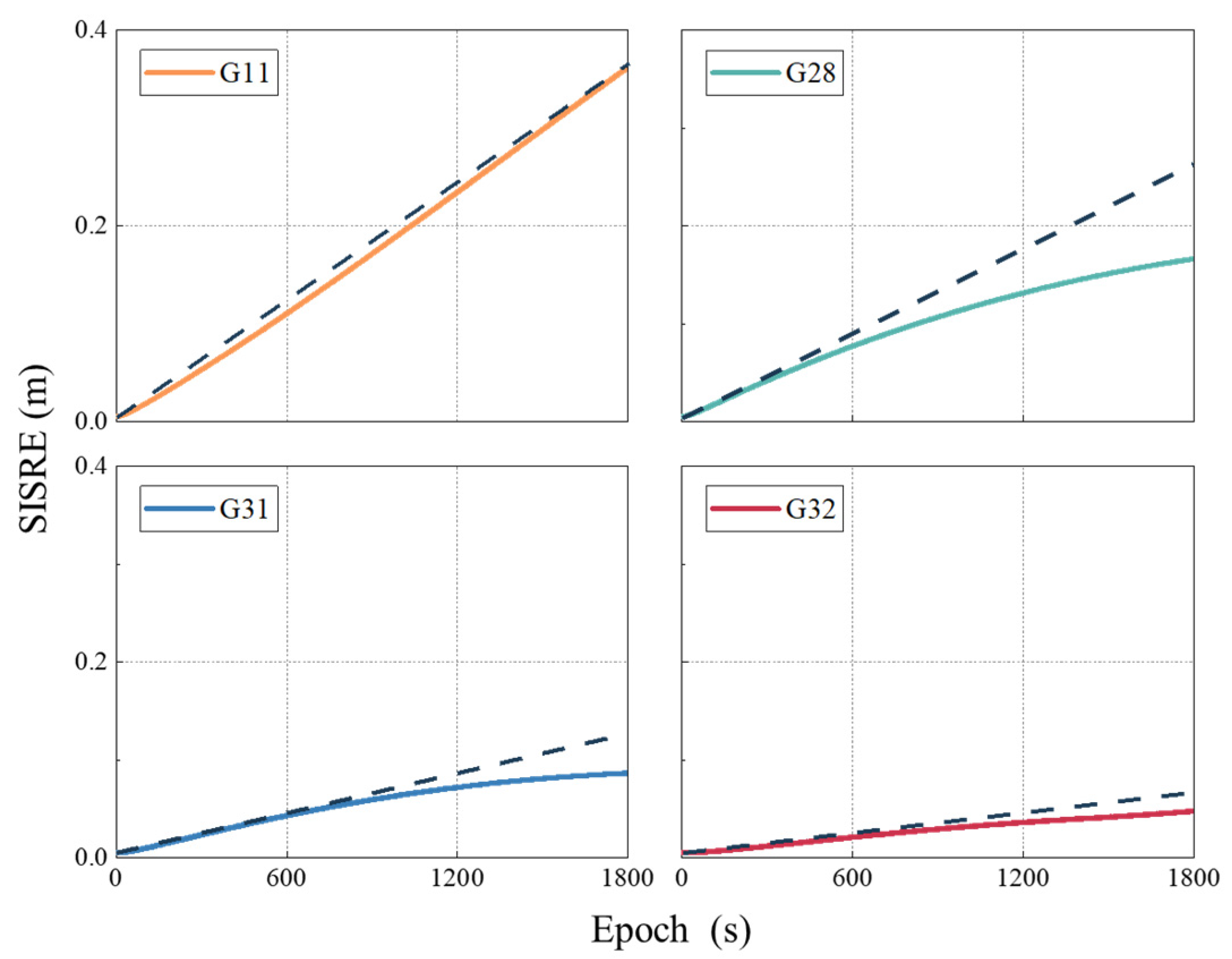
- Linear envelope was employed to fit the growth relationship between SISRE and SSR aging;
- (3)
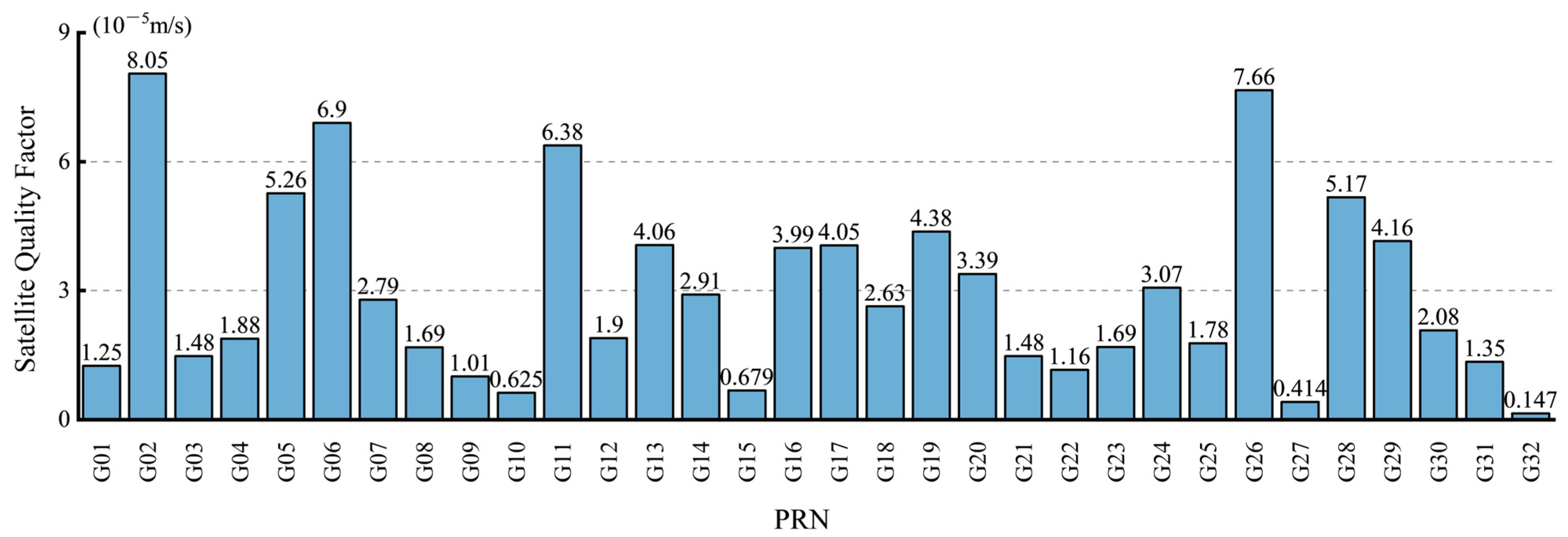
- The slope was used as the quantified degradation parameter, resulting in the development of a table of degradation parameters;
- (4)
- In practical applications, the parameter is calculated based on the interruption times in the SSR and the corresponding degradation parameters obtained from the table for the relevant satellites.
2.4. Mathematical Model Under INS Positional Constraints
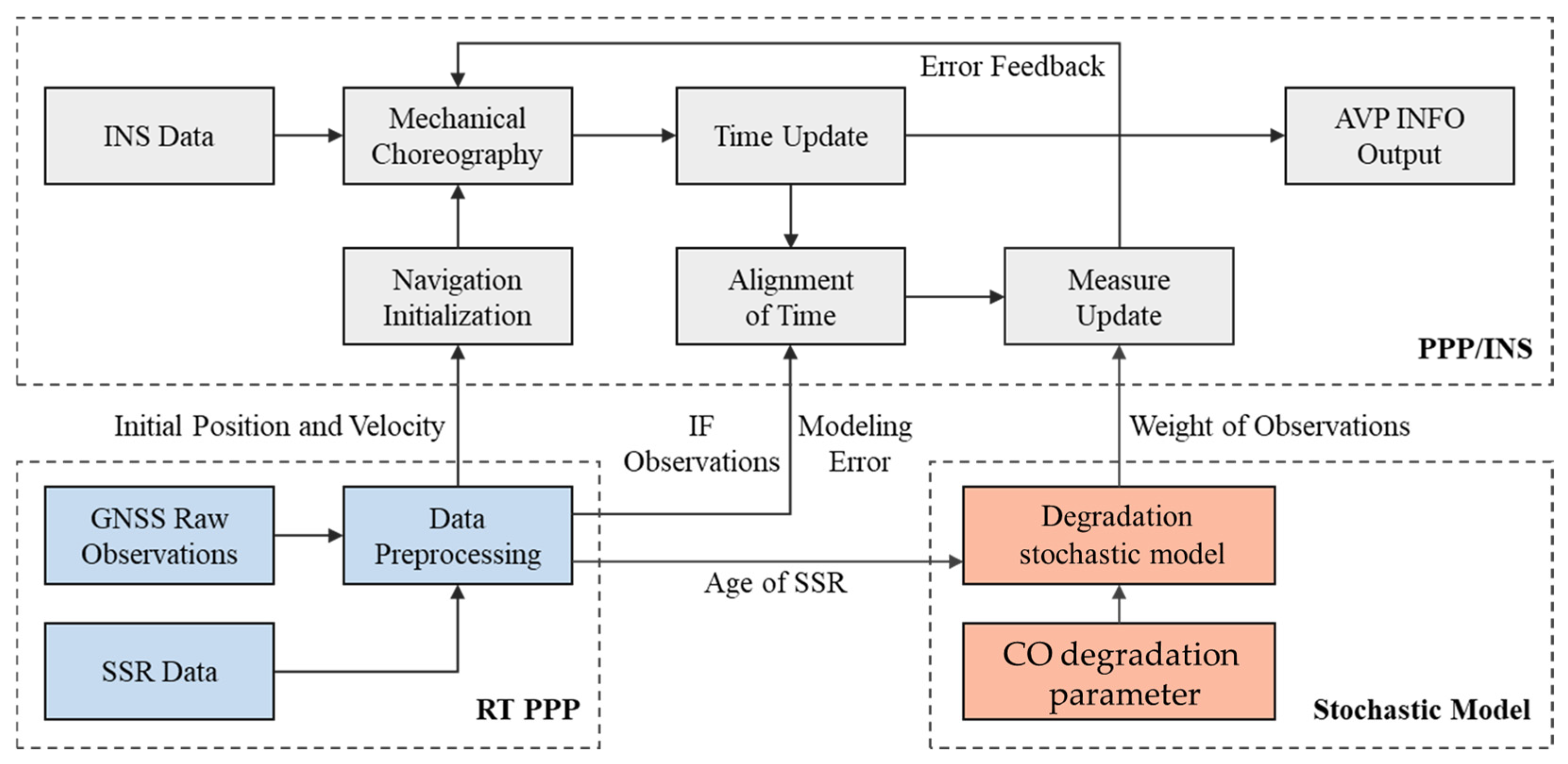
2.5. System Architecture of the Positioning System
3. Experiment and Results
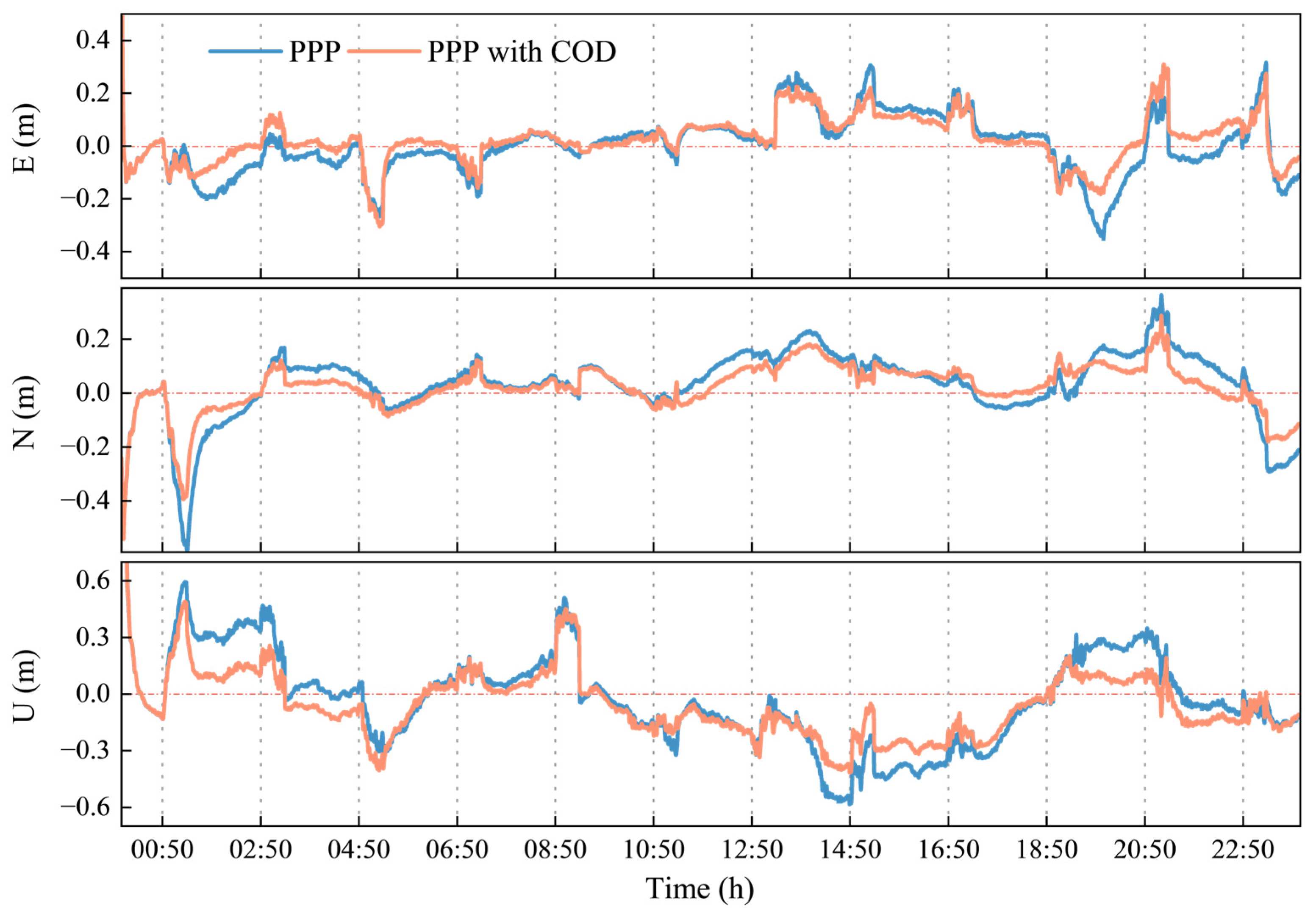
3.1. Validation of COD Stochastic Model
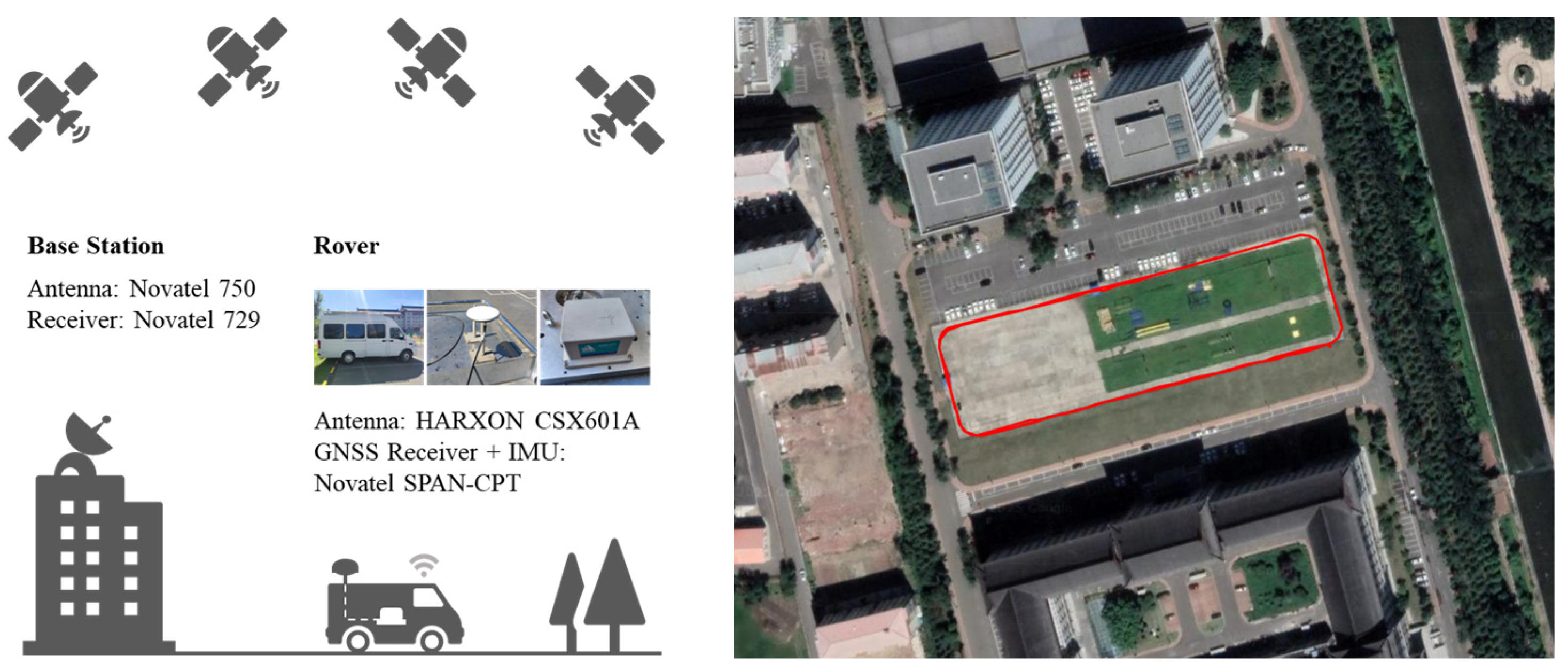
3.2. Dynamic Testing Data Collection and Processing Strategies
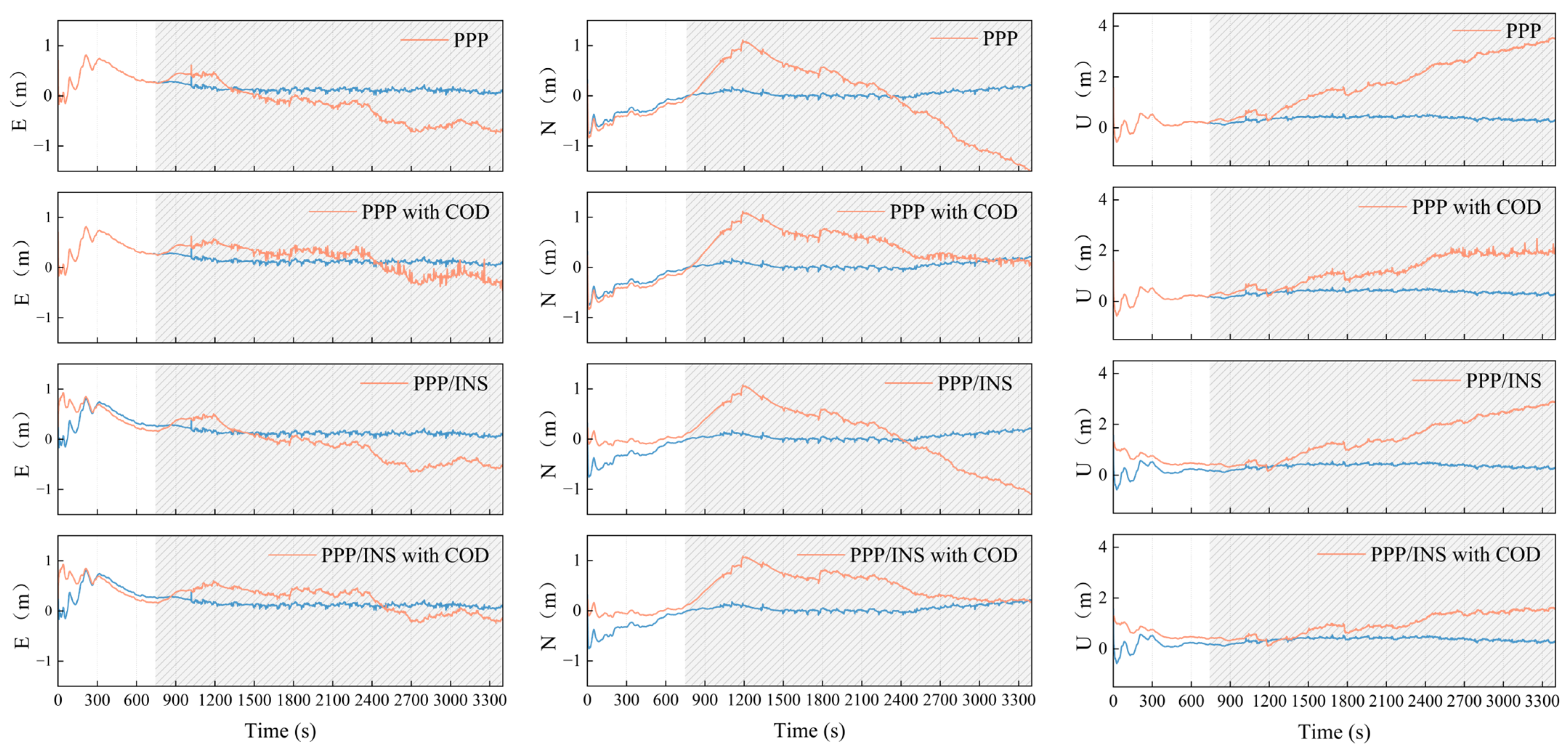
3.3. Dynamic Test
4. Discussion
5. Conclusions
- (1)
- Compared to the traditional fixed equivalent weight stochastic model, the COD stochastic model exhibits a significantly enhanced ability to alleviate positioning degradation. With the COD stochastic model, the horizontal and 3D positioning accuracy increase by an average of 12% and 17% when the SSR lag ranges from 5 to 30 min. When the SSR age reaches 30 min, the horizontal positioning accuracy is 0.131 m and the 3D positioning accuracy is 0.269 m, showing improvements of 23.2% and 19.0%, respectively.
- (2)
- The incorporation of INS position constraints into the tightly coupled PPP/INS model further improves its error suppression capability. Moreover, the PPP/INS model with COD demonstrates superior positioning accuracy under SSR interruptions. Dynamic experiments indicated that, during a half-hour interruption of SSR communication, the combination of the two methods significantly improves positioning accuracy. PPP with COD shows superior capabilities in error suppression, resulting in a 31.8% improvement in horizontal accuracy and a 48.8% enhancement in 3D accuracy. The PPP/INS with COD model offers the best accuracy maintenance, enhancing horizontal accuracy by 38.7% and 3D accuracy by 69.9%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, F.; Li, G.; Zhang, J.; Sun, Z.; Zhang, R.; Zhao, L. Ocean decimeter-level real-time BDS precise point positioning based on short message communication. GPS Solut. 2024, 28, 39. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, Z.; Yang, F.; Liu, X.; Zhang, J. Improved Multi-GNSS PPP Partial Ambiguity Resolution Method Based on Two-Step Sorting Criterion. Remote Sens. 2023, 15, 3319. [Google Scholar] [CrossRef]
- Choy, S.; Harima, K. Satellite delivery of high-accuracy GNSS precise point positioning service: An overview for Australia. J. Spat. Sci. 2019, 64, 197–208. [Google Scholar] [CrossRef]
- Akpınar, B.; Aykut, N.O. Determining the Coordinates of Control Points in Hydrographic Surveying by the Precise Point Positioning Method. J. Navig. 2017, 70, 1241–1252. [Google Scholar] [CrossRef]
- Pan, L.; Gao, X.; Hu, J.; Ma, F.; Zhang, Z.; Wu, W. Performance assessment of real-time multi-GNSS integrated PPP with uncombined and ionospheric-free combined observables. Adv. Space Res. 2021, 67, 234–252. [Google Scholar] [CrossRef]
- Cheng, S.; Cheng, J.; Zang, N.; Cai, J.; Fan, S.; Zhang, Z.; Song, H. Adaptive non-holonomic constraint aiding Multi-GNSS PPP/INS tightly coupled navigation in the urban environment. GPS Solut. 2023, 27, 152. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, M.; Cai, B.; Rizos, C.; Wang, J. An accurate train positioning method using tightly-coupled GPS + BDS PPP/IMU strategy. GPS Solut. 2022, 26, 67. [Google Scholar] [CrossRef]
- Yan, C.; Wang, Q.; Zhang, Y.; Ke, F.; Gao, W.; Yang, Y. Analysis of GNSS clock prediction performance with different interrupt intervals and application to real-time kinematic precise point positioning. Adv. Space Res. 2020, 65, 978–996. [Google Scholar] [CrossRef]
- Alkan, R.M.; Erol, S.; Mutlu, B. Real-time multi-GNSS Precise Point Positioning using IGS-RTS products in Antarctic region. Polar Sci. 2022, 32, 100844. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, G.; Chen, G.; Sun, W.; Pan, L. Signal-in-Space and Positioning Performance of BDS Open Augmentation Service. Math. Probl. Eng. 2022, 2022, 1–11. [Google Scholar] [CrossRef]
- Sun, J.; Liu, J.; Yang, Y.; Fan, S.; Yu, W. (Eds.) China Satellite Navigation Conference (CSNC) 2017 Proceedings; Springer: Singapore, 2017; Volume III. [Google Scholar]
- Liu, T.; Yuan, Y.; Zhang, B.; Wang, N.; Tan, B.; Chen, Y. Multi-GNSS precise point positioning (MGPPP) using raw observations. J. Geod. 2017, 91, 253–268. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Zhang, X.; Zhang, Y.; Guo, B.; Wang, R.; Klotz, J.; Wickert, J. Real-time high-rate co-seismic displacement from ambiguity-fixed precise point positioning: Application to earthquake early warning. Geophys. Res. Lett. 2013, 40, 295–300. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Wang, L.; Wang, X.; Yuan, H. Assessment of Multiple GNSS Real-Time SSR Products from Different Analysis Centers. ISPRS Int. J. Geo-Inf. 2018, 7, 85. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, Y.; Chen, J.; Chen, Q.; Xu, K.; Wang, B. Performance Assessment of Multi-GNSS Real-Time Products from Various Analysis Centers. Remote Sens. 2023, 15, 140. [Google Scholar] [CrossRef]
- Nie, Z.; Wang, B.; Wang, Z.; He, K. An offshore real-time precise point positioning technique based on a single set of BeiDou short-message communication devices. J. Geod. 2020, 94, 78. [Google Scholar] [CrossRef]
- Mu, X.; Wang, L.; Shu, B.; Tian, Y.; Li, X.; Lei, T.; Huang, G.; Zhang, Q. Performance Analysis of Multi-GNSS Real-Time PPP-AR Positioning Considering SSR Delay. Remote Sens. 2024, 16, 1213. [Google Scholar] [CrossRef]
- Hadas, T.; Bosy, J. IGS RTS precise orbits and clocks verification and quality degradation over time. GPS Solut. 2015, 19, 93–105. [Google Scholar] [CrossRef]
- Yue, C.; Dang, Y.; Gu, S.; Wang, H.; Zhang, J. Optimization of undifferenced and uncombined PPP stochastic model based on covariance component estimation. GPS Solut. 2022, 26, 119. [Google Scholar] [CrossRef]
- Mikoś, M.; Kazmierski, K.; Hadas, T.; Sośnica, K. Stochastic modeling of the receiver clock parameter in Galileo-only and multi-GNSS PPP solutions. GPS Solut. 2024, 28, 14. [Google Scholar] [CrossRef]
- Zhao, Q.; Guo, J.; Zuo, H.; Gong, X.; Guo, W.; Gu, S. Comparison of time transfer of IF-PPP, GIM-PPP, and RIM-PPP. GPS Solut. 2023, 27, 99. [Google Scholar] [CrossRef]
- Kazmierski, K.; Hadas, T.; Sośnica, K. Weighting of Multi-GNSS Observations in Real-Time Precise Point Positioning. Remote Sens. 2018, 10, 84. [Google Scholar] [CrossRef]
- Tang, L.; Wang, J.; Cui, B.; Zhu, H.; Ge, M.; Schuh, H. Multi-GNSS precise point positioning with predicted orbits and clocks. GPS Solut. 2023, 27, 162. [Google Scholar] [CrossRef]
- Gao, Z.; Ge, M.; Shen, W.; Li, Y.; Chen, Q.; Zhang, H.; Niu, X. Evaluation on the impact of IMU grades on BDS + GPS PPP/INS tightly coupled integration. Adv. Space Res. 2017, 60, 1283–1299. [Google Scholar] [CrossRef]
- Elsheikh, M.; Abdelfatah, W.; Noureldin, A.; Iqbal, U.; Korenberg, M. Low-Cost Real-Time PPP/INS Integration for Automated Land Vehicles. Sensors 2019, 19, 4896, Correction to Sensors 2022, 22, 5568. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, H.; Ge, M.; Niu, X.; Shen, W.; Wickert, J.; Schuh, H. Tightly coupled integration of multi-GNSS PPP and MEMS inertial measurement unit data. GPS Solut. 2017, 21, 377–391. [Google Scholar] [CrossRef]
- Elmezayen, A.; El-Rabbany, A. Ultra-Low-Cost Tightly Coupled Triple-Constellation GNSS PPP/MEMS-Based INS Integration for Land Vehicular Applications. Geomatics 2021, 1, 258–286. [Google Scholar] [CrossRef]
- Li, Z.; Gao, J.; Wang, J.; Yao, Y. PPP/INS tightly coupled navigation using adaptive federated filter. GPS Solut. 2017, 21, 137–148. [Google Scholar] [CrossRef]
- Gu, S.; Dai, C.; Fang, W.; Zheng, F.; Wang, Y.; Zhang, Q.; Lou, Y.; Niu, X. Multi-GNSS PPP/INS tightly coupled integration with atmospheric augmentation and its application in urban vehicle navigation. J. Geod. 2021, 95, 64. [Google Scholar] [CrossRef]
- Lass, C.; Ziebold, R. Development of Precise Point Positioning Algorithm to Support Advanced Driver Assistant Functions for Inland Vessel Navigation. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2021, 15, 781–789. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Xiao, J. Estimating GNSS satellite clock error to provide a new final product and real-time services. GPS Solut. 2024, 28, 17. [Google Scholar] [CrossRef]
- Xiao, J.; Li, H.; Kang, Q.; Sun, Y. Improving Stochastic Model of GNSS Precise Point Positioning with Triple-Frequency Geometry-Free Combination. J. Surv. Eng. 2024, 150, 04024002. [Google Scholar] [CrossRef]
- IGS. IGS State Space Representation (SSR); Format Version 1.00; IGS: Tokyo, Japan, 2020. [Google Scholar]
- Chen, J.; Zhang, Y.; Yu, C.; Wang, A.; Song, Z.; Zhou, J. Models and performance of SBAS and PPP of BDS. Satell. Navig. 2022, 3, 4. [Google Scholar] [CrossRef]
- Li, Y.; Li, B.; Gao, Y. Improved PPP Ambiguity Resolution Considering the Stochastic Characteristics of Atmospheric Corrections from Regional Networks. Sensors 2015, 15, 29893–29909. [Google Scholar] [CrossRef]
- Kazmierski, K.; Sośnica, K.; Hadas, T. Quality assessment of multi-GNSS orbits and clocks for real-time precise point positioning. GPS Solut. 2018, 22, 11. [Google Scholar] [CrossRef]
- Maciuk, K. Satellite clock stability analysis depending on the reference clock type. Arab. J. Geosci. 2019, 12, 28. [Google Scholar] [CrossRef]
- Li, F.; Liang, Y.; Xu, J.; Wu, M. Advances in satellite atomic clock technologies for the GNSS. Meas. Sci. Technol. 2024, 35, 15027. [Google Scholar]
- Shu, B.; Liu, H.; Feng, Y.; Xu, L.; Qian, C.; Yang, Z. Analysis of Factors Affecting Asynchronous RTK Positioning with GNSS Signals. Remote Sens. 2019, 11, 1256. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Broadcast versus precise ephemerides: A multi-GNSS perspective. GPS Solut. 2015, 19, 321–333. [Google Scholar] [CrossRef]
- Rife, J.; Pullen, S.; Enge, P.; Pervan, B. Paired overbounding for nonideal LAAS and WAAS error distributions. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 1386–1395. [Google Scholar] [CrossRef]
- Shu, B.; Wang, L.; Zhang, Q.; Huang, G. Evalution of multi-GNSS orbit and clock extrapolating error and their influence on real-time PPP during outages of SSR correction. Acta Geod. Cartogr. Sin. 2021, 50, 1738–1750. [Google Scholar]
- Nassar, S.; El-Sheimy, N. A combined algorithm of improving INS error modeling and sensor measurements for accurate INS/GPS navigation. GPS Solut. 2006, 10, 29–39. [Google Scholar] [CrossRef]
- Lai, L.; Zhao, D.; Xu, T.; Cheng, Z.; Guo, W.; Li, L. Improving Vehicle Positioning Performance in Urban Environment with Tight Integration of Multi-GNSS PPP-RTK/INS. Remote Sens. 2022, 14, 5489. [Google Scholar] [CrossRef]
- Soloviev, A. Tight Coupling of GPS and INS for Urban Navigation. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1731–1746. [Google Scholar] [CrossRef]
- Chen, W.; Hu, C.; Gao, S.; Chen, Y.; Ding, X. Error Correction Models and Their Effects on GPS Precise Point Positioning. Surv. Rev. 2013, 41, 238–252. [Google Scholar] [CrossRef]



| Age of SSR (s) | BADG | |||||
|---|---|---|---|---|---|---|
| PPP | PPP with COD | Improvement | ||||
| Horizontal/3D (m) | Horizontal/3D (m) | Horizontal/3D (m) | ||||
| 300 | 0.13 | 0.30 | 0.13 | 0.30 | 0 | 0 |
| 400 | 0.18 | 0.32 | 0.18 | 0.31 | 1.0% | 1.5% |
| 500 | 0.18 | 0.33 | 0.18 | 0.32 | 1.5% | 2.7% |
| 600 | 0.19 | 0.33 | 0.18 | 0.32 | 2.7% | 4.3% |
| 700 | 0.20 | 0.35 | 0.19 | 0.33 | 3.5% | 5.6% |
| 800 | 0.21 | 0.36 | 0.20 | 0.33 | 4.6% | 7.0% |
| 900 | 0.22 | 0.38 | 0.21 | 0.35 | 5.2% | 8.3% |
| 1000 | 0.23 | 0.41 | 0.22 | 0.37 | 6.5% | 9.8% |
| 1200 | 0.26 | 0.48 | 0.24 | 0.42 | 8.3% | 12.2% |
| 1500 | 0.30 | 0.57 | 0.27 | 0.49 | 10.0% | 14.5% |
| 1800 | 0.45 | 0.71 | 0.39 | 0.59 | 12.5% | 16.7% |
| Station (The SSR Age Is 1800s) | PPP | PPP with COD | Improvement | |||
| Horizontal/3D (m) | Horizontal/3D (m) | Horizontal/3D (m) | ||||
| BABG | 0.45 | 0.71 | 0.39 | 0.59 | 12.50% | 16.70% |
| DEAR | 0.39 | 0.69 | 0.34 | 0.57 | 12.82% | 17.39% |
| FALK | 0.41 | 0.72 | 0.35 | 0.61 | 14.63% | 15.28% |
| CUSV | 0.37 | 0.7 | 0.31 | 0.58 | 14.10% | 17.50% |
| Contents | Processing Strategy. |
|---|---|
| GNSS/INS Data Collection Sensors | Novatel SPAN-CPT |
| Position Reference Source | RTK (1 cm, RMS) |
| Cut-off Elevation Angle | 10° |
| Observables and Frequency | GPS L1/L2 |
| Processing Time Interval | GNSS: 1 Hz, INS: 100 Hz |
| Sources of SSR Data | CAS0 |
| Calibration of Satellite Orbits and Clocks | Broadcast ephemeris and SSR real-time corrections |
| Receiver Antenna Phase Center Offset | Corrected with the up-to-date igs14.atx file |
| Initial Alignment of INS | Dynamic alignment |
| Accelerometer Stability | 0.049 rad2/s |
| Gyroscopes Stability | 2.424 × 10−3 rad/s |
| Angular Random Walk | 2.612 × 10−10 rad2/s3 |
| Velocity Random Walk | 1.661 × 10−5 m2/s5 |
| Model Strategy | Horizontal/3D (m) | Improvement | Error Increment (m) | Improvement | ||||
|---|---|---|---|---|---|---|---|---|
| PPP | 1.02 | 2.58 | — | 1.76 | 3.75 | — | ||
| PPP with COD | 0.64 | 1.60 | 37.3% | 38.0% | 1.20 | 1.92 | 31.8% | 48.8% |
| PPP/INS | 0.82 | 2.08 | 19.6% | 19.4% | 1.27 | 2.85 | 27.8% | 24.0% |
| PPP/INS with COD | 0.62 | 1.32 | 39.2% | 48.8% | 1.08 | 1.13 | 38.7% | 69.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhao, L.; Yang, F.; Zhang, J.; Shi, J.; Zheng, C. Improved Performance of RT-PPP During Communication Outages Based on Position Constraints and Stochastic Model Optimization. Remote Sens. 2025, 17, 1969. https://doi.org/10.3390/rs17121969
Liu X, Zhao L, Yang F, Zhang J, Shi J, Zheng C. Improved Performance of RT-PPP During Communication Outages Based on Position Constraints and Stochastic Model Optimization. Remote Sensing. 2025; 17(12):1969. https://doi.org/10.3390/rs17121969
Chicago/Turabian StyleLiu, Xiaosong, Lin Zhao, Fuxin Yang, Jie Zhang, Jinjian Shi, and Chuanlei Zheng. 2025. "Improved Performance of RT-PPP During Communication Outages Based on Position Constraints and Stochastic Model Optimization" Remote Sensing 17, no. 12: 1969. https://doi.org/10.3390/rs17121969
APA StyleLiu, X., Zhao, L., Yang, F., Zhang, J., Shi, J., & Zheng, C. (2025). Improved Performance of RT-PPP During Communication Outages Based on Position Constraints and Stochastic Model Optimization. Remote Sensing, 17(12), 1969. https://doi.org/10.3390/rs17121969






