Robust Pose Estimation for Noncooperative Spacecraft Under Rapid Inter-Frame Motion: A Two-Stage Point Cloud Registration Approach

Abstract

This paper addresses the challenge of robust pose estimation for spacecraft under rapid inter-frame motion, proposing a two-stage point cloud registration framework. The first stage computes coarse pose estimation by leveraging Fast Point Feature Histogram (FPFH) descriptors with random sample and consensus (RANSAC) for correspondence matching, effectively handling significant positional displacements. The second stage refines the solution through geometry-aware fine registration using raw point cloud data, enhancing precision through a multi-scale iterative ICP-like framework. To validate the approach, we simulate time-of-flight (ToF) sensor measurements by rendering NASA’s public 3D spacecraft models and obtain 3D point clouds by back-projecting the depth measurements to 3D space. Comprehensive experiments demonstrate superior performance over several state-of-the-art methods in both accuracy and robustness under rapid inter-frame motion scenarios. The dual-stage architecture proves effective in maintaining tracking continuity while mitigating error accumulation from fast relative motion, showing promise for autonomous spacecraft proximity operations.

1. Introduction

In the vast expanse of space, the precise determination of a space target’s position and orientation—known as pose estimation—is a task of paramount importance. It is the cornerstone of numerous space missions, ranging from routine satellite operations to complex tasks such as autonomous docking, orbital maintenance, and planetary exploration [1,2,3]. Accurate pose estimation enables spacecraft to navigate safely, perform intricate maneuvers, and interact with other objects in space with the required precision. As space missions become increasingly ambitious, the demand for robust and reliable pose estimation techniques has never been greater. Despite the critical nature of this task, achieving accurate pose estimation in space is fraught with challenges. One of the most significant hurdles is the rapid inter-frame motion that spacecraft experience, particularly during aggressive orbital maneuvers or when operating in close proximity to other fast-moving objects [4,5].

Recent advancements in spacecraft pose estimation have explored diverse sensor configurations, including monocular [6], stereo [7], and time-of-flight (ToF) imaging systems [5]. Monocular vision approaches often rely on monocular or stereo vision systems combined with feature-based methods, such as template matching or 2D keypoint descriptors (e.g., SIFT [8], ORB [9]). While computationally efficient and effective in structured environments, they inherently suffer from depth ambiguity and struggle with rapid inter-frame motion, sparse textures, and extreme lighting variations common in space scenarios, requiring extensive prior knowledge of target geometry—a critical limitation when operating with uncooperative space objects lacking predefined models [10]. In contrast, depth-enabled modalities such as stereo vision and ToF sensors overcome this constraint by directly acquiring 3D structural measurements through point cloud generation [4,11,12,13]. Recent advances in 3D sensing have shifted focus to point cloud registration techniques. This capability transforms the pose estimation challenge into a temporal point cloud registration problem, where relative transformations between sequential frames can be solved through geometric correspondence alignment.

Iterative Closest Point (ICP) [14] and its variants (e.g., Generalized-ICP [15] and Robust-ICP [16]) are widely used for fine pose refinement but require accurate initial guesses, making them prone to failure under large displacements. To address this, hybrid frameworks combining global and local registration have emerged. For instance, feature descriptors like FPFH [17] and SHOT [18], paired with RANSAC [19], are employed for coarse alignment. More recently, deep learning techniques have been introduced to learn 3D local descriptors. 3DMatch [20] and 3DSmoothNet [21] pioneered this approach by employing a Siamese Network for feature extraction. FCGF [22] eliminates the need for keypoint detection by computing descriptors in a single pass using a fully convolutional neural network. Predator [23] leverages an attention mechanism to detect salient points in overlapping regions, enhancing robustness in low-overlap scenarios. GeoTransformer [24] learns geometric features for superpoint matching, demonstrating strong resilience to low overlap and rigid transformations. However, these transformer-based methods present critical limitations for spacecraft applications. First, their reliance on large-scale annotated training data conflicts with the scarcity of spacecraft point cloud datasets, which are inherently limited by mission-specific configurations and the prohibitive costs of space environment simulations. Second, the computational complexity of transformer operations—particularly cross-attention mechanisms—poses challenges for real-time execution on radiation-hardened spacecraft processors with stringent power constraints. These dual limitations of data dependency and computational intensity motivated our adoption of FPFH for coarse registration. As a handcrafted descriptor, FPFH operates in a training-free manner with low computational complexity, ensuring three key advantages: (1) immediate deployment without data collection or model fine-tuning, (2) deterministic runtime performance on resource-constrained hardware, and (3) inherent robustness to the sparse and irregular point distributions typical in spacecraft scenarios. Notably, while modern descriptors like FCGF and GeoTransformer reduce outlier proportions, no existing method can fully eliminate erroneous correspondences, particularly under extreme noise or partial observations. This underscores the necessity for robust estimators. Random Sample Consensus (RANSAC) [19] is a widely used algorithm for robust estimation in the presence of outliers. It iteratively samples minimal subsets of correspondences to generate pose hypotheses, which are then evaluated against the full correspondence set. However, its efficiency deteriorates in high-outlier scenarios, requiring exponentially more iterations to achieve reliable results. To address this, various RANSAC variants have been proposed to enhance efficiency and robustness. GC-RANSAC [25] improves local optimization by alternating between graph cuts and model refitting. CG-SAC [26] leverages keypoint normals and a compatibility-guided strategy to reduce sampling randomness. SAC-COT [27] ranks and samples ternary loops from the compatibility graph for more precise estimation. SC2-PCR [28] introduces a second-order spatial compatibility (SC2) metric, which emphasizes global rather than local consistency, allowing for more effective inlier identification and robust registration. Beyond RANSAC-based approaches, Branch-and-Bound (BnB) methods [29,30,31] explore the 6D parameter space to find globally optimal solutions. While these methods ensure optimality, they suffer from high computational costs, particularly in large correspondence sets with high outlier ratios. Another line of point cloud registration consists of optimization-based methods. Optimization-based methods mitigate the impact of outliers by employing robust loss functions that downweight outlier contributions during iterative estimation. Fast Global Registration (FGR) [32] formulates a dense objective using a scaled Geman–McClure estimator as the penalty function and reduces the influence of local minima through Graduated Nonconvexity (GNC). Yang et al. [31] extended GNC to operate directly with standard nonminimal solvers, creating a versatile framework for spatial perception tasks such as object localization and PCR. However, both FGR and GNC struggle with local minima when dealing with extremely low inlier ratios or in the absence of a good initial guess.

In the context of spacecraft-specific applications, model-based approaches leveraging prior CAD data have gained traction. Ref. [33] integrated ICP with Kalman filtering to track pose under orbital motion, yet their method suffered from error accumulation during high-speed maneuvers. Deep learning techniques, such as PointNet-based architectures [34], have also been explored for direct pose regression. However, these methods demand extensive training data and struggle to generalize to unseen spacecraft geometries or dynamic lighting. To simulate realistic on-orbit conditions, synthetic datasets generated via rendering tools (e.g., Blender, Unity) have become pivotal. Pioneering work by [35] utilized NASA’s 3D models to train vision-based detectors, but their focus was limited to RGB imagery, ignoring depth sensor challenges like noise and sparsity. Recent studies introduced physics-based ToF sensor simulations [4], enabling evaluation of registration algorithms under varying noise levels and motion blur.

Motivated by this paradigm, our work specifically addresses the precision enhancement of point cloud-based pose determination under challenging orbital relative motion conditions. Instead of applying robust loss functions directly in global registration, we introduce a two-stage refinement strategy. The first stage of our framework focuses on computing a coarse pose estimation by leveraging Fast Point Feature Histogram (FPFH) descriptors [17] in conjunction with RANSAC-based correspondence matching [19]. This combination is particularly effective in handling significant positional displacements, making it well-suited for scenarios involving rapid inter-frame motion. The use of FPFH descriptors allows for the efficient computation of geometric features, while RANSAC helps to mitigate the impact of outliers, ensuring a more reliable initial pose estimation. In the second stage, we refine the coarse pose estimation through a geometry-aware fine registration process. This stage utilizes raw point cloud data and employs an ICP-like framework. By incorporating the coarse pose, we can generate more accurate correspondences for more accurate pose, which is crucial for tracking the spacecraft’s motion over time. This refinement process significantly enhances the precision of the pose estimation, ensuring that the final result is both accurate and reliable. The proposed two-stage framework builds on these foundations by uniquely combining FPFH-RANSAC for robustness to large displacements and motion-constrained ICP for precision. Unlike prior works, the integration of temporal continuity constraints directly addresses error propagation in high-speed scenarios, a gap highlighted in recent benchmarks for autonomous spacecraft navigation. This dual strategy bridges the trade-off between computational efficiency and accuracy, advancing the state of the art for dynamic on-orbit applications.

To validate the effectiveness of our proposed framework, we have developed a comprehensive dataset that simulates time-of-flight (ToF) sensor measurements. This dataset is generated by rendering NASA’s public 3D spacecraft models, followed by back-projection to create synthetic 3D point clouds. The diversity of this dataset allows us to thoroughly test and evaluate our method under different scenarios, ensuring its robustness and versatility. An illustration of the simulated ToF image sequence is presented in Figure 1. Our experiments demonstrate that the proposed two-stage registration framework outperforms conventional methods in both accuracy and robustness. Specifically, our approach achieves an angular error of less than 2.0° and a translational error of less than 10 cm, showcasing its superior performance in dynamic environments. The dual-stage architecture not only maintains tracking continuity but also effectively mitigates error accumulation from fast relative motion, making it a promising solution for autonomous spacecraft proximity operations. The primary novelty of our work lies in the design of a two-stage point cloud registration framework that builds upon conventional ICP-based fine registration. In the coarse registration stage, we introduce a feature-based alignment mechanism enhanced with a length-invariant outlier rejection strategy, combined with a RANSAC-based pose estimation scheme. This allows us to robustly compute an initial pose even in the presence of significant noise and outliers. The resulting coarse pose initialization significantly reduces the likelihood of local minima during the subsequent fine registration stage, thereby improving convergence and stability. This design proves particularly effective in scenarios involving rapid inter-frame motion, which are common in spacecraft operations. In conclusion, the development of our two-stage point cloud registration framework represents a significant advancement in the field of spacecraft pose estimation. By addressing the challenges posed by rapid inter-frame motion and providing a more accurate and robust solution, our work paves the way for safer and more efficient space missions. Additionally, the comprehensive dataset we have contributed will serve as a valuable resource for further research and development in this area.

The main contributions of this work are threefold:

• Two-stage Point Cloud Registration Framework: We propose a novel two-stage point cloud registration framework tailored for pose estimation of noncooperative spacecraft. This approach incorporates a length-invariant outlier rejection mechanism in the coarse alignment stage, followed by an ICP-based fine registration. The design significantly improves robustness and accuracy under fast inter-frame motion, as demonstrated through extensive quantitative evaluations.
• Synthetic Benchmark Dataset for Spacecraft Pose Estimation: We construct a comprehensive synthetic dataset using 8 diverse CAD models of spacecraft, each with 10 independently generated sequences and a total of 12,000 annotated frames. The dataset provides accurate ground truth poses and is designed to support rigorous benchmarking under a wide range of motion and viewing conditions.
• Practical Adaptability for Onboard Applications: The proposed framework is designed with computational efficiency and data generalizability in mind, making it suitable for onboard processing in resource-constrained spacecraft systems. Unlike many deep learning-based methods, our approach avoids the need for large-scale training data and delivers real-time inference performance, which is validated across diverse simulated ToF scenarios.

The remainder of this paper is organized as follows. Section 2 details our novel two-stage point cloud registration methodology, presenting both the coarse alignment mechanism for initial pose approximation and the refined fine registration stage for precision tracking. Section 3 validates the proposed approach through extensive experiments on our newly created benchmark dataset, featuring quantitative comparisons with state-of-the-art methods across multiple evaluation metrics. Finally, Section 5 concludes the paper by summarizing key findings, discussing practical implications for on-orbit servicing missions, and outlining directions for future research in spaceborne perception systems.

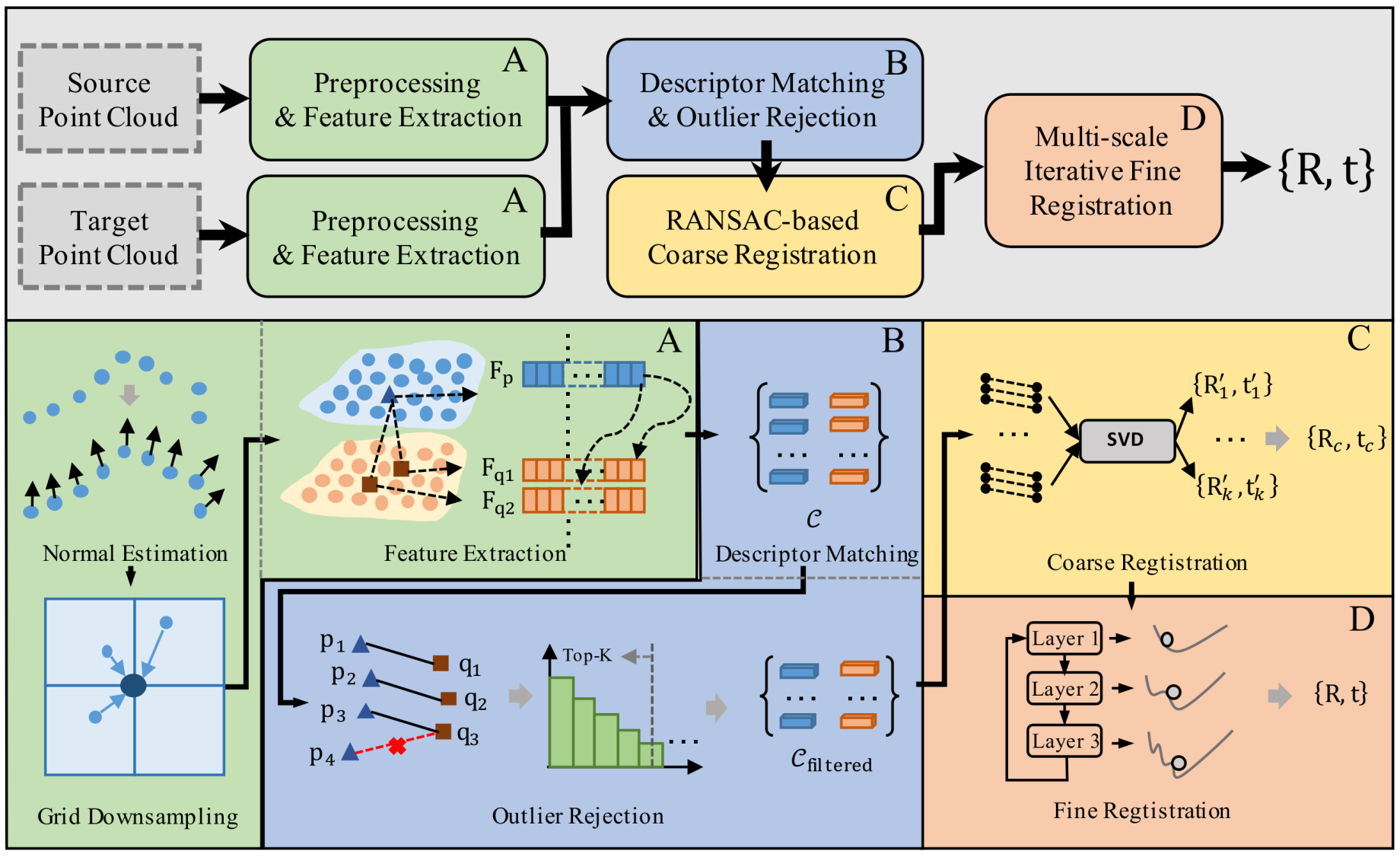
2. Materials and Methods

Spacecrafts in close-range proximity often exhibit abrupt rotational/translational displacements between consecutive frames. This violates the “small-motion assumption” required by traditional iterative optimization methods (e.g., ICP and its variants), causing severe convergence issues. Conventional registration pipelines relying solely on fine registration are highly susceptible to local minima when initial pose errors exceed their narrow convergence basins. This is exacerbated by sparse geometries and sensor noise in space environments. To address these challenges, firstly, our method introduces a robust coarse registration stage leveraging efficient geometric descriptors for correspondence matching, followed by outlier rejection and robust parameter estimation via RANSAC. This provides a globally consistent initial pose estimate Secondly, a fine registration stage is initialized with the coarse alignment result and then performs multi-scale iterative fine optimization. This hierarchical architecture explicitly decouples large-motion estimation from precision refinement, ensuring both convergence reliability and high accuracy.

2.1. Problem Statement

Given a sequential point cloud observation of a noncooperative spacecraft ${\left\{{\mathcal{P}}_t\right\}}_{t=0}^T$ where ${\mathcal{P}}_t={\{{\mathbf{p}}_t^i\in {\mathbb{R}}^3\}}_{i=1}^{N_t}$ represents the 3D point cloud captured at time step t, we aim to continuously estimate the spacecraft’s 6-DOF pose ${\mathbf{T}}_t\in SE\left(3\right)$ through point cloud registration. The pose transformation between consecutive frames should satisfy:

$${\mathbf{T}}_t=arg\underset{\mathbf{T}\in SE\left(3\right)}{min}\sum _{i=1}^{N_t}{∥\mathbf{T}\circ {\mathbf{p}}_t^i-{\mathbf{q}}_t^i∥}^2$$

(1)

where ${\mathbf{T}}_t=\left[\begin{array}{cc}{\mathbf{R}}_t& {\mathbf{t}}_t\\ \mathbf{0}& 1\end{array}\right]$ denotes the homogeneous transformation matrix comprising rotation ${\mathbf{R}}_t\in SO\left(3\right)$ and translation ${\mathbf{t}}_t\in {\mathbb{R}}^3$ and ${\mathbf{q}}_t^i$ represents the corresponding point in the previous frame ${\mathcal{P}}_{t-1}$. The operator ∘ applies rigid transformation to points. An illustration of the pipeline of our proposed method is presented in Figure 2.

2.2. Feature-Based Coarse Registration

2.2.1. Point Cloud Preprocessing

Point cloud normals are necessary and essential for feature extraction and descriptor generation; we compute them via Principal Component Analysis (PCA) on local neighborhoods. For each point ${\mathbf{p}}_i\in \mathcal{P}$, its neighborhood is defined as ${\mathcal{N}}_i=\{{\mathbf{p}}_j|\parallel {\mathbf{p}}_j-{\mathbf{p}}_i{\parallel }_2<r\}$, and then we can compute the covariance matrix as

$${\mathbf{C}}_i={\displaystyle \frac{1}{|{\mathcal{N}}_i|}}\sum _{j\in {\mathcal{N}}_i}({\mathbf{p}}_j-{\mu }_i){({\mathbf{p}}_j-{\mu }_i)}^{\top }$$

(2)

where ${\mu }_i={\displaystyle \frac{1}{|{\mathcal{N}}_i|}}{\sum }_{j\in {\mathcal{N}}_i}{\mathbf{p}}_j$. Eigen decompostion is applied to ${\mathbf{C}}_i$: ${\mathbf{C}}_i{\mathbf{v}}_k={\lambda }_k{\mathbf{v}}_k,{\lambda }_0\le {\lambda }_1\le {\lambda }_2$, and finally, the normal vector is selected as ${\mathbf{n}}_i={\mathbf{v}}_0$, which is the eigenvector for the smallest eigenvalue.

Since the raw point cloud is too dense for feature extraction, for efficiency, we use voxel downsampling to downsample the original point clouds. On the other hand, voxel downsampling outputs more smooth point clouds. The point cloud is discretized into cubic voxels with edge length s: the voxel grid is a collection of $\mathcal{V}={\bigcup }_{m,n,l}{V}_{m,n,l}$, then the voxel coordinates is computed as

$$V_{m,n,l}=\left\{{\mathbf{p}}_i|m=\lfloor {\displaystyle \frac{x_i}{s}}\rfloor ,n=\lfloor {\displaystyle \frac{y_i}{s}}\rfloor ,l=\lfloor {\displaystyle \frac{z_i}{s}}\rfloor \right\}.$$

(3)

Finally, the downsampled point is computed as

$${\widehat{\mathbf{p}}}_{m,n,l}={\displaystyle \frac{1}{|V_{m,n,l}|}}\sum _{{\mathbf{p}}_i\in V_{m,n,l}}{\mathbf{p}}_i.$$

(4)

Then, noise suppression is applied via k-nearest neighbor statistics: the mean distance is computed as

$${\overline{d}}_i={\displaystyle \frac{1}{k}}\sum _{j=1}^k{\parallel {\mathbf{p}}_i-{\mathbf{p}}_j^{\left(k\right)}\parallel }_2.$$

(5)

The thresholding is determined by ${\mathcal{P}}_{\mathrm{filtered}}=\left\{{\mathbf{p}}_i\left|{\overline{d}}_i\le {\mu }_d+\alpha {\sigma }_d\right.\right\}$, where ${\mu }_d={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\overline{d}}_i,{\sigma }_d=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{({\overline{d}}_i-{\mu }_d)}^2}.$

2.2.2. Feature Extraction and Matching

The FPFH [17] is widely adopted for 3D feature extraction and matching. We briefly review the computation of FPFH as follows. First, the Simplified Point Feature Histogram (SPFH) is computed. For each point ${\mathbf{p}}_i$ with normal ${\mathbf{n}}_i$ and neighbors ${\mathbf{p}}_j\in {\mathcal{N}}_i$:

$$\begin{array}{cc}\hfill {\alpha }_j& =arctan\left({\mathbf{n}}_j^{\top }{\displaystyle \frac{{\mathbf{p}}_j-{\mathbf{p}}_i}{\parallel {\mathbf{p}}_j-{\mathbf{p}}_i\parallel }}\right)\hfill \\ \hfill {\varphi }_j& ={\mathbf{u}}_i^{\top }{\displaystyle \frac{{\mathbf{p}}_j-{\mathbf{p}}_i}{d}}\hfill \\ \hfill {\theta }_j& =arctan\left({\mathbf{n}}_i^{\top }({\mathbf{w}}_j\times {\mathbf{u}}_i),{\mathbf{n}}_i^{\top }{\mathbf{w}}_j\right)\hfill \end{array}$$

(6)

where:

$$d=\parallel {\mathbf{p}}_j-{\mathbf{p}}_i{\parallel }_2,{\mathbf{u}}_i={\displaystyle \frac{{\mathbf{p}}_j-{\mathbf{p}}_i}{d}},{\mathbf{w}}_j={\mathbf{n}}_j\times {\mathbf{u}}_i$$

(7)

Then, FPFH is constructed as

$$\mathrm{FPFH}\left({\mathbf{p}}_i\right)=\mathrm{SPFH}\left({\mathbf{p}}_i\right)+{\displaystyle \frac{1}{|{\mathcal{N}}_i|}}\sum _{j\in {\mathcal{N}}_i}{\displaystyle \frac{1}{d_j}}\mathrm{SPFH}\left({\mathbf{p}}_j\right)$$

(8)

with distance weighting $d_j={\parallel {\mathbf{p}}_j-{\mathbf{p}}_i\parallel }_2$.

Once we get the FPFH descriptor, which is a 33-dimensional vector, we perform robust feature matching. Several matching criteria are adopted for more robust feature matching. First, the ratio test is performed. For two nearest neighbors ${\mathbf{q}}_1,{\mathbf{q}}_2$:

$$\mathrm{Match}\mathrm{valid}\mathrm{if}:{\displaystyle \frac{D_f({\mathbf{f}}_{\mathbf{p}},{\mathbf{f}}_{{\mathbf{q}}_1})}{D_f({\mathbf{f}}_{\mathbf{p}},{\mathbf{f}}_{{\mathbf{q}}_2})}}<\tau$$

(9)

where $D_f({\mathbf{f}}_a,{\mathbf{f}}_b)={\parallel {\mathbf{f}}_a-{\mathbf{f}}_b\parallel }_2$ and $\tau \in [0.8,0.95]$. In addition to the ratio test, we propose another criterion. Define k-nearest neighborhoods:

$$\begin{array}{cc}\hfill {\mathcal{N}}_k\left(\mathbf{p}\right)& =\{{\mathbf{q}}_1,\dots ,{\mathbf{q}}_k|D_f({\mathbf{f}}_{\mathbf{p}},{\mathbf{f}}_{{\mathbf{q}}_i})\mathrm{sorted}\}\hfill \\ \hfill {\mathcal{N}}_k\left(\mathbf{q}\right)& =\{{\mathbf{p}}_1,\dots ,{\mathbf{p}}_k|D_f({\mathbf{f}}_{\mathbf{q}},{\mathbf{f}}_{{\mathbf{p}}_j})\mathrm{sorted}\}\hfill \end{array}$$

(10)

The final correspondence set is constructed as:

$$\mathcal{C}=\left\{(\mathbf{p},\mathbf{q})\right|\mathbf{q}\in {\mathcal{N}}_k\left(\mathbf{p}\right)\wedge \mathbf{p}\in {\mathcal{N}}_k\left(\mathbf{q}\right)\}$$

(11)

2.2.3. RANSAC-Based Pose Estimation

Given initial correspondences $\mathcal{C}={\left\{({\mathbf{p}}_i,{\mathbf{q}}_i)\right\}}_{i=1}^M$, we introduce pairwise length invariance for outlier rejection. For two correspondences $({\mathbf{p}}_a,{\mathbf{q}}_a)$ and $({\mathbf{p}}_b,{\mathbf{q}}_b)$:

$$\Delta l_{ab}=\left|\parallel {\mathbf{p}}_a-{\mathbf{p}}_b{\parallel }_2-{\parallel {\mathbf{q}}_a-{\mathbf{q}}_b\parallel }_2\right|$$

(12)

the distance is computed via robust kernel:

$$s_{ab}=max\left(0,1-{\displaystyle \frac{\Delta l_{ab}^2}{{\sigma }_l^2}}\right)$$

(13)

where ${\sigma }_l$ controls geometric tolerance (typically 0.1 times median edge length). The voting score is aggregated next. For N random pairs, only top-k matches survive and the filtered correspondence set is constructed as follows:

$$\mathrm{Score}\left(c_i\right)=\sum _{j=1}^N{s}_{ij}·\mathbb{I}(\Delta l_{ij}<3{\sigma }_l)$$

(14)

$${\mathcal{C}}_{\mathrm{filtered}}=\left\{{\mathbf{c}}_i\right|\mathrm{Score}\left({\mathbf{c}}_i\right)\in \mathrm{Top}-\mathrm{K}\left({\left\{\mathrm{Score}\left({\mathbf{c}}_j\right)\right\}}_{j=1}^M\right)\}$$

(15)

This outlier rejection mechanism effectively improves the quality of point correspondences, which enhances the accuracy and robustness of the subsequent fine registration. By filtering out inconsistent matches based on length invariance, the estimated coarse pose is more reliable, providing a well-initialized alignment that prevents the optimization from falling into local minima. This is particularly beneficial in scenarios with large inter-frame motion, as demonstrated in the experimental section. After outlier rejection, RANSAC is applied for pose estimation. Randomly sample 3 correspondences and solve:

$$\begin{array}{cc}\hfill & \underset{\mathbf{R},\mathbf{t}}{min}\sum _{k=1}^3{\parallel \mathbf{R}{\mathbf{p}}_k+\mathbf{t}-{\mathbf{q}}_k\parallel }^2\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\mathbf{R}\in SO\left(3\right),\mathbf{t}\in {\mathbb{R}}^3\hfill \end{array}$$

(16)

where this equation has close form solution via SVD decomposition. For model verification, compute inlier count:

$$\mathrm{IR}=\sum _{({\mathbf{p}}_i,{\mathbf{q}}_i)}\mathbb{I}\left(\parallel \mathbf{R}{\mathbf{p}}_i+\mathbf{t}-{\mathbf{q}}_i{\parallel }_2<{ϵ}_{\mathrm{th}}\right)$$

(17)

Finally, we refine the pose with all survived inliers, which is repeated for for K iterations (typically 10–20). The best transformation is updated as follows:

$${\mathbf{T}}^{*}=arg\underset{\mathbf{T}\in SE\left(3\right)}{min}\sum _{({\mathbf{p}}_i,{\mathbf{q}}_i)\in {\mathcal{C}}_{\mathrm{inlier}}}{\parallel \mathbf{T}\circ {\mathbf{p}}_i-{\mathbf{q}}_i\parallel }^2.$$

(18)

2.3. Geometry-Based Fine Registration

After obtaining a coarse pose estimation from RANSAC-based alignment, there is still room for refinement due to inaccuracies in feature positions. These inaccuracies can arise from sensor noise, imperfect feature extraction, or outlier correspondences. To address this, we refine the pose by leveraging the raw point cloud geometry through an iterative process that involves regenerating correspondences and solving for an improved transformation using a weighted SVD approach. Given a coarse transformation ${\mathbf{T}}_c=\left[{\mathbf{R}}_c\right|{\mathbf{t}}_c]$, we apply it to the source point cloud $\mathbf{P}={\left\{{\mathbf{p}}_i\right\}}_{i=1}^N$ to obtain transformed points:

$${\mathbf{p}}_i^{\prime }={\mathbf{R}}_c{\mathbf{p}}_i+{\mathbf{t}}_c.$$

(19)

For each transformed point ${\mathbf{p}}_i^{\prime }$, we search for the nearest neighbor ${\mathbf{q}}_j$ in the target point cloud $\mathbf{Q}={\left\{{\mathbf{q}}_j\right\}}_{j=1}^M$ using Euclidean distance:

$${\mathbf{q}}_j=arg\underset{{\mathbf{q}}_j\in \mathbf{Q}}{min}\parallel {\mathbf{p}}_i^{\prime }-{\mathbf{q}}_j\parallel .$$

(20)

This process generates a new set of correspondences $\left\{({\mathbf{p}}_i,{\mathbf{q}}_j)\right\}$, which better reflect the true alignment. Once correspondences are established, we refine the transformation by solving a weighted least-squares optimization problem. The objective is to minimize:

$$\sum _i{w}_i{\parallel {\mathbf{R}}_p{\mathbf{p}}_i+\mathbf{t}-{\mathbf{q}}_i\parallel }^2,$$

(21)

where $w_i$ is a robust weight determined using a kernel function of the point-wise residuals:

$$w_i=\varphi (\parallel {\mathbf{R}}_c{\mathbf{p}}_i+{\mathbf{t}}_c-{\mathbf{q}}_i\parallel ),$$

(22)

and $\varphi (·)$ is a robust Cauchy loss to mitigate the influence of outliers. Then, we compute the weighted centroid of both point sets:

$$\overline{\mathbf{p}}={\displaystyle \frac{{\sum }_i{w}_i{\mathbf{p}}_i}{{\sum }_i{w}_i}},\overline{\mathbf{q}}={\displaystyle \frac{{\sum }_i{w}_i{\mathbf{q}}_i}{{\sum }_i{w}_i}}.$$

(23)

The covariance matrix is given by:

$$\mathbf{H}=\sum _i{w}_i({\mathbf{p}}_i-\overline{\mathbf{p}}){({\mathbf{q}}_i-\overline{\mathbf{q}})}^T.$$

(24)

Using singular value decomposition (SVD) $\mathbf{H}=\mathbf{U}\Sigma {\mathbf{V}}^T$, the optimal rotation is obtained as $\mathbf{R}=\mathbf{V}{\mathbf{U}}^T$. If $det\left(\mathbf{R}\right)<0$, we enforce a proper rotation by flipping the last column of $\mathbf{V}$ as $\mathbf{V}[:,3]\leftarrow -\mathbf{V}[:,3]$. The optimal translation is then given by $\mathbf{t}=\overline{\mathbf{q}}-\mathbf{R}\overline{\mathbf{p}}$. To accelerate convergence and improve robustness, we implement a multi-scale framework: (1) start with a downsampled coarse point cloud to quickly establish an initial refinement; (2) iteratively refine the pose at increasing resolutions; (3) at each scale, update correspondences and recompute the transformation; (4) stop when convergence criteria (e.g., transformation change below a threshold) are met.

2.4. Point Cloud Dataset Construction

Let the spacecraft CAD model be represented as triangular mesh $\mathcal{M}={\{{\mathbf{v}}_i\in {\mathbb{R}}^3\}}_{i=1}^N$ with surface normals $\left\{{\mathbf{n}}_i\right\}$. The perspective projection follows:

$$\left[\begin{array}{c}u\\ vs.\\ 1\end{array}\right]={\displaystyle \frac{1}{z_c}}\mathbf{K}\left[\mathbf{R}\right|\mathbf{t}]\left[\begin{array}{c}{\mathbf{v}}_w\\ 1\end{array}\right],$$

(25)

where:

• ${\mathbf{v}}_w\in {\mathbb{R}}^3$: 3D vertex in world coordinates
• $\mathbf{R}\in SO\left(3\right)$, $\mathbf{t}\in {\mathbb{R}}^3$: Camera extrinsic parameters
• $\mathbf{K}=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$: Intrinsic matrix
• $(u,v)$: Pixel coordinates in image plane

For each pixel coordinate $(u,v)$, its normalized coordinate is given by:

$$(x_n,y_n,1)=({\displaystyle \frac{u-c_x}{f_x}},{\displaystyle \frac{v-c_y}{f_y}},1).$$

(26)

Then, its corresponding 3D point in the camera coordinate is computed by scaling the normalized coordinate with depth value $d_{uv}$, which is given by:

$${\mathbf{v}}_{cam}=(d_{uv}·{\displaystyle \frac{u-c_x}{f_x}},d_{uv}·{\displaystyle \frac{v-c_y}{f_y}},d_{uv}).$$

(27)

This formula can be rewritten in the matrix form as follows:

$${\mathbf{v}}_{cam}=d_{uv}·{\mathbf{K}}^{-1}\left[\begin{array}{c}u\\ vs.\\ 1\end{array}\right],{\mathbf{K}}^{-1}=\left[\begin{array}{ccc}{\displaystyle \frac{1}{f_x}}& 0& -{\displaystyle \frac{c_x}{f_x}}\\ 0& {\displaystyle \frac{1}{f_y}}& -{\displaystyle \frac{c_y}{f_y}}\\ 0& 0& 1\end{array}\right].$$

(28)

For each pixel coordinate $(u,v)$, cast a ray from camera origin $\mathbf{o}$ through the pixel:

$$\mathbf{r}\left(t\right)=\mathbf{o}+t·{\mathbf{d}}_{uv},t\ge 0,$$

(29)

where the ray direction ${\mathbf{d}}_{uv}$ is computed as:

$${\mathbf{d}}_{uv}={\mathbf{R}}^{\top }{\mathbf{K}}^{-1}\left[\begin{array}{c}u\\ v\\ 1\end{array}\right].$$

(30)

The depth value $d_{uv}$ is obtained by solving the ray-mesh intersection:

$$d_{uv}=min\{t>0|\mathbf{r}\left(t\right)\cap \mathcal{M}\ne \varnothing \}.$$

(31)

For each valid pixel $(u,v)$ with depth $d_{uv}$, the 3D point ${\mathbf{p}}_w$ in world coordinates is obtained by converting ${\mathbf{v}}_{cam}$ with $\left[\mathbf{R}\right|\mathbf{t}]$:

$${\mathbf{p}}_w={\mathbf{R}}^{\top }\left({\mathbf{v}}_{cam}-\mathbf{t}\right).$$

(32)

where ${\mathbf{v}}_{cam}$ is computed by back-projecting the depth pixel with Equation (28). To simulate orbital motion, we render sequences with controlled viewpoint transitions. The process for synthetic data generation is summarized in Algorithm 1.

Algorithm 1 Synthetic point cloud generation.

1: Initialize camera trajectory ${\left\{{\mathbf{T}}_k\right\}}_{k=1}^N$ with orbital dynamics 2: for each frame k do 3:    Ray cast CAD model $\mathcal{M}$ at pose ${\mathbf{T}}_k$→ Get depth map ${\mathcal{D}}_k$ 4:    Add noise: ${\tilde{\mathcal{D}}}_k={\mathcal{D}}_k+{ϵ}_{\mathrm{ToF}}$ 5:    Back-project: ${\mathcal{P}}_k=\left\{{\mathbf{p}}_i\right|{\mathbf{p}}_i=\mathrm{Equation}\left(32\right)\left({\tilde{d}}_i\right)\}$ 6:    Apply sensor artifacts: $${\mathcal{P}}_k\leftarrow {\mathcal{P}}_k\setminus \left\{\mathbf{p}\right|\angle ({\mathbf{n}}_{\mathbf{p}},{\mathbf{v}}_{\mathrm{ray}})>{\theta }_{\max }\}$$ (33) 7: end for

3. Results

To comprehensively evaluate the proposed two-stage point cloud registration framework, we conducted systematic experiments under varying motion dynamics and sensing conditions.

3.1. Dataset

This study utilized 3D models of eight NASA spacecraft obtained from official NASA repositories: Aura (Earth Observing System spacecraft built by Northrop Grumman, Redondo Beach, CA, USA); Chandra X-ray Observatory (space telescope built by Northrop Grumman, Redondo Beach, CA, USA, operated by Smithsonian Astrophysical Observatory, Cambridge, MA, USA); Deep Space 1 (technology demonstrator spacecraft built by Jet Propulsion Laboratory, Pasadena, CA, USA); ICESat-2 (Ice, Cloud and land Elevation Satellite-2 with ATLAS instrument developed by NASA Goddard Space Flight Center, Greenbelt, MD, USA; spacecraft bus by Northrop Grumman, Gilbert, AZ, USA); Jason-1 (oceanography satellite built by Thales Alenia Space, Cannes, France for CNES, and Jet Propulsion Laboratory, Pasadena, CA, USA for NASA); Juno (Jupiter orbiter built by Lockheed Martin Space, Denver, CO, USA, operated by Jet Propulsion Laboratory, Pasadena, CA, USA); MESSENGER (Mercury orbiter built by Johns Hopkins University Applied Physics Laboratory, Laurel, MD, USA); TOPEX/Poseidon (oceanography satellite built by Fairchild Industries, Germantown, MD, USA with NASA instruments by Jet Propulsion Laboratory, Pasadena, CA, USA). All digital models were sourced from NASA’s publicly available 3D model repositories [36], covering diverse configurations including satellites, orbital transfer vehicles, and exploration probes. Each model is converted into watertight meshes with triangle counts ranging from 50 K to 200 K faces. Each model has 10 sequences, where each sequence contained 150 frames rendered with the algorithm in Section 2.4. Four examples of the simulated normal maps of various spacecraft are illustrated in Figure 3. For pose trajectory simulation, the initial transformation is randomly sampled from 6D pose space and the incremental Euler angle and translation along each axis are randomly increased within $[0.5^{\circ },2.0^{\circ }]$ and [−50 cm, 50 cm] for subsequent frames, generating challenging trajectories with sudden maneuvers and introducing discontinuous jumps in angular and positional velocity.

3.2. Evaluation Metrics

To quantitatively assess the performance of feature- and geometry-based point cloud registration algorithms, we adopt three accuracy metrics: Relative Rotation Error (RRE) computes the angular deviation between estimated ${\widehat{\mathbf{R}}}_n$ and ground truth ${\mathbf{R}}_{n,gt}$ rotations:

$$\mathrm{RRE}={\displaystyle \frac{1}{N_{total}}}\sum _{n=1}^{N_{total}}{\displaystyle \frac{180}{\pi }}arccos\left({\displaystyle \frac{\mathrm{tr}\left({\widehat{\mathbf{R}}}_n^{\top }{\mathbf{R}}_{n,\mathrm{gt}}\right)-1}{2}}\right),$$

(34)

where $tr(·)$ denotes the matrix trace. Relative Translation Error (RTE) evaluates Euclidean distance between estimated ${\mathbf{t}}_n$ and ground truth ${\mathbf{t}}_{n,gt}$ translations:

$$\mathrm{RTE}={\displaystyle \frac{1}{N_{total}}}\sum _{n=1}^{N_{total}}{\parallel {\mathbf{t}}_n-{\mathbf{t}}_{\mathrm{n},\mathrm{gt}}\parallel }_2,$$

(35)

where ${\parallel ·\parallel }_2$ represents the Euclidean norm and $N_{total}=12,000$ is the total number of all tested frames. The transformation Root Mean Squared Error (RMSE) measures the Euclidean distance error between the transformed source point cloud and target point cloud:

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{|{\mathcal{C}}^{*}|}}\sum _{(p_{x_i}^{*},q_{y_i}^{*})\in {\mathcal{C}}^{*}}{∥\mathbf{T}\circ p_{x_i}^{*}-q_{y_i}^{*}∥}_2^2},$$

(36)

where $\mathbf{T}$ is the predicted transformation and $C^{*}$ are the ground truth correspondences.

3.3. Implementation Details

All experiments are carried out on an Intel i9-9900K CPU at 3.7 GHZ. We use C++ and PCL library to implement the proposed algorithm. The voxel size s is set to 2.5, 5.0, 7.5, and 10 cm, respectively, for experiments on efficiency and accuracy. All spacecraft models are scaled into a cube with 3 m edge length and placed at 3 m to 10 m in front of the virtual ToF camera. The intrinsic parameters of principal point for ToF imaging are the center of the image with a resolution of $512\times 512$, and the focal length is set to 525.

3.4. Comparison to Other Methods

3.4.1. Quantitative Comparison

We compare our method with several state-of-the-art pose estimation methods, including four representative traditional methods ICP [14], NDT [37], LSG-CPD [38], RobustICP [16], and two recent learning-based methods, i.e., IDAM [39] and RPM-Net [40]. We use zero-mean Gaussian noise with standard deviation $\sigma$ = 2 cm to simulate the real noise level. The experimental results, as summarized in

Table 1. Comparison results with relative rotation and translation error metrics. The best results are highlighted in bold, and the second-best are underlined.

Sequences	ICP		NDT		LSG-CPD		RobustICP		IDAM		RPM-Net		Ours
	RRE	RTE	RRE	RTE	RRE	RTE	RRE	RTE	RRE	RTE	RRE	RTE	RRE	RTE
Aura	6.76	28.21	8.01	31.28	0.89	8.01	3.37	17.37	1.21	10.29	1.14	11.45	1.07	13.17
Chandra	7.87	26.09	7.17	31.77	3.00	12.78	3.23	7.96	1.96	15.63	1.99	10.26	2.02	4.10
DeepSpace	18.37	97.30	23.60	113.96	2.58	10.01	3.27	28.71	3.45	11.78	3.01	9.23	1.66	9.13
ICESat-2	9.14	42.57	12.91	68.36	1.31	9.06	5.40	15.22	2.05	8.89	1.57	8.87	2.37	12.70
Jason-1	3.27	13.62	3.59	12.24	2.62	8.78	8.99	5.98	2.78	12.45	2.26	7.25	4.08	7.55
Juno	6.30	30.16	2.68	32.86	1.00	14.32	2.55	9.37	2.51	13.69	1.75	10.23	0.52	10.40
Messenger	7.78	27.33	8.16	32.14	2.09	4.53	2.80	16.25	1.92	5.01	1.88	11.47	1.78	5.68
Topex	32.33	26.84	19.95	28.48	2.55	7.54	4.00	8.59	2.66	7.88	3.24	8.01	1.71	4.79
Average	11.48	36.52	10.76	43.87	2.01	9.38	4.20	13.68	2.32	10.70	2.10	9.59	1.90	8.44

, demonstrate the effectiveness of the proposed dual-stage framework compared to state-of-the-art registration methods across various spacecraft sequences. On average, our method achieves the lowest rotation error (RRE: 1.90∘) and translation error (RTE: 8.44 cm), outperforming traditional approaches like ICP (RRE: 11.48°, RTE: 36.52 cm) and NDT (RRE: 10.76°, RTE: 43.87 cm), as well as recent learning-based methods such as IDAM (RRE: 2.32°, RTE: 10.70 cm) and RPM-Net (RRE: 2.10°, RTE: 9.59 cm). Notably, our framework excels in scenarios with aggressive motion, as evidenced by its superior performance on the DeepSpace sequence (RRE: 1.66°, RTE: 9.13 cm) and Chandra sequence (RTE: 4.10 cm), where fast inter-frame displacements challenge conventional algorithms. While LSG-CPD and RPM-Net exhibit competitive accuracy in certain cases (e.g., Aura and Messenger), our method maintains consistent robustness across all sequences, particularly under large positional shifts. The geometry-aware refinement stage contributes significantly to error reduction, as shown by the lower RTE in critical cases like Topex (4.79 cm vs. LSG-CPD’s 7.54 and RobustICP’s 8.59 cm). These results validate the dual-stage architecture’s ability to balance coarse-to-fine registration, effectively mitigating error accumulation from rapid motion while ensuring high precision—a critical requirement for autonomous spacecraft operations.

3.4.2. Robustness to Noise

To evaluate our method’s resilience to sensor imperfections, we inject zero-mean Gaussian noise with standard deviations ranging from $\sigma =1$ to 5 cm (relative to original point cloud coordinates) into the test sequences. As shown in

Table 2. Comparison results with different levels of noise. The best results are highlighted in bold, and the second-best are underlined.

Sequences	ICP		NDT		LSG-CPD		RobustICP		IDAM		RPM-Net		Ours
	RRE	RTE	RRE	RTE	RRE	RTE	RRE	RTE	RRE	RTE	RRE	RTE	RRE	RTE
$\sigma$ = 1 cm	11.89	48.92	10.07	28.51	1.44	6.31	3.04	10.61	2.20	9.58	1.58	9.22	1.76	8.02
$\sigma$ = 2 cm	11.48	36.52	10.76	43.89	2.01	9.38	4.20	13.68	2.32	10.70	2.10	9.59	1.90	8.44
$\sigma$ = 3 cm	9.21	39.37	8.55	37.45	2.76	13.02	4.99	15.88	3.14	12.23	3.00	11.05	2.48	9.54
$\sigma$ = 4 cm	9.86	34.17	8.41	39.12	3.26	13.85	5.83	16.47	5.98	14.69	4.97	12.89	1.85	8.93
$\sigma$ = 5 cm	11.02	44.86	9.29	44.51	5.07	18.46	7.82	18.60	7.23	17.85	6.27	15.61	3.14	12.24
Average	10.69	40.77	9.41	38.70	2.91	12.20	5.18	15.05	4.17	13.01	3.58	11.67	2.23	9.43

, the proposed method demonstrates remarkable robustness against varying levels of sensor noise, outperforming both traditional and deep learned registration techniques. Across all noise levels ($\sigma =1$ to 5 cm), our approach achieves the lowest average rotation error (RRE: 2.23°) and translation error (RTE: 9.43 cm), significantly surpassing traditional methods like ICP (RRE: 10.69°, RTE: 40.77 cm) and NDT (RRE: 9.41°, RTE: 38.70 cm). Notably, under severe noise conditions ($\sigma$ = 5 cm), our method maintains superior performance with RRE and RTE values of 3.14° and 12.24 cm, respectively—outperforming even learning-based methods such as RPM-Net (RRE: 6.27°, RTE: 15.61 cm) and IDAM (RRE: 7.23°, RTE: 17.85 cm). The dual-stage architecture, combining coarse feature-based alignment with geometry-aware refinement effectively mitigates noise interference, as evidenced by the minimal error escalation ($\Delta$ RRE: 1.38°, $\Delta$ RTE: 4.22 cm), as noise increases from $\sigma$ = 1 cm to 5 cm. In contrast, methods like LSG-CPD and RobustICP exhibit sharper error degradation (e.g., LSG-CPD’s RTE rises from 6.31 cm to 18.46 cm). The results highlight the framework’s resilience to noise, attributed to its multi-scale iterative refinement that prioritizes geometric consistency over raw descriptor matching. This capability is critical for real-world spacecraft operations, where sensor measurements are inherently noisy, and precise pose estimation under uncertainty remains paramount.

3.4.3. Qualitative Results

The quantitative advantages of our method are further corroborated through visual comparisons under varying noise levels. Heavy Sensor Noise: As shown in Figure 4, our method maintains precise alignment even under severe noise ($\sigma$ = 5 cm). The two-stage architecture successfully preserves structural contours through its outlier rejection module, enabling correct identification of solar panel edges obscured by noise. Rapid Spinning Motion: The third row of Figure 4 illustrates trajectory estimations during high-speed rotation. Our method closely follows the ground truth (blue) through effective outlier rejection and model fitting in the coarse stage and multiscale iterative framework in fine registration. Complex Geometric Structures: The last row of Figure 4 demonstrates our superiority in handling spacecraft with intricate components. Our feature-aware matching correctly associates asymmetric protrusions through effective coarse matching to align docking ports with antenna masts successfully. These visual results confirm that our method simultaneously addresses three critical challenges in spaceborne perception: noise resilience through hierarchical filtering, motion robustness via predictive alignment, and structural awareness via discriminative feature matching.

3.5. Ablation Study

To validate our architectural design, we conduct ablation studies comparing three variants: (1) coarse-only using initial alignment without refinement, (2) fine-only without initialization, and (3) full coarse-to-fine approach. Quantitative results are shown in

Table 3. Ablation study on registration components. The best results are highlighted in bold.

Configuration	RRE (°)		RTE (cm)
	Mean	Std	Mean	Std
Coarse-only	5.32	1.15	12.87	2.42
Fine-only	8.71	2.63	14.25	3.38
Full (Ours)	1.90	0.73	8.44	1.02

. In addition, the effectiveness of the coarse stage for addressing the limitation of FPFH and how our method improve the inlier ratio is discussed; the results are presented in Figure 5.

We conducted experiments to evaluate the limitations of the coarse-only method using FPFH features and demonstrate the effectiveness of our proposed efficient outlier rejection strategy. The results, as shown in Figure 5, highlight significant improvements in inlier ratio (IR) after applying our method, particularly in scenarios with repetitive structures (e.g., solar panels) that inherently generate high outlier ratios. Several conclusions can be reached: Outlier Rejection in Repetitive Structures: In the second row, the solar panel region initially exhibited a large number of false matches due to its repetitive geometry. Our outlier rejection method successfully eliminated nearly all outliers, improving the IR by nearly 10× (e.g., from 7.70% to 76.00% in the fourth column). Robustness to Extreme Outliers: The first five rows show initial IRs below 10%, validating our method’s capability to handle scenarios with severe outlier contamination. Post-rejection, the IRs consistently exceeded 50%, with the highest reaching 87% (sixth row, fourth column). Impact of Survival Matches: Columns 2–4 illustrate IRs under varying survival match counts (1000, 500, 100). As the number of survival matches decreases, the IR progressively increases, demonstrating that our method efficiently prioritizes high-quality correspondences. For instance, in the sixth row, reducing survival matches from 1000 to 100 improved the IR from 13.44% to 87.00% (6.47× enhancement). In summary, the substantial IR improvements directly address the computational inefficiency of RANSAC in high-outlier regimes. By reducing outlier proportions, our method minimizes the required RANSAC iterations, thereby enhancing both computational efficiency and registration accuracy. These results underscore the practicality of our approach for real-world applications involving complex geometries and aggressive motion.

Several key conclusions can be drawn from the analysis: Coarse-stage Limitations: The coarse-only variant achieves moderate accuracy (5.32°) but suffers from residual alignment errors, particularly in handling symmetric structures where multiple plausible solutions exist. Fine-stage Sensitivity: The fine-only implementation demonstrates severe performance degradation (8.71°), with higher probability trapped in local minima due to poor initialization. This confirms our hypothesis that traditional optimization-based refinement cannot compensate for inadequate initial guesses in noncooperative scenarios. Synergy Analysis: The full pipeline reduces errors by 64.3% (rotation) and 34.4% (translation) compared to the best individual component, proving the necessity of our hierarchical design. The coarse stage provides initialization within the convergence basin (avg. initial error < 5.32°), enabling the robustness and accuracy in fine stage. This study verifies that neither component alone suffices for space-grade precision, while their integration creates complementary advantages: the learning-based coarse stage ensures global convergence, and the optimization-based fine stage guarantees physical plausibility.

To further validate the necessity and effectiveness of our proposed coarse-to-fine two-stage registration framework, we conduct ablation experiments under challenging scenarios with large inter-frame motions. Specifically, the source and target point clouds are sampled from sequential frames with increasing temporal intervals (10, 20, 30, 40, 50), where larger intervals correspond to rapid relative motions. As shown in Figure 6, directly applying fine registration without a robust initial pose estimation fails to converge to the global optimum, as the algorithm becomes trapped in local minima due to the substantial misalignment. In contrast, our coarse registration stage reliably provides a near-optimal initial transformation for intervals up to 40, achieving successful alignment even under severe pose discrepancies. This coarse alignment effectively narrows the search space for the subsequent fine registration stage, enabling iterative refinement to further minimize the registration error. Notably, when the interval exceeds 50, the motion magnitude surpasses the coarse stage’s capability, highlighting the practical bounds of our method. These experiments confirm that the coarse-to-fine pipeline is critical for handling large motions, balancing robustness and accuracy in spacecraft pose estimation tasks.

3.6. Runtime Performance Analysis

The computational-accuracy trade-off of our point cloud registration pipeline is systematically evaluated through voxel size variations, as summarized in

Table 4. Performance analysis under varying voxel sizes.

	RRE (°)	RTE (cm)	Time (ms)
s = 2.5 cm	1.49	7.22	179
s = 5 cm	1.90	8.44	99
s = 7.5 cm	2.45	12.25	88
s = 10 cm	4.23	15.78	67

. The qualitative results are presented in Figure 7. Three distinct operational regimes emerge from this analysis. High-Precision Mode (2.5 cm): Achieves sub-1.5° angular accuracy at the cost of computational intensity (179 ms/frame), suitable for critical docking phases requiring millimeter-level precision. Balanced Mode (5 cm): Maintains 1.9°/8.44 cm accuracy while keeping processing time below 100 ms, striking an optimal balance for most orbital servicing tasks. This configuration satisfies the 10 Hz update rate required by standard spaceborne computers. Real-Time Mode (10 cm): Enables 15FPS performance (67 ms/frame) through aggressive downsampling, demonstrating potential for rapid motion tracking despite increased errors (4.23°/15.78 cm). This analysis confirms our method’s adaptability to mission requirements—from precision-oriented operations to time-critical tracking scenarios.

4. Discussion

The proposed two-stage point cloud registration framework demonstrates strong potential for spacecraft pose estimation under challenging conditions such as rapid inter-frame motion and sensor noise. By combining a feature-based coarse alignment with a geometry-aware fine refinement, the method effectively balances robustness, accuracy, and computational efficiency. A key strength of this approach lies in its ability to circumvent the local minima issue commonly faced by traditional ICP-based optimization methods. The introduction of a length-invariant outlier rejection strategy significantly improves correspondence quality prior to RANSAC, resulting in a more reliable coarse pose initialization. This initialization serves as a strong prior for the subsequent fine registration stage, which leverages multi-scale iterative refinement to ensure precision even in cases with large initial misalignments. Another notable advantage is the framework’s suitability for real-time deployment on resource-constrained spacecraft systems. Unlike deep learning-based methods, which often require extensive training data and substantial inference resources, the proposed method is entirely training-free and exhibits deterministic performance. This makes it a practical choice for onboard processing where computational budgets and data availability are limited. The robustness of the method under sensor noise and motion dynamics has been extensively validated using a synthetically generated benchmark dataset. However, a potential limitation is that the simulation-based dataset, while diverse and realistic, may not capture all physical complexities of actual on-orbit environments, such as unmodeled reflectance properties or unexpected occlusions. Additionally, although the current framework excels in rigid registration scenarios, handling deformable or articulated spacecraft components remains an open challenge. In future work, we plan to extend the method’s applicability to more complex real-world datasets and consider integration with visual-inertial fusion frameworks. Furthermore, incorporating uncertainty modeling or confidence estimation into the registration pipeline may enhance robustness in ambiguous or degenerate cases.

5. Conclusions

In this work, we present a robust two-stage framework for spacecraft pose estimation tailored to address challenges posed by rapid inter-frame motion. By integrating FPFH-based coarse registration with RANSAC and a geometry-aware multi-scale fine registration stage, the proposed method effectively handles large positional displacements while achieving high precision. Experimental validation using simulated ToF sensor data derived from NASA spacecraft models demonstrates the framework’s superiority in accuracy and robustness over existing approaches, particularly under aggressive orbital maneuvers. The architecture’s ability to mitigate error accumulation from fast relative motion and maintain tracking continuity highlights its potential for real-world autonomous spacecraft proximity operations. This work advances the state of the art in pose estimation by balancing computational efficiency with registration fidelity, offering a promising solution for dynamic space missions requiring reliable and real-time navigation capabilities.