Sensing Lunar Dust Density Using Radio Science Signals of Opportunity
Abstract
1. Introduction
2. Lunar RO
3. Lunar Dust Density Estimate and Uncertainty
4. Results and Discussion
4.1. GRAIL RO Frequency Residual
4.2. GRAIL RO Electron Density
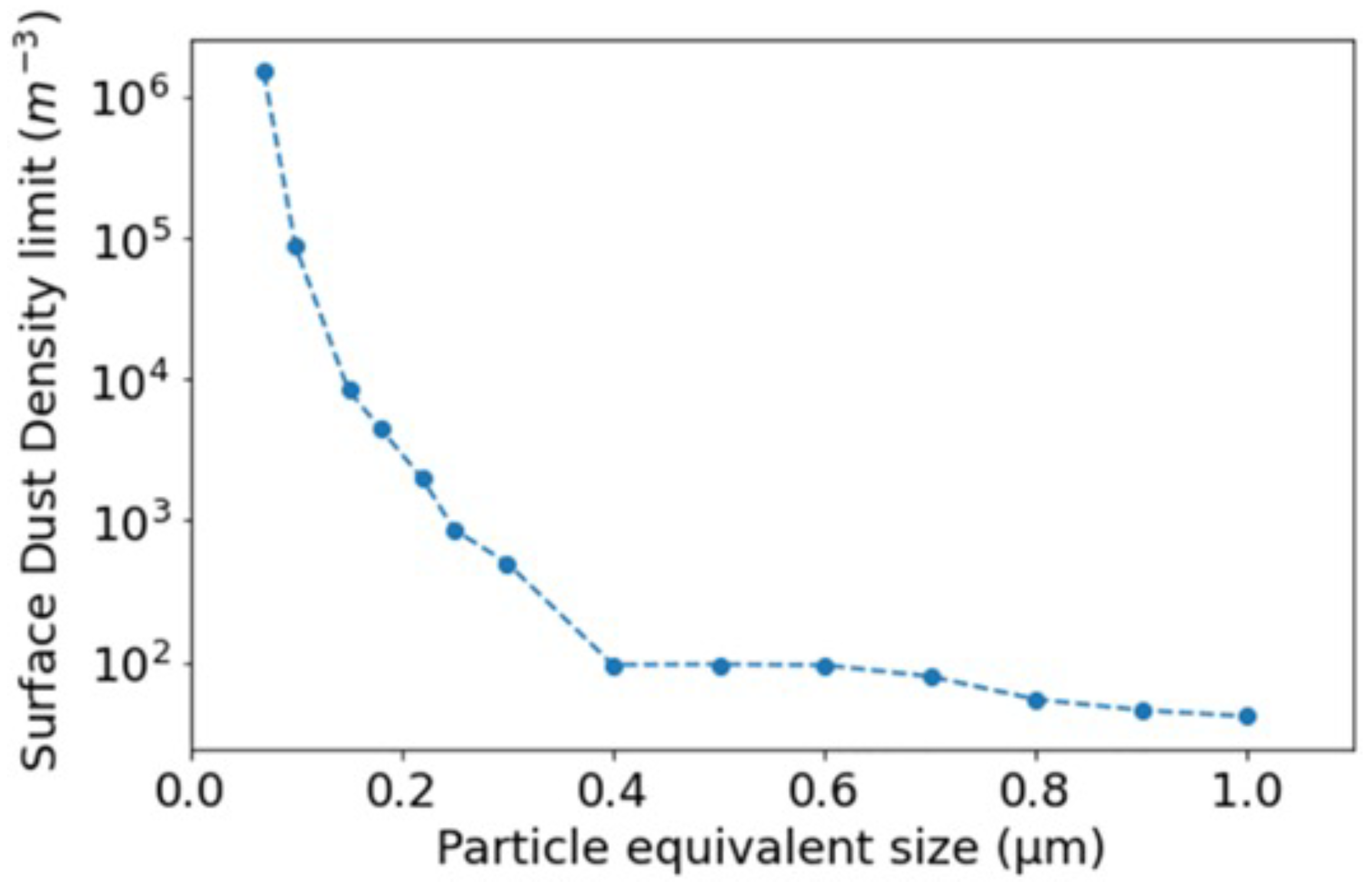
4.3. GRAIL RO Dust Density Profile Estimate
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Criswell, D.R. Horizon-Glow and the Motion of Lunar Dust. In Proceedings of the Photon and Particle Interactions with Surfaces in Space; Grard, R.J.L., Ed.; Astrophysics and Space Science Library. Springer: Dordrecht, The Netherlands, 1973; Volume 37, p. 545. [Google Scholar] [CrossRef]
- Rennilson, J.J.; Criswell, D.R. Surveyor Observations of Lunar Horizon-Glow. Moon 1974, 10, 121–142. [Google Scholar] [CrossRef]
- Glenar, D.A.; Stubbs, T.J.; McCoy, J.E.; Vondrak, R.R. A reanalysis of the Apollo light scattering observations, and implications for lunar exospheric dust. Planet. Space Sci. 2011, 59, 1695–1707. [Google Scholar] [CrossRef]
- Horányi, M.; Szalay, J.R.; Kempf, S.; Schmidt, J.; Grün, E.; Srama, R.; Sternovsky, Z. A permanent, asymmetric dust cloud around the Moon. Nature 2015, 522, 324–326. [Google Scholar] [CrossRef] [PubMed]
- Sharma, H.; Hedman, M.M.; Wooden, D.H.; Colaprete, A.; Cook, A.M. Constraining Low-Altitude Lunar Dust Using the LADEE-UVS Data. J. Geophys. Res. Planets 2021, 126, e2021JE006935. [Google Scholar] [CrossRef]
- Stubbs, T.; Glenar, D.; Farrell, W.; Vondrak, R.; Collier, M.; Halekas, J.; Delory, G. On the role of dust in the lunar ionosphere. Planet. Space Sci. 2011, 59, 1659–1664. [Google Scholar] [CrossRef]
- Reasoner, D.L.; Burke, W.J. Direct observation of the lunar photoelectron layer. Lunar Planet. Sci. Conf. Proc. 1972, 3, 2639. [Google Scholar]
- Vyshlov, A.S.; Savich, N.A.; Vasilyev, M.B.; Samoznaev, L.N.; Sidorenko, A.I.; Shtern, D.Y. Some results of cislunar plasma research. In NASA Special Publication; NASA: Washington, DC, USA, 1976; Volume 397, pp. 81–85. [Google Scholar]
- Imamura, T.; Nabatov, A.; Mochizuki, N.; Iwata, T.; Hanada, H.; Matsumoto, K.; Noda, H.; Kono, Y.; Liu, Q.; Futaana, Y.; et al. Radio occultation measurement of the electron density near the lunar surface using a subsatellite on the SELENE mission. J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef]
- Choudhary, R.K.; Ambili, K.M.; Choudhury, S.; Dhanya, M.B.; Bhardwaj, A. On the origin of the ionosphere at the Moon using results from Chandrayaan-1 S band radio occultation experiment and a photochemical model. Geophys. Res. Lett. 2016, 43, 10025–10033. [Google Scholar] [CrossRef]
- Tripathi, K.R.; Choudhary, R.K.; Ambili, K.M.; Bindu, K.R.; Manikantan, R.; Parikh, U. A study on the characteristic features of the lunar ionosphere using dual frequency radio science (DFRS) experiment onboard Chandrayaan-2 orbiter. Mon. Not. R. Astron. Soc. Lett. 2022, 515, L61–L66. [Google Scholar] [CrossRef]
- Dalba, P.A.; Withers, P. Cassini Radio Occultation Observations of Titan’s Ionosphere: The Complete Set of Electron Density Profiles. J. Geophys. Res. Space Phys. 2019, 124, 643–660. [Google Scholar] [CrossRef]
- Ambili, K.M.; Choudhary, R.K. Three-dimensional distribution of ions and electrons in the lunar ionosphere originated from the photochemical reactions. Mon. Not. R. Astron. Soc. 2021, 510, 3291–3300. [Google Scholar] [CrossRef]
- Xie, L.; Zhang, X.; Li, L.; Zhou, B.; Zhang, Y.; Yan, Q.; Feng, Y.; Guo, D.; Yu, S. Lunar Dust Fountain Observed Near Twilight Craters. Geophys. Res. Lett. 2020, 47, e2020GL089593. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, J.; Lin, Y.; Wei, Y.; Li, L.; Zhang, X.; Lin, H.; Xie, L. Key Questions of Solar Wind–Moon Interaction. Space Sci. Technol. 2023, 3, 0060. [Google Scholar] [CrossRef]
- Phipps, P.H.; Withers, P. Radio occultations of the Io plasma torus by Juno are feasible. J. Geophys. Res. Space Phys. 2017, 122, 1731–1750. [Google Scholar] [CrossRef]
- Withers, P.; Stubbs, T.; Mazarico, E. A theoretical assessment of the feasibility of potential Lunar Reconnaissance Orbiter radio occultation observations of the lunar ionosphere. Adv. Space Res. 2021, 67, 4099–4109. [Google Scholar] [CrossRef]
- Wang, J.; He, X.; Cao, Y. Modeling Electrostatic Levitation of Dust Particles on Lunar Surface. IEEE Trans. Plasma Sci. 2008, 36, 2459–2466. [Google Scholar] [CrossRef]
- Yeo, L.H.; Wang, X.; Deca, J.; Hsu, H.W.; Horányi, M. Dynamics of electrostatically lofted dust on airless planetary bodies. Icarus 2021, 366, 114519. [Google Scholar] [CrossRef]
- Wang, X.; Schwan, J.; Hsu, H.W.; Grün, E.; Horányi, M. Dust charging and transport on airless planetary bodies. Geophys. Res. Lett. 2016, 43, 6103–6110. [Google Scholar] [CrossRef]
- Schwan, J.; Wang, X.; Hsu, H.W.; Grün, E.; Horányi, M. The charge state of electrostatically transported dust on regolith surfaces. Geophys. Res. Lett. 2017, 44, 3059–3065. [Google Scholar] [CrossRef]
- Dove, A.; Horányi, M.; Robertson, S.; Wang, X. Laboratory investigation of the effect of surface roughness on photoemission from surfaces in space. Planet. Space Sci. 2018, 156, 92–95. [Google Scholar] [CrossRef]
- Hood, N.; Carroll, A.; Mike, R.; Wang, X.; Schwan, J.; Hsu, H.W.; Horányi, M. Laboratory Investigation of Rate of Electrostatic Dust Lofting Over Time on Airless Planetary Bodies. Geophys. Res. Lett. 2018, 45, 13206–13212. [Google Scholar] [CrossRef]
- Orger, N.C.; Toyoda, K.; Masui, H.; Cho, M. Experimental investigation on silica dust lofting due to charging within micro-cavities and surface electric field in the vacuum chamber. Adv. Space Res. 2019, 63, 3270–3288. [Google Scholar] [CrossRef]
- Carroll, A.; Hood, N.; Mike, R.; Wang, X.; Hsu, H.W.; Horányi, M. Laboratory measurements of initial launch velocities of electrostatically lofted dust on airless planetary bodies. Icarus 2020, 352, 113972. [Google Scholar] [CrossRef]
- Örger, N.; Cordova Alarcon, J.R.; Toyoda, K.; Cho, M. Lunar Surface Charging and Electrostatic Lofting of Lunar Dust Particles under Different Solar Wind Conditions and Solar Ultraviolet Radiation. In Proceedings of the 13th Space Environment Symposium, Tokyo, Japan, 1–2 November 2016. [Google Scholar]
- Orger, N.C.; Cordova Alarcon, J.R.; Toyoda, K.; Cho, M. Lunar dust lofting due to surface electric field and charging within Micro-cavities between dust grains above the terminator region. Adv. Space Res. 2018, 62, 896–911. [Google Scholar] [CrossRef]
- Yang, Y.M.; Oudrhiri, K.; Withers, P.; Erwin, D.A.; Buccino, D.R.; Haha, I. Investigating Lunar Ionosphere Using GRAIL Radio Science Signals. In Proceedings of the 2024 EGU General Assembly Conference Abstracts, Vienna, Austria, 14–19 April 2024; p. 12526. [Google Scholar] [CrossRef]








| Spacecraft | Radio Frequency | RO Period | Uncertainty | Uncertainty |
|---|---|---|---|---|
| Chandrayaan-1 | S-band | 2009 July | el/m3 | (0.1 m) |
| SELENE | S- and X-band | 2008–2009 | el/m3 | (0.1 m) |
| GRAIL | X-band | 2012 | el/m3 | (0.1 m) |
| Chandrayaan-2 | S- and Ka-band | 2019–2021 | el/m3 | (0.1 m) |
| LRO | S-band | Still active | el/m3 | (0.1 m) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oudrhiri, K.; Yang, Y.-M.; Erwin, D. Sensing Lunar Dust Density Using Radio Science Signals of Opportunity. Remote Sens. 2025, 17, 1940. https://doi.org/10.3390/rs17111940
Oudrhiri K, Yang Y-M, Erwin D. Sensing Lunar Dust Density Using Radio Science Signals of Opportunity. Remote Sensing. 2025; 17(11):1940. https://doi.org/10.3390/rs17111940
Chicago/Turabian StyleOudrhiri, Kamal, Yu-Ming Yang, and Daniel Erwin. 2025. "Sensing Lunar Dust Density Using Radio Science Signals of Opportunity" Remote Sensing 17, no. 11: 1940. https://doi.org/10.3390/rs17111940
APA StyleOudrhiri, K., Yang, Y.-M., & Erwin, D. (2025). Sensing Lunar Dust Density Using Radio Science Signals of Opportunity. Remote Sensing, 17(11), 1940. https://doi.org/10.3390/rs17111940






