SeqConv-Net: A Deep Learning Segmentation Framework for Airborne LiDAR Point Clouds Based on Spatially Ordered Sequences
Abstract
1. Introduction
1.1. Related Work
1.1.1. Traditional Segmentation Methods
1.1.2. Deep Learning-Based Methods
1.2. Motivations
1.3. Contributions
- (1).
- Spatially Ordered Sequence Perspective: We innovatively propose the idea of spatially ordered sequences, where different elevation points at the same planar position can be viewed as a sequence from low to high, with the sequence values containing elevation information. This operates point cloud semantic segmentation as a sequence generation task of the same length, providing a new way to process point cloud data.
- (2).
- SeqConv-Net Point Cloud Semantic Segmentation Architecture: Based on the spatially ordered sequence perspective, we design an RNN+CNN point cloud semantic segmentation architecture called SeqConv-Net and innovatively use RNN hidden states as CNN inputs to fuse planar spatial information.
- (3).
- Construction and Validation of SeqConv-Net: We design the first network based on the SeqConv-Net architecture and validate its feasibility. Experiments show that our SeqConv-Net design is not only efficient and reliable but also interpretable. Compared to previous methods, it significantly improves the speed of point cloud semantic segmentation in large scenes while maintaining accuracy.
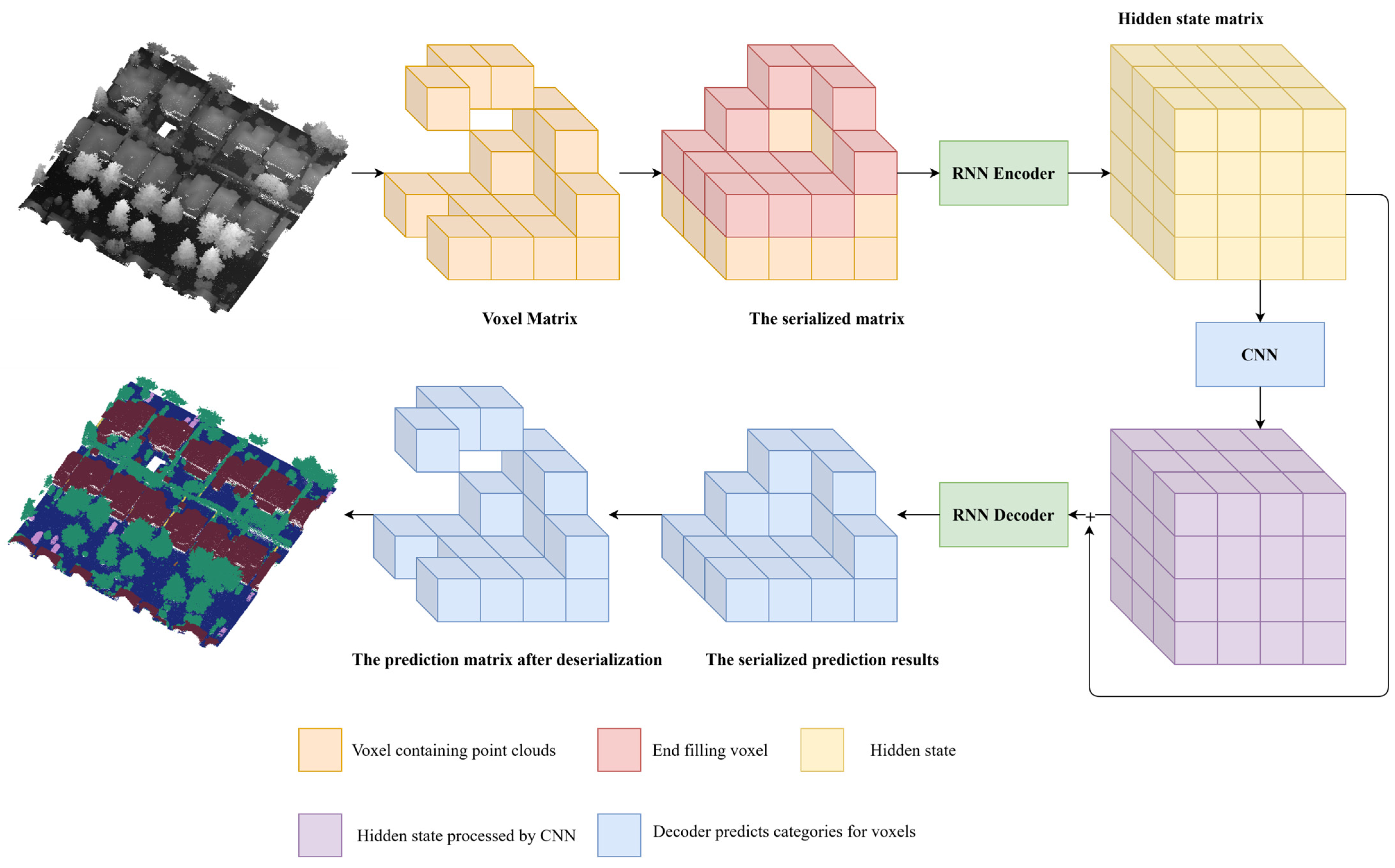
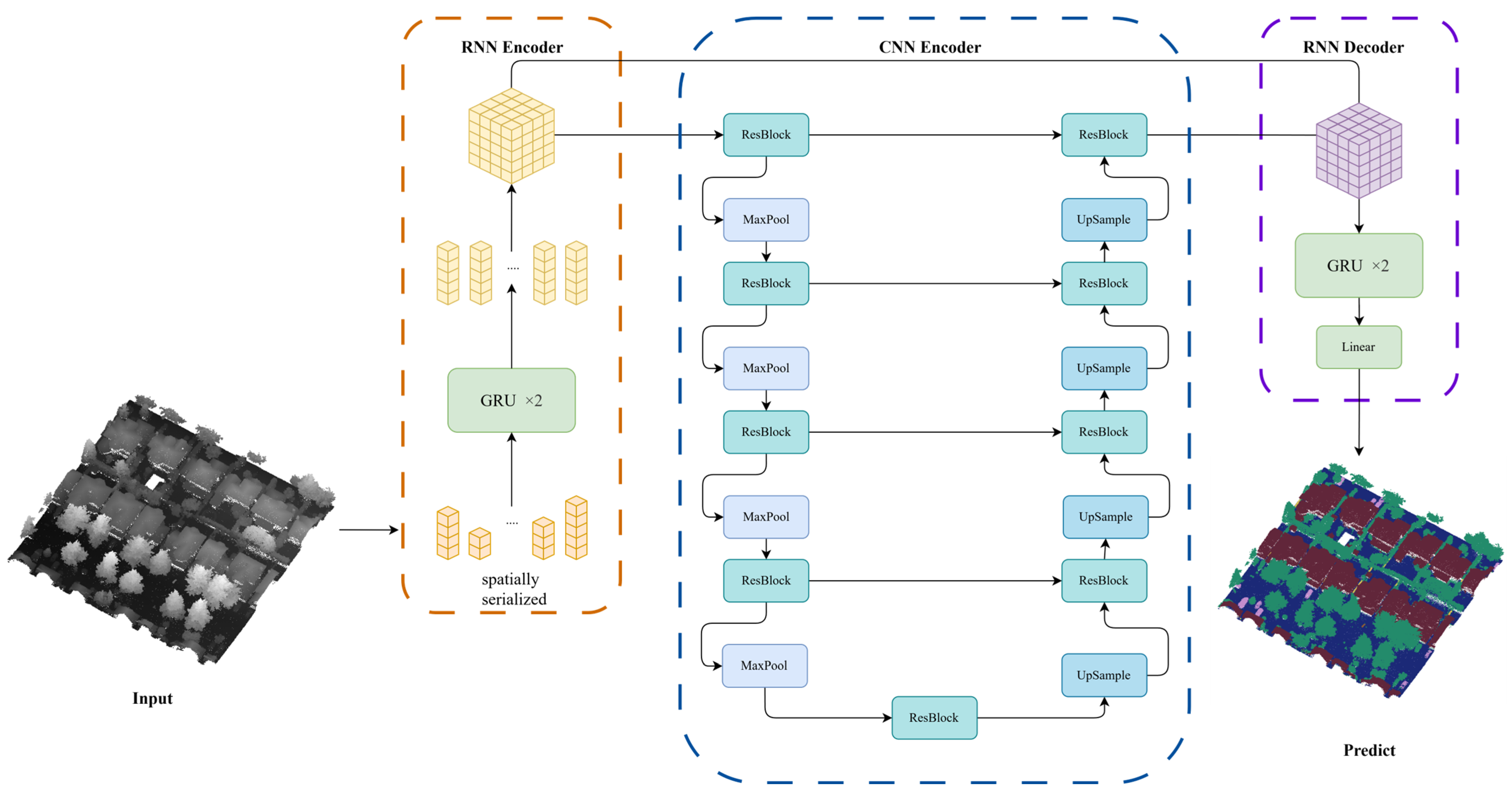
2. Point Cloud Semantic Segmentation Framework
2.1. Architecture Overview
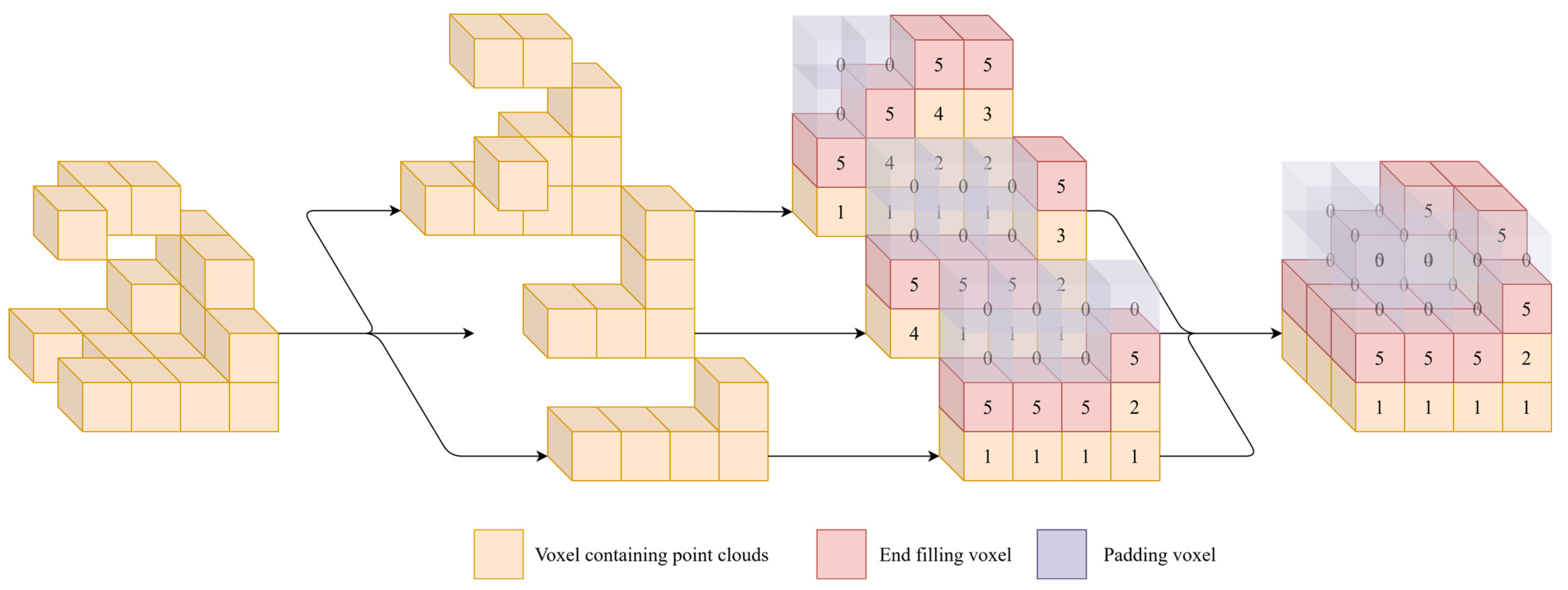
2.2. Spatially Ordered Sequences
2.2.1. The Concept of Spatially Ordered Sequences
- (1).
- Avoids issues with absolute elevation: Traditional methods using elevation coordinates may face inconsistencies or computational complexity due to variations in elevation range or noise. Using indices as elevation representations converts elevation information into relative positional relationships, avoiding instability caused by absolute elevation values and enhancing model robustness.
- (2).
- Fast generation of spatially related sequences: The index-based elevation representation allows for accelerated sequence generation using sorting algorithms. By sorting the sequence and using the indices of valid positions as input, spatial sequences can be quickly generated. This serialized representation facilitates efficient computer processing and significantly reduces preprocessing time compared to methods like KNN, especially for large-scale point cloud data.
- (3).
- Utilizes NLP embedding methods: By using integer indices as elevation representations, we can leverage embedding techniques from NLP, mapping indices to high-dimensional vector spaces for computation. This embedding representation captures relationships between elevations and provides richer feature representations for deep learning models, enhancing their expressive power.
- (4).
- Efficient voxel-to-point cloud recovery: During prediction, the network can sequentially output predictions for each valid position and use the indices to restore the correspondence between predictions and original voxels. This recovery process is computationally efficient and does not introduce additional losses.
2.2.2. Generation Algorithm for Spatially Ordered Sequences
2.2.3. Differences Between Spatially Ordered Sequences and NLP Sequences
2.3. Spatial Information Processing
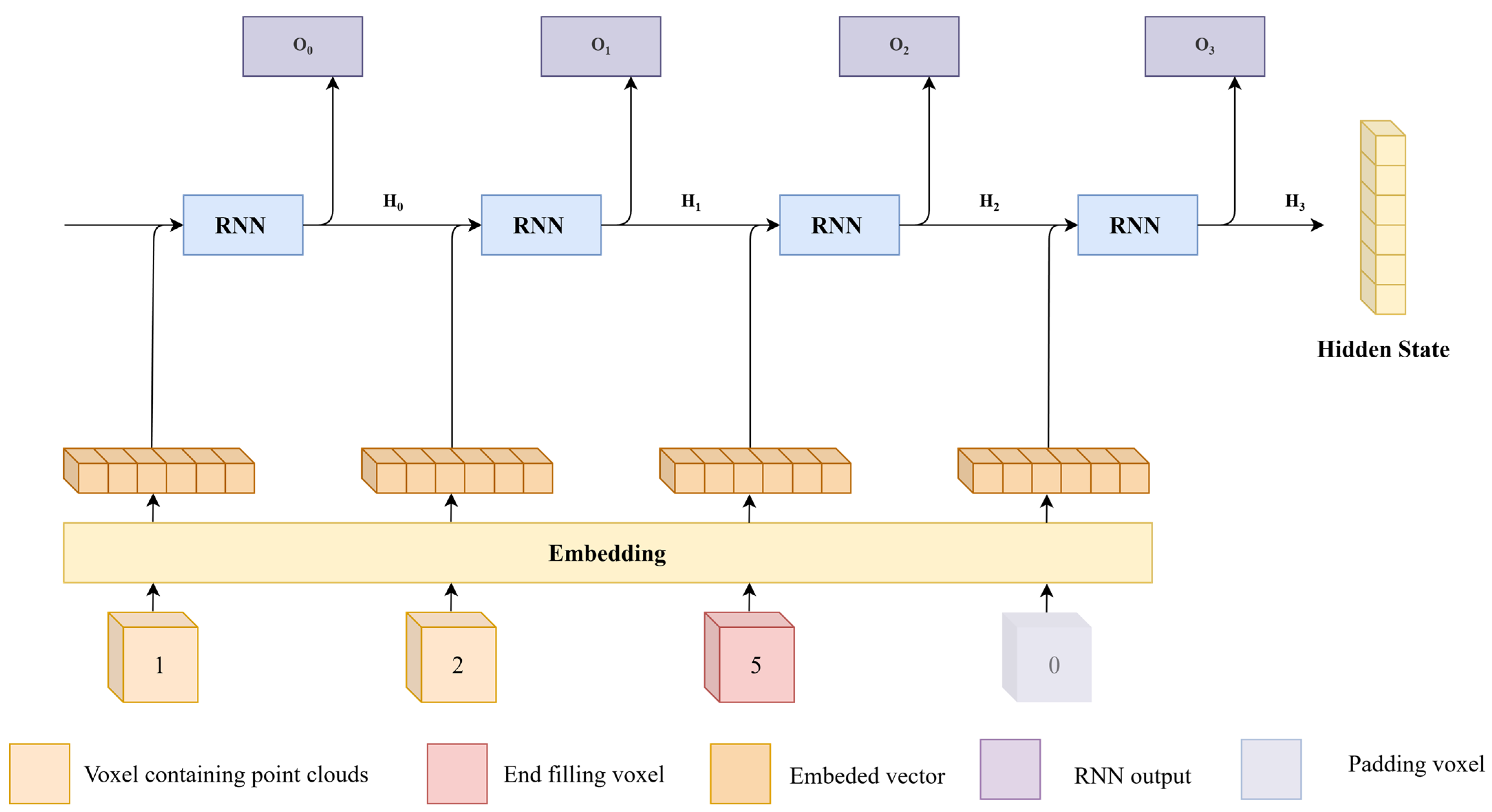
2.3.1. Elevation Information Extraction Using RNNs
2.3.2. Planar Information Fusion and Extraction Using CNNs
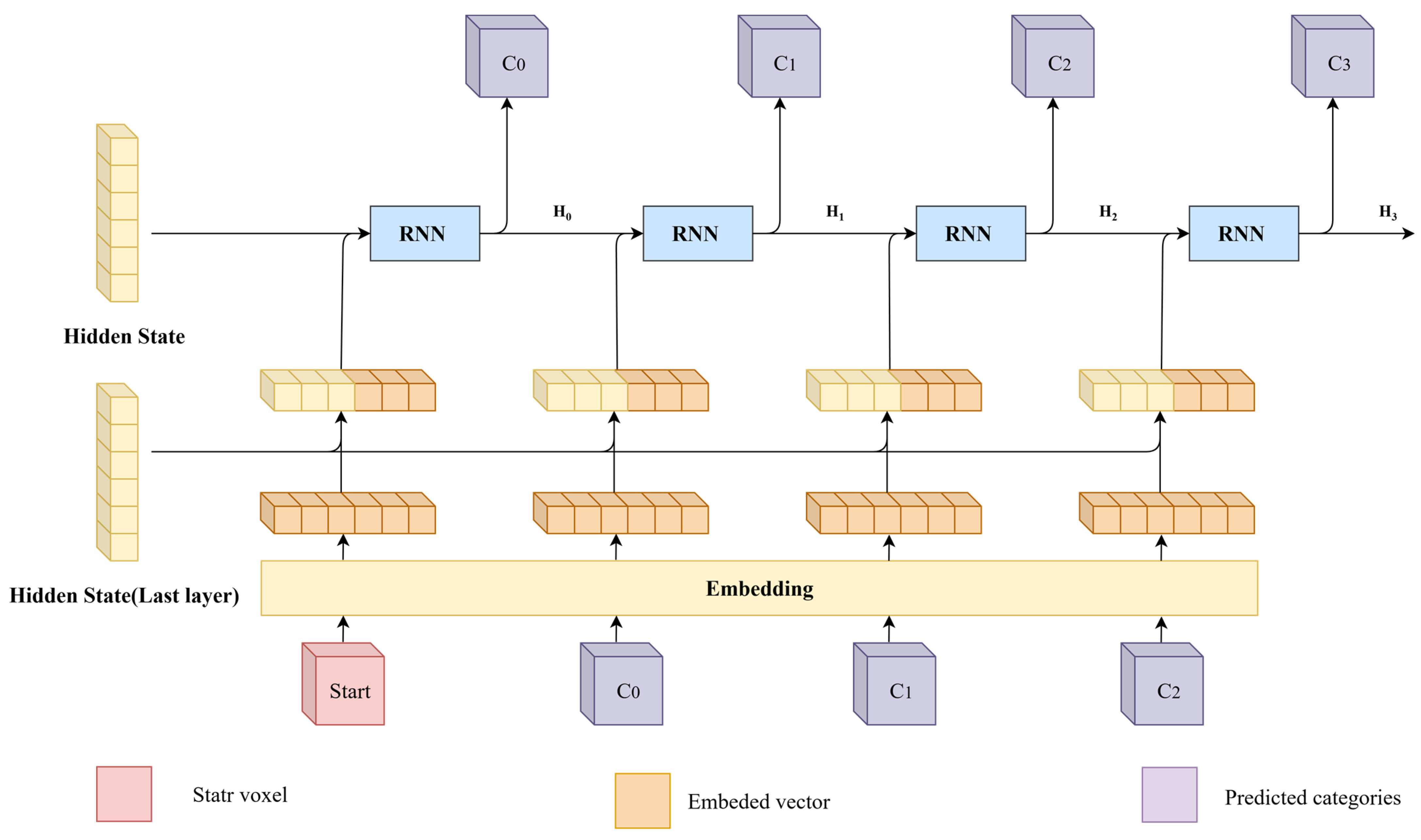
2.3.3. Prediction
3. Experimental Results and Analysis
3.1. Data Preprocessing and Augmentation
3.1.1. Sequence Loss
- (1).
- From the global accuracy perspective, even at the maximum resolution of one meter, the model’s mIOU remains at 0.93.
- (2).
- The impact of serialization on object classification accuracy is within an acceptable range, and higher resolutions lead to greater serialization loss.
- (3).
- The accuracy differences between different object classes are mainly due to their inherent geometric features and spatial distribution characteristics, rather than the serialization process itself.
3.1.2. Elevation Truncation
3.2. Experiments
3.2.1. Network Structure
3.2.2. Elevation Embedding
3.2.3. Implementation Details and Evaluation Metrics
3.2.4. Results
3.3. Ablation Studies
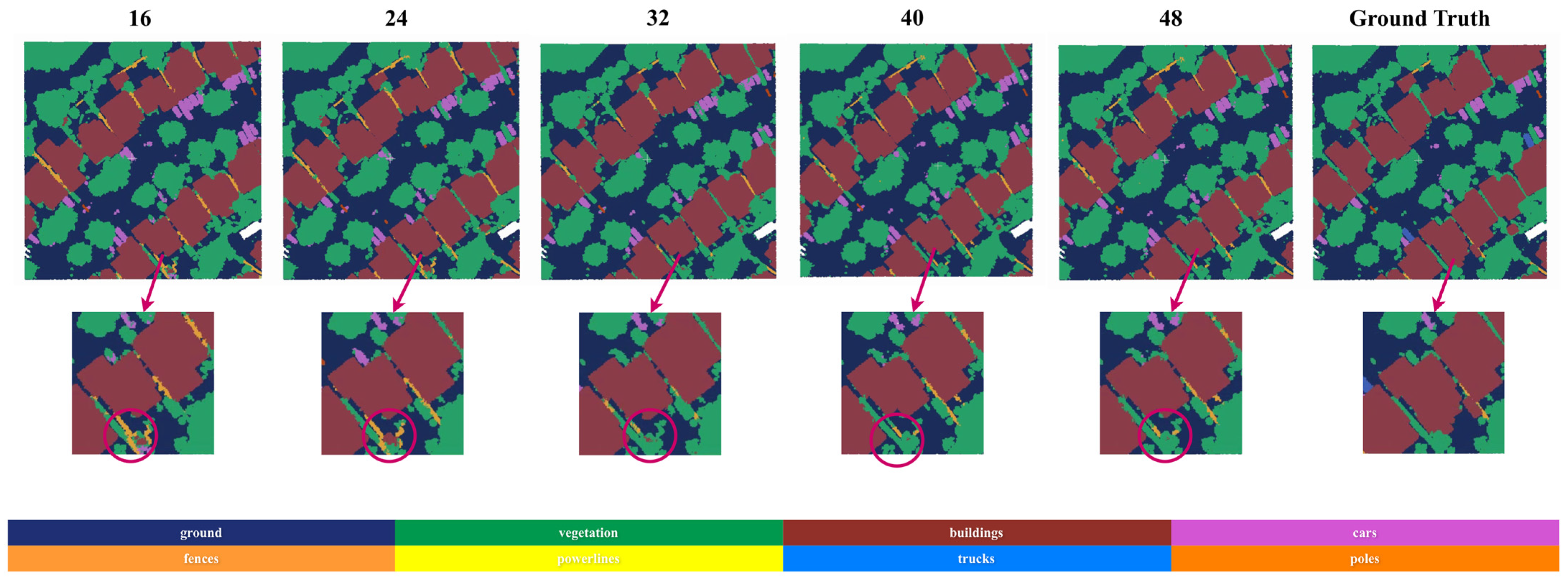
3.3.1. Hidden State Dimension
3.3.2. Spatial Sequence Resolution
3.3.3. Exploring Hidden Variables
- (1).
- The focus of different channels on specific object features indicates that the model does not simply encode elevations but learns spatial information perception through the CNN, which enables the model to learn feature separation methods.
- (2).
- The complementary feature distribution across channels shows that the model achieves effective information decomposition and reorganization, not just simple encoding.
- (3).
- The correspondence between features and the DSM confirms that the hidden variable mapping process has practical physical significance.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef] [PubMed]
- Qi, R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph CNN for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Thomas, H.; Qi, C.R.; Deschaud, J.-E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. KPConv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6411–6420. [Google Scholar]
- Robert, D.; Raguet, H.; Landrieu, L. Efficient 3D semantic segmentation with superpoint transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 17195–17204. [Google Scholar]
- Pauly, M.; Keiser, R.; Gross, M. Multi-scale feature extraction on point-sampled surfaces. Comput. Graph. Forum 2003, 22, 281–289. [Google Scholar] [CrossRef]
- Rabbani, T.; Van Den Heuvel, F.; Vosselmann, G. Segmentation of point clouds using smoothness constraint. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2006, 36, 248–253. [Google Scholar]
- Golovinskiy, A.; Funkhouser, T. Min-cut based segmentation of point clouds. In Proceedings of the IEEE 12th International Conference on Computer Vision Workshops (ICCV Workshops), Kyoto, Japan, 27 September–4 October 2009; pp. 39–46. [Google Scholar]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Papon, J.; Abramov, A.; Schoeler, M.; Worgotter, F. Voxel cloud connectivity segmentation-supervoxels for point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; pp. 2027–2034. [Google Scholar]
- Rusu, R.B.; Marton, Z.C.; Blodow, N.; Dolha, M.E.; Beetz, M. Functional object mapping of kitchen environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Nice, France, 22–26 September 2008; pp. 3525–3532. [Google Scholar]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J. 3D object recognition in cluttered scenes with local surface features: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2270–2287. [Google Scholar] [CrossRef]
- Lai, K.; Bo, L.; Ren, X.; Fox, D. A large-scale hierarchical multi-view RGB-D object dataset. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 1817–1824. [Google Scholar]
- Qi, R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. RandLA-Net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11108–11117. [Google Scholar]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. PointCNN: Convolution on X-transformed points. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar] [CrossRef]
- Boulch, A. ConvPoint: Continuous convolutions for point cloud processing. Comput. Graph. 2020, 88, 24–34. [Google Scholar] [CrossRef]
- Wu, W.; Qi, Z.; Fuxin, L. PointConv: Deep convolutional networks on 3D point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9621–9630. [Google Scholar]
- Wu, B.; Wan, A.; Yue, X.; Keutzer, K. SqueezeSeg: Convolutional neural nets with recurrent CRF for real-time road-object segmentation from 3D LiDAR point cloud. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1887–1893. [Google Scholar]
- Milioto, A.; Vizzo, I.; Behley, J.; Stachniss, C. RangeNet++: Fast and accurate LiDAR semantic segmentation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4213–4220. [Google Scholar]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-view convolutional neural networks for 3D shape recognition. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar]
- Le, T.; Duan, Y. PointGrid: A deep network for 3D shape understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 9204–9214. [Google Scholar]
- Meng, H.Y.; Gao, L.; Lai, Y.K.; Manocha, D. VV-Net: Voxel VAE net with group convolutions for point cloud segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8500–8508. [Google Scholar]
- Graham, B.; Engelcke, M.; Van Der Maaten, L. 3D semantic segmentation with submanifold sparse convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 9224–9232. [Google Scholar]
- Liu, Z.; Tang, H.; Lin, Y.; Han, S. Point-voxel CNN for efficient 3D deep learning. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 16259–16268. [Google Scholar]
- Guo, M.H.; Cai, J.X.; Liu, Z.N.; Mu, T.J.; Martin, R.R.; Hu, S.M. PCT: Point cloud transformer. Comput. Vis. Media 2021, 7, 187–199. [Google Scholar] [CrossRef]
- Akwensi, P.H.; Wang, R.; Guo, B. Preformer: A memory-efficient transformer for point cloud semantic segmentation. Int. J. Appl. Earth Obs. Geoinf. 2024, 128, 103730. [Google Scholar] [CrossRef]
- Liang, D.; Zhou, X.; Xu, W.; Zhu, X.; Zou, Z.; Ye, X.; Tan, X.; Bai, X. PointMamba: A simple state space model for point cloud analysis. arXiv 2024, arXiv:2402.10739. [Google Scholar]
- Zhang, T.; Yuan, H.; Qi, L.; Zhang, J.; Zhou, Q.; Ji, S.; Yan, S.; Li, X. Point Cloud Mamba: Point cloud learning via state space model. arXiv 2024, arXiv:2403.00762. [Google Scholar] [CrossRef]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar] [CrossRef]
- Varney, N.; Asari, V.K.; Graehling, Q. DALES: A large-scale aerial LiDAR data set for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020; pp. 186–187. [Google Scholar]
- Cho, K.; van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention (MICCAI); Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C.D. GloVe: Global vectors for word representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]




| Resolution | Ground | Vegetation | Buildings | Cars | Fences | Powerlines | Trucks | Poles | mIOU |
|---|---|---|---|---|---|---|---|---|---|
| 0.25 | 0.991 | 0.974 | 0.997 | 0.995 | 0.976 | 0.995 | 0.995 | 0.994 | 0.990 |
| 0.5 | 0.978 | 0.936 | 0.994 | 0.983 | 0.926 | 0.986 | 0.983 | 0.981 | 0.971 |
| 1 | 0.956 | 0.886 | 0.985 | 0.934 | 0.815 | 0.962 | 0.951 | 0.952 | 0.930 |
| Truncation | Ground | Vegetation | Cars | Trucks | Powerlines | Fences | Poles | Buildings | mIOU |
|---|---|---|---|---|---|---|---|---|---|
| NO | 0.915 | 0.943 | 0.927 | 0.977 | 0.955 | 0.828 | 0.973 | 0.990 | 0.938 |
| YES | 0.915 | 0.943 | 0.927 | 0.977 | 0.955 | 0.828 | 0.973 | 0.990 | 0.938 |
| Method | Powerline | Low Vegetation | Impervious Surfaces | Car | Fence | Roof | Facade | Shrub | Tree | OA | Speed |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PointNet++ | 57.9 | 79.6 | 90.6 | 66.1 | 31.5 | 91.6 | 54.3 | 41.6 | 77.0 | 65.58 | 24.6 s |
| KPConv | 63.1 | 82.3 | 91.4 | 72.5 | 25.2 | 94.4 | 60.3 | 44.9 | 81.2 | 68.37 | 6.27 s |
| DGCNN | 44.6 | 71.2 | 81.8 | 42.0 | 11.8 | 93.8 | 64.3 | 46.4 | 81.7 | 59.73 | 6.81 s |
| PointCNN | 61.5 | 82.7 | 91.8 | 75.8 | 35.9 | 92.7 | 57.8 | 49.1 | 78.1 | 69.49 | - |
| ConvPoint | 58.8 | 80.9 | 90.7 | 65.9 | 34.3 | 90.3 | 52.4 | 39.1 | 77.0 | 65.49 | - |
| RandLA-Net | 68.8 | 82.1 | 91.3 | 76.6 | 43.8 | 91.1 | 61.9 | 45.2 | 77.4 | 70.91 | 3.2 s |
| Ours | 38.5 | 82.7 | 94.1 | 78.9 | 67.5 | 89.3 | 46.3 | 57.5 | 85.1 | 71.10 | 2.1 s |
| Method | Input Points | mIOU | Speed |
|---|---|---|---|
| PointNet++ | 8192 | 0.683 | 726.6 s |
| KPConv | 8192 | 0.726 | 186.9 s |
| DGCNN | 8192 | 0.665 | 203.2 s |
| PointCNN | 8192 | 0.584 | - |
| ConvPoint | 8192 | 0.674 | - |
| PointTransformer | 8192 | 0.749 | 698.7 s |
| PReFormer | 8192 | 0.709 | - |
| PointMamba | 8192 | 0.733 | 90.7 s |
| PointCloudMamba | 8192 | 0.747 | 115.6 s |
| Ours | - | 0.755 | 8.01 s |
| Ground | Vegetation | Buildings | Cars | Trucks | Poles | Powerlines | Fences | mIOU | Speed | |
|---|---|---|---|---|---|---|---|---|---|---|
| 16 | 0.942 | 0.839 | 0.930 | 0.655 | 0.396 | 0.679 | 0.607 | 0.406 | 0.682 | 4.05 s |
| 24 | 0.950 | 0.851 | 0.931 | 0.685 | 0.412 | 0.681 | 0.658 | 0.453 | 0.702 | 4.26 s |
| 32 | 0.953 | 0.870 | 0.932 | 0.732 | 0.453 | 0.704 | 0.717 | 0.495 | 0.732 | 5.56 s |
| 40 | 0.952 | 0.896 | 0.932 | 0.763 | 0.522 | 0.701 | 0.704 | 0.501 | 0.747 | 6.02 s |
| 48 | 0.964 | 0.919 | 0.934 | 0.751 | 0.532 | 0.706 | 0.724 | 0.511 | 0.755 | 8.01 s |
| Ground | Vegetation | Buildings | Cars | Trucks | Poles | Power Lines | Fences | mIOU | Speed | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.943 | 0.839 | 0.930 | 0.512 | 0.214 | 0.682 | 0.651 | 0.210 | 0.622 | 1.51 s |
| 0.5 | 0.953 | 0.870 | 0.932 | 0.732 | 0.453 | 0.704 | 0.717 | 0.495 | 0.732 | 8.01 s |
| 0.25 | 0.955 | 0.865 | 0.925 | 0.713 | 0.421 | 0.692 | 0.653 | 0.512 | 0.717 | 30.9 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, B.; Yao, C.; Ma, H.; Wang, J.; Xu, J. SeqConv-Net: A Deep Learning Segmentation Framework for Airborne LiDAR Point Clouds Based on Spatially Ordered Sequences. Remote Sens. 2025, 17, 1927. https://doi.org/10.3390/rs17111927
Guo B, Yao C, Ma H, Wang J, Xu J. SeqConv-Net: A Deep Learning Segmentation Framework for Airborne LiDAR Point Clouds Based on Spatially Ordered Sequences. Remote Sensing. 2025; 17(11):1927. https://doi.org/10.3390/rs17111927
Chicago/Turabian StyleGuo, Bin, Chunjing Yao, Hongchao Ma, Jie Wang, and Junhao Xu. 2025. "SeqConv-Net: A Deep Learning Segmentation Framework for Airborne LiDAR Point Clouds Based on Spatially Ordered Sequences" Remote Sensing 17, no. 11: 1927. https://doi.org/10.3390/rs17111927
APA StyleGuo, B., Yao, C., Ma, H., Wang, J., & Xu, J. (2025). SeqConv-Net: A Deep Learning Segmentation Framework for Airborne LiDAR Point Clouds Based on Spatially Ordered Sequences. Remote Sensing, 17(11), 1927. https://doi.org/10.3390/rs17111927






