On-Orbit Performance and Hyperspectral Data Processing of the TIRSAT CubeSat Mission
Abstract
1. Introduction
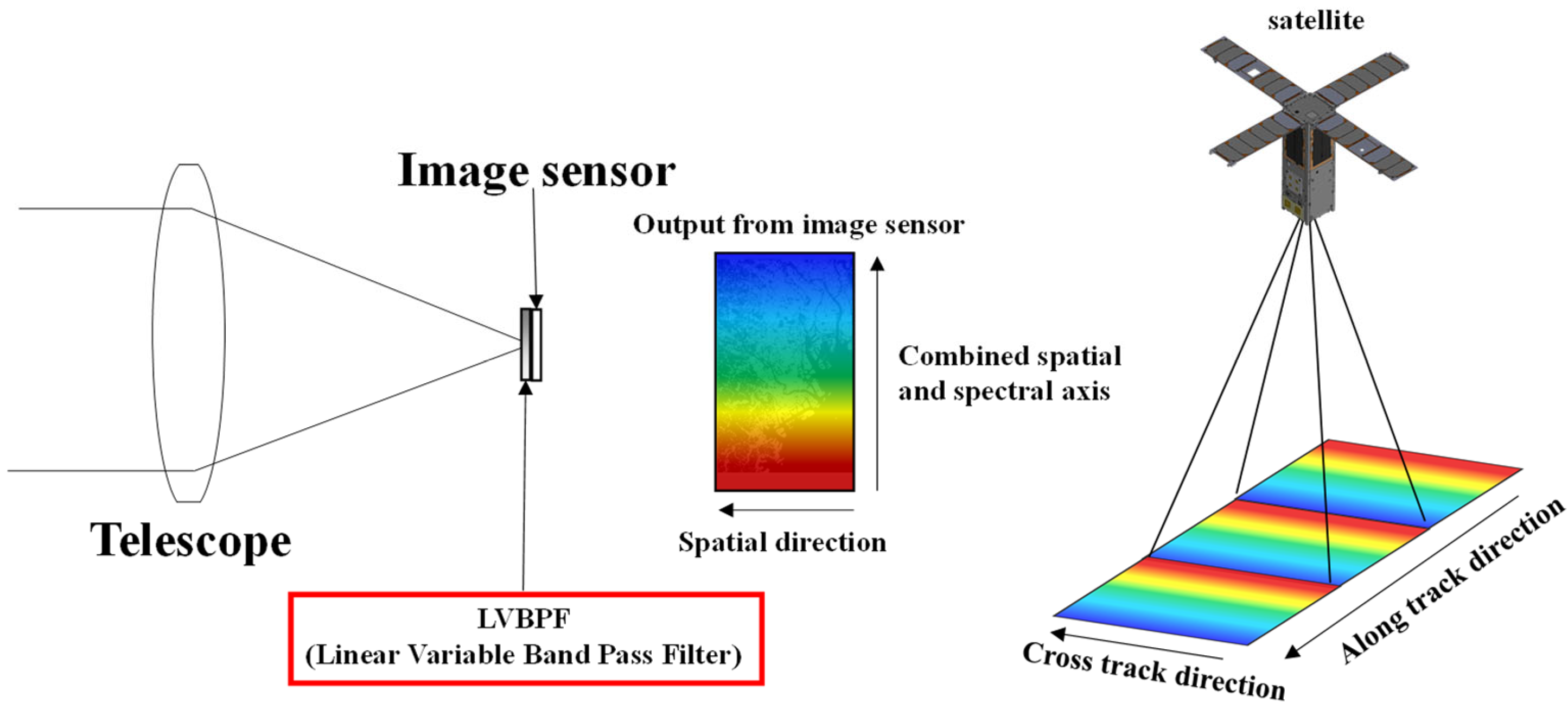
2. Development of a Linear Variable Band-Pass Filter-Based Hyperspectral Camera
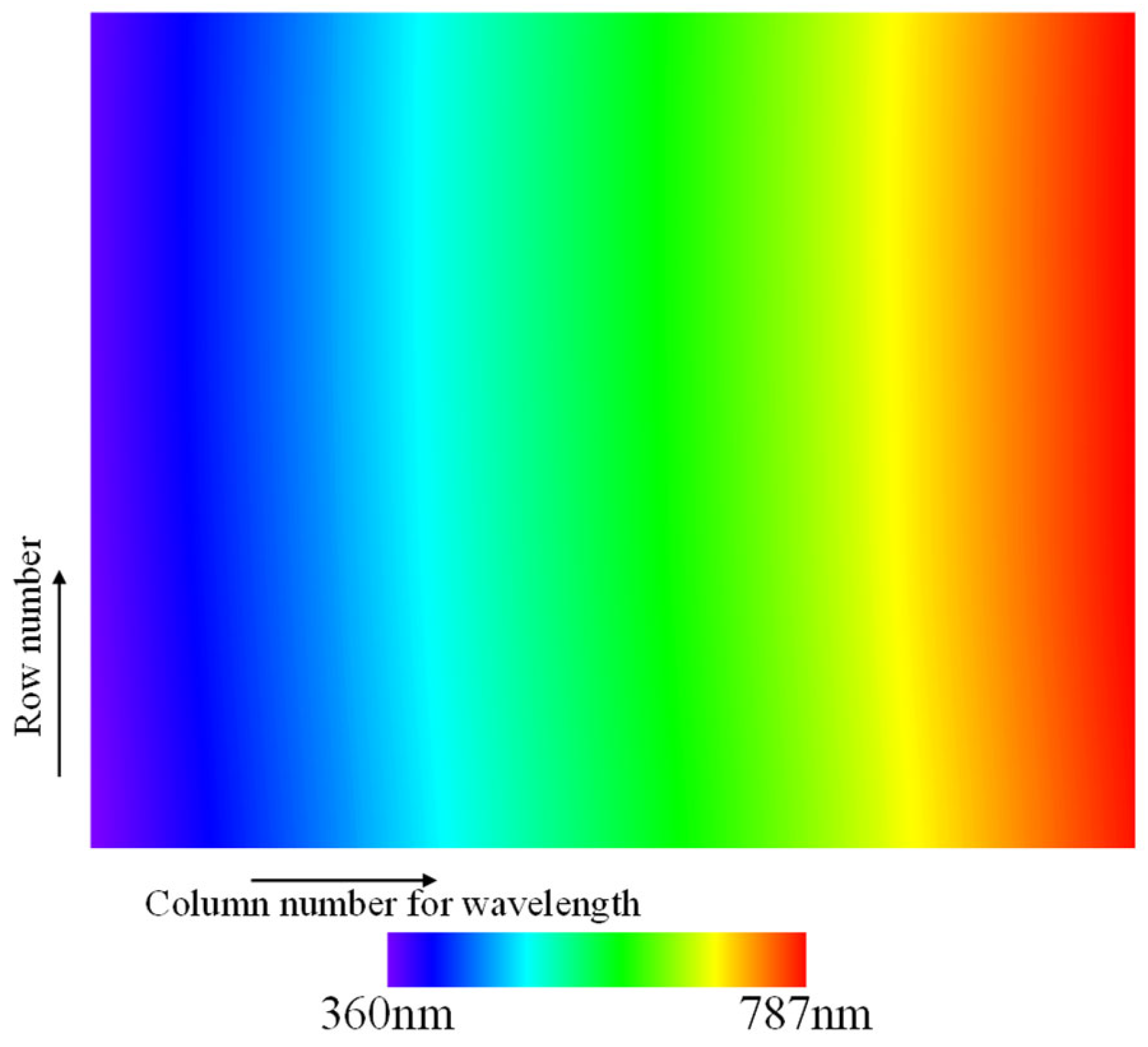
2.1. Observation Method of LVBPF-Based Hyperspectral Camera
2.2. Specification
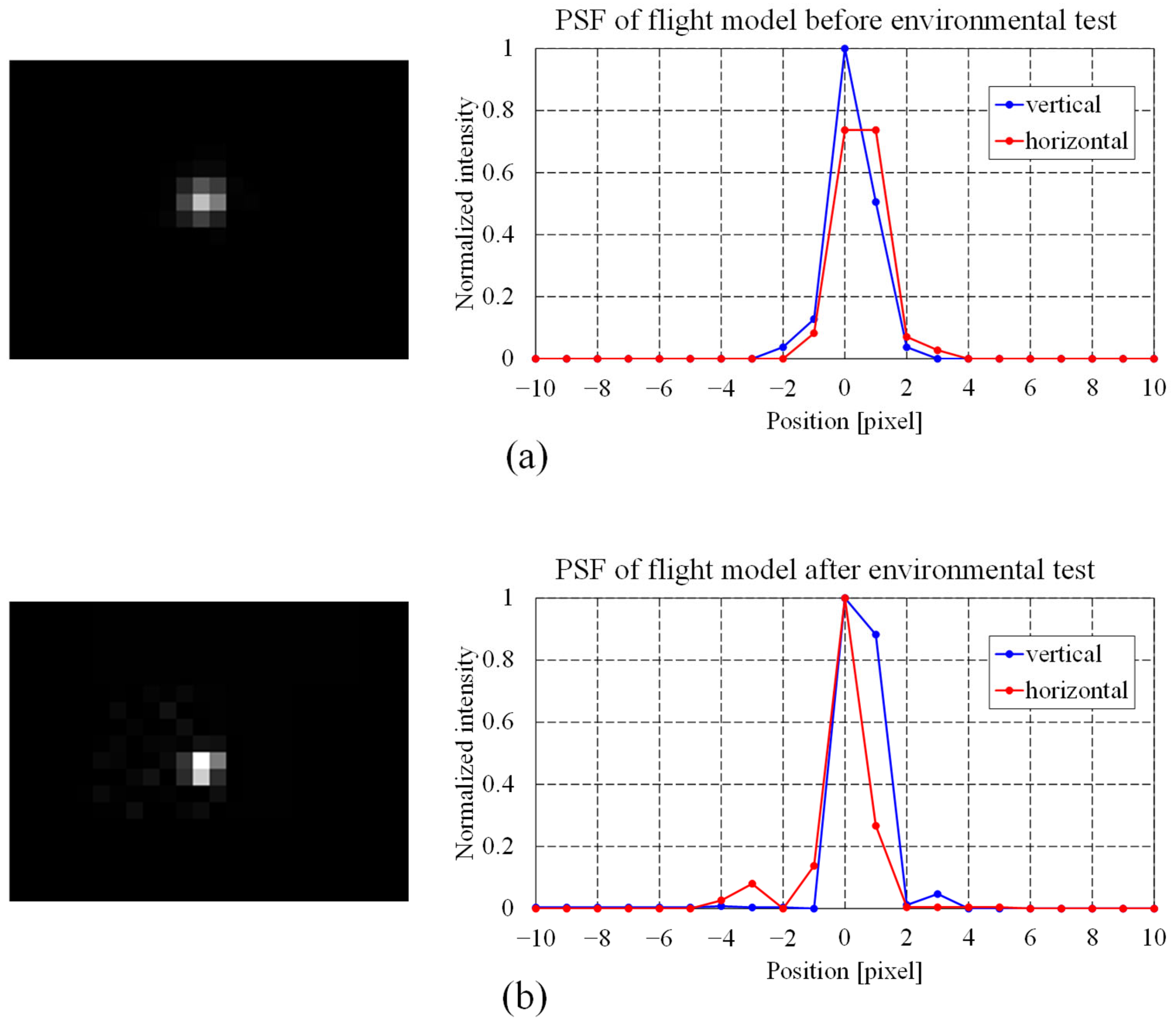
2.3. Pre-Flight Test on Ground
2.3.1. Imaging Performance
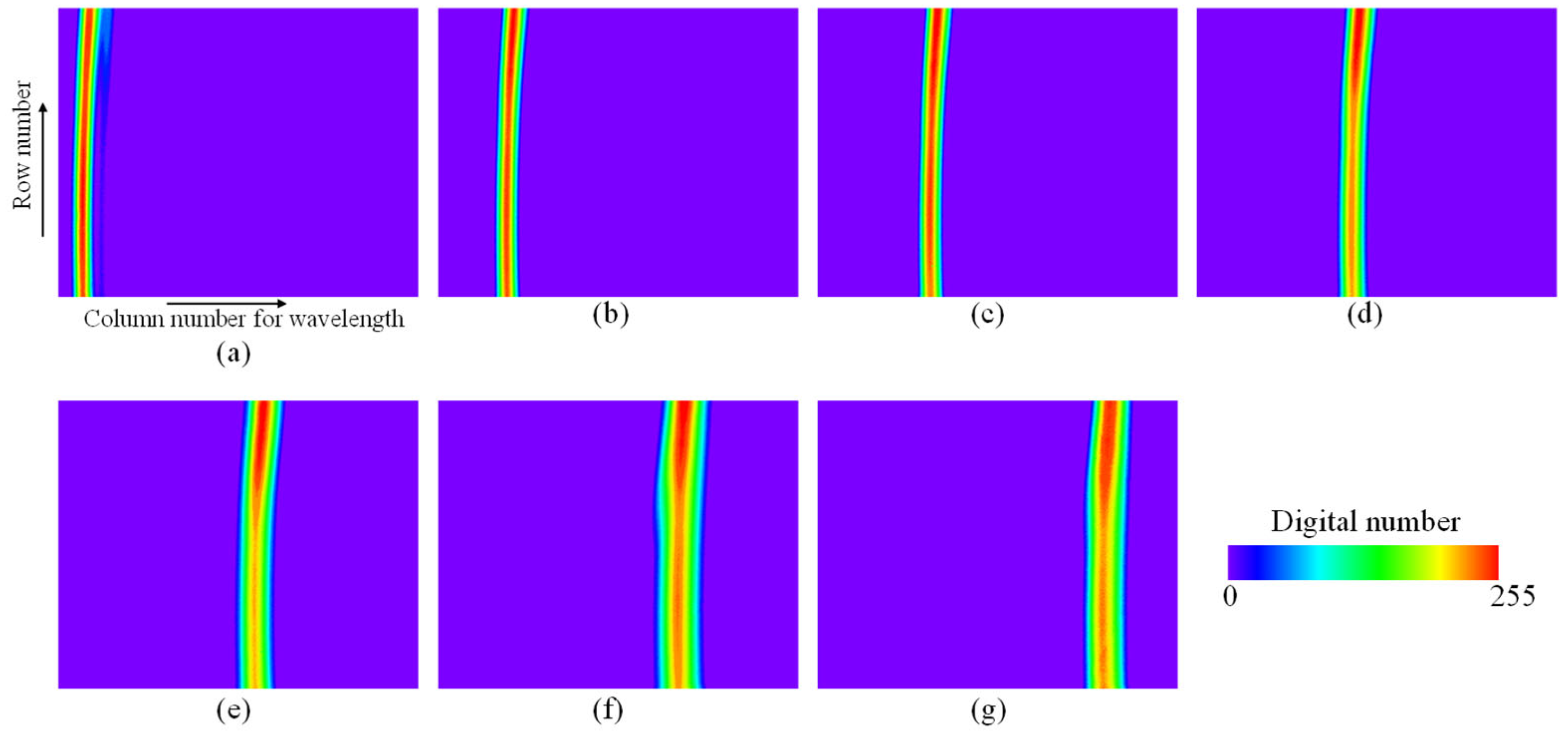
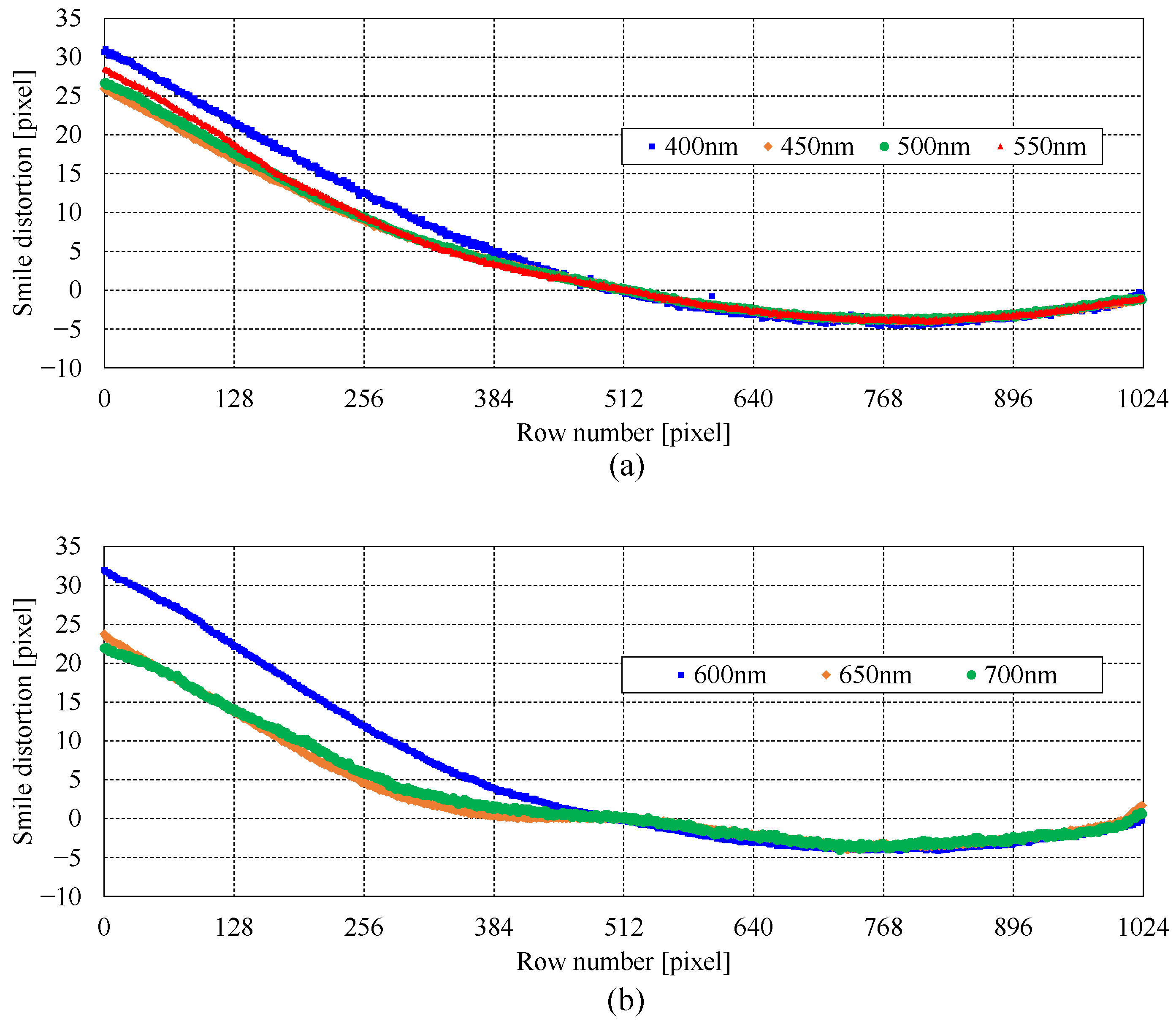
2.3.2. Spectral Calibration
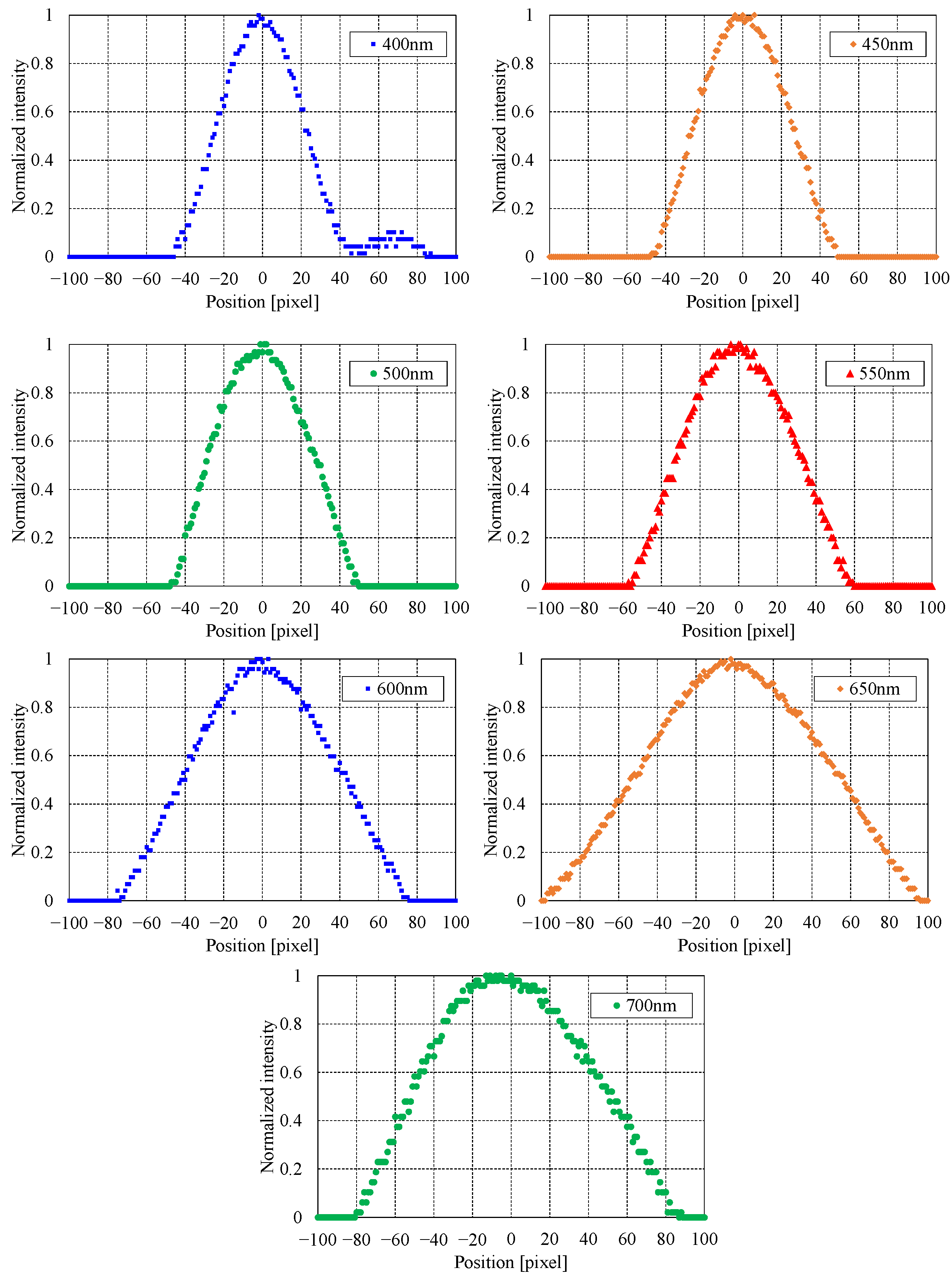
2.3.3. Spectral Performance Measurement
3. Description of Satellite Bus for TIRSAT
3.1. Introduction of TIRSAT
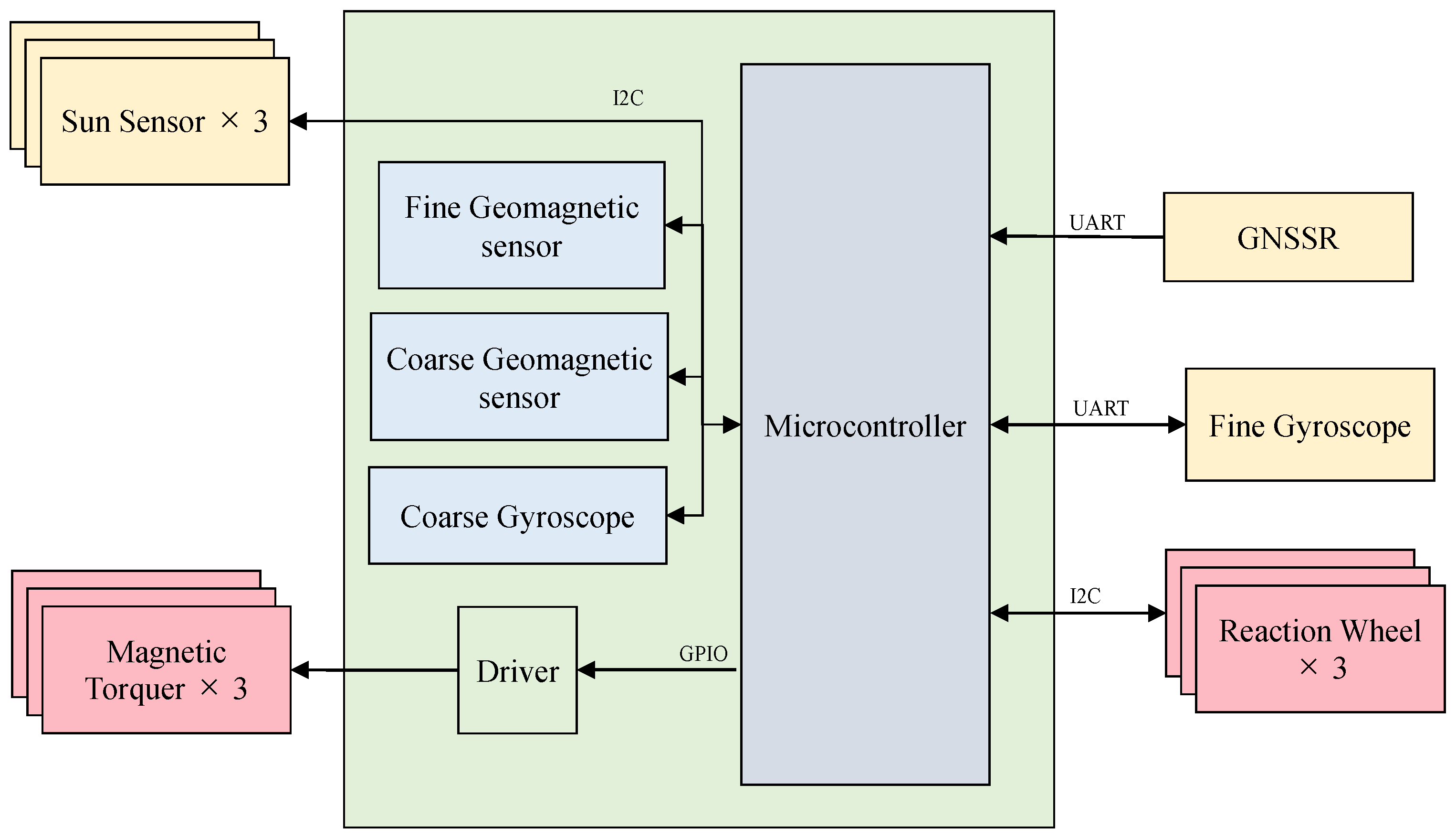
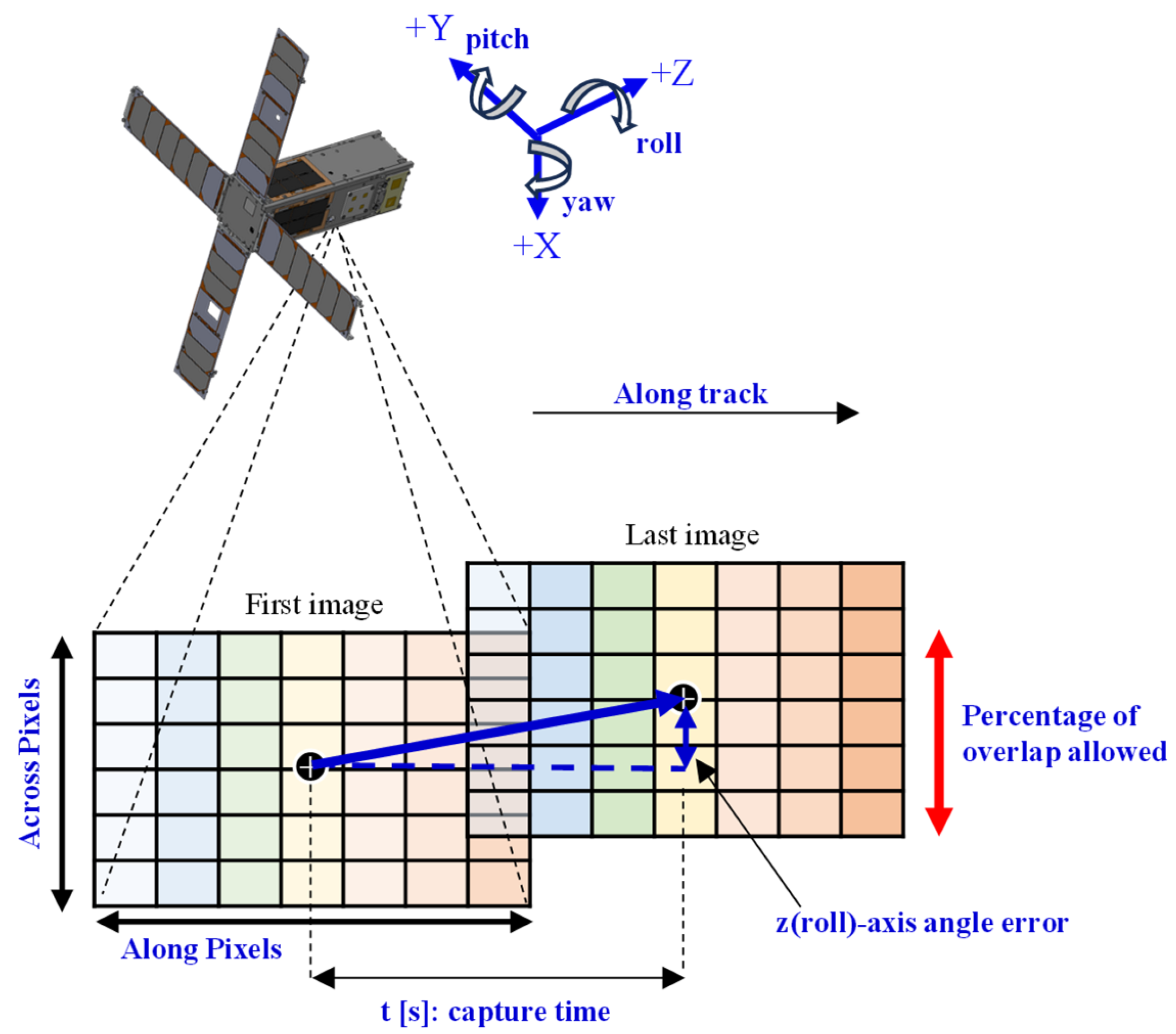
3.2. Attitude Determination and Control Subsystem of TIRSAT
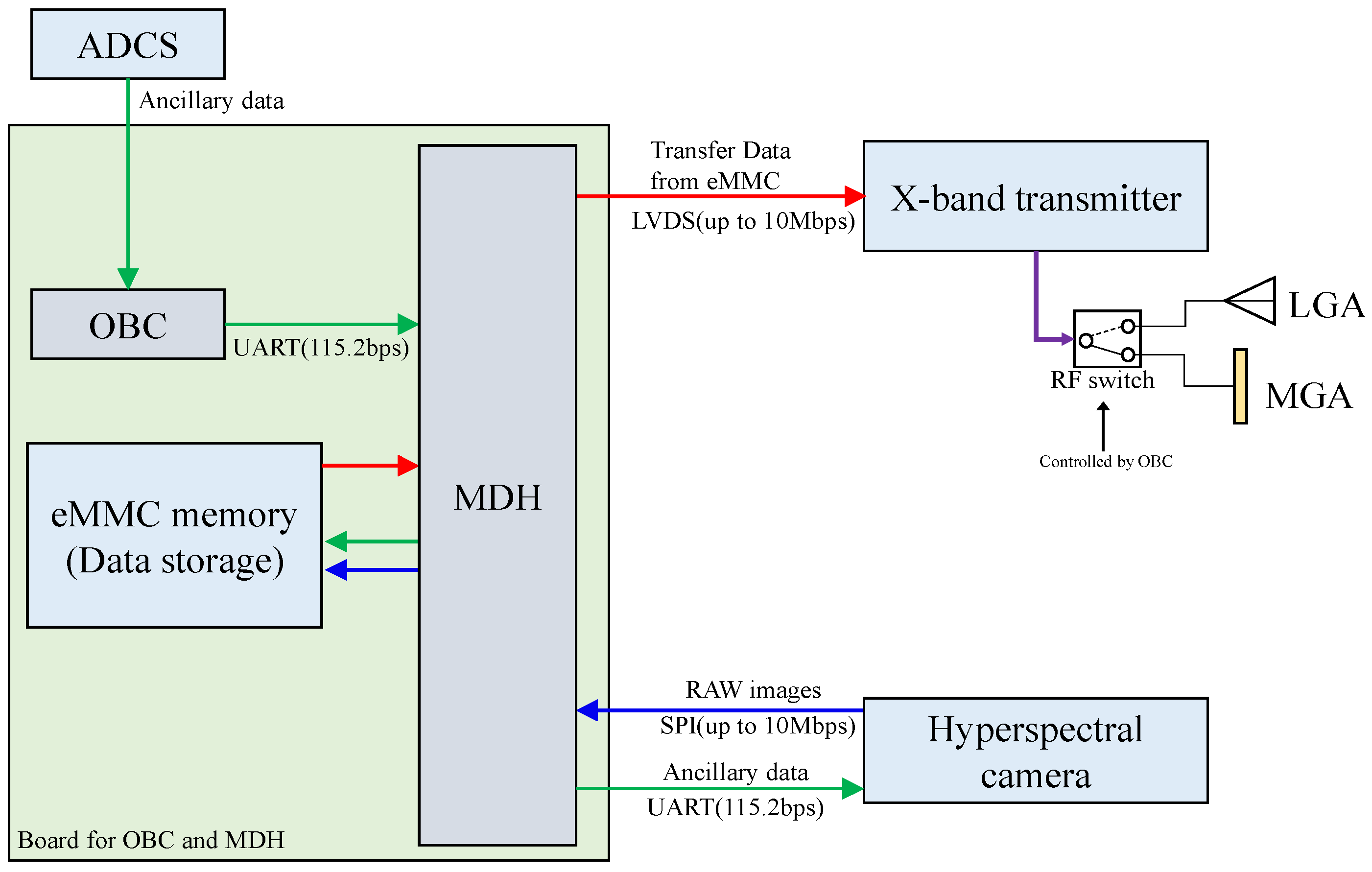
3.3. Mission Data Handling and Communication Subsystem
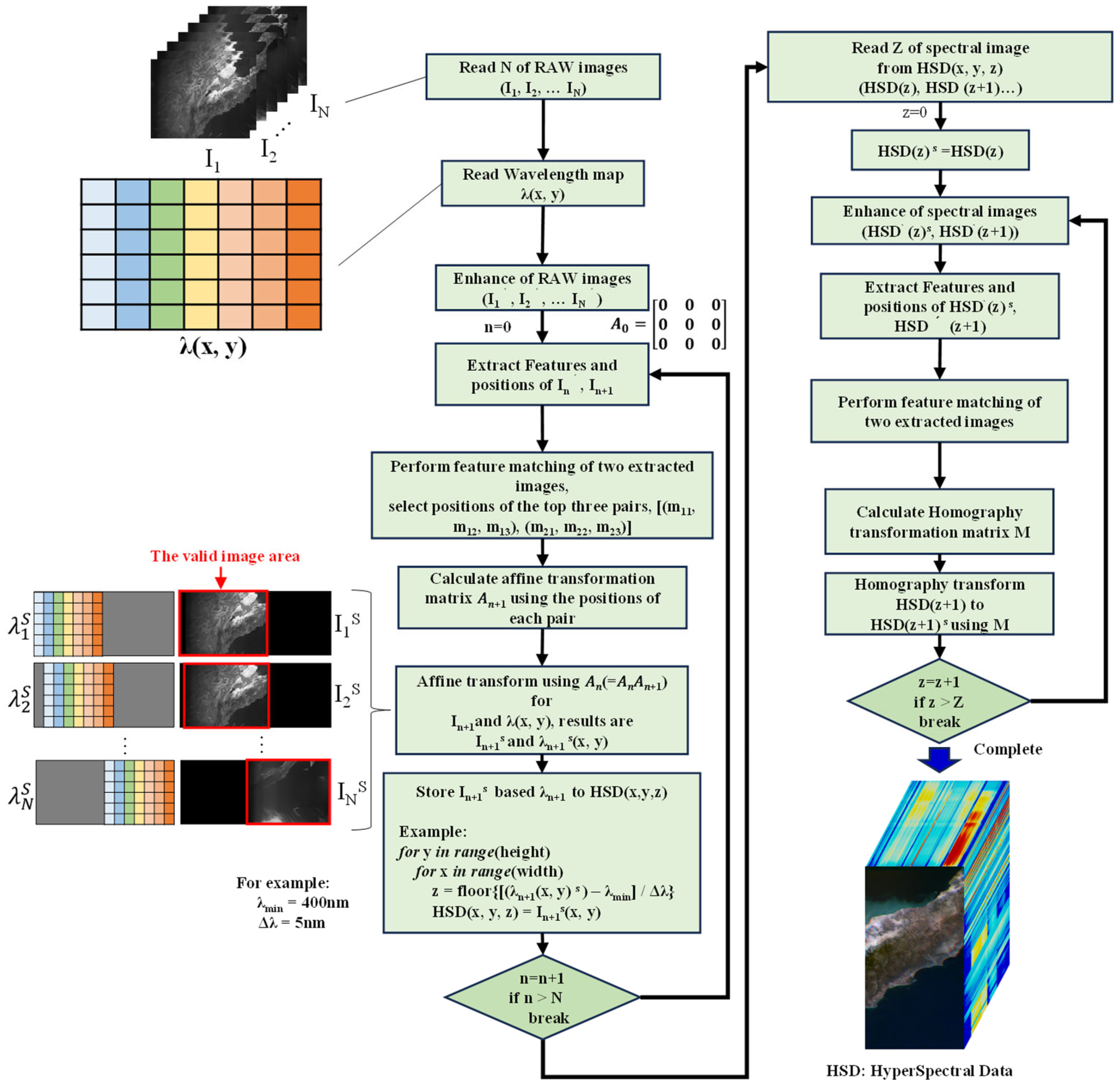
4. Data-Construction Method for LVBPF-Based Hyperspectral Data
5. On-Orbit Results
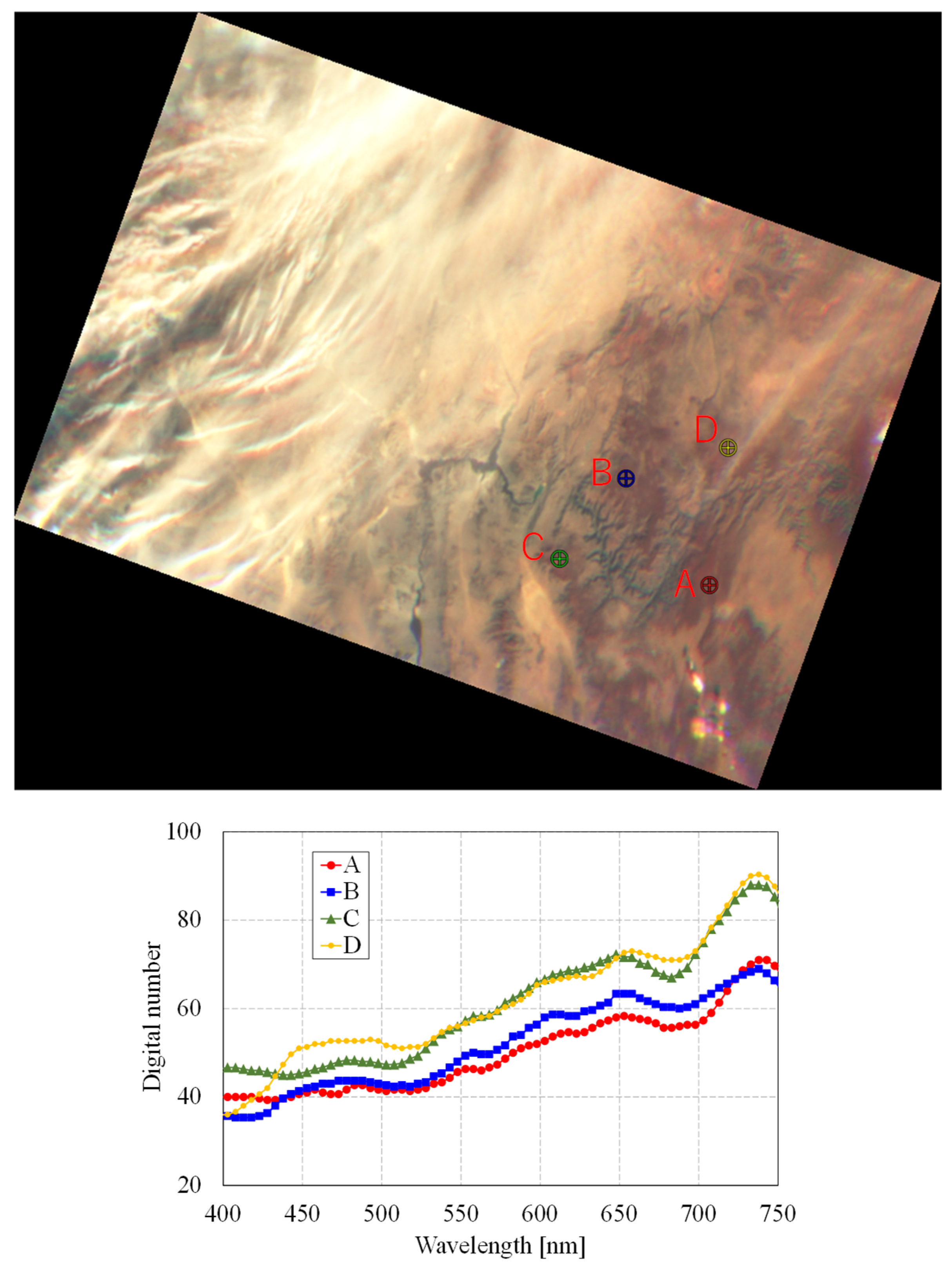
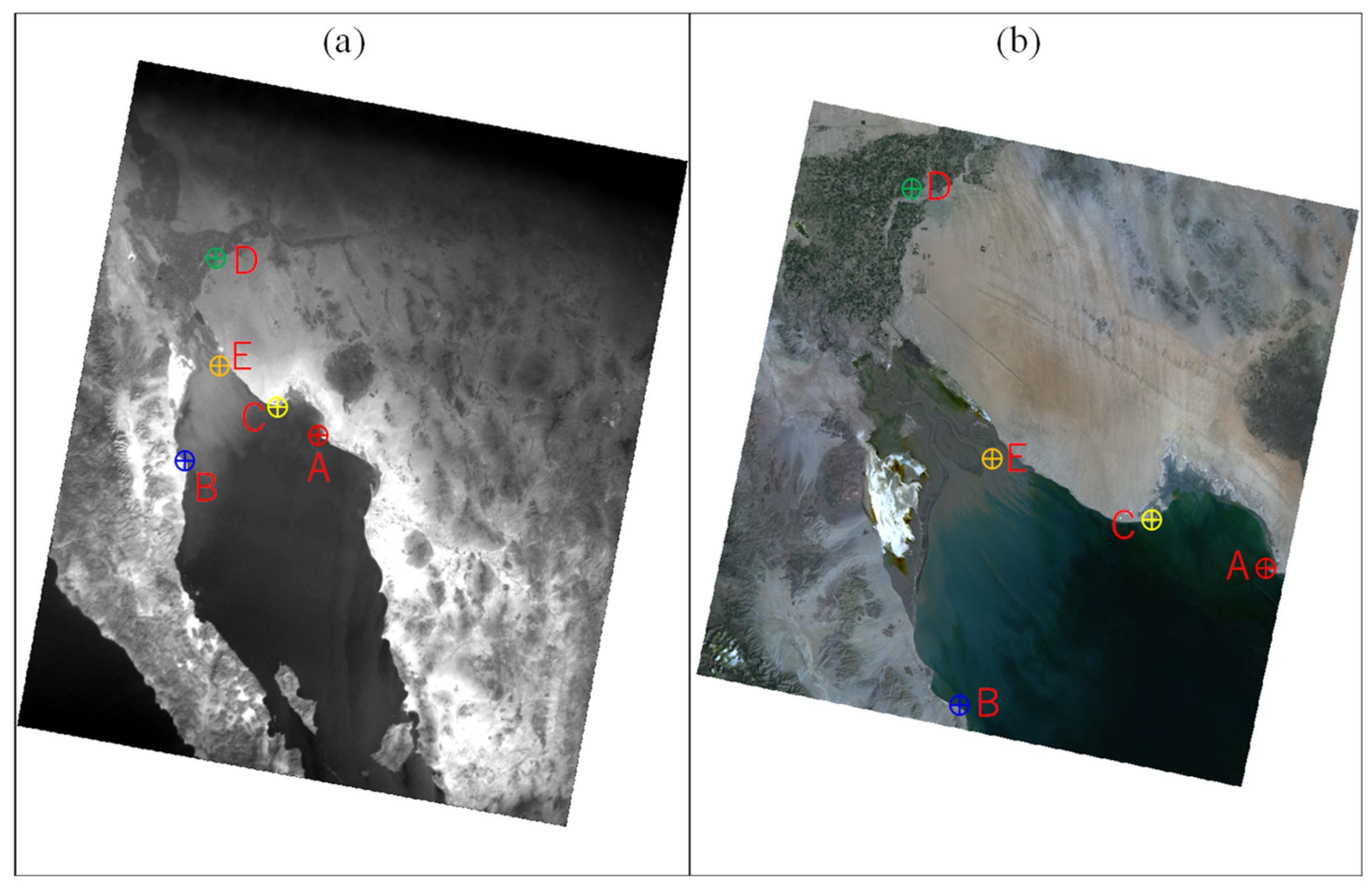
5.1. Observation Result and Validation of Data-Construction Method
5.2. On-Orbit Analysis Results of the Satellite Bus Performances
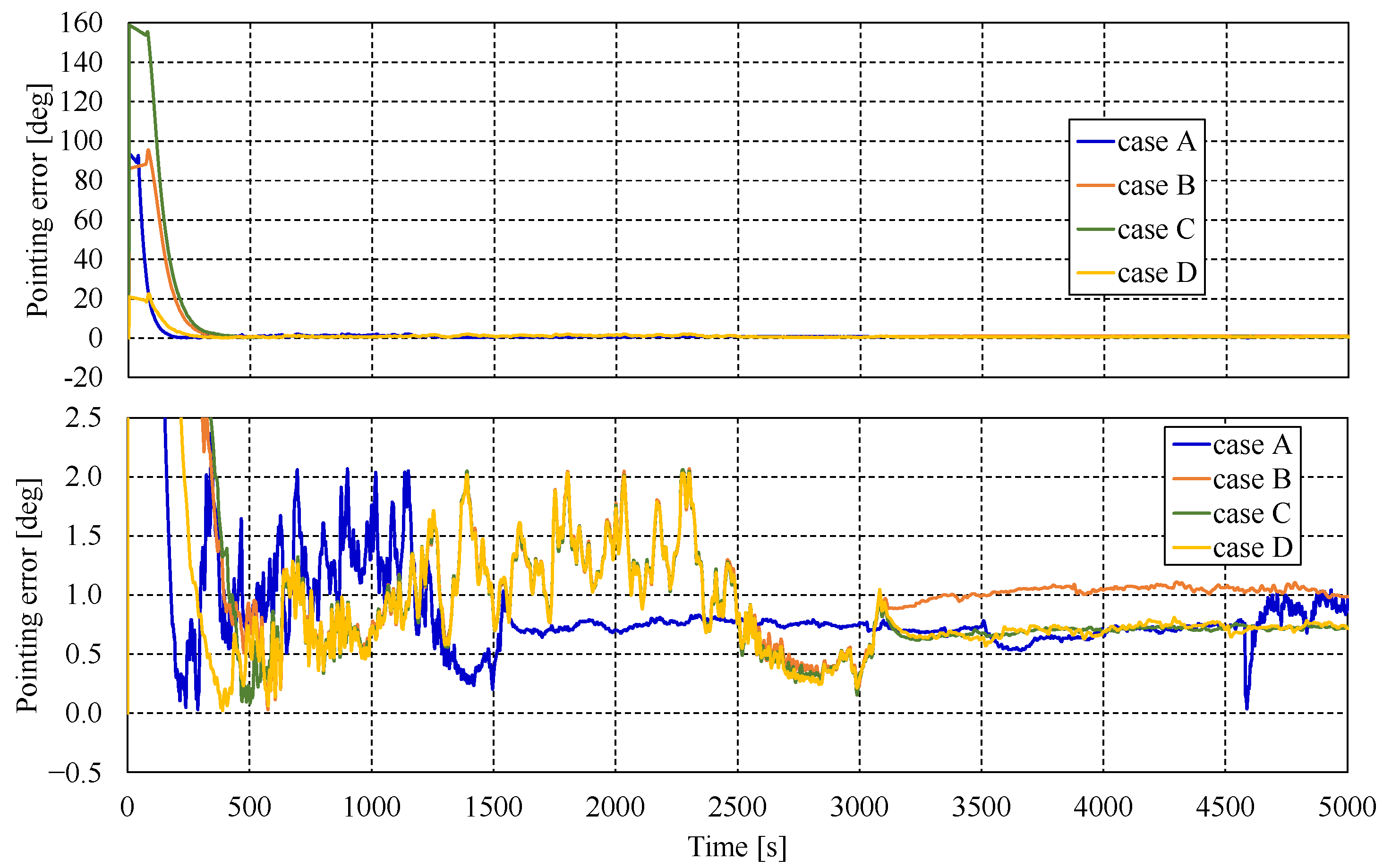
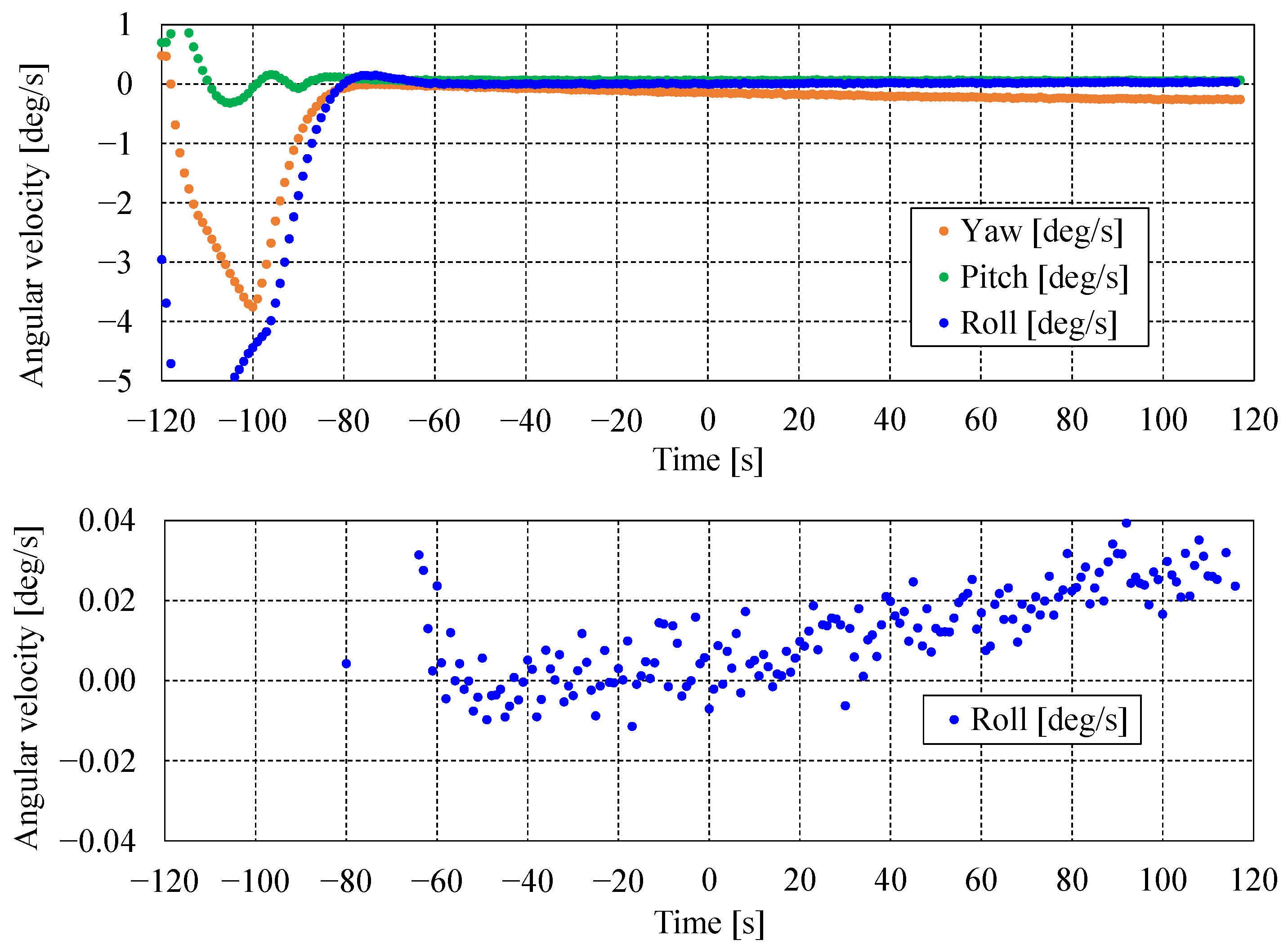
5.2.1. Evaluation of Attitude Precision and Stability
5.2.2. Thermal Analysis
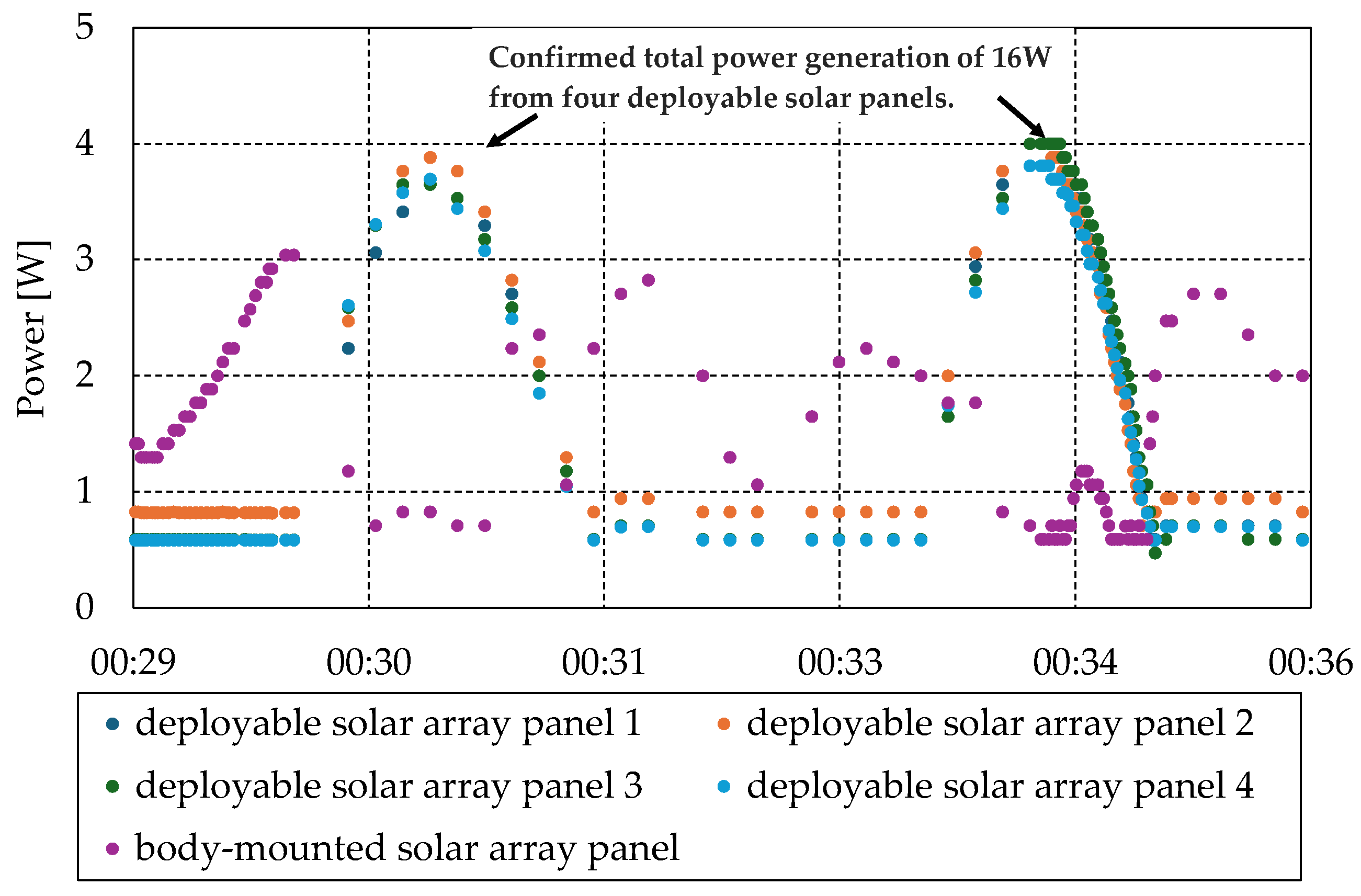
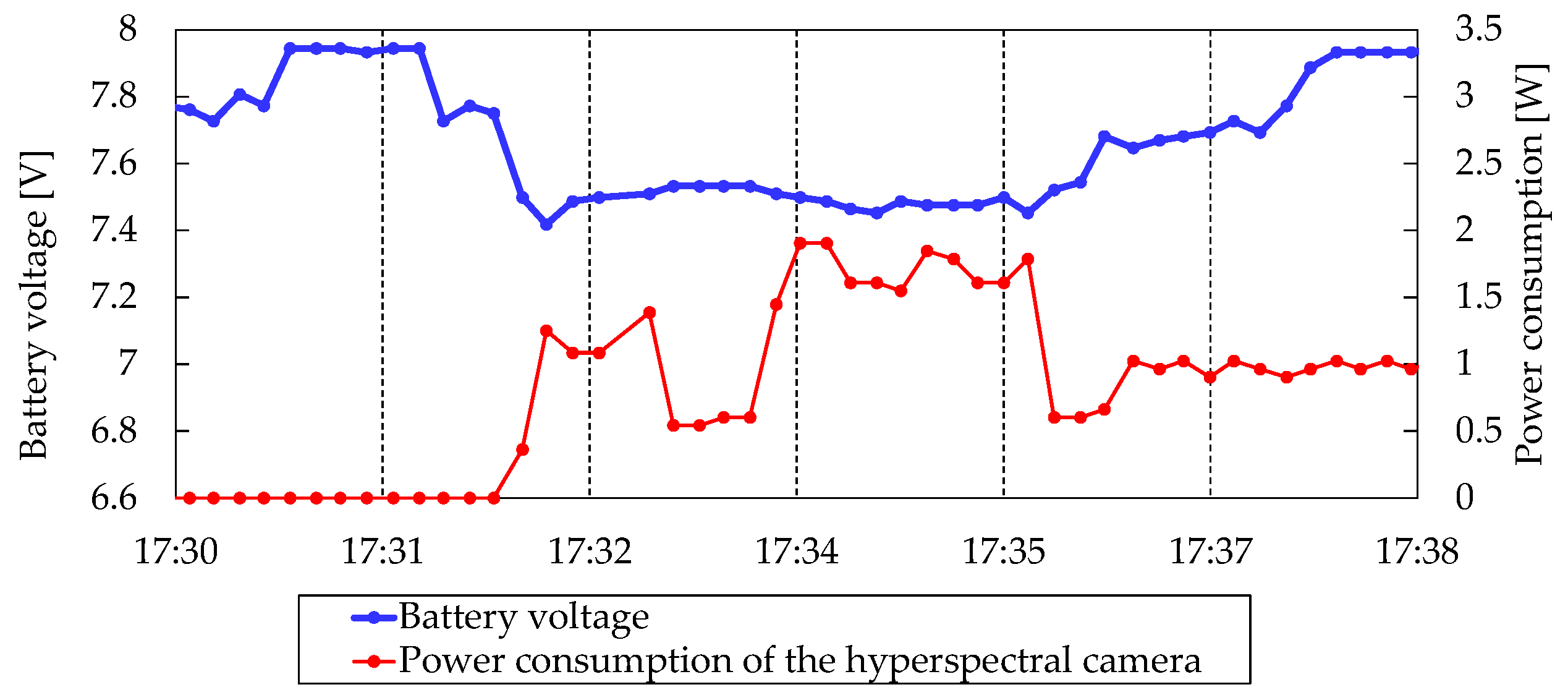
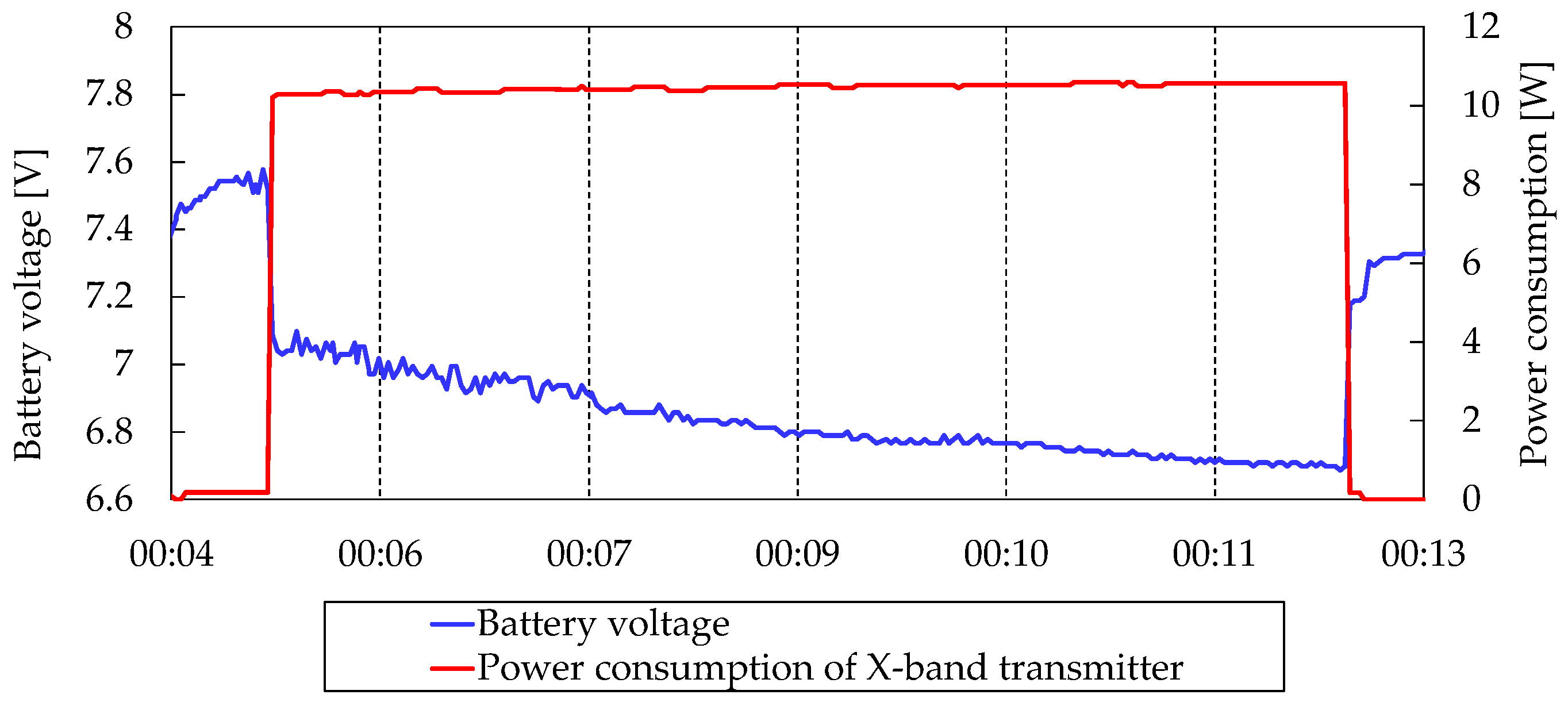
5.2.3. Power Control Subsystem
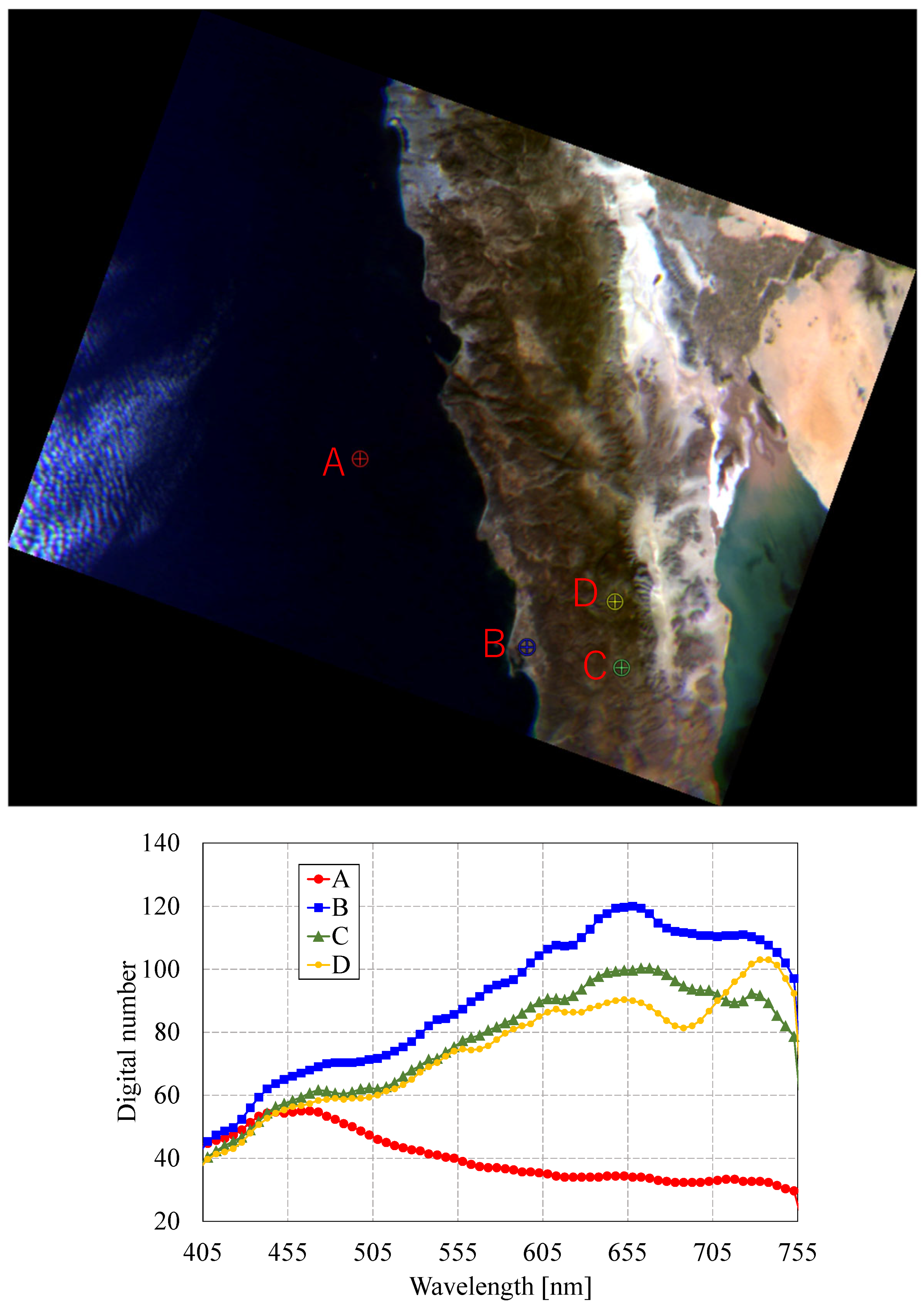
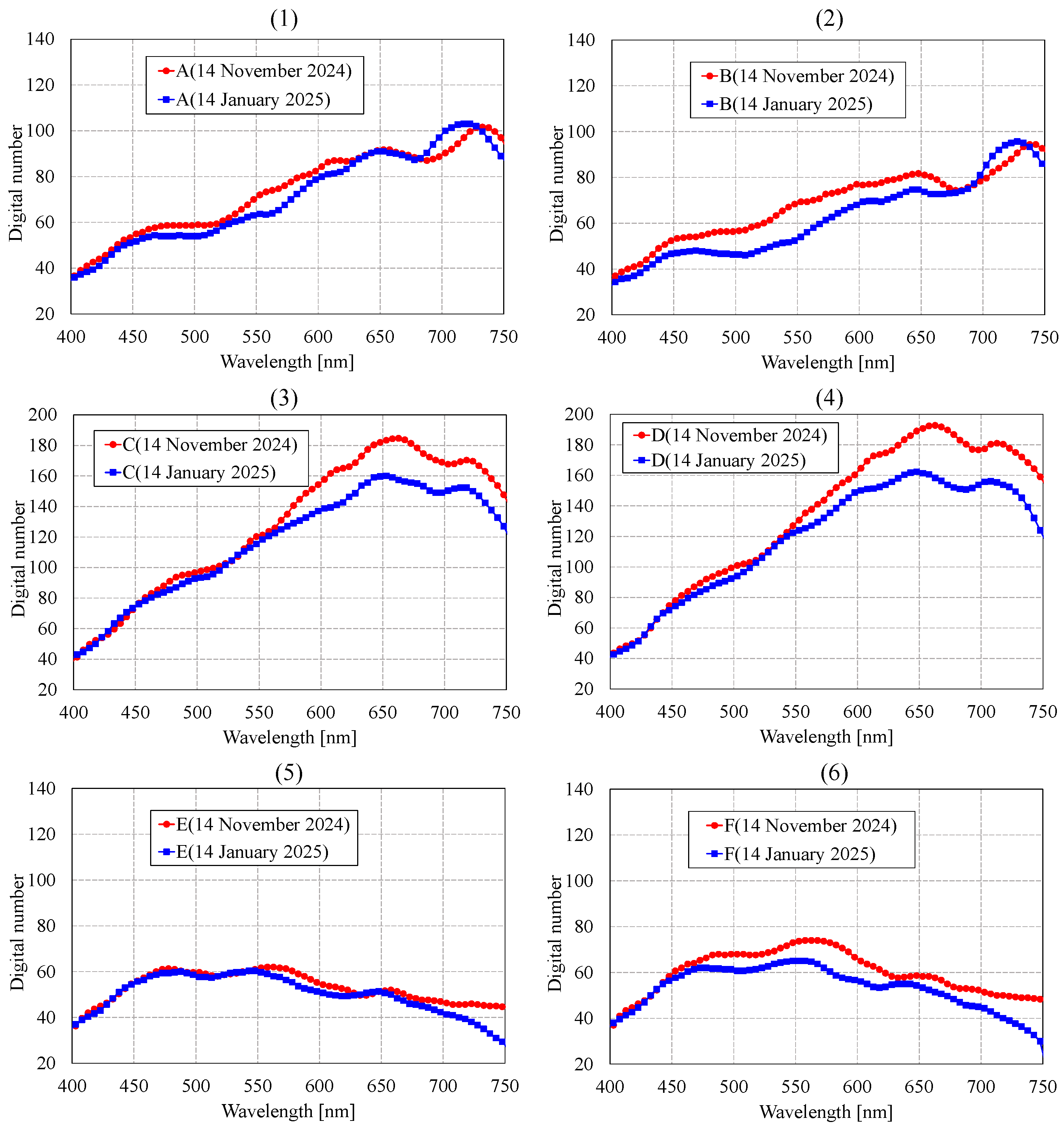
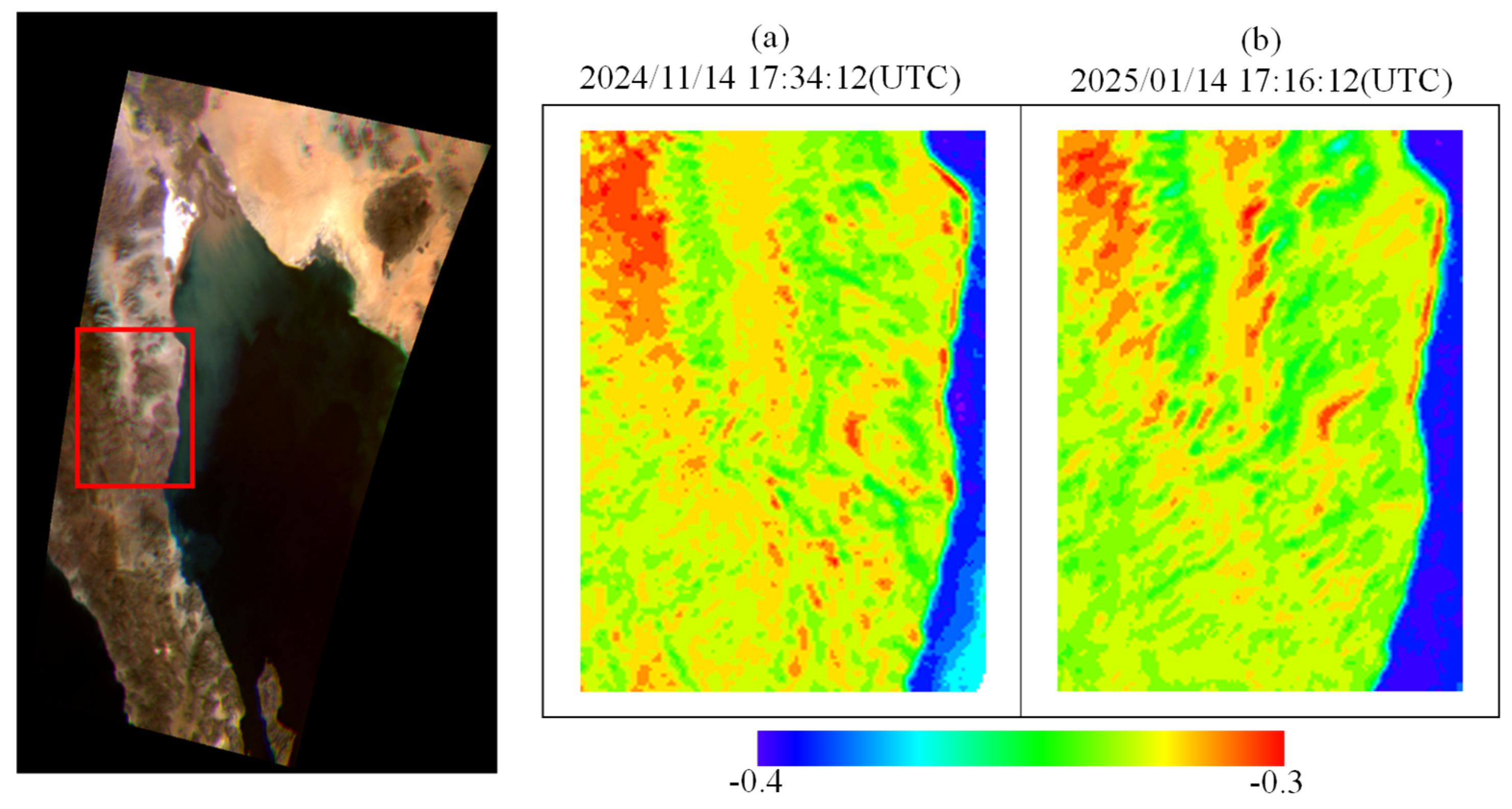
5.3. Comparison of Hyperspectral Data Across Two Time Periods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thenkabail, P.S.; Lyon, J.G.; Huete, A. Hyperspectral Remote Sensing of Vegetation; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar] [CrossRef]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent advances of hyperspectral imaging technology and applications in agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Transon, J.; Raphael, D.; Alexandre, M.; Pierre, D. Survey of hyperspectral earth observation applications from space in the sentinel-2 context. Remote Sens. 2018, 10, 157. [Google Scholar] [CrossRef]
- Lucke, R.L.; Corson, M.; McGlothlin, N.R.; Butcher, S.D.; Wood, D.L.; Korwan, D.; Li, R.R.; Snyder, W.A.; Davis, C.O.; Chen, D.T. Hyperspectral imager for the coastal ocean: Instrument description and first images. Appl. Opt. 2011, 50, 1501–1516. [Google Scholar] [CrossRef] [PubMed]
- Pearlman, J.S.; Barry, P.S.; Segal, C.C.; Shepanski, J.; Beiso, D.; Carman, S.L. Hyperion a space-based imaging spectrometer. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1160–1173. [Google Scholar] [CrossRef]
- Loizzo, R.; Guarini, R.; Longo, F.; Scopa, T.; Formaro, R.; Facchinetti, C.; Varacalli, G. Prisma: The Italian Hyperspectral Mission. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Shen-En, Q. Hyperspectral satellites, evolution, and development history. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7032–7056. [Google Scholar] [CrossRef]
- Iwasaki, A.; Tanii, J.; Kashimura, O.; Ito, Y. Prelaunch Status of Hyperspectral Imager Suite (HISUI). In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019. [Google Scholar] [CrossRef]
- Boshuizen, C.R.; Mason, J.; Klupar, P.; Spanhake, S. Results from the Planet Labs Flock Constellation. In Proceedings of the 28th AIAA/USU Conference on Small Satellites, Logan, UT, USA, 4–7 August 2014. [Google Scholar]
- Areda, E.E.; Cordova-Alarcon, J.R.; Masui, H.; Cho, M. Development of Innovative CubeSat Platform for Mass Production. Appl. Sci. 2022, 12, 9087. [Google Scholar] [CrossRef]
- DelPozzo, S.; Williams, C. Nano/Microsatellite Market, Forecast, 10th ed.; SpaceWorks Enterprises, Inc.: Atlanta, GA, USA, 2020. [Google Scholar] [CrossRef]
- Curnick, D.J.; Davies, A.J.; Duncan, C.; Freeman, R.; Jacoby, D.M.; Shelley, H.T.; Rossi, C.; Wearn, O.R.; Williamson, M.J.; Pettorelli, N. SmallSats: A new technological frontier in ecology and conservation? Remote Sens. Ecol. Conserv. 2022, 8, 139–150. [Google Scholar] [CrossRef]
- Erik, K. Satellite Constellations—2024 Survey, Trends and Economic Sustainability. In Proceedings of the International Astronautical Congress, IAC, Milan, Italy, 14–18 October 2024; pp. 14–18. [Google Scholar] [CrossRef]
- Bakken, S.; Henriksen, M.B.; Birkeland, R.; Langer, D.D.; Oudijk, A.E.; Berg, S.; Pursley, Y.; Garrett, J.L.; Gran-Jansen, F.; Honoré-Livermore, E.; et al. HYPSO-1 CubeSat: First Images and In-Orbit Characterization. Remote Sens. 2023, 15, 755. [Google Scholar] [CrossRef]
- Esposito, M.; Dijk, C.V.; Vercruyssen, N.; Conticello, S.S.; Manzillo, P.F.; Koeleman, R.; Delauré, B.; Benhadj, I. Demonstration in Space of a Smart Hyperspectral Imager for Nanosatellites. In Proceedings of the 32th Annual AIAA/USU Conference on Small Satellites, SSC18-I-07, Logan, UT, USA, 4–9 August 2018. [Google Scholar]
- Introduction of Wyvern’s Hyperspectral Satellites. Available online: https://wyvern.space/our-products/generation-one-hyperspectral-satellites/ (accessed on 9 April 2025).
- Tikka, T.; Makynen, J.; Shimoni, M. Hyperfield—Hyperspectral small satellites for improving life on Earth. In Proceedings of the 2023 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2023. [Google Scholar] [CrossRef]
- Joshua, M.; Salvaggio, K.; Keremedjiev, M.; Roth, K.; Foughty, E. Planet’s upcoming VIS-SWIR hyperspectral satellites. In Hyperspectral/Multispectral Imaging and Sounding of the Environment; Optica Publishing Group: Munich, Germany, 2023. [Google Scholar] [CrossRef]
- Aoyanagi, Y. On-orbit demonstration of a linear variable band-pass filter based miniaturized hyperspectral camera for CubeSats. J. Appl. Remote Sens. 2024, 18, 044512. [Google Scholar] [CrossRef]
- Mika, A.M. Linear-Wedge Spectrometer. In Proceedings of the SPIE, Imaging Spectroscopy of the Terrestrial Environment, Orlando, FL, USA, 1 September 1990; Volume 1298. [Google Scholar] [CrossRef]
- Song, S.; Gibson, D.; Ahmadzadeh, S.; Chu, H.O.; Warden, B.; Overend, R.; Macfarlane, F.; Murray, P.; Marshall, S.; Aitkenhead, M.; et al. Low-cost hyper-spectral imaging system using a linear variable bandpass filter for agritech applications. Appl. Opt. 2020, 59, A167–A175. [Google Scholar] [CrossRef] [PubMed]
- Dami, M.; De Vidi, R.; Aroldi, G.; Belli, F.; Chicarella, L.; Piegari, A.; Sytchkova, A.; Bulir, J.; Lemarquis, F.; Lequime, M.; et al. Ultra Compact Spectrometer Using Linear Variable Filters. In Proceedings of the International Conference on Space Optics 2010, Rhodes, Greece, 4–8 October 2010. [Google Scholar] [CrossRef][Green Version]
- Rahmlow, T.D., Jr.; Cote, W.; Johnson, R., Jr. Hyperspectral imaging using a Linear Variable Filter (LVF) based ultra-compact camera. In Proceedings of the SPIE, Photonic Instrumentation Engineering VII, San Francisco, CA, USA, 1–6 February 2020; Volume 11287. [Google Scholar] [CrossRef]
- Aoyanagi, Y.; Matsumoto, T.; Obata, T.; Nakasuka, S. Design of 3U-CubeSat Bus Based on TRICOM Experience to Improve Versatility and Easiness of AIT. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2021, 19, 252–258. [Google Scholar] [CrossRef]
- Verspieren, Q.; Matsumoto, T.; Aoyanagi, Y.; Fukuyo, T.; Obata, T.; Nakasuka, S.; Kwizera, G.; Abakunda, J. Store-and-Forward 3U CubeSat Project TRICOM and Its Utilization for Development and Education: The Cases of TRICOM-1R and JPRWASAT. Trans. Jpn. Soc. Aeronaut. Space Sci. 2020, 63, 206–211. [Google Scholar] [CrossRef]
- Ikari, S.; Hosonuma, T.; Suzuki, T.; Fujiwara, M.; Sekine, H.; Takahashi, R.; Arai, H.; Shimada, Y.; Nakamura, H.; Suzumoto, R.; et al. Development of Compact and Highly Capable Integrated AOCS module for CubeSats. J. Evol. Space Act. 2023, 1, 63. [Google Scholar] [CrossRef]
- Nakajima, S.; Funase, R.; Nakasuka, S.; Ikari, S.; Tomooka, M.; Aoyanagi, Y. Command centric architecture (C2A): Satellite software architecture with a flexible reconfiguration capability. Acta Astronaut. 2020, 171, 208–214. [Google Scholar] [CrossRef]







| Item | Specification |
|---|---|
| Size | 3.6 cm × 3.6 cm × 2.4 cm |
| Weight | 35 g |
| Ground sampling distance | 450 m/pixel |
| Swath | 460 km |
| Available wavelength range | 400–770 nm |
| Spectral sampling distance | 5 nm |
| Spectral resolution | 18.1 nm |
| Number of bands | 75 bands |
| Focal length of telescope lens | 8 mm |
| F-number of telescope lens | F/2.5 |
| Detector format | 1280 along track × 1024 cross track |
| Pixel size | 5.3 μm |
| Dynamic range | 8-bit |
| Item | Specification |
|---|---|
| Size | 10.1 mm × 8 mm |
| Thickness | 0.5 mm |
| Spectral detection range | 380–850 nm |
| Dispersion | 67.7 nm/mm |
| Peak transmission | 65% |
| Spectral blocking property | <1% |
| Half bandwidth | 15 nm at 430 nm 20.6 nm at 780 nm |
| Item | Specification |
|---|---|
| Size | 117 mm × 117 mm × 381 mm |
| Weight | 4.97 kg |
| Attitude Determination and Control Subsystem | Three-axis stabilization control using geomagnetic sensor, MEMS gyroscope, three-sun sensor, GPS receiver, magnetic torque, and reaction wheel |
| Electrical Power Subsystem | Solar array panel: four deployable panels, four body-mounted panels Maximum power generation: 20 W Typical power consumption: 10 W Battery: 5.8 Ah, nominal 8 V (lithium ion battery) |
| Communication Subsystem | Telemetry/command: S-band Command uplink: 4 kbps, Telemetry downlink: 4 kbps–64 kbps Mission data downlink: X-band (5 Mbps, 10 Mbps) |
| Orbit | Sun-synchronous sub-recurrent orbit Altitude: 680 km (approximately); inclination: 98 degrees |
| Item | Specification |
|---|---|
| Reaction wheel | Three-axis mounted Max angular momentum: 3 mNms (nominal) 5 mNms (peak) |
| Magnetic torquer | Three-axis mounted Magnetic moment: 0.35 Am2 |
| Sun sensor | Three-surface mounted Accuracy: ≤0.5°(3σ) |
| Fine geomagnetic sensor | Resolution: 13 nT |
| Fine gyroscope | Random noise: 4.36 × 10−5 rad/s (1σ) |
| Microcontroller | Clock: 80 MHz; ROM: 512 kiB; RAM: 128 KiB |
| Item | Attitude-Control Accuracy (Roll, Pitch) | Attitude-Control Accuracy (Yaw) | Attitude Stability (Roll) |
|---|---|---|---|
| Requirements | 7.3° | 5.8° | 0.048°/s |
| Item | (1) Sequentially Synthesized | (2) Affine | (3) Homography | (4) Proposed Method |
|---|---|---|---|---|
| Image enhancement | - | Gamma correction (gamma = 2.0) | ||
| Unsharp masking | ||||
| Feature detection | AKAZE | |||
| Transformation | Affine | Homography and RANSAC | (1) + (2) | |
| Library | OpenCV, pillow | |||
| Location | TIRSAT | Landsat-9 | Distance [km] | ||
|---|---|---|---|---|---|
| Latitude [°] | Longitude [°] | Latitude [°] | Longitude [°] | ||
| A | 31.7117 | −113.8237 | 31.3447 | −113.6420 | 44.297 |
| B | 30.9371 | −114.7187 | 31.4722 | −114.9723 | 64.209 |
| C | 31.4933 | −114.0276 | 31.9123 | −114.1741 | 48.612 |
| D | 33.0178 | −114.7806 | 32.4926 | −114.8430 | 58.692 |
| E | 32.1983 | −114.7021 | 31.6918 | −114.5939 | 57.241 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aoyanagi, Y.; Doi, T.; Arai, H.; Shimada, Y.; Yasuda, M.; Yamazaki, T.; Sawazaki, H. On-Orbit Performance and Hyperspectral Data Processing of the TIRSAT CubeSat Mission. Remote Sens. 2025, 17, 1903. https://doi.org/10.3390/rs17111903
Aoyanagi Y, Doi T, Arai H, Shimada Y, Yasuda M, Yamazaki T, Sawazaki H. On-Orbit Performance and Hyperspectral Data Processing of the TIRSAT CubeSat Mission. Remote Sensing. 2025; 17(11):1903. https://doi.org/10.3390/rs17111903
Chicago/Turabian StyleAoyanagi, Yoshihide, Tomofumi Doi, Hajime Arai, Yoshihisa Shimada, Masakazu Yasuda, Takahiro Yamazaki, and Hiroshi Sawazaki. 2025. "On-Orbit Performance and Hyperspectral Data Processing of the TIRSAT CubeSat Mission" Remote Sensing 17, no. 11: 1903. https://doi.org/10.3390/rs17111903
APA StyleAoyanagi, Y., Doi, T., Arai, H., Shimada, Y., Yasuda, M., Yamazaki, T., & Sawazaki, H. (2025). On-Orbit Performance and Hyperspectral Data Processing of the TIRSAT CubeSat Mission. Remote Sensing, 17(11), 1903. https://doi.org/10.3390/rs17111903





