Abstract
The Total Precipitable Water (TPW) is a key variable of atmospheres, and its spatiotemporal distribution is of great importance in global climate change. This paper addresses the TPW retrieval over both sea and land surfaces from the data acquired by the Microwave Humidity Sounder II (MWHS-II) on Fengyun 3D (FY-3D) satellite. First, the Back Propagation Neural Network (BPNN) algorithms are developed with the spatiotemporal matching samples of the MWHS-II data with the fifth-generation European Centre for Medium-Range Weather Forecast (ECMWF) atmospheric reanalysis (ERA5) data. Then, the TPWs at spatial resolutions of 0.25° in longitude and latitude between 65°S and 65°N over both sea and land surfaces are retrieved from the pixel-aggregated FY-3D MWHS-II data in 2022. Finally, the TPWs retrieved in this work are validated with the radiosonde TPWs over both sea and land surfaces, and they are also compared to the F18 Special Sensor Microwave Imager Sounder (SSMIS) TPWs over sea surfaces. The results indicate that the BPNN algorithms developed in this work are valid and superior to the D-matrix method, the Ridge method, the Lasso method, the physical method, the random forest (RF) method, the support vector machine (SVM) method, and the eXtreme Gradient Boosting (XGBoost) method. Against the radiosonde TPWs, the mean error (ME), the root mean square error (RMSE), and mean absolute error (MAE) of the TPWs retrieved in this work are −1.17 mm, 3.46 mm, and 2.63 mm over sea surfaces, respectively, and they are −0.80 mm, 4.04 mm, and 3.13 mm over land surfaces, respectively. The TPWs retrieved in this work are much more accurate than the F18 SSMIS TPWs.
1. Introduction
The Total Precipitable Water (TPW) is a key physical parameter in the study of the global energy balance and water cycle. Its spatiotemporal distribution and variations significantly affect global climate change, making it highly valuable for weather and climate applications [1]. Currently, TPW products are mainly obtained through three methods: the radiosonde observations, the satellite remote sensing, and the reanalysis data. The radiosonde observations provide accurate TPW by measuring humidity profiles and integrating the water vapor content of the entire atmospheric column. However, the radiosonde observations are expensive and have uneven spatial distribution, especially in oceanic regions where stations are sparse. Additionally, radiosondes typically conduct measurements only twice a day, limiting their ability to monitor rapidly changing weather processes [2]. Another method to obtain TPW is through satellite remote sensing, which can be divided into optical, infrared, and microwave remote sensing. The optical remote sensing has a high spatial resolution, but it is greatly affected by clouds. The infrared remote sensing also cannot effectively retrieve water vapor information under cloudy conditions. In contrast, the microwave remote sensing can penetrate cloud layers and collect data in cloudy conditions, enabling all-weather TPW observation [3]. However, the accuracy of microwave remote sensing retrieval is strongly influenced by the surface emissivity, which usually has large value and uncertainty over land, which makes it difficult to distinguish atmospheric signals from surface emission. Fortunately, the microwave sea surface emissivity has smaller value and less variation in contrast to microwave land surface emissivity. Therefore, the TPW retrieval over sea surfaces is far more accurate than that over land surfaces. Most existing studies focus on the TPW retrieval over sea surfaces [4].
The TPW retrieval from satellite microwave radiometer data has a history of several decades, and many methods have been developed, including the empirical methods, the semi-empirical methods, the physics-based methods, and the neural network methods [5,6,7]. These methods generally perform retrieval by establishing linear or nonlinear relationships between TPW and the brightness temperatures (TB) in microwave channels. Currently, microwave radiometers primarily use two water vapor absorption lines, located at 22.235 GHz and 183.31 GHz, to detect atmospheric moisture information. Grody et al. first validated the strong correlation between water vapor content and TB at the 22.235 GHz water vapor absorption line and proposed an empirical method to retrieve atmospheric water vapor content from microwave radiometer observations [8]. Alishouse et al. utilized the Special Sensor Microwave Imager (SSM/I) observations to simultaneously retrieve the TPW and cloud liquid water content over sea surfaces [9]. According to a radiative transfer model, Wang et al. developed a semi-empirical algorithm to retrieve the total water vapor content over sea surfaces from the Tropical Rainfall Measuring Mission (TRMM) Microwave Imager (TMI) data under clear-sky conditions [10]. Bobylev et al. developed a neural network algorithm to retrieve water vapor content over the Arctic Ocean [11] from the combined SSM/I data and the data acquired by the Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E). In contrast to the 22.23 GHz channel, the channels centered at the 183.31 GHz water vapor absorption line offer higher spatial resolution and observation accuracy, and have been widely used to retrieve TPW in recent years. The modern advanced satellite microwave radiometers, such as the Advanced Microwave Sounding Unit B (AMSU-B), the Microwave Humidity Sounder (MHS), and the Advanced Technology Microwave Sounder (ATMS), are equipped with the 183.31 GHz channels. Boukabara et al. proposed a variational retrieval algorithm and established a comprehensive microwave retrieval system (MiRS). With the data in the 183.31 GHz channels, the TPW retrieval accuracy was significantly improved [12]. Liu et al. developed a physics-based algorithm to retrieve TPW from the ATMS observations in the 165.50 GHz and 183.31 GHz channels [13].
The Fengyun-3 (FY-3) series are China’s second generation of polar-orbiting meteorological satellites. The fourth satellite in the series, FY-3D, was successfully launched from the Taiyuan Satellite Launch Center on November 15, 2017. It is China’s main operational low Earth orbit afternoon satellite. There are ten advanced remote sensing instruments on FY-3D, and one of them is the Microwave Humidity Sounder II (MWHS-II) [14]. As listed in Table 1, the MWHS-II has four frequency bands and fifteen channels. Among these, the 118.75 GHz oxygen-absorption band is used for the first time on a polar-orbiting meteorological satellite. This band has eight oxygen absorption channels at the Quasi-vertical (QV) polarization, which are mainly used to detect atmospheric temperature profiles. The 183.31 GHz water vapor absorption band has five channels at the QV polarization, which are primarily used to retrieve atmospheric humidity profiles. In addition, two window channels are centered at 89.0 GHz and 150.0 GHz at the Quasi-horizontal (QH) polarization, respectively, and they are used to collect emission and scattering from both the Earth surfaces and atmospheres. The equivalent noise temperature difference (NEΔT) is 1.0 K in the channels 1 and 8~15, 1.6 K in the channels 4~7, 2.0 K in the channel 3, and 3.6 K in the channel 2 [15]. FY-3D MWHS-II cross-track scans Earth surfaces and atmospheres with the 15 channels, and the Earth Incidence Angle (EIA) mainly ranges between 0° and 65°. According to the instrument parameters, the FY-3D MWHS-II’s observations can be used to retrieve TPW. To date, there is no research or algorithm regarding the TPW retrieval from the FY-3D MWHS-II data over both sea and land surfaces found in the literature.

Table 1.
Instrument parameters of FY-3D MWHS-II.
Therefore, this work focuses on the TPW retrieval from FY-3D MWHS-II data over both sea surfaces and land surfaces. Besides the introduction, this article is organized as follows: Section 2 describes the materials; Section 3 presents the methods; Section 4 gives the results; and Section 5 and Section 6 are devoted to the discussion and conclusions, respectively.
It should be noted that this article is a revised and expanded version of a paper entitled “Retrieval of global total precipitable water over sea surfaces from MWHS-II/FY-3D data using the BP neural network”, which was accepted and presented at the Photonics & Electromagnetics Research Symposium (PIERS), Chengdu, China, 21–25 April 2024 [16].
2. Materials
In this work, the following data in 2022 are used: the FY-3D MWHS-II Level 1 (L1) data, the fifth-generation of European Centre for Medium-range Weather Forecast (ECMWF) atmospheric reanalysis (ERA5) data, the radiosonde data, the F18 Special Sensor Microwave Imager Sounder (SSMIS) TPW product, the Terra and Aqua combined Moderate Resolution Imaging Spectroradiometer (MODIS) land cover (MCD12C1) product, and the Global 30 Arc-Second Elevation (GTOPO30) data.
The FY-3D MWHS-II L1 data, downloaded from the Fengyun Satellite Data Center (https://satellite.nsmc.org.cn, accessed on 10 September 2024), contain the TBs at top of atmosphere (TOA) in the fifteen channels listed in Table 1, the geolocation (longitude and latitude), the observation time, the EIA, etc.
The ERA5 data (https://cds.climate.copernicus.eu, accessed on 15 September 2024) contain hourly estimates of a lot of atmospheric, land, and oceanic climate variables with spatial resolutions of 0.25° in longitude and latitude [17]. Against the TPW obtained by the Global Navigation Satellite System (GNSS), the root mean square error (RMSE) of the TPW extracted from the ERA5 data is about 1.8 mm [18,19], and the global standard deviations are usually lower than 3 mm [20]. Because of its high spatiotemporal resolutions and accuracy, the ERA5 TPW is used to build the training and testing datasets below in this work.
The radiosonde data, provided by the University of Wyoming in the United States of America (USA) (http://weather.uwyo.edu/upperair/sounding.html, accessed on 6 October 2024), have climate parameters at 0:00 and 12:00 UTC every day, such as the profiles of atmospheric temperature and humidity, wind speed and direction, etc. Although the radiosonde data are accurate, the sparse distribution of the radiosonde stations and the low temporal resolution hinder their use as the references for model training. The TPWs extracted from the radiosonde atmospheric humidity profiles are used to validate the retrieved TPWs in this work. The extraction equation is given by [21]:
where is the TPW, is the air density, is the gravitational acceleration, denotes the specific humidity at pressure , and is the pressure at Earth surface.
The F18 SSMIS TPW product (http://www.remss.com, accessed on 1 November 2024) is generated from the observations acquired by the SSMIS on the U.S. Defense Meteorological Satellite Program (DMSP) F18 satellite in terms of the radiative transfer model [22], and it provides TPWs over sea surfaces with spatial resolutions of 0.25° in longitude and latitude. The validation results indicated that the F18 SSMIS TPWs are accurate. Therefore, The F18 SSMIS TPWs are used to cross-validate the results over sea surfaces in this work.
The MCD12C1 product (https://search.earthdata.nasa.gov, accessed on 20 September 2024), generated from the observations of the MODIS [23], provides global land cover types with spatial resolutions of 0.05° (approximately 5.6 km) in longitude and latitude. According to the standards of the International Geosphere-Biosphere Programme (IGBP), the MCD12C1 product divides global land surfaces into 17 major categories, including 11 natural vegetation types, three human-developed and land mosaic types, and three non-vegetated land types. The land cover types extracted from the MCD12C1 product are used as one of the input features of the neural network over land surfaces.
The GTOPO30 dataset (https://www.usgs.gov, accessed on 10 September 2024) is a global digital elevation model (DEM) produced by the U.S. Geological Survey (USGS). It covers global land areas with a spatial resolution of 30 arc-seconds (approximately 1 km) [24]. The GTOPO30 dataset provides elevation information for the entire globe and is widely used in geographic and climate change research, hydrological analysis, and ecological modeling. In this work, the GTOPO30 elevation data are used to determine the Earth surface–atmosphere boundary and used as one of the input features of the neural network over land surfaces.
Except for the ERA5 data and the F18 SSMIS TPW data, all the data introduced above are firstly pixel-aggregated into the 0.25° × 0.25° grid space. Then, the TBs in the MWHS-II channels 10 to 15 are re-calibrated using the results in [25]. Finally, two datasets mainly containing the spatiotemporal samples between FY-3D MWHS-II TBs and the ERA5 TPWs in 2022 are collected for sea surfaces and land surfaces, respectively. The matching criteria are (1) collocation between 65 °S and 65 °N in the 0.25° × 0.25° grid space, (2) at least 25 km away from coastlines, and (3) a maximum absolute time difference of less than one minute (|Δt| < 1.0 min). According to the above criteria, a total of 14,107,205 matching samples over sea surfaces and 6,300,924 matching samples over land surfaces are collected. Figure 1 displays the spatial distribution of the matching samples over both sea surfaces and land surfaces. The matching samples are densely distributed in high latitude regions, followed by the tropical regions and the mid-latitude regions. In most regions, the number of matching samples is greater than fifteen. Table 2 lists the monthly distribution of the matching samples. Over land surfaces, the number of matching samples ranges between 465,000 and 549,000, whereas it is approximately doubled over sea surfaces. The spatiotemporal distribution of the matching samples is determined by many factors, such as the satellite orbit, the matching criteria, and so on. In general, the matching samples have good spatiotemporal representativeness, and can be used to develop the TPW retrieval algorithm.
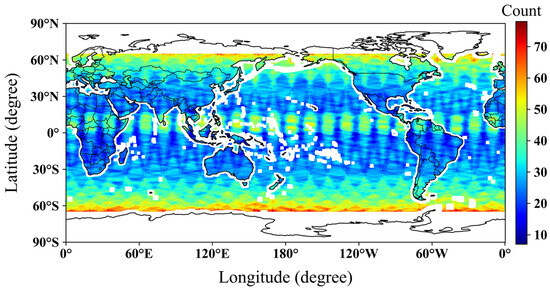
Figure 1.
Spatial distribution of the matching samples over both sea surfaces and land surfaces.

Table 2.
Monthly distribution of the matching samples in 2022.
It should be noted that the features in the two datasets have different units, e.g., the TBs are in Kelvin, while the elevation is in kilometers. To eliminate the impact of different units of input features on the output and accelerate the convergence of the neural network training, all the input data in the two datasets are converted into the z-scores using the following equation
where μ and σ are the mean and the standard deviation of input feature x, respectively; and zi is the z-score of input xi.
3. Methods
3.1. Back Propagation Neural Network
To retrieve TPW over both sea surfaces and land surfaces, the Back Propagation Neural Network (BPNN) [26] is adopted in this work. As shown in Figure 2, the BPNN consists of the input layer, the hidden layer(s), and the output layer.
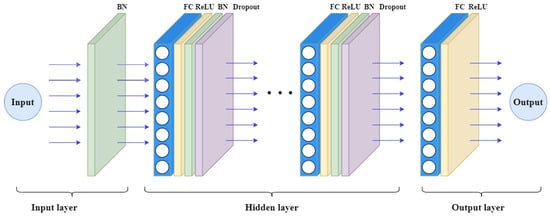
Figure 2.
Architecture of the Back Propagation Neural Network (BPNN) for TPW Retrieval.
Because of the large differences between land surfaces and sea surfaces, two BPNNs are designed for the TPW retrieval over sea and land surfaces, respectively. As we know, the hyperparameter selection is essential for optimizing the performance of neural networks. In this work, 80% of the matching samples are randomly selected as training data and the remaining 20% are used as the testing data. With the training and testing datasets, ablation experiments are conducted with the following candidate settings: the number of hidden layer(s) of 1, 2, 3 or 4, the number of neurons per hidden layer of 32, 64, 128 or 256, the loss function of Mean Square Error (MSE) Loss, Mean Absolute Error (MAE) Loss, Huber Loss or Log-Cosh Loss, and the dropout rate of 0.0, 0.1, 0.2, 0.3 or 0.5. The results of ablation experiments indicate that for sea surfaces, the BPNN with a single hidden layer of 128 neurons, the MSE Loss function, and the dropout rate of 0.1 provides the best balance between predicting accuracy and computational efficiency. For land surfaces, the BPNN with a two-hidden-layer of 64 neurons per layer, the MSE Loss function, and the dropout rate of 0.2 shows superior performance. These optimized settings ensure the robustness and generalization of the BPNNs across diverse atmospheres and Earth surfaces, highlighting the importance of tailoring hyperparameters to the specific retrieval task.
Because the atmospheric humidity is coupled with the atmospheric temperature, besides the TBs in the water vapor absorption channels, the use of TBs in the oxygen-absorption channels can improve the humidity retrieval accuracy [27]. In addition, the TBs in the MWHS-II channels 1 (89.0 GHz) and 10 (150.0 GHz) can provide information from Earth surfaces. Therefore, the TBs in all the fifteen MWHS-II channels are used in TPW retrieval in this work. Over sea surfaces, 19 input features are used, and they are the 15 TBs extracted from the FY-3D MWHS-II L1 data, the month of the year, the geolocation (latitude and longitude), and the EIA. Because of relatively small values and narrow dynamic ranges, the sea surface emissivities in the MWHS-II channels 1 (89.0 GHz) and 10 (150.0 GHz) are not taken into account. Over land surfaces, due to the complexity of land surfaces, besides the 19 input features for sea surfaces, another six variables are selected as input features: the GTOPO30 elevation, the MCD12C1 land cover type, and four land surface emissivities in the MWHS-II channels 1 (89.0 GHz) and 10 (150.0 GHz) at both vertical and horizontal polarizations.
The microwave land surface emissivities can be modeled using the physical models [28,29,30,31], the semi-empirical models [32,33,34], and the empirical models [35,36]. Most of them either cannot provide the needed level of accuracy for quantitative remote sensing or are only applied to specific land cover types. With only four parameters, the Hewison’s model calculates land surface emissivities between 20 GHz and 200 GHz at arbitrary EIA and polarization. The land surface emissivity at p (p = v or h, which denotes vertical polarization or horizontal polarization, respectively) polarization is given by [34]
where is the frequency; θ is the EIA; is the root mean square height of land surface; and c is the speed of light. is the power reflectivity at p polarization, which is expressed by
where Q is the depolarization coefficient; and are, respectively, the power reflectivity at vertical polarization and horizontal polarization for a specular land surface, and they are expressed by
with
in which is the effective relative permittivity of a specular surface, is the effective static permittivity, is the high frequency limit, and is the effective relaxation frequency.
The three permittivity coefficients (, and ) and the depolarization coefficient Q in the above equations are listed in Table IV in [34]. Due to its simplicity and applicability, the Hewison’s model is adopted in this work.
The ablation experiments also show that the use of squares of the TBs instead of the TBs themselves can improve the model’s sensitivity to the TB’s nonlinear variations, and the use of exponential value of the elevation instead of the elevation itself can reduce the scaling effect of elevation data on the model and enhance the model’s generalization capability and stability.
The hidden layer is composed of a fully connection (FC), a Rectified Linear Unit (ReLU) activation function, a batch normalization (BN), and a dropout. The ReLU activation function accelerates convergence and mitigates the gradient vanishing problem. The BN layer stabilizes the training process, and the dropout reduces the risk of overfitting and gradient explosion [37].
The output layer consists of one neuron, which corresponds to the TPW and is fully connected to the neurons in the previous layer, and the ReLU activation function and the MSE loss function are applied.
Figure 3 demonstrates the flowchart of the data processing and TPW retrieval in this work, including the establishment of the training and testing datasets, the development of the BPNNs, the TPW retrieval, and the validation and comparison. Once the structures and settings are determined, the BPNNs are trained using the error back-propagation method fed with the training data and testing data. To ensure effective training and reproducibility, the BPNNs are trained for 100 epochs with a batch size of 64 using the Adam optimizer, which provides stable and efficient convergence.
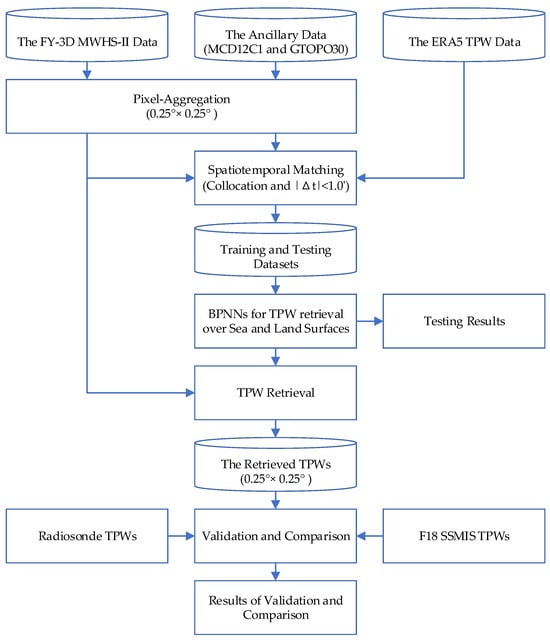
Figure 3.
Flowchart of the data processing and TPW retrieval.
Figure 4 displays the testing results of the trained BPNNs with testing dataset over sea surfaces and land surfaces. The scatters are basically distributed around the diagonals, and the predicted TPWs are linearly related to the ERA5 TPWs. Over sea surfaces, the mean error (ME), the RMSE, the MAE, and the determinant coefficient (R2) are 0.04 mm, 2.04 mm, 1.47 mm, and 0.98, respectively. Over land surfaces, the scatters are relatively more dispersed in contrast to those over sea surfaces, and the ME, the RMSE, MAE, and R2 are 0.06 mm, 2.60 mm, 1.75 mm, and 0.97, respectively. The results indicate that the predicting errors over land surfaces are slightly greater than those over sea surfaces. This is mainly attributed to the complex of land surfaces, especially the uncertainties of land surface emissivities, which are estimated by the Hewison’s model and less accurate over sparsely vegetated areas and bare areas [34,38].
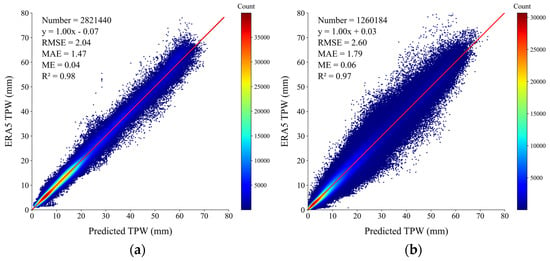
Figure 4.
Scatterplots of the predicted TPWs versus the ERA5 TPWs of the testing dataset (a) over sea surfaces and (b) over land surfaces.
Land cover types have impact on TPW retrieval [39]. Figure 5 shows the testing results across the 17 MODIS land cover types. The predicted TPWs are highly linear related to the ERA5 TPWs with R2 greater than or equal to 0.92, except that over the snow and ice areas, which is 0.86. The ME ranges between −0.56 mm and 0.35 mm. The RMSE (MAE) varies from 1.47 (1.03) mm to 3.49 (2.47) mm depending on land cover types. Overall, the retrieval errors over the three non-vegetated or sparsely vegetated areas (the water bodies, snow and ice, and barren or sparsely vegetated areas) are smallest, followed by the retrieval errors over the 11 natural vegetation areas, whereas the retrieval errors over the three human-developed and mosaic areas (the croplands, urban and built-up, and cropland/natural vegetation mosaic areas) are largest. The largest retrieval errors over the three human-developed and mosaic areas may be attributed to the high spatial heterogeneity of land surfaces, as well as the strong anthropogenic influences and dynamic surface–atmosphere coupling effect. In contrast, the non-vegetated or sparsely vegetated areas and the natural vegetation areas are relatively more homogeneous and their properties are also more stable, which is beneficial to the TPW retrieval. In general, the testing results in this work basically agree with those in [39,40]. The results indicate that the BPNN in this work is not only applicable to all land cover types, but also has excellent performance.
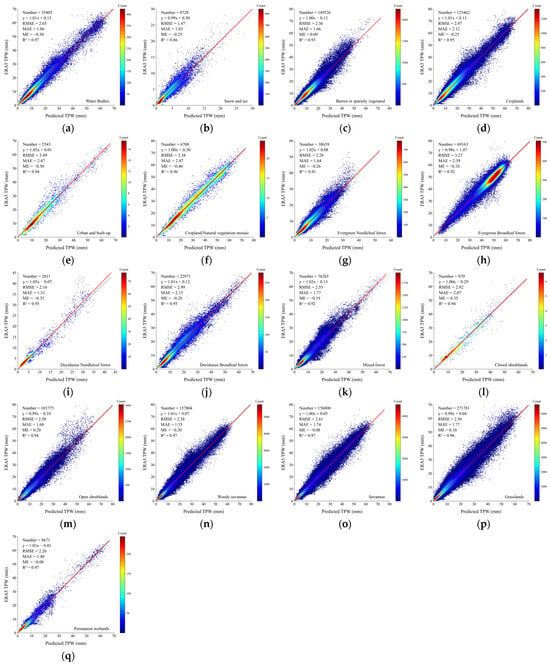
Figure 5.
Scatterplots of the predicted TPWs in this work versus the ERA5 TPWs over (a) the water bodies areas, (b) the snow and ice areas, (c) the barren or sparsely vegetated areas, (d) the croplands areas, (e) the urban and built-up areas, (f) the cropland/natural vegetation mosaic areas, (g) the evergreen needleleaf forest areas, (h) the evergreen broadleaf forest areas, (i) the deciduous needleleaf forest areas, (j) the deciduous broadleaf forest areas, (k) the mixed forest areas, (l) the closed shrublands areas, (m) the open shrublands areas, (n) the woody savannas areas, (o) the savannas areas, (p) the grassland areas, and (q) the permanent wetland areas.
Although the BPNNs adopted in this work are data-driven models, their design is fundamentally guided by physical knowledge. Traditional physical retrieval methods explicitly describe the radiative transfer process using physical models, and relate the simulated TBs to TPWs. In contrast, the neural network approach learns nonlinear relations between TBs and TPW in terms of large number of training samples, without explicitly involving physical models. However, through training with well-selected samples and input features, the network can implicitly learn the underlying physical relationships. The construction of the input features reflects the physically-informed design. For example, the TBs in the 183.31 GHz channels are strongly sensitive to TPW, while the 118.75 GHz channels are mainly used to detect atmospheric temperature profiles, and the window channels at 89.0 GHz and 150.0 GHz provide surface emission information and scattering. Furthermore, over land surfaces, additional inputs, such as elevation, land cover types, and land surface emissivities, are included to account for the complex land–atmosphere interactions. These features are selected in terms of known physical mechanisms. Thus, the neural network architecture and input feature design are not purely statistical, but rather constructed in a way that incorporates atmospheric radiative transfer theory, which enhances both the retrieval accuracy and the model interpretability.
To further evaluate the contribution and importance of input features in TPW retrieval, the SHapley Additive exPlanations (SHAP) method is used. The SHAP is a model interpretation technique rooted in cooperative game theory, and it quantifies feature importance by calculating the marginal contribution of each feature to the model’s output [41]. Figure 6 presents the SHAP analysis results of the BPNNs over both sea surfaces and land surfaces. Over sea surfaces, the five most important features are the TB9, TB1, EIA, TB13, and TB10, respectively, while the five least important features are TB4, the longitude, TB3, TB2, and the month, respectively, where the TBi denotes the TB in the MWHS-II channel i. Over land surfaces, the five most important features are TB15, TB13, TB8, TB9, and TB6, respectively, whereas the five least important features are the land cover types, TB3, longitude, TB2, and the month, respectively. The land surface emissivities in the channels 1 (89.0 GHz) and 10 (150.0 GHz) and the elevation also make significant contributions to the TPW retrieval over land surfaces. Over both sea and land surfaces, the TBs in the MWHS-II oxygen-absorption channels centered at 118.75 GHz have obvious contributions to the TPW retrieval. The SHAP results justify from another side that the selection of the input features is reasonable.
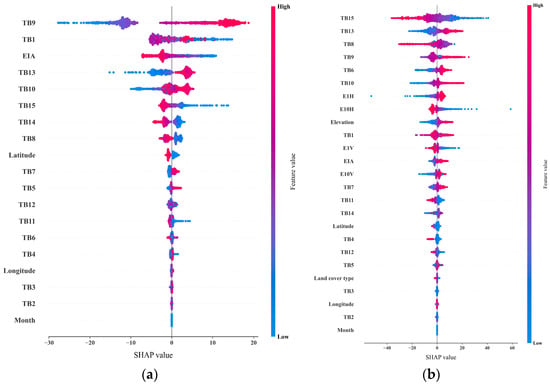
Figure 6.
SHapley Additive exPlanations (SHAP) values of the input features over (a) sea surfaces and (b) land surfaces (TBi denotes the brightness temperature in the MWHS-II channel i, while EiV and EiH stand for the land surface emissivities in the MWHS-II channel i at vertical and horizontal polarizations, respectively).
In general, the BPNNs are well designed, and both the training and testing results show that the BPNNs have good accuracy, strong robustness, and generalization capability in TPW retrieval.
3.2. Comparison to Other Commonly Used Methods
To further evaluate the retrieval performance, the BPNNs developed in this work are compared to seven commonly used methods with the same training data and testing data in Section 2. The seven methods are the D-matrix method [42], the Ridge method [43], the Lasso method [44], the physical method [45], the random forest (RF) method [46], the support vector machine (SVM) method [47], and the eXtreme Gradient Boosting (XGBoost) method [48]. The first three methods are statistical ones, while the last three methods are the machine learning ones. The D-matrix method is a strategy used to solve systems of linear equations by expressing them as matrices and reducing them to a specific form. The Ridge method, also known as L2 regularization, is a technique used in linear regression to address the problem of multicollinearity among predictor variables. It combats overfitting by adding a penalty term (L2 regularization) to the ordinary least squares (OLS) objective function, and achieves realistic and reliable results. The Lasso method is a regression method based on least absolute shrinkage and selection operator and it is an important technique in regression analysis for variables selection and regularization. The Lasso method helps remove irrelevant data features and prevents overfitting. This allows features with weak influence to be clearly identified as the coefficients of less important variables are shrunk toward zero. The physical method establishes the relationship between TPW and microwave radiometer brightness temperatures by simplifying the radiative transfer process. The RF method is a commonly-used machine learning algorithm, trademarked by Leo Breiman and Adele Cutler, which combines the output of multiple decision trees to reach a single result. Its ease of use and flexibility have fueled its adoption, as it handles both classification and regression problems. The SVM method is a supervised machine learning algorithm used for classification and regression tasks. It aims to find the optimal hyperplane in an N-dimensional space to separate data points into different classes. The algorithm maximizes the margin between the closest points of different classes. The physical method is not applied to the TPW retrieval over land surfaces in this work because of its poor performance over land surfaces [45].
The following six standard statistical metrics are used for quantitative analysis: the ME, the MAE, the RMSE, the mean squared logarithmic error (MSLE), the mean absolute percentage error (MAPE), and R2, which are given by the following equations, respectively,
where N is the number of the matching samples; and are the ith predicted TPW and ERA5 TPW, respectively; and are the mean of the predicted TPWs and the mean of the ERA5 TPWs, respectively.
Besides the testing results of the seven methods, the testing results of the BPNNs are also listed in Table 3 for convenience. Over sea surfaces, the ME, MAE, RMSE, MAPE, MSLE, and R2 of the BPNN in this work are 0.04 mm, 1.47 mm, 2.04 mm, 0.01 mm, 8.64%, and 0.982, respectively. Except for the ME, the BPNN in this work is far superior to the seven methods on other statistical metrics. Over land surfaces, the ME, MAE, RMSE, MSLE, MAPE, and R2 of the BPNN in this work are, respectively, 0.06 mm, 1.79 mm, 2.60 mm, 0.03 mm, 15.53%, and 0.967, which are slightly worse than those of the BPNN over sea surfaces. However, the BPNN over land surfaces is superior to other six methods on all metrics. It should be noted that the XGBoost method achieved good results only second to the BPNNs in this work. In general, the BPNNs in this work have good performance in TPW retrieval over both sea and land surfaces.

Table 3.
Comparison between the results obtained by the BPNNs in this work and the results obtained by the seven commonly used methods.
4. Results
4.1. Retrieved TPWs
The TPWs are retrieved from the FY−3D MWHS-II data in 2022 at a spatial resolution of 0.25° × 0.25° using the BPNNs developed in Section 3. Taking the results on 1 January, 1 April, 1 July, and 1 October 2022 as examples, Figure 7 displays the spatiotemporal distribution and variation of the TPWs over both sea and land surfaces. The four days are selected because they are good representatives of the four seasons. The TPW mainly ranges between 0.0 and 75.0 mm, and shows an obvious latitudinal dependence: TPWs are highest in tropical regions and gradually decrease toward higher latitudes. The relatively high TPWs in the tropics are primarily attributed to intense evaporation and deep convection, especially over the tropical Pacific, Indian, and Atlantic Oceans, the Amazon Basin, the rainforests of West Africa, and the Southeast Asian archipelago.
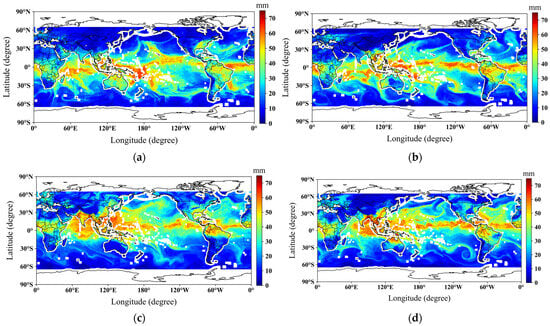
Figure 7.
Maps of the total precipitable water at spatial resolution of 0.25 in longitude and latitude retrieved from the FY−3D MWHS-II data on (a) 1 January 2022, (b) 1 April 2022, (c) 1 July 2022, and (d) 1 October 2022.
Globally, the TPWs over sea surfaces exhibit distinct latitude-dependent structures. The areas with large TPWs are approximately concentrated between 30°S and 30°N, associated with tropical moisture-rich environments driven by strong sea surface evaporation and deep convective systems. In the mid-latitudes (30–60° in northern and southern hemispheres), obvious moisture transport belts are observed, largely influenced by subtropical high-pressure systems and mid-latitude cyclonic activity. These transport features vary with seasons: they move southward in January (winter in north hemisphere) and northward in July (summer in north hemisphere), which is mirrored against the seasonal movement of the Intertropical Convergence Zone (ITCZ). The strengthening of these features in summer seasons leads to pronounced TPW increases in tropical and subtropical ocean regions. Additionally, TPW distribution in the mid-latitudes tends to be more zonally uniform in winter, whereas in summer, enhanced baroclinic activity introduces stronger meridional (north–south) asymmetry.
In contrast to sea surfaces, TPW distribution over land surfaces is more complex due to surface heterogeneity and the influences of terrain, and exhibits stronger seasonal variations. The large TPWs are primarily observed in the Central African Basin, the Southeast Asian archipelago (including Indonesia), and the tropical rainforest regions of Central and South America. These areas are strongly influenced by tropical monsoons, deep convection, and abundant precipitation, maintaining high water vapor levels all through the year. In the Northern Hemisphere mid-latitudes, TPWs over land surfaces are generally lower, especially in winter, due to the dominance of dry continental air masses under cold high-pressure systems. For instance, over eastern China, strong seasonal variation is observed: in summer, TPW increases significantly under the influence of the East Asian summer monsoon and moist southwesterly flows, particularly in the Yangtze River basin. In contrast, western China remains relatively dry throughout the year due to its inland location, complex terrain, and limited moisture transport, resulting in weaker seasonal variation and overall lower TPWs.
4.2. Validation and Comparison
The TPWs retrieved in this work are validated with the TPWs extracted from the radiosonde data provided by the University of Wyoming in the USA. The TPWs retrieved in this work are matched to the radiosonde data with the following two criteria: (1) the radiosonde stations fall in the 0.25° × 0.25° grid at least 25 km away from the continent coastlines, and (2) the absolute time difference is less than 3 h. As shown in Figure 8, 16 deep-sea radiosonde stations located on islands and 135 continent stations are qualified. The TPWs of the radiosonde data are calculated using Equation (1). A total of 4613 matching TPWs over sea surfaces and 71,577 matching TPWs over land surfaces were collected in 2022.
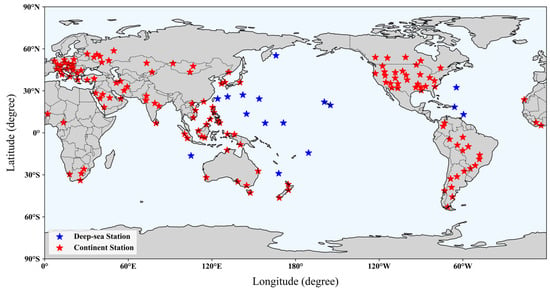
Figure 8.
The spatial distribution of the selected radiosonde stations.
It should be noted that the deep-sea radiosonde stations are located on islands, which are higher than sea surfaces in altitude. This will lead to the results that the retrieved TPWs over sea surfaces are slightly larger than the TPWs extracted from the radiosonde data. Bock et al. proposed an altitude correction term for TPW [49], which is given by
where Δω is the correction term for the TPW ω, and h is the altitude of the deep-sea radiosonde station in meters.
The TPWs at deep-sea stations are corrected by adding the Δω. After the altitude correction, the retrieved TPWs are more consistent with the radiosonde TPWs. Figure 9 displays the scatterplots of the TPWs retrieved in this work versus the radiosonde TPWs. The TPWs retrieved in this work are highly linearly related to the radiosonde TPWs with determinant coefficients (R2) greater than 0.96. The scatters over sea surfaces are more concentrated around the diagonal than those over land surfaces. Over sea surfaces, the ME, the RMSE, and MAE are, respectively, −1.17 mm, 3.46 mm, and 2.63 mm, while over land surfaces, they are −0.80 mm, 4.04 mm, and 3.13 mm, respectively. Compared to the radiosonde TPWs, the TPWs in this work are systematically underestimated, especially in the heterogeneous moisture fields. This is primarily attributed to the spatial scale effects: the radiosonde TPWs were measured at stations (points), while the TPWs in this work were retrieved over the 0.25° × 0.25° grids. The underestimation was also observed in other gridded datasets, e.g., the ERA5 TPWs [18]. It should be noted that the ERA5 TPWs are used as the truths of the training/testing samples in this work, and the underestimation was finally transferred to the outputs of the BPNNs in TPW retrieval. Further investigation shows that there is a bimodal distribution of TPWs in Figure 9. The first peak centered at about 38 mm is linked to a strong convective activity and a warming of sea surface temperature in the tropical regions, while the second peak appears to be associated with drier conditions over subtropical and mid-latitude sea surfaces, where convection is not so strong. In addition, the seasonal variation is another reason forming the bimodal distribution of TPWs. The retrieved TPWs over land surfaces have relatively larger errors than those over sea surfaces because of the larger variations in both land surfaces and atmospheres, and the complex interaction between them. In general, the TPWs retrieved in this work are accurate enough against the radiosonde TPWs over both sea surfaces and land surfaces.
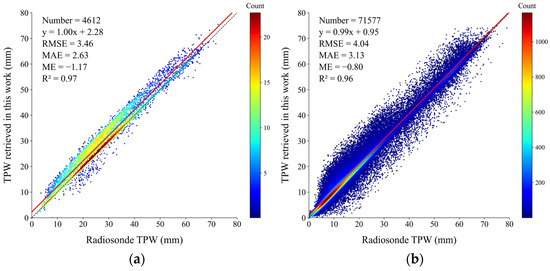
Figure 9.
Scatterplots of the TPWs retrieved in this work versus the radiosonde TPWs (a) over sea surfaces and (b) over land surfaces.
The TPWs retrieved in this work are also compared to the F18 SSMIS TPWs in 2022. As introduced in Section 2, the F18 SSMIS TPW product only provides TPWs over sea surfaces, and thus the comparison is conducted only over sea surfaces. Figure 10 displays the maps of the F18 SSMIS TPWs on 1 January, 1 April, 1 July, and 1 October of 2022. Because of the narrow width of the F18 SSMIS swaths, gaps exist between the observations of two neighboring orbits, which is not observed in Figure 7. The TPWs in Figure 7 and Figure 10 are not only similar in spatial distribution, but also have similar values.
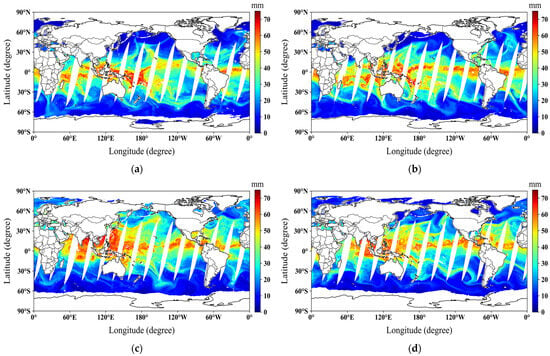
Figure 10.
Maps of the F18 SSMIS TPWs on (a) 1 January, (b) 1 April, (c) 1 July, and (d) 1 October of 2022.
Besides a qualitative comparison, a quantitative comparison is also conducted in this work, which needs matching samples. However, due to the large difference between the satellite orbits, the number of the matching samples between the TPWs in this work and the F18 SSMIS TPWs is small and their spatiotemporal distribution is generally uneven. In addition, the F18 SSMIS TPWs also contain retrieval errors, and consequently it is difficult to determine which one is more accurate. Therefore, the F18 SSMIS TPWs are also validated against the radiosonde TPWs. With the matching criteria presented above, 1559 matching samples between the F18 SSMIS TPWs and radiosonde TPWs are collected, and they are displayed in Figure 11. Against the radiosonde TPWs, the ME, the RMSE, and MAE of F18 SSMIS TPWs are, respectively, 0.86 mm, 4.24 mm, and 3.37 mm. The RMSE and MAE of F18 SSMIS TPWs are 0.78 mm and 0.74 mm larger than those of the TPWs retrieved in this work, respectively. The determinant coefficient (R2) of the F18 SSMIS TPWs is 0.92, which is also less than that of the TPWs retrieved in this work. Therefore, a conclusion can be made that the TPWs retrieved in this work are more consistent with the radiosonde TPWs than the F18 SSMIS TPWs; in other words, the TPWs retrieved in this work are more accurate than the F18 SSMIS TPWs.
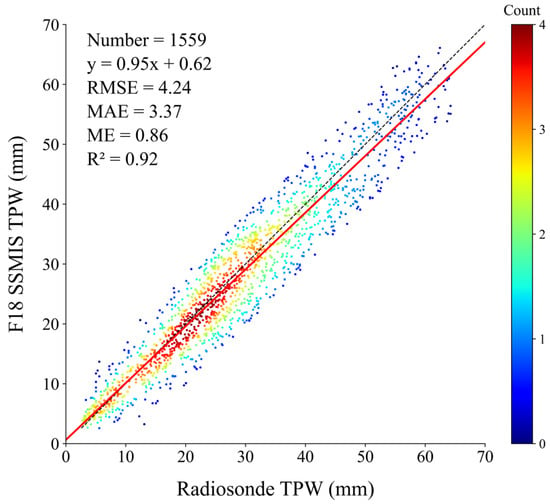
Figure 11.
Scatterplot of the F18 SSMIS TPWs versus the radiosonde TPWs.
5. Discussion
Although the BPNNs developed in this work can efficiently handle the nonlinear relationships between the TBs and TPW and accurate TPWs were obtained over both sea and land surfaces, some limitations are worth noting, such as the data dependency, physical interpretability, generalization ability, and error control. In the future, collaborative optimization of “data-physics-algorithm” is needed, combined with knowledge in the field of meteorology, to improve the TPW retrieval accuracy, especially over land surfaces.
In the validation, the radiosonde TPWs were measured at points, while the TPWs in this work were retrieved over the 0.25° × 0.25° grids. The spatial scale mismatch may produce errors in the validation. In addition, as shown in Figure 8, the spatial distribution of the radiosonde stations is strongly uneven, and some regions, such as plateaus and oceans, lack representative sites. The radiosonde stations collect TPWs only at 0:00 and 12:00 every day. The lack of spatiotemporal representativeness of the radiosonde TPWs may also introduce uncertainty into the validation results.
Although the BPNNs developed in this work have the capability to describe the regional and seasonal variations of the TPWs, the model performance in different climatic zones and the spatial distribution of the TPW retrieval errors across seasons should be analyzed. However, because of the sparsely spatiotemporal distribution of the radiosonde stations, it is difficult to collect a sufficient number of matching samples, and thus the evaluation and analysis may also be biased. In addition, one year of data are not enough for the model training, the TPW retrieval and validation. In the future, long-term training/testing datasets will be constructed for model training, and long-term TPWs over the globe will be retrieved from the FY-3D MWHS-II data, and the accuracy and stability should be fully evaluated.
6. Conclusions
This paper presented the TPW retrieval from the FY-3D MWHS-II L1 data at spatial resolution of 0.25° in longitude and latitude over both sea and land surfaces. The results indicated that the BPNN algorithms developed in this work are valid and accurate, which are superior to the D-matrix method, the Ridge method, the Lasso method, the physical method, the RF method, the SVM method, and the XGBoost method. Against the radiosonde TPWs, the ME, the RMSE, and MAE of the TPWs retrieved from the FY-3D MWHS-II data in this work are −1.17 mm, 3.46 mm, and 2.63 mm over sea surfaces, respectively, while they are −0.80 mm, 4.04 mm, and 3.13 mm over land surfaces, respectively. The TPWs retrieved in this work were averagely underestimated against the radiosonde TPWs, which may be attributed to the discrepancy between the ERA5 TPWs and the radiosonde TPWs. The results also showed that the TPWs retrieved in this work are much more accurate than the F18 SSMIS TPWs. The results not only highlight the performance advantage of neural networks but also demonstrate their capability to retrieve TPWs over both sea and land surfaces, particularly when guided by physically-informed feature design and interpretation techniques, such as the SHAP.
In the future, long-term training/testing datasets will be constructed for model training, and long-term TPWs over both sea and land surfaces will be retrieved from the FY-3D MWHS-II data and validated against the radiosonde TPWs.
Author Contributions
Conceptualization, Y.Z. and G.-M.J.; methodology, Y.Z. and G.-M.J.; software, Y.Z.; validation, Y.Z. and G.-M.J.; formal analysis, G.-M.J.; investigation, G.-M.J.; resources, Y.Z.; data curation, Y.Z.; writing—original draft preparation, Y.Z.; writing—review and editing, G.-M.J.; visualization, Y.Z.; supervision, G.-M.J.; project administration, G.-M.J.; funding acquisition, G.-M.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Key Research and Development Program of China under Grant 2021YFB3900401, and in part by the National Natural Science Foundation of China under Grant 41871222.
Data Availability Statement
Data available on request due to privacy restrictions.
Acknowledgments
The authors would like to thank the editors and anonymous reviewers for their constructive suggestions, which helped them to improve the quality and presentation of this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zveryaev, I.I.; Allan, R.P. Water vapor variability in the tropics and its links to dynamics and precipitation. J. Geophys. Res. Atmos. 2005, 110, D21. [Google Scholar] [CrossRef]
- Ji, D.; Shi, J.; Letu, H.; Li, W.; Zhang, H.; Shang, H. A Total precipitable water product and its trend analysis in recent years based on passive microwave radiometers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7324–7335. [Google Scholar] [CrossRef]
- Ji, D.; Shi, J.; Xiong, C.; Wang, T.; Zhang, Y. A total precipitable water retrieval mthod over land using the combination of passive microwave and optical remote sensing. Remote Sens. Environ. 2017, 191, 313–327. [Google Scholar] [CrossRef]
- Schröder, M.; Lockhoff, M.; Forsythe, J.M.; Cronk, H.Q.; Vonder Haar, T.H.; Bennartz, R. The GEWEX water vapor assessment: Results from intercomparison, trend, and homogeneity analysis of total column water vapor. J. Appl. Meteorol. Climatol. 2016, 55, 1633–1649. [Google Scholar] [CrossRef]
- Alshawaf, F.; Fuhrmann, T.; Knöpfler, A.; Luo, X.; Mayer, M.; Hinz, S.; Heck, B. Accurate estimation of atmospheric water vapor using GNSS observations and surface meteorological data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3764–3771. [Google Scholar] [CrossRef]
- Czajkowski, K.P.; Goward, S.N.; Shirey, D.; Walz, A. Thermal remote sensing of near-surface water vapor. Remote Sens. Environ. 2002, 79, 253–265. [Google Scholar] [CrossRef]
- Firsov, K.M.; Chesnokova, T.Y.; Bobrov, E.V.; Klitochenko, I.I. Total water vapor content retrieval from sun photometer data. Atmos. Ocean. Opt. 2013, 26, 281–284. [Google Scholar] [CrossRef]
- Grody, N.C.; Gruber, A.; Shen, W.C. Atmospheric water content over the tropical pacific derived from the nimbus-6 scanning microwave spectrometer. J. Appl. Meteorol. Climatol. 1980, 19, 986–996. [Google Scholar] [CrossRef]
- Alishouse, J.C.; Snyder, S.A.; Vongsathorn, J.; Ferraro, R.R. Determination of oceanic total precipitable water from the SSM/I. IEEE Trans. Geosci. Remote Sens. 1990, 28, 811–816. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, J.; Wang, H.; Feng, W.; Wang, Y. Physical statistical algorithm for precipitable water vapor inversion on land surface based on multi-source remotely sensed data. Sci. China Earth Sci. 2015, 58, 2340–2352. [Google Scholar] [CrossRef]
- Bobylev, L.P.; Zabolotskikh, E.V.; Mitnik, L.M.; Mitnik, M.L. Atmospheric water vapor and cloud liquid water retrieval over the arctic ocean using satellite passive microwave sensing. IEEE Trans. Geosci. Remote Sens. 2009, 48, 283–294. [Google Scholar] [CrossRef]
- Boukabara, S.A.; Garrett, K.; Chen, W.; Iturbide-Sanchez, F.; Grassotti, C.; Kongoli, C.; Meng, H. MiRS: An all-weather 1DVAR satellite data assimilation and retrieval system. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3249–3272. [Google Scholar] [CrossRef]
- Liu, H.; Tang, S.; Hu, J.; Zhang, S.; Deng, X. An improved physical split-window algorithm for precipitable water vapor retrieval exploiting the water vapor channel observations. Remote Sens. Environ. 2017, 194, 366–378. [Google Scholar] [CrossRef]
- Zhang, P.; Lu, Q.; Hu, X.; Gu, S.; Yang, L.; Min, M.; Xian, D. Latest progress of the chinese meteorological satellite program and core data processing technologies. Adv. Atmos. Sci. 2019, 36, 1027–1045. [Google Scholar] [CrossRef]
- Carminati, F.; Atkinson, N.; Candy, B.; Lu, Q. Insights into the microwave instruments onboard the fengyun-3d satellite: Data quality and assimilation in the met office NWP System. Adv. Atmos. Sci. 2021, 38, 1379–1396. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, G. Retrieval of Global Total Precipitable Water over Sea Surfaces from MWHS-II/FY-3D Data Using the BP Neural Network. In Proceedings of the 2024 Photonics & Electromagnetics Research Symposium (PIERS), Chengdu, China, 8–11 January 2024; pp. 1–5. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Thépaut, J.-N. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, C.; Chen, B.; Dai, W. Consistency evaluation of precipitable water vapor derived from ERA5, ERA5-interim, GNSS, and radiosonde over china. Radio Sci. 2019, 54, 561–571. [Google Scholar] [CrossRef]
- Wang, S.; Xu, T.; Nie, W.; Jiang, C.; Yang, Y.; Fang, Z.; Li, M.; Zhang, Z. Evaluation of precipitable water vapor from five reanalysis products with ground-based GNSS observations. Remote Sens. 2020, 12, 1817. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Blewitt, G. Global comparisons of ERA5 and the operational HRES tropospheric delay and water vapor products with GPS and MODIS. Earth Space Sci. 2021, 8, e2020EA001417. [Google Scholar] [CrossRef]
- Gurbuz, G.; Jin, S. Long-term variations of precipitable water vapor estimated from GPS, MODIS and radiosonde observations in Turkey. Int. J. Climatol. 2017, 37, 5170–5180. [Google Scholar] [CrossRef]
- Kroodsma, R.A.; Berg, W.; Wilheit, T.T. Special sensor microwave imager/sounder updates for the global precipitation measurement V07 data suite. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5303511. [Google Scholar] [CrossRef]
- Sulla-Menashe, D.; Gray, J.M.; Abercrombie, S.P.; Friedl, M.A. Hierarchical mapping of annual global land cover 2001 to present: The MODIS collection 6 land cover product. Remote Sens. Environ. 2019, 222, 183–194. [Google Scholar] [CrossRef]
- Miliaresis, G.C.; Argialas, D.P. Segmentation of physiographic features from the global digital elevation model/GTOPO30. Comput. Geosci. 1999, 25, 715–728. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, G. Intercalibration of FY-3D MWHS-II Water Vapor Absorption Channels Against S-NPP ATMS Channels Using the Double Difference Method. In Proceedings of the 2024 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2024), Athens, Greece, 7–12 July 2024; pp. 6255–6258. [Google Scholar]
- Yu, W.; Xu, X.; Jin, S.; Ma, Y.; Liu, B.; Gong, W. BP neural network retrieval for remote sensing atmospheric profile of ground-based microwave radiometer. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4502105. [Google Scholar] [CrossRef]
- Meng, S.; Zhang, T.; Jiang, G.; Ye, H. Retrieval of Atmospheric Temperature and Humidity Profiles from FY-3E MWTS and MWHS Data Using Deep Learning Neural Networks. In Proceedings of the Fifth International Conference on Geoscience and Remote Sensing Mapping (ICGRSM 2023), Lianyungang, China, 15–17 December 2023; Volume 12980, pp. 564–569. [Google Scholar]
- Boyarskii, D.A.; Etkin, V.S. Two flow model of wet snow microwave emissivity. In Proceedings of the IGARSS ’94-1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; pp. 2068–2070. [Google Scholar]
- Weng, F.; Yan, B.; Grody, N.C. A microwave land emissivity model. J. Geophys. Res. 2001, 106, 20115–20123. [Google Scholar] [CrossRef]
- Chen, K.S.; Wu, T.D.; Tsang, L.; Li, Q.; Shi, J.; Fung, A.K. Emission of roughsur faces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Kurum, M.; Lang, R.H.; O’Neill, P.E.; Joseph, A.T.; Jackson, T.J.; Cosh, M.H. A first-order radiative transfer model for microwave radiometry of forest canopies at L-band. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3167–3179. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Njoku, E.G.A. A semiempirical model for interpreting microwave emission from semiarid land surfaces as seen from space. IEEE Trans. Geosci. Remote Sens. 1990, 28, 384–393. [Google Scholar] [CrossRef]
- Wiesmann, A.; Mätzler, C. Microwave emission model of layered snowpacks. Remote Sens. Environ. 1999, 70, 307–316. [Google Scholar] [CrossRef]
- Hewison, T.J. Airborne measurements of forest and agricultural land surface emissivity at millimeter wavelengths. IEEE Trans. Geosci. Remote Sens. 2002, 39, 393–400. [Google Scholar] [CrossRef]
- Biswas, S.K.; Farrar, S.; Gopalan, K.; Santos-Garcia, A.; Jones, W.L.; Bilanow, S. Intercalibration of microwave radiometer brightness temperatures for the global precipitation measurement mission. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1465–1477. [Google Scholar] [CrossRef]
- Zhang, W.-L.; Jiang, G.-M. Intercalibration of FY-3C MWRI over forest warm-scenes based on microwave radiative transfer model. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5301011. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Tian, Y.; Peters-Lidard, C.D.; Harrison, K.W.; Prigent, C.; Norouzi, H.; Aires, F.; Masunaga, H. Quantifying uncertainties in land-surface microwave emissivity retrievals. IEEE Trans. Geosci. Remote Sens. 2013, 52, 829–840. [Google Scholar] [CrossRef]
- Xia, X.; Fu, D.; Shao, W.; Jiang, R.; Wu, S.; Zhang, P.; Xia, X. Retrieving precipitable water vapor over land from satellite passive microwave radiometer measurements using automated machine learning. Geophys. Res. Lett. 2023, 50, e2023GL105197. [Google Scholar] [CrossRef]
- Kazumori, M. Precipitable water vapor retrieval over land from GCOM-W/AMSR2 and its application to numerical weather prediction. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6663–6666. [Google Scholar]
- Mangalathu, S.; Hwang, S.H.; Jeon, J.S. Failure mode and effects analysis of rc members based on machine-learning-based shapley additive explanations (SHAP) approach. Eng. Struct. 2020, 219, 110927. [Google Scholar] [CrossRef]
- Li, J.; Huang, H. Retrieval of atmospheric profiles from satellite sounder measurements by use of the discrepancy principle. Appl. Opt. 1999, 38, 916–923. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Munoz-Mari, J.; Gomez-Chova, L.; Guanter, L.; Calbet, X. Nonlinear statistical retrieval of atmospheric profiles from MetOp-IASI and MTG-IRS infrared sounding data. IEEE Trans. Geosci. Remote Sens. 2011, 50, 1759–1769. [Google Scholar] [CrossRef]
- Al-Obeidat, F.; Spencer, B.; Alfandi, O. Consistently accurate forecasts of temperature within buildings from sensor data using ridge and lasso regression. Future Gener. Comput. Syst. 2020, 110, 382–392. [Google Scholar] [CrossRef]
- Miao, J.; Kunzi, K.; Heygster, G.; Lachlan-Cope, T.A.; Turner, J. Atmospheric water vapor over antarctica derived from Special Sensor Microwave/Temperature 2 Data. J. Geophys. Res. Atmos. 2001, 106, 10187–10203. [Google Scholar] [CrossRef]
- Di Paola, F.; Ricciardelli, E.; Cimini, D.; Cersosimo, A.; Di Paola, A.; Gallucci, D.; Viggiano, M. MiRTaW: An algorithm for atmospheric temperature and water vapor profile estimation from ATMS measurements using a random forests technique. Remote Sens. 2018, 10, 1398. [Google Scholar] [CrossRef]
- Ghaffari-Razin, S.R.; Majd, R.D.; Hooshangi, N. Regional modeling and forecasting of precipitable water vapor using least square support vector regression. Adv. Space Res. 2023, 71, 4725–4738. [Google Scholar] [CrossRef]
- Xu, J.; Liu, Z.; Hong, G.; Cao, Y. A new machine-learning-based calibration scheme for MODIS thermal infrared water vapor product using BPNN, GBDT, GRNN, KNN, MLPNN, RF, and XGBoost. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5001412. [Google Scholar] [CrossRef]
- Bock, O.; Bouin, M.-N.; Walpersdorf, A.; Lafore, J.-P.; Janicot, S.; Guichard, F.; Agusti-Panareda, A. Comparison of ground-based GPS precipitable water vapour to independent observations and NWP model reanalyses over Africa. Q. J. R. Meteorol. Soc. 2007, 133, 2011–2027. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).