ASTER GDEM Correction Based on Stacked Ensemble Learning and ICEsat-2/ATL08: A Case Study from the Qilian Mountains
Abstract
1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
2.2.1. ASTER GDEM
2.2.2. ICESat-2/ATL08 Product
2.2.3. Field Measurements
2.2.4. Land Cover Type
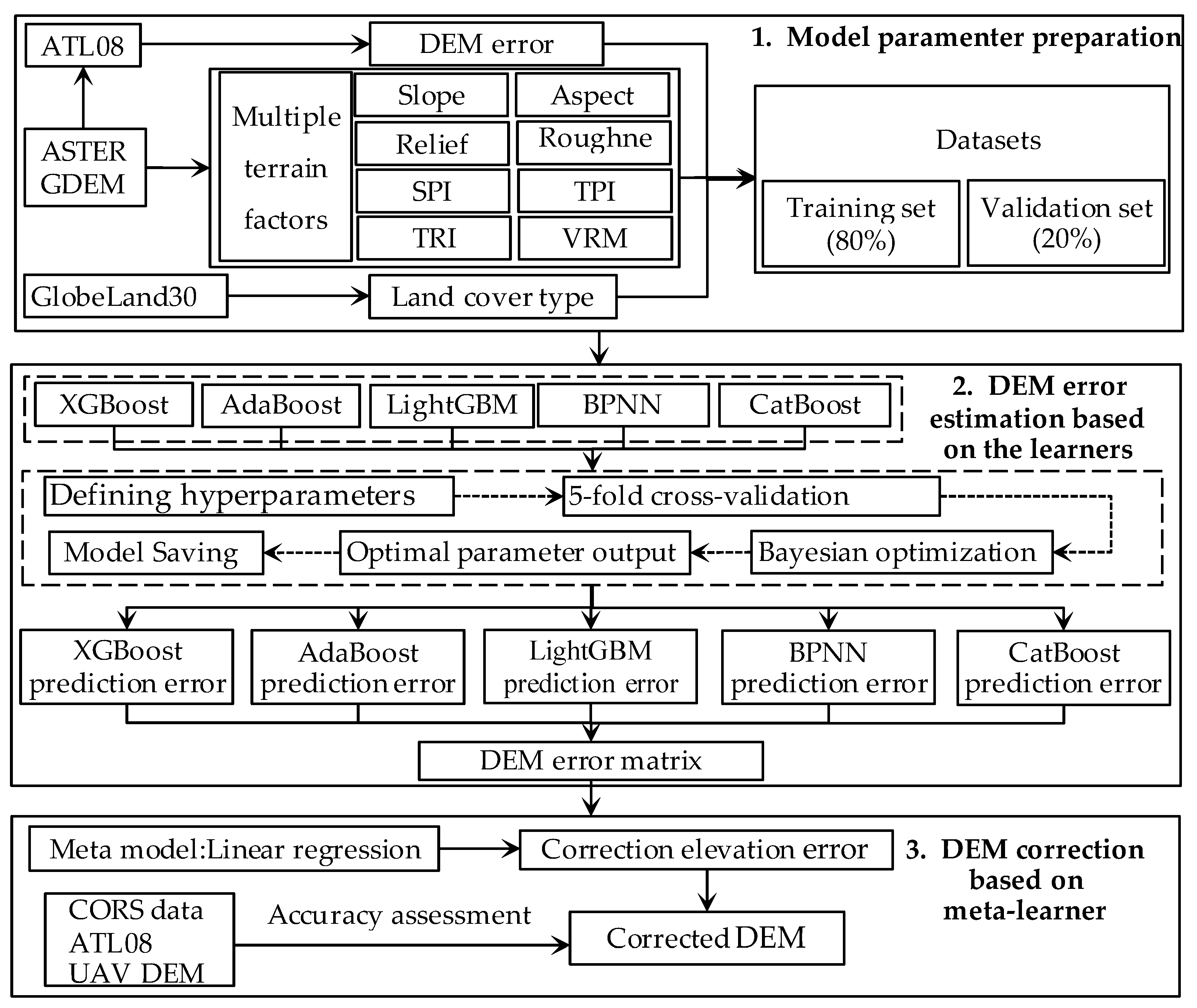
3. Methods
3.1. Model Parameters Preparation
3.2. DEM Error Estimation Based on the Learners
3.2.1. Hyperparameter Settings for Five Learners
3.2.2. Learner Training Based on Training and Validation Sets
3.2.3. Construction of DEM Error Matrix
3.3. DEM Correction Based on Stack Ensemble Learning
3.4. Accuracy Assessment Methods
4. Results
4.1. Accuracy Evaluation of DEM
4.1.1. DEM Accuracy Evaluation Based on CORS and ATL08 Products
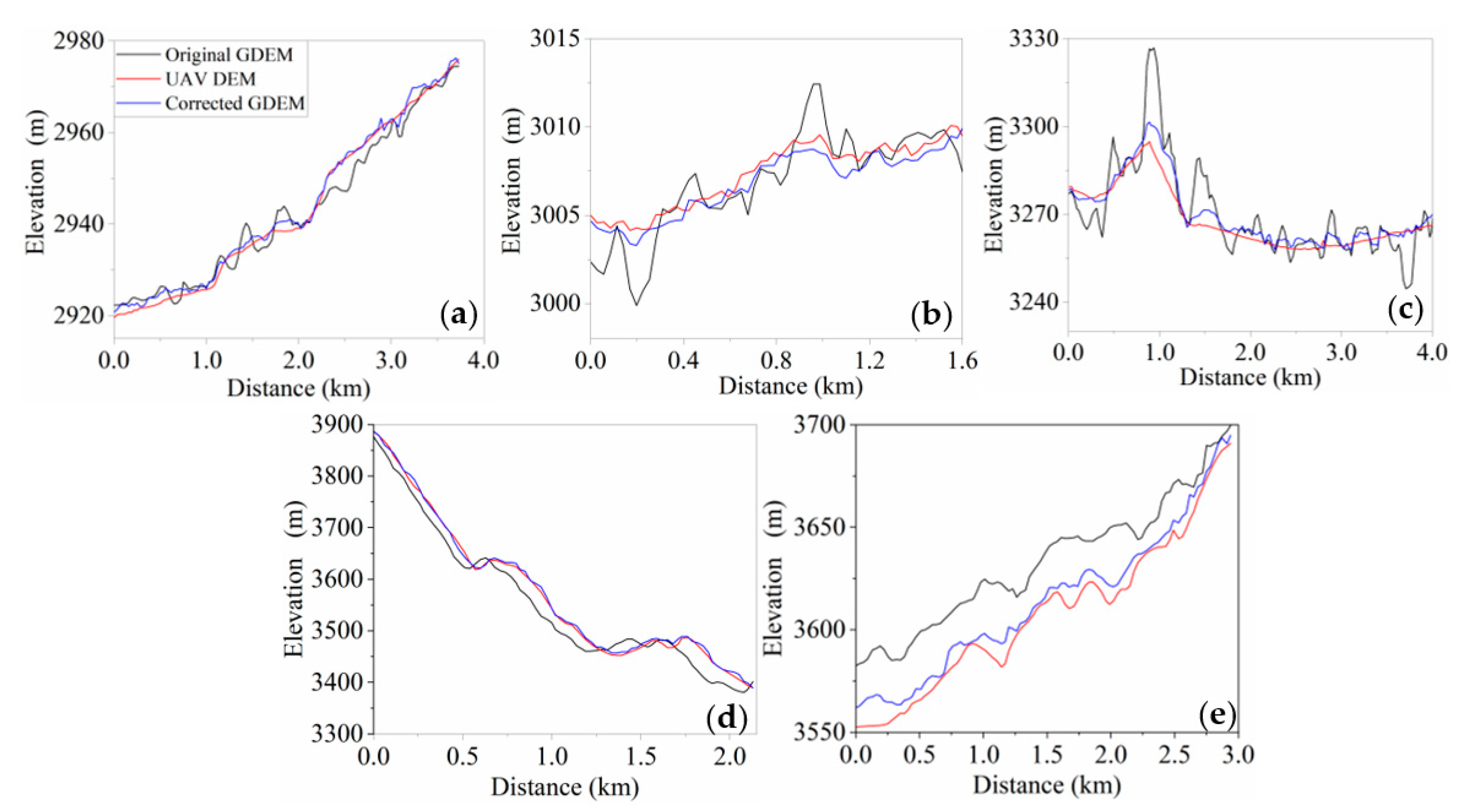
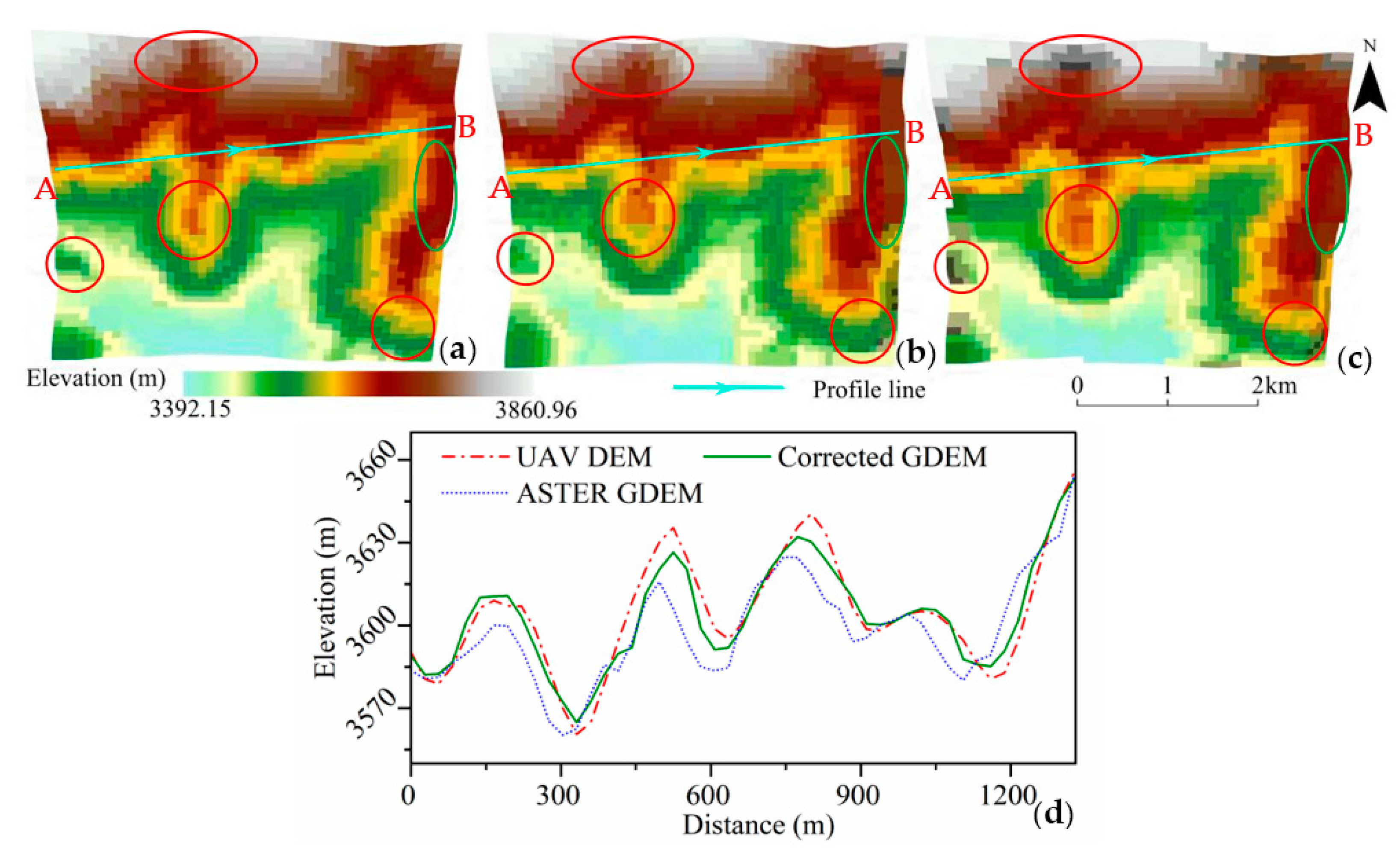
4.1.2. Accuracy Analysis Based on UAV DEM
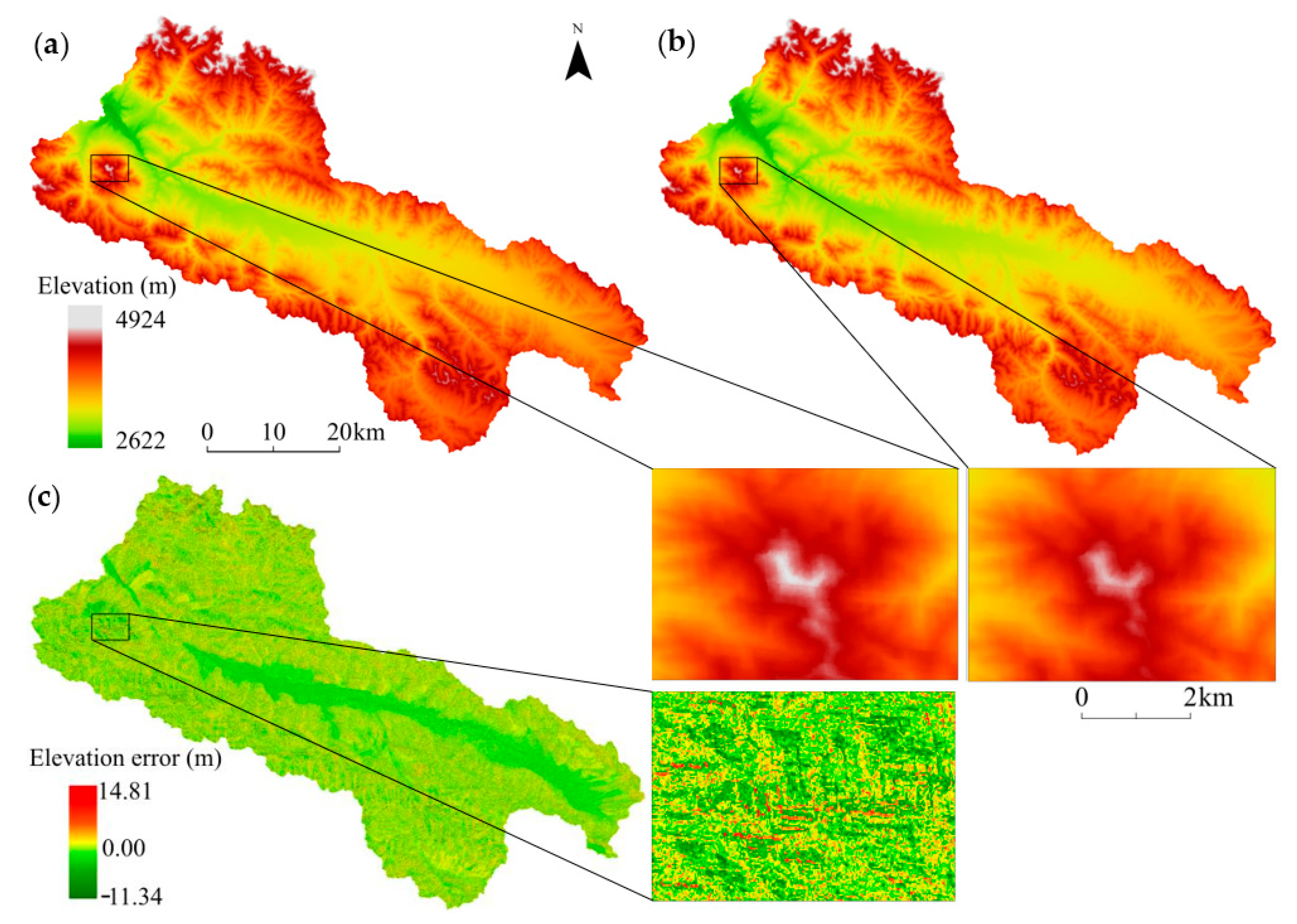
4.2. DEM Correction Results
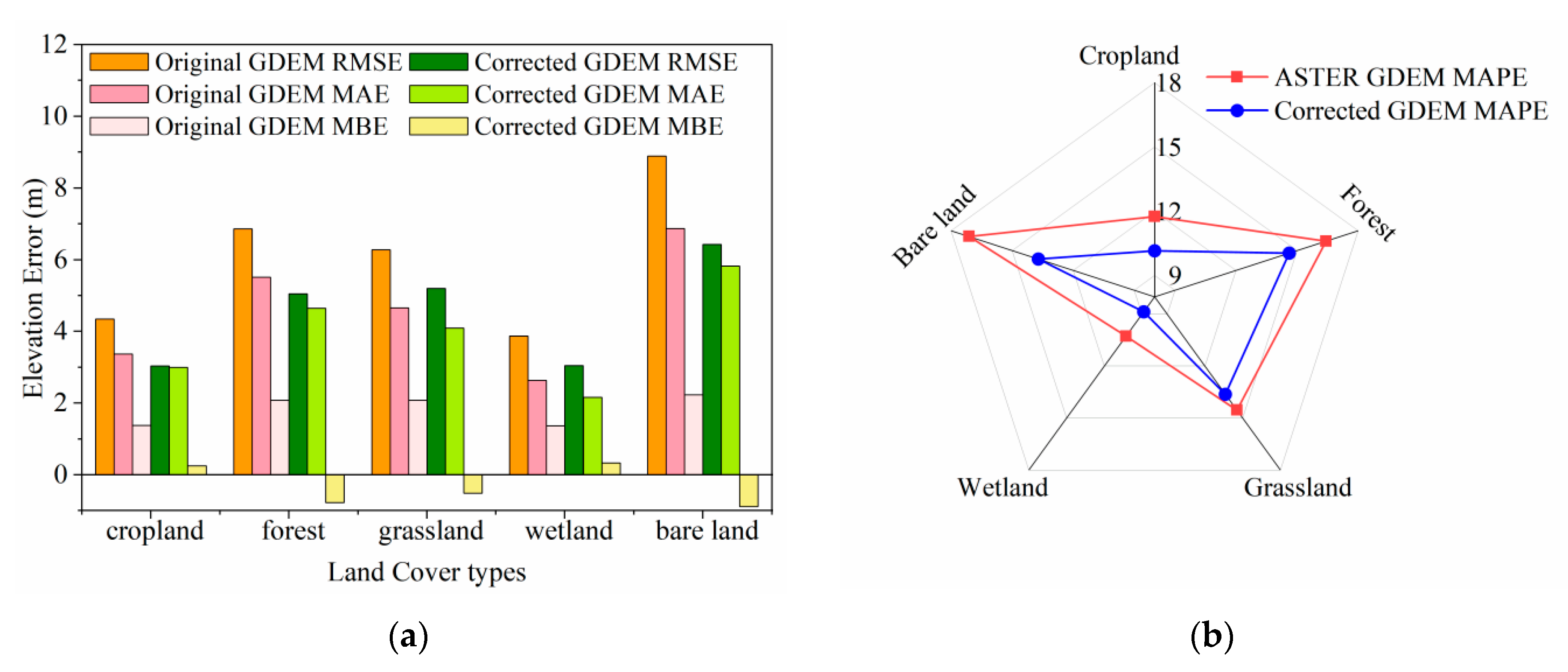
4.2.1. Comparison of Results Before and After GDEM Correction
4.2.2. Three Factors Affecting GDEM Elevation Accuracy
- (1)
- Impact of Slope
- (2)
- Impact of Aspect
- (3)
- Impact of Land Cover Type
4.3. Performance Comparison Between SEL and Five ML Models
5. Discussion
5.1. Comparison of GDEM Correction Between ATL08 with 20 m and 100 m Intervals
5.2. Comparison of Hyperparameter Optimization on the Accuracy of ML Models
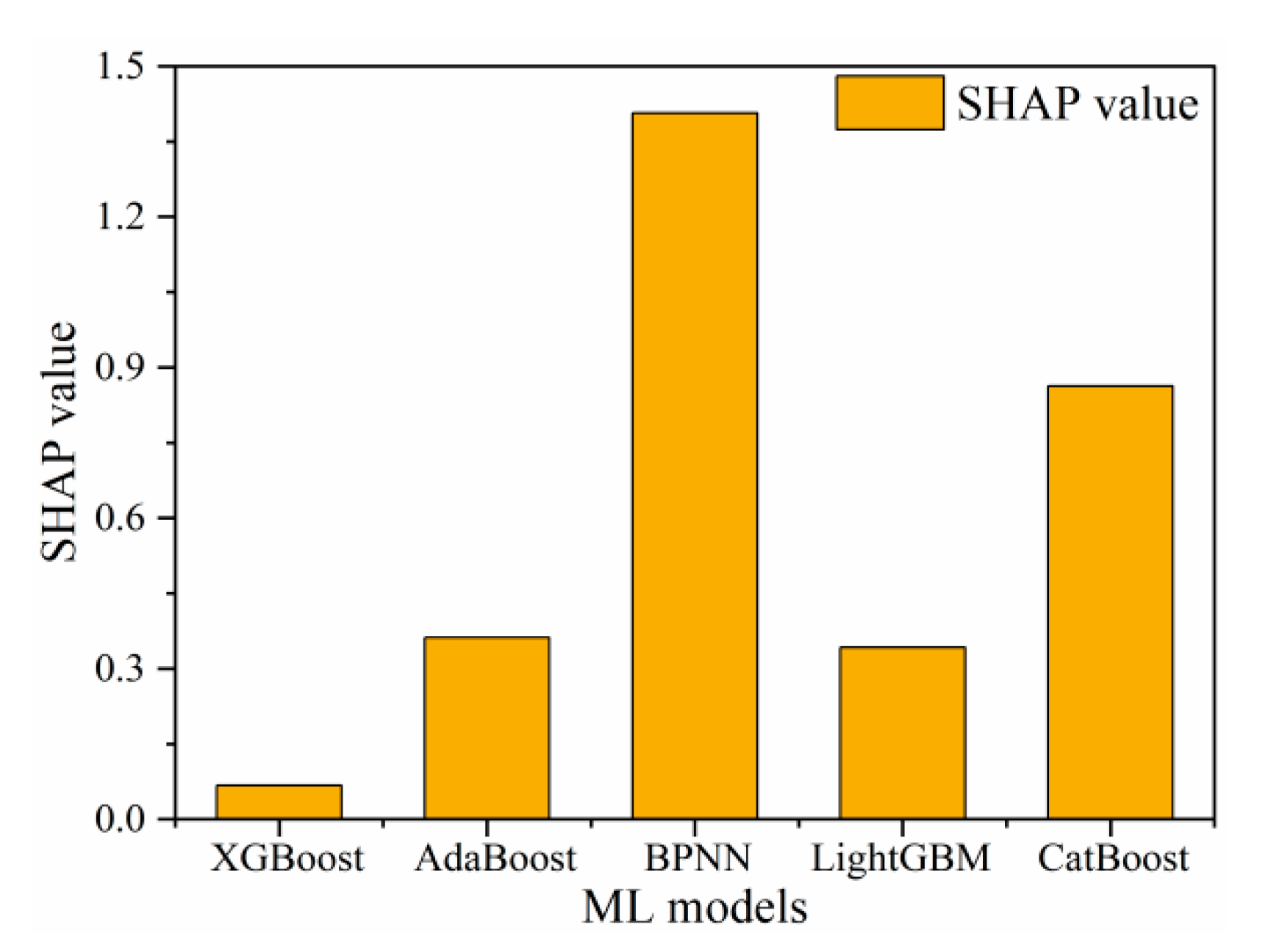
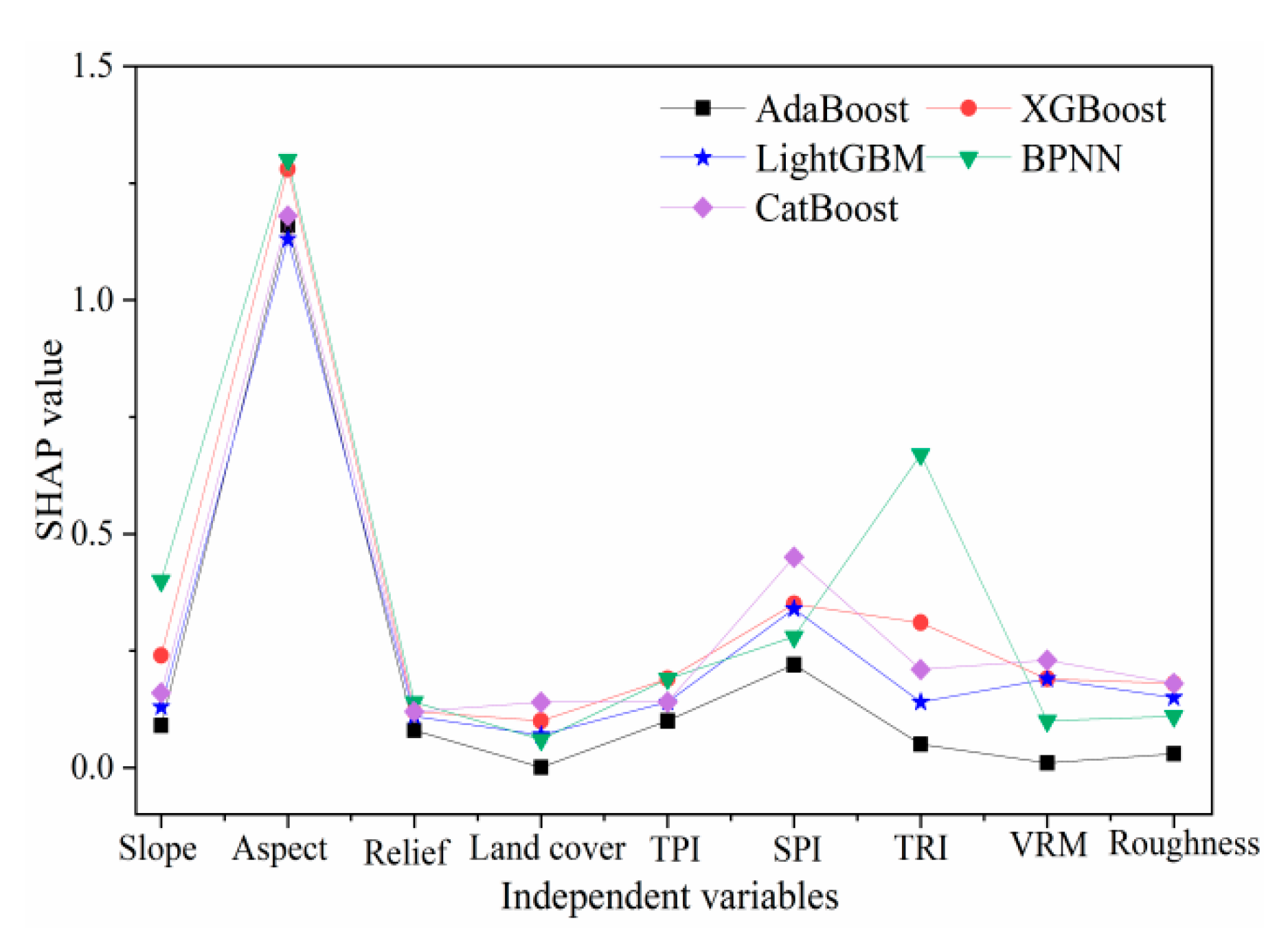
5.3. Comparison of the Importance of ML Models and Independent Variables
5.4. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wilson, J.P. Environmental Applications of Digital Terrain Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2018; pp. 50–150. [Google Scholar]
- Jordan, G.; Meijninger, B.M.; Van Hinsbergen, D.J.; Meulenkamp, J.E.; Van Dijk, P.M. Extraction of morphotectonic features from DEMs: Development and applications for study areas in Hungary and NW Greece. Int. J. Appl. Earth Obs. Geoinf. 2005, 7, 163–182. [Google Scholar] [CrossRef]
- He, F.; Gu, L.; Wang, T.; Zhang, Z. The synthetic geo-ecological environmental evaluation of a coastal coal-mining city using spatiotemporal big data: A case study in Longkou, China. J. Clean. Prod. 2017, 142, 854–866. [Google Scholar] [CrossRef]
- Hoja, D.; Reinartz, P.; Schroeder, M. Comparison of DEM generation and combination methods using high resolution optical stereo imagery and interferometric SAR data. Rev. Fr. Photogramm. Télédétect. 2006, 4, 89–94. [Google Scholar]
- Rastogi, G.; Agrawal, R.; Ajai, A. Bias corrections of CartoDEM using ICESat-GLAS data in hilly regions. GISci. Remote Sens. 2015, 52, 571–585. [Google Scholar] [CrossRef]
- Guth, P.L.; Geoffroy, T.M. LiDAR point cloud and ICESat-2 evaluation of 1 second global digital elevation models: Copernicus wins. Trans. GIS 2021, 25, 2245–2261. [Google Scholar] [CrossRef]
- Tachikawa, T.; Hato, M.; Kaku, M.; Iwasaki, A. Characteristics of ASTER GDEM version 2. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 3657–3660. [Google Scholar]
- Arefi, H.; Reinartz, P. Accuracy Enhancement of ASTER Global Digital Elevation Models Using ICESat Data. Remote Sens. 2011, 3, 1323–1343. [Google Scholar] [CrossRef]
- Del Rosario González-Moradas, M.; Viveen, W.; Vidal-Villalobos, R.A.; Villegas-Lanza, J.C. A performance comparison of SRTM v. 3.0, AW3D30, ASTER GDEM3, Copernicus and TanDEM-X for tectonogeomorphic analysis in the south American Andes. Catena 2023, 228, 107160. [Google Scholar] [CrossRef]
- Weifeng, X.; Jun, L.; Dailiang, P.; Jinge, J.; Hongxuan, X.; Hongyue, Y.; Jun, Y. Multi-source DEM accuracy evaluation based on ICESat-2 in Qinghai-Tibet Plateau, China. Int. J. Digit. Earth 2023, 17, 2297843. [Google Scholar] [CrossRef]
- Carrera-Hernandez, J.J. Not all DEMs are equal: An evaluation of six globally available 30 m resolution DEMs with geodetic benchmarks and LiDAR in Mexico. Remote Sens. Environ. 2021, 261, 112474. [Google Scholar] [CrossRef]
- Uuemaa, E.; Ahi, S.; Montibeller, B.; Muru, M.; Kmoch, A. Vertical accuracy of freely available global digital elevation models (ASTER, AW3D30, MERIT, TanDEM-X, SRTM, and NASADEM). Remote Sens. 2020, 12, 3482. [Google Scholar] [CrossRef]
- Richter, R. Correction of satellite imagery over mountainous terrain. Appl. Opt. 1998, 37, 4004–4015. [Google Scholar] [CrossRef]
- Xu, W.; Li, J.; Peng, D.; Yin, H.; Jiang, J.; Xia, H.; Wen, D. Vertical Accuracy Assessment and Improvement of Five High-Resolution Open-Source Digital Elevation Models Using ICESat-2 Data and Random Forest: Case Study on Chongqing, China. Remote Sens. 2024, 16, 1903. [Google Scholar] [CrossRef]
- Bagheri, H.; Schmitt, M.; Zhu, X.X. Fusion of Urban TanDEM-X raw DEMs using variational models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4761–4774. [Google Scholar] [CrossRef]
- Bagheri, H.; Schmitt, M.; Zhu, X.X. Fusion of TanDEM-X and Cartosat-1 DEMs using TV-norm regularization and ANN-predicted weights. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3369–3372. [Google Scholar]
- Okolie, C.J.; Smit, J.L. A systematic review and meta-analysis of Digital elevation model (DEM) fusion: Pre-processing, methods and applications. ISPRS J. Photogramm. Remote Sens. 2022, 188, 1–29. [Google Scholar] [CrossRef]
- Saberi, A.; Kabolizadeh, M.; Rangzan, K.; Abrehdary, M. Accuracy assessment and improvement of SRTM, ASTER, FABDEM, and MERIT DEMs by polynomial and optimization algorithm: A case study (Khuzestan Province, Iran). Open Geosci. 2023, 15, 20220455. [Google Scholar] [CrossRef]
- Ouyang, Z.; Zhou, C.; Xie, J.; Zhu, J.; Zhang, G.; Ao, M. SRTM DEM correction using ensemble machine learning algorithm. Remote Sens. 2023, 15, 3946. [Google Scholar] [CrossRef]
- Yang, X.; Li, L.; Chen, L.; Chen, L.; Shen, Z. Improving ASTER GDEM accuracy using land use-based linear regression methods: A case study of Lianyungang, East China. ISPRS Int. J. Geo-Inf. 2018, 7, 145. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q. A practical method for SRTM DEM correction over vegetated mountain areas. ISPRS J. Photogramm. Remote Sens. 2014, 87, 216–228. [Google Scholar] [CrossRef]
- Pham, H.T.; Marshall, L.; Johnson, F.; Sharma, A. A method for combining SRTM DEM and ASTER GDEM2 to improve topography estimation in regions without reference data. Remote Sens. Environ. 2018, 210, 229–241. [Google Scholar] [CrossRef]
- Okolie, C.; Adeleke, A.; Mills, J.; Smit, J.; Maduako, I.; Bagheri, H.; Komar, T.; Wang, S. Assessment of explainable tree-based ensemble algorithms for the enhancement of Copernicus digital elevation model in agricultural lands. Int. J. Image Data Fusion 2024, 15, 430–460. [Google Scholar] [CrossRef]
- Yue, L.; Shen, H.; Zhang, L.; Zheng, X.; Zhang, F.; Yuan, Q. High-quality seamless DEM generation blending SRTM-1, ASTER GDEM v2 and ICESat/GLAS observations. ISPRS J. Photogramm. Remote Sens. 2017, 123, 20–34. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, H.; Jiang, B.; Meng, L.; Guan, H.; Xu, M.; Cui, Y.; Kong, F.; Yin, Y.; Wang, M. An innovative approach for improving the accuracy of digital elevation models for cultivated land. Remote Sens. 2020, 12, 3401. [Google Scholar] [CrossRef]
- Chen, C.; Yang, S.; Li, Y. Accuracy assessment and correction of SRTM DEM using ICESat/GLAS data under data coregistration. Remote Sens. 2020, 12, 3435. [Google Scholar] [CrossRef]
- Geiß, C.; Schrade, H.; Pelizari, P.A.; Taubenböck, H. Multistrategy ensemble regression for mapping of built-up density and height with Sentinel-2 data. ISPRS J. Photogramm. Remote Sens. 2020, 170, 57–71. [Google Scholar] [CrossRef]
- Li, Y.; Li, L.; Chen, C.; Liu, Y. Correction of global digital elevation models in forested areas using an artificial neural network-based method with the consideration of spatial autocorrelation. Int. J. Digit. Earth 2023, 16, 1568–1588. [Google Scholar] [CrossRef]
- Xu, W.; Li, J.; Peng, D.; Jiang, J.; Xia, H.; Wen, D. Comparison of five methods for improving the accuracy of SRTM3 DEM and TanDEM-X DEM in the Qinghai-Tibet Plateau using ICESat-2 data. Int. J. Digit. Earth 2024, 17, 2391036. [Google Scholar] [CrossRef]
- Dong, Y.; Shortridge, A.M. A regional ASTER GDEM error model for the Chinese Loess Plateau. Int. J. Remote Sens. 2019, 40, 1048–1065. [Google Scholar] [CrossRef]
- Okolie, C.; Adeleke, A.; Smit, J.; Mills, J.; Ogbeta, C.; Maduako, I. Performance analysis of Bayesian optimised gradient-boosted decision trees for digital elevation model (DEM) error correction: Interim results. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, 10, 179–183. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, S.; Yuan, B.; Mu, H.; Xia, Z.; Tang, P.; Fang, H.; Wang, Z.; Du, P. Error-Reduced Digital Elevation Model of the Qinghai-Tibet Plateau using ICESat-2 and Fusion Model. Sci. Data 2024, 11, 588. [Google Scholar] [CrossRef]
- Nguyen, C.; Starek, M.J.; Tissot, P.E.; Cai, X.; Gibeaut, J. Ensemble neural networks for modeling DEM error. ISPRS Int. J. Geo-Inf. 2019, 8, 444. [Google Scholar] [CrossRef]
- Hu, M.; Ji, S. Accuracy evaluation and improvement of common DEM in Hubei Region based on ICESat/GLAS data. Earth Sci. Inform. 2022, 15, 221–231. [Google Scholar] [CrossRef]
- Wu, Z.; Yao, F.; Zhang, J.; Ma, E.; Yao, L.; Dong, Z. Genetic Programming Guided Mapping of Forest Canopy Height by Combining LiDAR Satellites with Sentinel-1/2, Terrain, and Climate Data. Remote Sens. 2023, 16, 110. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Chang, X.L.; Liang, J.; He, R. Influence of frozen ground on hydrological processes in alpine regions: A case study in an upper reach of the Heihe River. J. Glaciol. Geocryol. 2016, 5, 1362–1372. [Google Scholar]
- Zhang, Y.; Ye, C.; Yang, R.; Li, K. Reconstructing Snow Cover under Clouds and Cloud Shadows by Combining Sentinel-2 and Landsat 8 Images in a Mountainous Region. Remote Sens. 2024, 16, 188. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, Y.; Ye, C.; Liu, J. An integrated approach to reconstructing snow cover under clouds and cloud shadows on Sentinel-2 Time-Series images in a mountainous area. J. Hydrol. 2023, 619, 129264. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J. GlobeLand30: Operational global land cover mapping and big-data analysis. Sci. China Earth Sci 2018, 61, 1533–1534. [Google Scholar] [CrossRef]
- Yazdi, M.F.; Kamel, S.R.; Chabok, S.J.M.; Kheirabadi, M. Flight delay prediction based on deep learning and Levenberg-Marquart algorithm. J. Big Data 2020, 7, 106. [Google Scholar] [CrossRef]
- Różycka, M.; Migoń, P.; Michniewicz, A. Topographic Wetness Index and Terrain Ruggedness Index in geomorphic characterization of landslide terrains, on examples from the Sudetes, SW Poland. Z. Geomorphol. 2017, 61, 61–80. [Google Scholar] [CrossRef]
- Avand, M.; Janizadeh, S.; Tien Bui, D.; Pham, V.H.; Ngo, P.T.T.; Nhu, V.H. A tree-based intelligence ensemble approach for spatial prediction of potential groundwater. Int. J. Digit. Earth 2020, 13, 1408–1429. [Google Scholar] [CrossRef]
- Anokye, M.; Cui, X.; Yang, F.; Wang, P.; Sun, Y.; Ma, H.; Amoako, E.O. Optimizing multi-classifier fusion for seabed sediment classification using machine learning. Int. J. Digit. Earth 2023, 17, 2295988. [Google Scholar] [CrossRef]
- Goel, P.K.; Degroot, M.H. Information about hyperparameters in hierarchical models. J. Am. Stat. Assoc. 1981, 76, 140–147. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Probst, P.; Boulesteix, A.L.; Bischl, B. Tunability: Importance of hyperparameters of machine learning algorithms. J. Mach. Learn. Res. 2019, 20, 1–32. [Google Scholar]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Peng, Y.; Gong, D.; Deng, C.; Li, H.; Cai, H.; Zhang, H. An automatic hyperparameter optimization DNN model for precipitation prediction. Appl. Intell. 2022, 52, 2703–2719. [Google Scholar] [CrossRef]
- Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Thomas, J.; Ullmann, T.; Becker, M.; Boulesteix, A.L.; et al. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2023, 13, e1484. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. Segmentation of the mean of heteroscedastic data via cross-validation. Stat. Comput. 2011, 21, 613–632. [Google Scholar] [CrossRef]
- Cai, W.; Wei, R.; Xu, L.; Ding, X. A method for modelling greenhouse temperature using gradient boost decision tree. Inf. Process. Agric. 2022, 9, 343–354. [Google Scholar] [CrossRef]
- Yates, L.A.; Aandahl, Z.; Richards, S.A.; Brook, B.W. Cross validation for model selection: A review with examples from ecology. Ecol. Monogr. 2023, 93, e1557. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, W.; Liu, Z.; Tan, J. TBM performance prediction with Bayesian optimization and automated machine learning. Tunn. Undergr. Space Technol. 2020, 103, 103493. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. Super ensemble learning for daily streamflow forecasting: Large-scale demonstration and comparison with multiple machine learning algorithms. Neural Comput. Appl. 2021, 33, 3053–3068. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Hu, J.Z.; Chen, G.; Ma, Y.; Zhao, P. A D-InSAR method to improve snow depth estimation accuracy. Chin. Sci. Bull. 2022, 67, 3064–3080. [Google Scholar] [CrossRef]
- Lu, R.; Liu, S.; Duan, H.; Kang, W.; Zhi, Y. Combining the SHAP Method and Machine Learning Algorithm for Desert Type Extraction and Change Analysis on the Qinghai–Tibetan Plateau. Remote Sens. 2024, 16, 4414. [Google Scholar] [CrossRef]
- Podobnikar, T. Production of integrated digital terrain model from multiple datasets of different quality. Int. J. Geogr. Inf. Sci. 2005, 19, 69–89. [Google Scholar] [CrossRef]
- Podobnikar, T. Methods for visual quality assessment of a digital terrain model. Surv. Perspect. Integr. Environ. Soc. 2009, 2, 1–10. [Google Scholar]
- Varga, M.; Bašić, T. Accuracy validation and comparison of global digital elevation models over Croatia. Int. J. Remote Sens. 2015, 36, 170–189. [Google Scholar] [CrossRef]
- Fang, H.-Y.; Guo, M. Aspect-induced differences in soil erosion intensity in a gullied hilly region on the Chinese Loess Plateau. Environ. Earth Sci. 2015, 74, 5677–5685. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Yu, C.; Wang, Q.; Zhang, Z.; Zhong, Z.; Ding, Y.; Lai, T.; Huang, H.; Shen, P. Multi-source data joint processing framework for DEM calibration and fusion. Int. J. Appl. Earth Obs. Geoinf. 2025, 139, 104484. [Google Scholar] [CrossRef]





| Data Types | Datasets | Satellite/Instrument Type | Application |
|---|---|---|---|
| DEM data | ASTER GDEM V3 | Terra/ASTER | DEM correction and terrain parameters extraction |
| ICESat-2 product | ATL08 (V6) | ICESat-2/ATLAS | DEM errors and accuracy validation |
| Field measurements | UAV DEM | CHCNAV P330 pro | DEM accuracy validation |
| CORS Data | CHCNAV i80 GNSS | ||
| Land cover type | GlobeLand30 2020 | - | Extraction of land cover types |
| Sample Area Name | Sample Area Number | Altitude (m) | Coverage Type | Mean Slope | Flight Date | Flight Altitude (m) |
|---|---|---|---|---|---|---|
| Arou | A | 2965~3035 | Grassland | 1.8° | 1 April 2023 | 120 |
| Baishiya | B | 3006~3101 | Grassland | 0.3° | 2 April 2023 | 85 |
| Ebao | C | 3291~3385 | Grassland | 1.6° | 7 April 2023 | 90 |
| Mangzhayakou | D | 3404~4031 | Grassland, Bare ground | 23.6° | 8 April 2023 | 150 |
| Jingyangling | E | 3535~3763 | Grassland | 8.8° | 10 April 2023 | 150 |
| Learner | Hyperparameter | Parameter Meaning | Value Range | Optimum |
|---|---|---|---|---|
| XGBoost2.0 | Colsample_bytree | Proportion of random features sampled per tree | (0.30, 0.90) | 0.89 |
| Learning_rate | Learning rate | (0.00, 0.20) | 0.01 | |
| Max_depth | Maximum depth of tree to prevent overfitting | (3, 10) | 7 | |
| N_estimators | Number of weak learners | (100, 300) | 295 | |
| Subsample | Proportion of samples randomly sampled per tree | (0.00, 1.00) | 0.80 | |
| Gamma | Minimum value of branching loss performed by leaf nodes | (0.00, 0.30) | 0.20 | |
| AdaBoost | Max_depth | Maximum depth of tree | (0, 10) | 10 |
| Learning_rate | Learning rate | (0.01, 0.20) | 0.10 | |
| Loss | Loss function | Linear, square, exponential | Exponential | |
| N_estimators | Number of weak learners | (100, 500) | 50 | |
| LightGBM | Feature_fraction | Proportion of random features sampled per tree | (0.00, 1.00) | 0.86 |
| Learning_rate | Learning rate | (0.01, 0.20) | 0.10 | |
| Max_depth | Maximum depth of tree | (3, 10) | 9 | |
| N_estimators | Number of weak learners | (100, 500) | 200 | |
| Subsample | Proportion of samples randomly sampled per tree | (0.00, 1.00) | 0.98 | |
| L2_leaf_reg | Preventing overfitting | (0, 1000) | 200 | |
| CatBoost | Learning_rate | Learning rate | (0.01, 0.20) | 0.01 |
| Max_depth | Maximum depth of tree | (3, 10) | 4 | |
| N_estimators | Number of weak learners | (100, 500) | 366 | |
| Subsample | Proportion of samples randomly sampled per tree | (0.00, 50.00) | 42.20 | |
| L2_leaf_reg | Preventing overfitted | (0, 1000) | 3 | |
| RSM | Random subspace method | (0.30, 0.90) | 0.89 | |
| BP Neural Network | Activation | Activation function | Relu | Relu |
| Hidden_layer_ sizes | Hidden layer | (1, 100) | 50 | |
| Optimizer | Optimization model | Adam, sgd, rmsprop | Adam | |
| Neurons | Number of neurons | (1, 10,000) | 1000 |
| Overall Accuracy (m) | CORS Validation (m) | ATL08 Validation (m) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | MBE | RMSE | MAE | MBE | RMSE | MAE | MBE | |
| Original GDEM | 7.15 | 5.93 | 2.05 | 4.77 | 3.56 | −0.36 | 6.44 | 5.01 | 2.00 |
| Corrected GDEM | 4.13 | 3.67 | 1.08 | 3.58 | 3.27 | −0.38 | 4.08 | 3.62 | 0.46 |
| Slope | Original GDEM | Corrected GDEM | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE (m) | MAE (m) | MBE (m) | MAPE (%) | RMSE (m) | MAE (m) | MBE (m) | MAPE (%) | |
| ≤5° | 4.21 | 2.57 | 1.09 | 7.95 | 2.24 | 1.92 | −0.26 | 5.96 |
| 5–10° | 4.89 | 3.88 | 1.12 | 11.47 | 2.97 | 2.27 | 0.44 | 6.75 |
| 10–15° | 6.16 | 4.96 | 1.25 | 14.21 | 4.11 | 2.87 | 1.03 | 8.28 |
| 15–20° | 7.10 | 5.82 | 1.73 | 16.31 | 5.53 | 3.69 | 0.94 | 10.36 |
| ≥20° | 8.16 | 6.57 | 2.41 | 18.17 | 6.22 | 5.02 | 0.34 | 13.58 |
| Aspect | Original GDEM | Corrected GDEM | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE (m) | MAE (m) | MBE (m) | MAPE (%) | RMSE (m) | MAE (m) | MBE (m) | MAPE (%) | |
| North | 6.96 | 5.44 | 3.29 | 15.51 | 4.34 | 3.74 | 1.40 | 14.08 |
| Northeastern | 6.29 | 4.85 | 1.86 | 13.76 | 4.29 | 3.62 | −0.38 | 12.34 |
| East | 6.01 | 4.67 | 0.66 | 13.18 | 4.14 | 3.63 | 0.38 | 12.10 |
| Southeast | 6.27 | 4.81 | 0.12 | 13.62 | 4.32 | 3.81 | 1.54 | 12.10 |
| South | 6.30 | 4.83 | −0.39 | 13.71 | 4.01 | 3.12 | 0.62 | 12.97 |
| Southwestern | 6.25 | 4.86 | 2.36 | 13.84 | 4.14 | 3.69 | −1.03 | 12.16 |
| West | 6.58 | 5.15 | 3.55 | 14.74 | 4.10 | 3.59 | 2.06 | 13.07 |
| Northwestern | 6.95 | 5.51 | 3.93 | 15.70 | 4.64 | 3.90 | 2.44 | 13.94 |
| Model | RMSE (m) | MAE (m) | MAPE (%) |
|---|---|---|---|
| XGBoost | 5.99 | 4.65 | 13.21 |
| AdaBoost | 5.92 | 4.58 | 13.02 |
| LightGBM | 5.89 | 4.57 | 12.98 |
| CatBoost | 5.90 | 4.58 | 12.99 |
| BPNN | 6.01 | 4.61 | 13.06 |
| SEL | 4.08 | 3.78 | 11.58 |
| RF | 6.75 | 5.06 | 14.26 |
| ATL08 (100 m) | ATL08 (20 m) | |||||
|---|---|---|---|---|---|---|
| RMSE (m) | MAE (m) | MAPE (%) | RMSE (m) | MAE (m) | MAPE (%) | |
| Original GDEM | 7.61 | 6.11 | 14.32 | 6.94 | 5.01 | 14.51 |
| Corrected GDEM | 4.63 | 3.67 | 12.69 | 4.08 | 3.62 | 11.58 |
| Models | Before Bayesian Optimization | After Bayesian Optimization | ||||
|---|---|---|---|---|---|---|
| RMSE (m) | MAE (m) | MAPE (%) | RMSE (m) | MAE (m) | MAPE (%) | |
| XGBoost | 7.12 | 5.88 | 15.21 | 5.99 | 4.65 | 13.21 |
| AdaBoost | 7.33 | 6.20 | 15.02 | 5.92 | 4.58 | 13.02 |
| LightGBM | 7.24 | 6.11 | 15.98 | 5.89 | 4.57 | 12.98 |
| CatBoost | 7.18 | 6.02 | 15.99 | 5.90 | 4.58 | 12.99 |
| BPNN | 7.09 | 5.84 | 15.06 | 6.01 | 4.61 | 13.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Q.; Zhang, Y.; Ma, Y.; Yang, R.; Lei, K. ASTER GDEM Correction Based on Stacked Ensemble Learning and ICEsat-2/ATL08: A Case Study from the Qilian Mountains. Remote Sens. 2025, 17, 1839. https://doi.org/10.3390/rs17111839
Wei Q, Zhang Y, Ma Y, Yang R, Lei K. ASTER GDEM Correction Based on Stacked Ensemble Learning and ICEsat-2/ATL08: A Case Study from the Qilian Mountains. Remote Sensing. 2025; 17(11):1839. https://doi.org/10.3390/rs17111839
Chicago/Turabian StyleWei, Qi, Yanli Zhang, Yalong Ma, Ruirui Yang, and Kairui Lei. 2025. "ASTER GDEM Correction Based on Stacked Ensemble Learning and ICEsat-2/ATL08: A Case Study from the Qilian Mountains" Remote Sensing 17, no. 11: 1839. https://doi.org/10.3390/rs17111839
APA StyleWei, Q., Zhang, Y., Ma, Y., Yang, R., & Lei, K. (2025). ASTER GDEM Correction Based on Stacked Ensemble Learning and ICEsat-2/ATL08: A Case Study from the Qilian Mountains. Remote Sensing, 17(11), 1839. https://doi.org/10.3390/rs17111839







