A 3D Reconstruction of Gas Cloud Leakage Based on Multi-Spectral Imaging Systems
Abstract
1. Introduction
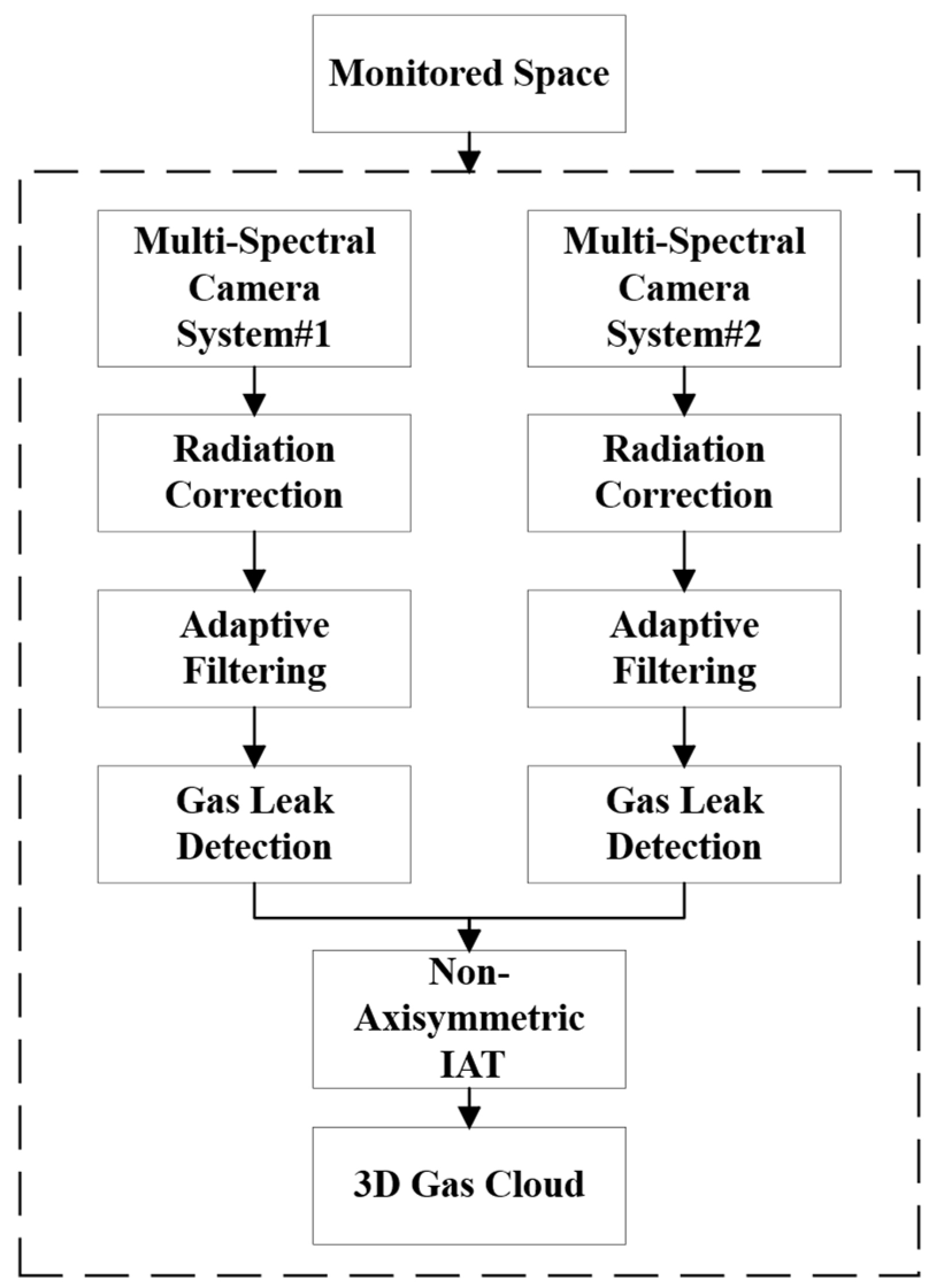
2. Multi-Spectral Imaging System-Based Three-Dimensional Reconstruction Methods
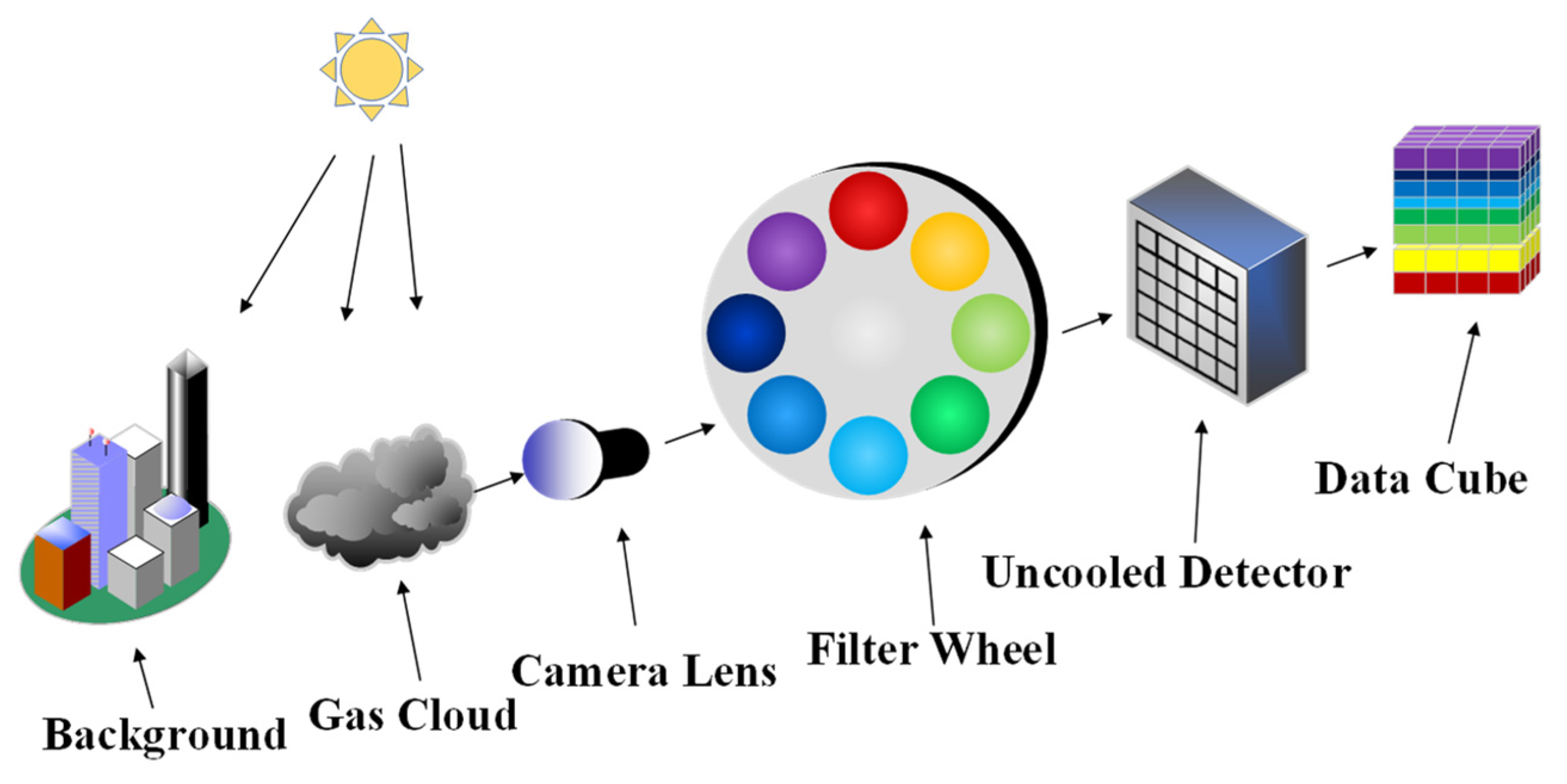
2.1. Principle of Infrared Telemetry
2.2. Multi-Spectral Imaging System
2.3. Three-Dimensional Reconstruction of Gas Clouds Based on Multi-Spectral Imaging Systems
2.3.1. Radiometric Correction
2.3.2. Adaptive Filtering
2.3.3. Gas Leak Detection
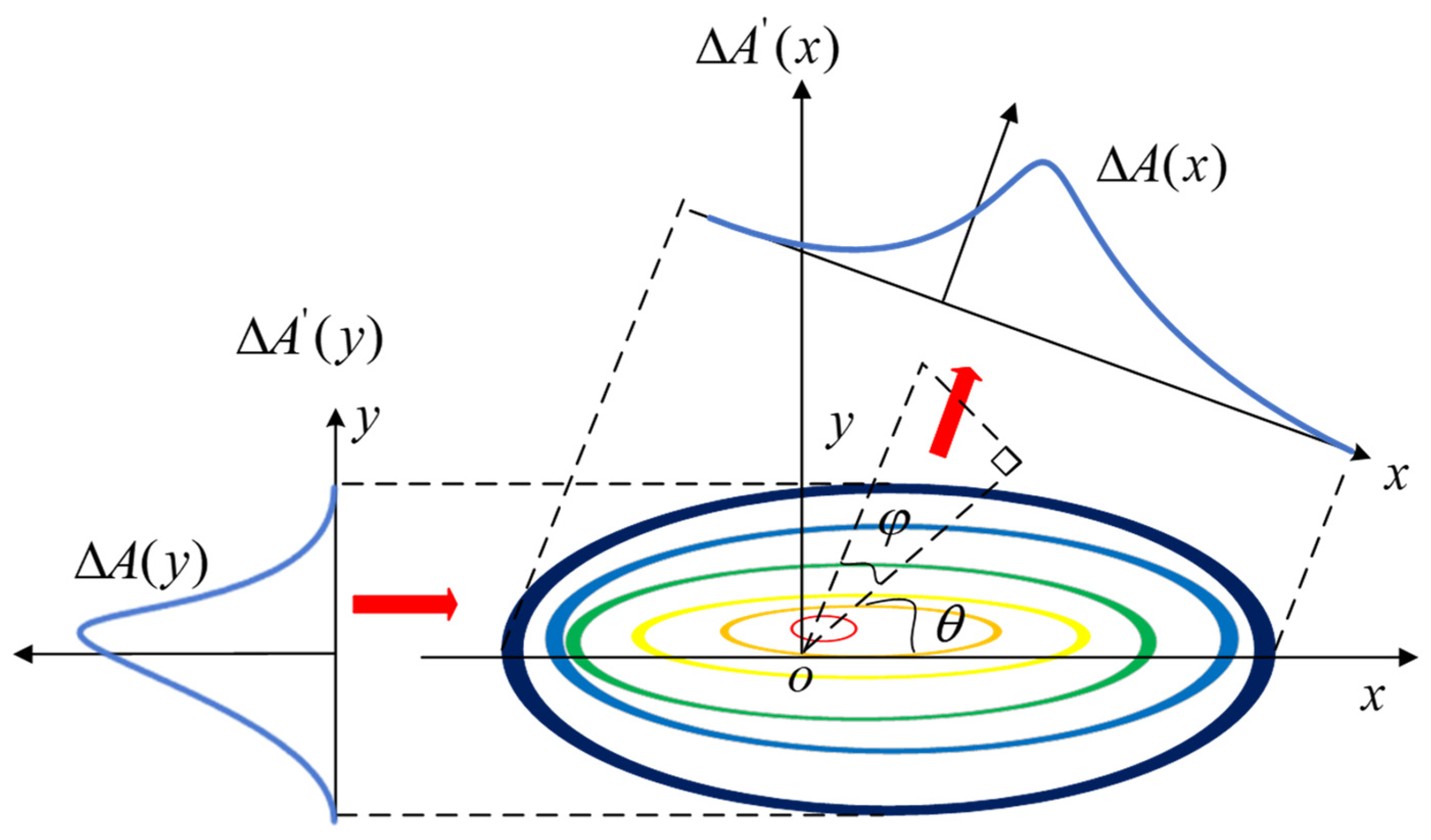
2.3.4. Non-Axisymmetric IAT
3. Results
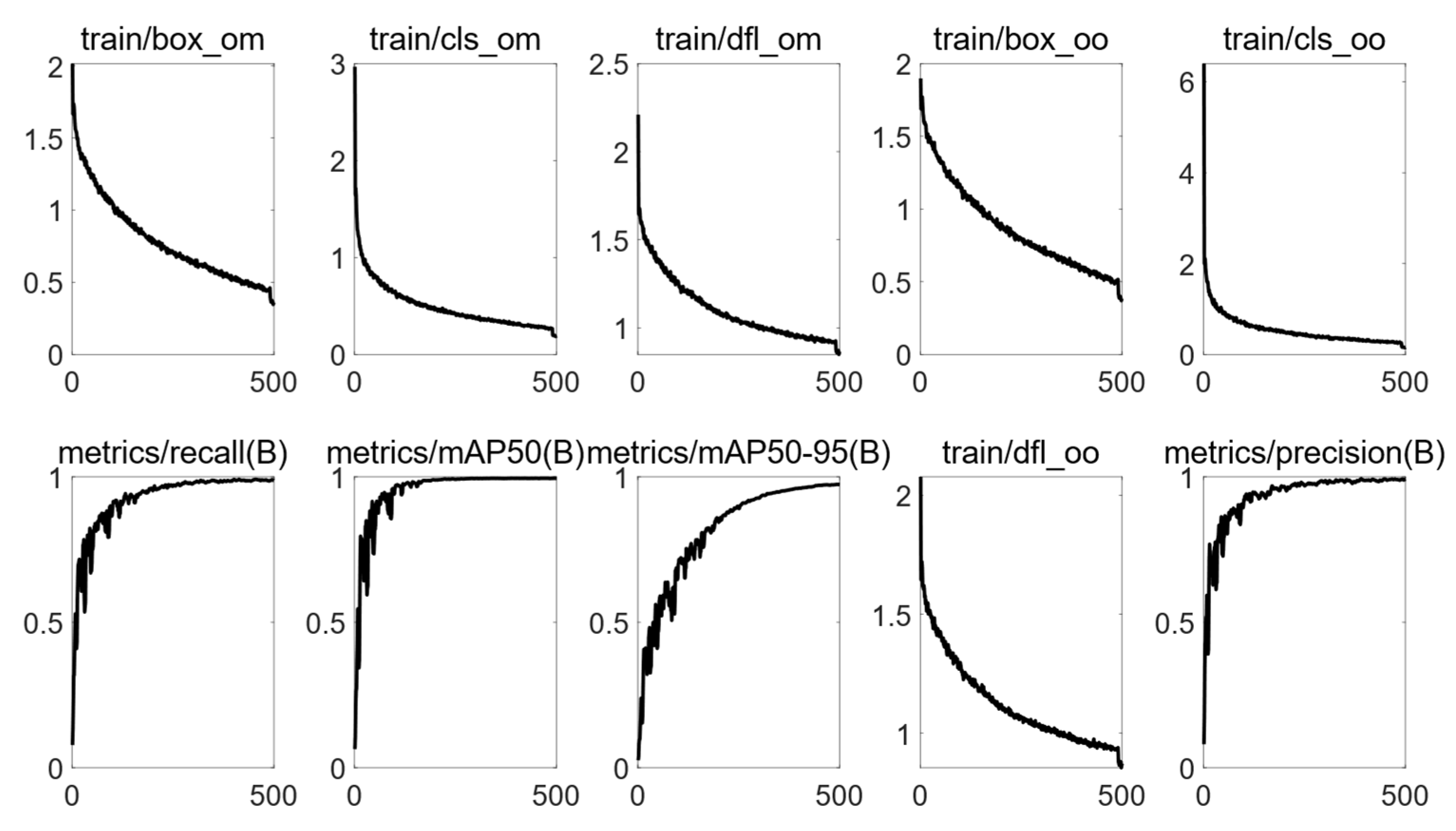
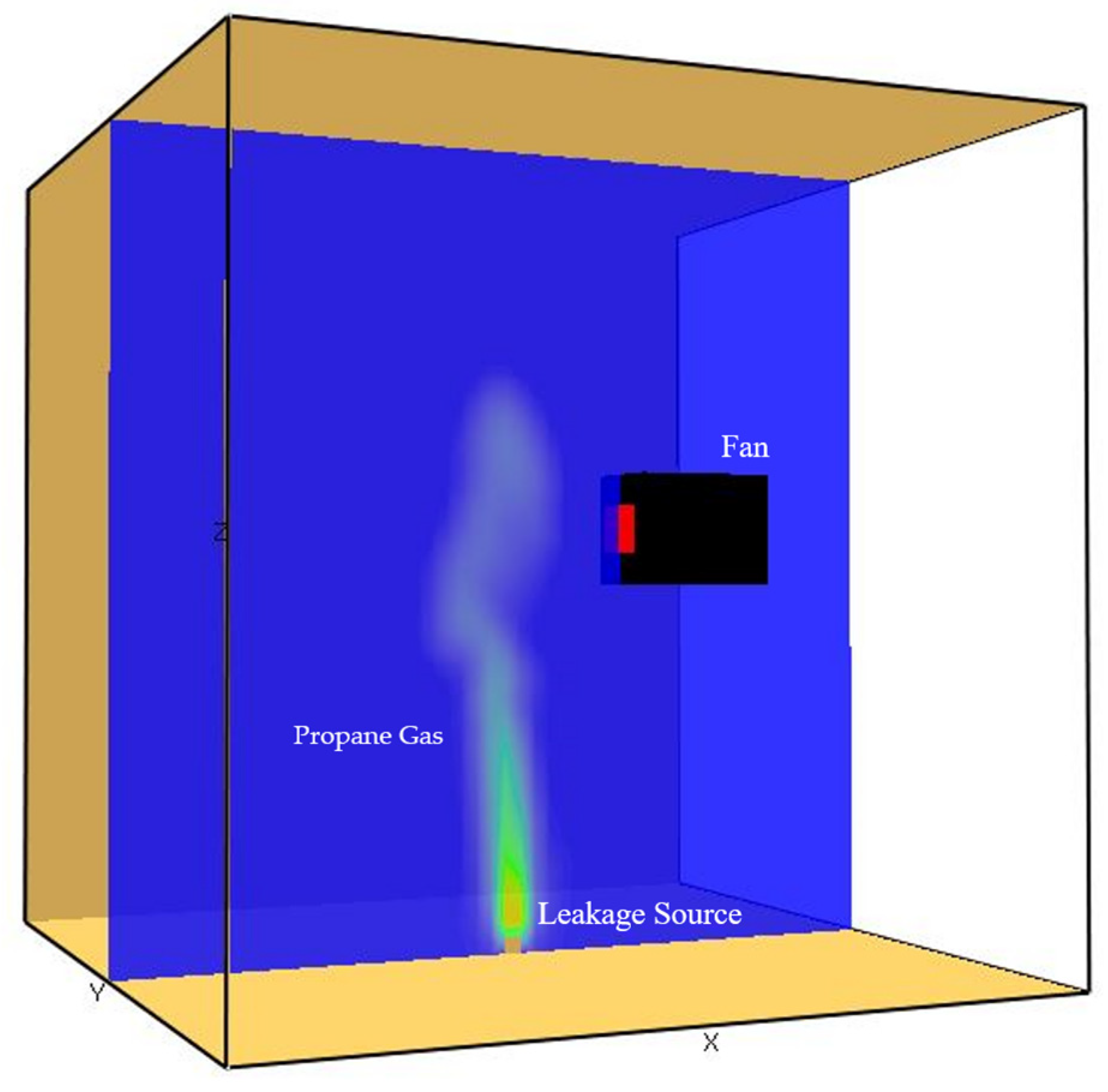
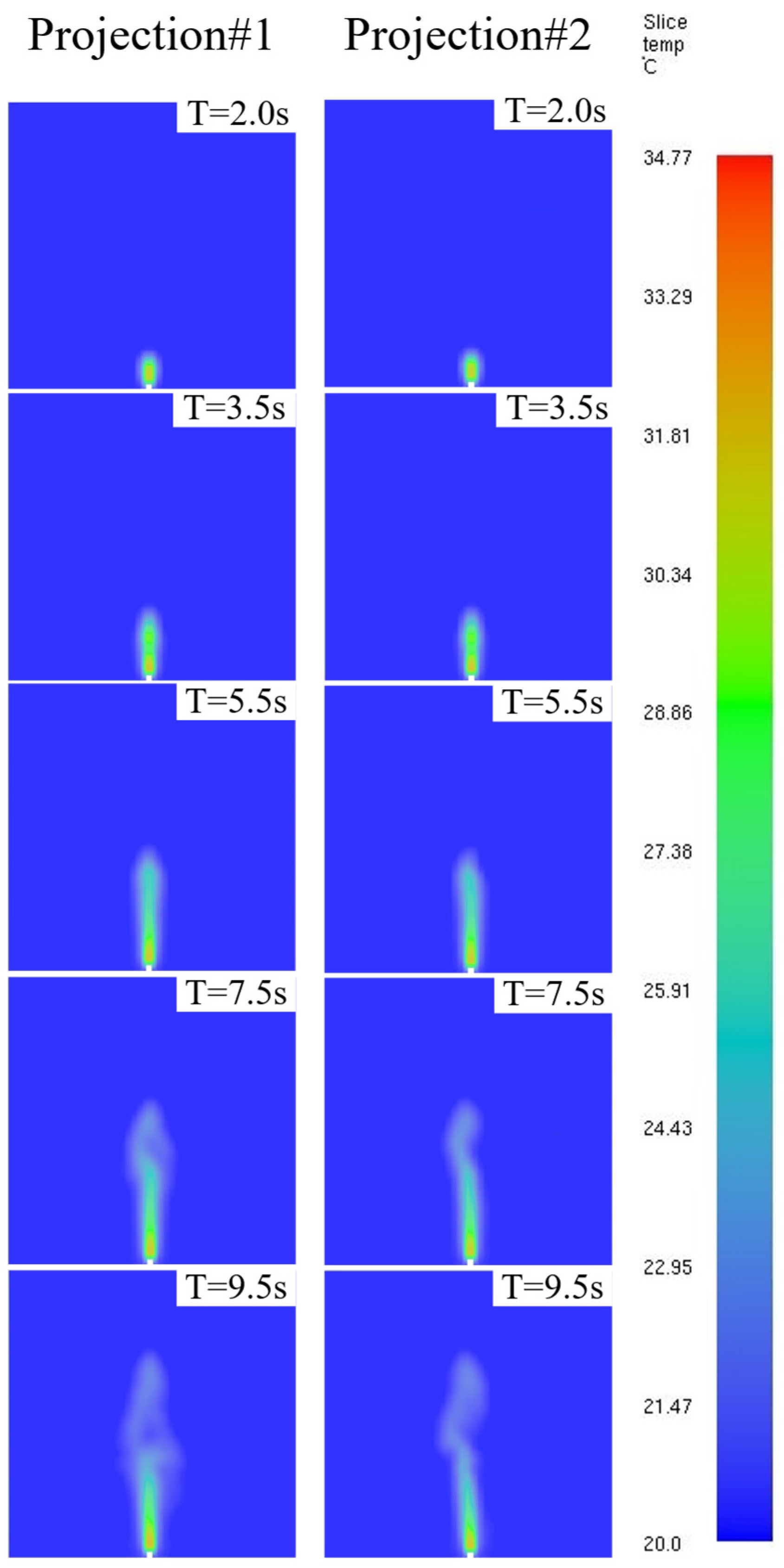
3.1. Simulation Experiment
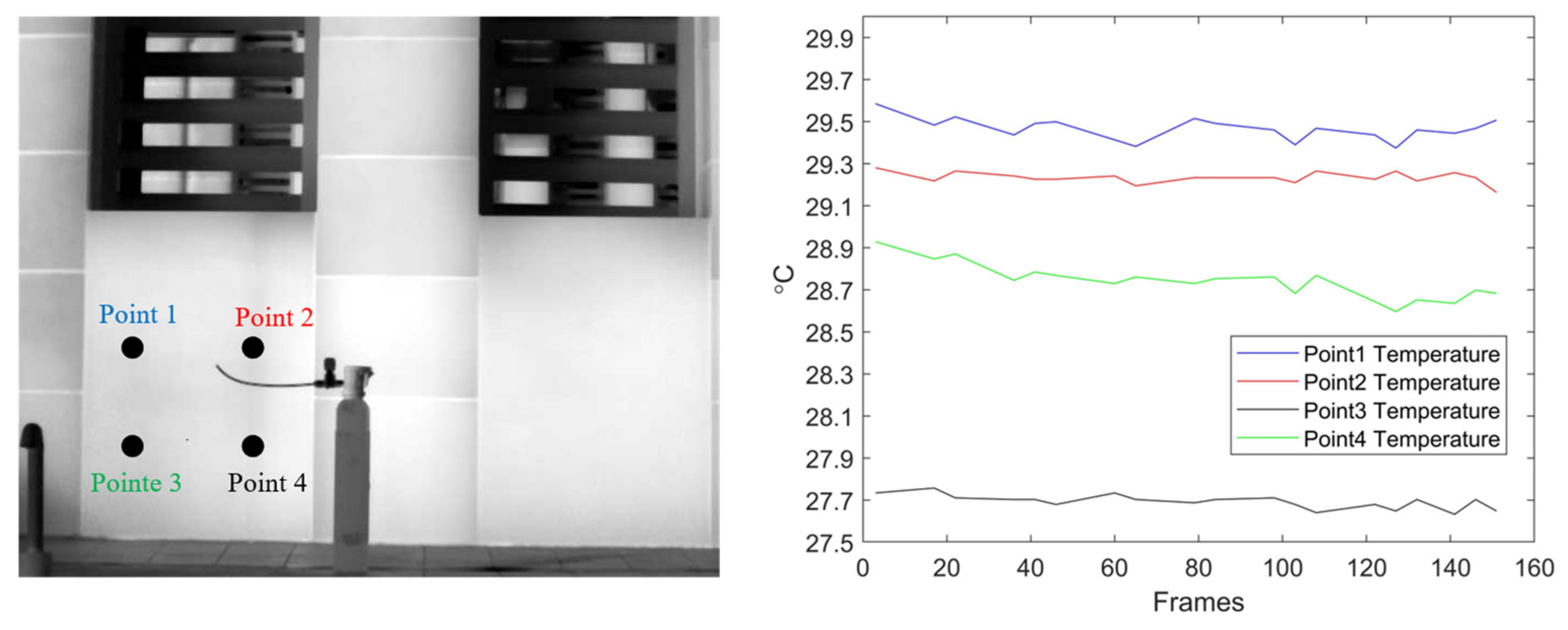
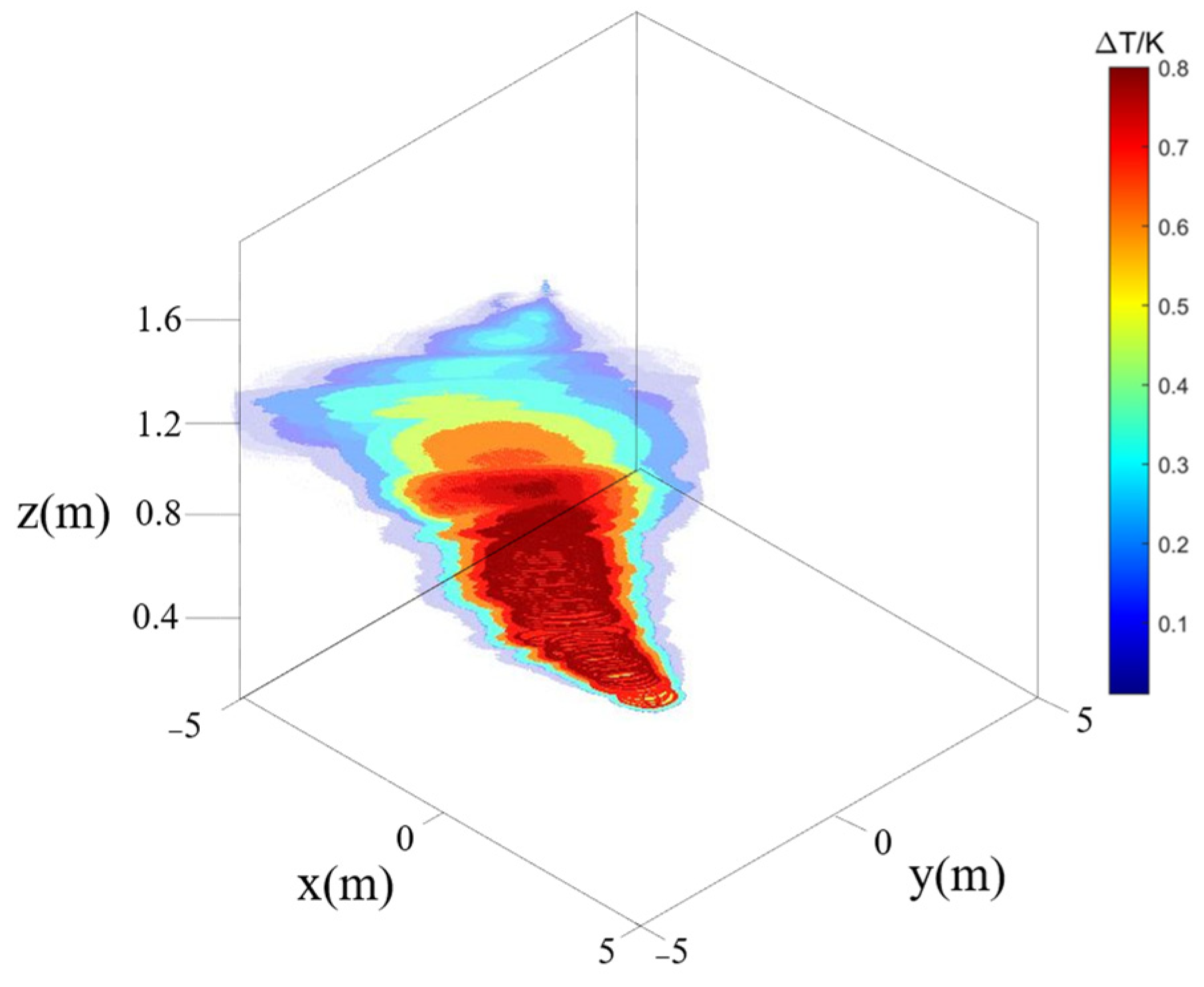
3.2. Field Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IAT | Inverse Abel transform |
| 3D | Three-dimensional |
References
- Wigley, T.M. Coal to gas: The influence of methane leakage. Clim. Chang. 2011, 108, 601–608. [Google Scholar] [CrossRef]
- Bradley, D.; Chamberlain, G.A.; Drysdale, D.D. Large vapour cloud explosions, with particular reference to that at Buncefield. Phil. Trans. R. Soc. A 2012, 370, 544–566. [Google Scholar] [CrossRef]
- Okamoto, K.; Ichikawa, T.; Fujimoto, J.; Kashiwagi, N.; Nakagawa, M.; Hagiwara, T.; Honma, M. Prediction of evaporative diffusion behavior and explosion damage in gasoline leakage accidents. Process. Saf. Environ. Prot. 2021, 148, 893–902. [Google Scholar] [CrossRef]
- Mitchell, A.L.; Tkacik, D.S.; Roscioli, J.R.; Herndon, S.C.; Yacovitch, T.I.; Martinez, D.M.; Vaughn, T.L.; Williams, L.L.; Sullivan, M.R.; Floerchinger, C.; et al. Measurements of Methane Emissions from Natural Gas Gathering Facilities and Processing Plants: Measurement Results. Environ. Sci. Technol. 2015, 49, 3219–3227. [Google Scholar] [CrossRef] [PubMed]
- Meribout, M. Gas leak-detection and measurement systems: Prospects and future trends. IEEE Trans. Instrum. Meas. 2021, 70, 4505813. [Google Scholar] [CrossRef]
- Xiaoming, C.H.I. Experimental Research and Analysis of Infrared Imaging Detection Technology for Gas Leakage in Petrochemical Enterprises. Infrared Technol. 2024, 46, 947–956. [Google Scholar]
- Hong, T.; Culp, J.T.; Kim, K.-J.; Devkota, J.; Sun, C.; Ohodnicki, P.R. State-of-the-art of methane sensing materials: A review and perspectives. TrAC Trends Anal. Chem. 2020, 125, 115820. [Google Scholar] [CrossRef]
- Rouet-Leduc, B.; Hulbert, C. Automatic detection of methane emissions in multispectral satellite imagery using a vision transformer. Nat. Commun. 2024, 15, 3801. [Google Scholar] [CrossRef]
- Wu, W.; Liu, Y.; Rogers, B.M.; Xu, W.; Dong, Y.; Lu, W. Monitoring gas flaring in Texas using time-series sentinel-2 MSI and landsat-8 OLI images. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103075. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, F.; Jiao, Y.; Wang, C.; Li, X.; Zhang, Q. Optical Filter Selection for Photoacoustic Sensors of Multicomponent Gases: Considering Cross Interference. IEEE Trans. Instrum. Meas. 2023, 72, 6008808. [Google Scholar] [CrossRef]
- Irakulis-Loitxate, I.; Roger, J.; Gorroño, J.; Valverde, A.; Guanter, L. Detection of Methane Point Sources with High-Resolution Satellites. Environ. Sci. Proc. 2023, 28, 29. [Google Scholar] [CrossRef]
- Wang, P.; Tang, G.; Liu, S.; Yang, Y.; Zhu, S.; Wang, S.; Liu, X.; Lu, J.; Wang, J.; Li, C.; et al. Study on the lower limit of gas detection based on the snapshot infrared multispectral imaging system. Opt. Express 2024, 32, 27919–27930. [Google Scholar] [CrossRef]
- Ren, M.; Wang, S.; Zhou, J.; Zhuang, T.; Yang, S. Multispectral detection of partial discharge in SF6 gas with silicon photomultiplier-based sensor array. Sens. Actuators A Phys. 2018, 283, 113–122. [Google Scholar] [CrossRef]
- Li, K.; Duan, S.; Pang, L.; Li, W.; Yang, Z.; Hu, Y.; Yu, C. Chemical Gas Telemetry System Based on Multispectral Infrared Imaging. Toxics 2023, 11, 83. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Xu, L.; Xu, H.; Shen, X.; Deng, Y.; Xu, H.; Liu, J.; Liu, W. Three-dimensional reconstruction of a leaking gas cloud based on two scanning FTIR remote-sensing imaging systems. Opt. Express 2022, 30, 25581–25596. [Google Scholar] [CrossRef]
- Yan, B.; Li, S.; Fang, J.; Zeng, D.; Chen, S.; Chen, H. 3D reconstruction of gas cloud concentration field with high temporal and spatial resolution based on an imaging-type FTIR. Opt. Express 2024, 32, 33174–33195. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Shi, Z.; Zi, C.; Chen, L.; Cao, X. Concentration-aware real-time 3D reconstruction of leaking gas clouds based on two-view bandpass optical gas imaging. Opt. Express 2025, 33, 5310. [Google Scholar] [CrossRef]
- Watremez, X.; Labat, N.; Audouin, G.; Lejay, B.; Marcarian, X.; Dubucq, D.; Marblé, A.; Foucher, P.-Y.; Poutier, L.; Danno, R.; et al. Remote Detection and Flow rates Quantification of Methane Releases Using Infrared Camera Technology and 3D Reconstruction Algorithm. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 26–28 September 2016. [Google Scholar]
- Zeng, Y.; Morris, J.; Sanders, A.; Mutyala, S.; Zeng, C. Methods to determine response factors for infrared gas imagers used as quantitative measurement devices. J. Air Waste Manag. Assoc. 2017, 67, 1180–1191. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, Z.; Khan, H.A.; Kootstra, G. Improving Radiometric Block Adjustment for UAV Multispectral Imagery under Variable Illumination Conditions. Remote Sens. 2024, 16, 3019. [Google Scholar] [CrossRef]
- Kedzierski, M.; Wierzbicki, D.; Sekrecka, A.; Fryskowska, A.; Walczykowski, P.; Siewert, J. Influence of Lower Atmosphere on the Radiometric Quality of Unmanned Aerial Vehicle Imagery. Remote Sens. 2019, 11, 1214. [Google Scholar] [CrossRef]
- Ochs, M.; Schulz, A.; Bauer, H.-J. High dynamic range infrared thermography by pixelwise radiometric self calibration. Infrared Phys. Technol. 2009, 53, 112–119. [Google Scholar] [CrossRef]
- Barber, R.; Rodriguez-Conejo, M.A.; Melendez, J.; Garrido, S. Design of an Infrared Imaging System for Robotic Inspection of Gas Leaks in Industrial Environments. Int. J. Adv. Robot. Syst. 2015, 12, 23. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, P.; Peng, H.; Yu, Y.; Zhang, L.; Yao, J.; Qin, J.; Sun, Z.; He, M.; Yang, X. Using angular two-point correlations to self-calibrate the photometric redshift distributions of decals dr9. Mon. Not. R. Astron. Soc. 2023, 520, 161–179. [Google Scholar] [CrossRef]
- Haykin, S.S. Adaptive Filter Theory; Prentice Hall: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Wang, A.; Chen, H.; Liu, L.; Chen, K.; Lin, Z.; Han, J.; Ding, G. YOLOv10: Real-Time End-to-End Object Detection. arXiv 2024, arXiv:2405.14458. [Google Scholar]
- Ali, M.L.; Zhang, Z. The YOLO Framework: A Comprehensive Review of Evolution, Applications, and Benchmarks in Object Detection. Computers 2024, 13, 336. [Google Scholar] [CrossRef]
- Hu, J.; Wei, Y.; Chen, W.; Zhi, X.; Zhang, W. CM-YOLO: Typical Object Detection Method in Remote Sensing Cloud and Mist Scene Images. Remote Sens. 2025, 17, 125. [Google Scholar] [CrossRef]
- Hickstein, D.D.; Gibson, S.T.; Yurchak, R.; Das, D.D.; Ryazanov, M. A direct comparison of high-speed methods for the numerical Abel transform. Rev. Sci. Instrum. 2019, 90, 065115. [Google Scholar] [CrossRef]
- Zhang, L.; Schaeffer, H. Stability and error estimates of BV solutions to the Abel inverse problem. Inverse Probl. 2018, 34, 105003. [Google Scholar] [CrossRef]
- Ruan, H.; Wan, B. A New Method for Asymmetrical Abel Inversion Using Fourier-Bessel Expansions. Int. J. Infrared Millim. Waves 2000, 21, 1973–1987. [Google Scholar] [CrossRef]
- Nguyen, T.-A.; Kondo, K.; Kakuta, N. Simultaneous near-infrared measurement of temperature and flow fields of a thermal plume arising in water. J. Vis. 2024, 28, 265–278. [Google Scholar] [CrossRef]
- NIST. FDS and Smokeview. Available online: https://pages.nist.gov/fds-smv/ (accessed on 28 November 2024).
- Wvan Aarle, W.; Palenstijn, W.J.; Cant, J.; Janssens, E.; Bleichrodt, F.; Dabravolski, A.; De Beenhouwer, J.; Batenburg, K.J.; Sijbers, J. Fast and Flexible X-ray Tomography Using the ASTRA Toolbox. Opt. Express 2016, 24, 25129–25147. [Google Scholar] [CrossRef] [PubMed]



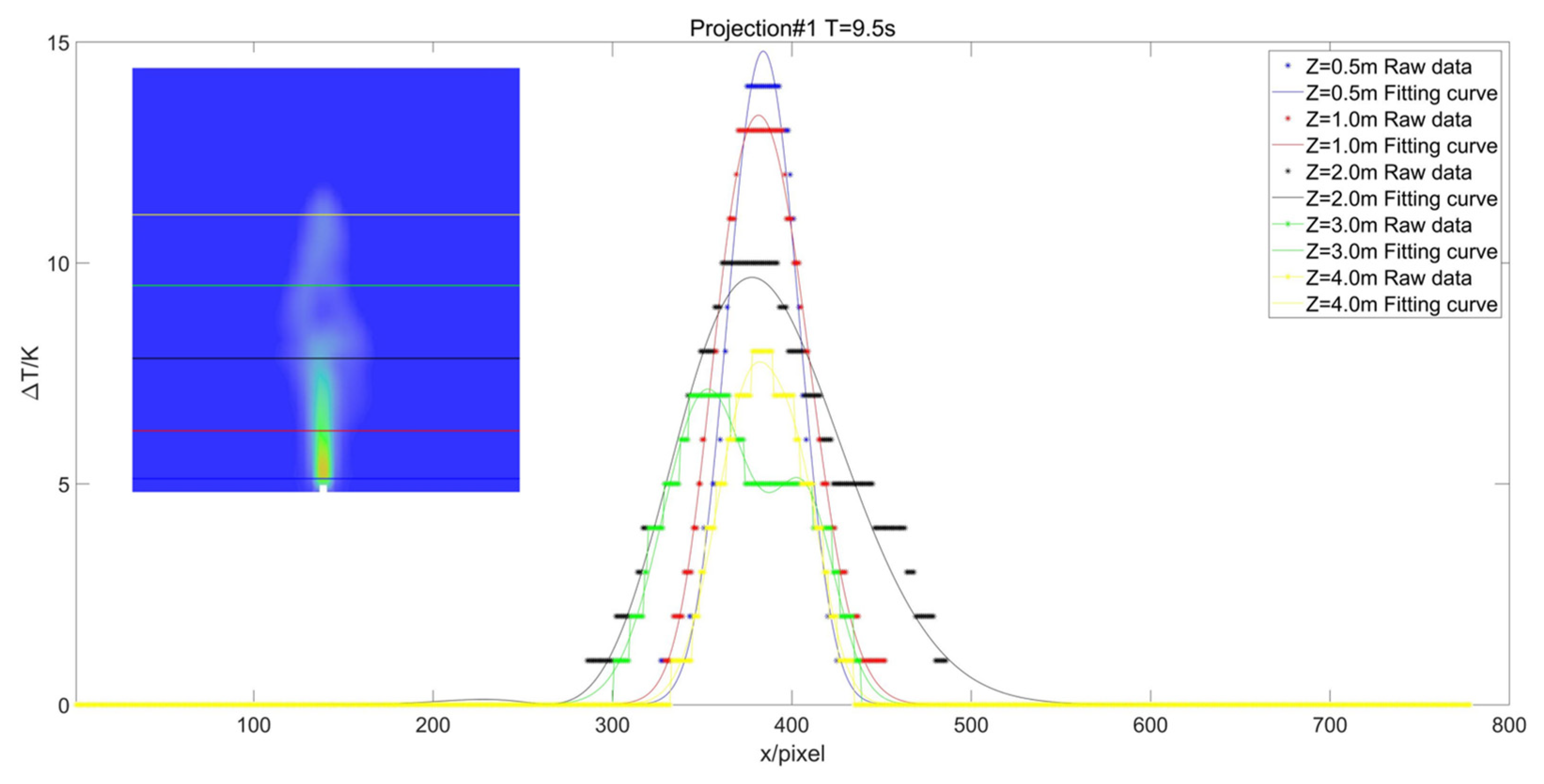

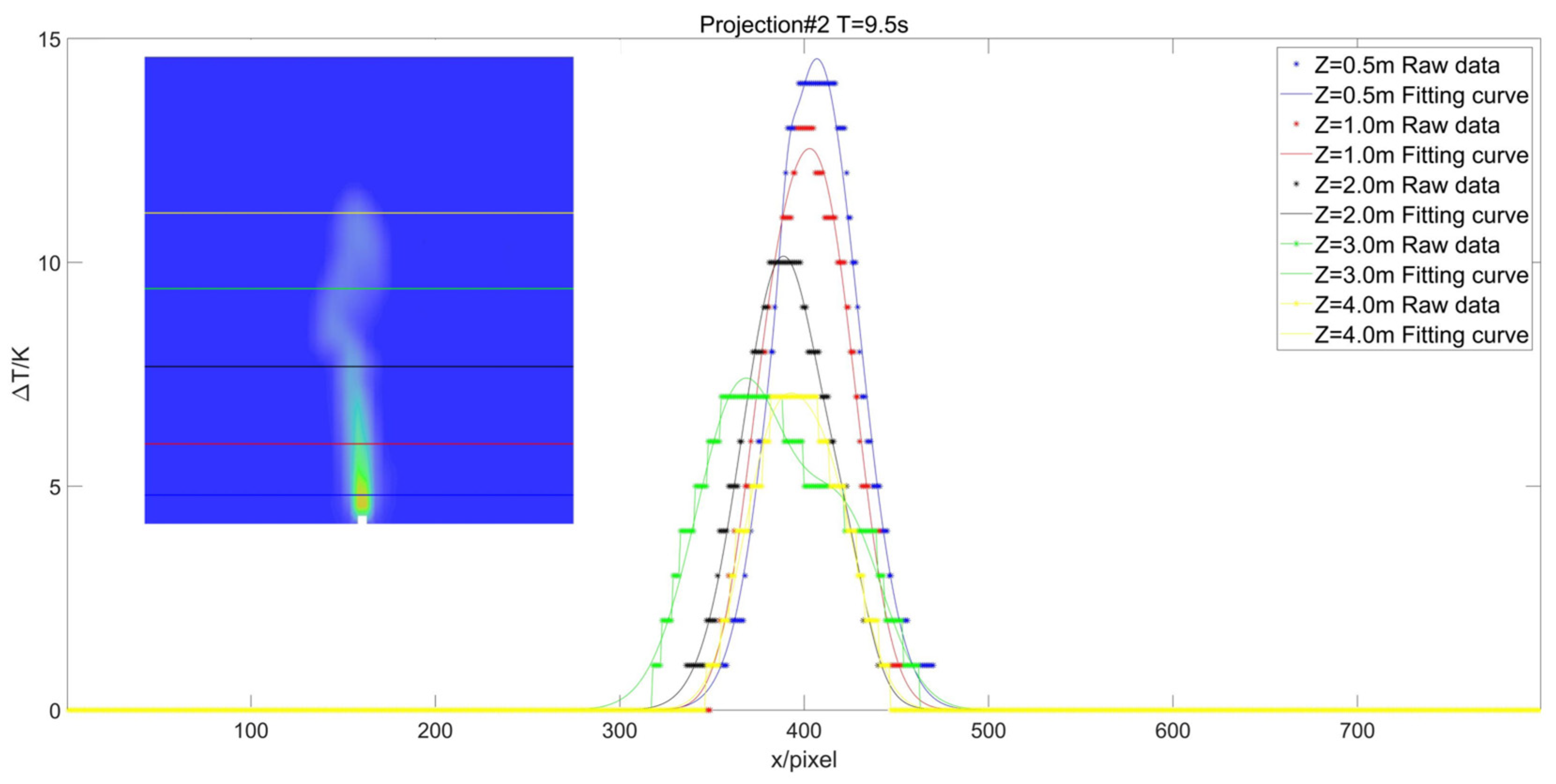



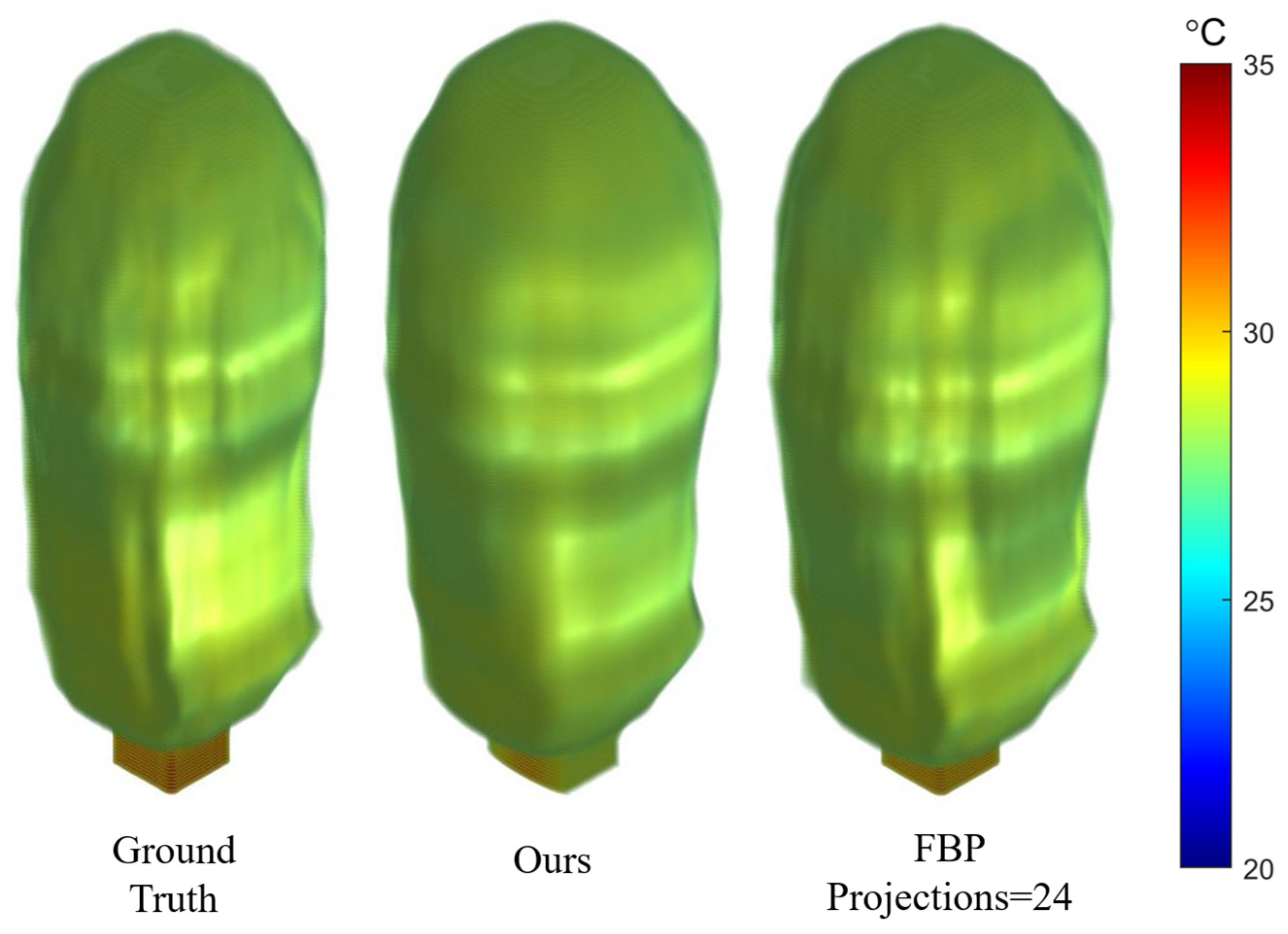
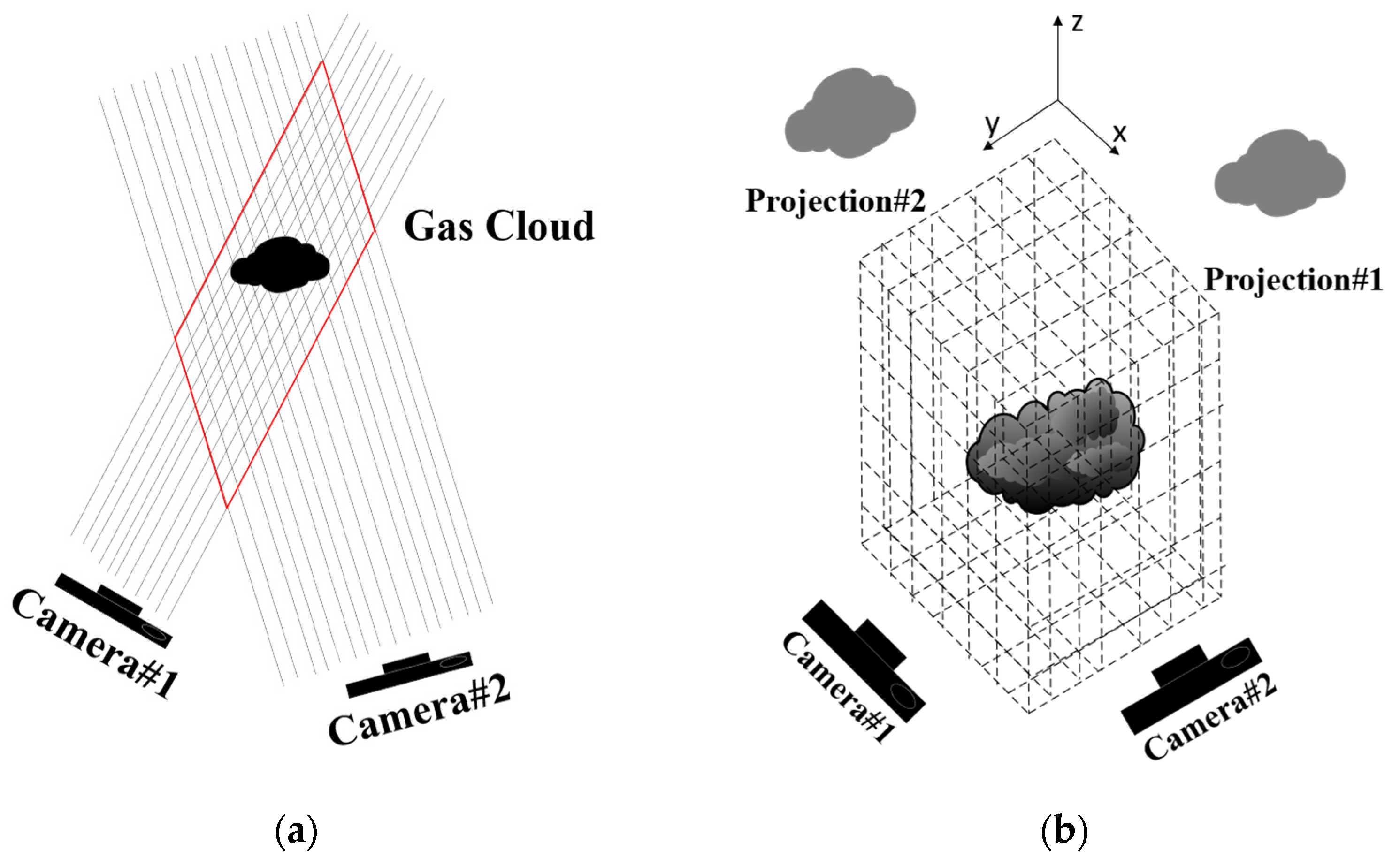


| Parameters | Substance |
|---|---|
| Spatial resolution | 640 × 12 pixels |
| Pixel spacing | 14 μm |
| Field of view (horizontal × vertical) | 10.24° × 8.20° |
| Detector frame rate | 30 Hz |
| Response wave band | 8~14 μm |
| Temperature measurement range | −20 °C~150 °C |
| Temperature accuracy | ±2 °C or ±2% of the readout (whichever is greater) @ ambient temperature −20 °C to 60 °C |
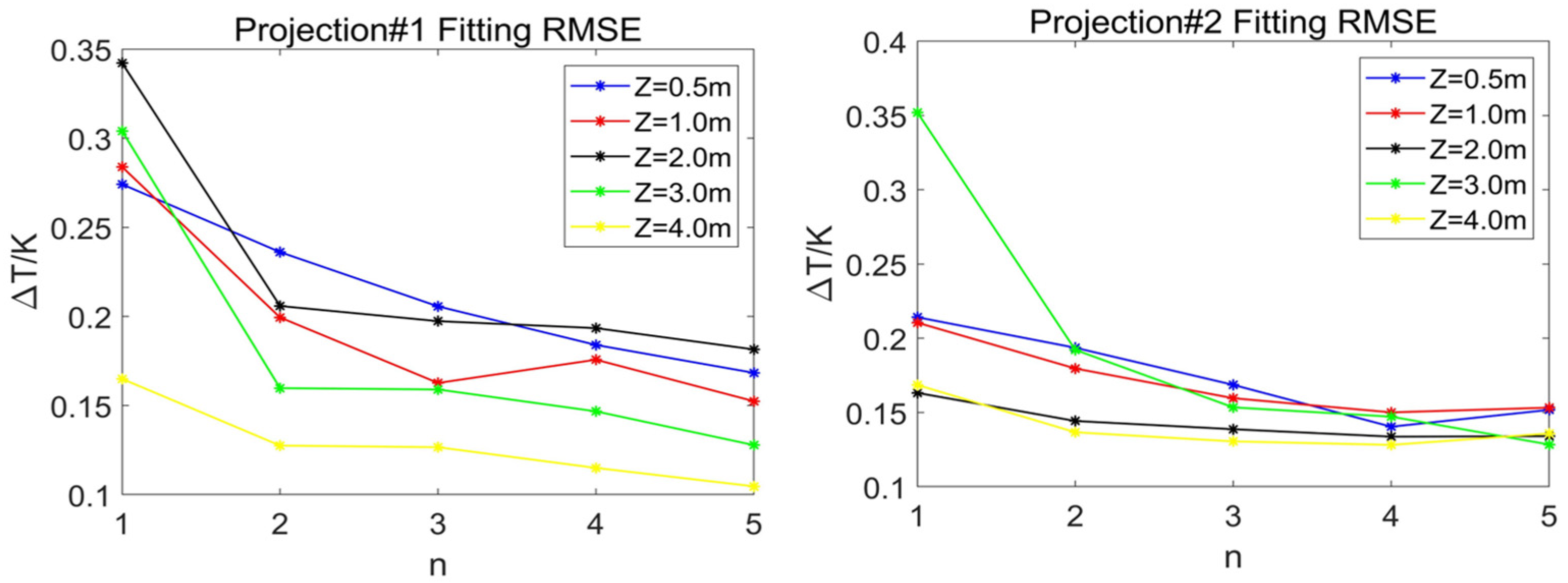
| Average RMSE | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 |
|---|---|---|---|---|---|
| projection#1 | 0.2137 | 0.1949 | 0.2241 | 0.1795 | 0.1278 |
| projection#2 | 0.1738 | 0.1707 | 0.1429 | 0.1947 | 0.1400 |
| Method | PSNR | SSIM | Time |
|---|---|---|---|
| FBP (Projections = 18) | 18.99 | 0.873 | 28.99 ms |
| FBP (Projections = 24) | 29.51 | 0.995 | 32.67 ms |
| ART (Iterations = 1000) | 10.05 | 0.640 | 43.85 ms |
| ART (Iterations = 50,000) | 13.60 | 0.794 | 440.26 ms |
| SART (Iterations = 50) | 9.34 | 0.635 | 22.15 ms |
| SART (Iterations = 400) | 27.96 | 0.992 | 80.98 ms |
| Ours | 25.63 | 0.940 | 15.67 ms |
| Position | PSNR | SSIM |
|---|---|---|
| Z = 0.5 m | 25.63 | 0.940 |
| Z = 1.0 m | 24.46 | 0.924 |
| Z = 2.0 m | 17.96 | 0.751 |
| Z = 3.0 m | 19.05 | 0.868 |
| Z = 4.0 m | 18.94 | 0.850 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Xu, L. A 3D Reconstruction of Gas Cloud Leakage Based on Multi-Spectral Imaging Systems. Remote Sens. 2025, 17, 1786. https://doi.org/10.3390/rs17101786
Zhang L, Xu L. A 3D Reconstruction of Gas Cloud Leakage Based on Multi-Spectral Imaging Systems. Remote Sensing. 2025; 17(10):1786. https://doi.org/10.3390/rs17101786
Chicago/Turabian StyleZhang, Lei, and Liang Xu. 2025. "A 3D Reconstruction of Gas Cloud Leakage Based on Multi-Spectral Imaging Systems" Remote Sensing 17, no. 10: 1786. https://doi.org/10.3390/rs17101786
APA StyleZhang, L., & Xu, L. (2025). A 3D Reconstruction of Gas Cloud Leakage Based on Multi-Spectral Imaging Systems. Remote Sensing, 17(10), 1786. https://doi.org/10.3390/rs17101786





