A Detection and Cover Integrated Waveform Design Method with Good Correlation Characteristics and Doppler Tolerance
Abstract
1. Introduction
- Strong applicability. At present, the mainstream probing and jamming integrated waveform is mainly realized by a simple combination waveform or time/frequency division multiplexing, such as an LFM-Barker code integrated waveform, etc. However, this kind of method has obvious limitations in engineering implementation: the waveform construction method is limited by the preset basis function combination mode, and the design freedom is limited. Compared with these methods, the proposed method establishes an objective function to optimize the waveform itself, which is not limited by the type of adversary detection waveform, has higher design freedom, and is applicable to a wide range of scenarios.
- Stable performance. At present, there are two typical realization modes of an integrated waveform: Suppression interference mostly adopts a noise modulation waveform, which mainly suppresses the interference through the noise-like nature of the waveform. This interference style requires a high jamming–signal ratio (JSR), and is difficult to realize in practical applications. Deception jamming generally adopts signal forwarding architecture. Although it can achieve a coherent jamming effect, it has inherent defects such as strict isolation requirements and high hardware implementation complexity. Compared with the above methods, the proposed method considers the low interference-to-signal ratio scenario from the perspective of deception jamming, and does not need to forward the enemy detection signal to achieve a stable jamming effect, and the detection performance is better than the mainstream integrated waveform.
2. Problem Statement
3. Problem Optimization
3.1. Simplifying the Objective Function
3.2. Gradient Descent
| Algorithm 1 Gradient Optimization of detection and cover integrated waveform |
|
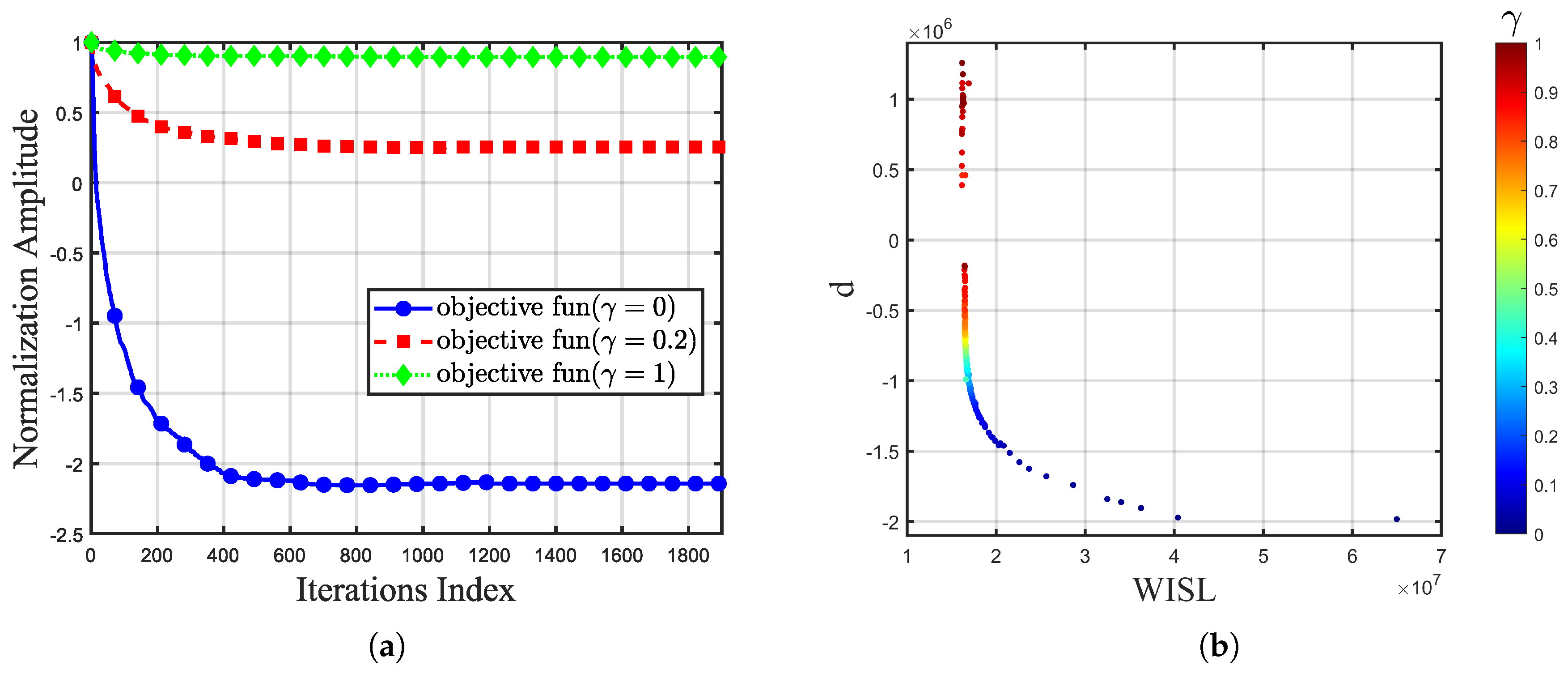
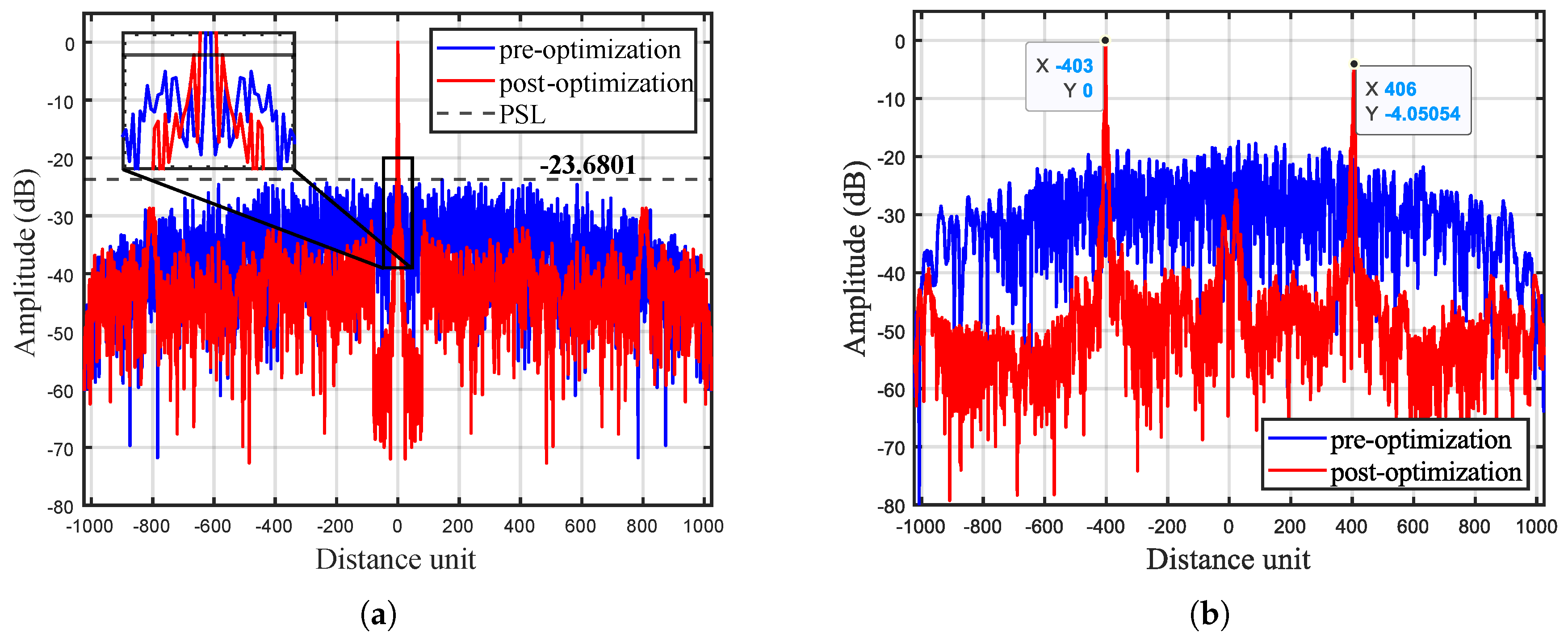
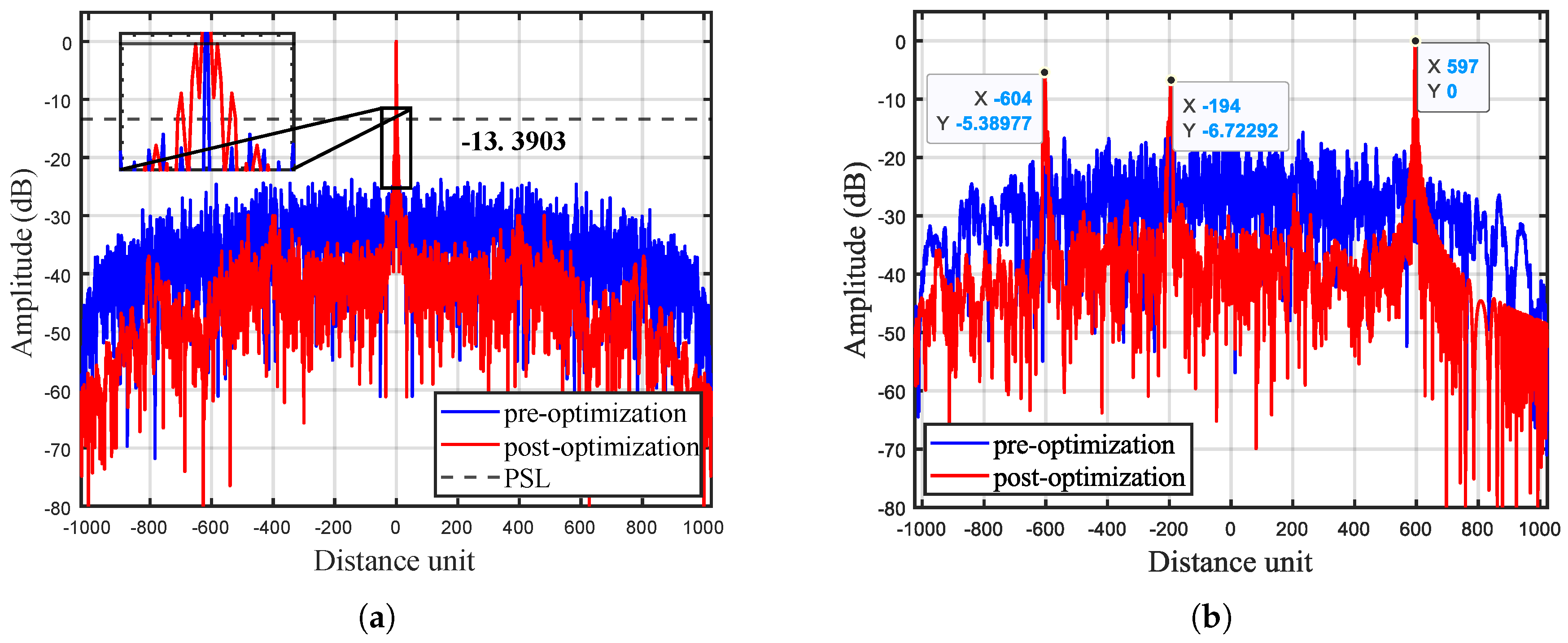
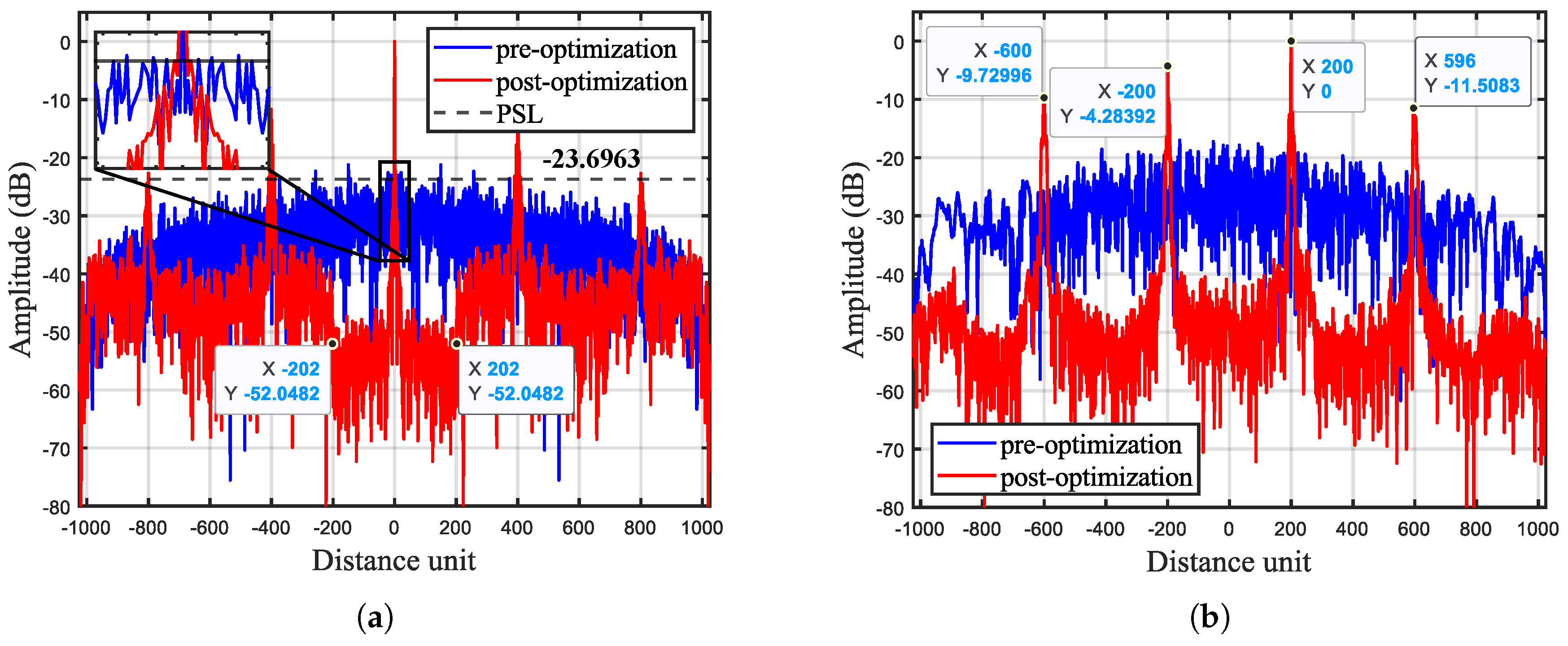
4. Simulations and Experimental Results
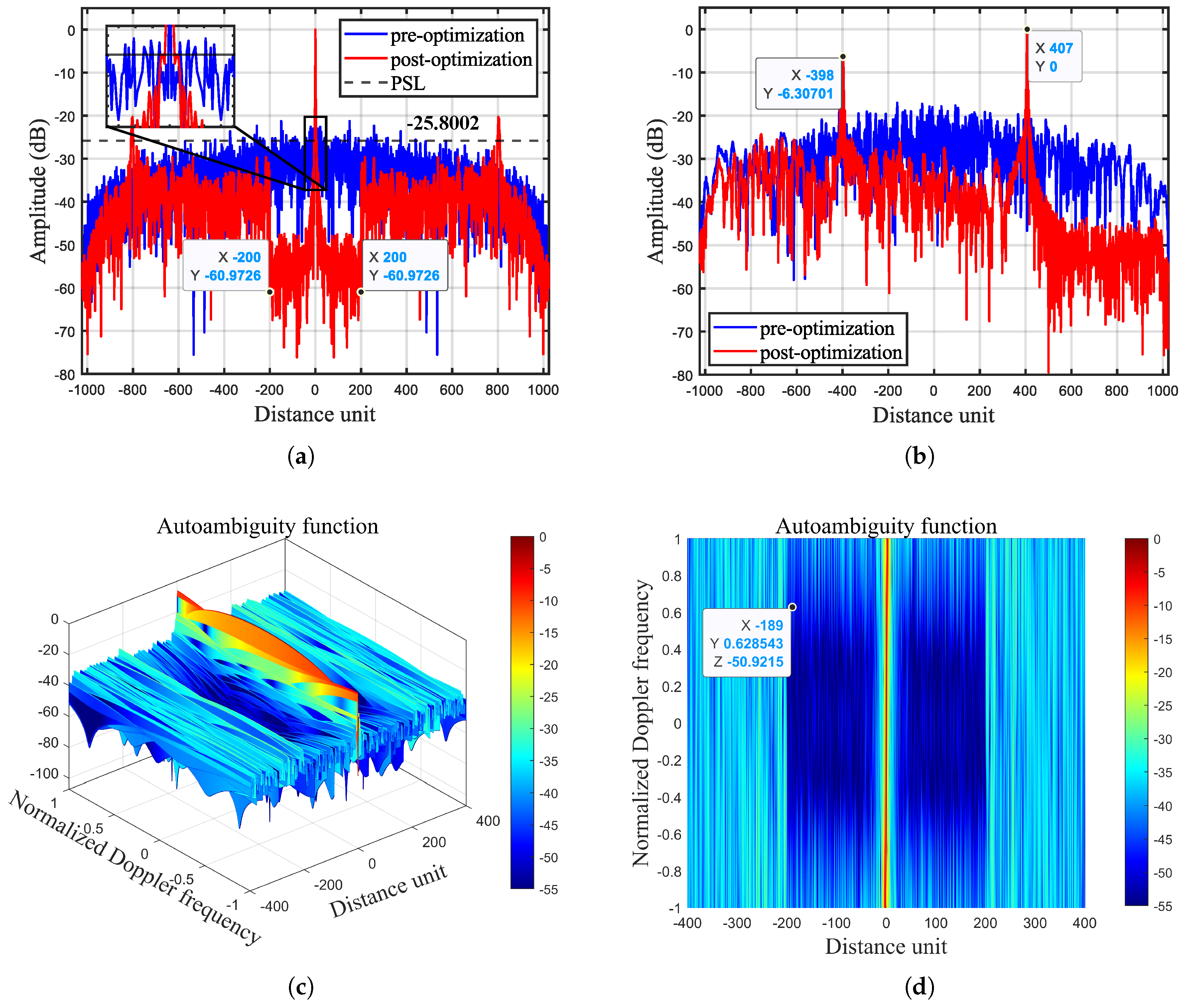
4.1. Numerical Results
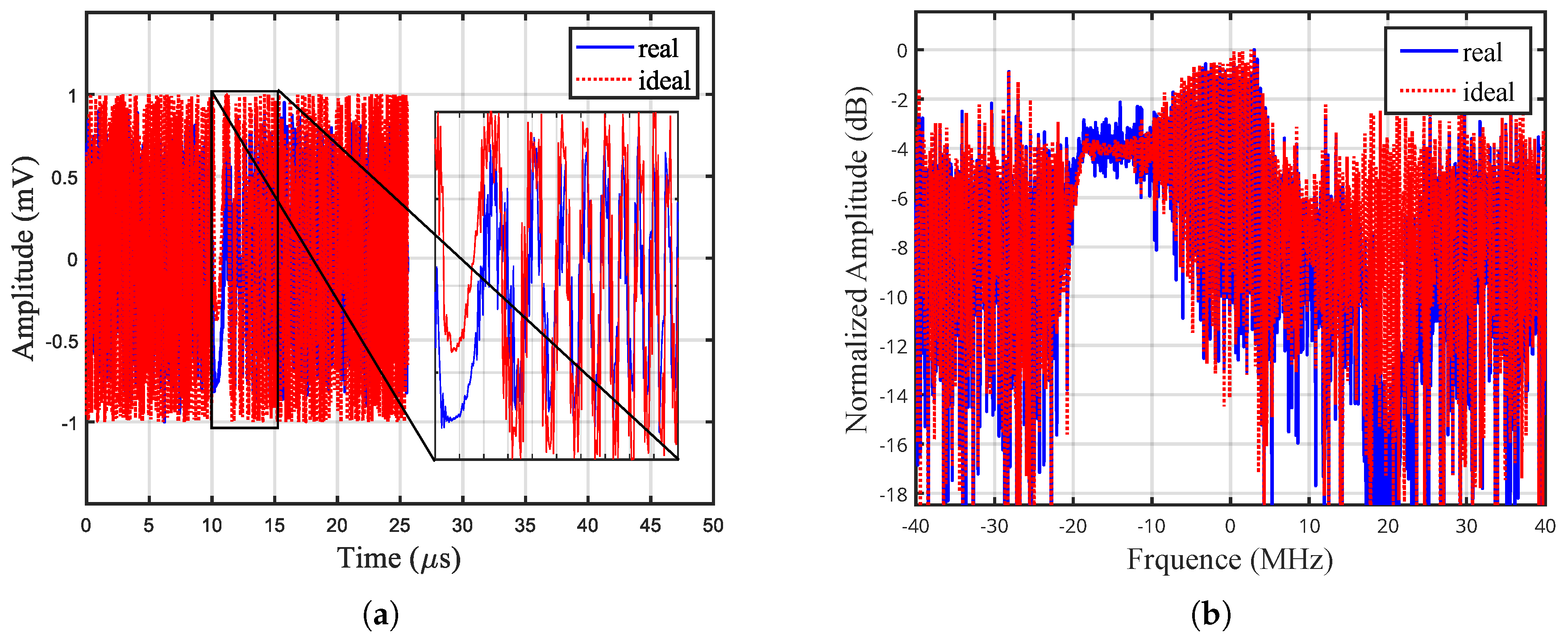
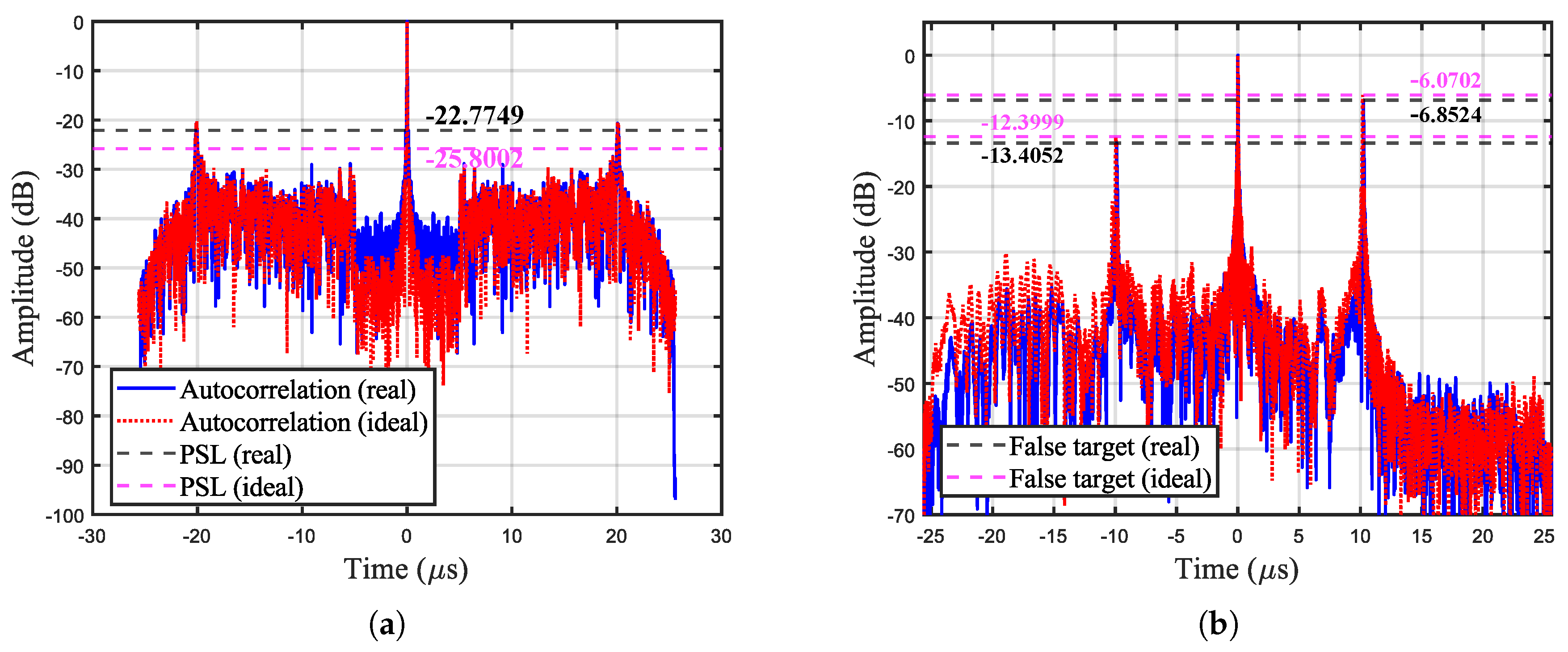
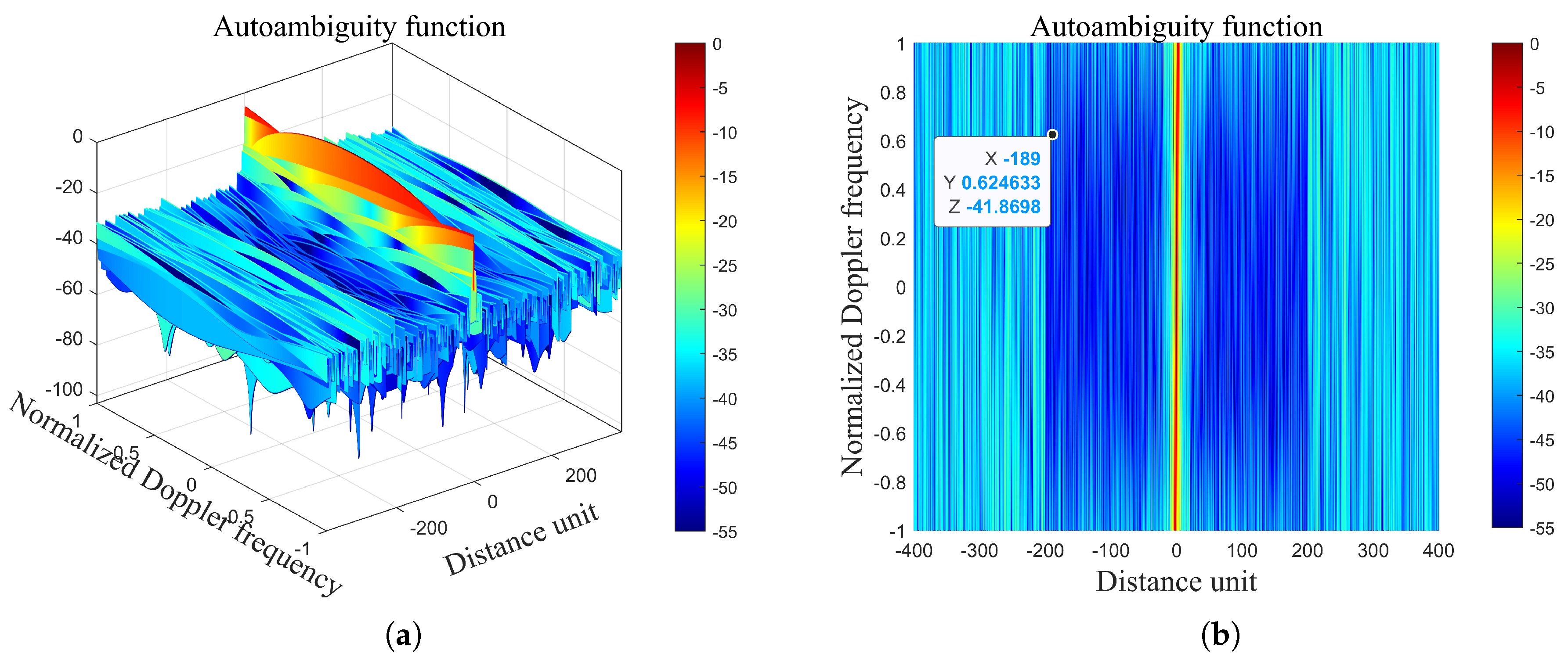
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, M.; Li, Y.; Wei, J.; Zhu, E. Joint Design of OFDM-LFM Waveforms and Receive Filter for MIMO Radar in Spatial Heterogeneous Clutter. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Xie, Z.; Wu, L.; Huang, X.; Fan, C.; Zhu, J.; Liu, W. Cross Ambiguity Function Shaping of Cognitive MIMO Radar: A Synergistic Approach to Antenna Placement and Waveform Design. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–13. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, Y.; Zhang, T.; Cui, G.; Tay, W.P. Integrated Transmit Waveform and RIS Phase Shift Design for LPI Detection and Communication. IEEE Trans. Wireless Commun. 2024, 23, 5663–5679. [Google Scholar] [CrossRef]
- Li, H.; Chen, S. Electromagnetic Scattering Characteristics and Radar Identification of Sea Corner Reflectors: Advances and Prospects. J. Radars 2023, 12, 738–761. [Google Scholar] [CrossRef]
- Luo, Y.; Guo, L.; Zuo, Y.; Liu, W. Time-Domain Scattering Characteristics and Jamming Effectiveness in Corner Reflectors. IEEE Access 2021, 9, 15696–15707. [Google Scholar] [CrossRef]
- Li, Y.; Huang, D.; Xing, S.; Wang, X. A Review of Synthetic Aperture Radar Jamming Technique. J. Radars 2020, 9, 753–764. [Google Scholar] [CrossRef]
- Wu, Q.; Zhao, F.; Ai, X.; Liu, X.; Xiao, S. Two-Dimensional Blanket Jamming Against ISAR Using Nonperiodic ISRJ. IEEE Sens. J. 2019, 19, 4031–4038. [Google Scholar] [CrossRef]
- Xu, Z.; Tang, B.; Ai, W.; Zhu, J. Relative Entropy Based Jamming Signal Design Against Radar Target Detection. IEEE Trans. Signal Process. 2025, 73, 1200–1215. [Google Scholar] [CrossRef]
- Li, F.; Zhao, Y.; Qiao, X. A waveform design method for suppressing range sidelobes in desired intervals. Signal Process. 2014, 96, 203–211. [Google Scholar] [CrossRef]
- An, M.; Yin, J.; Wang, T.; Li, Y. Quantitative Impacts of Different Polarization Operating Modes and Waveforms on Weather Observables for Polarimetric Phased Array Radar. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–22. [Google Scholar] [CrossRef]
- Zhu, J.; Yin, T.; Guo, W.; Zhang, B.; Zhou, Z. An underwater target azimuth trajectory enhancement approach in BTR. Appl. Acoust. 2025, 230, 110373. [Google Scholar] [CrossRef]
- Wang, F.; Li, N.; Pang, C.; Li, Y.; Wang, X. Algorithm for Designing PCFM Waveforms for Simultaneously Polarimetric Radars. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–16. [Google Scholar] [CrossRef]
- Xu, Z.; Tang, B.; Ai, W.; Xie, Z.; Zhu, J. Radar Transceiver Design for Extended Targets Based on Optimal Linear Detector. IEEE Trans. Aerosp. Electron. Syst. 2025, 1–12. [Google Scholar] [CrossRef]
- He, H.; Stoica, P.; Li, J. Waveform design with stopband and correlation constraints for cognitive radar. In Proceedings of the 2010 2nd International Workshop on Cognitive Information Processing, Elba, Italy, 14–16 June 2010; pp. 344–349. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Huang, Y.; Piezzo, M.; Farina, A. A new radar waveform design algorithm with improved feasibility for spectral coexistence. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1029–1038. [Google Scholar] [CrossRef]
- Rowe, W.; Stoica, P.; Li, J. Spectrally Constrained Waveform Design. IEEE Signal Process Mag. 2014, 31, 157–162. [Google Scholar] [CrossRef]
- Gerlach, K.; Frey, M.R.; Steiner, M.J.; Shackelford, A. Spectral Nulling on Transmit via Nonlinear FM Radar Waveforms. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1507–1515. [Google Scholar] [CrossRef]
- Yuan, Y.; Liu, X.; Zhang, T.; Cui, G.; Kong, L. Reinforcement-Learning-Enhanced Adaption of Signal Power and Modulation for LPI Radar System. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 8555–8568. [Google Scholar] [CrossRef]
- Celentano, S.; Farina, A.; Timmoneri, L.; Foglia, G. Co-existence of AESA (Active Electronically Scanned Array) radar and Electronic Warfare (EW) systems on board of a military ship. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–5. [Google Scholar]
- Chen, K.; Xie, C.; Yang, F.; Huang, M.; Chen, Y.; Qu, S.W.; Yang, S. Integrated Radar and Communication Design With Low Probability of Intercept Based on 4-D Antenna Arrays. IEEE Trans. Antennas Propag. 2022, 70, 8496–8506. [Google Scholar] [CrossRef]
- Kay, S.M.; Thanos, J.H. Optimal transmit signal design for active sonar/radar. In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002; pp. II-1513–II-1516. [Google Scholar]
- Shao, C.; Tang, S. Optimization research of radar and jammer integration share signal design. Microcomputer Inf. 2010, 26, 208–210. [Google Scholar]
- Zhang, Y.; Chen, T. Integrated Radar and Jammer Signal Modulated by Bi-phase Encoding Signal of Spatiotemporal Chaos. Mod. Radar. 2006, 15–18. [Google Scholar]
- Yang, D.; Liu, Y.; Tang, S.; Wu, S. Optimization design of radar/jammer share signal modulated by binary phase encoding signal of chaos. Comput. Simul. 2011, 28, 30–33, 37. [Google Scholar]
- Han, G.; He, J.; Pan, Q. Optimization design of radar and jammer integration signal based on improved chaos genetic algorithm. Comput. Eng. Appl. 2014, 50, 212–215. [Google Scholar]
- Tan, L.; Jiang, Q.; Liu, F. Detection and jamming integration signal of orthogonal comb waveform. J. Detect. Control. 2016, 38, 78–81. [Google Scholar]
- Li, C.; Wu, G.; Li, G.; Xue, H. Shared Waveform Design for Integrated Detection and Jamming Signal Based on Smart Noise Jamming of Convolution Modulation. In Proceedings of the 2023 8th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 8–10 July 2023; pp. 564–569. [Google Scholar]
- Li, Q.; Wang, Y.; Shang, K. Design and performance simulation for the detection and jamming integrated signal waveform. J. Detect. Control. 2016, 42, 39–44. [Google Scholar]
- Pralon, L.; Beltrao, G.; Barreto, A.; Cosenza, B. On the Analysis of PM/FM Noise Radar Waveforms Considering Modulating Signals with Varied Stochastic Properties. Sensors 2021, 21, 1727. [Google Scholar] [CrossRef]
- Cao, R.; Li, M.; Ding, D. Design of Integrated Detection-Jamming Signal Based on Noise Frequency Modulation and Phase-Coded. In Proceedings of the 2023 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Qingdao, China, 14–17 May 2023; pp. 1–2. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, Y.; Hu, X.; Xiao, Y. Integrated waveform optimization design of detection and jamming based on DQN. Syst. Eng. Electron. 2023, 45, 638–646. [Google Scholar]
- Deng, Y.; Wei, X. Design and Processing of Integrated Signal for Co-Frequency Detection and Jamming Based on Timing Constraint. In Proceedings of the 2024 6th International Conference on Electronic Engineering and Informatics (EEI), Chongqing, China, 28–30 June 2024; pp. 1738–1743. [Google Scholar]
- Li, C.; Wu, G. A Shared Waveform Design and Processing Method for Integrated Radar Detection and Coherent Jamming Signal. In Proceedings of the 2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 17–19 June 2022; pp. 373–380. [Google Scholar]
- Wang, F.; Xia, X.G.; Pang, C.; Cheng, X.; Li, Y.; Wang, X. Joint Design Methods of Unimodular Sequences and Receiving Filters With Good Correlation Properties and Doppler Tolerance. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Zhu, J.; Xie, Z.; Jiang, N.; Song, Y.; Han, S.; Liu, W.; Huang, X. Delay-Doppler Map Shaping through Oversampled Complementary Sets for High-Speed Target Detection. Remote Sens. 2024, 16, 2898. [Google Scholar] [CrossRef]
- Yin, T.; Guo, W.; Zhu, J.; Wu, Y.; Zhang, B.; Zhou, Z. Underwater Broadband Target Detection by Filtering Scanning Azimuths Based on Features of Subband Peaks. IEEE Sens. J. 2025, 25, 13601–13609. [Google Scholar] [CrossRef]
- Wang, F.; Pang, C.; Zhou, J.; Li, Y.; Wang, X. Design of Complete Complementary Sequences for Ambiguity Functions Optimization With a PAR Constraint. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Lin, C.t. On the Ambiguity Function of Random Binary-Phase-Coded Waveforms. IEEE Trans. Aerosp. Electron. Syst. 1985, AES-21, 432–436. [Google Scholar] [CrossRef]
- Wang, Y.C.; Dong, L.; Xue, X.; Yi, K.C. On the Design of Constant Modulus Sequences with Low Correlation Sidelobes Levels. IEEE Commun. Lett. 2012, 16, 462–465. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, L.; Jiang, R.; Hu, J.; Xu, S. Radar Jamming Decision-Making in Cognitive Electronic Warfare: A Review. IEEE Sens. J. 2023, 23, 11383–11403. [Google Scholar] [CrossRef]
- Xiong, J.; Cui, G.; Fan, T.; Li, Y.; Yu, X.; Kong, L.; Yang, X. Tangential Maneuvering Target Detection for Airborne Cognitive Radar. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 401–415. [Google Scholar] [CrossRef]
- Rybicki, B.W.; Nelson, J.K. Train Offline, Refine Online: Improving Cognitive Tracking Radar Performance with Approximate Policy Iteration and Deep Neural Networks. IEEE Trans. Radar Syst. 2025, 3, 57–70. [Google Scholar] [CrossRef]
- Wicks, M.C.; Mokole, E.L.; Blunt, S.D.; Schneible, R.S.; Amuso, V.J. Principles of Waveform Diversity and Design; IET Press: Rijeka, Croatia, 2011. [Google Scholar]
- Pillai, S.R.; Pillai, S.U.; Selesnick, I.W.; Li, K.Y. Waveform Diversity: Theory & Applications; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Gini, F.; Maio, A.D.; Patton, L. Waveform Design and Diversity for Advanced Radar Systems; IET Press: London, UK, 2012. [Google Scholar]
- The MathWorks, Inc. Optimization Toolbox User’s Guide. Available online: https://ww2.mathworks.cn/help/pdfdoc/optim/optim.pdf/ (accessed on 5 March 2025).
- Jin, G.; Deng, Y.; Wang, R.; Wang, W.; Wang, P.; Long, Y.; Zhang, Z.M.; Zhang, Y. An Advanced Nonlinear Frequency Modulation Waveform for Radar Imaging With Low Sidelobe. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6155–6168. [Google Scholar] [CrossRef]
- Wu, L.; Palomar, D.P. Sequence Design for Spectral Shaping via Minimization of Regularized Spectral Level Ratio. IEEE Trans. Signal Process. 2019, 67, 4683–4695. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, N. Discrete Phase Coded Sequence Set Design for Waveform-Agile Radar Based on Alternating Direction Method of Multipliers. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4238–4252. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Wang, F.; Li, N.; Wu, Z.; Pang, C.; Zhang, L.; Li, Y. A Detection and Cover Integrated Waveform Design Method with Good Correlation Characteristics and Doppler Tolerance. Remote Sens. 2025, 17, 1775. https://doi.org/10.3390/rs17101775
Guo H, Wang F, Li N, Wu Z, Pang C, Zhang L, Li Y. A Detection and Cover Integrated Waveform Design Method with Good Correlation Characteristics and Doppler Tolerance. Remote Sensing. 2025; 17(10):1775. https://doi.org/10.3390/rs17101775
Chicago/Turabian StyleGuo, Haoting, Fulai Wang, Nanjun Li, Zezhou Wu, Chen Pang, Lei Zhang, and Yongzhen Li. 2025. "A Detection and Cover Integrated Waveform Design Method with Good Correlation Characteristics and Doppler Tolerance" Remote Sensing 17, no. 10: 1775. https://doi.org/10.3390/rs17101775
APA StyleGuo, H., Wang, F., Li, N., Wu, Z., Pang, C., Zhang, L., & Li, Y. (2025). A Detection and Cover Integrated Waveform Design Method with Good Correlation Characteristics and Doppler Tolerance. Remote Sensing, 17(10), 1775. https://doi.org/10.3390/rs17101775





