Refinement of Trend-to-Trend Cross-Calibration Total Uncertainties Utilizing Extended Pseudo Invariant Calibration Sites (EPICS) Global Temporally Stable Target
Abstract
1. Introduction
1.1. Trend-to-Trend Cross-Calibration Using Global EPICS
1.2. Spectral Band Adjustment Factor Estimation for Cross-Calibration
1.3. T2T Cross-Calibration Uncertainty
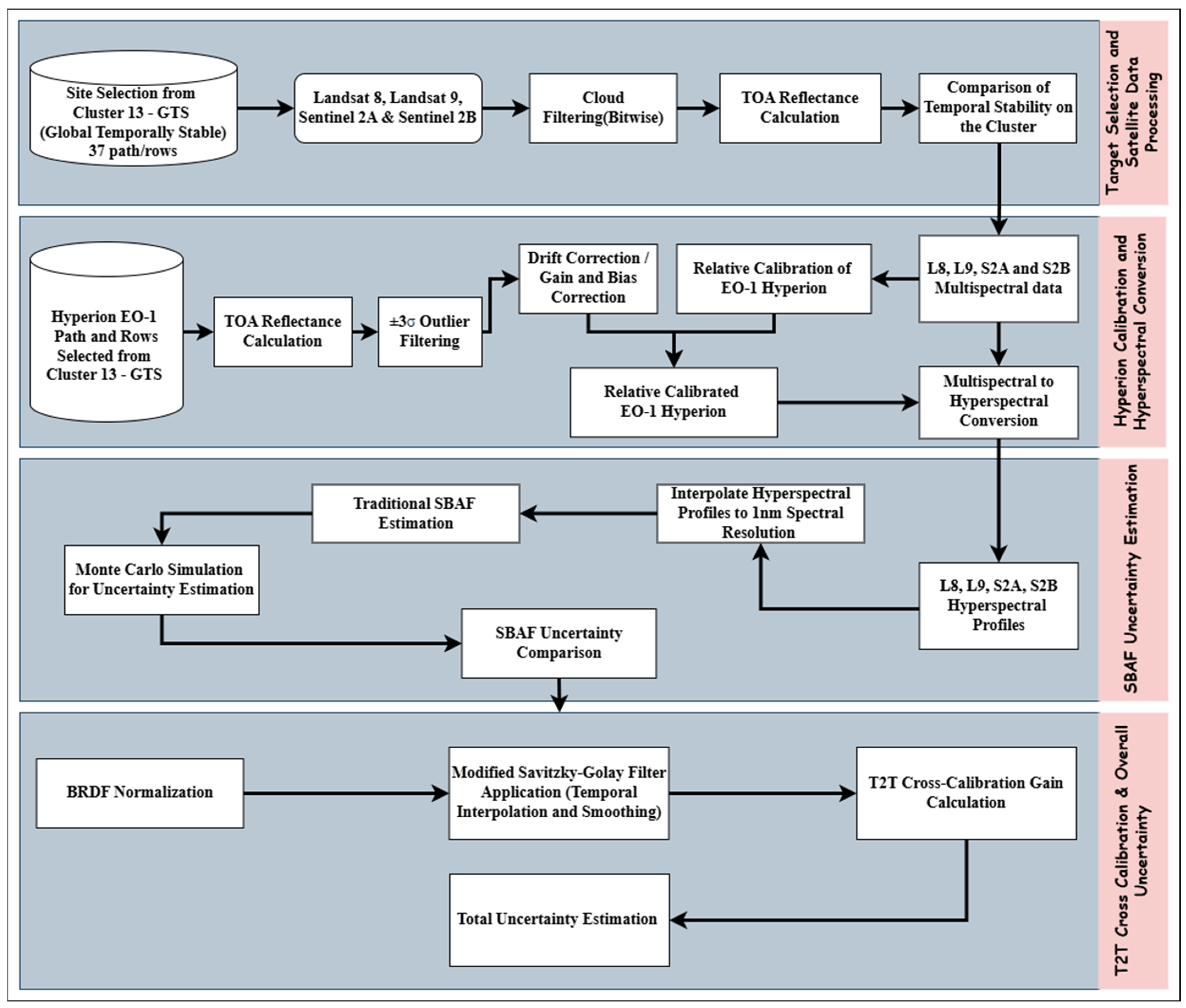
2. Materials and Methods
2.1. Sensor Overview
2.1.1. Landsat 8, 9
2.1.2. Sentinel 2A, 2B
2.1.3. Earth Observing-1 (Hyperion)
2.2. Data Processing
2.2.1. Selection of Sites from EPICS Cluster 13-GTS
2.2.2. Creation of Zonal Mask for Satellite Images
2.2.3. Cloud Screening from Selected Scenes
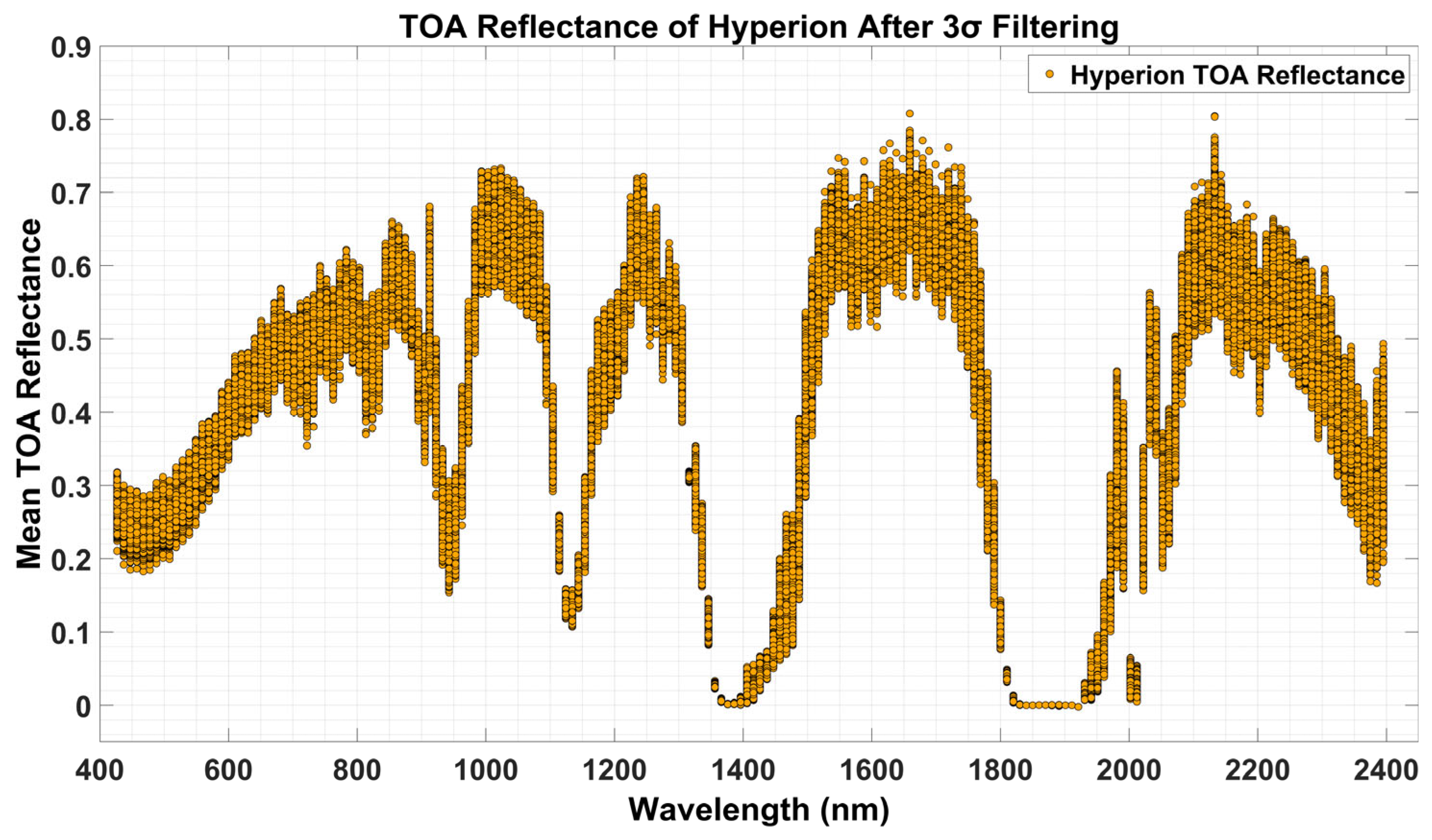
2.2.4. Filtering Outliers
2.2.5. Temporal Stability Comparison
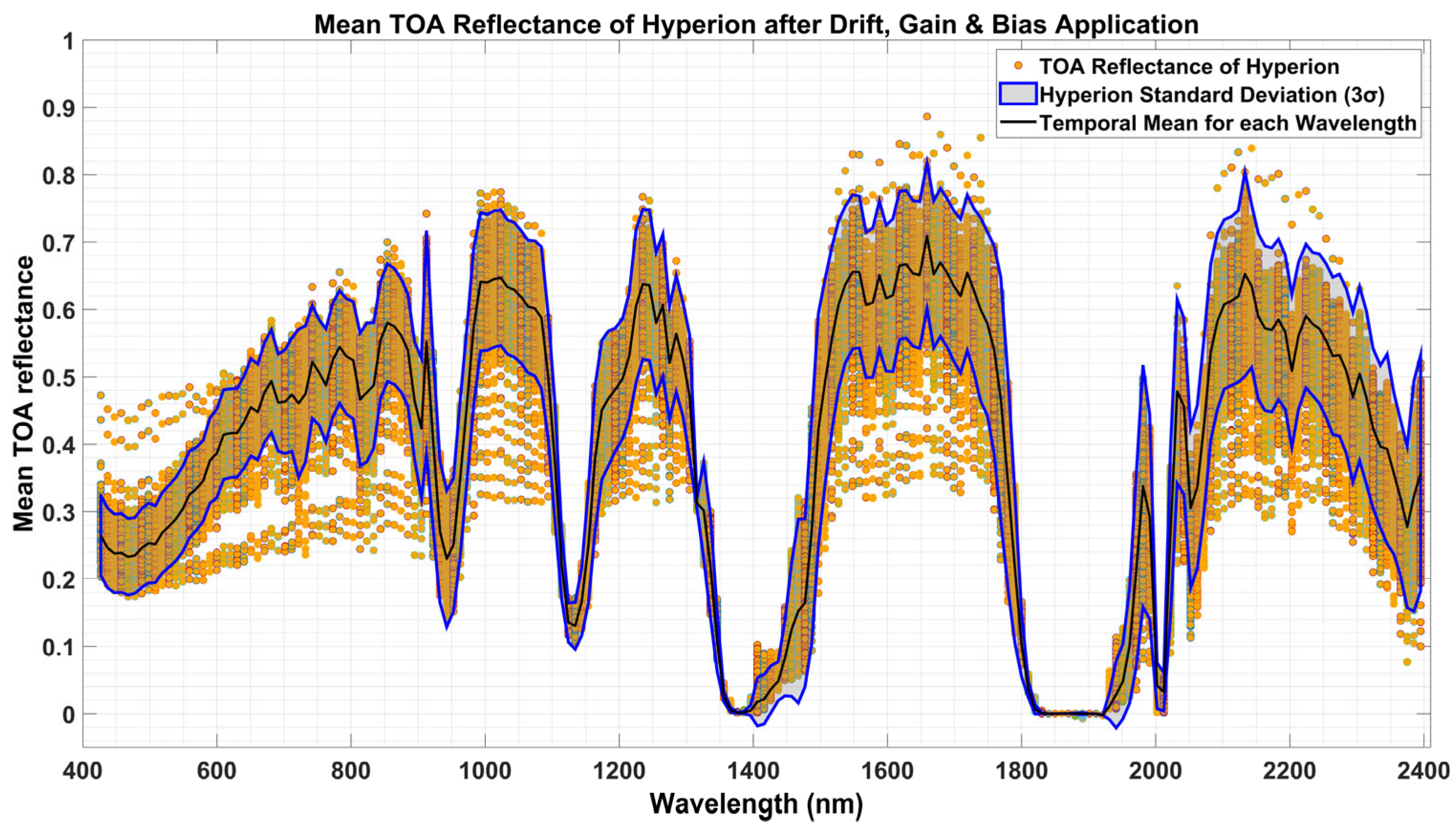
2.2.6. Drift Gain and Bias Correction on EO-1 Hyperion
2.3. Estimation of Satellite Hyperspectral Profile
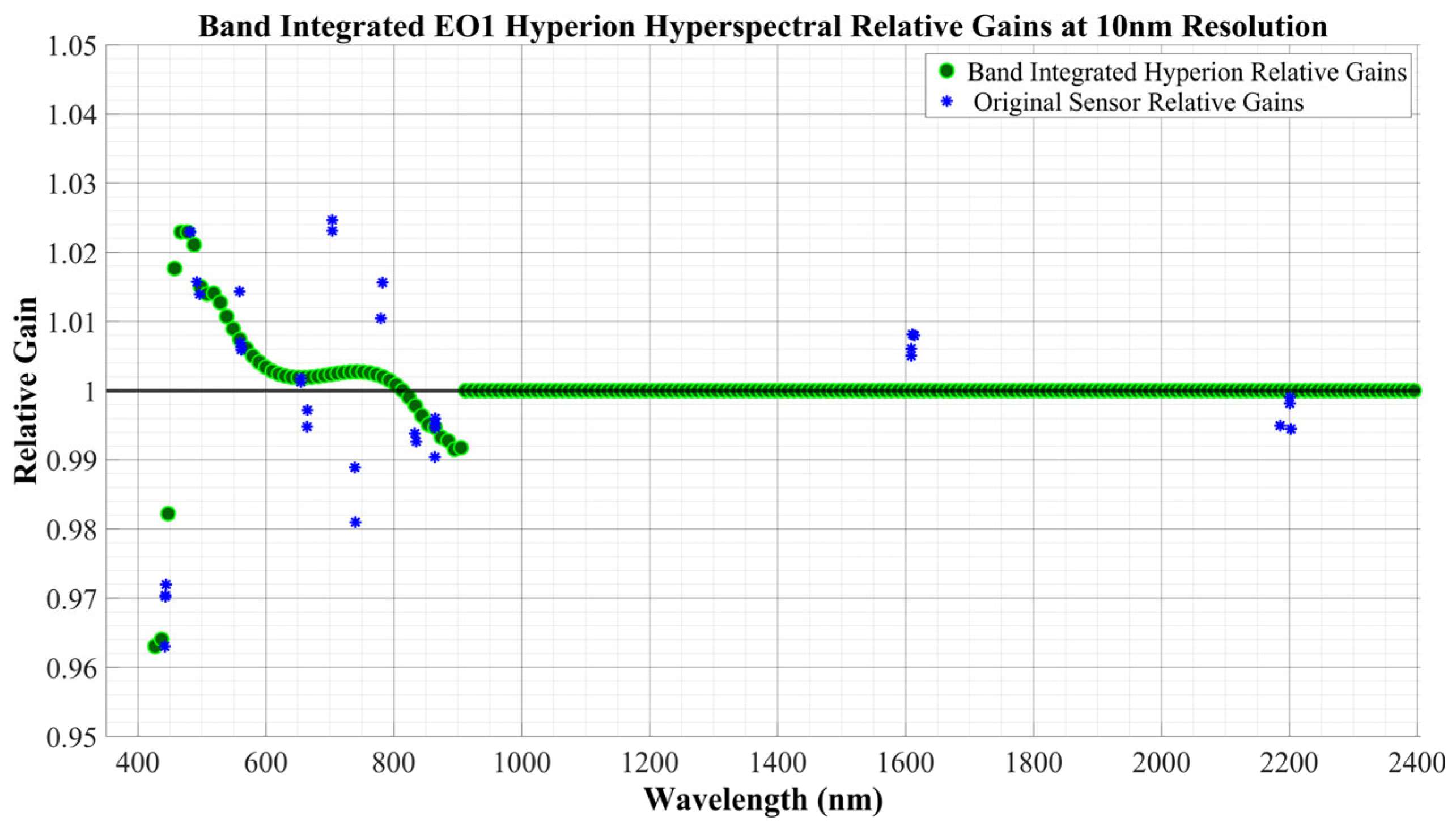
2.4. Relative Calibration on Hyperion
2.4.1. Interpolation of Super-Spectral Gains
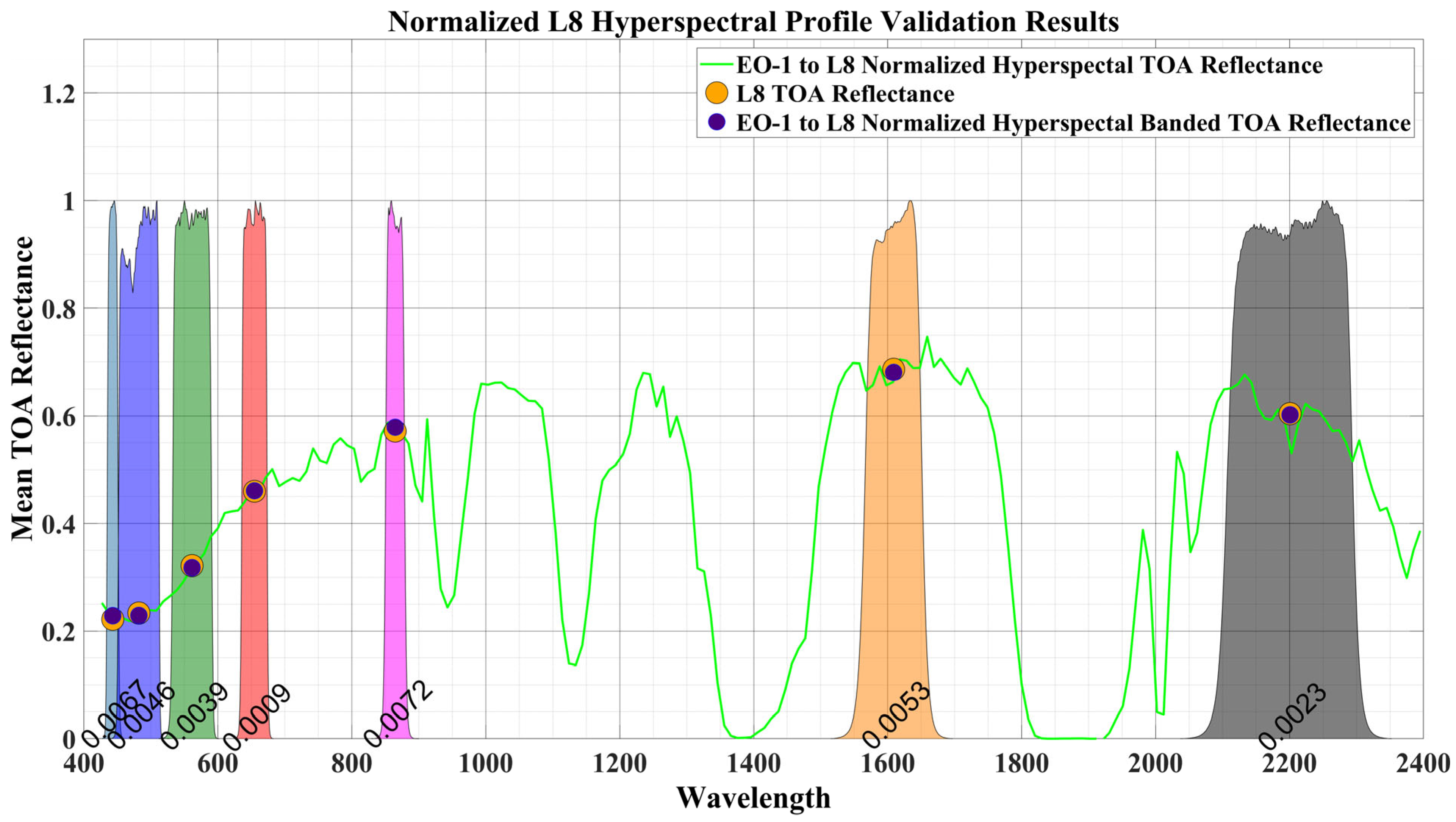
2.4.2. Normalized Hyperspectral Profile After Relative Gain Calibration
2.5. Makima Interpolation on Hyperspectral Profiles
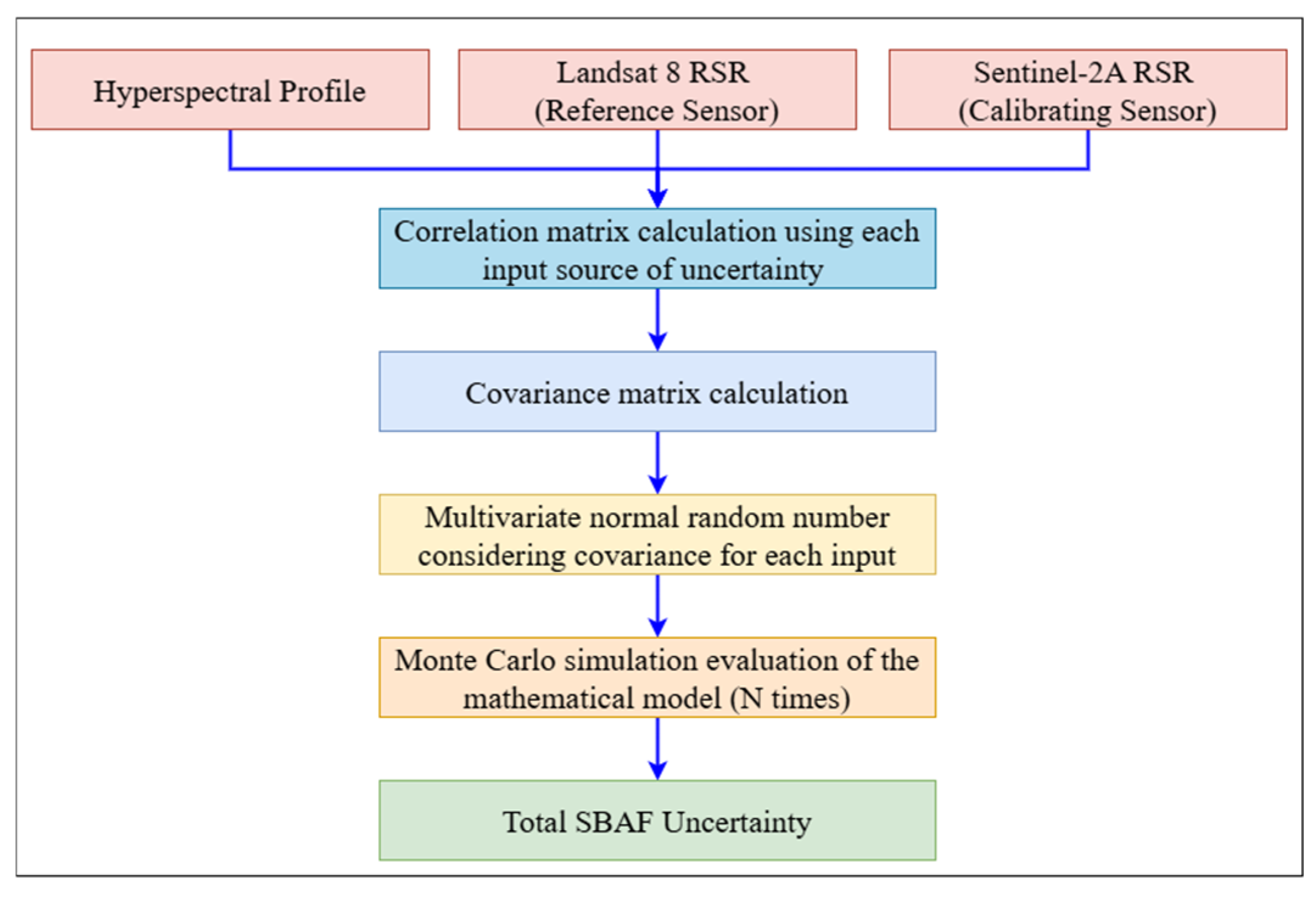
2.6. EPICS Global SBAF and Uncertainty Estimation Using Monte Carlo Simulation
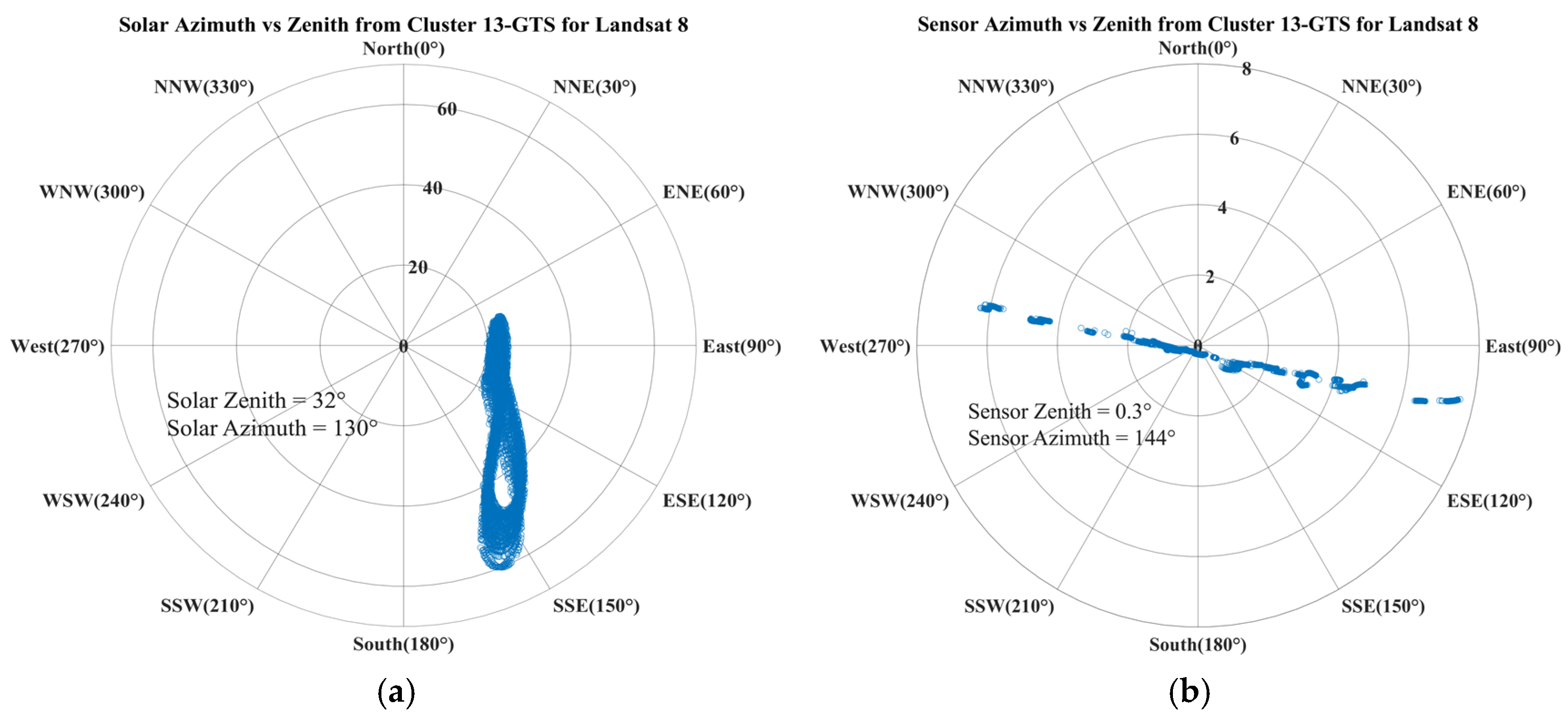
2.7. BRDF Normalization
- View Zenith Angle = 0.3°
- View Azimuth Angle = 144°
- Solar Zenith Angle = 32°
- Solar Azimuth Angle = 130°
2.8. Temporal Interpolation Using MSG Filter
2.9. T2T Cross-Calibration Gain
2.10. Total Uncertainty Estimation
3. Results
3.1. Sites Selected from Cluster 13-GTS
3.2. Temporal Stability of Cluster 13-GTS vs. GC13
3.3. Normalized Hyperspectral Profiles After Relative Calibration
3.4. Hyperspectral Profiles at 1 nm Spectral Resolution Interpolation
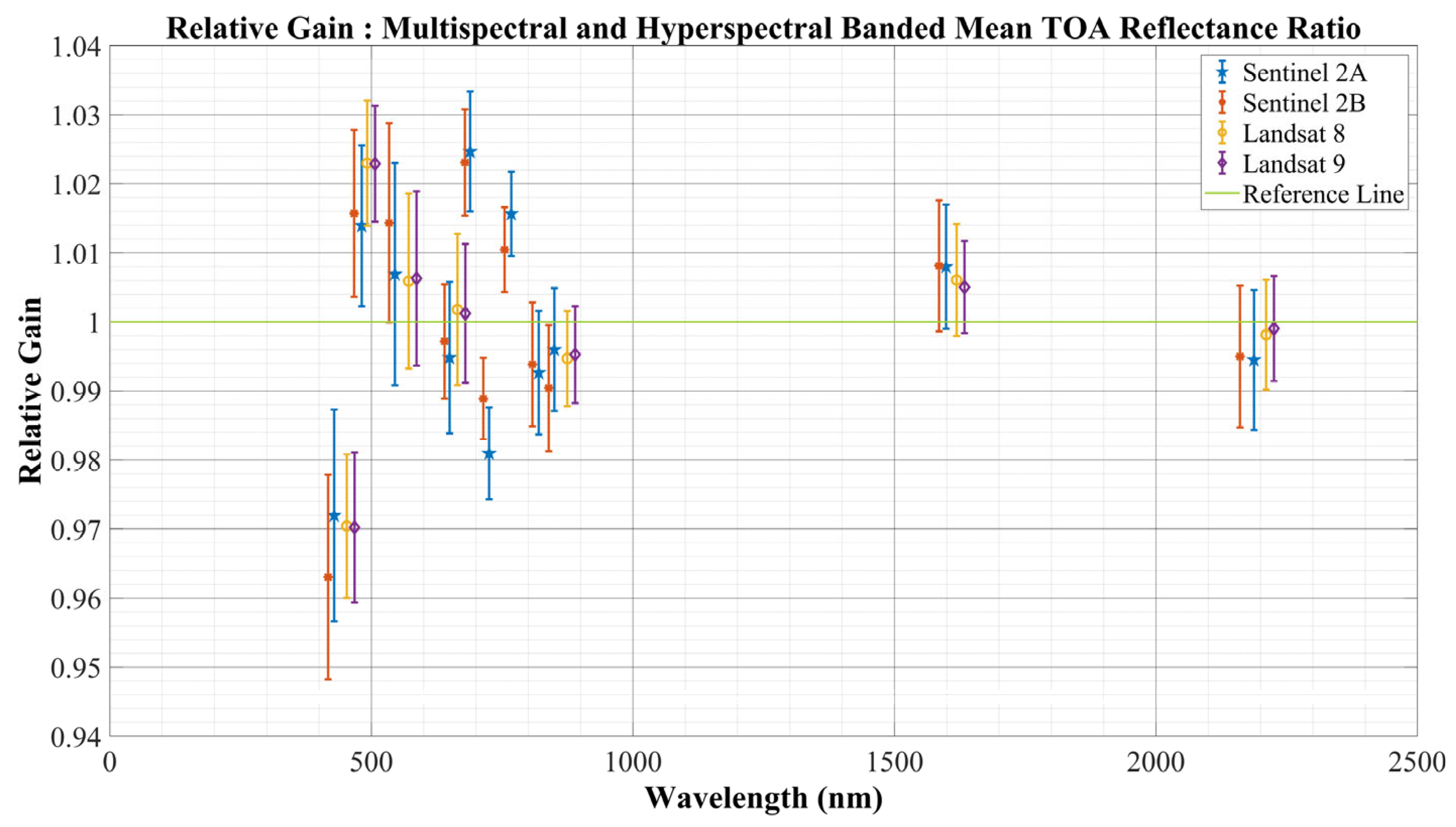
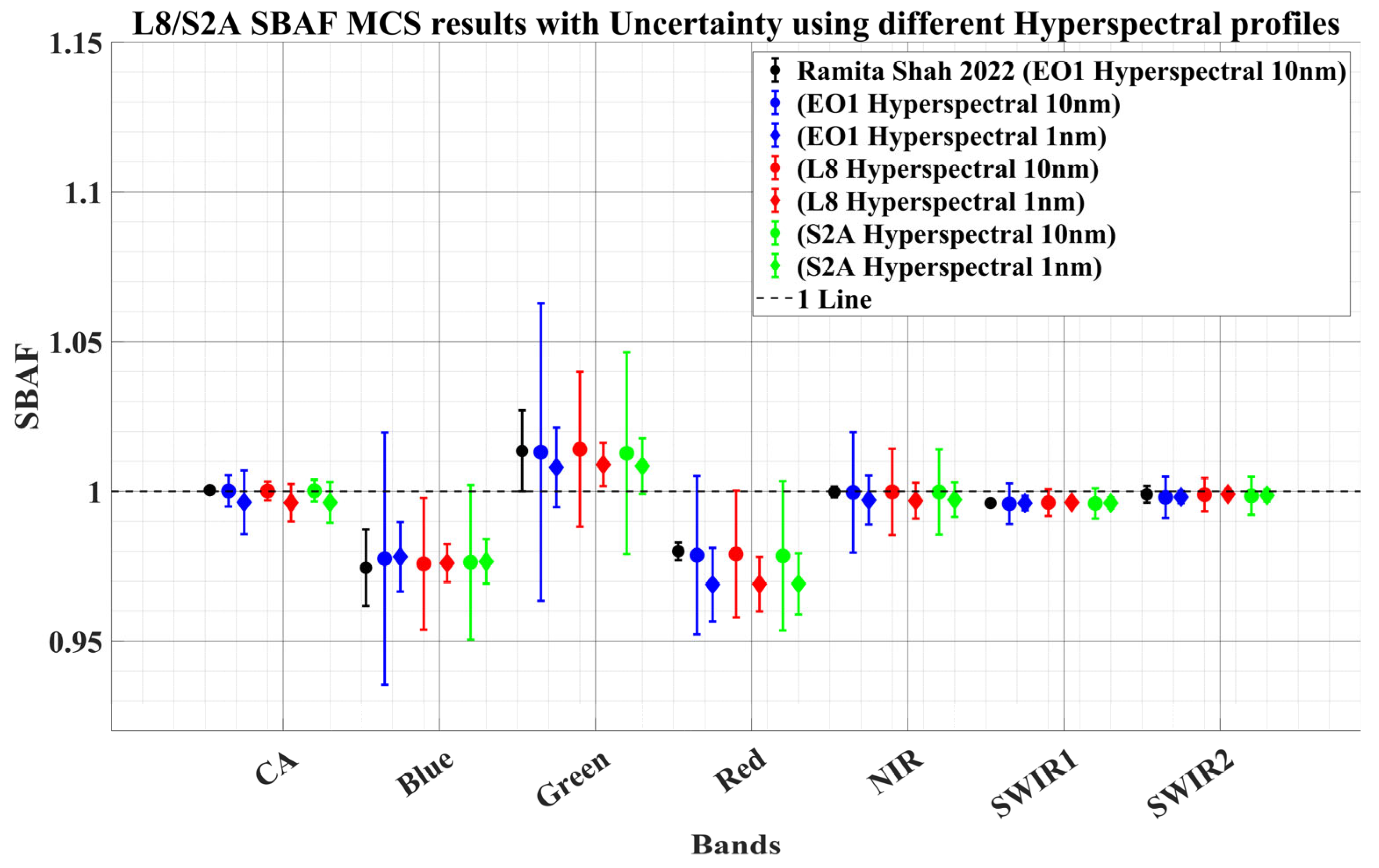
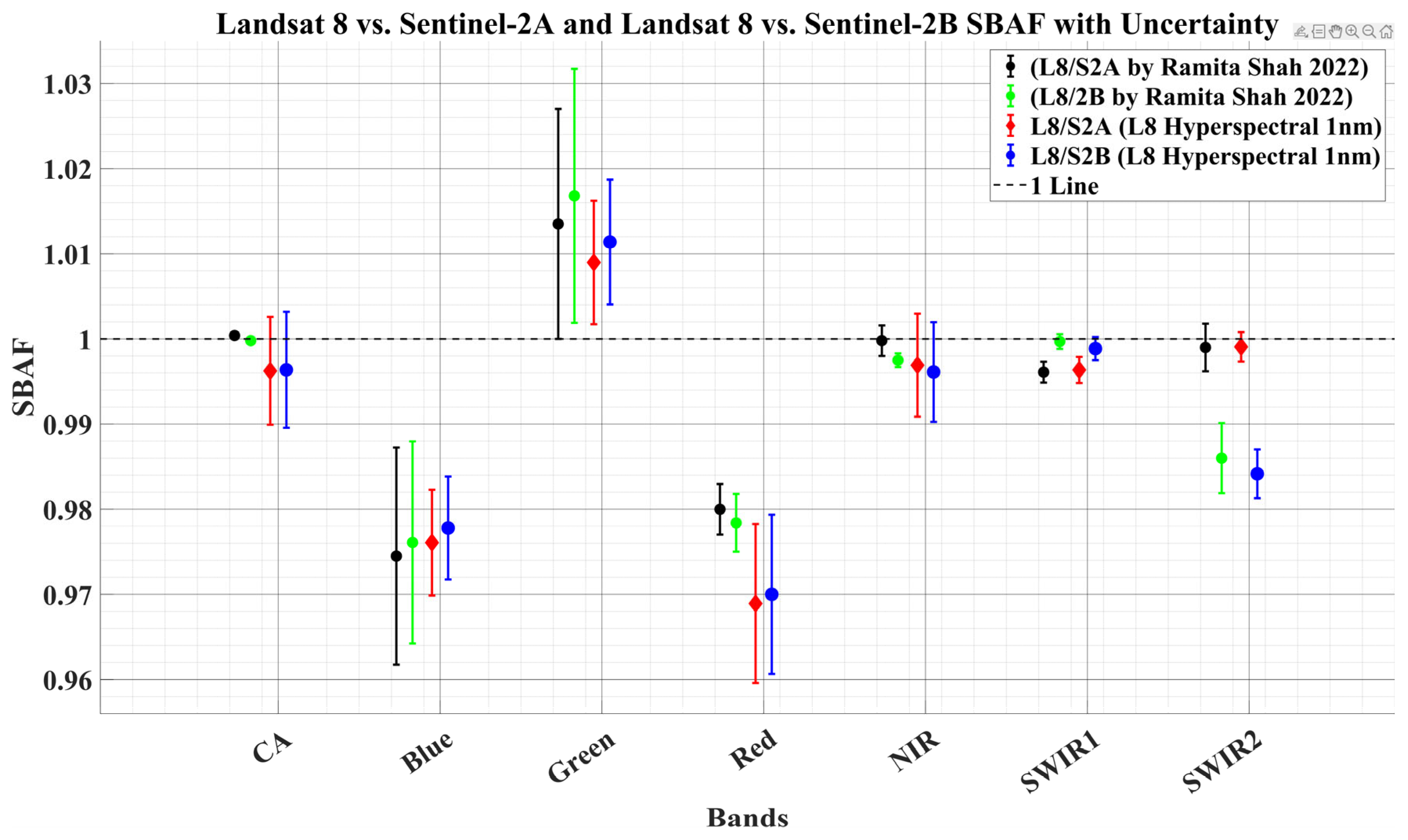
3.5. Global SBAF Estimation Using Different Hyperspectral Profiles
Derived SBAF Using Monte Carlo Simulation for Different Hyperspectral Profiles
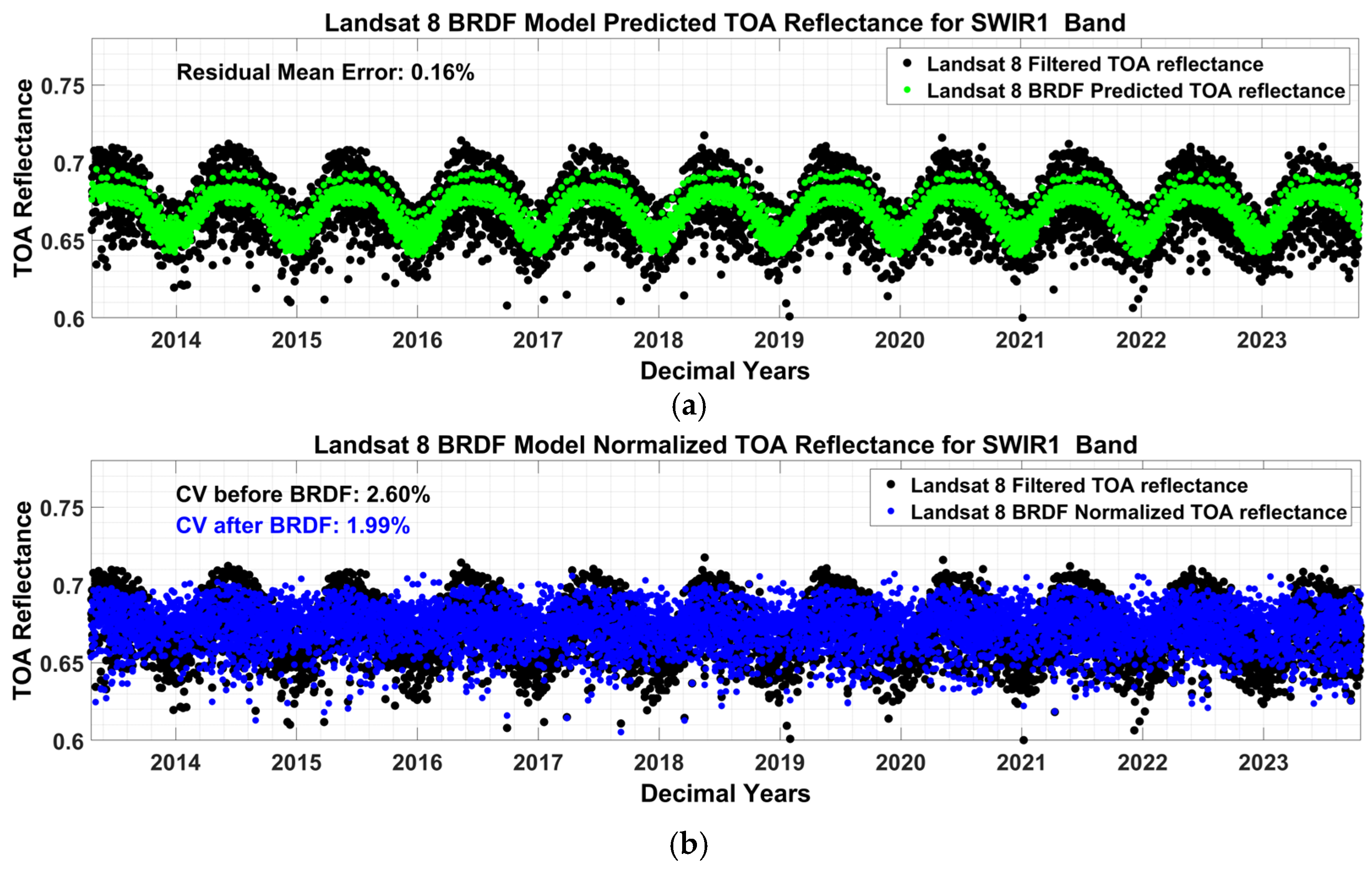
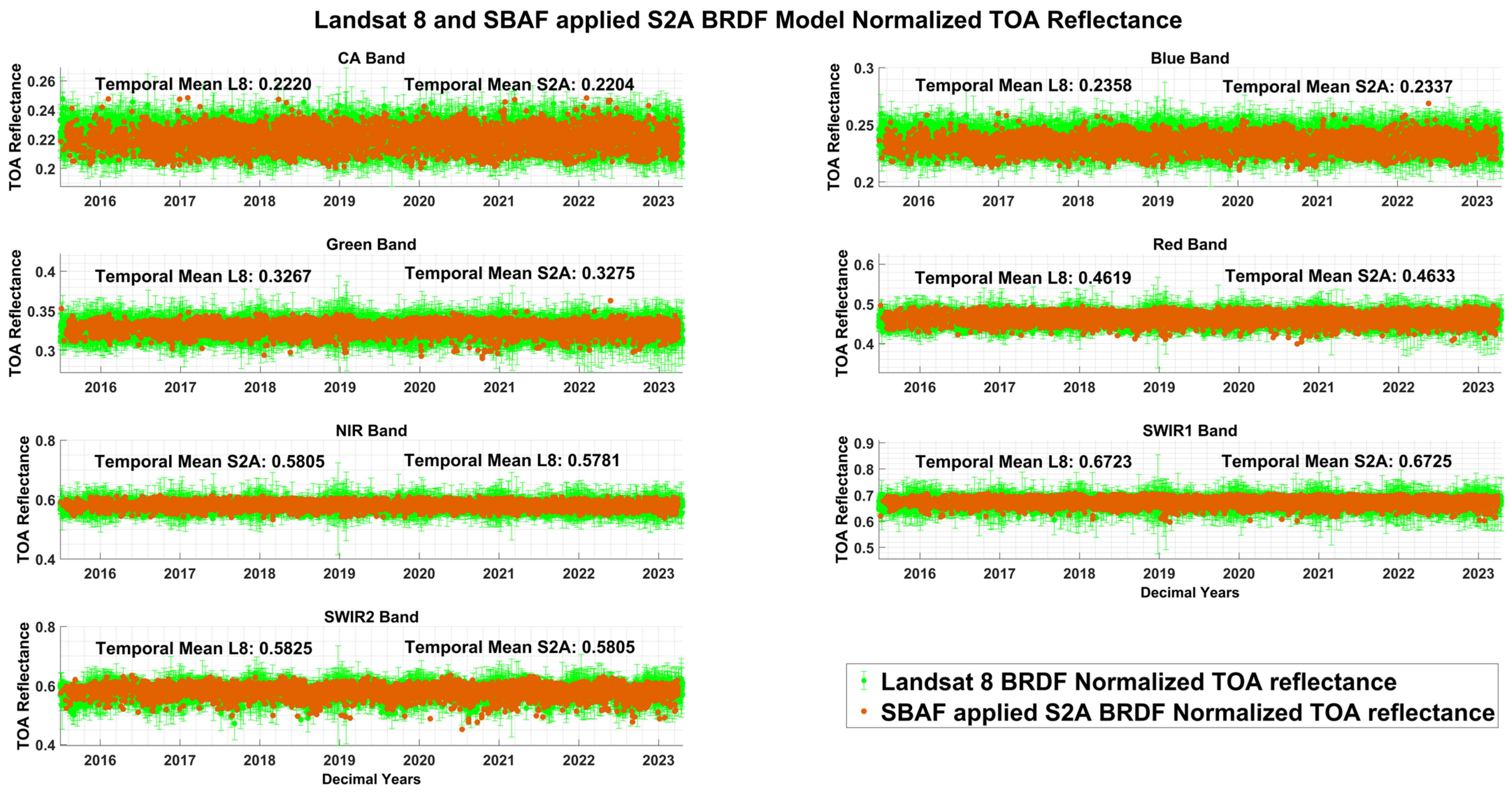
3.6. BRDF Normalized TOA Reflectance
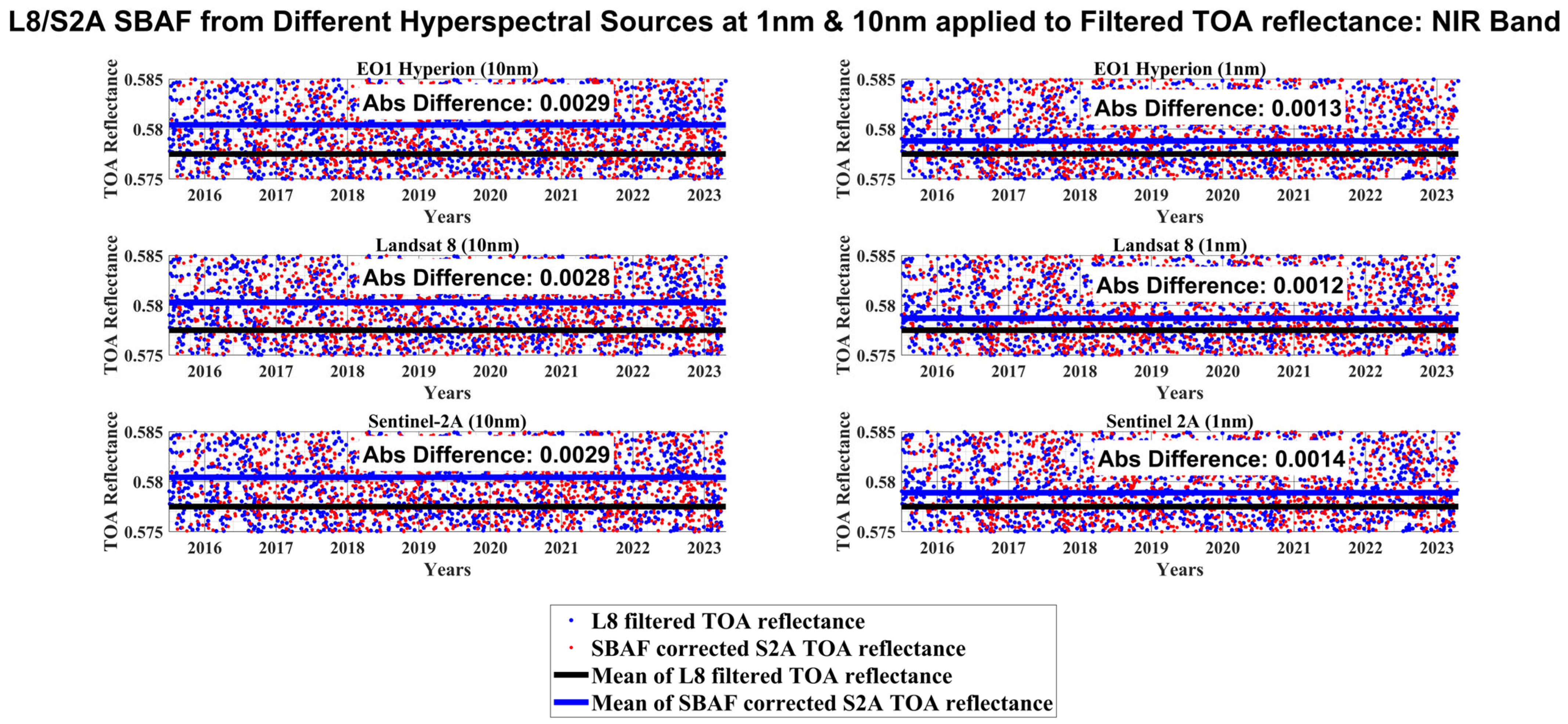
3.7. Trend Identification Using MSG Filter
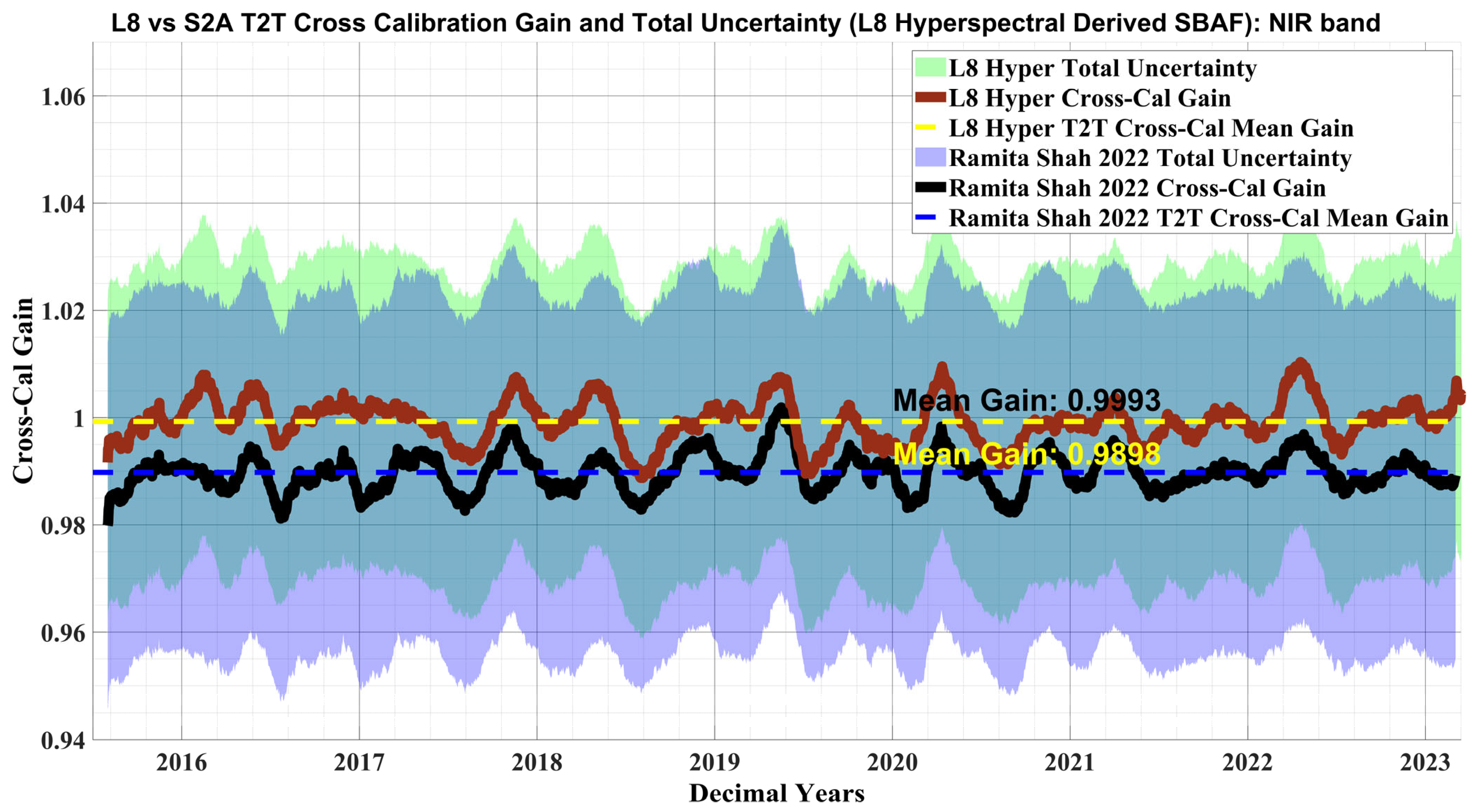
3.8. T2T Cross Calibration Gain Validation
3.9. Total T2T Cross-Calibration Uncertainty Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Wang, D.; Morton, D.; Masek, J.; Wu, A.; Nagol, J.; Xiong, X.; Levy, R.; Vermote, E.; Wolfe, R. Impact of Sensor Degradation on the MODIS NDVI Time Series. Remote Sens. Environ. 2012, 119, 55–61. [Google Scholar] [CrossRef]
- Dinguirard, M.; Slater, P.N. Calibration of Space-Multispectral Imaging Sensors: A Review. Remote Sens. Environ. 1999, 68, 194–205. [Google Scholar] [CrossRef]
- Sterckx, S.; Livens, S.; Adriaensen, S. Rayleigh, Deep Convective Clouds, and Cross-Sensor Desert Vicarious Calibration Validation for the PROBA-V Mission. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1437–1452. [Google Scholar] [CrossRef]
- Chander, G.; Meyer, D.J.; Helder, D.L. Cross Calibration of the Landsat-7 ETM+ and EO-1 ALI Sensor. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2821–2831. [Google Scholar] [CrossRef]
- Teillet, P.M.; Barker, J.L.; Markham, B.L.; Irish, R.R.; Fedosejevs, G.; Storey, J.C. Radiometric Cross-Calibration of the Landsat-7 ETM+ and Landsat-5 TM Sensors Based on Tandem Data Sets. Remote Sens. Environ. 2001, 78, 39–54. [Google Scholar] [CrossRef]
- Lacherade, S.; Fougnie, B.; Henry, P.; Gamet, P. Cross Calibration over Desert Sites: Description, Methodology, and Operational Implementation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1098–1113. [Google Scholar] [CrossRef]
- Helder, D.L.; Basnet, B.; Morstad, D.L. Optimized Identification of Worldwide Radiometric Pseudo-Invariant Calibration Sites. Can. J. Remote Sens. 2010, 36, 527–539. [Google Scholar] [CrossRef]
- Shrestha, M.; Leigh, L.; Helder, D. Classification of North Africa for Use as an Extended Pseudo Invariant Calibration Sites (EPICS) for Radiometric Calibration and Stability Monitoring of Optical Satellite Sensors. Remote Sens. 2019, 11, 875. [Google Scholar] [CrossRef]
- Shrestha, M.; Hasan, M.N.; Leigh, L.; Helder, D. Extended Pseudo Invariant Calibration Sites (EPICS) for the Cross-Calibration of Optical Satellite Sensors. Remote Sens. 2019, 11, 1676. [Google Scholar] [CrossRef]
- Khakurel, P.; Leigh, L.; Kaewmanee, M.; Pinto, C.T. Extended Pseudo Invariant Site-Based Trend-to-Trend Cross-Calibration of Optical Satellite Sensors. Remote Sens. 2021, 13, 1545. [Google Scholar] [CrossRef]
- Shah, R.; Leigh, L.; Kaewmanee, M.; Pinto, C.T. Validation of Expanded Trend-to-Trend Cross-Calibration Technique and Its Application to Global Scale. Remote Sens. 2022, 14, 6216. [Google Scholar] [CrossRef]
- Fajardo Rueda, J.; Leigh, L.; Kaewmanee, M.; Byregowda, H.; Teixeira Pinto, C. Derivation of Hyperspectral Profiles for Global Extended Pseudo Invariant Calibration Sites (EPICS) and Their Application in Satellite Sensor Cross-Calibration. Remote Sens. 2025, 17, 216. [Google Scholar] [CrossRef]
- Fajardo Rueda, J.; Leigh, L.; Teixeira Pinto, C.; Kaewmanee, M.; Helder, D. Classification and Evaluation of Extended Pics (Epics) on a Global Scale for Calibration and Stability Monitoring of Optical Satellite Sensors. Remote Sens. 2021, 13, 3350. [Google Scholar] [CrossRef]
- Fajardo Rueda, J.; Leigh, L.; Pinto, C.T. A Global Mosaic of Temporally Stable Pixels for Radiometric Calibration of Optical Satellite Sensors Using Landsat 8. Remote Sens. 2024, 16, 2437. [Google Scholar] [CrossRef]
- Fajardo Rueda, J.; Leigh, L.; Teixeira Pinto, C. Identification of Global Extended Pseudo Invariant Calibration Sites (EPICS) and Their Validation Using Radiometric Calibration Network (RadCalNet). Remote Sens. 2024, 16, 4129. [Google Scholar] [CrossRef]
- Landsat Next|Landsat Science. Available online: https://landsat.gsfc.nasa.gov/satellites/landsat-next/ (accessed on 17 November 2024).
- Pinto, C.T.; Shrestha, M.; Hasan, N.; Leigh, L.; Helder, D. SBAF for Cross-Calibration of Landsat-8 OLI and Sentinel-2 MSI over North African PICS. Proc. SPIE 2018, 10764, 294–304. [Google Scholar] [CrossRef]
- Karki, P.B.; Kaewmanee, M.; Leigh, L.; Pinto, C.T. The Development of Dark Hyperspectral Absolute Calibration Model Using Extended Pseudo Invariant Calibration Sites at a Global Scale: Dark EPICS-Global. Remote Sens. 2023, 15, 2141. [Google Scholar] [CrossRef]
- Landsat 8 Data Users Handbook|U.S. Geological Survey. Available online: https://www.usgs.gov/landsat-missions/landsat-8-data-users-handbook (accessed on 30 October 2024).
- Gross, G.; Helder, D.; Begeman, C.; Leigh, L.; Kaewmanee, M.; Shah, R. Initial Cross-Calibration of Landsat 8 and Landsat 9 Using the Simultaneous Underfly Event. Remote Sens. 2022, 14, 2418. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Li, J.; Roy, D.P.; Atzberger, C.; Zhou, G. A Global Analysis of Sentinel-2A, Sentinel-2B and Landsat-8 Data Revisit Intervals and Implications for Terrestrial Monitoring. Remote Sens. 2017, 9, 902. [Google Scholar] [CrossRef]
- Revel, C.; Lonjou, V.; Marcq, S.; Desjardins, C.; Fougnie, B.; Coppolani-Delle Luche, C.; Guilleminot, N.; Lacamp, A.S.; Lourme, E.; Miquel, C.; et al. Sentinel-2A and 2B Absolute Calibration Monitoring. Eur. J. Remote Sens. 2019, 52, 122–137. [Google Scholar] [CrossRef]
- Ungar, S.G.; Pearlman, J.S.; Mendenhall, J.A.; Reuter, D. Overview of the Earth Observing One (EO-1) Mission. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1149–1159. [Google Scholar] [CrossRef]
- Franks, S.; Neigh, C.S.R.; Campbell, P.K.; Sun, G.; Yao, T.; Zhang, Q.; Huemmrich, K.F.; Middleton, E.M.; Ungar, S.G.; Frye, S.W. EO-1 Data Quality and Sensor Stability with Changing Orbital Precession at the End of a 16 Year Mission. Remote Sens. 2017, 9, 412. [Google Scholar] [CrossRef]
- Jing, X.; Leigh, L.; Helder, D.; Teixeira Pinto, C.; Aaron, D. Lifetime Absolute Calibration of the EO-1 Hyperion Sensor and Its Validation. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9466–9475. [Google Scholar] [CrossRef]
- Chen, L.; Hu, X.; Xu, N.; Zhang, P. The Application of Deep Convective Clouds in the Calibration and Response Monitoring of the Reflective Solar Bands of FY-3A/MERSI (Medium Resolution Spectral Imager). Remote Sens. 2013, 5, 6958–6975. [Google Scholar] [CrossRef]
- Landsat Collection 2 Quality Assessment Bands|U.S. Geological Survey. Available online: https://www.usgs.gov/Landsat-missions/Landsat-collection-2-quality-assessment-bands (accessed on 27 February 2025).
- Document Library. Available online: https://sentiwiki.copernicus.eu/web/document-library#Library-S2-Documents (accessed on 3 March 2025).
- Chander, G.; Mishra, N.; Helder, D.L.; Aaron, D.B.; Angal, A.; Choi, T.; Xiong, X.; Doelling, D.R. Applications of Spectral Band Adjustment Factors (SBAF) for Cross-Calibration. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1267–1281. [Google Scholar] [CrossRef]
- Gascon, F.; Bouzinac, C.; Thépaut, O.; Jung, M.; Francesconi, B.; Louis, J.; Lonjou, V.; Lafrance, B.; Massera, S.; Gaudel-Vacaresse, A.; et al. Copernicus Sentinel-2A Calibration and Products Validation Status. Remote Sens. 2017, 9, 584. [Google Scholar] [CrossRef]
- Farhad, M.M.; Kaewmanee, M.; Leigh, L.; Helder, D. Radiometric Cross Calibration and Validation Using 4 Angle BRDF Model between Landsat 8 and Sentinel 2A. Remote Sens. 2020, 12, 806. [Google Scholar] [CrossRef]
- Kaewmanee, M. Pseudo Invariant Calibration Sites: PICS Evolution. In Proceedings of the CALCON 2018, Logan, UT, USA, 18–20 June 2018. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Z. Physiol. Chem. 1951, 40, 1832. [Google Scholar] [CrossRef]
- Taubenböck, H.; Habermeyer, M.; Roth, A.; Dech, S. Automated Allocation of Highly Structured Urban Areas in Homogeneous Zones from Remote Sensing Data by Savitzky-Golay Filtering and Curve Sketching. IEEE Geosci. Remote Sens. Lett. 2006, 3, 532–536. [Google Scholar] [CrossRef]
- Markham, B.; Barsi, J.; Kvaran, G.; Ong, L.; Kaita, E.; Biggar, S.; Czapla-Myers, J.; Mishra, N.; Helder, D. Landsat-8 Operational Land Imager Radiometric Calibration and Stability. Remote Sens. 2014, 6, 12275–12308. [Google Scholar] [CrossRef]
- Czapla-Myers, J.; McCorkel, J.; Anderson, N.; Thome, K.; Biggar, S.; Helder, D.; Aaron, D.; Leigh, L.; Mishra, N. The Ground-Based Absolute Radiometric Calibration of Landsat 8 OLI. Remote Sens. 2015, 7, 600–626. [Google Scholar] [CrossRef]










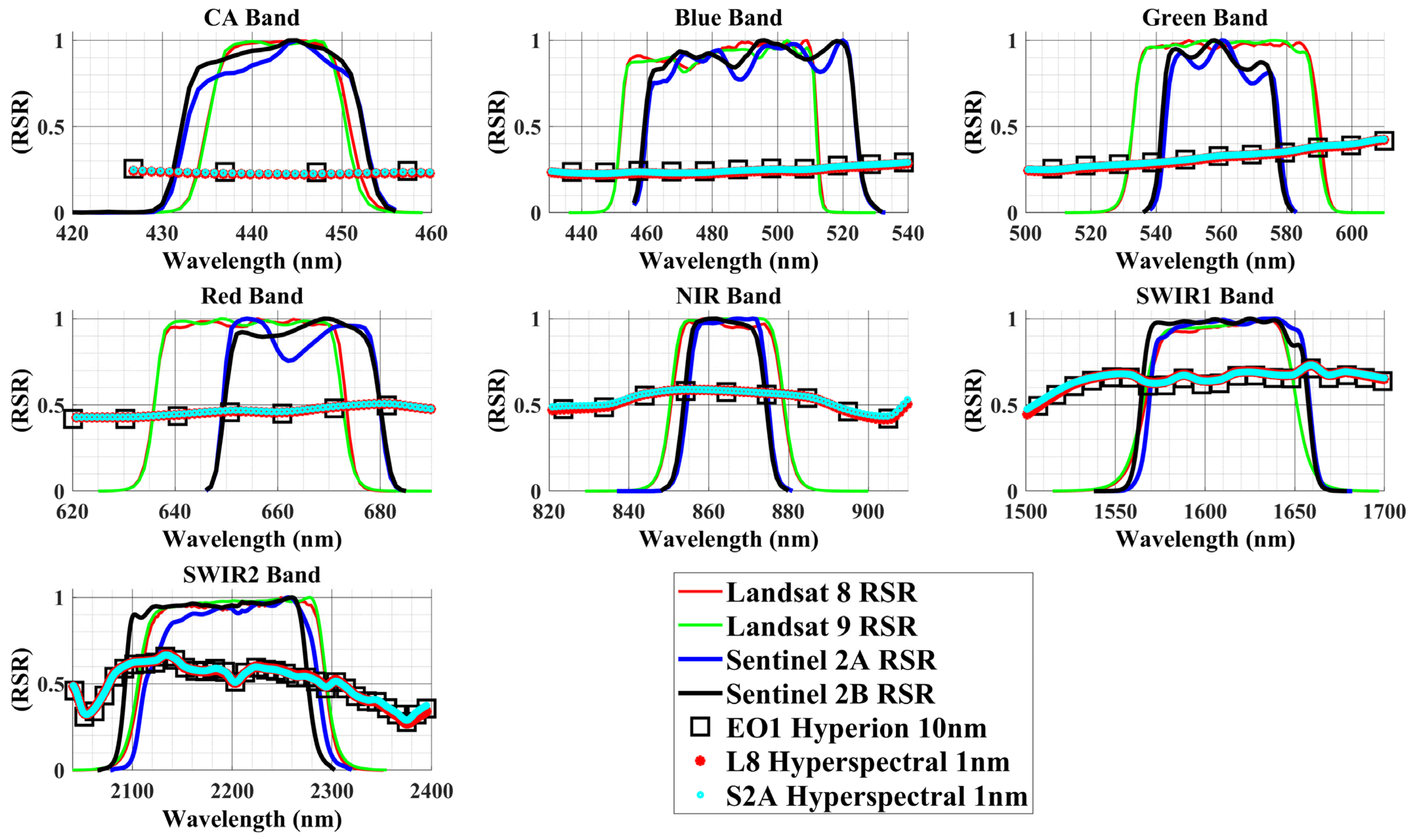

| Landsat 8 | Landsat 9 | Sentinel 2A | Sentinel 2B | EO-1 Hyperion | |
|---|---|---|---|---|---|
| No. of Scenes Acquired | 7000 | 1299 | 6307 | 6385 | 1569 |
| No. of Sites | 40 WRS-2 paths/rows | 40 WRS-2 paths/rows | 35 Tiles | 35 Tiles | 127 paths/rows |
| Acquisition Date Range | 2013–2023 | 2021–2023 | 2015–2023 | 2017–2023 | 2001–2017 |
| No. of Spectral Bands | 7 Multispectral bands | 7 Multispectral bands | 11 Multispectral bands | 11 Multispectral bands | 242 (196 Calibrated Hyperspectral Bands) |
| Temporal Resolution | 16 Days | 16 Days | 10 Days | 10 Days | 16 Days |
| Cluster Classification | CA (443 nm) | Blue (482 nm) | Green (561.4 nm) | Red (654.6 nm) | NIR (864.7 nm) | SWIR1 (1608.9 nm) | SWIR2 (2200.7 nm) | |
|---|---|---|---|---|---|---|---|---|
| GC13 | Coefficient of Variation (%) | 2.98 | 2.99 | 2.48 | 3.56 | 2.56 | 2.57 | 3.89 |
| Cluster 13-GTS | Coefficient of Variation (%) | 3.06 | 2.95 | 2.15 | 2.71 | 2.18 | 2.07 | 3.48 |
| Absolute Difference (Unit Reflectance) | CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|---|
| Before Relative Calibration of EO1 Hyperion | 0.67 | 0.46 | 0.39 | 0.09 | 0.72 | 0.53 | 0.23 |
| After Relative Calibration of EO1 Hyperion | 0.16 | 0.06 | 0.32 | 0.02 | 0.46 | 0.22 | 0.27 |
| Mean Absolute Difference (Unit Reflectance) | CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|---|
| Before Relative Calibration of EO1 Hyperion | −0.70 | 0.52 | 0.23 | 0.10 | −0.32 | 0.40 | −0.11 |
| After Relative Calibration of EO1 Hyperion | −0.19 | 0.06 | 0.16 | −0.01 | −0.13 | 0.33 | −0.10 |
| Hyperspectral Source | Bands | |||||||
|---|---|---|---|---|---|---|---|---|
| CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 | ||
| Shah et al. [11] EO-1 Hyperion (10 nm) | SBAF Mean | 1.0004 | 0.9745 | 1.0135 | 0.9800 | 0.9998 | 0.9961 | 0.9990 |
| 3σ (%) | 0.02 | 1.26 | 1.35 | 0.27 | 0.18 | 0.12 | 0.27 | |
| New EO-1 Hyperion (10 nm) | SBAF Mean | 1.0001 | 0.9775 | 1.0131 | 0.9787 | 0.9997 | 0.9959 | 0.9980 |
| 3σ (%) | 0.52 | 4.21 | 4.97 | 2.64 | 2.01 | 0.68 | 0.69 | |
| New EO-1 Hyperion (1 nm) | SBAF Mean | 0.9964 | 0.9781 | 1.0080 | 0.9689 | 0.9971 | 0.9961 | 0.9981 |
| 3σ (%) | 1.06 | 1.16 | 1.33 | 1.22 | 0.82 | 0.24 | 0.20 | |
| Landsat 8 (10 nm) | SBAF Mean | 1.0001 | 0.9758 | 1.0140 | 0.9791 | 0.9998 | 0.9962 | 0.9989 |
| 3σ (%) | 0.31 | 2.20 | 2.58 | 2.12 | 1.44 | 0.45 | 0.56 | |
| Landsat 8 (1 nm) | SBAF Mean | 0.9962 | 0.9761 | 1.0090 | 0.9690 | 0.9969 | 0.9963 | 0.9991 |
| 3σ (%) | 0.63 | 0.63 | 0.72 | 0.91 | 0.60 | 0.15 | 0.18 | |
| Sentinel 2A (10 nm) | SBAF Mean | 1.0002 | 0.9763 | 1.0127 | 0.9785 | 0.9998 | 0.9960 | 0.9985 |
| 3σ (%) | 0.36 | 2.58 | 3.37 | 2.49 | 1.42 | 0.50 | 0.64 | |
| Sentinel 2A (1 nm) | SBAF Mean | 0.9963 | 0.9766 | 1.0084 | 0.9691 | 0.9972 | 0.9961 | 0.9986 |
| 3σ (%) | 0.68 | 0.75 | 0.93 | 1.02 | 0.58 | 0.18 | 0.20 | |
| Gain and Standard Deviation | Bands | ||||||
|---|---|---|---|---|---|---|---|
| CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 | |
| Mean Ratio | 1.0077 | 1.0072 | 1.0001 | 1.0077 | 0.9993 | 0.9985 | 1.0009 |
| Std Dev | 0.0047 | 0.0045 | 0.0040 | 0.0054 | 0.0040 | 0.0041 | 0.0052 |
| Hyperspectral Source | Gain and Total Uncertainty | Bands | ||||||
|---|---|---|---|---|---|---|---|---|
| CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 | ||
| Shah et al. EO1 (10 nm) | Mean Gain | 1.0030 | 1.0168 | 0.9947 | 0.9815 | 0.9881 | 0.9939 | 0.9952 |
| Uncertainty (%) | 3.32 | 3.37 | 3.16 | 3.80 | 3.29 | 3.73 | 5.23 | |
| L8 Hyperspectral | Mean Gain | 1.0077 | 1.0072 | 1.0001 | 1.0077 | 0.9993 | 0.9985 | 1.0009 |
| Uncertainty (%) | 4.79 | 4.56 | 3.68 | 4.31 | 3.65 | 3.48 | 5.32 | |
| Cluster | Hyperspectral Source | Sources of Uncertainty (%) | Bands | ||||||
|---|---|---|---|---|---|---|---|---|---|
| CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 | |||
| GC13 | EO1 Hyperion 10 nm | UTotal | 3.32 | 3.37 | 3.16 | 3.80 | 3.29 | 3.73 | 5.23 |
| 13-GTS | Simulated Landsat 8 (1 nm) | UTemporal-Spatial | 2.99 | 2.84 | 2.18 | 2.71 | 2.17 | 2.00 | 3.45 |
| UBRDF | 0.21 | 0.22 | 0.21 | 0.33 | 0.21 | 0.05 | 0.06 | ||
| USBAF | 3.16 | 2.95 | 2.19 | 2.67 | 2.14 | 2.04 | 3.53 | ||
| USensor | 2 | 2 | 2 | 2 | 2 | 2 | 2 | ||
| UTotal | 4.79 | 4.56 | 3.68 | 4.31 | 3.65 | 3.48 | 5.32 | ||
| Hyperspectral Source | Gain and Total Uncertainty | Bands | ||||||
|---|---|---|---|---|---|---|---|---|
| CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 | ||
| Shah et al. EO1 (10 nm) | Gain | 0.998 | 0.9978 | 0.9912 | 0.9971 | 0.9977 | 0.9981 | 0.9954 |
| Uncertainty (%) | 3.45 | 3.44 | 3.01 | 3.45 | 3.23 | 3.68 | 5.13 | |
| Simulated L8 | Gain | 1.0000 | 0.9983 | 1.0004 | 0.9964 | 0.9966 | 0.9970 | 0.9967 |
| Uncertainty (%) | 4.74 | 4.54 | 3.61 | 4.17 | 3.58 | 3.43 | 5.36 | |
| Hyperspectral Source | Gain and Total Uncertainty | Bands | ||||||
|---|---|---|---|---|---|---|---|---|
| CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 | ||
| Shah et al. EO1 (10 nm) | Gain | 1.0091 | 1.0136 | 0.9939 | 0.9733 | 1.0031 | 0.994 | 1.0044 |
| Uncertainty (%) | 3.41 | 3.39 | 3.08 | 3.74 | 3.3 | 3.68 | 4.99 | |
| Simulated L8 (1 nm) | Gain | 0.9873 | 0.9815 | 0.9840 | 1.0061 | 1.0060 | 1.0102 | 1.0186 |
| Uncertainty (%) | 5.31 | 5.21 | 4.28 | 4.80 | 4.29 | 4.13 | 5.77 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samaranayake, M.; Kaewmanee, M.; Leigh, L.; Fajardo Rueda, J. Refinement of Trend-to-Trend Cross-Calibration Total Uncertainties Utilizing Extended Pseudo Invariant Calibration Sites (EPICS) Global Temporally Stable Target. Remote Sens. 2025, 17, 1774. https://doi.org/10.3390/rs17101774
Samaranayake M, Kaewmanee M, Leigh L, Fajardo Rueda J. Refinement of Trend-to-Trend Cross-Calibration Total Uncertainties Utilizing Extended Pseudo Invariant Calibration Sites (EPICS) Global Temporally Stable Target. Remote Sensing. 2025; 17(10):1774. https://doi.org/10.3390/rs17101774
Chicago/Turabian StyleSamaranayake, Minura, Morakot Kaewmanee, Larry Leigh, and Juliana Fajardo Rueda. 2025. "Refinement of Trend-to-Trend Cross-Calibration Total Uncertainties Utilizing Extended Pseudo Invariant Calibration Sites (EPICS) Global Temporally Stable Target" Remote Sensing 17, no. 10: 1774. https://doi.org/10.3390/rs17101774
APA StyleSamaranayake, M., Kaewmanee, M., Leigh, L., & Fajardo Rueda, J. (2025). Refinement of Trend-to-Trend Cross-Calibration Total Uncertainties Utilizing Extended Pseudo Invariant Calibration Sites (EPICS) Global Temporally Stable Target. Remote Sensing, 17(10), 1774. https://doi.org/10.3390/rs17101774







