Abstract
The time-varying gravity field models derived from the Gravity Recovery and Climate Experiment (GRACE) satellite mission suffer from pronounced longitudinal stripe errors in the spatial domain. A potential way to mitigate such errors is to combine GRACE data with observations from other sources. In this study, we investigate the impacts on GRACE monthly gravity field solutions of incorporating the GPS data collected by the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE) mission. To that end, we produce GRACE/GOCE combined monthly gravity field solutions through combination on the normal equation level and compare them with the GRACE-only solutions, for which we have considered the state-of-the-art ITSG-Grace2018 solutions. Analysis in the spectral domain reveals that the combined solutions have a notably lower noise level beyond degree 30, with cumulative errors up to degree 96 being reduced by 31%. A comparison of the formal errors reveals that the addition of GOCE GPS data mainly improves (near-) sectorial coefficients and resonant orders, which cannot be well determined by GRACE alone. In the spatial domain, we also observe a significant reduction by at least 30% in the noise of recovered mass changes after incorporating the GOCE GPS data. Furthermore, the signal-to-noise ratios of mass changes over 180 large river basins were improved by 8–20% (dependent on the applied Gaussian filter radius). These results demonstrate that the GOCE GPS data can augment the GRACE monthly gravity field solutions and support a future GOCE-type mission for tracking more accurate time-varying gravity fields.
1. Introduction
Accurate time-varying gravity field models are of great significance to understanding large-scale mass transport in the Earth system. In the past two decades, they were mostly obtained with the highly precise K-Band ranging (KBR) measurements from the Gravity Recovery and Climate Experiment (GRACE) mission [1] and its successor, the GRACE Follow-On (GRACE-FO) mission [2]. Currently, the GRACE time-varying gravity field models are typically generated monthly by many analysis centers. Although the monthly gravity field solutions have been improved greatly in the past two decades, they still cannot reach the pre-launch baseline accuracy, which was anticipated to be no larger than 0.66 mm for the cumulative geoid height errors up to degree and order 120 [3]. Among others, the solutions suffer from pronounced errors, which leave longitudinal stripe structures in the spatial domain, and have troubled almost all geoscience applications of GRACE time-varying gravity field solutions. To suppress such errors, one typically applies a filter to the gravity field solutions in the post-processing stage. For that purpose, a number of filters have been proposed for specific applications [4,5,6,7]. Unfortunately, filtering suppresses not only noise, but also the signals in the gravity field solutions.
The near-polar orbits of GRACE lead to inherent anisotropic sensitivity of the observing system, especially for the KBR measurements, which are more sensitive to longitudinal gravity field variations than to latitudinal ones. As such, almost all known error sources can introduce stripy errors in the final GRACE gravity field solutions, e.g., instrumentation noise, errors in the de-aliasing models, and sub-Nyquist artifacts [8,9,10,11,12]. A potential way to improve the GRACE temporal gravity field solutions is to combine GRACE data with observations from other sources. Mass transports at and below the Earth’s surface can induce changes in the Earth’s gravity field, which can be observed by GRACE. On the other hand, they also can cause deformation of the solid Earth, which can be sensed, by the Global Navigation Satellite System (GNSS) data collected by ground stations, among others. It has been demonstrated that the GNSS-derived station displacements can constrain and improve the GRACE-only solutions [13,14,15]. However, such observations are limited by uneven spatial coverage (dense over lands and sparse over oceans) and potential contamination by various non-mass change signals. The spaceborne GNSS technique, which employs the high-low satellite-to-satellite tracking mode, can compensate for these deficiencies. In fact, its ability to retrieve temporal gravity field variations has been verified in many studies and there is a consensus that it can contribute to bridging the gap between GRACE and GRACE-FO [16,17,18,19,20,21,22].
In this study, we consider the Global Positioning System (GPS) data collected by the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE) mission. The GOCE satellite flew in a very low orbit (~250 km), which made it more sensitive to the Earth’s gravity field. However, it has been recognized that the GOCE GPS data suffer from, large ionosphere-induced errors, among others, which has limited their application to temporal gravity field recovery [23,24]. Later, with tailed algorithms to suppress ionosphere-induced errors in the observations, the GOCE GPS data have been demonstrated to be able to recover temporal variations of gravity fields [18,25,26]. Importantly, the GOCE satellite flew in a more inclined orbit than GRACE (96.6° versus 89°). This makes it free from the sub-Nyquist artifacts, which lead to notable longitudinal stripe errors in the GRACE gravity field solutions [11]. All this suggests that GOCE may improve the GRACE-only gravity field solutions. The potential value of the GOCE data on GRACE monthly solutions has been assessed in [27]. For that purpose, the authors considered both the GPS and satellite gravity gradiometry (SGG) data for 1 year from November 2009 to December 2010 and generated both unconstrained and optimally filtered solutions. For unconstrained solutions, the improvements were primarily confined to high degrees beyond 60, which could mostly be attributed to the incorporation of SGG data. For optimally filtered solutions, they showed that the impacts of GOCE data stayed well below the GRACE noise level. Nevertheless, the data processing accuracy has been improved continuously for both GRACE and GOCE in the past decade. Therefore, the impacts of the GOCE data on the GRACE time-varying gravity field models might have changed and this has motivated us to reassess the potential value of the GOCE data. Considering that the SGG data cannot contribute to low-degree gravity terms, which contain the most time-varying signals, due to the measurement bandwidth (5–100 mHz) [28], we only consider the GOCE GPS data in this study.
To demonstrate the potential value of the GOCE GPS data, two sets of monthly gravity field solutions are generated, covering the entire GOCE mission period from November 2009 to October 2013. One is the GRACE-only solutions, for which we consider the state-of-the-art ITSG-Grace2018 monthly gravity solutions generated by the Institute of Geodesy, Graz University of Technology [29]. The other is the GRACE/GOCE combined solutions, for which the combination is performed on the normal equation (NEQ) level. The GRACE NEQs are those accompanied with the ITSG-Grace2018 solutions. For GOCE, they are established in-house based on the GOCE kinematic orbits. To assess the value of the incorporation of the GOCE GPS data, the two sets of solutions will be compared in both spatial and spectral domains.
2. Materials and Methods
In this section, we first present the data and models adopted for GOCE monthly gravity field modeling. Then, we focus on the method used for the combination of GRACE and GOCE data on the NEQ level.
2.1. Data and Models
In this study, we use the Position and Navigation Data Analyst (PANDA) software to perform the data processing. It has been widely used in satellite precise orbit determination [30,31,32] and in Earth’s gravity field modeling [33,34], where the classical dynamic approach has been adopted. For this study, the kinematic orbits of the GOCE satellite are taken as pseudo-observations for gravity field modeling. The data processing mainly involves two steps: first, a dynamic orbit is computed through fitting to the kinematic orbit; second, daily NEQs containing the spherical harmonic coefficients (SHCs) are constructed and accumulated into monthly NEQs, which are finally inverted to obtain the monthly gravity field solutions. More details about the data processing can be found in [17].
Table 1 gives an overview of the data and models used for GOCE-based gravity field modeling. For time-varying gravity field modeling, a high-quality a priori static gravity field model should be adopted [10]. To that end, we use the static part of the GOCO06s model up to degree and order 200 [35]. The solid Earth and pole tides are modeled according to the IERS 2010 conventions [36]. The ocean tides are described by the state-of-the-art FES2014b model [37], up to degree and order 180. For non-tidal atmosphere and ocean variations, we adopt the official AOD1B products. We mention that the old version of RL06 has been used, though the latest version of RL07 is currently available. This is in order to stay consistent with the ITSG-Grace2018 solutions, for which AOD1B RL06 products were used. For third-body perturbations, the Sun, Moon, and planet positions are calculated based on the Jet Propulsion Laboratory (JPL) planetary and lunar ephemerides DE440 [38]. Additionally, although the non-gravitational forces imposed on the GOCE satellite were compensated to a large extent in the along-track direction by the drag-free attitude control system, there still exists a considerable amount of residual disturbances. In this study, we use the GOCE common mode accelerometer data, which are provided in the EGG_CCD product [39], to account for these residual disturbances. It has been shown that omitting the residual disturbances would degrade the low-degree gravity terms [18]. At this point, it should be noted that the residual disturbances were neglected in [27]. Therefore, it is likely that the contribution of GOCE GPS data to the GRACE monthly gravity field solutions has been underestimated.
For GOCE kinematic orbits, we have used those generated in [26]. The orbits are computed based on the raw observation approach and exhibit better performance in terms of orbit precision and gravity field recovery, when compared to the first release of GOCE level 2 SST_PSO products [26], which were adopted in [27]. Furthermore, the kinematic orbits are processed with an epoch-difference scheme during gravity field recovery. That is, we use position differences between adjacent epochs instead of the positions themselves for gravity field recovery. It has been proved that the epoch-difference scheme can mitigate constant or slowly-varying systematic errors in the kinematic orbits and background force models [17]. These systematic errors usually lead to non-stationary noise, which is an almost insurmountable difficulty for stochastic modeling of observation noise. As a result, the low-degree gravity terms can be notably improved with the epoch-difference scheme, when compared to the traditional undifferenced one. The reader is referred to [17] for more details. Additionally, to account for colored noise in the observations, we adopt the well-known frequency-dependent data weighting (FDDW) method proposed in [40], with which optimal data weighting can be achieved.
In this study, the data processing arc length is set equal to 24 h. The parameters consist of satellite initial position and velocity, accelerometer biases, and monthly gravity field in the form of SHCs. The accelerometer scale factors are fixed to 1, since they are precise down to a level of better than 10−3 [41]. Regarding the accelerometer biases, they are estimated as piecewise constants with a 1.5 h interval. Nevertheless, it has been shown that the epoch-difference scheme is quite insensitive to the choice of estimation interval of accelerometer biases [17]. Finally, the SHCs are estimated up to degree and order 96 to stay consistent with the NEQs accompanied with the ITSG-Grace2018 solutions.
In general, the adopted models and input data in this study have been notably improved when compared to those adopted in [27]. Certainly, this would contribute to an increased accuracy of GOCE data processing. Importantly, it would improve the ability of GOCE to retrieve temporal gravity field variations and increase the potential value of GOCE data to GRACE monthly gravity field solutions.

Table 1.
Data and models used for GOCE-based gravity field modeling.
Table 1.
Data and models used for GOCE-based gravity field modeling.
| Background Force Models | Description |
|---|---|
| Earth’s gravity field | GOCO06s [35] (200 200) |
| Solid Earth and pole tides | IERS Conventions 2010 [36] |
| Ocean tides | FES2014b [37] (180 180) |
| Ocean pole tides | Desai [42] (30 30) |
| Atmosphere and ocean de-aliasing | AOD1B RL06 [43] |
| Third-body perturbations | DE440 [38] |
| General relativistic effects | IERS Conventions 2010 [36] |
| Reference frames | |
| Conventional inertial reference frame | IERS Conventions 2010 [36] |
| Precession/nutation | IAU 2006/2000A [36] |
| Earth orientation parameters | IERS EOP 08 C04 |
| Input data | |
| Satellite kinematic orbits | 30 s sampling |
| Satellite attitudes | GOCE star tracker quaternions (EGG_IAQ product, ESA [39]) |
| Satellite non-gravitational accelerations | GOCE common-mode accelerations (EGG_CCD product, ESA [39]) |
| Estimated parameters | |
| Initial state vector | Position and velocity per arc |
| Accelerometer bias | Piece-wise linear with an interval of 3 h |
| Spherical harmonic coefficients | Between degrees 2 and 96 |
2.2. Data Combination
The GOCE and GRACE data are combined on the NEQ level. The monthly NEQs are generated during the compilation of monthly gravity field solutions and more details can be found in [17,44]. The combined monthly NEQ system is formed as:
with
where N denotes the normal matrix, b the right-hand side vector, dx the SHC correction vector to the a priori reference gravity model x0, σ2 the variance factor, and the subscript i = 1, 2 signifies GOCE and GRACE, respectively. The monthly NEQs of GOCE are derived from the kinematic orbits in-house, as described above. For GRACE, we consider those accompanied with the ITSG-Grace2018 solutions, which are released in the SINEX format (https://www.iers.org/IERS/EN/Organization/AnalysisCoordinator/SinexFormat/sinex.html, accessed on 28 April 2024). Apart from the right-hand side vector b and normal matrix N, additional information is provided in the SINEX files, including the a priori parameter vector x0 (i.e., the a priori gravity field), the solution vector x (i.e., x0 + dx), the maximum gravity degree lmax, the number of observations n (reduced by pre-eliminated parameters), the number of unknowns u, the weighted square sum of pre-fit residuals lTPl, the gravitational constant GM (the gravity constant times the mass of the Earth), the equatorial radius of Earth R, and the tide system (zero tide/tide free). It should be noted that both GRACE and GOCE NEQs must refer to the common Earth constants (GM and R) and a priori gravity field before combination, otherwise the individual NEQs have to be updated, as shown in [45]. Since both the GRACE and GOCE NEQs refer to the same Earth constants (GM = 3.986004415 × 1014 m3/s2, R = 6378136.3 m) in this study, the scaling of individual NEQs is not necessary anymore. For the a priori gravity field, we have adopted the static part of the GOCO06s model as the common reference xref, which is also the background field for GOCE-based gravity field modeling. To adapt the GRACE NEQs to this a priori model, the corresponding right-hand side vector must be updated as follows:
the square sum of the pre-fit residuals, which will be used in the variance component estimation (VCE) method as shown in [45], also have to be adapted:
where lTPl, N, b, x, and x0 are the square sum of the pre-fit residuals, normal matrix, right-hand side vector, solution vector, and a priori parameter vector recorded in the SINEX files, respectively.
Finally, the variance factors σ2 are computed based on the VCE method, which we have referred to the Appendix in [45]. Note that the VCE-derived weights (1/σ2) should equal 1.0 in theory, if statistically optimal data weighting was applied when forming the NEQs. Figure 1 shows the weights of the NEQs for each month. It can be seen that this is true in both cases. For the GOCE NEQs, the VCE-based weights vary between 0.98 and 1.00 with an average of 0.99. The GRACE NEQs get slightly larger weights, which vary between 1.06 and 1.08, with an average of 1.07. The results demonstrate that the input data have been appropriately weighted during the establishment of the NEQs in both cases.
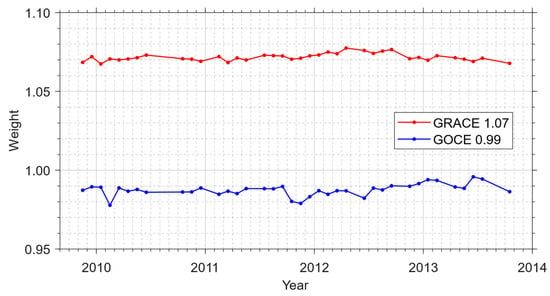
Figure 1.
The VCE-based weights of GRACE and GOCE NEQs for each monthly solution. The average values are displayed in the legend.
3. Results
Based on the above strategies, we have generated the monthly gravity field solutions covering the entire GOCE mission period from November 2009 to October 2013. We mention that 10 months within this period have been excluded from the analysis, mainly due to data outages of either GRACE or GOCE. For GRACE, 7 months are missing due to battery incapacity after 2011. These include January and June of 2011, May and October of 2012, and March, August, and September of 2013. For GOCE, 3 months, from July to September in 2010, are excluded due to data outage. In the following sections, we assess the potential value of GOCE data on GRACE monthly gravity field solutions in both the spectral and spatial domains.
3.1. Analysis in the Spectral Domain
To analyze the impact of the GOCE GPS data on the GRACE monthly gravity field solutions in the spectral domain, we first inspect the formal error characteristics of the two sets of solutions. The formal errors can be interpreted as the uncertainties of the estimates. They are fully dependent on the sensitivity and geometry of the observations. Thus, a comparison between the two sets of formal errors allows us to distinguish the SHCs most influenced by the incorporation of GOCE data in terms of estimation uncertainties. For that purpose, we calculate the RMS (root mean square) over the formal error time series for each SHC, which is displayed in Figure 2. In general, the two formal errors exhibit similar patterns. The formal errors of (near-)sectorial SHCs with equal degree and order are notably larger than those of (near-)zonal terms with zero order. This can be explained by the inherent anisotropic sensitivity of the GRACE KBR measurements, which are more sensitive to the longitudinal gravity field variations than to the latitudinal ones. Besides, large formal errors can be observed for orders that are close to integer multiples of 15. This typical structure in GRACE solutions can be attributed to orbit resonance effects [46,47]. A cross-comparison between the two formal errors tells us that the formal errors for the (near-)sectorial SHCs and resonance orders are notably reduced when GOCE data are incorporated. This can be clearly observed in Figure 2c, which shows the RMS reduction percentage in the GRACE/GOCE combined solutions with respect to the GRACE-only ones. On the one hand, this means that the observing system of GRACE/GOCE is more isotropic compared to that of GRACE, implying that the (near-)sectorial terms can be better determined in the GRACE/GOCE combined case. On the other hand, the results indicate that the incorporation of GOCE data can reduce the orbit resonance effects in the GRACE-only solutions, which is beneficial to the determination of resonance orders. Finally, due to the polar gap issue of GOCE, its impacts on the (near-)zonal terms, especially those of high degrees, are hardly discernible as expected.
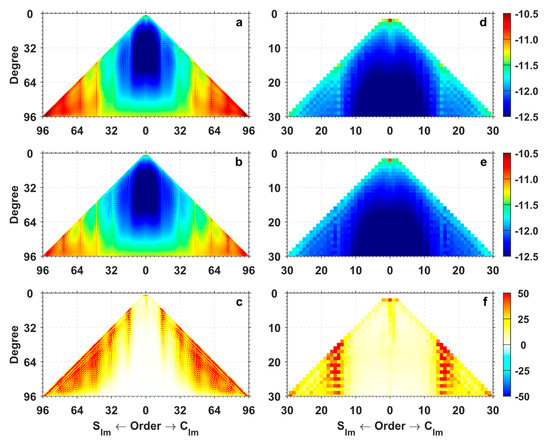
Figure 2.
RMS (log10 representation) of formal errors for the GRACE-only (a,d), GRACE/GOCE combined (b,e) monthly solutions, and the RMS reduction percentage in the GRACE/GOCE combined solutions with respect to the GRACE-only ones (c,f). The left and right columns are complete to degree and order 96 and 30, respectively. Clm and Slm denote the SHC with degree l and order m.
Additionally, one can see that the incorporation of GOCE data can also reduce the formal errors of the degree two SHCs (Figure 2f). Of particular interest is the C20 coefficient, which exhibits large formal errors here and can only be poorly determined using the GRACE data [47]. For scientific applications, it is necessary to replace the C20 coefficients of the GRACE monthly solutions with those from other sources, such as those derived from satellite laser ranging (SLR) data [48,49], or those determined with the so-called GRACE-OBP approach [50,51]. To investigate the impacts of GOCE data, we compare the C20 time series from the GRACE-only and GRACE/GOCE combined monthly solutions, as well as the SLR-derived values (denoted as ‘SLR-TN14’) and those determined with the GRACE-OBP approach. For the GRACE-OBP approach, we have used the high degree terms from the GRACE-only solutions to determine the C20 coefficient together with the three degree 1 terms. Certainly, the combined solutions can also be used for that purpose within the GRACE-OBP approach, but our test experiment shows that the impacts are minor. Figure 3 shows the C20 time series from different solutions, where the mean value of each solution has been subtracted from the corresponding time series. Although the mean value becomes closer to that of SLR-TN14 after incorporating the GOCE data, as presented in the legends, the differences among different solutions are all within 1.1 × 10−11. At this point, one should not compare the GRACE-OBP approach with others, since it cannot determine the absolute C20 [50,51]. However, this is not an issue for time-varying gravity field recovery. Generally speaking, large discrepancies can be observed among the four time series. Table 2 further lists the statistical results in terms of standard deviation (STD) and correlation coefficient between the C20 time series. The results reveal that the GRACE-only C20 time series is closer to SLR-TN14, while the GRACE/GOCE combined solutions exhibit better consistency with the time series based on the GRACE-OBP approach. To shed more light on this issue, we further fit the C20 time series to a deterministic model consisting of offset, linear trend, annual, and semi-annual terms and compute the RMS of post-fit residuals. As a result, the RMS (3.7 × 10−11) in the case of the combined solution is remarkably smaller than that (5.7 × 10−11) in the GRACE-only solution case. Assuming that the variations in C20 can be well described by the deterministic model [52], the results indicate that the C20 term can be better recovered through the incorporation of the GOCE data. Finally, for other degree 2 terms, which can be well determined based on GRACE data alone, the time series of the GRACE-only and GRACE/GOCE combined solutions agree very well with each other, and the correlation coefficients between the two time series all exceed 0.96.
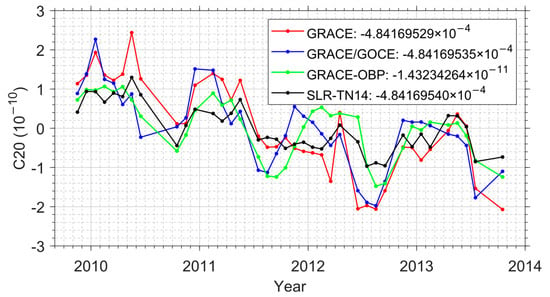
Figure 3.
C20 coefficients from different solutions. The mean values are presented in the legends and have been subtracted from the corresponding time series.

Table 2.
Statistics of the differences between C20 coefficients from different solutions.
As performed for the formal errors, we also calculate the RMS over the correction time series for each SHC with respect to the a priori gravity field, i.e., the static part of the GOCO06s model. Figure 4 displays the degree amplitudes in terms of geoid heights for both solutions and their associated formal errors. Regarding the degree amplitudes for the solutions, it can be seen that below degree 30, the degree amplitude decreases as the degree increases. This is consistent with the behavior of signals induced by Earth’s mass transport [53]. For these low degrees, the GRACE-only and GRACE/GOCE combined solutions agree very well with each other, except for degree 2, at which a notable discrepancy appears between the two solutions. This is mainly caused by the large differences in the C20 terms, as mentioned above. Beyond degree 30, the degree amplitude gradually increases, which is evidence that noise becomes dominant. It is clear that the degree amplitudes are lower in the combined solution above degree 30, indicating that the combined solution suffers from a lower noise level. Table 3 further lists the cumulative geoid heights up to degree 30 and 96 for the two solutions. It reveals that the difference of the cumulative geoid heights up to degree 30 is minor (3%), while they are reduced by 31% up to degree 96 when the GOCE data are incorporated. As far as the formal error is considered, we can see that the degree amplitudes of the combined solution are lower than those of the GRACE-only solution in the entire degree range. From the above results, it is sensible to induce that the incorporation of GOCE data can notably reduce the noise while retaining the signal in the gravity field solutions, which will be demonstrated later in the spatial domain. Finally, for this assessment, one can also first restore the full monthly solutions by adding back the static reference gravity field model and subtracting another high-quality static model from the restored full monthly solutions, and then calculate the RMS over the difference time series for each SHC. We have performed a test experiment with the GOCO05c model [54] and found that such an operation did not alter the above conclusions.
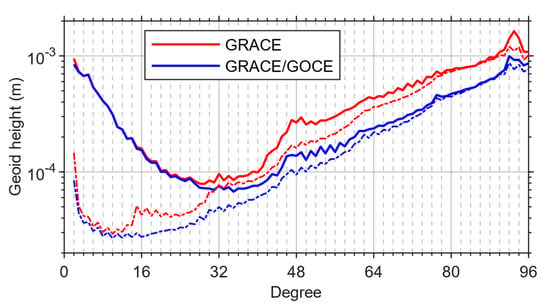
Figure 4.
Degree amplitudes in terms of geoid heights for different solutions (solid) and their associated formal errors (dot-dashed) (RMS values in the considered time span).

Table 3.
Cumulative geoid heights (mm) up to degree 30 and 96 of different solutions (RMS values in the considered time span).
Finally, we also perform a Fisher-test on each SHC to test the significance of the recovered temporal variations as performed in [55]. For that purpose, the full model is composed of bias, linear, annual, and semi-annual terms and the reduced model only includes the bias term. This allows us to test the significance of the recovered temporal variations consisting of linear trends, annual, and semi-annual terms. Figure 5 displays the cumulative distribution function of the recovered temporal variations signifying the significance of each SHC for the considered two solutions and their differences. In general, the function values for the combined solution are larger than those for the GRACE-only solution (bottom plots in Figure 5), except for the (near-)zonal terms due to the polar gap of GOCE. In the combined solutions case, there are 4509 SHCs with cumulative distribution functions larger than 0.90, while the number is 4273 in the GRACE-only solution case. The Fisher-test addresses that the combined solution can offer more significant temporal variations than the GRACE-only solution.
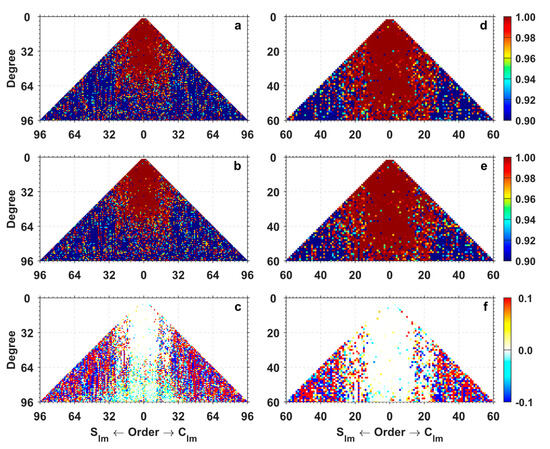
Figure 5.
Cumulative distribution function of the recovered temporal variations signifying the significance of each SHC determined with the Fisher-test for the GRACE-only (a,d), GRACE/GOCE combined solutions (b,e), and their differences as (GRACE/GOCE)-(GRACE) (c,f). The left and right columns are complete to degree and order 96 and 60, respectively.
3.2. Analysis in the Spatial Domain
In this section, we assess the potential value of the incorporation of GOCE data to recover mass changes in the spatial domain. For that purpose, we consider both unfiltered and filtered solutions. For the latter, we use the Gaussian filter to mitigate the high-frequency noise in the gravity field solutions [53]. To take into consideration the impact of the Gaussian filter width on the final results, two radii are considered: 150 km and 300 km. Hereafter, the corresponding solutions are denoted as the ‘G150’ and ‘G300’ filtered solutions, respectively. In addition, for the poorly determined C20 terms and the missing degree 1 terms, we have used those derived from the GRACE-OBP approach [50,56] for both solutions in the following computation.
To facilitate the analysis in the spatial domain, the monthly SHCs are first transformed to gridded mass changes in terms of equivalent water heights (EWHs), following [53]. To account for the Earth’s oblateness, additional correction has been applied according to [57]. Considering that mass changes (if they exist) are mainly linear or/and seasonal [58], we fit the mass change time series to a deterministic model, which is composed of offset, linear trend, annual, and semi-annual terms. By this means, we obtain the dominant mass change signals from the deterministic model, as well as the mass change residuals by subtracting the dominant signals from the ‘observed’ mass changes. Then, the mass change signals are calculated as the RMS of mass change time series derived from the trend and seasonal terms. Accordingly, the noise is calculated as the RMS over the residual mass change time series. After that, we further compute the signal-to-noise ratio (SNR) as SNR = RMSsignal/RMSresidual. This allows us to assess the impacts of the incorporation of GOCE data on the signals, noise, and SNRs of the recovered mass changes through a comparison between the GRACE-only and GRACE/GOCE combined solutions. One thing worth mentioning is that the adopted deterministic model can only grasp the most dominant signals. As a result, residual signals, e.g., inter-annual signals, may exist and remain in the residual mass changes. In some cases, this may lead to an overestimation of the noise and an underestimation of the signals. However, as these residual signals are usually minor compared to the dominant signals, their impacts are expected to be small for the current analysis.
3.2.1. Gridded Mass Changes
Figure 6 displays the geographical maps of the derived gridded RMS of mass changes (gridded signals) inferred from different solutions. For the GRACE-only solutions, it can be seen that the recovered gridded signals from the unfiltered and G150 filtered solutions exhibit prominent south–north stripes at low to middle latitudes and it is difficult to identify the signals there. One can also observe latitude-dependent patterns in the GRACE-only solutions. Since the accuracy of the GRACE gravity field solutions also exhibits such patterns [34], one may conclude that the recovered signals suffer from large uncertainties. For the combined solutions, the south–north stripes and latitude-dependent patterns are notably reduced. In the case of the G150 filtered solutions, typical signals at low to middle latitudes start to become visible, e.g., those over the Amazon River basin, Central and South Africa, and Southeast Asia. In the case of the G300 filtered solutions, high-frequency noise is mitigated to a large extent and the typical signals can be clearly observed in both the GRACE-only and combined solutions. As far as the differences of the recovered signals are concerned, one can see that they are mainly confined to low to middle latitudes and the differences are minor over the polar regions. This is in line with expectations, considering the polar gap in the GOCE ground tracks. Additionally, for the unfiltered and G150 filtered solutions, the recovered gridded signals inferred from the combined solutions are notably smaller than those from the GRACE-only solutions. This can be owed to the large uncertainties in the recovered gridded signals, particularly for the GRACE-only solutions, which will be shown later. For the G300 filtered solutions, the signals can be realistically recovered. The differences become minor and good consistency is achieved between the two solutions.
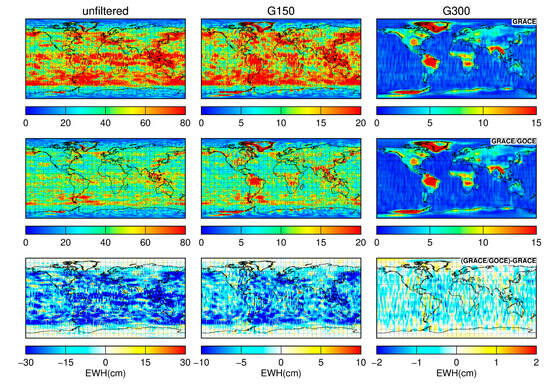
Figure 6.
Gridded mass change RMS in terms of EWHs derived from GRACE-only (top), GRACE/GOCE combined (center) solutions, and their differences (bottom). From left to right, the plots display the results based on unfiltered, G150, and G300 filtered solutions, respectively.
Figure 7 shows the geographical distribution of the gridded RMS of mass change residuals (gridded noise) inferred from different solutions. We can see that the RMS residuals in the case of the combined solutions are systematically smaller at low to middle latitudes than those for the GRACE-only solutions. Over the polar regions, the differences are negligible. Given that the residuals are noise-dominated, this implies that the combined solutions have a lower noise level than the GRACE-only solutions at low to middle latitudes. The ocean areas and the Sahara Desert are usually selected to quantify the noise in the GRACE gravity field solutions. Mass changes over oceans have been largely removed by the applied background force models, as described in [59], and residuals there are thus expected to be dominated by noise. The Sahara Desert exhibits minimal temporal mass variations. As such, residuals there are mostly noise. We compute the weighted mean of the gridded RMS residuals over oceans and the Sahara Desert, for which the weight is determined by the cosine of latitude, and list the results in Table 4. It can be seen that RMS residuals over oceans in the combined solution case are substantially reduced by at least 34% for both unfiltered and filtered solutions, when compared to those in the GRACE-only solution case. As for the Sahara Desert (10°W−30°E, 20°N−30°N), the RMS residuals are reduced by at least 30% after incorporating the GOCE data for both unfiltered and filtered solutions. As such, we conclude that the mass changes recovered from the combined solutions suffer from a remarkably lower noise level when compared to the GRACE-only solutions, which is consistent with the results obtained in the spectral analysis.
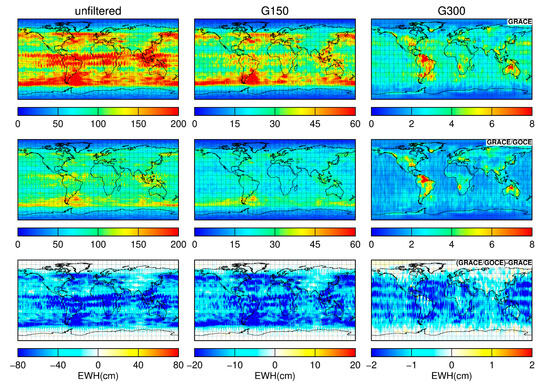
Figure 7.
Same as in Figure 6, but for the gridded RMS of mass change residuals.

Table 4.
Weighted mean of the gridded RMS of mass change residuals (cm) over oceans and the Sahara Desert (the weight is determined by the cosine of latitude).
Figure 8 shows the geographical distribution of the gridded SNR of mass changes inferred from different solutions. In general, the SNRs in the case of the combined solutions are larger than those in the GRACE-only case. This becomes obvious as the filter radius increases, particularly over land areas with prominent mass changes, e.g., in Central and South Africa. We further calculate the weighted mean of gridded SNRs over the land areas and list the results in Table 5. One can see that the SNRs of the combined solutions are improved by 2%, 13%, and 15% for the unfiltered, G150, and G300 filtered solutions, respectively, when compared to those of the GRACE-only solutions. We would stress that the improved SNRs in the combined solutions mainly benefit from the notably lower noise level, but not the stronger signal, as can be observed in Figure 6 and Figure 7. These results demonstrate that GOCE data can enhance the GRACE-only solutions and improve the recovery of time-varying gravity fields.
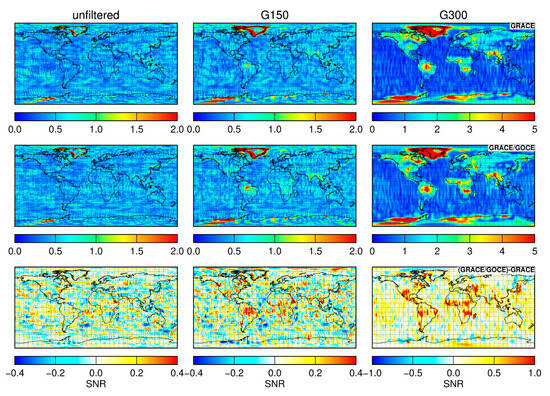
Figure 8.
Geographical distribution of the gridded SNR for the GRACE-only (top), GRACE/GOCE combined (center) solutions, and their differences (bottom). From left to right, the plots display the results based on unfiltered, G150, and G300 filtered solutions, respectively.

Table 5.
Weighted mean of the gridded SNR of mass changes (cm) over land areas (the weight is determined by the cosine of latitude).
3.2.2. Regional Mass Changes
To investigate the potential value of GOCE data in regional mass changes of different temporal behaviors, we first consider the Amazon River basin (~6.22 106 km2) and Greenland (~2.26 106 km2) as the targets. The Amazon River basin exhibits prominent seasonal mass variations, which are known to be of primarily hydrological origin [60,61]. As for Greenland, mass changes there are known to show seasonal variations superimposed by a strong negative long-term trend. The seasonal variations are mainly associated with summer ice melting, followed by winter gains, and the strong negative trend variations are mainly due to the long-term ice loss [62,63,64,65,66].
Figure 9 shows the mean mass change time series over the Amazon River basin and Greenland recovered from different solutions. For the Amazon River basin, we also consider the mass change time series inferred from the WaterGAP Global Hydrology Model (WGHM), which is a well-established global hydrological model that can output total water storage changes [67]. Overall, the time series derived from the two gravity field solutions agree very well with each other over both regions. This is particularly true for the filtered solutions. For the time series of the Amazon River basin, a relatively large discrepancy can be observed for the unfiltered solutions of April 2012 (marked by a right arrow in the top-left plot). For this month, the accelerometer onboard GRACE was powered off on April 19 to reduce battery load and the GRACE-only solution was generated based on only 18 days of data. As a result, the gravity field solution for this month was determined with a worse quality compared to other months. Incorporation of GOCE data can significantly mitigate the noise in the solution of this month and the SHC formal errors and degree amplitudes are notably reduced. Nevertheless, one can see that the Gaussian filter can effectively suppress the noise, and the GRACE-only solution for this month exhibits excellent consistency with the combined solution after filtering.
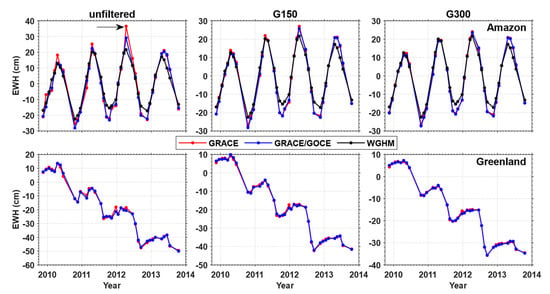
Figure 9.
Time series of mean mass changes over the Amazon River basin (top) and Greenland (bottom) inferred from the unfiltered (left), G150 (center), and G300 (right) filtered solutions. The WGHM solutions are not filtered. The right arrow in the top-left plot points to April 2012.
Table 6 summarizes the annual amplitudes, phases, the associated formal errors, and SNRs over the Amazon River basin, derived from different solutions. It can be seen that the recovered signals from the considered two gravity filed solutions agree very well with each other; the differences are always confined to the 1-σ error margins and are mostly negligible. On the other hand, the associated formal errors in the case of the combined solutions are not larger than those in the GRACE-only case (dependent on the filter radius). As such, better SNRs are achieved with the combined solutions. Furthermore, for the unfiltered solutions, the GRACE/GOCE combined solution exhibits a better consistency with WGHM than the GRACE-only solution. Specifically, the derived annual amplitudes and phases are closer to those from WGHM (cf. Table 6), and the mass change time series presents a stronger correlation and smaller difference in STD with respect to that derived from WGHM (cf. Table 7). As to the filtered solutions, the differences in the correlation coefficient and STD become negligible. In addition, one may note that the annual amplitude derived from the gravity field solutions is notably larger than that derived from WGHM. This is consistent with what is reported in [67], but specific reasons remain unclear to us. As for the mass change trends over Greenland, the results are more beneficial to the combined solution, compared to those over the Amazon River basin (cf. Table 8). With smaller formal errors and larger SNRs, the trend signals are slightly stronger (even though the differences are negligible) in the combined solution. These results reveal that the combined solutions are capable of offering better mass change recoveries over the two target regions.

Table 6.
Annual amplitudes (cm), phases (deg), the associated formal errors, and SNRs of mass changes over the Amazon River basin recovered from different solutions. The phases are defined using the cosine convention with reference epoch 1 January 2010.

Table 7.
Correlation coefficients and STDs (cm) of the differences between the WGHM and gravity field solutions.

Table 8.
Mass change trends, the associated formal errors (Gt/year), and SNRs over Greenland recovered from different solutions. The time interval is from November 2009 to October 2013.
Finally, to make the analysis more comprehensive, we further investigate the impacts of GOCE GPS data on the retrieval of temporal mass variations over 180 large river basins around the globe. The 180 large river basins and their boundaries are taken from the TRIP model [68]. For each river basin, we calculate the signals (RMS mass changes from linear and seasonal terms), noise (RMS mass change residuals), and SNRs for both unfiltered and filtered solutions. The results are shown in Figure 10. In general, the SNRs of mass changes inferred from the combined solutions are larger than those from the GRACE-only solutions (bottom row of Figure 10). On average, the SNRs are improved by 11%, 20%, and 8% for the unfiltered, G150, and G300 filtered solutions, respectively (cf. Table 9), when the GOCE data are incorporated. Nevertheless, the mass changes cannot be realistically recovered from the unfiltered and G150 filtered solutions. This is particularly true for the river basins with relatively small areas, for which the SNRs of mass changes are generally lower than 1. A Gaussian filter with a 300 km radius seems to be adequate for most of the river basins. In that case, the SNRs exceed 1 for 87% and 89% of the 180 river basins for the GRACE-only and GRACE/GOCE combined solutions, respectively. While good consistency between the signals inferred from the two solutions can be observed in Figure 10c, the mass changes suffer from a lower noise level in the case of the combined solutions for most of the river basins (Figure 10f). As such, the combined solution delivers larger SNRs for 73% of the 180 river basins when a Gaussian filter with a 300 km radius is applied.
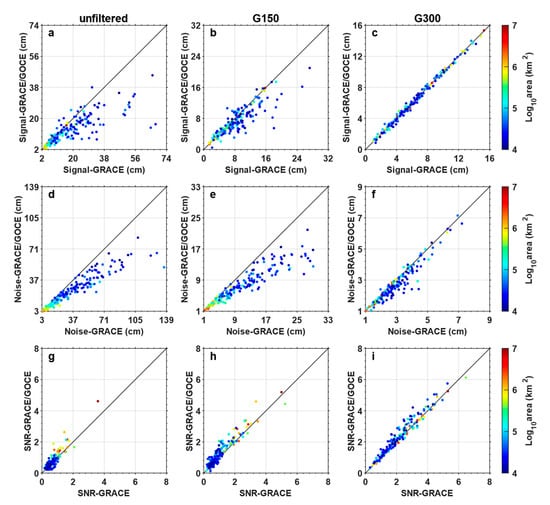
Figure 10.
Signals (a–c), noise (d–f), and SNRs (g–i) over 180 large river basins around the globe inferred from the GRACE-only (X-axis) and GRACE/GOCE combined (Y-axis) solutions.

Table 9.
Mean of the SNRs of mass changes over 180 large river basins inferred from different solutions.
All these results make us conclude that the incorporation of GOCE data can augment the GRACE-only gravity filed solutions and provide better regional mass change estimates.
4. Discussion
As described in the main text, our results are more positive than those presented in [27], for both unfiltered and filtered solutions. In [27], the authors considered the period from November 2009 to December 2010, and 11 monthly gravity field solutions were generated (3 months were excluded due to GOCE data outage, as mentioned before). Among them, 4 months from November 2009 to February 2010 are regarded as ‘bad’, during which GRACE experienced a short orbit repeating period with only 7 days, and the remaining 7 months are regarded as ‘good’. For unfiltered solutions, the authors obtained rather different results for good and bad months regarding the impacts of GOCE data. For bad months, the degree amplitudes of the estimated SHC corrections were reduced in the entire degree range after incorporating the GOCE data, while they were mainly limited to high degrees above 60 for good months. In our case, however, the differences between the good and bad months are minor and the degree amplitudes are all notably reduced beyond degree 30, as can be seen in Figure 11. Here we only show four of the good months for the sake of brevity. Other good months exhibit similar patterns. The large discrepancies between our results and those presented in [27] can be explained by the following aspects: (i) data processing accuracy for both GRACE and GOCE has been notably improved in the past decade. This is true for both background force models and instrumentation data, as explained in the main text. As such, the GOCE GPS data are now able to recover temporal gravity field variations, as can be seen in Figure 12 which displays the trends and annual mass changes derived from the GOCE, GRACE, and GRACE/GOCE combined solutions after applying a Gaussian filter with 750 km radius. Here, the GOCE monthly solutions are generated based on the NEQs, which are compiled from the GOCE kinematic orbits, as described earlier in this article. One can see that the GOCE GPS data can reproduce the signals in many areas as GRACE does, e.g., those over the Amazon River basin, Central and South Africa, and Southeast Asia. Importantly, these results are in line with those recently presented in [18], which has proved the effectiveness of the GOCE GPS data in time-varying gravity field recovery with reprocessed precise science orbits. (ii) Different GOCE data were incorporated. The previous study considered both the GPS and SGG data of GOCE, while we only considered the GPS data. However, due to the measurement bandwidth (5–100 mHz), the SGG data would unlikely alter the SHCs below degree 27, which contain the most time-varying signals. (iii) Different data processing strategies were adopted. While this study was based on the classical dynamic approach to gravity field modeling, the acceleration approach was adopted in [27]. Although these two approaches are equivalent in theory, specific implementations may lead to different results. For instance, the orbit and gravity field parameters were separately estimated in the acceleration approach adopted in [27], while all parameters were simultaneously adjusted in this study. Such different implementations can notably impact the final gravity field solutions [69].
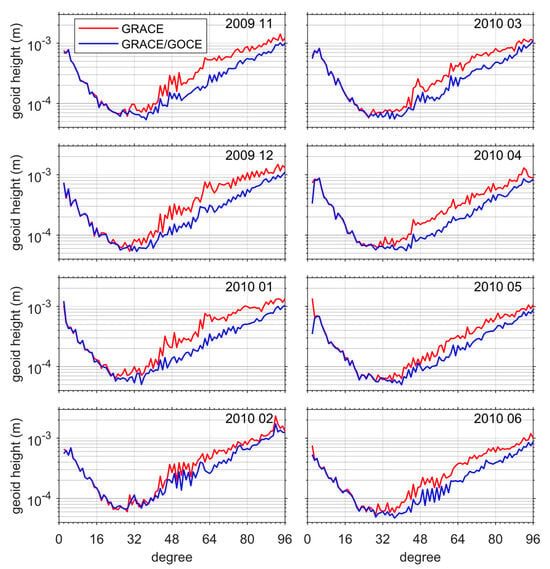
Figure 11.
Degree amplitudes in terms of geoid heights for different monthly solutions generated in this study. Note that in [27] the 4 months in the left column are regarded as bad and those in the right column are good.
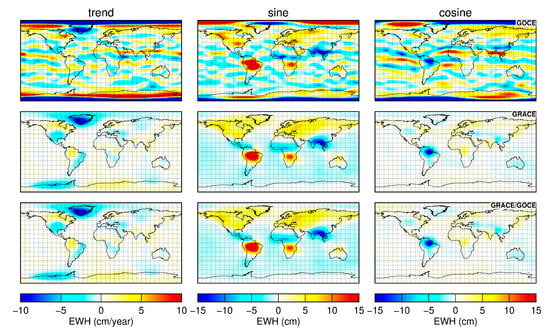
Figure 12.
The trend and annual mass changes inferred from different solutions after applying a Gaussian filter with 750 km radius. From top to bottom, the plots are for the GOCE GPS, GRACE-only, and GRACE/GOCE combined solutions, respectively.
As to the filtered gravity field solutions, the large discrepancies between the results may be partly attributed to the applied filters. In this study, we used a simple isotropic Gaussian filter, while in [27] the authors applied an optimal filter, in which the monthly solutions were constrained by a signal variance–covariance matrix [5]. In our case, it is also likely that the impacts of GOCE GPS data could be reduced, even to a negligible level as in [27], if such an optimal filter is applied. However, one has to keep in mind that even an optimal filter would inevitably dampen the gravity field signals [5]. On the other hand, this is also beyond the scope of this study. After all, what we seek here is to improve the unfiltered solutions by combining the GRACE data with information from other sources.
5. Conclusions
In this study, we reassessed the potential value of GOCE GPS data on GRACE monthly gravity field solutions. This is motivated by the increased accuracy of data processing for both GRACE and GOCE in the past decade. To that end, the GRACE and GOCE data are combined on the NEQ level based on the VCE method. For GRACE, we considered the NEQs accompanied with the state-of-the-art ITSG-Grace2018 monthly gravity field solutions generated by the Institute of Geodesy, Graz University of Technology. For GOCE, the NEQs are generated in-house from satellite kinematic orbits using the classical dynamic approach. Importantly, the kinematic orbits have been processed with an epoch-difference scheme, which has been proved to be able to reduce non-stationary errors originating from the observations and applied force models, and eventually facilitates an optimal data weighting with the well-known frequency-dependent data weighting method. In this way, we have produced the GRACE/GOCE combined monthly gravity field solutions for the entire GOCE mission period from November 2009 to October 2013. They are then confronted with the GRACE-only solutions, i.e., the ITSG-Grace2018 monthly solutions, in both spectral and spatial domains to evaluate the added value of the GOCE GPS data on GRACE monthly solutions.
Analysis in the spectral domain shows that GOCE data mainly improve the (near-)sectorial SHCs and resonance orders, as evidenced by the notably reduced formal errors of these terms in the combined solutions compared to the GRACE-only solutions. The improved (near-)sectorial terms indicate that incorporation of GOCE data can improve the anisotropy of the GRACE observing system, which is known to be more sensitive to longitudinal gravity field variations than to latitudinal ones. The improved resonance orders signify that GOCE data can reduce the orbit resonance effects in the GRACE-only solutions. Analysis of degree amplitudes of SHCs in terms of geoid heights reveals that GOCE data can remarkably reduce the degree amplitudes beyond degree 30, which are dominated by noise. Specifically, the cumulative geoid heights up to degree 30 and 96 in the case of the GRACE/GOCE combined solutions are reduced by 3 and 31%, respectively, when compared to the GRACE-only solutions. These results demonstrate that the incorporation of GOCE data can significantly reduce the noise in the GRACE-only solutions.
Analysis in the spatial domain shows that the combined solutions are able to provide better results than the GRACE-only solutions. On the one hand, the combined solutions suffer from a notably lower noise level compared to the GRACE-only solutions. The gridded mass change residuals over oceans are reduced by at least 34% when the GOCE data are incorporated. This is true for both unfiltered and Gaussian filtered solutions. On the other hand, the mass changes can be better recovered from the combined solutions. Specifically, differences in the signals inferred from the two solutions over the Amazon River basin and Greenland are negligible, while the formal errors of the estimates are reduced. Furthermore, the SNRs of mass changes inferred from the G300 filtered solutions over 180 large river basins around the globe are improved by 8% on average, after incorporating the GOCE data.
These results demonstrate that, with the improved data processing accuracy for both GRACE and GOCE in the past decade, the incorporation of GOCE GPS data can notably improve the GRACE monthly gravity field solutions.
Author Contributions
Conceptualization, X.G. and H.Z.; Formal analysis, X.G. and Y.L.; Funding acquisition, X.G. and Z.L.; Methodology, X.G. and H.Z.; Software, X.G. and Y.S.; Validation, X.G. and Y.L.; Visualization, X.G. and Y.L.; Writing—original draft, X.G., Y.L. and H.Z.; Writing—review and editing, Y.S. and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 41931074, 42374102, 41904009, 42171426).
Data Availability Statement
All datasets used in this study are publicly available. The GOCE kinematic orbits: http://ftp.tugraz.at/outgoing/ITSG/tvgogo/orbits/GOCE_ROTI (accessed on 28 April 2024), and descriptions about the orbits can be found in Zehentner and Mayer-Gürr [26]. The GOCE EGG_CCD and EGG_IAQ products: https://doi.org/10.5270/esa-8sfucze (accessed on 28 April 2024), and descriptions about the products can be found in [39]. The ITSG-Grace2018 monthly gravity field solutions and the associated normal equations in the SINEX format: http://ftp.tugraz.at/outgoing/ITSG/GRACE/ITSG-Grace_operational/monthly (accessed on 28 April 2024), and descriptions about the solutions can be found in https://www.tugraz.at/institute/ifg/downloads/gravity-field-models/itsg-grace2018 (accessed on 28 April 2024), and [29]. The gravity field model GOCO06s: http://icgem.gfz-potsdam.de/tom_longtime (accessed on 28 April 2024), and descriptions about the model can be found in [35]. The SLR-TN14: ftp://isdcftp.gfz-potsdam.de/grace-fo/DOCUMENTS/TECHNICAL_NOTES/TN-14_C30_C20_SLR_GSFC.txt (accessed on 28 April 2024), and descriptions can be found in [49]. The 180 larger river basins and their boundaries are available at the website of the TRIP model: http://hydro.iis.u-tokyo.ac.jp/~taikan/TRIPDATA/TRIPDATA.html (accessed on 28 April 2024).
Acknowledgments
The numerical calculations in this research have been done on the HPC platform of Huazhong University of Science and Technology.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the Global Mass Change Data Record: GRACE Follow-On Instrument and Science Data Performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Kim, J. Simulation Study of a Low-Low Satellite-to-Satellite Tracking Mission. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2000. [Google Scholar]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Klees, R.; Revtova, E.A.; Gunter, B.C.; Ditmar, P.; Oudman, E.; Winsemius, H.C.; Savenije, H.H.G. The design of an optimal filter for monthly GRACE gravity models. Geophys. J. Int. 2008, 175, 417–432. [Google Scholar] [CrossRef]
- Kusche, J.; Schmidt, R.; Petrovic, S.; Rietbroek, R. Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model. J. Geod. 2009, 83, 903–913. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, P.; Tang, L.; Luo, Z. A New GRACE Filtering Approach Based on Iterative Image Convolution. J. Geophys. Res. Solid Earth 2023, 128, e2023JB026553. [Google Scholar] [CrossRef]
- Flechtner, F.; Neumayer, K.-H.; Dahle, C.; Dobslaw, H.; Fagiolini, E.; Raimondo, J.-C.; Güntner, A. What Can be Expected from the GRACE-FO Laser Ranging Interferometer for Earth Science Applications? Surv. Geophys. 2016, 37, 453–470. [Google Scholar] [CrossRef]
- Zhou, H.; Tang, L.; Tan, D.; Duan, H.; Pail, R.; Luo, Z.; Zhou, Z. Impacts of frequency-dependent instrument noise for next-generation gravimetric mission on determining temporal gravity field model. J. Geod. 2023, 97, 23. [Google Scholar] [CrossRef]
- Ditmar, P.; Teixeira da Encarnação, J.; Hashemi Farahani, H. Understanding data noise in gravity field recovery on the basis of inter-satellite ranging measurements acquired by the satellite gravimetry mission GRACE. J. Geod. 2012, 86, 441–465. [Google Scholar] [CrossRef]
- Peidou, A.; Pagiatakis, S. Stripe Mystery in GRACE Geopotential Models Revealed. Geophys. Res. Lett. 2020, 47, e2019GL085497. [Google Scholar] [CrossRef]
- Pagiatakis, S.; Peidou, A. The Intriguing Structure of Stripes in GRACE Geopotential Models. Remote Sens. 2021, 13, 4362. [Google Scholar] [CrossRef]
- Kusche, J.; Schrama, E.J.O. Surface mass redistribution inversion from global GPS deformation and Gravity Recovery and Climate Experiment (GRACE) gravity data. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Razeghi, M.; Han, S.C.; McClusky, S.; Sauber, J. A Joint Analysis of GPS Displacement and GRACE Geopotential Data for Simultaneous Estimation of Geocenter Motion and Gravitational Field. J. Geophys. Res. Solid Earth 2019, 124, 12241–12263. [Google Scholar] [CrossRef]
- Carlson, G.; Werth, S.; Shirzaei, M. Joint Inversion of GNSS and GRACE for Terrestrial Water Storage Change in California. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023135. [Google Scholar] [CrossRef] [PubMed]
- Weigelt, M.; van Dam, T.; Jäggi, A.; Prange, L.; Tourian, M.J.; Keller, W.; Sneeuw, N. Time-variable gravity signal in Greenland revealed by high-low satellite-to-satellite tracking. J. Geophys. Res. Solid Earth 2013, 118, 3848–3859. [Google Scholar] [CrossRef]
- Guo, X.; Ditmar, P.; Zhao, Q.; Xiao, Y. Improved recovery of temporal variations of the Earth’s gravity field from satellite kinematic orbits using an epoch-difference scheme. J. Geod. 2020, 94, 69. [Google Scholar] [CrossRef]
- Arnold, D.; Grombein, T.; Schreiter, L.; Sterken, V.; Jaggi, A. Reprocessed precise science orbits and gravity field recovery for the entire GOCE mission. J. Geod. 2023, 97, 67. [Google Scholar] [CrossRef] [PubMed]
- Teixeira da Encarnação, J.; Visser, P.; Arnold, D.; Bezdek, A.; Doornbos, E.; Ellmer, M.; Guo, J.; van den Ijssel, J.; Iorfida, E.; Jäggi, A.; et al. Description of the multi-approach gravity field models from Swarm GPS data. Earth Syst. Sci. Data 2020, 12, 1385–1417. [Google Scholar] [CrossRef]
- Zhang, C.; Shum, C.K.; Bezděk, A.; Bevis, M.; de Teixeira da Encarnação, J.; Tapley, B.D.; Zhang, Y.; Su, X.; Shen, Q. Rapid Mass Loss in West Antarctica Revealed by Swarm Gravimetry in the Absence of GRACE. Geophys. Res. Lett. 2021, 48, e2021GL095141. [Google Scholar] [CrossRef]
- Bezděk, A.; Sebera, J.; Teixeira da Encarnação, J.; Klokočník, J. Time-variable gravity fields derived from GPS tracking of Swarm. Geophys. J. Int. 2016, 205, 1665–1669. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, Q. A new approach to Earth’s gravity field modeling using GPS-derived kinematic orbits and baselines. Remote Sens. 2019, 11, 1728. [Google Scholar] [CrossRef]
- Jäggi, A.; Bock, H.; Meyer, U.; Beutler, G.; van den Ijssel, J. GOCE: Assessment of GPS-only gravity field determination. J. Geod. 2014, 89, 33–48. [Google Scholar] [CrossRef]
- Visser, P.N.A.M.; van der Wal, W.; Schrama, E.J.O.; van den Ijssel, J.; Bouman, J. Assessment of observing time-variable gravity from GOCE GPS and accelerometer observations. J. Geod. 2014, 88, 1029–1046. [Google Scholar] [CrossRef]
- Guo, X.; Ditmar, P.; Zhao, Q.; Klees, R.; Farahani, H.H. Earth’s gravity field modelling based on satellite accelerations derived from onboard GPS phase measurements. J. Geod. 2017, 91, 1049–1068. [Google Scholar] [CrossRef]
- Zehentner, N.; Mayer-Gürr, T. Precise orbit determination based on raw GPS measurements. J. Geod. 2015, 90, 275–286. [Google Scholar] [CrossRef]
- Farahani, H.H.; Ditmar, P.; Klees, R. Assessment of the added value of data from the GOCE satellite mission to time-varying gravity field modelling. J. Geod. 2014, 88, 157–178. [Google Scholar] [CrossRef]
- Rummel, R.; Yi, W.; Stummer, C. GOCE gravitational gradiometry. J. Geod. 2011, 85, 777–790. [Google Scholar] [CrossRef]
- Kvas, A.; Behzadpour, S.; Ellmer, M.; Klinger, B.; Strasser, S.; Zehentner, N.; Mayer-Gürr, T. ITSG-Grace2018: Overview and Evaluation of a New GRACE-Only Gravity Field Time Series. J. Geophys. Res. Solid Earth 2019, 124, 9332–9344. [Google Scholar] [CrossRef]
- Guo, X.; Geng, J.; Chen, X.; Zhao, Q. Enhanced orbit determination for formation-flying satellites through integrated single- and double-difference GPS ambiguity resolution. GPS Solut. 2020, 24, 14. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, Q. M-estimation-based robust and precise baseline determination for formation-flying satellites. GPS Solut. 2021, 25, 48. [Google Scholar] [CrossRef]
- Wang, C.; Guo, J.; Zhao, Q.; Ge, M. Improving the Orbits of the BDS-2 IGSO and MEO Satellites with Compensating Thermal Radiation Pressure Parameters. Remote Sens. 2022, 14, 641. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, Q. GRACE time-varying gravity field solutions based on PANDA software. Geod. Geodyn. 2018, 9, 162–168. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, Q.; Ditmar, P.; Sun, Y.; Liu, J. Improvements in the monthly gravity field solutions through modeling the colored noise in the GRACE data. J. Geophys. Res. Solid Earth 2018, 123, 7040–7054. [Google Scholar] [CrossRef]
- Kvas, A.; Brockmann, J.M.; Krauss, S.; Schubert, T.; Gruber, T.; Meyer, U.; Mayer-Gürr, T.; Schuh, W.-D.; Jäggi, A.; Pail, R. GOCO06s—A satellite-only global gravity field model. Earth Syst. Sci. Data 2021, 13, 99–118. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. (Eds.) IERS Conventions (2010); Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Lyard, F.H.; Allain, D.J.; Cancet, M.; Carrère, L.; Picot, N. FES2014 global ocean tide atlas: Design and performance. Ocean Sci. 2021, 17, 615–649. [Google Scholar] [CrossRef]
- Park, R.S.; Folkner, W.M.; Williams, J.G.; Boggs, D.H. The JPL Planetary and Lunar Ephemerides DE440 and DE441. Astron. J. 2021, 161, 105. [Google Scholar] [CrossRef]
- ESA. GOCE L1b Products User Handbook. Technical Note, GOCE-GSEG-EOPG-TN-06-0137, Issue 2, Revision 0. 2008. Available online: https://earth.esa.int/eogateway/documents/20142/37627/GOCE-Level-1b-Products-User-Handbook (accessed on 12 December 2023).
- Ditmar, P.; Klees, R.; Liu, X. Frequency-dependent data weighting in global gravity field modeling from satellite data contaminated by non-stationary noise. J. Geod. 2007, 81, 81–96. [Google Scholar] [CrossRef]
- Bouman, J.; Fiorot, S.; Fuchs, M.; Gruber, T.; Schrama, E.; Tscherning, C.; Veicherts, M.; Visser, P. GOCE gravitational gradients along the orbit. J. Geod. 2011, 85, 791–805. [Google Scholar] [CrossRef]
- Desai, S.D. Observing the pole tide with satellite altimetry. J. Geophys. Res. 2002, 107, 7-1–7-13. [Google Scholar] [CrossRef]
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Poropat, L.; Thomas, M.; Dahle, C.; Esselborn, S.; König, R.; Flechtner, F. A new high-resolution model of non-tidal atmosphere and ocean mass variability for de-aliasing of satellite gravity observations: AOD1B RL06. Geophys. J. Int. 2017, 211, 263–269. [Google Scholar] [CrossRef]
- Kvas, A.; Mayer-Gürr, T. GRACE gravity field recovery with background model uncertainties. J. Geod. 2019, 93, 2543–2552. [Google Scholar] [CrossRef]
- Meyer, U.; Jean, Y.; Kvas, A.; Dahle, C.; Lemoine, J.M.; Jäggi, A. Combination of GRACE monthly gravity fields on the normal equation level. J. Geod. 2019, 93, 1645–1658. [Google Scholar] [CrossRef]
- Seo, K.W.; Wilson, C.R.; Han, S.C.; Waliser, D.E. Gravity Recovery and Climate Experiment (GRACE) alias error from ocean tides. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J. The unexpected signal in GRACE estimates of C20. J. Geod. 2017, 91, 897–914. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Loomis, B.D.; Rachlin, K.E.; Luthcke, S.B. Improved Earth Oblateness Rate Reveals Increased Ice Sheet Losses and Mass-Driven Sea Level Rise. Geophys. Res. Lett. 2019, 46, 6910–6917. [Google Scholar] [CrossRef]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Y.; Guo, X.; Guo, J. Estimating C30 coefficients for GRACE/GRACE-FO time-variable gravity field models using the GRACE-OBP approach. J. Geod. 2023, 97, 20. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J. C20 and C30 Variations from SLR for GRACE/GRACE-FO Science Applications. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025459. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Fecher, T.; Pail, R.; Gruber, T. GOCO05c: A New Combined Gravity Field Model Based on Full Normal Equations and Regionally Varying Weighting. Surv. Geophys. 2017, 38, 571–590. [Google Scholar] [CrossRef]
- Meyer, U.; Jäggi, A.; Beutler, G. Monthly gravity field solutions based on GRACE observations generated with the Celestial Mechanics Approach. Earth Planet. Sci. Lett. 2012, 345–348, 72–80. [Google Scholar] [CrossRef]
- Sun, Y.; Ditmar, P.; Riva, R. Statistically optimal estimation of degree-1 and C20 coefficients based on GRACE data and an ocean bottom pressure model. Geophys. J. Int. 2017, 210, 1305–1322. [Google Scholar] [CrossRef]
- Ditmar, P. Conversion of time-varying Stokes coefficients into mass anomalies at the Earth’s surface considering the Earth’s oblateness. J. Geod. 2018, 92, 1401–1412. [Google Scholar] [CrossRef] [PubMed]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 5, 358–369. [Google Scholar] [CrossRef]
- Mayer-Gürr, T.; Behzadpur, S.; Ellmer, M.; Kvas, A.; Klinger, B.; Strasser, S.; Zehentner, N. ITSG-Grace2018—Monthly, Daily and Static Gravity Field Solutions from GRACE; GFZ Data Services: Potsdam, Germany, 2018. [Google Scholar] [CrossRef]
- Xavier, L.; Becker, M.; Cazenave, A.; Longuevergne, L.; Llovel, W.; Filho, O.C.R. Interannual variability in water storage over 2003–2008 in the Amazon Basin from GRACE space gravimetry, in situ river level and precipitation data. Remote Sens. Environ. 2010, 114, 1629–1637. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. The 2009 exceptional Amazon flood and interannual terrestrial water storage change observed by GRACE. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Siemes, C.; Ditmar, P.; Riva, R.E.M.; Slobbe, D.C.; Liu, X.L.; Farahani, H.H. Estimation of mass change trends in the Earth’s system on the basis of GRACE satellite data, with application to Greenland. J. Geod. 2013, 87, 69–87. [Google Scholar] [CrossRef]
- Velicogna, I.; Wahr, J. Time-variable gravity observations of ice sheet mass balance: Precision and limitations of the GRACE satellite data. Geophys. Res. Lett. 2013, 40, 3055–3063. [Google Scholar] [CrossRef]
- Schrama, E.J.O.; Wouters, B.; Rietbroek, R. A mascon approach to assess ice sheet and glacier mass balances and their uncertainties from GRACE data. J. Geophys. Res. Solid Earth 2014, 119, 6048–6066. [Google Scholar] [CrossRef]
- Ran, J.; Ditmar, P.; Klees, R.; Farahani, H.H. Statistically optimal estimation of Greenland Ice Sheet mass variations from GRACE monthly solutions using an improved mascon approach. J. Geod. 2018, 92, 299–319. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, A.; Ivins, E.R.; Geruo, A.; Barletta, V.R.; Bentley, M.J.; Bettadpur, S.; Briggs, K.H.; Bromwich, D.H.; Forsberg, R.; Galin, N.; et al. A reconciled estimate of ice-sheet mass balance. Science 2012, 338, 1183–1189. [Google Scholar] [CrossRef] [PubMed]
- Müller Schmied, H.; Cáceres, D.; Eisner, S.; Flörke, M.; Herbert, C.; Niemann, C.; Peiris, T.A.; Popat, E.; Portmann, F.T.; Reinecke, R.; et al. The global water resources and use model WaterGAP v2.2d: Model description and evaluation. Geosci. Model Dev. 2021, 14, 1037–1079. [Google Scholar] [CrossRef]
- Oki, T.; Sud, Y.C. Design of Total Runoff Integrating Pathways (TRIP)—A global river channel network. Earth Interact. 1998, 2, 1–36. [Google Scholar] [CrossRef]
- Meyer, U.; Jäggi, A.; Beutler, G.; Bock, H. The impact of common versus separate estimation of orbit parameters on GRACE gravity field solutions. J. Geod. 2015, 89, 685–696. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).