A Deep-Learning-Based Error-Correction Method for Atmospheric Motion Vectors
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.1.1. AMV Data
2.1.2. Reanalysis Data
2.2. Data Preprocessing
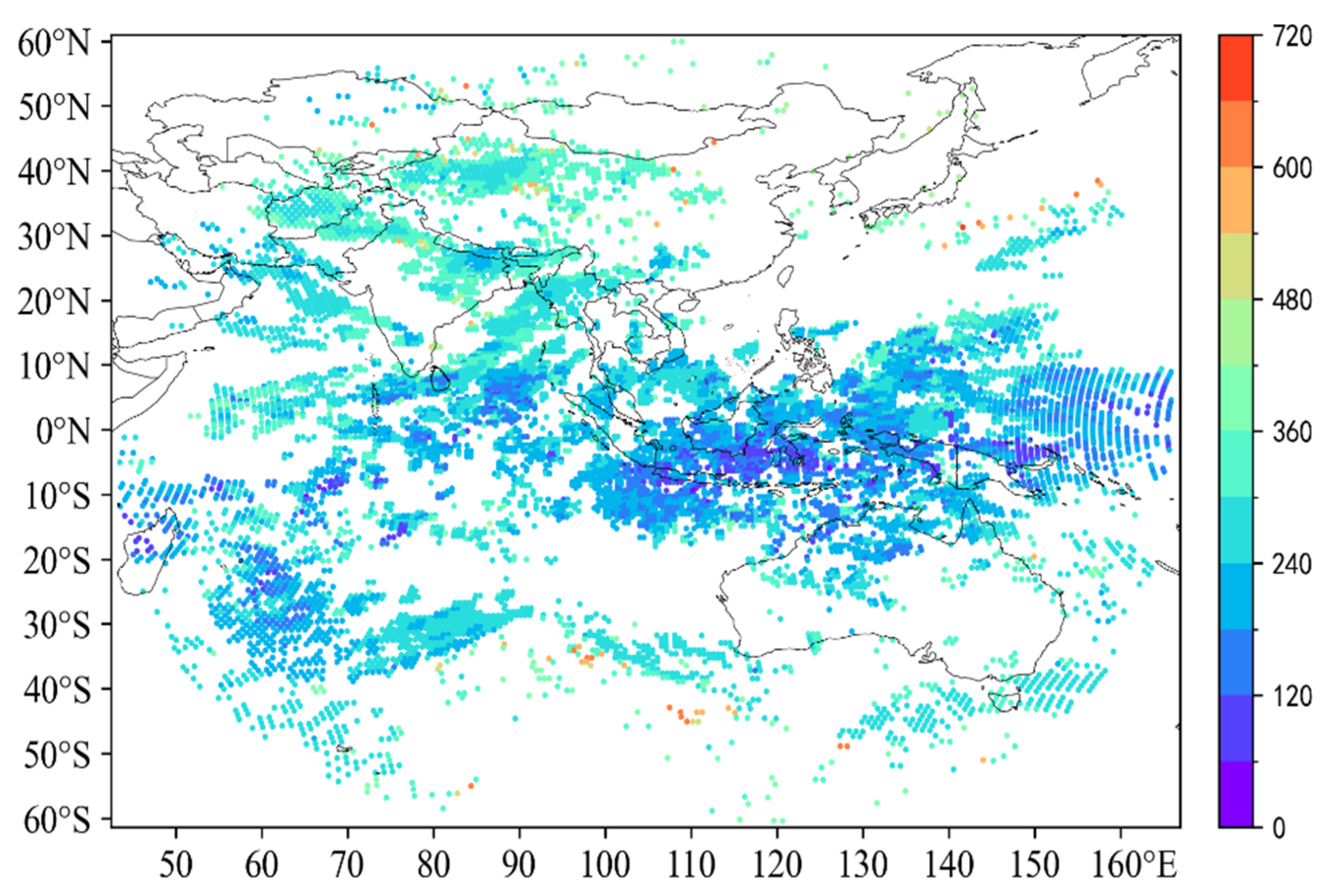
2.3. Data Quality Evaluation
3. Model
3.1. U-Net
3.2. Long Short-Term Memory
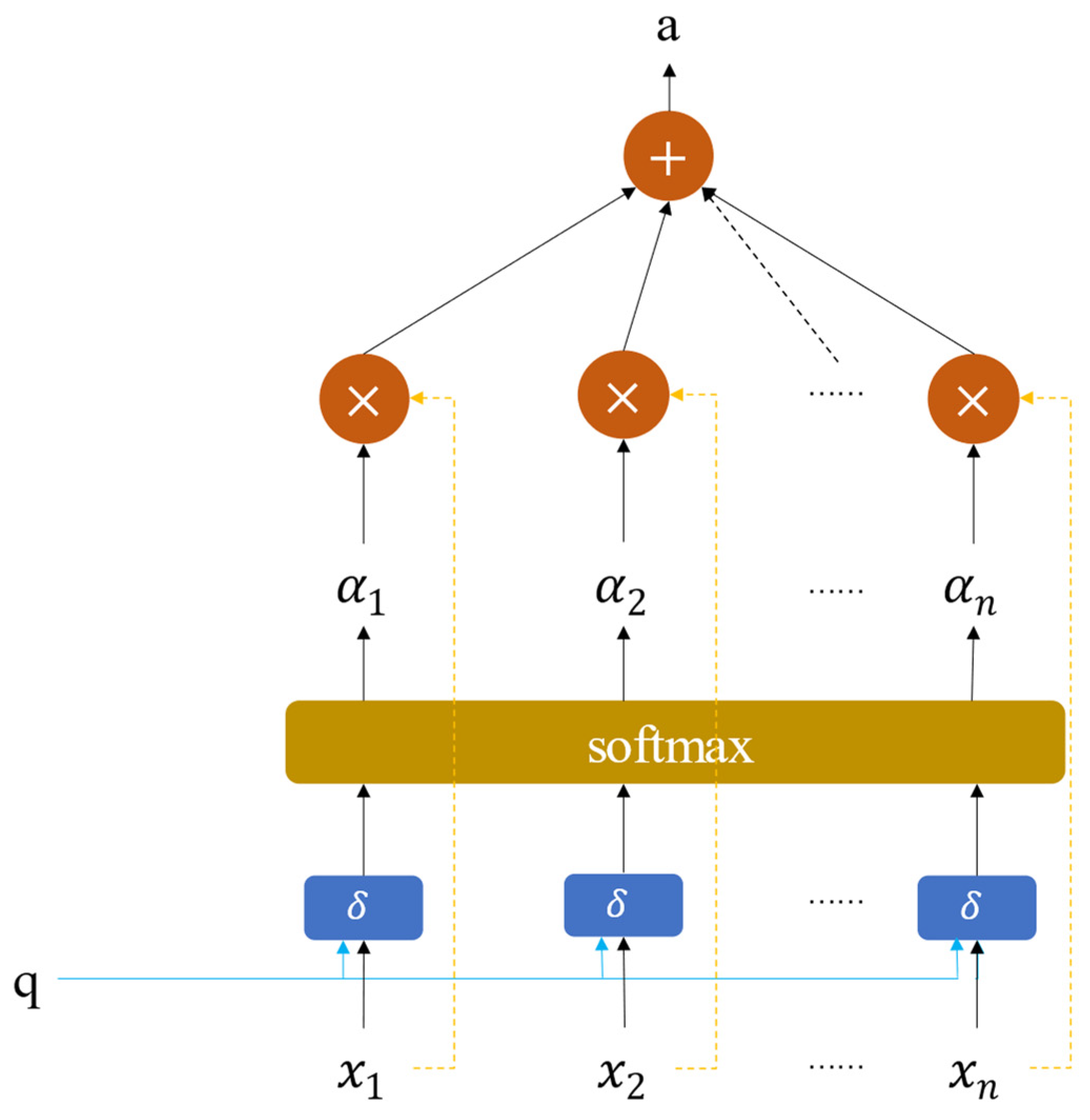
3.3. Attention Mechanism
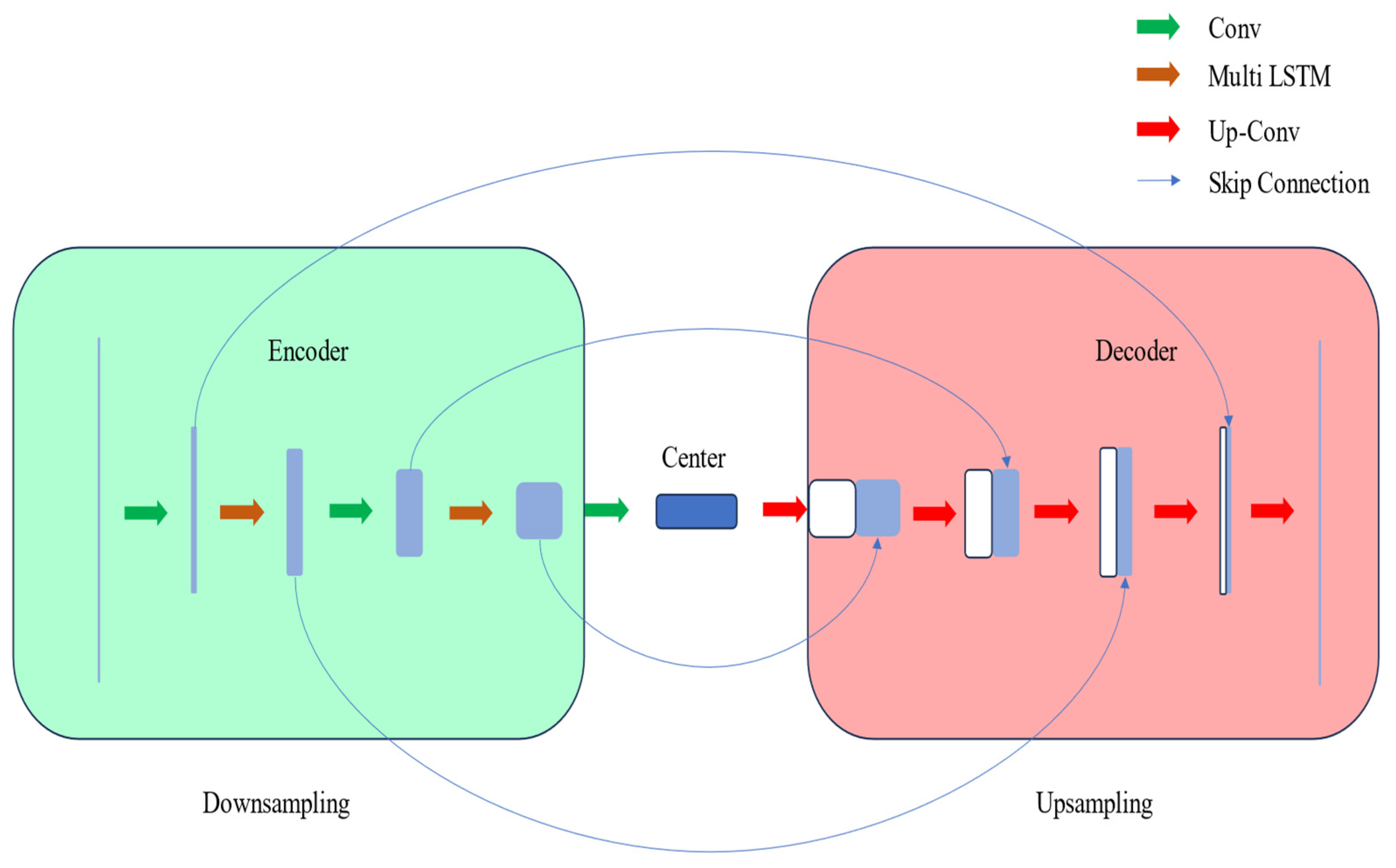
3.4. AMVCN
4. Results
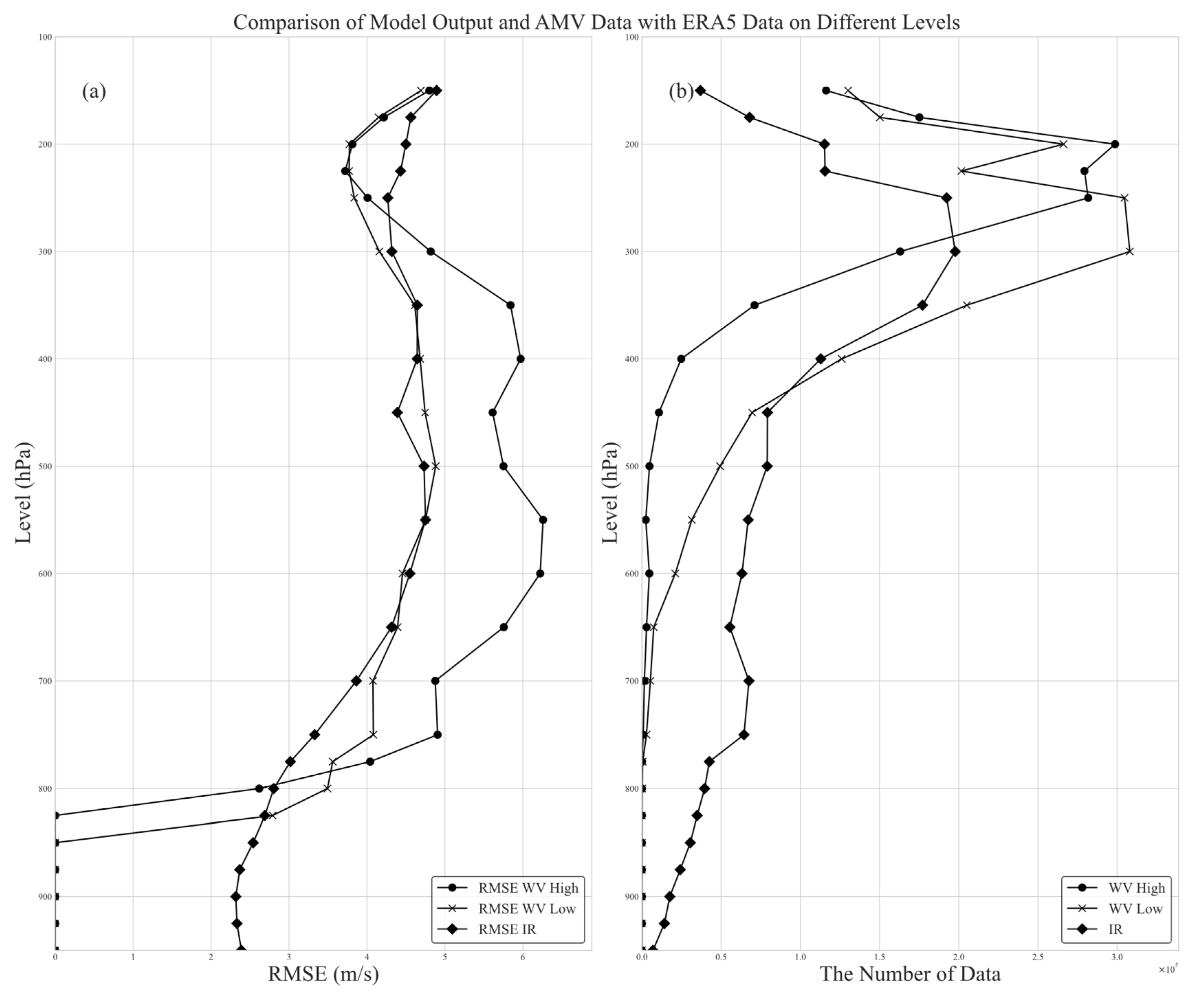
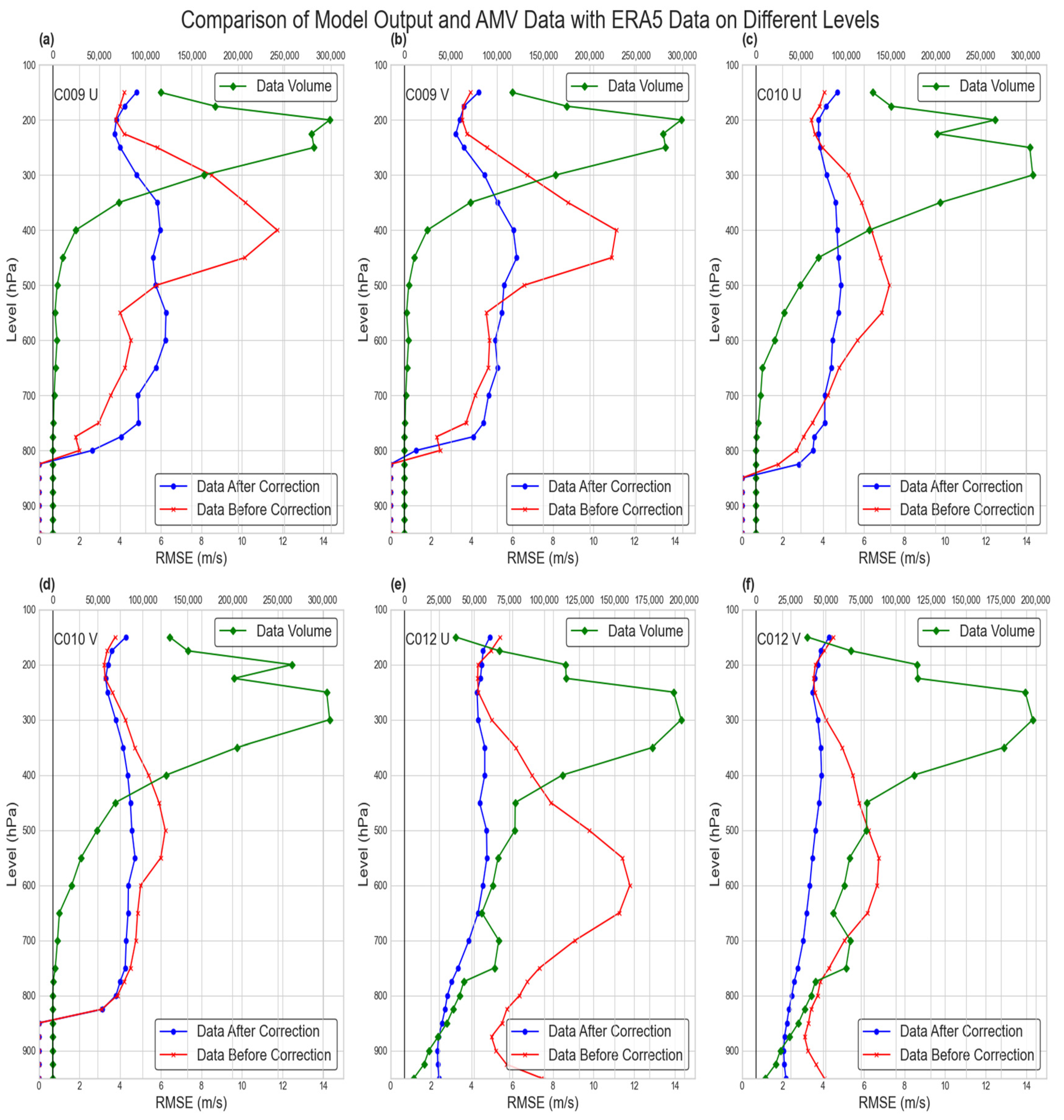
4.1. Quality Evaluation
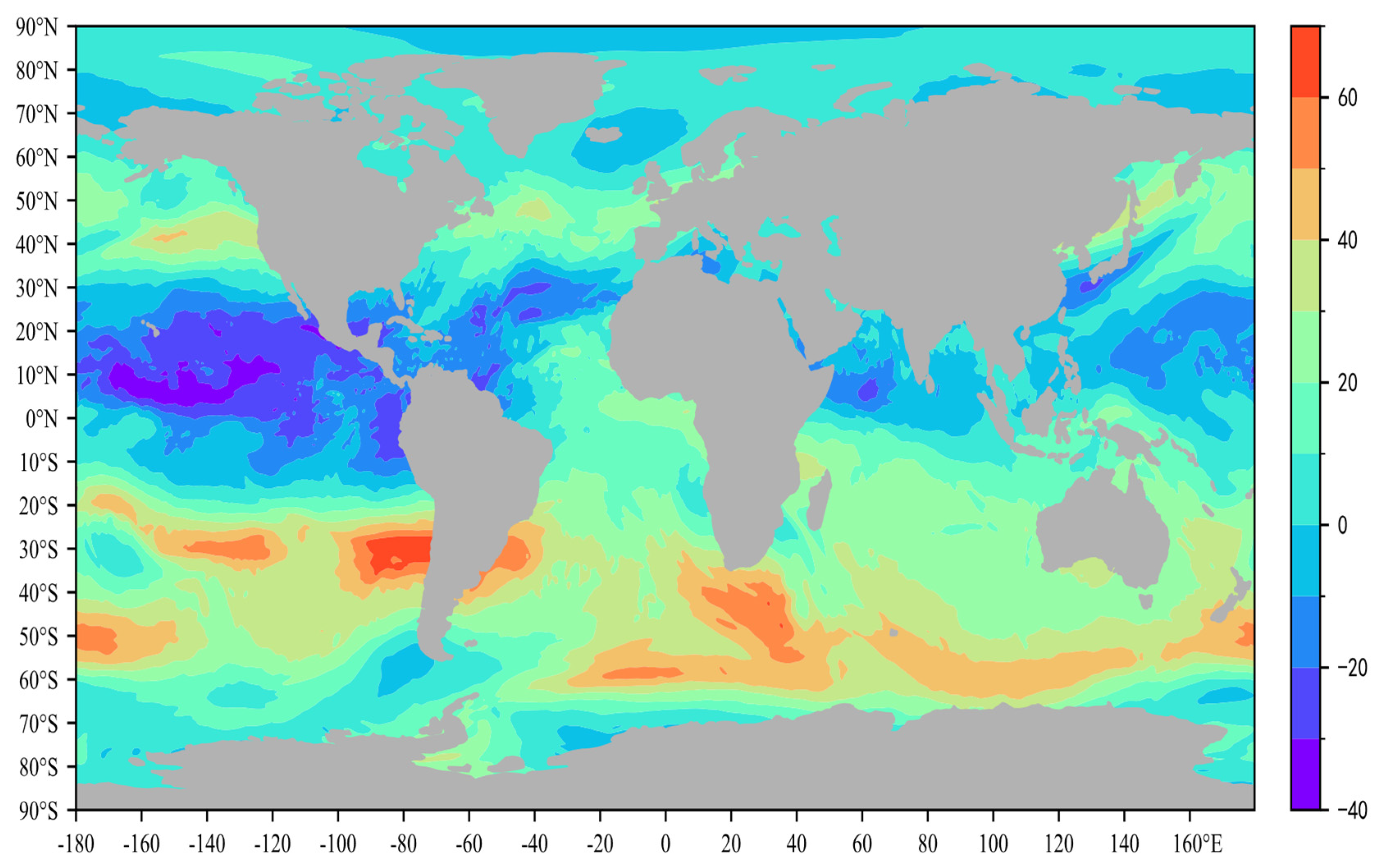
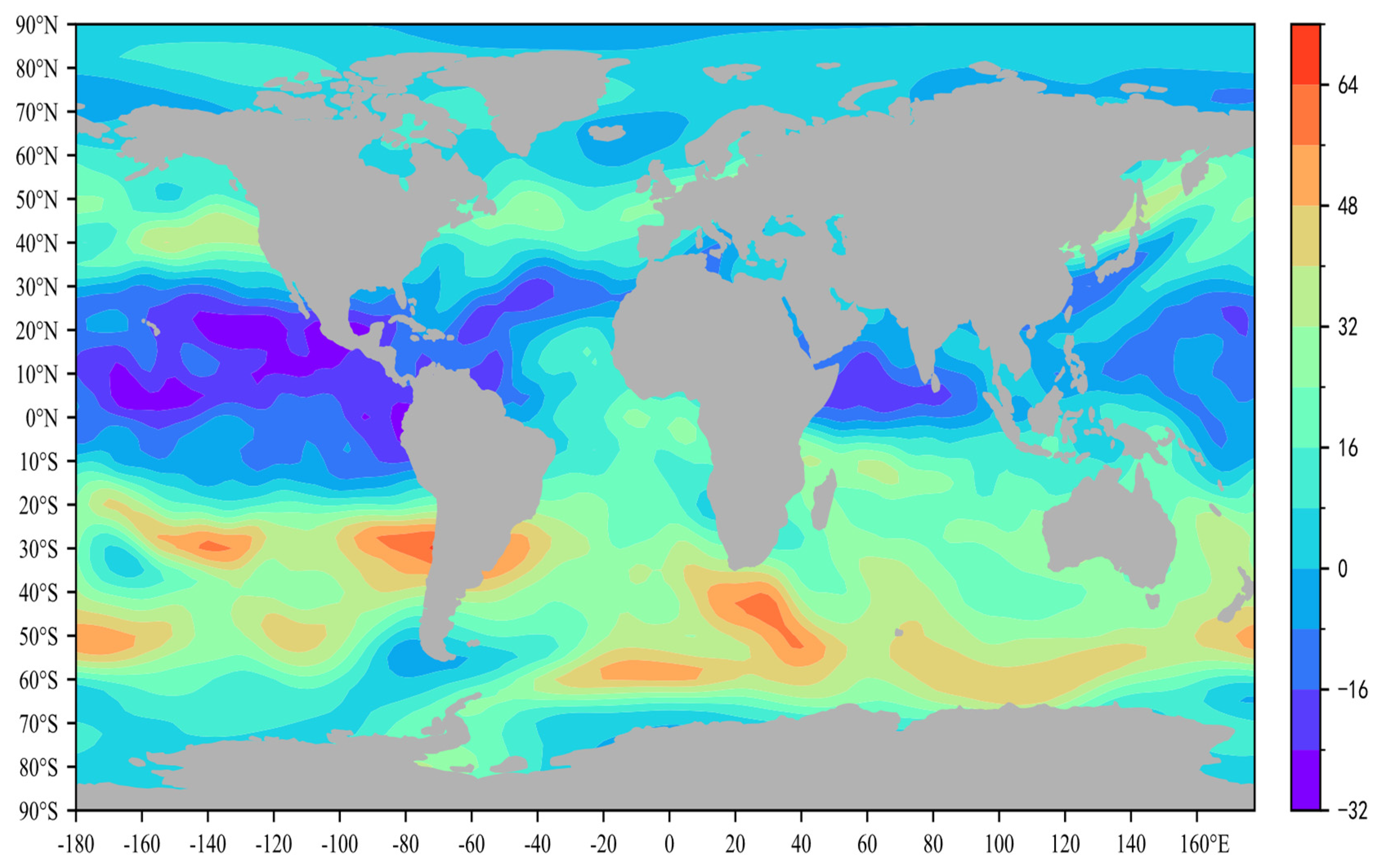
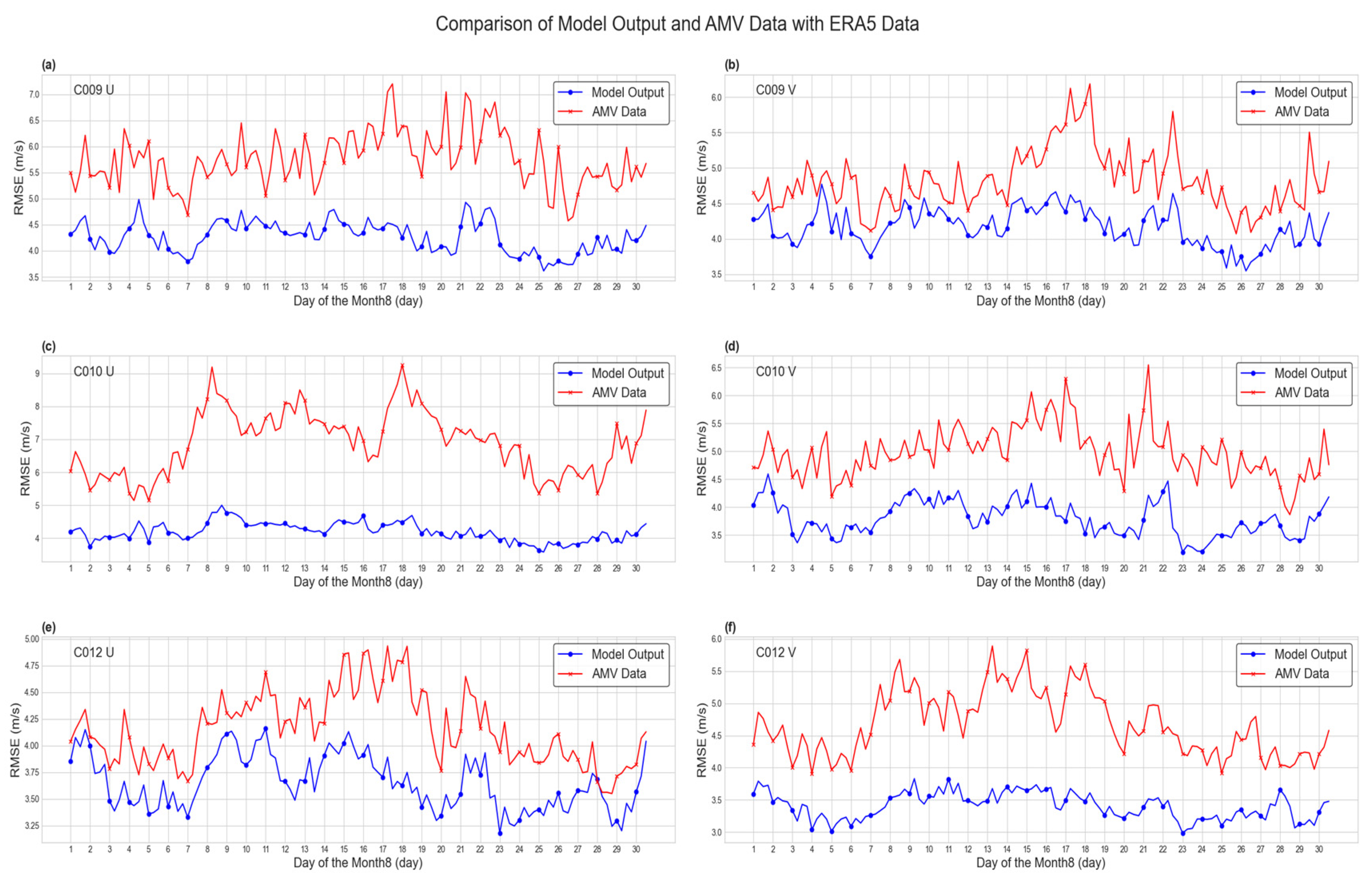
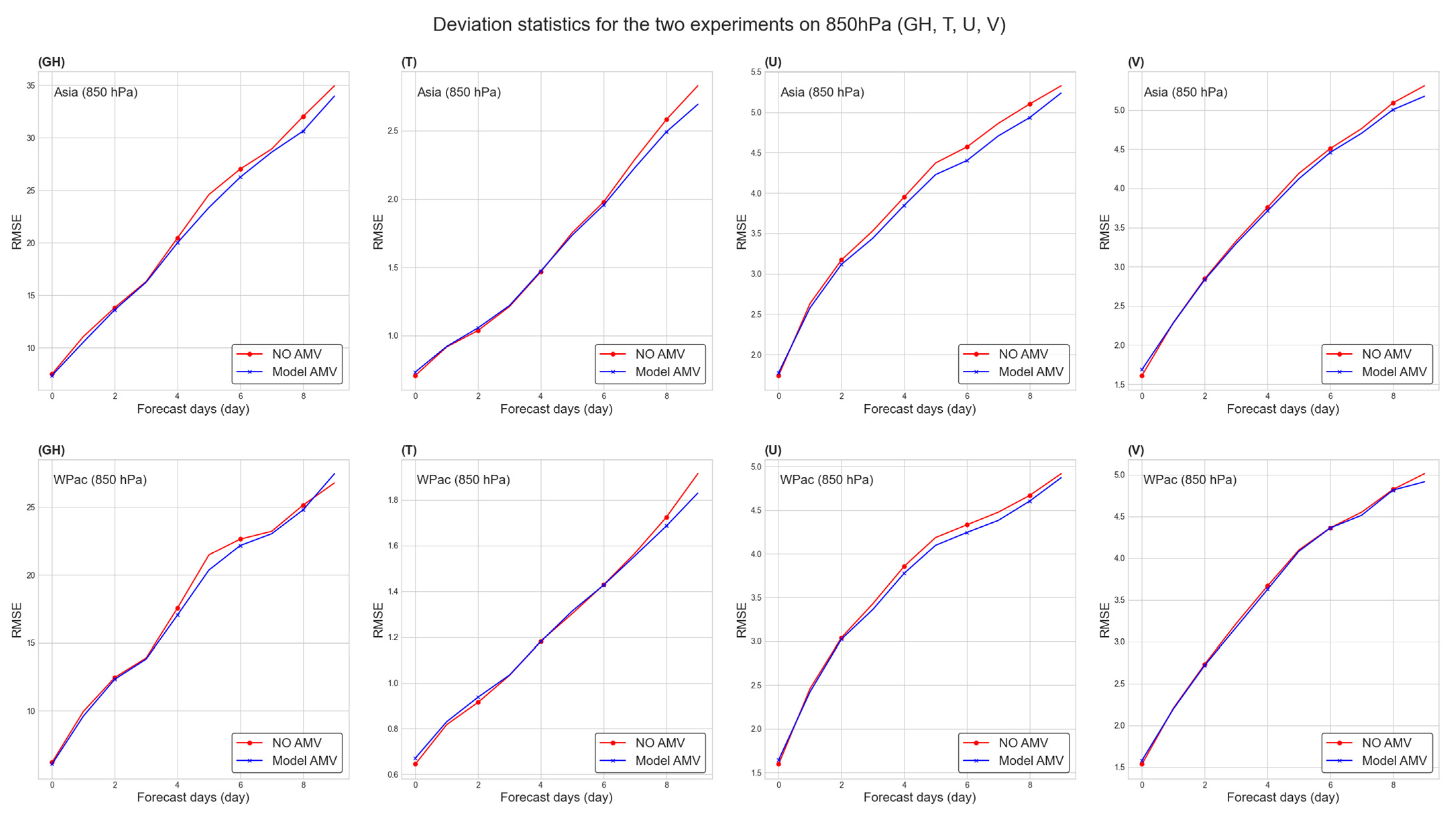
4.2. Meteorological Element Forecast Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baker, W.E.; Emmitt, G.D.; Robertson, F.; Atlas, R.M.; Molinari, J.E.; Bowdle, D.A.; Paegle, J.; Hardesty, R.M.; Menzies, R.T.; Krishnamurti, T.N.; et al. Lidar-Measured Winds from Space: A Key Component for Weather and Climate Prediction. Bull. Am. Meteorol. Soc. 1995, 76, 869–888. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, S. Numerical experiments of the prediction of typhoon tracks by using satellite cloud-derived wind. J. Trop. Meteorol. 1999, 15, 347–355. [Google Scholar]
- Yerong, F. Application of Cloud Tracked Wind Data in Tropical Cyclone Movement Forecasting. Meteorology 1999, 25, 11–16. [Google Scholar]
- Bing, Z.; Haiming, X.; Guoxiong, W.; Jinhai, H. Numerical simulation of CMWDA with impacting on torrential rain forecast. Acta Meteorol. Sin. 2002, 60, 308–317. [Google Scholar]
- Zhaorong, Z.; Jishan, X. Assimilation of cloud-derived winds and its impact on typhoon forecast. J. Trop. Meteorol. 2004, 20, 225–236. [Google Scholar]
- Bormann, N.; Thépaut, J.-N. Impact of MODIS Polar Winds in ECMWF’s 4DVAR Data Assimilation System. Mon. Weather Rev. 2004, 132, 929–940. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, X.-H.; Chen, B.-Y.; Liu, H.; Wu, R.; Han, Q.; Feng, X.; Li, Y.; Zhang, Z. FY-4 geostationary meteorological satellite imaging characteristics and its application prospects. J. Mar. Meteorol 2017, 37, 1–12. [Google Scholar]
- Zhang, Z.-Q.; Lu, F.; Fang, X.; Tang, S.; Zhang, X.; Xu, Y.; Han, W.; Nie, S.; Shen, Y.; Zhou, Y. Application and development of FY-4 meteorological satellite. Aerosp. Shanghai 2017, 34, 8–19. [Google Scholar]
- Xie, Q.; Li, D.; Yang, Y.; Ma, Y.; Pan, X.; Chen, M. Impact of assimilating atmospheric motion vectors from Himawari-8 and clear-sky radiance from FY-4A GIIRS on binary typhoons. Atmos. Res. 2023, 282, 106550. [Google Scholar] [CrossRef]
- Liang, J. Impact Study of Assimilating Geostationary Satellite Atmospheric Motion Vectors on Typhoon Numerical Forecasting; Chengdu University of Information Technology: Chengdu, China, 2020; pp. 1–6. Available online: https://cnki.sris.com.tw/kns55/brief/result.aspx?dbPrefix=CJFD (accessed on 24 April 2024).
- Velden, C.S.; Bedka, K.M. Identifying the Uncertainty in Determining Satellite-Derived Atmospheric Motion Vector Height Attribution. J. Appl. Meteorol. Climatol. 2009, 48, 450–463. [Google Scholar] [CrossRef]
- Sun, X.J.; Zhang, C.L.; Fang, L.; Lu, W.; Zhao, S.J.; Ye, S. A review of the technical system of spaceborne Doppler wind lidar and its assessment method. Natl. Remote Sens. Bull. 2022, 26, 1260–1273. [Google Scholar] [CrossRef]
- Yang, C.Y.; Lu, Q.F.; Jing, L. Numerical experiments of assimilation and forecasts by using dualchannels AMV products of FY-2 C based on height reassignment. J. PLA Univ. Sci. Technol. 2012, 13, 694–701. [Google Scholar]
- Wan, X.; Tian, W.; Han, W.; Wang, R.; Zhang, Q.; Zhang, X. The evaluation of FY-2E reprocessed IR AMVs in GRAPES. Meteor. Mon. 2017, 43, 1–10. [Google Scholar]
- Yaodeng, C.; Jie, S.; Shuiyong, F.; Cheng, W. A study of the observational error statistics and assimilation applications of the FY-4A satellite atmospheric motion vector. J. Atmos. Sci. 2021, 44, 418–427. [Google Scholar]
- Key, J.; Maslanik, J.; Schweiger, A. Classification of merged AVHRR and SMMR Arctic data with neural networks. Photogramm. Eng. Remote Sens. 1989, 55, 1331. [Google Scholar]
- Ziyi, D.; Zhenhong, D.; Sensen, W.; Yadong, L.; Feng, Z.; Renyi, L. An automatic marine mesoscale eddy detection model based on improved U-Net network. Haiyang Xuebao 2022, 44, 123–131. [Google Scholar] [CrossRef]
- Santana, O.J.; Hernández-Sosa, D.; Smith, R.N. Oceanic mesoscale eddy detection and convolutional neural network complexity. Int. J. Appl. Earth Obs. Geoinf. 2022, 113, 102973. [Google Scholar] [CrossRef]
- Dai, L.; Zhang, C.; Xue, L.; Ma, L.; Lu, X. Eyed tropical cyclone intensity objective estimation model based on infrared satellite image and relevance vector machine. J. Remote Sens. 2018, 22, 581–590. [Google Scholar] [CrossRef]
- Hess, P.; Boers, N. Deep Learning for Improving Numerical Weather Prediction of Heavy Rainfall. J. Adv. Model. Earth Syst. 2022, 14, e2021MS002765. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Hao, X.; Zhang, G.; Ma, S. Deep Learning. Int. J. Semant. Comput. 2016, 10, 417–439. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.W.M.; van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Pouyanfar, S.; Sadiq, S.; Yan, Y.; Tian, H.; Tao, Y.; Reyes, M.P.; Shyu, M.-L.; Chen, S.-C.; Iyengar, S.S. A Survey on Deep Learning: Algorithms, Techniques, and Applications. ACM Comput. Surv. 2018, 51, 1–36. [Google Scholar] [CrossRef]
- Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Hasan, M.; Van Essen, B.C.; Awwal, A.A.S.; Asari, V.K. A State-of-the-Art Survey on Deep Learning Theory and Architectures. Electronics 2019, 8, 292. [Google Scholar] [CrossRef]
- Huang, D.; Li, M.; Song, W.; Wang, J. Performance of convolutional neural network and deep belief network in sea ice-water classification using SAR imagery. J. Image Graph. 2018, 23, 1720–1732. [Google Scholar]
- Brajard, J.; Carrassi, A.; Bocquet, M.; Bertino, L. Combining data assimilation and machine learning to emulate a dynamical model from sparse and noisy observations: A case study with the Lorenz 96 model. J. Comput. Sci. 2020, 44, 101171. [Google Scholar] [CrossRef]
- Bonavita, M.; Laloyaux, P. Machine Learning for Model Error Inference and Correction. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002232. [Google Scholar] [CrossRef]
- Rasp, S.; Lerch, S. Neural Networks for Postprocessing Ensemble Weather Forecasts. Mon. Weather Rev. 2018, 146, 3885–3900. [Google Scholar] [CrossRef]
- Wan, X.; Gong, J.; Han, W.; Tian, W. The evaluation of FY-4A AMVs in GRAPES_RAFS. Meteorol. Mon. 2019, 45, 458–468. [Google Scholar]
- Jiang, S.; Shu, X.; Wang, Q.; Yan, Z. Evolution characteristics of wave energy resources in Guangdong coastal area based on long time series ERA-Interim reanalysis data. Mar. Sci. Bull. 2021, 40, 550–558. [Google Scholar]
- Tan, H.; Shao, Z.; Liang, B.; Gao, H. A comparative study on the applicability of ERA5 wind and NCEP wind for wave simulation in the Huanghai Sea and East China Sea. Mar. Sci. Bull. 2021, 40, 524–540. [Google Scholar]
- Geng, S.; Han, C.; Xu, S.; Yang, J.; Shi, X.; Liang, J.; Liu, Y.; Shuangquan, W. Applicability Analysis of ERA5 Surface Pressure and Wind Speed Reanalysis Data in the Bohai Sea and North Yellow Sea. Mar. Bull. 2023, 42, 159–168. [Google Scholar]
- Chen, K.; Xie, X.; Zhang, J.; Zou, J.; Yi, Z. Accuracy analysis of the retrieved wind from HY-2B scatterometer. J. Trop. Oceanogr. 2020, 39, 30–40. [Google Scholar] [CrossRef]
- Ebuchi, N. Evaluation of NSCAT-2 Wind Vectors by Using Statistical Distributions of Wind Speeds and Directions. J. Oceanogr. 2000, 56, 161–172. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Y.n.; Luo, J. Deep learning for processing and analysis of remote sensing big data: A technical review. Big Earth Data 2022, 6, 527–560. [Google Scholar] [CrossRef]
- Pan, X.; Lu, Y.; Zhao, K.; Huang, H.; Wang, M.; Chen, H. Improving Nowcasting of Convective Development by Incorporating Polarimetric Radar Variables into a Deep-Learning Model. Geophys. Res. Lett. 2021, 48, e2021GL095302. [Google Scholar] [CrossRef]
- Zhou, K.; Zheng, Y.; Dong, W.; Wang, T. A Deep Learning Network for Cloud-to-Ground Lightning Nowcasting with Multisource Data. J. Atmos. Ocean. Technol. 2020, 37, 927–942. [Google Scholar] [CrossRef]
- Weyn, J.A.; Durran, D.R.; Caruana, R. Improving Data-Driven Global Weather Prediction Using Deep Convolutional Neural Networks on a Cubed Sphere. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002109. [Google Scholar] [CrossRef]
- Zeng, M.; Zhang, G.; Li, Y.; Luo, Y.; Hu, G.; Huang, Y.; Liang, C. Combined multi-branch selective kernel hybrid-pooling skip connection residual network for seismic random noise attenuation. J. Geophys. Eng. 2022, 19, 863–875. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and rainfall forecasting by two long short-term memory-based models. J. Hydrol. 2020, 583, 124296. [Google Scholar] [CrossRef]
- Wang, F.; Cao, Y.; Wang, Q.; Zhang, T.; Su, D. Estimating Precipitation Using LSTM-Based Raindrop Spectrum in Guizhou. In Atmosphere 2023, 14, 1031. [Google Scholar] [CrossRef]
- Parasyris, A.; Alexandrakis, G.; Kozyrakis, G.V.; Spanoudaki, K.; Kampanis, N.A. Predicting Meteorological Variables on Local Level with SARIMA, LSTM and Hybrid Techniques. Atmosphere 2022, 13, 878. [Google Scholar] [CrossRef]





| Channels | Data | RMSE/(m/s) | MAE/(m/s) | R |
|---|---|---|---|---|
| C009 | AMV | 5.804 | 0.790 | 0.951 |
| Correction | 4.962 () | 0.706 () | 0.967 () | |
| Mdole | 4.278 () | 0.694 () | 0.974 () | |
| C010 | AMV | 4.832 | 0.954 | 0.965 |
| Correction | 4.438 () | 0.866 () | 0.972 () | |
| Mdole | 4.178 () | 0.894 () | 0.974 () | |
| C012 | AMV | 6.889 | 1.118 | 0.885 |
| Correction | 6.601 () | 0.973 () | 0.900 () | |
| Mdole | 4.195 () | 0.805 () | 0.956 () |
| Channels | Data | RMSE/(m/s) | MAE/(m/s) | R |
|---|---|---|---|---|
| C009 | AMV | 5.010 | 0.733 | 0.855 |
| Correction | 4.416 ) | 0.666 ) | 0.886 ) | |
| Mdole | 3.816 ) | 0.635 ) | 0.912 ) | |
| C010 | AMV | 4.164 | 0.872 | 0.892 |
| Correction | 3.948 ) | 0.802 ) | 0.905 ) | |
| Mdole | 3.665 ) | 0.804 ) | 0.916 ) | |
| C012 | AMV | 4.684 | 0.867 | 0.816 |
| Correction | 4.504 ) | 0.765 ) | 0.837 ) | |
| Mdole | 3.416 ) | 0.680 ) | 0.899 ) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Leng, H.; Zhao, J.; Zhao, Y.; Zhao, C.; Li, B. A Deep-Learning-Based Error-Correction Method for Atmospheric Motion Vectors. Remote Sens. 2024, 16, 1562. https://doi.org/10.3390/rs16091562
Cao H, Leng H, Zhao J, Zhao Y, Zhao C, Li B. A Deep-Learning-Based Error-Correction Method for Atmospheric Motion Vectors. Remote Sensing. 2024; 16(9):1562. https://doi.org/10.3390/rs16091562
Chicago/Turabian StyleCao, Hang, Hongze Leng, Jun Zhao, Yanlai Zhao, Chengwu Zhao, and Baoxu Li. 2024. "A Deep-Learning-Based Error-Correction Method for Atmospheric Motion Vectors" Remote Sensing 16, no. 9: 1562. https://doi.org/10.3390/rs16091562
APA StyleCao, H., Leng, H., Zhao, J., Zhao, Y., Zhao, C., & Li, B. (2024). A Deep-Learning-Based Error-Correction Method for Atmospheric Motion Vectors. Remote Sensing, 16(9), 1562. https://doi.org/10.3390/rs16091562





