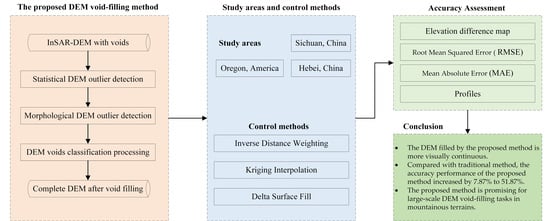
InSAR Digital Elevation Model Void-Filling Method Based on Incorporating Elevation Outlier Detection
Abstract
1. Introduction
2. Materials and Methods
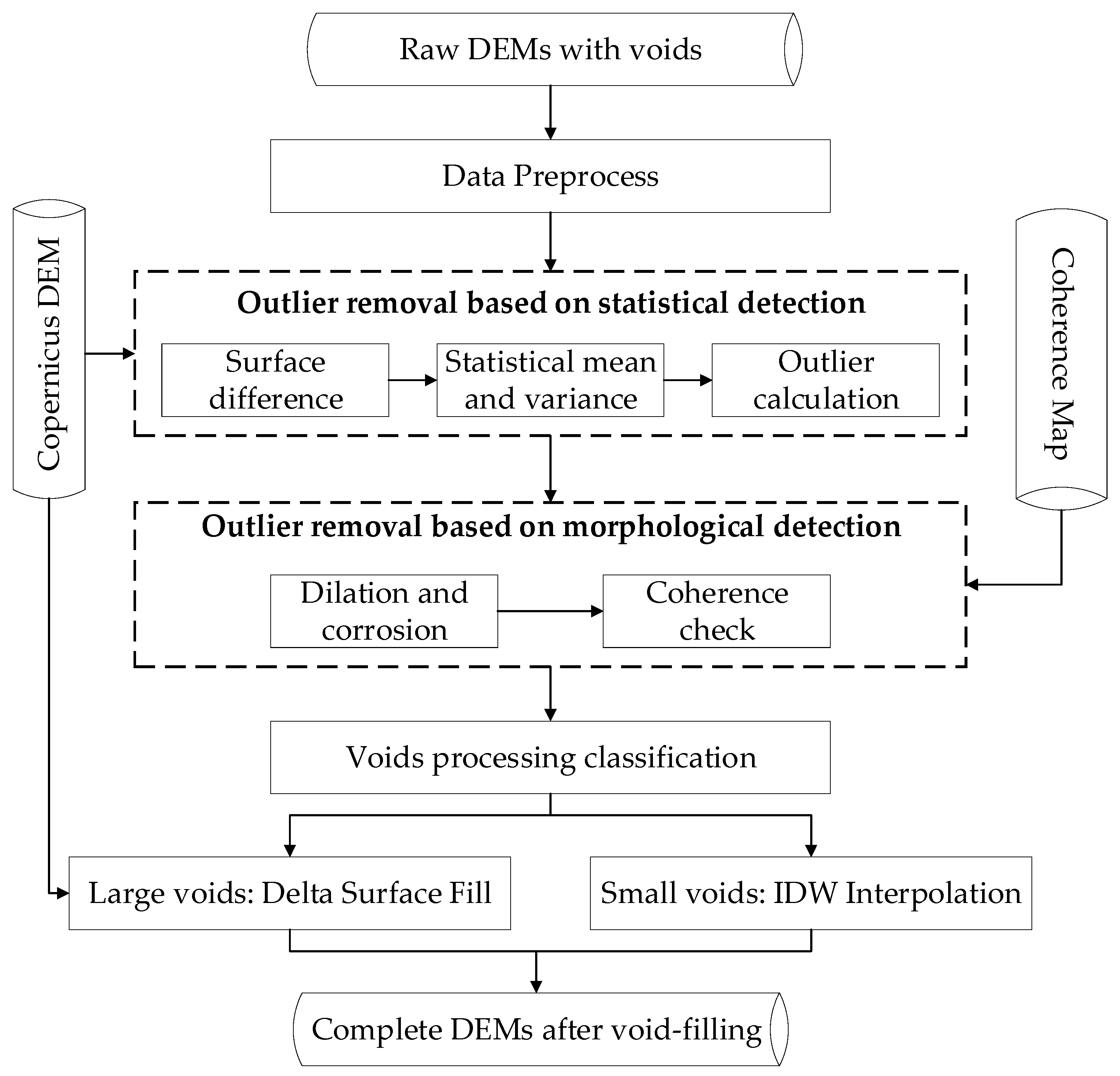
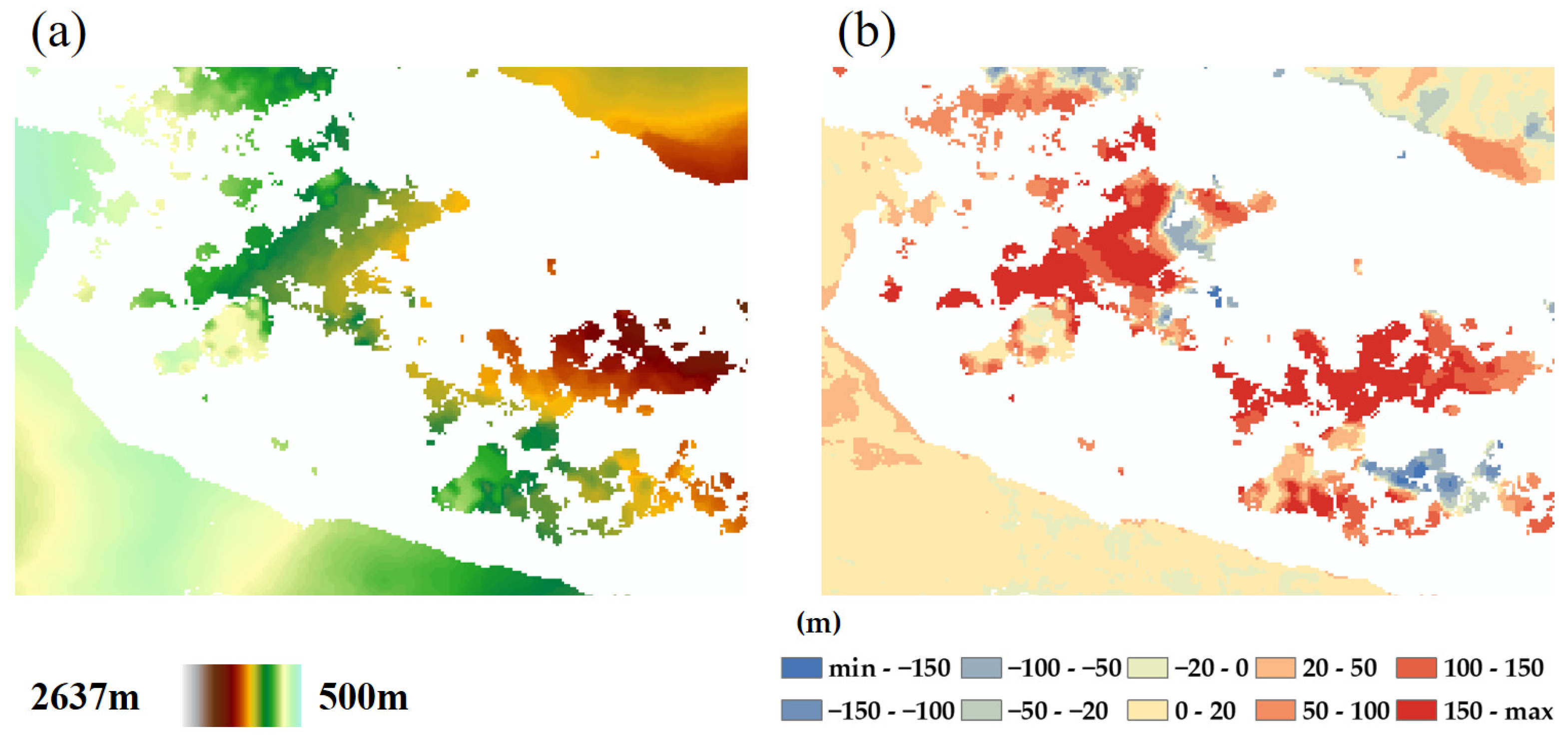
2.1. DEM Outlier Detection and Removal
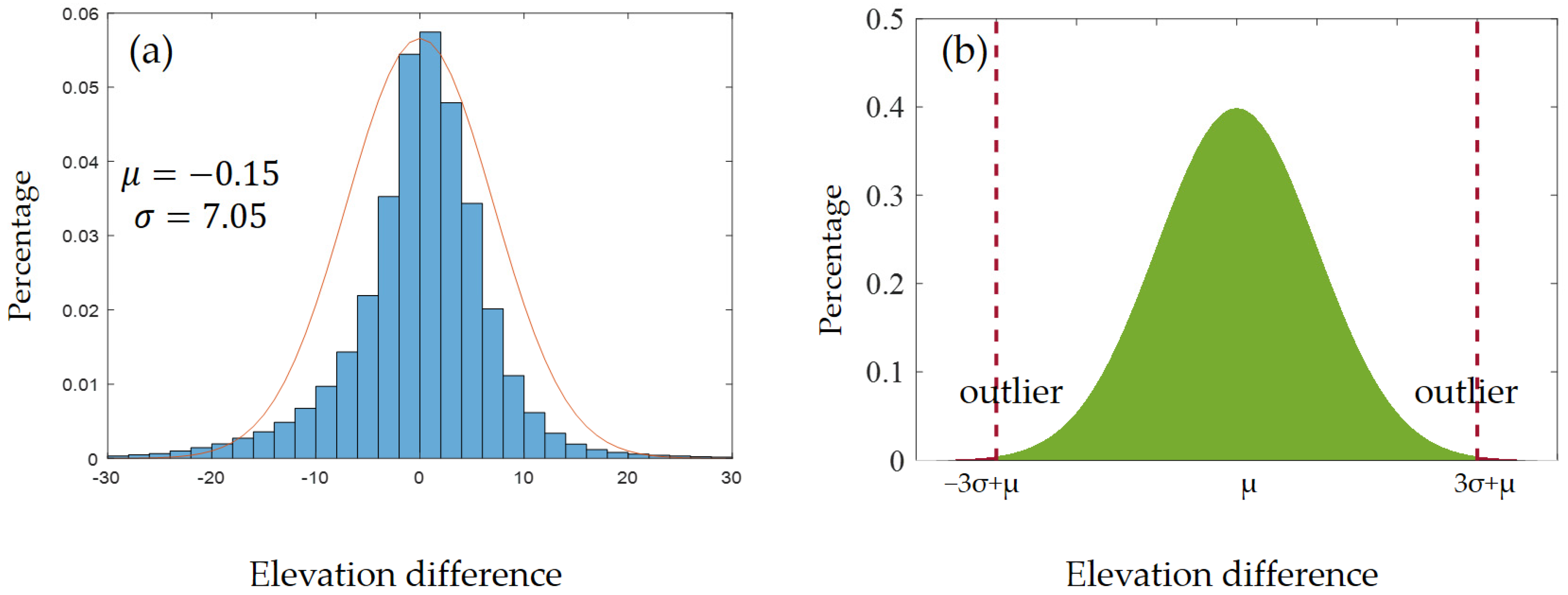
2.1.1. DEM Outlier Removal Based on Statistical Detection
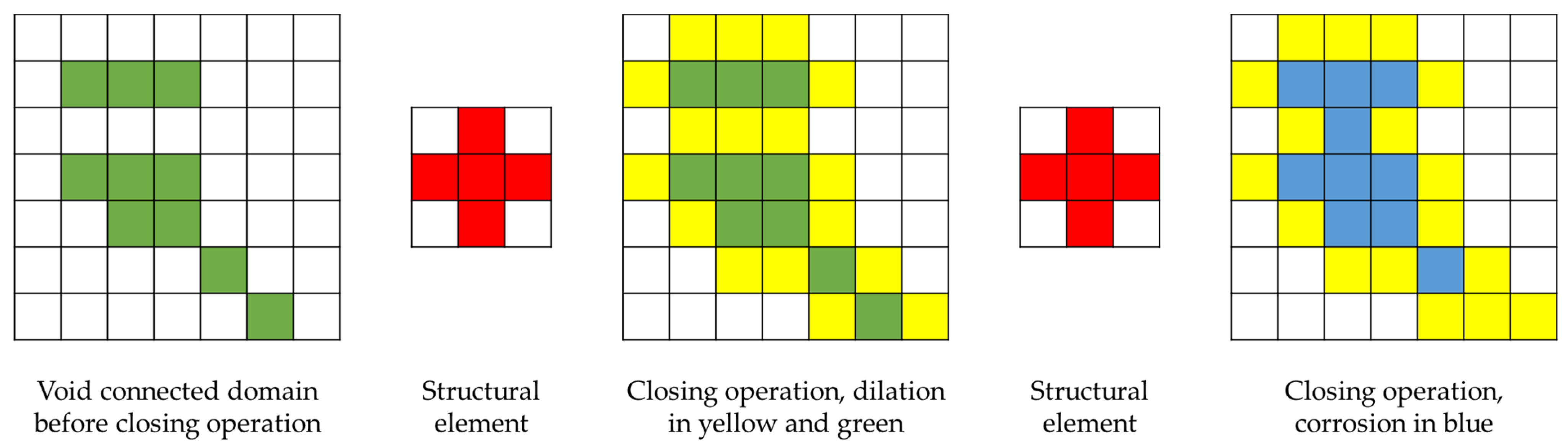
2.1.2. DEM Outlier Removal Based on Morphological Detection
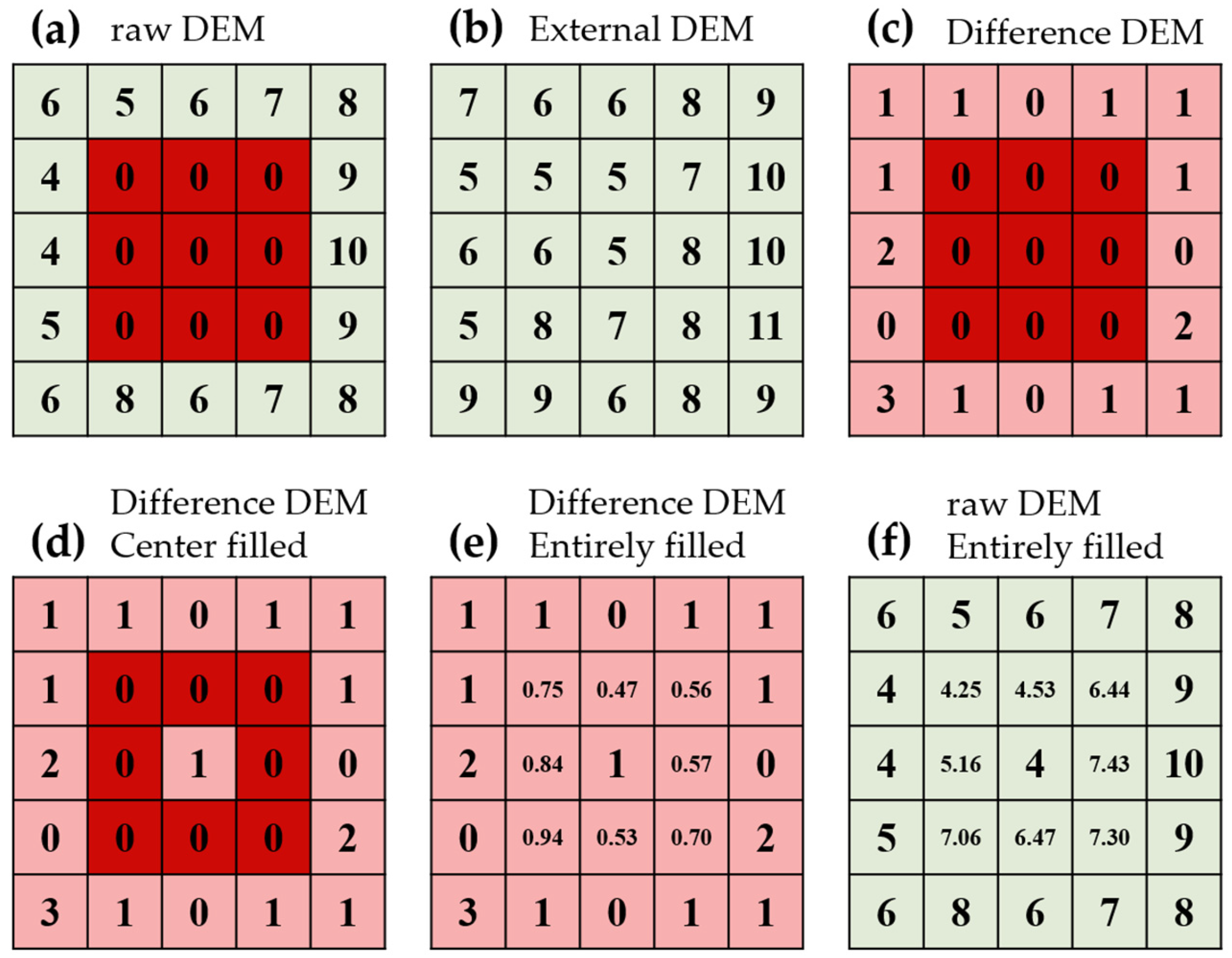
2.2. Delta Surface Fill
- Computing the delta surface of raw DEMs and external DEMs;
- Internal filling of delta surface voids;
- Delta surface voids’ edge interpolation;
- Combining external DEMs and the delta surface.
2.3. Study Area and Experimental Data
3. Results
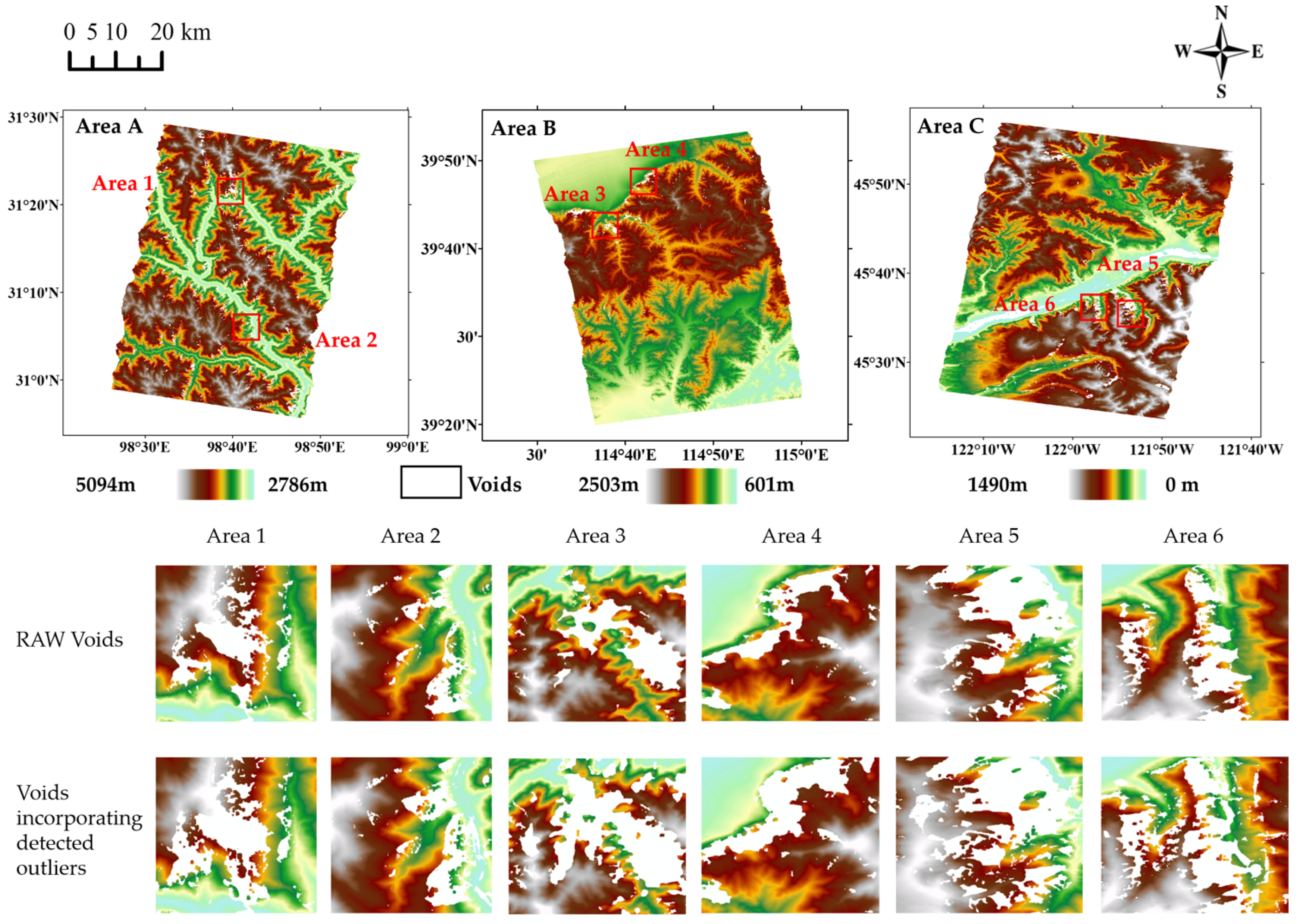
3.1. Void-Filling Results via Different Methods
3.2. Elevation Difference Analysis
3.3. Important Terrain Void-Filling Performance Analysis by Profile
4. Discussion
4.1. The Impact of Elevation Outlier Removal on DEM Void Filling
4.2. Suitable Situations and Future Improvement Directions of the Proposed Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lakshmi, S.E.; Yarrakula, K. Review and critical analysis on digital elevation models. G Eofizika 2018, 35, 103–284. [Google Scholar] [CrossRef]
- Tarolli, P. High-resolution topography for understanding Earth surface processes: Opportunities and challenges. Geomorphology 2014, 216, 295–312. [Google Scholar] [CrossRef]
- Badura, J.; Przybylski, B.A. Application of digital elevation models to geological and geomorphological studies-some examples. Przegląd Geol. 2005, 53, 977–983. [Google Scholar]
- Wechsler, S. Uncertainties associated with digital elevation models for hydrologic applications: A review. Hydrol. Earth Syst. Sci. 2007, 11, 1481–1500. [Google Scholar] [CrossRef]
- Racoviteanu, A.E.; Manley, W.F.; Arnaud, Y.; Williams, M.W. Evaluating digital elevation models for glaciologic applications: An example from Nevado Coropuna, Peruvian Andes. Glob. Planet. Chang. 2007, 59, 110–125. [Google Scholar] [CrossRef]
- Zhou, G.; Bao, X.; Ye, S.; Wang, H.; Yan, H. Selection of optimal building facade texture images from UAV-based multiple oblique image flows. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1534–1552. [Google Scholar] [CrossRef]
- Geymen, A. Digital elevation model (DEM) generation using the SAR interferometry technique. Arab. J. Geosci. 2014, 7, 827–837. [Google Scholar] [CrossRef]
- Zheng, W.; Hu, J.; Lu, Z.; Hu, X.; Sun, Q.; Liu, J.; Zhu, J.; Li, Z. Enhanced Kinematic Inversion of 3-D Displacements, Geometry, and Hydraulic Properties of a North-South Slow-Moving Landslide in Three Gorges Reservoir. J. Geophys. Res. Solid Earth 2023, 128, e2022JB026232. [Google Scholar] [CrossRef]
- Hirt, C. Artefact detection in global digital elevation models (DEMs): The Maximum Slope Approach and its application for complete screening of the SRTM v4.1 and MERIT DEMs. Remote Sens. Environ. 2018, 207, 27–41. [Google Scholar] [CrossRef]
- Dowding, S.; Kuuskivi, T.; Li, X. Void fill of SRTM elevation data—Principles, processes and performance. In ASPRS Images to Decision: Remote Sensing Foundation for GIS Applications; ASPRS: Bethesda, MD, USA, 2004; pp. 12–16. [Google Scholar]
- Ma, H.; Zhou, W.; Zhang, L. DEM refinement by low vegetation removal based on the combination of full waveform data and progressive TIN densification. ISPRS J. Photogramm. Remote Sens. 2018, 146, 260–271. [Google Scholar] [CrossRef]
- Yan, W.Y. Scan line void filling of airborne LiDAR point clouds for hydroflattening DEM. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6426–6437. [Google Scholar] [CrossRef]
- Grohman, G.; Kroenung, G.; Strebeck, J. Filling SRTM voids: The delta surface fill method. Photogramm. Eng. Remote Sens. 2006, 72, 213–216. [Google Scholar]
- Reuter, H.I.; Nelson, A.; Jarvis, A. An evaluation of void-filling interpolation methods for SRTM data. Int. J. Geogr. Inf. Sci. 2007, 21, 983–1008. [Google Scholar] [CrossRef]
- Luedeling, E.; Siebert, S.; Buerkert, A. Filling the voids in the SRTM elevation model—A TIN-based delta surface approach. ISPRS J. Photogramm. Remote Sens. 2007, 62, 283–294. [Google Scholar] [CrossRef]
- Hall, O.; Falorni, G.; Bras, R.L. Characterization and quantification of data voids in the shuttle radar topography mission data. IEEE Geosci. Remote Sens. Lett. 2005, 2, 177–181. [Google Scholar] [CrossRef]
- Dong, G.; Huang, W.; Smith, W.A.; Ren, P. A shadow constrained conditional generative adversarial net for SRTM data restoration. Remote Sens. Environ. 2020, 237, 111602. [Google Scholar] [CrossRef]
- Wecker, L.; Samavati, F.; Gavrilova, M. Contextual void patching for digital elevation models. Vis. Comput. 2007, 23, 881–890. [Google Scholar] [CrossRef]
- Ling, F.; Zhang, Q.; Wang, C. Filling voids of SRTM with Landsat sensor imagery in rugged terrain. Int. J. Remote Sens. 2007, 28, 465–471. [Google Scholar] [CrossRef]
- Crippen, R.E.; Hook, S.J.; Fielding, E.J. Nighttime ASTER thermal imagery as an elevation surrogate for filling SRTM DEM voids. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Hogan, J.; Smith, W.A. Refinement of digital elevation models from shadowing cues. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1181–1188. [Google Scholar]
- Dong, G.; Huang, W.; Smith, W.A.; Ren, P. Filling voids in elevation models using a shadow-constrained convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2019, 17, 592–596. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. The CGIAR-CSI SRTM 90 m Database. 2008, Volume 15, p. 5. Available online: http://srtm.csi.cgiar.org (accessed on 3 November 2023).
- Huber, M.; Osterkamp, N.; Marschalk, U.; Tubbesing, R.; Wendleder, A.; Wessel, B.; Roth, A. Shaping the global high-resolution TanDEM-X digital elevation model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7198–7212. [Google Scholar] [CrossRef]
- Robinson, N.; Regetz, J.; Guralnick, R.P. EarthEnv-DEM90: A nearly-global, void-free, multi-scale smoothed, 90m digital elevation model from fused ASTER and SRTM data. ISPRS J. Photogramm. Remote Sens. 2014, 87, 57–67. [Google Scholar] [CrossRef]
- Li, S.; Hu, G.; Cheng, X.; Xiong, L.; Tang, G.; Strobl, J. Integrating topographic knowledge into deep learning for the void-filling of digital elevation models. Remote Sens. Environ. 2022, 269, 112818. [Google Scholar] [CrossRef]
- Qiu, Z.; Yue, L.; Liu, X. Void filling of digital elevation models with a terrain texture learning model based on generative adversarial networks. Remote Sens. 2019, 11, 2829. [Google Scholar] [CrossRef]
- López, C. Improving the elevation accuracy of digital elevation models: A comparison of some error detection procedures. Trans. GIS 2000, 4, 43–64. [Google Scholar] [CrossRef]
- Chen, C.; Liu, F.; Li, Y.; Yan, C.; Liu, G. A robust interpolation method for constructing digital elevation models from remote sensing data. Geomorphology 2016, 268, 275–287. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y. A robust multiquadric method for digital elevation model construction. Math. Geosci. 2013, 45, 297–319. [Google Scholar] [CrossRef]
- Schultz, H.; Riseman, E.M.; Stolle, F.R.; Woo, D.-M. Error detection and DEM fusion using self-consistency. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 1174–1181. [Google Scholar]
- Zhang, K.; Gann, D.; Ross, M. Detection of Low Elevation Outliers in TanDEM-X DEMs With Histogram and Adaptive TIN. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5101213. [Google Scholar] [CrossRef]
- Ghannadi, M.A.; Alebooye, S.; Izadi, M.; Moradi, A. A method for Sentinel-1 DEM outlier removal using 2-D Kalman filter. Geocarto Int. 2022, 37, 2237–2251. [Google Scholar] [CrossRef]
- González, C.; Bachmann, M.; Bueso-Bello, J.-L.; Rizzoli, P.; Zink, M. A fully automatic algorithm for editing the tandem-x global dem. Remote Sens. 2020, 12, 3961. [Google Scholar] [CrossRef]
- Chukwuocha, A.C. Outlier based selection and accuracy updating of digital elevation models for urban area projects. Afr. J. Environ. Sci. Technol. 2018, 12, 258–267. [Google Scholar]
- Zhang, W.; Wang, W.; Chen, L. Constructing DEM based on InSAR and the relationship between InSAR DEM’s precision and terrain factors. Energy Procedia 2012, 16, 184–189. [Google Scholar] [CrossRef]
- Felicísimo, A.M. Parametric statistical method for error detection in digital elevation models. ISPRS J. Photogramm. Remote Sens. 1994, 49, 29–33. [Google Scholar] [CrossRef]
- Curran-Everett, D. Explorations in statistics: Standard deviations and standard errors. Adv. Physiol. Educ. 2008, 32, 203–208. [Google Scholar] [CrossRef] [PubMed]
- Höhle, J.; Höhle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef]
- Sathymoorthy, D.; Palanikumar, R.; Sagar, B. Morphological segmentation of physiographic features from DEM. Int. J. Remote Sens. 2007, 28, 3379–3394. [Google Scholar] [CrossRef]
- Haralick, R.M.; Sternberg, S.R.; Zhuang, X. Image analysis using mathematical morphology. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 532–550. [Google Scholar] [CrossRef] [PubMed]
- U.S. Geological Survey. 1/3rd Arc-Second Digital Elevation Models (DEMs)—USGS National Map 3DEP Downloadable Data Collection; US Geological Survey: Reston, VA, USA, 2023.
- Ferreira, Z.A.; Cabral, P. Vertical Accuracy Assessment of ALOS PALSAR, GMTED2010, SRTM and Topodata Digital Elevation Models. In Proceedings of the GISTAM, Online, 23–25 April 2021; pp. 116–124. [Google Scholar]
- Stoker, J.; Miller, B. The accuracy and consistency of 3d elevation program data: A systematic analysis. Remote Sens. 2022, 14, 940. [Google Scholar] [CrossRef]
- Zheng, X.; Xiong, H.; Yue, L.; Gong, J. An improved ANUDEM method combining topographic correction and DEM interpolation. Geocarto Int. 2016, 31, 492–505. [Google Scholar] [CrossRef]

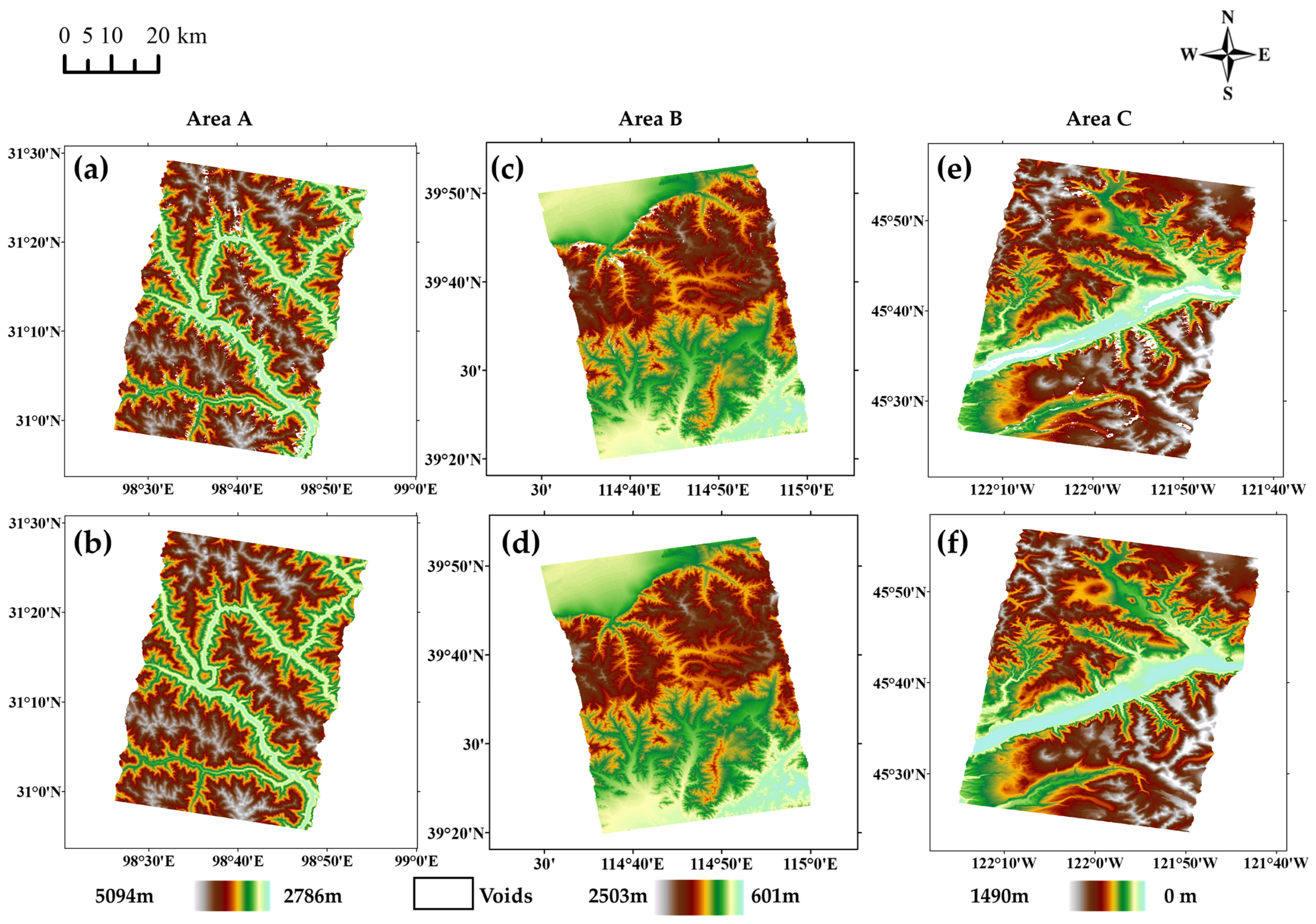


| Location | Landform | Datatype | Data Source | Spatial Resolution | Image Size (Pixels) | Void Pixels | |
|---|---|---|---|---|---|---|---|
| Area A | Sichuan, China | Plateau, bare ground | Raw DEM | TanDEM-X | 10 m | 5538 × 4572 | 654,907 |
| Reference DEM | ALOS PALSAR | 12.5 m | 4430 × 3658 | - | |||
| Area B | Hebei, China | Mountain, low vegetation | Raw DEM | TanDEM-X | 10 m | 6016 × 4818 | 176,085 |
| Reference DEM | ALOS PALSAR | 12.5 m | 4813 × 3854 | - | |||
| Area C | Oregon, America | Mountain, High vegetation | Raw DEM | TanDEM-X | 10 m | 6043 × 4986 | 807,757 |
| Reference DEM | LiDAR | 10 m | 6054 × 6001 | - |
| Raw DEM Voids (%) | Detected Outliers (%) | Reliable Area (%) | |
|---|---|---|---|
| Area 1 | 18.72 | 8.18 | 73.10 |
| Area 2 | 10.74 | 5.94 | 83.32 |
| Area 3 | 16.82 | 17.16 | 66.02 |
| Area 4 | 13.52 | 6.95 | 79.53 |
| Area 5 | 27.66 | 9.97 | 62.37 |
| Area 6 | 18.29 | 11.23 | 70.48 |
| RMSE (m) | Improvement (%) | ||||
|---|---|---|---|---|---|
| IDW | Kriging | DSF | Proposed Method | Compared to DSF | |
| Area 1 | 47.40 | 47.00 | 26.76 | 22.15 | 17.23 |
| Area 2 | 16.18 | 15.80 | 12.82 | 8.73 | 31.90 |
| Area 3 | 46.60 | 46.39 | 38.58 | 18.57 | 51.87 |
| Area 4 | 39.17 | 38.90 | 29.82 | 15.04 | 49.56 |
| Area 5 | 33.75 | 33.10 | 16.65 | 15.34 | 7.87 |
| Area 6 | 23.44 | 23.03 | 19.35 | 17.63 | 8.89 |
| MAE (m) | Improvement (%) | ||||
|---|---|---|---|---|---|
| IDW | Kriging | DSF | Proposed Method | Compared to DSF | |
| Area 1 | 21.98 | 21.77 | 14.18 | 11.14 | 21.44 |
| Area 2 | 9.12 | 8.96 | 7.18 | 5.67 | 21.03 |
| Area 3 | 28.43 | 28.29 | 22.87 | 13.58 | 40.62 |
| Area 4 | 17.44 | 17.39 | 13.24 | 8.48 | 35.95 |
| Area 5 | 20.70 | 20.32 | 13.19 | 12.13 | 8.04 |
| Area 6 | 17.34 | 17.13 | 15.16 | 14.09 | 7.06 |
| MAE of Line 1 (m) | MAE of Line 2 (m) | |||||||
|---|---|---|---|---|---|---|---|---|
| IDW | Kriging | DSF | Proposed Method | IDW | Kriging | DSF | Proposed Method | |
| Area 1 | 42.45 | 42.46 | 20.64 | 14.74 | 35.17 | 35.17 | 6.75 | 5.82 |
| Area 2 | 17.57 | 17.14 | 8.10 | 6.37 | 7.45 | 7.01 | 4.80 | 4.58 |
| Area 3 | 39.94 | 39.78 | 34.70 | 13.80 | 51.72 | 51.72 | 40.25 | 18.57 |
| Area 4 | 38.86 | 38.61 | 27.46 | 8.30 | 22.26 | 22.00 | 16.44 | 10.84 |
| Area 5 | 37.46 | 36.30 | 13.64 | 12.58 | 15.10 | 15.10 | 13.28 | 10.67 |
| Area 6 | 27.60 | 26.81 | 17.85 | 17.29 | 16.29 | 15.47 | 12.69 | 13.30 |
| RMSE (m) | MAE (m) | |
|---|---|---|
| separate large and small voids process | 14.56 | 11.55 |
| unify large and small voids process | 14.72 | 11.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Gui, R.; Hu, J.; Fu, H.; Yuan, Y.; Jiang, K.; Liu, L. InSAR Digital Elevation Model Void-Filling Method Based on Incorporating Elevation Outlier Detection. Remote Sens. 2024, 16, 1452. https://doi.org/10.3390/rs16081452
Hu Z, Gui R, Hu J, Fu H, Yuan Y, Jiang K, Liu L. InSAR Digital Elevation Model Void-Filling Method Based on Incorporating Elevation Outlier Detection. Remote Sensing. 2024; 16(8):1452. https://doi.org/10.3390/rs16081452
Chicago/Turabian StyleHu, Zhi, Rong Gui, Jun Hu, Haiqiang Fu, Yibo Yuan, Kun Jiang, and Liqun Liu. 2024. "InSAR Digital Elevation Model Void-Filling Method Based on Incorporating Elevation Outlier Detection" Remote Sensing 16, no. 8: 1452. https://doi.org/10.3390/rs16081452
APA StyleHu, Z., Gui, R., Hu, J., Fu, H., Yuan, Y., Jiang, K., & Liu, L. (2024). InSAR Digital Elevation Model Void-Filling Method Based on Incorporating Elevation Outlier Detection. Remote Sensing, 16(8), 1452. https://doi.org/10.3390/rs16081452