Spatial Parameter Identification for MIMO Systems in the Presence of Non-Gaussian Interference

Abstract

Reliable identification of spatial parameters for multiple-input multiple-output (MIMO) systems, such as the number of transmit antennas (NTA) and the direction of arrival (DOA), is a prerequisite for MIMO signal separation and detection. Most existing parameter estimation methods for MIMO systems only consider a single parameter in Gaussian noise. This paper develops a reliable identification scheme based on generalized multi-antenna time-frequency distribution (GMTFD) for MIMO systems with non-Gaussian interference and Gaussian noise. First, a new generalized correlation matrix is introduced to construct a generalized MTFD matrix. Then, the covariance matrix based on time-frequency distribution (CM-TF) is characterized by using the diagonal entries from the auto-source signal components and the non-diagonal entries from the cross-source signal components in the generalized MTFD matrix. Finally, by making use of the CM-TF, the Gerschgorin disk criterion is modified to estimate NTA, and the multiple signal classification (MUSIC) is exploited to estimate DOA for MIMO system. Simulation results indicate that the proposed scheme based on GMTFD has good robustness to non-Gaussian interference without prior information and that it can achieve high estimation accuracy and resolution at low and medium signal-to-noise ratios (SNRs).

1. Introduction

The increasing number of wireless devices, together with the requirements for effectiveness and reliability of information transmission, have led to the development of various new communication technologies for addressing unprecedented challenges [1,2,3,4]. Among them, the multiple-input multiple-output (MIMO) technology with sensing capability has been a research hotspot [5]. The self-learning and adaptive abilities of the MIMO system are mainly manifested in the ability to adaptively select the best transmission parameters and modes according to the surrounding communication environment. Nevertheless, the adaptive transmission at the transmitter results in strong randomness of the received signal, which puts forward higher requirements on the signal processing at the receiver [6,7]. Therefore, MIMO signal processing without prior information has great potential. In blind MIMO signal processing, accurate antenna number estimation is the key to blind channel estimation, blind coding recognition, and blind signal demodulation [8]. By estimating the number of transmit antennas (NTA), the exact number of desired users can be obtained, and the users can be effectively regulated to alleviate the interference between them. Direction-of-arrival (DOA) estimation is used to determine the angle and position of the signal from the array of received data [9]. The effective information of the user’s location obtained by DOA estimation is crucial for distinguishing the target user from the interfering users and obtaining accurate and reliable transmission of information. Through the joint estimation of the NTA and the DOA, the desired user information can be accurately distinguished from the background noise/interference by exploiting the different characteristics of spatial information carried by each path, thereby improving the performance of MIMO systems.

To obtain target location through DOA estimation, many algorithms have been proposed, including the beamforming algorithm, maximum likelihood algorithm, multiple signal classification (MUSIC) algorithm, rotation-invariant subspace (ESPRIT) algorithm, and subspace fitting algorithm. By leveraging the characteristics and properties of signal, noise, array structure, etc., these methods greatly enhance the estimation accuracy. In MIMO systems, early DOA estimation can be achieved by beamforming techniques, such as the Capon algorithm [10]. Although this method is simple and feasible, it cannot achieve high-resolution angle estimation. To solve this problem, a series of subspace-based DOA estimation algorithms have been proposed. The classical subspace-based methods include the MUSIC algorithm and ESPRIT algorithm. The improved algorithms based on these two methods have been extensively studied. In [11], Meng et al. combined MUSIC with the quantum algorithm to obtain signal subspace and noise subspace with lower computational complexity. In [12], Karthikeyan et al. investigated one-dimensional ESPRIT, Unitary ESPRIT, and Multidimensional ESPRIT algorithms, and then the simulation results were verified using the universal software radio peripheral network series (USRP-N210). By employing beamforming technology to calculate the phase difference of the received signal as a reference, Kumar et al. presented an improved algorithm that can increase the system capacity and extend ESPRIT to non-orthogonal multiple access MIMO systems [13]. However, all these improvements involve eigenvalue decomposition (EVD) or inversion of the covariance matrix, so they are computationally complex. The propagator method can avoid such operations and improve the estimation performance [14]. In recent years, DOA estimation has also made breakthroughs in many fields. DOA estimation using radar systems equipped with uniform rectangular arrays provides the basis for future urban unmanned aerial vehicle development [15]. Zhang et al. realized super-resolution angle estimation under arbitrary geometric MIMO-EMVS arrays, bringing a new perspective to signal processing [16]. In [17], Liang et al. proposed a novel deep neural network to explore the problem of DOA estimation under strong noise. Zhang et al. also investigated a feasible DOA estimation method in the presence of strong noise interference [18]. In [19], Wen et al. estimated the DOA of a source oriented toward non-line-of-sight propagation in an intelligent reflecting surface-aided wireless communication scenario, which became a major breakthrough in wireless communication.

Most studies on DOA estimation are based on the assumption of Gaussian background interference. However, due to various artificial and physical interference, the actual communication environment may contain complex noise/interference. In the case of colored noise/interference, Cong et al. eliminated the influence of colored noise through generalized noise reconstruction [20]. Chen et al. employed an optimization method similar to minimum variance distortionless response and got a DOA estimation expression based on the mapping between eigenvalues [21]. After eliminating noise, Du et al. derived Bayesian tensor factorization, a fitted real-valued model, and approximate factor matrices, which led to higher estimation accuracy [22]. For impulsive noise/interference, DOA tracking algorithms based on the equivalent covariance matrices constructed by phased fractional moments were proposed in [23,24]. Based on the filtering theory, An et al. proposed an effective pretreatment filtering technology to cut out the impulse mixed in the received data [25]. Su et al. employed a diagonal beam spectrum feature to suppress non-Gaussian noise and enhance array gain [26]. In [27], Gong et al. adopted the infinite norm normalization preprocessing method to alleviate the impact of pulse noise/interference, thus ensuring the performance of the DOA estimation algorithm. Additionally, Dong et al. extended the DOA estimation under impulsive interference to non-circular signal environments [28]. To handle the non-uniform noise/interference, a sparse reconstruction DOA estimation method combining vectorized and reduced signal covariance matrices was proposed in [29]. In [30], Zuo et al. eliminated non-uniform interference by constructing two Toeplitz correlation matrices and achieved higher estimation accuracy.

The aforementioned works relate to DOA estimation. On the other hand, the existing estimation methods for the NTA of MIMO can be mainly divided into two categories: information theoretic criterion (ITC)-based methods [31,32,33] and feature-based methods [34,35,36,37,38,39]. Based on ITC, the problem of estimating the number of transmit antennas is transformed into a model selection problem. Such methods determine the number of transmitting antennas by selecting the minimum Kullback–Leibler length for each candidate model. Somekh et al. determined the number of transmitting antennas in MIMO systems by using the minimum description length and Akaike information criterion [31]. This method does not require setting a threshold subjectively and has low algorithm complexity. Shi et al. developed a method that can adaptively estimate the number of transmit antennas in MIMO systems based on the Schur complementarity test [32]. This method has low computational complexity and does not depend on the number of receive antennas in the MIMO system. Hassan et al. designed two ITC-based algorithms that are insensitive to the spatial correlation of the MIMO channel and can effectively estimate the number of transmit antennas [33]. Feature-based estimation methods use the features extracted from MIMO signals to transform the problem of estimating the number of transmit antennas into a multivariate hypothesis testing problem. Such methods are easier to implement than the methods based on information theory. In [34], a method was proposed to identify the number of base station antennas by using the orthogonality of pilot signals. Since this method needs to estimate the channel parameters and noise power, it has high computational complexity. Mohammadkarim et al. developed a method for estimating the number of transmitting antennas based on high-order statistics [35]. This method has high robustness to frequency offset but requires prior information on noise variance. In [36], two methods were proposed to estimate the number of transmitting antennas based on a covariance matrix. The two methods do not require prior information such as training sequence and noise power. In [37], the eigenvalue of high-order moments was exploited to design an estimation method based on hypothesis testing. In [38], the random matrix theory was used to simultaneously detect the number of antennas and AoAs when a transmitter with multiple antennas is present. Ref. [39] designed a hypothesis-testing algorithm based on stochastic matrix theory for MIMO-OFDM systems. In order to effectively estimate the number of signals within a specific range, the Akaike information criterion and the minimum description length algorithm based on beam space were proposed [40]. Zhao et al. designed a convolutional neural network model based on the mapping relationship between signal covariance matrix and source number and realized the joint estimation of source number and DOA [41]. In a non-Gaussian interference environment, Zhang et al. adopted a clustering algorithm based on a generalized correlation matrix to detect the number of transmitted antennas in MIMO systems, avoiding the need for prior information on transmitted signals [42]. Yan et al. established a multi-target off-grid model, which can automatically identify the number of source signals and perform DOA estimation [43].

In most existing works, the NTA and DOA are estimated under the Gaussian noise/ interference. However, non-Gaussian noise/interference is also very prevalent in the actual communication scenario, such as atmospheric noise, urban noise, and environmental noise in shallow sea acoustic communication. These noises have serious trailing characteristics in their probability distribution, so they do not completely obey the Gaussian distribution [44]. The existing works suffer from degraded performance or even become invalid in non-Gaussian noise/interference. Therefore, non-Gaussian noise/interference poses a great challenge to the estimation of the NTA and DOA. Consequently, this paper investigates the joint estimation of the NTA and DOA for a MIMO system with non-Gaussian noise/interference.

To realize a joint estimation of the NTA and DOA in Gaussian noise and non-Gaussian interference, a reliable estimation method is presented using the generalized multi-antenna time-frequency distribution (GMTFD) matrix. The GMTFD matrix is constructed based on the analysis of the generalized correlation matrix, and the joint estimation method is designed by using the quasi-covariance matrix from the GMTFD matrix. The main contributions of the proposed method are as follows:

• The proposed method introduces a new generalized correlation matrix, constructs a GMTFD matrix, analyzes the characteristics of the GMTFD matrix, characterizes the covariance matrix, and establishes a quasi-covariance matrix by using the GMTFD matrix.
• The similarity transformation of the quasi-covariance matrix is conducted based on the Gerschgorin disk criterion, and the objective function is constructed based on the radius and eigenvalues of the Gerschgorin disk to determine the number of transmit antennas in the MIMO system.
• Signal subspace and noise subspace are obtained by EVD of the quasi-covariance matrix, and the DOA estimation is carried out using the subspace method.
• The proposed method does not require prior information, such as channel coefficient, noise power, interference power, etc., and it can realize the joint estimation of the NTA and DOA for a MIMO system in the presence of Gaussian noise and non-Gaussian interference.

2. System Model

Consider a MIMO system equipped with $M_t$ antennas at the transmitting terminal and $M_r$ antennas at the receiving terminal ($M_r>M_t$). Assume that there are $M_t$ far-field, narrow-band, incoherent signals. The baseband modulation is M-PSK (phase shift keying) or M-QAM (quadrature amplitude modulation) ($M\ge 4$). Let the signal wavelength be $\lambda$ and the speed of light be c. Then, the time delay $\Delta t$ between adjacent receive antennas can be expressed as

$$\Delta t=\frac{dcos{\theta }_{m_t}}{c},$$

(1)

where d represents the distance between any two adjacent antennas, ${\theta }_{m_t}$ denotes the nominal azimuth DOA for the $m_t$-th signal, and ${\theta }_{m_t}\in (0,\pi )$, $m_t=1,2,\dots ,M_t$. Taking the origin of the receive antennas as the reference point, the time delay $\Delta t$ between each receive antenna and the reference point is defined as

$$\Delta t=\left[0,\frac{dcos{\theta }_{m_t}}{c},\frac{2dcos{\theta }_{m_t}}{c},\cdots ,\frac{(M_r-1)dcos{\theta }_{m_t}}{c}\right].$$

(2)

The time delay $\Delta t$ of these adjacent receive antennas can be converted into the phase shift as

$$e^{-j\omega \Delta t}=e^{-j2\pi \left(\frac{d}{\lambda }\right)cos{\theta }_{m_t}}.$$

(3)

Then, the phase shift between each receive antenna and the reference point is expressed as

$$\Delta \phi =\left[0,e^{-j2\pi \left(\frac{d}{\lambda }\right)cos{\theta }_{m_t}},e^{-j2\pi \left(\frac{2d}{\lambda }\right)cos{\theta }_{m_t}},\cdots ,e^{-j2\pi \left(\frac{(M_r-1)d}{\lambda }\right)cos{\theta }_{m_t}}\right].$$

(4)

Moreover, the signal of the m-th receive antenna at time instant t can be represented as

$$y_m\left(t\right)=\sum _{k=1}^{M_t}{h}_k{s}_k\left(t\right)e^{-j2\pi \left(\frac{(m-1)d}{\lambda }\right)cos\left({\theta }_k\right)}+Z_m\left(t\right)+w_m\left(t\right),$$

(5)

where $s_k\left(t\right)$, $Z_m\left(t\right)$, and $w_m\left(t\right)$ denote the signal transmitted, the non-Gaussian interference, and the additive Gaussian white noise (AWGN), respectively, and $h_k$ is the propagation attenuation coefficient of the k-th transmit signal. Therefore, the array output observed at time instant t can be represented as

$$\begin{array}{cc}\hfill \mathbf{y}\left(t\right)& =\sum _{k=1}^{M_t}{h}_k{s}_k\left(t\right)\mathbf{a}\left({\theta }_k\right)+\mathbf{Z}\left(t\right)+\mathbf{w}\left(t\right)\hfill \\ \hfill & =\mathbf{A}\tilde{\mathbf{s}}\left(t\right)+\mathbf{Z}\left(t\right)+\mathbf{w}\left(t\right),\hfill \end{array}$$

(6)

where $\tilde{\mathbf{s}}\left(t\right)={\left[h_1{s}_1\left(t\right),h_2{s}_2\left(t\right),\dots ,h_{M_t}{s}_{M_t}\left(t\right)\right]}^T$ denotes the source matrix, ${(·)}^T$ denotes the matrix transpose, $h_1,h_2,...,h_{M_t}$ is the signal propagation attenuation coefficient, and $\mathbf{Z}\left(\mathbf{t}\right)$ is the $M_r\times 1$ non-Gaussian interference vector. The alpha-stable distribution is employed to model non-Gaussian interference, $\mathbf{w}\left(\mathbf{t}\right)$ is the $M_r\times 1$ additive Gaussian noise vector, and $\mathbf{A}$ is the array steering vector as follows:

$$\begin{array}{cc}\hfill \mathbf{A}& =\left[\mathbf{a}\left({\theta }_1\right),\mathbf{a}\left({\theta }_2\right),\dots ,\mathbf{a}\left({\theta }_{M_t}\right)\right]\hfill \\ \hfill & =\left[\begin{array}{ccc}1& \cdots & 1\\ e^{(-j2\pi d/\lambda )cos{\theta }_1}& \cdots & e^{(-j2\pi d/\lambda )cos{\theta }_{M_t}}\\ ⋮& ⋮& ⋮\\ e^{(-j2\pi d/\lambda )\left(M_r-1\right)cos{\theta }_1}& \cdots & e^{(-j2\pi d/\lambda )\left(M_r-1\right)cos{\theta }_{M_t}}\end{array}\right].\hfill \end{array}$$

(7)

3. Generalized MTFD Matrix Construction

Most of the existing NTA and DOA estimation methods rely on the second-order statistical characteristics of the received signal, such as the covariance matrix and the time-frequency distribution matrix. However, in non-Gaussian interference, a large amount of impulsive interference makes the variance of the received signal go to infinity, especially the impulsive interference characterized by $\alpha$-stable distribution [45]. This interference does not have a finite second-order moment, and its covariance matrix is unbounded, which degrades the performance of the methods using the covariance or time-frequency distribution. To solve the above problems, a generalized MTFD matrix is introduced to characterize the spatial feature information of the received signal under non-Gaussian interference, so as to realize the effective estimation of NTA and DOA.

Generalized MTFD is a 3D array containing time, frequency, and space, which uses the $(t,f)$ information between antennas at different spatial positions to characterize a set of communication signals and their interrelations under non-Gaussian interference [46]. Given that the generalized MTFD is an extension of the generalized TFD in the spatial domain, we first define the generalized TFD here. For the received signal $y_i\left(t\right)$ on the i-th antenna, the Wigner–Ville distribution (WVD) is the Fourier transform (FT) of its instantaneous generalized autocorrelation function $K_{y_i}(t,\tau )$,

$$W_{y_i}(t,f)=\underset{\tau \to f}{F}\left\{K_{y_i}(t,\tau )\right\}={\int }_{\mathbb{R}}{K}_{y_i}(t,\tau )e^{-j2\pi f\tau }d\tau ,$$

(8)

where $K_{y_i}(t,\tau )$ is defined as

$$K_{y_i}(t,\tau )=\mathbb{E}\left\{\psi \left[y_i\left(t+\frac{\tau }{2}\right)\right]\psi \left[y_i^{†}\left(t-\frac{\tau }{2}\right)\right]\right\},$$

(9)

and where $\psi \left[y_i\left(t\right)\right]=exp\left(\frac{{\left|y_i\left(t\right)\right|}^p}{J}\right)(1\le p\le 2)$ is a nonlinear transformation, ${(·)}^{*}$ represents the conjugation operation, and J is the compression factor.

However, the WVD uses bilinear transformation instead of linear transformation, which will generate serious cross-terms when processing multi-component signals. These undesirable cross-terms can be minimized by convolving WVD with the associated 2D-TF kernel [47], which can be expressed as

$${\rho }_{y_i}(t,f)=W_{y_i}{(t,f)}_{\underset{tf}{**}}\gamma (t,f),$$

(10)

where ${\rho }_{y_i}(t,f)$ represents quadratic generalized TFD, $\underset{tf}{**}$ denotes double convolution, and $\gamma (t,f)$ is a 2D smooth kernel of t and f used to reduce cross-terms generated during WVD processing. After replacing a convolution with a signal delay, one has

$${\rho }_{y_i}(t,f)=\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}{K}_{y_i}(t,\tau )\right\},$$

(11)

where $R(t,\tau )$ is the delay kernel function of generalized TFD and is defined as the inverse FT of $\gamma (t,f)$. It is expressed as follows:

$$R(t,\tau )={\underset{f\to \tau }{F}}^{-1}\left\{\gamma (t,f)\right\}={\int }_{\mathbb{R}}\gamma (t,f)e^{j2\pi \tau f}df.$$

(12)

It can be seen from the above analysis that generalized TFD is obtained by the FT of convolution of the delay kernel function and the generalized autocorrelation function, which is similar to traditional TFD. As mentioned before, generalized MTFD is an extension of generalized TFD, which means it can be defined by the delay kernel function and the generalized time-dependent correlation matrix. The generalized time-dependent correlation matrix can be represented as

$$\begin{array}{cc}\hfill {\mathbf{G}}_{\mathbf{y}\mathbf{y}}(t,\tau )& =\mathbb{E}\left\{\overleftrightarrow{\mathbf{y}}\left(t+\frac{\tau }{2}\right){\overleftrightarrow{\mathbf{y}}}^{†}\left(t-\frac{\tau }{2}\right)\right\}\hfill \\ \hfill & \simeq \mathbf{A}{\Sigma }_{\mathrm{G}}(t,\tau ){\mathbf{A}}^{†}+{\varpi }_{\mathrm{G}}^2\delta \left(t\right)\mathbf{I},\hfill \end{array}$$

(13)

where ${\Sigma }_{\mathrm{G}}(t,\tau )$ is the generalized signal correlation matrix, and ${\varpi }_{\mathrm{G}}^2\mathbf{I}$ is the generalized interference correlation matrix.

We note that only when ${\mathbf{G}}_{\mathbf{y}\mathbf{y}}(t,\tau )$ is bounded can the generalized MTFD effectively suppress non-Gaussian interference. Therefore, we give the proof of the boundedness of ${\mathbf{G}}_{\mathbf{y}\mathbf{y}}(t,\tau )$.

Theorem 1.

If the generalized time-dependent correlation matrix ${\mathbf{G}}_{\mathbf{y}\mathbf{y}}(t,\tau )$ is bounded, the $(i,m)$-th element of ${\mathbf{G}}_{\mathbf{y}\mathbf{y}}(t,\tau )$ is bounded, which can be represented as

$$-\infty <G_{im}=\mathbb{E}\left\{\frac{y_i(t+\frac{\tau }{2})y_m^{*}(t-\frac{\tau }{2})}{\psi \left[y_i(t+\frac{\tau }{2})\right]\psi \left[y_m(t-\frac{\tau }{2})\right]}\right\}<\infty .$$

(14)

Proof. 

See Appendix A.  □

Given that ${\mathbf{G}}_{\mathbf{y}\mathbf{y}}(t,\tau )$ is bounded, based on the extended Wiener–Khintchine theorem, the generalized MTFD of the received signal can be estimated as the FT of the time-varying generalized correlation matrix, which can be expressed as

$$\begin{array}{cc}\hfill {\mathit{\rho }}_{yy}(t,f)& =\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}{\mathbf{G}}_{\mathbf{y}\mathbf{y}}(t,\tau )\right\}\hfill \\ \hfill & =\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}\left(\mathbf{A}{\Sigma }_{\mathrm{G}}(t,\tau ){\mathbf{A}}^{†}+{\varpi }_{\mathrm{G}}^2\delta \left(\tau \right)\mathbf{I}\right)\right\}.\hfill \end{array}$$

(15)

Based on the linear property and the convolution operation of FT, the generalized MTFD of the received signal can be expressed as

$${\mathit{\rho }}_{yy}(t,f)=\mathit{A}\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}{\Sigma }_{\mathbf{G}}(t,\tau )\right\}{\mathit{A}}^{†}+{\varpi }_{\mathrm{G}}^2\mathit{I}\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}{\delta }_{(}\tau )\right\}.$$

(16)

The expansion form of the generalized MTFD of the received signal can be expressed as

$$\begin{array}{cc}\hfill {\mathit{\rho }}_{yy}(t,f)& =\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}{\mathbf{G}}_{\mathbf{y}\mathbf{y}}(t,\tau )\right\}\hfill \\ \hfill & =\begin{array}{c}\hfill \left[\begin{array}{cccc}{\rho }_{y_1,y_1}(t,f)& {\rho }_{y_1,y_2}(t,f)& \cdots & {\rho }_{y_1,y_{M_r}}(t,f)\\ {\rho }_{y_2,y_1}(t,f)& {\rho }_{y_2,y_2}(t,f)& \cdots & {\rho }_{y_2,y_{M_r}}(t,f)\\ ⋮& ⋮& ⋮& ⋮\\ {\rho }_{y_{M_r,y_1}}(t,f)& {\rho }_{y_{M_r},y_2}(t,f)& \cdots & {\rho }_{y_{M_r},y_{M_r}}(t,f)\end{array}\right].\end{array}\hfill \end{array}$$

(17)

In the generalized MTFD matrix, the diagonal terms are the generalized auto-TFD terms of the signal, which are defined as

$${\rho }_{y_i,y_i}(t,f)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }R(t-\xi ,\tau ){\overleftrightarrow{y}}_i\left(\xi +\frac{\tau }{2}\right){\overleftrightarrow{y}}_i^{*}\left(\xi -\frac{\tau }{2}\right)e^{-j2\pi \tau f}d\xi dt.$$

(18)

The non-diagonal terms are the generalized cross-TFD terms of the signal and are defined as

$${\rho }_{y_i,y_j}(t,f)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }R(t-\xi ,\tau ){\overleftrightarrow{y}}_i\left(\xi +\frac{\tau }{2}\right){\overleftrightarrow{y}}_j^{*}\left(\xi -\frac{\tau }{2}\right)e^{-j2\pi \tau f}d\xi dt.$$

(19)

Therefore, the diagonal and off-diagonal entries of the signal-generalized MTFD matrix play the roles of autocorrelation and cross-correlation, respectively.

The generalized MTFD extends the noise power in the $(t,f)$ while focusing on the source signal power within the instantaneous bandwidth. By replacing the generalized correlation matrix of the signal with ${\mathbf{G}}_{\mathbf{y}\mathbf{y}}(t,\tau )$ and by defining ${\mathit{\rho }}_{yy}(t,f)$, the generalized MTFD matrix can be employed to characterize the signal covariance matrix to make it adapt to many traditional second-order-based array processing methods [48].

To reduce the computational complexity, only the effective information of the generalized MTFD matrix is used to extract the transmitted signal information. Specifically, the TF points $(t_s,f_s)$ with sufficient energy are selected through threshold processing, and the points with negligible energy are eliminated [46]. This process can be expressed as

$$Keep(t_s,f_s)if∥{\mathit{\rho }}_{yy}\left(t_s,f_s\right)∥>\epsilon ,$$

(20)

where $\epsilon$ denotes the selection threshold, typically, $\epsilon =5\%$ of the points with maximum energy [49]. It is defined as a parameter related to the generalized auto-TFD terms of the signal

$$\epsilon \ge 0.05\times max\left({\rho }_{\mathrm{avg}}\right),$$

(21)

where ${\rho }_{avg}$ is the average of the generalized auto-TFD terms of the signal, and it is expressed as

$${\rho }_{\mathrm{avg}}(t,f)=\frac{1}{M_r}\sum _{i=1}^{M_r}{\rho }_{y_i{y}_i}(t,f).$$

(22)

Based on the effective TF points of the generalized MTFD matrix selected by Equation (20), the quasi-covariance matrix of the signal is constructed as

$${\widehat{\mathit{\rho }}}_{yy}(t,f)=\frac{1}{n}\sum _{i=1}^n{\rho }_{yy}\left(t_i,f_i\right),$$

(23)

where n represents the number of selected TF points.

Compared with the traditional signal covariance matrix, the quasi-covariance matrix reduces interference and improves the algorithm’s performance by selecting the high-energy TF points.

4. Joint Estimation Based on the Generalized MTFD Matrix

4.1. Estimation of the Number of Transmit Antennas

In this paper, the number of antennas is estimated using the radius of the Gerschgorin disk. Firstly, similarity transformation is performed on the quasi-covariance matrix ${\widehat{\mathit{\rho }}}_{yy}(t,f)$ to obtain the radius of the Gerschgorin disk of ${\widehat{\mathit{\rho }}}_{yy}(t,f)$. Then, the number of transmit antennas is estimated by constructing the objective function based on the radius of the Gerschgorin disk. As previously mentioned, the expansion of the quasi-covariance matrix can be expressed as

$$\begin{array}{cc}\hfill & {\widehat{\mathit{\rho }}}_{yy}(t,f)=\left[\begin{array}{cccc}{\widehat{\rho }}_{y_1,y_1}(t,f)& {\widehat{\rho }}_{y_1,y_2}(t,f)& \cdots & {\widehat{\rho }}_{y_1,y_{M_r}}(t,f)\\ {\widehat{\rho }}_{y_2,y_1}(t,f)& {\widehat{\rho }}_{y_2,y_2}(t,f)& \cdots & {\widehat{\rho }}_{y_2,y_{M_r}}(t,f)\\ ⋮& ⋮& ⋮& ⋮\\ {\widehat{\rho }}_{y_{M_r,y_1}}(t,f)& {\widehat{\rho }}_{y_{M_r},y_2}(t,f)& \cdots & {\widehat{\rho }}_{y_{M_r},y_{M_r}}(t,f)\end{array}\right].\hfill \end{array}$$

(24)

Firstly, the quasi-covariance matrix is divided into blocks to obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\widehat{\mathit{\rho }}}_{yy}(t,f)& =\left[\begin{array}{cccc}{\widehat{\rho }}_{y_1,y_1}(t,f)& {\widehat{\rho }}_{y_1,y_2}(t,f)& \cdots & {\widehat{\rho }}_{y_1,y_{M_r}}(t,f)\\ {\widehat{\rho }}_{y_2,y_1}(t,f)& {\widehat{\rho }}_{y_2,y_2}(t,f)& \cdots & {\widehat{\rho }}_{y_2,y_{M_r}}(t,f)\\ ⋮& ⋮& ⋮& ⋮\\ {\widehat{\rho }}_{y_{M_r,y_1}}(t,f)& {\widehat{\rho }}_{y_{M_r},y_2}(t,f)& \cdots & {\widehat{\rho }}_{y_{M_r},y_{M_r}}(t,f)\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}{\widehat{\mathit{\rho }}}_1(t,f)& \widehat{\rho }\\ {\widehat{\rho }}^{†}& {\widehat{\mathit{\rho }}}_{M_r{M}_r}(t,f)\end{array}\right],\hfill \end{array}\end{array}$$

(25)

where $\widehat{\rho }$ is a vector formed by the first $M_r-1$ elements of the $M_r$-th column of the quasi-covariance matrix ${\widehat{\mathit{\rho }}}_{yy}(t,f)$, and ${\widehat{\mathit{\rho }}}_1(t,f)$ is a square matrix consisting of the first $M_r-1$ rows and the first $M_r-1$ columns of the matrix ${\widehat{\mathit{\rho }}}_{yy}(t,f)$. This implies that ${\widehat{\mathit{\rho }}}_1(t,f)$ is the sequential principal minor of ${\widehat{\mathit{\rho }}}_{yy}(t,f)$. The matrix ${\widehat{\mathit{\rho }}}_1(t,f)$ can be further expressed as

$${\widehat{\mathit{\rho }}}_1(t,f)={\mathbf{U}}_1{\mathbf{\Lambda }}_1{\mathbf{U}}_1^{†},$$

(26)

where ${\mathbf{\Lambda }}_1$ is a diagonal matrix composed of eigenvalues

$${\mathbf{\Lambda }}_1=diag\left({\mu }_1,{\mu }_2,{\mu }_3,\cdots ,{\mu }_{M_r-1}\right),$$

(27)

and where ${\mathbf{U}}_1$ is a unitary matrix composed of eigenvectors of ${\widehat{\mathit{\rho }}}_1(t,f)$

$${\mathbf{U}}_1=\left[{\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3,\cdots ,{\mathbf{u}}_{M_r-1}\right].$$

(28)

The eigenvalues of the quasi-covariance matrix ${\widehat{\mathit{\rho }}}_{yy}(t,f)$ and its block matrix ${\widehat{\mathit{\rho }}}_1(t,f)$ satisfy the relationship

$${\ell }_1\ge {\mu }_1\ge {\ell }_2\ge {\mu }_2\ge \cdots \ge {\ell }_{M_r-1}\ge {\mu }_{M_r-1}\cdots \ge {\ell }_{M_r},$$

(29)

where ${\ell }_1\ge {\ell }_2\cdots \ge {\ell }_{M_r}$ represent the eigenvalues of the matrix ${\widehat{\mathit{\rho }}}_{yy}(t,f)$. Then, the matrix ${\mathbf{U}}_2=\left[\begin{array}{cc}{\mathbf{U}}_1& \mathbf{0}\\ \mathbf{0}& 1\end{array}\right]$ is constructed, and a similar transformation is performed on the quasi-covariance matrix ${\widehat{\mathit{\rho }}}_{yy}(t,f)$ as follows:

$$\begin{array}{cc}\hfill {\widehat{\mathit{\rho }}}_2(t,f)& ={\mathbf{U}}_2^{†}{\widehat{\mathit{\rho }}}_{yy}(t,f){\mathbf{U}}_2\hfill \\ \hfill & =\left[\begin{array}{cc}{\mathbf{\Lambda }}_1& {\mathbf{U}}_1^{†}\widehat{\rho }\\ {\widehat{\rho }}^{†}{\mathbf{U}}_1& {\widehat{\rho }}_{M_r{M}_r}(t,f)\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{ccccc}{\mu }_1& 0& \cdots & 0& {\rho }_1\\ 0& {\mu }_2& \cdots & 0& {\rho }_2\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & {\mu }_{M_r-1}& {\rho }_{M_r-1}\\ {\rho }_1^{*}& {\rho }_2^{*}& \cdots & {\rho }_{M_r-1}^{*}& {\widehat{\rho }}_{y_{M_r},y_{M_r}}(t,f)\end{array}\right].\hfill \end{array}$$

(30)

According to the Gerschgorin disk principle, the radius of the i-th Gerschgorin disk can be written as

$$r_i=\left|{\rho }_i\right|.$$

(31)

To scale the radius of the Gerschgorin disk, a diagonal matrix $\mathit{P}$ is constructed as

$$\mathbf{P}=diag\left(b_1,b_2,\cdots ,b_{M_r-1},b_{M_r}\right),$$

(32)

where $b_i=\left|{\ell }_i-{\ell }_{i+1}\right|,\left(i=1,\cdots ,M_r-1\right)$, and $b_{M_r}=\frac{1}{M_r-1}{\sum }_{i=1}^{M_r-1}{b}_i$. Using $\mathit{P}$ to perform a similar transformation on ${\widehat{\mathit{\rho }}}_2(t,f)$ yields

$$\begin{array}{cc}\hfill {\widehat{\mathit{\rho }}}_3(t,f)& =\mathbf{P}{\widehat{\rho }}_2(t,f){\mathbf{P}}^{-1}\hfill \\ \hfill & =\left[\begin{array}{ccccc}{\mu }_1& 0& \cdots & 0& \frac{b_1}{b_{M_r}}{\rho }_1\\ 0& {\mu }_2& \cdots & 0& \frac{b_2}{b_{M_r}}{\rho }_2\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & {\mu }_{M_r-1}& \frac{b_{M_r-1}}{b_{M_r}}{\rho }_{M_r-1}\\ \frac{b_{M_r}}{b_1}{\rho }_1^{*}& \frac{b_{M_r}}{b_2}{\rho }_2^{*}& \cdots & \frac{b_{M_r}}{b_{M_r-1}}{\rho }_{M_r-1}^{*}& {\widehat{\rho }}_{y_{M_r},y_{M_r}}(t,f)\end{array}\right].\hfill \end{array}$$

(33)

Based on matrix theory, ${\widehat{\mathit{\rho }}}_3(t,f)$ is obtained by performing a similar transformation on ${\widehat{\mathit{\rho }}}_2(t,f)$ so that it has the same eigenvalues as ${\widehat{\mathit{\rho }}}_2(t,f)$, and the center of the Gerschgorin disk remains unchanged. However, the radius of the Gerschgorin disk is compressed by a factor of $b_i/b_{M_r}$, which can increase the distance between the noise radius and the signal radius.

According to the above analysis, the objective function based on the Gerschgorin disk criterion is modified as

$$G\left(k\right)=\frac{1}{\frac{1}{M_r-1}{\sum }_{i=1}^{M_r-1}{b}_i}\left(b_k{r}_k-\frac{D_n}{M_r-1}\sum _{i=1}^{M_r-1}{b}_i{r}_i\right),$$

(34)

where $D_n=t_D/ln\left(N/M_r\right)$. The value of $G\left(k\right)$ starts with $k=1$, and the iteration stops when it takes a non-negative value for the first time. The estimation of the number of antennas is obtained as ${\widehat{M}}_t=k-1$.

The method of estimation of the number of transmit antennas is summarized in Algorithm 1.

Algorithm 1: Estimation of the NTA via the GMTFD matrix

Input: The GMTFD matrix ${\mathit{\rho }}_{yy}(t,f)$

1. The effective TF points of the GMTFD matrix are selected by Equation (20).

2. The quasi-covariance matrix ${\widehat{\mathit{\rho }}}_{yy}(t,f)$ is constructed according to Equation (23).

3. Perform a similar transformation on the matrix ${\widehat{\mathit{\rho }}}_{yy}(t,f)$ using Equation (30).

4. Estimate the radius of the Gerschgorin disk according to Equation (31).

5. Use the center of the Gerschgorin disk to compress the radius of the Gerschgorin disk.

Start iteration

6. Construct the objective function based on the Gerschgorin disk criterion according to Equation (34).

7. Update the objective function for $k=k+1$.

8. Until the objective function takes a non-negative value for the first time.

Terminate iteration

Output: ${\widehat{M}}_t=k-1$

4.2. DOA Estimation

In this paper, a subspace algorithm is employed to estimate the DOA of the MIMO signal. Assume that $M_t$ source signals of the system are incoherent, and $M_t$ vectors in the matrix $\mathit{A}$ of the received signal are linear and non-uniform. The DOA estimation of the signal is determined by the characteristic structure of the matrix, so the implementation of DOA estimation requires the EVD of the quasi-covariance matrix.

Let the eigenvalues of matrix ${\widehat{\mathit{\rho }}}_{yy}(t,f)$ be ${\ell }_1\ge {\ell }_2\cdots \ge {\ell }_{M_r}$ and the eigenvalues of matrix $\mathbf{A}\underset{\tau \to f}{F}\left\{\left.R{(t,\tau )}_{\underset{t}{*}}{\Sigma }_{\mathrm{G}}(t,\tau )\right\}{\mathbf{A}}^{†}\right.$ be ${\lambda }_1\ge {\lambda }_2\cdots \ge {\lambda }_{M_r}$. Then, the relationship between ℓ and $\lambda$ can be expressed as ${\ell }_i={\lambda }_i+{\varpi }_{\mathrm{G}}^2\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}\delta \left(\tau \right)\right\}$, $i=1,2,\dots ,M_r$. Since A has full rank, the $M_r-M_t$ smallest eigenvalues of ${\widehat{\mathit{\rho }}}_{yy}(t,f)$ are equal to ${\varpi }_{\mathrm{G}}^2\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}\delta \left(\tau \right)\right\}$, i.e.,

$${\ell }_i=\left\{\begin{array}{c}{\lambda }_i+{\varpi }_{\mathrm{G}}^2\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}\delta \left(\tau \right)\right\}i=1,2,\dots ,M_t\hfill \\ {\varpi }_{\mathrm{G}}^2\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}\delta \left(\tau \right)\right\}i=M_t+1,M_t+2,\dots ,M_r\hfill \end{array}\right..$$

(35)

The EVD of ${\widehat{\mathit{\rho }}}_{yy}(t,f)$ can be simplified as

$$\begin{array}{cc}\hfill {\widehat{\mathit{\rho }}}_{yy}(t,f)=& \sum _{i=1}^{M_t}\left({\lambda }_i+{\varpi }_{\mathrm{G}}^2\mathbf{I}\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}\delta \left(\tau \right)\right\}\right)v_i{v}_i^H\hfill \\ & +\sum _{i=M_t+1}^{M_r}\left({\varpi }_{\mathrm{G}}^2\mathbf{I}\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}\delta \left(\tau \right)\right\}\right)v_i{v}_i^H,\hfill \end{array}$$

(36)

where $v_i^H{v}_j={\delta }_{i,j}$ is the orthogonal eigenvector of ${\widehat{\mathit{\rho }}}_{yy}(t,f)$. Then, we have

$${\widehat{\mathit{\rho }}}_{yy}(t,f)v_i={\varpi }_{\mathrm{G}}^2\mathbf{I}\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}\delta \left(\tau \right)\right\}{v}_i,i=1,2,\dots ,M_r,$$

(37)

which means $({\widehat{\mathit{p}}}_{yy}(t,f)-{\varpi }_{\mathrm{G}}^2\mathbf{I}\underset{\tau \to f}{F}\{R{(t,\tau )}_{\underset{t}{*}}\delta \left(\tau \right)\})v_i=0,i=M_t+1,M_t+2,\dots ,M_r$. The quasi-covariance matrix of the received signal satisfies

$${\widehat{\mathit{p}}}_{yy}(t,f)-{\varpi }_{\mathrm{G}}^2\mathbf{I}\underset{\tau \to f}{F}\left\{R{(t,\tau )}_{\underset{t}{*}}\delta \left(\tau \right)\right\}=\mathbf{A}\underset{\tau \to f}{F}\left\{\left.R{(t,\tau )}_{\underset{t}{*}}{\Sigma }_{\mathrm{G}}(t,\tau )\right\}{\mathbf{A}}^{†}\right.$$

(38)

and

$$\mathbf{A}\underset{\tau \to f}{F}\left\{\left.R{(t,\tau )}_{\underset{t}{*}}{\Sigma }_{\mathrm{G}}(t,\tau )\right\}{\mathbf{A}}^{†}\right.v_i=0,i=M_t+1,M_t+2,\dots ,M_r.$$

(39)

We can obtain

$${\mathbf{A}}^{†}{v}_i=0,i=M_t+1,M_t+2,\dots ,M_r.$$

(40)

This suggests that the subspace spanned by the eigenvectors $v_{M_t+1},v_{M_t+2},\dots ,v_{M_r}$ is orthogonal to the complement subspace spanned by the steering vectors in A.

Therefore, based on the eigenvectors of ${\widehat{\mathit{\rho }}}_{yy}(t,f)$, the steering vectors orthogonal to the noise subspace can be used to estimate the DOA of the signal [46].

4.2.1. MUSIC Algorithm

The MUSIC algorithm exploits the orthogonality of the signal subspace and the noise subspace to find the corresponding signal azimuth angle by constructing an objective function and searching its minimum value. The problem of searching the minimum value is usually transformed into a problem of searching the maximum value by taking the reciprocal form, and the objective function becomes

$$P_{\mathrm{MUSIC}}\left(\theta \right)=\frac{1}{{\sum }_{i=M_t+1}^{M_r}{\left|a\left(\theta \right){\widehat{v}}_i\right|}^2}.$$

(41)

In the MUSIC algorithm, $\theta$ is traversed. Then, the value corresponding to each spectral peak in the MUSIC space spectrum corresponds to the azimuth of a real signal.

The method of DOA estimation based on MUSIC is summarized in Algorithm 2.

Algorithm 2: DOA estimation based on the GMTFD-MUSIC

Input: The GMTFD matrix ${\mathit{\rho }}_{yy}(t,f)$

1. The effective TF points of the GMTFD matrix are selected by Equation (20).

2. The quasi-covariance matrix ${\widehat{\mathit{\rho }}}_{yy}(t,f)$ is constructed according to Equation (23).

3. Do the EVD of ${\widehat{\mathit{\rho }}}_{yy}(t,f)$ according to Equation (36).

4. Obtain the signal subspace and noise subspace according to the descending arrangement of the

eigenvalues.

Start iteration

5. The signal direction $\theta$ is substituted into the spatial spectrum of the original data in turn.

6. Search the spectrum peak to obtain the maximum matching angle as the DOA using Equation (41).

Terminate iteration

Output: $\theta$

4.2.2. ESPRIT Algorithm

For a uniform MIMO antenna array, the adjacent sub-antennas in this array have fixed spacing, which reflects the fixed relationship between the adjacent sub-antennas and represents the rotation invariance between the sub-antennas. The ESPRIT algorithm exploits the rotation invariance between sub-antennas to estimate the DOA of a MIMO system.

The ESPRIT algorithm assumes that there are two identical sub-antenna arrays and that the spacing between them is known. Also, it is assumed that the received signal of the first $M_r-1$ elements in the MIMO array constitutes subarray 1, and the received signal of the next $M_r-1$ elements constitutes subarray 2. Then, the steering vectors of the two sub-antenna arrays satisfy the relationship

$$A_2=A_1\varphi ,$$

(42)

where $\varphi$ is determined by the DOA information of the signals and the relative positions of the two subarrays. EVD is carried out on the signal model of subarray 1 and subarray 2 to obtain the signal subspaces of the two subarrays, respectively. Combined with the rotation invariant relation between two subarrays, we have

$$U_{s2}=U_{s1}\psi .$$

(43)

After the eigenvalues $\{{\psi }_1,{\psi }_2,\dots ,{\psi }_{M_t}\}$ are determined by performing the EVD of $\psi$, the azimuth of the transmit signals can be obtained, which can be expressed as

$${\theta }_k=arccos\frac{j\lambda log{\psi }_k}{2\pi d}.$$

(44)

The method of DOA estimation based on ESPRIT is summarized in Algorithm 3.

Algorithm 3: DOA estimation based on the GMTFD-ESPRIT

Input: The GMTFD matrix ${\mathit{\rho }}_{yy}(t,f)$

1. The effective TF points of the GMTFD matrix are selected by Equation (20).

2. The quasi-covariance matrix ${\widehat{\mathit{\rho }}}_{yy}(t,f)$ is constructed according to Equation (23).

3. Perform the EVD of ${\widehat{\mathit{\rho }}}_{yy}(t,f)$ according to Equation (36).

4. Obtain the eigenvector $v_s$ corresponding to the signal subspace.

5. Take the first $M_t-1$ rows and the last $M_t-1$ rows of $v_s$ to form the matrices $U_{s1}$ and $U_{s2}$,

respectively.

6. Use the least squares method to obtain the transformation matrix $\psi$.

Start iteration

7. Determine the eigenvalue ${\psi }_i$ of $\psi$.

8. Update the estimation of DOA according to Equation (44).

Terminate iteration

Output: $\theta$

4.3. Computational Complexity Analysis

In order to evaluate the efficiency of the proposed algorithm, we analyze its complexity in this subsection. The complexity analysis is shown as:

(1)

The computation complexity of the GMTFD is $O(M_r^2(4L\times logL+L(N-1)+L^2\times logL)+M_r+M_r^2)$, where L is the number of samples.

(2)

The MUSIC computation complexity is $O(M_r^3+M_r^2+M_r+N_{\theta }\times M_r+M_t^2+M_t)$, where $N_{\theta }$ denotes the DOA search scope.

(3)

The ESPRIT computation complexity is $O(M_r^3+M_r\times M_t^2+M_t^3+M_r)$.

(4)

The NTA estimation computation complexity based on the Gerschgorin disk principle is $O(M_r^2+M_r\times M_t^2)$.

From the above analysis, it can be proved that the complexity of the proposed NTA estimation algorithm is $O(M_r^2(4L\times logL+L(N-1)+L^2\times logL)+M_r+2M_r^2+M_r\times M_t^2)$, the complexity of the MUSIC based on the GMTFD is $O(M_r^2(4L\times logL+L(N-1)+L^2\times logL)+2M_r+2M_r^2+M_r^3+N_{\theta }\times M_r+M_t^2+M_t)$, and the complexity of the ESPRIT based on the GMTFD is $O(M_r^2(4L\times logL+L(N-1)+L^2\times logL)+2M_r+M_r^2+M_r^3+M_r\times M_t^2+M_t^3+M_r)$. Numerical analyses show that the proposed NTA and DOA estimation algorithm suffers from high computational complexity after employing GMTFD. However, its performance is significantly enhanced in the presence of non-Gaussian interference.

5. Simulations

5.1. Parameter Settings

This section presents numerical results to analyze the effectiveness and reliability of the proposed estimation method for MIMO systems under different situations. Assume that there are three equal power uncorrelated sources at ${\theta }_1={20}^{\circ }$, ${\theta }_2={40}^{\circ }$, and ${\theta }_3={60}^{\circ }$, respectively. The settings of other simulation parameters are as follows: the modulation mode is QPSK, the signal length is $N=800$, the number of receive antennas is $M_r=8$, the distance between adjacent receive antennas is $d=0.5\lambda$, the wavelength of the MIMO antennas is $\lambda =10$ m, the signal-to-interference ratio (SIR) is 16, the received interference is a mixture of AWGN and non-Gaussian interference, the characteristic index of alpha-stable noise is $\alpha =1.8$, the number of Monte Carlo experiments is denoted by T, and $T=800$. For the performance of NTA identification, the probability of detection $P_d$ is employed as a performance measure, which is defined as

$$P_d=Pr\left[M_t={\widehat{M}}_t\right],$$

(45)

where ${\widehat{M}}_t$ is the estimate of $M_t$. The performance of the DOA estimation is evaluated by the root-mean-square error (RMSE), which is expressed as

$$RMSE=\sqrt{\frac{1}{T{M}_t}{\sum }_{i=1}^T{\sum }_{k=1}^{M_t}{|{\widehat{\theta }}_i\left(k\right)-{\theta }_k|}^2},$$

(46)

where ${\widehat{\theta }}_i\left(k\right)$ represents the k-th target angle measured at time i.

5.2. Simulation Results

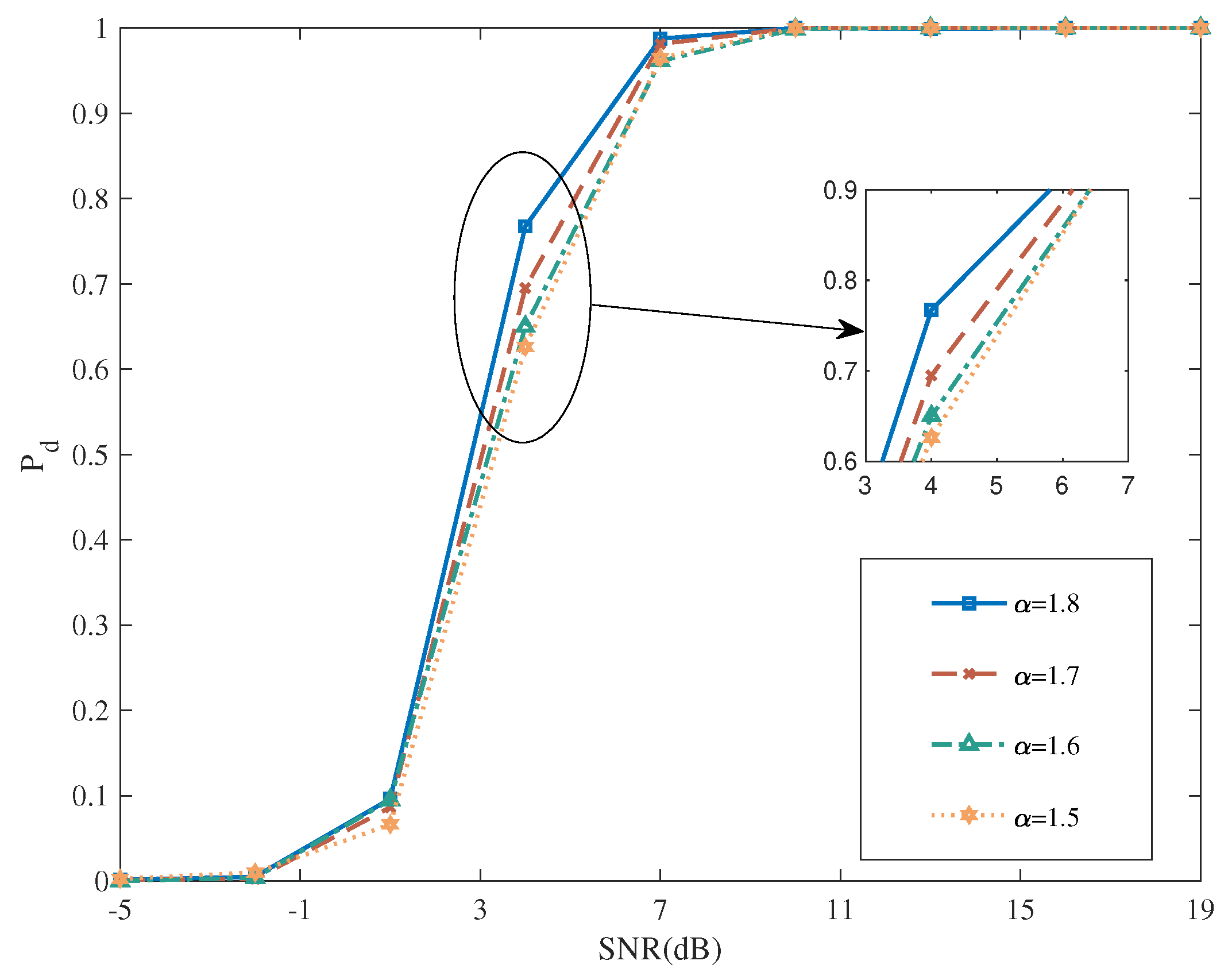
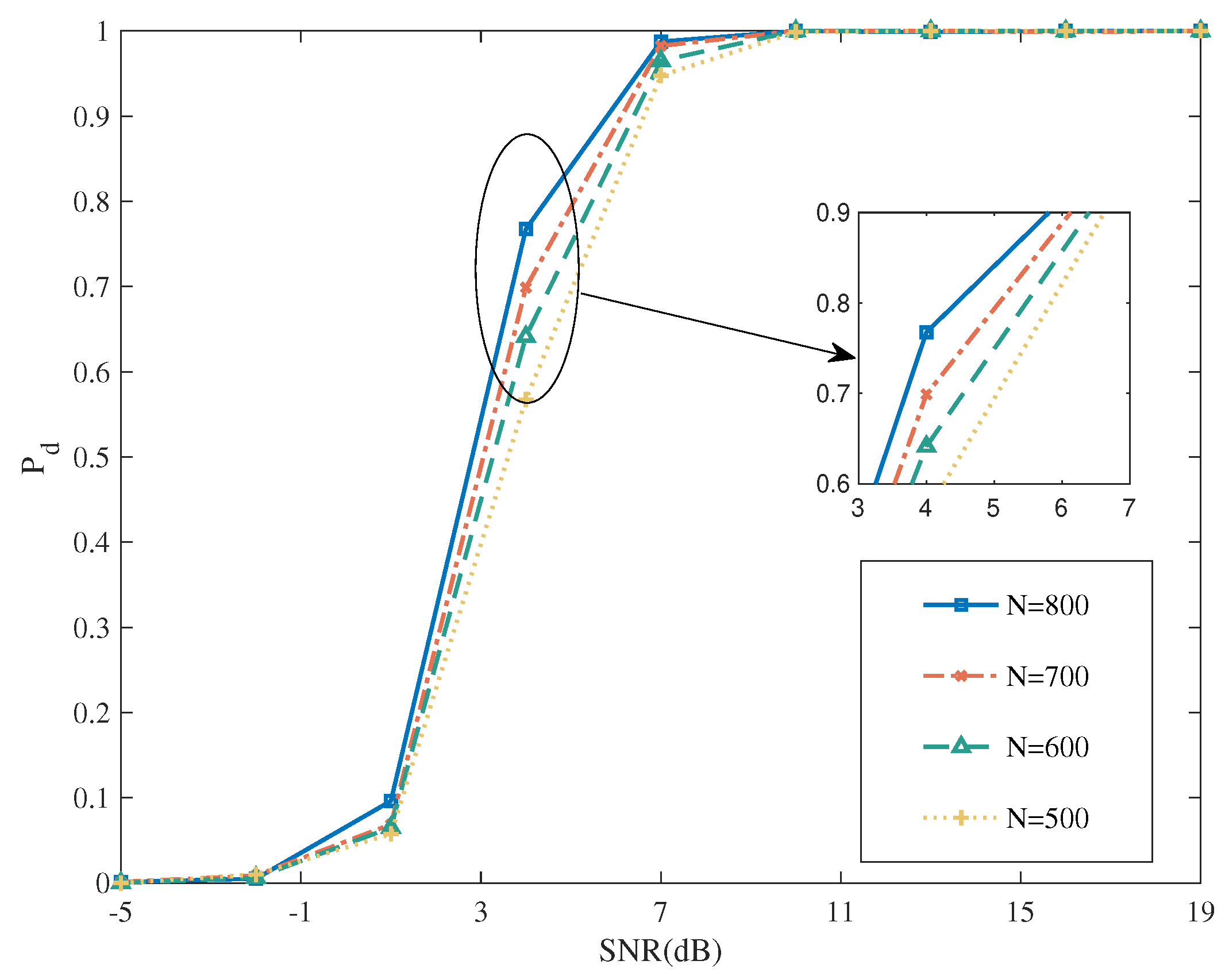
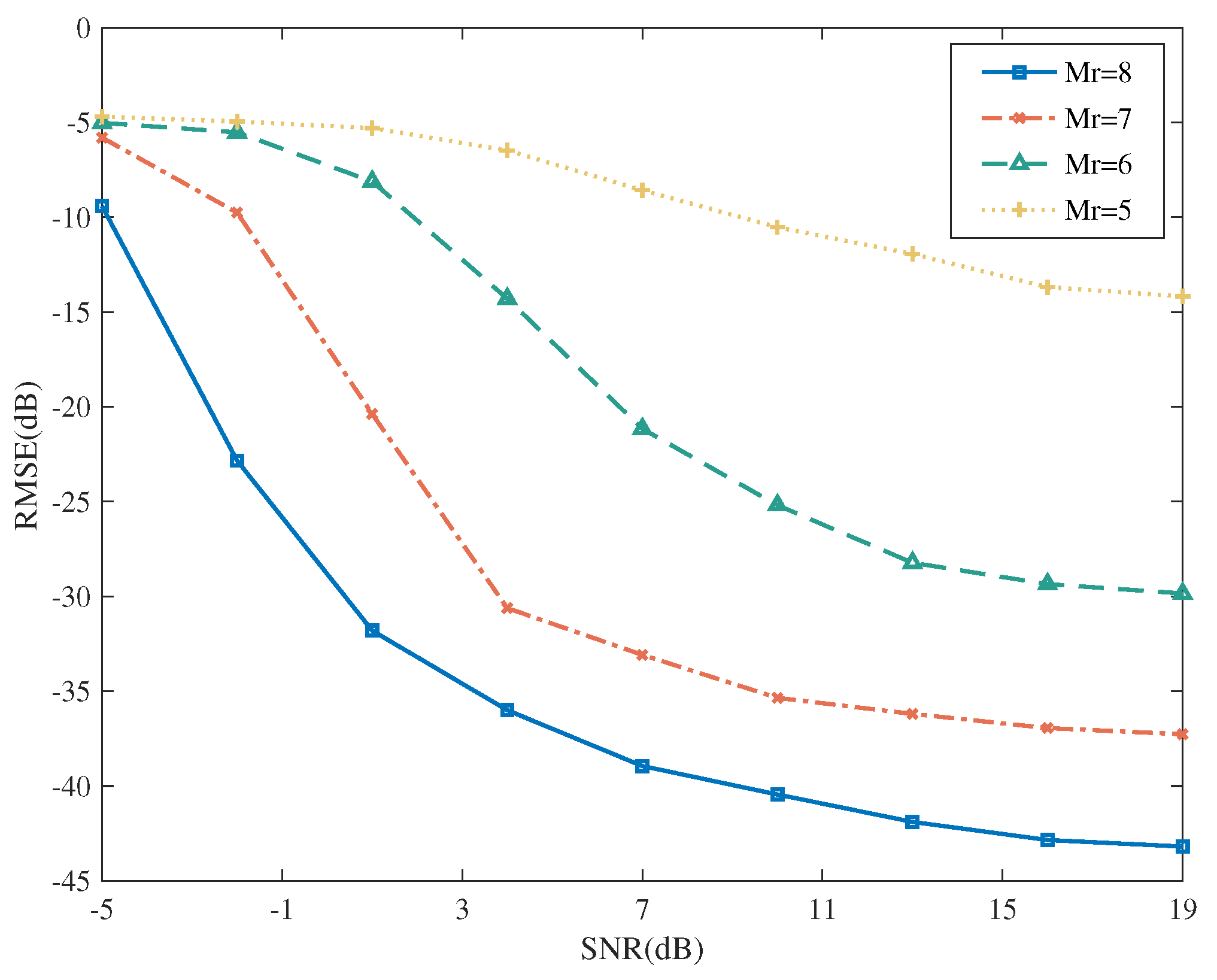
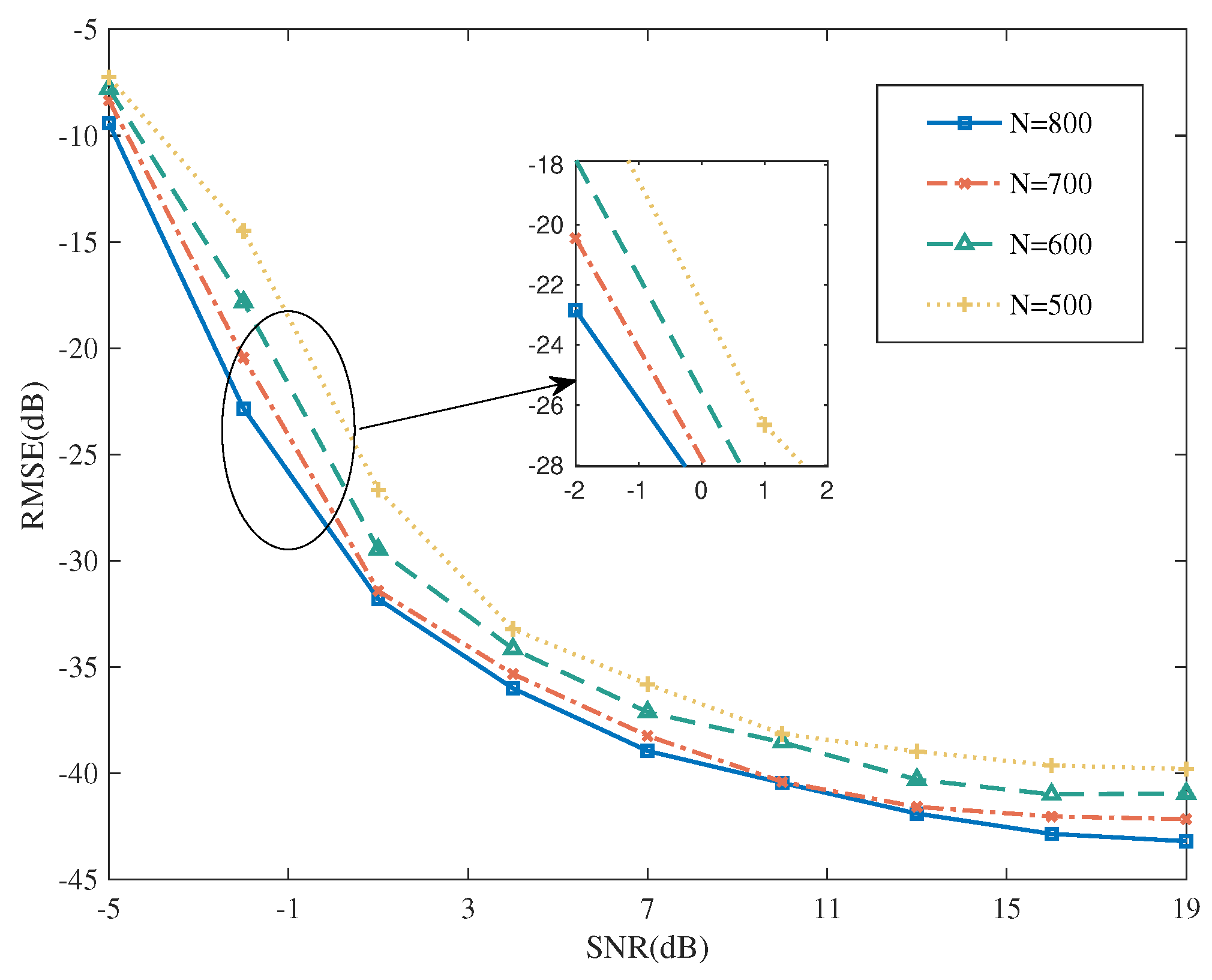
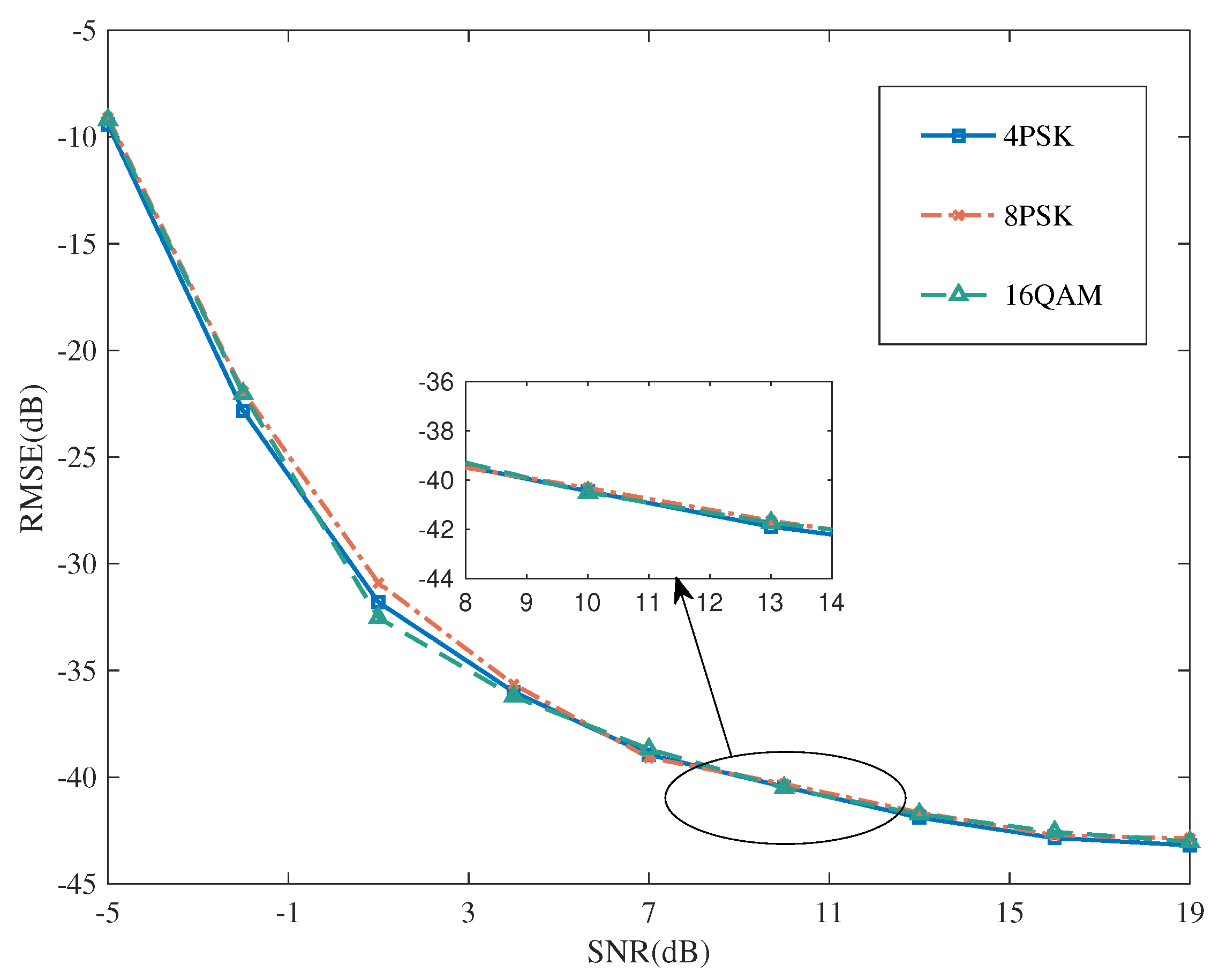
5.2.1. Performance for NTA Estimations

Figure 1 shows the estimation accuracy of the NTA of the proposed method under different settings of the alpha-stable noise interference characteristic index $\alpha$. In the simulation experiment, $N=800$, $M_r=8$, $SIR=16$, the modulation mode is QPSK, and $\alpha =1.8$, $\alpha =1.7$, $\alpha =1.6$, and $\alpha =1.5$ are set sequentially. It can be found from Figure 1 that the estimation performance of the proposed method is continuously improved as the value of $\alpha$ increases. When $\alpha =1.5$ and $SNR=6$ dB, the average estimation accuracy of the NTA is about $80\%$. When the value of $\alpha$ increases to $\alpha =1.8$, the average estimation accuracy of the NTA is more than $90\%$.

Figure 2 presents the influence of signal length on the estimation accuracy of the NTA when $\alpha =1.8$, $M_r=8$, $SIR=16$, and the modulation mode is QPSK. Different signal lengths $N=500$, $N=600$, $N=700$, and $N=800$ are considered. As shown in Figure 2, the estimation performance of the proposed method increases with the signal length N. When $N=500$ and $SNR=6$ dB, the average estimation accuracy of the NTA is about $75\%$. When the value of N increases to $N=800$, the average estimation accuracy of the NTA is more than $90\%$.

Figure 3 shows the estimation accuracy of the NTA under different modulation modes when $\alpha =1.8$, $M_r=8$, $SIR=16$, and $N=800$. It can be observed from Figure 3 that the change in modulation mode does not affect the average estimation accuracy of the proposed method. This is because the proposed method uses the characteristics of a GMTFD matrix to construct detection statistics and thresholds, and the modulation mode does not affect the detection statistics and thresholds. Thus, it does not affect the estimation performance of the proposed method.

Figure 4 presents the performance comparison between the GMTFD-based algorithm proposed in this paper and the WME, SM-PET, and HOM-HT algorithms for the estimation of the NTA under different SNR and SIR, when $\alpha =1.5$, $M_r=8$, $N=800$, and the modulation mode is QPSK. As illustrated in Figure 4, the performance of the WME, SM-PET, and HOM-HT algorithms degrades seriously in non-Gaussian interference, while the GMTFD-based method can effectively estimate the number of antennas, which validates the effectiveness of the proposed algorithm.

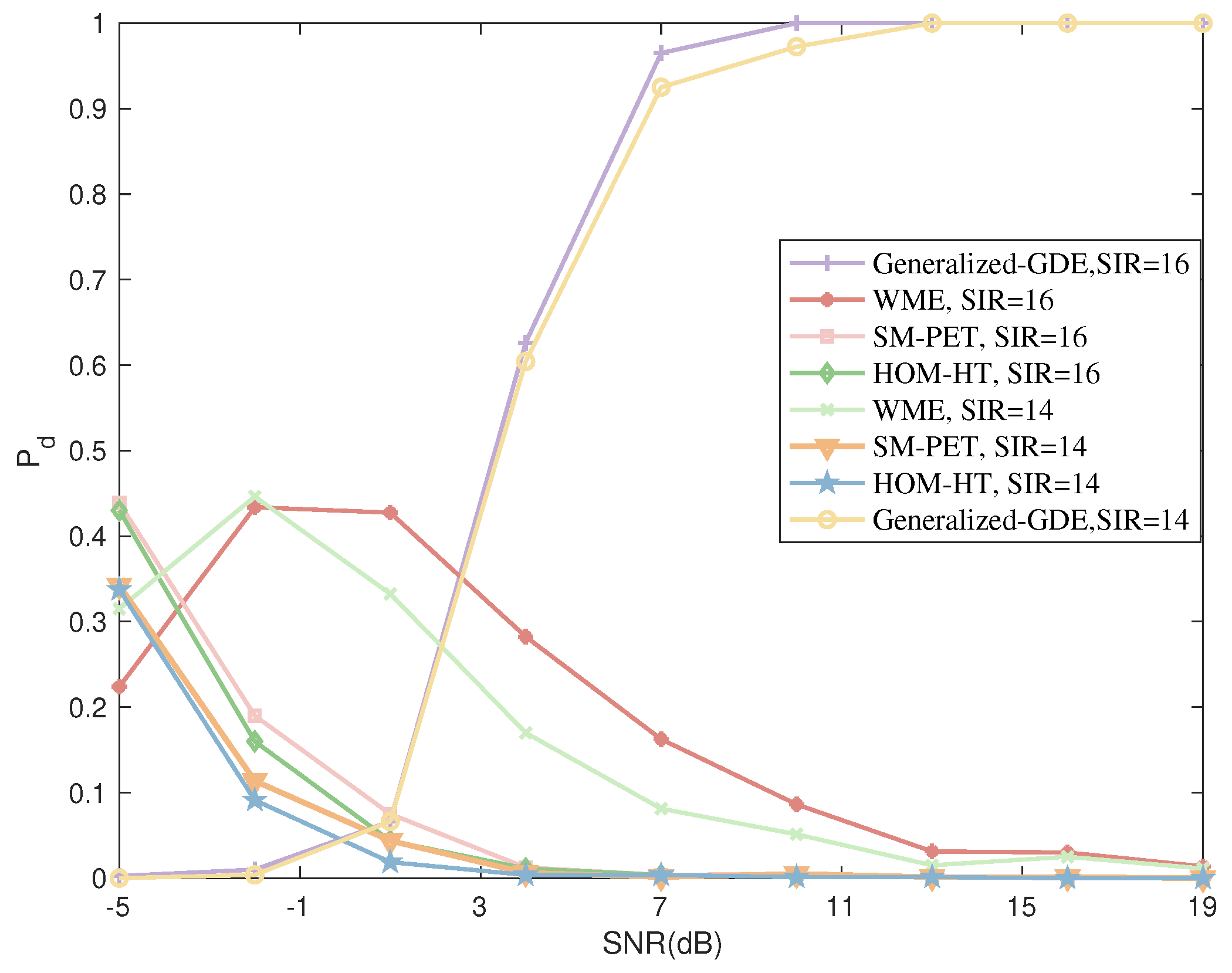
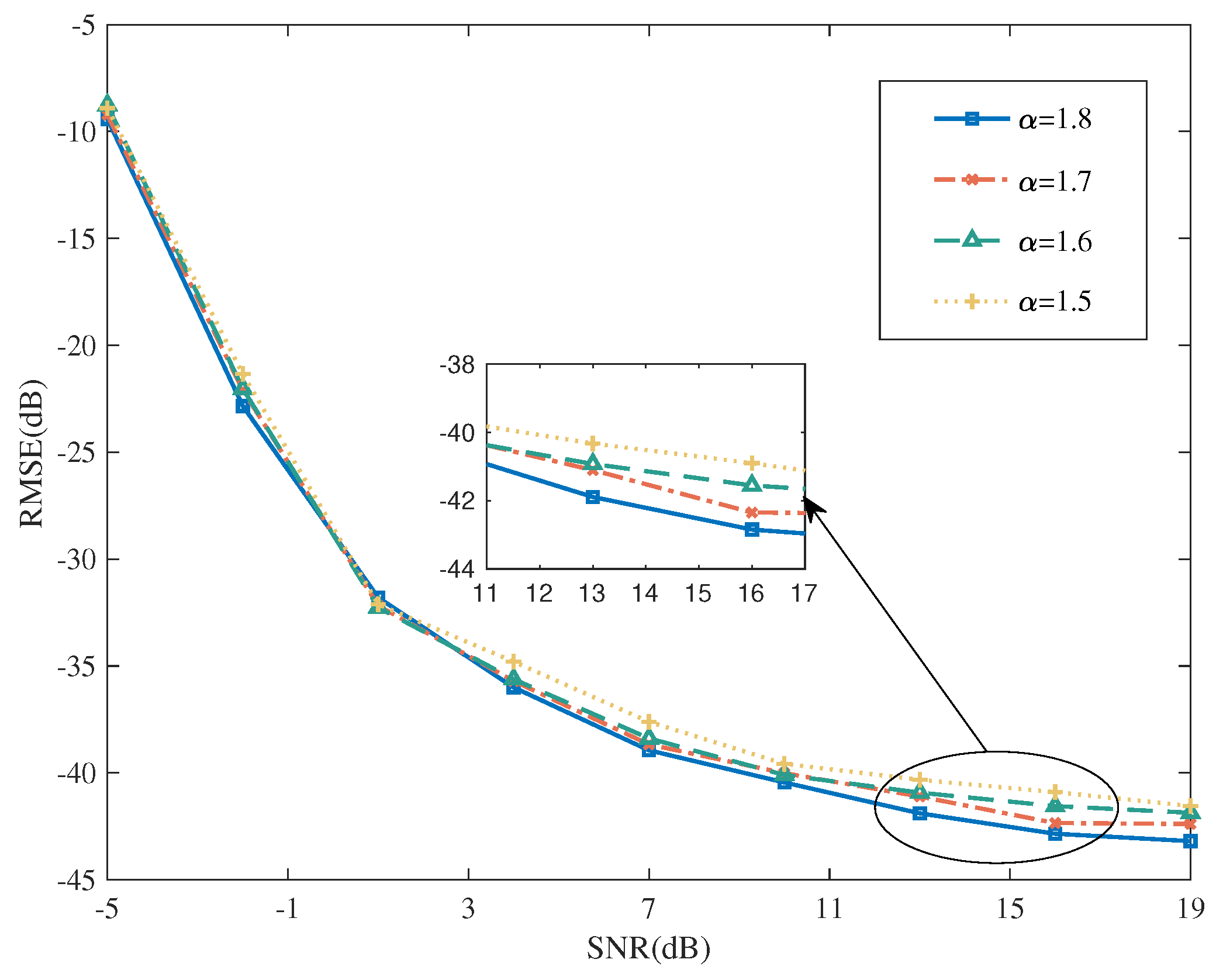
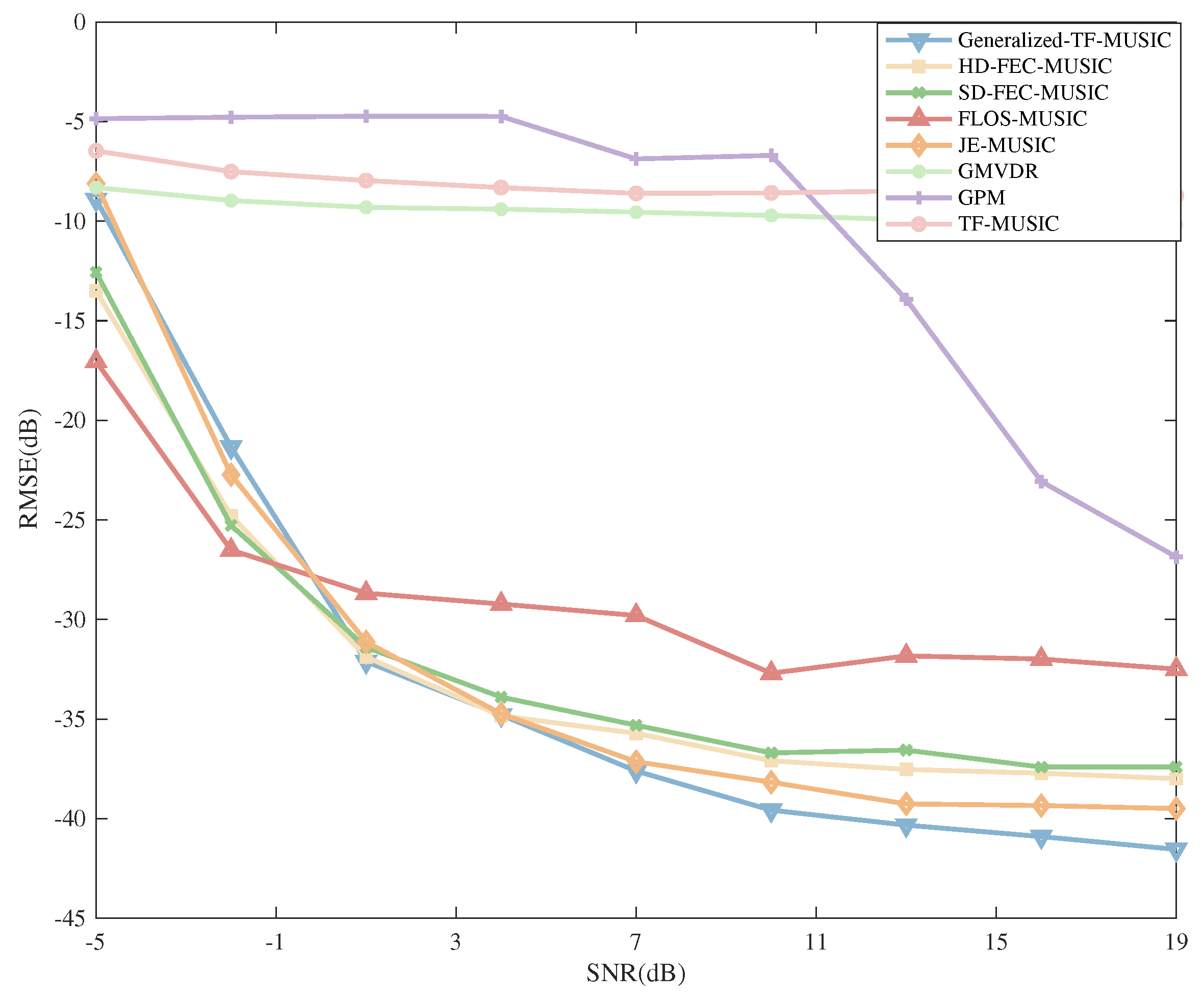
5.2.2. Performance for DOA Estimations

Figure 5 shows the RMSE of the DOA estimation of the proposed method under different settings of the alpha-stable noise interference characteristic index $\alpha$. In the simulation experiment, $N=800$, $M_r=8$, $SIR=16$, the modulation mode is QPSK, and $\alpha =1.8$, $\alpha =1.7$, $\alpha =1.6$, and $\alpha =1.5$ are set sequentially. It can be found from Figure 5 that the estimation performance of the proposed method is continuously improved as the value of $\alpha$ increases. When $\alpha =1.5$ and $SNR=7$ dB, the RMSE of the DOA estimation is about −36 dB. When the value of $\alpha$ increases to $\alpha =1.8$, the RMSE of the DOA estimation is close to −40 dB. This is because, as the value of $\alpha$ becomes larger, the amount of peak pulse interference in the received signal will decrease, which will improve the correlation of the signal, thus affecting the estimation performance.

Figure 6 illustrates the influence of the number of receive antennas on the estimation accuracy of the DOA when $N=800$, $\alpha =1.8$, $SIR=16$, and the modulation mode is QPSK. Different numbers of receive antennas $M_r=5$, $M_r=6$, $M_r=7$, and $M_r=8$ are considered. As shown in Figure 6, the estimation performance of the proposed method increases with the number of receive antennas $M_r$. When $M_r=5$ and $SNR=7$ dB, the RMSE of DOA estimation is about −7 dB. When the value of $M_r$ increases to $M_r=8$, the RMSE of DOA estimation is about −40 dB. As the number of receive antennas $M_r$ increases, the number of generalized correlation matrix elements of the received signal increases, making the statistics closer to the theoretical distribution, thus leading to higher recognition performance.

Figure 7 presents the influence of signal length on the accuracy of DOA estimation when $\alpha =1.8$, $M_r=8$, $SIR=16$, and the modulation mode is QPSK. Different signal lengths $N=500$, $N=600$, $N=700$, and $N=800$ are considered. As shown in Figure 7, the estimation performance of the proposed method increases with the signal length N. When $N=500$ and $SNR=7$ dB, the RMSE of the DOA estimation is about −35 dB. When the value of N increases to $N=800$, the RMSE of the DOA estimation reduces to −40 dB. Similar to the change in the number of receive antennas, as the signal length N increases, the number of generalized correlation matrix elements of the received signal increases, making the statistics closer to the theoretical distribution, thus improving the method’s recognition performance.

Figure 8 shows the estimation accuracy of the DOA under different modulation modes when $\alpha =1.8$, $M_r=8$, $SIR=16$, and $N=800$. It can be observed from Figure 8 that the change in modulation mode does not affect the average estimation accuracy of the proposed method. This is because the proposed method uses the characteristics of a GMTFD matrix to construct detection statistics and thresholds, and the modulation mode does not affect the detection statistics and thresholds. Thus, it does not affect the estimation performance of the proposed method.

Figure 9 presents the performance comparison between the GMTFD-based algorithms proposed in this paper and the traditional MTFD-based algorithms in DOA estimation, when $\alpha =1.8$, $M_r=8$, $SIR=16$, $N=800$, and the modulation mode is QPSK. As illustrated in Figure 9, against the background of non-Gaussian interference, the estimation performance of the Generalized-TF-MUSIC and Generalized-TF-ESPRIT algorithms is better than the TF-MUSIC and TF-ESPRIT algorithms.

We adopted several DOA estimation methods that can deal with non-Gaussian interference to compare with the proposed Generalized-TF-MUSIC in the simulation setup of the DOA estimation. Examples are the generalized propagator algorithm (GPM), generalized beamforming algorithm (GMVDR), MUSIC based on correlation entropy (JE-MUSIC), fractional low order MUSIC (FLOS-MUSIC), MUSIC based on soft decision/hard decision (SD-FEC-MUSIC/HD-FEC-MUSIC), and TF-MUSIC. Figure 10 shows the performance comparison between the GMTFD-based algorithms proposed in this paper and other identification methods in the DOA estimation, when $\alpha =1.5$, $M_r=8$, $SIR=16$, $N=800$, and the modulation mode is QPSK. It is clear from Figure 10 that the DOA estimation performance of the proposed Generalized-TF-MUSIC algorithm is better than the other seven algorithms, which verifies the effectiveness of the proposed algorithm.

6. Discussion

The introduction of a generalized MTFD matrix can improve the adaptability of MIMO communication systems to non-Gaussian interference. This paper presents a method of spatial parameter estimation using a GMTFD matrix against non-Gaussian interference and Gaussian noise. The model considers the effects of various communication system parameters and has universal applicability. Based on the complexity analysis and simulation results, the proposed method is compared and verified in detail.

As shown in Figure 1 and Figure 5, the proposed method has good adaptability to non-Gaussian interference. This is mainly because the generalized MTFD compresses the strong pulse amplitude of non-Gaussian interference by introducing nonlinear transformation and extracts the subspace information according to the quasi-covariance matrix constructed by the generalized MTFD, so as to effectively extract the information of NTA and DOA. As shown in Figure 2 and Figure 7, with the increase in signal length, the performance of the proposed method becomes better. This is because the quasi-covariance matrix is closer to the theoretical value. As shown in Figure 3 and Figure 8, the modulation type of the MIMO system does not affect the performance of this method because it does not contribute to the construction of generalized MTFD. As shown in Figure 4 and Figure 9, the proposed method achieves better resolution performance than traditional methods. This is because the generalized MTFD matrix adopted in this paper can suppress the non-Gaussian interference while concentrating the signal energy around the instantaneous frequency, which improves the effective SNR of the signal. However, although the proposed method has the above advantages, it also has some limitations.

Although it can effectively suppress non-Gaussian interference, the computational complexity of this method is very high. The computational complexity mainly comes from the calculation of the MTFD matrix. In future work, we will further improve the calculation of the MTFD of the proposed method.

7. Conclusions

This paper proposed a reliable scheme to identify the NTA and DOA of MIMO systems in complex environments. The generalized covariance matrix was introduced to construct the GMTFD matrix with strong adaptability to non-Gaussian interference. By making use of the GMTFD matrix, the spatial parameters are estimated for MIMO systems in the presence of non-Gaussian interference and Gaussian noise. The proposed scheme exhibits superior stability and robustness compared to existing methods, even in the absence of a priori information about the communication system, such as modulation types and channel coefficients. The results indicated the effectiveness and practicability of the proposed method, which has high estimation accuracy and resolution under low SNR conditions at the expense of high computational complexity.