Seismic Data Reconstruction Using a Phase-Shift-Plus-Interpolation-Based Apex-Shifted Hyperbolic Radon Transform
Abstract
1. Introduction
2. Methods
2.1. Stolt-Stretch-Based Apex Shifted Hyperbolic Radon Transform
2.2. PSPI Operator
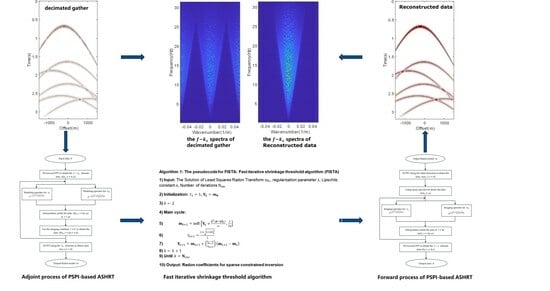
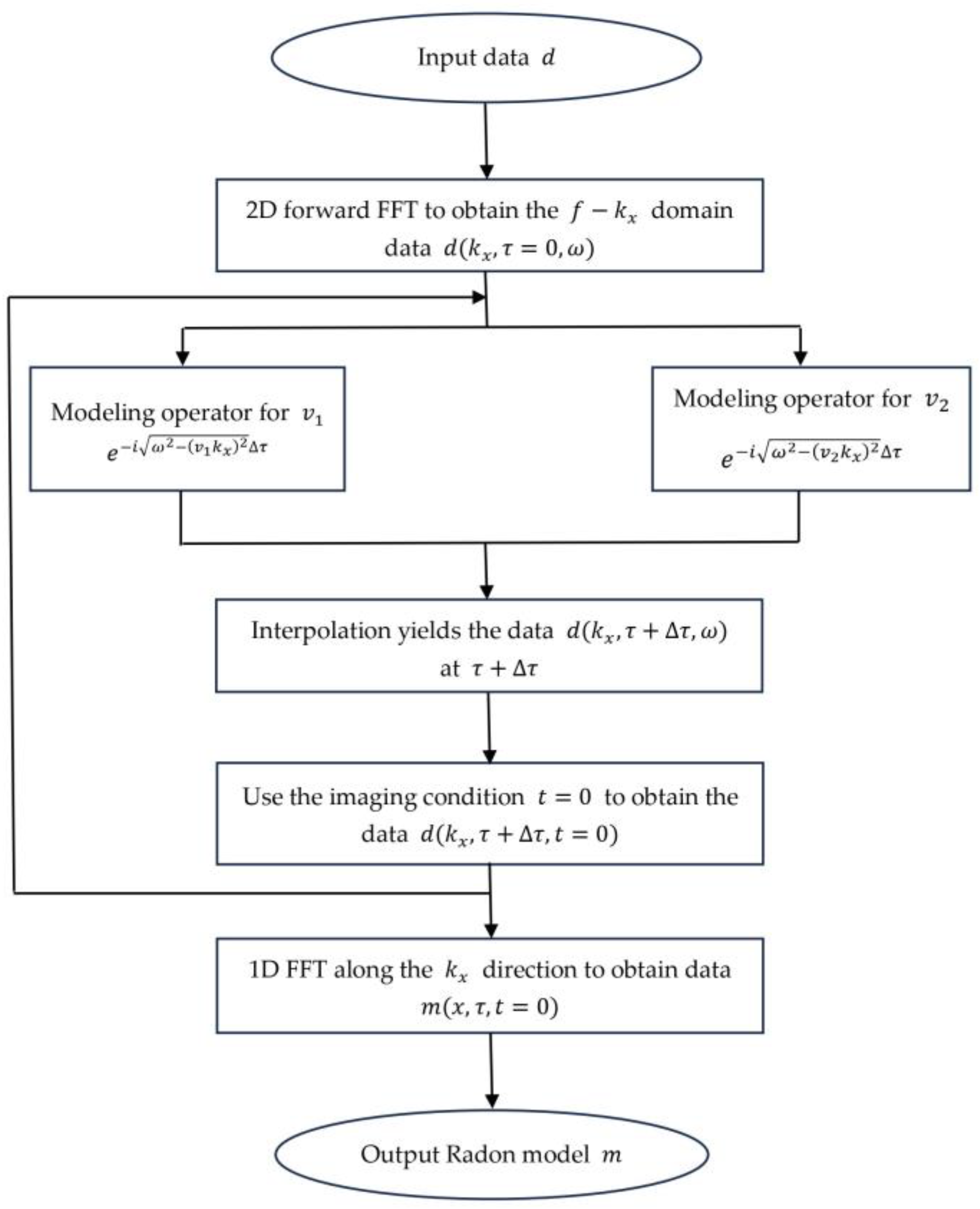
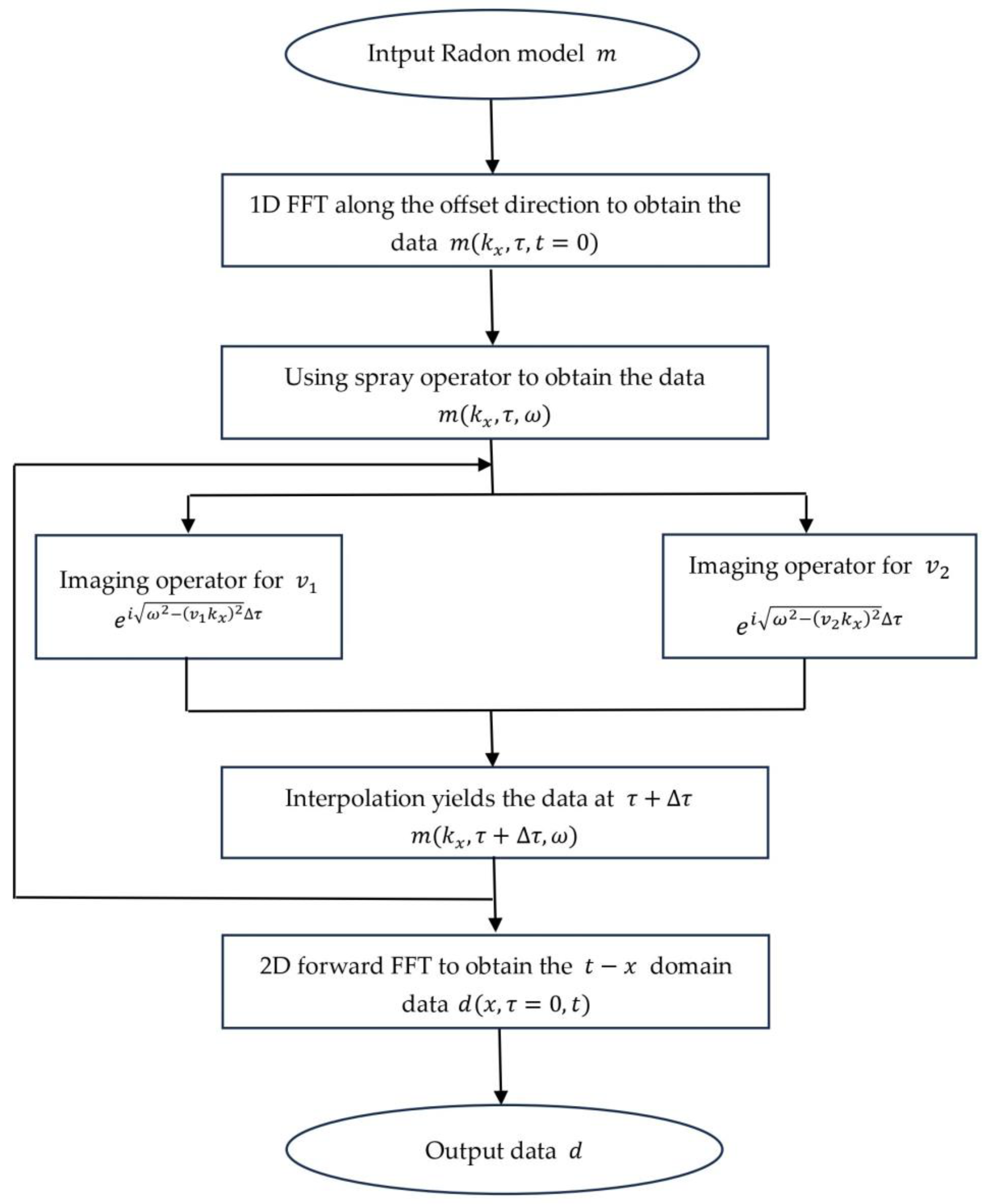
2.3. PSPI-Based Apex-Shifted Hyperbolic Radon Transform
2.4. Sparsity Promotion of Apex-Shifted Hyperbolic Radon Transform
| Algorithm 1: The pseudocode for FISTA: Fast iterative shrinkage threshold algorithm (FISTA) |
| 1) Input: The Solution of Least Squares Radon Transform , regularization parameter , Lipschitz constant , Number of iterations 2) Initialization: 3) 4) Main cycle: 5) |
| 6) |
| 7) |
| 8) |
| 9) Until 10) Output: Radon coefficients for sparse constrained inversion |
3. Results
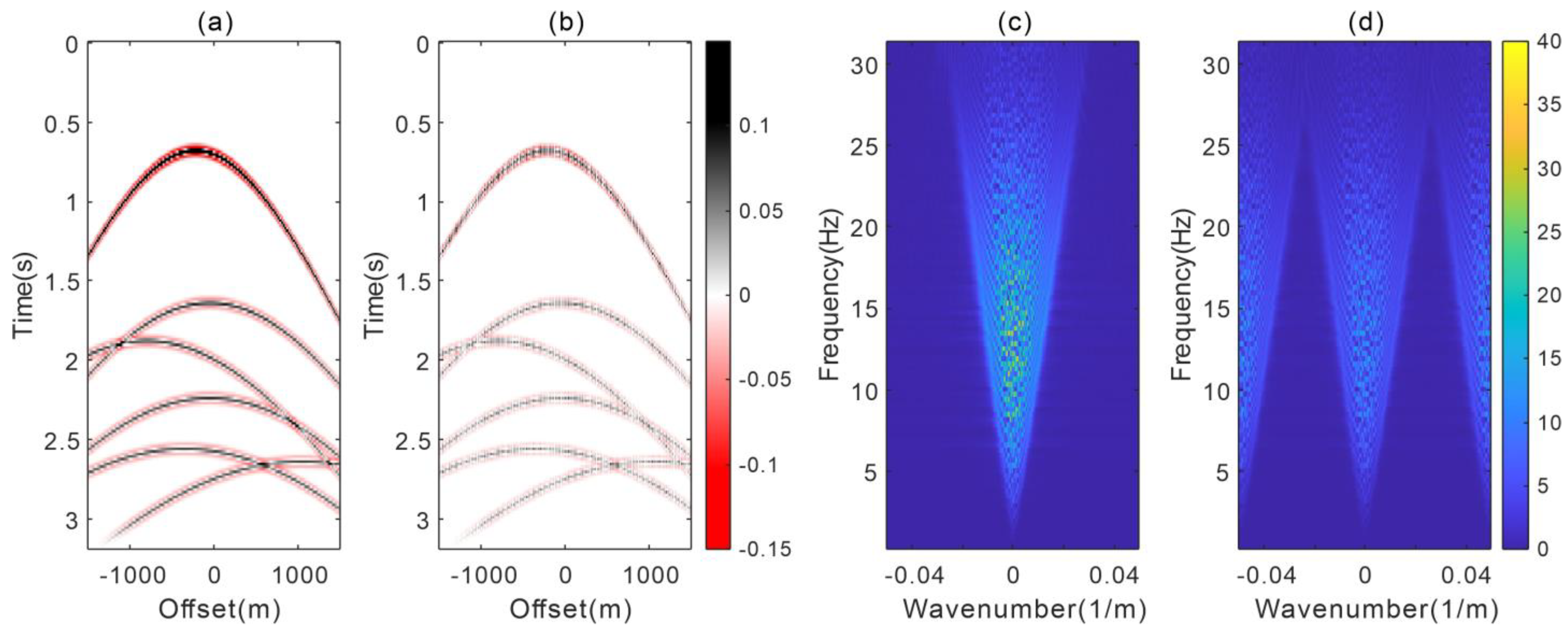
3.1. Synthetic Example
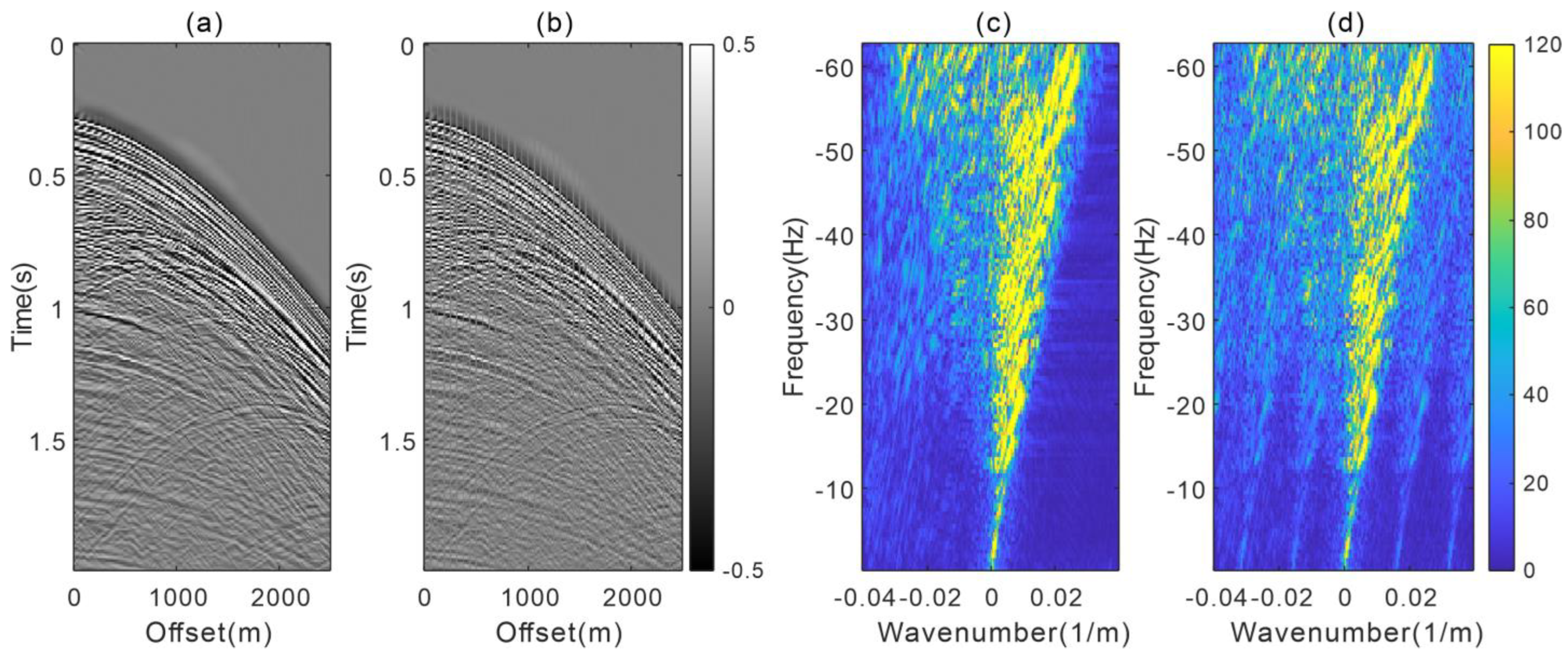
3.2. Field Example
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vermeer, G.J.O. Seismic Wavefield Sampling; Society of Exploration Geophysicists and Shell Research BV: Houston, TX, USA, 1990. [Google Scholar]
- Chen, Y.; Chen, K.; Shi, P.; Wang, Y. Irregular seismic data reconstruction using a percentile-half-thresholding algorithm. J. Geophys. Eng. 2014, 11, 065001. [Google Scholar] [CrossRef]
- Trad, D. Five-dimensional interpolation: Recovering from acquisition constraints. Geophysics 2009, 74, 123–132. [Google Scholar] [CrossRef]
- Duijndam, A.J.W.; Schonewille, M.A. Nonuniform fast Fourier transform. Geophysics 1999, 64, 539–551. [Google Scholar] [CrossRef]
- Ouyang, Z.; Zhang, L.; Wang, H.; Yang, K. High-Dimensional Seismic Data Reconstruction Based on Linear Radon Transform–Constrained Tensor CANDECOM/PARAFAC Decomposition. Remote Sens. 2022, 14, 6275. [Google Scholar] [CrossRef]
- Trad, D.; Ulrych, T.; Sacchi, M. Accurate interpolation with high resolution time-variant Radon transforms. Geophysics 2002, 67, 644–656. [Google Scholar] [CrossRef]
- Wang, J.; Ng, M.; Perz, M. Seismic data interpolation by greedy local Radon transform. Geophysics 2010, 75, WB225–WB234. [Google Scholar] [CrossRef]
- Hollander, Y.; Yilmaz, O. An acceleration method for the anti-leakage parabolic Radon transform for seismic data interpolation. In Proceedings of the SEG International Exposition and Annual Meeting, San Antonio, TX, USA, 15–20 September 2019; SEG: Houston, TX, USA, 2019; p. D033S045R005. [Google Scholar] [CrossRef]
- Naghizadeh, M.; Sacchi, M. Beyond alias hierarchical scale curvelet interpolation of regularly and irregularly sampled seismic data. Geophysics 2010, 75, 189–202. [Google Scholar] [CrossRef]
- Kong, L.Y.; Yu, S.W.; Chen, L. Application of compressive sensing to seismic data reconstruction. Acta Seismol. Sin. 2012, 34, 659–666. [Google Scholar]
- Gan, S.; Wang, S.; Chen, Y.; Zhang, Y.; Jin, Z. Dealiased seismic data interpolation using seislet transform with low-frequency constraint. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2150–2154. [Google Scholar]
- Fomel, S. Towards the seislet transform. In Proceedings of the 2006 SEG Annual Meeting, New Orleans, LO, USA, 1–6 October 2006; pp. 2847–2851. [Google Scholar]
- Liu, Y.; Fomel, S. OC-seislet: Seislet transform construction with differential offset continuation. Geophysics 2010, 75, 235–245. [Google Scholar] [CrossRef]
- Gong, X.; Wang, S.; Zhang, T. Velocity analysis using high-resolution semblance based on sparse hyperbolic Radon transform. J. Appl. Geophys. 2016, 134, 146–152. [Google Scholar] [CrossRef]
- Dix, C.H. Seismic velocities from surface measurements. Geophysics 1955, 20, 68–86. [Google Scholar] [CrossRef]
- Trad, D. Interpolation and multiple attenuation with migration operators. Geophysics 2003, 68, 2043–2054. [Google Scholar] [CrossRef]
- Trad, D.; Siliqi, R.; Poole, G.; Boelle, J. Fast and robust deblending using Apex shifted Radon transform. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Sabbione, J.I.; Sacchi, M.D.; Velis, D.R. Microseismic data denoising via an apex-shifted hyperbolic Radon transform. In Proceedings of the 83rd Annual International Meeting, SEG, Expanded Abstracts, Houston, TX, USA, 22–27 September 2013; pp. 2155–2161. [Google Scholar] [CrossRef]
- Karimpouli, S.; Malehmir, A.; Hassani, H.; Khoshdel, H.; Nabi-Bidhendi, M. Automated diffraction delineation using an apex-shifted Radon transform. J. Geophys. Eng. 2015, 12, 199–209. [Google Scholar] [CrossRef]
- Li, C.; Peng, S.; Zhao, J.; Cui, X.; Du, W.; Satibekova, S. Polarity-preserved diffraction extracting method using modified apex-shifted Radon transform and double-branch Radon transform. J. Geophys. Eng. 2018, 15, 1991–2000. [Google Scholar] [CrossRef]
- Seher, T. A high-resolution apex-shifted hyperbolic Radon transform and its application to multiple attenuation. In Proceedings of the SEG International Exposition and Annual Meeting, Houston, TX, USA, 24–29 September 2017; SEG: Houston, TX, USA, 2017; p. SEG-2017-17640537. [Google Scholar]
- Yang, F.; Wang, D.; Hu, B.; Zhu, H.; Sun, J. 3D surface-related multiples elimination based on improved apex-shifted Radon transform. Acta Geophys. 2021, 69, 1679–1696. [Google Scholar] [CrossRef]
- Ibrahim, A.; Sacchi, M.D. Fast simultaneous seismic source separation using Stolt migration and demigration operators. Geophysics 2015, 80, WD27–WD36. [Google Scholar] [CrossRef]
- Ibrahim, A.; Terenghi, P.; Sacchi, M.D. Wavefield reconstruction using a Stolt-based asymptote and apex shifted hyperbolic Radon transform. In Proceedings of the 2015 SEG Annual Meeting, New Orleans, LO, USA, 18–23 October 2015. SEG Technical Program Expanded Abstracts. [Google Scholar] [CrossRef]
- Gong, X.; Wang, S.; Du, L. Seismic data reconstruction using a sparsity-promoting apex shifted hyperbolic radon-curvelet transform. Stud. Geophys. Geod. 2018, 62, 450–465. [Google Scholar] [CrossRef]
- Gong, X.; Yu, C.; Wang, Z. Separation of prestack seismic diffractions using an improved sparse apex-shifted hyperbolic Radon transform. Explor. Geophys. 2017, 48, 476–484. [Google Scholar] [CrossRef]
- Yilmaz, O.G. Seismic Data Analysis: Processing, Inversion, and Interpretation of Seismic Data, 2nd ed.; Investigations in Geophysics; SEG: Houston, TX, USA, 2001. [Google Scholar]
- Gazdag, J.; Sguazzero, P. Migration of seismic data by phase shift plus interpolation. Geophysics 1984, 49, 124–131. [Google Scholar] [CrossRef]
- Gazdag, J. Wave equation migration with the phase-shift method. Geophysics 1978, 43, 1342–1351. [Google Scholar] [CrossRef]
- Claerbout, J. Earth Soundings Analysis: Processing Versus Inversion; Blackwell Scientific Publications: Hoboken, NJ, USA, 1992. [Google Scholar]
- Beck, A.; Teboulle, M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 2009, 18, 2419–2434. [Google Scholar] [CrossRef] [PubMed]
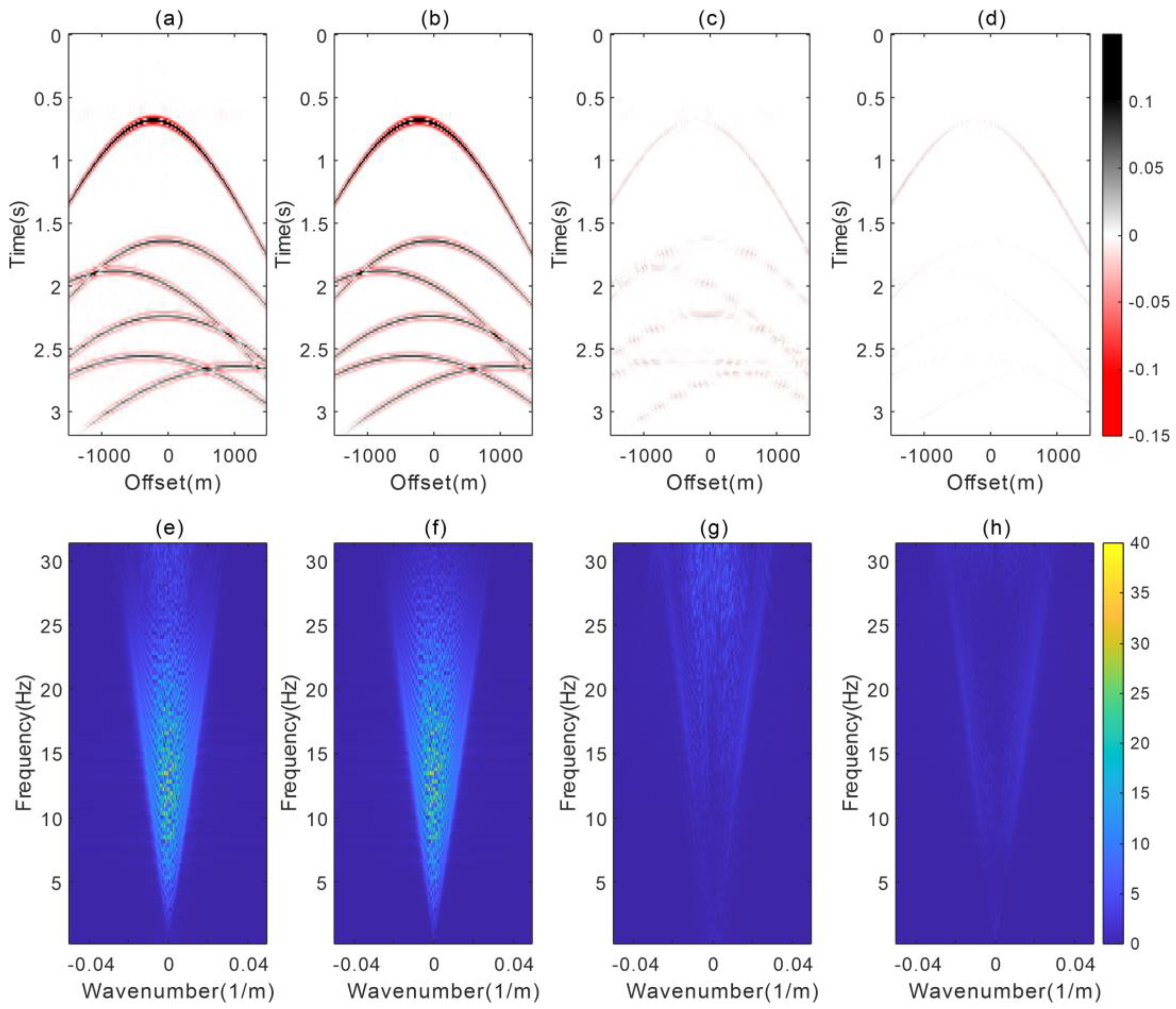
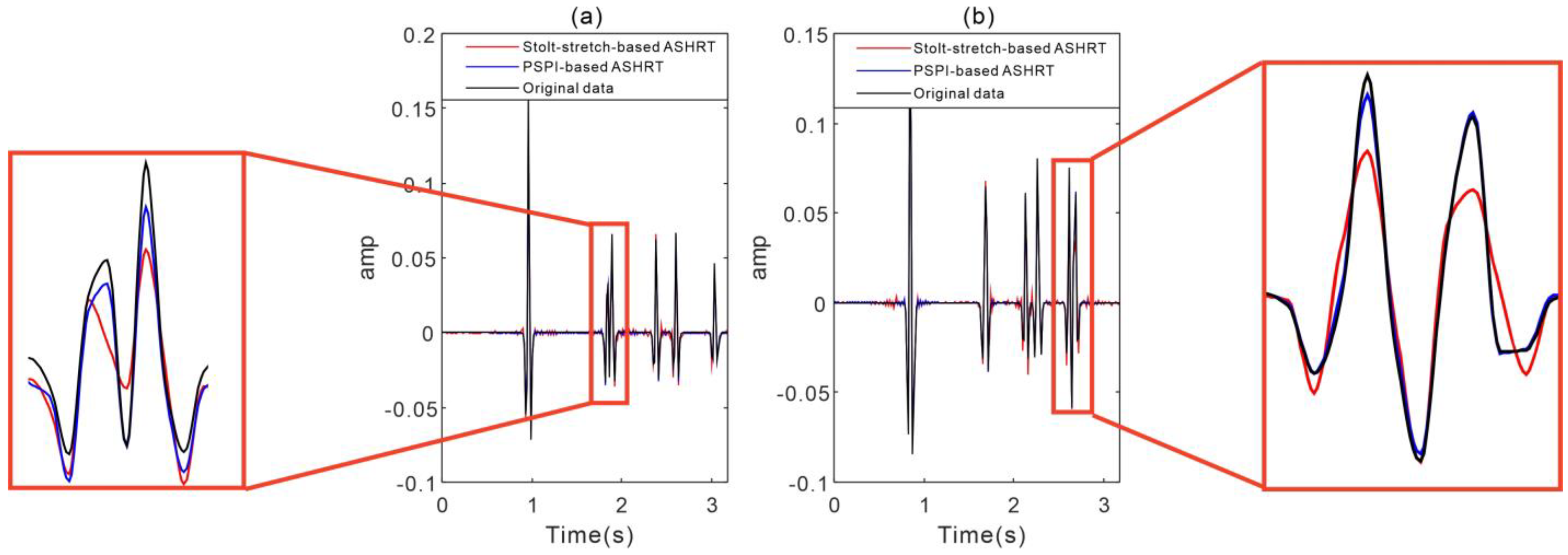
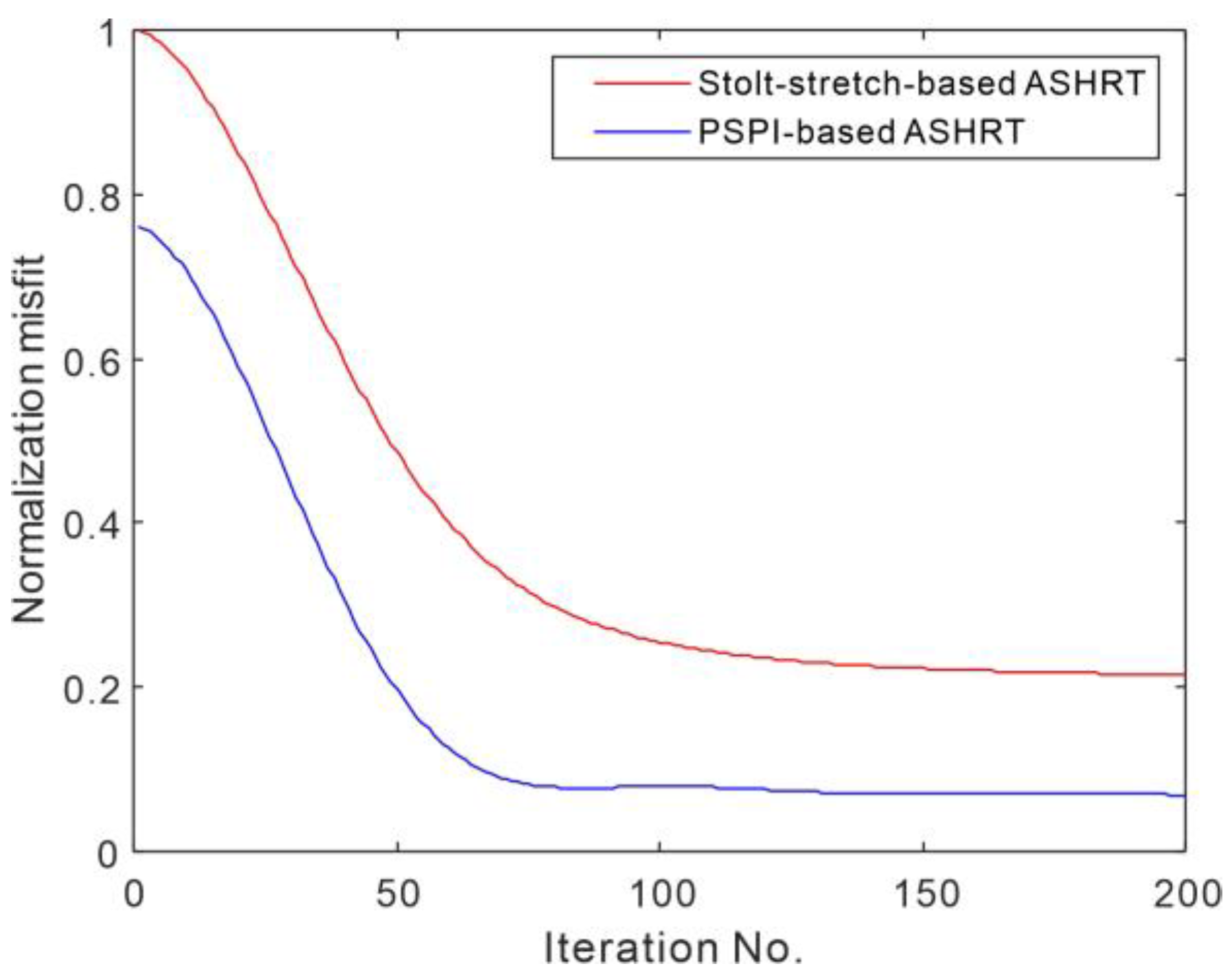

| PSNR/db | SNR/db | MES | |
|---|---|---|---|
| Stolt-stretch-based ASHRT | 48.70 | 13.79 | 1.35 × 10−5 |
| PSPI-based ASHRT | 53.27 | 22.90 | 4.71 × 10−6 |
| PSNR/db | SNR/db | MES | |
|---|---|---|---|
| Stolt-stretch-based ASHRT | 20.66 | 6.56 | 0.0086 |
| PSPI-based ASHRT | 22.13 | 8.00 | 0.0061 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Gong, X.; Hu, B. Seismic Data Reconstruction Using a Phase-Shift-Plus-Interpolation-Based Apex-Shifted Hyperbolic Radon Transform. Remote Sens. 2024, 16, 1114. https://doi.org/10.3390/rs16071114
Wang Y, Gong X, Hu B. Seismic Data Reconstruction Using a Phase-Shift-Plus-Interpolation-Based Apex-Shifted Hyperbolic Radon Transform. Remote Sensing. 2024; 16(7):1114. https://doi.org/10.3390/rs16071114
Chicago/Turabian StyleWang, Yue, Xiangbo Gong, and Bin Hu. 2024. "Seismic Data Reconstruction Using a Phase-Shift-Plus-Interpolation-Based Apex-Shifted Hyperbolic Radon Transform" Remote Sensing 16, no. 7: 1114. https://doi.org/10.3390/rs16071114
APA StyleWang, Y., Gong, X., & Hu, B. (2024). Seismic Data Reconstruction Using a Phase-Shift-Plus-Interpolation-Based Apex-Shifted Hyperbolic Radon Transform. Remote Sensing, 16(7), 1114. https://doi.org/10.3390/rs16071114