Abstract
Lake volume variation is closely related to climate change and human activities, which can be monitored by multi-source remote-sensing data from space. Although there are usually two routine ways to construct the lake volume by the digital elevation model (DEM) or satellite altimetric data combined with the lake area, rarely has a comparison been made between the two methods. Therefore, we conducted a comparison between the two methods in Texas for 14 lakes with abundant validation data. First, we constructed the lake hypsometric curve by five commonly applied DEMs (SRTM, ASTER, ALOS, GMTED2010, and NED) or satellite altimetric products combined with the gauge lake area. Second, the lake volume was estimated by combining the hypsometric curve with the gauge lake area time series. Finally, the estimation error has been quantitatively calculated. The results show that the relative lake volume estimation error (rVSD) of the altimetric data (4%) is only 10–18% of that of the DEMs (22–41%), and the DEM with the highest resolution (NED) has the least rVSD with an average of 22%. Therefore, for large-scale lake monitoring, we suggest the application of satellite altimetric data with the lake area to estimate the lake volume of large lakes, and the application of high-resolution DEM with the lake area to calculate the lake volume of small lakes that are gapped by satellite altimetric data.
1. Introduction
Since the 1990s, more and more researchers have begun to study lake dynamics from space by multi-source remote-sensing data [1,2,3,4]. Lake area and lake water level are two commonly remotely sensed parameters by satellite images or satellite altimetric data. In addition, lake volume variation can also be estimated by combining multi-source remote-sensing data [5,6,7]. Lake volume is closely related to regional water resource utilization and management, human activities, and climate change.
Unlike directly measured water level records, lake volumes are usually estimated by integrating water levels with hypsometric curves. The hypsometric curve describes the relationship between the water level and the water area, and it is usually constructed by a bathymetric survey map [8]. However, it is hard to access large-scale lake volume information, due to the expensive station maintenance cost or limited data-sharing policy [9,10]. The remote-sensing technique is an effective tool for large-scale lake monitoring. Traditionally, to obtain a precise lake hypsometric curve, high-precision lake bathymetric survey work should be performed [8]. However, such survey work is time-consuming, expensive, and labor-intensive. Therefore, more and more researchers try to construct the hypsometric curve and estimate lake volumes by satellite remote-sensing data as listed in Table 1.
To estimate lake volume variations by multi-source remote-sensing data, the digital elevation model (DEM) or satellite altimetric data are usually applied. Accordingly, there are mainly two methods, and the first method is to combine the DEM with the lake area (DEM + A). For example, Yao, et al. [11] applied the Shuttle Radar Topography Mission (SRTM), Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER), Huanjing images, and Landsat images to study the lake volume variations in the Inner Tibetan Plateau. Qiao, et al. [12] combined the SRTM and Landsat images to estimate the lake volume dynamics in the Tibetan Plateau. Fang, et al. [13] applied the SRTM data and Landsat images to study the lake volume changes in China. Besides the DEM+A method, satellite altimetric data are also usually applied with lake area data to estimate lake volumes (Altimetry + A). For example, Li, et al. [14] applied multiple altimetric data with Landsat images to study the lake volume variations in the Tibetan Plateau. Schwatke, et al. [15] combined altimetric products (Database for Hydrological Time Series of Inland Waters, DAHITI [16]) with Landsat images to study the lakes in Texas. Busker, et al. [17] applied DAHITI products with the Global Surface Water (GSW) dataset [4] to study worldwide lakes. Tortini, et al. [18] applied the Global Reservoirs and Lakes Monitor (G-REALM) altimetric products [19] with MODIS data, and produced the lake volume products of worldwide lakes.
Although the studies listed above estimate lake volume variations by combining the DEM or satellite altimetric data with the lake area, only part of them have evaluated the volume estimation error [15,17,18], and the estimation error of the two methods has not been compared. To figure out which method (DEM + A or Altimetry + A) is more suitable for lake volume estimation, we performed a comparison study of the two methods in the same lakes, and the estimation error was quantitatively evaluated by the gauge data.

Table 1.
List of relevant studies on lake volume estimation using multi-source remote-sensing data. Note that the resolution of raster data is shown in parentheses.
Table 1.
List of relevant studies on lake volume estimation using multi-source remote-sensing data. Note that the resolution of raster data is shown in parentheses.
| Research | Study Area | Remote-Sensing Data | Hypsometric Curve | Time Series Data | Volume Error |
|---|---|---|---|---|---|
| Yao et al. [11] | 871 lakes in the Inner Tibetan Plateau | ASTER/SRTM (1 arc) + Huanjing (30 m) & Landsat (30 m) | Monotonic cubic spline fitting | Remotely sensed water area | Not quantitively evaluated |
| Qiao et al. [12] | 315 lakes in the Tibetan Plateau | SRTM (1 arc) | Linear regression | Remotely sensed water area | Not specifically evaluated |
| Fang et al. [13] | 760 lakes in China | SRTM (1 arc) | Four different curves: linear, power law, segmented linear, and quadratic polynomial relationships | Remotely sensed water area | Not specifically evaluated |
| Li et al. [14] | 52 lakes in the Tibetan Plateau | Multiple altimetric data + Landsat (30 m) | Second-order polynomial fitting | Remotely sensed water area or water level | Not specifically evaluated |
| Schwatke et al. [15] | 28 lakes in Texas | DAHITI altimetric product + Landsat (30 m) | New modified Strahler approach | All heights derived from remotely sensed water area or water level | 2.8–14.9% (average: 8.3%) |
| Busker et al. [17] | 137 lakes worldwide | DAHITI altimetric product + GSW (30 m) | Linear regression | Remotely sensed water area or water level | Average: 7.42% (validated at 18 lakes) |
| Tortini et al. [18] | 347 lakes worldwide | G-REALM altimetric product + MODIS (500 m) | Linear regression | All heights derived from remotely sensed water area or water level | 0.87 km3 (validated at Lake Sakakawea) |
| This study | Texas | 1. SRTM (1 arc), ASTER (1 arc), ALOS (1 arc), GMTED2010 (7.5 arc), and NED (1/3 arc) 2. DAHITI altimetric product + Gauge water area | Linear regression | Gauge water area | 1. Average: 22–41% 2. Average: 4% |
2. Study Area and Materials
2.1. Study Area and Gauge Data
To evaluate the lake volume estimation error by the DEM + A or the Altimetry + A method, we selected lakes in Texas State of the United States of America as our study area. The climate and water resources in Texas change greatly from its arid western desert to humid eastern forests. In addition, the mean annual precipitation also changes greatly from 20 cm to 140 cm [20].
As shown in Figure 1, our study lakes are mainly located in East Texas with abundant reservoirs and massive open-access hydrological data. We selected 14 regulated reservoirs monitored by satellite altimetric data as our study lakes (Table A1). The study lakes are of various sizes (average area: 12–678 km2, average volume: 0.06–4.90 km3). Among the study lakes, there are five large lakes (lake area > 100 km2 and lake volume > 1 km3) and nine small lakes.
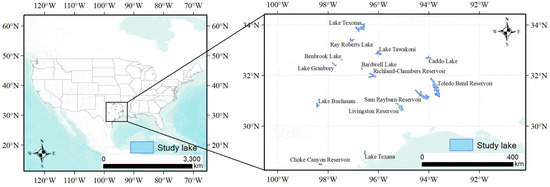
Figure 1.
Location of the study lakes in Texas.
We obtained hydrological gauge data from the Texas Water Development Board (TWDB) via https://waterdatafortexas.org/ (accessed on 25 June 2020), which provides daily water level, water area, and water volume for about 120 reservoirs. Lake gauges provide near-real-time water level measurements, and TWDB website provides daily averaged water level values. TWDB also translates water levels into water areas and water volumes by combining the water level measurements with hypsometric curves. The hypsometric curves are produced from surveys and bathymetric models of each lake, and they indicate the water area and water volume corresponding to different water levels. The details of hypsometric curves and the corresponding survey reports are also provided by the TWDB website. Therefore, gauge water area and water volume are of high quality. In this study, gauge water area was used for lake volume estimation, while gauge water level and gauge water volume were used for validation. Considering that some dams were built before 2000, we estimated lake volumes after 2000.
2.2. Digital Elevation Model
We used five open-access DEMs as listed in Table 2, which contains four global DEMs and National Elevation Dataset (NED) in the United States of America. The four global DEMs includes SRTM, ASTER Global Digital Elevation Model, ALOS World 3D-30 m (AW3D30), and Global Multi-resolution Terrain Elevation Data 2010 (GMTED2010).

Table 2.
Basic information of multi-source DEMs we used.
SRTM was produced by National Aeronautics and Space Administration (NASA) and United States Geological Survey (USGS). We used SRTM PLUS data (v3.0) [21], which were released in 2013, and the spatial resolution is 1 arc (about 30 m). SRTM was generated from 11-day global C-band Interferometric Synthetic Aperture Radar (INSAR) data from the space shuttle Endeavour in 2000. SRTM is the first high-precision global DEM with an elevation measurement error of 9 m (90% percentile of error), but it only covers 80% of land surface area from 56°N to 60°S [21].
ASTER was jointly produced by NASA and Japan’s Ministry of Economy, Trade, and Industry (METI). We adopted ASTER v3.0 released in 2019 with a spatial resolution of 1 arc [22]. ASTER was generated from 1.3 million stereo images acquired by TERRA satellite. ASTER has a high spatial coverage (83°N–83°S), which covers 99% of land surface area. In addition, ASTER data are of robust quality and the vertical precision is about 17 m (90% quantile of error), because it is merged from multiple-year observations from 2000 to 2013. However, the original data source of ASTER is optical images, so ASTER is vulnerable to cloud cover.
ALOS data were released by Japan Aerospace Exploration Agency (JAXA). We used ALOS v2.2 released in 2019 with a spatial resolution of 1 arc [23]. ALOS data were developed from vertical, forward, and backward stereo images acquired by PRISM sensor onboard ALOS satellite. Although the original ALOS data (AW3D DEM) have a spatial resolution of 5 m, the public data resolution is 30 m. AW3D DEM (5 m) has a vertical and horizontal root-mean-square error (RMSE) of 5 m [23]. Similar to ASTER data, ALOS data are also composited from multi-year images, and the data quality is relatively stable. However, there is a lot of data loss at a high latitude above 60° due to cloud and ice coverage.
GMTED2010 database was released in 2010 and developed by USGS and The National Geospatial-Intelligence Agency (NGA). Its main data source is SRTM, Canada DEM, reference 3D data of SPOT5, and ICESat data. The database has three spatial resolutions, including 30 arc, 15 arc, and 7.5 arc. In our study, we adopted 7.5 arc data spanning from 84°N to 56°S with a vertical precision of 26–30 m [24].
Until now, NED database is the most precise public DEM released by USGS. NED database is the product of the 3D Elevation Program (3DEP), including high-resolution thematic DEM (1 m, 3 m, and 5 m). However, the spatial coverage is not high and there are obvious data gaps. In addition, NED also provides seamless DEM with a coarser resolution (1/3 arc, 1 arc, and 2 arc), and it has a wider spatial coverage. In this study, we adopted 1/3 arc seamless NED product, which was produced from laser radar cloud data with a vertical precision of ~3 m (90% quantile of error) [25].
2.3. Satellite Altimetric Data
We collected satellite altimetric products from DAHITI via http://dahiti.dgfi.tum.de/en/ (accessed on 25 June 2020), which provides open-access altimetric water level products for global lakes. The database was developed by the Deutsches Geodätisches Forschungsinstitut der Technischen Universität München (DGFI-TUM) in 2013 [16]. The altimetric products are derived from multiple satellite altimeters, and the detailed data source and time span of each altimetric product are listed in Table A1.
3. Method
3.1. Estimation Principle of Lake Volume Variation
Assuming the lake shape is regular as in Figure 2a, the lake area (A) and lake water level (L) are linearly correlated and the hypsometric curve is shown in Equation (1) with a first-order polynomial [12,17,18]. Gauge records provide real water level range ( to ), while only part of the water level was observed by remote-sensing data. DEM provides elevation above lake surface elevation (, and satellite altimetric data provide periodic observations ranging from to . When satellite water level is , variable lake volume () above can be estimated by integrating lake area against from to [11,13,17] (Figure 2b and Equation (2)).
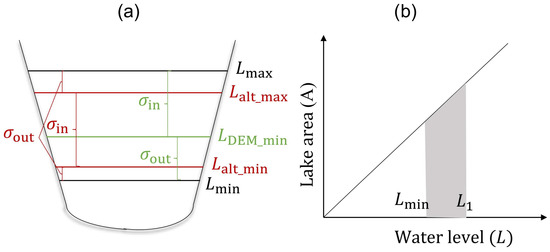
Figure 2.
Schematic diagram of satellite elevation scope and lake volume variation estimation method: (a) lake shape and satellite elevation scope (altimetric data (red) and DEM (green)); and (b) principle of lake volume variation estimation.
In constructing lake hypsometric curve, remote-sensing data are limited to its elevation scope. As shown in Figure 2a, the dynamic water level range of DEM and satellite altimetric data are shown in green and red. For DEM, although it cannot provide lake topography below the water surface, it can provide terrain elevation information above the lake surface. For altimetric data, although they can provide periodical lake water levels, they cannot capture some extreme levels due to their low temporal resolution.
Using the hypsometric curve with gauge water area time series, we derived the water level and water volume time series. Considering that the hypsometric curve is derived from remotely sensed data with limited elevation scope, we separate water volume estimation error into two parts: and (Figure 2a). and are the estimation error when the gauge water level is within and outside the remotely sensed elevation scope.
3.2. Lake Volume Estimation by DEM and Satellite Altimetric Data
This study performed two groups of control experiments (Figure 3) to evaluate the performance of DEM and satellite altimetric data in lake volume monitoring. DEM and satellite altimetric data differ in their way of deriving the lake hypsometric curve. After obtaining the hypsometric curve, lake water level and volume time series were derived by combining gauge water area time series.
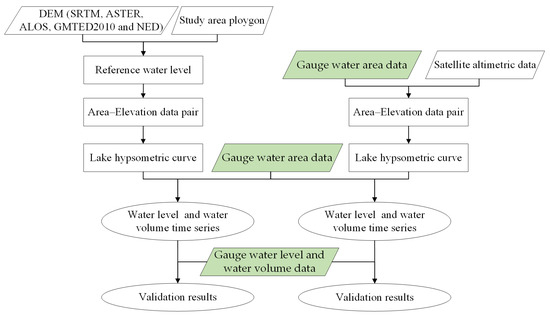
Figure 3.
Workflow diagram of lake volume estimation by DEMs and satellite altimetric data.
For the five DEMs we studied, we obtain synchronized water area and water level data pairs. By calculating the enclosed area at each elevation, lake hypsometric curve can be estimated. Different from DEM, satellite altimetric data only provide periodical lake water levels. To establish lake hypsometric curve, we obtained the corresponding gauge water area in the same day.
To derive the hypsometric curve by DEM, we processed each DEM as follows:
- First, outlining the boundary of study area. With the aid of Google Earth software, we roughly sketched out the boundary of each study area, including the study lake and its surroundings.
- Second, deriving lake reference water level . For the elevation data within each study area, we used the mode as and further checked by DEM. As in Figure 4a, the lake surface of Lake Buchanan is a hydro-flattened surface and the mode represents the lake surface level.
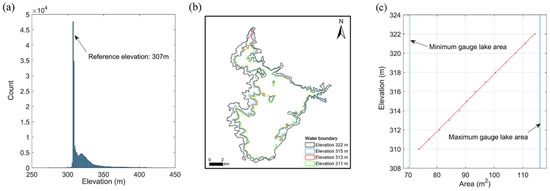 Figure 4. Process of lake hypsometric curve derivation at Lake Buchanan by ALOS data: (a), histogram of elevation data of DEM; (b), examples of enclosed lake area above the reference elevation (307 m); and (c) the relationship between elevation and enclosed lake area.
Figure 4. Process of lake hypsometric curve derivation at Lake Buchanan by ALOS data: (a), histogram of elevation data of DEM; (b), examples of enclosed lake area above the reference elevation (307 m); and (c) the relationship between elevation and enclosed lake area. - Third, obtaining the elevation–area data pairs. Using , we calculated the maximum connected area enclosed by contour line from to at a step length of 1 m. Take contour as an example: we extracted the region below , carried out morphological open operation first to ignore small patches, then carried out morphological close operation to fill small bridges, and then estimated the maximum eight-connected area. As shown in Figure 4b, some contours are shown. As the elevation increases, the enclosed lake area also increases, and the islands in the lake submerged. After estimating the enclosed area of each contour, we derived 40 elevation–area data pairs. In addition, we removed data pairs with an area of less than 3 km2, which may be small pools around the study lake.
- Finally, establishing the lake hypsometric curve. The data pairs obtained in the last step describe the potential relationship between lake area and water level. From gauge lake area records, the area variation range is known. Assuming the area ranges from to , the corresponding elevation–area data pairs within the range are extracted. If there are more than five data pairs, they are used to establish the lake hypsometric curve. Otherwise, the elevation–area data pairs within the range of to are used. As shown in Figure 4c, data pairs within the gauge lake area range are kept, and the elevation and lake area have a good linear correlation relationship.
3.3. Evaluation Metrics
Using daily gauge water level and water volume data, we evaluated the water level and water volume estimation error of DEM and altimetric data. In this study, we applied five evaluation metrics: dynamic water level coverage (DWLC), water level and water volume estimation error ( and ), and relative water level and water volume estimation error (rHSD and rVSD).
Specifically speaking, DWLC (Equation (3)) is the ratio of satellite elevation scope to gauge water level range, which describes the water level range ratio observed by remote-sensing data. HSD (Equation (4)) and VSD (Equation (5)) are the standard error of water level and water volume estimates, which describes the estimation precision and ignores system bias. rHSD (Equation (6)) and rVSD (Equation (7)) are the ratio of HSD and VSD to water level and water volume variation range. Considering that absolute water level and water volume differs greatly among different sizes of lakes, the relative precision is more comparable among different lakes.
where are the -th validation data pair, the number of validation data pairs, estimated water level, gauge water level, estimated water volume, and gauge water volume, respectively. and ( and ) are the 95% and 5% quantile of gauge water level (water volume).
4. Results
4.1. Water Level and Volume Estimated by DEMs
Table 3 lists the lake water level and volume estimation error of the five DEMs. The results show that the water level and volume error (HSD and VSD) differ greatly among the five DEMs. The average HSD varies from 0.62 m to 2.28 m, and the average VSD varies from 0.20 km3 to 0.53 km3.

Table 3.
Validation results of water level and volume estimated by DEMs. DWLC indicates dynamic water level coverage; HSD and VSD are water level and water volume estimation error. Note: Large lakes have an average area greater than 100 km2 and average volume greater than 1 km3. In addition, the best results among the five DEMs are in bold.
Overall, the NED has the least water level and volume estimation error, followed by the ALOS, SRTM, ASTER, and GMTED2010, which is in line with the reported vertical precision of each DEM as listed in Table 2. Specifically, the NED outperforms the other four DEMs in large lakes, and the VSD is 32–54% of that of the other four DEMs. ALOS outperforms the other four DEMs in small lakes, and the VSD is 31–56% of that of the other four DEMs.
Usually, the HSD and DWLC are assumed to be closely related to the VSD, and a smaller HSD and a larger DWLC contribute to a more precise hypsometric curve. Although the hypsometric curve is constructed from elevation–area data pairs above the lake surface at the time of the DEM acquisition, it is applied to estimate water volumes at all gauge water levels. Therefore, if the DWLC is high, the hypsometric curve is more applicable to subhydroflattened surface levels. Taking the Richland–Chambers Reservoir as an example (Table 3), the NED and ALOS have a comparable HSD (0.16 m vs. 0.16 m), while the NED has a greater DWLC (93% vs. 58%), and the VSD of the NED is much smaller than that of the ALOS (0.03 km3 vs. 0.08 km3), which is mainly attributed to the high DWLC of the NED.
The validation results indicate that the HSD plays a more important role than the DWLC in lake volume estimation. Our correlation analysis results show that the HSD is significantly correlated with the VSD (r = 0.61, p-value = 0.00), while no obvious correlation relationship is found between the DWLC and VSD (r = 0.17, p-value = 0.15). For all lakes, although GMTED2010 has the widest average DWLC, it has the largest average water level and volume estimation error. In contrast, although the NED has the lowest average DWLC, it achieves the least average water level and volume estimation error, especially for large lakes.
4.2. Water Level and Volume Estimated by Satellite Altimetric Data
The validation results of satellite altimetric data are listed in Table 4. Overall, the water level and volume estimation results are of high precision with an average of 0.21 m and 0.04 km3, and there is no obvious difference between large and small lakes. For dynamic water level coverage, the altimetric data capture a large part of the water level variations, and the average DWLC is 71%. However, the DWLC ranges greatly among lakes, ranging from 37% to 100%. In terms of water level retrieval, the satellite altimetric data provide accurate estimates, and the HSD varies from 0.02 m to 0.66 m with an average of 0.21 m. Similarly, the lake volume estimation error is also small, and the VSD varies from 0.00 km3 to 0.17 km3 with an average of 0.04 km3.

Table 4.
Validation results of water level and volume estimated by satellite altimetric data.
4.3. Comparison between DEM and Altimetric Data in Lake Volume Estimation
The relative lake volume estimation error statistics are shown in Table 5. For the altimetric data, the rVSD is comparable between large lakes and small lakes. However, except for the NED, large lakes usually have a greater rVSD than that of small lakes. In addition, Table 5 shows that the altimetric data outperforms the DEM in lake volume estimation, especially for large lakes. For all lakes, the average rVSD of the altimetric data is 4%, which is 10–18% of that of the DEMs (22–41%). For large lakes, the altimetric data show great superiority, and the average rVSD is 4%, which is 6–21% of that of the DEMs (19–63%). For small lakes, the altimetric data also show an advantage in lake volume estimation, and the rVSD is 11–27% of that of the DEMs.

Table 5.
Comparison of relative lake volume estimation error between DEMs and satellite altimetric data. Note that the best results of the six sets of data are in bold.
The distribution details of the rVSD are shown in Figure 5 by boxplots in three colors. To be specific, the estimation error within and outside the remotely sensed elevation scope ( and ) are shown in blue and green boxplots, and the whole estimation error is shown in red boxplots. The results show that the change of and are usually synchronous, and they are positively correlated with a correlation coefficient r = 0.49 (p-value = 0.00). Furthermore, is generally larger and more spread-out than . This suggests that water volume estimates outside the remotely sensed elevation scope have a higher uncertainty than that of estimates inside the scope, which is in line with Busker et al. [17] and Weekley and Li [26]. Therefore, this further suggests that a wider scope contributes to a more precise hypsometric curve.
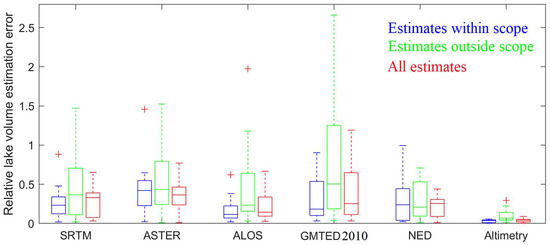
Figure 5.
Distribution of relative lake volume estimation error of DEMs and altimetric data. Note that blue, green, and red indicate lake volume estimates within remotely sensed elevation scope, outside remotely sensed elevation scope, and all estimates, respectively. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. Outliers are plotted individually using the ‘+’ marker symbol.
5. Discussion
5.1. Comparison with Previous Study
The main objective of this study is to compare the DEM and altimetric data in lake volume estimation, and the gauge area and linear regression are applied for the two groups of experiments. We derived the lake volume time series of 14 lakes in Texas. Validated by the gauge water volumes, we derived the lake volume estimation error. Compared with the previous studies listed in Table 1, our study has evaluated the volume estimation error by the DEM + A method and the Altimetry + A method in the same time.
Our validation results show that the average relative volume estimation error is 4% for altimetric data, while it is 8.3% for Schwatke et al. [15] and 7.42% for Busker et al. [17]. Our estimation error is about half that of previous studies, because we used the gauge water area to construct the final lake volume time series, while previous studies used remotely sensed water area. The gauge water area is more precise than the remotely sensed water area, because it is based on the gauge water level and hypsometric curve derived from surveys and bathymetric models. However, the remotely sensed water area is usually extracted from optical images, but the area extraction precision is usually affected by obscuration (clouds and vegetation) and an insufficient image resolution [27].
In addition, we applied a linear regression to represent the hypsometric curve. Although some previous studies also applied the linear regression [12,17,18], some studies applied a more complicated regression, such as the new modified Strahler approach [15] and multi-order polynomial regression [14]. For lakes with an irregular shape, a more complicated regression maybe more applicable.
5.2. Implication for Large-Scale Lake Volume Monitoring
For large-scale lake volume monitoring, the DEM and altimetric data are suggested to be combined for lake volume monitoring, because the DEM usually has a wide spatial coverage while the altimetric data usually have a limited coverage. In this study, we utilized four global DEMs (SRTM, ASTER, ALOS, and GMTED2010), which cover 80–99% of the terrestrial surface, including most lakes on the Earth. In contrast, most lakes on the Earth are not covered by conventional altimetric data, especially for small lakes [19], because conventional altimetric satellites provide strip observations, and the strip distance ranges from dozens to hundreds of kilometers. For example, Topex/Poseidon and ERS, the two best-known families of altimetric satellites, have an orbital interval of 315 km and 80 km at the equator.
For lakes monitored by both the DEM and altimetric data, the altimetric data are usually more suitable than the DEM for lake volume estimation, because altimetric data usually have a better vertical precision and a wider dynamic water level coverage than that of the DEM. In this study, the water level estimation error ranges from 0.62 m to 2.28 m for DEMs, while it is 0.21 m for satellite altimetric data. Especially, for some lakes with small water level fluctuations, a DEM with a low spatial resolution may not be able to provide a precise description of the lake topography. Taking the Livingston Reservoir as an example (Figure 6), the lake area and water level have small fluctuations with a range of 67.48 km2 and 2.05 m. From the elevation–area data pairs (the first row in Figure 6) within the water area range, we found that there are abundant data pairs for the altimetric data, while there are only three data pairs for the NED. Therefore, the hypsometric curve constructed by the altimetric data is more reliable, and the estimated water level and volume estimates correspond well with the gauge records, especially for some extremes. Statistically, the water level and lake volume estimation error of the altimetric data is much smaller than the best-performed DEM NED (HSD: 0.02 m vs. 0.29 m; VSD: 0.01 km3 vs. 0.16 km3). In addition, the DEM provides terrain elevation above the lake surface depending on the time of DEM acquisition. Unlike the DEM, the altimetric data usually provide periodic observations and the repeat cycle varies from 10 days to 35 days, which contributes to a high DWLC and a reliable hypsometric curve.
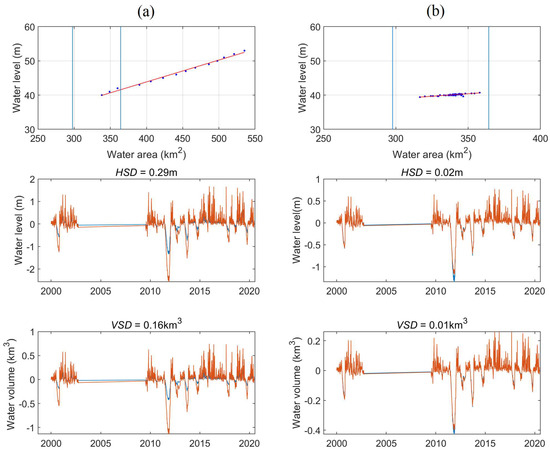
Figure 6.
Water level and volume estimation results of NED (a) and satellite altimetric data (b) for Livingston Reservoir. Each example includes the following: (1) the elevation−area relationship; (2) estimated (orange) and gauge (blue) water level time series; and (3) estimated (orange) and gauge (blue) water volume time series. Water level and volume estimation error HSD and VSD are marked.
For lakes with multiple DEMs, the DEM with the highest resolution seems to perform the best, especially for large lakes. Among the five DEMs we studied, the NED generally has the smallest HSD and VSD, even though its DWLC is low, as in the Sam Rayburn Reservoir and Livingston Reservoir (Table 3). The good performance of the NED is mainly attributed to its low HSD. In general, the NED has an obvious superiority in terrain elevation measurement, and a high-resolution DEM may allow for a better estimation of the hypsometric curve and lake volumes.
5.3. Implication for Individual Lake Volume Monitoring
For individual lake monitoring, the selection of optimal remote-sensing data is more random, both the data quality and elevation scope should be specially considered.
Some data quality problems may impact the vertical precision of altimetric data and DEMs. For different satellite altimetric data, they are some common data problems: systematic elevation bias and waveform pollution. When we are integrating multi-satellite and multi-track altimetric data into long-term water level products, systematic elevation bias should be considered and removed [7]. Furthermore, there are waveform pollution problems for some small lakes with complex surroundings, and waveforms should be selected and retracked [28,29]. Unlike the common quality problems among satellite altimeters, the quality problem differs among DEMs with different imaging types. For low-resolution DEMs, such as the GMTED2010, they have some difficulties in the lake boundary description, especially for small lakes. Take Bardwell Lake (area: 12 km2, volume: 0.06 km3) as an example (Figure 7): the GMTED2010 has the lowest spatial resolution (7.5 arc), while the NED has the highest spatial resolution (1/3 arc). It is hard to distinguish the lake boundary in the GMTED2010, while it can be clearly described by the NED with many details. For high-resolution DEMs, such as the NED, they tend to have image mosaic problems. For example, in Ray Roberts Lake (Figure 7), there is a significant mosaic strip and the water level differs greatly on the two sides of the strip, which may be the main reason why the NED has the greatest water level estimation error in Ray Roberts Lake among the 14 lakes we studied (Table 3). A high-resolution image tends to have a small frame size and there are mosaic problems when we are mosaicking multiple images into a seamless DEM product. In addition, for an SAR Interferometry mode (SARIN) DEM, such as the SRTM, although the radar signal can penetrate clouds and reach earth surface, there are projection reduction, midway stagnation, shadows casting, and other problems on the slope [30,31]. For optical stereo-pair mode DEMs, such as the ASTER and ALOS, they are susceptible to cloud cover [32].
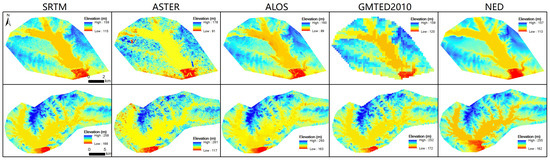
Figure 7.
Comparison of five DEMs (SRTM, ASTER, ALOS, GMTED2010, and NED) for small lake Bardwell Lake (the first row) and large lake Ray Roberts Lake (the second row).
In addition, the dynamic water level coverage for different remote-sensing data should also be considered. For altimetric data, the water level time series may have some time gaps, and some high and low water levels are not captured. For example, the altimetric time series of Lake Tawakoni is derived from Jason-2 and Jason-3 (Table A1), and there is a data gap during August 2013 to March 2015. However, the gauge water level dropped about 1.21 m during the time gap, which accounts for the 26% of the gauge water level range. Therefore, the altimetric data perform worse than the ALOS in lake volume estimation due to the smaller DLWC. Different from the multi-temporal satellite altimetric data, the dynamic water level coverage of each DEM is more random depending on the time of data acquisition. To make full use of multiple DEMs, the DEM with the lowest lake surface elevation can be specifically selected for each individual lake, as with Weekley and Li [26].
6. Conclusions
In this study, we applied five commonly applied DEMs (SRTM, ASTER, ASTER, GMTED2010, and NED) and satellite altimetric data combined with the gauge water areas to estimate the lake volumes of 14 Texas lakes, and the water volume estimation error was quantitatively evaluated by the gauge lake volumes. The main conclusions are as follows:
- For the DEM + A method, the average relative water volume estimation error varies from 22% to 41%, and the DEM with the highest resolution (NED) has the least relative water volume estimation error, followed by the ALOS, SRTM, ASTER, and GMTED2010.
- For the Altimetry + A method, the average relative water volume estimation error is 4%. Satellite altimetric data could provide more precise lake volume estimates than the commonly applied DEMs, and the estimation error is only 10–18% of that of the five DEMs. Especially for large lakes, the estimation error is only 6–21% of that of the five DEMs.
- For lake volume estimation, the Altimetry + A method is more suggested for large lakes, while the DEM + A method is more suggested for small lakes that are gapped by conventional altimeters. Meanwhile, for lakes with multiple DEMs, the DEM with the highest resolution is more suggested.
Finally, it’s worth noting that the Surface Water and Ocean Topography (SWOT) mission was launched on 16 December 2022, which will give us the first global survey of nearly all water on the Earth’s surface, based on a new type of radar called Ka-band radar interferometry, which will make high-resolution measurements of earth’s land surface like the SRTM every 21 days with a balance of global coverage and frequent sampling [33]. It will provide lake water level, water area, and lake surface slope at the same time. It is expecting to see a new paradigm for global lake volume monitoring.
Author Contributions
Conceptualization, methodology, validation, investigation, data curation, writing—original draft preparation, and visualization, C.Y.; writing—review and editing, F.Z.; project administration, C.L.; funding acquisition, C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Second Tibetan Plateau Scientific Expedition and Research Program (STEP) under Grant 2019QZKK0206 and Major Program of the National Natural Science Foundation of China under Grant 42090015.
Data Availability Statement
The data presented in this study are available upon request from the first author (yctina@whu.edu.cn) or the corresponding author (liucx@radi.ac.cn).
Acknowledgments
The authors would like to thank the Texas Water Development Board for providing the gauge data, DAHITI for providing the lake satellite altimetric products, and NASA, USGS, METI, JAXA, and NGA for providing the multi-source DEMs.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Texas reservoirs’ names, with their location, average area and volume, satellite altimetric data source, and time span.
Table A1.
Texas reservoirs’ names, with their location, average area and volume, satellite altimetric data source, and time span.
| Name | Longitude (°) | Latitude (°) | Average Area (km2) | Average Volume (km3) | Satellite Altimetric Data | Time Span |
|---|---|---|---|---|---|---|
| Toledo Bend Reservoir | 31.56 | −93.79 | 678 | 4.90 | ICESat, Jason-2, Jason-3, Sentinel-3A | 2003–2020 |
| Sam Rayburn Reservoir | 31.15 | −94.23 | 422 | 3.16 | Jason-2, Jason-3 | 2008–2020 |
| Livingston Reservoir | 30.76 | −95.13 | 338 | 2.16 | Envisat, SARAL/AltiKa, Sentinel-3B | 2002–2020 |
| Lake Texoma | 33.90 | −96.62 | 300 | 3.01 | Envisat, SARAL/AltiKa | 2002–2016 |
| Richland–Chambers Reservoir | 32.00 | −96.20 | 163 | 1.21 | Jason-1, Jason-2, Jason-3 | 2002–2020 |
| Lake Tawakoni | 32.86 | −95.96 | 137 | 0.92 | Jason-2, Jason-3 | 2008–2020 |
| Caddo Lake | 32.71 | −94.01 | 116 | 0.19 | Envisat, SARAL/AltiKa | 2002–2016 |
| Ray Roberts Lake | 33.41 | −97.02 | 106 | 0.86 | Jason-2, Jason-3 | 2008–2020 |
| Lake Buchanan | 30.80 | −98.41 | 76 | 0.81 | Envisat, Jason-2, Jason-3, SARAL/AltiKa | 2002–2020 |
| Choke Canyon Reservoir | 28.49 | −98.31 | 74 | 0.49 | Jason-1, Jason-2, Jason-3 | 2002–2020 |
| Lake Texana | 28.93 | −96.54 | 36 | 0.18 | Envisat | 2002–2010 |
| Lake Granbury | 32.41 | −97.75 | 29 | 0.15 | Envisat, Cryosat-2, SARAL/AltiKa | 2002–2017 |
| Benbrook Lake | 32.63 | −97.47 | 13 | 0.09 | Envisat, Cryosat-2, SARAL/AltiKa | 2002–2016 |
| Bardwell Lake | 32.28 | −96.66 | 12 | 0.06 | Envisat, SARAL/AltiKa | 2002–2015 |
References
- Alsdorf, D.E.; Rodríguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45, RG2002. [Google Scholar] [CrossRef]
- Ji, L.; Gong, P.; Wang, J.; Shi, J.; Zhu, Z. Construction of the 500-m Resolution Daily Global Surface Water Change Database (2001–2016). Water Resour. Res. 2018, 54, 10270–10292. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.C.; Nino, F.; Abarca Del Rio, R.; Cazenave, A.; et al. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Birkett, C.; Lettenmaier, D.P. Global monitoring of large reservoir storage from satellite remote sensing. Water Resour. Res. 2012, 48, W09504. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. Estimating water volume variations in lakes and reservoirs from four operational satellite altimetry databases and satellite imagery data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar] [CrossRef]
- Yuan, C.; Gong, P.; Liu, C.; Ke, C. Water-volume variations of Lake Hulun estimated from serial Jason altimeters and Landsat TM/ETM+ images from 2002 to 2017. Int. J. Remote Sens. 2018, 40, 670–692. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, Y.; Zhu, L.; Wang, J.; Li, J.; Chen, D. Estimation and trend detection of water storage at Nam Co Lake, central Tibetan Plateau. J. Hydrol. 2011, 405, 161–170. [Google Scholar] [CrossRef]
- The Ad Hoc Group; Vörösmarty, C.; Askew, A.; Grabs, W.; Barry, R.G.; Birkett, C.; Döll, P.; Goodison, B.; Hall, A.; Jenne, R.; et al. Global water data: A newly endangered species. Eos Trans. Am. Geophys. Union 2001, 82, 54–58. [Google Scholar] [CrossRef]
- Yu, C.Q.; Gong, P.; Yin, Y.Y. China’s water crisis needs more than words. Nature 2011, 470, 307. [Google Scholar] [CrossRef]
- Yao, F.; Wang, J.; Yang, K.; Wang, C.; Walter, B.A.; Crétaux, J.F. Lake storage variation on the endorheic Tibetan Plateau and its attribution to climate change since the new millennium. Environ. Res. Lett. 2018, 13, 064011. [Google Scholar] [CrossRef]
- Qiao, B.; Zhu, L.; Yang, R. Temporal-spatial differences in lake water storage changes and their links to climate change throughout the Tibetan Plateau. Remote Sens. Environ. 2019, 222, 232–243. [Google Scholar] [CrossRef]
- Fang, Y.; Li, H.; Wan, W.; Zhu, S.; Wang, Z.; Hong, Y.; Wang, H. Assessment of Water Storage Change in China’s Lakes and Reservoirs over the Last Three Decades. Remote Sens. 2019, 11, 1467. [Google Scholar] [CrossRef]
- Li, X.; Long, D.; Huang, Q.; Han, P.; Zhao, F.; Wada, Y. High-temporal-resolution water level and storage change data sets for lakes on the Tibetan Plateau during 2000–2017 using multiple altimetric missions and Landsat-derived lake shoreline positions. Earth Syst. Sci. Data 2019, 11, 1603–1627. [Google Scholar] [CrossRef]
- Schwatke, C.; Dettmering, D.; Seitz, F. Volume Variations of Small Inland Water Bodies from a Combination of Satellite Altimetry and Optical Imagery. Remote Sens. 2020, 12, 1606. [Google Scholar] [CrossRef]
- Schwatke, C.; Dettmering, D.; Bosch, W.; Seitz, F. DAHITI—An innovative approach for estimating water level time series over inland waters using multi-mission satellite altimetry. Hydrol. Earth Syst. Sci. 2015, 19, 4345–4364. [Google Scholar] [CrossRef]
- Busker, T.; de Roo, A.; Gelati, E.; Schwatke, C.; Adamovic, M.; Bisselink, B.; Pekel, J.-F.; Cottam, A. A global lake and reservoir volume analysis using a surface water dataset and satellite altimetry. Hydrol. Earth Syst. Sci. 2019, 23, 669–690. [Google Scholar] [CrossRef]
- Tortini, R.; Noujdina, N.; Yeo, S.; Ricko, M.; Birkett, C.M.; Khandelwal, A.; Kumar, V.; Marlier, M.E.; Lettenmaier, D.P. Satellite-based remote sensing data set of global surface water storage change from 1992 to 2018. Earth Syst. Sci. Data 2020, 12, 1141–1151. [Google Scholar] [CrossRef]
- Birkett, C.; Reynolds, C.; Beckley, B.; Doorn, B. From Research to Operations: The USDA Global Reservoir and Lake Monitor. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 19–50. [Google Scholar] [CrossRef]
- Wurbs, R.A.; Ayala, R.A. Reservoir evaporation in Texas, USA. J. Hydrol. 2014, 510, 1–9. [Google Scholar] [CrossRef]
- Rodríguez, E.; Morris, C.S.; Belz, J.E. A global assessment of the SRTM Performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- Gesch, D.; Oimoen, M.; Danielson, J.; Meyer, D. Validation of the ASTER global digital elevation model version 3 over the conterminous United States. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41-B4, 143. [Google Scholar] [CrossRef]
- Takaku, J.; Tadono, T.; Tsutsui, K. Generation of High Resolution Global DSM from ALOS PRISM. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40-4, 243–248. [Google Scholar] [CrossRef]
- Danielson, J.J.; Gesch, D.B. Global Multi-Resolution Terrain Elevation Data 2010 (GMTED2010); U.S. Geological Survey Open-File Report 2011, 2011-1073; USGS Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2011. [CrossRef]
- Gesch, D.B.; Oimoen, M.J.; Evans, G.A. Accuracy Assessment of the U.S. Geological Survey National Elevation Dataset, and Comparison with Other Large-Area Elevation Datasets—SRTM and ASTER; U.S. Geological Survey Open-File Report 2014, 2014-1008; U.S. Geological Survey: Reston, VA, USA, 2014. [CrossRef]
- Weekley, D.; Li, X. Tracking lake surface elevations with proportional hypsometric relationships, Landsat imagery, and multiple DEMs. Water Resour. Res. 2021, 57, e2020WR027666. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Zhang, S.; Wu, J. Detecting, Extracting, and Monitoring Surface Water from Space Using Optical Sensors: A Review. Rev. Geophys. 2018, 56, 333–360. [Google Scholar] [CrossRef]
- Okeowo, M.A.; Lee, H.; Hossain, F.; Getirana, A. Automated Generation of Lakes and Reservoirs Water Elevation Changes from Satellite Radar Altimetry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3465–3481. [Google Scholar] [CrossRef]
- Jiang, L.; Nielsen, K.; Andersen, O.B.; Bauer-Gottwein, P. CryoSat-2 radar altimetry for monitoring freshwater resources of China. Remote Sens. Environ. 2017, 200, 125–139. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Uuemaa, E.; Ahi, S.; Montibeller, B.; Muru, M.; Kmoch, A. Vertical Accuracy of Freely Available Global Digital Elevation Models (ASTER, AW3D30, MERIT, TanDEM-X, SRTM, and NASADEM). Remote Sens. 2020, 12, 3482. [Google Scholar] [CrossRef]
- Tonooka, H.; Tachikawa, T. ASTER Cloud Coverage Assessment and Mission Operations Analysis Using Terra/MODIS Cloud Mask Products. Remote Sens. 2019, 11, 2798. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT Mission and Its Capabilities for Land Hydrology. Surv. Geophys. 2015, 37, 307–337. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).