S3L: Spectrum Transformer for Self-Supervised Learning in Hyperspectral Image Classification

Abstract

In the realm of Earth observation and remote sensing data analysis, the advancement of hyperspectral imaging (HSI) classification technology is of paramount importance. Nevertheless, the intricate nature of hyperspectral data, coupled with the scarcity of labeled data, presents significant challenges in this domain. To mitigate these issues, we introduce a self-supervised learning algorithm predicated on a spectral transformer for HSI classification under conditions of limited labeled data, with the objective of enhancing the efficacy of HSI classification. The S3L algorithm operates in two distinct phases: pretraining and fine-tuning. During the pretraining phase, the algorithm learns the spatial representation of HSI from unlabeled data, utilizing a masking mechanism and a spectral transformer, thereby augmenting the sequence dependence of spectral features. Subsequently, in the fine-tuning phase, labeled data is employed to refine the pretrained weights, thereby improving the precision of HSI classification. Within the comprehensive encoder–decoder framework, we propose a novel spectral transformer module specifically engineered to synergize spatial feature extraction with spectral domain analysis. This innovative module adeptly navigates the complex interplay among various spectral bands, capturing both global and sequential spectral dependencies. Uniquely, it incorporates a gated recurrent unit (GRU) layer within the encoder to enhance its ability to process spectral sequences. Our experimental evaluations across several public datasets reveal that our proposed method, distinguished by its spectral transformer, achieves superior classification performance, particularly in scenarios with limited labeled samples, outperforming existing state-of-the-art approaches.

1. Introduction

Hyperspectral imaging (HSI), a pioneering remote sensing technology, has proven its distinct benefits across various domains in recent years. This technology surpasses traditional imaging by offering richer, more detailed data for precise object identification and analysis. It achieves this by capturing continuous spectral information ranging from visible light to near-infrared bands. The evolution of HSI has not only revolutionized traditional Earth observation and environmental monitoring but also demonstrated its exceptional application value in urban planning, disaster management, and agriculture [1,2,3,4]. However, the intricate and high-dimensional nature of hyperspectral data poses significant challenges to effective data analysis and processing. This complexity necessitates ongoing research to discover more efficient data processing and analysis methods.

In the initial stages, traditional methods such as support vector machines (SVMs) [5,6], random forests (RFs) [7], k-NN [8], and PCA [9] were commonly employed for hyperspectral image classification. Among these, the SVM model, despite its compactness, struggled with identifying an appropriate nonlinear kernel function. RF, by integrating multiple decision trees, exhibited superior generalization capabilities but demanded substantial computational resources. While k-NN offered flexibility by adjusting the k value to suit different problems, it often underperformed with category-imbalanced datasets. PCA, based on linear assumptions, found it challenging to handle nonlinear data structures. Furthermore, these traditional methods typically relied on manually designed features and lacked the capacity to extract deep features, rendering them often ineffective for hyperspectral image classification tasks.

In recent years, the swift advancement of deep learning technology has significantly propelled hyperspectral image classification technology. The goal is to harness the capabilities of sophisticated neural network architectures for more robust and efficient classification. Early deep learning methods, such as stacked autoencoders (SAEs) and deep belief networks (DBNs) [10], set the groundwork by emphasizing feature extraction through fully connected layers. However, these methods’ reliance on fully connected layers led to a large number of network parameters and necessitated diverse training data.

To mitigate these issues, the convolutional neural network (CNN) [11] was introduced into HSI classification. Qing et al. [12] proposed a multiscale residual convolutional neural network model, MRA-NET, for hyperspectral image classification, focusing on efficient channel attention network fusion. Bhatti et al. [13] introduced the local similarity projection Gabor filter (LSPGF) algorithm for hyperspectral image classification, combining dimensionality reduction via local similarity projection and 2D Gabor filtering with CNN-based feature extraction. Several researchers have employed 3D CNNs for hyperspectral image classification tasks. Yue et al. [14] proposed an HSI classification method based on adaptive spatial pyramid constraint (ASPC), which leverages the global spatial neighborhood information of labeled samples to enhance the model’s generalization ability in scenarios with limited training data. Zhu et al. [15] integrated global convolutional long short-term memory and a global joint attention mechanism to address the challenge of insufficient and imbalanced sample data, introducing the SSDGL framework for HSI classification. Despite their success, these methods still grapple with the challenge that CNNs are local and translation-invariant, potentially failing to capture long-range dependencies in hyperspectral data. The self-attention mechanism, a key feature of the transformer architecture, allows the model to dynamically weigh and integrate information from the entire input spectrum [16]. The transformer model’s self-attention mechanism enables it to capture long-range dependencies in the data, and transformers are permutation-invariant, making them more suitable for processing unordered feature sets [17]. Sun et al. [18] proposed a spectral–spatial feature tag transformer (SSFTT) method for HSI classification, which captures spectral–spatial features and high-level semantic features, outperforming several state-of-the-art methods. Yang et al. [19] proposed a hyperspectral image transformer (HiT) classification network that embeds convolution operations into the transformer structure to capture subtle spectral differences and convey local spatial context information.

Despite substantial advancements in HSI classification using deep learning, these methods continue to face challenges. End-to-end supervised learning often necessitates a large number of labeled samples to optimize deep models. To mitigate these issues, strategies such as lightweight modeling [20], active learning [21], and self-supervised pretraining modeling (SSL) have been introduced. These methods aim to enhance generalization capabilities and utilize unlabeled raw data, which are more readily available than labeled samples. In this paper, we introduce a spectral transformer-based self-supervised learning algorithm (S3L) for HSI classification when labeled data are scarce. The goal is to optimize the performance of hyperspectral image classification. This method comprises two stages: pretraining and fine-tuning. In the pretraining stage, a mask mechanism is employed to learn the spatial representation of HSI, and the spectral features are modeled through the spectral transformer module. In the fine-tuning stage, labeled data are used to optimize pretraining weights and enhance classification accuracy. Experimental results on multiple public datasets demonstrate that the proposed method achieves state-of-the-art performance.

The main contributions are summarized as follows:

1. We propose a unique spectral transformer structure specifically designed to capture and model the complex relationships between different spectral bands in hyperspectral images. This structure enhances the model’s sensitivity to spectral information, allowing it to more accurately capture subtle changes in HSI data.

2. We adopt a pretraining and fine-tuning strategy, using a mask mechanism and a spectral transformer to learn the spatial representation of HSI from unlabeled data. This approach enhances the sequence dependence of spectral features and learns robust spatial representation of the hyperspectral image by introducing a mask mechanism.

3. Experimental results on multiple public datasets demonstrate that the proposed S3L outperforms other methods, achieving state-of-the-art performance.

In the subsequent sections, we delve into the specifics of the proposed S3L. Section 2 reviews previous work. Section 3 provides a detailed introduction to the S3L. In Section 4, we carry out comparative and ablation experiments and analyze the results to further validate the effectiveness of the proposed S3L. Finally, Section 5 offers a comprehensive summary of the entire text.

2. Related Work

2.1. Hyperspectral Image Classification

HSI classification serves as a foundational pillar for applications of HSI, finding extensive utility across various domains including agriculture, forestry, urban planning, military defense, and environmental surveillance. The realm of hyperspectral image classification algorithms bifurcates into two primary categories: conventional methodologies and those predicated on deep learning techniques.

(1) Traditional methods: HSI classification has predominantly concentrated on extracting spectral features. Tang et al. [22] introduced two manifold-based sparse representation algorithms aimed at addressing the instability issues of ℓ1-based sparse representation. By integrating local structure and smoothness properties into the sparse representation, they significantly enhanced classification performance. Gu et al. [23] developed a novel framework, multistructural element nonlinear multikernel learning (MultiSE-NMKL), which merges spectral and spatial features. This approach generates extended morphological profiles (EMPs) using multistructural elements to encapsulate spatial–spectral information. Furthermore, it employs nonlinear multikernel learning (NMKL) to derive optimal combination kernels from predefined linear basis kernels, thereby boosting classification accuracy. Samaniego et al. [24] outlined a general strategy to identify the Euclidean metric in a low-dimensional space that minimizes the variance for a specific class label. This method primarily addresses challenges in remote sensing, pattern recognition, and statistics by improving classification accuracy through ensemble prediction, tackling the issue of nonlinear relationships in object classification. Ren et al. [25] proposed an innovative classification technique that enhances HSI classification by integrating random forests with label constraints. This method leverages spectral and spatial information through principal component analysis and morphological profiling. By incorporating spatial continuity label constraints into a random forest classifier, it achieves superior accuracy over traditional random forest and support vector machine (SVM) methods.

Banki et al. [26] introduced a wavelet-based kernel function for SVMs, termed the wavelet kernel, to advance HSI classification. This kernel demonstrates its effectiveness in comparison with traditional Gaussian and polynomial kernels in remote sensing applications. Hsu et al. [27] presented a classification method that utilizes a learning dictionary to amalgamate spectral and spatial information into a joint sparse representation, addressing the challenge of dimensionality reduction in HSI analysis. Melgani et al. [6] conducted a thorough evaluation of SVMs for hyperspectral remote sensing image classification. They compared the SVMs’ efficiency and effectiveness against traditional feature reduction techniques and other nonparametric classifiers. Additionally, they explored various multiclass strategies to overcome the challenges of applying binary SVMs to multiclass problems in hyperspectral data analysis. Zhang et al. [7] introduced a cascaded random forest (CRF) method that enhances the random forest algorithm by integrating a hierarchical random subspace method for feature selection with boosting. This combination, along with a novel out-of-bag error method for updating sample weights, aims to improve classification performance without risking overfitting. Heras et al. [28] advocated for the use of extreme learning machines (ELMs) in classifying hyperspectral images for land cover classification. They introduced two ELM-based techniques to integrate spectral and spatial information, which not only improved classification accuracy and efficiency but also reduced execution time compared to similar technologies. Li et al. [29] proposed the robust sparse representation-based classification (RSRC) method and its extension, the joint RSRC (JRSRC), to overcome the limitations of traditional SRC methods. By effectively handling outliers in HSI classification, these methods demonstrated improved performance over existing techniques, including orthogonal matching pursuit and other popular classifiers.

(2) Deep Learning: Deep learning-based algorithms for hyperspectral image classification can be broadly categorized into three main approaches: convolutional neural network (CNN)-based methods (encompassing both 2D and 3D architectures), attention mechanism-based methods, and those leveraging transformer architectures. Lu et al. [30] proposed an evolutionary block-based CNN (EB-CNN), which employs a genetic algorithm to automatically determine the optimal CNN architecture for hyperspectral image classification. Zhou et al. [31] introduced multiscale convolutional gradient features (MCGFs), refined through pseudo-Siamese networks, to capture finer common features and overcome the limitations of traditional handcrafted features and deep learning methods requiring extensive training. Cai et al. [32] introduced the transformer network (TRN) into the field of automatic modulation classification, highlighting its ability to fuse global information of sample sequences to improve classification accuracy, especially in low signal-to-noise ratios. TRN outperforms other deep models and traditional methods in terms of classification accuracy. Hong et al. [33] developed a general multimodal deep learning (MDL) framework that combines data fusion and network architecture strategies to extend from pixel-level classification to spatial information modeling using CNNs. Wu et al. [34] proposed a deep learning-based framework, CCR-Net, which utilizes convolutional neural networks and a novel cross-channel reconstruction module to classify multimodal remote sensing data. Yu et al. [35] proposed an image-based global learning framework of a dual-channel convolutional network (DCCN) that optimizes the utilization of global and multiscale information for HSI classification. Qing et al. [36] introduced a 3D self-attention multiscale feature fusion network (3DSA-MFN) for HSI classification, incorporating 3D multihead self-attention to capture interactive features over long distances and effectively fuse spatial and spectral features. Zhong et al. [37] introduced a spectral space transform network (SSTN), with spatial attention and spectral correlation modules, and a factorized architecture search (FAS) framework for hyperspectral image classification. Peng et al. [38] used a dual-branch structure to capture fine-grained spatial information and extract spectral features, proposing a CASST method for hyperspectral image classification, which achieved better accuracy than the existing transformer classification model. Qing et al. [39] utilized spectral attention and self-attention mechanisms to extract spectral–spatial features and proposed an end-to-end transformer model, SAT Net, for hyperspectral image classification.

2.2. Self-Supervised Learning

Deep learning methodologies predominantly rely on data-driven approaches, necessitating extensive efforts in data collection and annotation—a process that is both time-consuming and resource-intensive. Self-supervised learning [40] emerges as a potent solution, capable of extracting visual features from vast quantities of unlabeled images or videos, thereby significantly reducing the dependency on labeled datasets for deep learning applications. Within the realm of self-supervision theory, Teng et al. [41] introduced an innovative approach that leverages data from downstream tasks to refine unlabeled data, enhancing self-supervised learning. This method primarily addresses the challenges arising when the conditional independence (CI) condition is not met, which otherwise leads to a marked increase in sample complexity for downstream tasks. Bansal et al. [42] established a novel upper bound to gauge the generalization gap of classifiers, while Huang et al. [43] developed a technique to mathematically evaluate data augmentation through the introduction of a specific metric. This metric provides an upper limit on the error rate for downstream classification tasks, offering a theoretical framework to comprehend the impact of contrastive learning on the generalization capabilities within self-supervised learning.

In the domain of image representation learning, Pandey et al. [44] unveiled a cutting-edge semisupervised method for 2D medical image segmentation. This method employs contrastive learning (CL) on image patches to capture local feature representations, coupled with a novel consistency regularization (CR) strategy. This combination effectively addresses the issue of confirmation bias and fosters improved feature-space clustering. Park et al. [45] introduced an innovative model, RUC, designed to tackle the challenges of misprediction and overconfidence frequently encountered in unsupervised image clustering techniques. RUC’s innovation lies in its use of pseudolabels from existing image clustering models as a noisy dataset, which may include misclassified samples. Through a retraining process, RUC aims to rectify misaligned knowledge, thus alleviating the overconfidence issue in predictions. In the realm of video representation learning, Jenni et al. [46] introduced an innovative self-supervised approach for learning video representations attuned to changes in motion dynamics. This method trains a neural network to differentiate between video sequences and their temporally transformed counterparts, eliminating the need for manual labeling. Han et al. [47] developed a vision-centric self-supervised technique for video representation learning that enhances information–noise contrastive estimation (InfoNCE) training. This enhancement is achieved through two key innovations: the inclusion of semantic class positive samples to boost performance and the introduction of a novel self-supervised cotraining strategy. This strategy leverages the complementary information from different visual perspectives (RGB flow and optical flow) to generate positive samples from one view based on another. In the domain of 3D feature learning, Xie et al. [48] put forward an unsupervised pretraining methodology for 3D point cloud comprehension, diverging from the traditional focus on advanced scene understanding tasks. This method employs unsupervised pretraining on a vast dataset of 3D scenes, utilizing a unified architecture, source datasets, and contrastive losses to achieve performance that outstrips recent state-of-the-art results in segmentation and detection tasks across six diverse indoor and outdoor, real and synthetic datasets. The notable enhancement in performance underscores the adaptability of the learned representations across different domains.

3. Methodology

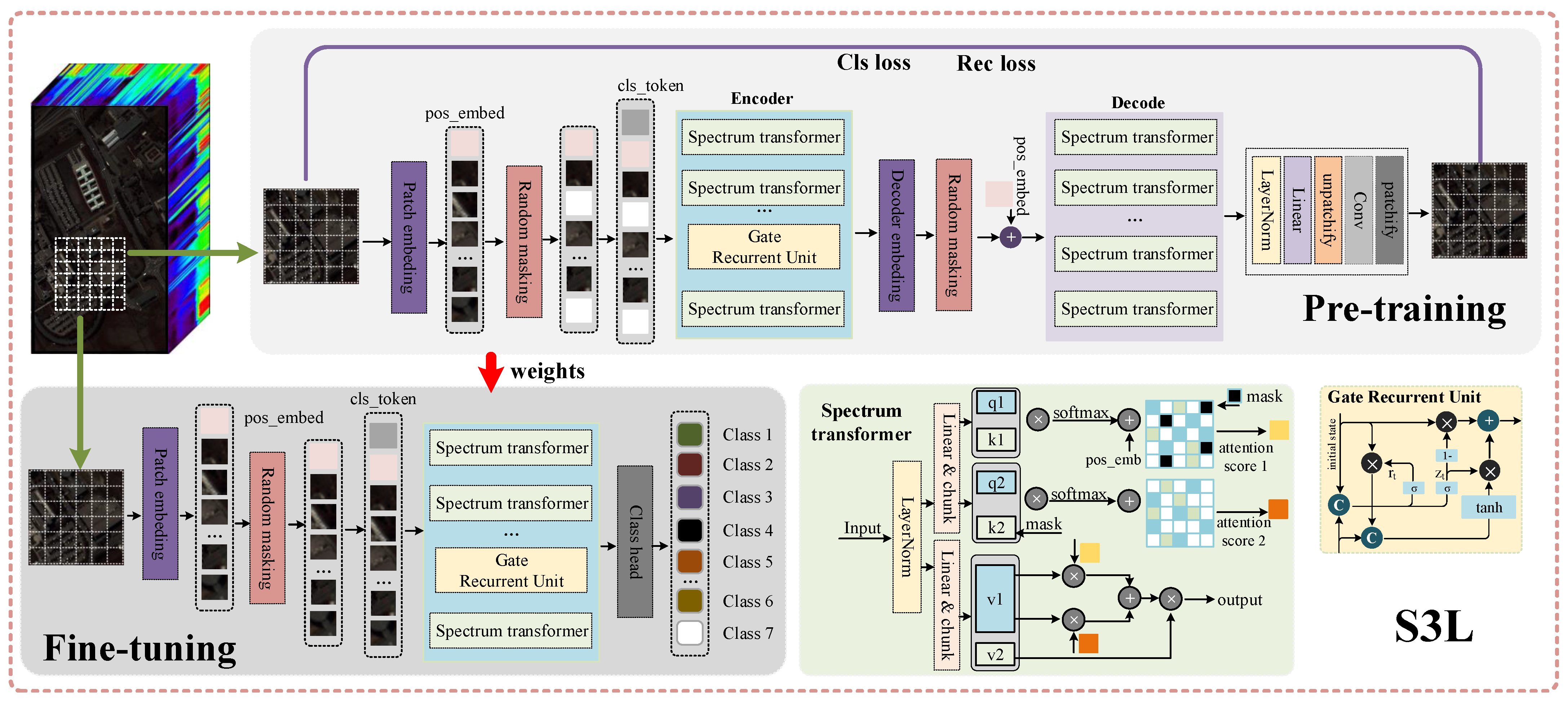
In order to achieve efficient classification performance with limited HSI annotation data, we propose a self-supervised learning algorithm, S3L (spectral–spatial self-learning), which deeply processes spectral features. The design of S3L is inspired by current state-of-the-art techniques in self-supervised learning, particularly their effectiveness in processing high-dimensional feature spaces. The overall architecture of this algorithm is shown in Figure 1. At the core of S3L is its unique spectral transformer architecture, specifically designed to parse and learn from the complexity and high dimensionality of HSI data. The introduction of the spectral transformer structure aims to enhance the model’s sensitivity to spectral information and capture subtle changes in HSI data more accurately. The S3L algorithm is divided into two main stages: pretraining and fine-tuning. In the pretraining stage, we adopt an innovative approach that does not rely on labeled data but introduces a mask mechanism to learn a robust spatial representation of hyperspectral images. The goal of this stage is to enable the model to autonomously learn and understand the intrinsic structure and characteristics of HSI data without explicit label guidance. Concurrently, the introduction of the spectral transformer enables the model to conduct in-depth modeling of spectral features in HSI data, capturing richer and more detailed information. To further enhance the model’s sequential dependence on spectral features, we innovatively couple the gated recurrent unit (GRU) module with the transformer’s encoder module. This coupling not only improves the model’s ability to process time series data but also enhances its ability to understand and represent spectral features. In this way, S3L can handle spatiotemporal dynamic changes in HSI data more effectively, providing more accurate classification performance.

Throughout the pretraining process, we continually optimize and adjust the model’s parameters through a comprehensive optimization strategy, encompassing both classification and reconstruction functions. This strategy ensures that the model can glean as much effective information as possible during the pretraining phase, laying a solid foundation for the subsequent fine-tuning phase. Upon entering the fine-tuning phase, we introduce limited labeled data to further refine and optimize the model weights obtained during the pretraining phase. The goal of this stage is to enable the model to adapt more accurately to specific classification tasks and further enhance the accuracy of hyperspectral image classification. Through the robust feature representation obtained in the pretraining stage coupled with the fine adjustments in the fine-tuning stage, S3L can significantly improve the overall performance of classification tasks.

In the following section, we first delve into the details of the spectral transformer module in S3L, explaining its design concept and working mechanism. We then explore the pretraining and fine-tuning process of S3L and how these two stages interact with and complement each other to advance the hyperspectral image classification task.

3.1. Spectrum Transformer

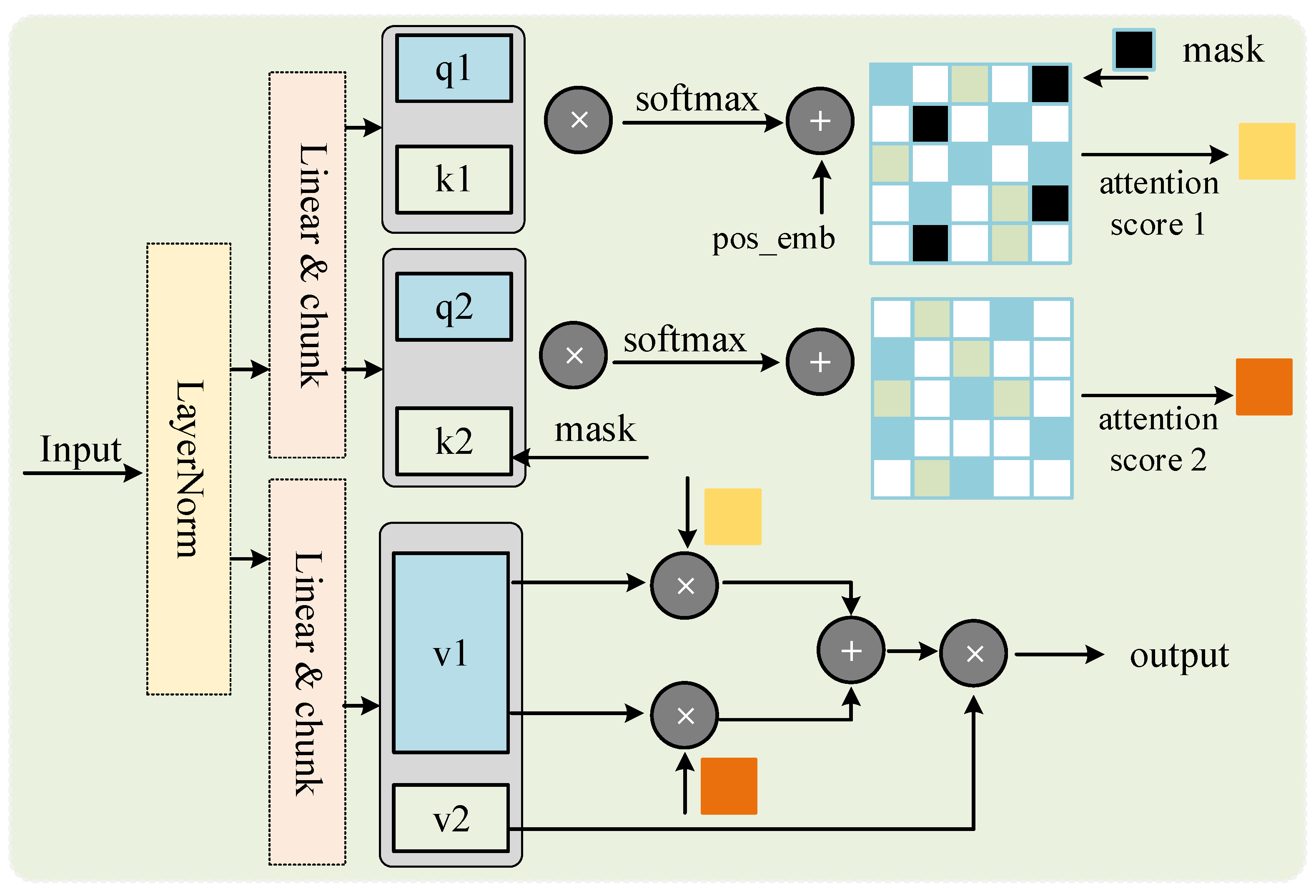
Masked image modeling in self-supervised learning methods is a transformative technology, particularly crucial in HSI classification. Existing masking methods primarily focus on modeling spatial features, often overlooking the importance of spectral features. To address this, we propose a unique spectral transformer structure specifically designed to capture and model the complex relationships between different spectral bands in hyperspectral images, as depicted in Figure 2.

Specifically, for the input hyperspectral feature matrix, we first normalize it to eliminate scale differences between different bands. Next, we perform carefully designed partitioning and splicing operations on the spectral features. This not only preserves the integrity of the spatial features but also significantly enhances the model’s ability to capture spectral sequential feature dependencies when processing input shifts by introducing changes in spectral dimensions. We further linearly map the normalized feature vectors to recalibrate the spectral dimensions, a step that critically influences the model’s ability to understand and process spectral data.

By further dividing, we obtain two components, v and $gate$, which play a central role in the model. Additionally, the feature vector generates $query$ and $key$ through another linear mapping, two components crucial in the transformer architecture. We further divide them, resulting in different linear components (such as $q1$, $q2$, $k1$, and $k2$), and through multiple position shifts, we enable the model to more deeply understand and model the complex interactions between spectral features. For $k2$, we adopt an innovative random masking strategy. By setting the value of the mask part to zero, the model can ignore certain noncritical parts and focus on more important information. We also introduce rotational position encoding to enhance the model’s understanding of sequential relationships in hyperspectral sequence data. Next, the input data are padded to fit the needs of the transformer model and facilitate parallel processing of spectral features. This step enables the model to efficiently capture different granularity levels in the spectral data. Simultaneously, the mask is also padded accordingly to ensure its consistency with the input data length. The core of the transformer model lies in its attention mechanism. We obtain the final similarity matrix by calculating the similarity between $query$ and $key$ and adjusting it using the relative position deviation. These attention weights are then applied to the feature variables V, producing the output matrix $att2$. For $k1$ and $q1$, we adopt a similar approach to obtain the feature output $att1$. By weighting information at different locations, the model is able to obtain a more accurate and richer data representation. Finally, by weighted combination of $att1$ and $att2$, we obtain the final feature output. This approach enables the model to effectively handle complex relationships between adjacent pixels and spectral features, further enhancing the performance of S3L. The entire implementation process of the spectral transformer demonstrates in detail how to effectively improve the accuracy of hyperspectral image classification through carefully designed structures and strategies. The detailed execution process is shown in Algorithm 1.

Algorithm 1 Spectrum transformer

1: Input: Hyperspectral feature matrix x 2: Output: Processed feature matrix 3: Normalize x to obtain $normed\_x$ 4: if$self.shift\_tokens$ is true then 5:    Split and concatenate $normed\_x$ to introduce spectral dimension variations 6: end if 7: Apply linear mapping to $normed\_x$, split into v and $gate$ 8: Generate query and key from $normed\_x$, split into $q1$, $q2$, $k1$, and $k2$ 9: if mask exists then 10:    Apply masking to $k2$, setting masked values to 0 11:    Apply rotary position encoding to $q1$, $q2$, $k1$, $k2$ to enhance sequence understanding 12: end if 13: Pad input data for suitable reorganization and chunking 14: Apply the same padding to the mask to match the input data length 15: Compute similarity $sim$ between queries and keys with relative position bias 16: Apply attention mechanism to v to produce output matrices $att1$ and $att2$ 17: Weight and combine $att1$ and $att2$ to obtain the final feature output 18: Enhance performance by processing relationships between adjacent pixels and spectral features 19: return Final feature output

3.2. Self-Supervised Pretraining

During the pretraining phase, our goal is to extract robust spatial and spectral features from hyperspectral images using a self-supervised learning approach, which does not require labeled data. We achieve this by implementing a masking mechanism that randomly occludes parts of the input hyperspectral images, creating an information bottleneck. This compels the model to predict the occluded region’s content based solely on the surrounding unoccluded context, thereby enhancing the model’s understanding of spatial and spectral dependencies in the data. The entire procedure is delineated in Algorithm 2.

Drawing inspiration from the work of Sun et al. [49], a variety of dimensionality reduction techniques were explored, including linear discriminant analysis (LDA), independent component analysis (ICA), local linear embedding (LLE), and principal component analysis (PCA). LDA is designed to enhance the separation between classes, yet it may falter with hyperspectral data where class distinctions are subtle. ICA aims to identify independent components, a challenge in hyperspectral imagery due to the often-correlated spectral signatures of materials. LLE prioritizes preserving the local structure of data, potentially overlooking broader trends. Conversely, PCA focuses on capturing components with significant variance, effectively mitigating noise by discarding low-variance elements. This attribute of PCA not only addresses the noise issue prevalent in hyperspectral imagery but also adeptly manages the sparsity associated with high-dimensional data spaces. To effectively handle noise and redundant information in hyperspectral images, we employ the principal component analysis (PCA) algorithm for data preprocessing. PCA linearly transforms the original hyperspectral data $I\in {\mathbb{R}}^{H\times W\times C}$ into a new coordinate system, the basis of which is the data’s principal component direction. The PCA-processed data are denoted as $I_p\in {\mathbb{R}}^{H\times W\times L}$, where L signifies the number of spectral channels postdimensionality reduction. We then use a sliding window of size $s\times s$ to divide $I_p$ into N small blocks of size $s\times s\times L$. Each small block is represented as $P\in {\mathbb{R}}^{s\times s\times L}$, where $N=(H-s+1)(W-s+1)$.

Algorithm 2 Pretraining process for hyperspectral image classification

1: Initialize model parameters $\theta$. 2: for each training epoch $epoch=1,2,\dots ,E$ do 3:    for each batch $(X,Y)$ in the training set do 4:      Generate a masked version of the input $X_{masked}$. 5:      Transfer $X_{masked}$ to the computation device (e.g., GPU). 6:      Compute the reconstruction loss $L_{rec}$. 7:      if labelled data is available then 8:         Compute the classification loss $L_{cls}$. 9:      end if 10:      Calculate the total loss $L=\alpha L_{cls}+\beta L_{rec}$. 11:      Update the model parameters $\theta$ to minimize L. 12:    end for 13:    Update the learning rate. 14: end for 15: Save the model state.

For these small patches P, we apply random mask operations and add positional encoding. The processed data are then passed through the encoder and decoder, which are composed of spectral transformers in sequence. In the encoder’s penultimate layer, we incorporate a GRU network structure to capture the sequential dependence of spectral features while maintaining the capture of global dependencies. This is necessary as our proposed spectral transformer performs multiple splits and calibrations when handling spectral dimensions, which may overlook the spectral continuity between adjacent pixels.

To optimize the entire pretraining process, we use two loss functions: classification loss (Cls loss) and reconstruction loss (Rec loss). The classification loss aims to preserve the model’s discriminative ability during pretraining, even when faced with incomplete spectral information. This is achieved by making accurate class predictions on unoccluded parts of the image, thereby enhancing the model’s ability to infer global information from partial data. The classification loss is expressed as

$$\mathrm{Cls}=-\sum _{i=1}^N{y}_{i}log\left(p_i\right)$$

(1)

where $y_i$ is the true class label and $p_i$ is the class probability predicted by the model.

The reconstruction loss is designed to aid the model in learning the complex structure of hyperspectral images, deeply exploring spatial–spectral features by reconstructing the mask area, and identifying subtle spectral differences of different ground objects. This enables comprehensive characterization of hyperspectral images, capturing more spatial and spectral details. The reconstruction loss is expressed as mean square error (MSE):

$$\mathrm{Rec}=\frac{1}{N}\sum _{i=1}^N{(I_i-{\widehat{I}}_i)}^2$$

(2)

where $I_i$ is the pixel value of the original image and ${\widehat{I}}_i$ is the pixel value of the reconstructed image.

3.3. Fine-Tuning

Following the initial deep learning and feature extraction in the pretraining phase, the model undergoes further refinement to enhance its performance in specific classification tasks. Fine-tuning primarily involves adjusting the pretrained weights using labeled data to align the learned features more accurately with the dataset’s specific categories. The network structure during the fine-tuning phase largely mirrors the pretrained model. The key distinction is the exclusive use of the encoder, omitting the decoder. The encoder employs the spectrum transformer to amalgamate and process spectral data, ensuring that the spatial and spectral features align with the labeled data. This method preserves the original spatial and spectral representation during refinement, enhancing its consistency with the labeled data.

A classification head is incorporated during the fine-tuning process, positioned at the model’s end. This component transforms the rich spectral–spatial features into category probability distributions. It is optimized to map learned representations to specific categories effectively, thereby minimizing classification errors. The classification head also strikes a balance between the generalized representation acquired during pretraining and the detailed information necessary for precise classification, ensuring the model’s final output accurately predicts hyperspectral image class labels. It is important to note that a lower learning rate is maintained throughout the fine-tuning process. This strategy preserves the general features acquired during pretraining while facilitating necessary model adjustments for new classification tasks. Consequently, the fine-tuning process can optimize the model and make necessary adjustments while retaining its robust feature extraction capabilities, thereby enhancing the model’s performance in specific tasks. In summary, the fine-tuning phase is a refinement and enhancement of the pretraining phase. It fine-tunes the learned features and adjusts the network structure to better suit specific classification tasks. This process not only boosts the model’s accuracy but also ensures its comprehensive understanding and effective processing of hyperspectral images. Through fine-tuning, our model exhibits superior performance across a range of complex classification scenarios.

4. Datasets and Experimental Setting

This section commences with an introduction to three publicly accessible datasets, followed by a quantitative and qualitative comparative analysis with other sophisticated methods. Subsequently, we perform a series of ablation experiments to evaluate and highlight the efficacy of each component within the S3L framework.

4.1. Datasets

Our research utilizes four renowned hyperspectral image datasets, Indian Pines (IN), University of Pavia (UP), Salinas (SA), and Houston 2013, to assess the performance of our proposed method. These datasets, widely recognized in the hyperspectral image processing domain, offer hyperspectral images with diverse characteristics, facilitating a thorough evaluation of our method’s effectiveness and generalizability.

Table 1. Summary of hyperspectral image datasets.

	IN	UP	SA	Houston
Region or country	Indiana, USA	Pavia, Italy	California, USA	Texas, USA
Sensor type	AVIRIS	ROSIS	AVIRIS	ITRES CASI
Number of bands	200	103	204	144
Wavelength ($\mathsf{\mu }$m)	0.4–2.5	0.43–0.86	0.4–2.5	0.38–1.05
Spatial resolution	20 m	1.3 m	3.7 m	2.5 m
Image size	$145\times 145$	$610\times 340$	$512\times 217$	$349\times 1905$
Number of labeled samples	10,249	42,776	54,129	15,429
Number of classes	16	9	16	15

summarizes the basic information of the four datasets.

Table 2. The number of training and testing samples across the University of Pavia, Indian Pines, and Salinas datasets).

	Indian Pines			Salinas			University of Pavia
Class	Land Cover Type	Training	Testing	Land Cover Type	Training	Testing	Land Cover Type	Training	Testing
1	Alfalfa	20	46	Weeds-1	20	2009	Asphalt	20	6631
2	Corn-notill	20	1428	Weeds-2	20	3726	Meadows	20	18,649
3	Corn-mintill	20	830	Fallow	20	1976	Gravel	20	2099
4	Corn	20	237	Fallow-plow	20	1394	Trees	20	3064
5	Grass-past	20	483	Fallow-sm	20	2678	Metal sheets	20	1345
6	Grass-trees	20	730	Stubble	20	3959	Bare Soil	20	5029
7	Grass-pas-m	20	28	Celery	20	3579	Bitumen	20	1330
8	Hay-windr	20	478	Grapes	20	11,271	Bricks	20	3682
9	Oats	20	20	Soil	20	6203	Shadows	20	947
10	Soybean-n	20	972	Corn	20	3278
11	Soybean-m	20	2455	Lettuce-4wk	20	1068
12	Soybean-c	20	593	Lettuce-5wk	20	1927
13	Wheat	20	205	Lettuce-6wk	20	916
14	Woods	20	1265	Lettuce-7wk	20	1070
15	Buildings	20	386	Vineyard-unt	20	7268
16	Stone	20	93	Vineyard-t	20	1807
	Total	320	10,249	Total	320	54,129	Total	180	42,776

and

Table 3. The number of labeled training samples and testing samples of the Houston 2013 dataset.

	Land Cover Type	Training	Testing
1	Healthy Grass	20	1251
2	Stressed Grass	20	1254
3	Synthetic Grass	20	697
4	Trees	20	1244
5	Soil	20	1242
6	Water	20	325
7	Residential	20	1268
8	Commercial	20	1244
9	Road	20	1252
10	Highway	20	1227
11	Railway	20	1235
12	Parking Lot 1	20	1233
13	Parking Lot 2	20	469
14	Tennis Court	20	428
15	Running Track	20	660
	Total	300	15,029

illustrate the training and test samples.

Indian Pines: The Indian Pines dataset, captured by the Airborne Visible/Infrared Imaging Spectroradiometer (AVIRIS) in 1992, represents a 145 × 145 pixel region in northwest Indiana’s Indian Pines area. It comprises 21,025 samples, initially with 224 spectral bands in the 0.4 to 2.5 µm range. However, due to water absorption and noise, 24 bands were discarded, leaving 200 usable bands. The spatial resolution is 20 m. The dataset, known for its diverse class representation, includes 16 different classes with a total of 10,249 labeled samples, primarily consisting of agricultural land and natural perennial vegetation.

Salinas: The Salinas dataset, collected by the AVIRIS sensor in California’s Salinas Valley, is characterized by a high spatial resolution of 3.7 m per pixel. The original dataset includes 224 bands with a spectral range from 400 to 2500 nm. After excluding 20 bands due to water absorption, 204 bands were retained for analysis. The dataset, covering an area of 512 × 217 pixels or a total of 111,104 samples, includes 16 different categories with 54,129 labeled samples, featuring diverse landscapes such as vegetable plots, bare soil, and vineyards.

University of Pavia: The University of Pavia dataset, also known as PaviaU, was collected by the ROSIS-03 sensor in the urban area of Pavia, Northern Italy. It boasts a high geometric resolution of 1.3 m, consisting of 610 × 340 pixels, with a total of 207,400 samples. Initially, 115 frequency bands were included, 12 of which were discarded due to noise, leaving 103 frequency bands for our experiments. The dataset features urban landscapes with nine categories and 42,776 labeled samples, including various urban surfaces such as asphalt, bricks, grass, and trees.

Houston 2013: The Houston 2013 dataset, captured using CASI-1500 sensors, encompasses the University of Houston campus and adjacent regions. It comprises 349 by 1905 pixels, featuring a comprehensive collection of 144 spectral bands. These bands span a spectral range from 380 nm to 1050 nm, with each pixel representing a spatial resolution of 2.5 m. The dataset is categorized into 15 distinct classes, encompassing various natural and human-made surfaces such as grass, trees, soil, and water, among others. It includes a total of 15,029 labeled pixels, facilitating detailed analysis and classification tasks.

4.2. Implementation Details

We employed the PyTorch 1.13.1 library to construct an experimental framework for hyperspectral image classification. The system used for this experiment was equipped with an NVIDIA GPU 4090 (Santa Clara, CA, USA), boasting 24 GB of memory, and operated within a Python 3.8 environment. In the experiment, we configured 20 training samples per category, set the window sizes to 27, and established a batch size of 512. We ran the model for 300 epochs with a learning rate of $1\times {10}^{-3}$. Regarding the mask settings, we maintained a mask ratio of 0.8 and an MLP ratio of 2.0, and we assigned 128 to the number of hidden channels. The dimensions of both the model’s encoder and decoder were set to 128. However, they differed in complexity: the encoder consisted of two layers, while the decoder was more intricate with six layers. Each layer contained eight‘ attention heads. We set the temperature to 1.0 and the hierarchical loss rate to 0.005. The model was trained using the Adam optimizer. To minimize the effects of random sampling, we conducted the experiment multiple times, each time with different initial training samples.

4.3. Comparative Analysis

To assess the efficacy of our proposed method, we juxtapose it with eight distinct methods: HybridSN [50], 3DAES [51], SSFTT [18], FDSSC [52], DCFSL [53], CLB [54], and DBDA [55]. HybridSN [50] is a spectral–spatial 3D-CNN supplemented with a spatial 2D-CNN. This method jointly extracts spatial–spectral features from a multitude of spectral bands and further learns a spatial representation at a more abstract level. 3DAES [51] is a semisupervised Siamese network that incorporates an autoencoder module and a Siamese network. This network explores information in large volumes of unlabeled data and rectifies it with a limited set of labeled samples. SSFTT [18] captures spectral–spatial features and high-level semantic features using a spectral–spatial feature extraction module and a transformer encoder module. FDSSC [52] is an end-to-end fast dense spectral–spatial convolution framework. It employs different convolution kernel sizes to extract spectral and spatial features, respectively, and utilizes a densely connected structure for deep learning of features. DCFSL [53] employs a conditional adversarial domain adaptation strategy to address the few-shot learning and domain adaptation problems within a unified framework. CLB [54] is an unsupervised framework that leverages contrastive learning methods and transformer models for hyperspectral image classification. DBDA [55] is a dual-branch dual-attention mechanism network that captures a vast number of spectral and spatial features contained in HSI. It uses channel attention blocks and spatial attention blocks to refine and optimize the extracted feature maps.

4.3.1. Quantitative Analysis

Table 4. Comparative analysis of quantitative classification outcomes using various algorithms on the IN dataset. The best performing results are shown in bold.

Class No.	HybridSN	DCFSL	3DAES	SSFTT	FDSSC	CLB	DBDA	Proposed
1	91.87 ± 3.2	95.26 ± 2.3	95.50 ± 0.9	100.00 ± 0.0	91.38 ± 5.8	94.59 ± 2.7	88.95 ± 6.1	88.47 ± 5.5
2	58.38 ± 5.4	58.86 ± 7.6	88.79 ± 1.4	87.54 ± 8.3	91.32 ± 6.7	88.59 ± 7.2	93.34 ± 2.1	94.82 ± 0.7
3	82.77 ± 6.3	66.92 ± 9.1	70.78 ± 4.8	86.22 ± 7.4	89.60 ± 8.6	77.12 ± 3.5	96.97 ± 2.2	95.27 ± 0.8
4	77.38 ± 8.7	84.61 ± 5.3	77.82 ± 6.2	98.94 ± 0.6	81.78 ± 7.9	85.33 ± 4.4	33.22 ± 9.4	84.13 ± 8.1
5	94.41 ± 4.5	77.91 ± 8.8	85.31 ± 3.6	92.08 ± 5.1	98.20 ± 0.9	46.25 ± 8.9	95.15 ± 1.8	96.70 ± 3.3
6	70.61 ± 7.1	87.45 ± 4.1	54.11 ± 9.5	97.11 ± 2.0	96.22 ± 3.1	65.89 ± 9.3	91.86 ± 1.1	100.00 ± 0.0
7	93.89 ± 2.6	97.83 ± 0.6	100.00 ± 0.0	100.00 ± 0.0	98.75 ± 0.8	100.00 ± 0.0	98.68 ± 0.6	94.40 ± 5.6
8	80.55 ± 6.4	89.50 ± 3.7	61.06 ± 8.6	99.07 ± 0.6	97.58 ± 0.5	34.30 ± 8.2	72.00 ± 6.9	93.16 ± 4.3
9	98.27 ± 1.2	97.02 ± 0.7	96.49 ± 1.2	100.00 ± 0.0	98.70 ± 1.3	89.82 ± 7.8	100.00 ± 0.0	100.00 ± 0.0
10	91.11 ± 0.9	69.07 ± 9.6	85.88 ± 2.8	88.70 ± 7.0	77.37 ± 8.4	84.31 ± 5.9	90.28 ± 3.4	85.74 ± 6.5
11	97.16 ± 2.5	65.86 ± 8.0	98.90 ± 1.1	84.86 ± 9.8	90.90 ± 7.5	88.18 ± 6.6	70.50 ± 7.7	88.69 ± 4.7
12	76.39 ± 8.9	58.28 ± 9.4	87.11 ± 2.2	76.18 ± 8.6	85.33 ± 5.1	89.32 ± 3.9	97.04 ± 1.5	96.77 ± 0.8
13	88.73 ± 7.2	96.93 ± 0.5	99.49 ± 0.5	98.90 ± 1.1	92.46 ± 4.8	89.60 ± 5.7	98.60 ± 1.4	92.53 ± 6.3
14	96.72 ± 2.3	87.36 ± 9.5	97.84 ± 1.6	97.81 ± 1.2	96.64 ± 1.3	100.00 ± 0.0	100.00 ± 0.0	100.00 ± 0.0
15	74.90 ± 9.8	68.37 ± 8.7	99.20 ± 0.8	94.51 ± 2.9	84.92 ± 7.4	92.65 ± 4.6	86.73 ± 8.2	94.47 ± 3.1
16	78.03 ± 7.3	96.83 ± 2.2	96.30 ± 3.7	100.00 ± 0.0	82.19 ± 9.1	73.80 ± 8.4	89.76 ± 9.9	88.73 ± 5.4
OA (%)	83.17 ± 2.1	81.99 ± 1.8	87.78 ± 2.9	91.14 ± 2.5	91.24 ± 2.2	88.43 ± 1.9	91.65 ± 1.7	93.45 ± 1.5
AA (%)	82.13 ± 2.8	80.73 ± 3.4	89.20 ± 1.9	91.68 ± 2.5	85.56 ± 2.7	85.38 ± 2.1	87.09 ± 2.9	92.20 ± 1.4
Kappa × 100	77.10 ± 2.5	79.36 ± 2.2	91.62 ± 1.8	89.24 ± 2.6	87.90 ± 2.3	88.67 ± 1.7	91.16 ± 1.2	92.78 ± 2.0

displays the quantitative experimental results of various methods on the IN dataset. The proposed method consistently outperforms other techniques across various indicators. Specifically, S3L achieves an OA of 93.45%, which is 1.8% higher than the closest competitor, DBDA, and significantly surpasses traditional methods such as HybridSN. In the AA domain, the proposed method again leads with 92.2%, slightly higher than SSFTT’s 91.68%. This underscores the balanced performance of the proposed method across different categories. SSFTT can achieve higher classification performance with limited labeled samples. For instance, the OA of the SSFTT method is improved by 9.58% over the HybridSN method and 3.83% over the 3DAES method. The addition of methods like CLB and DBDA, which utilize contrastive learning and attention mechanisms, respectively, are beneficial for handling classification boundary issues. As shown in the per-class accuracy results, our proposed method can handle boundary information better, achieving 100% accuracy for Classes 6, 9, and 14.

Table 5. Comparativeanalysis of quantitative classification outcomes using various algorithms on the SA dataset. The best performing results are shown in bold.

Class No.	HybridSN	DCFSL	3DAES	SSFTT	FDSSC	CLB	DBDA	Proposed
1	86.16 ± 5.7	97.37 ± 0.6	96.99 ± 0.3	94.64 ± 2.6	94.25 ± 5.2	92.34 ± 7.8	93.42 ± 6.9	94.17 ± 5.8
2	88.67 ± 6.8	96.19 ± 0.2	99.10 ± 0.8	97.84 ± 1.7	95.55 ± 3.3	93.45 ± 7.1	94.26 ± 5.8	97.68 ± 2.2
3	91.49 ± 7.9	89.84 ± 8.0	92.07 ± 4.8	96.38 ± 3.2	94.69 ± 7.3	93.68 ± 8.8	94.56 ± 5.1	96.31 ± 3.6
4	90.72 ± 8.0	99.47 ± 0.4	91.60 ± 3.4	95.05 ± 8.7	93.59 ± 5.6	92.36 ± 6.2	92.60 ± 7.4	97.26 ± 2.7
5	88.45 ± 5.3	91.46 ± 7.2	90.67 ± 8.7	89.90 ± 7.6	92.12 ± 5.7	91.96 ± 5.4	90.55 ± 6.7	92.97 ± 7.0
6	93.24 ± 7.4	98.69 ± 0.4	99.20 ± 0.8	96.70 ± 3.3	88.43 ± 7.6	87.43 ± 8.3	88.45 ± 5.7	91.53 ± 8.4
7	89.79 ± 6.2	97.53 ± 1.1	99.87 ± 0.1	98.40 ± 1.6	95.39 ± 3.6	92.20 ± 7.5	89.37 ± 8.6	91.46 ± 8.5
8	93.56 ± 8.7	88.72 ± 9.3	83.40 ± 6.1	89.67 ± 7.2	90.15 ± 8.4	92.77 ± 7.3	91.25 ± 6.5	93.34 ± 6.6
9	92.91 ± 7.7	94.54 ± 0.4	98.58 ± 1.0	93.01 ± 6.3	92.20 ± 5.8	92.87 ± 9.6	94.56 ± 8.2	97.68 ± 2.3
10	95.18 ± 6.6	89.60 ± 7.0	91.87 ± 8.0	92.13 ± 9.1	91.81 ± 8.8	89.66 ± 7.9	91.29 ± 6.4	96.18 ± 3.7
11	92.01 ± 5.5	96.70 ± 3.3	93.55 ± 0.4	94.20 ± 5.8	94.83 ± 6.1	94.67 ± 7.4	90.64 ± 5.9	98.47 ± 1.5
12	94.20 ± 6.7	97.62 ± 0.1	97.08 ± 0.9	89.00 ± 5.8	90.87 ± 6.4	86.28 ± 7.6	87.99 ± 8.2	88.49 ± 5.4
13	95.55 ± 7.8	99.16 ± 0.7	98.34 ± 0.2	91.26 ± 6.5	83.87 ± 7.9	88.45 ± 8.4	88.38 ± 5.6	89.36 ± 7.1
14	91.39 ± 8.6	96.06 ± 1.1	96.05 ± 2.7	89.02 ± 8.6	86.44 ± 5.3	85.10 ± 6.7	88.08 ± 7.5	92.72 ± 7.2
15	89.95 ± 9.8	77.59 ± 8.0	89.31 ± 7.1	92.98 ± 6.2	91.70 ± 7.3	89.98 ± 5.4	90.47 ± 7.7	93.87 ± 6.1
16	91.72 ± 5.6	91.56 ± 6.8	88.49 ± 9.0	86.84 ± 7.2	90.53 ± 8.4	90.97 ± 6.9	89.28 ± 5.5	92.55 ± 7.4
OA (%)	92.50 ± 1.7	92.70 ± 1.5	92.13 ± 1.8	93.01 ± 1.6	92.83 ± 1.9	92.27 ± 3.3	92.17 ± 2.7	94.87 ± 3.1
AA (%)	93.75 ± 3.4	92.87 ± 2.8	92.47 ± 2.5	94.26 ± 2.8	93.51 ± 3.4	93.87 ± 3.4	92.20 ± 3.8	94.31 ± 3.2
Kappa × 100	92.61 ± 1.9	92.31 ± 3.3	92.68 ± 2.7	92.34 ± 2.5	92.03 ± 2.0	92.49 ± 2.6	92.10 ± 2.8	92.46 ± 2.4

showcases the experimental results on the SA dataset. The OA, AA, and Kappa values of the proposed S3L are 94.87%, 94.31%, and 92.46, respectively, which surpass the corresponding values of other methods. 3DAES and SSFTT also achieved competitive results, with OA values of 92.13% and 93.01%, AA values of 92.47% and 94.26%,and Kappa values of 92.68 and 92.34, respectively. The proposed S3L obtains additional semantic information by processing spectral and spatial data, effectively capturing and utilizing spectral and spatial features in hyperspectral images.

Table 6. Comparative analysis of quantitative classification outcomes using various algorithms on the PU dataset. The best performing results are shown in bold.

Class No.	HybridSN	DCFSL	3DAES	SSFTT	FDSSC	CLB	DBDA	Proposed
1	85.26 ± 5.4	86.68 ± 7.1	98.99 ± 6.3	88.58 ± 8.2	97.56 ± 1.8	90.42 ± 7.4	96.83 ± 3.9	98.76 ± 1.2
2	98.13 ± 0.2	91.57 ± 8.8	98.51 ± 1.7	96.79 ± 5.1	91.53 ± 6.6	96.41 ± 0.7	96.55 ± 3.2	95.46 ± 3.5
3	62.08 ± 6.1	74.35 ± 5.2	84.53 ± 8.4	96.60 ± 7.5	90.23 ± 6.8	77.28 ± 5.9	51.34 ± 8.1	87.75 ± 4.4
4	73.44 ± 7.3	92.59 ± 8.6	94.16 ± 5.4	87.37 ± 6.2	85.60 ± 7.8	97.09 ± 2.9	90.46 ± 5.6	91.37 ± 2.3
5	93.63 ± 8.7	98.58 ± 0.5	99.96 ± 0.3	99.62 ± 6.4	88.06 ± 7.6	96.14 ± 1.0	98.48 ± 1.7	92.13 ± 2.5
6	98.97 ± 6.5	78.59 ± 5.7	77.67 ± 8.2	94.94 ± 7.9	94.01 ± 3.4	71.26 ± 6.3	93.36 ± 7.4	97.10 ± 2.9
7	90.58 ± 7.2	84.73 ± 8.5	81.26 ± 6.6	92.63 ± 5.5	86.93 ± 7.7	84.30 ± 8.3	43.93 ± 6.0	96.47 ± 2.5
8	80.70 ± 8.9	77.26 ± 7.3	91.92 ± 6.7	87.66 ± 5.9	83.95 ± 8.1	94.32 ± 7.6	93.29 ± 6.4	86.25 ± 6.0
9	60.47 ± 5.6	97.46 ± 1.3	97.62 ± 0.1	94.04 ± 7.0	86.88 ± 6.9	95.65 ± 5.2	97.73 ± 4.0	89.27 ± 5.7
OA (%)	85.97 ± 1.9	85.65 ± 1.5	91.56 ± 1.8	90.65 ± 1.7	89.13 ± 1.7	90.45 ± 1.4	92.55 ± 1.6	94.64 ± 1.5
AA (%)	84.13 ± 2.8	84.75 ± 3.2	92.77 ± 2.6	93.44 ± 1.5	90.86 ± 2.0	90.42 ± 1.9	83.10 ± 1.8	92.78 ± 1.7
Kappa × 100	88.39 ± 1.2	84.94 ± 1.2	94.06 ± 0.9	91.77 ± 1.5	93.13 ± 2.0	89.94 ± 1.3	91.30 ± 1.8	93.54 ± 1.6

presents the quantitative experimental results of various methods on the PU dataset. The proposed method, S3L, achieved an overall accuracy (OA) of 94.64% and an average accuracy (AA) of 92.78%, demonstrating its consistent performance across all categories and its effective integration of spectral and spatial features. The Kappa coefficient is 93.54, the second highest, indicating a high agreement between the predicted and actual class labels. Among other methods, 3DAES and SSFTT performed commendably, with overall accuracy rates of 91.56% and 90.65% respectively. FDSSC, known for its rapid and accurate feature learning, excelled in Class 1 and Class 6 but fell short in other categories. This discrepancy may be attributed to the method’s emphasis on speed, potentially compromising its accuracy in complex scenes. SSFTT and CLB also demonstrated notable performance, particularly in Class 2 and Class 3 for SSFTT, and Class 2 and Class 4 for CLB, indicating their effective feature extraction capabilities.

Table 7. Estimated comparative analysis of quantitative classification outcomes using various algorithms on the Houston 2013 dataset. The best performing results are shown in bold.

Class No.	HybridSN	DCFSL	3DAES	SSFTT	FDSSC	CLB	DBDA	Proposed
1	48.23 ± 7.2	88.12 ± 8.1	64.89 ± 5.6	91.78 ± 0.5	82.67 ± 6.4	37.54 ± 7.9	74.32 ± 8.5	81.23 ± 5.1
2	84.68 ± 6.8	63.89 ± 9.4	82.56 ± 7.3	78.42 ± 8.2	85.29 ± 5.5	85.77 ± 6.1	87.13 ± 9.1	87.59 ± 0.8
3	75.47 ± 8.7	67.83 ± 7.5	88.24 ± 6.9	80.57 ± 5.8	80.86 ± 9.8	72.74 ± 8.3	87.72 ± 7.1	88.19 ± 0.9
4	69.28 ± 9.5	74.52 ± 8.4	71.97 ± 7.2	90.98 ± 0.7	73.64 ± 6.5	76.08 ± 5.4	27.83 ± 8.9	77.05 ± 7.6
5	85.14 ± 7.4	69.79 ± 5.9	79.76 ± 8.6	87.07 ± 6.7	91.57 ± 0.6	87.58 ± 8.8	87.73 ± 9.0	90.09 ± 6.2
6	87.39 ± 8.0	87.84 ± 7.7	90.67 ± 9.4	90.92 ± 5.3	90.89 ± 7.8	91.16 ± 6.6	92.07 ± 5.7	93.94 ± 0.5
7	65.79 ± 6.3	92.49 ± 8.9	53.92 ± 7.0	93.02 ± 0.6	60.72 ± 5.5	93.02 ± 0.7	75.18 ± 6.9	87.53 ± 8.7
8	91.33 ± 9.2	82.18 ± 6.0	93.02 ± 0.8	92.36 ± 7.6	92.95 ± 5.8	91.76 ± 9.7	93.02 ± 0.9	93.02 ± 0.7
9	71.87 ± 8.1	92.27 ± 7.9	48.68 ± 6.7	93.02 ± 0.8	26.01 ± 9.0	83.02 ± 5.2	85.24 ± 7.3	86.12 ± 8.2
10	86.72 ± 0.5	66.38 ± 7.4	80.72 ± 6.4	82.60 ± 8.0	72.21 ± 9.3	77.61 ± 5.9	83.84 ± 6.8	78.68 ± 7.2
11	88.90 ± 8.6	71.71 ± 5.4	89.74 ± 7.8	77.68 ± 6.1	85.16 ± 9.0	81.80 ± 8.4	92.47 ± 0.8	81.65 ± 7.3
12	69.02 ± 6.8	69.68 ± 9.1	79.12 ± 8.2	70.36 ± 7.4	80.90 ± 5.6	81.16 ± 9.9	89.03 ± 8.7	89.71 ± 0.6
13	80.14 ± 7.6	92.31 ± 8.3	92.45 ± 0.5	91.82 ± 6.9	85.57 ± 5.7	83.20 ± 8.5	91.42 ± 7.9	85.49 ± 6.4
14	90.70 ± 8.4	81.36 ± 7.1	91.28 ± 6.2	91.71 ± 9.8	91.53 ± 5.9	93.02 ± 0.6	93.02 ± 0.7	93.02 ± 0.8
15	65.77 ± 9.6	76.63 ± 8.8	91.33 ± 0.6	89.87 ± 6.3	76.19 ± 7.5	86.48 ± 8.1	80.17 ± 5.4	88.33 ± 9.9
OA (%)	74.32 ± 1.5	73.75 ± 4.8	80.21 ± 1.9	83.05 ± 1.7	82.68 ± 1.6	83.52 ± 1.8	85.24 ± 1.9	86.50 ± 1.2
AA (%)	75.24 ± 1.4	77.92 ± 1.6	81.17 ± 2.5	84.40 ± 2.8	77.03 ± 1.7	79.39 ± 1.5	82.58 ± 1.9	85.25 ± 1.3
Kappa × 100	66.89 ± 1.2	66.71 ± 1.5	82.42 ± 1.6	81.79 ± 1.4	81.33 ± 1.8	82.27 ± 1.7	86.41 ± 1.9	85.85 ± 1.6

presents a comparative analysis of the performance metrics for various methodologies applied to the Houston 2013 dataset. The method proposed in this study attains an overall accuracy (OA) of 86.50%, an average accuracy (AA) of 85.25%, and a Kappa coefficient of 85.85. Concurrently, the SSFTT and FDSSC methods demonstrate robust performance, with SSFTT excelling in Class 4 with a 90.98% accuracy rate, and FDSSC achieving the highest classification accuracy in Class 5 at 91.57%. Nonetheless, when juxtaposed with the outcomes from other datasets, a marginal decline in the performance of all evaluated methods on the Houston 2013 dataset is observed. This decrement can likely be attributed to the larger size and the more complex spatial and spectral characteristics of the Houston 2013 dataset compared to the others.

4.3.2. Qualitative Analysis

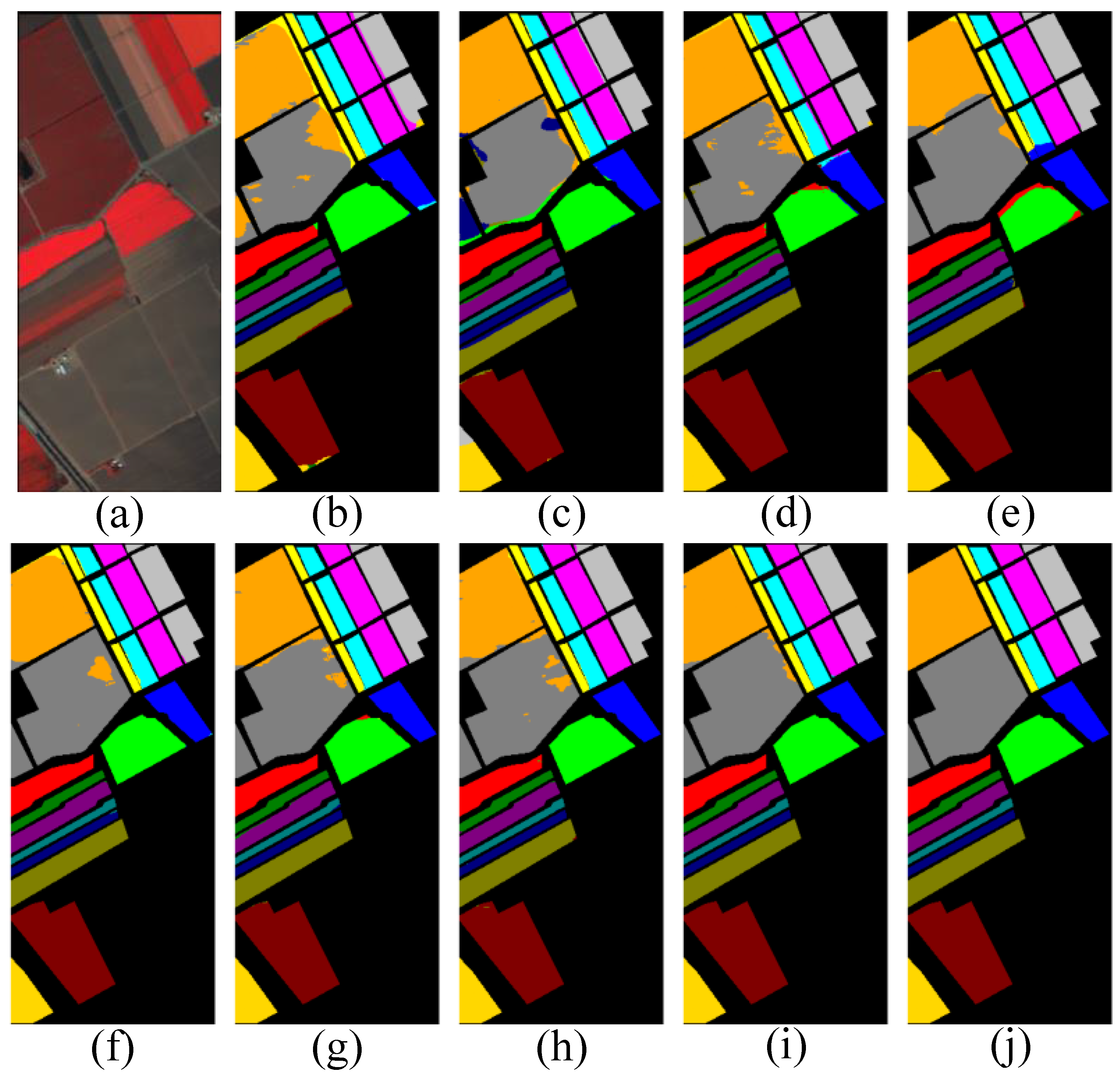
Figure 3 presents the visual results of the hyperspectral image classification task on the Indian Pines (IN) dataset. The classification results of different methods (HybridSN, 3DAES, SSFTT, FDSSC, DCFSL, CLB, and DBDA) and the ground truth are displayed in sections a–i. It is evident that the proposed method excels in preserving plot boundaries and minimizing classification errors, particularly in identifying complex surfaces such as Building–Grass–Trees–Drives and Stone–Steel–Towers. The classification results of the proposed method are more coherent and the color blocks are more compact, indicating higher classification accuracy and spatial continuity. For different types of crops, such as corn (Corn-notill, Corn-mintill, Corn) and soybeans (Soybean-notill, Soybean-mintill, Soybean-clean) with varying farming methods, the proposed method appears to distinguish more accurately between different farming statuses. This is reflected in the classification results in the figure, with clear color distinctions and fewer misclassifications. When analyzing large areas of single color such as wheat fields (Wheat) and fallow fields (Fallow, Fallow-rough plow, Fallow-smooth), the proposed method effectively reduces noise and misclassification areas, demonstrating smoother and more consistent classification results.

Figure 4 displays the visualization results of the hyperspectral image classification task on the Salinas Area (SA) dataset. The proposed method proves effective in identifying small plots and complex boundaries, such as vineyards (Grapes), lettuce (Lettuce-4wk to Lettuce-7wk), and Vineyard-untrained, accurately depicting the edges of plots. Compared to other methods, oversmoothing is reduced, thereby better preserving the spatial characteristics of the original features. Additionally, the results of the proposed method are more distinct in color distinction, reducing confusion and misclassification, especially between categories with similar colors, such as lettuce at different stages. Throughout the visualization outcomes, objects categorized as Grapes and Fallow-plow exhibit a higher propensity for misclassification.

Figure 5 illustrates the visualization results of the hyperspectral image classification task on the PU dataset. When classifying urban structures such as buildings, roads, and lanes, the proposed method produces more refined and coherent results, better preserving the structural features of the buildings, such as metal surfaces and brick distinctions. Furthermore, S3L effectively reduces noise, displaying a more uniform and consistent classification. Throughout the visualization outcomes, objects categorized as Meadows and Bare Soil exhibit a higher propensity for misclassification.

Figure 6 presents the comparative visualization outcomes for various methodologies applied to the Houston 2013 dataset, with inaccurately classified regions delineated by yellow boxes. The analysis reveals that HybridSN, DCFSL, and SSFTT exhibit a higher incidence of misclassifications, particularly with indistinct demarcations between Tennis Court and Running Track areas. Both CLB and the newly introduced S3L method encounter some classification inaccuracies within the Healthy Grass categories. Conversely, FDSSC and the novel S3L method demonstrate superior qualitative visualization outcomes. Notably, S3L stands out for its minimal misclassifications, distinct boundary delineations, and adeptness at accurately classifying small-area features as well as features possessing similar spectral signatures. Throughout the visualization outcomes, objects categorized as Stressed Grass and Water exhibit a higher propensity for misclassification.

Figure 7 presents the visualization curves of the proposed S3L method during training and validation on three hyperspectral datasets: IN, UP, and SA. For the IN dataset, the initial training loss of S3L is high, reflecting the uncertainty in the initial model. As the number of epochs increases, it eventually stabilizes around 0.2, indicating effective model convergence, with the validation accuracy stabilizing at approximately 91%. The training accuracy of S3L on the UP dataset approaches 100%, the validation accuracy nears 94%, and the final training loss is close to 0.1. The performance on the SA dataset mirrors that of the IN and UP datasets, with a similar pattern observed: the training loss significantly decreases and levels off, with the training set accuracy nearing 100% and the validation set accuracy approaching 93%.

4.4. Ablation Experiment

To validate the effectiveness of each proposed module, we designed several sets of ablation experiments. In Experiment 1, the spectral transformer module was replaced with the standard transformer module (Exp 1) to evaluate the performance of the standard transformer in processing hyperspectral data. In Experiment 2, the GRU module (Exp 2) was removed to analyze its contribution to the order dependence of captured spectral features. No pretraining was performed in Experiment 3 (Exp 3). The experimental results are displayed in

Table 8. Comparison of ablation experiment results (UP, IN, SA datasets). The best performing results are shown in bold.

Experimental	UP		IN		SA
	OA (%)	Kappa	OA (%)	Kappa	OA (%)	Kappa
Full	94.64	0.9354	93.5	0.925	91.8	0.910
Exp 1	91.2	0.905	90.3	0.895	88.5	0.880
Exp 2	92.7	0.920	91.8	0.910	89.9	0.895
Exp 3	87.3	0.865	86.5	0.850	84.7	0.835

.

When replacing the spectral transformer module with the classic transformer module, performance deteriorates on all datasets. OA on the UP dataset dropped to 91.2%, and Kappa dropped to 0.905; on the IN dataset, OA dropped to 90.3%, and Kappa dropped to 0.895; and on the SA dataset, OA dropped to 88.5%, and Kappa dropped to 0.880. This demonstrates the critical role of the specialized design of the spectral transformer in processing hyperspectral data for the overall performance of the model. Classic transformers, while effective in various tasks, may not be as proficient as spectral transformers in capturing complex spectral dependencies in hyperspectral data.

In the experiment of removing the GRU module, although the performance decreased, the impact was less than that of Experiment 1. The OA on the UP dataset is 92.7% and the Kappa is 0.920; the IN dataset has an OA of 91.8% and a Kappa of 0.910; and the SA dataset has an OA of 89.9% and a Kappa of 0.895. This result illustrates the important role of the GRU module in the model, especially in capturing the order dependence of spectral features. However, the model can still maintain good performance even without the GRU module, indicating that other components (such as the spectral transformer) also play a significant role in the model.

The experimental results without pretraining performed the worst on all indicators. On the UP dataset, OA dropped to 87.3%, and Kappa dropped to 0.865; on the IN dataset, OA dropped to 86.5%, and Kappa dropped to 0.850; and on the SA dataset, OA dropped to 84.7%, and Kappa dropped to 0.835. This significant performance drop underscores the importance of the pretraining phase. Pretraining allows the model to learn robust feature representations without labeled data, providing a solid foundation for the fine-tuning phase.

5. Conclusions

This paper introduces a self-supervised learning algorithm, S3L, based on the spectral transformer for HSI classification. The S3L algorithm operates in two stages: pretraining and fine-tuning. During the pretraining stage, a mask mechanism is employed to learn the spatial representation of HSI, and spectral features are modeled through the spectral transformer module. In the fine-tuning stage, labeled data are utilized to optimize pretraining weights and enhance classification accuracy. Additionally, a GRU layer is integrated into the algorithm to strengthen the sequence dependence of spectral features. Experimental results on multiple datasets demonstrate that the S3L algorithm performs commendably when labeled samples are limited and is competitive with current advanced methods. Future work will explore the application of S3L in a broader range of remote sensing data classification tasks and further optimize the algorithm structure.

While the proposed method has demonstrated remarkable performance, it is not without its limitations. Compared to convolutional neural networks (CNNs), the self-supervised learning (S3L) approach, which leverages the transformer architecture, encounters certain deployment challenges. Primarily, the intricate self-attention mechanism inherent to transformers demands substantial memory during inference, posing significant demands on hardware resources. Additionally, the scarcity of hardware platforms capable of accelerating transformer models represents another critical issue that needs addressing. Moving forward, our research will focus on developing a lightweight transformer architecture and exploring hardware acceleration capabilities for transformer-based models. Furthermore, the training, fine-tuning, and testing processes have been confined to a single dataset. Future efforts will aim to extend these processes across diverse datasets, enhancing the method’s adaptability and robustness.