MVP-Stereo: A Parallel Multi-View Patchmatch Stereo Method with Dilation Matching for Photogrammetric Application
Abstract
1. Introduction
1.1. Traditional MVS Methods
1.2. Learning-Based MVS Methods
1.3. Our Contributions
2. Methods
2.1. Patchmatch Stereo
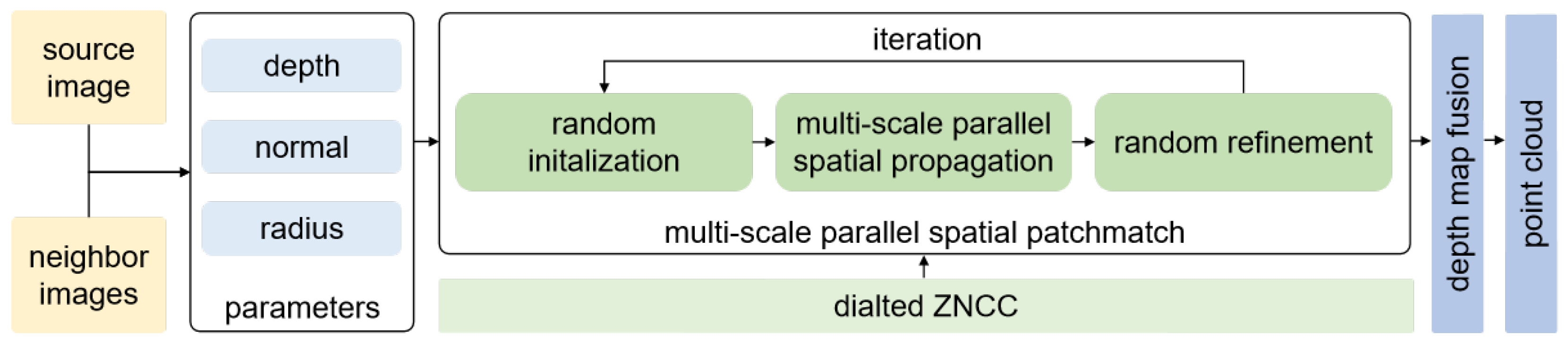
2.2. MVP-Stereo
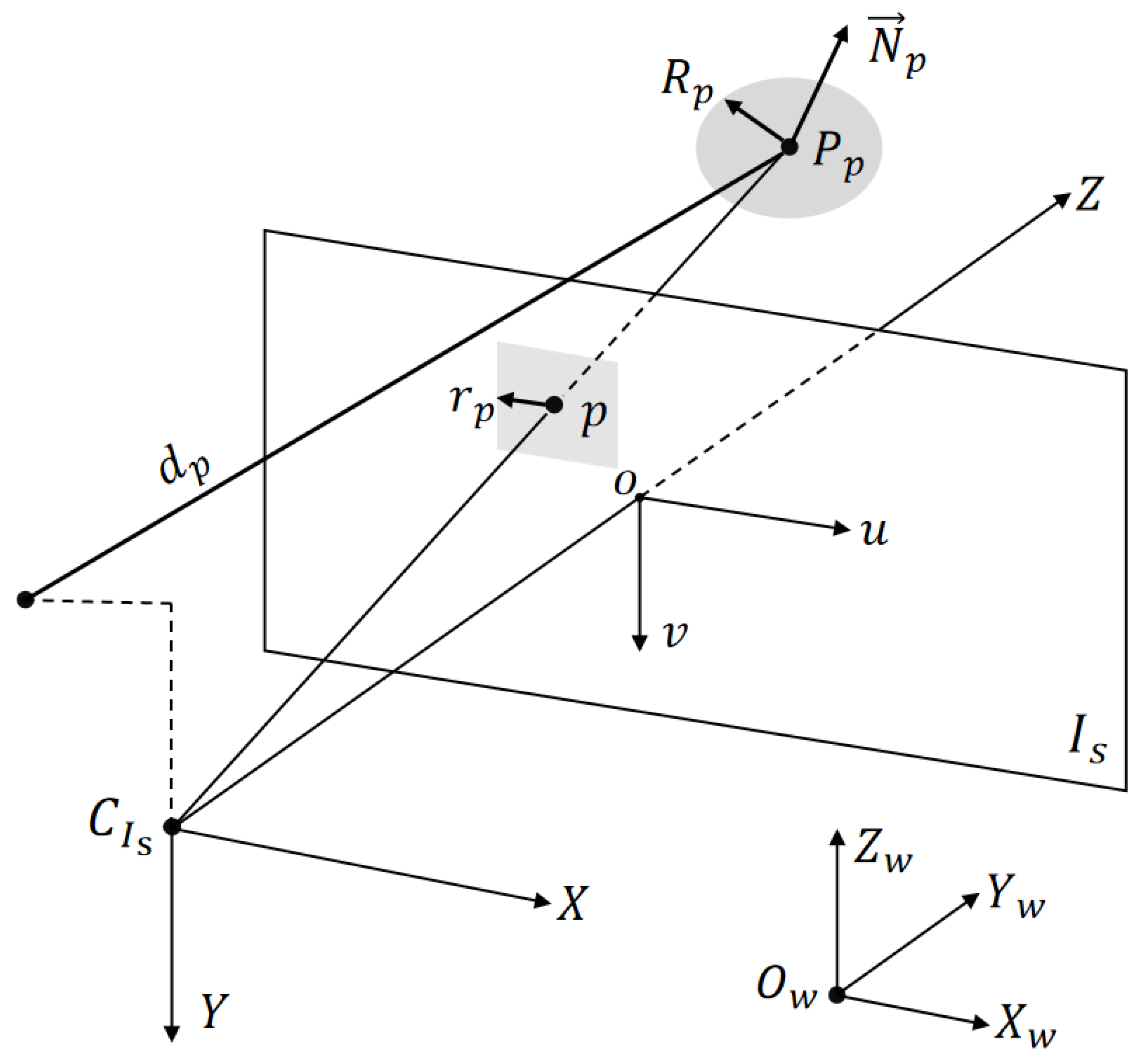
2.2.1. Estimated Parameter
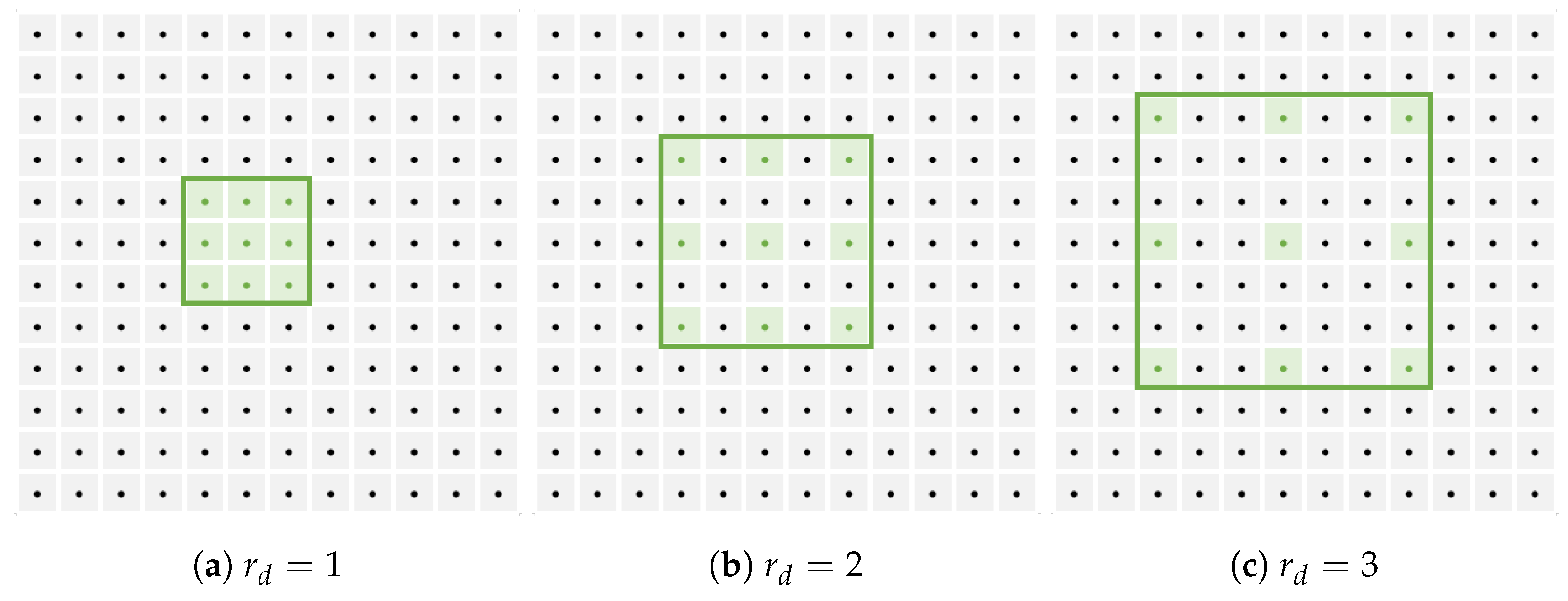
2.2.2. Multi-View Dilated ZNCC
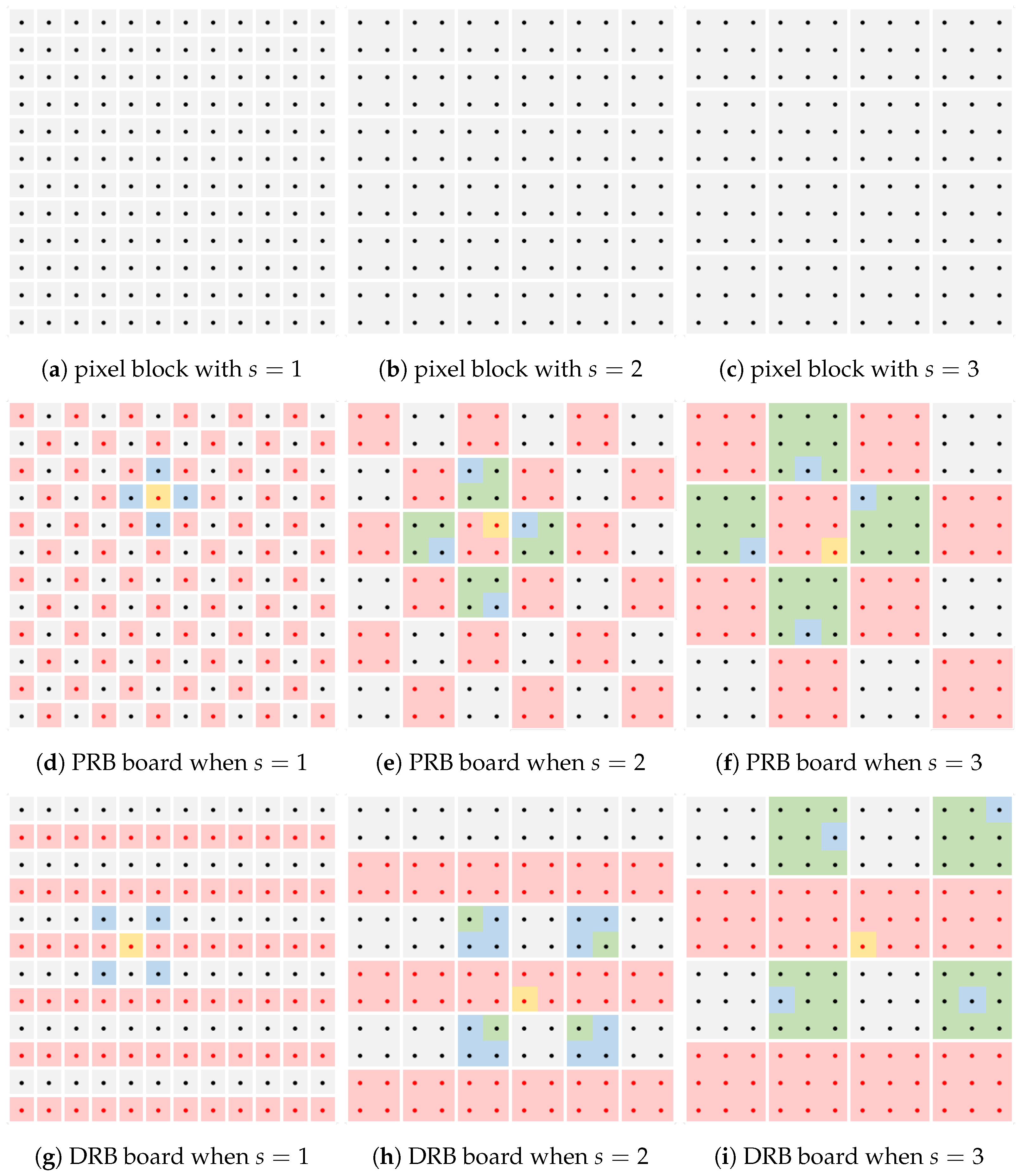
2.2.3. Multi-Scale Parallel Patchmatch
3. Experiments
3.1. Datasets
3.2. Implementation
3.3. Evaluation Metrics
3.4. Experiments on the Strecha Dataset
3.5. Experiments on the ETH3D Benchmark
3.6. Ablation Experiments
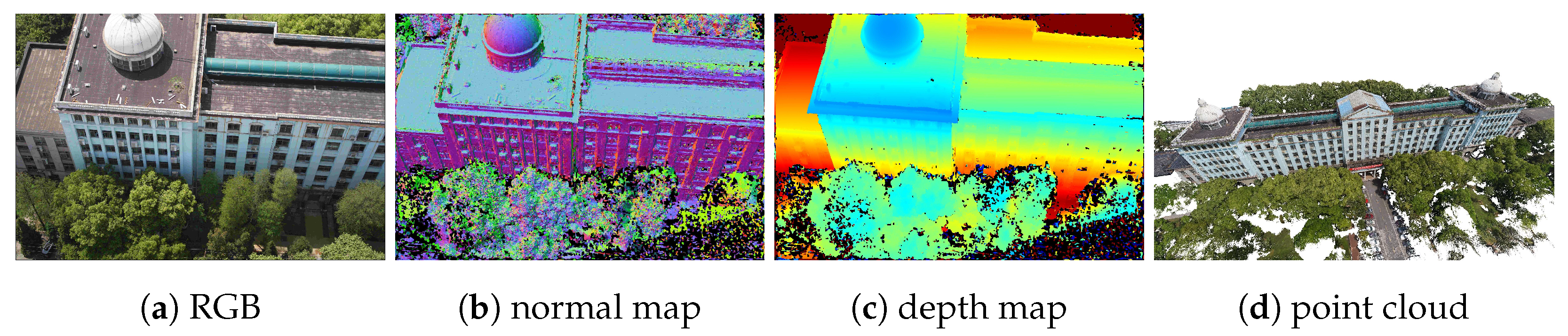
3.7. Experiments on the UAV Dataset
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Gruen, A. Multi-image matching for DSM generation from IKONOS imagery. ISPRS J. Photogramm. Remote Sens. 2006, 60, 195–211. [Google Scholar] [CrossRef]
- Gomez, C.; Setiawan, M.A.; Listyaningrum, N.; Wibowo, S.B.; Hadmoko, D.S.; Suryanto, W.; Darmawan, H.; Bradak, B.; Daikai, R.; Sunardi, S.; et al. LiDAR and UAV SfM-MVS of Merapi volcanic dome and crater rim change from 2012 to 2014. Remote Sens. 2022, 14, 5193. [Google Scholar] [CrossRef]
- Corradetti, A.; Seers, T.; Mercuri, M.; Calligaris, C.; Busetti, A.; Zini, L. Benchmarking different SfM-MVS photogrammetric and iOS LiDAR acquisition methods for the digital preservation of a short-lived excavation: A case study from an area of sinkhole related subsidence. Remote Sens. 2022, 14, 5187. [Google Scholar] [CrossRef]
- Nan, L.; Wonka, P. Polyfit: Polygonal surface reconstruction from point clouds. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2353–2361. [Google Scholar]
- Han, W.; Xiang, S.; Liu, C.; Wang, R.; Feng, C. Spare3d: A dataset for spatial reasoning on three-view line drawings. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 14690–14699. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Randla-net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11108–11117. [Google Scholar]
- Xiang, S.; Yang, A.; Xue, Y.; Yang, Y.; Feng, C. Self-supervised Spatial Reasoning on Multi-View Line Drawings. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12745–12754. [Google Scholar]
- Li, Y.; Ge, Z.; Yu, G.; Yang, J.; Wang, Z.; Shi, Y.; Sun, J.; Li, Z. Bevdepth: Acquisition of reliable depth for multi-view 3d object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 1477–1485. [Google Scholar]
- Schonberger, J.L.; Frahm, J.M. Structure-from-motion revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Moulon, P.; Monasse, P.; Perrot, R.; Marlet, R. Openmvg: Open multiple view geometry. In Proceedings of the Reproducible Research in Pattern Recognition: First International Workshop, RRPR 2016, Cancún, Mexico, 4 December 2016; Revised Selected Papers 1. Springer: Berlin/Heidelberg, Germany, 2017; pp. 60–74. [Google Scholar]
- Gruen, A. Adaptive least squares correlation: A powerful image matching technique. S. Afr. J. Photogramm. Remote Sens. Cartogr. 1985, 14, 175–187. [Google Scholar]
- Gruen, A.; Baltsavias, E.P. Geometrically constrained multiphoto matching. Photogramm. Eng. Remote Sens. 1988, 54, 633–641. [Google Scholar]
- Gruen, A. Least squares matching: A fundamental measurement algorithm. In Close Range Photogrammetry and Machine Vision; Whittler Publishing: Caithness, UK, 1996. [Google Scholar]
- Agouris, P.; Schenk, T. Automated aerotriangulation using multiple image multipoint matching. Photogramm. Eng. Remote Sens. 1996, 62, 703–710. [Google Scholar]
- Shen, S. Accurate multiple view 3d reconstruction using patch-based stereo for large-scale scenes. IEEE Trans. Image Process. 2013, 22, 1901–1914. [Google Scholar] [CrossRef]
- Galliani, S.; Lasinger, K.; Schindler, K. Massively parallel multiview stereopsis by surface normal diffusion. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 873–881. [Google Scholar]
- Fei, D.; Qingsong, Y.; Teng, X. A GPU-PatchMatch multi-view dense matching algorithm based on parallel propagation. Acta Geod. Cartogr. Sin. 2020, 49, 181. [Google Scholar]
- Vu, H.H.; Labatut, P.; Pons, J.P.; Keriven, R. High accuracy and visibility-consistent dense multiview stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 889–901. [Google Scholar] [CrossRef]
- Li, S.; Siu, S.Y.; Fang, T.; Quan, L. Efficient multi-view surface refinement with adaptive resolution control. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part I 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 349–364. [Google Scholar]
- Zhou, Y.; Shen, S.; Hu, Z. Detail preserved surface reconstruction from point cloud. Sensors 2019, 19, 1278. [Google Scholar] [CrossRef]
- Kazhdan, M.; Chuang, M.; Rusinkiewicz, S.; Hoppe, H. Poisson surface reconstruction with envelope constraints. In Proceedings of the Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2020; Volume 39, pp. 173–182. [Google Scholar]
- Yan, Q.; Xiao, T.; Qu, Y.; Yang, J.; Deng, F. An Efficient and High-Quality Mesh Reconstruction Method with Adaptive Visibility and Dynamic Refinement. Electronics 2023, 12, 4716. [Google Scholar] [CrossRef]
- Waechter, M.; Moehrle, N.; Goesele, M. Let there be color! Large-scale texturing of 3D reconstructions. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Proceedings, Part V 13. Springer: Berlin/Heidelberg, Germany, 2014; pp. 836–850. [Google Scholar]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A comparison and evaluation of multi-view stereo reconstruction algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; IEEE: Piscataway, NJ, USA, 2006; Volume 1, pp. 519–528. [Google Scholar]
- Gruen, A. Development and status of image matching in photogrammetry. Photogramm. Rec. 2012, 27, 36–57. [Google Scholar] [CrossRef]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the art in high density image matching. Photogramm. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef]
- Faugeras, O.; Keriven, R. Variational Principles, Surface Evolution, PDE’s, Level Set Methods and the Stereo Problem; IEEE: Piscataway, NJ, USA, 2002. [Google Scholar]
- Vogiatzis, G.; Esteban, C.H.; Torr, P.H.; Cipolla, R. Multiview stereo via volumetric graph-cuts and occlusion robust photo-consistency. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 2241–2246. [Google Scholar] [CrossRef] [PubMed]
- Hiep, V.H.; Keriven, R.; Labatut, P.; Pons, J.P. Towards high-resolution large-scale multi-view stereo. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1430–1437. [Google Scholar]
- Cremers, D.; Kolev, K. Multiview stereo and silhouette consistency via convex functionals over convex domains. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1161–1174. [Google Scholar] [CrossRef]
- Goesele, M.; Snavely, N.; Curless, B.; Hoppe, H.; Seitz, S.M. Multi-view stereo for community photo collections. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio De Janeiro, Brazil, 14–21 October 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–8. [Google Scholar]
- Furukawa, Y.; Ponce, J. Accurate, dense, and robust multiview stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 1362–1376. [Google Scholar] [CrossRef]
- Yu, J.; Zhu, Q.; Yu, W. A dense matching algorithm of multi-view image based on the integrated multiple matching primitives. Acta Geod. Cartogr. Sin. 2013, 42, 691. [Google Scholar]
- Hongrui, Z.; Shenghan, L. Dense High-definition Image Matching Strategy Based on Scale Distribution of Feature and Geometric Constraint. Acta Geod. Cartogr. Sin. 2018, 47, 790. [Google Scholar]
- Rothermel, M.; Wenzel, K.; Fritsch, D.; Haala, N. SURE: Photogrammetric surface reconstruction from imagery. In Proceedings of the LC3D Workshop, Berlin, Germany, 4–5 December 2012; Volume 8. [Google Scholar]
- Li, Y.; Liang, F.; Changhai, C.; Zhiyun, Y.; Ruixi, Z. A multi-view dense matching algorithm of high resolution aerial images based on graph network. Acta Geod. Cartogr. Sin. 2016, 45, 1171. [Google Scholar]
- Xu, Q.; Tao, W. Multi-scale geometric consistency guided multi-view stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5483–5492. [Google Scholar]
- Xu, Q.; Kong, W.; Tao, W.; Pollefeys, M. Multi-scale geometric consistency guided and planar prior assisted multi-view stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 4945–4963. [Google Scholar] [CrossRef] [PubMed]
- Merrell, P.; Akbarzadeh, A.; Wang, L.; Mordohai, P.; Frahm, J.M.; Yang, R.; Nistér, D.; Pollefeys, M. Real-time visibility-based fusion of depth maps. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio De Janeiro, Brazil, 14–21 October 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–8. [Google Scholar]
- Hirschmuller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 328–341. [Google Scholar] [CrossRef]
- Hernandez-Juarez, D.; Chacón, A.; Espinosa, A.; Vázquez, D.; Moure, J.C.; López, A.M. Embedded real-time stereo estimation via semi-global matching on the GPU. Procedia Comput. Sci. 2016, 80, 143–153. [Google Scholar] [CrossRef]
- Kuhn, A.; Hirschmüller, H.; Scharstein, D.; Mayer, H. A tv prior for high-quality scalable multi-view stereo reconstruction. Int. J. Comput. Vis. 2017, 124, 2–17. [Google Scholar] [CrossRef]
- Bleyer, M.; Rhemann, C.; Rother, C. Patchmatch stereo-stereo matching with slanted support windows. In Proceedings of the BMVC, Dundee, UK, 29 August–2 September 2011; Volume 11, pp. 1–11. [Google Scholar]
- Cernea, D. OpenMVS: Multi-View Stereo Reconstruction Library. Available online: https://cdcseacave.github.io/openMVS (accessed on 20 December 2023).
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Zheng, E.; Dunn, E.; Jojic, V.; Frahm, J.M. Patchmatch based joint view selection and depthmap estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1510–1517. [Google Scholar]
- Schönberger, J.L.; Zheng, E.; Frahm, J.M.; Pollefeys, M. Pixelwise view selection for unstructured multi-view stereo. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part III 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 501–518. [Google Scholar]
- Kuhn, A.; Lin, S.; Erdler, O. Plane completion and filtering for multi-view stereo reconstruction. In Proceedings of the Pattern Recognition: 41st DAGM German Conference, DAGM GCPR 2019, Dortmund, Germany, 10–13 September 2019; Proceedings 41. Springer: Berlin/Heidelberg, Germany, 2019; pp. 18–32. [Google Scholar]
- Romanoni, A.; Matteucci, M. Tapa-mvs: Textureless-aware patchmatch multi-view stereo. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 10413–10422. [Google Scholar]
- Xu, Z.; Liu, Y.; Shi, X.; Wang, Y.; Zheng, Y. Marmvs: Matching ambiguity reduced multiple view stereo for efficient large scale scene reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 5981–5990. [Google Scholar]
- Wang, Y.; Guan, T.; Chen, Z.; Luo, Y.; Luo, K.; Ju, L. Mesh-guided multi-view stereo with pyramid architecture. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2039–2048. [Google Scholar]
- Stathopoulou, E.K.; Battisti, R.; Cernea, D.; Georgopoulos, A.; Remondino, F. Multiple View Stereo with quadtree-guided priors. ISPRS J. Photogramm. Remote Sens. 2023, 196, 197–209. [Google Scholar] [CrossRef]
- Yuan, Z.; Cao, J.; Li, Z.; Jiang, H.; Wang, Z. SD-MVS: Segmentation-Driven Deformation Multi-View Stereo with Spherical Refinement and EM optimization. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 22–25 February 2024; Volume 38. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. Mvsnet: Depth inference for unstructured multi-view stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 767–783. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Shen, T.; Fang, T.; Quan, L. Recurrent mvsnet for high-resolution multi-view stereo depth inference. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5525–5534. [Google Scholar]
- Gu, X.; Fan, Z.; Zhu, S.; Dai, Z.; Tan, F.; Tan, P. Cascade cost volume for high-resolution multi-view stereo and stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 15–19 June 2020; pp. 2495–2504. [Google Scholar]
- Wang, F.; Galliani, S.; Vogel, C.; Speciale, P.; Pollefeys, M. Patchmatchnet: Learned multi-view patchmatch stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14194–14203. [Google Scholar]
- Mi, Z.; Di, C.; Xu, D. Generalized binary search network for highly-efficient multi-view stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12991–13000. [Google Scholar]
- Yan, Q.; Wang, Q.; Zhao, K.; Li, B.; Chu, X.; Deng, F. Rethinking disparity: A depth range free multi-view stereo based on disparity. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 3091–3099. [Google Scholar]
- Ikehata, S. Scalable, Detailed and Mask-Free Universal Photometric Stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 13198–13207. [Google Scholar]
- Ju, Y.; Shi, B.; Chen, Y.; Zhou, H.; Dong, J.; Lam, K.M. GR-PSN: Learning to estimate surface normal and reconstruct photometric stereo images. IEEE Trans. Vis. Comput. Graph. 2023, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Logothetis, F.; Mecca, R.; Budvytis, I.; Cipolla, R. A CNN based approach for the point-light photometric stereo problem. Int. J. Comput. Vis. 2023, 131, 101–120. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, J.; Mao, S.; Ji, M.; Wang, G.; Chen, Z.; Zhang, T.; Yuan, X.; Dai, Q.; Fang, L. GigaMVS: A benchmark for ultra-large-scale gigapixel-level 3D reconstruction. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7534–7550. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Strecha, C.; Von Hansen, W.; Van Gool, L.; Fua, P.; Thoennessen, U. On benchmarking camera calibration and multi-view stereo for high resolution imagery. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–8. [Google Scholar]
- Schops, T.; Schonberger, J.L.; Galliani, S.; Sattler, T.; Schindler, K.; Pollefeys, M.; Geiger, A. A multi-view stereo benchmark with high-resolution images and multi-camera videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3260–3269. [Google Scholar]










| Datasets | Scene | Image Number | Resolution |
|---|---|---|---|
| Strecha [66] | Fountain, Herzjesu | 11, 8 | |
| ETH3D [67] | (courtyard, electro, facade, meadow, playground, terrace) 1, (delivery_area, kicker, office, pipes, relief, relief_2, terrains) 2, (boulders, observatory, terrace_2) 3, (botanical_garden, bridge, door, exhibition_hall, lecture_room, living_room, lounge, old_computer, statue) 4 | (38, 45, 76, 15, 38, 23) 1, (44, 31, 26, 14, 31, 31, 42) 2, (26, 27, 13) 3, (30, 110, 7, 68, 23, 65, 10, 54, 11) 4 | around |
| UAV | P104 | 104 | |
| P114 | 114 | ||
| P139 | 139 |
| Method | Fountain | Herzjesu | ||||
|---|---|---|---|---|---|---|
| Quality (%) | Quality (%) | |||||
| Time (s)↓ | Td = 2 cm↑ | Td = 10 cm↑ | Time (s)↓ | Td = 2 cm↑ | Td = 10 cm↑ | |
| COLMAP [47] | 1046.88 | 82.7 | 97.5 | 709.14 | 69.1 | 93.1 |
| OpenMVS [15,44] | 191.13 | 77.1 | 90.7 | 150.48 | 65.5 | 82.2 |
| Gipuma [16] | 235.58 | 69.3 | 83.8 | 134.34 | 28.3 | 45.5 |
| ACMM [37] | 321.66 | 85.3 | 97.4 | 141.26 | 73.1 | 93.2 |
| ACMMP [38] | 395.48 | 84.8 | 97.2 | 248.28 | 72.6 | 93.5 |
| Ours | 81.21 | 80.6 | 93.1 | 54.10 | 65.6 | 84.6 |
| Method | = 2 cm (%) | = 10 cm (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Time (s)↓ | comp↑ | acc↑ | F1↑ | comp↑ | acc↑ | F1↑ | ||
| indoor | COLMAP [47] | 1869.33 | 59.65 | 91.95 | 70.41 | 82.82 | 98.11 | 89.28 |
| OpenMVS [15,44] | 2263.08 | 75.92 | 82.00 | 78.33 | 88.84 | 95.20 | 91.68 | |
| Gipuma [16] | 767.00 | 31.44 | 86.33 | 41.86 | 52.22 | 98.31 | 65.41 | |
| ACMM [37] | 1332.72 | 72.73 | 90.99 | 79.84 | 88.22 | 97.79 | 92.50 | |
| ACMMP [38] | 3284.78 | 86.90 | 91.36 | 88.86 | 97.34 | 97.76 | 97.53 | |
| SD-MVS [53] | 3055.56 | 87.49 | 89.88 | 88.50 | 97.40 | 97.70 | 97.53 | |
| Ours | 533.67 | 76.23 | 73.51 | 74.46 | 85.83 | 95.28 | 90.08 | |
| outdoor | COLMAP [47] | 1025.33 | 72.98 | 92.04 | 80.81 | 89.70 | 98.64 | 93.79 |
| OpenMVS [15,44] | 1459.67 | 86.41 | 81.93 | 84.09 | 96.48 | 96.32 | 96.40 | |
| Gipuma [16] | 458.00 | 45.30 | 78.78 | 55.16 | 62.40 | 97.36 | 75.18 | |
| ACMM [37] | 662.07 | 79.17 | 89.63 | 83.58 | 90.43 | 98.85 | 94.35 | |
| ACMMP [38] | 1711.67 | 86.58 | 90.55 | 88.32 | 97.01 | 98.79 | 97.87 | |
| SD-MVS [53] | 1451.45 | 86.71 | 86.22 | 87.50 | 97.06 | 96.35 | 97.53 | |
| Ours | 293.33 | 79.79 | 82.71 | 81.13 | 88.93 | 96.92 | 92.71 | |
| = 2 cm (%) | = 10 cm (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| d-Z | MSP | C2F | comp↑ | acc↑ | F1↑ | comp↑ | acc↑ | F1↑ | |
| indoor | × | × | × | 50.09 | 82.21 | 59.39 | 67.14 | 97.51 | 78.23 |
| ✓ | × | × | 59.19 | 77.44 | 65.26 | 72.79 | 95.77 | 81.69 | |
| ✓ | ✓ | × | 61.20 | 78.56 | 67.07 | 74.01 | 95.90 | 82.51 | |
| ✓ | ✓ | ✓ | 70.07 | 74.39 | 71.43 | 82.97 | 94.70 | 88.09 | |
| outdoor | × | × | × | 51.10 | 76.57 | 59.70 | 65.60 | 97.48 | 77.30 |
| ✓ | × | × | 61.35 | 74.37 | 66.43 | 73.57 | 97.08 | 83.02 | |
| ✓ | ✓ | × | 64.13 | 74.95 | 68.68 | 76.23 | 97.13 | 84.82 | |
| ✓ | ✓ | ✓ | 69.97 | 72.08 | 70.60 | 80.70 | 95.23 | 87.32 | |
| = 2 cm (%) | = 10 cm (%) | ||||||
|---|---|---|---|---|---|---|---|
| comp↑ | acc↑ | F1↑ | comp↑ | acc↑ | F1↑ | ||
| indoor | 1 | 27.49 | 51.49 | 33.73 | 45.06 | 76.63 | 54.91 |
| 2 | 66.24 | 71.99 | 68.34 | 80.51 | 93.23 | 86.10 | |
| 4 | 68.84 | 73.73 | 70.47 | 82.36 | 94.39 | 87.64 | |
| 6 | 70.07 | 74.39 | 71.43 | 82.97 | 94.70 | 88.09 | |
| outdoor | 1 | 30.80 | 53.73 | 37.98 | 49.18 | 86.35 | 61.22 |
| 2 | 64.93 | 71.25 | 67.47 | 76.00 | 95.52 | 84.20 | |
| 4 | 68.77 | 72.22 | 69.98 | 79.62 | 95.88 | 86.68 | |
| 6 | 69.97 | 72.08 | 70.60 | 80.70 | 95.23 | 87.32 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Kang, J.; Xiao, T.; Liu, H.; Deng, F. MVP-Stereo: A Parallel Multi-View Patchmatch Stereo Method with Dilation Matching for Photogrammetric Application. Remote Sens. 2024, 16, 964. https://doi.org/10.3390/rs16060964
Yan Q, Kang J, Xiao T, Liu H, Deng F. MVP-Stereo: A Parallel Multi-View Patchmatch Stereo Method with Dilation Matching for Photogrammetric Application. Remote Sensing. 2024; 16(6):964. https://doi.org/10.3390/rs16060964
Chicago/Turabian StyleYan, Qingsong, Junhua Kang, Teng Xiao, Haibing Liu, and Fei Deng. 2024. "MVP-Stereo: A Parallel Multi-View Patchmatch Stereo Method with Dilation Matching for Photogrammetric Application" Remote Sensing 16, no. 6: 964. https://doi.org/10.3390/rs16060964
APA StyleYan, Q., Kang, J., Xiao, T., Liu, H., & Deng, F. (2024). MVP-Stereo: A Parallel Multi-View Patchmatch Stereo Method with Dilation Matching for Photogrammetric Application. Remote Sensing, 16(6), 964. https://doi.org/10.3390/rs16060964






