Abstract
Multimodal remote sensing data classification can enhance a model’s ability to distinguish land features through multimodal data fusion. In this context, how to help models understand the relationship between multimodal data and target tasks has become the focus of researchers. Inspired by the human feedback learning mechanism, causal reasoning mechanism, and knowledge induction mechanism, this paper integrates causal learning, reinforcement learning, and meta learning into a unified remote sensing data classification framework and proposes causal meta-reinforcement learning (CMRL). First, based on the feedback learning mechanism, we overcame the limitations of traditional implicit optimization of fusion features and customized a reinforcement learning environment for multimodal remote sensing data classification tasks. Through feedback interactive learning between agents and the environment, we helped the agents understand the complex relationships between multimodal data and labels, thereby achieving full mining of multimodal complementary information.Second, based on the causal inference mechanism, we designed causal distribution prediction actions, classification rewards, and causal intervention rewards, capturing pure causal factors in multimodal data and preventing false statistical associations between non-causal factors and class labels. Finally, based on the knowledge induction mechanism, we designed a bi-layer optimization mechanism based on meta-learning. By constructing a meta training task and meta validation task simulation model in the generalization scenario of unseen data, we helped the model induce cross-task shared knowledge, thereby improving its generalization ability for unseen multimodal data. The experimental results on multiple sets of multimodal datasets showed that the proposed method achieved state-of-the-art performance in multimodal remote sensing data classification tasks.
1. Introduction
Remote sensing data classification has research significance in the fields of urban planning, mining exploration, and agriculture [1,2,3,4,5]. In recent years, with the rapid development of sensor technology, a variety of remote sensing data sources have been provided to support remote sensing data classification tasks. For example, a hyperspectral image (HSI) is able to reflect fine spectral information of ground objects [6,7] but is susceptible to factors such as weather and has challenges in distinguishing ground objects with similar spectral reflectance. In contrast, light detection and ranging (LiDAR) is not sensitive to weather conditions, and the elevation information it contains helps the model distinguish between objects with similar spectral information but different heights [8]. Multimodal remote sensing data classification can improve a model’s ability to distinguish ground objects through multimodal data fusion, which has attracted extensive attention from researchers in recent years.
In the process of multimodal data fusion, a key problem is how to help models understand the relationship between multimodal data and target tasks? The difficulty of solving this problem lies in the following: On the one hand, the coupling relationship between task-related information and task-unrelated information in multimodal data is often tight and complex, which makes it difficult for the model to accurately distinguish the two. For example, there may be spectral noise in HSI, and there may also be noise in LiDAR due to the scattering effect of multipath effects. It is frustrating that the noise information is not only difficult to directly observe and interfere with, but also often brings serious interference to the model learning process. On the other hand, the association pattern between multimodal data and target tasks often changes dynamically with specific context information. Take HSI and LiDAR for example, where different classes of ground objects in urban scenes often have inconsistent heights and different spectral reflectances (difference in ground object materials), so multimodal data fusion tends to make comprehensive use of HSI and LiDAR. However, in a forest scene with a similar height of trees, attention to LiDAR information can lead to intermodal information interference. The dynamic change in the association pattern requires the model to fully understand the dependency between the context information and the multimodal data fusion, which necessitates higher requirements of its intelligence.
In order to accurately capture task-related information from multimodal data, inspired by the human visual system’s focus on only the key information in a visual scene, researchers have developed a variety of attention mechanisms. These attention mechanisms have been designed to adaptively emphasize task-related information and suppress task-unrelated information in model learning. Gao et al. [9] proposed an adaptive feature fusion module to adjust the model’s degree of attention to different modalities through dynamic attention allocation. However, this method only models the global importance of multimodal data, and the noise information contained in the data is also a concern when a certain modality is emphasized.Considering the consistency of multimodal data in describing objects, the mutual supervision between multimodal data can help the model to capture task-related information. To solve this problem, Zhang et al. [10] proposed a mutual guidance attention module that highlights key task-based information and suppresses useless noise information by establishing mutual supervision between different modal information flows. In order to more fully mine the consistency information among multimodal data, Song et al. [11] developed a cross-modal attention fusion module that learns the global dependency relationship between multimodal data by establishing deep interactions between them, and then uses this dependency relationship to improve the model’s ability to capture task-related information. However, the optimization of attention mechanisms in the above methods often relies on establishing statistical associations between multimodal data and labels, thus minimizing the empirical risk of the model on the training data. It should be noted that overemphasis on statistical dependencies between multimodal data and labels can lead models to establish false statistical associations between non-causal factors (such as spectral noise) and labels. For example, ground objects in a certain region can show abnormal spectral responses within a certain band due to weather factors. If the model establishes a statistical correlation between abnormal spectral responses and labels, the model will often mistakenly emphasize abnormal spectral information. In addition, multimodal remote sensing data classification tasks usually face high labeling costs, which makes it difficult to obtain sufficient labeled training data in practical applications. This problem of data sparsity leads to the possibility that the training data may not accurately reflect the real data distribution. In this context, simply minimizing the empirical risk of the model on the training data may make it difficult for the model to achieve satisfactory generalization performance on unseen multimodal data.
Fortunately, the human causal reasoning mechanism and knowledge induction mechanism provide solutions to the above problems. On the one hand, humans are able to identify causal associations that are truly related to each other from appearances, rather than through statistical learning. For example, although “fish” are usually found in water and the two show a high statistical dependence, humans can clearly recognize that there is a non-causal relationship between “water” and “fish”. Inspired by this, if a causal reasoning mechanism can be built into the model learning process, it can be made to cut out the false statistical association between non-causal factors and labels, and learn the real causal effect between data and labels. On the other hand, humans are able to generalize core knowledge from different tasks, so they can effectively deal with unseen tasks. For example, by practicing addition and subtraction exercises, students can deduce the rules of addition and subtraction operations from them, so that they can perform exercises correctly when they encounter addition and subtraction exercises that they have not seen in practice. Inspired by this, if a knowledge induction mechanism can be established in the process of model optimization, a model can escape the limitations of fitting training data in the learning process, and can generalize cross-task shared knowledge from different multimodal remote sensing data classification tasks to improve its generalization ability for unseen multimodal data.
In order to capture complex association patterns among multimodal data, researchers have conducted extensive explorations. Considering that the association modes of multi-modal data are often closely related to the above information, Xue et al. [12] proposed a self-calibrated convolution, which captures multi-scale context information of multimodal data. The weight of multi-scale context information is adjusted adaptively by spectral and spatial self-attention. Roy et al. [13], taking into account the differences among multimodal data, customized a personalized feature learning mode for HSI and LiDAR, and captured HSI rich spatial-spectral information by convolution and LiDAR spatial structure information for a morphological expansion layer and erosion layer. Finally, multimodal data were integrated using an additive operation. However, simple additive operations struggle to capture complex nonlinear relationships between multimodal data. Therefore, Wang et al. [14] proposed a spatial-spectral mutual guided module to realize cross-modal information fusion of multimodal spatial and spectral information, and to improve the semantic correlation between multimodal spectrum and spatial information by using adaptive, multi-scale and mutual learning technologies. Further, in order to fully capture the local and global associations of multimodal data, Du et al. [15] proposed a spatial-spectral graph network, which uses image block-based convolution to preserve the local structures of multimodal data and uses the information transfer mechanism of graph neural networks to capture the global associations. The above one-step multimodal data fusion method has significant limitations in the mining of complex association patterns: The multimodal data only go through one forward process in the fusion process and cannot evaluate the quality of the current fusion strategy and make adaptive adjustments to it. Such a one-step fusion process limits the model’s ability to mine complex association patterns. In addition, the optimization process of the multimodal data fusion strategies of these methods is often implicit and is not directly guided by the gradient of classification loss. It is difficult to ensure that the model truly understands the complex role relationship between multimodal data and labels in feature fusion, which can lead to the model incorrectly suppressing task-related information or emphasizing task-unrelated information.
Fortunately, the human feedback learning mechanism has provided a solution to this problem; specifically, humans can understand the complex relationships between things through interactive feedback with the environment. For example, chemists combine different chemicals during experiments and obtain feedback signals by observing the reaction phenomena between them. Based on this feedback signal, chemists can better understand the interaction between chemical substances and the effect of this interaction relationship on the reaction phenomenon, and then modify their experimental operations to obtain the expected experimental results. Inspired by this, if a task-oriented feedback mechanism can be established in the process of multimodal feature fusion, the model could fully understand how the current multimodal data fusion strategy acts on the target task and adjust its multimodal data fusion strategy according to its performance in the target task, fully capturing and intelligently adapting to complex association patterns among multimodal data.
In summary, the key issue that this paper aims to address is how to establish feedback learning mechanisms, causal inference mechanisms, and knowledge induction mechanisms in multimodal remote sensing data classification tasks?
To address this issue, we integrated reinforcement learning, causal learning, and meta-learning into a unified multimodal remote sensing data classification framework and proposed a causal meta-reinforcement learning framework. Specifically, to establish a feedback learning mechanism and causal reasoning mechanism, we customized a reinforcement learning environment for multimodal remote sensing data classification tasks and designed causal distribution prediction actions, classification rewards, and causal intervention rewards. Through this approach, on the one hand, intelligent agents can understand the complex relationships between multimodal data and labels in their interaction feedback with the environment. On the other hand, intelligent agents can distinguish causal and non-causal factors in multimodal data using the feedback and incentive of reward signals, and can accurately capture purely causal factors by mining multimodal complementary information. To establish a knowledge induction mechanism, inspired by meta-learning scenario simulation training, we constructed meta training tasks and meta validation tasks, and based on this, we constructed a bi-layer optimization mechanism. By simulating a scenario of generalizing visible multimodal data to unseen multimodal data, we encouraged the intelligent entities to induce cross-task shared knowledge, thereby improving their generalization ability on unseen multimodal data. The contributions of this paper are as follows:
- (1)
- Causal meta-reinforcement learning (CMRL) is proposed, which simulates the human feedback learning mechanism, causal inference mechanism, and knowledge induction mechanism to fully mine multimodal complementary information, accurately capture true causal relationships, and reasonably induce cross-task shared knowledge;
- (2)
- Escaping the limitations of implicit optimization of fusion features, a reinforcement learning environment was customized for the classification of multimodal remote sensing data. Through the interaction feedback between intelligent agents and multimodal data, full mining of multimodal complementary information was achieved;
- (3)
- Surpassing the traditional learning model of establishing statistical associations between data and labels, causal reasoning was introduced for the first time into multimodal remote sensing data classification tasks. Causal distribution prediction actions, classification rewards, and causal intervention rewards were designed to encourage intelligent agents to capture pure causal factors and cut out false statistical associations between non-causal factors and labels;
- (4)
- The shortcomings of the optimization mode that minimizes the empirical risk of the model on training data under sparse training samples were revealed, and a targeted bi-layer optimization mechanism based on meta-learning was proposed. By encouraging agents to induce cross-task shared knowledge during scenario simulation, their generalization ability on unseen test data was improved.
2. Relate Work
2.1. Reinforcement Learning
In recent years, reinforcement learning has achieved tremendous success in fields such as game AI [16,17,18], robotics [19,20,21], and autonomous driving [22,23,24]. In particular, with its integration into large-capacity deep neural networks, reinforcement learning has surpassed expert human performance in certain scenarios, such as Go [25] and StarCraft [26]. Reinforcement learning, inheriting the trial-and-error learning mechanism from psychology and the principles of optimal control [27,28], can learn optimal strategies through the interaction feedback between an agent and environment under predefined human rules [29]. Early reinforcement learning methods were plagued by the curse of dimensionality, as they typically stored and iterated states in a tabular form, making it difficult to handle tasks with large-scale or continuous actions. Mnih et al. [30] first combined deep learning with Q-learning, introducing the deep Q-network (DQN), which provided a deep learning solution for reinforcement learning and surpassed human expert levels in several classic games. Building on DQN, researchers further explored and proposed solutions like the double DQN [31] to mitigate overestimation issues, as well as the deep recurrent Q-network (DRQN) [32] for partially observable Markov decision processes.
However, these methods are unable to handle continuous action scenarios, limiting the application of reinforcement learning in real-world settings. To address this issue, the theory of policy gradients [33] was proposed. Overcoming the limitations of value iteration and policy iteration, this theory directly learns the policy function, mapping states to the probability distribution of actions without the need to discretize the action space. Based on this theory, Lillicrap et al. [34] proposed the deep deterministic policy gradient (DDPG), consisting of an actor network for directly outputting deterministic actions, and a critic network for evaluating future expected returns based on input states. By optimizing these networks, agents can learn action strategies that maximize future expected returns under the motivation of reward function signals. However, as an offline reinforcement learning algorithm, DDPG struggles with the complex dynamic changes and real-time decision-making demands of real-world scenarios. Proximal policy optimization [35], updating through experience trajectories and calculating advantage functions to assess the relative advantage of each action over the average, allows for policy updates using samples obtained from online sampling, effectively resolving this issue.
It is noteworthy that, despite the promising feedback learning mechanism of reinforcement learning for learning multimodal data fusion strategies, its potential in multimodal data fusion tasks remains underexplored. This paper is the first to utilize the reinforcement learning framework for multimodal remote sensing data classification, learning multimodal remote sensing data fusion strategies through agent interaction and feedback with a customized environment and providing a new reinforcement learning paradigm for multimodal remote sensing data classification.
2.2. Causal Learning
Causal learning focuses on discovering and understanding the true causal relationships between entities, rather than statistical dependencies, offering new solutions for enhancing the generality and credibility of deep models [36]. In recent years, researchers have spent time exploring the potential of causal learning in various deep learning tasks. Wang et al. [37] considered causal factors that have a real causal relationship with labels as cross-domain invariant, transferable knowledge in domain generalization tasks. By intervening in the features, they effectively mined invariant causal factors with strong generalization capabilities. Liu et al. [38] proposed a cross-modal causal conceptual reasoning framework for visual question answering tasks, discovering the underlying causal structure between visual and language modalities through causal intervention. Lin et al. [39] focused on using causal learning to eliminate the diagnostic errors induced by task-irrelevant information in data during medical diagnostic tasks, thereby enhancing the model’s credibility and generality in this domain. Zhang et al. [40] constructed a structural causal model (SCM) for person re-identification tasks and developed the SCM through backdoor adjustment, achieving effective mining of pure causal factors.
Although the causal reasoning mechanism of causal learning holds promise for helping models discover the real causal connections between data and labels, thus enhancing credibility in multimodal data fusion tasks, its potential in this area has not yet been fully explored. This paper is the first to construct a causal inference mechanism for multimodal remote sensing data classification tasks. Combining this mechanism with the feedback learning mechanism of reinforcement learning enables agents to capture pure causal factors during their interactions with the environment. This method removes the false statistical association between non-causal factors and labels, providing a new causal perspective for multimodal remote sensing data classification.
2.3. Meta-Learning
Meta-learning, as an method for “learning to learn”, has garnered widespread attention in recent years due to its unique knowledge induction mechanism, which allows models to find shared knowledge across tasks from a large number of similar yet different meta-tasks [41,42,43].
Yu et al. [44] created zero-sample face manipulation meta-tasks to simulate unseen external attacks and shared meta-knowledge across tasks within a meta-learning optimization framework. Jia et al. [45] constructed pseudo-classes through data augmentation in an unsupervised setting and built meta-tasks based on these. They simulated small-sample classification scenarios for unseen classes by reallocating the meta-labels in each meta-task, achieving the induction of general knowledge for small-sample classification. Lv et al. [46] used meta-learning for drug discovery tasks to facilitate cross-task knowledge transfer, reducing the model’s dependency on large data volumes. Wang et al. [47] integrated graph learning with meta-learning into a unified framework for cross-domain small-sample hyperspectral image classification, utilizing the knowledge induction mechanism of meta-learning to learn general node aggregation functions.
Despite the potential of the knowledge induction mechanism of meta-learning to help models induce general knowledge for multimodal data fusion from meta-tasks, thereby enhancing their generalization performance on unseen multimodal data, its potential in multimodal data fusion tasks has not been fully explored. This paper establishes meta-training and meta-validation tasks and uses a bi-layer optimization mechanism to induce shared multimodal data fusion knowledge across tasks, providing a new meta-optimization mechanism for multimodal remote sensing data classification.
3. Method
3.1. Framework of CMRL
A flow chart of the overall structure of CMRL is illustrated in Figure 1: In the first phase, the optimal multimodal data fusion strategy is learned based on a meta-optimization mechanism. In this phase, first, multimodal data are input into the meta-task generation module to obtain meta-training tasks and meta-validation tasks. Then, in the learning process of meta training and meta-validation tasks, based on a bi-layer optimization framework, agents learn the optimal multimodal data fusion strategy through feedback interactions in a predefined reinforcement learning environment.
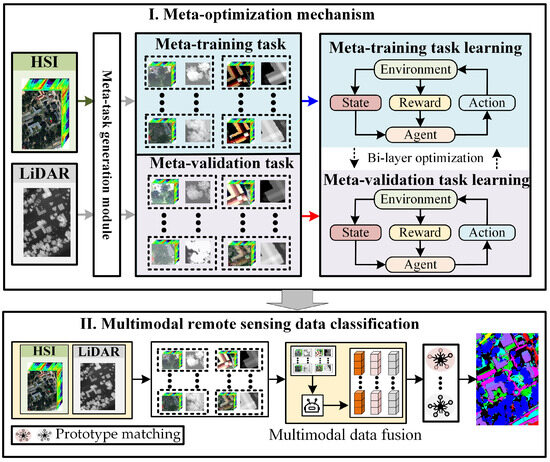
Figure 1.
The overall structure flow chart of CMRL.
In the second phase, the task of classifying multimodal remote sensing data is completed. In this stage, first, paired multimodal samples are obtained from multimodal data. Then, based on the strategy learned in the previous phase, agents fuse the multimodal samples to obtain the corresponding causal fusion features. Finally, the causal fusion features are subjected to prototype matching to obtain the corresponding class probability vectors, thereby completing the classification task of multimodal remote sensing data.
Next, we provide a detailed introduction to the meta-optimization mechanism, meta-training task learning, and meta-validation task learning:
3.1.1. Meta-Optimization Mechanisms
Figure 2 shows the framework of the meta-optimization mechanism. In this section, we will elaborate on the workflow of the meta-optimization mechanism, which is primarily divided into two parts: meta-task construction and bi-layer optimization.
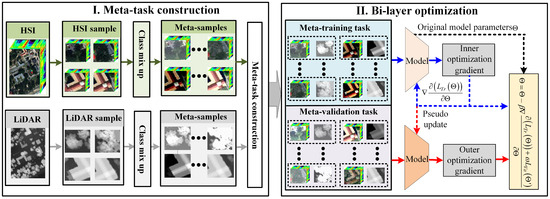
Figure 2.
Framework of meta-optimization mechanism.
- (1)
- Meta-task construction: First, multimodal data are input into the meta-task generation module, where meta-samples are generated based on a class mixing strategy. Then, an equal number of meta-samples from each class are randomly selected to construct meta-training tasks and meta-validation tasks;
- (2)
- Bi-layer optimization: First, in the inner optimization, calculate the model’s meta-training loss on meta-training tasks, pseudo-update the model based on this loss, and save the optimization gradients of the meta-training tasks. Then, in the outer optimization, calculate the meta-validation loss of the model after pseudo-updates on meta-validation tasks, and perform meta-updates on the model considering both meta-training and meta-validation losses.
3.1.2. Meta-Training Task Learning
Figure 3 shows the framework of meta training task learning. In this section, we will elucidate the workflow of the meta-training task:
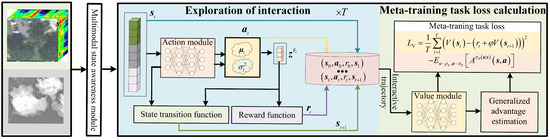
Figure 3.
Framework of meta-training task learning.
- (1)
- Exploration of interaction: First, input multimodal data from the meta-training task into the multimodal state perception module to obtain the state , where t represents the time step. Then, input into the action module to obtain causal distribution predictions , and obtain causal fusion features by sampling from the causal distribution. Next, use the state transition function to update the state to and calculate classification rewards and causal intervention rewards to obtain the total reward . Finally, repeat the above process until a predefined number of interactions is reached, obtaining an interaction trajectory;
- (2)
- Meta-training task loss calculation: First, estimate the state values for each time step in the interaction trajectory using a state value network. Then, calculate the value loss by computing the difference between the state value estimate and the future expected rewards. Simultaneously, use the generalized advantage estimation (GAE) [48] algorithm based on the state value estimate to obtain the advantage function. Calculate the policy loss based on the advantage function. Finally, compute the meta-training loss.
3.1.3. Meta-Validation Task Learning
In this section, we will elucidate the workflow of the meta-validation task:
First, the agent predicts the causal distribution of multimodal data in the meta-validation task based on the current action policy. It then obtains causal fusion features by sampling from the causal distribution. Next, it calculates class prototypes based on the causal fusion features of multimodal data from various classes in the meta-validation task. Class predictions are obtained through prototype matching. Finally, the meta-validation loss is calculated based on the class predictions and labels.
3.2. Modeling Multimodal Remote Sensing Data Classification as an MDP
Reinforcement learning can leverage exploration and interaction with the environment to understand intricate associations between actions and the environment. In the task of classifying multimodal remote sensing data, this characteristic of reinforcement learning has the potential to assist models in comprehending the complex relationships between multimodal data and labels. This, in turn, would allow the model to capture task-related complementary information from multimodal data.
However, there is currently a lack of research customizing reinforcement learning environments specifically for the task of multimodal remote sensing data classification. This poses a challenge in realizing the full potential of reinforcement learning for this task. Therefore, we modeled the multimodal remote sensing data classification problem as a Markov decision process (MDP) and customized its states, state transition function, actions, and rewards. Below, we provide a detailed explanation of the modeling process:
3.2.1. State and State Transition Function
The state is a comprehensive description of the environment at any given moment. It not only reflects the current attributes of the environment but also contains key information the agent needs to make decisions. Therefore, the state is the foundation for an agent to learn and understand its environment, ensuring it can learn effective behavior strategies based on complete information. The state transition reveals how the current state and the actions of the agent together affect the future state of the environment. This defines how the environment responds to the actions of the agent and is the basis for the agent to understand the complex interactions between its actions and the environment. This section introduces the design of the state and the design of the state transition function:
First, considering the existence of modal heterogeneity, data from different modalities often have inconsistent data dimensions. Therefore, we used a dimension unification module to unify the dimensions of samples from both modalities:
where and represent the meta-samples of the two modalities, and their generation methods are described in Section 3.4. and represent the dimensionally unified HSI and LiDAR, respectively, and and are the learnable dimension unification parameters for each modality.
Then, we divide the data from the two modalities into a series of spatial tokens along the spatial dimension and use encoders to obtain state-aware features for both modalities:
where (▪) represents the Transformer encoder. and are the spatial tokens for the two modalities; , h, and w are the spatial dimensions of the two-modal data; and and are the state-aware features of the two modalities.
Finally, we define the state as the concatenation of the state-aware features of the two modalities and the causal fusion features, and define the following state transition function:
where represents the causal fusion feature at time step , which is determined by the agent’s action being the initial causal fusion feature, which can be expressed as .
The advantage of this design lies in the fact that the state transition function replaces the causal fusion feature of the previous time step with that of the current time step at each time step, while retaining the unmerged state-aware features of the two modalities. This helps the agent understand the potential connections between the causal fusion feature and multimodal data, allowing it to optimize and adjust its action strategies accordingly.
3.2.2. Designing Actions and Rewards Based on Causal Intervention
In CMRL, the main goal of the agent is to discover the optimal action strategy that maximizes cumulative rewards through continuous exploration and feedback interactions. The achievement of this goal depends on the proper design of the actions and the reward mechanism. The design of actions needs to consider the characteristics of the environment and task requirements. Rewards, as the environment’s immediate feedback for specific actions of the agent, quantify the effectiveness of each action in achieving the target task. By imposing rewards and punishment feedback, the agent is guided to learn how to optimize its behavior strategy. In this section, we elaborate on the design of actions and rewards:
Inspired by human causal reasoning mechanisms, we treat information related to classes in multimodal data as causal factors, while information independent of classes is considered non-causal factors, such as spectral noise caused by weather or collection equipment. Multimodal data are a mix of causal and non-causal factors. Our goal is to capture causal factors to learn the true causal associations between multimodal data and class labels. Causal factors should meet three conditions: (1) causal factors are mutually independent, (2) they contain sufficient task-relevant information, and (3) they are distinct from non-causal factors. Therefore, to enable the agent to intelligently capture causal factors from multimodal data, we designed the following actions and rewards:
- (1)
- Predicting actions from causal distribution
Inspired by the variational autoencoder, we designed an action module that predicts the causal distribution in multimodal data based on the current state perceived by the agent. To ensure the mutual independence of causal factors, in this paper, the prior distribution of the causal distribution was designed as a multivariate Gaussian distribution with independent components. The output of the action module is the predicted action for the causal distribution in the multimodal data, which can be expressed as
where and represent the mean and variance of the causal distribution predicted at time step t, respectively.
Next, sampling is performed from the causal distribution using reparameterization [49] to obtain causal fusion features:
where represents a standard multivariate Gaussian distribution, with ∼ denoting the sampling operation.
Finally, we minimize the difference between the causal distribution and the prior distribution (standard multivariate Gaussian distribution) using the following KL divergence constraint:
where T represents the predefined total number of time steps, and (▪) represents the KL divergence.
- (2)
- Classification rewards
To ensure that the causal fusion features contain sufficient task-relevant information, we designed a prototype matching reward mechanism that provides reward signals to the agent by comparing the similarity between the causal fusion features and class prototypes.
Specifically, first, we computed class prototypes based on the collection of classes from the meta-training task, and obtained class predictions for causal fusion features by calculating the distance between causal fusion features and class prototypes. For the causal fusion feature at time step t, its probability prediction for class class c can be represented as
where is the class label for , and (▪) is the distance metric, which is the Euclidean distance in this case. is the class prototype and can be represented as
where R is the number of samples in the class set, is the causal fusion feature of the t-th sample in the c-th class.
Finally, we can calculate the cross-entropy between class predictions and the true labels to obtain the classification reward for the t-th time step:
where is the true class label, is the class prediction, and is the reward coefficient.
- (3)
- Causal intervention reward
To ensure a sufficient separation between causal and non-causal factors, we use causal intervention. If we can control the non-causal factors in multimodal data, we can disrupt their spurious statistical associations with class labels, thus capturing pure causal factors.However, the effectiveness of this mechanism relies on accurate interventions for non-causal factors, which are often challenging to directly observe and manipulate.
Based on the analysis of HSI in existing research [50], we observed that the high-frequency components tend to contain more noise information, while the low-frequency components contain more key class-discrimination information. This observation inspired us to adopt a simplified assumption that noise primarily manifests as high-frequency characteristics. Consequently, we simulated noise variations in real-world scenarios to implement causal intervention by perturbing the high-frequency components of HSI. Specifically, first, we utilized Fourier transformation to decompose the HSI into low-frequency components and high-frequency components :
where (▪) represents the Fourier transform.
Then, we perturbed the high-frequency components to find the non-causal factors and obtained the counterfactual HSI by performing an inverse Fourier transform:
where (▪) represents the inverse Fourier transform, and represents the high-frequency components obtained after performing the Fourier transform on the randomly selected HSI.
Afterward, the counterfactual state is obtained by feeding and the corresponding input into the state perception module, and then it is input into the action module to obtain the counterfactual causal fusion features .
Finally, the classification reward is calculated based on , and the causal intervention reward is obtained by calculating the mean squared error between the classification rewards corresponding to and :
where , corresponds to class predictions based on counterfactual causal fusion features. Causal intervention reward is obtained by constraining the consistent causal effects between counterfactual causal fusion features and causal fusion features, which can break the causal relationship between non-causal factors and class labels, ensuring a sufficient separation between causal factors and non-causal factors.
- (4)
- Total reward
The total reward can be represented as follows:
where is the weighting coefficient.
3.3. Policy Gradient-Based Reinforcement Learning
This section aims to optimize the action strategies of the agent. Specifically, in this paper, the action of the agent is to predict the causal distribution of multimodal data, while the prior distribution of the causal distribution is assumed to be a multivariate Gaussian distribution. Based on this assumption, the actions of the agent are often high-dimensional and continuous. At this time, reinforcement learning schemes based on value iteration or policy iteration are often difficult to apply. Fortunately, policy gradient theory provides a solution for dealing with such situations. Policy gradient theory optimizes the policy by maximizing the expected return, without the need to solve complex value functions. The commonly used policy loss can be expressed as
where . represents the distribution of state at time step t, and is the discount factor. is a parameterized policy network that, based on state , outputs the corresponding action , corresponding to the action module in this paper.
is the advantage function, which is used to quantify how much additional reward the current policy network’s output action, relative to the expected average performance, can bring given the state . The advantage function can be represented as follows:
where represents the expected reward of the agent taking action in state , and is the expected reward of following the current policy in state . The optimization goal of the model is to improve the current policy by maximizing the advantage function, thereby achieving the maximization of expected rewards.
However, it is often difficult to directly obtain the expected reward for the agent taking action in a given state . Therefore, we use GAE to fit the advantage function. GAE uses a weighted average of a series of temporal difference residuals to estimate the advantage function. The advantage function at the nth time step t can be represented as:
where , (▪) is the value module used to assess the expected value of an input state. is the discount factor.
From the above equation, it can be seen that the optimization of the action module is closely related to the advantage function, and the quality of the advantage function depends on the accuracy of the state value network’s evaluation of state values. Therefore, we optimize this by minimizing the following value loss:
3.4. Knowledge Induction Mechanism
The knowledge induction mechanism is designed to help models deduce cross-task shared knowledge from a multitude of tasks by simulating scenarios where the model generalizes on unseen data. This is achieved through the construction of meta-training tasks and meta-validation tasks. Meta-training tasks simulate the available multimodal data to train the model, while meta-validation tasks simulate unseen multimodal data. The model’s performance on these new data is evaluated to validate its generalization capability. The knowledge induction mechanism mainly consists of two parts: meta-task construction and bi-layer optimization.
3.4.1. Meta-Task Construction
To construct the meta-training and meta-validation tasks, we developed a class-mixing-based meta-task generation module. This module is designed to ensure that the meta-training and meta-validation tasks adequately reflect the diversity of real-world data. Specifically, we employed a class-mixing strategy to generate meta-samples, which are used to expand the original training data and form the meta-training and meta-validation sets. The class-mixing strategy involves combining different modal samples from the same class (for example, HSI and LiDAR) to create new meta-samples. These meta-samples can be represented as
where and are the multimodal meta-samples, and are the original HSI and LiDAR samples randomly selected from the same class sample set, and is the mixing coefficient, which can be expressed as . Meta-samples can be considered as interpolations within the real data distribution, allowing them to more comprehensively cover the actual data distribution.
During construction of the meta-training and meta-validation tasks, we uniformly sample multimodal data from each class of the meta-training and meta-validation sets, ensuring that the model can learn each class in a balanced manner. It is important to note that, in each meta-update process, the samples in both the meta-training and meta-validation tasks are newly generated meta-samples. This method ensures the diversity of the meta-training tasks and the novelty of the meta-validation tasks.
3.4.2. Bi-Layer Optimization
During the inner optimization, we train the model using meta-training tasks and perform pseudo-updates on the model using gradient descent:
where represents the model parameters before the update, is the learning rate for inner layer optimization, and represents the meta-training tasks. denotes the meta-training loss with model parameters . The meta-training loss can be expressed as
where and are weight coefficients.
In the outer layer optimization, we calculate the loss of the pseudo-updated model during the meta-validation tasks to assess the model’s generalization ability for new tasks. This process involves combining the meta-training loss and meta-validation loss to perform a meta-update on the model:
where is the meta-learning rate, and represents the meta-validation tasks. denotes the meta-validation loss corresponding to the model parameters . The meta-validation loss can be expressed as
where is the class prediction for the meta-validation task based on causal fusion features, which can be obtained by measuring the similarity between the causal fusion features and the class prototypes. Through this approach, the learning objective of the model is not merely to achieve optimal performance in the meta-training tasks, but rather to learn the cross-task shared knowledge that can be generalized to unseen meta-validation tasks. This, in turn, enables the accurate classification of unseen multimodal data.
4. Experiment
4.1. Dataset
We selected three sets of HSI and LiDAR datasets to validate the performance of the algorithm proposed in this paper, the training set contained training samples and meta-samples, where the training samples consisted of 20 samples per class randomly selected from the dataset, and the meta-samples were generated based on the training samples using a class-mixing strategy. The validation set was composed of validate samples obtained through random selection from the dataset, ensuring no overlap with the training samples. The remaining samples in the dataset were allocated to the testing set as test samples. The specific distribution of train, validate, and test samples in each dataset is shown in Table 1. Below, we provide a comprehensive description of the three datasets involved in the experiments.

Table 1.
The number of train, validate, and test samples for each dataset.
- (1)
- MUUFL Dataset [51]: The MUUFL dataset was collected at the University of Southern Mississippi in Gulfport, covering 11 classes of ground objects. The data were acquired in November 2010 using Gemini LiDAR and CASI-1500 equipment. These devices were synchronized on the same flight platform to collect hyperspectral image data and LiDAR data simultaneously, ensuring spatial and temporal consistency between the two types of data. Both the hyperspectral images and LiDAR data consist of 325 × 220 pixels with a spatial resolution of 1 m. The hyperspectral images have 64 bands, and the LiDAR data record precise elevation information of the terrain. Dataset available at: https://github.com/GatorSense/MUUFLGulfport (accessed on 21 January 2024).
- (2)
- Houston Dataset [52]: Funded by the National Science Foundation of the United States and collected by the Airborne Laser Mapping Center, the Houston dataset covers 15 classes of ground objects in and around the University of Houston campus. This multimodal dataset primarily consists of two parts: hyperspectral data and LiDAR data. Both types of data have the same spatial resolution of 2.5 m and include 349 × 1905 pixels. The HSI covers 144 spectral bands from 380 nm to 1050 nm. The LiDAR data records precise elevation information of the terrain. Dataset available at: http://dase.grss-ieee.org/ (accessed on 21 January 2024).
- (3)
- Trento Dataset [53]: The Trento dataset was collected in the rural areas south of Trento, Italy, encompassing 6 classes of ground objects, including various natural features and artificial agricultural structures. This dataset integrates hyperspectral images captured by an airborne hyperspectral imager and LiDAR data obtained from an aerial laser scanning system. Both modalities have a consistent spatial resolution and consist of 166 × 600 pixels. The hyperspectral images include 63 spectral bands, and the LiDAR data records precise elevation information of the terrain. Dataset available at: https://github.com/tyust-dayu/Trento (accessed on 21 January 2024).
4.2. Experimental Setting
All experiments were conducted on a computer equipped with a 3.80 GHz Intel Core i7-10700KF CPU, 32 GB RAM, produced by Intel Corporation headquartered in Santa Clara, California, USA, and an RTX 3090Ti GPU, with PyTorch 2.1.1 as the experimental environment. The comparison methods included unimodal approaches: convolutional recurrent neural networks (CRNN) [54]; multimodal decision fusion methods: hierarchical random walk network (HRWN) [55]; and multimodal feature fusion methods: two-branch convolution neural network (TBCNN) [56], patch-to-patch convolution neural network (PTP-CNN) [57], coupled adversarial learning based classification (CALC) [58], and multimodal fusion transformer (MFT) [59].
To ensure fairness in the comparative experiments, the parameter settings for each method followed their original configurations. For the unimodal methods, we trained the models using 20 HSI samples per class. For the multimodal methods, we trained the models using 20 paired HSI and LiDAR samples per class. In all experiments, AdamW was used as the optimizer, with an episode setting of 2000, an inner layer optimization learning rate of 0.001, a meta-learning rate of 0.001, a patch size of 7, a predefined number of time steps set to 5, and an inner layer optimization count of 5. To balance the diversity of samples in the meta-training/meta-validation tasks and computational efficiency, we set the number of samples per class in the meta-task to 20. To eliminate the impact of randomness on the experiments, all experimental results are the average of 10 runs. Three evaluation metrics were chosen, including overall accuracy (OA), average accuracy (AA) per class, and the Kappa coefficient.
4.3. Comparative Experiments
The experimental results of CMRL and its comparative methods on the three datasets are shown in Table 1, Table 2 and Table 3, in each row, the optimal metric is bolded. From these, it can be observed that

Table 2.
Classification accuracy for the MUUFL dataset.

Table 3.
Classification accuracy of the Houston dataset.
- (1)
- Compared to the unimodal methods, multimodal methods exhibited a higher classification accuracy. This was because, due to the phenomena of “different objects have the same spectra” and “the same objects have different spectra” in HSI, some samples may have had low class distinguishability, making it difficult for the unimodal methods that only use HSI to achieve satisfactory performance. In contrast, the multimodal methods could combine LiDAR information to enhance the model’s ability to differentiate features when such phenomena occurred;
- (2)
- Compared to the multimodal decision fusion methods, the multimodal feature fusion methods demonstrated a higher classification performance. This is because the multimodal decision fusion methods integrate the output information of the classifiers. When noise exists in multimodal data, the noise interference from different modalities might accumulate during the decision-making process, leading to inaccurate class predictions. On the other hand, multimodal feature fusion methods can establish deep interactions between multimodal data, more effectively mining class-distinguishing information;
- (3)
- CMRL showed the highest classification performance across all three datasets, demonstrating its superiority in multimodal remote sensing data classification tasks. In particular, it showed a clear classification advantage for challenging classes like “mixed ground surface” and “sidewalk.” The former often contains complex noise information, while the latter is frequently obscured by structures such as buildings and trees, presenting significant intra-class variability and blurred inter-class boundaries. The superior performance of CMRL can be attributed to the following factors: On one hand, its feedback learning mechanism and causal inference mechanism allow the agent to fully understand which information in the multimodal data has a causal relationship with the labels. This enables the agent to cut off false statistical associations between non-causal factors (like noise information and obstructed heterogeneous ground features) and labels, achieving precise mining of real causal effects. On the other hand, the knowledge induction mechanism of CMRL enables the agent to learn cross-task shared knowledge, which can help it achieve higher generalization performance on unseen multimodal data.
4.4. Visual Analysis
4.4.1. Classification Accuracy Maps
In this section, we demonstrate how we visualized the classification accuracy maps of CMRL and its comparative methods on three datasets, as shown in Figure 4, Figure 5 and Figure 6. It can be observed that CMRL exhibited the best continuity in the classification accuracy diagrams across all three datasets, especially in some easily confusable classes. For example, in the Trento dataset, the classes “buildings” (green) and “roads” (yellow) are both made of concrete material, hence they have similar spectral curves. However, LiDAR elevation data helps distinguish these two types of features. Benefiting from the feedback learning mechanism of reinforcement learning, CMRL showed the strongest capability among all comparative methods in capturing multimodal complementary information, resulting in the least confusion and misclassification in these two classes.
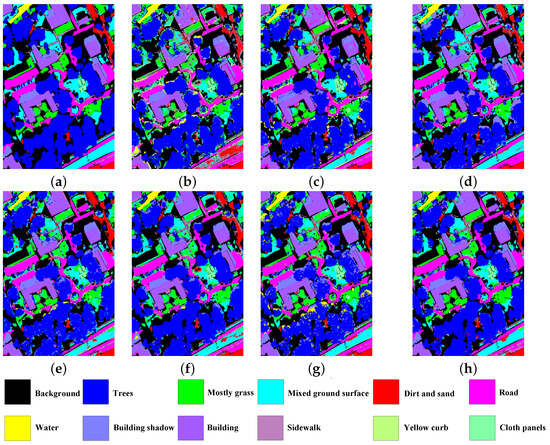
Figure 4.
Classification accuracy map for the MUUFL dataset. (a) Label map (b) CRNN (c) HRWN (d) TBCNN (e) PTPCNN (f) CALC (g) MFT (h) CMRL.

Figure 5.
Classification accuracy map for the Houston dataset. (a) Label map (b) CRNN (c) HRWN (d) TBCNN (e) PTPCNN (f) CALC (g) MFT (h) CMRL.
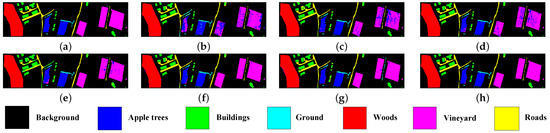
Figure 6.
Classification accuracy map for the Trento dataset. (a) Label map (b) CRNN (c) HRWN (d) TBCNN (e) PTPCNN (f) CALC (g) MFT (h) CMRL.
4.4.2. t-SNE Maps
In this section, using the Trento dataset as an example, we present the t-SNE diagrams of CMRL and its comparative methods, as shown in Figure 7. It can be observed that CMRL demonstrated the highest intra-class consistency and inter-class separability, especially for the easily confusable classes “buildings” and “roads”. The other methods showed a mix of these two classes, while CMRL almost entirely avoided this phenomenon. This indicates that CMRL could effectively capture class-distinguishing information in multimodal data, possessing the best feature learning ability.
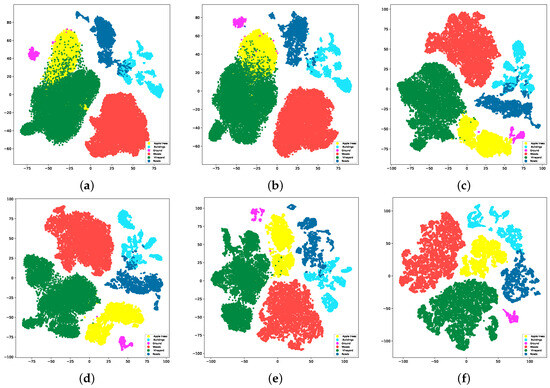
Figure 7.
t-SNE map for the Trento dataset. (a) CRNN (b) TBCNN (c) PTPCNN (d) CALC (e) MFT (f) CMRL.
4.4.3. Ablation Study
To validate the effectiveness of the components in this paper, we constructed ablation models, as shown in Table 4 and Table 5. In Table 4, the checkmark indicates preserved components, while the cross indicates degraded components. In Table 5, the optimal metric in each row is bolded. Below, we introduce the design principles of these models.

Table 4.
Classification accuracy for the Trento dataset.

Table 5.
Baseline models.
Baseline-A: The initial causal fusion features were directly used for multimodal remote sensing data classification tasks through prototype matching, and the model was updated using cross-entropy loss.
Baseline-B: Built upon Baseline-A by adding a reinforcement learning (RL) feedback learning mechanism, exclusively using classification rewards as the reward signal and updating the model using value loss and policy loss.
Baseline-C: Enhanced Baseline-B by incorporating a causal learning (CL) causal inference mechanism, specifically adding causal intervention rewards and constraints on the KL divergence of the causal distribution.
CMRL: Further developed Baseline-C by integrating a meta-learning (ML) knowledge induction mechanism, which involved constructing meta-training tasks and meta-validation tasks, and updating the model using a bi-layer optimization mechanism.
Table 5 and Table 6 show the classification accuracy of each model on the three datasets, from which the following results can be observed:

Table 6.
Impact of different components on OA (%).
- (1)
- Compared to Baseline-A, Baseline-B improved the classification performance on three datasets by 2.81%, 2.21%, and 2.23%, respectively. This was because the feedback learning mechanism of reinforcement learning allows the agent to interact with a custom environment to understand the complex association mechanisms between its actions (predictions about the causal distribution) and the multimodal remote sensing data classification task. It can adjust and optimize action strategies based on immediate feedback from rewards. This iterative feedback structure enhances the model’s ability to capture task-relevant complementary information in multimodal data. The experimental performance also validated the effectiveness of the feedback learning mechanism of reinforcement learning in multimodal remote sensing data classification tasks;
- (2)
- Compared to Baseline-B, Baseline-C improved the classification performance on three datasets by 1.08%, 0.91%, and 1.42%, respectively. This was because the causal reasoning mechanism of causal learning helps the model identify causal and non-causal factors in multimodal data. This mechanism effectively reduces the influence of spectral noise in HSI by disrupting the false statistical association between non-causal factors and labels through causal intervention, helping the model establish a true causal relationship between multimodal data and labels. The experimental performance also validated the effectiveness of the causal reasoning mechanism of causal learning in multimodal remote sensing data classification tasks;
- (3)
- Compared to Baseline-C, CMRL improved the classification performance on three datasets by 2.24%, 2.03%, and 1.23%, respectively. This was because the knowledge induction mechanism of meta-learning helps the model reveal cross-task shared knowledge applicable to unseen multimodal data from a large number of similar yet different meta-tasks. This effectively alleviates the issue of the limited model generalization capability caused by data distribution bias between training and test samples. The experimental performance also validated the effectiveness of the knowledge induction mechanism of meta-learning in multimodal remote sensing data classification tasks.
5. Conclusions
This paper integrated reinforcement learning, causal learning, and meta-learning into a unified framework, inspired by the human cognitive mechanisms of feedback learning, causal inference, and knowledge induction. The proposed CMRL addresses key challenges in multimodal remote sensing data classification tasks, such as the difficulty in mining multimodal complementary information, suppressing interference from non-causal factors, and generalizing to unseen data. First, the feedback learning mechanism based on reinforcement learning enables the agent to fully understand the complex associations between multimodal remote sensing data and labels, capturing class-discriminative multi-modal complementary information from noisy data. Second, the causal inference mechanism based on causal intervention helps the model to establish the true causal connections between multimodal remote sensing data and labels, accurately suppressing interference from non-causal factors. Lastly, the knowledge induction mechanism based on meta-learning assists the model in capturing cross-task shared knowledge from meta-training and meta-validation tasks, enhancing the model’s generalization capabilities on unseen multimodal remote sensing data. Experiments on three multimodal remote sensing datasets demonstrated that CMRL achieved state-of-the-art performance, offering a new paradigm in reinforcement learning, a novel perspective on causal learning, and an innovative meta-optimization mechanism for multimodal remote sensing data classification. However, this paper adopted a rather simplistic assumption about noise when conducting the causal interventions, which may not be applicable to all types and sources of noise. In future work, we will further explore more realistic causative intervention methods to accurately simulate different types and sources of noise.
Author Contributions
W.Z., X.W., H.W. and Y.C. provided significant contributions to the work. W.Z. and Y.C. provided the method ideas for this study; W.Z. and H.W. performed the experiments; X.W. analyzed the data; W.Z. and X.W. wrote the original paper; Y.C. reviewed and edited the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China under Grant 62176259, Grant 62373364, Grant 62303468, by the Key Research and Development Program of Jiangsu Province under Grant BE2022095, and by the China Postdoctoral Science Foundation Grant 2023M733757, the Natural Science Foundation of Jiangsu Province under Grant BK20221116. (Corresponding author: Yuhu Cheng).
Data Availability Statement
The locations of these observers were generated by computer simulation. lt is easy to generate the simulation with the method in the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, Y.; Li, W.; Zhang, M.; Wang, S.; Tao, R.; Du, Q. Graph information aggregation cross-domain few-shot learning for hyperspectral image classification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 1912–1925. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Wang, W.; Wang, J.; Cai, Y.; Yang, Z.; Li, J. Hyper-LGNet: Coupling local and global features for hyperspectral image classification. Remote Sens. 2022, 14, 5251. [Google Scholar] [CrossRef]
- Datta, D.; Mallick, P.K.; Reddy, A.V.N.; Mohammed, M.A.; Jaber, M.M.; Alghawli, A.S.; Al-qaness, M.A.A. A hybrid classification of imbalanced hyperspectral images using ADASYN and enhanced deep subsampled multi-grained cascaded forest. Remote Sens. 2022, 14, 4853. [Google Scholar] [CrossRef]
- Xing, C.; Cong, Y.; Duan, C.; Wang, Z.; Wang, M. Deep network with irregular convolutional kernels and self-expressive property for classification of hyperspectral images. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 10747–10761. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Deng, W.; Zheng, Z.; Zhong, Y.; Guan, Q.; Lin, W.; Zhang, L.; Li, D. A spectral-spatial-dependent global learning framework for insufficient and imbalanced hyperspectral image classification. IEEE Trans. Cybern. 2021, 52, 11709–11723. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Chong, Y.; Pan, S.; Wang, Y.; Nie, C. Spatial-spectral unified adaptive probability graph convolutional networks for hyperspectral image classification. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3650–3664. [Google Scholar] [CrossRef] [PubMed]
- Ren, Q.; Tu, B.; Liao, S.; Chen, S. Hyperspectral image classification with iformer network feature extraction. Remote Sens. 2022, 14, 4866. [Google Scholar] [CrossRef]
- Dong, W.; Yang, T.; Qu, J.; Zhang, T.; Xiao, S.; Li, Y. Joint contextual representation model-informed interpretable network with dictionary aligning for hyperspectral and LiDAR classification. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 6804–6818. [Google Scholar] [CrossRef]
- Gao, H.; Feng, H.; Zhang, Y.; Xu, S.; Zhang, B. AMSSE-Net: Adaptive multiscale spatial–spectral enhancement network for classification of hyperspectral and LiDAR data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5531317. [Google Scholar] [CrossRef]
- Zhang, T.; Xiao, S.; Dong, W.; Qu, J.; Yang, Y. A mutual guidance attention-based multi-level fusion network for hyperspectral and LiDAR classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 5509105. [Google Scholar] [CrossRef]
- Song, L.; Feng, Z.; Yang, S.; Zhang, X.; Jiao, L. Discrepant bi-directional interaction fusion network for hyperspectral and LiDAR data classification. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5510605. [Google Scholar] [CrossRef]
- Xue, Z.; Yu, X.; Tan, X.; Liu, B.; Yu, A.; Wei, X. Multiscale deep learning network with self-calibrated convolution for hyperspectral and LiDAR data collaborative classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5514116. [Google Scholar] [CrossRef]
- Roy, S.K.; Deria, A.; Hong, D.; Ahmad, M.; Plaza, A.; Chanussot, J. Hyperspectral and LiDAR data classification using joint CNNs and morphological feature learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5530416. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Shi, Y.; Lai, J.; Tan, X. AM3Net: Adaptive mutual-learning-based multimodal data fusion network. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 5411–5426. [Google Scholar] [CrossRef]
- Du, X.; Zheng, X.; Lu, X.; Wang, X. Hyperspectral and LiDAR representation with spectral-spatial graph network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 9231–9245. [Google Scholar] [CrossRef]
- Oh, I.; Rho, S.; Moon, S.; Son, S.; Lee, H.; Chung, J. Creating pro-level AI for a real-time fighting game using deep reinforcement learning. IEEE Trans. Games 2021, 14, 212–220. [Google Scholar] [CrossRef]
- Donge, V.S.; Lian, B.; Lewis, F.L.; Davoudi, A. Multi-agent graphical games with inverse reinforcement learning. IEEE Trans. Control Netw. Syst. 2022, 10, 841–852. [Google Scholar] [CrossRef]
- Justesen, N.; Bontrager, P.; Togelius, J.; Risi, S. Deep learning for video game playing. IEEE Trans. Games 2019, 12, 1–20. [Google Scholar]
- Matarese, M.; Sciutti, A.; Rea, F.; Rossi, S. Toward robots’ behavioral transparency of temporal difference reinforcement learning with a human teacher. IEEE Trans. Hum. Mach. Syst. 2021, 51, 578–589. [Google Scholar] [CrossRef]
- Zhang, L.; Hou, Z.; Wang, J.; Liu, Z.; Li, W. Robot navigation with reinforcement learned path generation and fine-tuned motion control. IEEE Robot. Autom. 2023, 8, 4489–4496. [Google Scholar] [CrossRef]
- Garaffa, L.C.; Basso, M.; Konzen, A.A.; de Freitas, E.P. Reinforcement learning for mobile robotics exploration: A survey. IEEE Trans. Neural Netw. Learn. Sys. 2023, 8, 3796–3810. [Google Scholar] [CrossRef]
- Wu, J.; Huang, Z.; Lv, C. Uncertainty-aware model-based reinforcement learning: Methodology and application in autonomous driving. IEEE Trans. Intell. Veh. 2022, 8, 194–203. [Google Scholar] [CrossRef]
- Shu, H.; Liu, T.; Mu, X.; Cao, D. Driving tasks transfer using deep reinforcement learning for decision-making of autonomous vehicles in unsignalized intersection. IEEE Trans. Veh. Technol. 2021, 71, 41–52. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhao, H. A survey of deep RL and IL for autonomous driving policy learning. IEEE Trans. Intell. Transp. Syst. 2021, 23, 14043–14065. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [PubMed]
- Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P.; et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar]
- Wang, X.; Gu, Y.; Cheng, Y.; Liu, A.; Chen, C.P. Approximate policy-based accelerated deep reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 1820–1830. [Google Scholar] [CrossRef] [PubMed]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Bai, Z.; Hao, P.; Shangguan, W.; Cai, B.; Barth, M.J. Hybrid reinforcement learning-based eco-driving strategy for connected and automated vehicles at signalized intersections. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15850–15863. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [PubMed]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double Q-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 2094–2100. [Google Scholar]
- Baek, J.; Kaddoum, G. Online partial offloading and task scheduling in SDN-fog networks with deep recurrent reinforcement learning. IEEE Internet Things J. 2022, 9, 11578–11589. [Google Scholar] [CrossRef]
- Kohl, N.; Stone, P. Policy gradient reinforcement learning for fast quadrupedal locomotion. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 2619–2624. [Google Scholar]
- Lilicrap, T.; Hunt, J.; Pritzel, A.; Hess, N.; Erez, T.; Silver, D.; Wiestra, D. Continuous control with deep reinforcement learning. In Proceedings of the International Conference on Representation Learning, San Juan, PR, USA, 2–4 May 2016; pp. 1–14. [Google Scholar]
- Cheng, Y.; Huang, L.; Wang, X. Authentic boundary proximal policy optimization. IEEE Trans. Cybern. 2021, 52, 9428–9438. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Xiao, L.; Cao, X.; Foroosh, H. Multiple adverse weather conditions adaptation for object detection via causal intervention. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 46, 1742–1756. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, F.; Chen, Z.; Wu, Y.-C.; Hao, J.; Chen, G.; Heng, P.-A. Contrastive-ace: Domain generalization through alignment of causal mechanisms. IEEE Trans. Image Process. 2023, 32, 235–250. [Google Scholar] [CrossRef]
- Liu, Y.; Li, G.; Lin, L. Cross-modal causal relational reasoning for event-level visual question answering. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 11624–11641. [Google Scholar] [PubMed]
- Lin, J.; Wang, K.; Chen, Z.; Liang, X.; Lin, L. Towards causality-aware inferring: A sequential discriminative approach for medical diagnosis. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 13363–13375. [Google Scholar] [CrossRef]
- Zhang, Y.-F.; Zhang, Z.; Li, D.; Jia, Z.; Wang, L.; Tan, T. learning domain invariant representations for generalizable person re-identification. IEEE Trans. Image Process. 2023, 32, 509–523. [Google Scholar] [CrossRef]
- Nag, S.; Raychaudhuri, D.S.; Paul, S.; Roy-Chowdhury, A.K. Reconstruction Guided Meta-Learning for Few Shot Open Set Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 15394–15405. [Google Scholar] [CrossRef] [PubMed]
- Hospedales, T.; Antoniou, A.; Micaelli, P.; Storkey, A. Meta-learning in neural networks: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 5149–5169. [Google Scholar]
- Coskun, H.; Zia, M.Z.; Tekin, B.; Bogo, F.; Navab, N.; Tombari, F.; Sawhney, H.S. Domain-specific priors and meta learning for few-shot first-person action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 6659–6673. [Google Scholar] [CrossRef]
- Yu, B.; Li, X.; Li, W.; Zhou, J.; Lu, J. Discrepancy-aware meta-learning for zero-shot face manipulation detection. IEEE Trans. Image Process. 2023, 32, 3759–3773. [Google Scholar] [CrossRef] [PubMed]
- Ye, H.-J.; Han, L.; Zhan, D.-C. Revisiting unsupervised meta-learning via the characteristics of few-shot tasks. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 3721–3737. [Google Scholar] [CrossRef]
- Lv, Q.; Chen, G.; Yang, Z.; Zhong, W.; Chen, C.Y.-C. Meta learning with graph attention networks for low-data drug discovery. IEEE Trans. Neural Netw. Learn. Sys. 2023, 1–13. [Google Scholar] [CrossRef]
- Wang, H.; Wang, X.; Cheng, Y. Graph meta transfer network for heterogeneous few-shot hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5501112. [Google Scholar] [CrossRef]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.I.; Abbeel, P. High-dimensional continuous control using generalized advantage estimation. arXiv 2015, arXiv:1506.02438. [Google Scholar]
- Jiao, P.; Guo, X.; Jing, X.; He, D.; Wu, H.; Pan, S.; Gong, M.; Wang, W. Temporal network embedding for link prediction via vae joint attention mechanism. IEEE Trans. Neural Netw. Learn. Sys. 2022, 33, 7400–7413. [Google Scholar] [CrossRef]
- Wang, S.; Li, L.; Li, X.; Zhang, J.; Zhao, L.; Su, X.; Chen, F. textcolorredA denoising network based on frequency-spectral- spatial-feature for hyperspectral image. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2023, 16, 6693–6710. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, Y.; Tu, B.; Zhou, C.; Li, Q. Multiview hierarchical network for hyperspectral and LiDAR data classification. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2022, 15, 1454–1469. [Google Scholar] [CrossRef]
- Debes, C.; Merentitis, A.; Heremans, R.; Hahn, J.; Frangiadakis, N.; van Kasteren, T.; Liao, W.; Bellens, R.; Pižurica, A.; Gautama, S.; et al. Hyperspectral and LiDAR data fusion: Outcome of the 2013 GRSS data fusion contest. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2014, 7, 2405–2418. [Google Scholar] [CrossRef]
- Shen, X.; Deng, X.; Geng, J.; Jiang, W. SFE-FN: A shuffle feature enhancement-based fusion network for hyperspectral and LiDAR classification. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5501605. [Google Scholar] [CrossRef]
- Wu, H.; Prasad, S. Convolutional recurrent neural networks for hyperspectral data classification. Remote Sens. 2017, 9, 298. [Google Scholar] [CrossRef]
- Zhao, X.; Tao, R.; Li, W.; Li, H.-C.; Du, Q.; Liao, W.; Philips, W. Joint classification of hyperspectral and LiDAR data using hierarchical random walk and deep CNN architecture. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7355–7370. [Google Scholar] [CrossRef]
- Xu, X.; Li, W.; Ran, Q.; Du, Q.; Gao, L.; Zhang, B. Multisource remote sensing data classification based on convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 937–949. [Google Scholar] [CrossRef]
- Zhang, M.; Li, W.; Du, Q.; Gao, L.; Zhang, B. Feature extraction for classification of hyperspectral and LiDAR data using patch-to-patch CNN. IEEE Trans. Cybern. 2020, 50, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Ding, K.; Fu, W.; Li, S.; Guo, A. Coupled adversarial learning for fusion classification of hyperspectral and LiDAR data. Inf. Fusion 2023, 93, 118–131. [Google Scholar] [CrossRef]
- Roy, S.K.; Deria, A.; Hong, D.; Rasti, B.; Plaza, A.J.; Chanussot, J. Multimodal fusion transformer for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5515620. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).