An Adaptive IMM Algorithm for a PD Radar with Improved Maneuvering Target Tracking Performance
Abstract
1. Introduction
2. Review of the Classical IMM Algorithm
2.1. Model Interaction
2.2. Parallel Filtering of Models
2.3. The Updates of Model Probability
2.4. Model Estimation Fusion
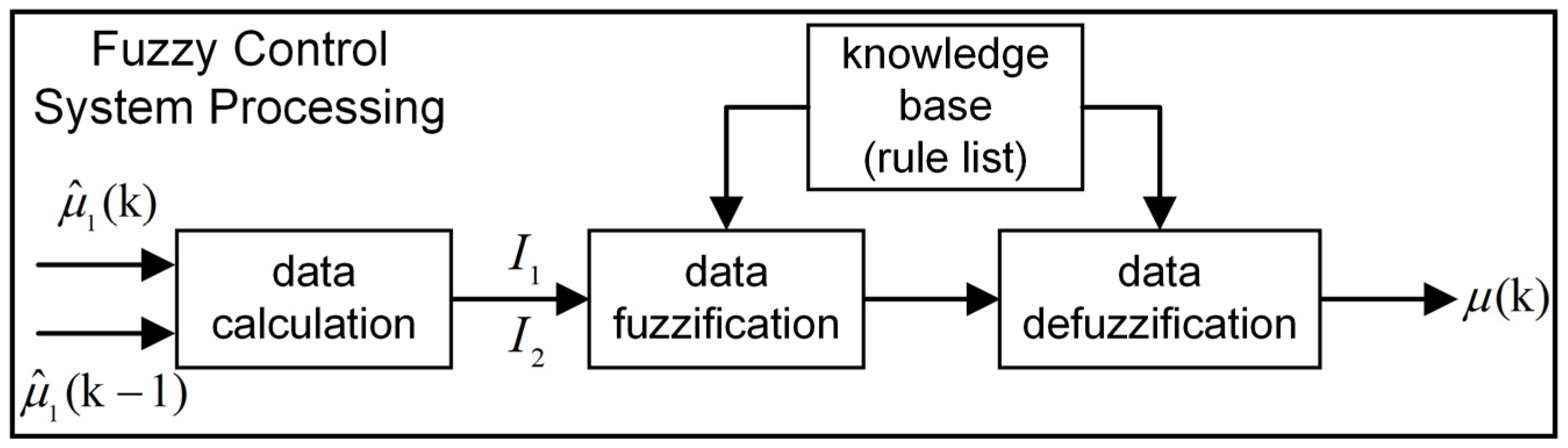
3. The Design of the ATPFC-IMM Algorithm
| Algorithm 1: Implementation pseudocode for the proposed ATPFC-IMM algorithm in a single cycle. |
| Background: The classical IMM algorithm. |
| Function: Accelerating model switching and updating model probabilities. |
| 1: Input: The probability information of each model. |
| 2: Computation: |
| (1) Likelihood function ratio: for () do for () do ; end for end for |
| (2) Correction function: . |
| 3: Correction of probability transfer matrix: for () do ; end for |
| 4: Normalization of probability transfer matrix: . |
| 5: Re-Updating: |
| Inputting the model probability information into the fuzzy control system: for () do ; end for |
| 6: The currently obtained model probabilities are kept for the next moment of the algorithm update: . |
| 7: Output: (1). The re-updating probability of each model: . (2). Model state estimation fusion: . 8: Return , ; |
3.1. The Correction of the Probability Transfer Matrix
3.2. The Design of the Fuzzy Control System
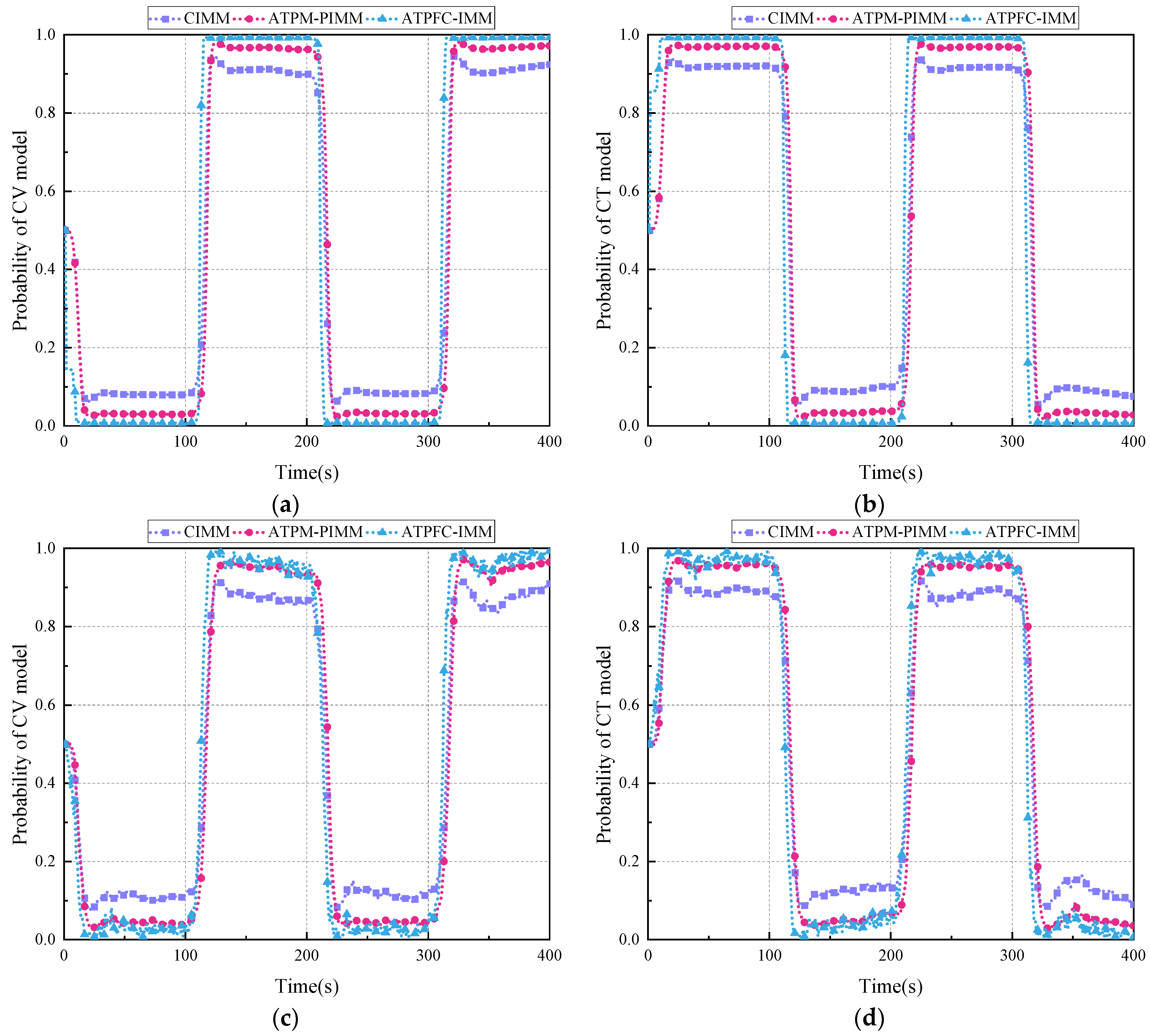
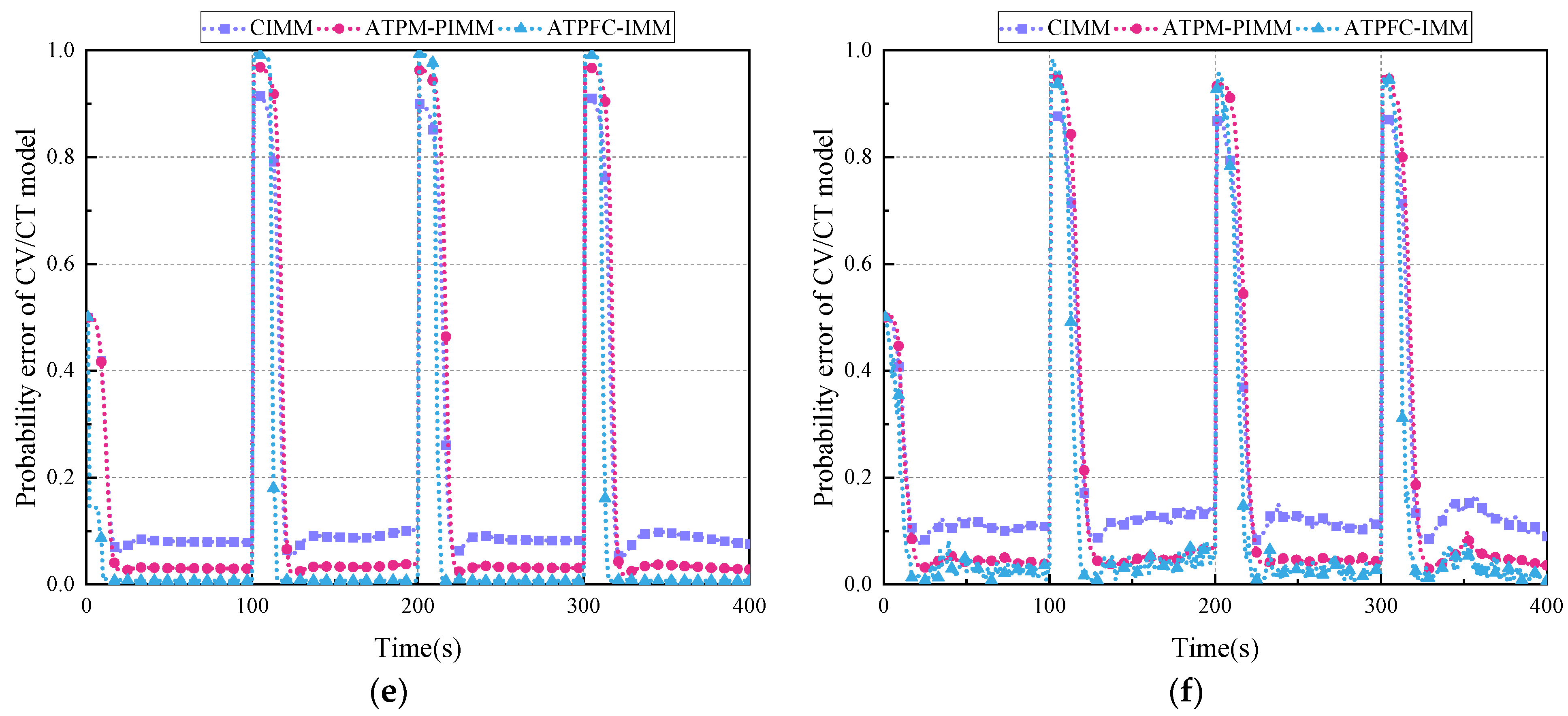
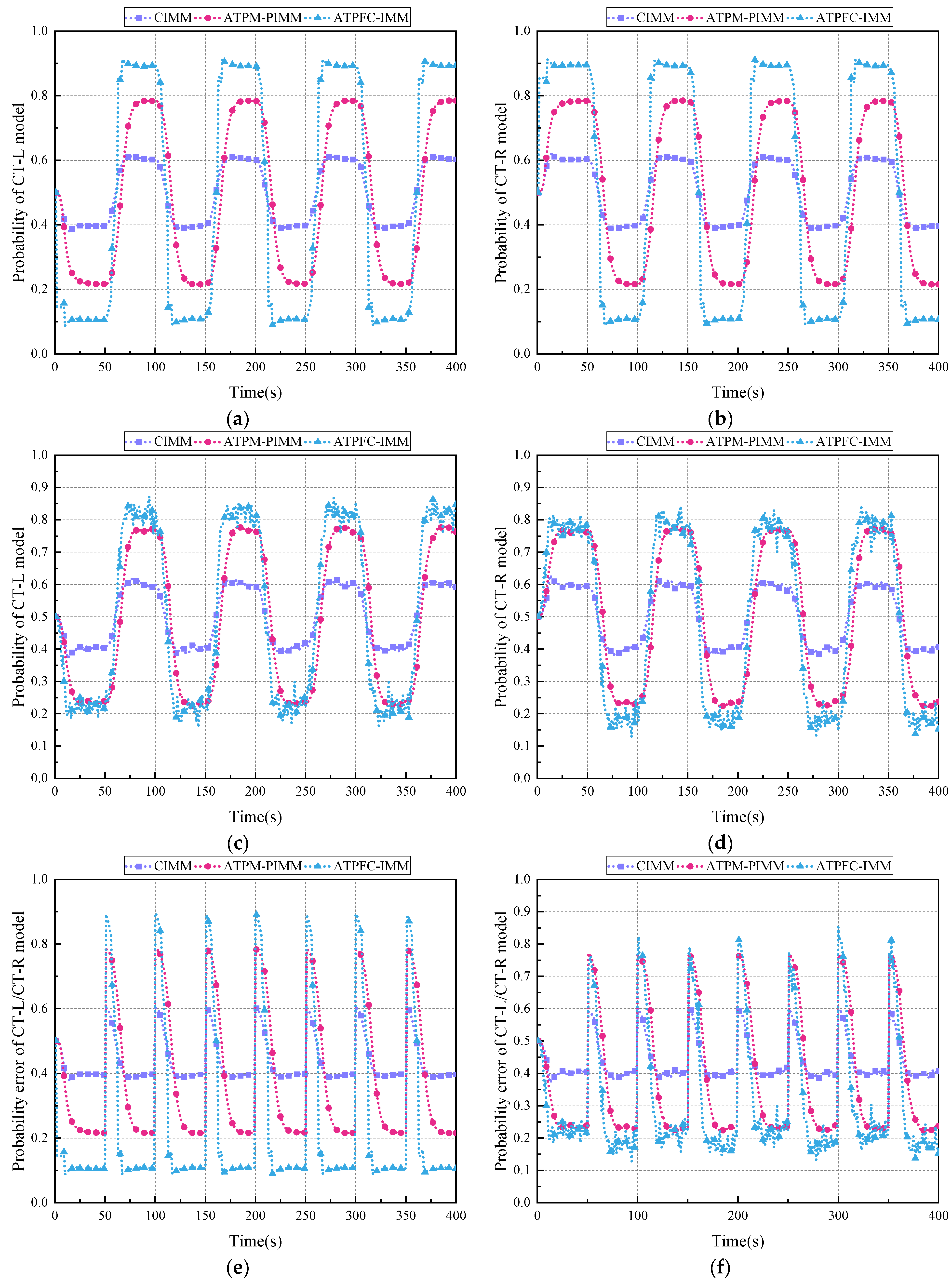
4. Simulation and Analysis
4.1. Experiment 1
4.2. Experiment 2
4.3. Experiment 3
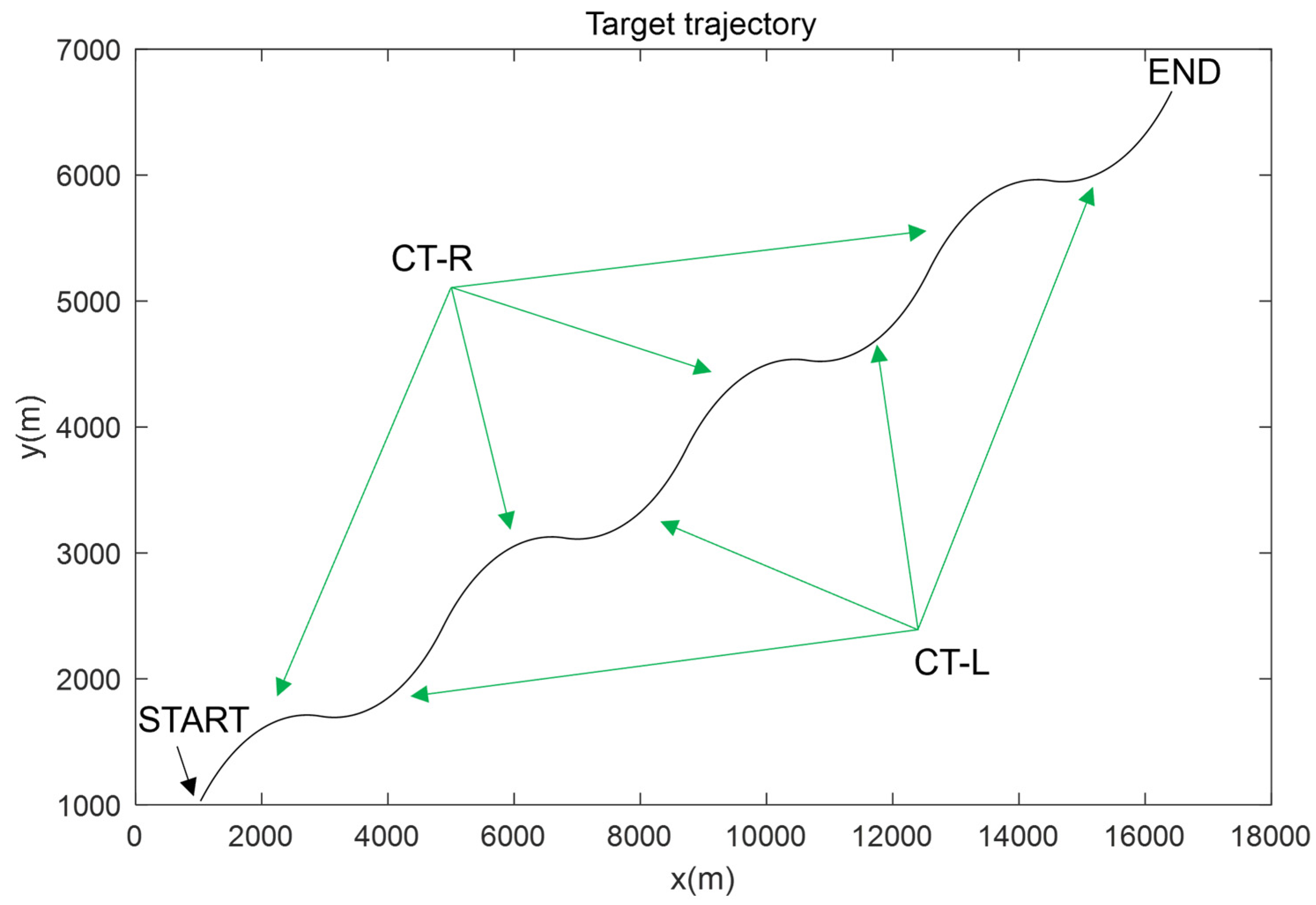
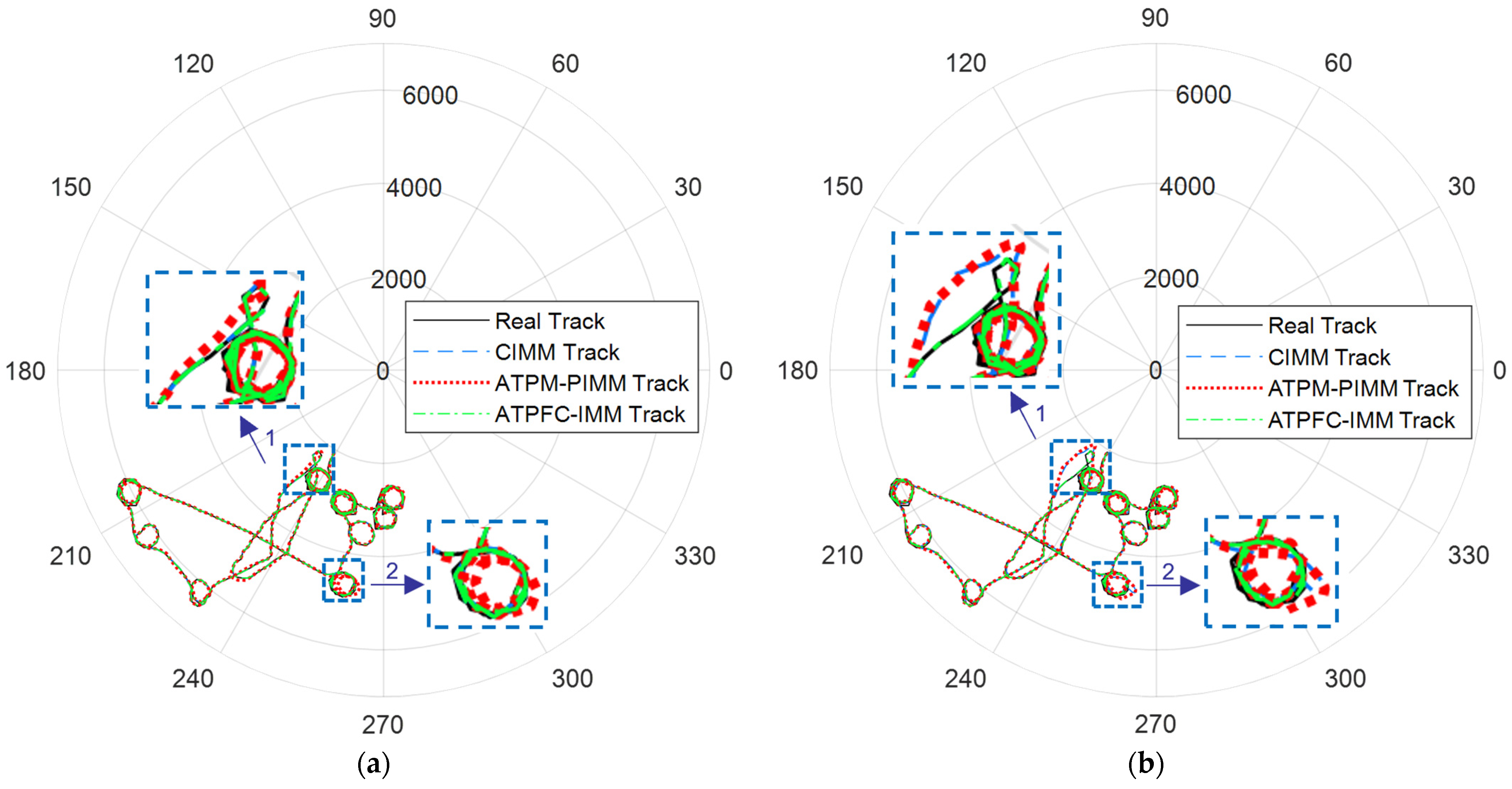
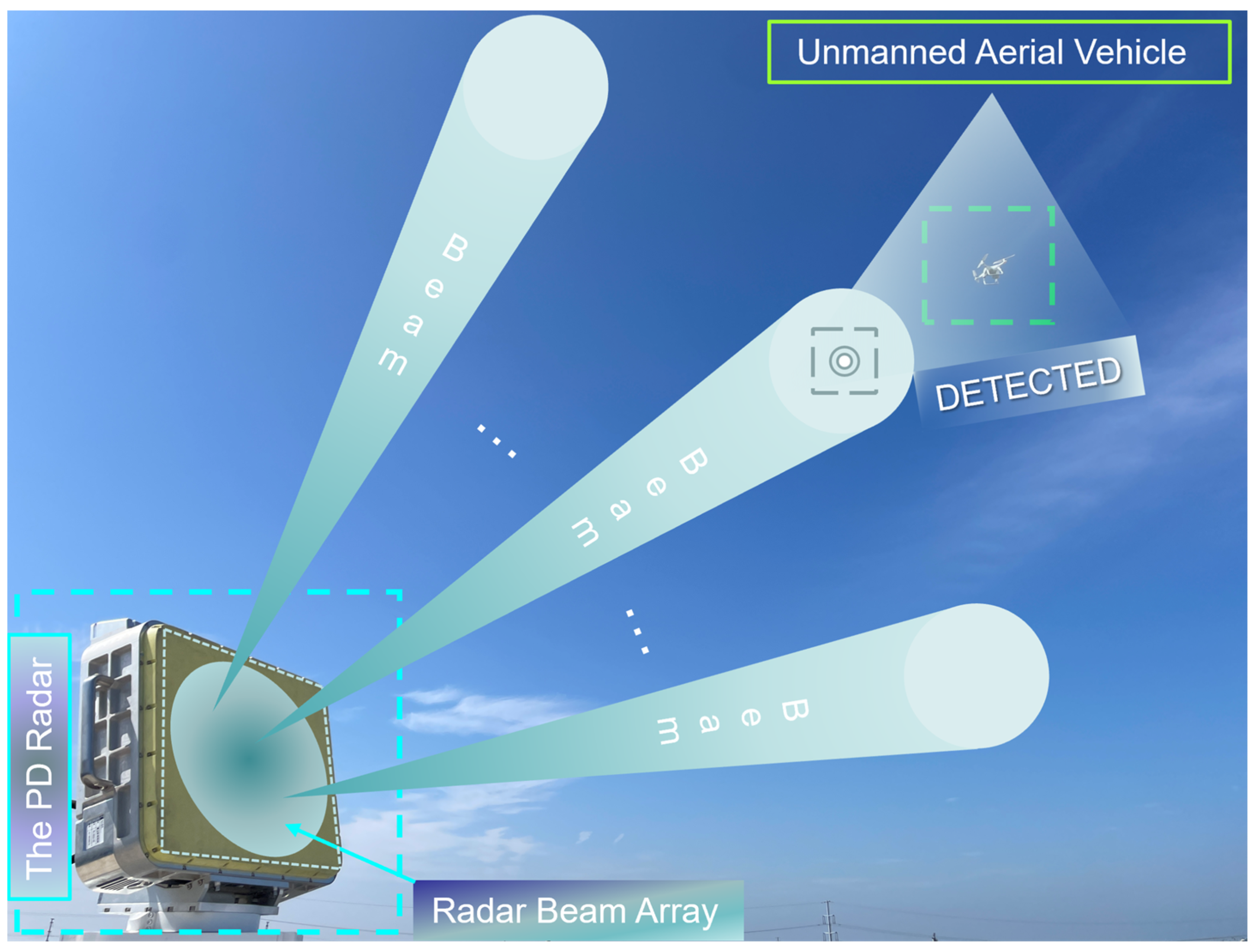
5. Application and Analysis
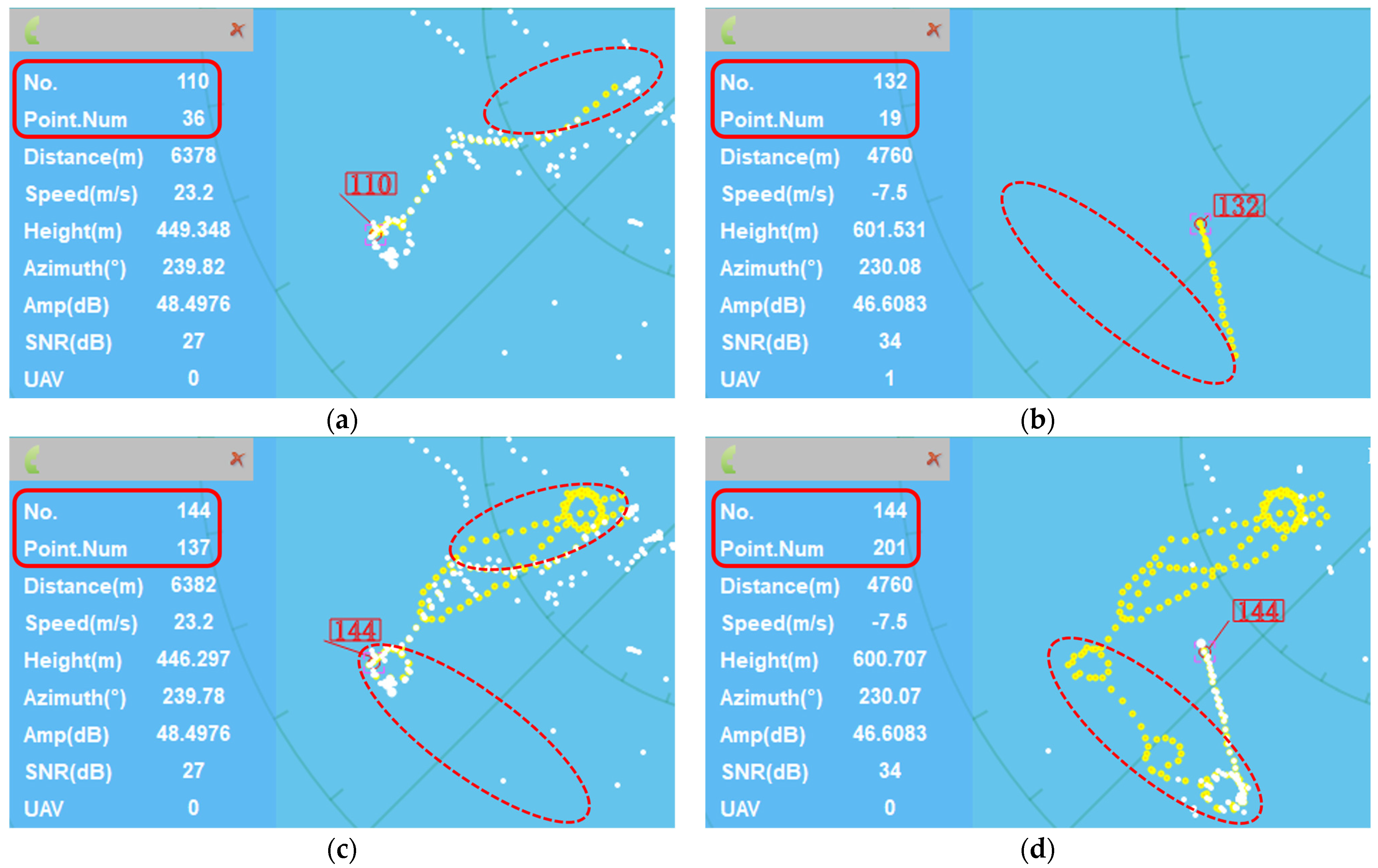
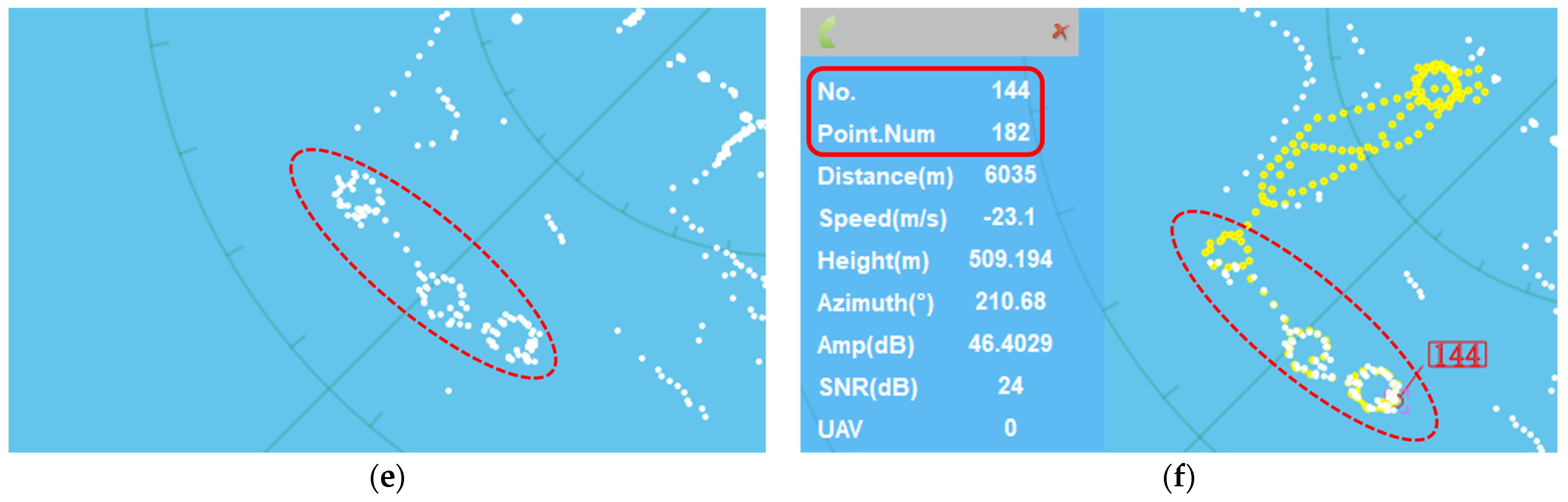
5.1. Case 1 (Circular Maneuvering)
5.2. Case 2 (Continuous-Turning Maneuvers)
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pu-Wen, F.; Chang-Qiang, H.; Lin-Ping, C.; Xiao-Ju, Y. Research on adaptive Markov matrix IMM tracking algorithm. Syst. Eng. Electron. 2013, 35, 2269–2274. [Google Scholar]
- Hong, T.; Liang, H.; Yang, Q.; Fang, L.; Kadoch, M.; Cheriet, M. A Real-Time Tracking Algorithm for Multi-Target UAV Based on Deep Learning. Remote Sens. 2023, 15, 2. [Google Scholar] [CrossRef]
- Xie, G.; Sun, L.; Wen, T.; Hei, X.; Qian, F. Adaptive Transition Probability Matrix-Based Parallel IMM Algorithm. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2980–2989. [Google Scholar] [CrossRef]
- Bao, T.; Zhang, Z.; Sabahi, M.F. An Improved Radar and Infrared Sensor Tracking Fusion Algorithm Based on IMM-UKF. In Proceedings of the 16th IEEE International Conference on Networking, Sensing and Control (ICNSC), Banff, AL, Canada, 9–11 May 2019; pp. 420–423. [Google Scholar]
- Peng, H.; Cheng, T.; Li, X. De-correlated unbiased sequential filtering based on best unbiased linear estimation for target tracking in Doppler radar. J. Syst. Eng. Electron. 2020, 31, 1167–1177. [Google Scholar] [CrossRef]
- Han, B.; Huang, H.; Lei, L.; Huang, C.; Zhang, Z. An Improved IMM Algorithm Based on STSRCKF for Maneuvering Target Tracking. IEEE Access 2019, 7, 57795–57804. [Google Scholar] [CrossRef]
- Lu, C.; Feng, W.; Li, W.; Zhang, Y.; Guo, Y. An adaptive IMM filter for jump Markov systems with inaccurate noise covariances in the presence of missing measurements. Digit. Signal Process. 2022, 127, 103529. [Google Scholar] [CrossRef]
- Gao, L.; Xing, J.; Ma, Z.; Sha, J.; Meng, X. Improved IMM Algorithm for Nonlinear Maneuvering Target Tracking. In Proceedings of the International Workshop on Information and Electronics Engineering (IWIEE)/International Conference on Information, Computing and Telecommunications (ICICT), Harbin, China, 10–11 March 2012; pp. 4117–4123. [Google Scholar]
- Lan, J.; Li, X.R.; Jilkov, V.P.; Mu, C. Second-Order Markov Chain Based Multiple-Model Algorithm for Maneuvering Target Tracking. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 3–19. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X.; Zeng, L.; Dai, S.; Zhang, M.; Lian, F. Filtering in Triplet Markov Chain Model in the Presence of Non-Gaussian Noise with Application to Target Tracking. Remote Sens. 2023, 15, 5543. [Google Scholar] [CrossRef]
- Yuan, Z.; Wenbin, L.U.; Bo, Y.; Shifei, T.A.O.; Haosu, Z.; Yu, C. Improved IMM algorithm based on support vector regression for UAV tracking. J. Syst. Eng. Electron. 2022, 33, 867–876. [Google Scholar] [CrossRef]
- Rui, Z.; Guo-Ping, H.U. Target Tracking Algorithm Based on IMM/MSPDAF Data Fusion of Multi-Sensor. Mod. Def. Technol. 2010, 38, 123–127. [Google Scholar]
- Xu, D.; Cheng, S.; Bao, S. Interacting Multiple Model Algorithm Based on Adaptive Transition Probability. Acta Electron. Sin. 2017, 45, 2113–2120. [Google Scholar]
- Hwang, I.; Seah, C.E.; Lee, S.J. A Study on Stability of the Interacting Multiple Model Algorithm. IEEE Trans. Autom. Control 2017, 62, 901–906. [Google Scholar] [CrossRef]
- Li, W.L.; Jia, Y.M. An Information Theoretic Approach to Interacting Multiple Model Estimation. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1811–1825. [Google Scholar] [CrossRef]
- Huai, L.; Li, B.; Yun, P.; Song, C.; Wang, J. Weighted Maximum Correntropy Criterion-Based Interacting Multiple-Model Filter for Maneuvering Target Tracking. Remote Sens. 2023, 15, 4513. [Google Scholar] [CrossRef]
- Dong, X.D.; Zhang, X.F.; Zhao, J.; Sun, M.; Wu, Q.H. Multi-Maneuvering Sources DOA Tracking with Improved Interactive Multi-Model Multi-Bernoulli Filter for Acoustic Vector Sensor (AVS) Array. IEEE Trans. Veh. Technol. 2021, 70, 7825–7838. [Google Scholar] [CrossRef]
- Ge, Q.B.; Hu, X.M.; Li, Y.Y.; He, H.L.; Song, Z.H. A Novel Adaptive Kalman Filter Based on Credibility Measure. IEEE CAA J. Autom. Sin. 2023, 10, 103–120. [Google Scholar] [CrossRef]
- Jondhale, S.R.; Deshpande, R.S. Kalman Filtering Framework-Based Real Time Target Tracking in Wireless Sensor Networks Using Generalized Regression Neural Networks. IEEE Sens. J. 2019, 19, 224–233. [Google Scholar] [CrossRef]
- Baidoo, E.; Hu, J.R.; Zhan, L. Kalman filtering method for sparse off-grid angle estimation for bistatic multiple-input multiple-output radar. Iet Radar Sonar Navig. 2020, 14, 313–319. [Google Scholar] [CrossRef]
- RadhikaM, N.; Parthasarathy, S.S.; Mallick, M. IMM-CKF and Posterior Cramér-Rao Lower Bound for a Highly Maneuvering Target. Solid State Technol. 2020, 63, 1591–1607. [Google Scholar]
- Yang, Z.; Gao, R.; He, W. A Review of The Research on Kalman Filtering in Power System Dynamic State Estimation. In Proceedings of the IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference, Chongqing, China, 18–20 June 2021. [Google Scholar] [CrossRef]
- Shmaliy, Y.S.; Zhao, S.; Ahn, C.K. Kalman and UFIR state estimation with coloured measurement noise using backward Euler method. Iet Signal Process. 2020, 14, 64–71. [Google Scholar] [CrossRef]
- Chen, B.-S.; Yang, C.-Y.; Liao, F.-K.; Liao, J.-F. Mobile Location Estimator in a Rough Wireless Environment Using Extended Kalman-Based IMM and Data Fusion. IEEE Trans. Veh. Technol. 2009, 58, 1157–1169. [Google Scholar] [CrossRef]
- Quanan, G.; Yunjian, X. Kalman Filter Algorithm for Sports Video Moving Target Tracking. In Proceedings of the 2020 International Conference on Advance in Ambient Computing and Intelligence (ICAACI), Ottawa, ON, Canada, 12–13 September 2020; pp. 26–30. [Google Scholar]
- Kim, B.; Yi, K.; Yoo, H.-J.; Chong, H.-J.; Ko, B. An IMM/EKF Approach for Enhanced Multitarget State Estimation for Application to Integrated Risk Management System. IEEE Trans. Veh. Technol. 2015, 64, 876–889. [Google Scholar] [CrossRef]
- Du, X.; Ao, Q.; Qi, L. Application of Improved Interactive Multimodel Algorithm in Player Trajectory Feature Matching. Complexity 2021, 4, 2993675. [Google Scholar] [CrossRef]
- Jiang, Z.; Huynh, D.Q. Multiple Pedestrian Tracking from Monocular Videos in an Interacting Multiple Model Framework. IEEE Trans. Image Process. 2018, 27, 1361–1375. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.; Zhou, G.-q.; He, J.-b. A Novel Adaptive Markov Matrix IMM Algorithm using Multi-Sensor Fusion. Int. J. Simul. Syst. Sci. Technol. 2016, 17, 53.1–53.5. [Google Scholar]
- Xiao, J.; Wang, H.; Xu, W.; Xu, D.; Cao, J. Application of an Adaptive IMM Algorithm with Optimized Tracking Performance in PD Radar. In Proceedings of the 16th UK-Europe-China Workshop on Millimetre Waves and Terahertz Technologies (UCMMT), Guangzhou, China, 31 August–3 September 2023. [Google Scholar] [CrossRef]
- Guo, Q.; Teng, L. Maneuvering Target Tracking with Multi-Model Based on the Adaptive Structure. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 865–871. [Google Scholar] [CrossRef]
- Sabilla, I.A.; Meirisdiana, M.; Sunaryono, D.; Husni, M. Best Ratio Size of Image in Steganography using Portable Document Format with Evaluation RMSE, PSNR, and SSIM. In Proceedings of the 4th IEEE International Conference on Computer and Informatics Engineering (IC2IE), Depok, Indonesia, 14–15 September 2021; pp. 289–294. [Google Scholar]
- Zhou, Z.; Liu, J.-M.; Li, Z.-X. Adaptive multiple-model tracking algorithm based on STC-IMM structure. Control Decis. 2013, 28, 1226–1230. [Google Scholar]

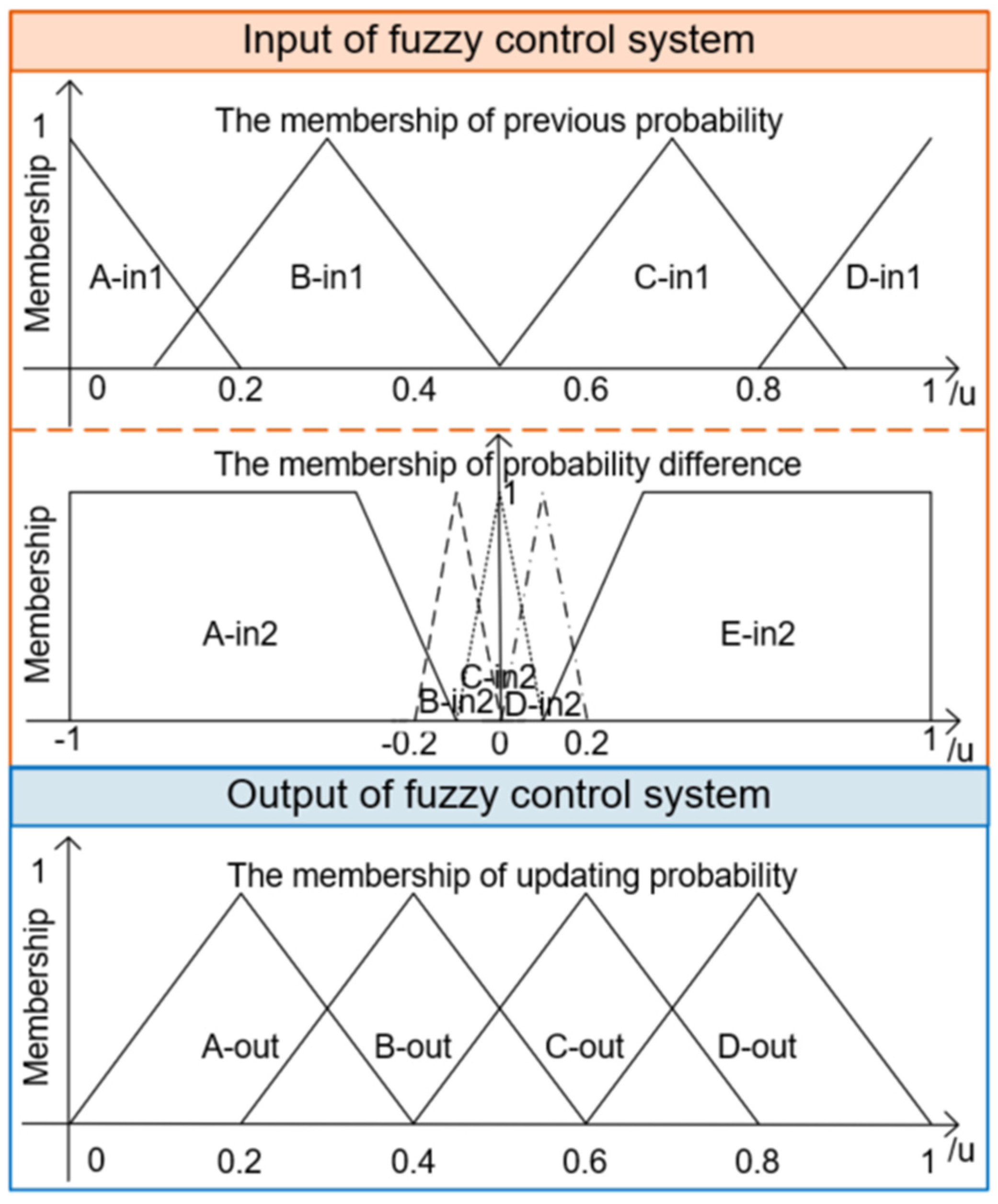





| Output | Input-2 | |||||
|---|---|---|---|---|---|---|
| A-in2 | B-in2 | C-in2 | D-in2 | E-in2 | ||
| Input -1 | A-in1 | A-out | A-out | A-out | B-out | C-out |
| B-in1 | A-out | A-out | B-out | C-out | D-out | |
| C-in1 | A-out | B-out | C-out | D-out | D-out | |
| D-in1 | B-out | C-out | D-out | D-out | D-out | |
| Algorithm | Measurement Noise | RMSE of x-Axis/(m) | RMSE of y-Axis/(m) | RMSE of Position/(m) |
|---|---|---|---|---|
| CIMM | Unadded | 7.6171 | 11.9254 | 15.3929 |
| ATPM-PIMM [3] | 6.6795 | 10.6392 | 13.7303 | |
| ATPFC-IMM | 6.4601 | 10.4568 | 13.3856 | |
| CIMM | Added | 16.5781 | 19.5356 | 26.2282 |
| ATPM-PIMM [3] | 15.9144 | 18.6876 | 25.2220 | |
| ATPFC-IMM | 15.7616 | 18.5622 | 24.8715 |
| Algorithm | Measurement Noise | RMSE of x-Axis/(m) | RMSE of y-Axis/(m) | RMSE of Position/(m) |
|---|---|---|---|---|
| CIMM | Unadded | 5.3504 | 5.6552 | 8.6531 |
| ATPM-PIMM [3] | 4.7714 | 5.4412 | 8.0322 | |
| ATPFC-IMM | 3.0197 | 3.1945 | 4.9433 | |
| CIMM | Added | 13.7502 | 14.2969 | 20.1896 |
| ATPM-PIMM [3] | 13.4140 | 14.0470 | 19.8215 | |
| ATPFC-IMM | 9.0937 | 9.5531 | 13.3783 |
| Algorithm | Measurement Noise | RMSE of x-Axis/(m) | RMSE of y-Axis/(m) | RMSE of Position/(m) |
|---|---|---|---|---|
| CIMM | Unadded | 6.3057 | 12.7035 | 14.9693 |
| ATPM-PIMM [3] | 6.1202 | 12.8428 | 14.8355 | |
| ATPFC-IMM | 4.6364 | 9.5192 | 11.0814 | |
| CIMM | Added | 15.7992 | 23.9586 | 28.8754 |
| ATPM-PIMM [3] | 15.8645 | 23.8320 | 28.8369 | |
| ATPFC-IMM | 13.9693 | 21.0919 | 25.4698 |
| Algorithm | Measurement Noise | RMSE of x-Axis/(m) | RMSE of y-Axis/(m) | RMSE of Position/(m) |
|---|---|---|---|---|
| CIMM | Unadded | 4.7026 | 7.1481 | 9.2974 |
| ATPM-PIMM [3] | 4.4345 | 6.5464 | 8.5476 | |
| ATPFC-IMM | 3.6148 | 4.7559 | 6.5612 | |
| CIMM | Added | 12.8534 | 19.4745 | 23.6441 |
| ATPM-PIMM [3] | 11.9888 | 18.4349 | 22.3480 | |
| ATPFC-IMM | 11.6783 | 17.7896 | 21.5809 |
| Algorithm | Measurement Noise | RMSE of x-Axis/(m) | RMSE of y-Axis/(m) | RMSE of Position/(m) |
|---|---|---|---|---|
| CIMM | Unadded | 33.5938 | 37.0065 | 55.7760 |
| ATPM-PIMM [3] | 28.8964 | 33.7882 | 49.5958 | |
| ATPFC-IMM | 20.9961 | 22.8124 | 33.8124 | |
| CIMM | Added | 58.1596 | 56.8049 | 82.7898 |
| ATPM-PIMM [3] | 54.6615 | 54.1209 | 78.0547 | |
| ATPFC-IMM | 46.5514 | 46.9047 | 66.5357 |
| Indicators | Specifications | Indicators | Specifications |
|---|---|---|---|
| Range | >7 km | Height | >400 m |
| Ranging Accuracy | <15 m | Azimuth Accuracy | <0.6° |
| Pitch Accuracy | <0.6° | Distance Resolution | <30 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Xiao, J.; Xu, D.; Wang, H.; Cao, J. An Adaptive IMM Algorithm for a PD Radar with Improved Maneuvering Target Tracking Performance. Remote Sens. 2024, 16, 1051. https://doi.org/10.3390/rs16061051
Xu W, Xiao J, Xu D, Wang H, Cao J. An Adaptive IMM Algorithm for a PD Radar with Improved Maneuvering Target Tracking Performance. Remote Sensing. 2024; 16(6):1051. https://doi.org/10.3390/rs16061051
Chicago/Turabian StyleXu, Wenwen, Jiankang Xiao, Dalong Xu, Hao Wang, and Jianyin Cao. 2024. "An Adaptive IMM Algorithm for a PD Radar with Improved Maneuvering Target Tracking Performance" Remote Sensing 16, no. 6: 1051. https://doi.org/10.3390/rs16061051
APA StyleXu, W., Xiao, J., Xu, D., Wang, H., & Cao, J. (2024). An Adaptive IMM Algorithm for a PD Radar with Improved Maneuvering Target Tracking Performance. Remote Sensing, 16(6), 1051. https://doi.org/10.3390/rs16061051