Accounting for Geometric Anisotropy in Sparse Magnetic Data Using a Modified Interpolation Algorithm
Abstract
1. Introduction
2. Influence Analysis of Geometric Anisotropy of Variogram
2.1. Principles of Kriging Interpolation Algorithm
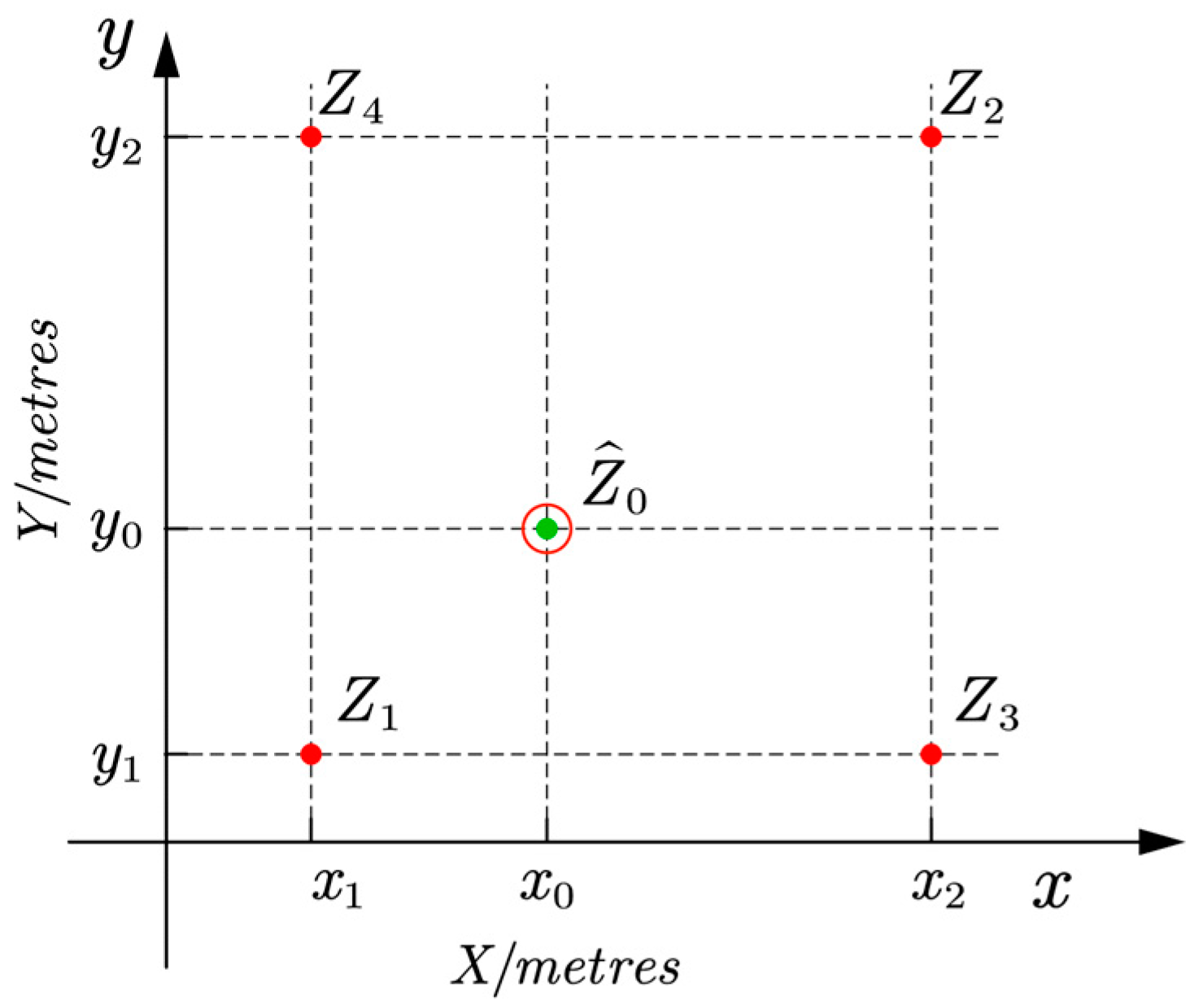
2.1.1. Regionalized Variable
2.1.2. Principle of Interpolation
2.1.3. Variogram
2.1.4. Experimental Variogram
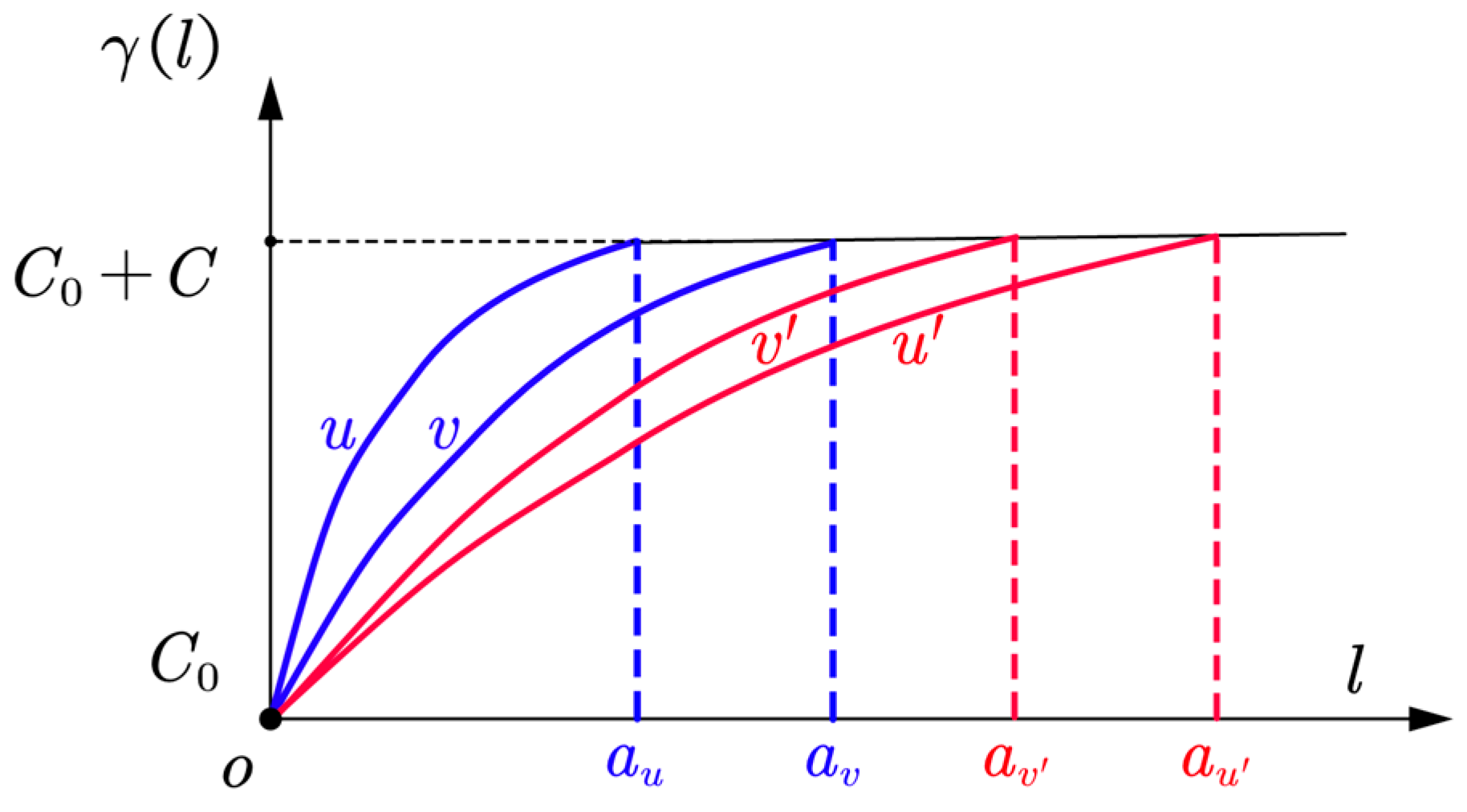
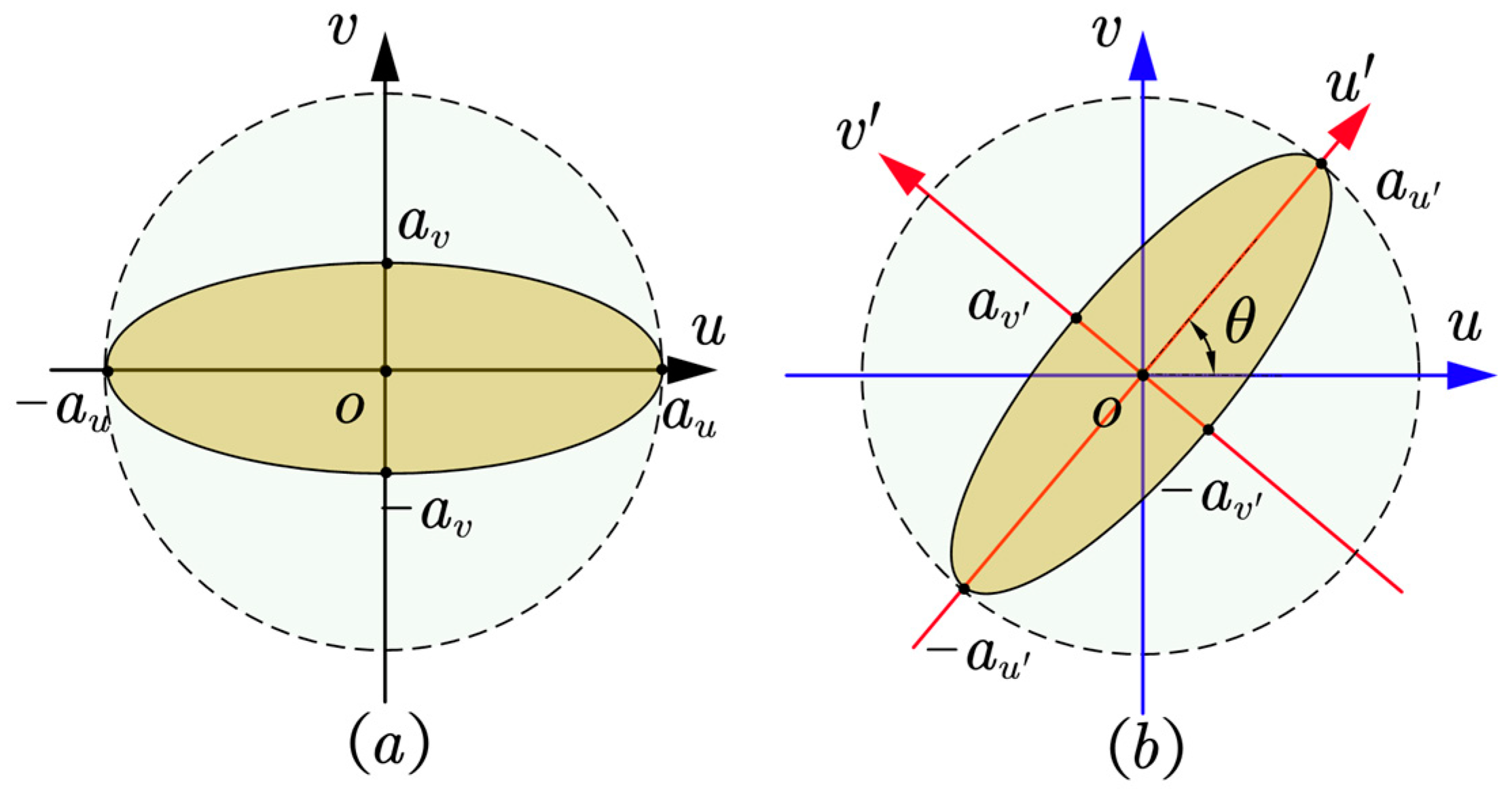
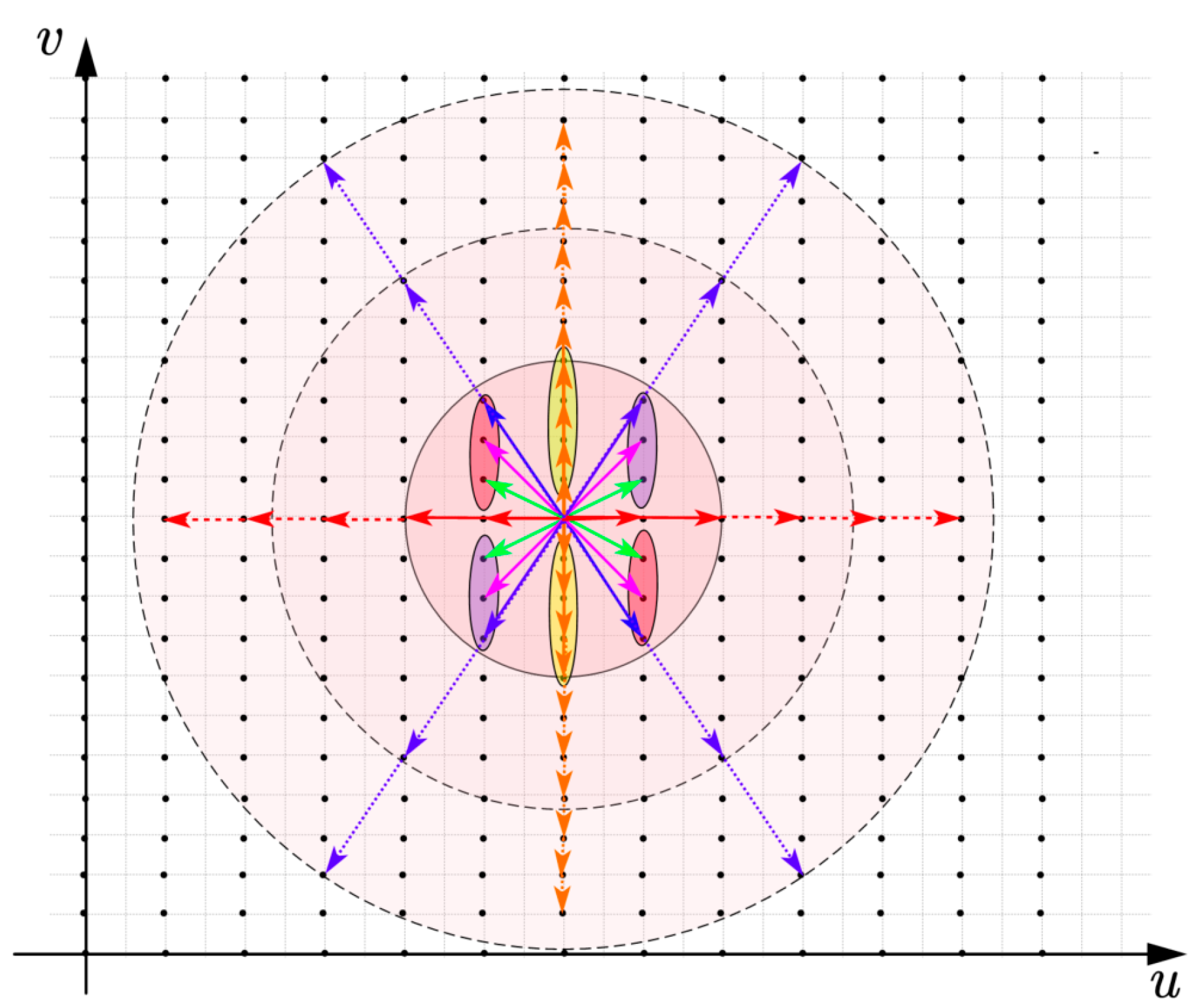
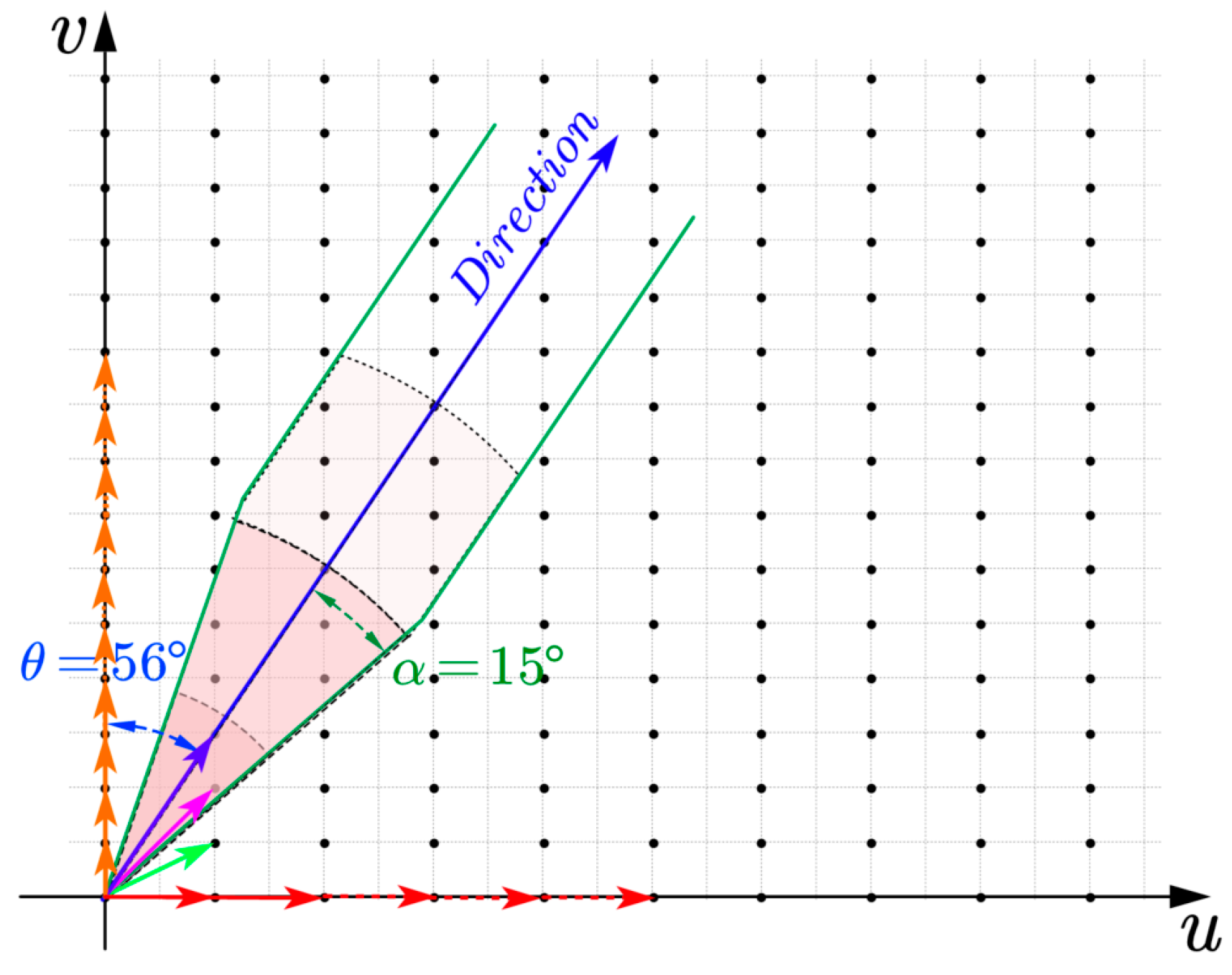
2.2. Analysis of Geometric Anisotropy of Experimental Variogram
- (1)
- If the geomagnetic trend is distributed along the direction (orange arrows), the number of sampling data is sufficient and the interval is small, thus the resolution is high and the magnetic trend in this direction can be better represented;
- (2)
- If the geomagnetic trend is distributed along the direction (red arrows), the number of sampling data and interval are significantly lower than that along the direction , which can properly reflect the geomagnetic trend in this direction. If the sampling interval in this direction is increased, and the data become more and more sparse, its resolution will be reduced and the interpolation accuracy will be reduced, too;
- (3)
- If the geomagnetic trend is distributed along the blue line, the number of sampling points in this direction is extremely reduced (the number of blue arrows), and the sampling interval is significantly larger than the above two methods, which makes the details of geomagnetic changes in this direction easy to be ignored, thus reducing the accuracy of interpolation. At this time, in order to increase the number of samples, the area in the azimuth direction is often expanded by setting the tolerance in the azimuth direction and the lag distance tolerance, as shown in Figure 6 for the blue direction expansion in Figure 5, where the azimuth angle and the azimuth tolerance .
3. Construction Method of Geomagnetic Map Based on Geometric Anisotropy Correction of Variogram
3.1. Geometric Anisotropy Correction Formula
- The characteristic direction of the geomagnetic map is consistent with the surveying direction
- 2.
- The characteristic direction of the geomagnetic map is inconsistent with the surveying direction
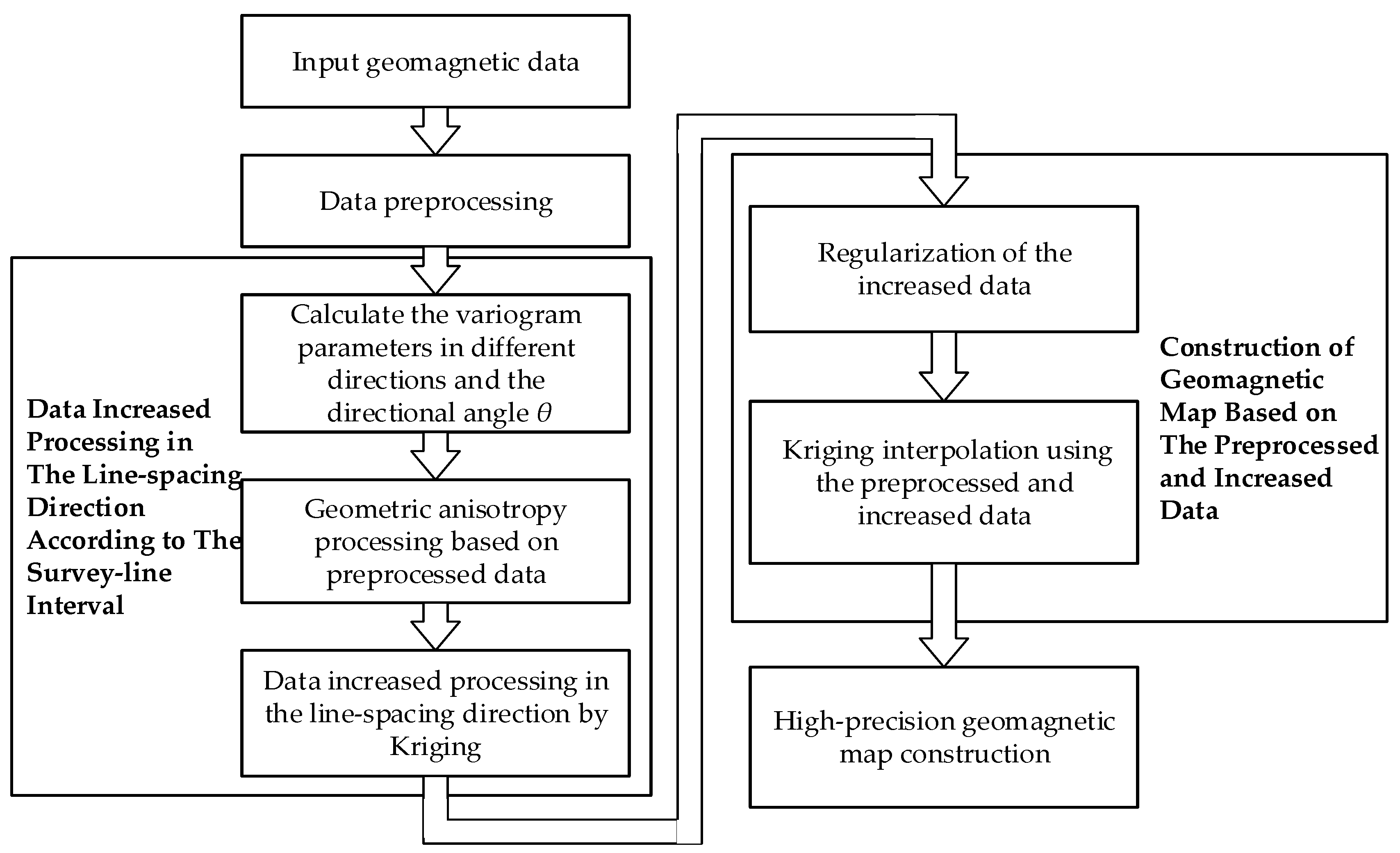
3.2. Geomagnetic Interpolation Algorithm Based on Geometric Anisotropy Correction of Variogram
- (1)
- Data Increase Processing
- (2)
- Construction of Geomagnetic Map
4. Simulation
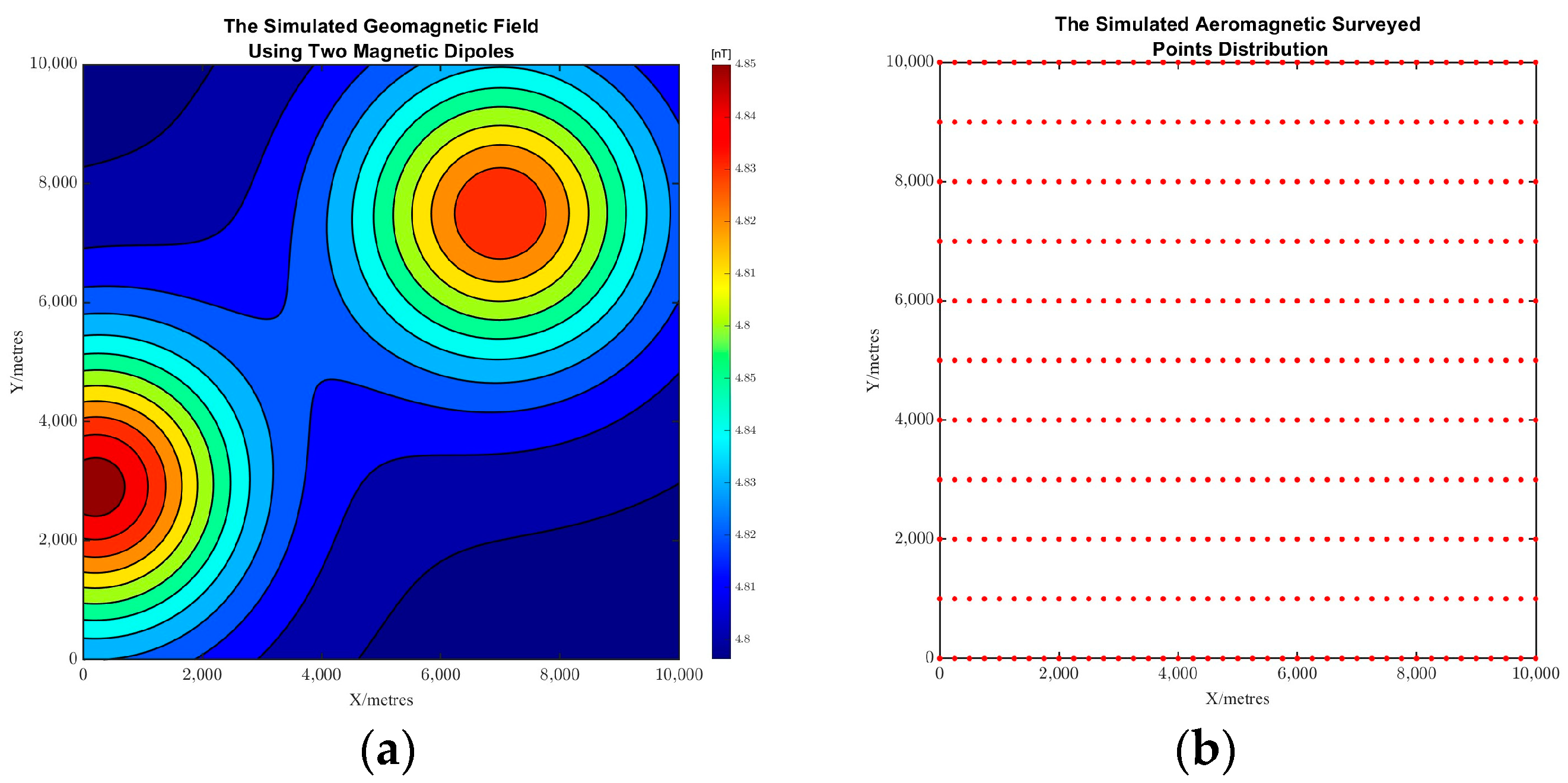
4.1. Simulation of Geomagnetic Field Using Two Magnetic Dipoles
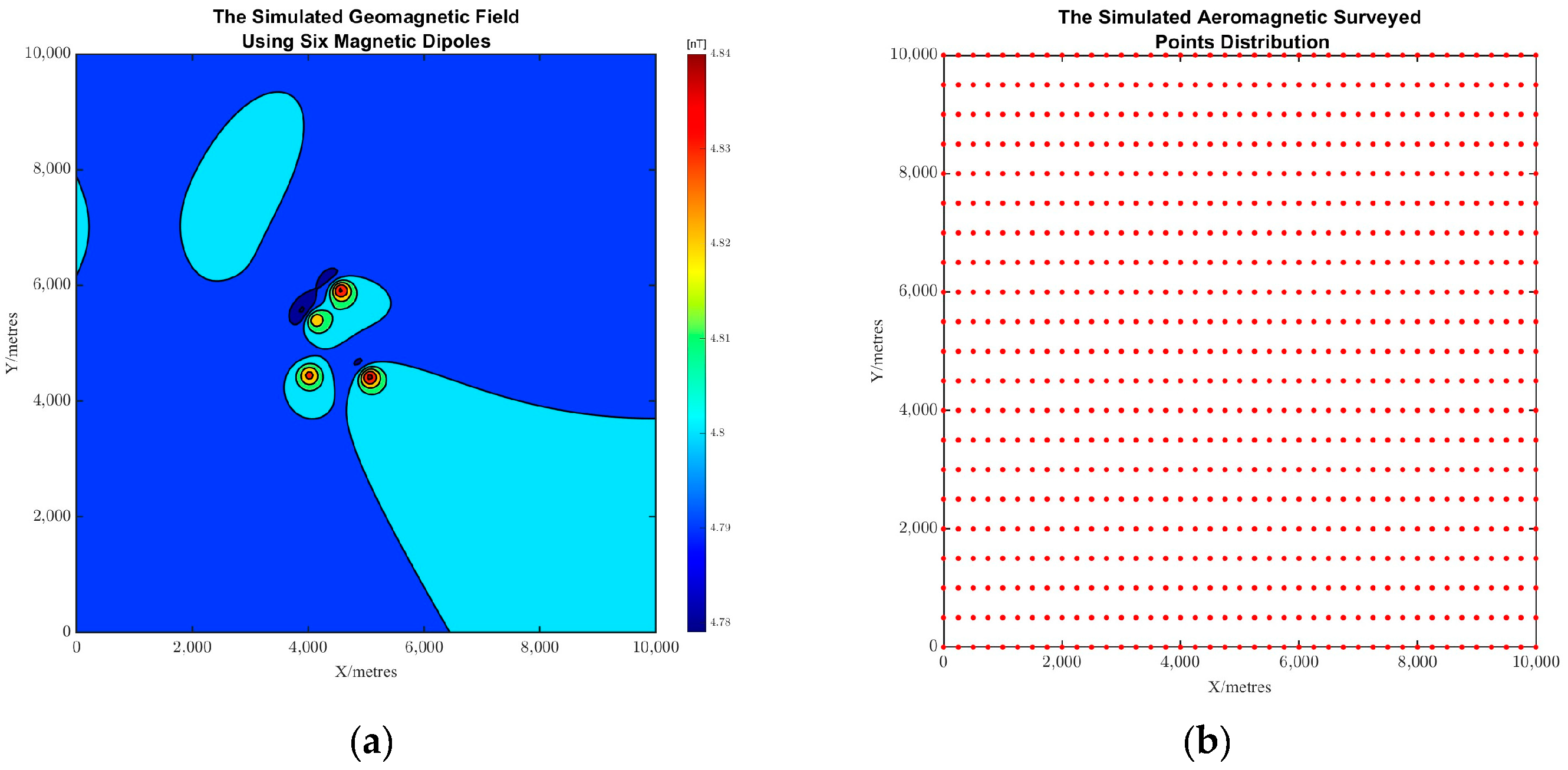
4.2. Simulation of Geomagnetic Field Using Multiple Magnetic Dipoles
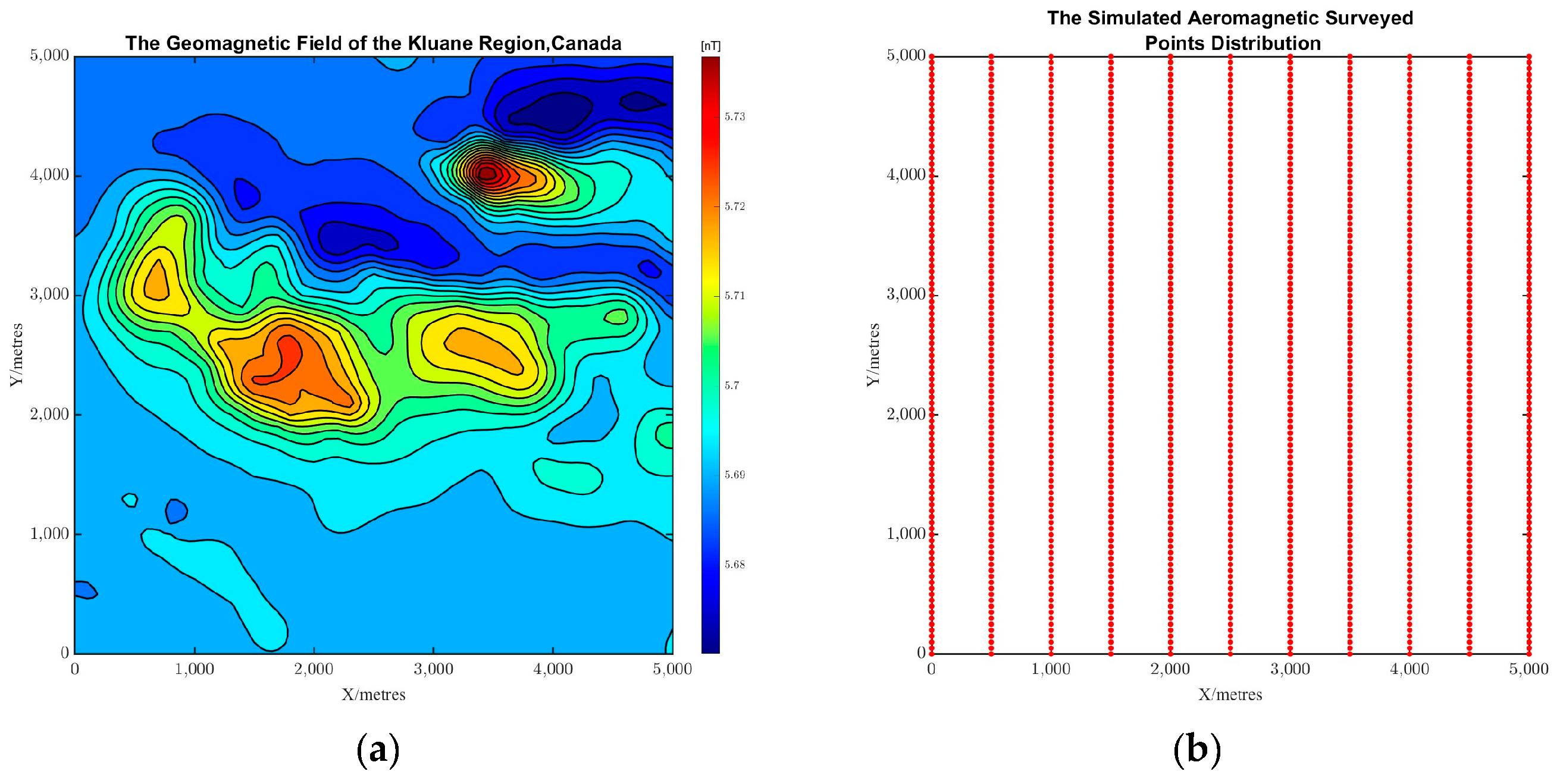
5. Experiments
6. Conclusions
- The influence of geometric anisotropy caused by the sparsity of geomagnetic data on the variability of geomagnetic map construction is analyzed;
- The geometric anisotropy correction formula of the variogram of sparse data is derived;
- A geomagnetic interpolation algorithm based on geometric anisotropy correction of variogram is proposed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, W. Aeromagnetic Survey. In Encyclopedia of Engineering Geology; Encyclopedia of Earth Sciences Series; Bobrowsky, P.T., Marker, B., Eds.; Springer: Cham, Switzerland, 2018; pp. 13–18. ISBN 978-3-319-73568-9. [Google Scholar]
- Colin, R. Aeromagnetic Surveys: Principles, Practice and Interpretation|Sebas Sanguil—Academia.Edu. Available online: https://www.academia.edu/16883197/Aeromagnetic_Surveys_Principles_Practice_and_Interpretation (accessed on 10 January 2024).
- Reid, A.B. Aeromagnetic Survey Design. Geophysics 1980, 45, 973–976. [Google Scholar] [CrossRef]
- DB63/T 1933-2021; Technical Specification for Aerial Magnetic Survey of UAV. Administration for Market Regulation of Qinghai Province: Xining, China, 2021. (In Chinese)
- DZ-T-0142-1994; Technical Specification for Airborne Magnetic Survey. Ministry of Land and Resources: Beijing, China, 1994. (In Chinese)
- Xie, X.; Zhao, D.; Liu, C.; Fu, L. Comparative study on different preparation methods of geomagnetic reference map. Eng. Surv. Mapp. 2023, 32, 13–20. (In Chinese) [Google Scholar] [CrossRef]
- Huang, H.; Liu, Q.; Wang, J.; Chen, J.; Yu, X. Kriging-Based Study on the Visualization of Magnetic Method Data. In Proceedings of the 2012 International Conference on Image Analysis and Signal Processing, Hangzhou, China, 9–11 November 2013. [Google Scholar]
- Yang, G.; Zhang, G.; Li, S. Application of universal Kriging interpolation in geomagnetic map. J. Chin. Inert. Technol. 2008, 16, 162–166. (In Chinese) [Google Scholar]
- Cai, C.; Cao, Z.; Zhang, X.; Li, S. A Study for Optimizing the Indoor Geomagnetic Reference Map. J. Geod. Geodyn. 2017, 37, 647–650. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, N.; Lin, C.; Lin, P.; Xu, L.; Liu, Y. Construction Method of Geomagnetic Reference Map for Satellite Communication Navigation through Kriging Method. J. Phys. Conf. Ser. 2021, 2033, 012034. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics; Springer: Berlin/Heidelberg, Germany, 1995; ISBN 978-3-662-03100-1. [Google Scholar]
- Sun, H. Principle of Geostatistics and Application; China University of Mining and Technology Press: Xuzhou, China, 1990. (In Chinese) [Google Scholar]
- Mcbratney, A.B.; Webster, R. Choosing Functions for Semi-Variograms of Soil Properties and Fitting Them to Sampling Estimates. J. Soil Sci. 1986, 37, 617–639. [Google Scholar] [CrossRef]
- Ai, S.; Ding, X.; Tolle, F.; Wang, Z.; Zhao, X. Latest Geodetic Changes of Austre Lovénbreen and Pedersenbreen, Svalbard. Remote Sens. 2019, 11, 2890. [Google Scholar] [CrossRef]
- Cressie, N.A.C. Statistics for Spatial Data; Wiley series in probability and mathematical statistics; Wiley: New York, NY, USA, 1993; ISBN 978-0-471-00255-0. [Google Scholar]
- Oliver, M.A.; Webster, R. Kriging: A Method of Interpolation for Geographical Information Systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Chen, L.; Cao, J.; Wu, M. Research on Spatial Domain Numerical Methods for Potential Field Continuation in Geomagnetic Navigation; National Defense Industry Press: Arlington, VA, USA, 2015; p. 133. (In Chinese) [Google Scholar]
- Yu, Z.; Pan, M.; Liu, Z. Research on magnetic anomaly detection method assisted by geomagnetic map. J. Phys. Conf. Ser. 2023, 12, 62. [Google Scholar] [CrossRef]
- Open Government Portal|Open Government[EB/OL]. Available online: https://search.open.canada.ca/en/od/ (accessed on 20 March 2023).




| No. | Position | Radius of the Sphere/Meters | ||
|---|---|---|---|---|
| X/Meters | Y/Meters | Z/Meters | ||
| 1 | 200 | 2900 | −4000 | 400 |
| 2 | 7000 | 7500 | −4400 | 400 |
| Variogram Model | ME (nT) | MAE (nT) | RMSE (nT) |
|---|---|---|---|
| Spherical Variogram | 40.6872 | 2.9604 | 4.7042 |
| Improved Variogram | 4.54835 | 0.6291 | 0.7985 |
| No. | Position | Radius of the Sphere/Meters | ||
|---|---|---|---|---|
| X/Meters | Y/Meters | Z/Meters | ||
| 1 | 1000 | 7000 | −1000 | 80 |
| 2 | 5000 | 4500 | −200 | 63 |
| 3 | 4500 | 6000 | −200 | 63 |
| 4 | 4000 | 4500 | −250 | 63 |
| 5 | 4000 | 5500 | −200 | 63 |
| 6 | 5000 | 5000 | −200 | 14 |
| Variogram Model | ME (nT) | MAE (nT) | RMSE (nT) |
|---|---|---|---|
| Spherical Variogram | 229.81627 | 1.6513 | 11.4462 |
| Improved Variogram | 195.9085 | 0.7501 | 7.0059 |
| Variogram Model | ME (nT) | MAE (nT) | RMSE (nT) |
|---|---|---|---|
| Spherical Variogram | 131.7929 | 10.0630 | 17.4667 |
| Improved Variogram | 92.8156 | 7.7730 | 14.4882 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, Q.; Pan, M.; Chen, D.; Liu, Z.; Yan, L.; Xu, Y.; Ding, Z.; Yu, Z.; Liu, X.; et al. Accounting for Geometric Anisotropy in Sparse Magnetic Data Using a Modified Interpolation Algorithm. Remote Sens. 2024, 16, 883. https://doi.org/10.3390/rs16050883
Li H, Zhang Q, Pan M, Chen D, Liu Z, Yan L, Xu Y, Ding Z, Yu Z, Liu X, et al. Accounting for Geometric Anisotropy in Sparse Magnetic Data Using a Modified Interpolation Algorithm. Remote Sensing. 2024; 16(5):883. https://doi.org/10.3390/rs16050883
Chicago/Turabian StyleLi, Haibin, Qi Zhang, Mengchun Pan, Dixiang Chen, Zhongyan Liu, Liang Yan, Yujing Xu, Zengquan Ding, Ziqiang Yu, Xu Liu, and et al. 2024. "Accounting for Geometric Anisotropy in Sparse Magnetic Data Using a Modified Interpolation Algorithm" Remote Sensing 16, no. 5: 883. https://doi.org/10.3390/rs16050883
APA StyleLi, H., Zhang, Q., Pan, M., Chen, D., Liu, Z., Yan, L., Xu, Y., Ding, Z., Yu, Z., Liu, X., Wan, K., & Dai, W. (2024). Accounting for Geometric Anisotropy in Sparse Magnetic Data Using a Modified Interpolation Algorithm. Remote Sensing, 16(5), 883. https://doi.org/10.3390/rs16050883







