Abstract
In the realm of neural network-based noise reduction, conventional models predominantly address Gaussian and blur artifacts across entire images. However, they encounter notable challenges when directly applied to periodic noise characteristics of high-resolution infrared sequential imagery. The high resolution also complicates the construction of suitable datasets. Our study introduces an innovative strategy that transforms two-dimensional images into one-dimensional signals, eliminating the need for processing the full image. We have developed a simulated dataset that closely mirrors natural infrared line scanning images derived from the FLIR dataset. To address low-frequency periodic noise, we propose two neural-network-based denoising approaches. The first employs a neural network to deduce noise from the one-dimensional signal, while the second utilizes discrete Fourier transforms for noise prediction within the frequency domain. Our experimental results highlight the Restormer model’s exemplary performance in direct noise prediction, where denoised images attain a PSNR of around 41 and an SSIM close to 0.9 on simulated data, leaving minimal residual noise in the actual denoised images. Further, we investigate the influence of Fourier coefficients, as predicted by neural networks, on the denoising process in the second approach. Employing 12 frequency coefficients, the Restormer and NAFNet models both reach a PSNR near 34 and an SSIM of approximately 0.842.
1. Introduction
The continuous development of infrared detector manufacturing technology has resulted in widespread attention towards the application of scanning-type infrared line detectors in extensive field-of-view imaging. The imaging methods of infrared line detectors can primarily be categorized into scanning and push-broom modes [1,2]. Due to their wide-angle scanning capability, infrared line detectors find extensive use in military reconnaissance [3,4] and remote sensing imaging [2,5]. However, limitations in the production level and processes of infrared detectors, coupled with various external environmental interferences, contribute to the presence of different types of noise in infrared line scanning images, including salt-and-pepper noise, non-uniform stripe noise, periodic noise, and various forms of high-frequency mixed noises. As a result, research focused on denoising techniques specifically for infrared line detectors has emerged as a popular area of study.
For infrared image salt-and-pepper noise, traditional image denoising algorithms can be categorized into neighborhood pixel-based methods and NLM (non-local mean) algorithms. Neighborhood pixel-based denoising methods, including arithmetic mean method, Gaussian filtering algorithm, bilateral filtering, and guided filtering, primarily estimate the denoised pixel by considering its relationship with neighboring pixels within a window. These algorithms are computationally efficient but only utilize pixel information within the window, neglecting the entire frame’s image information. NLM algorithms, such as the BM3D algorithm, operate on image blocks rather than windows, searching for similar image blocks throughout the entire frame for denoising. However, due to the need for searching within the entire frame, these algorithms significantly increase computational complexity.
Infrared line detectors are susceptible to electrical interference, leading to wide-striped noise in scanning images. This type of noise exhibits periodic variations in brightness. It should be noted that this striped noise differs from the noise caused by the non-uniformity of the infrared detectors [6]. The striped noise resulting from the non-uniformity of infrared line detectors appears as narrow horizontal noise in the scanning images due to different response levels in each infrared detection unit. Consequently, noise reduction algorithms aimed at correcting the non-uniformity in infrared detectors [7,8,9] typically leverage the characteristic of noise appearing in the form of narrow horizontal stripes in the images. In reference [7], guided filtering was first applied to the non-uniform correction of infrared focal plane array detectors. They designed a one-dimensional guided filtering window, achieving effective stripe denoising. References [8,9] combined guided filtering with wavelet transform, applying guided filtering to the vertical frequency domain after wavelet transformation, resulting in excellent denoising of stripe noise. However, a challenge arises when addressing periodic noise in infrared line detectors caused by electrical interference due to their high imaging speed. This periodic noise manifests as vertically alternating bright and dark stripes in a slow, gradual manner. Several hundred columns in the image are affected for a single noise period. Given that periodic noise cannot be represented by narrow stripes in the image, the effectiveness of applying the non-uniformity correction algorithm to mitigate the periodic noise of infrared line detectors is limited.
The traditional periodic stripe noise, caused by electromechanical interference, is characterized by small noise periods and rapid variations. It exhibits prominent peak noise in the frequency domain and is commonly addressed through frequency-based noise elimination [10,11]. Infrared column detectors offer fast scanning speeds and often exhibit periodic noise resulting from electrical interference, characterized by low-frequency vertical stripes alternating between brightness and darkness in the image. When the image is transformed into the frequency domain, the periodic noise becomes mixed in the low-frequency range, making it challenging to identify distinct peak noise in the high-frequency range. Consequently, direct application of frequency trap filters for noise suppression in the frequency domain becomes difficult.
In recent years, there has been a rapid development in the computing power of computer hardware, which has led to the widespread application of deep learning in the field of image denoising. Various network models, including residual networks [12], dense networks [13], recursive networks [14], multi-scale networks [15], encoder–decoder networks [16], attention operations [17,18], self-similarity techniques [19], non-local operations [20], and NAFNet (nonlinear activation free network) [21], have been proposed for image denoising. Particularly, in the post-2020 era, there has been a gradual shift from CNN (convolutional neural network)-based neural network models to transformer-based neural networks [22,23]. Transformers exhibit stronger feature extraction capabilities, leading to the proposal of numerous transformer-based network models for image preprocessing [24,25,26,27,28,29,30,31,32,33,34,35]. Additionally, in 2017, K. Zhang et al. [12] suggested that while using neural networks for predicting denoised images can introduce edge effects, utilizing network predictions for denoising the noise in images produces superior outcomes.
The neural network models discussed earlier primarily address Gaussian and blurry noise in images. The input of such networks is full-frame noisy images, and the output is target images free of noise. Due to the fact that both input and output are full-frame images, a certain level of image resolution is required. However, infrared line images boast an extremely high resolution, typically consisting of tens of thousands of columns. Consequently, directly applying such networks to infrared scanning images is challenging. Moreover, constructing a dataset for infrared scanning images poses difficulties due to their ultra-high resolution. In light of the features of long-period noise in the aforementioned infrared line detectors, the absence of visible noise points in the frequency domain, and the exceptionally high resolution of these images, this study scrutinizes the characteristics of periodic noise in infrared line detectors. To address this, it converts two-dimensional images into one-dimensional signals and introduces two viable denoising methods based on neural networks. One approach involves directly predicting noise using a one-dimensional signal, where the neural network takes a one-dimensional signal as input and outputs the predicted one-dimensional periodic noise. Another approach involves predicting noise in the frequency domain through DFT (discrete Fourier transform), where the neural network takes partial DFT frequency coefficients of a one-dimensional signal as input and outputs the predicted periodic noise signal’s partial DFT frequency coefficients. Experimental analysis demonstrates the efficacy of both denoising methods, with the Restormer spatial domain network model exhibiting superior denoising performance.
This paper presents the following main contributions:
- (1)
- It conducts a comprehensive analysis of the characteristics of periodic noise in infrared line detectors and proposes a method to convert the image into a one-dimensional signal for denoising. This approach addresses the challenge of using the entire frame image as the input and output of the neural network model for denoising, which is particularly difficult due to the high resolution of the infrared line scanning image.
- (2)
- Two denoising algorithms are introduced. One algorithm directly predicts the periodic noise in the image from the one-dimensional signal, while the other algorithm combines the Fourier transform with the neural network to forecast the Fourier coefficients of the noise signal. These methods overcome the issue of not being able to denoise such periodic noise directly using frequency domain trap filters. Experimental results demonstrate that both methods achieve certain denoising effects. Notably, the Restormer-based method, which directly predicts the periodic noise in the image from the one-dimensional signal, achieves the best denoising performance. Additionally, this paper thoroughly examines the impact of the number of predicted Fourier coefficients on the denoising effect of the image in the second method.
- (3)
- By transforming the Flir infrared dataset, this study generates a simulated dataset that exhibits image characteristics similar to real infrared line images. The experiment verifies that utilizing this simulated dataset for training the network produces a certain denoising effect on real infrared line scanning images. This approach resolves the difficulty of constructing a dataset using actual infrared line scanning images.
The article is organized as follows. Section 2 is divided into two parts: Materials and Methods. The Section 2.1 introduces the characteristics of periodic noise in infrared line scan detectors and distinguishes this noise from traditional periodic noise caused by electrical interference. The Section 2.2 describes two neural network-based denoising methods: one predicts noise in the spatial domain using neural networks, while the other predicts the frequency domain coefficients of periodic noise using neural networks. Section 3 qualitatively and quantitatively analyzes the denoising performance of the algorithms using simulated datasets. Additionally, the algorithms are qualitatively analyzed using real infrared line scan datasets. Moreover, this paper conducts ablation experiments on the number of Fourier coefficients predicted by neural networks to investigate their impact on denoising effectiveness. Specific discussions are carried out in Section 4, and Section 5 concludes the article.
2. Materials and Methods
2.1. Characteristics of Periodic Noise in Infrared Line Detectors
2.1.1. General Periodic Noise
Periodic noise in images is commonly caused by electrical or motor interference during the image acquisition process. It manifests as recurring disturbances or shocks within the image. Examples of such noise typically include high-frequency noise, as depicted in Figure 1a with high-frequency grid noise. Removing such high-frequency periodic noise directly in the spatial domain is generally challenging. However, these disturbances often exhibit evident high-frequency noise points in the frequency domain’s high-frequency components, as illustrated in Figure 1b. Consequently, denoising this type of noise can be achieved directly in the frequency domain using trap filters such as Gaussian filters and Butterworth notch filters. Due to their specific nature as high-frequency noise points in the frequency domain, the periodic noise can be effectively suppressed without compromising the overall image contour and details by applying trap filters. The effect of a Butterworth notch filter on Figure 1a is demonstrated in Figure 1c, while Figure 1d displays the frequency domain image after applying a Butterworth notch filter to Figure 1b. It is clear from the figures that the trap filter significantly reduces the periodic noise in the denoised image, preserving object integrity and substantially improving the overall quality.

Figure 1.
General periodic noise image, the image after frequency domain filtering, and the corresponding Fourier spectrum images. (a) Image depicting the manifestation of periodic noise induced by electrical interference; (b) The Fourier spectrum image of the noisy image after applying a 2D Hanning window; (c) Image obtained after effective denoising using a trap filter; (d) Image resulting from the application of a trap filter for efficient frequency domain filtering.
2.1.2. Periodic Noise of the Infrared Line Array Detector
The imaging methods of infrared detectors can be categorized into two types: staring imaging and scanning imaging. Infrared focal plane array detectors are commonly used for detectors that employ the staring imaging method, whereas the infrared line detectors addressed in this paper utilize the scanning imaging method. During the imaging process, the infrared line detector is required to move and scan the objects within the scene. The underlying imaging principle is depicted in Figure 2.
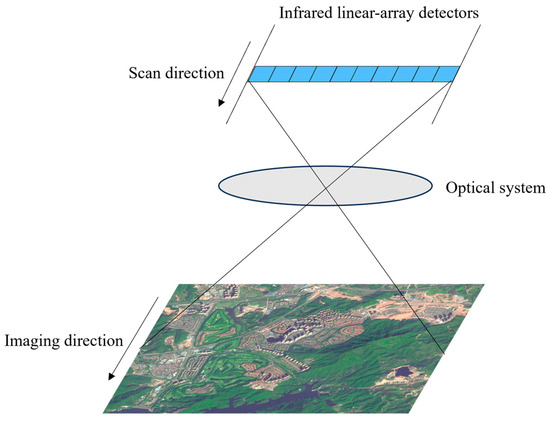
Figure 2.
Imaging method of infrared line array detector.
In contrast to general image periodic noise, infrared line array detectors consist of multiple detection units and offer fast imaging speed, resulting in high-resolution scanning images with extended noise periods. This noise is visually represented in the image through vertical periodic variations of brightness and darkness, as depicted in Figure 3a. The higher resolution and longer periods of the image cause the periodic noise of the infrared line array detector to predominantly exist in the low-frequency part of the image spectrum. The spectrum analysis of the infrared line array scanning image shown in Figure 3b reveals the absence of apparent image noise points, indicating a low intensity of periodic noise in the infrared line array image. Consequently, due to the lack of visible noise points in the Fourier spectrum image, the direct usage of trap filters in the frequency domain for image denoising becomes challenging.

Figure 3.
Authentic infrared line scan image and the corresponding Fourier spectrum image. (a) Infrared line scan image; (b) Fourier spectrum image.
The infrared line scanning images were captured using a blackbody to ensure a pure background, as illustrated in Figure 4a. Statistical analysis was performed on the acquired infrared line scanning images in both the row and column directions, as depicted in Figure 4b and Figure 4c, respectively. In Figure 4b, the vertical axis represents the average value of each row in the infrared line images, while in Figure 4c, it represents the average value of each column. The aforementioned images reveal that the scanning imaging technique is employed by the infrared line detector. However, the presence of electrical interference introduces periodic variations in image intensity along the column direction. This interference manifests as vertical bright and dark stripes within the images.
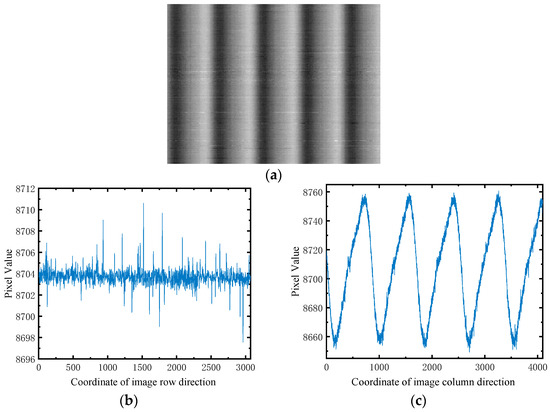
Figure 4.
Blackbody captures infrared line scanning image and generates statistical results for both the row and column directions. (a) Infrared line scanning image captured by blackbody; (b) Statistical results of the image in the row direction; (c) Statistical results of the image in the column direction.
To enhance the analysis of periodic noise fluctuations in infrared line scanning images and the variations in peak noise values, we acquired a dataset comprising 40 frames of 3072 × 4096 infrared line scanning images at four distinct time intervals using a black body as the source. Figure 5 presents the statistical outcome of the histogram displaying the periodicity of the infrared image dataset, while Figure 6 showcases the statistical results concerning the peak noise values.
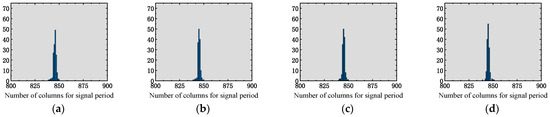
Figure 5.
Statistical analysis of the histogram depicting the periodicity magnitude of noise in infrared scanning images. (a) Time Period 1; (b) Time Period 2; (c) Time Period 3; (d) Time Period 4.

Figure 6.
Statistical analysis of peak-to-peak noise values in infrared line scanning images. (a) Time Period 1; (b) Time Period 2; (c) Time Period 3; (d) Time Period 4.
Figure 5 demonstrates the consistent periodicity of the noise in the infrared scanning image, with a period of approximately 845 columns. In Figure 6, the peak-to-peak values of the periodic noise in the infrared images are presented, indicating a signal peak at around 8755 and a signal valley at around 8655. The amplitude of the periodic signal remains constant.
2.2. Enhancing Neural Network-Based Method for Periodic Noise Denoising in Infrared Line Array Images
The development of neural networks has greatly enhanced their ability to extract features. Specifically, after the proposal of the Transformer, neural network models such as Vit, Uformer, and Restormer demonstrate significantly improved feature extraction capabilities compared to the traditional CNN-based ResNet model. Furthermore, recent years have witnessed the emergence of NAFNet, a network based on new activation functions that exhibits even more powerful feature-extraction abilities than networks based on Relu and Gelu. In Equation (3), if we employ the one-dimensional signal with a size of 1 × 4096 as the input and the periodic noise signal as the training label for neural network denoising, this approach significantly reduces the number of model parameters compared to neural networks that process entire 3072 × 4096 image frames as input and output. Moreover, due to the low frequency of periodic signals in infrared line scanning images, by utilizing Fourier transform, we can store the first Fourier coefficients and use them to reconstruct the periodic noise signal. Another feasible training approach involves using the initial Fourier coefficients of signal as input and the initial Fourier coefficients of noise as labels for neural network training. This method remarkably reduces the dimensionality of the input–output vectors in contrast to neural networks that use as input and as the label, thereby significantly mitigating the training difficulty of the neural network model. However, the values of the first Fourier coefficients are considerably larger than , which poses challenges for modeling the network.
2.2.1. Analysis of Denoising for Infrared Line Scanning Image Periodic Noise
The fast imaging speed of the infrared line array results in a low periodic noise frequency and the absence of noticeable noise spots in the frequency domain. Consequently, direct denoising of the array using a notch filter is not possible. Additionally, the infrared line array detector has a large number of detection units. In this experiment, the infrared line detector utilized had 3072 detection units, providing a highly detailed scanning image with thousands of columns. However, existing neural networks for image denoising typically operate on whole-frame images as input and output. Directly applying such a neural network for denoising the entire frame of the infrared line scan image would require a computationally expensive and large-scale neural network model to be constructed.
Periodic noise in infrared scanning images is classified as additive noise, which is elucidated by the image signal model presented in Equation (1).
Within the Equation (1), the variable represents the original infrared image encompassing noise, while the variable signifies the ideal infrared image devoid of any noise. Moreover, the variable is indicative of the periodic noise resulting from electromechanical interference, whereas the variable represents various other forms of noise. Based on the analysis of periodic noise in Figure 4, it is observed that the infrared scanning image exhibits periodic noise solely in the columnar direction. Consequently, an initial step can be performed by computing the mean value for each column of the image and subsequently transforming the image into a one-dimensional signal, as illustrated in Equation (2). Subsequently, the mean can be subtracted from the one-dimensional signal according to Equation (3).
The frame resolution for the infrared line image experiment is 3072 × 4096. In this experiment, denotes image pixel and represents the number of rows in one frame, where is equal to 3072 and . The signal is a one-dimensional representation that contains the mean values of each column in the image. The vector mean is calculated using the , and is obtained by subtracting the mean value from the one-dimensional image vector. By leveraging the powerful feature extraction capability of neural networks, the periodic noise signal is extracted from the image , allowing for the completion of image denoising using Equation (4).
The image mentioned is the denoised image, . The shape of the periodic noise signal s is shown in Figure 4c, with the means of the signal’s peaks and valleys close to zero.
2.2.2. Dataset Construction
Infrared line scan images exhibit remarkably high resolution. Nevertheless, this characteristic poses a series of challenges in constructing datasets suitable for neural network training. The abundance of pixels and intricate details in high-resolution images results in a substantial increase in dataset size. The task of collecting, annotating, and storing such a voluminous dataset is daunting. Moreover, the unique nature of infrared line detector imaging technology makes it arduous to acquire a substantial number of infrared line images with non-periodic noise for use as labels in model training. In light of stringent constraints, this study rigorously analyzes the collected infrared line images that entail periodic noise. Subsequently, the Flir infrared dataset (https://www.flir.com/oem/adas/adas-dataset-form/ (accessed on 1 December 2023)) is employed to fabricate a simulated dataset of infrared line scan images. The Flir infrared dataset mainly covers the mid-wave infrared and long-wave infrared bands. By training the model with this simulated training set, effective denoising of real infrared line scan images is achieved.
In two separate time periods, a significant number of infrared column images were captured, which encompassed periodic noise. For every frame image, the maximum and minimum values were meticulously documented. These findings are visually depicted in Figure 7.
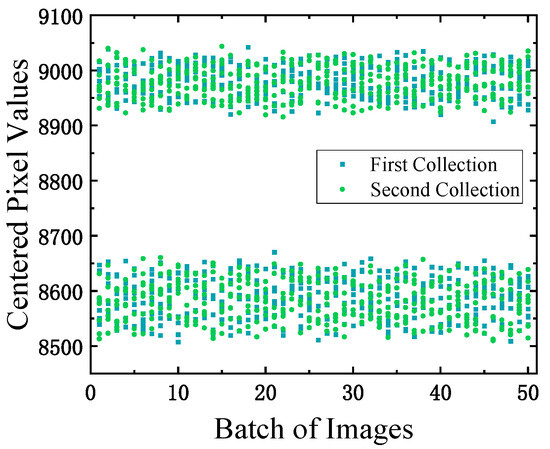
Figure 7.
Statistics of the maximum and minimum values in infrared line scanning images.
The infrared column image data in Figure 7 represent 14-bit data, exhibiting a fluctuation range of [8500, 9100], with a range size of 600. Figure 6 illustrates the fluctuation range of the periodic noise data in the infrared column image, which ranges from [8655, 8755], with a size of 100. To obtain pure background periodic noise images, multiple frames are captured using a blackbody source, followed by conducting statistical analysis on the column direction of the images. The one-dimensional signal in the column direction is depicted in Figure 4c. Assuming the one-dimensional periodic noise signal under pure background is denoted as , it undergoes mean removal processing, as depicted in Equation (5).
The variable represents a one-dimensional periodic noise signal that has undergone mean normalization. It exhibits fluctuations within a range of approximately [−50, 50], corresponding to a total range of 100. Based on Equations (2) and (3), the input for the neural network is the mean normalized one-dimensional signal derived from the image. By applying mean normalization, the input analog image dataset aligns its fluctuation range with the actual infrared image. In order to generate dataset that closely resemble real data, this study employs a scaling transformation on the Flir infrared image dataset, as demonstrated in Equation (6).
The interpolated image, , is derived from the Flir infrared dataset and has been enlarged. It has dimensions of 4096 columns by 3277 rows. The functions and are utilized to ascertain the minimum and maximum values of the image, correspondingly. The transformed image, , represents the outcome of applying a scaling transformation to . During the training process using the simulated dataset, the model takes input , as depicted in Equation (7).
The simulated image exhibits a pixel value fluctuation range of 500, while the fluctuation range of is 100. The value fluctuation range of is approximately 600, which is similar to the fluctuation range observed in real infrared scanning images, making it a reasonable comparison. Notably, this paper addresses the phase shift issue of periodic noise during the process of adding such noise. Figure 4c depicts a one-dimensional statistical graph of periodic noise in the infrared scanning image, showing a noise period size of approximately 845 columns. To generate image datasets with varying phase-shifted periodic noise within the same scene, each frame consists of a 3072 × 4096 Flir dataset image without noise. It is necessary to incorporate 845 frames of periodic noise images with different phase shifts, all with a resolution of 3072 × 4096. These images are then used to create corresponding datasets of 845 frames representing the same scene, each frame containing different phase-shifted periodic noise. The collection of 845 frames with varying phase shifts is obtained by column-wise offsetting and cropping from a 3072 × 16,384 pure background infrared scanning periodic noise image, resulting in images with a resolution of 3072 × 4096.
2.2.3. Neural Network Denoising Algorithm for Periodic Noise in Infrared Scanning Image in the Spatial Domain
In the denoising training process in the spatial domain, the model takes as its input, as referenced in Equation (7). The label consists of the noise vector , which is added to each frame image in the constructed simulated infrared image set, as also mentioned in Equation (7). The main objective is to leverage the powerful feature extraction capability of neural networks to accurately extract the image periodic noise vector from , making it as similar as possible to the added noise vector . This, in turn, facilitates the removal of periodic noise in the infrared column image using Equation (4). Figure 8 showcases the flowchart of the spatial domain neural network denoising algorithm.
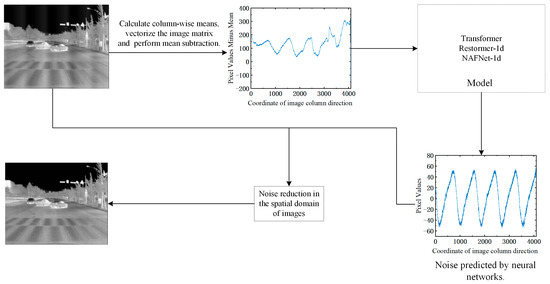
Figure 8.
Flowchart of the spatial domain neural network denoising algorithm.
The comprehensive algorithmic procedure is delineated systematically as follows:
- Step 1: To transform the image matrix into a one-dimensional vector, the mean value of each column of the image is calculated, resulting in a one-dimensional vector representation. To mitigate the fluctuation of the vector magnitude, the mean value is subtracted from the one-dimensional vector, yielding the input vector for the neural network model.
- Step 2: The input of a one-dimensional vector into a neural network results in the prediction of a one-dimensional periodic noise vector by the model for infrared column images.
- Step 3: The denoised image is obtained by applying Equation (4) to the periodic noise signal .
2.2.4. Neural Network Denoising Algorithm for Periodic Noise in Infrared Scanning Image in the Frequency Domain
In this section, we will analyze the training and prediction processes of the frequency domain neural network model separately. Firstly, we will examine the model training process in detail. Drawing upon Figure 4, which presents the period signal acquired by the infrared line detector, there is a possibility that the signal solely manifests at specific low-frequency frequencies. Consequently, the algorithm implemented in this paper extracts the frequency components of the periodic noise from these specific frequencies. Initially, the one-dimensional signal undergoes Fourier transformation as represented by Equation (8), serving as the input for the model.
In this case, is set to 4096, . represents the number of frequencies that will be truncated from the Fourier complex sequence . The truncations need to preserve enough frequencies to accurately reconstruct a periodic signal with noise. For instance, truncating the first 100 frequencies of , with = 100, yields the input for the network model. The real and imaginary parts of the truncated frequencies are then rearranged according to Equation (9).
In Equation (9), . The term corresponds to the mathematical operation of extracting the real part of a complex number, while refers to the operation of extracting the imaginary part. The input for the neural network model consists of a one-dimensional vector with a length of . Likewise, the periodic noise signal is subjected to Fourier transformation, resulting in Fourier coefficients . Next, frequencies are extracted, serving as the training labels for the neural network, as depicted in Equation (10).
The label vector is utilized for training neural networks. It is a one-dimensional vector with a length of . This following content aims to outline the process of utilizing the trained network model for the purpose of denoising infrared scanning images. Specifically, for an infrared scanning image denoted as , which possesses a frame resolution of 3072 × 4096 and is affected by periodic noise, the initial step involves transforming it into a one-dimensional signal, denoted as , employing Equations (2) and (3). Subsequently, Equation (8) is utilized to conduct a DFT transformation on the one-dimensional signal , leading to the DFT coefficients, termed as . Furthermore, Equation (9) facilitates the acquisition of a one-dimensional input vector, , which corresponds to the neural network model and has a length of . Finally, by inputting into the trained neural network, the output vector, termed , is obtained.
To transform the coefficients in vector into complex form, we apply the procedure outlined in Equation (11).
For a given value , the function produces a complex number where the real part is denoted by and the imaginary part by . Leveraging the properties of the discrete Fourier transform, the periodic noisy signal can be restored from , as demonstrated in Equation (12).
In Equation (12), . Subsequently, the denoised image is obtained by subtracting the predicted periodic noise from the image using Equation (4). The flowchart of the overall algorithm is shown in Figure 9.
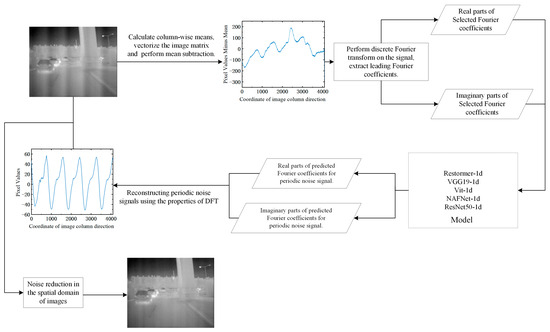
Figure 9.
Overall flowchart of frequency neural network denoising algorithm.
The comprehensive algorithmic procedure is delineated systematically as follows:
- Step 1: To transform the image matrix into a one-dimensional vector, the average value is computed for each column of the image. This process results in a one-dimensional vector representation of the image. In order to mitigate fluctuations in vector magnitudes, the mean value is subtracted from the one-dimensional image vector.
- Step 2: To obtain the input for the neural network model, we perform the calculation of the discrete Fourier transform (DFT) transformation coefficients for a one-dimensional vector. The Fourier coefficients are truncated based on the frequency of periodic noise in the detector. We select the first Fourier coefficients and rearrange the real and imaginary parts of the truncated coefficients using Equation (10).
- Step 3: The neural network model takes a one-dimensional vector as input and generates an output vector . By utilizing Equation (11), the truncated Fourier coefficient vector of periodic noise is obtained.
- Step 4: The periodic noise in the model-predicted images can be effectively reconstructed by employing Equation (12).
- Step 5: Using Equation (4) and periodic noise , the denoised image is obtained.
3. Results
3.1. The Impact of Frequency Numbers on Denoising Effectiveness
Equations (8) and (9) suggest that the algorithm of the frequency domain neural network model, following the Fourier transformation of one-dimensional image signals, selectively focuses on the initial Fourier coefficients instead of considering the entire set. By inputting these Fourier coefficients into the neural network output model, the first coefficients of periodic noise can be extracted. Subsequently, employing Equations (11) and (12), the periodic noise signal within the reconstructed signal can be recovered based on these initial Fourier coefficients, effectively accomplishing the image denoising process. The objective of the experiments in this section is to examine the impact of the number of truncated Fourier coefficients on the reconstruction of periodic noise signals.
The periodic vertical stripe changes in the infrared array image can be observed in Figure 3 and Figure 4. These changes can be attributed to the fast imaging speed of the infrared array detector, leading to a longer noise period and lower noise frequency. Upon undergoing Fourier transformation, the noise frequency should be present in the low-frequency Fourier coefficients. Figure 10 illustrates the selection of various Fourier coefficients in the experiment to reconstruct the periodic signal using Equations (11) and (12). From Figure 10, it is evident that for values greater than 12, the reconstructed periodic signal closely resembles the original periodic signal. When , the reconstructed periodic signal exhibits a similar transformation pattern to the original periodic signal, yet with some deviations. Notably, for N equal to 3, the reconstructed signal, though still periodic, significantly differs from the “Origin” signal.
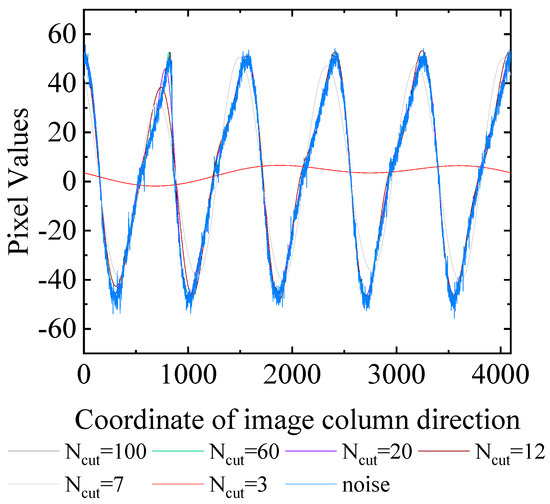
Figure 10.
The impact of the number of Fourier coefficient truncation on the reconstruction of periodic signals.
The experimental results presented in Figure 10 demonstrate that the periodic noise in the infrared line image predominantly exists within the low-frequency region. By selectively capturing a subset of relevant Fourier coefficients, the image denoising algorithm is capable of effectively reconstructing the periodic noise signal within the infrared line scanning image.
3.2. Verification of Denoising Effectiveness Using Simulated Datasets
3.2.1. Analysis of Image Denoising Effects by Different Algorithms
This study utilizes Flir infrared array images to construct a simulated infrared line scanning image dataset, addressing the challenges associated with the high resolution and the acquisition of a pure noise-free image dataset for actual infrared line scanning images. The constructed dataset is then utilized to train a model and conduct a quantitative analysis of the denoising effect of the algorithm. In the neural network training process, the spatial domain neural network takes as the input, which represents the noise vector added to each frame image in the simulated infrared line scanning image dataset, as described in Equation (7). Additionally, the frequency domain neural network algorithm extracts 100 frequency components ( = 100) from the one-dimensional vector , obtained through Fourier transform and frequency truncation as stated in Equation (9), resulting in a one-dimensional input vector of size . The label in this case is the one-dimensional vector , obtained through the Fourier transform and truncation of the periodic noise signal added to the simulated dataset, as described in Equation (10). The overall dataset utilized for model training consists of 420 frames extracted from the Flir dataset, with 210 frames collected during the day and another 210 frames collected at night.
Random phase-shifted periodic noise was introduced to 420 image frames, which were extracted from the Flir dataset. Prior to and following the denoising process, the PSNR and SSIM values of the images were computed. The outcomes of the experimental analysis are visually illustrated in Figure 11.
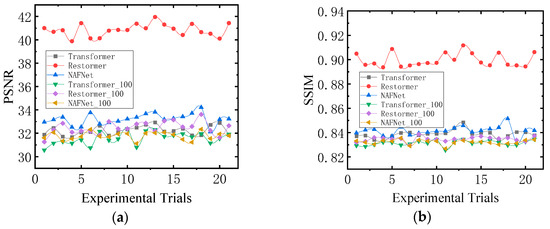
Figure 11.
PSNR and SSIM of simulated dataset denoising effects. (a) presents the denoising PSNR results of spatial algorithms and frequency domain algorithms on the dataset. (b) presents the denoising SSIM results of spatial algorithms and frequency domain algorithms on the dataset.
In Figure 11, the x-axis represents the sequence of experiments, with each group of experimental results indicating the average denoising outcome of 20 image frames. To quantitatively demonstrate the denoising effect of the 420-image frames, the results were divided into four sets, each comprising 105 image frames. The average PSNR and SSIM results are provided in Table 1 and Table 2, respectively. Among the models used, Transformer, Restormer, and NAFNet represent the direct extraction of noise signals from the spatial domain. Conversely, Transformer_100, Restormer_100, and NAFNet_100 involve the extraction of 100 Fourier coefficients from the frequency domain through neural networks, which are then utilized for denoising purposes. The Transformer model solely employs the Encode module with 12 blocks and 20 attention heads. Its model size is approximately 1.4 GB. As for the Restormer and NAFNet models, their sizes are approximately 258 MB and 384 MB, respectively. The denoising results obtained from Algorithm, Figure 11, and Table 1 and Table 2 indicate that the Restormer neural network model offers the most effective denoising solution by directly extracting noise from the image. This approach yields a denoised image with a PSNR value close to 41 and an SSIM value close to 0.90. In contrast, the Transformer and NAFNet models exhibit lower capability in directly extracting periodic noise from the signal. Furthermore, the frequency domain neural network algorithm demonstrates a certain level of denoising effect when the number of frequency truncations is N. This effect is comparable to the Transformer and NAFNet models’ ability to extract periodic noise directly from the signal’s spatial domain. These findings suggest that while having fewer input and output parameters is advantageous for model convergence in the neural network, the larger values of the frequency coefficients after the Fourier transformation of the signal pose difficulties in network fitting, ultimately resulting in no significant improvement in the denoising effect of the model.

Table 1.
PSNR for denoising in simulated dataset.

Table 2.
SSIM for denoising in simulated dataset.
In order to better compare the denoising effects of different models, this experiment selected four frames of images from the dataset for qualitative analysis. The denoising effect images are depicted in Figure 12. The highlighted region in the red box of Figure 12 indicates areas where the denoising results of various algorithms are suboptimal. It is evident that utilizing Restormer to directly extract periodic noise from the spatial domain achieves the most effective denoising results, producing a denoised image that closely resembles the original image without noise. While other methods have some degree of denoising effects, the resulting images may exhibit areas that are somewhat unsatisfactory.
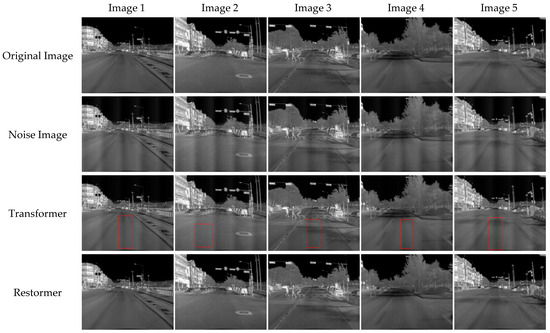

Figure 12.
Denoising effect images of different model algorithms. The selected area within the red box in the figure is chosen to highlight some residual noise present in the denoised image.
This experiment aims to comprehensively analyze the denoising effects of different algorithms by plotting the noise curves extracted from the noisy images, as depicted in Figure 13. In this context, “noise” refers to the periodically added noise signal. The findings from Figure 13 demonstrate that the periodic noise signals extracted by various neural network denoising models align with the trends of the added periodic noise, albeit with slight disparities in amplitude. Specifically, in Figure 13b–d, the periodic noise extracted by each algorithm closely resembles the added periodic noise. Additionally, the corresponding denoised images in Figure 12 exhibit successful removal of image periodic noise, resulting in effective denoising. However, in Figure 13a, the noise directly extracted from the image space domain using the Transformer model exhibits a smaller amplitude, despite having a consistent periodicity with the added noise. Consequently, the image denoised using the Transformer algorithm in Figure 12 exhibits a moderate denoising effect. Notably, the Restormer_100 model demonstrates discrepancies in the fitted Fourier frequency coefficients. Although the reconstructed noise signal from this model aligns with the added periodic signal in trend, it deviates numerically, resulting in some line noise in the denoised images generated by this model.
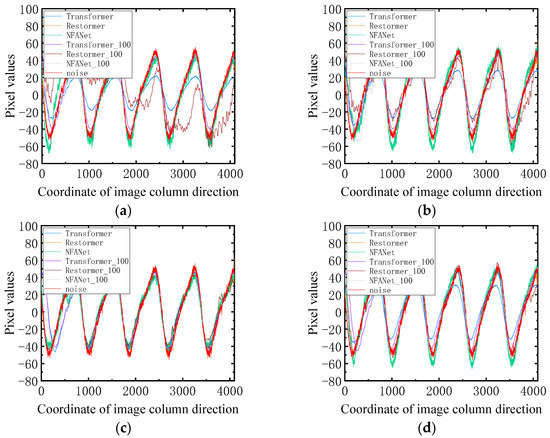
Figure 13.
Periodic noise reconstructed by different models. (a–d) respectively represent the one-dimensional noise curves extracted by each model from Image 1, Image 2, Image 3, and Image 4 in Figure 12.
3.2.2. The Effect of Different on the Denoising Performance of Frequency Domain Neural Networks
Section 3.1 examines the feasibility of reconstructing periodic noise signals by utilizing only the initial Fourier coefficients. This section employs experimental analysis to assess the denoising performance of neural network models defined in Equations (9) and (10) while employing different numbers of frequency coefficients N. Theoretically, reducing the number of input–output parameters in a neural network model facilitates network fitting. For this experiment, we selected = 100, 60, and 12 as the frequencies respective to the coefficients, and subsequently trained Transformer, Restormer, and NAFNet network models. The obtained results for the denoised images’ PSNR and SSIM are presented in Figure 14.
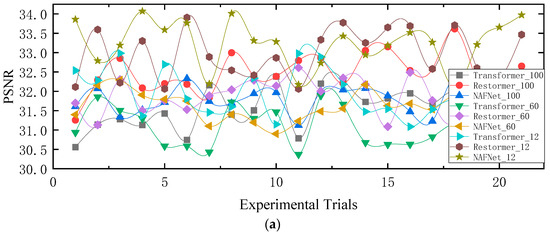
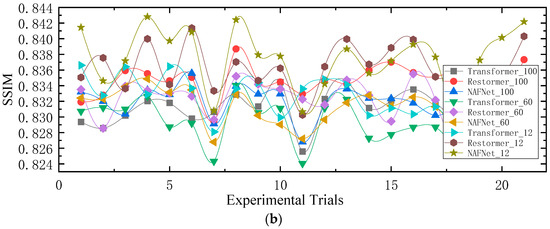
Figure 14.
PSNR and SSIM values for various neural networks with . The suffix in the model names in the diagram indicates the number of periodic noise frequencies predicted by the model. Transformer_100, Restormer_100, and NAFNet_100 indicate that the model predicts 100 periodic noise frequencies. Transformer_60, Restormer_60, and NAFNet_60 indicate a prediction of 60 periodic noise frequencies. Transformer_12, Restormer_12, and NAFNet_12 indicate a prediction of 12 periodic noise frequencies. (a) denotes the denoising PSNR results of various frequency domain algorithms on the dataset. (b) denotes the denoising SSIM results of various frequency domain algorithms on the dataset.
The data in Table 3 and Table 4 represent, respectively, the PSNR and SSIM values of predicting model denoising images with different frequency coefficients. Each image dataset in Table 3 and Table 4 consists of 30 frames of images. Figure 14 illustrates the experimental order on the horizontal axis, with each group of results representing the average denoising outcomes of 20 image frames. The experimental results demonstrate a slight enhancement in denoising performance for the Restormer, Transformer, and NAFNet models when = 12, exhibiting higher PSNR and SSIM values for the denoised images. An observation during the model training process reveals that smaller values of lead to faster convergence of the models, but also pose a higher risk of overfitting.

Table 3.
PSNR for various neural networks with .

Table 4.
SSIM for various neural networks with .
3.3. Experimental Analysis of Real Infrared Scanning Line Image
This section of the experiment aims to validate the denoising capability of a neural network model trained on a simulated infrared line scanning image dataset when applied to real long-wave infrared line scan images. Two frames of infrared line scanning images with a resolution of 3072 × 4096 were carefully selected for analysis, and the results for denoising using various algorithms are presented in Figure 15. Among these algorithms, Two-circle [10] and local Threshold [11] are designed specifically for removing periodic noise in the frequency domain. However, as observed from the figure, the denoising effect achieved by these two frequency-domain-based algorithms is not significant, as noticeable periodic vertical stripe noise remains visible in the image. This discrepancy may be attributed to the relatively low intensity of periodic noise in infrared scanning image, resulting in the absence of apparent noise points in the image’s frequency domain. Consequently, even after applying a trap filter for noise removal, the overall denoising effect on the image is not substantial. When examining the spatial domain neural network models (Transformer, Restormer, and NAFNet) and frequency domain neural network models (Transformer_100, Restormer_100, and NAFNet_100), it is worth noting that the frequency truncation is set to 100 in the latter category of models.
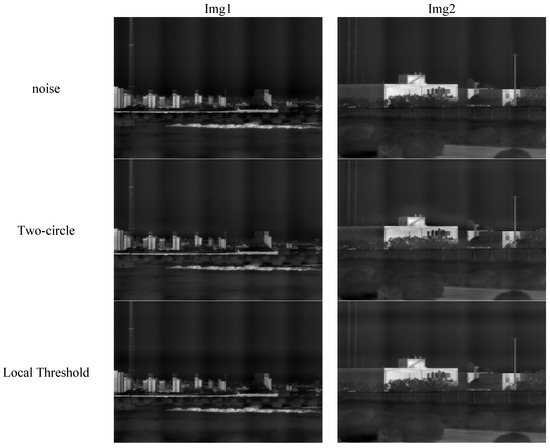
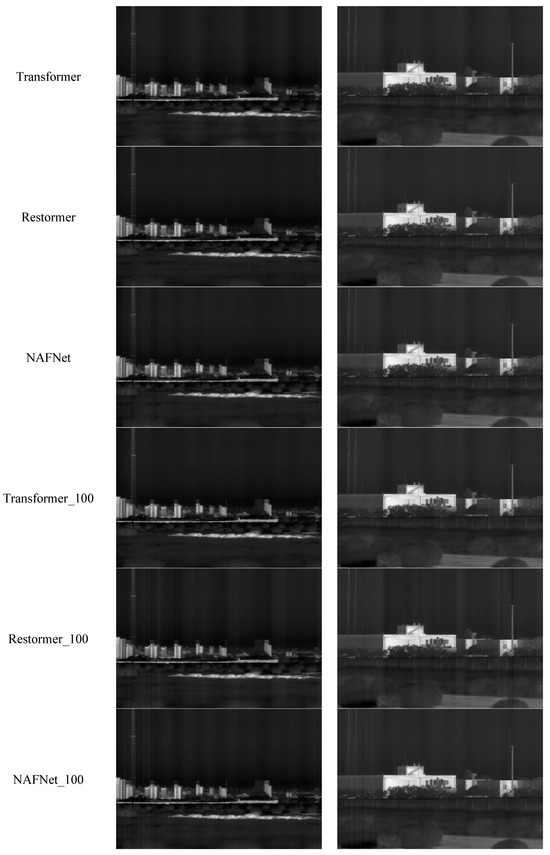
Figure 15.
Real infrared line scanning denoised image.
Based on Figure 15, the neural network-processed images demonstrate notable improvement in denoising compared to the original noisy images. Among the models, the Restormer model exhibits the most effective denoising, which aligns with the denoising outcomes discussed in Section 3.2.1. This superior performance of the Restormer model may be attributed to its enhanced ability to extract periodic noise from signals with small values, surpassing the capabilities of the NAFNet and Transformer models. Conversely, when utilizing neural networks to eliminate periodic noise in the frequency domain, the substantial values of Fourier coefficients introduce a deviation between the Fourier coefficients of the extracted periodic noise and the genuine periodic signal. Consequently, this deviation results in a less effective denoising when reconstructing the periodic signal using Fourier coefficients, in contrast to the direct utilization of the Restormer model for noise extraction from the spatial domain of the image.
4. Discussion
This research paper addresses the issue of long-period vertical stripe noise that arises from external electrical interference during the imaging process of infrared line scanning detectors. This type of periodic noise presents as vertical stripes with periodic fluctuations in brightness and darkness on the infrared line scanning image. Fourier spectrum analysis reveals the absence of prominent noise points in the spectrum image of the periodic noise, rendering traditional notch filtering in the frequency domain of the image ineffective for noise removal. Given the exceptionally high resolution of infrared line scanning images, training a neural network to perform denoising by taking the entire frame image as input and output is currently infeasible. Consequently, this paper utilizes infrared line scanning images captured by employing a blackbody as a pure background. It is discovered that this particular type of periodic noise exhibits signal changes in a periodic manner along the columns of the image. By calculating the mean value of each column in the infrared line scanning image and converting the image into a one-dimensional vector, the periodic signal can be extracted from the one-dimensional vector using a neural network. This approach significantly reduces the scale of the neural network and accelerates its convergence.
Periodic signals can be reconstructed by utilizing Fourier coefficients in Fourier inverse transformation to recover the underlying periodic noise. Moreover, in the case of infrared line scanning images, where the frequency of the periodic noise is relatively low, it is possible to reconstruct the entire periodic noise by selectively retaining a finite number of Fourier coefficients. Building upon the aforementioned analysis, this paper proposes two distinct approaches for utilizing neural networks to extract periodic noise. One approach involves using a one-dimensional image signal as the input to the neural network, while the output is a sequence depicting the periodic noise. The alternative approach involves utilizing a subset of the Fourier coefficients obtained from performing a Fourier transformation on the one-dimensional image signal. These coefficients serve as the input to the neural network, giving rise to the output consisting of a subset of the Fourier coefficients of the periodic signal. Both approaches leverage the powerful feature-extraction capability of neural networks. The first method involves directly predicting the periodic noise signal within the image from the one-dimensional image signal. The second method predicts the Fourier coefficients of the periodic signal from the Fourier coefficients of the one-dimensional image signal.
Creating a dataset for neural network training that includes a significant number of non-periodic noise infrared line images poses challenges due to the high resolution of these images and the distinctive features of infrared line detector imaging technology. This study addresses this issue by conducting an analysis of infrared scanning images and utilizing the Flir infrared image dataset to generate a simulated dataset of infrared line scanning images for training neural networks. Furthermore, the impact of the number of Fourier coefficients in the second denoising method on the denoising effect was examined. The experimental results demonstrated that decreasing the number of Fourier coefficients led to an improvement in the denoising effect to some extent. It is important to note that reducing the Fourier coefficients increases the risk of overfitting during the neural network training process. Finally, the trained neural network model was employed to denoise natural infrared line scanning images that contained periodic noise. The experimental results indicated that all models exhibited a certain degree of denoising on the infrared line scanning images, which was similar to the simulated image dataset. The Restormer, which directly extracts periodic noise from the one-dimensional signal of the image, demonstrated the best denoising effect, thereby validating the feasibility of the algorithm proposed in this study.
Future work can be explored from the following perspectives:
- (1)
- This paper presents two denoising methods specifically designed for mitigating long-period low-frequency noise in infrared line scanning images. It does not involve the development of a new network model. However, it opens up possibilities for the future design of a more effective denoising network model to address this particular type of one-dimensional signal.
- (2)
- Infrared array detectors possess high real-time imaging capabilities and generate substantial amounts of data. Image processing for such detectors is commonly carried out using embedded devices. Therefore, it is crucial to design network models that minimize memory usage and enhance model computation speed, thus meeting the real-time requirements of the devices. The task of transplanting the model network into embedded devices poses a significant challenge.
5. Conclusions
The research presented herein tackles the persistent challenge of vertical stripe noise in infrared line scanning detectors, predominantly attributed to low-frequency electrical interference during the imaging sequence. The study advances a novel paradigm that reconceptualizes these images as one-dimensional signals by meticulously analyzing pure background infrared line scanning images. Two innovative neural-network-based noise-reduction techniques are introduced to downsize the neural network’s complexity and enhance convergence speed. The first method employs the one-dimensional image signal as input, generating an output delineating the periodic noise sequence. The second method utilizes the Fourier coefficients derived from the one-dimensional image signal through Fourier transformation as input, producing output that comprises the selective Fourier coefficients of the periodic signal. Both methodologies have been rigorously validated through simulations and empirical testing on actual imagery, exhibiting remarkable noise attenuation capabilities. Notably, the application of Restormer for direct extraction of periodic noise from one-dimensional signals has demonstrated superlative noise reduction efficacy, delivering denoised images that are virtually devoid of any detectable periodic noise artifacts.
Author Contributions
Conceptualization, W.C. and B.L.; methodology, B.L.; software, B.L.; validation, B.L.; formal analysis, B.L.; resources, W.C., Y.Z., Y.M., L.L. and B.L.; data curation, W.C. and B.L.; writing—original draft preparation, B.L.; writing—review and editing, Y.Z., W.C. and B.L.; supervision, B.L.; funding acquisition, W.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data generated or analyzed during this study are included in this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bouali, M.; Sato, O.; Polito, P. An algorithm to improve the detection of ocean fronts from whiskbroom scanner images. Remote Sens. Lett. 2015, 6, 942–951. [Google Scholar] [CrossRef]
- Valenzuela, W.E.; Figueroa, M.; Pezoa, J.E.; Meza, P. A digital architecture for striping noise compensation in push-broom hyperspectral cameras. In Applications of Digital Image Processing XXXVIII; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9599, p. 95992H. [Google Scholar]
- Lou, C.; Zhang, Y.; Liu, Y. Small Target Detection of Infrared Linear Array Image Based on Complemented Gradient Enhancement. Acta Opt. Sin. 2021, 41, 2104001. [Google Scholar] [CrossRef]
- Mu, J.; Li, W.; Rao, J.; Wei, H.; Li, F. Infrared small target detection using tri-layer template local difference measure. Opt. Precis. Eng. 2022, 30, 869–882. [Google Scholar] [CrossRef]
- Li, K.; Li, W.-L.; Han, C.-P. The method based on L1 norm optimization model for stripe noise removal of remote sensing image. J. Infrared Millim. Waves 2021, 40, 272–283. [Google Scholar]
- Song, S.; Yang, G.; Zhou, X. Line array time delay integral CCD sweep image non-uniformity correction method. Procedia Comput. Sci. 2020, 174, 216–223. [Google Scholar]
- Cao, Y.; Yang, M.Y.; Tisse, C.-L. Effective Strip Noise Removal for Low-Textured Infrared Images Based on 1-D Guided Filtering. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 2176–2188. [Google Scholar] [CrossRef]
- Wang, E.; Jiang, P.; Hou, X.; Zhu, Y.; Peng, L. Infrared Stripe Correction Algorithm Based on Wavelet Analysis and Gradient Equalization. Appl. Sci. 2019, 9, 1993. [Google Scholar] [CrossRef]
- Wang, E.; Jiang, P.; Li, X.; Li, X.; Cao, H. Infrared stripe correction algorithm based on wavelet decomposition and total variation guided filtering. J. Eur. Opt. Soc. Rapid Publ. 2020, 16, 1. [Google Scholar] [CrossRef]
- Hamd, M.H. Auto detection and removal of frequency domain periodic noise. In Proceedings of the 2014 IEEE Global Summit on Computer & Information Technology (GSCIT), Sousse, Tunisia, 14–16 June 2014; pp. 1–4. [Google Scholar]
- Yadav, V.P.; Singh, G.; Anwar, M.I.; Khosla, A. Periodic noise removal using local thresholding. In Proceedings of the 2016 Conference on Advances in Signal Processing (CASP), Pune, India, 9–11 June 2016; pp. 114–117. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image restoration. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 2480–2495. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Wen, B.; Fan, Y.; Loy, C.C.; Huang, T.S. Non-local recurrent network for image restoration. In Proceedings of the Advances in Neural Information Processing Systems 31, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.-H.; Shao, L. Multi-stage progressive image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 14821–14831. [Google Scholar]
- Yue, Z.; Zhao, Q.; Zhang, L.; Meng, D. Dual adversarial network: Toward real-world noise removal and noise generation. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; pp. 41–58. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Sun, G.; Kong, Y.; Fu, Y. Accurate and Fast Image Denoising via Attention Guided Scaling. IEEE Trans. Image Process. 2021, 30, 6255–6265. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, K.; Li, K.; Zhong, B.; Fu, Y. Residual non-local attention networks for image restoration. arXiv 2019, arXiv:1903.10082. [Google Scholar]
- Hu, X.; Ma, R.; Liu, Z.; Cai, Y.; Zhao, X.; Zhang, Y.; Wang, H. Pseudo 3d autocorrelation network for real image denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 16175–16184. [Google Scholar]
- Plotz, T.; Roth, S. Neural nearest neighbors networks. In Proceedings of the Advances in Neural Information Processing Systems 31, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Chen, L.; Chu, X.; Zhang, X.; Sun, J. Simple baselines for image restoration. In European Conference on Computer Vision; Springer Nature: Cham, Switzerland, 2022; pp. 17–33. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Chen, Z.; Zhang, Y.; Gu, J.; Kong, L.; Yang, X. Recursive generalization transformer for image super-resolution. arXiv 2023, arXiv:2303.06373. [Google Scholar]
- Chen, Z.; Zhang, Y.; Gu, J.; Zhang, Y.; Kong, L.; Yuan, X. Cross aggregation transformer for image restoration. Adv. Neural Inf. Process. Syst. 2022, 35, 25478–25490. [Google Scholar]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. Swinir: Image restoration using swin transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021. [Google Scholar]
- Shi, S.; Gu, J.; Xie, L.; Wang, X.; Yang, Y.; Dong, C. Rethinking alignment in video superresolution transformers. arXiv 2022, arXiv:2207.08494. [Google Scholar]
- Wang, Z.; Cun, X.; Bao, J.; Liu, J. Uformer: A general u-shaped transformer for image restoration. arXiv 2021, arXiv:2106.03106. [Google Scholar]
- Yang, F.; Yang, H.; Fu, J.; Lu, H.; Guo, B. Learning texture transformer network for image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.-H. Restormer: Efficient transformer for high resolution image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Zhang, J.; Zhang, Y.; Gu, J.; Dong, J.; Kong, L.; Yang, X. Xformer: Hybrid xshaped transformer for image denoising. arXiv 2023, arXiv:2303.06440. [Google Scholar]
- Zhang, J.; Zhang, Y.; Gu, J.; Zhang, Y.; Kong, L.; Yuan, X. Accurate image restoration with attention retractable transformer. arXiv 2022, arXiv:2210.01427. [Google Scholar]
- Liang, J.; Cao, J.; Fan, Y.; Zhang, K.; Ranjan, R.; Li, Y.; Timofte, R.; Van Gool, L. Vrt: A video restoration transformer. arXiv 2022, arXiv:2201.12288. [Google Scholar]
- Shao, W.; Ge, Y.; Zhang, Z.; Xu, X.; Wang, X.; Shan, Y.; Luo, P. Dynamic token normalization improves vision transformer. arXiv 2021, arXiv:2112.02624. [Google Scholar]
- Zhang, Z.; Jiang, Y.; Jiang, J.; Wang, X.; Luo, P.; Gu, J. Star: A structure-aware lightweight transformer for real-time image enhancement. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 4106–4115. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).