Optimizing the Deployment of Ground Tracking Stations for Low Earth Orbit Satellite Constellations Based on Evolutionary Algorithms
Abstract
1. Introduction
2. Problem Definition
2.1. Variable Structure Optimization
2.2. Objective Functions
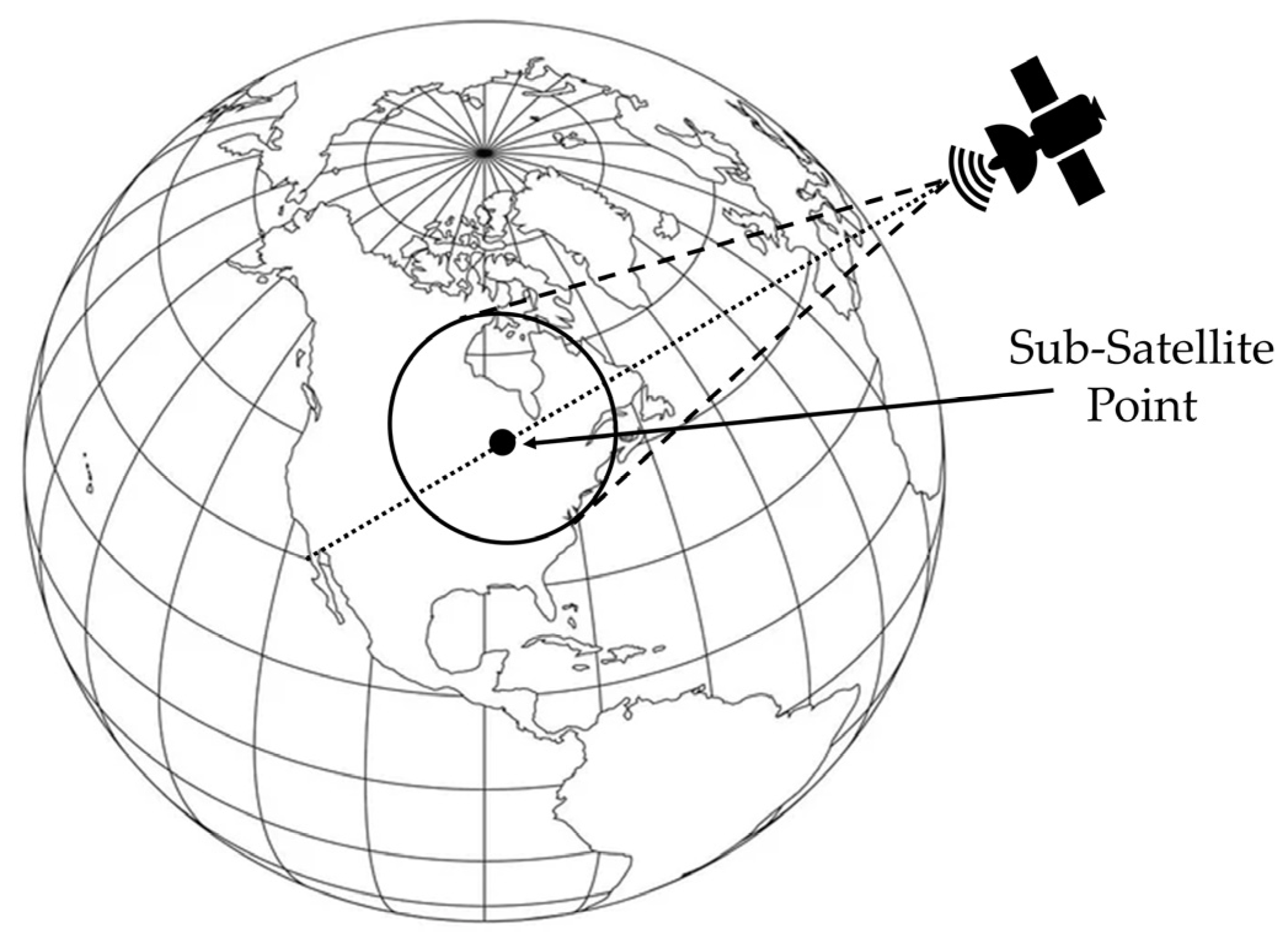
2.3. Calculation of the Satellite Position Dilution of Precision
2.4. Intersatellite Links for SPDOP
3. Methodology
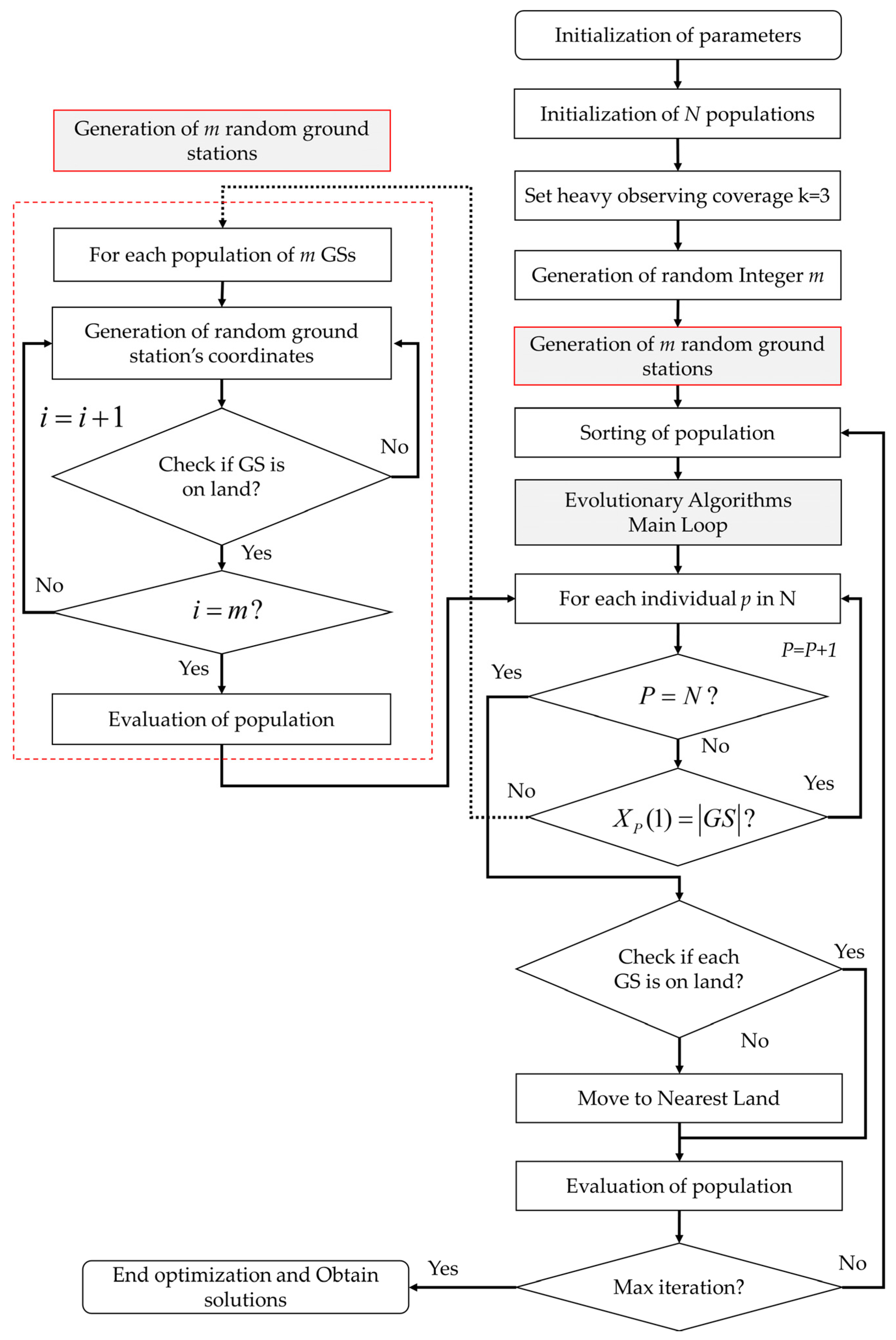
3.1. Objective and Methodology for Global Deployment
| Algorithm 1. Optimal deployment method for global distribution of GSs | |
| Step 0: | Initialize the parameters: evolutionary algorithm parameters, number of populations N and maximum iteration (It). |
| Step 1: | For a given k-heavy coverage of k = 3, generate N random integer values (according to the size of population), each in the interval . |
| Step 2: | For each random integer m, generate m random coordinates, and check whether each set corresponds to land. |
| Step 3: | For each population, evaluate the following objectives: the number of GSs and the observing rate according to the k-heavy coverage, in addition to the evaluation of the distance between the two nearest GSs in the population. |
| Step 4: | Sort the population according to a non-dominated solution. |
| Step 5: | Apply the main loop of the evolutionary algorithm (Appendix A) with all operations of crossover, mutation and selection. |
| Step 6: | For each individual P in the population, check whether the value of the number of GSs (XP(1) refers to the variable of the number of GSs used as expressed in Equation (1) or whether it is changed (due to crossover and mutation operators) relative to the total number of GSs (|GS|). If the number of GSs (nGS) in a population has changed due to the crossover and mutation operations, generate a new deployment of GSs according to the new nGS (the same as for the generation of the initial populations). |
| Step 7: | Due to crossover, mutation operations could change the variables; check the coordinates of GSs to see whether they correspond to land. |
| Step 8: | Find the nearest land, and move the GSs here. |
| Step 9: | Evaluate each individual population through the objective function. |
| Step 10: | Check the number of iterations, and if iteration It <= Itmax (maximum iteration), go to Step 4; else, end of optimization. |
3.2. Objectives and Methodology for Regional Deployment
| Algorithm 2. Optimal deployment method for local distribution of GSs. | |
| Step 0: | Initialize the parameters of the algorithm and population size of N individuals. |
| Step 1: | Define the number m of GSs that are used for optimal deployment. |
| Step 2: | For each population, generate m random GSs in the selected regional area. |
| Step 3: | Evaluate the objective function of each population (mean SPDOP) of visible satellites in addition to the sub-objective of the distance between the nearest GSs in the same population. |
| Step 4: | Sort the population according to the ranking of min mean (SPDOP) and distance between GSs. |
| Step 5: | Apply the main loop of evolutionary algorithms (Appendix A) with all operations of selection, crossover and mutation of individuals (or GSs). |
| Step 6: | After each crossover and mutation operation, check whether the GS is in a regional area. |
| Step 7: | If any ground station is outside the regional area, move it to the nearest regional land. |
| Step 8: | Evaluate the objective function of each population (mean SPDOP) of visible satellites in addition to the sub-objective of the distance between the nearest GSs in the same population. |
| Step 9: | Sort the population based on the ranking of the min mean (SPDOP) and the distance between GSs. |
| Step 10: | Check the number of iterations (generation), and if it does not reach the max iterations go to Step 5; else, end the algorithm. |
4. Results
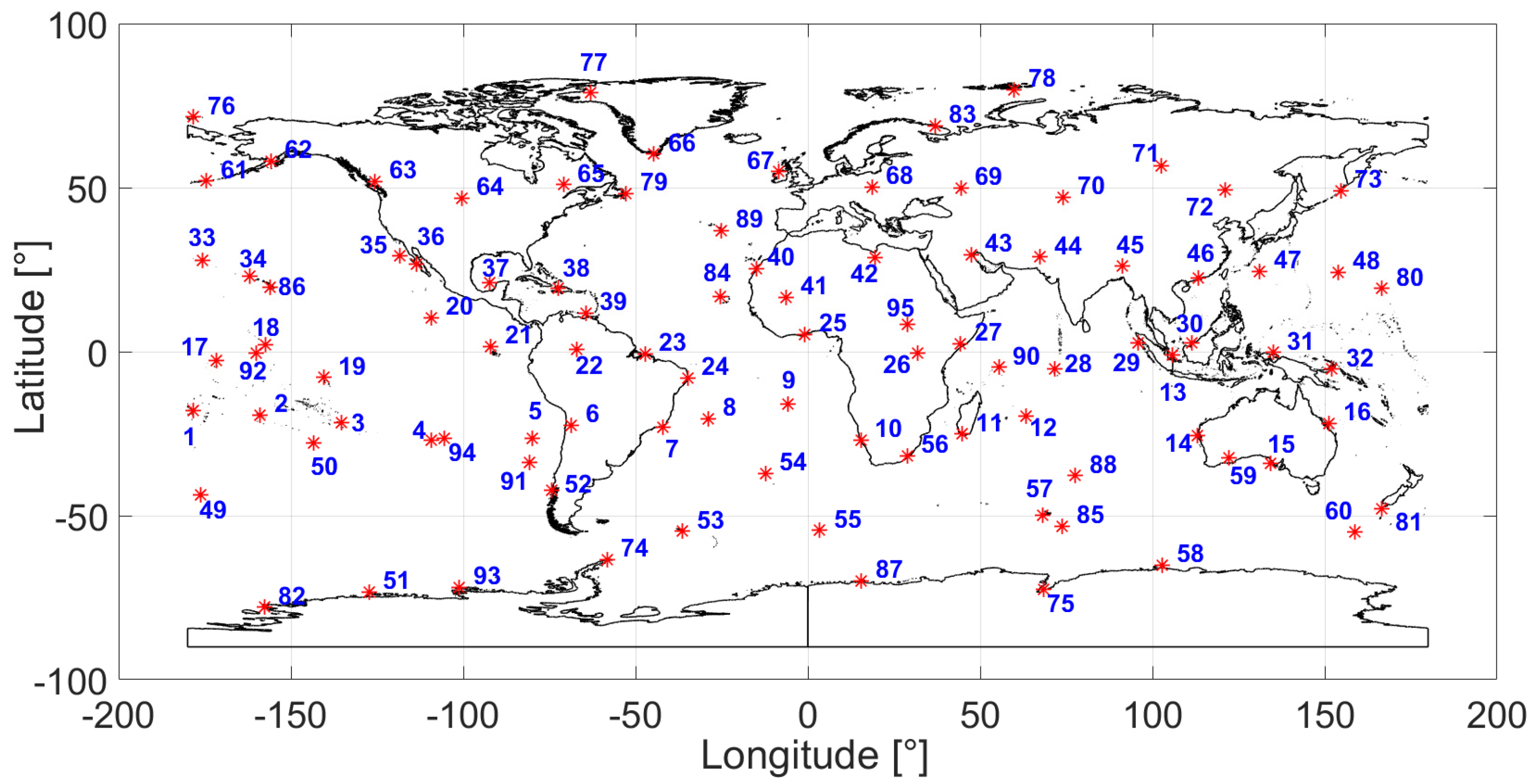
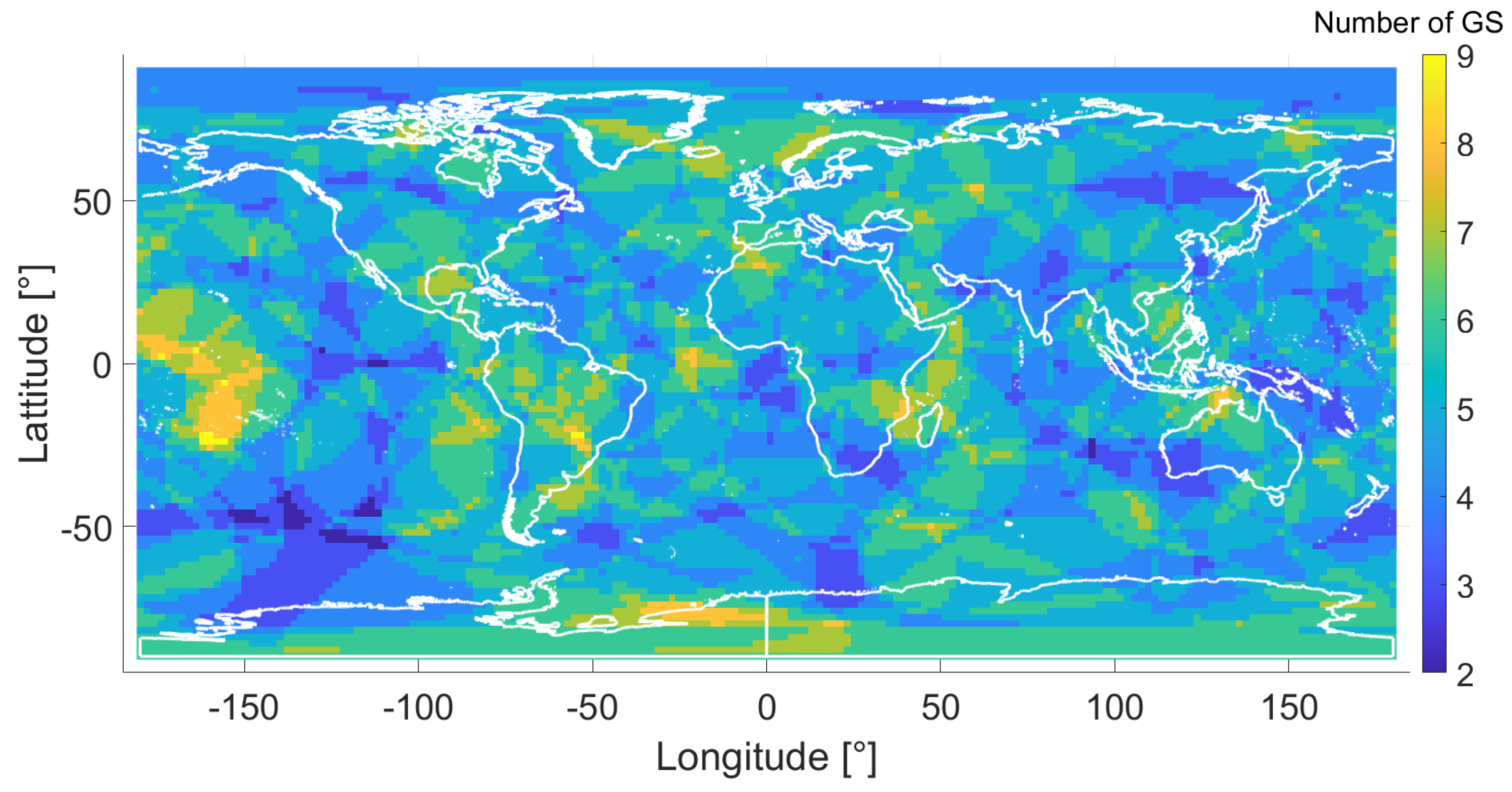
4.1. Global Deployment Optimization
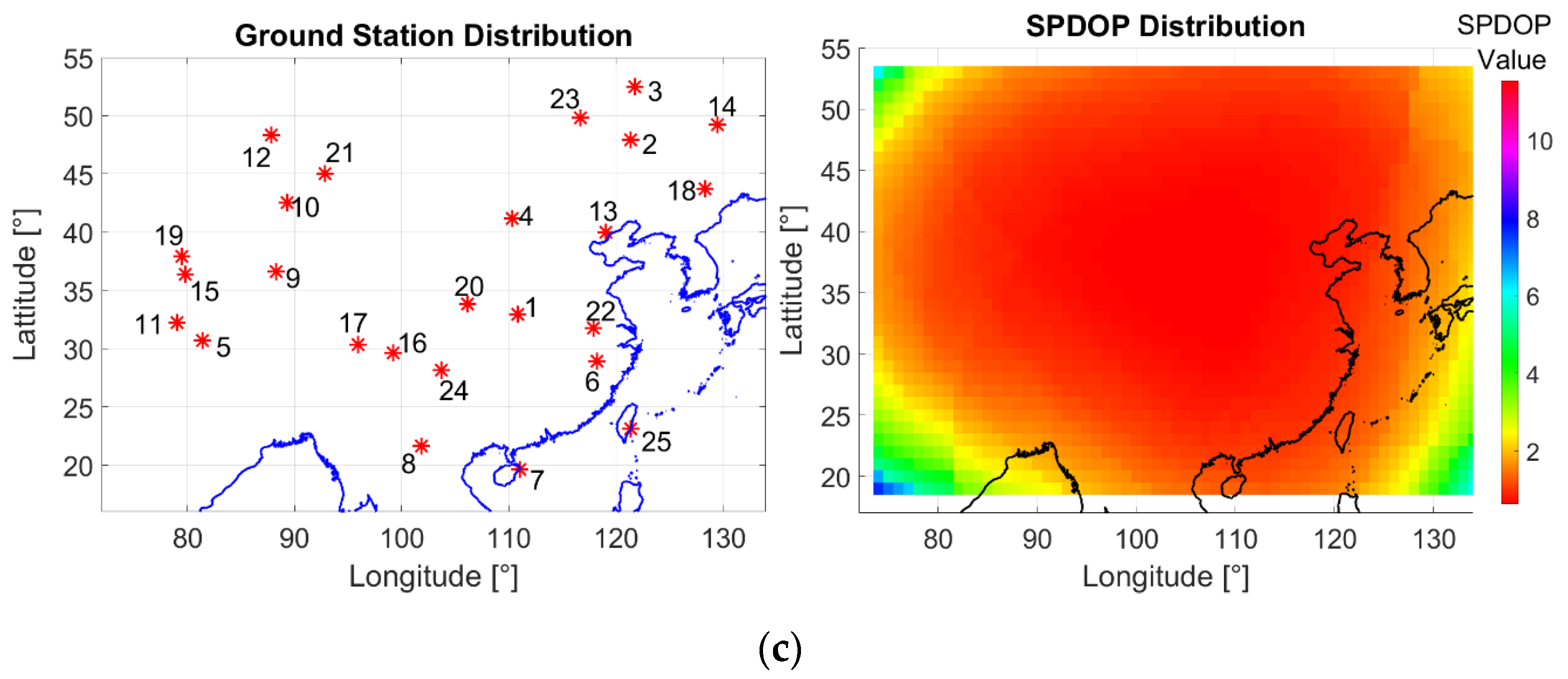
- SPDOP Distribution
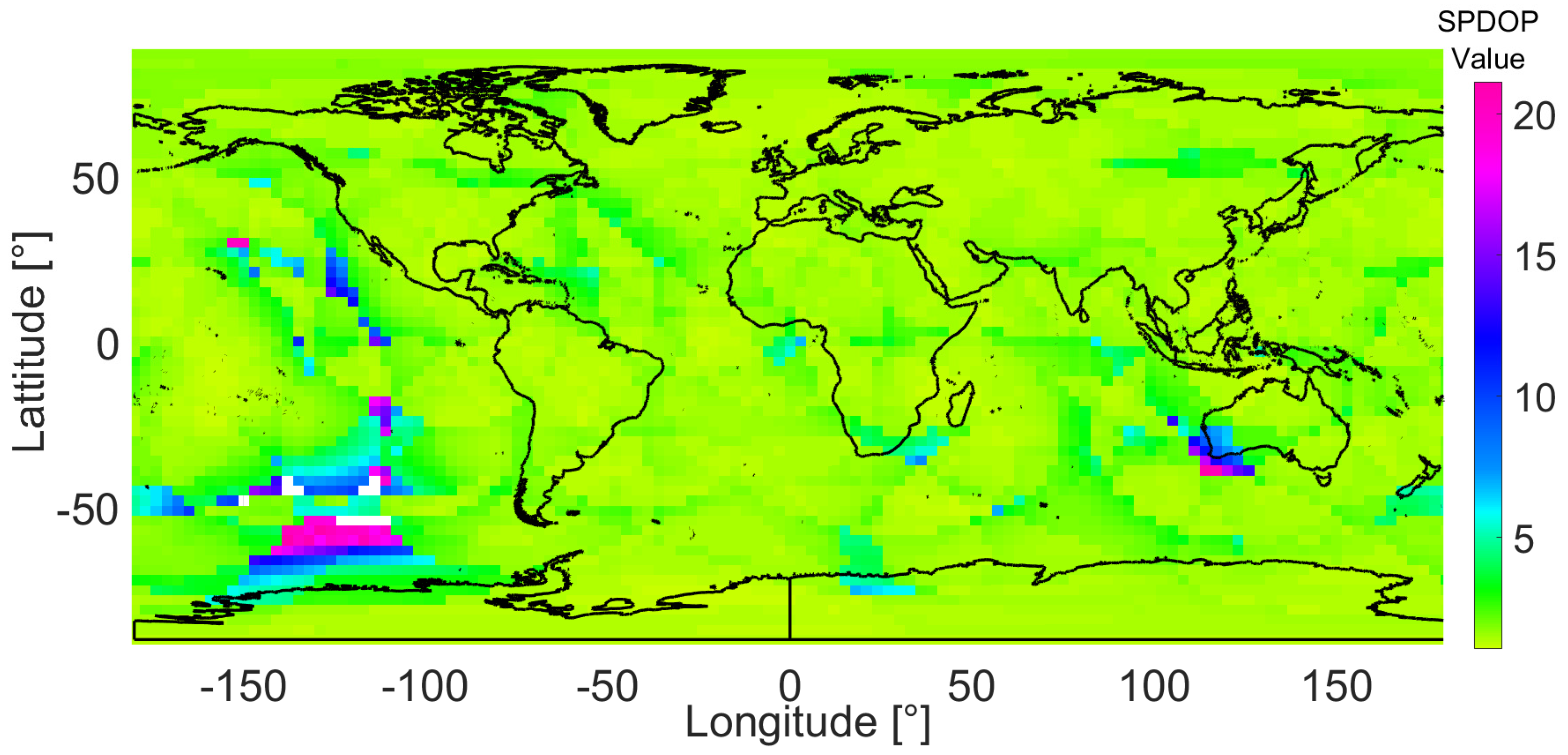
4.2. Regional Deployment Optimization
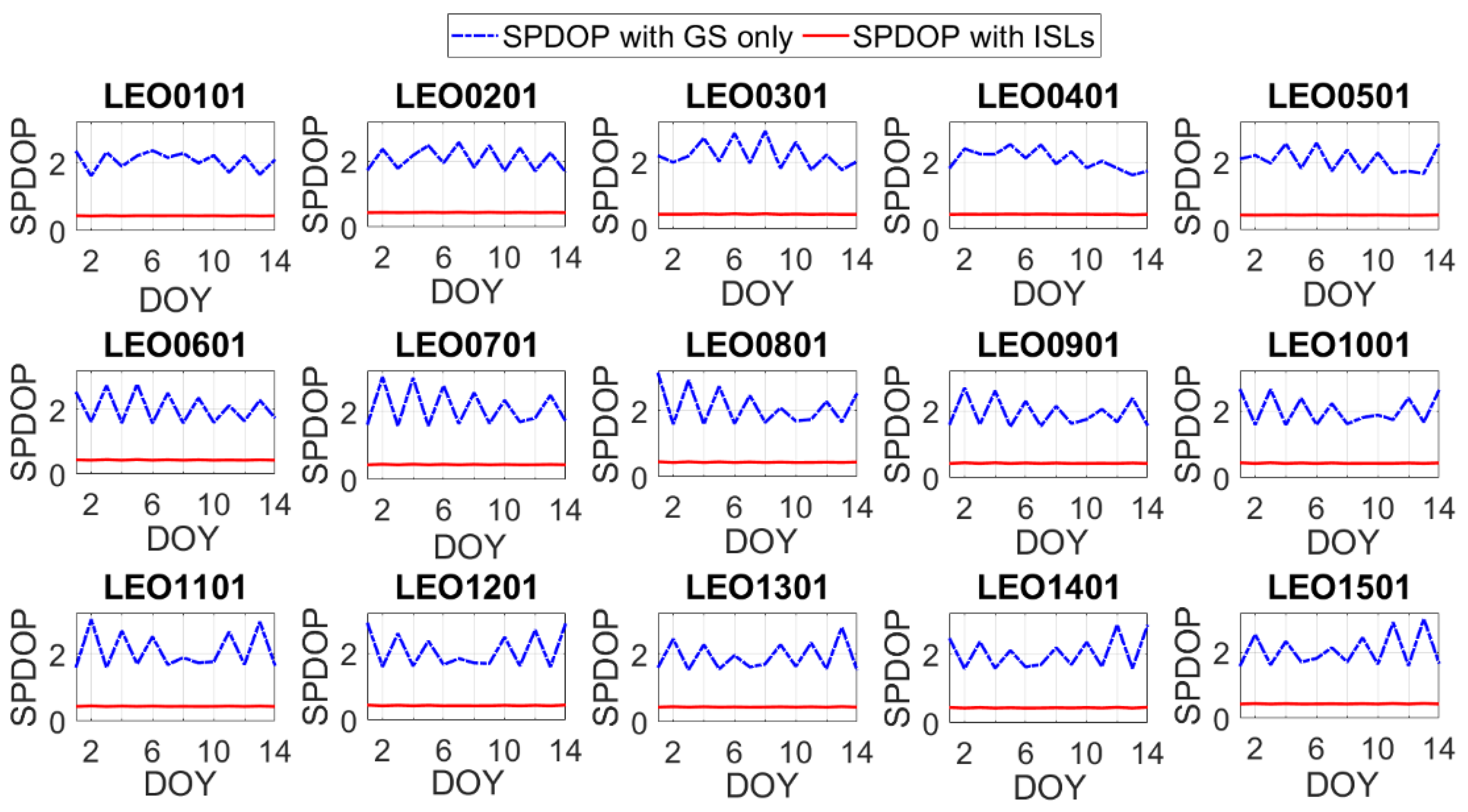
- SPDOP with Ground Stations and Intersatellite Links
5. Discussion
5.1. Global Deployment Optimization
5.2. Regional Deployment Optimization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Hybrid Method with Integration of Non-Dominated Sorting Genetic Algorithm-III (NSGA-III), Strength Pareto Evolutionary Algorithm-II (SPEA-II), and Multi-Objective Particle Swarm Optimization (MOPSO)
| Algorithm A1. Overall procedure of the hybrid method of evolutionary algorithms (HMEAs). | |
| Step 0 | Initialize the parameters of each algorithm NSGA-III, SPEA-II and MOPSO. |
| Step 1 | Generate a random population of N individuals, and evaluate the fitness. |
| Step 2 | Sort the population according to the ranking based on non-dominated solutions. |
| Step 3 | Truncate the population into three sub-populations of [N/3] individuals for each. |
| Step 4 | Fit each sub-population to the individual structure of the used algorithm, because the initialization used the NSGA-III individual structure. Submit each sub-population for processing to each algorithm: the first with NSGA-III, the second with SPEA-II and the last with MOPSO. |
| Step 5 | After each sub-population is processed in the corresponding population, fit to the NSGA-III individual structure and merge all sub-populations of [N/3] to the whole solution of N individuals. |
| Step 6 | Update the new archive with the truncation of the merged population after sorting according to the raw fitness of SPEA-II. |
| Step 7 | Check the number of generations it; if it > MaxIt? end optimization; else, it = it + 1, and go to Step 2. |
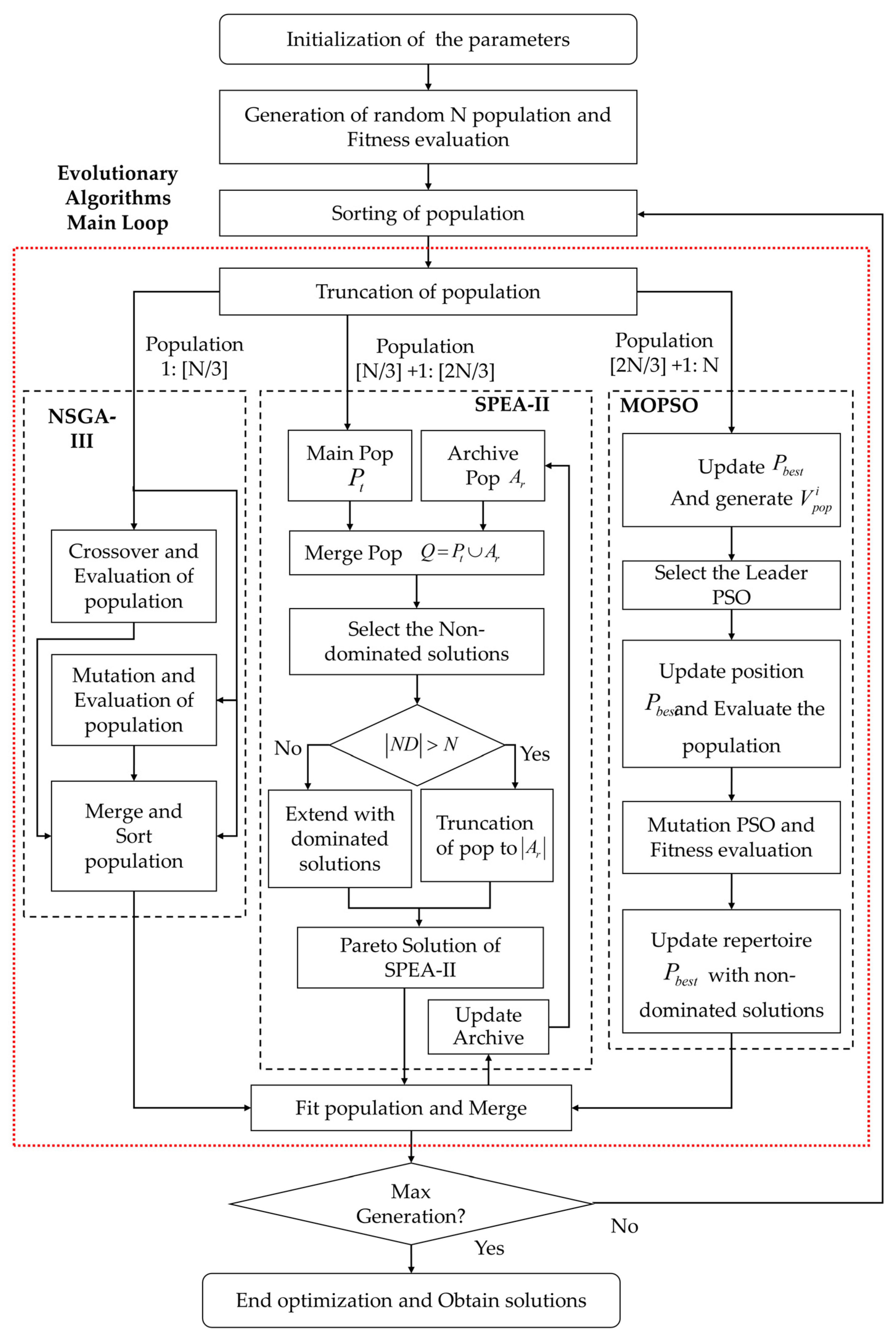
- Apply the operator of the crossover to a random number of crossover individuals , which is calculated by the probability of crossover of the NSGA-III parameter as .
- Apply the operator of the mutation to a random number of mutated individuals , which is calculated by the probability of mutation of the NSGA-III parameters as .
- Merge the main population and individuals that have undergone crossover and mutation to select the next new population by sorting based on ND solutions.
- Merge the main population and archive population, and after fitness evaluation, select the ND solutions based on the strength and raw operator.
- According to the number of individuals in ND solutions, extend the ND solutions by the dominant solution if the number of ND solutions is less than the archive size, or truncate the ND solutions if the size exceeds the archive size.
- The new population is the solution improved by SPEA-II, while the new archive is updated after merging all sub-populations.
- Update the best population and generate the velocity for each particle (individual), and the repertory is updated according to the non-dominated sorting solution of the sub-population.
- For each individual, select a leader from the repertory, and that particle should move toward its leader.
- Update the particle velocity after the selection of a leader; therefore, update the position and evaluate the individuals in the population.
- Apply the mutation according to the number of mutates for the MOPSO mutation parameter and evaluate the mutated individuals.
References
- Joerger, M.; Gratton, L.; Pervan, B.; Cohen, C.E. Analysis of Iridium-augmented GPS for floating carrier phase positioning. Navigation 2010, 57, 137–160. [Google Scholar] [CrossRef]
- Tan, Z.; Qin, H.; Cong, L.; Zhao, C. New method for positioning using IRIDIUM satellite signals of opportunity. IEEE Access 2019, 7, 83412–83423. [Google Scholar] [CrossRef]
- Ke, M.; Lv, J.; Chang, J.; Dai, W.; Tong, K.; Zhu, M. Integrating GPS and LEO to accelerate convergence time of precise point positioning. In Proceedings of the 2015 International Conference on Wireless Communications & Signal Processing (WCSP), Nanjing, China, 15–17 October 2015; pp. 1–5. [Google Scholar]
- Li, X.; Ma, F.; Li, X.; Lv, H.; Bian, L.; Jiang, Z.; Zhang, X. LEO constellation-augmented multi-GNSS for rapid PPP convergence. J. Geod. 2019, 93, 749–764. [Google Scholar] [CrossRef]
- Ge, H.; Li, B.; Nie, L.; Ge, M.; Schuh, H. LEO constellation optimization for LEO enhanced global navigation satellite system (LeGNSS). Adv. Space Res. 2020, 66, 520–532. [Google Scholar] [CrossRef]
- Li, M.; Xu, T.; Guan, M.; Gao, F.; Jiang, N. LEO-constellation-augmented multi-GNSS real-time PPP for rapid re-convergence in harsh environments. GPS Solut. 2021, 26, 29. [Google Scholar] [CrossRef]
- Nie, X.; Li, M.; Ma, F.; Wang, L.; Zhang, X. LEO Constellation Design Based on Dual Objective Optimization and Study on PPP Performance. In China Satellite Navigation Conference (CSNC 2021) 2021 Proceedings; Yang, C., Xie, J., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2021; Volume 773, pp. 197–207. [Google Scholar]
- Zhang, Y.; Li, Z.; Li, R.; Wang, Z.; Yuan, H.; Song, J. Orbital design of LEO navigation constellations and assessment of their augmentation to BDS. Adv. Space Res. 2020, 66, 1911–1923. [Google Scholar] [CrossRef]
- Han, Y.; Wang, L.; Fu, W.; Zhou, H.; Li, T.; Xu, B.; Chen, R. LEO navigation augmentation constellation design with the multi-objective optimization approaches. Chin. J. Aeronaut. 2021, 34, 265–278. [Google Scholar] [CrossRef]
- Yang, M.; Dong, X.; Hu, M. Design and simulation for hybrid LEO communication and navigation constellation. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; pp. 1665–1669. [Google Scholar]
- He, X.; Hugentobler, U. Design of Mega-Constellations of LEO Satellites for Positioning. In China Satellite Navigation Conference (CSNC 2018) 2018 Proceedings; Sun, J., Yang, C., Guo, S., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2018; Volume 497, pp. 663–673. [Google Scholar]
- Guan, M.; Xu, T.; Gao, F.; Nie, W.; Yang, H. Optimal walker constellation design of LEO-based global navigation and augmentation system. Remote Sens. 2020, 12, 1845. [Google Scholar] [CrossRef]
- Dvorkin, V.; Karutin, S. Optimization of the global network of tracking stations to provide GLONASS users with precision navigation and timing service. Gyroscopy Navig. 2013, 4, 181–187. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Dai, T.; Wang, L.; Wang, J. Real-time GPS satellite clock offset determination based on the TIN global station-selecting method. J. Geomat. Sci. Technol. 2017, 34, 441–444. [Google Scholar]
- Zhang, R.; Yang, Y.; Zhang, Q.; Huang, G.; Wang, L.; Qu, W.; Zhao, H. Optimal Estimation of Dynamic Parameters of BDS Orbit for Optimal Selection of Tracking Stations. J. Geod. Geodyn. 2016, 36, 216–220. [Google Scholar] [CrossRef]
- Shah Sadman, A.A.M.; Hossam-E-Haider, M. Study of GNSS Parameters and Environmental Factors over Bangladesh Intended for Selecting Ideal Ground Station Location for SBAS. In Proceedings of the 2021 2nd Global Conference for Advancement in Technology (GCAT), Bangalore, India, 1–3 October 2021; pp. 1–6. [Google Scholar]
- Yang, X.; Wang, Q.; Xue, S. Random optimization algorithm on GNSS monitoring stations selection for ultra-rapid orbit determination and real-time satellite clock offset estimation. Math. Probl. Eng. 2019, 2019, 7579185. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Q.; Huang, G.; Wang, L.; Qu, W. Impact of tracking station distribution structure on BeiDou satellite orbit determination. Adv. Space Res. 2015, 56, 2177–2187. [Google Scholar] [CrossRef]
- Zhang, R.; Tu, R.; Zhang, P.; Fan, L.; Han, J.; Wang, S.; Hong, J.; Lu, X. Optimization of ground tracking stations for BDS-3 satellite orbit determination. Adv. Space Res. 2021, 68, 4069–4087. [Google Scholar] [CrossRef]
- Zhang, R.; Tu, R.; Zhang, P.; Fan, L.; Han, J.; Lu, X. Orbit determination of BDS-3 satellite based on regional ground tracking station and inter-satellite link observations. Adv. Space Res. 2021, 67, 4011–4024. [Google Scholar] [CrossRef]
- Liu, X.; Ge, Y.; Zhao, C.; Li, B.; Zhou, R. A Study on Global Monitoring Station Optimization Deployment Method Based on Navigation Satellite Quadruple Observing Coverage. In Proceedings of the 2021 International Conference on Communications, Information System and Computer Engineering (CISCE), Beijing, China, 14–16 May 2021; pp. 394–399. [Google Scholar]
- Kopacz, J.; Roney, J.; Herschitz, R. Optimized ground station placement for a mega constellation using a genetic algorithm. In Proceedings of the 33rd Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 3–8 August 2019; p. SSC19-WP11-05. [Google Scholar]
- Carlton-Wippern, K.C. Satellite Position Dilution of Precision (SPDOP). In Proceedings of the 1997 AAS/AIAA Astrodynamics Specialist Conference, Sun Valley, ID, USA, 4–7 August 1997; pp. 133–146. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Ge, H.; Li, B.; Ge, M.; Shen, Y.; Schuh, H. Improving BeiDou precise orbit determination using observations of onboard MEO satellite receivers. J. Geod. 2017, 91, 1447–1460. [Google Scholar] [CrossRef]
- Wu, F.; Kubo, N.; Yasuda, A. Performance Evaluation of GPS Augmentation Using Quasi-Zenith Satellite System. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1249–1261. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Zhang, R.; Tu, R.; Fan, L.; Zhang, P.; Liu, J.; Han, J.; Lu, X. Contribution analysis of inter-satellite ranging observation to BDS-2 satellite orbit determination based on regional tracking stations. Acta Astronaut. 2019, 164, 297–310. [Google Scholar] [CrossRef]
- Kur, T.; Liwosz, T.; Kalarus, M. The application of inter-satellite links connectivity schemes in various satellite navigation systems for orbit and clock corrections determination: Simulation study. Acta Geod. Geophys. 2021, 56, 1–28. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Y.; Hu, X.; Chen, J.; Guo, R.; Tang, C.; Zhou, S.; Zhao, L.; Xu, J. Inter-satellite link enhanced orbit determination for BeiDou-3. J. Navig. 2020, 73, 115–130. [Google Scholar] [CrossRef]
- Xie, X.; Geng, T.; Zhao, Q.; Cai, H.; Zhang, F.; Wang, X.; Meng, Y. Precise orbit determination for BDS-3 satellites using satellite-ground and inter-satellite link observations. GPS Solut. 2019, 23, 40. [Google Scholar] [CrossRef]
- He, X.; Hugentobler, U.; Schlicht, A.; Nie, Y.; Duan, B. Precise orbit determination for a large LEO constellation with inter-satellite links and the measurements from different ground networks: A simulation study. Satell. Navig. 2022, 3, 22. [Google Scholar] [CrossRef]
- NOAA. National Oceanic and Atmospheric Administration. Available online: www.ngdc.noaa.gov (accessed on 10 August 2023).
- Heris, M.K. NSGA-III: Non-dominated Sorting Genetic Algorithm, the Third Version—MATLAB Implementation. Yarpiz. 2016. Available online: https://yarpiz.com/456/ypea126-nsga3 (accessed on 15 April 2023).
- Mostapha, K.H. Strength Pareto Evolutionary Algorithm 2 (SPEA2). Available online: https://www.mathworks.com/matlabcentral/fileexchange/52871-strength-pareto-evolutionary-algorithm-2-spea2 (accessed on 20 September 2023).
- Víctor, M.-C. Multi-Objective Particle Swarm Optimization (MOPSO). Available online: https://www.mathworks.com/matlabcentral/fileexchange/62074-multi-objective-particle-swarm-optimization-mopso (accessed on 11 August 2023).





| Variables | Min Number of GSs () | Max Number of GSs () | Longitudes [°] | Latitudes [°] |
|---|---|---|---|---|
| Value | 60 | 150 | 180W~180E | 85S~85N |
| Algorithm | Parameter | Value |
|---|---|---|
| Non-dominated sorting genetic algorithm-III (NSGA-III) | Crossover probability | 0.8 |
| Mutation probability | 0.2 | |
| Mutation rate | 0.05 | |
| Multi-objective particle swarm optimization (MOPSO) | Inertia weight | 0.4 |
| Damping rate | 0.5 | |
| Inflation rate | 0.5 | |
| Mutation rate | 0.1 | |
| Personal learning | 1 | |
| Global learning | 2 | |
| Strength Pareto evolutionary algorithm-II (SPEA-II) | Crossover probability | 0.5 |
| Mutation probability | 0.5 | |
| Number archive to population ratio | 1/3 |
| Coordinates | Longitude [°] | Latitude [°] |
|---|---|---|
| Value | 75E~135E | 17N~55N |
| Scenario Case | 1 | 2 | 3 |
|---|---|---|---|
| Number of GSs used | 15 | 20 | 25 |
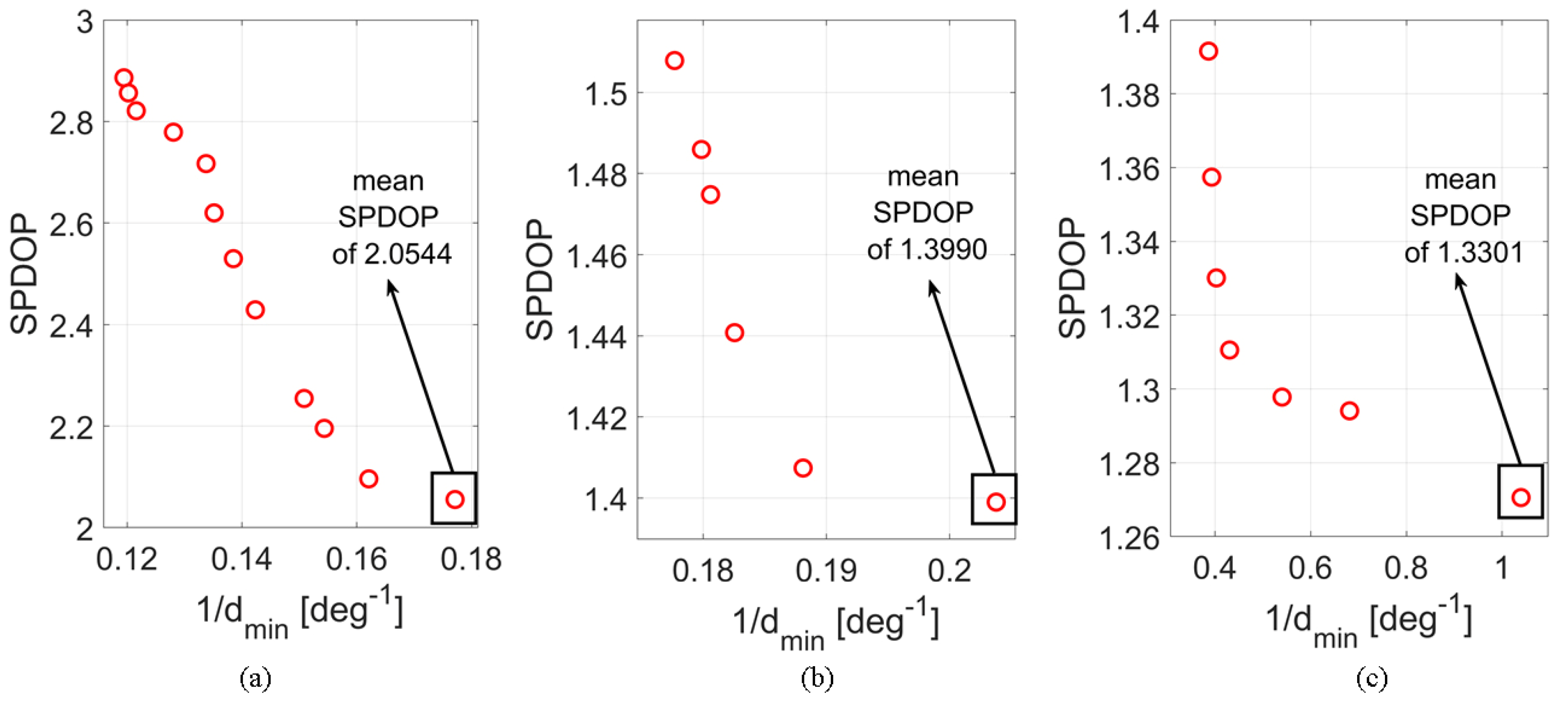
| Scenario | Mean SPDOP | Max SPDOP | Std of SPDOP |
|---|---|---|---|
| 15 GSs | 2.0544 | 11.5266 | 0.7973 |
| 20 GSs | 1.3990 | 9.0000 | 0.4701 |
| 25 GSs | 1.3301 | 7.5696 | 0.4687 |
| Scheme | Mean SPDOP | Std SPDOP | Observation |
|---|---|---|---|
| Scheme 1 | 207.97 | 189.43 | 30 GSs (focus on Eastern hemisphere) |
| Scheme 2 | 149.43 | 126.17 | 30 GSs (globally distributed) |
| Deployment | Parameters | Mean SPDOP | Max SPDOP | Min SPDOP |
|---|---|---|---|---|
| 15 GSs | GSs only | 2.058 | 3.143 | 1.516 |
| GSs and ISLs | 0.439 | 0.453 | 0.435 | |
| 20 GSs | GSs only | 1.403 | 2.063 | 1.077 |
| GSs and ISLs | 0.422 | 0.437 | 0.409 | |
| 25 GSs | GSs only | 1.330 | 1.945 | 1.011 |
| GSs and ISLs | 0.409 | 0.425 | 0.396 |
| Parameters | Max | Min | Mean | Std |
|---|---|---|---|---|
| Value | 64 | 37 | 51.43 | 8.68 |
| Parameter | Single-Heavy Observing Coverage 1-HC | Double-Heavy Observing Coverage 2-HC | Triple-Heavy Observing Coverage 3-HC | Quadruple-Heavy Observing Coverage 4-HC |
|---|---|---|---|---|
| Value | 100% | 100% | 97.37% | 92.01% |
| Satellite’s Orbit | GEO | IGSO | MEO | LEO |
| Mean SPDOP with GSs only | 475.72 | 354.27 | 185.10 | 2.06 |
| Std of SPDOP | 2.57 | 136.27 | 148.65 | 0.79 |
| Mean SPDOP with GSs + ISLs | 12.00 | 2.12 | 2.67 | 0.44 |
| Std of SPDOP | 0.75 | 0.91 | 1.34 | 0.09 |
| Reference | [29] | / | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kralfallah, M.; Wu, F.; Tahir, A.; Oubara, A.; Sui, X. Optimizing the Deployment of Ground Tracking Stations for Low Earth Orbit Satellite Constellations Based on Evolutionary Algorithms. Remote Sens. 2024, 16, 810. https://doi.org/10.3390/rs16050810
Kralfallah M, Wu F, Tahir A, Oubara A, Sui X. Optimizing the Deployment of Ground Tracking Stations for Low Earth Orbit Satellite Constellations Based on Evolutionary Algorithms. Remote Sensing. 2024; 16(5):810. https://doi.org/10.3390/rs16050810
Chicago/Turabian StyleKralfallah, Mansour, Falin Wu, Afnan Tahir, Amel Oubara, and Xiaohong Sui. 2024. "Optimizing the Deployment of Ground Tracking Stations for Low Earth Orbit Satellite Constellations Based on Evolutionary Algorithms" Remote Sensing 16, no. 5: 810. https://doi.org/10.3390/rs16050810
APA StyleKralfallah, M., Wu, F., Tahir, A., Oubara, A., & Sui, X. (2024). Optimizing the Deployment of Ground Tracking Stations for Low Earth Orbit Satellite Constellations Based on Evolutionary Algorithms. Remote Sensing, 16(5), 810. https://doi.org/10.3390/rs16050810






