The Extreme Rainfall Events of the 2020 Typhoon Season in Vietnam as Seen by Seven Different Precipitation Products
Abstract
1. Introduction
2. Data
- Ground-based instruments: this includes rain gauges obtained from automatic weather stations and weather radars.
- Precipitation estimations from geostationary satellites (GEO): the study utilizes data from the Advanced Geo-synchronous Radiation Imager (AGRI) on board the Chinese FengYun-4A satellite and the Advanced Meteorological Imager (AMI) on board the South Korean GEO-KOMPSAT-2A satellite.
- Precipitation estimation from a space-borne radar on a low Earth orbit (LEO) platform: the Dual-frequency Precipitation Radar on board the NASA-JAXA GPM-CO satellite.
- Multi-satellite products with different levels of calibration and latency: specifically, the Integrated Multi-satellitE Retrievals for GPM (IMERG) Early and Final runs.
- Model reanalysis: the “Total precipitation” variable of the ERA5-Land product by ECMWF (European Centre for Medium-Range Weather Forecasts).
2.1. Ground Reference Data: Automatic Rain Gauge Stations
2.2. Ground Weather Radar Precipitation Product
2.3. Space-Borne Radar Product: GPM-DPR
2.4. Geostationary Satellite-Based Products: GEO-KOMPSAT-2A and FengYun-4A
2.4.1. GEO-KOMPSAT-2A
2.4.2. FengYun-4A
2.5. Multi-Satellite Products and Model Reanalysis: IMERG and ERA5-Land
2.5.1. IMERG
2.5.2. ERA5-Land
2.6. Study Period: Heavy Rainfall Events between August and November 2020
2.7. Data Availability and Coverage
3. Methods
3.1. A Shared Spatial Grid for a Multi-Platform Analysis
3.2. Towards a Uniform Dataset: Products Intersection
3.3. Error Metrics
3.3.1. Categorical Indices
3.3.2. Continuous Indices
4. Results
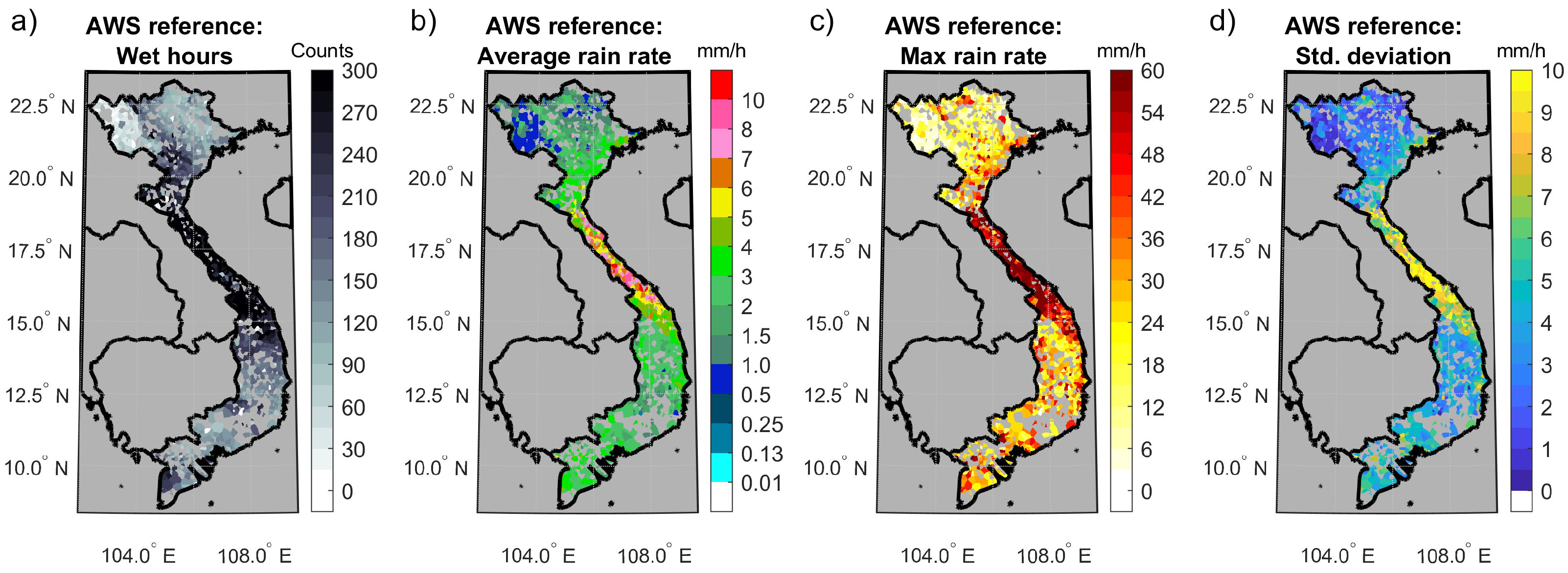
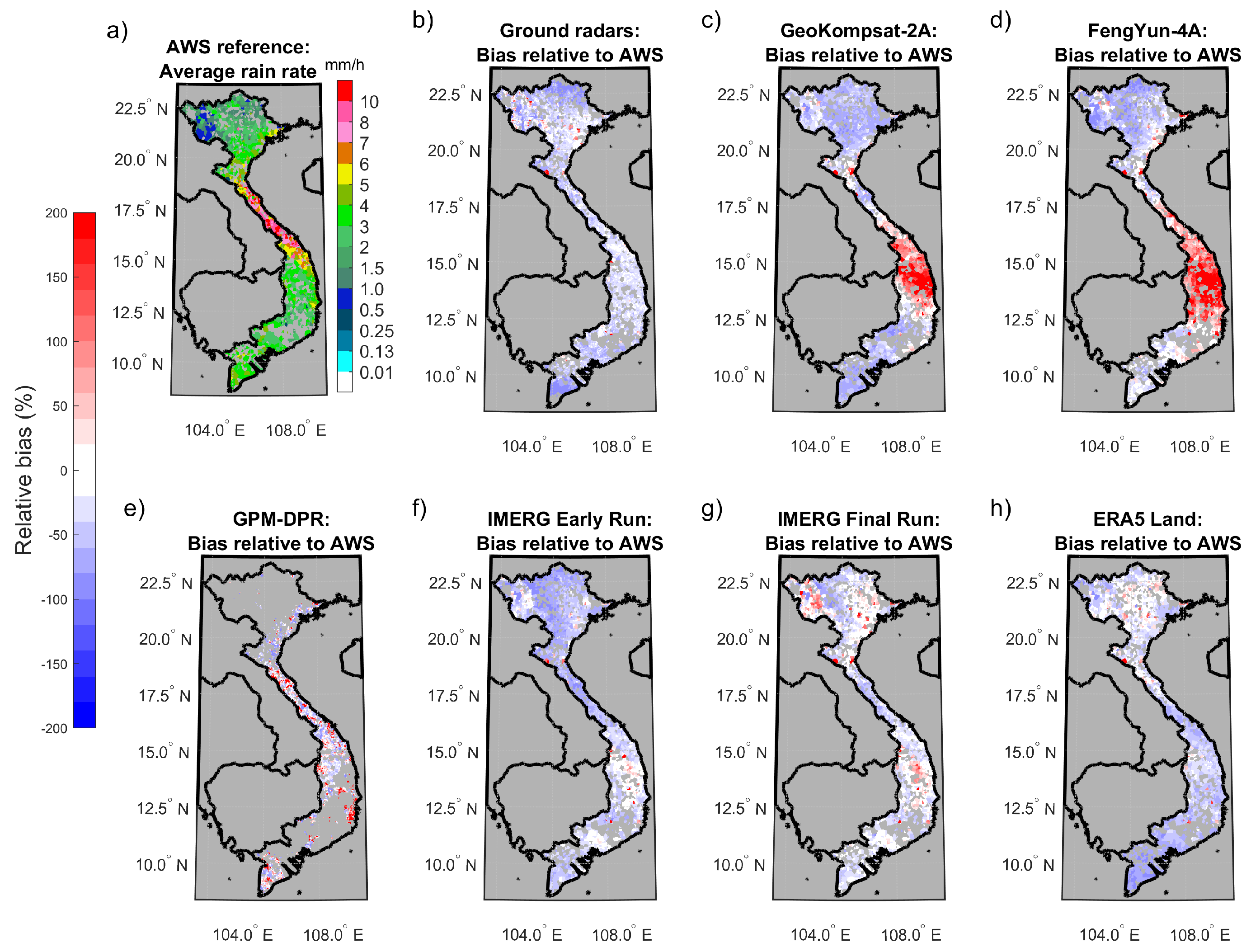
4.1. Spatial Distribution of Average Values
4.2. Rainfall Area Detection
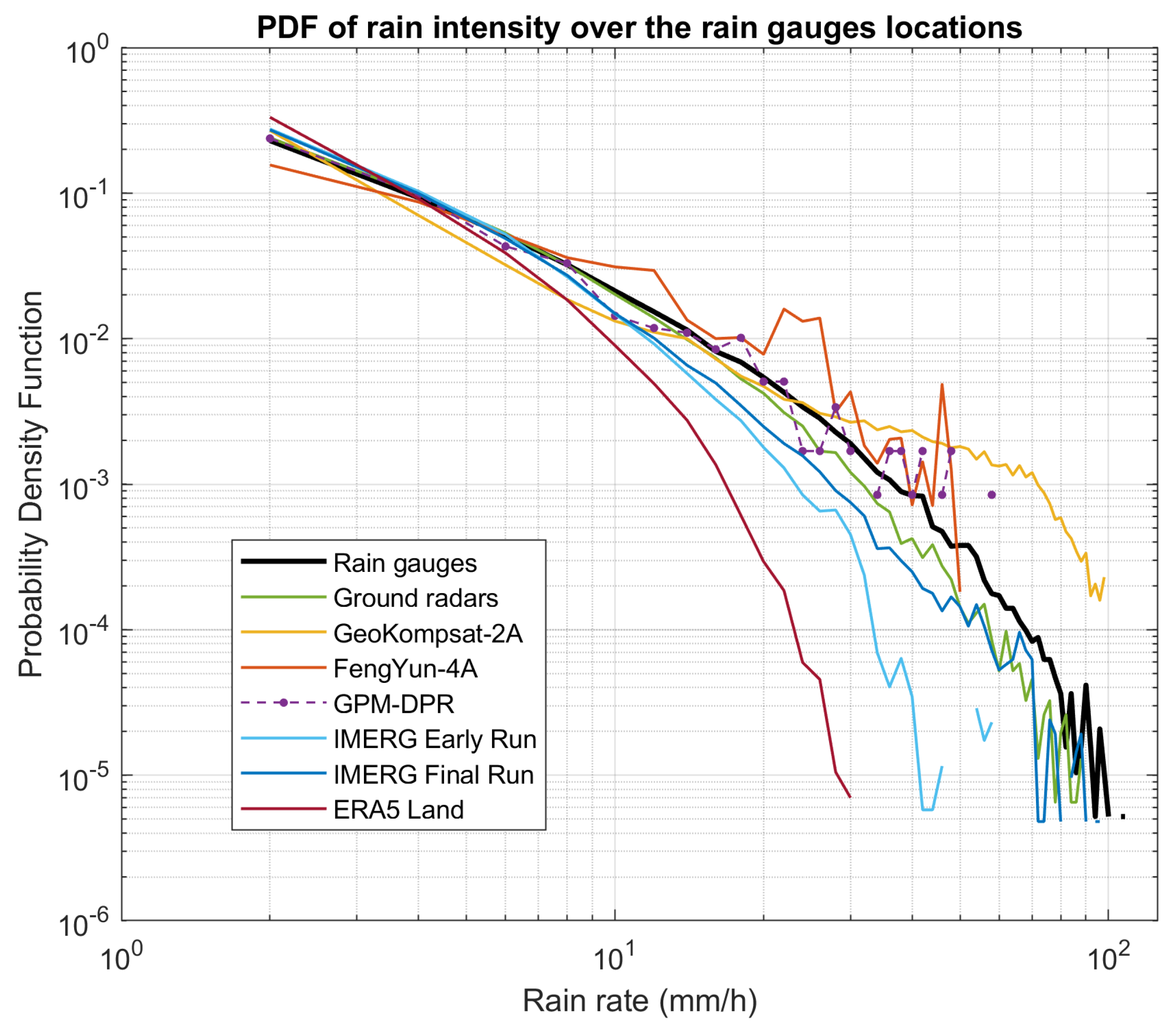
4.3. Overall Distribution of the Estimated Rain Rates
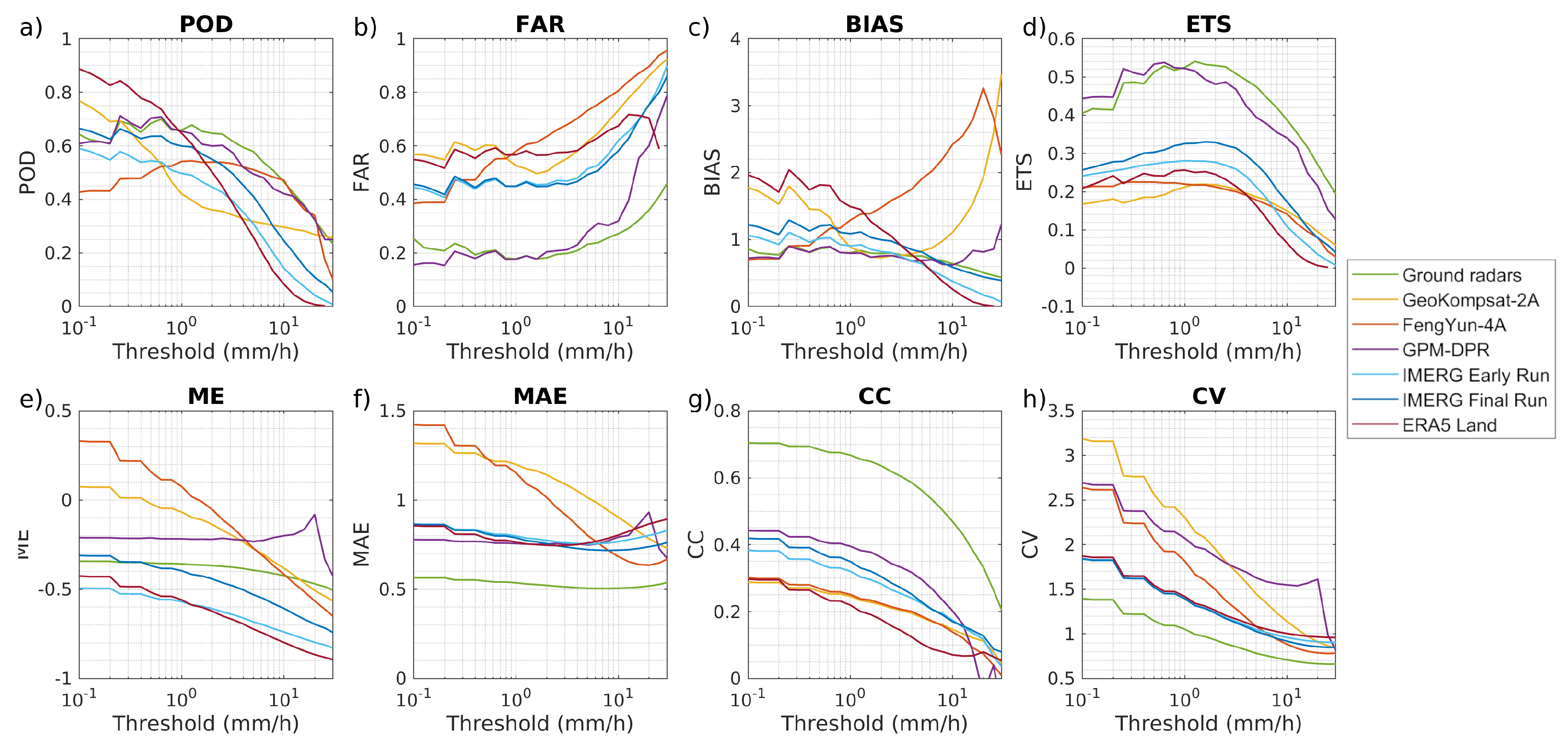
4.4. High-Resolution Rain Rate Estimates
Other Metrics: mKGE and P50
4.5. Sensitivity Analysis
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AGRI | Advanced Geosynchronous Radiation Imager |
| AMI | Advanced Meteorological Imager |
| AWS | Automatic Weather Station |
| mBIAS | Multiplicative bias (categorical) |
| CC | Correlation Coefficient |
| CHIRPS | Climate Hazards Group InfraRed Precipitation with Station data |
| CMORPH | Climate Prediction Center Morphing Technique |
| CSI | Critical Success Index |
| DPR | Dual-frequency Precipitation Radar (active sensor) |
| ECMWF | European Centre for Medium-range Weather Forecasts |
| ERA5-Land | ECMWF ReAnalysis ver. 5 |
| ETS | Equitable Threat Score |
| FAR | False Alarm Ratio |
| FY-4A | Fengyun 4A |
| GEO | Geostationary Earth orbit |
| GK-2A | GEO-KOMPSAT-2A |
| GPCC | Global Precipitation Climatology Centre |
| GPM | Global Precipitation Mission |
| GPM-CO | Global Precipitation Mission Core Observatory |
| GSMaP | Global Satellite Mapping of Precipitation |
| IMERG | Integrated Multi-satellitE Retrievals, version 06 |
| IR | Infra-Red passive sensor |
| JAXA | Japan Aerospace Exploration Agency |
| JMA | Japan Meteorological Agency |
| JWA | Japan Weather Association |
| KMA | Korean Meteorological Administration |
| LEO | Low Earth Orbit |
| MAE | Mean Absolute Error |
| ME | Mean Error or relative bias |
| mKGE | Modified Kling–Gupta Efficiency |
| MW | MicroWave passive sensor |
| NASA | National Aeronautics and Space Administration |
| NCN | National Centre for Hydro-Meteorological Network |
| NRT | Near Real-Time |
| P50 | Probability to find the estimate inside 50% of the observation |
| POD | Probability Of Detection |
| QPE | Quantitative Precipitation Estimation |
| RG | Rain Gauge |
| RMSD | Root Mean Square Deviation |
| TRMM | Tropical Rainfall Measuring Mission |
| VNMHA | The Vietnam Meteorological and Hydrological Administration |
References
- Luu, L.N.; Scussolini, P.; Kew, S.; Philip, S.; Hariadi, M.H.; Vautard, R.; Van Mai, K.; Van Vu, T.; Truong, K.B.; Otto, F.; et al. Attribution of typhoon-induced torrential precipitation in Central Vietnam, October 2020. Clim. Chang. 2021, 169, 24. [Google Scholar] [CrossRef]
- Ortiz-Vargas, A.; Sebesvari, Z. Technical Report: Floods in Central Viet Nam. In Interconnected Disaster Risks 2020/2021; United Nations University-Institute for Environment and Human Security (UNU-EHS): Bonn, Germany, 2021. [Google Scholar] [CrossRef]
- Puca, S.; Porcu’, F.; Rinollo, A.; Vulpiani, G.; Baguis, P.; Balabanova, S.; Campione, E.; Ertürk, A.; Gabellani, S.; Iwanski, R.; et al. The validation service of the hydrological SAF geostationary and polar satellite precipitation products. Nat. Hazards Earth Syst. Sci. 2014, 14, 871–889. [Google Scholar] [CrossRef]
- Schwaller, M.R.; Morris, K.R. A Ground Validation Network for the Global Precipitation Measurement Mission. J. Atmos. Ocean. Technol. 2011, 28, 301–319. [Google Scholar] [CrossRef]
- Kidd, C.; Shige, S.; Vila, D.; Tarnavsky, E.; Yamamoto, M.K.; Maggioni, V.; Maseko, B. The IPWG Satellite Precipitation Validation 17 Effort. In Satellite Precipitation Measurement: Volume 2; Springer International Publishing: Cham, Switzerland, 2020; pp. 453–470. [Google Scholar] [CrossRef]
- Dos Reis, J.B.C.; Rennó, C.D.; Lopes, E.S.S. Validation of Satellite Rainfall Products over a Mountainous Watershed in a Humid Subtropical Climate Region of Brazil. Remote Sens. 2017, 9, 1240. [Google Scholar] [CrossRef]
- Deo, A.; Munchak, S.J.; Walsh, K.J.E. Cross Validation of Rainfall Characteristics Estimated from the TRMM PR, a Combined PR–TMI Algorithm, and a C-POL Ground Radar during the Passage of Tropical Cyclone and Nontropical Cyclone Events over Darwin, Australia. J. Atmos. Ocean. Technol. 2018, 35, 2339–2358. [Google Scholar] [CrossRef] [PubMed]
- Dandridge, C.; Lakshmi, V.; Bolten, J.; Srinivasan, R. Evaluation of Satellite-Based Rainfall Estimates in the Lower Mekong River Basin (Southeast Asia). Remote Sens. 2019, 11, 2709. [Google Scholar] [CrossRef]
- Stephens, C.M.; Pham, H.T.; Marshall, L.A.; Johnson, F.M. Which Rainfall Errors Can Hydrologic Models Handle? Implications for Using Satellite-Derived Products in Sparsely Gauged Catchments. Water Resour. Res. 2022, 58, e2020WR029331. [Google Scholar] [CrossRef]
- Gummadi, S.; Dinku, T.; Shirsath, P.B.; Kadiyala, M.D.M. Evaluation of multiple satellite precipitation products for rainfed maize production systems over Vietnam. Sci. Rep. 2022, 12, 485. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.H.; Masih, I.; Mohamed, Y.A.; Van der Zaag, P. Validating Rainfall-Runoff Modelling Using Satellite-Based and Reanalysis Precipitation Products in the Sre Pok Catchment, the Mekong River Basin. Geosciences 2018, 8, 164. [Google Scholar] [CrossRef]
- Mohammed, I.N.; Bolten, J.D.; Srinivasan, R.; Lakshmi, V. Satellite observations and modeling to understand the Lower Mekong River Basin streamflow variability. J. Hydrol. 2018, 564, 559–573. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Win, K.W.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Assessment of GPM and TRMM Multi-Satellite Precipitation Products in Streamflow Simulations in a Data-Sparse Mountainous Watershed in Myanmar. Remote Sens. 2017, 9, 302. [Google Scholar] [CrossRef]
- Gunathilake, M.B.; Zamri, M.N.M.; Alagiyawanna, T.P.; Samarasinghe, J.T.; Baddewela, P.K.; Babel, M.S.; Jha, M.K.; Rathnayake, U.S. Hydrologic Utility of Satellite-Based and Gauge-Based Gridded Precipitation Products in the Huai Bang Sai Watershed of Northeastern Thailand. Hydrology 2021, 8, 165. [Google Scholar] [CrossRef]
- Xia, X.; Liu, Y.; Jing, W.; Yao, L. Assessment of Four Satellite-Based Precipitation Products Over the Pearl River Basin, China. IEEE Access 2021, 9, 97729–97746. [Google Scholar] [CrossRef]
- Li, R.; Shi, J.; Ji, D.; Zhao, T.; Plermkamon, V.; Moukomla, S.; Kuntiyawichai, K.; Kruasilp, J. Evaluation and Hydrological Application of TRMM and GPM Precipitation Products in a Tropical Monsoon Basin of Thailand. Water 2019, 11, 818. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Soe, K.M.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Applications of TRMM- and GPM-Era Multiple-Satellite Precipitation Products for Flood Simulations at Sub-Daily Scales in a Sparsely Gauged Watershed in Myanmar. Remote Sens. 2019, 11, 140. [Google Scholar] [CrossRef]
- Trinh-Tuan, L.; Matsumoto, J.; Ngo-Duc, T.; Nodzu, M.I.; Inoue, T. Evaluation of satellite precipitation products over Central Vietnam. Prog. Earth Planet. Sci. 2019, 6, 54. [Google Scholar] [CrossRef]
- Mohsan, M.; Acierto, R.A.; Kawasaki, A.; Zin, W.W. Preliminary Assessment of GPM Satellite Rainfall over Myanmar. J. Disaster Res. 2018, 13, 22–30. [Google Scholar] [CrossRef]
- Luong, B.N.; Van, Q.D. Accuracy of Integrated Multi-SatelliE Retrievals for GPM Satellite Rainfall Product over North Vietnam. Pol. J. Environ. Stud. 2021, 30, 5657–5667. [Google Scholar] [CrossRef]
- Nodzu, M.I.; Jun, M.; Long, T.T.; Ngo-Duc, T. Precipitation estimation performance by Global Satellite Mapping and its dependence on wind over northern Vietnam. Prog. Earth Planet. Sci. 2019, 6, 58. [Google Scholar] [CrossRef]
- Le, H.M.; Sutton, J.R.P.; Bui, D.D.; Bolten, J.D.; Lakshmi, V. Comparison and Bias Correction of TMPA Precipitation Products over the Lower Part of Red–Thai Binh River Basin of Vietnam. Remote Sens. 2018, 10, 1582. [Google Scholar] [CrossRef]
- Hai, B.T.; Tuan, N.V. Nghiên cứu đánh giá và so sánh các đữ liệu mưa vệ tinh độ phân giải cao lưu vực sông Cả. Vietnam J. Hydrometeorol. 2018, 11, 695. Available online: https://vjol.info.vn/index.php/TCKHTV/article/view/59946 (accessed on 9 November 2023).
- Le, M.H.; Lakshmi, V.; Bolten, J.; Bui, D.D. Adequacy of Satellite-derived Precipitation Estimate for Hydrological Modeling in Vietnam Basins. J. Hydrol. 2020, 586, 124820. [Google Scholar] [CrossRef]
- Tran, T.N.D.; Le, M.H.; Zhang, R.; Nguyen, B.Q.; Bolten, J.D.; Lakshmi, V. Robustness of gridded precipitation products for vietnam basins using the comprehensive assessment framework of rainfall. Atmos. Res. 2023, 293, 106923. [Google Scholar] [CrossRef]
- Petracca, M.; D’Adderio, L.P.; Porcu’, F.; Vulpiani, G.; Sebastianelli, S.; Puca, S. Validation of GPM Dual-Frequency Precipitation Radar (DPR) Rainfall Products over Italy. J. Hydrometeorol. 2018, 19, 907–925. [Google Scholar] [CrossRef]
- Yin, G.; Baik, J.; Park, J. Comprehensive analysis of GEO-KOMPSAT-2A and FengYun satellite-based precipitation estimates across Northeast Asia. GIScience Remote Sens. 2022, 59, 782–800. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated Multi-satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement: Volume 1; Springer International Publishing: Cham, Switzerland, 2020; pp. 343–353. [Google Scholar] [CrossRef]
- Muñoz Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Muñoz Sabater, J. ERA5-Land Hourly Data from 1950 to Present; Copernicus Climate Change Service (C3S) Climate Data Store (CDS), 2019; Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.e2161bac?tab=overview (accessed on 9 November 2023). [CrossRef]
- Makihara, Y. A Method for Improving Radar Estimates of Precipitation by Comparing Data from Radars and Raingauges. J. Meteorol. Soc. Jpn. Ser. II 1996, 74, 459–480. [Google Scholar] [CrossRef]
- Kimpara, C.; Tonouchi, M.; Hoa, B.T.K.; Hung, N.V.; Cuong, N.M.; Akaeda, K. Quantitative Precipitation Estimation by Combining Rain gauge and Meteorological Radar Network in Viet Nam. VN J. Hydrometeorol. 2020, 5, 36–50. [Google Scholar] [CrossRef]
- Iguchi, T.; Seto, S.; Meneghini, R.; Yoshida, N.; Awaka, J.; Le, M.; Chandrasekar, V.; Brodzik, S.; Kubota, T.; Takahashi, N. GPM/DPR Level-2 Algorithm Theoretical Basis Document; NASA GPM, 2021. Available online: https://gpm.nasa.gov/sites/default/files/2022-06/ATBD_DPR_V07A.pdf (accessed on 3 November 2023).
- Hirose, H.; Shige, S.; Yamamoto, M.K.; Higuchi, A. High Temporal Rainfall Estimations from Himawari-8 Multiband Observations Using the Random-Forest Machine-Learning Method. J. Meteorol. Soc. Jpn. Ser. II 2019, 97, 2019–2040. [Google Scholar] [CrossRef]
- Shin, D.; Seo, D.; Kim, D. Algorithm Theoretical Basis Document, Rainfall Intensity; National Meteorological Satellite Center, Korea Meteorological Administration, 2019; Available online: http://210.125.45.70/resources/common/pdf/GK2A_ATBD_RR_KOR_v1.0.pdf (accessed on 9 November 2023).
- Yang, J.; Zhang, Z.; Wei, C.; Lu, F.; Guo, Q. Introducing the New Generation of Chinese Geostationary Weather Satellites, Fengyun-4. Bull. Am. Meteorol. Soc. 2017, 98, 1637–1658. [Google Scholar] [CrossRef]
- NSMC-DataService. Spectral Response Parameters of FY-4A Satellite; National Satellite Meteorological Center, China Meteorological Administration, 2018; Available online: http://img.nsmc.org.cn/PORTAL/NSMC/DATASERVICE/SRF/FY4A/FY4A_AGRI_SRF_20180306.pdf (accessed on 9 November 2023).
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-SatellitE Retrievals for GPM (IMERG), Algorithm Theoretical Basis Document (ATBD) Version 06; NASA GPM, 2020. Available online: https://gpm.nasa.gov/sites/default/files/2020-05/IMERG_ATBD_V06.3.pdf (accessed on 9 November 2023).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Nguyen, Q.; Renwick, J.; Mcgregor, J. Variations of surface temperature and rainfall in Vietnam from 1971 to 2010. Int. J. Climatol. 2014, 34, 249–264. [Google Scholar] [CrossRef]
- Nurmi, P. Recommendations on the verification of local weather forecasts. ECMWF Tech. Memo. 2003, 430, 19. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Z.; Yan, S.; Peng, J. Do ERA5 and ERA5-land precipitation estimates outperform satellite-based precipitation products? A comprehensive comparison between state-of-the-art model-based and satellite-based precipitation products over mainland China. J. Hydrol. 2022, 605, 127353. [Google Scholar] [CrossRef]
- Lu, H.; Huang, Z.; Ding, L.; Lu, T.; Yuan, Y. Calibrating FY4A QPE using CMPA over Yunnan–Kweichow Plateau in summer 2019. Eur. J. Remote Sens. 2021, 54, 476–486. [Google Scholar] [CrossRef]
- Qiu, C.; Ding, L.; Zhang, L.; Xu, J.; Ma, Z. Quantitative Characteristics of the Current Multi-Source Precipitation Products over Zhejiang Province, in Summer, 2019. Water 2021, 13, 334. [Google Scholar] [CrossRef]
- Ramadhan, R.; Yusnaini, H.; Marzuki, M.; Muharsyah, R.; Suryanto, W.; Sholihun, S.; Vonnisa, M.; Harmadi, H.; Ningsih, A.P.; Battaglia, A.; et al. Evaluation of GPM IMERG Performance Using Gauge Data over Indonesian Maritime Continent at Different Time Scales. Remote Sens. 2022, 14, 1172. [Google Scholar] [CrossRef]
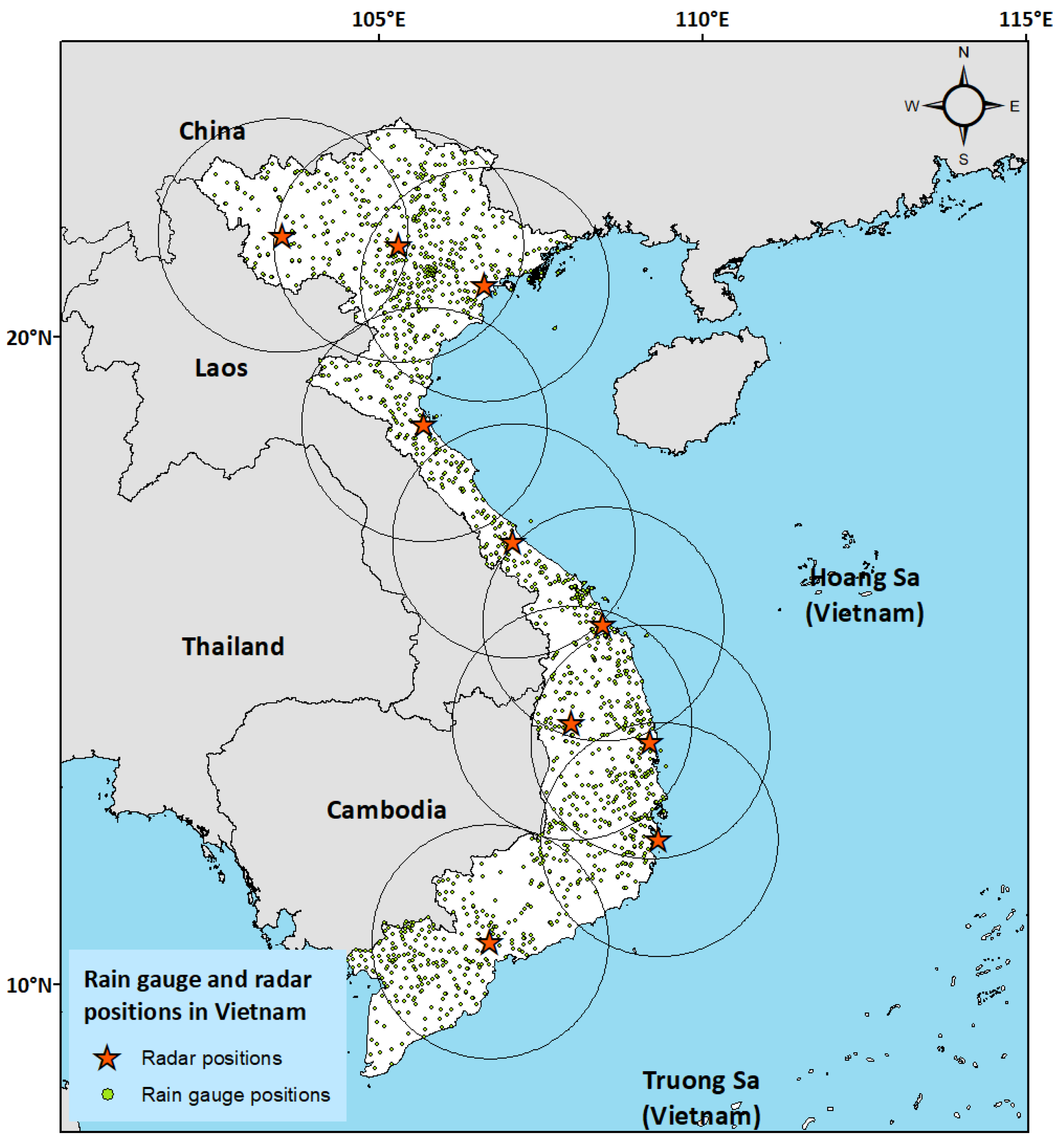


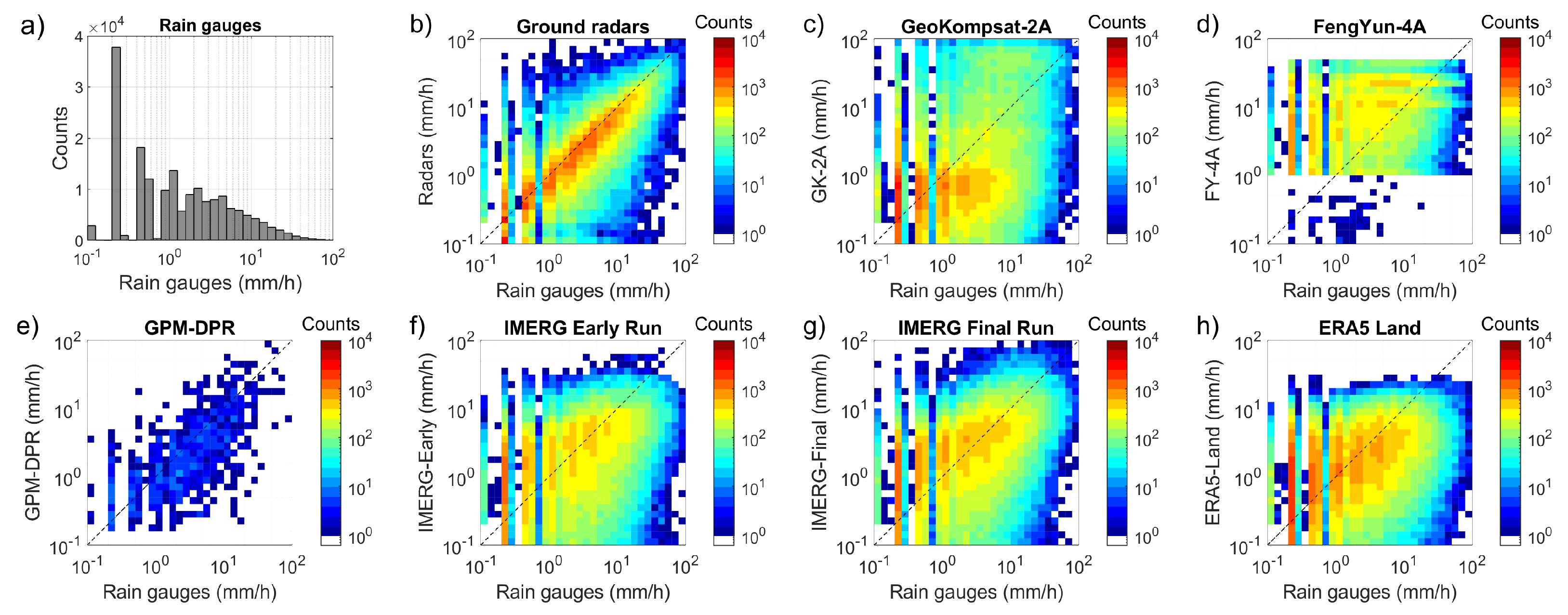

| Dataset | Period | Grid Resolution | Temporal Sampling | Coverage | Data Source | Latency |
|---|---|---|---|---|---|---|
| AWS (rain gauges) | 2008–present | point (avg. dist.: 8.6 km) | 10 min/1 h | country-wide | tipping bucket | ∼10 min/30 min–1 h |
| Radars | 2019–present | 1 km | 1 h | country-wide | C- and S-band | 15–30 min |
| GPM-DPR | 2014–present | 5 km | ∼1 overp./day | 245 km swath (global) | DPR (Ku + Ka) | 1 day |
| FY-4A | 2017–present | 4 km (nadir) | 1 h/3 h/6 h | full disk | VIS-IR | NRT |
| GK-2A | 2018–present | 2 km (nadir) | 10 min | full disk | IR + DPR | NRT |
| IMERG Early run | 2000–present | 30 min | global | MW + DPR + IR | 4 hours | |
| IMERG Final run | 2000–present | 30 min | global | MW + DPR + IR + rain gauges | 3.5 months | |
| ERA5-Land | 1950–present | ∼9 km | 1 h | global | ECMWF model | 2 to 3 months |
| This work | August 2020– November 2020 | 1 h | from 7°N–101°E to 24°N–111°E | 8 different sources | - |
| Case ID | Start (Date) | End (Date) | Duration (Hours [Days]) | Wet Ratio (%) | Average Rain Rate (mm/h) | Std. Deviation (mm/h) | Maximum Rain Rate (mm/h) |
|---|---|---|---|---|---|---|---|
| 1 | 31 July | 3 August | 73 [3] | 36.2 | 3.27 | 4.95 | 61.6 |
| 2 | 16 September | 20 September | 97 [4] | 29.9 | 2.89 | 5.86 | 106.6 |
| 3 | 5 October | 11 October | 145 [6] | 26.2 | 5.10 | 8.31 | 209.4 |
| 4 | 14 October | 21 October | 169 [7] | 31.2 | 3.83 | 6.83 | 96.8 |
| 5 | 27 October | 1 November | 121 [5] | 26.6 | 2.70 | 5.93 | 111.8 |
| 6 | 13 November | 17 November | 97 [4] | 23.6 | 1.48 | 3.63 | 289.7 |
| Whole dataset | August 2020 | November 2020 | 702 [29] | 28.8 | 3.49 | 6.57 | 289.7 |
| Product Coverage (% of Time) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Case ID | AWS | Radars | GK-2A | FY-4A | GPM-DPR | IMERG-Early | IMERG-Final | ERA5-Land |
| 1 | 90 | 100 | 100 | 100 | 4 | 100 | 100 | 99 |
| 2 | 97 | 100 | 100 | 98 | 8 | 100 | 100 | 99 |
| 3 | 95 | 100 | 100 | 100 | 9 | 100 | 100 | 98 |
| 4 | 98 | 100 | 100 | 100 | 15 | 100 | 100 | 99 |
| 5 | 94 | 100 | 100 | 100 | 25 | 100 | 100 | 99 |
| 6 | 97 | 100 | 100 | 100 | 9 | 100 | 100 | 99 |
| Whole dataset | 95 | 100 | 100 | 100 | 12 | 100 | 100 | 99 |
| Name | Equation | Range of Values | Optimal |
|---|---|---|---|
| Probability of detection | [0, 1] | (1) | |
| False alarm ratio | [0, 1] | (0) | |
| Multiplicative bias | [0–∞] | (1) | |
| Critical Success Index | [0, 1] | (1) | |
| Equitable threat score | [, 1] | (1) |
| Name | Equation | Range of Values | Optimal |
|---|---|---|---|
| Correlation coefficient | [−1, 1] | (1) | |
| Coefficient of variation | [0, ∞] | (0) | |
| Normalized mean error, or bias | [, ∞] | (0) | |
| Normalized mean absolute error | [0, ∞] | (0) | |
| Modified Kling–Gupta efficiency | [−∞, 1] | (1) | |
| Probability to have inside of | [0, 1] | (1) |
| Product | CSI | ETS | POD | FAR | mBIAS |
|---|---|---|---|---|---|
| Radars | 0.53 | 0.41 | 0.61 | 0.21 | 0.77 |
| GK-2A | 0.38 | 0.18 | 0.69 | 0.55 | 1.53 |
| FY-4A | 0.34 | 0.21 | 0.43 | 0.39 | 0.71 |
| IMERG-Early run | 0.40 | 0.25 | 0.55 | 0.41 | 0.92 |
| IMERG-Final run | 0.43 | 0.28 | 0.62 | 0.42 | 1.07 |
| ERA5-Land | 0.44 | 0.24 | 0.83 | 0.52 | 1.71 |
| GPM-DPR * | 0.55 | 0.45 | 0.61 | 0.15 | 0.72 |
| Product | CC | CV | ME | MAE | mKGE | ||
|---|---|---|---|---|---|---|---|
| Radars | 0.70 | 1.38 | −0.34 | 0.56 | 0.75 | 0.53 | 1.13 |
| GK-2A | 0.29 | 3.16 | 0.07 | 1.32 | 0.39 | 0.09 | 1.55 |
| FY-4A | 0.3 | 2.62 | 0.33 | 1.42 | 0.66 | 0.23 | 0.98 |
| IMERG-Early run | 0.38 | 1.82 | −0.50 | 0.86 | 0.5 | 0.21 | 1.00 |
| IMERG-Final run | 0.42 | 1.83 | −0.31 | 0.86 | 0.5 | 0.34 | 1.04 |
| ERA5-Land | 0.29 | 1.86 | −0.43 | 0.85 | 0.28 | 0.12 | 0.69 |
| GPM-DPR * | 0.44 | 2.67 | −0.21 | 0.78 | 0.75 | −0.17 | 2.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roversi, G.; Pancaldi, M.; Cossich, W.; Corradini, D.; Nguyen, T.T.N.; Nguyen, T.V.; Porcu’, F. The Extreme Rainfall Events of the 2020 Typhoon Season in Vietnam as Seen by Seven Different Precipitation Products. Remote Sens. 2024, 16, 805. https://doi.org/10.3390/rs16050805
Roversi G, Pancaldi M, Cossich W, Corradini D, Nguyen TTN, Nguyen TV, Porcu’ F. The Extreme Rainfall Events of the 2020 Typhoon Season in Vietnam as Seen by Seven Different Precipitation Products. Remote Sensing. 2024; 16(5):805. https://doi.org/10.3390/rs16050805
Chicago/Turabian StyleRoversi, Giacomo, Marco Pancaldi, William Cossich, Daniele Corradini, Thanh Thi Nhat Nguyen, Thu Vinh Nguyen, and Federico Porcu’. 2024. "The Extreme Rainfall Events of the 2020 Typhoon Season in Vietnam as Seen by Seven Different Precipitation Products" Remote Sensing 16, no. 5: 805. https://doi.org/10.3390/rs16050805
APA StyleRoversi, G., Pancaldi, M., Cossich, W., Corradini, D., Nguyen, T. T. N., Nguyen, T. V., & Porcu’, F. (2024). The Extreme Rainfall Events of the 2020 Typhoon Season in Vietnam as Seen by Seven Different Precipitation Products. Remote Sensing, 16(5), 805. https://doi.org/10.3390/rs16050805






