Influences of Different Factors on Gravity Wave Activity in the Lower Stratosphere of the Indian Region
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. GW Ep Extracted from the COSMIC-2 Temperature Profiles
2.3. Construction of the 3D Grids for Monthly LS GW Ep and Influencing Factors
2.4. Correlation Analysis and Dominance Analysis
3. Results
3.1. GW Climatology in the Indian Region
3.2. Distributions of the CCs and RICs of Different Influencing Factors
4. Discussion
4.1. Quantification of the Impacts of Selected Factors on LS GW Activities in the Indian Region
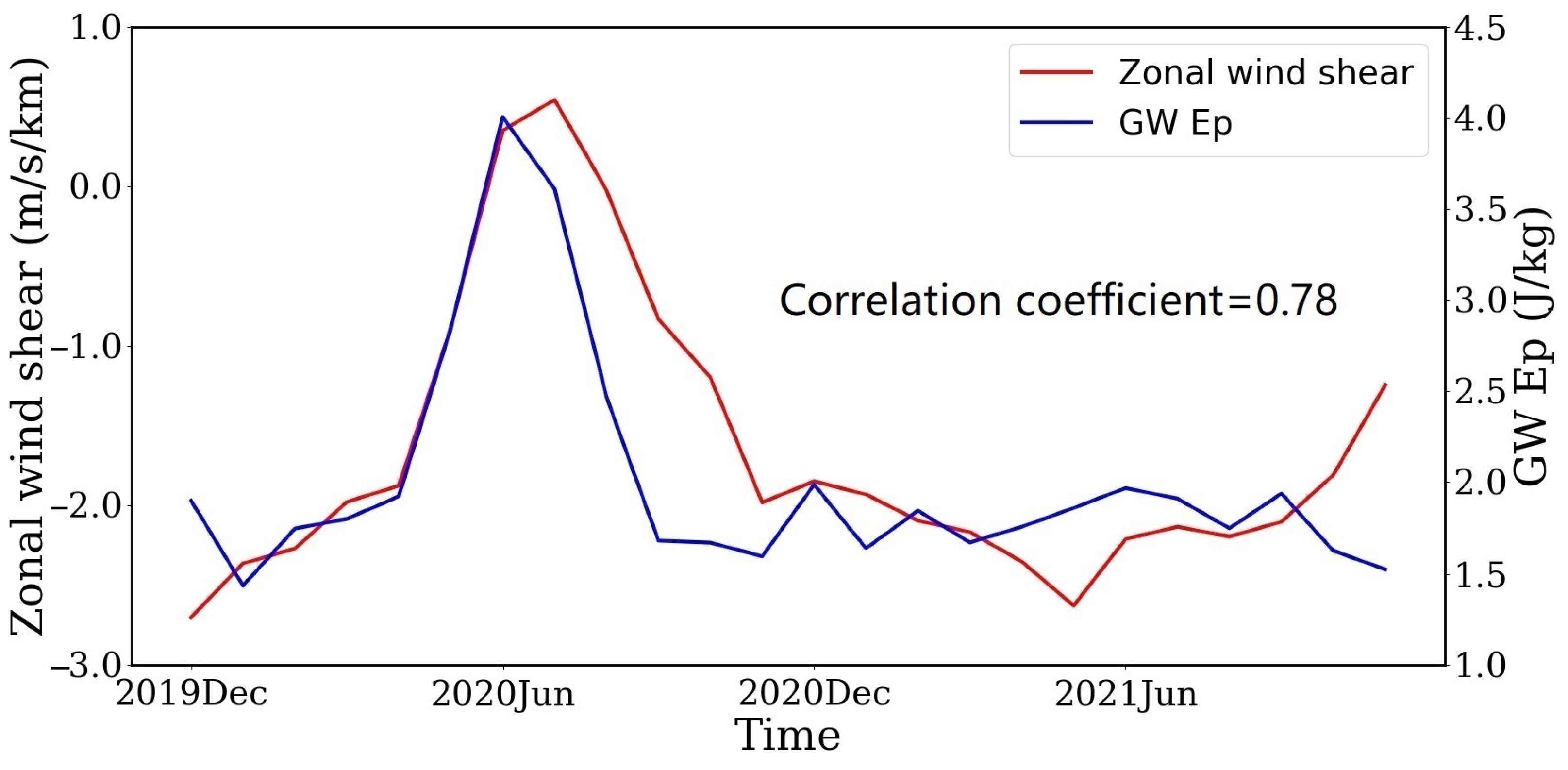
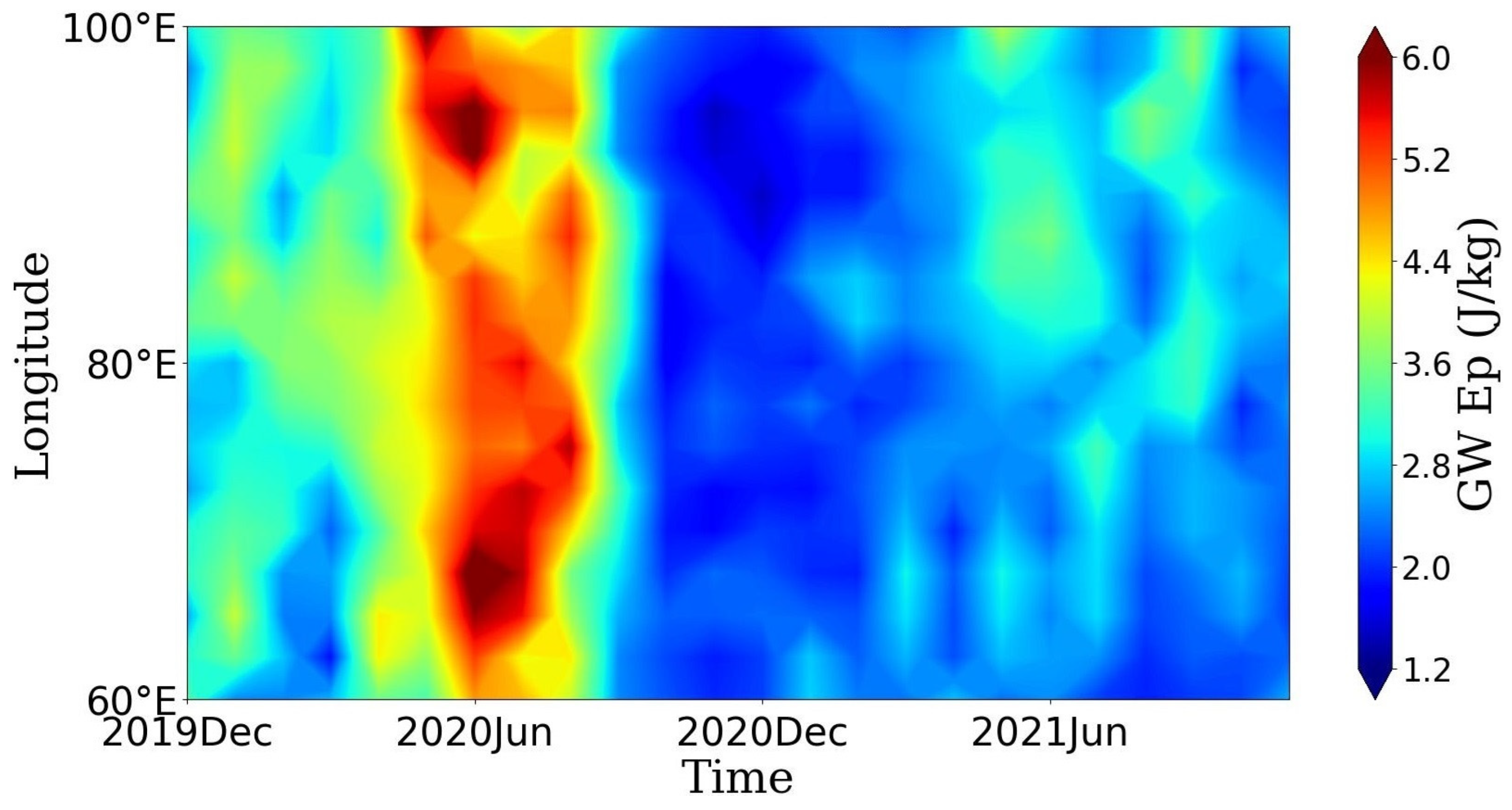
4.2. Analysis of the Impacts of Zonal Wind Speeds and Wind Shears on the LS GWs in Different Local Regions
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- John, S.R.; Kumar, K.K. TIMED/SABER observations of global gravity wave climatology and their interannual variability from stratosphere to mesosphere lower thermosphere. Clim. Dyn. 2012, 39, 1489–1505. [Google Scholar] [CrossRef]
- Hindley, N.P.; Wright, C.J.; Smith, N.D.; Mitchell, N.J. The southern stratospheric gravity wave hot spot: Individual waves and their momentum fluxes measured by COSMIC GPS-RO. Atmos. Chem. Phys. 2015, 15, 7797–7818. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, S.; Huang, C.; Huang, K.; Gong, Y.; Gan, Q. The interaction between the tropopause inversion layer and the inertial gravity wave activities revealed by radiosonde observations at a midlatitude station. J. Geophys. Res. Atmos. 2015, 120, 8099–8111. [Google Scholar] [CrossRef]
- Manzini, E.; McFarlane, N.A. The effect of varying the source spectrum of a gravity wave parameterization in a middle atmosphere general circulation model. J. Geophys. Res. Atmos. 1998, 103, 31523–31539. [Google Scholar] [CrossRef]
- Alexander, M.J.; Geller, M.; McLandress, C.; Polavarapu, S.; Preusse, P.; Sassi, F.; Sato, K.; Eckermann, S.; Ern, M.; Hertzog, A.; et al. Recent developments in gravity-wave effects in climate models and the global distribution of gravity-wave momentum flux from observations and models. Q. J. R. Meteorol. Soc. 2010, 136, 1103–1124. [Google Scholar] [CrossRef]
- Holton, J.R. The influence of gravity wave breaking on the general circulation of the middle atmosphere. J. Atmos. Sci. 1983, 40, 2497–2507. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Kim, Y.; Eckermann, S.D.; Chun, H. An overview of the past, present and future of gravity-wave drag parametrization for numerical climate and weather prediction models. Atmos. Ocean. 2003, 41, 65–98. [Google Scholar] [CrossRef]
- Alexander, S.P.; Shepherd, M.G. Planetary wave activity in the polar lower stratosphere. Atmos. Chem. Phys. 2010, 10, 707–718. [Google Scholar] [CrossRef]
- Watanabe, S.; Kawatani, Y.; Tomikawa, Y.; Miyazaki, K.; Takahashi, M.; Sato, K. General aspects of a T213L256 middle at-mosphere general circulation model. J. Geophys. Res. Atmos. 2008, 113, D12110. [Google Scholar] [CrossRef]
- Liu, H.L.; McInerney, J.M.; Santos, S.; Lauritzen, P.H.; Taylor, M.A.; Pedatella, N.M. Gravity waves simulated by high-resolution Whole Atmosphere Community Climate Model. Geophys. Res. Lett. 2014, 41, 9106–9112. [Google Scholar] [CrossRef]
- Holt, L.A.; Alexander, M.J.; Coy, L.; Molod, A.; Putman, W.; Pawson, S. Tropical waves and the quasi-biennial oscillation in a 7-km global climate simulation. J. Atmos. Sci. 2016, 73, 3771–3783. [Google Scholar] [CrossRef]
- Liu, X.; Yue, J.; Xu, J.; Garcia, R.R.; Russell, J.M., III; Mlynczak, M.; Wu, D.L.; Nakamura, T. Variations of global gravity waves derived from 14 years of SABER temperature observations. J. Geophys. Res. Atmos. 2017, 122, 6231–6249. [Google Scholar] [CrossRef]
- Scherllin-Pirscher, B.; Steiner, A.K.; Kirchengast, G.; Kuo, Y.H.; Foelsche, U. Empirical analysis and modeling of errors of atmospheric profiles from GPS radio occultation. Atmos. Meas. Tech. 2011, 4, 1875–1890. [Google Scholar] [CrossRef]
- Khaykin, S.M.; Hauchecorne, A.; Mzé, N.; Keckhut, P. Seasonal variation of gravity wave activity at midlatitudes from 7 years of COSMIC GPS and Rayleigh lidar temperature observations. Geophys. Res. Lett. 2015, 42, 1251–1258. [Google Scholar] [CrossRef]
- Leroy, S.S.; Gleisner, H. The stratospheric diurnal cycle in COSMIC GPS radio occultation data: Scientific applications. Earth Space Sci. 2022, 9, e2021EA002011. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. Atmos. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Tsuda, T.; Nishida, M.; Rocken, C.; Ware, R.H. A global morphology of gravity wave activity in the stratosphere revealed by the GPS occultation data (GPS/MET). J. Geophys. Res. 2000, 105, 7257–7273. [Google Scholar] [CrossRef]
- Ratnam, M.V.; Tetzlaff, G.; Jacobi, C. Global and seasonal variations of stratospheric gravity wave activity deduced from the CHAMP/GPS satellite. J. Atmos. Sci. 2004, 61, 1610–1620. [Google Scholar] [CrossRef]
- Anthes, R.; Schreiner, W. Six new satellites watch the atmosphere over Earth’s equator. Eos Trans. Am. Geophys. Union 2019, 100. [Google Scholar] [CrossRef]
- Schreiner, W.S.; Weiss, J.P.; Anthes, R.A.; Braun, J.; Chu, V.; Fong, J.; Hunt, D.; Kuo, Y.H.; Meehan, T.; Serafino, W.; et al. COSMIC-2 radio occultation constellation: First results. Geophys. Res. Lett. 2020, 47, e2019GL086841. [Google Scholar] [CrossRef]
- Pedatella, N.M.; Zakharenkova, I.; Braun, J.J.; Cherniak, I.; Hunt, D.; Schreiner, W.S.; Straus, P.R.; Valant-Weiss, B.L.; Vanhove, T.; Weiss, J.; et al. Processing and validation of FORMOSAT-7/COSMIC-2 GPS total electron content observations. Radio. Sci. 2021, 56, e2021RS007267. [Google Scholar] [CrossRef]
- Tien, J.Y.; Okihiro, B.B.; Esterhuizen, S.X.; Franklin, G.W.; Meehan, T.K.; Munson, T.N.; Robison, D.E.; Turbiner, D.; Young, L.E. Next generation scalable spaceborne GNSS science receiver. In Proceedings of the 2012 International Technical Meeting of the Institute of Navigation, Newport Beach, CA, USA, 30 January–1 February 2012; pp. 882–914. [Google Scholar]
- Alexander, S.P.; Tsuda, T.; Kawatani, Y.; Takahashi, M. Global distribution of atmospheric waves in the equatorial upper troposphere and lower stratosphere: COSMIC observations of wave mean flow interactions. J. Geophys. Res. 2008, 113, D24115. [Google Scholar] [CrossRef]
- Anthes, R.A. Exploring Earth’s atmosphere with radio occultation: Contributions to weather, climate and space weather. Atmos. Meas. Tech. Discuss. 2011, 4, 1077–1103. [Google Scholar] [CrossRef]
- Rakshit, G.; Jana, S.; Maitra, A. Gravity wave behavior in lower stratosphere during tropical cyclones over the Bay of Bengal. Radio. Sci. 2018, 53, 1356–1367. [Google Scholar] [CrossRef]
- Randel, W.J.; Wu, F.; Podglajen, A. Equatorial waves, diurnal tides and small-scale thermal variability in the tropical lower stratosphere from COSMIC-2 radio occultation. J. Geophys. Res. Atmos. 2021, 126, e2020JD033969. [Google Scholar] [CrossRef]
- Uccellini, L.W.; Koch, S.E. The synoptic setting and possible energy sources for mesoscale wave disturbances. Mon. Weather Rev. 1987, 115, 721–729. [Google Scholar] [CrossRef]
- Ern, M.; Arras, C.; Faber, A.; Frhlich, K.; Jacobi, C.; Kalisch, S.; Krebsbach, M.; Preusse, P.; Schmidt, T.; Wickert, J. Observations and ray tracing of gravity waves: Implications for global modeling. In Climate and Weather of the Sun-Earth System (CAWSES) Highlights from a Priority Program; Lubken, F.J., Ed.; Springer: Dordrecht, The Netherlands, 2013; pp. 383–408. [Google Scholar] [CrossRef]
- Ratnam, M.V.; Babu, A.N.; Rao, V.V.M.J.; Rao, S.V.B.; Rao, D.N. MST radar and radiosonde observations of inertia-gravity wave climatology over tropical stations: Source mechanisms. J. Geophys. Res. Atmos. 2008, 113, D07109. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, J.; Liu, L.; Wan, W. A global morphology of gravity wave activity in the stratosphere revealed by the 8-year SABER/TIMED data. J. Geophys. Res. 2012, 117, D21101. [Google Scholar] [CrossRef]
- Karoly, D.J.; Roff, G.L.; Reeder, M.J. Gravity wave activity associated with tropical convection detected in TOGA COARE sounding data. Geophys. Res. Lett. 1996, 23, 261–264. [Google Scholar] [CrossRef]
- Wright, C.J.; Gille, J.C. HIRDLS observations of gravity wave momentum fluxes over the monsoon regions. J. Geophys. Res. 2011, 116, D12103. [Google Scholar] [CrossRef]
- Jana, S.; Rakshit, G.; Maitra, A. Gravity wave activities associated with convective phenomena at a tropical location near land-sea boundary. Radio Sci. 2020, 55, e2019RS006952. [Google Scholar] [CrossRef]
- Sato, K.; Dunkerton, T.J. Estimates of momentum flux associated with equatorial Kelvin and gravity waves. J. Geophys. Res. Atmos. 1997, 102, 26247–26261. [Google Scholar] [CrossRef]
- Vincent, R.A.; Alexander, M.J. Gravity waves in the tropical lower stratosphere: An observational study of seasonal and interannual variability. J. Geophys. Res. 2000, 105, 17983–17993. [Google Scholar] [CrossRef]
- Rao, D.N.; Thulasiraman, S.; Rao, S.V.B.; Rao, T.N.; Kishore, P.; Ratnam, M.V.; Reddy, K.K. VHF radar observations of tropical easterly jet stream over Gadanki. Adv. Space Res. 2000, 26, 943–946. [Google Scholar] [CrossRef]
- Vasantha, B.; Ratnam, M.V.; Mohan, K.; Kamala, S.; Rao, D.N.; Rama, G.V. Characteristics of tropical easterly jet over Gadanki: Comparison with radiosonde and rawinsonde. Indian J. Radio Space Phys. 2002, 31, 130–139. [Google Scholar]
- Nath, D.; Ratnam, M.V.M.; Rao, V.V.M.J.; Murthy, B.V.K.; Rao, S.V.B. Gravity wave characteristics observed over a tropical station using high-resolution GPS radiosonde soundings. J. Geophys. Res. 2009, 114, D06117. [Google Scholar] [CrossRef]
- Fritts, D.C.; VanZandt, T.E. Spectral estimates of gravity wave energy and momentum fluxes. Part I: Energy dissipation, acceleration, and constraints. J. Atmos. Sci. 1993, 50, 3685–3694. [Google Scholar] [CrossRef]
- Wang, L.; Alexander, M.J. Gravity wave activity during stratospheric sudden warmings in the 2007–2008 Northern Hemi-sphere winter. J. Geophys. Res. 2009, 114, D18108. [Google Scholar] [CrossRef]
- Wang, L.; Alexander, M.J. Global estimates of gravity wave parameters from GPS radio occultation temperature data. J. Geophys. Res. Atmos. 2010, 115, D21122. [Google Scholar] [CrossRef]
- Xu, X.H.; Yu, D.C.; Luo, J. The spatial and temporal variability of global stratospheric gravity waves and their activity during sudden stratospheric warming revealed by COSMIC measurements. Adv. Atmos. Sci. 2018, 35, 1533–1546. [Google Scholar] [CrossRef]
- Luo, J.; Hou, J.L.; Xu, X.H. Variations of Stratospheric Gravity Waves Derived from Temperature Observations of Multi-GNSS Radio Occultation Missions. Remote Sens. 2021, 13, 4835. [Google Scholar] [CrossRef]
- Houchi, K.; Stoffelen, A.; Marseille, G.J.; De Kloe, J. Comparison of wind and wind shear climatologies derived from high-resolution radiosondes and the ECMWF model. J. Geophys. Res. 2010, 115, D22123. [Google Scholar] [CrossRef]
- Budescu, D.V. Dominance analysis: A new approach to the problem of relative importance of predictors in multiple regression. Psychol. Bull. 1993, 114, 542–551. [Google Scholar] [CrossRef]
- Azen, R.; Budescu, D.V. Comparing predictors in multivariate regression models: An extension of dominance analysis. J. Educ. Behav. Stat. 2006, 31, 157–180. [Google Scholar] [CrossRef]
- Tonidandel, S.; Lebreton, J.M. Relative Importance Analysis: A Useful Supplement to Regression Analysis. J. Bus. Psychol. 2011, 26, 1–9. [Google Scholar] [CrossRef]
- Kraha, A.; Turner, H.; Nimon, K.; Zientek, L.R.; Henson, R.K. Tools to support interpreting multiple regression in the face of multicollinearity. Front. Psychol. 2012, 3, 44. [Google Scholar] [CrossRef]
- Zhang, K.; Sebo, S.; McDonald, W.; Bhaskar, A.; Shuster, W.; Stewart, R.D.; Parolari, A.J. The role of inflow and infiltration (I/I) in urban water balances and streamflow regimes: A hydrograph analysis along the sewershed-watershed continuum. Water. Resour. Res. 2023, 59, e2022WR032529. [Google Scholar] [CrossRef]
- LeBreton, J.M.; Hargis, M.B.; Griepentrog, B.; Oswald, F.L.; Ployhart, R.E. A multidimensional approach for evaluating variables in organizational research and practice. Pers. Psychol. 2007, 60, 475–498. [Google Scholar] [CrossRef]
- Sasi, M.N.; Ramkumar, G.; Deepa, V.; Murthy, B.V.K. Inertia-gravity waves associated with tropical easterly jet over the Indian subcontinent during the south west monsoon period. Geophys. Res. Lett. 2000, 27, 3201–3204. [Google Scholar] [CrossRef]
- Kumar, K.K. VHF radar observations of convectively generated gravity waves: Some new insights. Geophys. Res. Lett. 2006, 33, L01815. [Google Scholar] [CrossRef]
- Fang, X.; Forbes, J.M.; Benna, M.; Montabone, L.; Curry, S.; Jakosky, B. The origins of longterm variability in Martian upper atmospheric densities. J. Geophys. Res. Space Phys. 2022, 127, e2021JA030145. [Google Scholar] [CrossRef]
- Romatschke, U.; Medina, S.; Houze, R.A. Regional, seasonal, and diurnal variations of extreme convection in the South Asian region. J. Clim. 2010, 23, 419–439. [Google Scholar] [CrossRef]
- Qie, X.S.; Wu, X.K.; Yuan, T.; Bian, J.C.; Lu, D.R. Comprehensive pattern of deep convective systems over the Tibetan Plateau–South Asian monsoon region based on TRMM data. J. Clim. 2014, 27, 6612–6626. [Google Scholar] [CrossRef]
- Zhang, F.; Tao, D. Effects of vertical wind shear on the predictability of tropical cyclones. J. Atmos. Sci. 2013, 70, 975–983. [Google Scholar] [CrossRef]
- Tsuda, T. Characteristics of atmospheric gravity waves observed using the MU (Middle and Upper atmosphere) radar and GPS (Global Positioning System) radio occultation. Proc. Jpn. Acad. Ser. B 2014, 90, 12–27. [Google Scholar] [CrossRef] [PubMed]
- Tao, D.; Zhang, F. Effects of vertical wind shear on the predictability of tropical cyclones: Practical versus intrinsic limit. J. Adv. Model. Earth Syst. 2015, 7, 1534–1553. [Google Scholar] [CrossRef]
- Miyahara, S.; Hayashi, Y.; Mahlman, J.D. Interactions between gravity waves and planetary-scale flow simulated by the GFDL ‘SKYHI’ general circulation model. J. Atmos. Sci. 1986, 43, 1844–1861. [Google Scholar] [CrossRef][Green Version]
- Alexander, S.P.; Tsuda, T.; Kawatani, Y. COSMIC GPS observations of Northern Hemisphere winter stratospheric gravity waves and comparisons with an atmospheric general circulation model. Geophys. Res. Lett. 2008, 35, 156–167. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Gray, L.J.; Dunkerton, T.J.; Hamilton, K.; Haynes, P.H.; Randel, W.J.; Holton, J.R.; Alexander, M.J.; Hirota, I.; Horinouchi, T.; et al. The quasi-biennial oscillation. Rev. Geophys. 2001, 39, 179–229. [Google Scholar] [CrossRef]
- Faber, A.; Llamedo, P.; Schmidt, T.; de la Torre, A.; Wickert, J. On the determination of gravity wave momentum flux from GPS radio occultation data. Atmos. Meas. Tech. 2013, 6, 3169–3180. [Google Scholar] [CrossRef]
- Schmidt, T.; Alexander, P.; de la Torre, A. Stratospheric gravity wave momentum flux from radio occultations. J. Geophys. Res. Atmos. 2016, 121, 4443–4467. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, J.; Luo, J.; Xu, X. Influences of Different Factors on Gravity Wave Activity in the Lower Stratosphere of the Indian Region. Remote Sens. 2024, 16, 761. https://doi.org/10.3390/rs16050761
Hou J, Luo J, Xu X. Influences of Different Factors on Gravity Wave Activity in the Lower Stratosphere of the Indian Region. Remote Sensing. 2024; 16(5):761. https://doi.org/10.3390/rs16050761
Chicago/Turabian StyleHou, Jialiang, Jia Luo, and Xiaohua Xu. 2024. "Influences of Different Factors on Gravity Wave Activity in the Lower Stratosphere of the Indian Region" Remote Sensing 16, no. 5: 761. https://doi.org/10.3390/rs16050761
APA StyleHou, J., Luo, J., & Xu, X. (2024). Influences of Different Factors on Gravity Wave Activity in the Lower Stratosphere of the Indian Region. Remote Sensing, 16(5), 761. https://doi.org/10.3390/rs16050761








