Abstract
Large rivers without hydrological data from remote sensing observations have recently become a hot research topic. The Irrawaddy River is among the major tropical rivers worldwide; however, published hydrological data on this river have rarely been obtained in recent years. In this paper, based on the existing measured the total suspended matter flux (FTSM) and discharge data for the Irrawaddy River, an inversion model of the total suspended matter concentration (CTSM) is constructed for the Irrawaddy River, and the CTSM and FTSM from 1990 to 2020 are estimated using the L1 products of Landsat-8 OLI/TIRS and Landsat-5 TM. The results show that over the last 30 years, the FTSM of the Irrawaddy River decreased at a rate of 3.9 Mt/yr, which is significant at the 99% confidence interval. An increase in the vegetation density of the Irrawaddy Delta has increased the land conservation capacity of the region and reduced the inflow of land-based total suspended matter (TSM). The FTSM of the Irrawaddy River was estimated by fusing satellite data and data measured at hydrological stations. The research method employed in this paper provides a new supplement to the existing hydrological data for large rivers.
1. Introduction
Total Suspended Matter (TSM) is an important indicator for assessing water quality. The collection and study of information on the concentration and flux of TSM (CTSM and FTSM, respectively) in large rivers is a current research hotspot. Recent studies have shown that the FTSM value in large deltaic rivers is declining, especially in Asia [1]. As more dams and other river projects are built and used, the transfer of water and sediment to the sea will decrease [2]. Over the past 60 years, nine major rivers in China [3], as well as the Mekong River [4] and the Ganges–Brahmaputra River [5], have demonstrated notable reductions in FTSM due to the construction of reservoirs and dams.
At present, the traditional estimation methods of FTSM are based mainly on station measurements [3,6,7] or hydroclimatic models [4]. Some of the abovementioned methods are disadvantageous due to being computationally intensive and undersupplied in terms of usable data, and some are excessively costly [8]. In large tropical rivers, installing and maintaining hydrological stations is very expensive; thus, the collection of river discharge and sediment data is limited. For these reasons, there is a growing interest in the scientific community to assess the FTSM in large rivers using remote sensing data [9]. Currently, numerous scholars have used various ocean color satellite sensors [10,11,12] to estimate FTSM values in study areas that include rivers, lakes, and nearshore waters. The integration of data from different satellites and the fusion of satellite data with in situ measurements from hydrological stations represent potential approaches for researching the variability in TSM fluxes within river systems [13,14,15].
Remote sensing is an efficient, low-cost, long-term indirect observation technique, and it plays an important role in several research areas, including hydrology [16,17]. The Irrawaddy River originates from the glaciers of the southeastern Himalayas at the confluence of the North Mai and Mali Rivers. The Irrawaddy River is considered to be one of the world’s major tropical river systems [18]. The river basin covers 60% of the territory of Myanmar and is home to more than 90% of the country’s population, who relies heavily on the river and its resources for their livelihoods [19]. The Irrawaddy River ranks fifth in the world in terms of the FTSM, and the mixed system of the Irrawaddy River and the Thanlwin River accounts for 20% of the total flux of material from the Himalayan–Tibetan orogenic belt [20]. However, in recent decades, the once-pristine Irrawaddy basin has been severely disturbed by increasing human activity, such as dam construction, agricultural development, deforestation, and land-based mining [21]. These disturbances have led to perceptible changes in the conditions of the Irrawaddy basin river channels [22]. The lack of publicly available local data on suspended fluxes and the paucity of long-term hydrological information—most scholarly studies to date have been based on historical data—present a formidable challenge for hydrological studies of the Irrawaddy River. Therefore, the use of long time series remote sensing data to estimate the FTSM in the Irrawaddy River can be an effective supplement to local hydrological data. Moreover, the use of multisource data to quantify the factors that influence the FTSM in the river can help identify the extent to which global changes are affecting the river and further clarify the mechanisms of land–ocean material exchange.
2. Materials and Methods
2.1. Study Area
The Irrawaddy River originates in the eastern part of the Qinghai–Tibetan Plateau (QTP). It is approximately 2100 km long and eventually discharges into the Indian Ocean. Most of the Irrawaddy Basin is located in Myanmar, with a small part being in the Chinese and Indian territories. The northern part of the basin is high in the mountains, and the southern part is a deltaic basin. The Irrawaddy River basin has a tropical monsoon climate, with heavy rainfall occurring from May to October and a dry season occurring from November to April. However, the average annual rainfall is spatially variable and ranges from approximately 500 mm in the central area of the basin to approximately 4000 mm in the northern mountains [23]. The mean daily temperature varies between 21 and 34 °C in the summer and between 11 and 23 °C in the colder seasons [24]. The Irrawaddy River has mean and maximum discharge rates of approximately 13,000 m3/s and 32,600 m3/s, respectively. The main sources of river water are snow and ice from the upper Tibetan Plateau and the contribution of precipitation to the basin [25]. The annual suspended matter transport is 325 ± 57 × 106 tons [19].
Furuichi calculated the monthly total discharge and suspended matter flux of the Irrawaddy River from 1966 to 1996 based on data provided by the Pyay hydrological station [19]. For comparison, our flux estimation section is located at the position shown in Figure 1C (i.e., before the river course of the Irrawaddy River bifurcates and is close to Pyay), which is conducive to building an inversion model based on the data recorded by the station. The location of the cross-section is considered to be the nontributary river channel, and the cross-section is close to Pyay to match the historical data.
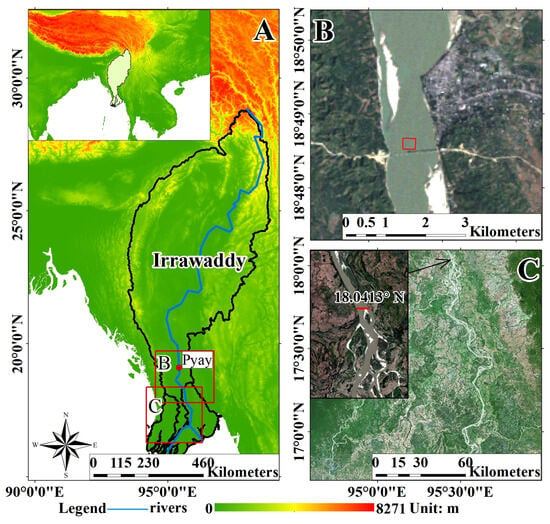
Figure 1.
(A) The location of the Irrawaddy River (blue line) and the basin (black line). (B) The location of the satellite image of the selected inversion modeling area (red box). (C) The location of the satellite image used to estimate the FTSM (red line).
2.2. Data
The reanalysis data used in this study included discharge and precipitation data. The discharge data are derived from the Global Flood Awareness System (GloFAS) [26], which is part of the Copernicus Emergency Management Service (CEMS). The dataset is simulated by a hydrological river routing model and global reanalysis grid runoff data. The difference between the discharge values and the actual values in the river basin, which were measured from the local hydrology station, was 10% or less. The spatial resolution of the raster data is 0.1° × 0.1°, and we used the monthly average discharge data from 1990 to 2020.
The precipitation data originate from the Global Precipitation Climatology Project (GPCP) [27]. The GPCP is a satellite precipitation product that combines the infrared and microwave data of dozens of geostationary satellites and polar orbiting satellites compiled by the Global Precipitation Climatology Center and corrected by data from multiple ground stations worldwide. The resolution of the data is 0.5° × 0.5°. This study used monthly average precipitation data from 1990 to 2020.
2.2.1. Remote Sensing Data
This study used Landsat data, including Landsat-8 Operational Land Imager (OLI)/Thermal Infrared Sensor (TIRS) L1 products (resolution: 30 m) and Landsat-5 Thermal Mapper (TM) L1 products (resolution: 30 m), as experimental satellite data. We also used Sentinel-2 data (resolution: 10 m) to verify the spectrum of the Landsat satellite data. These satellite data were downloaded from the official website of the United States Geological Survey (USGS) (https://earthexplorer.usgs.gov/, accessed on 1 October 2021). The Landsat satellite products provide images of the nontidal reaches of the Irrawaddy River (row and column number: 133-048) from 1990 to 2020. We selected at least one image for each season. After removing the unusable data covered by the cloud, we obtained a total of 205 images.
2.2.2. Land Use Data
GlobeLand30 [28], which is a 30 m spatial resolution global land cover dataset developed by China that uses the WGS-84 coordinate system, was used as the land classification data. The data include 10 primary types. The overall accuracy of the data is 85.72%, and the Kappa coefficient is 0.82.
2.2.3. Remote Sensing Data Preprocessing
The Landsat data used in this study were obtained from the USGS official website, and L1 standard data were downloaded. The data were geometrically corrected based on the digital elevation model (DEM) data. To obtain more accurate reflectivity data, the following steps need to be taken.
- (1)
- Radiometric Calibration
When comparing remote sensing data at different times, from different places or from different sensors, it is necessary to convert the gray value of the image into absolute radiance to calculate the spectral reflectance or spectral radiance of ground objects. We used the Radiometric Correction Radiometric Calibration function in ENVI 5.3 software to complete the radiometric calibration.
- (2)
- Atmospheric Correction
We used the Radiometric Correction—Atmospheric Correct Model—FLAASH Atmospheric Correct Model function in ENVI 5.3 software to complete the atmospheric correction. FLAASH is an improved model based on MODTRAN4 that has good accuracy in terms of hyperspectral and multispectral data correction. The Atmospheric Model is selected as Tropical according to the geographical location of the study area. Due to the unsatisfactory performance of the default aerosol model (Rural) in TSM inversion experiments for highly turbid water bodies [29,30], we opted to use the marine aerosol model.
- (3)
- Validation of Landsat Data with Sentinel Data
Due to the lack of measured spectral data for large river water bodies, we chose the star verification method to evaluate the atmospheric correction results. The basic process is to select two satellites (i.e., sensors) with similar bands and resolutions, then select images taken at the same time at the same location, and compare the reflectivity of each band on a pixel-by-pixel basis.
The Sentinel-2 MultiSpectral Instrument (MSI) is a sensor mounted on Sentinel-2A and Sentinel-2B. Sentinel-2 and Landsat-8 satellite data are widely used in water color remote sensing, and a variety of algorithms have been developed for fusing water color data from these two sensors [31,32]. In this study, for each river, two groups of Sentinel-2 L1C products (10 m resolution) are used to compare the Landsat-8 OLI products, and the location is selected as the overlapping area of the two sensors that covers the target river section. The selected Sentinel image acquisition times are 24 November 2018 at 4:11:39 and 16 May 2018 at 4:05:49. The selected Landsat image acquisition times are 24 November 2018 at 4:01:32 and 16 May 2018 at 4:01:14. Due to the close acquisition times, we believe that their remote sensing reflectances are sufficiently comparable.
Radiometric calibration and atmospheric correction of the Landsat 8 OLI images were carried out using ENVI 5.3 software. The Sentinel-2 images were corrected using SNAP software (V9.0.0; 29.06.2022 15:00 UTC.). A sensor transformation method developed by Zhang et al. (2018), which eliminates the difference between the OLI and MSI sensors, was used to improve the accuracy of our comparison [33]. See Table 1 for the specific transformation formula.

Table 1.
Transformation functions between the Sentinel-2 MSI and Landsat-8 OLI sensors using OLS regression [33].
3. Results
Since the main wavebands of the TSM inversion are near-infrared and blue light and the inversion model is based on the ratio of near-infrared to blue light wavebands, in each group of comparison images, we first resample the Sentinel image to the same resolution as the Landsat image. Then, we randomly take points in the river area, calculate the ratio of its near-infrared to its blue light wavebands, and compare the results of the two images. As shown in Figure 2, the results reveal that in the Irrawaddy River, the overall R = 0.75, and the root-mean-square error (RMSE) = 0.15. Our data are more accurate and reliable following FLAASH atmospheric correction and can therefore be used for FTSM estimation.
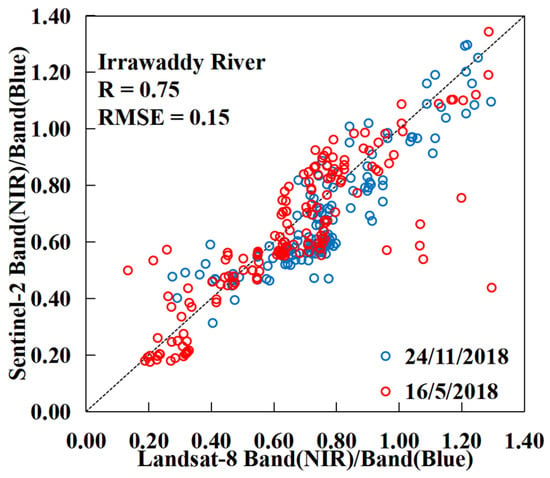
Figure 2.
Comparison of the ratios between the near-infrared and blue light wavebands determined using Landsat and Sentinel data.
For the atmospherically corrected data, we adopted the following method to collect the average remote sensing reflectance for the model [15,34]:
- We extracted the remote sensing reflectance for all bands within the selected 10 × 10 pixel area (Figure 1B).
- We applied Gaussian filtering.
- Pixels with deviations significantly exceeding the standard deviation were sequentially removed, ensuring that the variation coefficient (VC, SD/mean) was within 15%, and the mean of the remaining pixels was calculated.
3.1. Imputing Missing Data
In this study, L1 products of Landsat-8 OLI/TIRS sensors and L1 products of Landsat-5 TM sensors are used as experimental satellite data. Remote sensing images of the nontidal reaches of the Irrawaddy River were obtained for the period from 1990 to 2020 (Figure 1C). The image data distribution is shown in Figure 3.
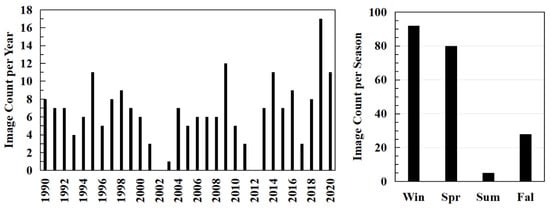
Figure 3.
Number of available remote sensing images in each year and season.
Due to the climatic characteristics of the geographical location of the study area, it is difficult to obtain noncloud, high-quality remote sensing images from complete time series, and thus, the adequacy of the research data cannot be guaranteed. In some years, there may be no data in summer or autumn. In such cases, we use the following method to fill in the missing data. First, we calculate the quarterly average CTSM of each season in a year according to the measured data from Pyay Station from 1966 to 1996, published by Furuichi and then, we calculate the CTSM ratio between seasons for all 30 years. This method can maximize the consistency of quarterly TSM trend changes between years. The results (Figure 4) show that most of the suspended solids are observed in the rainy season (i.e., May–October) each year.
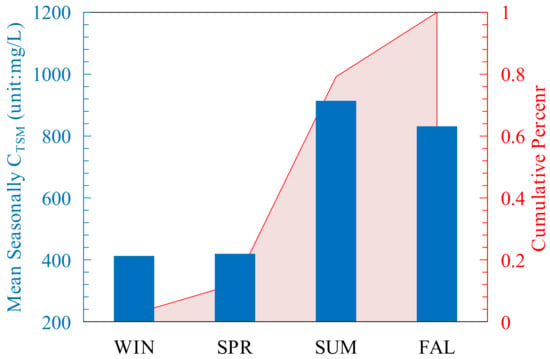
Figure 4.
Seasonal average CTSM trends in the Irrawaddy River calculated based on empirical data from the literature. The blue histogram shows the specific values of the seasonal average CTSM, and the red stacking curve shows the cumulative percentage of CTSM by season.
3.2. The M–K Test
The Mann–Kendall (M–K) test [35,36] is a climate diagnosis and prediction technique that can be used to determine whether an abrupt climate change occurred from a climate data series; if so, its occurrence time is expressed by the following equation:
where X is the value of the variable. A positive Z value suggests an upward trend in the variable, a negative Z value suggests a downward trend in the variable, and absolute Z values greater than 1.28, 1.64, and 2.32 signify the passing of significance tests at confidence levels of 90%, 95%, and 99%, respectively. The test result (i.e., Z value) reflects the overall trend in the variable.
The M–K abrupt change test can be used to determine whether there has been an abrupt change. Similarly, for variable series, we define the following expressions:
Then, whether there was an abrupt change in variable, Xn is analyzed based on the UFk and UBk values.
4. Results
4.1. The CTSM Inversion Model
The water color elements are generally highly correlated with the remote sensing reflectance in specific bands. After atmospheric correction, we obtained the surface reflectance product corresponding to the water body. The above parameters can be represented as:
where sr(λ) represents surface reflectance. Lω(λ) is the radiance of water surface reflection. Es(λ)E is solar irradiance. Rrs(λ) is remote sensing reflectance. θs is solar zenith angle. Solar irradiance is commonly considered approximately constant in the solar spectrum. The cos(θs) value remains consistent for the same pixel. Therefore, in the same remote sensing image, when calculating the ratio of different bands, the above expression can be simplified to:
According to the discharge and FTSM data provided by Furuichi from the Pyay station, we divided the FTSM by the river discharge to obtain the CTSM. We calculated the seasonal average reflectivity in a 10 × 10 pixel area on the section near Pyay (Figure 1B) using Landsat 5 TM images from 1990 to 1996 and compared it with the measured data to construct an inversion model for the CTSM in the Irrawaddy River. The ratio of near-infrared to blue light has a good correlation with the CTSM using the following expressions:
where a = 274.15 and b = 0.67. BandNIR/BandBlue represents the ratio of remote sensing reflectance between the near-infrared band and the blue band. A comparison of the inversion results with the measured data reveals that the results are positively correlated and distributed near the 1:1 line (R2 = 0.73, RMSE = 87.25; see Figure 5), thus indicating that the inversion model is suitable and that the inversion results are close to the measured data.
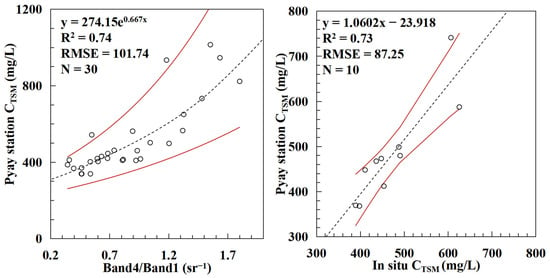
Figure 5.
Establishment and verification of the inversion model. There are 40 matching points in total. We used 30 points for modeling, and the remaining 10 points were used as validation datasets. The solid red line represents the 95% confidence interval.
4.2. Distribution of CTSM to the Irrawaddy River
Based on the CTSM inversion equation, we inverted 205 remotely sensed images for the CTSM. We calculated the arithmetic mean of the CTSM for each season during the 1990–2020 period. Based on these data, we plotted the seasonal distribution of CTSM in the Irrawaddy River, as shown in Figure 6. The trend of the distribution shows that the CTSM in the Irrawaddy River is more evenly distributed within the upper and lower reaches of the river, and relatively high CTSM values are found on the eastern bank of the river, which is presumably one of the main sources of suspended matter from land-based sources. The lowest CTSM levels of the year were observed during the spring (i.e., March–May), with the highest concentration being 480 mg/L and the lowest being approximately 380 mg/L; additionally, most of the CTSM concentration levels remained below 400 mg/L. During the summer (i.e., June–August) and autumn (i.e., September–November), the concentration of suspended matter increased significantly, with most of the river remaining at approximately 550 mg/L, the lowest concentration at approximately 450 mg/L, and the highest occurring at approximately 580 mg/L. In winter (i.e., December–February), the distribution of suspended matter concentrations was similar to but slightly greater than that in spring, as the suspended matter concentration in the main river channels remained at approximately 400 mg/L, with the highest concentration reaching 470 mg/L and the lowest reaching approximately 390 mg/L.
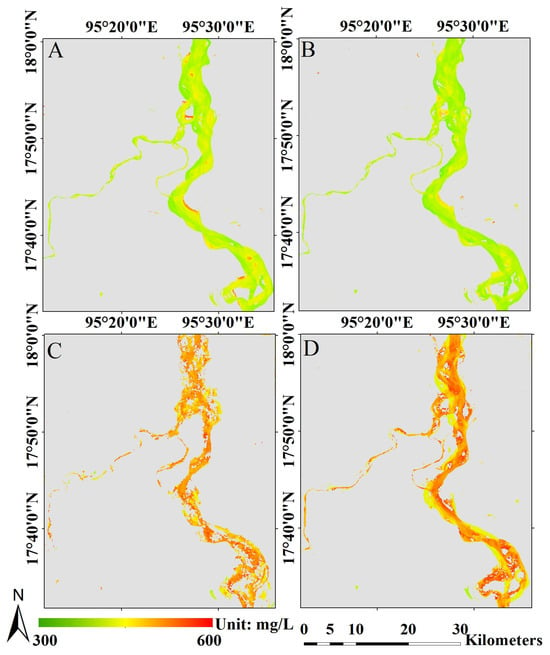
Figure 6.
Distribution trends in the Irrawaddy River CTSM in (A) winter, (B) spring, (C) summer, and (D) autumn.
After filling in the missing data with the measured data from the Pyay station from 1966 to 1996, we obtained the quarterly average CTSM dataset for the Irrawaddy River in the most recent 30 years. Based on this dataset, we calculated the annual average CTSM for each year, and the results are shown in Figure 7. Sentinel-2 satellite, with higher spatial and temporal resolution compared to Landsat, was utilized in our study with data spanning from 2015 to 2020. After numerical transformations (Table 1), we performed calculations for the CTSM using the same methodology. Despite discrepancies in the results due to differences in sensors, the inversion outcomes from both satellites exhibit consistent temporal trends over the studied period. Moreover, we also synchronously displayed the calculated results based on the measured dataset for the Pyay station. The results show that the inversion results of the satellite images are similar to the calculated results of the measured data in terms of their trend change and absolute values. The results showed that during the 1990–2020 period, the CTSM of the Irrawaddy River showed a downward trend.
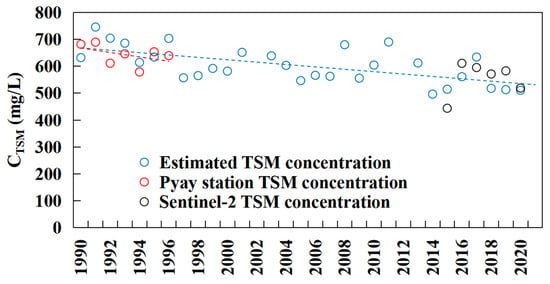
Figure 7.
Annual CTSM trend change in the Irrawaddy River. The blue circles represent the inversion results from Landsat, the red circles represent the in situ data results, the black circles represent the inversion results from Sentinel-2, the blue dotted line represents the linear regression of the inversion results from 1990 to 2020, and the red dotted line represents the linear regression of the in situ data from 1990 to 1996.
4.3. Changes in FTSM in the Irrawaddy River
The discharge data in this study are based on GloFAS data, and pixels with the same longitude and latitude as those in the flux calculation section were selected for calculation. When the spatial resolution of the discharge simulation data is 0.1°, there is a gap between the volume and the actual discharge. To increase the accuracy of the discharge data, we used the measured discharge from 1990 to 1996 to correct the linearity of the simulated discharge. The results showed that during 1990–1996, the simulated discharge was close to the measured discharge, and the trend change was consistent (R2 = 0.83, RMSE = 10.94 × 109 m3). The corrected results are shown in the right panel in Figure 8. Considering the discharge results in the M–K test formula, we calculate that, in the last 30 years, the discharge of the Irrawaddy River has reached 6.37 × 106 m3/year, and the results are significant at the 90% confidence interval (Z = −1.55, slope = −6.37 × 10−3).
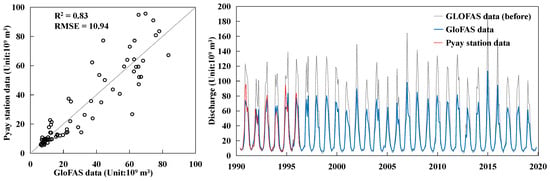
Figure 8.
The correction results (left) of and the corrected discharge changes (right) in the GloFAS discharge data based on the measured discharge data of the Pyay hydrologic station. The red dotted line is the discharge data measured from Pyay, the blue solid line is the corrected discharge data from the GloFAS, and the gray dotted line is the uncorrected discharge data from the GloFAS.
By multiplying the CTSM inversion dataset by the discharge of the corresponding section, we can estimate the change in the FTSM of the Irrawaddy River from 1990 to 2020 following unit conversion. Moreover, we synchronously display the results based on the measured dataset from the Pyay station and the estimation results from Sentinel-2. The results show (Figure 9) that the inversion results of the satellite images and the calculated results of the measured data are relatively similar in terms of their trend change and absolute values. The estimation results from Landsat and Sentinel-2 show consistent trends, further enhancing the credibility of the results. The results showed that the annual average FTSM of the Irrawaddy River during the 1990–2020 period displayed a downward trend. By incorporating the calculated seasonally averaged flux data into the M–K test formula, we calculated that in the last 30 years, the FTSM of the Irrawaddy River decreased at a rate of 3.9 mt/yr and was significant at the 99% confidence interval (slope = −3.91, Z = −3.28, p < 0.01). To reduce the data error, we calculated the annual averages of the data and then added the results to the measured dataset from the Pyay station before displaying them synchronously. The annual total FTSM change in the Irrawaddy River from 1966 to 2019 is plotted in Figure 9. The combination of measured and remote sensing data shows that the FTSM of the Irrawaddy River has been continuously declining for 55 years. Besset showed that the sediment supply to the Irrawaddy Delta decreased by approximately 30% between 1974 and 2014 [37]. The results of this study showed that the average annual total suspended solid flux in the Irrawaddy River was 340 mt/yr between 1966 and 1970 and 241 mt/yr between 2016 and 2020. The current transport flux of the Irrawaddy River has decreased by approximately 29.25%, which is very close to the results reported by Besset.
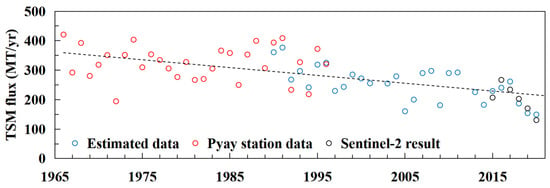
Figure 9.
Annual FTSM changes in the Irrawaddy River. The red circles refer to the measured FTSM data for Pyay station, the blue circles refer to the inverted FTSM data based on Landsat data, and the black circles refer to the inverted FTSM data based on Sentinel-2 data. The black dotted line is the linear fit of the change in the Irrawaddy River from 1966 to 2020.
5. Discussion
5.1. The FTSM of the Irrawaddy River Is Strongly Correlated with the CTSM and Discharge
The change in the FTSM depends on the change in river discharge and CTSM. We analyzed the correlation between the FTSM of the Irrawaddy River and its CTSM and discharge (Figure 10). The results show that in the Irrawaddy River, the FTSM is strongly and exponentially correlated with the CTSM and discharge, and both R2 values are greater than 0.9, which indicates that the contributions of the CTSM and discharge to the change in the FTSM in the Irrawaddy River are equivalent. Discharge had a greater correlation with the FTSM.
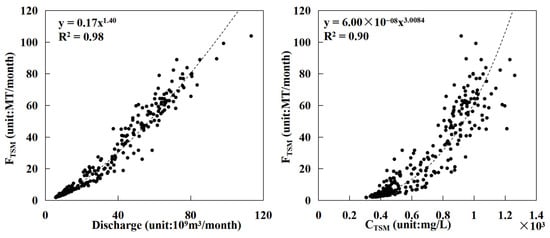
Figure 10.
Results of the correlation analysis between the FTSM and discharge (left) and between the FTSM and CTSM (right) in the Irrawaddy River from 1990 to 2020.
The discharge of the Irrawaddy River has been decreasing continuously since 1871 [38]. The M–K test results show that it has decreased at a rate of 6.37 × 106 m3 per year over the last 30 years. Moreover, the changes in precipitation and discharge trends in the basin are also somewhat similar (Figure 11). Precipitation directly changes river discharge and increases the likelihood that land-suspended logistics discharge into the river due to the land erosion caused by rainwater. In summary, it is clear that in the context of global change, natural changes, such as melting ice in the upper reaches of the Irrawaddy River basin and precipitation throughout the basin, can affect river discharge, thus changing the FTSM.
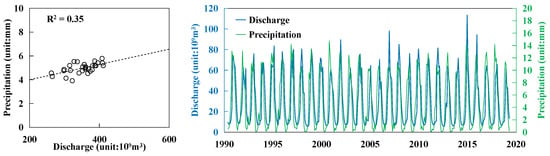
Figure 11.
Precipitation and discharge in the Irrawaddy River.
5.2. Influence of Suspended Matter Input from Land over the FTSM in the Irrawaddy River
One of the main sources of suspended matter in water bodies is land-based sediment yield. The characteristics of land classification in the basin are also important driving factors for the transport of CTSM in rivers. Changes in land use can change the transport of suspended matter from land to rivers. Deforestation, the conversion of forests to agricultural use, and the seasonal burning of farmland are examples of human activity that often increase the likelihood of suspended matter being washed into rivers during rainfall. Mining sand and gravel or sediment from the riverbed and riverbank will also change the content of suspended solids, thus affecting the stability of the riverbank and water quality.
Figure 12 shows the land classification results for the Irrawaddy River basin in 2000 and 2020. The land around the Irrawaddy River is mainly cropland. Agricultural activities and mining play key roles in the stability of riverine soils. Figure 13 shows that, except for the mutual conversion between vegetation types, most of the vegetation has been transferred to cropland, which is consistent with the conditions in Myanmar, a large agricultural country. A study noted that the distribution of mangroves in the Irrawaddy Delta decreased from 1978 to 2011, mainly due to the expansion of agriculture in this important economic region [25]. According to the land classification results, in the downstream Irrawaddy Delta (i.e., 15°N–20°N), the forest area decreased by approximately 144 km2, and the grassland and shrub land decreased by approximately 829 km2. The expansion of cultivated agricultural land in the lower reaches and the reduction in vegetation area may lead to a reduction in land stability in the Irrawaddy River Delta, which is not conducive to deltaic deposition, especially in the context of its sustained reduction in FTSM. In the upper reaches of the Irrawaddy Delta (i.e., 20°N–25°N), the total area of all types of vegetation increased by 1159 km2. The results in Figure 12 show that the vegetation coverage in the upper reaches of the delta has increased, some barelands and croplands have been converted to forests, and the artificial land area has increased. The region is attempting to restore its overall level of vegetation, and an increase in vegetation also increases the soil conservation capacity, which, in turn, reduces the contribution of land-based sediment yield to TSM; additionally, this may be one of the reasons for the reduction in downstream FTSM. Moreover, the agricultural center of gravity in the Irrawaddy River basin tends to shift to the lower reaches. Figure 14 describes the trend change in land types dominated by human activity and vegetation in the Irrawaddy Delta during 1991–2000, 2001–2010, and 2011–2020, as well as their correlations with the FTSM in the same period. The extent of human activity in the Irrawaddy Delta has gradually expanded over the last 30 years, and changes in the level of vegetation (R2 = 0.99) have a greater impact on the FTSM than human activity (R2 = 0.70). In general, the increase in vegetation in the upper reaches of the Irrawaddy Delta has enhanced the land conservation capacity of the region and reduced the sediment yield of terrestrial suspended solids, thus reducing the CTSM in the river.
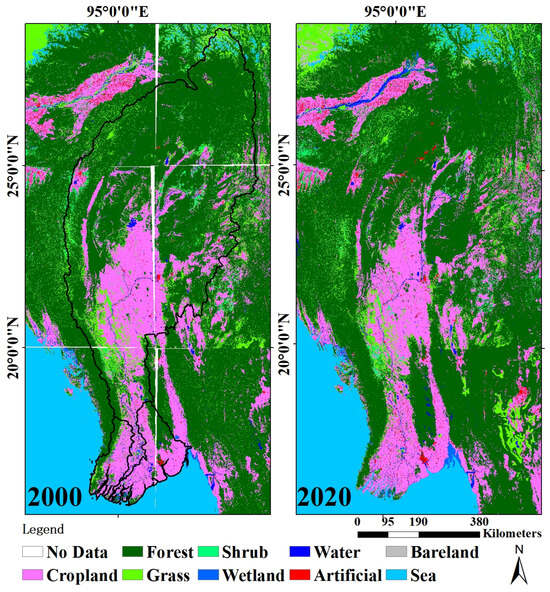
Figure 12.
Results of land classification in the Irrawaddy Basin.
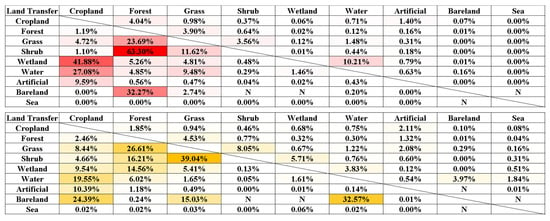
Figure 13.
The results of land transfer in the middle and upper reaches of the Irrawaddy River basin (red) and the lower reaches of the delta (yellow) represent the percentage of land area transferred from column elements to row elements; N represents no element transfer.
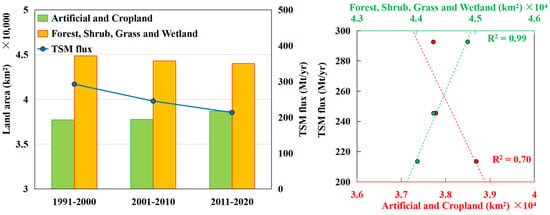
Figure 14.
(Left): land types dominated by human activity (yellow columns, which indicate artificial surface and cultivated land); land types dominated by vegetation (green columns, which indicate forests, shrubs, grasslands, and wetlands); and changes in FTSM over the three periods. (Right): the correlation between the area covered by land types dominated by human activity (red dots, indicating artificial surface and cultivated land) and the area covered by land types dominated by vegetation (green dots, indicating forests, shrubs, grasslands, and wetlands) and the change in FTSM.
6. Conclusions
In this study, an inversion model of the CTSM for the Irrawaddy River is constructed based on the existing measured FTSM and discharge data from the Irrawaddy River, and the CTSM for the Irrawaddy River from 1990 to 2020 is estimated using the L1 of the Landsat-8 OLI/TIRS and Landsat-5 TM products. Based on the CTSM and discharge data, we estimated the long-term change in the FTSM of the Irrawaddy River from 1990 to 2020, and our conclusions are described as follows:
- (1)
- The CTSM of the Irrawaddy River is evenly distributed between the upstream and downstream sections of the river. The waters with relatively high CTSM values are distributed along the east bank of the river channel, suggesting that the east bank may be among the main sources of terrestrial suspended solids. Considering the seasonal distribution trends, the CTSM in spring (i.e., March–May) was the lowest of the year. In summer (i.e., June–August) and autumn (i.e., September–November), the CTSM increases significantly. The CTSM in winter (i.e., December–February of the following year) is similar to but slightly greater than that in spring.
- (2)
- From 1990 to 2020, the CTSM of the Irrawaddy River exhibited a downward trend during the study period. Moreover, based on the discharge, we estimated the long-term change trend in the FTSM for the Irrawaddy River. Considering the calculated seasonally averaged flux results in the M–K test formula, we calculate that in the last 30 years, the FTSM in the Irrawaddy River decreased at a rate of 3.9 mt/yr and was significant at the 99% confidence interval (slope = −3.91, Z = −3.28, p < 0.01). The results of this study showed that between 1966 and 1970, the annual FTSM in the Irrawaddy River was 340 mt/yr; between 2016 and 2020, it was 241 mt/yr; and the current transport flux of the Irrawaddy River has decreased by approximately 29.25%.
The FTSM value of the Irrawaddy River is affected by discharge and CTSM, both of which strongly contribute to the FTSM. In terms of natural factors, the discharge of the Irrawaddy River itself has been experiencing a continuously decreasing trend for two centuries, and changes in the upstream freshwater input environment and precipitation are the major factors that have affected this change. In terms of human activity, the increase in vegetation in the upper reaches of the Irrawaddy Delta has increased the land conservation capacity of the region and reduced the inflow of terrestrial TSM.
Author Contributions
Conceptualization, Z.Z. and D.W.; methodology, Z.Z.; software, Z.Z. and J.H.; validation, X.H. and D.W.; formal analysis, Z.Z.; investigation, Z.Z.; resources, Z.Z., Q.Z. and F.G.; data curation, Z.Z. and F.G.; writing—original draft preparation, Z.Z.; writing—review and editing, D.W., Q.Z. and D.F.; visualization, Z.Z.; supervision, D.W.; project administration, D.W.; funding acquisition, D.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (Grant No. 2022YFC3104901), the Daya Bay Smart Ocean Intelligent Platform Project (contract No. 2020HZBXDYW04024), and the National Natural Science Foundation of China (contract No. 41476157).
Data Availability Statement
The data were retrieved from (1) United States Geological Survey (USGS), (2) Global Flood Awareness System (GloFAS), and (3) Global Precipitation Climatology Project (GPCP).
Acknowledgments
The authors would like to thank the USGS for excellent Landsat and Sentinel data. We also thank the satellite ground station and the satellite data processing and sharing center of SOED/SIO for help with the data processing. Our deepest gratitude goes to the editors and reviewers for their careful work and thoughtful suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, L.; Ni, J.; Chang, F.; Yue, Y.; Frolova, N.; Magritsky, D.; Borthwick, A.G.L.; Ciais, P.; Wang, Y.; Zheng, C.; et al. Global trends in water and sediment fluxes of the world’s large rivers. Sci. Bull. 2020, 65, 62–69. [Google Scholar] [CrossRef] [PubMed]
- Milliman, J.D.; Mei-e, R. River flux to the sea: Impact of human intervention on river systems and adjacent coastal areas. In Climate Change; Taylor & Francis: Abingdon, UK, 2021; pp. 57–83. [Google Scholar]
- Li, T.; Wang, S.; Liu, Y.; Fu, B.; Zhao, W. Driving forces and their contribution to the recent decrease in sediment flux to ocean of major rivers in China. Sci. Total Environ. 2018, 634, 534–541. [Google Scholar] [CrossRef] [PubMed]
- Darby, S.E.; Hackney, C.R.; Leyland, J.; Kummu, M.; Lauri, H.; Parsons, D.R. Fluvial sediment supply to a mega-delta reduced by shifting tropical-cyclone activity. Nature 2016, 539, 276–279. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Wang, D.; Gong, F.; He, X.; Bai, Y. A Study on the Flux of Total Suspended Matter in the Padma River in Bangladesh Based on Remote-Sensing Data. Water 2021, 13, 2373. [Google Scholar] [CrossRef]
- Portenga, E.W.; Bierman, P.R.; Trodick Jr, C.D.; Greene, S.E.; DeJong, B.D.; Rood, D.H.; Pavich, M.J. Erosion rates and sediment flux within the Potomac River basin quantified over millennial timescales using beryllium isotopes. GSA Bull. 2019, 131, 1295–1311. [Google Scholar] [CrossRef]
- Strick, R.J.; Ashworth, P.J.; Smith, G.H.S.; Nicholas, A.P.; Best, J.L.; Lane, S.N.; Parsons, D.R.; Simpson, C.J.; Unsworth, C.A.; Dale, J. Quantification of bedform dynamics and bedload sediment flux in sandy braided rivers from airborne and satellite imagery. Earth Surf. Process. Landf. 2019, 44, 953–972. [Google Scholar] [CrossRef]
- Rahman, M.M.; Goel, N.K.; Arya, D.S. Development of the Jamuneswari flood forecasting system: Case study in Bangladesh. J. Hydrol. Eng. 2012, 17, 1123–1140. [Google Scholar] [CrossRef]
- Gallay, M.; Martinez, J.M.; Mora, A.; Castellano, B.; Yépez, S.; Cochonneau, G.; Laraque, A. Assessing Orinoco river sediment discharge trend using MODIS satellite images. J. S. Am. Earth Sci. 2019, 91, 320–331. [Google Scholar] [CrossRef]
- Nechad, B.; Alvera-Azcaràte, A.; Ruddick, K.; Greenwood, N. Reconstruction of MODIS total suspended matter time series maps by DINEOF and validation with autonomous platform data. Ocean Dyn. 2011, 61, 1205–1214. [Google Scholar] [CrossRef]
- Gao, F.; Wang, Y.; Hu, X. Evaluation of the suitability of Landsat, MERIS, and MODIS for identifying spatial distribution patterns of total suspended matter from a self-organizing map (SOM) perspective. Catena 2019, 172, 699–710. [Google Scholar] [CrossRef]
- Pang, C.; Yu, W.; Yang, Y.; Han, D. An improved method for evaluating the seasonal variability of total suspended sediment flux field in the Yellow and East China Seas. Int. J. Sediment Res. 2011, 26, 1–14. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Zhu, G.; Liu, X.; Zhou, Y.; Xu, H.; Qin, B.; Liu, G.; Li, Y. Long-term remote monitoring of total suspended matter concentration in Lake Taihu using 250m MODIS-Aqua data. Remote Sens. Environ. 2015, 164, 43–56. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Chen, X.; Song, Q. Influence of the Three Gorges Dam on total suspended matters in the Yangtze Estuary and its adjacent coastal waters: Observations from MODIS. Remote Sens. Environ. 2014, 140, 779–788. [Google Scholar] [CrossRef]
- Liu, D.; Bai, Y.; He, X.; Pan, D.; Chen, C.-T.A.; Li, T.; Xu, Y.; Gong, C.; Zhang, L. Satellite-derived particulate organic carbon flux in the Changjiang River through different stages of the Three Gorges Dam. Remote Sens. Environ. 2019, 223, 154–165. [Google Scholar] [CrossRef]
- Crawford, C.J.; Roy, D.P.; Arab, S.; Barnes, C.; Vermote, E.; Hulley, G.; Gerace, A.; Choate, M.; Engebretson, C.; Micijevic, E.; et al. The 50-year Landsat collection 2 archive. Sci. Remote Sens. 2023, 8, 100103. [Google Scholar] [CrossRef]
- Chen, C.; Liang, J.; Yang, G.; Sun, W. Spatio-temporal distribution of harmful algal blooms and their correlations with marine hydrological elements in offshore areas, China. Ocean Coast. Manag. 2023, 238, 106554. [Google Scholar] [CrossRef]
- Syvitski, J.P.M.; Cohen, S.; Kettner, A.J.; Brakenridge, G.R. How important and different are tropical rivers?—An overview. Geomorphology 2014, 227, 5–17. [Google Scholar] [CrossRef]
- Furuichi, T.; Win, Z.; Wasson, R.J. Discharge and suspended sediment transport in the Ayeyarwady River, Myanmar: Centennial and decadal changes. Hydrol. Proc. 2009, 23, 1631–1641. [Google Scholar] [CrossRef]
- Robinson, R.A.J.; Bird, M.J.; Oo, N.W.; Hoey, T.B.; Maung Aye, M.; Higgitt, D.L.; Lu, X.X.; Sandar Aye, K.; Swe, A.; Tun, T.; et al. The Irrawaddy river sediment flux to the Indian Ocean: The original nineteenth-century data revisited. J. Geol. 2007, 115, 629–640. [Google Scholar] [CrossRef]
- Hennig, T. Damming the transnational Ayeyarwady basin. Hydropower and the water-energy nexus. Ren. Sust. Energy Rev. 2016, 65, 1232–1246. [Google Scholar] [CrossRef]
- SOBA. Synthesis Report State of the Basin Assessment; The World Bank: Yangon, Myanmar, 2017; Volume 1, p. 251. [Google Scholar]
- Chen, D.; Li, X.; Saito, Y.; Liu, J.P.; Duan, Y.; Liu, S.; Zhang, L. Recent evolution of the Irrawaddy (Ayeyarwady) Delta and the impacts of anthropogenic activities: A review and remote sensing survey. Geomorphology 2020, 365, 107231. [Google Scholar] [CrossRef]
- Chapman, H.; Bickle, M.; Thaw, S.H.; Thiam, H.N. Chemical fluxes from time series sampling of the Irrawaddy and Salween Rivers, Myanmar. Chem. Geol. 2015, 401, 15–27. [Google Scholar] [CrossRef]
- Webb, E.L.; Jachowski, N.R.A.; Phelps, J.; Friess, D.A.; Than, M.M.; Ziegler, A.D. Deforestation in the Ayeyarwady Delta and the conservation implications of an internationally-engaged Myanmar. Glob. Environ. Change 2014, 24, 321–333. [Google Scholar] [CrossRef]
- Alfieri, L.; Burek, P.; Dutra, E.; Krzeminski, B.; Muraro, D.; Thielen, J.; Pappenberger, F. GloFAS–global ensemble streamdischarge forecasting and flood early warning. Hydrol. Earth Sys. Sci. 2013, 17, 1161–1175. [Google Scholar] [CrossRef]
- Adler, R.; Wang, J.J.; Sapiano, M.; Huffman, G.; Chiu, L.; Xie, P.P.; NOAA CDR Program. Global Precipitation Climatology Project (GPCP) Climate Data Record (CDR), Version 2.3 (Monthly). Natl. Cent. Environ. Inf. 2016, 10, V56971M6. [Google Scholar] [CrossRef]
- Cao, X.; Chen, X.H.; Zhang, W.W.; Liao, A.; Chen, L.; Chen, Z.; Chen, J. Global cultivated land mapping at 30 m spatial resolution. Sci. Chin. Earth Sci. 2016, 59, 2275–2284. [Google Scholar] [CrossRef]
- Keukelaere, L.D.; Sterckx, S.; Adriaensen, S.; Knaeps, E.; Reusen, I.; Giardino, C.; Bresciani, M.; Hunter, P.; Neil, C.; Zande, D.V.; et al. Atmospheric correction of Landsat-8/OLI and Sentinel-2/MSI data using iCOR algorithm: Validation for coastal and inland waters. Eur. J. Remote Sens. 2018, 51, 525–542. [Google Scholar] [CrossRef]
- Bernardo, N.; Watanabe, F.; Rodrigues, T.; Alcântara, E. Atmospheric correction issues for retrieving total suspended matter concentrations in inland waters using OLI/Landsat-8 image. Adv. Space Res. 2017, 59, 2335–2348. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance dataset. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Shao, Z.; Cai, J.; Fu, P.; Hu, L.; Liu, T. Deep learning-based fusion of Landsat-8 and Sentinel-2 images for a harmonized surface reflectance product. Remote Sens. Environ. 2019, 235, 111425. [Google Scholar] [CrossRef]
- Zhang, H.K.; Roy, D.P.; Yan, L.; Li, Z.; Huang, H.; Vermote, E.; Skakun, S.; Roger, J.-C. Characterization of Sentinel-2A and Landsat-8 top of atmosphere, surface, and nadir BRDF adjusted reflectance and NDVI differences. Remote Sens. Environ. 2018, 215, 482–494. [Google Scholar] [CrossRef]
- Bailey, S.W.; Werdell, P.J. A multi-sensor approach for the on-orbit validation of ocean color satellite data products. Remote Sens. Environ. 2006, 102, 12–23. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank correlation methods. Br. J. Psychol. 1990, 25, 86–91. [Google Scholar] [CrossRef]
- Besset, M.; Anthony, E.J.; Bouchette, F. Multi-decadal variations in delta shorelines and their relationship to river sediment supply: An assessment and review. Earth Sci. Rev. 2019, 193, 199–219. [Google Scholar] [CrossRef]
- Stamp, L.D. The Irawadi River. Geogr. J. 1940, 95, 329–352. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).