Downscaling Land Surface Temperature Derived from Microwave Observations with the Super-Resolution Reconstruction Method: A Case Study in the CONUS
Abstract
1. Introduction
2. Materials
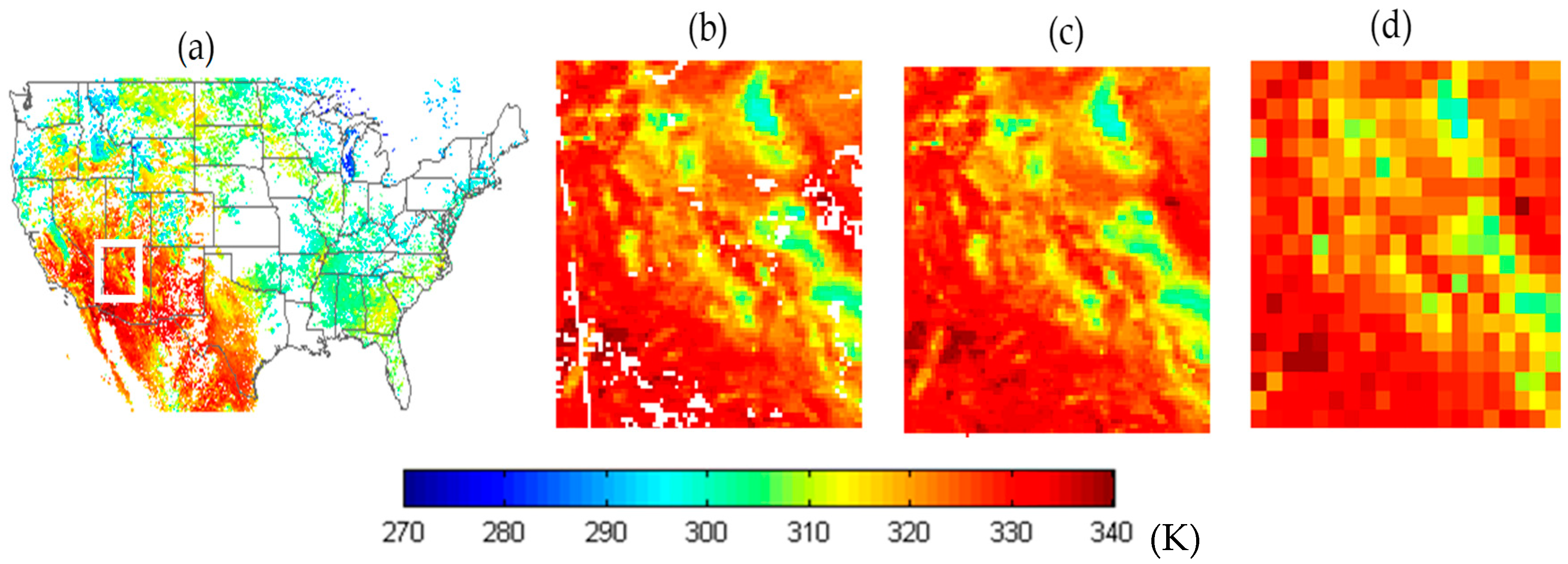
2.1. Satellite Data
2.2. In Situ Data
3. Methods
3.1. Multi-Image SRR
3.1.1. The ML-Based SRR
3.1.2. The POCS-Based SRR
3.2. Single-Image Super Resolution (SISR)
3.2.1. The Example-Based Method
3.2.2. The Self-Similarity Method
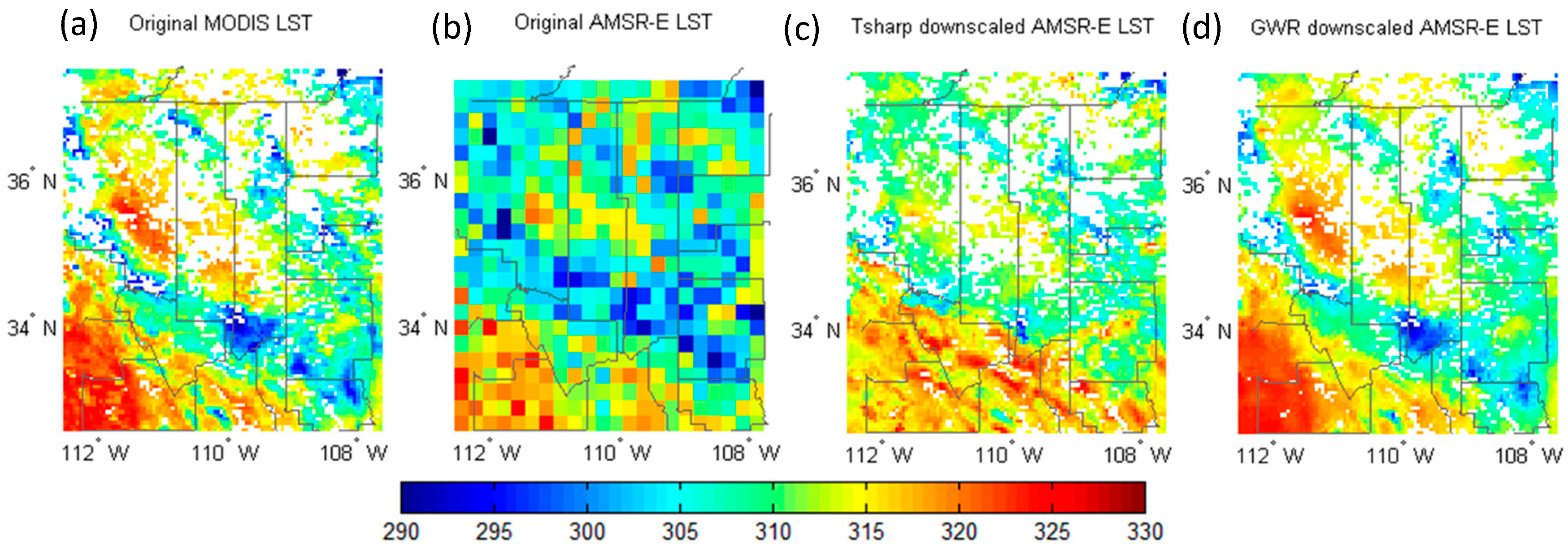
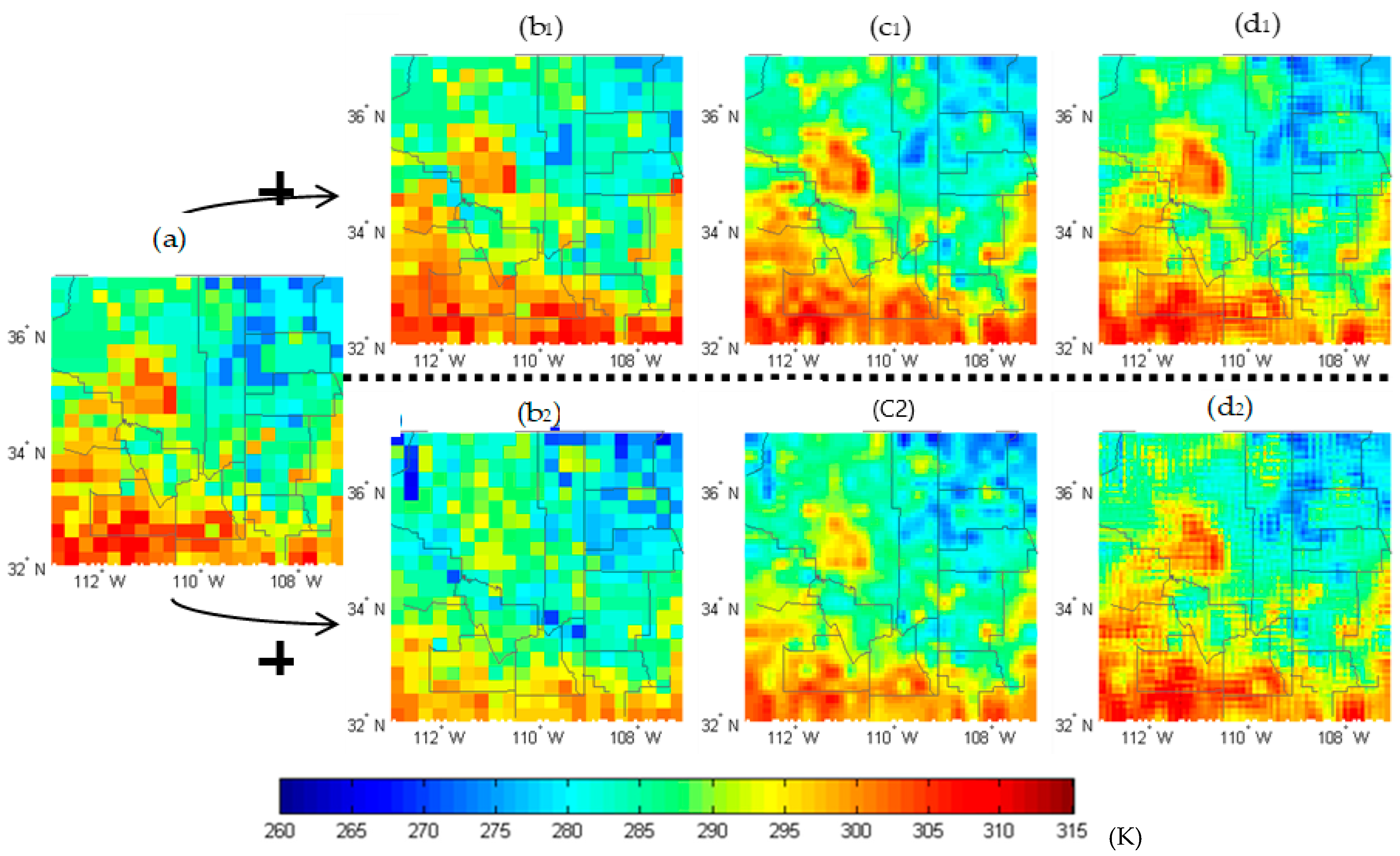
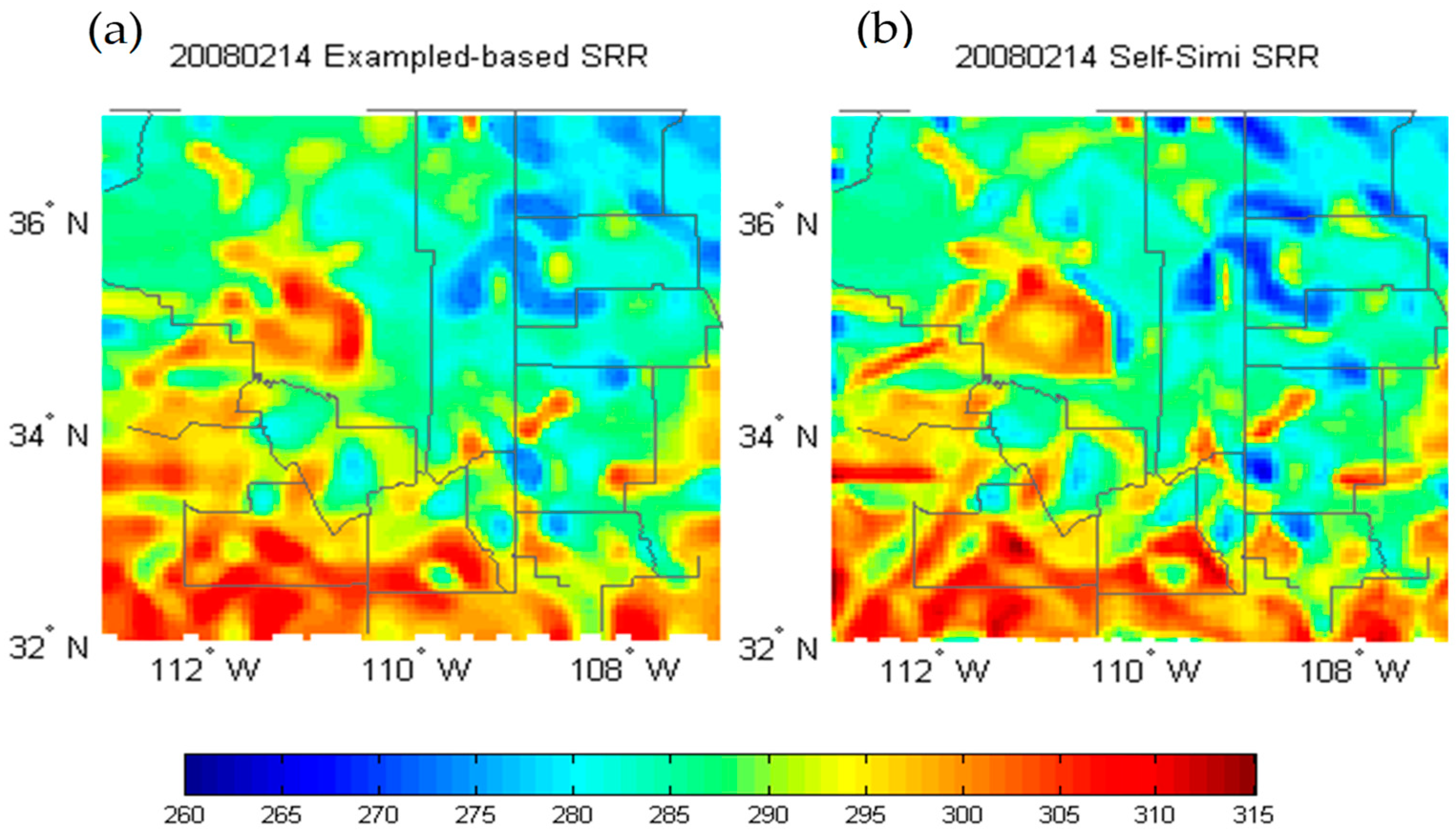
4. Results
4.1. Multiple-Image Downscaling
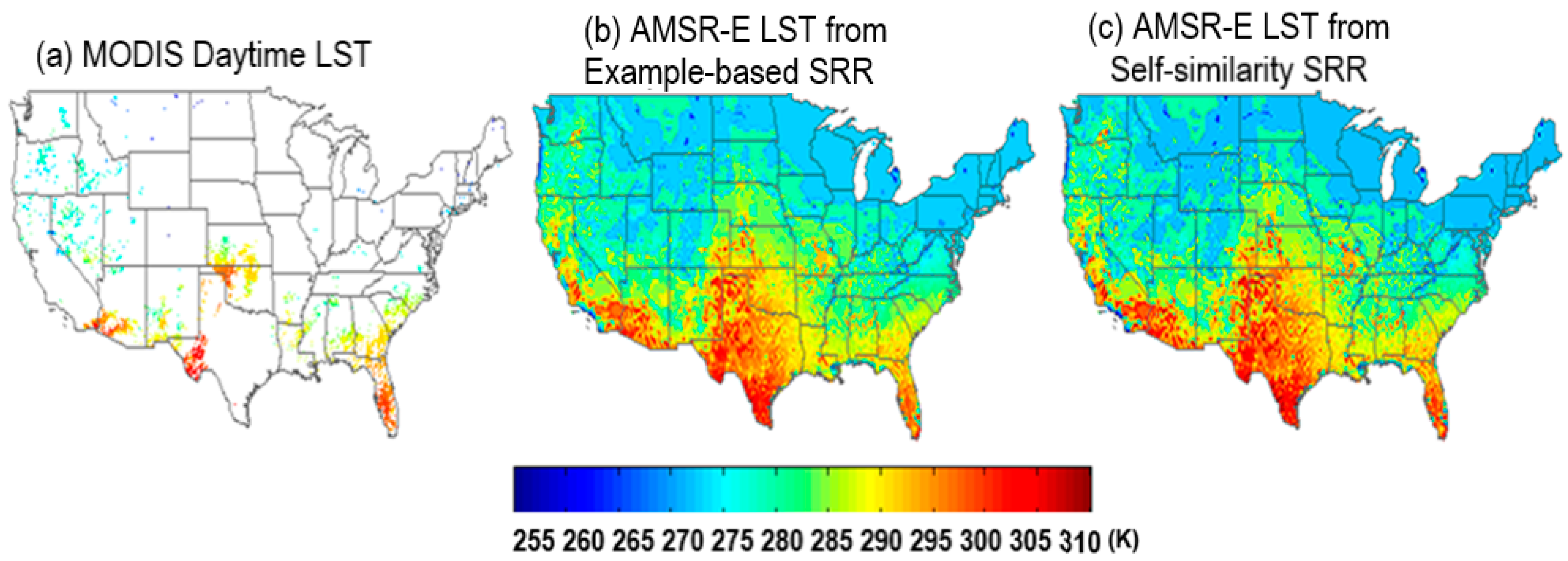
4.2. Single-Image Downscaling
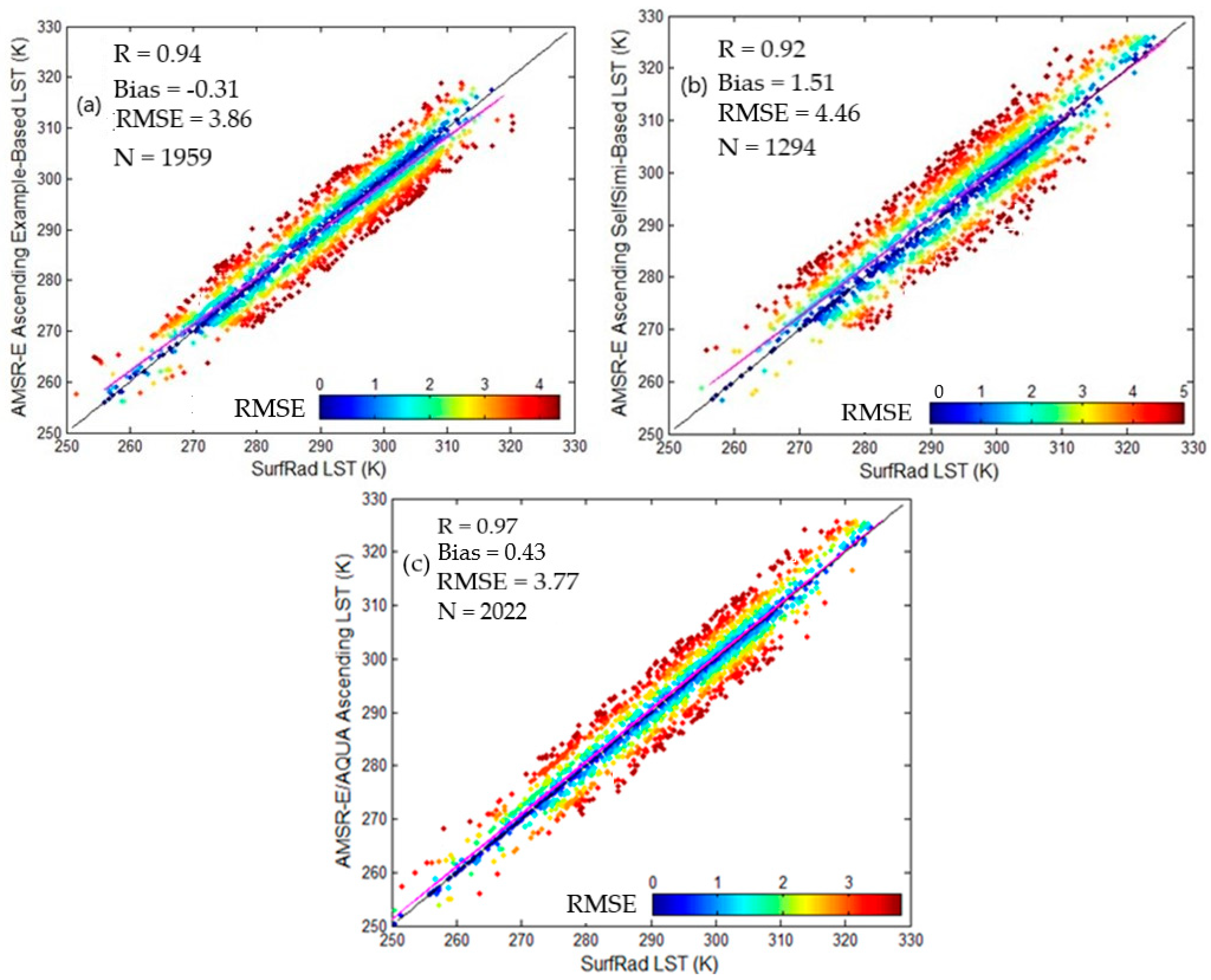
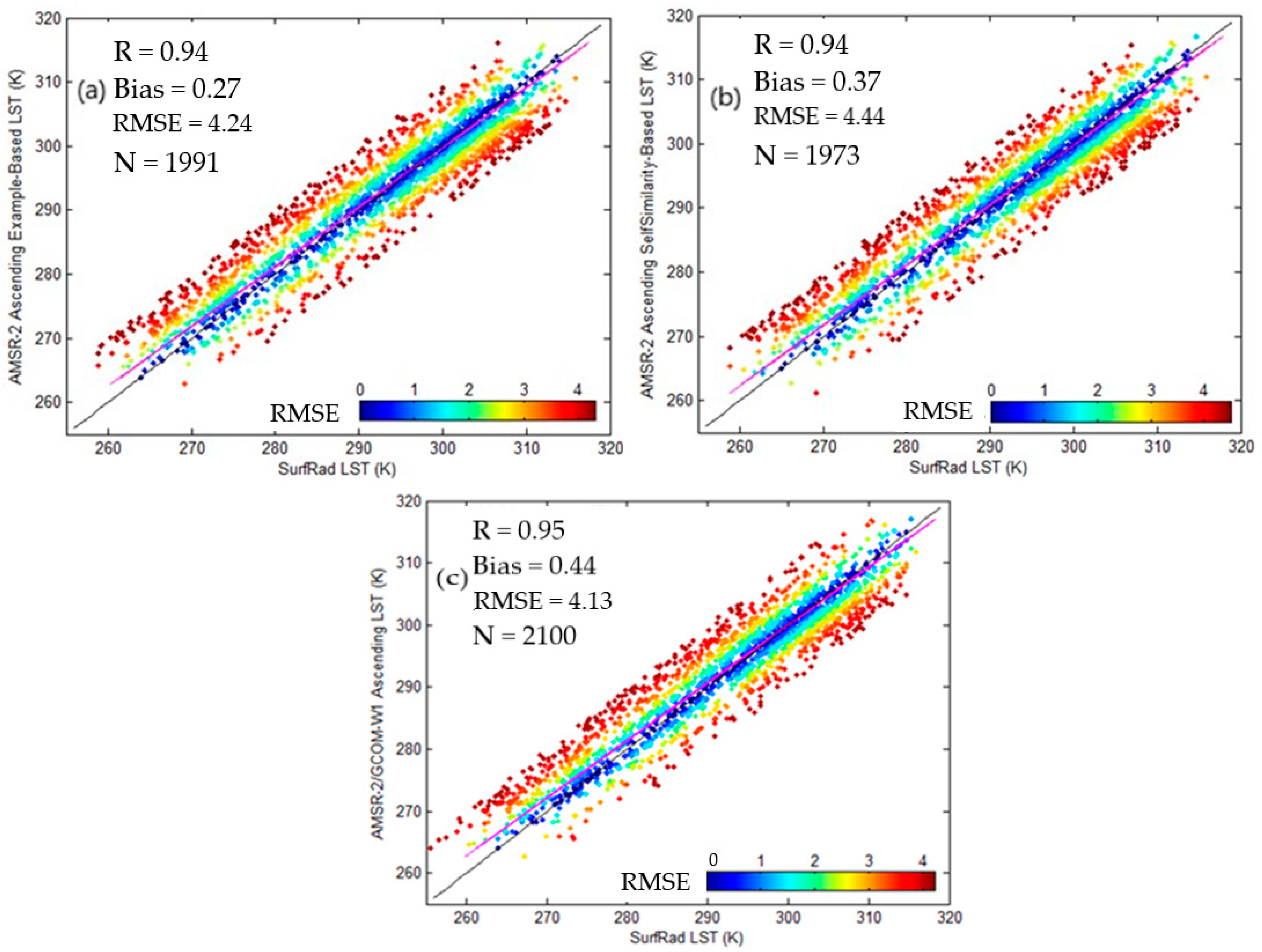
4.3. Results from the Validation against Ground Observations
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Houborg, R.; Starks, P.J.; Agam, N. A thermal-based remote sensing technique for routine mapping of land-surface carbon, water and energy fluxes from field to regional scales. Remote Sens. Environ. 2008, 112, 4227–4241. [Google Scholar] [CrossRef]
- Keramitsoglou, I.; Kiranoudis, C.T.; Weng, Q. Downscaling Geostationary Land Surface Temperature Imagery for Urban Analysis. IEEE Trans. Geosci. Remote Sens. 2013, 10, 1253–1257. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y. Monitoring surface urban heat island formation in a tropical mountain city using Landsat data (1987–2015). ISPRS J. Photogramm. Remote Sens. 2017, 133, 18–29. [Google Scholar] [CrossRef]
- Stathopoulou, M.; Cartalis, C. Downscaling AVHRR land surface temperatures for improved surface urban heat island intensity estimation. Remote Sens. Environ. 2009, 113, 2592–2605. [Google Scholar] [CrossRef]
- Hu, L.Q.; Brunsell, N.A. The impact of temporal aggregation of land surface temperature data for surface urban heat island (SUHI) monitoring. Remote Sens. Environ. 2013, 134, 162–174. [Google Scholar] [CrossRef]
- Leng, P.; Song, X.; Li, Z.L.; Ma, J.; Zhou, F.; Li, S. Bare surface soil moisture retrieval from the synergistic use of optical and thermal infrared data. Int. J. Remote Sens. 2014, 35, 988–1003. [Google Scholar] [CrossRef]
- Carlson, T. An overview of the ’triangle method’ for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Chauhan, N.S.; Miller, S.; Ardanuy, P. Spaceborne soil moisture estimation at high resolution: A microwave-optical/IR synergistic approach. Int. J. Remote Sens. 2003, 24, 4599–4622. [Google Scholar] [CrossRef]
- Lu, J.; Tang, R.; Tang, H.; Li, Z.L. Derivation of daily evaporative fraction based on temporal variations in surface temperature, air temperature, and net radiation. Remote Sens. 2013, 5, 5369–5396. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Alfieri, J.G.; Gao, F.; Hain, C.; Prueger, J.H.; Evett, S.; Colaizzi, P.; Howell, T.; Chavez, J.L. Mapping daily evapotranspiration at Landsat spatial scales during the BEAREX’08 field campaign. Adv. Water Resour. 2012, 50, 162–177. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 2. Surface moisture climatology. J. Geophys. Res. Atmos. 2007, 112, D11. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. J. Geophys. Res. Atmos. 2007, 112, D10. [Google Scholar] [CrossRef]
- Wang, P.X.; Li, X.W.; Gong, J.Y.; Song, C. Vegetation temperature condition index and its application for drought monitoring. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium 2001, Sydney, Australia, 9–13 July 2001; pp. 141–143. [Google Scholar]
- Wan, Z.M.; Wang, P.X.; Li, X.W. Using MODIS land surface temperature and normalized difference vegetation index products for monitoring drought in the southern Great Plains, USA. Int. J. Remote Sens. 2004, 25, 61–72. [Google Scholar] [CrossRef]
- Lorenz, D.J.; Otkin, J.A.; Svoboda, M.; Hain, C.R.; Anderson, M.C.; Zhong, Y. Predicting the US Drought Monitor (USDM) using precipitation, soil moisture, and evapotranspiration anomalies, part II: Intraseasonal drought intensification forecasts. J. Hydrometeorol. 2017, 18, 1963–1982. [Google Scholar] [CrossRef]
- Pinheiro, A.C.T.; Mahoney, R.; Privette, J.L.; Tucker, C.J. Development of a daily long term record of NOAA-14 AVHRR land surface temperature over Africa. Remote Sens. Environ. 2006, 103, 153–164. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. Land-surface temperature measurement from space: Physical principles and inverse modeling. IEEE Trans. Geosci. Remote Sens. 1989, 27, 268–278. [Google Scholar]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Wan, Z.; Li, Z. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar]
- Li, H.; Sun, D.; Yu, Y.; Wang, H.; Liu, Y.; Liu, Q.; Du, Y.; Wang, H.; Cao, B. Evaluation of the VIIRS and MODIS LST products in an arid area of Northwest China. Remote Sens. Environ. 2015, 142, 111–121. [Google Scholar] [CrossRef]
- Sun, D.; Pinker, R.T. Estimation of land surface temperature from a Geostationary Operational Environmental Satellite (GOES-8). J. Geophys. Res. 2003, 108, D11. [Google Scholar] [CrossRef]
- Sun, D.; Pinker, R.T.; Basara, J.B. Land surface temperature estimation from the next generation of Geostationary Operational Environmental Satellites: GOES M-Q. J. Appl. Meteorol. Climatol. 2004, 43, 363–372. [Google Scholar] [CrossRef]
- Sun, D.; Yu, Y.; Yang, H.; Liu, Q.; Shi, J. Inter-comparison of land surface temperature retrieved from GOES-East, GOES-West, and MODIS. Int. J. Digit. Earth 2013, 8, 476–494. [Google Scholar] [CrossRef]
- Sun, D.; Yu, Y.; Fang, L.; Liu, Y. Toward an operational land surface temperature algorithm for GOES. J. Appl. Meteor. Climatol. 2013, 52, 1974–1986. [Google Scholar] [CrossRef]
- McFarland, M.J.; Miller, R.L.; Neale, C.M.U. Land surface temperature derived from the SSM/I passive microwave brightness temperatures. IEEE Trans. Geosci. Remote Sens. 1990, 28, 839–845. [Google Scholar] [CrossRef]
- Davis, D.; Chen, Z.; Nwang, H.N.; Tsang, L.; Njoku, E. Solving inverse problems by Bayesian iterative inversion of a forward model with applications to parameter mapping using SMMR remote sensing data. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1182–1193. [Google Scholar] [CrossRef]
- Njoku, E.G. Surface Temperature Estimation over Land Using Satellite Microwave Radiometry; CRC Press: Boca Raton, FL, USA, 1993; pp. 1–28, Chapter 93-0446. [Google Scholar]
- Basist, A.; Grody, N.C.; Peterson, T.C.; Williams, C.N. Using the special sensor microwave/imager to monitor land surface temperatures, wetness, and snow cover. J. Appl. Meteor. 1998, 37, 888–911. [Google Scholar] [CrossRef]
- Njoku, E.G.; Li, L. Retrieval of land surface parameters using passive microwave measurements at 6 to 18 GHz. IEEE Trans. Geosci. Remote Sens. 1999, 37, 79–93. [Google Scholar] [CrossRef]
- Holmes, T.R.H.; de Jeu, R.A.M.; Owe, M.; Dolman, A.J. Land surface temperature from Ka band (37 GHz) passive microwave observations. J. Geophys. Res. 2009, 114, D04113. [Google Scholar] [CrossRef]
- André, C.; Ottlé, C.; Royer, A.; Maignan, F. Land surface temperature retrieval over circumpolar Arctic using SSM/I–SSMIS and MODIS data. Remote Sens. Environ. 2015, 162, 1–10. [Google Scholar] [CrossRef]
- Prigent, C.; Jimenez, C.; Aires, F. Toward “all weather,” long record, and real-time land surface temperature retrievals from microwave satellite observations. J. Geophys. Res. Atmos. 2016, 121, 5699–5717. [Google Scholar] [CrossRef]
- Ermida, S.L.; DaCamara, C.C.; Trigo, I.F.; Pires, A.C.; Ghent, D.; Remedios, J. Modelling directional effects on remotely sensed land surface temperature. Remote Sens. Environ. 2017, 190, 56–69. [Google Scholar] [CrossRef]
- Mao, K.B.; Shi, J.C.; Li, Z.L. A physics-based statistical algorithm for retrieving land surface temperature from AMSR-E passive microwave data. Sci. China Ser. D Earth Sci. 2007, 50, 1115–1120. [Google Scholar] [CrossRef]
- Mao, K.; Shi, J.; Tang, H.; Guo, Y.; Qiu, Y. A neural-network technique for retrieving land surface temperature from AMSR-E passive microwave data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium 2007, Barcelona, Spain, 23–27 July 2007; pp. 4422–4425. [Google Scholar]
- Sun, D.; Li, Y.; Zhan, X.; Houser, P.; Yang, C.; Chiu, L.; Yang, R. Land surface temperature derivation under all sky conditions through integrating AMSR-E/AMSR-2 and MODIS/GOES observations. Remote Sens. 2019, 11, 1704. [Google Scholar] [CrossRef]
- Kou, X.; Jiang, L.; Bo, Y.; Yan, S.; Chai, L. Estimation of land surface temperature through blending MODIS and AMSR-E data with the Bayesian maximum entropy method. Remote Sens. 2016, 8, 105. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Leng, P. A framework for the retrieval of all-weather land surface temperature at a high spatial resolution from polar-orbiting thermal infrared and passive microwave data. Remote Sens. Environ. 2017, 195, 107–117. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Göttsche, F.-M.; Zhan, W.; Liu, S.; Cao, R. A method based on temporal component decomposition for estimating 1-km all-weather land surface temperature by merging satellite thermal infrared and passive microwave observations. IEEE Trans. Geosci. Remote Sens. 2019, 7, 4670–4691. [Google Scholar] [CrossRef]
- Xu, S.; Cheng, J.; Zhang, Q. Reconstructing all-weather land surface temperature using the Bayesian maximum entropy method over the tibetan plateau and heihe river basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3307–3316. [Google Scholar] [CrossRef]
- Atkinson, P.M. Downscaling in remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 22, 106–114. [Google Scholar] [CrossRef]
- Jin, Y.; Ge, Y.; Wang, J.; Heuvelink, G.B.M.; Wang, L. Geographically Weighted Area-to-Point Regression Kriging for Spatial Downscaling in Remote Sensing. Remote Sens. 2018, 10, 579. [Google Scholar] [CrossRef]
- Nasrollahi, K.; Moeslund, T.B. Super-resolution: A comprehensive survey. Mach. Vis. Appl. 2014, 25, 1423–1468. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index-radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar]
- Gao, F.; Kustas, W.; Anderson, M. A data mining approach for sharpening thermal satellite imagery over land. Remote Sens. 2012, 4, 3287–3319. [Google Scholar] [CrossRef]
- Inamdar, A.K.; French, A. Disaggregation of GOES land surface temperatures using surface emissivity. Geophys. Res. Lett. 2009, 36, 1–5. [Google Scholar] [CrossRef]
- Essa, W.; Verbeiren, B.; van der Kwast, J.; Van de Voorde, T.; Batelaan, O. Evaluation of the DisTrad thermal sharpening methodology for urban areas. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 163–172. [Google Scholar] [CrossRef]
- Zakšek, K.; Oštir, K. Downscaling land surface temperature for urban heat island diurnal cycle analysis. Remote Sens. Environ. 2012, 117, 114–124. [Google Scholar] [CrossRef]
- Sun, D.; Kafatos, M. Note on the NDVI-LST relationship and the use of temperature-related drought indices over North America. Geophys. Res. Lett. 2007, 34, L24406. [Google Scholar] [CrossRef]
- Duan, S.; Li, Z. Spatial downscaling of MODIS land surface temperatures using geographically weighted regression: Case study in northern China. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6458–6469. [Google Scholar] [CrossRef]
- Li, W.; Ni, L.; Li, Z.; Duan, S.B.; Wu, H. Evaluation of machine learning algorithms in spatial downscaling of MODIS land surface temperature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2299–2307. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Yang, Y.; Cao, C.; Pan, X.; Li, X.; Zhu, X. Downscaling land surface temperature in an arid area by using multiple remote sensing indices with random forest regression. Remote Sens. 2017, 9, 789. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, N.; Cheng, J.; Xu, S. A Stepwise Downscaling Method for Generating High-Resolution Land Surface Temperature from AMSR-E Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5669–5681. [Google Scholar] [CrossRef]
- Akgun, T.; Altunbasak, Y.; Mersereau, R.M. Super-resolution reconstruction of hyperspectral images. IEEE Trans. Image Process 2005, 14, 1860–1875. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Ng, M.K.; Li, P.; Zhang, L. Super-resolution reconstruction algorithm to MODIS remote sensing images. Comput. J. 2009, 52, 90–100. [Google Scholar] [CrossRef]
- Zhang, H.; Zeyu Yang, Z.; Zhang, L.; Shen, H. Super-Resolution Reconstruction for Multi-Angle Remote Sensing Images Considering Resolution Differences. Remote Sens. 2014, 6, 637–657. [Google Scholar] [CrossRef]
- Galbraith, A.E.; Theiler, J.; Thome, K.J.; Ziolkowski, R.W. Resolution enhancement of multilook imagery for the multispectral thermal imager. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1964–1977. [Google Scholar] [CrossRef]
- Kawanishi, T.; Sezai, T.; Ito, Y.; Imaoka, K.; Takeshima, T.; Ishido, Y.; Shibata, A.; Miura, M.; Inahata, H.; Spencer, R.W. The Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E), NASDA’s contribution to the EOS for global energy and water cycle studies. IEEE Trans. Geosci. Remote Sens. 2003, 41, 184–194. [Google Scholar] [CrossRef]
- McCabe, M.F.; Gao, H.; Wood, E.F. Evaluation of AMSR-E-derived soil moisture retrievals using ground-based and PSR airborne data during SMEX02. J. Hydrometeorol. 2005, 6, 864–877. [Google Scholar] [CrossRef]
- Japan Aerospace Exploration Agency. GCOM-W1 “SHIZUKU” Data Users Handbook; Tsukuba Space Center, Japan Aerospace Exploration Agency: Ibaraki, Japan, 2013. [Google Scholar]
- Hulley, G.C.; Hook, S.J. Intercomparison of versions 4, 4.1 and 5 of the MODIS Land Surface Temperature and Emissivity products and validation with laboratory measurements of sand samples from the Namib desert, Namibia. Remote Sens. Environ. 2009, 113, 1313–1318. [Google Scholar] [CrossRef]
- Huete, A.; Justice, C.; van Leeuwen, W. MODIS Vegetation Index (MOD13). 1999. Available online: https://modis.gsfc.nasa.gov/data/atbd/atbd_mod13.pdf (accessed on 20 January 2024).
- Peng, X.; Wu, W.; Zheng, Y.; Sun, J.; Hu, T.; Wang, P. Correlation analysis of land surface temperature and topographic elements in Hangzhou, China. Sci. Rep. 2020, 10, 10451. [Google Scholar] [CrossRef] [PubMed]
- Gesch, D.; Oimoen, M.; Greenlee, S.; Nelson, C.; Steuck, M.; Tyler, D. The national elevation dataset. Photogramm. Engineer. Remote Sens. 2002, 68, 5–11. [Google Scholar]
- Park, S.C.; Park, M.K.; Kang, M.G. Super-resolution image reconstruction: A technical overview. IEEE Signal Process. Mag. 2003, 20, 21–36. [Google Scholar] [CrossRef]
- Irani, M.; Peleg, S. Improving resolution by image registration. CVGIP Graph. Models Image Process. 1991, 53, 231–239. [Google Scholar] [CrossRef]
- Shen, W.; Fang, L.; Chen, X.; Xu, H. Projection onto Convex Sets Method in Space-Frequency Domain for Super Resolution. J. Comput. 2014, 9, 1959–1966. [Google Scholar] [CrossRef]
- Trussell, H.; Civanlar, M. The feasible solution in signal restoration. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 201–212. [Google Scholar] [CrossRef]
- Aguena, M.L.; Mascarenhas, N.D. Multispectral image data fusion using POCS and super-resolution. Comput. Vis. Image Underst. 2006, 102, 178–187. [Google Scholar] [CrossRef]
- Tekalp, A.M.; Ozkan, M.K.; Sezan, M.I. High-resolution image reconstruction from lower-resolution image sequences and space-varying image restoration. In Proceedings of the ICASSP-92: 1992 IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 23–26 March 1992; Volume 3, pp. 169–172. [Google Scholar]
- Freeman, W.T.; Jones, T.R.; Pasztor, E.C. Example-based super-resolution. IEEE Comput. Graph. Appl. 2002, 22, 56–65. [Google Scholar] [CrossRef]
- Kim, K.I.; Kwon, Y. Example-based learning for single-image super-resolution. In Joint Pattern Recognition Symposium; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Said, E.H.; Homaifar, A.; Grossberg, M. Creating virtual sensors using learning based super-resolution and data fusion. In Proceedings of the 2009 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2009; pp. 1–9. [Google Scholar]
- Kim, C.; Choi, K.; Ra, J.B. Improvement on learning-based super-resolution by adopting residual information and patch reliability. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 1197–1200. [Google Scholar]
- Yang, C.Y.; Huang, J.B.; Yang, M.H. Exploiting self-similarities for single frame super-resolution. In Lecture Notes in Computer Science, Proceedings of the Asian Conference on Computer Vision, Queenstown, New Zealand, 8–12 November 2010; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Glasner, D.; Bagon, S.; Irani, M. Super-Resolution from a Single Image. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009. [Google Scholar] [CrossRef]
- Huang, J.B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar]
- Nasonov, A.V.; Krylov, A.S. Scale-space method of image ringing estimation. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 2793–2796. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Sun, D.; Zhan, X.; Houser, P.; Yang, C.; Qu, J.J. Downscaling Land Surface Temperature Derived from Microwave Observations with the Super-Resolution Reconstruction Method: A Case Study in the CONUS. Remote Sens. 2024, 16, 739. https://doi.org/10.3390/rs16050739
Li Y, Sun D, Zhan X, Houser P, Yang C, Qu JJ. Downscaling Land Surface Temperature Derived from Microwave Observations with the Super-Resolution Reconstruction Method: A Case Study in the CONUS. Remote Sensing. 2024; 16(5):739. https://doi.org/10.3390/rs16050739
Chicago/Turabian StyleLi, Yu, Donglian Sun, Xiwu Zhan, Paul Houser, Chaowei Yang, and John J. Qu. 2024. "Downscaling Land Surface Temperature Derived from Microwave Observations with the Super-Resolution Reconstruction Method: A Case Study in the CONUS" Remote Sensing 16, no. 5: 739. https://doi.org/10.3390/rs16050739
APA StyleLi, Y., Sun, D., Zhan, X., Houser, P., Yang, C., & Qu, J. J. (2024). Downscaling Land Surface Temperature Derived from Microwave Observations with the Super-Resolution Reconstruction Method: A Case Study in the CONUS. Remote Sensing, 16(5), 739. https://doi.org/10.3390/rs16050739






