Monitoring Soil Salinity Classes through Remote Sensing-Based Ensemble Learning Concept: Considering Scale Effects
Abstract
1. Introduction
2. Materials and Methods
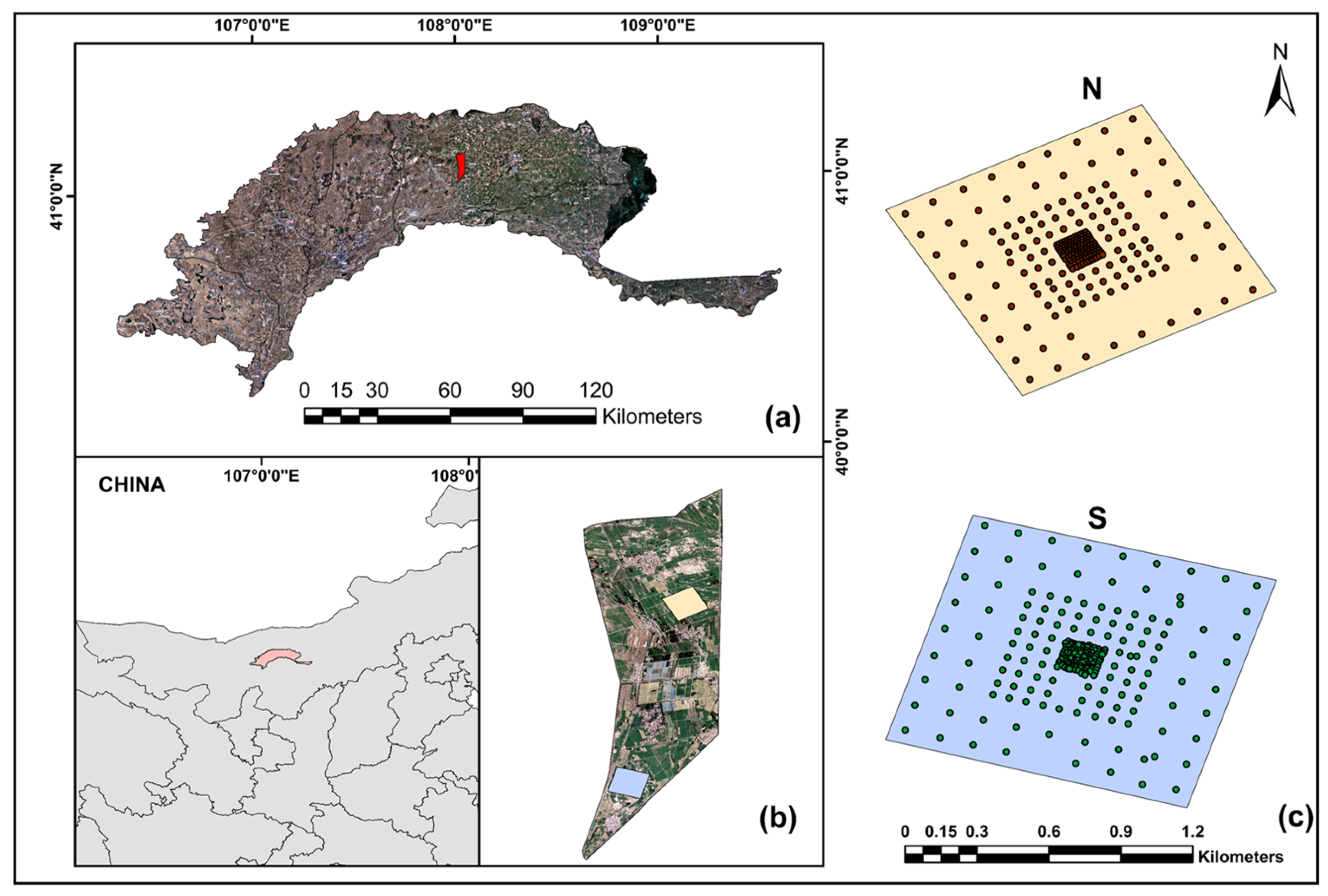
2.1. Study Area
2.2. Data Acquisition and Processing
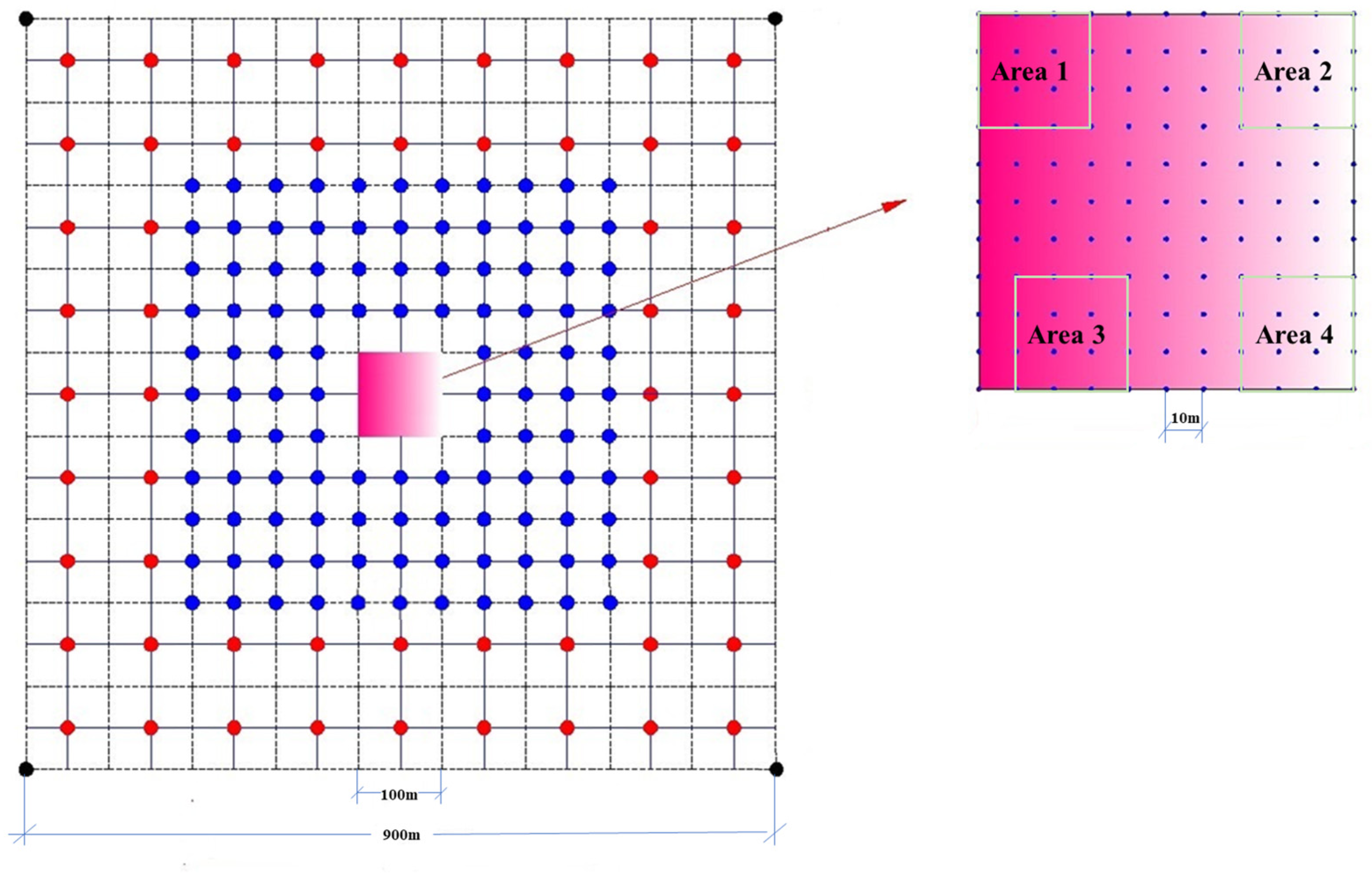
2.2.1. Salt Data Collection and Processing
2.2.2. Landsat 8 Data Acquisition and Processing
2.2.3. Remote Sensing Pixel-Scale Salt Content Acquisition
- (1)
- Normality test of the data
- (2)
- Variance function
- (3)
- Kriging interpolation
2.2.4. Classification Criteria for Soil Salinization
2.3. Spectral Index Construction
2.4. Feature Selection
3. Modeling Methods and Evaluation Metrics
3.1. Modeling Methods
3.2. Model Evaluation Metrics
4. Results and Analysis
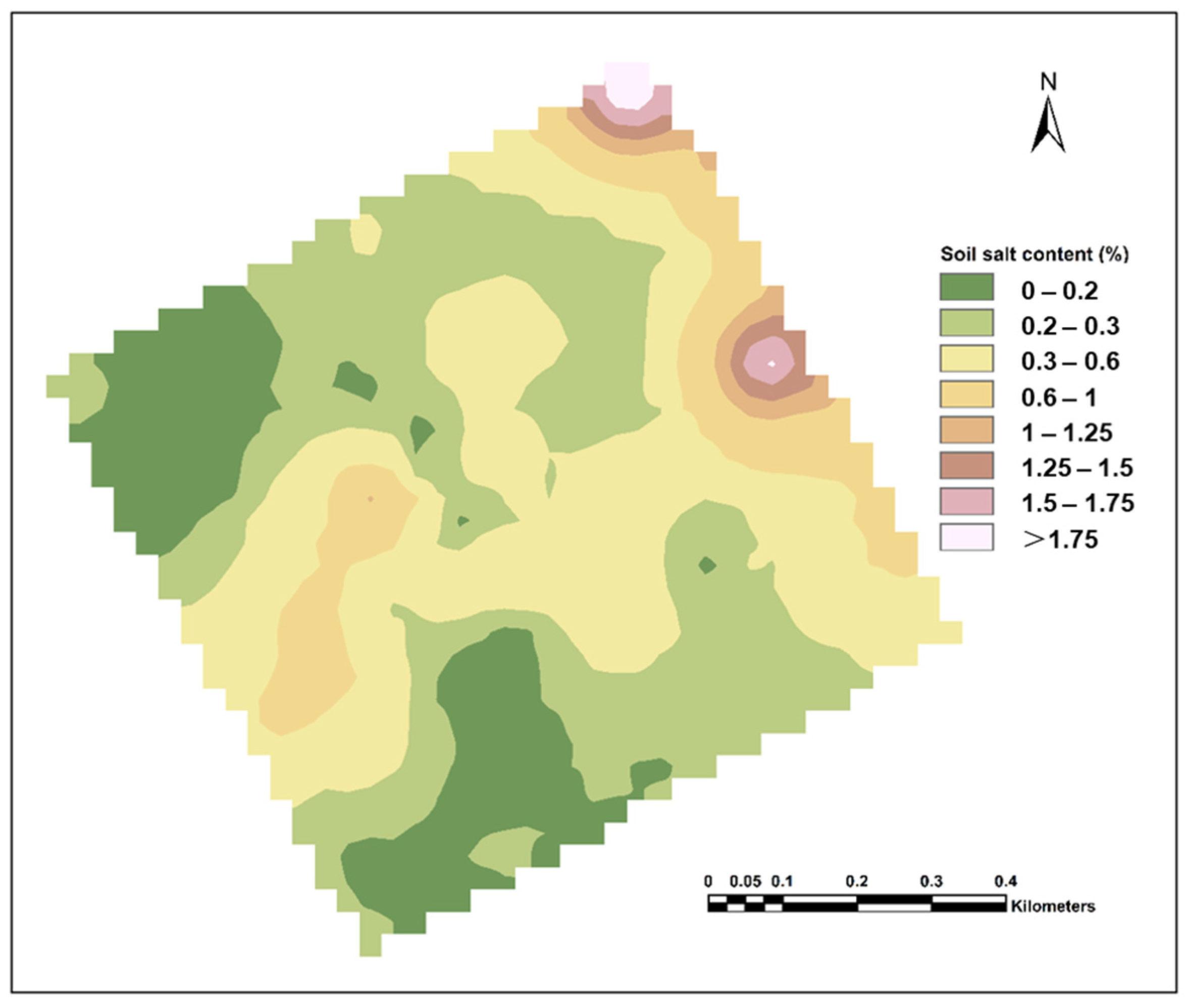
4.1. Descriptive Statistics of the Measured Soil Salinity
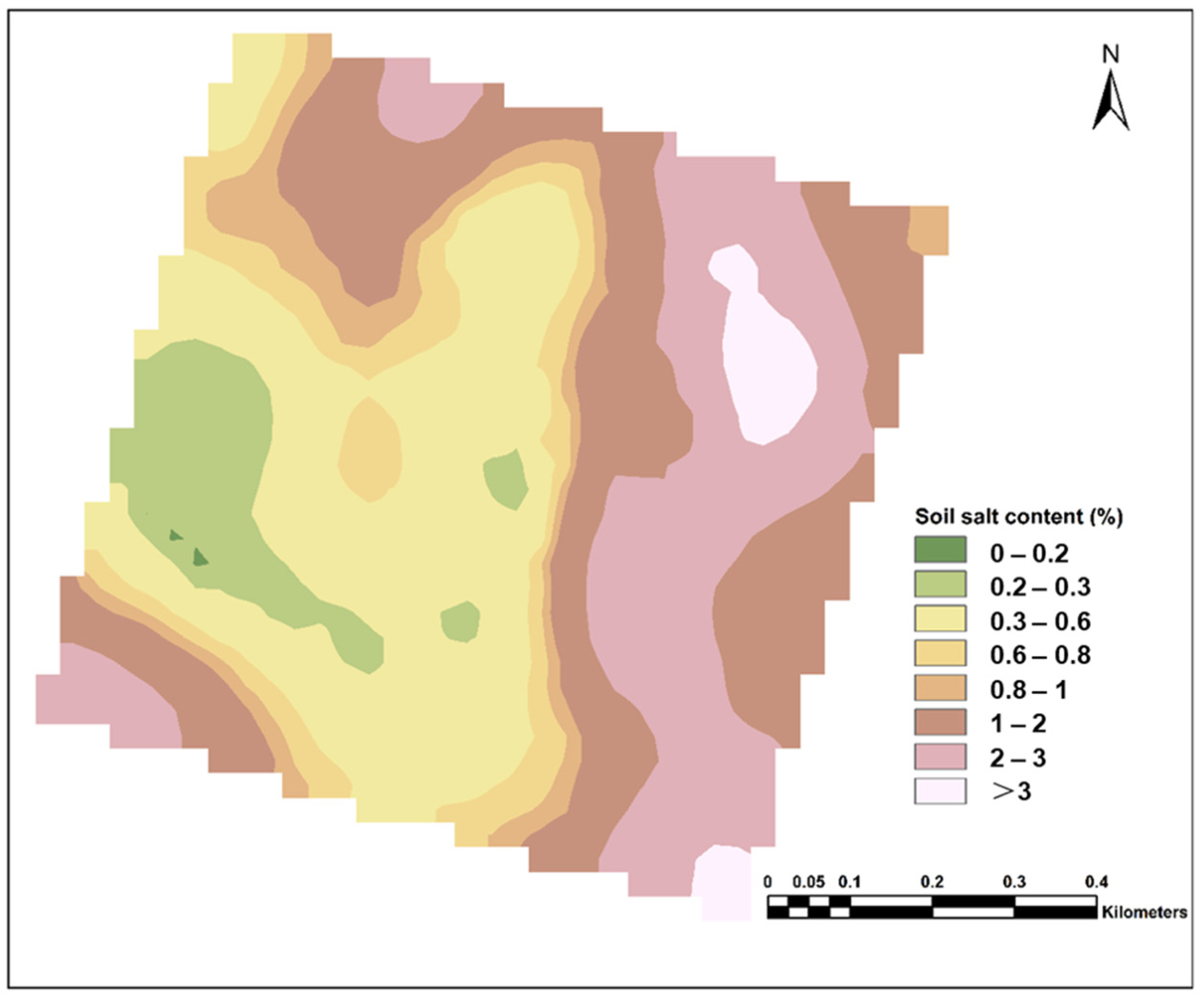
4.2. Transformation of “Point” to “Spatial” Scale for Soil Salinity Information Based on Geostatistical Methods
4.3. Model Results and Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Metternicht, G.I.; Zinck, J.A. Remote sensing of soil salinity: Potentials and constraints. Remote Sens. Environ. 2003, 85, 1–20. [Google Scholar] [CrossRef]
- Wang, J.; Zhen, J.; Hu, W.; Chen, S.; Lizaga, I.; Zeraatpisheh, M.; Yang, X. Remote sensing of soil degradation: Progress and perspective. Int. Soil Water Conserv. Res. 2023, 11, 429–454. [Google Scholar] [CrossRef]
- Farifteh, J.; Farshad, A.; George, R.J. Assessing salt-affected soils using remote sensing, solute modelling, and geophysics. Geoderma 2006, 130, 191–206. [Google Scholar] [CrossRef]
- Wang, J.; Ding, J.; Yu, D.; Teng, D.; He, B.; Chen, X.; Ge, X.; Zhang, Z.; Wang, Y.; Yang, X.; et al. Machine learning-based detection of soil salinity in an arid desert region, Northwest China: A comparison between Landsat-8 OLI and Sentinel-2 MSI. Sci. Total Environ. 2020, 707, 136092. [Google Scholar] [CrossRef] [PubMed]
- Abuelgasim, A.; Ammad, R. Mapping soil salinity in arid and semi-arid regions using Landsat 8 OLI satellite data. Remote Sens. Appl. 2019, 13, 415–425. [Google Scholar] [CrossRef]
- Wang, J.; Ding, J.; Ge, X.; Peng, J.; Hu, Z.W. Monitoring soil salinization based on remote sensing and proximal soil sensing: Progress and perspective. J. Remote Sens. 2023, 1–23. [Google Scholar] [CrossRef]
- Lobell, D.B.; Lesch, S.M.; Corwin, D.L.; Ulmer, M.G.; Anderson, K.A.; Potts, D.J.; Doolittle, J.A.; Motos, M.R.; Baltes, M.J. Regional-scale Assessment of Soil Salinity in the Red River Valley Using Multi-year MODIS EVI and NDVI. J. Environ. Qual. 2010, 39, 35–41. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ding, J.; Ma, X.; Zhang, Z.; Ge, X.; Lizaga, I.; Li, X.; Liang, J.; Chen, X.; Yuan, L.; et al. Capability of Sentinel-2 MSI data for monitoring and mapping of soil salinity in dry and wet seasons in the Ebinur Lake region, Xinjiang, China. Geoderma 2019, 353, 172–187. [Google Scholar] [CrossRef]
- Ge, X.; Ding, J.; Teng, D.; Wang, J.; Huo, T.; Jin, X.; Wang, J.; He, B.; Han, L. Updated soil salinity with fine spatial resolution and high accuracy. The synergy of Sentinel-2 MSI, environmental covariates and hybrid machine learning approaches. Catena 2022, 212, 106054. [Google Scholar] [CrossRef]
- Golestani, M.; Mosleh Ghahfarokhi, Z.; Esfandiarpour-Boroujeni, I.; Shirani, H. Evaluating the spatiotemporal variations of soil salinity in Sirjan Playa, Iran using Sentinel-2A and Landsat-8 OLI imagery. Catena 2023, 231, 107375. [Google Scholar] [CrossRef]
- Wang, L.; Hu, P.; Zheng, H.; Liu, Y.; Cao, X.; Hellwich, O.; Liu, T.; Luo, G.; Bao, A.; Chen, X. Integrative modeling of heterogeneous soil salinity using sparse ground samples and remote sensing images. Geoderma 2023, 430, 116321. [Google Scholar] [CrossRef]
- Abidine, M.M.O.; El Aboudi, A.; Kebd, A.; Aloueimine, B.B.; Dallahi, Y.; Soulé, A.; Vadel, A. Modeling the Spatial Variability of the Electrical Conductivity of the Soil Using Differents Spatial Interpolation Methods: Case of the Dawling National Park in Mauritania. Geogr. Tech. 2018, 13, 1–11. [Google Scholar] [CrossRef]
- Fu, T.; Gao, H.; Liu, J. Comparison of Different Interpolation Methods for Prediction of Soil Salinity in Arid Irrigation Region in Northern China. Agronomy 2021, 11, 1535. [Google Scholar] [CrossRef]
- Howari, F.M.; Goodell, P.C.; Miyamoto, S. Spectral properties of salt crusts formed on saline soils. J. Environ. Qual. 2002, 31, 1453–1461. [Google Scholar] [CrossRef]
- Cheng, L.; Aghakouchak, A.; Gilleland, E.; Katz, R.W. Non-stationary extreme value analysis in a changing climate. Clim. Chang. 2014, 127, 353–369. [Google Scholar] [CrossRef]
- Nie, M.; Huang, S.; Leng, G.; Zhou, Y.; Huang, Q.; Dai, M. Bayesian-based time-varying multivariate drought risk and its dynamics in a changing environment. Catena 2021, 204, 105429. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.P.; Huang, G.H.; Li, Y.F.; Liu, Y.R.; Zhou, X. Development of a multi-GCMs Bayesian copula method for assessing multivariate drought risk under climate change: A case study of the Aral Sea basin. Catena 2022, 212, 106048. [Google Scholar] [CrossRef]
- Davies, J.; Olley, J.; Hawker, D.; Mcbroom, J. Application of the Bayesian approach to sediment fingerprinting and source attribution. Hydrol. Process 2018, 32, 3978–3995. [Google Scholar] [CrossRef]
- Li, Y.; Gholami, H.; Song, Y.; Fathabadi, A.; Malakooti, H.; Collins, A.L. Source fingerprinting loess deposits in Central Asia using elemental geochemistry with Bayesian and GLUE models. Catena 2020, 194, 104808. [Google Scholar] [CrossRef]
- Fathabadi, A.; Jansen, J.D. Quantifying uncertainty of sediment fingerprinting mixing models using frequentist and Bayesian methods: A case study from the Iranian loess Plateau. Catena 2022, 217, 106474. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, T. Statistical interpretation of soil property profiles from sparse data using Bayesian compressive sampling. Géotechnique 2017, 67, 523–536. [Google Scholar] [CrossRef]
- Wang, C.; Li, X.; Zhang, J.; Liu, Y.; Situ, Z.; Gao, C.; Liu, J. Using Bayesian compressed sensing and sparse dictionaries to interpolate soil properties. Geoderma 2022, 428, 116162. [Google Scholar] [CrossRef]
- Luo, Y.; Weng, E.; Wu, X.; Gao, C.; Zhou, X.; Zhang, L. Parameter identifiability, constraint, and equifinality in data assimilation with ecosystem models. Ecol. Appl. 2009, 19, 571–574. [Google Scholar] [CrossRef]
- Heung, B.; Ho, H.C.; Zhang, J.; Knudby, A.; Bulmer, C.E.; Schmidt, M.G. An overview and comparison of machine-learning techniques for classification purposes in digital soil mapping. Geoderma 2016, 265, 62–77. [Google Scholar] [CrossRef]
- Tebaldi, C.; Knutti, R. The use of the multi-model ensemble in probabilistic climate projections. Philos. Trans. R. Soc. A 2007, 365, 2053–2075. [Google Scholar] [CrossRef]
- Baker, L.; Ellison, D. The wisdom of crowds—Ensembles and modules in environmental modelling. Geoderma 2008, 147, 1–7. [Google Scholar] [CrossRef]
- Peña, M.; van den Dool, H. Consolidation of Multimodel Forecasts by Ridge Regression: Application to Pacific Sea Surface Temperature. J. Clim. 2008, 21, 6521–6538. [Google Scholar] [CrossRef]
- Yan, J.; Sun, R.; Liu, T.; Duan, S. Domain-adaptation-based active ensemble learning for improving chemical sensor array performance. Sens. Actuators A-Phys. 2023, 357, 114411. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Nabiollahi, K.; Minasny, B.; Triantafilis, J. Comparing data mining classifiers to predict spatial distribution of USDA-family soil groups in Baneh region, Iran. Geoderma 2015, 253–254, 67–77. [Google Scholar] [CrossRef]
- Kim, D.; Yu, H.; Lee, H.; Beighley, E.; Durand, M.; Alsdorf, D.E.; Hwang, E. Ensemble learning regression for estimating river discharges using satellite altimetry data: The Central Congo River as a Test-bed. Remote Sens. Environ. 2019, 221, 741–755. [Google Scholar] [CrossRef]
- Cimusa Kulimushi, L.; Bigabwa Bashagaluke, J.; Prasad, P.; Heri-Kazi, A.B.; Lal Kushwaha, N.; Masroor, M.; Mohammed, S. Soil erosion susceptibility mapping using ensemble machine learning models: A case study of upper Congo river sub-basin. Catena 2023, 222, 106858. [Google Scholar] [CrossRef]
- Pham, K.; Kim, D.; Park, S.; Choi, H. Ensemble learning-based classification models for slope stability analysis. Catena 2021, 196, 104886. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Minasny, B.; Toomanian, N.; Zeraatpisheh, M.; Amirian-Chakan, A.; Triantafilis, J. Digital Mapping of Soil Classes Using Ensemble of Models in Isfahan Region, Iran. Soil. Syst. 2019, 3, 37. [Google Scholar] [CrossRef]
- Malone, B.P.; Minasny, B.; Odgers, N.P.; Mcbratney, A.B. Using model averaging to combine soil property rasters from legacy soil maps and from point data. Geoderma 2014, 232–234, 34–44. [Google Scholar] [CrossRef]
- Vaysse, K.; Lagacherie, P. Evaluating Digital Soil Mapping approaches for mapping GlobalSoilMap soil properties from legacy data in Languedoc- Roussillon (France). Geoderma Reg. 2015, 4, 20–30. [Google Scholar] [CrossRef]
- Rasaei, Z.; Bogaert, P. Spatial filtering and Bayesian data fusion for mapping soil properties: A case study combining legacy and remotely sensed data in Iran. Geoderma 2019, 344, 50–62. [Google Scholar] [CrossRef]
- Dasgupta, S.; Debnath, S.; Das, A.; Biswas, A.; Weindorf, D.C.; Li, B.; Shukla, A.K.; Das, S.; Saha, S.; Chakraborty, S. Developing regional soil micronutrient management strategies through ensemble learning based digital soil mapping. Geoderma 2023, 433, 116457. [Google Scholar] [CrossRef]
- Riggers, C.; Poeplau, C.; Don, A.; Bamminger, C.; Höper, H.; Dechow, R. Multi-model ensemble improved the prediction of trends in soil organic carbon stocks in German croplands. Geoderma 2019, 345, 17–30. [Google Scholar] [CrossRef]
- Song, X.; Wu, H.; Ju, B.; Liu, F.; Yang, F.; Li, D.; Zhao, Y.; Yang, J.; Zhang, G. Pedoclimatic zone-based three-dimensional soil organic carbon mapping in China. Geoderma 2020, 363, 114145. [Google Scholar] [CrossRef]
- Zhu, L.; Walker, J.P.; Shen, X. Stochastic ensemble methods for multi-SAR-mission soil moisture retrieval. Remote Sens. Environ. 2020, 251, 112099. [Google Scholar] [CrossRef]
- Nketia, K.A.; Asabere, S.B.; Ramcharan, A.; Herbold, S.; Erasmi, S.; Sauer, D. Spatio-temporal mapping of soil water storage in a semi-arid landscape of northern Ghana—A multi-tasked ensemble machine-learning approach. Geoderma 2022, 410, 115691. [Google Scholar] [CrossRef]
- Román Dobarco, M.; Arrouays, D.; Lagacherie, P.; Ciampalini, R.; Saby, N.P.A. Prediction of topsoil texture for Region Centre (France) applying model ensemble methods. Geoderma 2017, 298, 67–77. [Google Scholar] [CrossRef]
- Caubet, M.; Román Dobarco, M.; Arrouays, D.; Minasny, B.; Saby, N.P.A. Merging country, continental and global predictions of soil texture. Lessons from ensemble modelling in France. Geoderma 2019, 337, 99–110. [Google Scholar] [CrossRef]
- Castrignanò, A.; Buttafuoco, G. Geostatistical Stochastic Simulation of Soil Water Content in a Forested Area of South Italy. Biosyst. Eng. 2004, 87, 257–266. [Google Scholar] [CrossRef]
- Wu, J.; Vincent, B.; Yang, J.; Bouarfa, S.; Vidal, A. Remote Sensing Monitoring of Changes in Soil Salinity: A Case Study in Inner Mongolia, China. Sensors 2008, 8, 7035–7049. [Google Scholar] [CrossRef] [PubMed]
- Khan, N.M.; Rastoskuev, V.V.; Sato, Y.; Shiozawa, S. Assessment of hydrosaline land degradation by using a simple approach of remote sensing indicators. Agric. Water Manag. 2005, 77, 96–109. [Google Scholar] [CrossRef]
- Douaoui, A.E.K.; Nicolas, H.; Walter, C. Detecting salinity hazards within a semiarid context by means of combining soil and remote-sensing data. Geoderma 2006, 134, 217–230. [Google Scholar] [CrossRef]
- Allbed, A.; Kumar, L.; Aldakheel, Y.Y. Assessing soil salinity using soil salinity and vegetation indices derived from IKONOS high-spatial resolution imageries: Applications in a date palm dominated region. Geoderma 2014, 230–231, 1–8. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Minasny, B.; Sarmadian, F.; Malone, B.P. digital mapping of soil salinity in Ardakan region, central Iran. Geoderma 2014, 213, 15–28. [Google Scholar] [CrossRef]
- Yang, Y.; Dou, Y.; Liu, D.; An, S. Spatial pattern and heterogeneity of soil moisture along a transect in a small catchment on the Loess Plateau. J. Hydrol. 2017, 550, 466–477. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, Q.; Yang, H. Soil salinity distribution and its relationship with soil particle size in the lower reaches of Heihe River, Northwestern China. Environ. Earth Sci. 2016, 75, 810. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, F.; Zhang, X.; Chan, N.W.; Kung, H.; Ariken, M.; Zhou, X.; Wang, Y. Regional suitability prediction of soil salinization based on remote-sensing derivatives and optimal spectral index. Sci. Total Environ. 2021, 775, 145807. [Google Scholar] [CrossRef] [PubMed]
- Liao, K.; Lai, X.; Zhou, Z.; Zhu, Q. Combining the ensemble mean and bias correction approaches to reduce the uncertainty in hillslope-scale soil moisture simulation. Agric. Water Manag. 2017, 191, 29–36. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Chen, J.; Liu, S.; Jia, K.; Zhang, X.; Xiao, Z.; Fisher, J.; Mu, Q.; et al. Improving global terrestrial evapotranspiration estimation using support vector machine by integrating three process-based algorithms. Agric. For. Meteorol. 2017, 242, 55–74. [Google Scholar] [CrossRef]
- Zhang, R.; Xu, X.; Guo, J.; Sheng, Z. Multi-model ensemble approaches for simulation of evapotranspiration of karst agroforestry ecosystems. Agric. Water Manag. 2022, 273, 107869. [Google Scholar] [CrossRef]
- Zhao, K.; Wulder, M.; Hu, T.; Bright, R.M.; Brown, M.E. Detecting change-point, trend, and seasonality in satellite time series data to track abrupt changes and nonlinear dynamics: A Bayesian ensemble algorithm. Remote Sens. Environ. 2019, 232, 111181. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, F.; Sun, X.; Tan, K. Marine big data-driven ensemble learning for estimating global phytoplankton group composition over two decades (1997–2020). Remote Sens. Environ. 2023, 294, 113596. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Whitaker, C.J. Measures of Diversity in Classifier Ensembles and Their Relationship with the Ensemble Accuracy. Mach. Learn. 2003, 51, 181–207. [Google Scholar] [CrossRef]
- Akay, H. Spatial modeling of snow avalanche susceptibility using hybrid and ensemble machine learning techniques. Catena 2021, 206, 105524. [Google Scholar] [CrossRef]
- Sylvain, J.; Anctil, F.; Thiffault, E. Using bias correction and ensemble modelling for predictive mapping and related uncertainty: A case study in digital soil mapping. Geoderma 2021, 403, 115153. [Google Scholar] [CrossRef]
| Salinity Index | Formula | Reference |
|---|---|---|
| SI | [46] | |
| SI1 | [47] | |
| SI2 | [47] | |
| SI3 | [47] | |
| S1 | [48] | |
| S2 | [48] | |
| S3 | [48] | |
| S4 | [48] | |
| S5 | [48] | |
| S6 | [48] | |
| S7 | [11] | |
| S8 | [11] | |
| NDSI | [46] | |
| GAEX | [49] |
| Study Area | Area | Minimum (%) | Maximum (%) | Mean (%) | Median (%) | SD (%) | CV (%) |
|---|---|---|---|---|---|---|---|
| N | 1 | 0.10 | 0.44 | 0.25 | 0.25 | 0.11 | 44.18 |
| 2 | 0.21 | 1.12 | 0.49 | 0.43 | 0.29 | 58.61 | |
| 3 | 0.21 | 1.50 | 0.41 | 0.32 | 0.31 | 76.13 | |
| 4 | 0.21 | 0.66 | 0.34 | 0.27 | 0.15 | 43.93 | |
| S | 1 | 0.16 | 0.94 | 0.47 | 0.37 | 0.27 | 58.46 |
| 2 | 0.16 | 2.26 | 0.41 | 0.24 | 0.51 | 125.90 | |
| 3 | 0.18 | 0.73 | 0.40 | 0.38 | 0.16 | 39.58 | |
| 4 | 0.13 | 0.50 | 0.28 | 0.26 | 0.13 | 45.12 |
| Study Region | Minimum (%) | Maximum (%) | Mean (%) | Median (%) | SD (%) | CV (%) |
|---|---|---|---|---|---|---|
| N | 0.06 | 3.96 | 0.36 | 0.26 | 0.43 | 119.22 |
| S | 0.09 | 5.77 | 0.80 | 0.39 | 1.03 | 128.80 |
| Study Region | Theoretical Model | (%) | (m) | RSS | |||
|---|---|---|---|---|---|---|---|
| N | Exponential | 0.26 | 0.63 | 41.27 | 603.00 | 0.82 | 0.03 |
| S | Spherical | 0.23 | 1.16 | 19.46 | 762.00 | 0.97 | 0.07 |
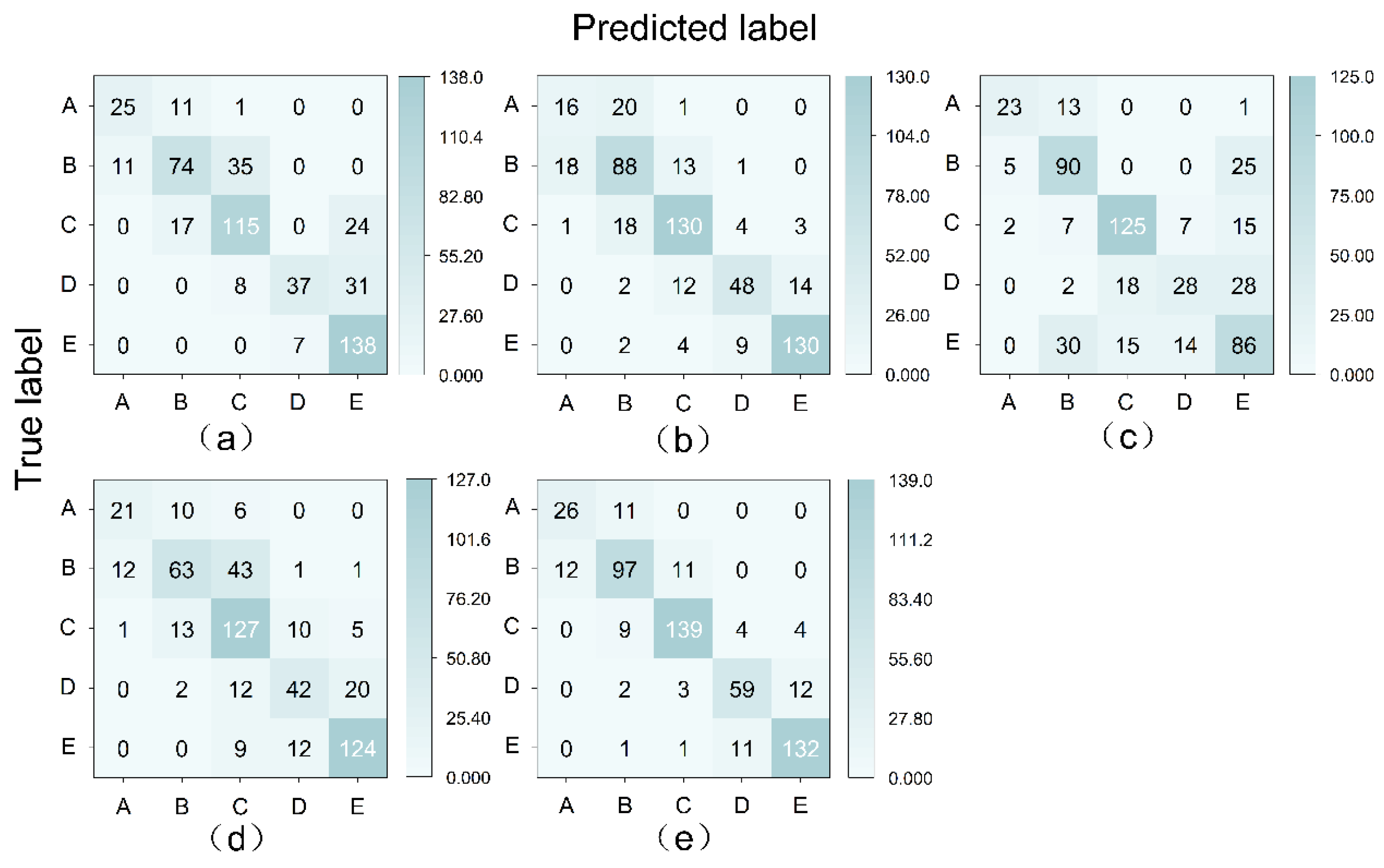
| Model | Category | Recall | Precision | F1-Score | Accuracy | Kappa |
|---|---|---|---|---|---|---|
| KDE-BC_S1 | Nonsaline | 0.68 | 0.69 | 0.68 | 0.73 | 0.64 |
| Slightly saline | 0.62 | 0.73 | 0.67 | |||
| Moderately saline | 0.74 | 0.72 | 0.73 | |||
| Strongly saline | 0.49 | 0.84 | 0.62 | |||
| Solonchak | 0.95 | 0.72 | 0.82 | |||
| KDE-BC_S3 | Nonsaline | 0.43 | 0.46 | 0.44 | 0.77 | 0.70 |
| Slightly saline | 0.73 | 0.68 | 0.70 | |||
| Moderately saline | 0.83 | 0.81 | 0.82 | |||
| Strongly saline | 0.63 | 0.77 | 0.70 | |||
| Solonchak | 0.90 | 0.88 | 0.89 | |||
| KDE-BC_S7 | Nonsaline | 0.62 | 0.77 | 0.69 | 0.66 | 0.55 |
| Slightly saline | 0.75 | 0.63 | 0.69 | |||
| Moderately saline | 0.80 | 0.79 | 0.80 | |||
| Strongly saline | 0.37 | 0.57 | 0.45 | |||
| Solonchak | 0.59 | 0.55 | 0.57 | |||
| KDE-BC_GAEX | Nonsaline | 0.57 | 0.62 | 0.59 | 0.71 | 0.61 |
| Slightly saline | 0.53 | 0.72 | 0.61 | |||
| Moderately saline | 0.81 | 0.64 | 0.72 | |||
| Strongly saline | 0.55 | 0.65 | 0.60 | |||
| Solonchak | 0.86 | 0.83 | 0.84 | |||
| KDE-BC_EL | Nonsaline | 0.70 | 0.68 | 0.69 | 0.85 | 0.80 |
| Slightly saline | 0.81 | 0.81 | 0.81 | |||
| Moderately saline | 0.89 | 0.90 | 0.90 | |||
| Strongly saline | 0.78 | 0.80 | 0.79 | |||
| Solonchak | 0.91 | 0.89 | 0.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Wu, J.; Xu, C. Monitoring Soil Salinity Classes through Remote Sensing-Based Ensemble Learning Concept: Considering Scale Effects. Remote Sens. 2024, 16, 642. https://doi.org/10.3390/rs16040642
Chen H, Wu J, Xu C. Monitoring Soil Salinity Classes through Remote Sensing-Based Ensemble Learning Concept: Considering Scale Effects. Remote Sensing. 2024; 16(4):642. https://doi.org/10.3390/rs16040642
Chicago/Turabian StyleChen, Huifang, Jingwei Wu, and Chi Xu. 2024. "Monitoring Soil Salinity Classes through Remote Sensing-Based Ensemble Learning Concept: Considering Scale Effects" Remote Sensing 16, no. 4: 642. https://doi.org/10.3390/rs16040642
APA StyleChen, H., Wu, J., & Xu, C. (2024). Monitoring Soil Salinity Classes through Remote Sensing-Based Ensemble Learning Concept: Considering Scale Effects. Remote Sensing, 16(4), 642. https://doi.org/10.3390/rs16040642









