An Adaptive INS/CNS/SMN Integrated Navigation Algorithm in Sea Area
Abstract
1. Introduction
2. Methodology
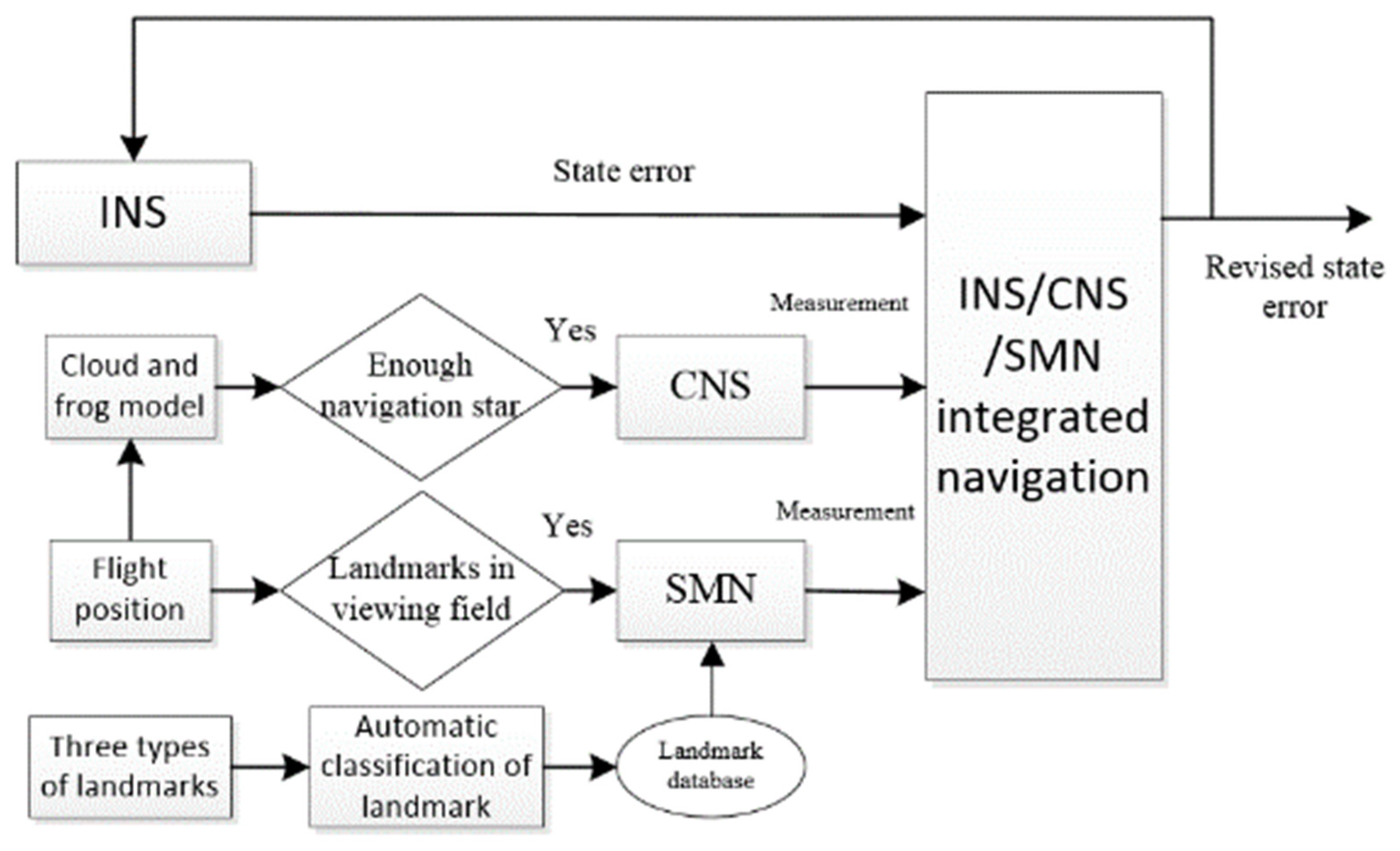
2.1. INS/CNS/SMN Adaptive Integrated Navigation Structure
- The development of the INS/CNS/SMN adaptive integrated navigation system, encompassing the formulation of the INS state equation, as well as the CNS and SMN measurement equations;
- Establishment of a cloud and fog model, serving as a foundational framework to determine the availability of CNS;
- Definition of three distinct types of sea area landmarks, accompanied by the introduction of an automatic classification model based on SVM. Additionally, the design of corresponding matching methods and strategies for these landmarks is presented.
2.1.1. State Equation of INS
2.1.2. Measurement Equation of CNS and SMN
- Measurement equation of CNS
- 2.
- Measurement Equation of SMN
2.1.3. Design of Kalman Filter
2.2. SMN in Sea Area
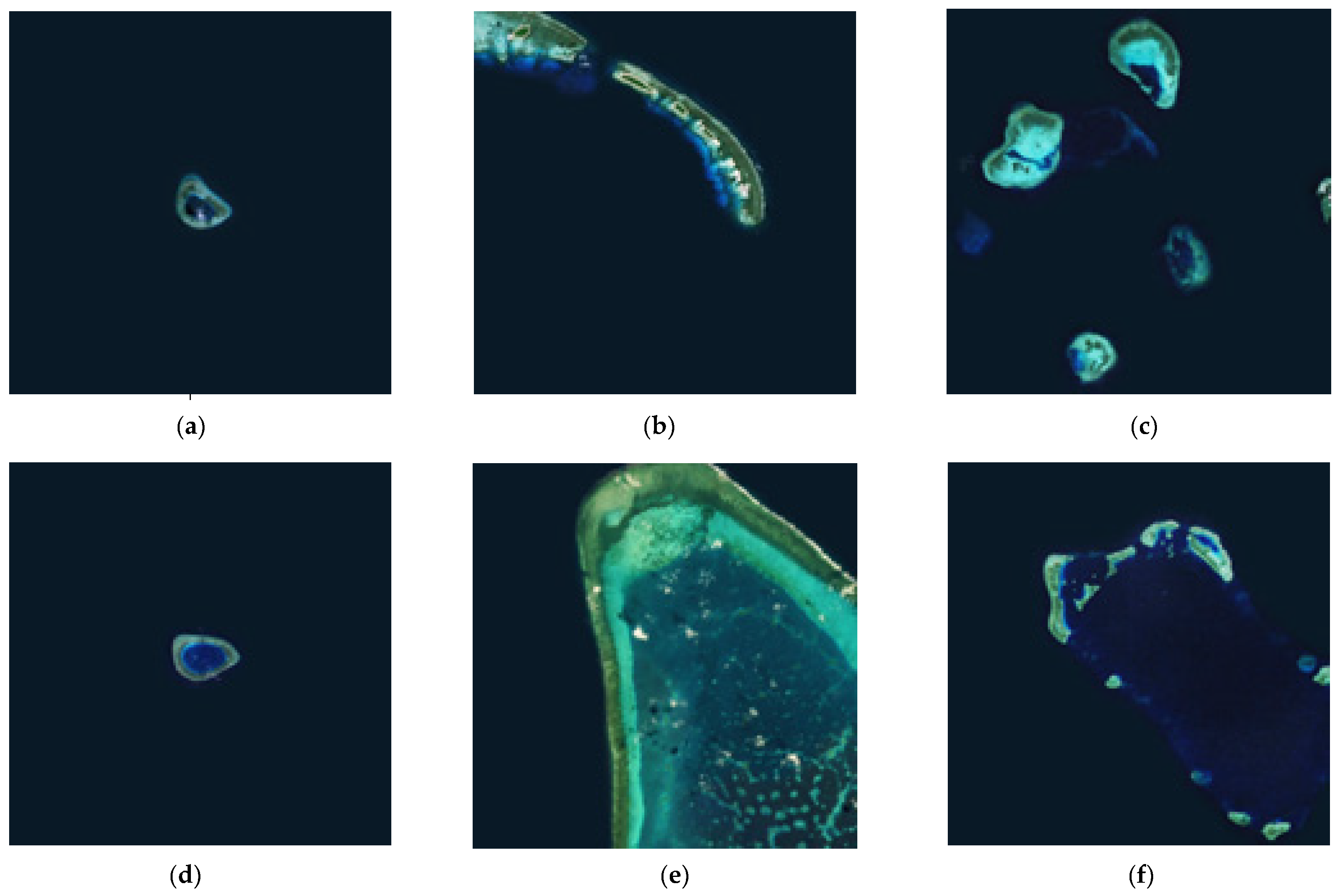
2.2.1. Definition of Sea Area Landmarks
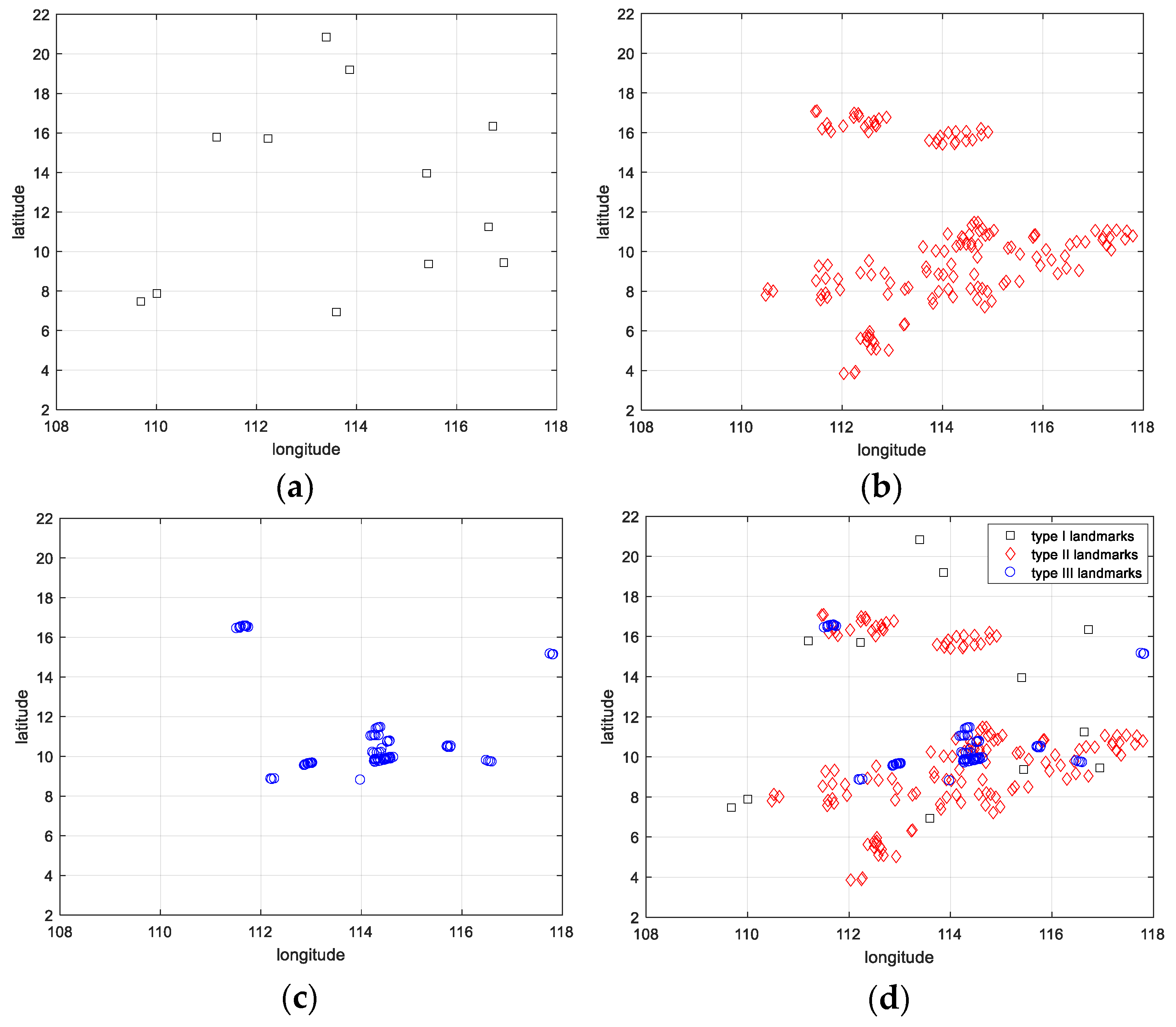
- Type I (isolated island): The proportion of landmark image pixels constitutes less than 3% of the field of view. The edge is well-defined, with no adjacent islands. The landmark solely retains the geographic information of the central point of the island;
- Type II (big island): The proportion of image pixels attributed to the landmark surpasses 3% in the field of view, exhibiting a clear shape. The landmark archives both the grayscale information of the image and the geographical coordinates of the image center;
- Type III (multi-island): There are more than two islands within the viewing field. The landmark records the triangular “edge-edge-edge” information formed by the central position of the base island and any other two islands.
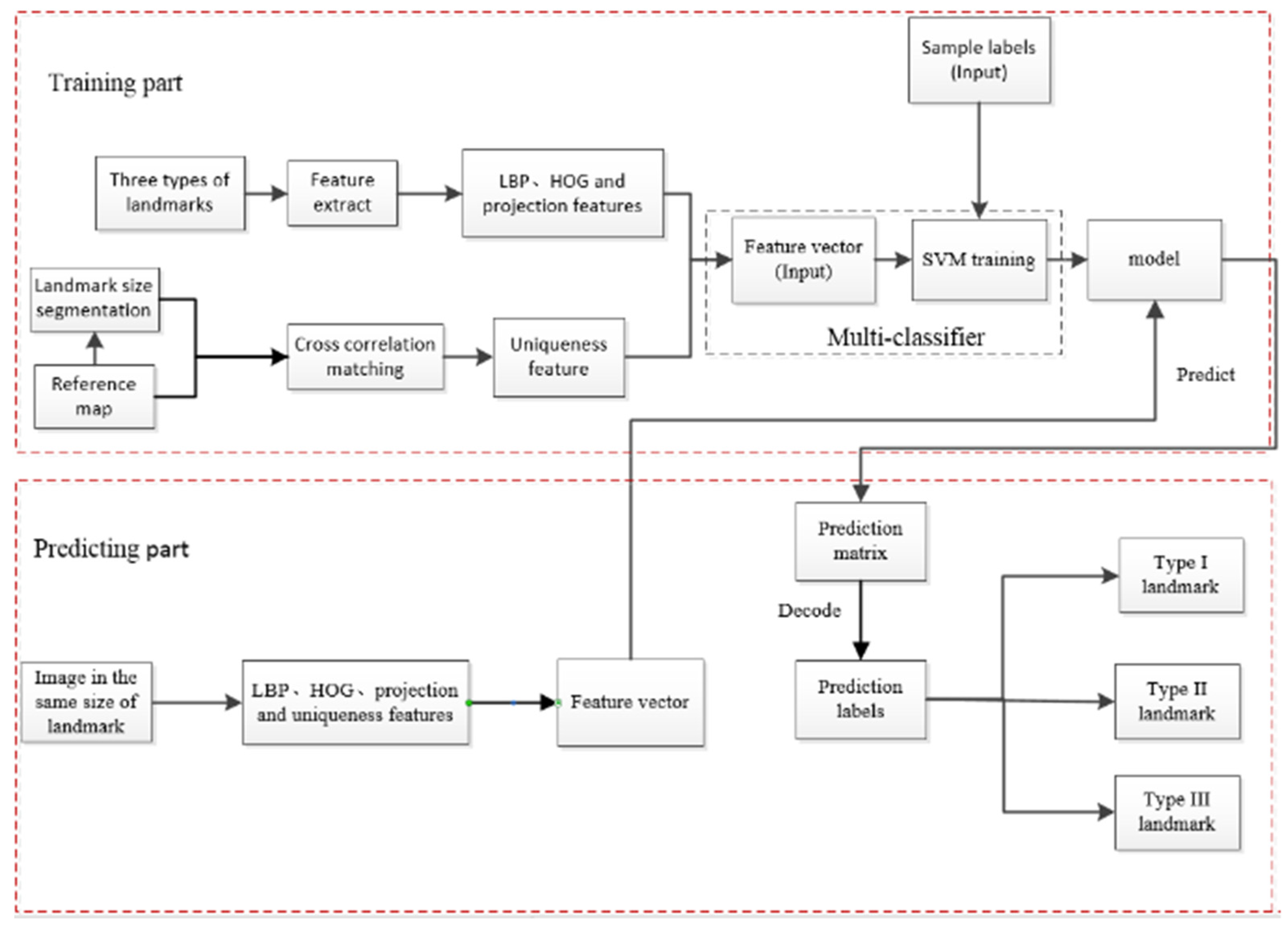
2.2.2. Automatic Classification Model of Sea Area Landmarks
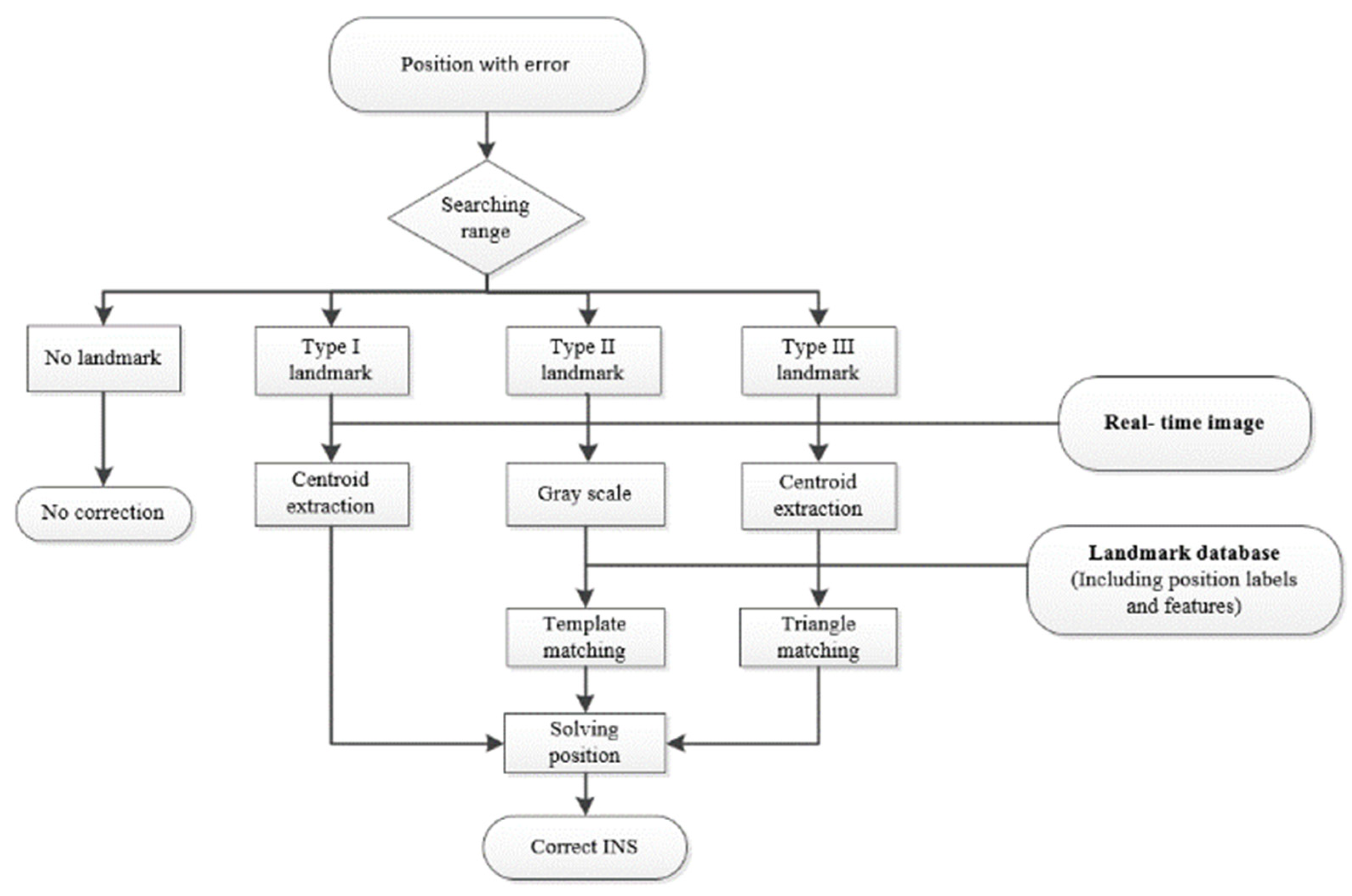
2.2.3. Multi–Mode Matching Strategies of Sea Area Landmarks
- Type I Landmarks: These landmarks, comprised of isolated islands without adjacent counterparts in the field of view, ensure the uniqueness of each landmark, obviating the need for matching. The detection of islands can be efficiently achieved through an image segmentation method [43]. Subsequently, the centroid of the island can be extracted using centroid extraction techniques [44], facilitating the determination of the aircraft’s current position;
- Type II Landmarks: Utilizing a variable step template matching algorithm [45], the matching position between the landmark and real-time image is derived through the analysis of gray information. This approach is employed to calculate the current position of the aircraft;
- Type III Landmarks: Introducing a consideration of the relative position relationship among islands, an “edge-edge-edge” information structure is formed by connecting the centroids of the three islands. This information is then employed for triangle matching [39,46], revealing the matching position between the landmark and real-time image, subsequently allowing for the computation of the aircraft’s current position.
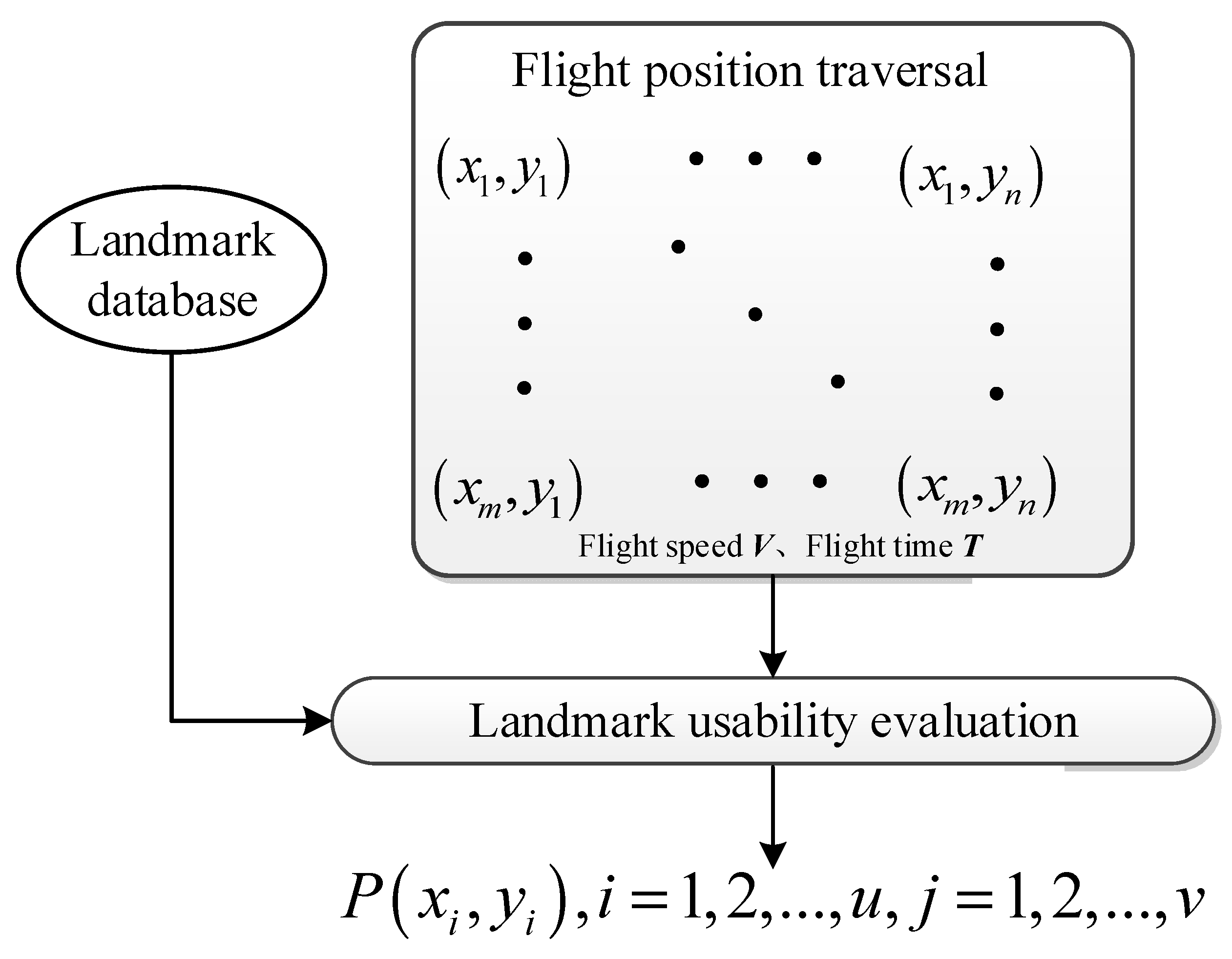
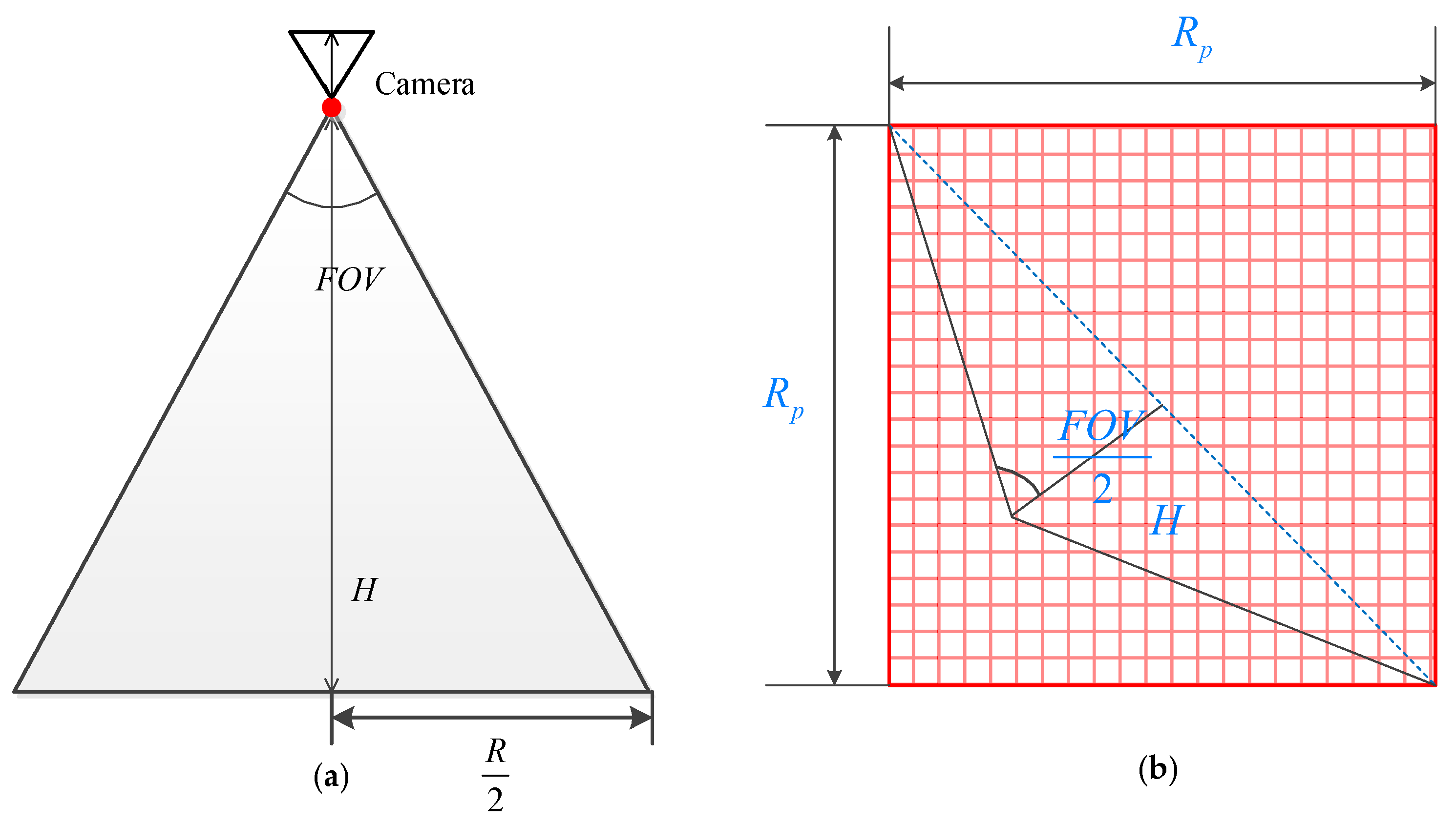
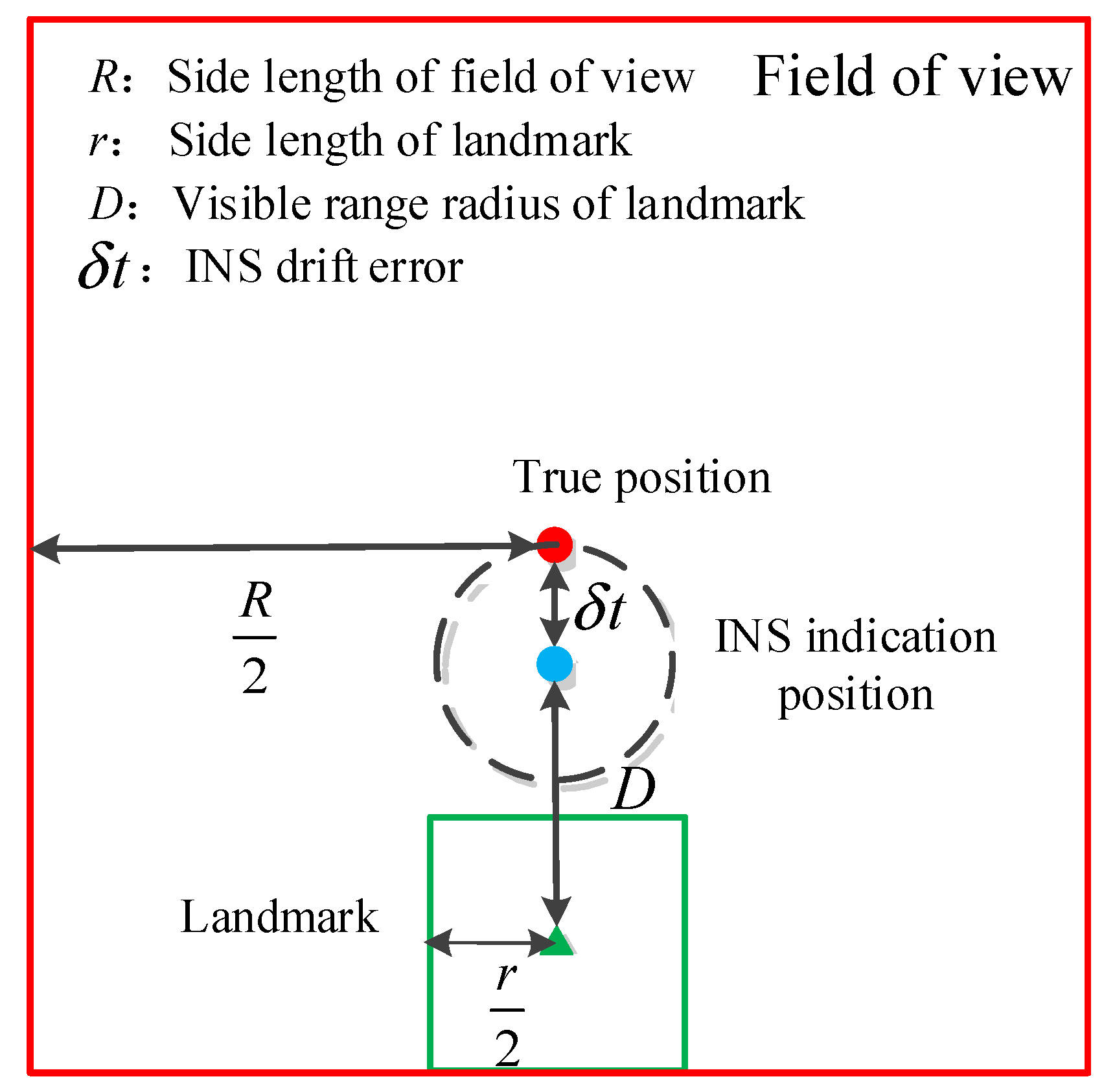
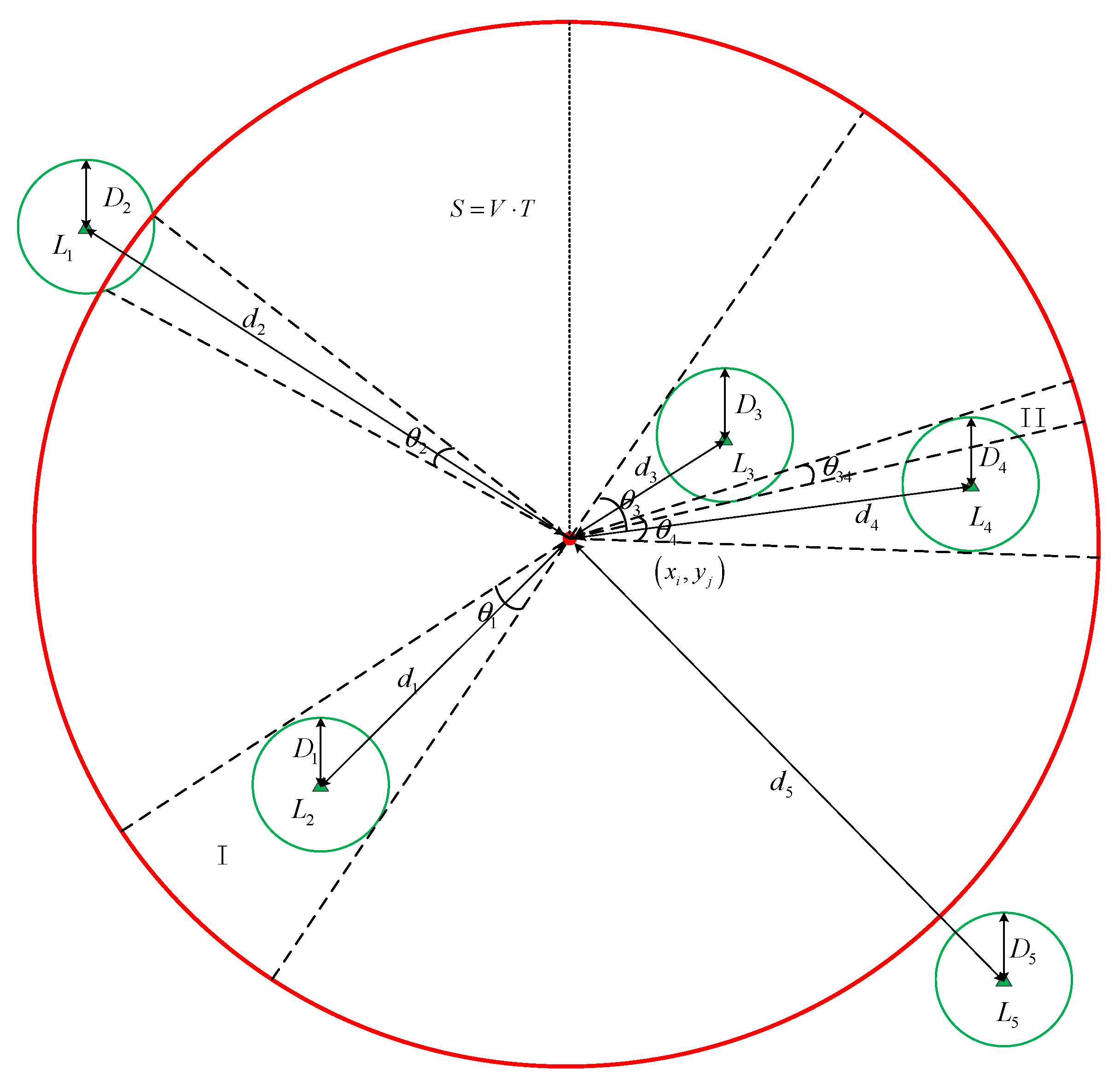
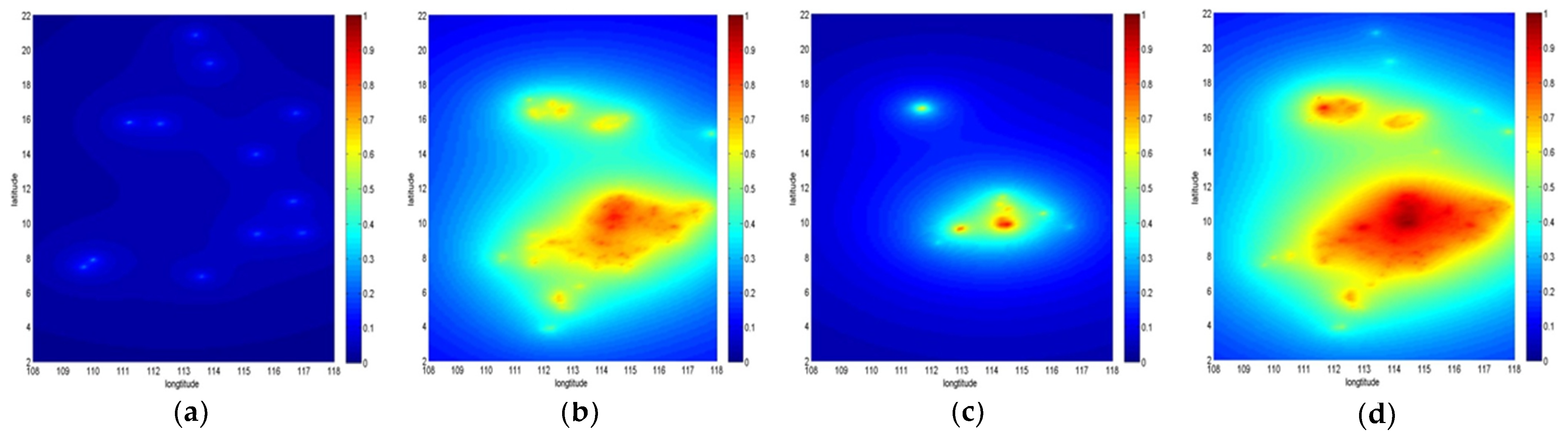
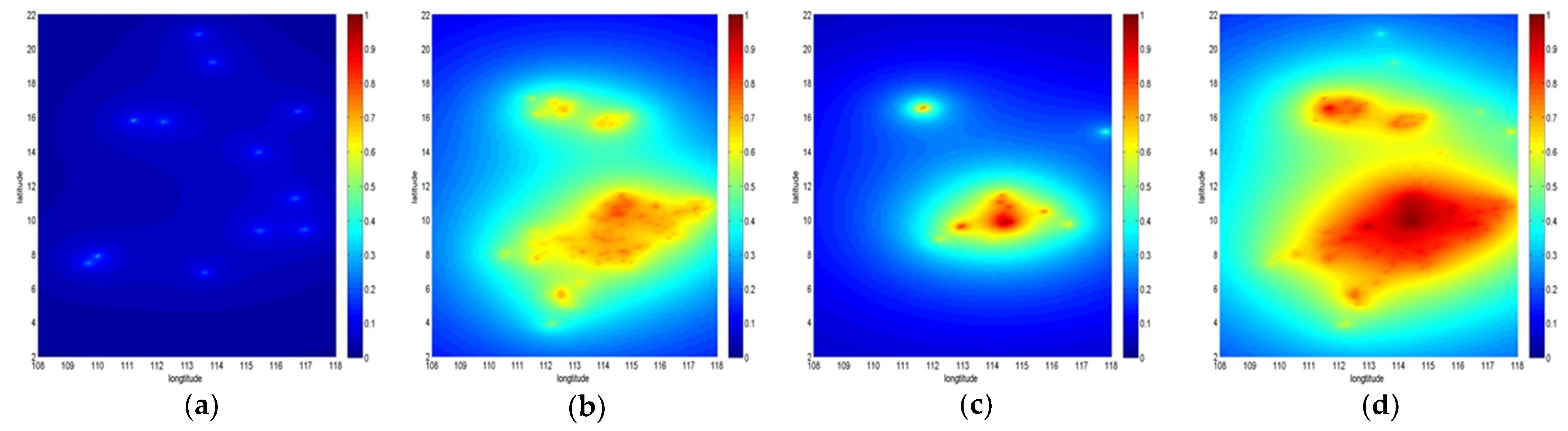
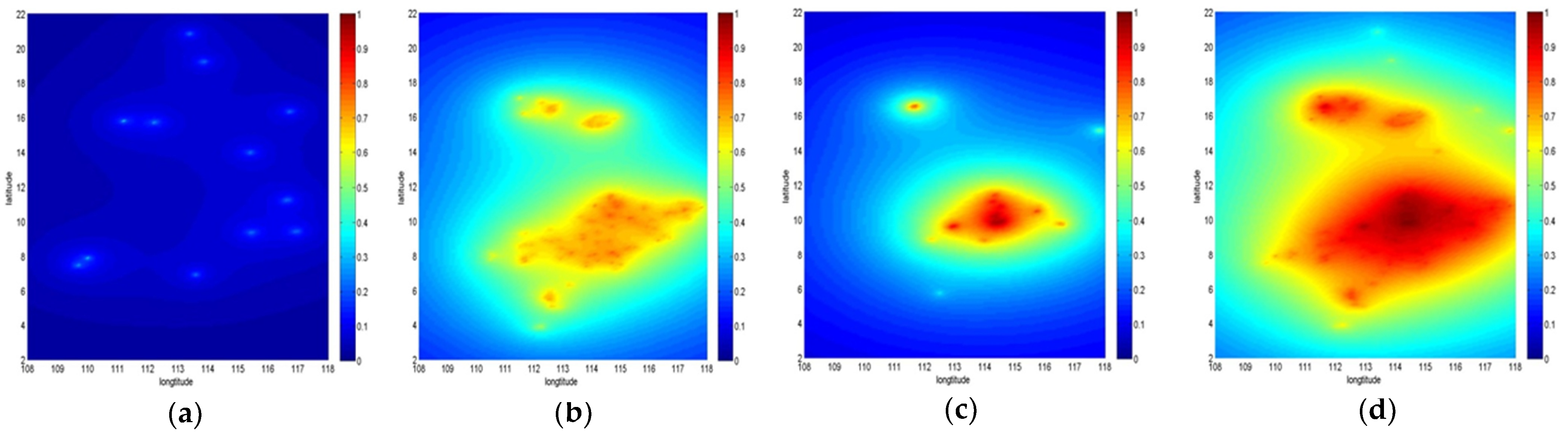
2.2.4. Usability Evaluation Algorithm of Sea Area Landmarks
- 1.
- Algorithm framework
- 2.
- Calculation of landmark visible range
- 3.
- Calculation of landmark observable probability
2.3. Cloud and Fog Model
2.3.1. Area and Size Model of the Cloud and Fog Area
2.3.2. Moving Model of Cloud and Fog Area with Time
2.3.3. Design of Weather Simulation Model
- Center position of cloud and fog;
- Side length, moving speed and direction of cloud and fog.
- Camera parameters: latitude, longitude, and altitude of the camera, the distance from the camera to the field of view;
- Parameters of cloud and fog: longitude and latitude of cloud and fog center, type of cloud and fog, and side length of cloud and fog.
- The intersection matrix between the camera field of view and the cloud and fog;
- The two composite images obtained by overlaying clouds and fog onto the upper and lower field of view of the camera;
- Matrix describing the cloud and fog coverage (parameter 00 represents no coverage of the camera by clouds and fog, 01 represents full coverage of the camera’s upper field of view by cloud and fog, 10 represents full coverage of the camera’s lower field of view by cloud and fog, 21 represents partial coverage of the camera’s upper field of view by cloud and fog and 22 represents partial coverage of the camera’s lower field of view by cloud and fog).
3. Results
3.1. Automatic Classification and Matching Algorithm of Three Types of Landmarks
- Landmark automatic classification
- 2.
- Landmark matching algorithm
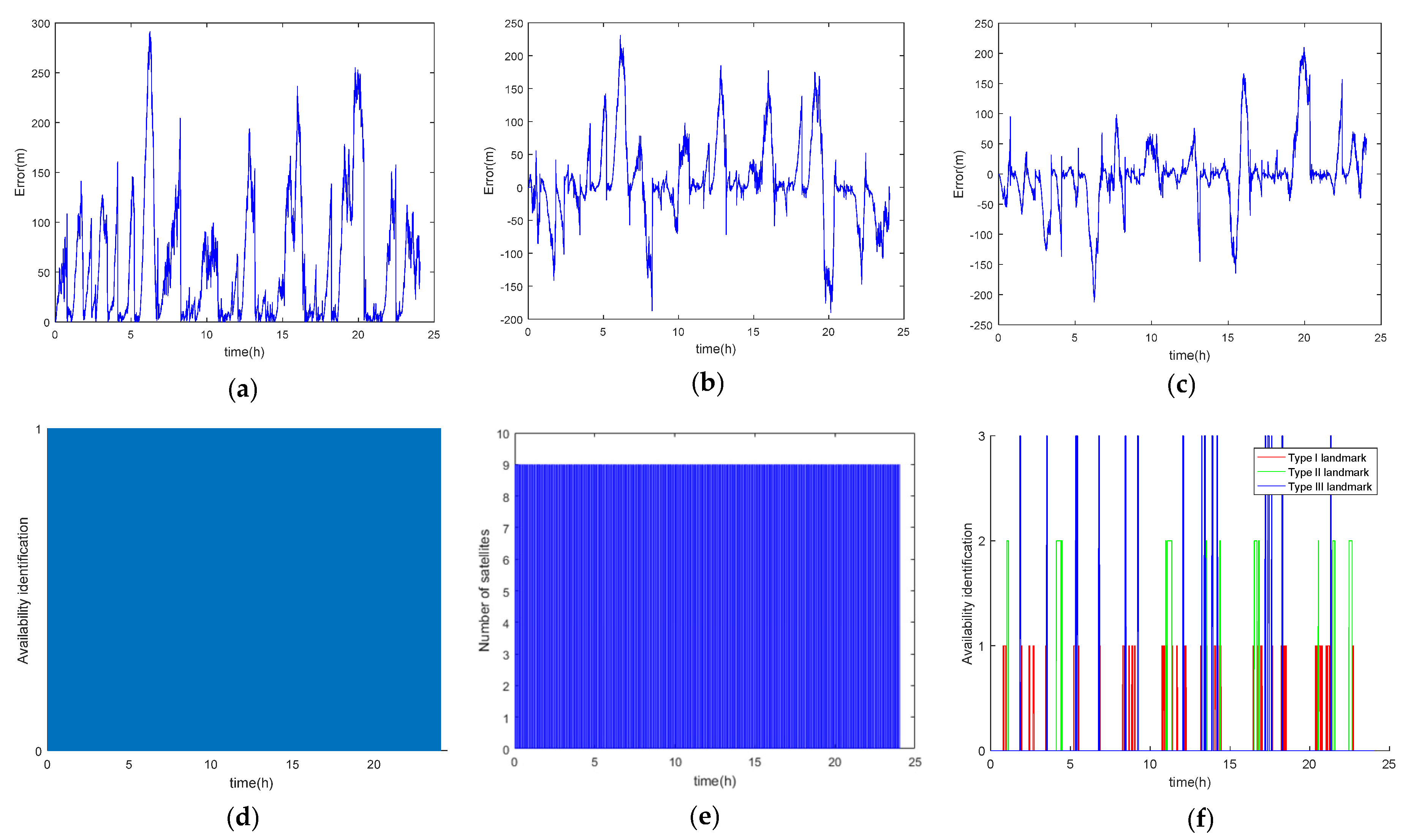
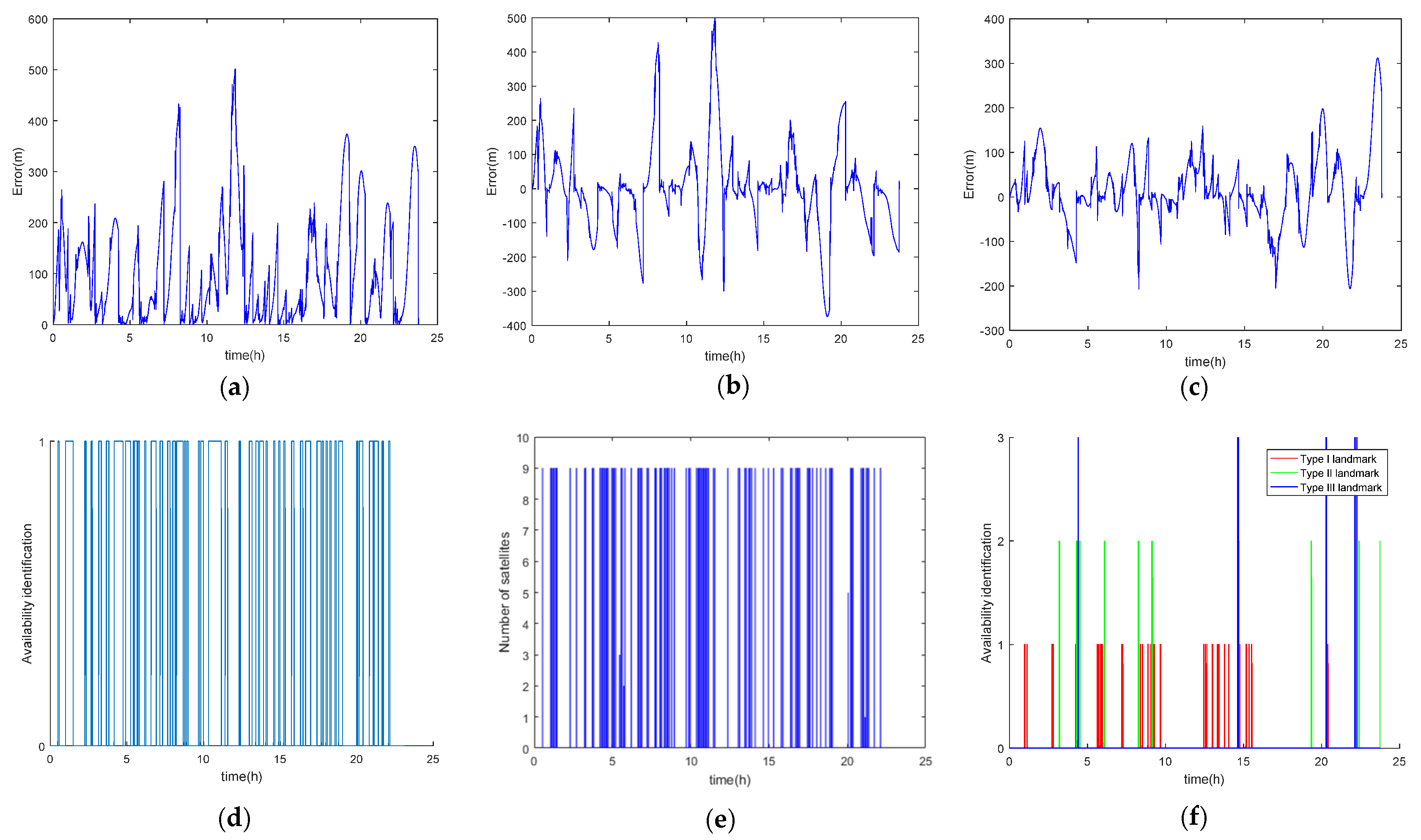
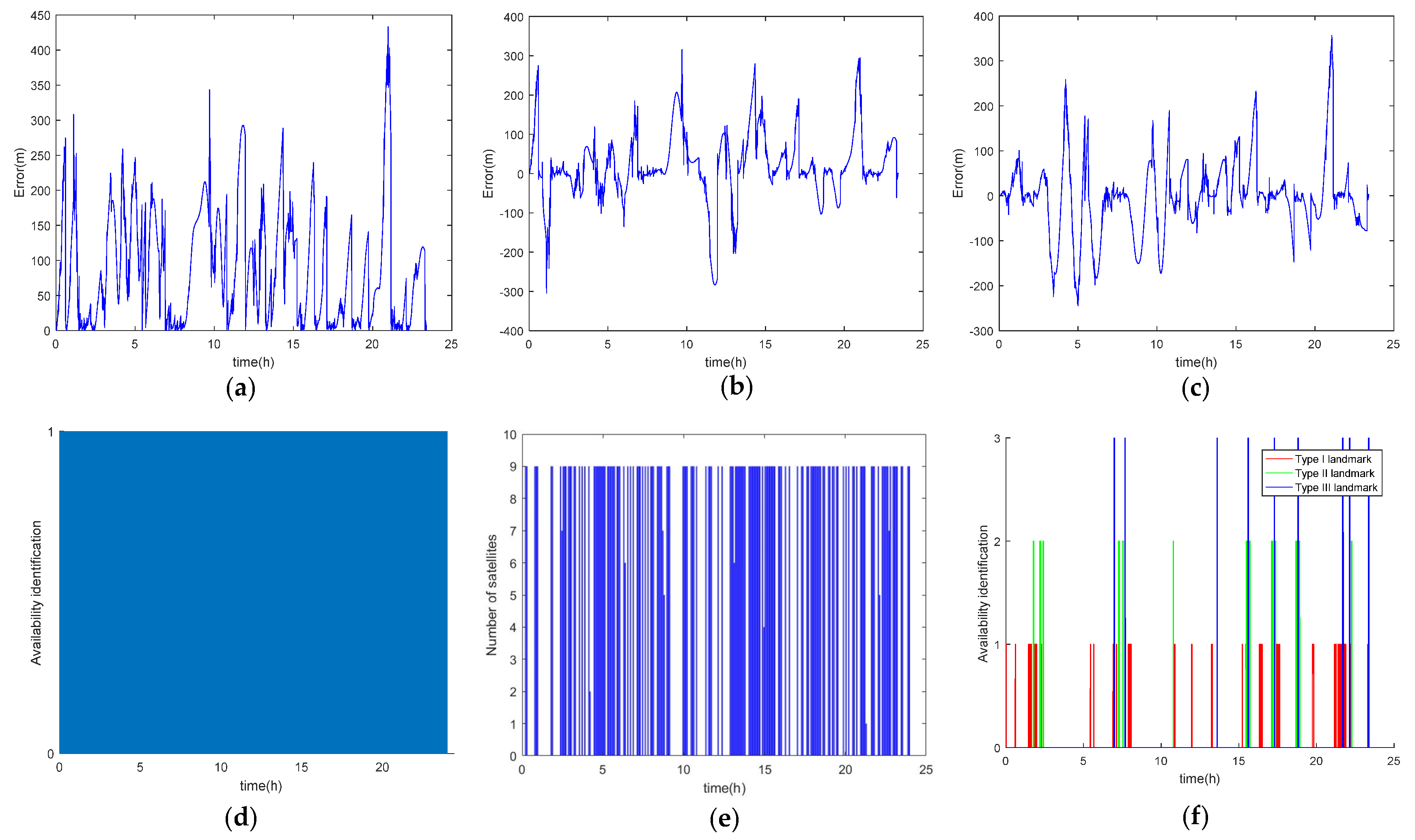
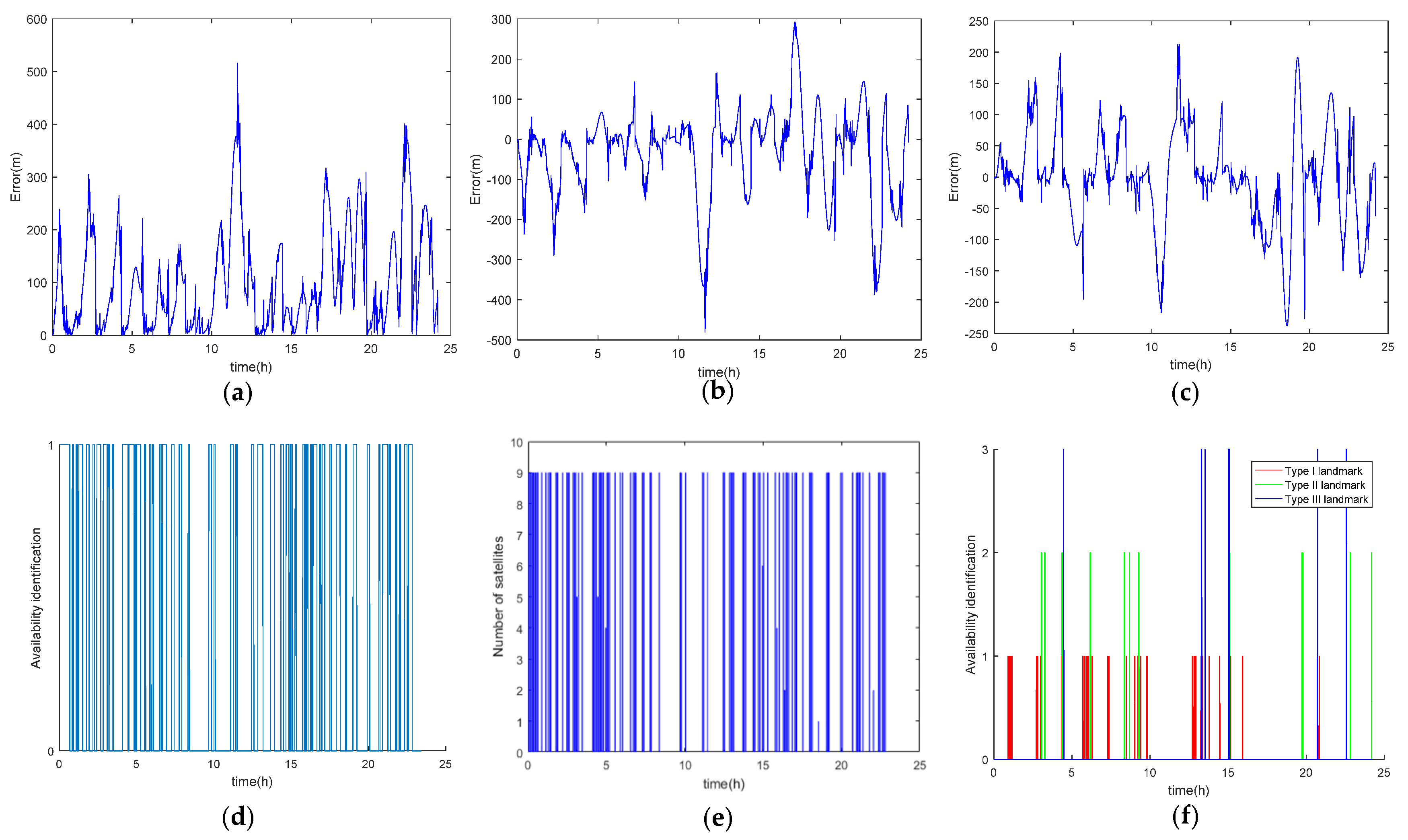
3.2. Landmark Usability Evaluation
3.3. CNS Availability
3.4. INS/CNS/SMN Adaptive Integrated Navigation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.Y. Theory and Application of Navigation System; Northwestern Polytechnic University Press: Xi’an, China, 2010. [Google Scholar]
- Barbour, N.; Schmidt, G. Inertial sensor technology trends. Sensors 2002, 1, 332–339. [Google Scholar] [CrossRef]
- Song, H.L.; Ma, Y.Q. Developing Trend of Inertial Navigation Technology and Requirement Analysis for Armament. Mod. Def. Technol. 2012, 40, 55–59. [Google Scholar]
- Dong, J.W.; Department, N.E. Analysis on inertial navigation technology. J. Instrum. Technol. 2017, 1, 41–43. [Google Scholar]
- Wang, S.Y.; Han, S.L.; Ren, X.Y. MEMS Inertial Navigation Technology and Its Application and Prospect. Control Inf. Technol. 2018, 6, 21–26. [Google Scholar]
- Lai, J.Z.; Yu, Y.Z.; Xiong, Z. SINS/CNS tightly integrated navigation positioning algorithm with nonlinear filter. Control Decis. 2012, 27, 1649–1653. [Google Scholar]
- Yang, S.J.; Yang, G.L.; Yi, H.L. Scheme design of autonomous integrated INS/CNS navigation systems for spacecraft. J. Chin. Inert. Technol. 2014, 22, 728–733. [Google Scholar]
- Quan, W.; Fang, J.; Li, J. INS/CNS/GNSS Integrated Navigation Technology. Syst. Eng. Electron. 2015, 33, 237–277. [Google Scholar]
- Qian, H.M.; Lang, X.K.; Qian, L.C. Ballistic missile SINS/CNS integrated navigation method. J. Beijing Univ. Aeronaut. Astronaut. 2017, 43, 857–864. [Google Scholar]
- Zhao, F.F.; Chen, C.Q.; He, W. A filtering approach based on MMAE for a SINS/CNS integrated navigation system. IEEE/CAA J. Autom. Sin. 2018, 5, 1113–1120. [Google Scholar] [CrossRef]
- Jia, W.B.; Wang, H.L.; Yang, J.F. Application of scene matching aided navigation in terminal guidance of ballistic missile. J. Tactical Missile Technol. 2009, 92, 62–65. [Google Scholar]
- Chen, F.; Xiong, Z.; Xu, Y.X. Research on the Fast Scene Matching Algorithm in the Inertial Integrated Navigation System. J. Astronaut. 2009, 30, 2308–2316. [Google Scholar]
- Du, Y.L. Research on Scene Matching Algorithm in the Vision-Aided Navigation System. Appl. Mech. Mater. 2011, 128, 229–232. [Google Scholar] [CrossRef]
- Li, Y.J.; Pan, Q.; Zhao, C.H. Natural-Landmark Scene Matching Vision Navigation Based on Dynamic Key-Frame. Phys. Procedia 2012, 24, 1701–1706. [Google Scholar] [CrossRef][Green Version]
- Yu, Q.F.; Shang, Y.; Liu, X.C. Full-parameter vision navigation based on scene matching for aircrafts. Sci. China Inf. Sci. 2014, 57, 1–10. [Google Scholar] [CrossRef][Green Version]
- Zhao, C.H.; Zhou, Y.H.; Lin, Z. Review of scene matching visual navigation for unmanned aerial vehicles. Sci. Sin. Inf. 2019, 49, 507–519. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.; Li, Y.; Xu, C. Map matching navigation method based on scene information fusion. Int. J. Model. Identif. Control 2022, 41, 110–119. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Y. Information fusion algorithm in INS/SMNS integrated navigation system. J. Beijing Univ. Aeronaut. Astronaut. 2009, 35, 292–295. [Google Scholar]
- Wang, Y.S.; Zeng, Q.H.; Liu, J.Y. INS/VNS integrated navigation method based on structured light sensor. In Proceedings of the 2016 China International Conference on Inertial Technology and Navigation, Beijing, China, 1 November 2016; pp. 511–516. [Google Scholar]
- Ning, X.; Gui, M.; Xu, Y.Z. INS/VNS/CNS integrated navigation method for planetary rovers. Aerosp. Sci. Technol. 2016, 48, 102–114. [Google Scholar] [CrossRef]
- Lu, J.; Lei, C.; Yang, Y. In-motion Initial Alignment and Positioning with INS/CNS/ODO Integrated Navigation System for Lunar Rovers. Adv. Space Res. 2017, 59, 3070–3079. [Google Scholar] [CrossRef]
- Lan, H.; Song, J.M.; Zhang, C.Y. Design and performance analysis of landmark-based INS/Vision Navigation System for UAV. Opt. Int. J. Light Electron Opt. 2018, 172, 484–493. [Google Scholar]
- Gou, B.; Cheng, Y.M.; de Ruiter, A.H. INS/CNS navigation system based on multi-star pseudo measurements. Aerosp. Sci. Technol. 2019, 95, 105506. [Google Scholar] [CrossRef]
- Shen, C.L.; Bu, Y.L.; Xu, X. Research on matching-area suitability for scene matching aided navigation. J. Aeronaut. 2010, 31, 553–563. [Google Scholar]
- Gong, X.P.; Cheng, Y.M.; Song, L. Automatic extraction algorithm of landmarks for scene-matching-based navigation. J. Comput. Simul. 2014, 31, 60–63. [Google Scholar]
- Zhu, R.; Karimi, H.A. Automatic Selection of Landmarks for Navigation Guidance. Trans. GIS 2015, 19, 247–261. [Google Scholar] [CrossRef]
- Yu, L.; Cheng, Y.M.; Liu, X.L. A method for reliability analysis and measurement error modeling based on machine learning in scene matching navigation (SMN). J. Northwestern Polytech. Univ. 2016, 34, 333–337. [Google Scholar]
- Wang, H.X.; Cheng, Y.M.; Liu, N. A Fast Selection Method of Landmarks for Terrain Matching Navigation. J. Northwestern Polytech. Univ. 2020, 38, 959–964. [Google Scholar] [CrossRef]
- Liu, X.C.; Wang, H.; Dan, F. An area-based position and attitude estimation for unmanned aerial vehicle navigation. Sci. China Technol. Sci. 2015, 58, 916–926. [Google Scholar] [CrossRef]
- Andrea, M.; Antonio, V. Improved Feature Matching for Mobile Devices with IMU. Sensors 2016, 16, 1243. [Google Scholar]
- Xiu, Y.; Zhu, S.; Rui, X.U. Optimal crater landmark selection based on optical navigation performance factors for planetary landing. Chin. J. Aeronaut. 2023, 36, 254–270. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V.N. Support Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Brabanter, J.D.; Lukas, L. Weighted least squares support vector machines: Robustness and sparse approximation. Neurocomputing 2002, 48, 85–105. [Google Scholar] [CrossRef]
- Khemchandani, R.; Chandra, S. Twin Support Vector Machines for Pattern Classification. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 905–910. [Google Scholar]
- Chen, J.; Ji, G. Weighted least squares twin support vector machines for pattern classification. In Proceedings of the 2010 the 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; pp. 242–246. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 886–893. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Carroll, M. Hartley transform phase cross correlation (PCC) based robust dynamic image matching in nuclear medicine. J. Nucl. Med. 2015, 56, 1746. [Google Scholar]
- Zhang, L.; Zhou, Y.; Lin, R.F. Fast triangle star pattern recognition algorithm. J. Appl. Opt. 2018, 39, 71–75. [Google Scholar]
- Chen, W.J.; Shao, Y.H.; Li, C.N. MLTSVM: A novel twin support vector machine to multi-label learning. Pattern Recognit. 2015, 52, 61–74. [Google Scholar] [CrossRef]
- Xu, S.; An, X. ML 2 S-SVM: Multi-label least-squares support vector machine classifiers. Electron. Libr. 2019, 37, 1040–1058. [Google Scholar] [CrossRef]
- Feng, P.; Qin, D.Y.; Ji, P. Multi-label learning algorithm with SVM based association. High Technol. Lett. 2019, 25, 97–104. [Google Scholar]
- Xu, J.D. A fast Ostu image segmentation method based on least square fitting. J. Chang. Univ. (Nat. Sci. Ed.) 2021, 33, 70–76. [Google Scholar]
- He, Y.; Wang, H.; Feng, L. Centroid extraction algorithm based on grey-gradient for autonomous star sensor. Opt. Int. J. Light Electron Opt. 2019, 194, 162932. [Google Scholar] [CrossRef]
- Cui, Z.J.; Qi, W.F.; Liu, Y.X. A fast image template matching algorithm based on normalized cross correlation. In Proceedings of the 2020 Conference on Computer Information Science and Artificial Intelligence (CISAI), Inner Mongolia, China, 25–27 September 2020; p. 12163. [Google Scholar]
- Guo, L.; Li, B.O.; Cao, Y. Star map recognition algorithm based on triangle matching and optimization. Electron. Des. Eng. 2018, 26, 137–140. [Google Scholar]
- Wang, S.H.; Han, Z.G.; Yao, Z.G. Analysis on cloud vertical structure over China and its neighborhood based on CloudSat data. J. Plateau Meteorol. 2011, 30, 38–52. [Google Scholar]
- Liu, S.J.; Wu, S.A.; Li, W.G. Study on spatial-temporal distribution of sea fog in the South China Sea from January to March based on FY-3B sea fog retrieval data. J. Mar. Meteorol. 2017, 37, 85–90. [Google Scholar]

| Month | Season | Low Cloud Radius (km) | Middle Cloud Radius (km) | High Cloud Radius (km) |
|---|---|---|---|---|
| 3–5 | spring | [74, 134] | [62, 122] | [65, 125] |
| 6–8 | summer | [60, 120] | [69.5, 130] | [93.7, 154] |
| 9–11 | autumn | [66, 126] | [67, 127] | [84, 144] |
| 12–2 | winter | [76, 136] | [68, 128] | [61, 121] |
| Month | Season | Low Cloud Speed (m/s) | Middle Cloud Speed (m/s) | High Cloud Speed (m/s) | Fog Speed (m/s) | Moving Direction | α (∘) |
|---|---|---|---|---|---|---|---|
| 3–5 | spring | [4, 16] | [14, 26] | [24, 36] | [1, 7] | east | 0 |
| 6–8 | summer | [9, 21] | [14, 26] | [39, 51] | [3, 9] | southwest | 225 |
| 9–11 | autumn | [11.8, 23.8] | [31.5, 43.5] | [50.3, 62.3] | [4.5, 10.5] | northeast | 45 |
| 12–2 | winter | [14, 26] | [34, 46] | [34, 46] | [5, 11] | northeast | 45 |
| Predict Number | Correct Number | Wrong Number | Prediction Accuracy | |
|---|---|---|---|---|
| Type I landmark | 3 | 3 | 0 | 100% |
| Type II landmark | 30 | 29 | 1 | 96.67% |
| Type III landmark | 16 | 15 | 1 | 93.75% |
| Height | Matching Probability | ||
|---|---|---|---|
| Type I Landmark | Type II Landmark | Type III Landmark | |
| H = 5000 m | 1 | 0.88 | 0.93 |
| H = 7500 m | 0.99 | 0.85 | 0.89 |
| H = 10,000 m | 0.96 | 0.81 | 0.83 |
| Altitude Range (m) | 8000–10,000 | 2000–5000 | 5000–8000 | 2000–10,000 |
|---|---|---|---|---|
| CNS effective probability | 1 | 0.79 | 0.91 | 0.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Z.; Cheng, Y.; Yao, S.; Li, Z. An Adaptive INS/CNS/SMN Integrated Navigation Algorithm in Sea Area. Remote Sens. 2024, 16, 612. https://doi.org/10.3390/rs16040612
Tian Z, Cheng Y, Yao S, Li Z. An Adaptive INS/CNS/SMN Integrated Navigation Algorithm in Sea Area. Remote Sensing. 2024; 16(4):612. https://doi.org/10.3390/rs16040612
Chicago/Turabian StyleTian, Zhaoxu, Yongmei Cheng, Shun Yao, and Zhenwei Li. 2024. "An Adaptive INS/CNS/SMN Integrated Navigation Algorithm in Sea Area" Remote Sensing 16, no. 4: 612. https://doi.org/10.3390/rs16040612
APA StyleTian, Z., Cheng, Y., Yao, S., & Li, Z. (2024). An Adaptive INS/CNS/SMN Integrated Navigation Algorithm in Sea Area. Remote Sensing, 16(4), 612. https://doi.org/10.3390/rs16040612






