Methodology for Regional Soil Organic Matter Prediction with Spectroscopy: Optimal Sample Grouping, Input Variables, and Prediction Model
Abstract
1. Introduction
2. Materials and Methods
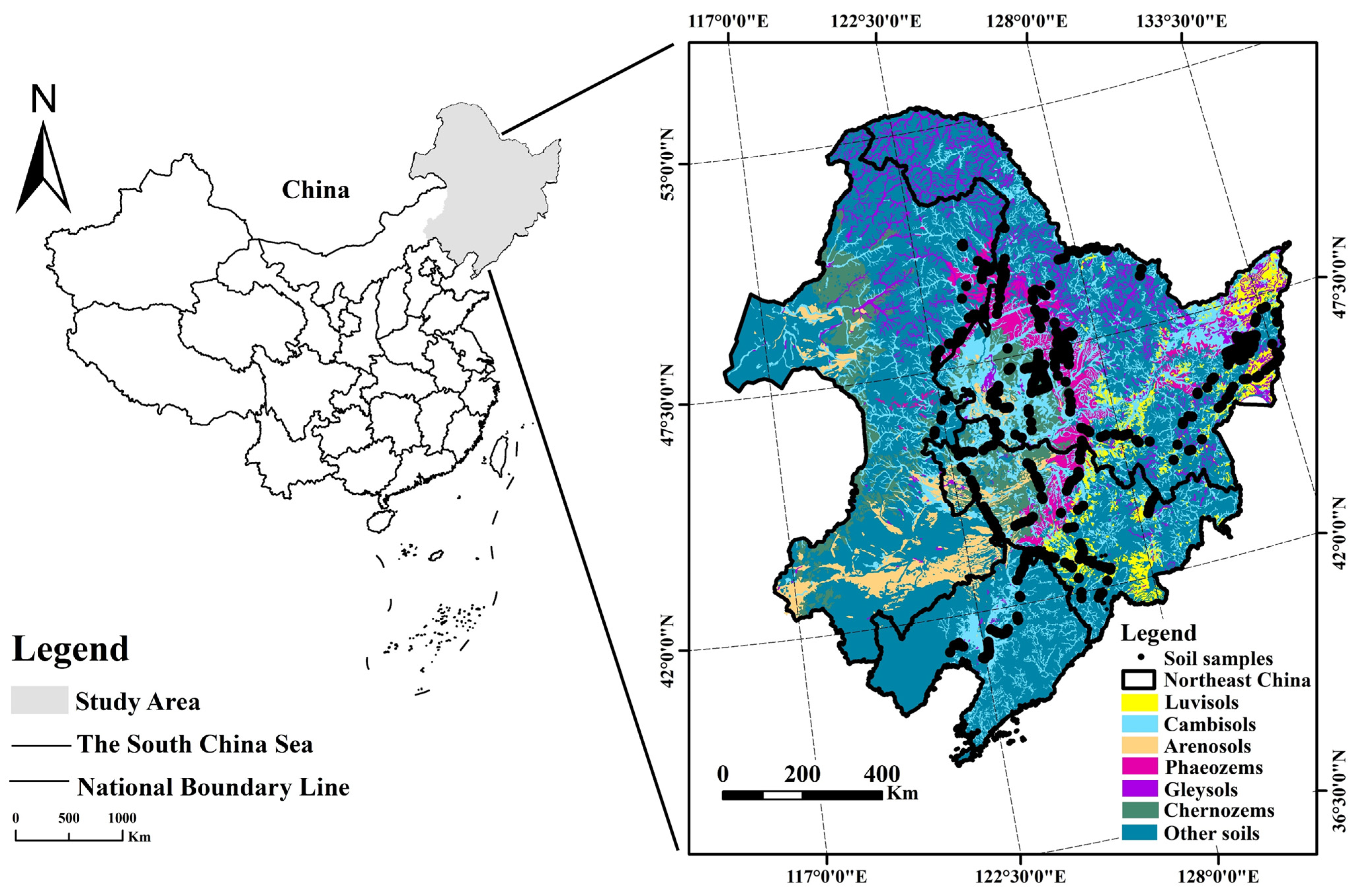
2.1. Overview of the Study Area
2.2. Soil Sample Collection and Processing
2.3. Soil Spectrometry
2.4. Spectral Data Preprocessing
- (1)
- Savitzky–Golay convolutional smoothing (S-G)
- (2)
- Continuum removal (CR)
- (3)
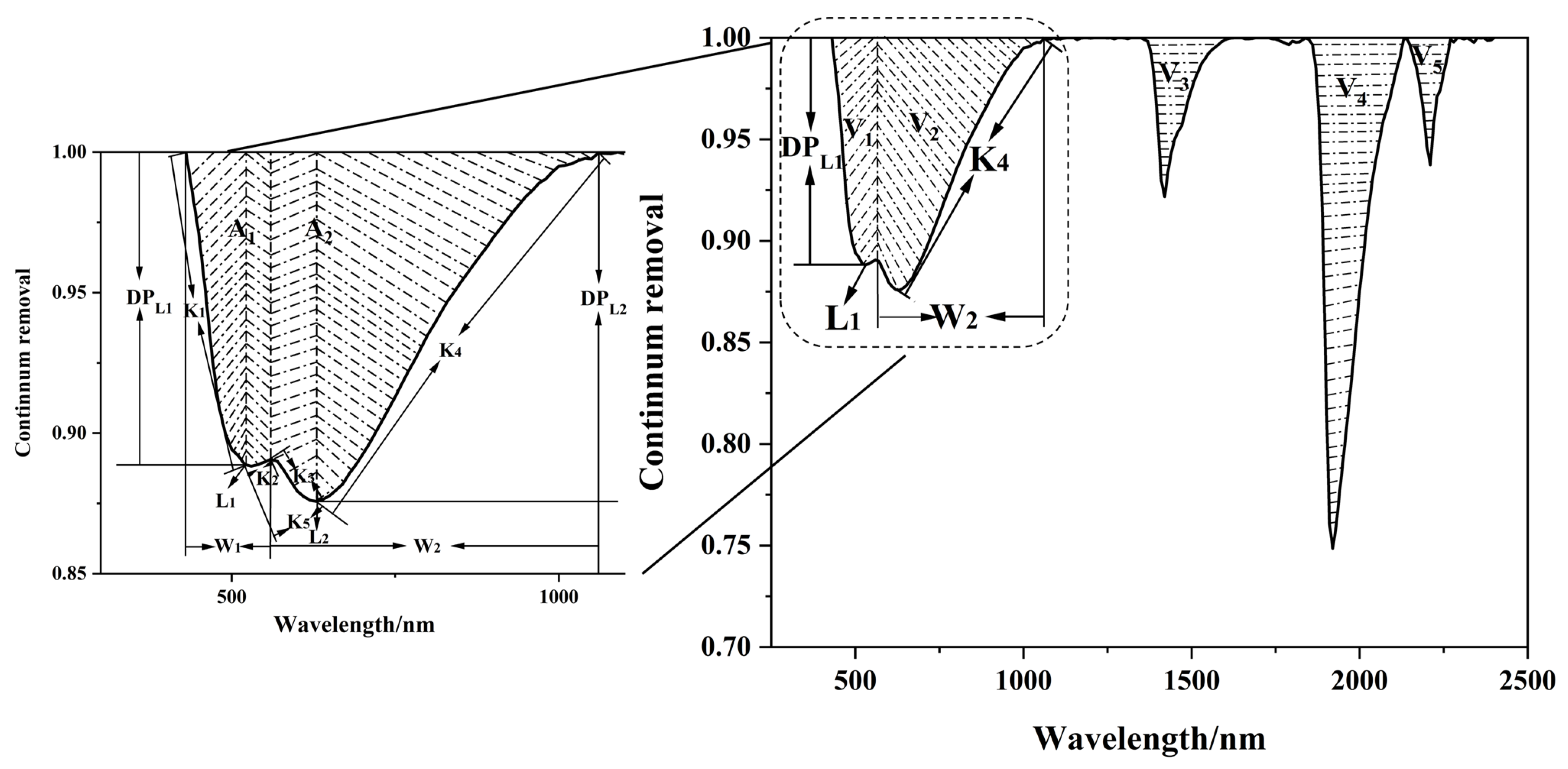
- Spectral characteristic parameters (SCPs)
- (4)
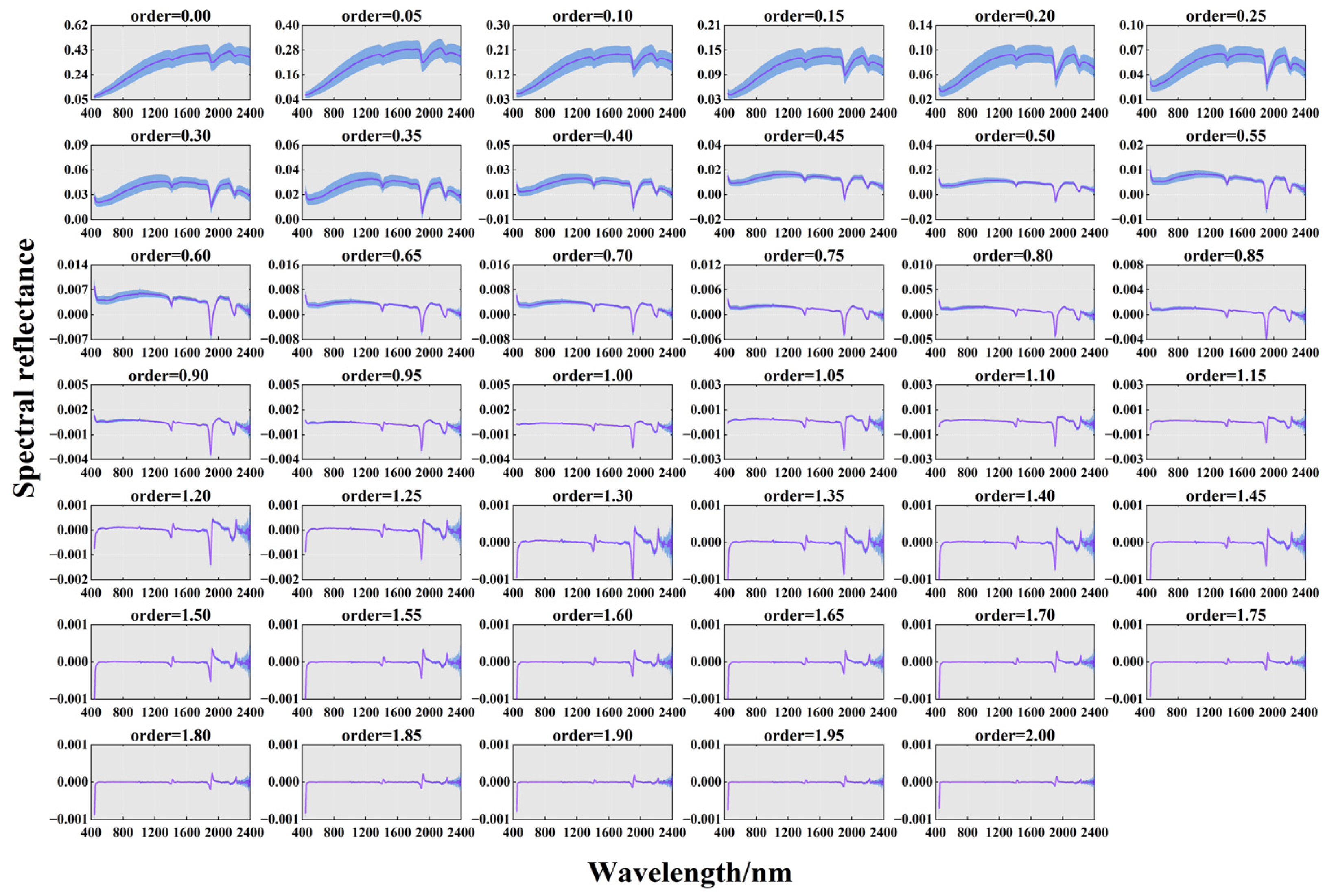
- Fractional-order differentiation (FOD)
2.5. Grouping Approach
2.5.1. No Groups
2.5.2. Traditional Grouping
2.5.3. Spectral Grouping
2.6. Models
2.6.1. Random Forest (RF)
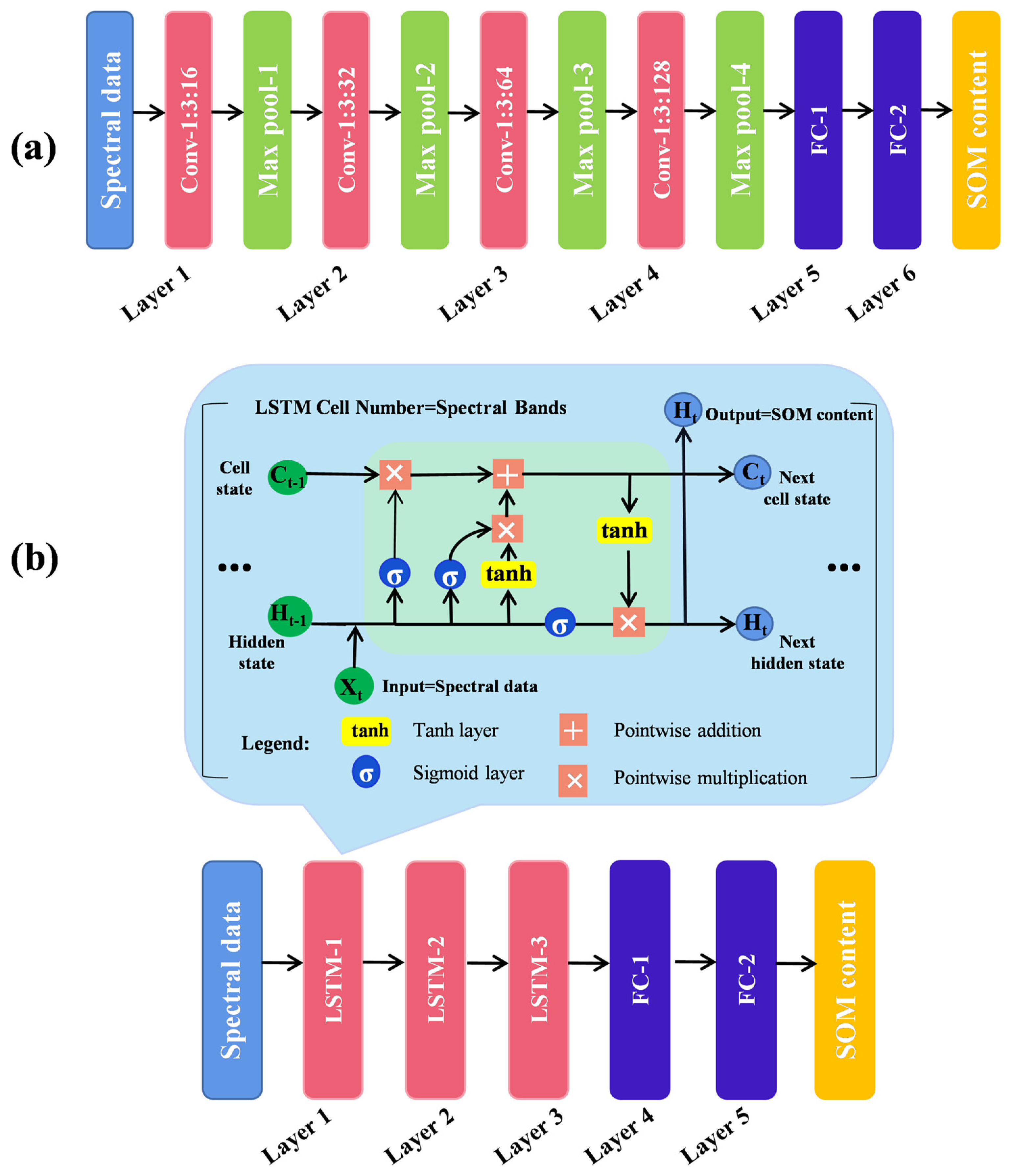
2.6.2. Convolutional Neural Network (CNN)
2.6.3. Long Short-Term Memory (LSTM)
2.7. Model Evaluation
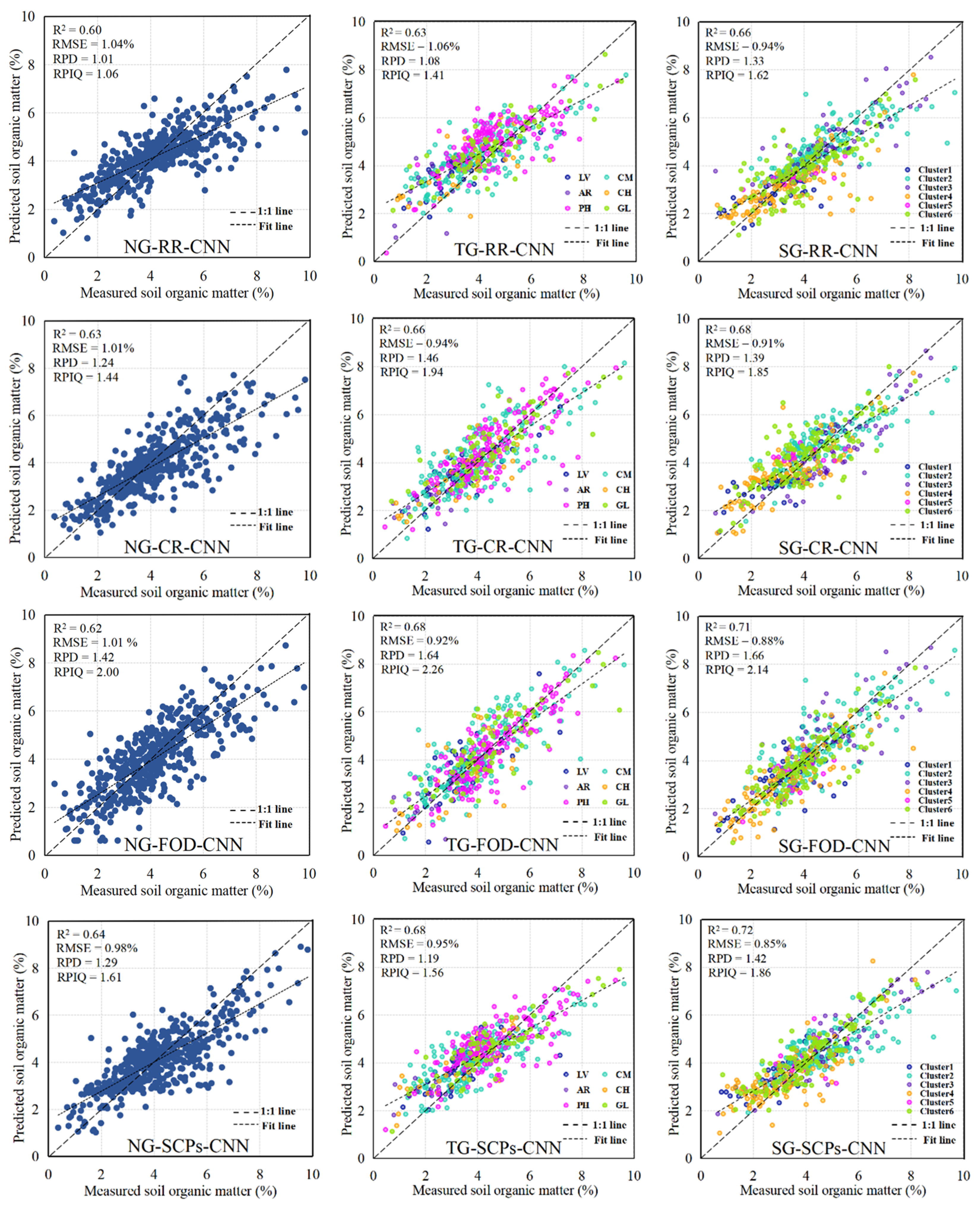
3. Results and Analyses
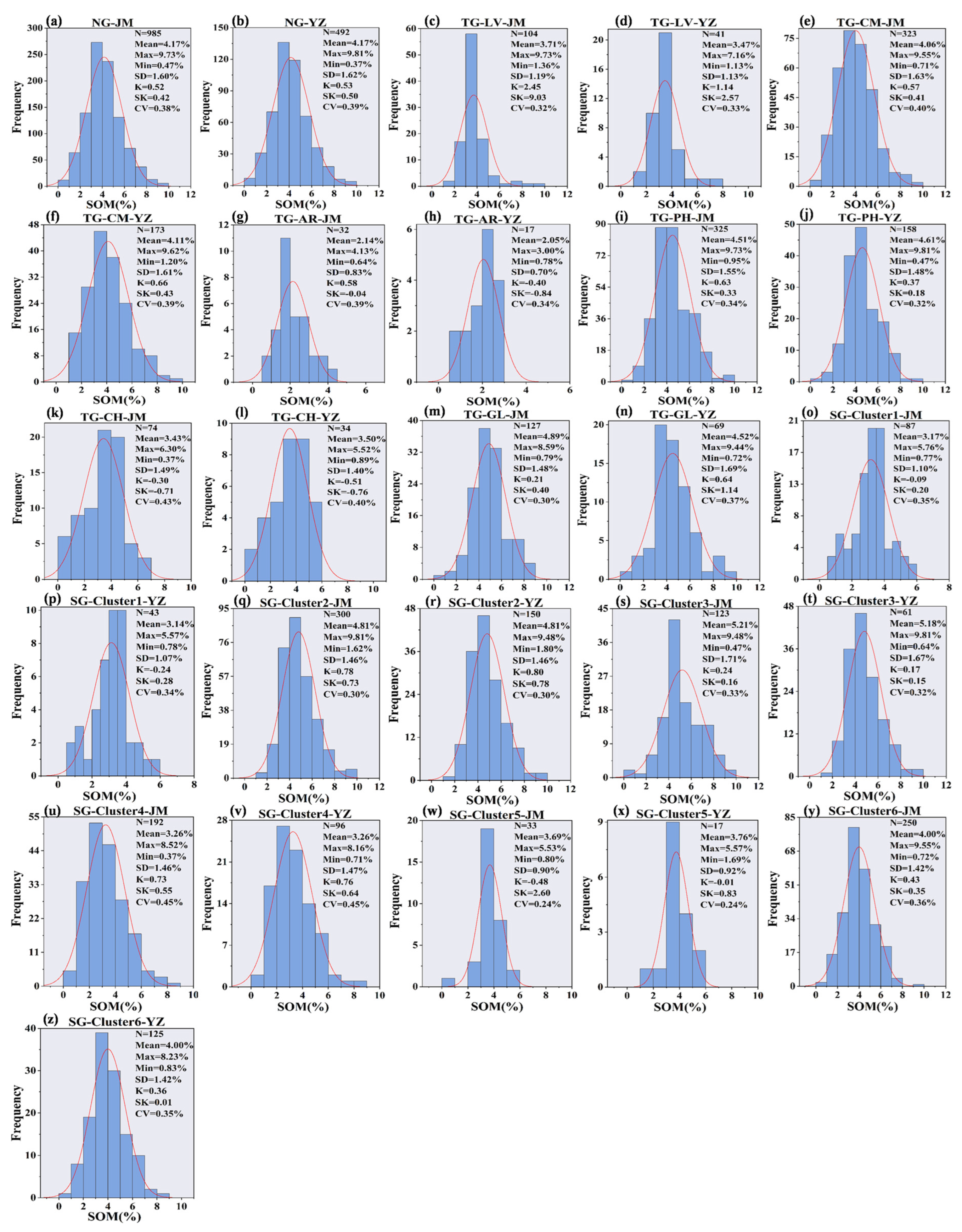
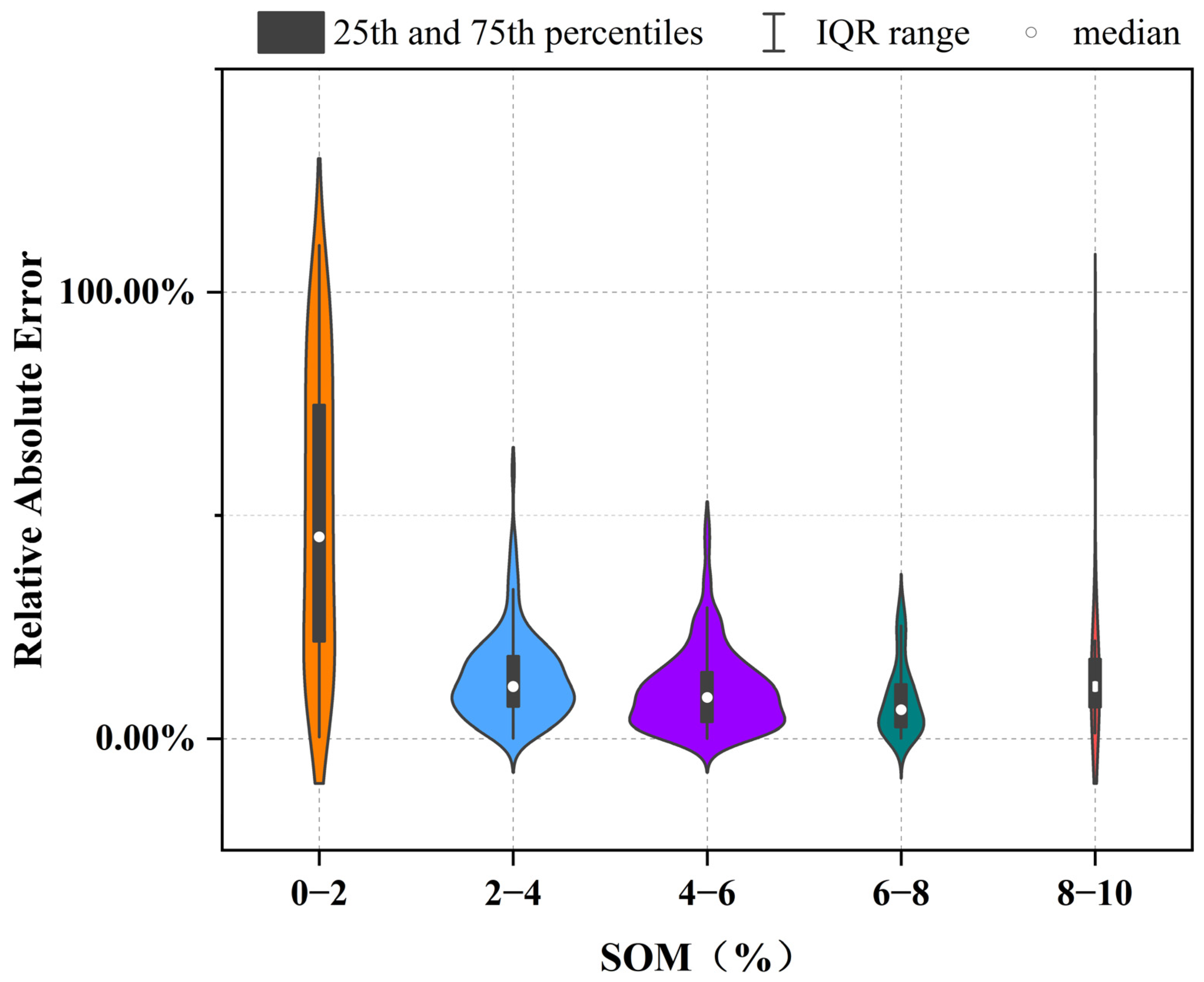
3.1. Descriptive Statistics of SOM Content for Different Grouping Methods
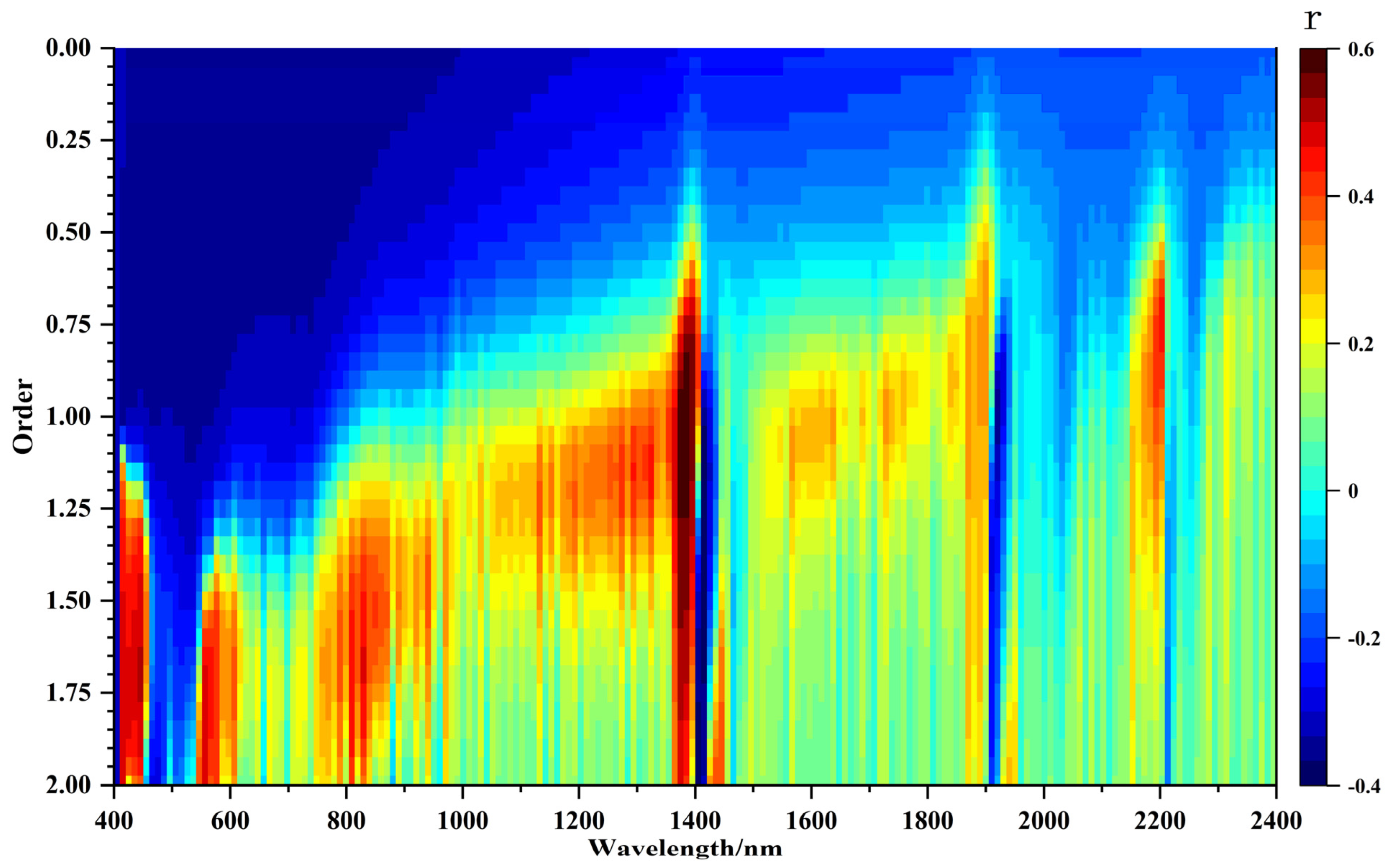
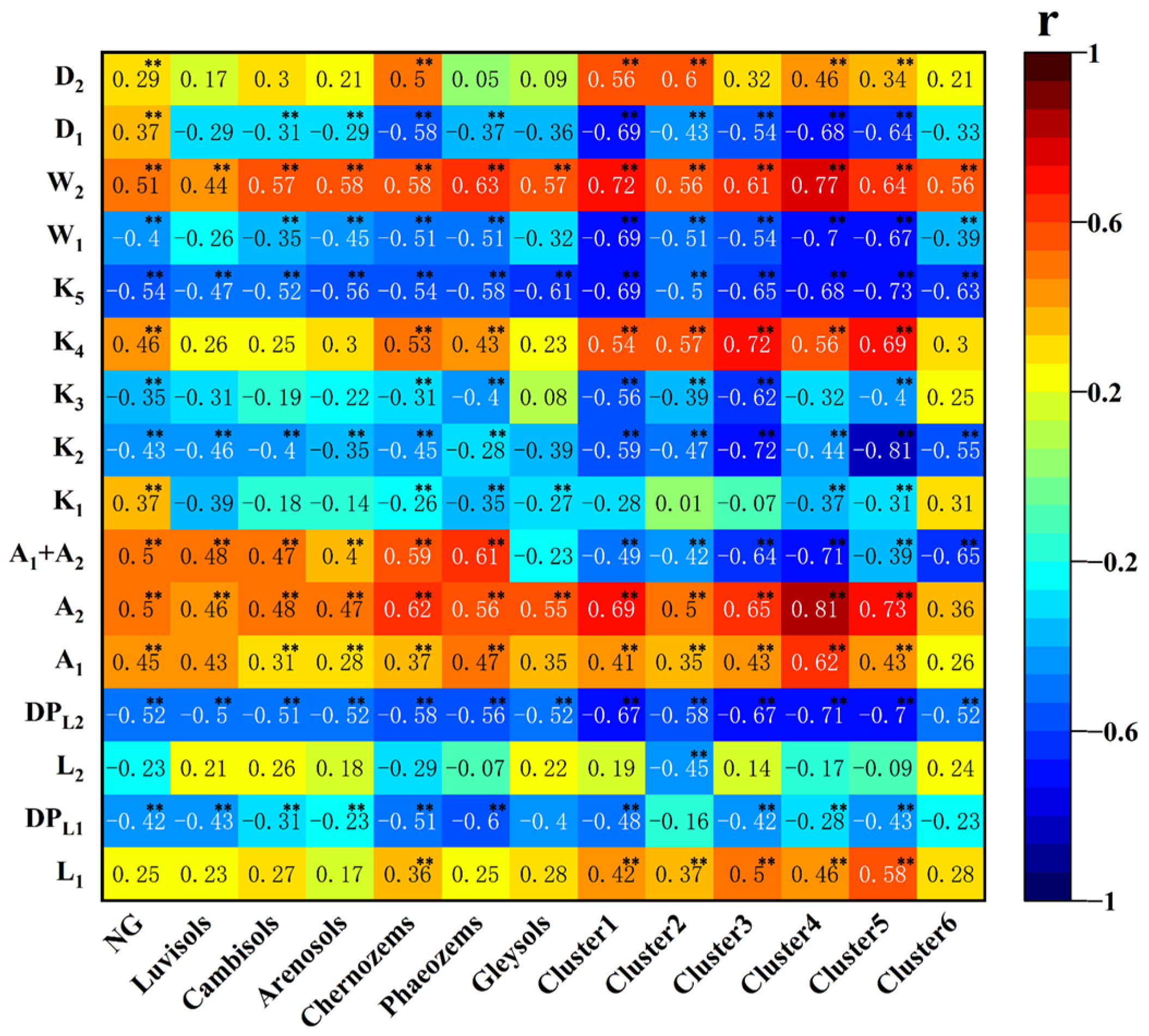
3.2. One-Dimensional Correlation between FOD Spectral Features and SOM Content
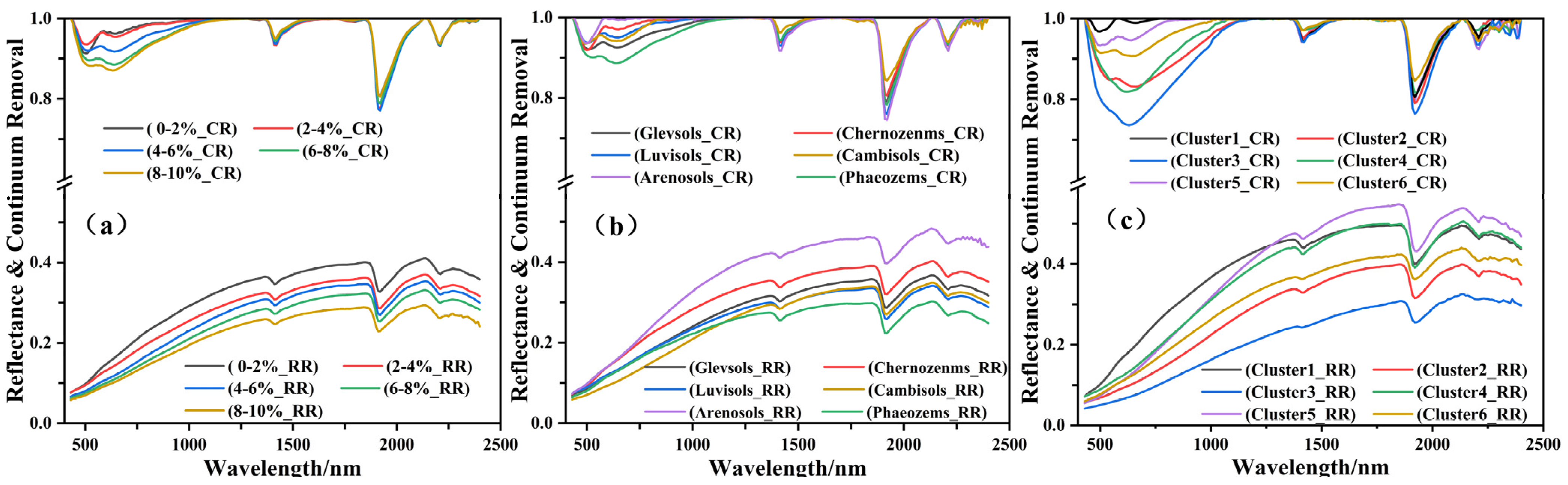
3.3. Spectral Characteristics of Soil Reflectance
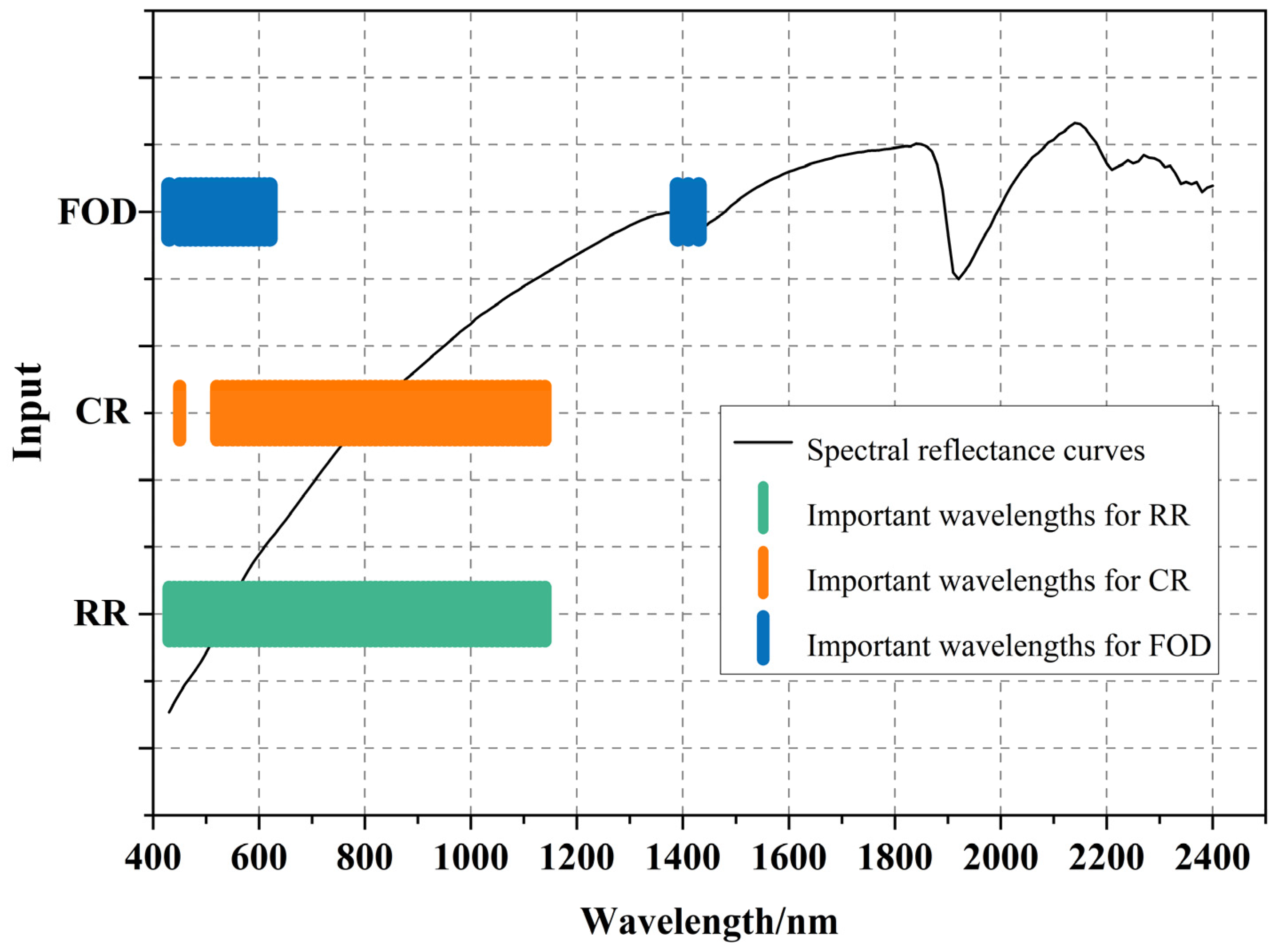
3.4. Spectral Variable Selection
3.5. Model Performance and Evaluation
4. Discussion
4.1. Impact of Deep Learning on the Performance of SOM Content Prediction Models
4.2. Comparison of Grouping Methods and Inputs
4.3. Research Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ge, X.; Ding, J.; Jin, X.; Wang, J.; Chen, X.; Li, X.; Liu, J.; Xie, B. Estimating Agricultural Soil Moisture Content through UAV-Based Hyperspectral Images in the Arid Region. Remote Sens. 2021, 13, 1562. [Google Scholar] [CrossRef]
- Rossel, R.V.; Behrens, T.; Ben-Dor, E.; Brown, D.J.; Demattê, J.A.M.; Shepherd, K.D.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V. A Global Spectral Library to Characterize the World’s Soil. Earth-Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef]
- Belyaev, B.I.; Belyaev, Y.V.; Katkovskii, L.V.; Tsikman, I.M. Estimation and Analysis of the Parameters of a Field Spectroradiometer Covering the Spectral Range 350–2500 Nm. J. Appl. Spectrosc. 2009, 76, 577–584. [Google Scholar] [CrossRef]
- Nocita, M.; Stevens, A.; van Wesemael, B.; Aitkenhead, M.; Bachmann, M.; Barthès, B.; Ben Dor, E.; Brown, D.J.; Clairotte, M.; Csorba, A.; et al. Chapter Four—Soil Spectroscopy: An Alternative to Wet Chemistry for Soil Monitoring. In Advances in Agronomy; Sparks, D.L., Ed.; Academic Press: Cambridge, MA, USA, 2015; Volume 132, pp. 139–159. [Google Scholar]
- Clark, R.N.; King, T.V.V.; Klejwa, M.; Swayze, G.A.; Vergo, N. High Spectral Resolution Reflectance Spectroscopy of Minerals. J. Geophys. Res. Solid Earth 1990, 95, 12653–12680. [Google Scholar] [CrossRef]
- Sanderman, J.; Baldock, J.A.; Dangal, S.R.S.; Ludwig, S.; Potter, S.; Rivard, C.; Savage, K. Soil Organic Carbon Fractions in the Great Plains of the United States: An Application of Mid-Infrared Spectroscopy. Biogeochemistry 2021, 156, 97–114. [Google Scholar] [CrossRef]
- Röder, L.L.; Fischer, H. Theoretical Investigation of Applicability and Limitations of Advanced Noise Reduction Methods for Wavelength Modulation Spectroscopy. Appl. Phys. B 2022, 128, 10. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Bor\uuvka, L.; Saberioon, M.M.; Kozák, J.; Vašát, R.; Němeček, K. Comparing Different Data Preprocessing Methods for Monitoring Soil Heavy Metals Based on Soil Spectral Features. Soil Water Res. 2015, 10, 218–227. [Google Scholar] [CrossRef]
- Bian, X. Spectral Preprocessing Methods. In Chemometric Methods in Analytical Spectroscopy Technology; Chu, X., Huang, Y., Yun, Y.-H., Bian, X., Eds.; Springer Nature: Singapore, 2022; pp. 111–168. ISBN 978-981-19162-5-0. [Google Scholar]
- Malenovskỳ, Z.; Homolová, L.; Zurita-Milla, R.; Lukeš, P.; Kaplan, V.; Hanuš, J.; Gastellu-Etchegorry, J.-P.; Schaepman, M.E. Retrieval of Spruce Leaf Chlorophyll Content from Airborne Image Data Using Continuum Removal and Radiative Transfer. Remote Sens. Environ. 2013, 131, 85–102. [Google Scholar] [CrossRef]
- Meng, X.; Bao, Y.; Zhang, X.; Wang, X.; Liu, H. Prediction of Soil Organic Matter Using Different Soil Classification Hierarchical Level Stratification Strategies and Spectral Characteristic Parameters. Geoderma 2022, 411, 115696. [Google Scholar] [CrossRef]
- Bayer, A.; Bachmann, M.; Müller, A.; Kaufmann, H. A Comparison of Feature-Based MLR and PLS Regression Techniques for the Prediction of Three Soil Constituents in a Degraded South African Ecosystem. Appl. Environ. Soil Sci. 2012, 2012, e971252. [Google Scholar] [CrossRef]
- Laukamp, C.; Rodger, A.; LeGras, M.; Lampinen, H.; Lau, I.C.; Pejcic, B.; Stromberg, J.; Francis, N.; Ramanaidou, E. Mineral Physicochemistry Underlying Feature-Based Extraction of Mineral Abundance and Composition from Shortwave, Mid and Thermal Infrared Reflectance Spectra. Minerals 2021, 11, 347. [Google Scholar] [CrossRef]
- Qiao, X.-X.; Wang, C.; Feng, M.-C.; Yang, W.-D.; Ding, G.-W.; Sun, H.; Liang, Z.-Y.; Shi, C.-C. Hyperspectral Estimation of Soil Organic Matter Based on Different Spectral Preprocessing Techniques. Spectrosc. Lett. 2017, 50, 156–163. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Liu, Y.; Zhang, Y.; Yu, L.; Chen, Y.; Liu, Y.; Cheng, H.; Liu, Y. Combination of Fractional Order Derivative and Memory-Based Learning Algorithm to Improve the Estimation Accuracy of Soil Organic Matter by Visible and near-Infrared Spectroscopy. Catena 2019, 174, 104–116. [Google Scholar] [CrossRef]
- Stenberg, B.; Viscarra Rossel, R.A.; Mouazen, A.M.; Wetterlind, J. Chapter Five—Visible and Near Infrared Spectroscopy in Soil Science. In Advances in Agronomy; Sparks, D.L., Ed.; Academic Press: Cambridge, MA, USA, 2010; Volume 107, pp. 163–215. [Google Scholar]
- Shi, Y.; Zhao, J.; Song, X.; Qin, Z.; Wu, L.; Wang, H.; Tang, J. Hyperspectral Band Selection and Modeling of Soil Organic Matter Content in a Forest Using the Ranger Algorithm. PLoS ONE 2021, 16, e0253385. [Google Scholar] [CrossRef]
- Jaconi, A.; Don, A.; Freibauer, A. Prediction of Soil Organic Carbon at the Country Scale: Stratification Strategies for near-Infrared Data. Eur. J. Soil Sci. 2017, 68, 919–929. [Google Scholar] [CrossRef]
- Genot, V.; Colinet, G.; Bock, L.; Vanvyve, D.; Reusen, Y.; Dardenne, P. Near Infrared Reflectance Spectroscopy for Estimating Soil Characteristics Valuable in the Diagnosis of Soil Fertility. J. Infrared Spectrosc. 2011, 19, 117–138. [Google Scholar] [CrossRef]
- Xu, M.; Chu, X.; Fu, Y.; Wang, C.; Wu, S. Improving the Accuracy of Soil Organic Carbon Content Prediction Based on Visible and Near-Infrared Spectroscopy and Machine Learning. Environ. Earth Sci. 2021, 80, 326. [Google Scholar] [CrossRef]
- Gogé, F.; Joffre, R.; Jolivet, C.; Ross, I.; Ranjard, L. Optimization Criteria in Sample Selection Step of Local Regression for Quantitative Analysis of Large Soil NIRS Database. Chemom. Intell. Lab. Syst. 2012, 110, 168–176. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, X.; Zou, B.; Wu, T. Exploring the Potential of Spectral Classification in Estimation of Soil Contaminant Elements. Remote Sens. 2017, 9, 632. [Google Scholar] [CrossRef]
- Ramirez-Lopez, L.; Behrens, T.; Schmidt, K.; Stevens, A.; Demattê, J.A.M.; Scholten, T. The Spectrum-Based Learner: A New Local Approach for Modeling Soil Vis–NIR Spectra of Complex Datasets. Geoderma 2013, 195–196, 268–279. [Google Scholar] [CrossRef]
- Xu, Z.; Zhao, X.; Guo, X.; Guo, J. Deep Learning Application for Predicting Soil Organic Matter Content by VIS-NIR Spectroscopy. Comput. Intell. Neurosci. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, Y.; Huang, H.; Li, A.; Yang, L.; Zhou, C. A CNN-LSTM Model for Soil Organic Carbon Content Prediction with Long Time Series of MODIS-Based Phenological Variables. Remote Sens. 2022, 14, 4441. [Google Scholar] [CrossRef]
- Wadoux, A.M.J.-C.; Padarian, J.; Minasny, B. Multi-Source Data Integration for Soil Mapping Using Deep Learning. Soil 2019, 5, 107–119. [Google Scholar] [CrossRef]
- Ng, W.; Minasny, B.; de Sousa Mendes, W.; Demattê, J.A.M. The Influence of Training Sample Size on the Accuracy of Deep Learning Models for the Prediction of Soil Properties with Near-Infrared Spectroscopy Data. Soil 2020, 6, 565–578. [Google Scholar] [CrossRef]
- Nelson, D.W.; Sommers, L.E. A Rapid and Accurate Procedure for Estimation of Organic Carbon in Soils. Proc. Indiana Acad. Sci. 1974, 84, 456–462. [Google Scholar]
- Pribyl, D.W. A Critical Review of the Conventional SOC to SOM Conversion Factor. Geoderma 2010, 156, 75–83. [Google Scholar] [CrossRef]
- Bao, Y.; Meng, X.; Ustin, S.; Wang, X.; Zhang, X.; Liu, H.; Tang, H. Vis-SWIR Spectral Prediction Model for Soil Organic Matter with Different Grouping Strategies. Catena 2020, 195, 104703. [Google Scholar] [CrossRef]
- Delwiche, S.R.; Reeves, J.B. A Graphical Method to Evaluate Spectral Preprocessing in Multivariate Regression Calibrations: Example with Savitzky–Golay Filters and Partial Least Squares Regression. Appl. Spectrosc. 2010, 64, 73–82. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Ting, H. Study on Spectral Features of Soil Fe2O3. Geogr. Geo-Inf. Sci. 2006. [Google Scholar] [CrossRef]
- Santos, M.J.; Hestir, E.L.; Khanna, S.; Ustin, S.L. Image Spectroscopy and Stable Isotopes Elucidate Functional Dissimilarity between Native and Nonnative Plant Species in the Aquatic Environment. New Phytol. 2012, 193, 683–695. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.; Zheng, L.; Zhao, Y.; Pei, X. Soil Nitrogen Content Forecasting Based on Real-Time NIR Spectroscopy. Comput. Electron. Agric. 2016, 124, 29–36. [Google Scholar] [CrossRef]
- Zhang, W.L.; Xu, A.G.; Zhang, R.L.; Ji, H.J.; Wu, S.X. Review of Soil Classification and Revision of China Soil Classification System. Sci. Agric. Sin. 2014, 47, 3214–3230. [Google Scholar]
- Shang, X.; Li, X.; Morales-Esteban, A.; Asencio-Cortés, G.; Wang, Z. Data Field-Based K-Means Clustering for Spatio-Temporal Seismicity Analysis and Hazard Assessment. Remote Sens. 2018, 10, 461. [Google Scholar] [CrossRef]
- Chen, X.; Li, H.; Zhang, S.; Chen, Y.; Fan, Q. High Spatial Resolution PM2.5 Retrieval Using MODIS and Ground Observation Station Data Based on Ensemble Random Forest. IEEE Access 2019, 7, 44416–44430. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; Alvarez de Andrés, S. Gene Selection and Classification of Microarray Data Using Random Forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Mustaqeem; Kwon, S. Optimal Feature Selection Based Speech Emotion Recognition Using Two-Stream Deep Convolutional Neural Network. Int. J. Intell. Syst. 2021, 36, 5116–5135. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A Review on the Long Short-Term Memory Model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Guerrero, C.; Wetterlind, J.; Stenberg, B.; Mouazen, A.M.; Gabarrón-Galeote, M.A.; Ruiz-Sinoga, J.D.; Zornoza, R.; Viscarra Rossel, R.A. Do We Really Need Large Spectral Libraries for Local Scale SOC Assessment with NIR Spectroscopy? Soil Tillage Res. 2016, 155, 501–509. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, Q.; Peng, J.; Ji, W.; Liu, H.; Li, X.; Viscarra Rossel, R.A. Development of a National VNIR Soil-Spectral Library for Soil Classification and Prediction of Organic Matter Concentrations. Sci. China Earth Sci. 2014, 57, 1671–1680. [Google Scholar] [CrossRef]
- Sotoodeh, K. The Mathematical Analysis and Review of Noise in Industrial Valves. JMST Adv. 2022, 4, 45–55. [Google Scholar] [CrossRef]
- Kale, K.V.; Solankar, M.M.; Nalawade, D.B.; Dhumal, R.K.; Gite, H.R. A Research Review on Hyperspectral Data Processing and Analysis Algorithms. Proc. Natl. Acad. Sci. India Sect. Phys. Sci. 2017, 87, 541–555. [Google Scholar] [CrossRef]
- Dotto, A.C.; Dalmolin, R.S.D.; Grunwald, S.; ten Caten, A.; Pereira Filho, W. Two Preprocessing Techniques to Reduce Model Covariables in Soil Property Predictions by Vis-NIR Spectroscopy. Soil Tillage Res. 2017, 172, 59–68. [Google Scholar] [CrossRef]
- Kharintsev, S.S.; Salakhov, M.K. A Simple Method to Extract Spectral Parameters Using Fractional Derivative Spectrometry. Spectrochim. Acta. A. Mol. Biomol. Spectrosc. 2004, 60, 2125–2133. [Google Scholar] [CrossRef]
- Jia, W.; Sun, M.; Lian, J.; Hou, S. Feature Dimensionality Reduction: A Review. Complex Intell. Syst. 2022, 8, 2663–2693. [Google Scholar] [CrossRef]
- Migenda, N.; Möller, R.; Schenck, W. Adaptive Dimensionality Reduction for Neural Network-Based Online Principal Component Analysis. PLoS ONE 2021, 16, e0248896. [Google Scholar] [CrossRef] [PubMed]
- Brown, D.J.; Shepherd, K.D.; Walsh, M.G.; Dewayne Mays, M.; Reinsch, T.G. Global Soil Characterization with VNIR Diffuse Reflectance Spectroscopy. Geoderma 2006, 132, 273–290. [Google Scholar] [CrossRef]
- Lao, C.; Chen, J.; Zhang, Z.; Chen, Y.; Ma, Y.; Chen, H.; Gu, X.; Ning, J.; Jin, J.; Li, X. Predicting the Contents of Soil Salt and Major Water-Soluble Ions with Fractional-Order Derivative Spectral Indices and Variable Selection. Comput. Electron. Agric. 2021, 182, 106031. [Google Scholar] [CrossRef]
- Tanaka, Y.; Kojima, R.; Ishida, S.; Yamashita, F.; Okuno, Y. Complex Network Prediction Using Deep Learning. arXiv 2021, arXiv:2104.03871. [Google Scholar]
- Pullanagari, R.R.; Dehghan-Shoar, M.; Yule, I.J.; Bhatia, N. Field Spectroscopy of Canopy Nitrogen Concentration in Temperate Grasslands Using a Convolutional Neural Network. Remote Sens. Environ. 2021, 257, 112353. [Google Scholar] [CrossRef]

| WRB | CSGC | Number | Total |
|---|---|---|---|
| Luvisols (LV) | Bleached baijiang soils | 145 | 1477 |
| Cambisols (CM) | Meadow soils | 496 | |
| Arenosols (AR) | Aeolian soils | 49 | |
| Phaeozems (PH) | Black soils | 483 | |
| Chernozems (CH) | Chernozems | 108 | |
| Gleysols (GL) | Aqueous soils | 196 |
| Layer | Kernel Size | Filters | Activation |
|---|---|---|---|
| Conv-1 | 3 | 16 | RELU |
| Max-pool-1 | 2 | - | - |
| Conv-2 | 3 | 32 | RELU |
| Max-pool-2 | 2 | - | - |
| Conv-3 | 3 | 64 | RELU |
| Max-pool-3 | 2 | - | - |
| Conv-4 | 3 | 128 | RELU |
| Max-pool-4 | 2 | - | - |
| FC-1 | - | 64 | RELU |
| FC-2 | - | 1 | Linear |
| Layer | Optimal Value |
|---|---|
| LSTM-1 | 128 |
| LSTM-2 | 64 |
| LSTM-3 | 32 |
| Dropout | 0.2 |
| FC-1 | 16 |
| FC-2 | 1 |
| Loss function | MSE |
| Optimizer | Adam |
| Learning rate | 0.001 |
| Epochs | 300 |
| Activation | RELU |
| GM | Type | N | Mean | Max | Min | SD | K | SK | CV |
|---|---|---|---|---|---|---|---|---|---|
| NG | 1477 | 4.17 | 9.81 | 0.37 | 1.61 | 0.44 | 0.52 | 0.39 | |
| TG | LV | 145 | 3.64 | 9.73 | 1.13 | 1.18 | 7.49 | 2.10 | 0.40 |
| CM | 496 | 4.08 | 9.62 | 0.71 | 1.62 | 0.40 | 0.60 | 0.37 | |
| AR | 49 | 2.11 | 4.13 | 0.64 | 0.78 | −0.09 | 0.37 | 0.42 | |
| CH | 483 | 3.45 | 6.30 | 0.37 | 1.46 | −0.73 | −0.35 | 0.34 | |
| PH | 108 | 4.56 | 9.81 | 0.47 | 1.53 | 0.26 | 0.55 | 0.33 | |
| GL | 196 | 4.76 | 9.44 | 0.72 | 1.56 | 0.60 | 0.34 | 0.39 | |
| SG | Cluster 1 | 130 | 3.16 | 5.76 | 0.77 | 1.08 | 0.18 | −0.14 | 0.34 |
| Cluster 2 | 450 | 4.81 | 9.48 | 1.62 | 1.46 | 0.73 | 0.79 | 0.30 | |
| Cluster 3 | 184 | 5.20 | 9.81 | 0.47 | 1.69 | 0.13 | 0.22 | 0.33 | |
| Cluster 4 | 288 | 3.26 | 8.52 | 0.37 | 1.46 | 0.55 | 0.74 | 0.45 | |
| Cluster 5 | 50 | 3.72 | 5.57 | 0.80 | 0.90 | 1.74 | −0.31 | 0.24 | |
| Cluster 6 | 375 | 4.00 | 9.55 | 0.72 | 1.42 | 0.22 | 0.40 | 0.35 |
| FOD | MACC | FOD | MACC | FOD | MACC | FOD | MACC |
|---|---|---|---|---|---|---|---|
| 0.00 | 0.532 | 0.05 | 0.532 | 0.10 | 0.532 | 0.15 | 0.532 |
| 0.20 | 0.532 | 0.25 | 0.533 | 0.30 | 0.533 | 0.35 | 0.532 |
| 0.40 | 0.532 | 0.45 | 0.532 | 0.50 | 0.532 | 0.55 | 0.531 |
| 0.60 | 0.531 | 0.65 | 0.53 | 0.70 | 0.529 | 0.75 | 0.527 |
| 0.80 | 0.549 | 0.85 | 0.58 | 0.90 | 0.597 | 0.95 | 0.604 |
| 1.00 | 0.603 | 1.05 | 0.606 | 1.10 | 0.598 | 1.15 | 0.592 |
| 1.20 | 0.585 | 1.25 | 0.578 | 1.30 | 0.578 | 1.35 | 0.577 |
| 1.40 | 0.574 | 1.45 | 0.57 | 1.50 | 0.566 | 1.55 | 0.561 |
| 1.60 | 0.556 | 1.65 | 0.55 | 1.70 | 0.543 | 1.75 | 0.54 |
| 1.80 | 0.545 | 1.85 | 0.549 | 1.90 | 0.551 | 1.95 | 0.553 |
| 2.00 | 0.554 |
| Model | GM | Inputs | R2 | RMSE | RPIQ | RPD |
|---|---|---|---|---|---|---|
| RF | NG | RR | 0.55 | 1.09 | 1.31 | 1.12 |
| CR | 0.58 | 1.05 | 1.21 | 1.03 | ||
| FOD | 0.57 | 1.06 | 1.51 | 1.09 | ||
| SCPs | 0.60 | 1.03 | 1.87 | 1.57 | ||
| TG | RR | 0.61 | 1.00 | 1.67 | 1.28 | |
| CR | 0.64 | 0.97 | 1.53 | 1.19 | ||
| FOD | 0.64 | 0.96 | 0.71 | 1.26 | ||
| SCPs | 0.65 | 0.95 | 1.61 | 1.33 | ||
| SG | RR | 0.63 | 0.97 | 1.59 | 1.28 | |
| CR | 0.66 | 0.95 | 1.36 | 1.16 | ||
| FOD | 0.69 | 0.90 | 1.53 | 1.34 | ||
| SCPs | 0.69 | 0.91 | 1.50 | 1.33 | ||
| CNN | NG | RR | 0.60 | 1.04 | 1.06 | 1.01 |
| CR | 0.63 | 1.01 | 1.44 | 1.24 | ||
| FOD | 0.62 | 1.01 | 2.00 | 1.42 | ||
| SCPs | 0.64 | 0.98 | 1.61 | 1.29 | ||
| TG | RR | 0.63 | 1.06 | 1.41 | 1.08 | |
| CR | 0.66 | 0.94 | 1.94 | 1.46 | ||
| FOD | 0.68 | 0.92 | 2.26 | 1.64 | ||
| SCPs | 0.68 | 0.95 | 1.56 | 1.19 | ||
| SG | RR | 0.66 | 0.94 | 1.62 | 1.33 | |
| CR | 0.68 | 0.91 | 1.85 | 1.39 | ||
| FOD | 0.71 | 0.88 | 2.40 | 1.66 | ||
| SCPs | 0.72 | 0.85 | 1.86 | 1.42 | ||
| LSTM | NG | RR | 0.61 | 1.02 | 1.64 | 1.35 |
| CR | 0.69 | 0.92 | 1.64 | 1.35 | ||
| FOD | 0.72 | 0.89 | 2.08 | 1.66 | ||
| SCPs | 0.72 | 0.87 | 1.79 | 1.41 | ||
| TG | RR | 0.63 | 1.00 | 1.52 | 1.15 | |
| CR | 0.69 | 0.89 | 1.47 | 1.34 | ||
| FOD | 0.73 | 0.85 | 2.00 | 1.67 | ||
| SCPs | 0.76 | 0.84 | 1.98 | 1.57 | ||
| SG | RR | 0.67 | 0.93 | 1.52 | 1.23 | |
| CR | 0.71 | 0.89 | 1.64 | 1.34 | ||
| FOD | 0.78 | 0.77 | 2.20 | 1.81 | ||
| SCPs | 0.82 | 0.69 | 2.62 | 1.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Dong, C.; Liu, H.; Meng, X.; Luo, C.; Han, Y.; Ai, H. Methodology for Regional Soil Organic Matter Prediction with Spectroscopy: Optimal Sample Grouping, Input Variables, and Prediction Model. Remote Sens. 2024, 16, 565. https://doi.org/10.3390/rs16030565
Zhang X, Dong C, Liu H, Meng X, Luo C, Han Y, Ai H. Methodology for Regional Soil Organic Matter Prediction with Spectroscopy: Optimal Sample Grouping, Input Variables, and Prediction Model. Remote Sensing. 2024; 16(3):565. https://doi.org/10.3390/rs16030565
Chicago/Turabian StyleZhang, Xinle, Chang Dong, Huanjun Liu, Xiangtian Meng, Chong Luo, Yongqi Han, and Hongfu Ai. 2024. "Methodology for Regional Soil Organic Matter Prediction with Spectroscopy: Optimal Sample Grouping, Input Variables, and Prediction Model" Remote Sensing 16, no. 3: 565. https://doi.org/10.3390/rs16030565
APA StyleZhang, X., Dong, C., Liu, H., Meng, X., Luo, C., Han, Y., & Ai, H. (2024). Methodology for Regional Soil Organic Matter Prediction with Spectroscopy: Optimal Sample Grouping, Input Variables, and Prediction Model. Remote Sensing, 16(3), 565. https://doi.org/10.3390/rs16030565







