Pentagram Arrays: A New Paradigm for DOA Estimation of Wideband Sources Based on Triangular Geometry
Abstract
1. Introduction
- Developing a new paradigm of pentagram arrays based on triangular geometry.
- Explanation of the theoretical principle of the superposition techniques.
- Clarification of the advantages of limiting the number of sensors in the array.
- The significance of designing an array with variable element spacing.
- Ability to maximize and minimize the array apertures.
- Addressing the issue of the DOA manifold matrix ambiguity problem.
- Application for DOA estimation algorithms of both azimuth and elevation angles.
- Conducting a large number of simulation experiments and analyses to validate the effectiveness of the geometry under different algorithms.
- -
- A single wideband signal (pulse signal) comes from a single azimuth DOA.
- -
- Two wideband signals with different frequencies and zero bandwidths (pulse signals) come from two closely related azimuth DOAs.
- -
- Two wideband signals with different frequencies and zero bandwidth (pulse signals) come from two far azimuth DOAs.
- -
- Two wideband signals with different frequencies and zero bandwidths (pulse signals) come from two far azimuth DOAs using different SNR values.
- -
- Two wideband signals with different frequencies and different bandwidths (without overlapping) come from two far azimuth DOAs.
- -
- Two wideband signals with the same frequencies and different bandwidths (with overlap) come from two far azimuth DOAs.
- -
- Four wideband signals with different frequencies and zero bandwidth (pulse signals) come from four far azimuth DOAs.
- -
- Four wideband signals with the same frequencies and different bandwidths (with overlap) come from four far azimuth DOAs.
2. The Proposed Array Geometry
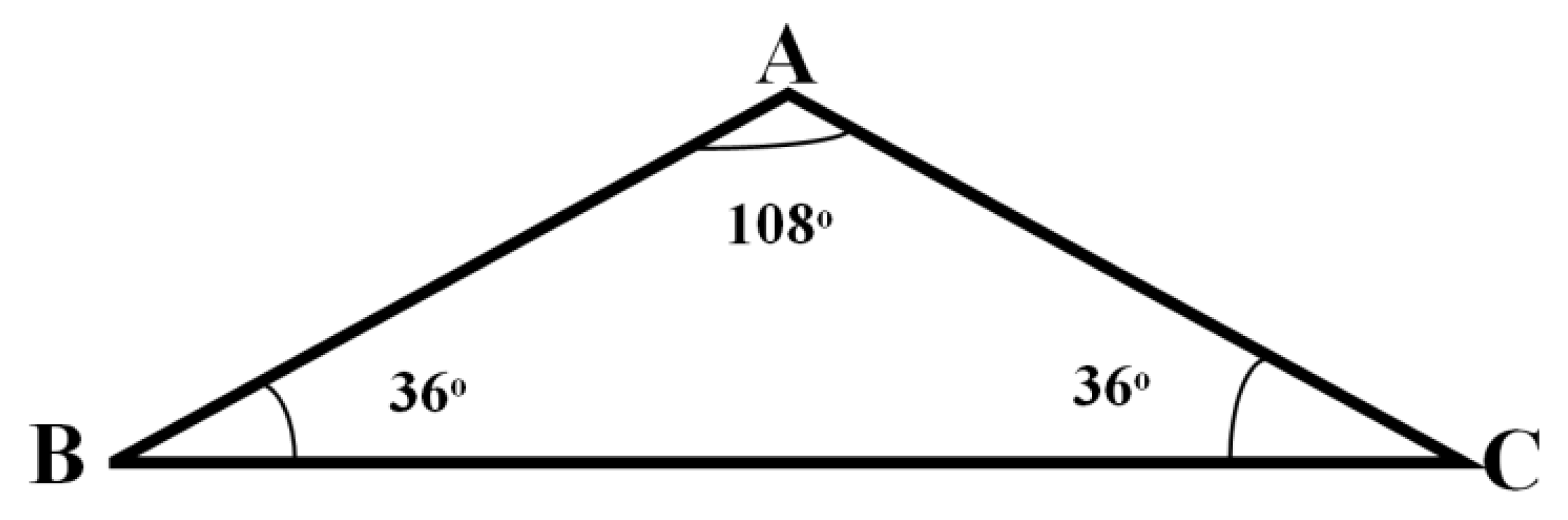
2.1. Pentagram and Triangular Geometry
2.2. Pentagram Geometry Analysis Based on Triangular Geometry
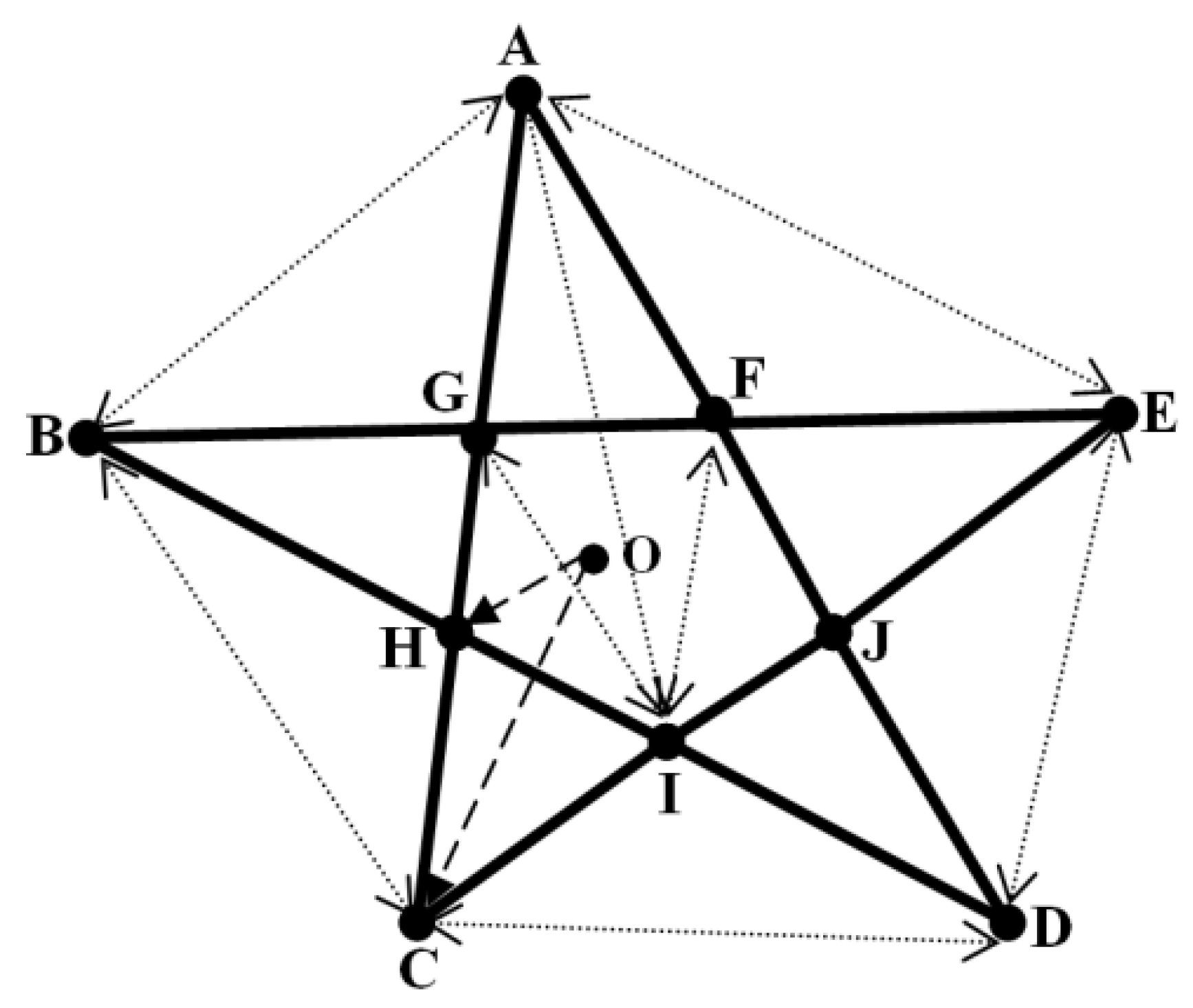
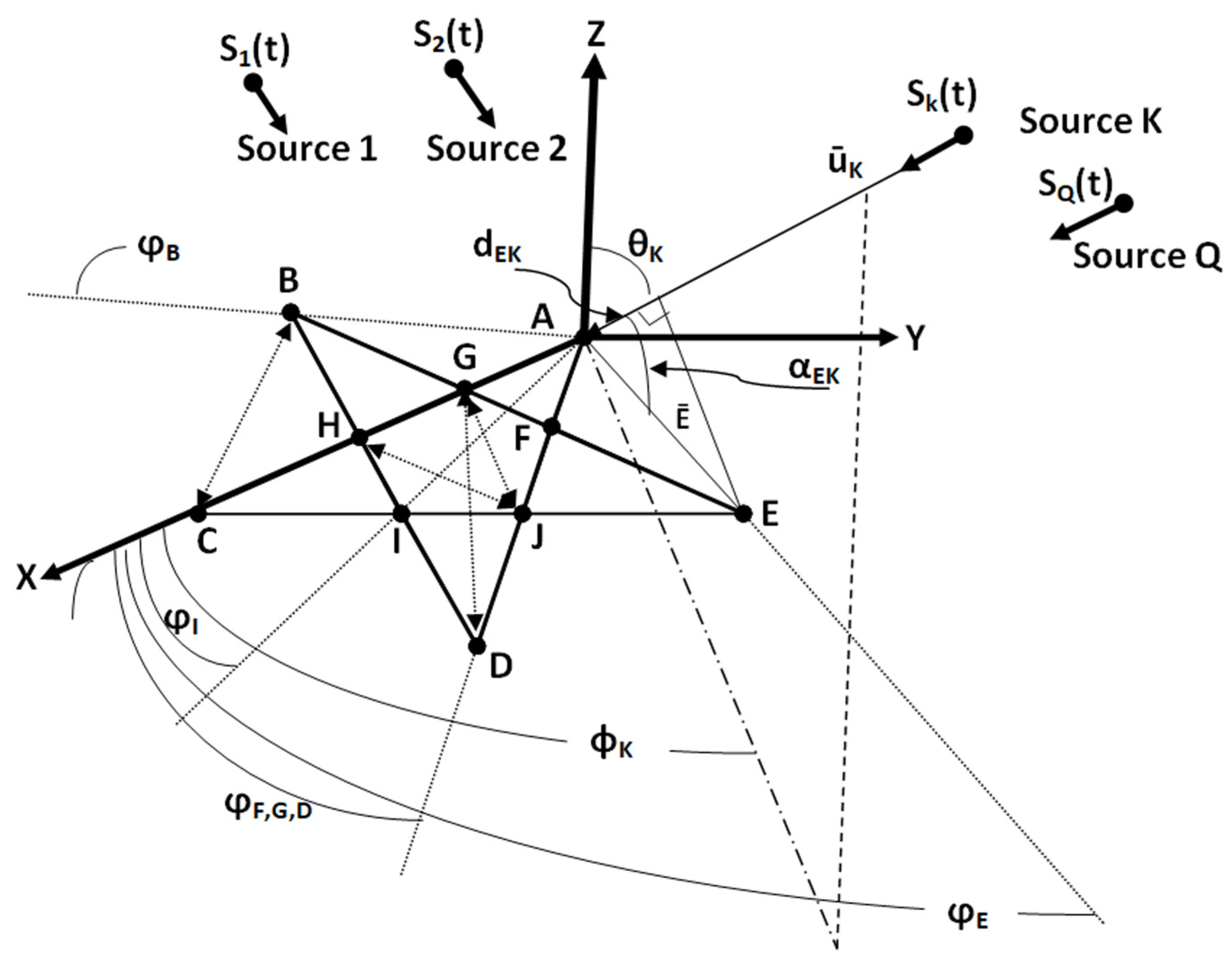
- The five outer vertices of the superposed triangles (pentagram) are named A, B, C, D, and E, and the five inner vertices are named F, G, H, I, and J.
- All five angles of the five outer vertices () have equal values of .
- All five inner angles of the five inner vertices () have equal values of .
- The lengths of the triangle sides between any two points (AB, BC, CD, DE, and EA) of the five outer vertices are equal; we named them L, and we have five Ls in total.
- The lengths of the triangle sides between the five outer vertices and any point of the five inner vertices (AF, AG, BG, BH, CH, CI, DI, DJ, EJ, and EF) are equal; we named them X, and we have ten Xs in total.
- The lengths of the triangle sides between two points of the five inner vertices (FG, GH, HI, IG, and JF) are equal (interconnection distances not included); we named them Y, and we have five Ys in total.
- The two straight lengths (interconnection) of triangle sides between any one point and the two points (opposite sides) of five interspersions (IF, IG, HJ, HF, and GJ) are equal; we named it P, and we have five Ps in total.
- The five lengths of triangle sides between the five headsails and the opposite (one) point of the five inner vertices (AI, BJ, CF, DG, and EH) are equal; we named them Z, and we have five Zs in total.
2.3. Pentagram Geometry Structure
3. DOA Array Signal Model
4. Results
4.1. Simulation Setup
4.1.1. Simulation Setup for Proposed Geometry Configuration
4.1.2. Simulation Setup for DOA Angular Accuracy and Resolution Performance of the Proposed Geometry
4.1.3. Simulation Setup for DOA Estimation Comparison of the Proposed Geometry with UCA and ULA Geometries
4.1.4. Simulation Setup for Proposed Geometry Performance Analysis
4.1.5. Simulation Setup for DOA Estimation Comparison Based on Different Frequencies with Different Bandwidths without Overlapping
4.1.6. Simulation Setup for DOA Estimation Comparison Based on Same Frequencies with Different Bandwidths with Overlapping
4.1.7. Simulation Setup for DOA Estimation Comparison Based on a Larger Number of Sources with Different Frequencies and Zero Bandwidths without Overlapping
4.1.8. Simulation Setup for DOA Estimation Comparison Based on Greater Number of Sources with Same Frequencies and Different Bandwidths with Overlapping
4.1.9. Simulation Setup for Different DOA Algorithm Performances Comparison Based on Proposed Geometry
4.2. Simulation Results
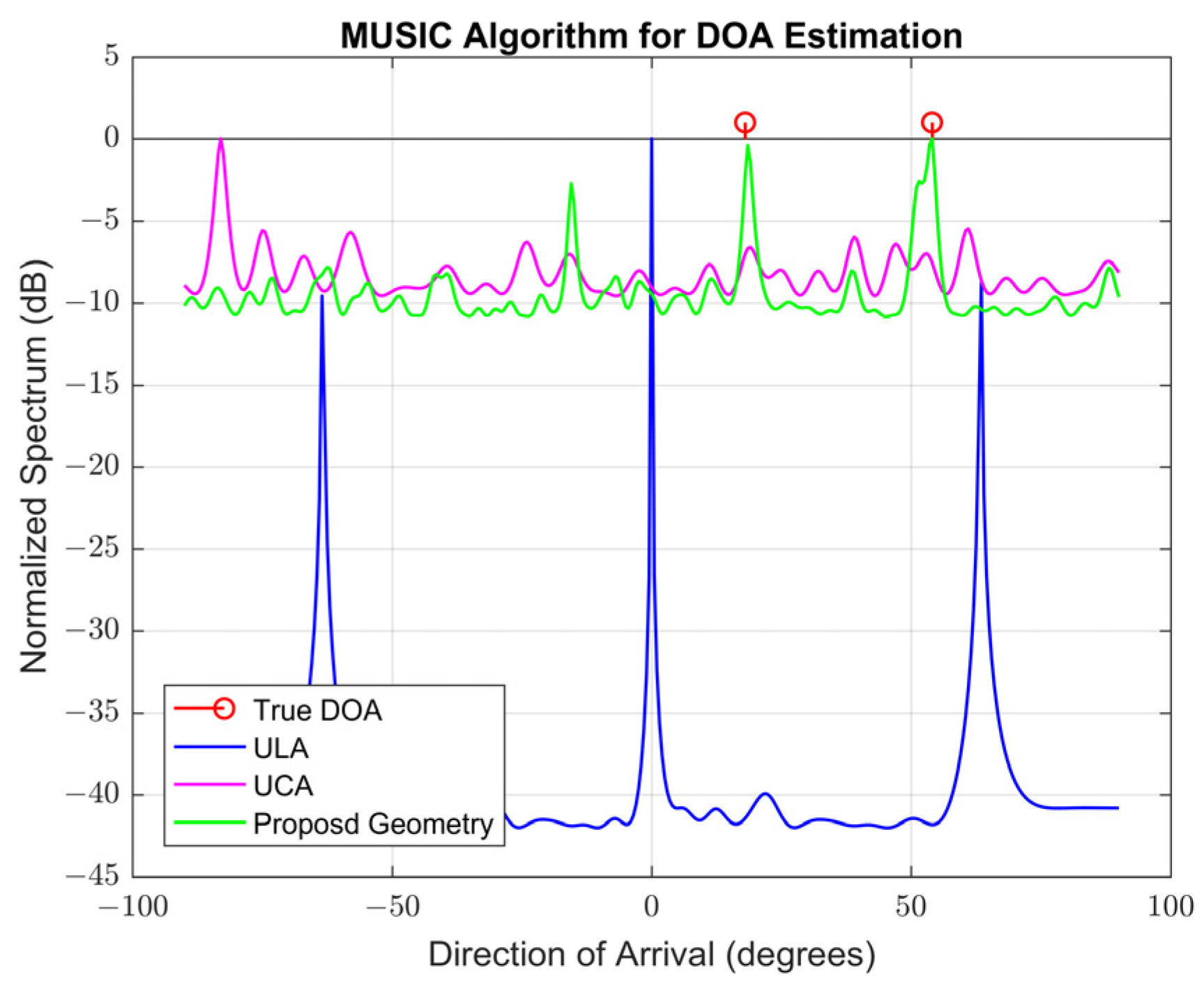
4.2.1. The 1-DOA Estimation of Proposed Geometry vs. ULA and UCA Geometries under the MUSIC Algorithm
4.2.2. The 1-DOA Angular Accuracy and Resolution Performance of the Proposed Geometry under the MUSIC Algorithm
4.2.3. The 1-DOA Estimation Performance Comparison of the Proposed Geometry with UCA and ULA Geometries
4.2.4. The 1-DOA Estimation Performance Analysis of the Proposed Geometry under the MUSIC Algorithm
4.2.5. The 1-DOA Estimation Performance Comparison of the Proposed Geometry with UCA and ULA Geometries Based on Different Frequencies with Different Bandwidths without Overlapping
4.2.6. The 1-DOA Estimation Performance Comparison of the Proposed Geometry with UCA and ULA Geometries Based on the Same Frequencies with Different Bandwidths with Overlapping
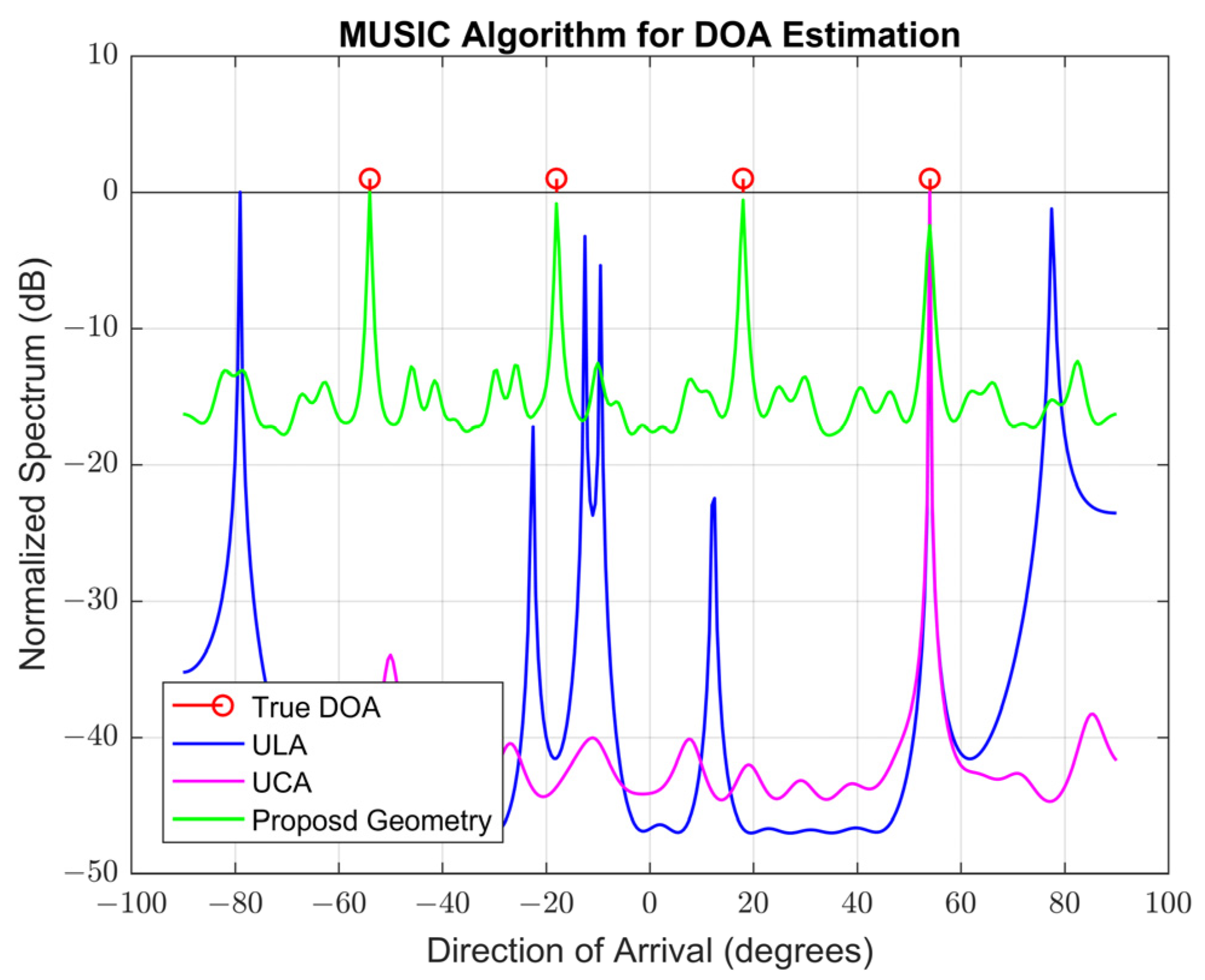
4.2.7. The 1-DOA Estimation Performance Comparison of the Proposed Geometry with UCA and ULA Geometries Based on a Larger Number of Wideband Sources
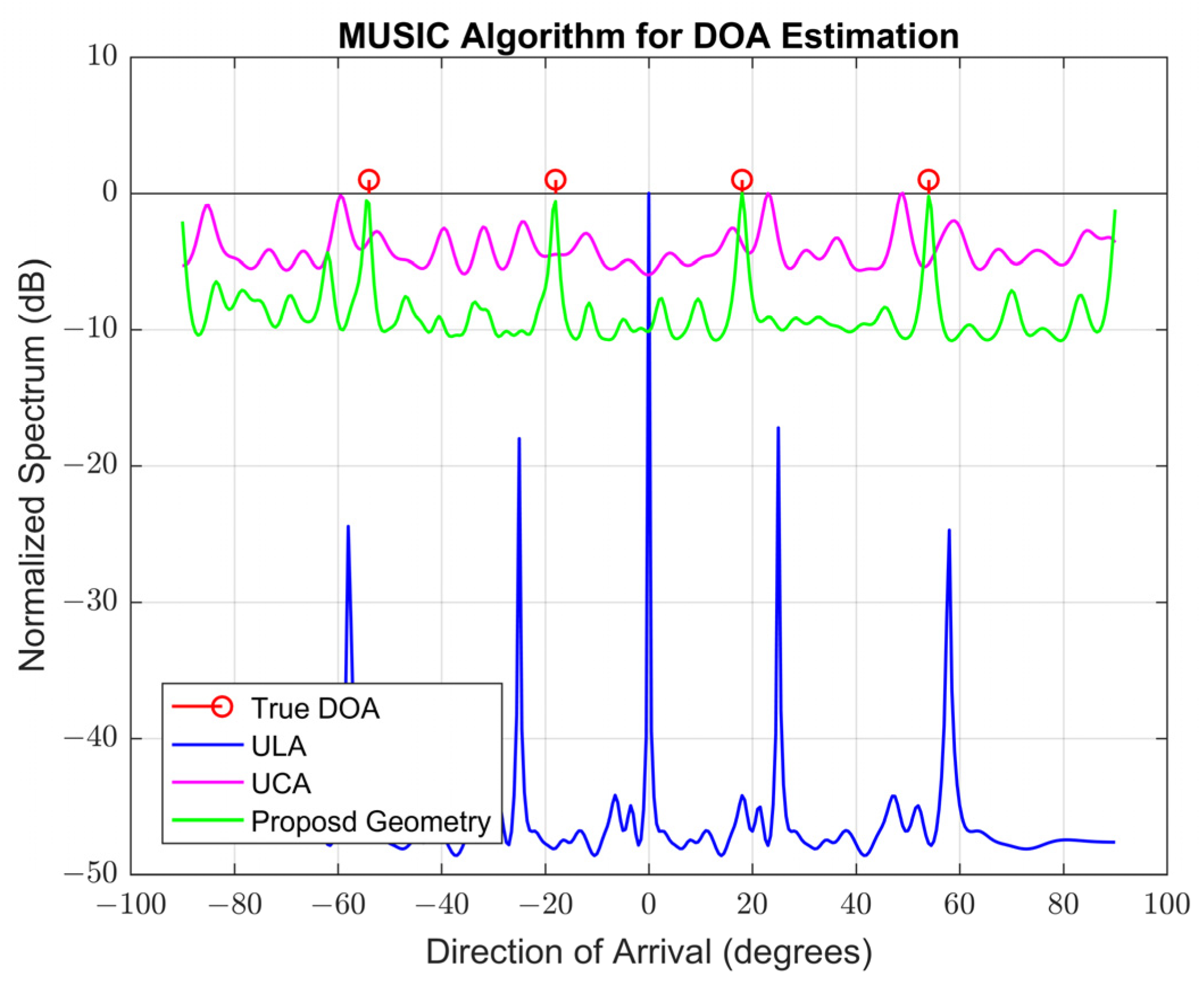
4.2.8. The 1-DOA Estimation Performance Comparison of the Proposed Geometry with UCA and ULA Geometries Based on a Larger Number of Wideband Sources with Frequency Overlapping
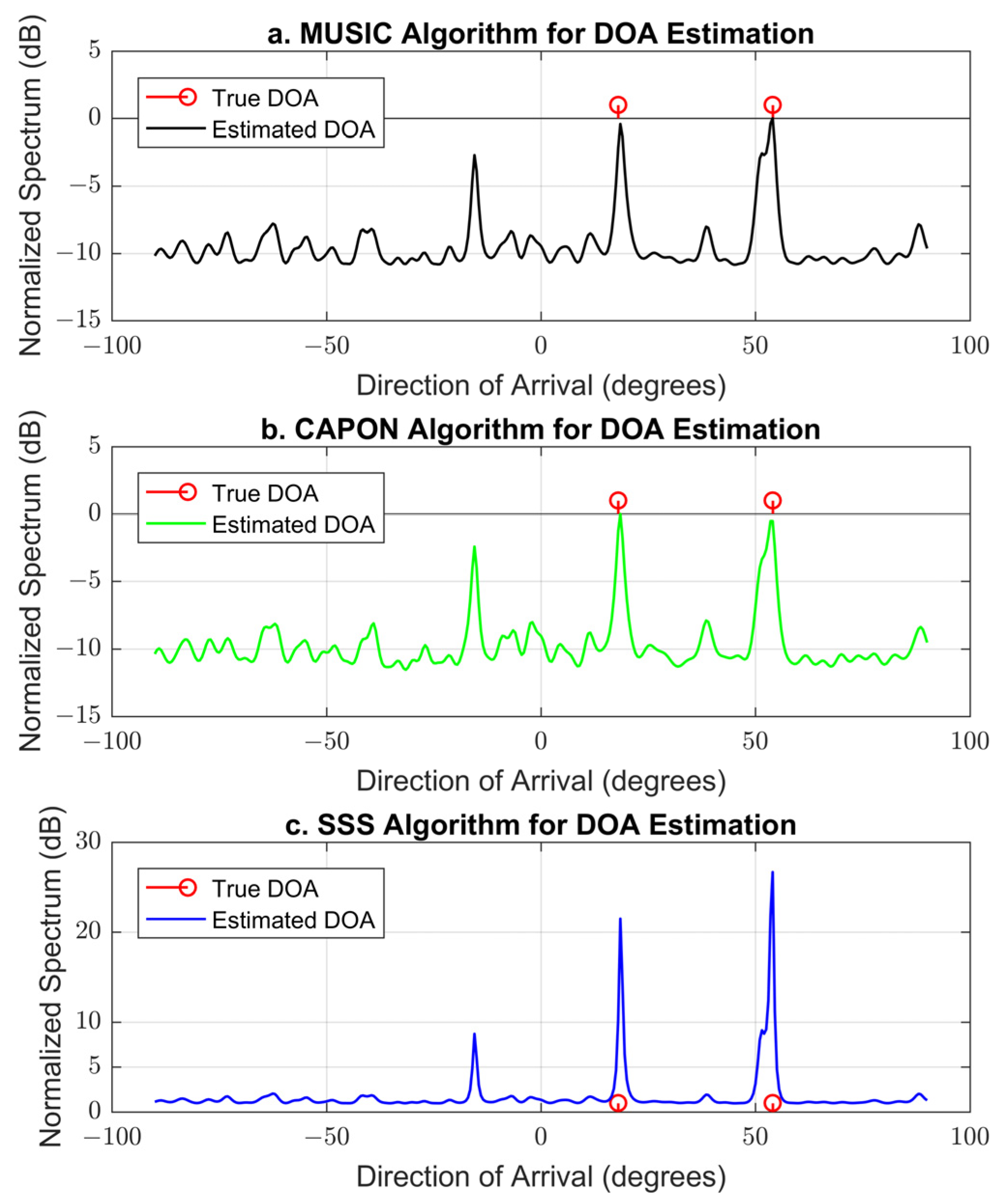
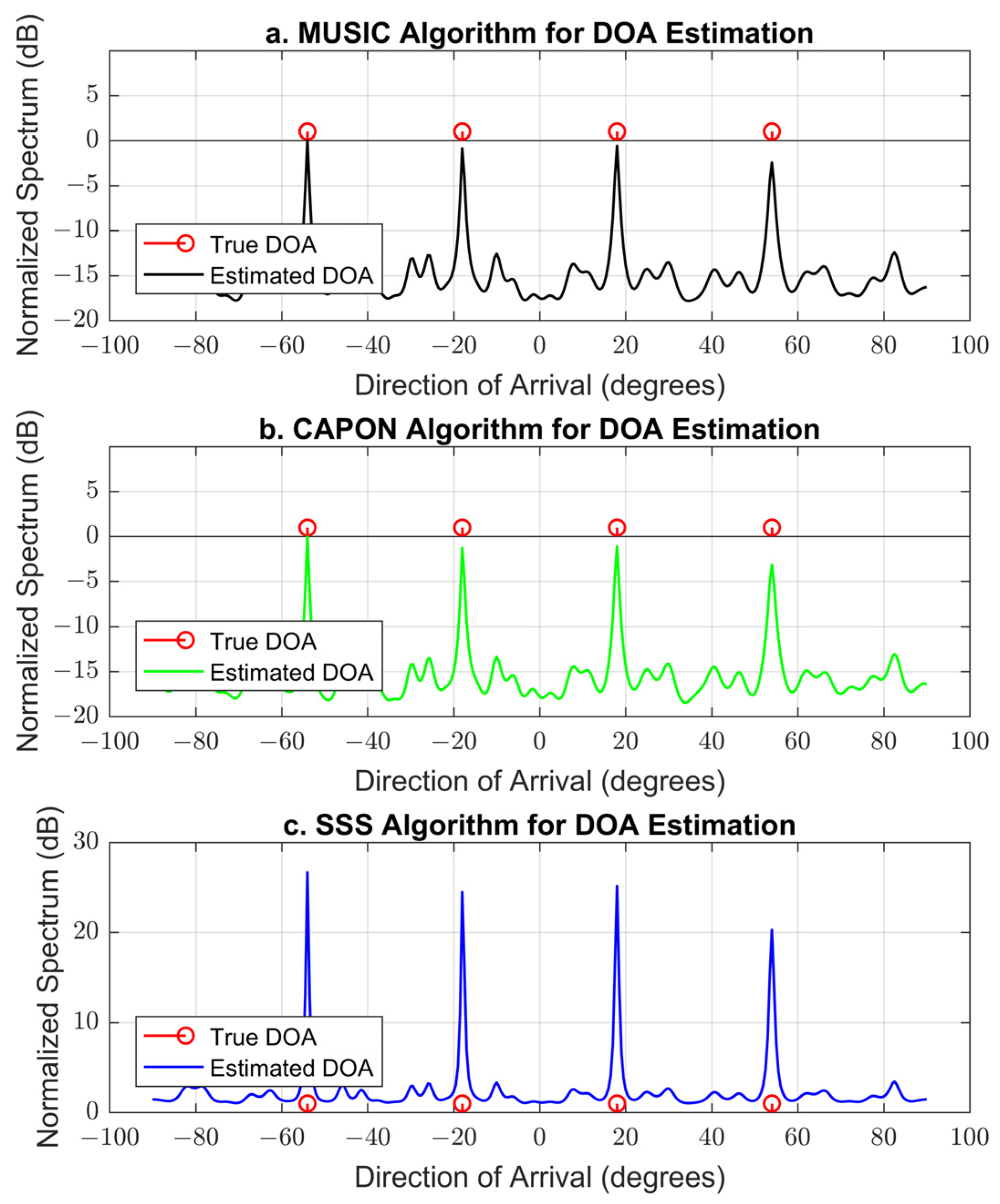
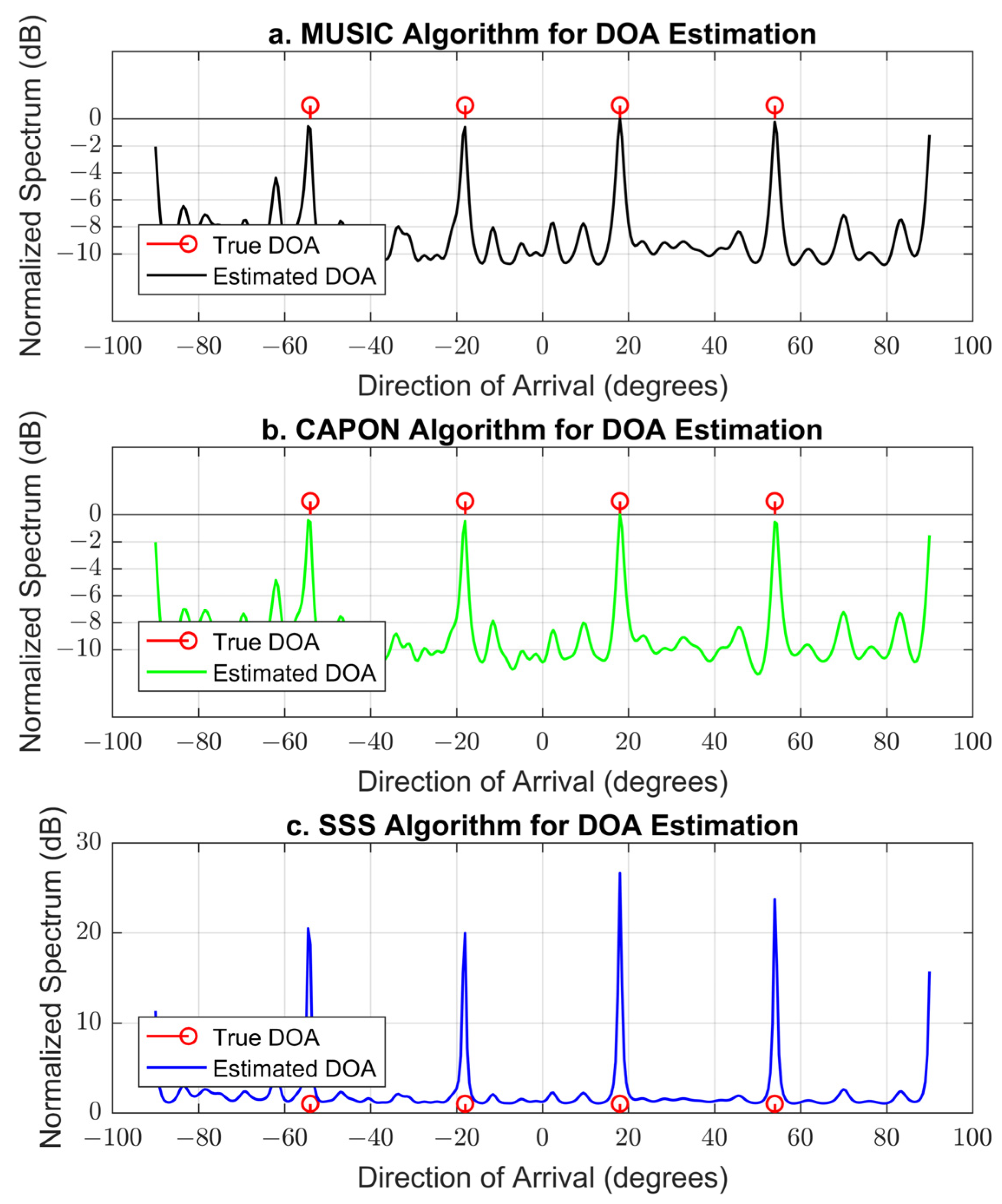
4.2.9. The 1-DOA Estimation Performance Comparison of Different DOA Algorithms Based on the Proposed Geometry
5. Discussion
- The proposed geometry used a fixed number of elements and variable element spacing to form various element configurations.
- These element configurations are selected and determined in accordance with the characteristics of the incident wideband signals and sources (from previous results, when bandwidth increases, element spacing decreases).
- Every element configuration is related to a specific antenna aperture and generates a particular manifold matrix.
- This particular manifold matrix has independent columns and satisfies the RIP condition.
- The covariance matrix for the incident wideband sources is obtained using this manifold matrix.
- Finally, the subspaces of this covariance matrix or its inversion are used to obtain unambiguous DOAs of the incident wideband sources by directly applying different DOA algorithms.
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chandran, S. Advances in Direction-of-Arrival Estimation; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Fallahi, R.; Roshandel, M. Effect of mutual coupling and configuration of concentric circular array antenna on the signal-to- interference performance in CDMA systems. Prog. Electromagn. Res. 2007, 76, 427–447. [Google Scholar] [CrossRef][Green Version]
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Stoica, P.; Moses, R.L. Introduction to Spectral Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Wax, M.; Shan, T.J.; Kailath, T. Spatio-temporal spectral analysis by eigenstructure methods. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 817–827. [Google Scholar] [CrossRef]
- Su, G.; Morf, M. The signal subspace approach for multiple wide-band emitter location. IEEE Trans. Acoust. Speech Signal Process. 1983, 31, 1502–1522. [Google Scholar]
- Wang, H.; Kaveh, M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 823–831. [Google Scholar] [CrossRef]
- Naidu, P.S. Sensor Array Signal Processing; CRC Press: New York, NY, USA, 2001. [Google Scholar]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Al-Sadoon, M.A.G.; Abduljabbar, N.A.; Ali, N.T.; Asif, R.; Zweid, A.; Alhassan, H.; Noras, J.M.; Abd-Alhameed, R.A. A More Efficient AOA Method for 2D and 3D Direction Estimation with Arbitrary Antenna Array Geometry. In BROADNETS 2018, LNICST; Sucasas, V., Mantas, G., Althunibat, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 263, pp. 419–430. [Google Scholar]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Trees, H.L.V. Optimum Array Processing, Part IV of Detection, Estimation and Modulation Theory; Wiley Interscience: New York, NY, USA, 2002. [Google Scholar]
- Wang, T.; Yang, L.S.; Lei, J.M.; Yang, S.Z. A modified MUSIC to estimate DOA of the coherent narrowband sources based on UCA. In Proceedings of the International Conference on Communication Technology (ICCT’06), Guilin, China, 27–30 November 2006. [Google Scholar]
- Mahmoud, K.R.; El-Adawy, M.; Ibrahem, S.M.M.; Bansal, R.; Zainud-Deen, S.H. A comparison between circular and hexagonal array geometries for smart antenna systems using particle swarm optimization algorithm. Prog. Electromagn. Res. 2007, 72, 75–90. [Google Scholar] [CrossRef]
- Gozasht, F.; Dadashzadeh, G.R.; Nikmehr, S. A comprehensive performance study of circular and hexagonal array geometries in the lms algorithm for smart antenna applications. Prog. Electromagn. Res. 2007, 68, 281–296. [Google Scholar] [CrossRef]
- Cand’es, E.; Romberg, J. Sparsity and incoherence in compressive sampling. Inverse Prob. 2007, 23, 969. [Google Scholar] [CrossRef]
- Ender, J.H.G. On compressive sensing applied to radar. Signal Process. 2010, 90, 1402–1414. [Google Scholar] [CrossRef]
- Ma, W.K.; Hsieh, T.H.; Chi, C.Y. DOA Estimation of quasi-stationary signals with less sensors than sources and unknown spatial noise covariance a khatri-rao subspace approach. IEEE Trans. Signal Process. 2010, 58, 2168–2180. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Han, K.; Nehorai, A. Wideband Direction of Arrival Estimation Using Nested Arrays. In Proceedings of the International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP05), St. Martin, France, 15–18 December 2013; IEEE: New York, NY, USA, 2013; pp. 188–191. [Google Scholar]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized co-prime array configurations for direction-of-arrival estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar] [CrossRef]
- Werner, D.H.; Haupt, R.L.; Werner, P.L. Fractal antenna engineering: The theory and design of fractal antenna arrays. IEEE Antennas Propag. Mag. 1999, 41, 37–59. [Google Scholar] [CrossRef]
- Spence, T.G.; Werner, D.H. Design of broadband planar arrays based on the optimization of aperiodic tilings. IEEE Trans. Antennas Propag. 2008, 56, 76–86. [Google Scholar] [CrossRef]
- Asghar, Z.S.; Ng, B.P. Aperiodic geometry design for DOA estimation of broadband sources using compressive sensing. Signal Process. 2019, 155, 96–107. [Google Scholar] [CrossRef]
- Agrawal, M.; Prasad, S. Broadband DOA Estimation Using Spatial-Only Modeling of Array Data. IEEE Trans. Signal Process. 2000, 48, 663–670. [Google Scholar] [CrossRef]
- Zatman, M. How Narrow Is Narrowband? IEE Proc. Radar Sonar Navig. 1998, 145, 85–91. [Google Scholar] [CrossRef]
- Whitney, L.E.; FSA; MAAA. Math Handbook of Formulas, Processes and Tricks, Geometry Version 2.9; Earl Whitney: Reno, NV, USA, 2015. [Google Scholar]
- Candes, E.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2004, 52, 489–509. [Google Scholar] [CrossRef]
- Cui, A.; Xu, T.; Yu, W.; He, P.; Xu, Z. An Array Interpolation Based Compressive Sensing DOA Method for Sparse Array. In Proceedings of the 3rd International Conference on Imaging, Signal Processing and Communication, Vancouver, BC, Canada, 26–28 August 2019; IEEE: New York, NY, USA, 2019; pp. 24–27. [Google Scholar]
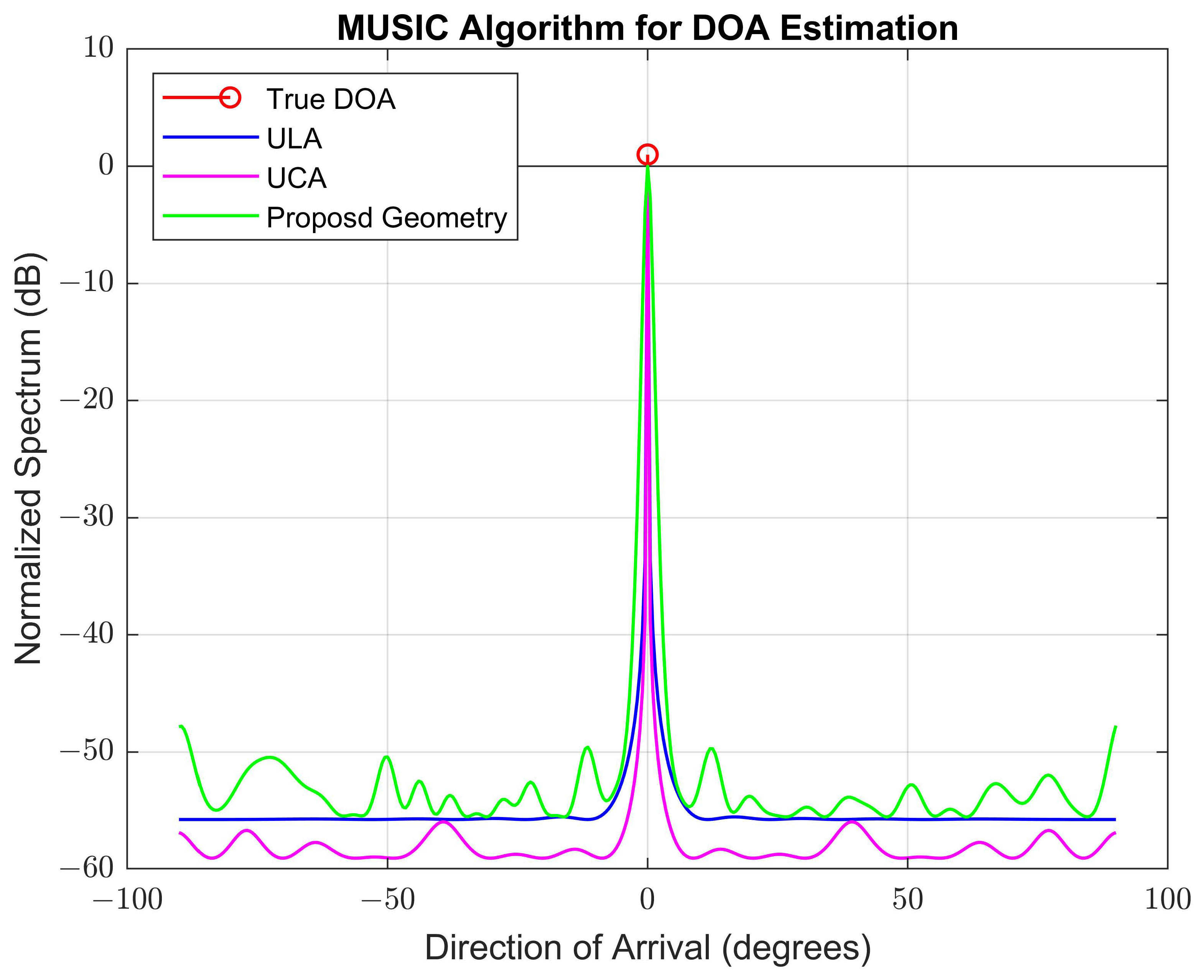
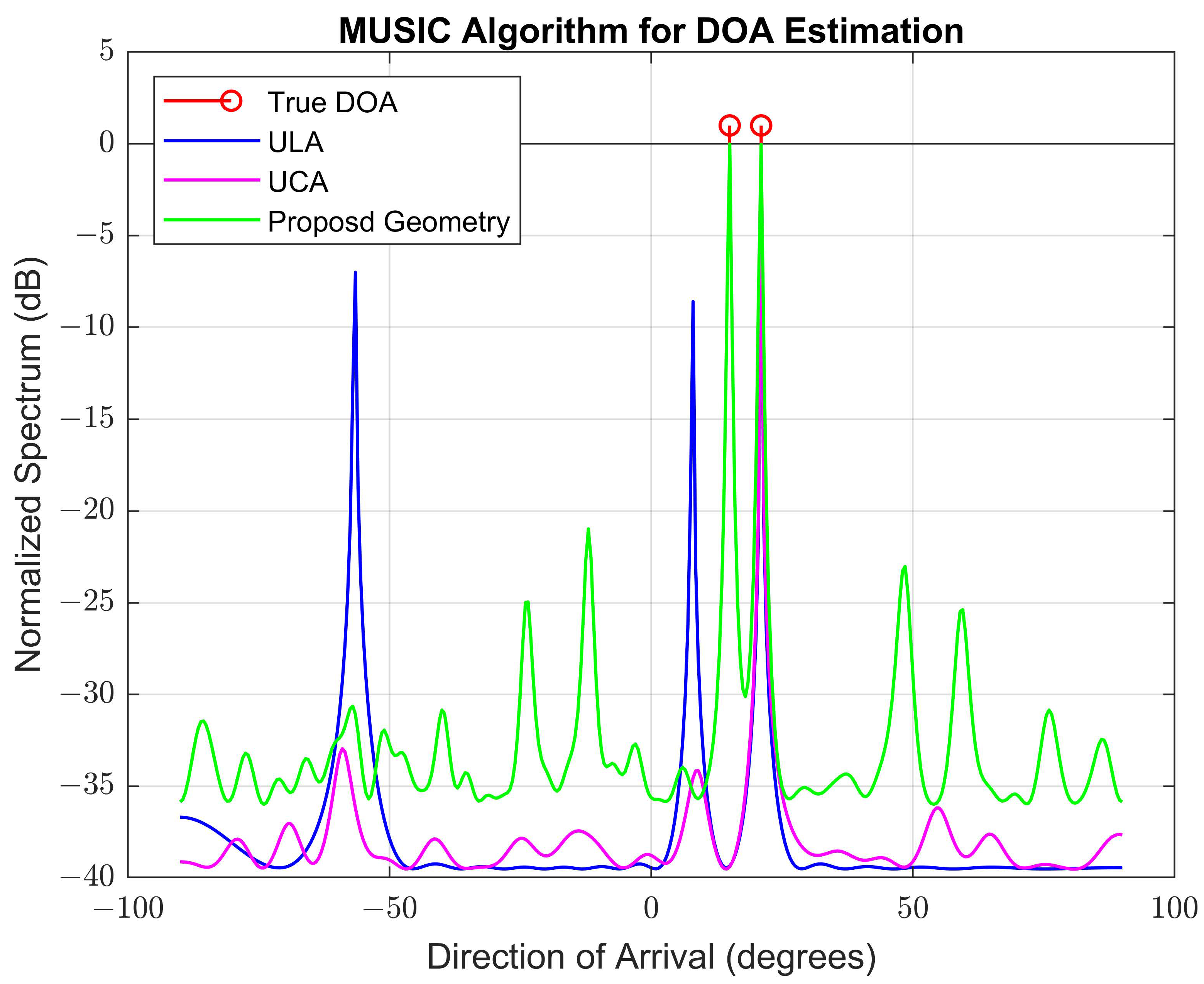
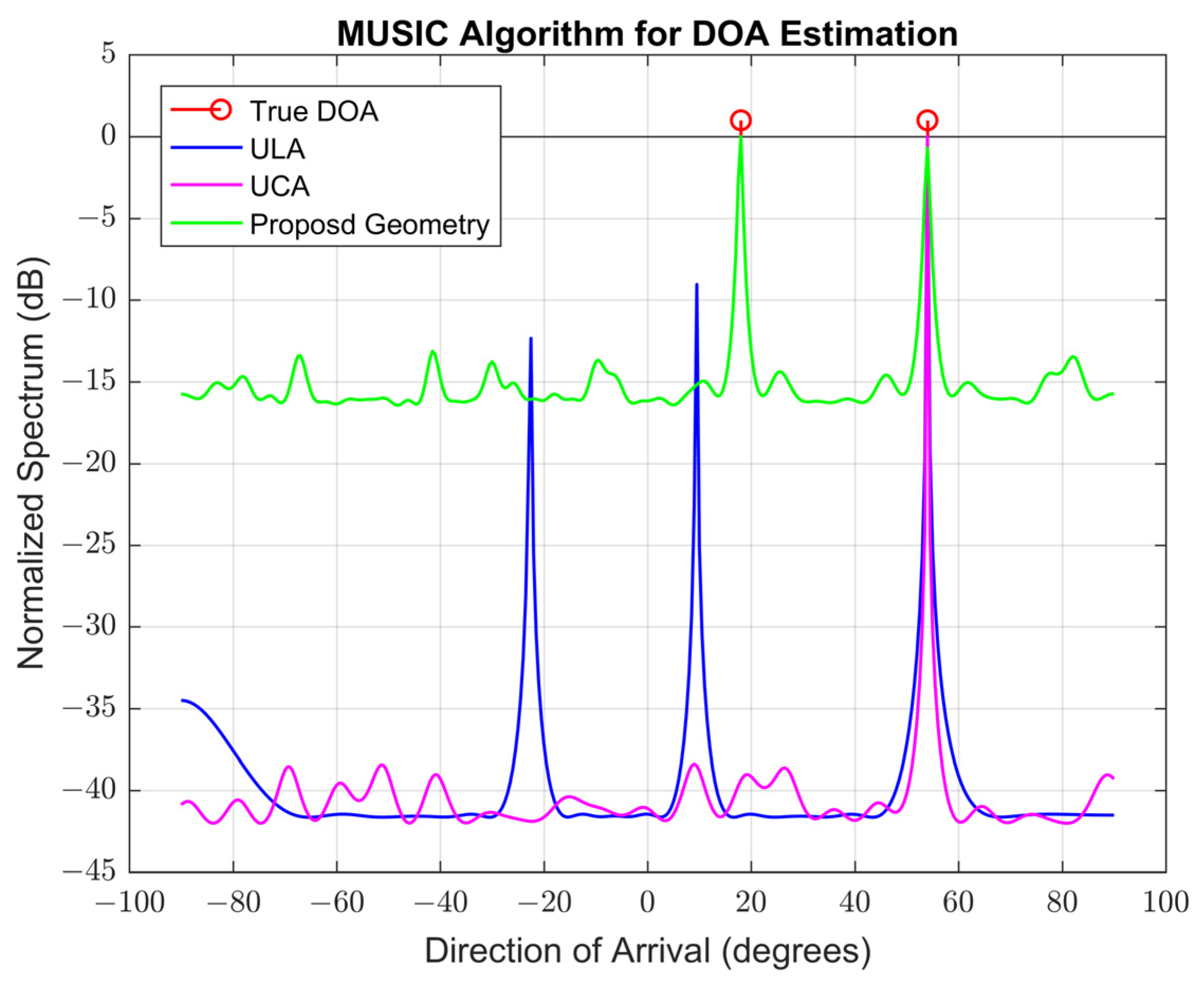

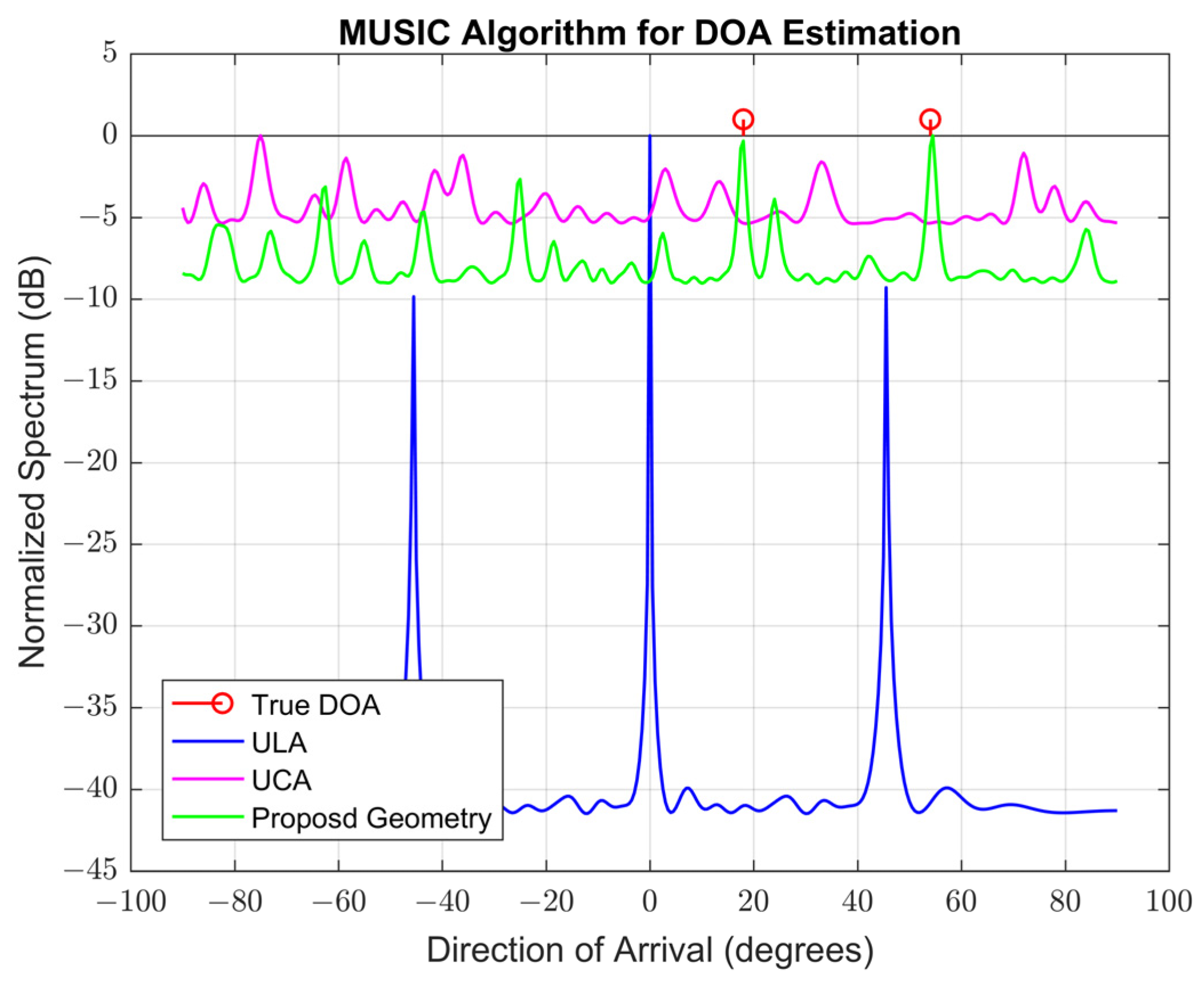
| Parameter | Symbol | ULA/UCA/Proposed | Notes |
|---|---|---|---|
| Number of sensors | M | 10 | Fixed number in the proposed geometry |
| Sampling frequency(GHz) | fs | 16 | For simulation |
| Center frequency (GHz) | f0 | 7.1 | One signal is considered |
| Bandwidth (GHz) | BW | 0 | Pulse signal |
| Wavelength of the incident signal (m) | λ | 0.042 | λ = c/f0 |
| Source elevation DOA (degrees) | 90 | Elevation kept as fixed | |
| Source azimuth DOA (degrees) | 0 | One source is considered | |
| Snapshots | N | 100 | Number of samples |
| Speed of propagation (light) m/s | c | - | |
| Signal-to-noise ratio (in dB) | SNR | 10 | - |
| Element spacing (in wavelength) | d | d = 0.5λ/R = 2.5λ/dX = 3.084λ | Element spacing for ULA/radius of UCA/base element spacing for proposed geometry |
| Element angle position (rad) | Phi | -/(2π/M)/- | Element distribution of the geometry |
| Parameter | Symbol | ULA/UCA/Proposed | Notes |
|---|---|---|---|
| Center frequency (GHz) | f0 | 7.1 and 13.7 | Two signals (different frequencies) are considered |
| Bandwidth (GHz) | BW | 0 and 0 | Pulse signals |
| Wavelength of the simulation (m) | λ | 0.0375 | λ2 < λ < λ1 |
| Wavelength for signal 7.1 (m) | λ1 | 0.0423 | λ1 = c/f0 |
| Wavelength for signal 13.4 (m) | λ2 | 0.0224 | λ 2 = c/f0 |
| Source azimuth DOA (degrees) | 15 and 21 | Two sources are considered | |
| Element spacing (in wavelength) | d | d = 0.5λ/R = 2.0λ/dX = 2.520λ | Element spacing for ULA/radius of UCA/base element spacing for proposed geometry |
| Parameter | Symbol | ULA/UCA/Proposed | Notes |
|---|---|---|---|
| Source azimuth DOA (degrees) | 18 and 54 | Two sources are considered | |
| Element spacing (in wavelength) | d | d = 0.5λ/R = 2.0λ/dX = 2.523λ | Element spacing for ULA/radius of UCA/base element spacing for proposed geometry |
| Parameter | Symbol | Proposed | Notes |
|---|---|---|---|
| Signal-to-noise ratio (in dB) | SNR | −25, 0, and 25 | The values range from low to high |
| Parameter | Symbol | ULA/UCA/Proposed | Notes |
|---|---|---|---|
| Bandwidth (GHz) | BW | 1.5 and 2.3 | 1.5 bandwidth of the signal 7.1 2.3 bandwidth of the signal 13.4 |
| Element spacing (in wavelength) | d | d = 0.5λ/R = 2.0λ/dX = 2.520λ | Element spacing for ULA/radius of UCA/base element spacing for proposed geometry |
| Parameter | Symbol | ULA/UCA/Proposed | Notes |
|---|---|---|---|
| Center frequency (GHz) | f0 | 8.0 and 8.0 | Two signals (same frequencies) |
| Wavelength of the simulation (m) | λ | 0.0375 | λ =λ1 = λ2 = c/f0 |
| Element spacing (in wavelength) | d | d = 0.5λ/R = 2.0λ/dX = 2.508λ | Element spacing for ULA/radius of UCA/base element spacing for proposed geometry |
| Parameter | Symbol | ULA/UCA/Proposed | Notes |
|---|---|---|---|
| Center frequency (GHz) | f0 | 3.6, 7.1, 9.2, and 13.4 | Four signals (different frequencies) are considered |
| Wavelength of the simulation (m) | λ | 0.0375 | λ4 < λ3 < λ < λ2 < λ1 |
| Wavelength for signal 1 (m) | λ1 | 0.0833 | λ1 = c/f0 |
| Wavelength for signal 2 (m) | λ2 | 0.0423 | λ2 = c/f0 |
| Wavelength for signal 3 (m) | λ3 | 0.0326 | λ3 = c/f0 |
| Wavelength for signal 4 (m) | λ4 | 0.0224 | λ4 = c/f0 |
| Source azimuth DOA (°) | −54, −18, 18, and 54 | Four sources are considered |
| Parameter | Symbol | ULA/UCA/Proposed | Notes |
|---|---|---|---|
| Center frequency (GHz) | f0 | 8.0, 8.0, 8.0, and 8.0 | Four signals (same frequency) |
| Wavelength of the simulation (m) | λ | 0.0375 | λ =λ1 = λ2 = λ3 = λ4 = c/f0 |
| Bandwidth (GHz) | BW | 1.5, 2.3, 3.5, and 4.3 | 1.5 bandwidth of the signal 1 2.3 bandwidth of the signal 2 3.5 bandwidth of the signal 3 4.3 bandwidth of the signal 4 |
| Element spacing (in wavelength) | d | d = 0.5λ/R = 1.0λ/dX = 1.099λ | Element spacing for ULA/radius of UCA/base element spacing for proposed geometry |
| Parameter | Symbol | MUSIC/CAPON/SSS | Notes |
|---|---|---|---|
| Scalar value (in wavelength) | ε | -/-/λ | Small scalar value added to avoid possible singularities (only for SSS) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalafalla, M.; Jiang, K.; Tian, K.; Feng, H.; Xiong, Y.; Tang, B. Pentagram Arrays: A New Paradigm for DOA Estimation of Wideband Sources Based on Triangular Geometry. Remote Sens. 2024, 16, 535. https://doi.org/10.3390/rs16030535
Khalafalla M, Jiang K, Tian K, Feng H, Xiong Y, Tang B. Pentagram Arrays: A New Paradigm for DOA Estimation of Wideband Sources Based on Triangular Geometry. Remote Sensing. 2024; 16(3):535. https://doi.org/10.3390/rs16030535
Chicago/Turabian StyleKhalafalla, Mohammed, Kaili Jiang, Kailun Tian, Hancong Feng, Ying Xiong, and Bin Tang. 2024. "Pentagram Arrays: A New Paradigm for DOA Estimation of Wideband Sources Based on Triangular Geometry" Remote Sensing 16, no. 3: 535. https://doi.org/10.3390/rs16030535
APA StyleKhalafalla, M., Jiang, K., Tian, K., Feng, H., Xiong, Y., & Tang, B. (2024). Pentagram Arrays: A New Paradigm for DOA Estimation of Wideband Sources Based on Triangular Geometry. Remote Sensing, 16(3), 535. https://doi.org/10.3390/rs16030535







