A Geodetic-Data-Calibrated Ice Flow Model to Simulate Historical and Future Response of Glaciers in Southeastern Tibetan Plateau
Abstract
1. Introduction
2. Study Area
3. Data and Methods
3.1. Datasets
3.1.1. Climate Datasets
3.1.2. Glacier Mass Balance Data
3.1.3. Ancillary Data Sets
3.2. Methods
3.2.1. Open Global Glacier Model Description
3.2.2. Model Spin-Up
3.2.3. Glacier Runoff Simulations
3.2.4. SETP Glacier Mass Balance Calculation Method
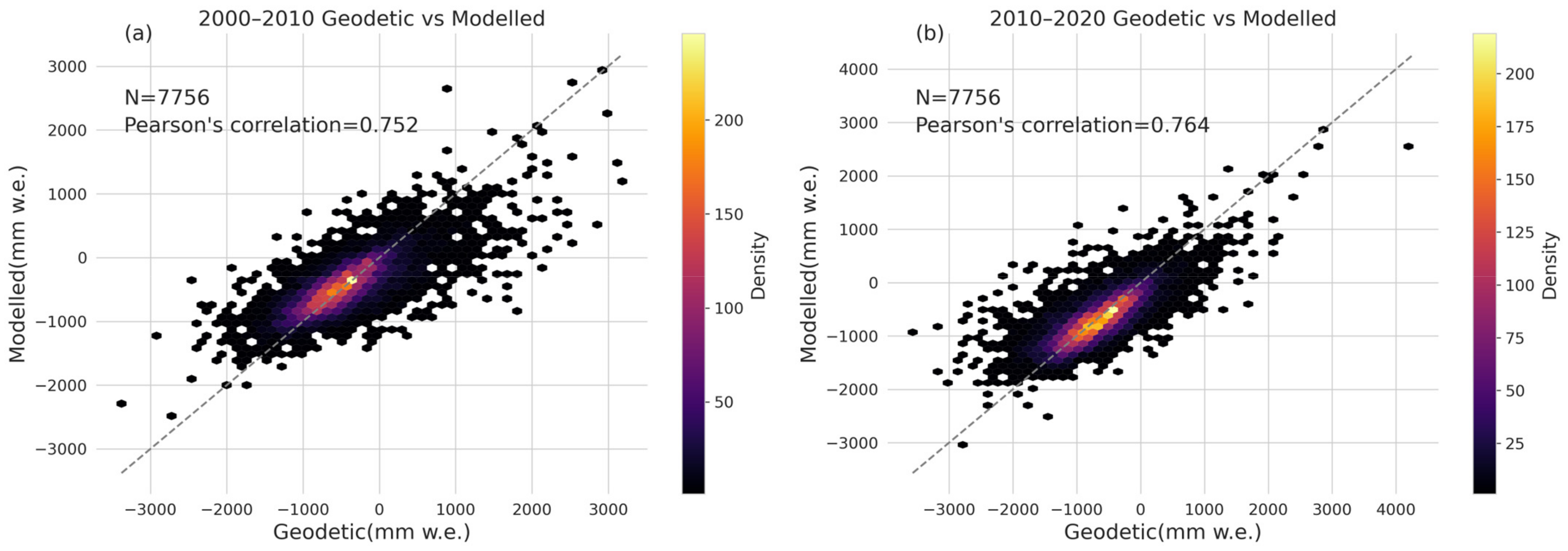
3.2.5. Model Calibration and Validation
4. Results
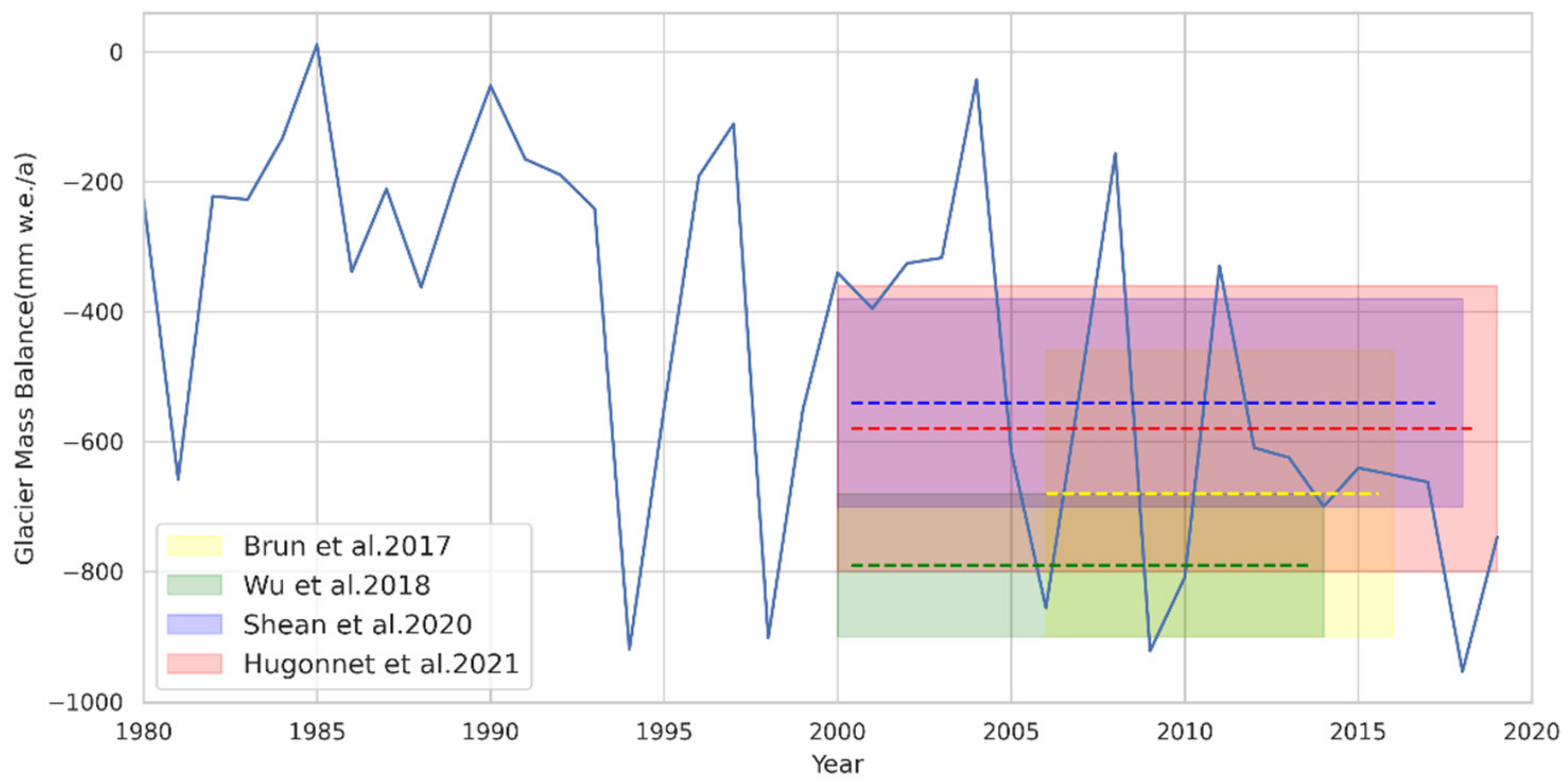
4.1. Glacier Mass Balance
4.2. Spatial Variability in Glacier Mass Balance
4.3. Future Dynamics of Maritime Glaciers
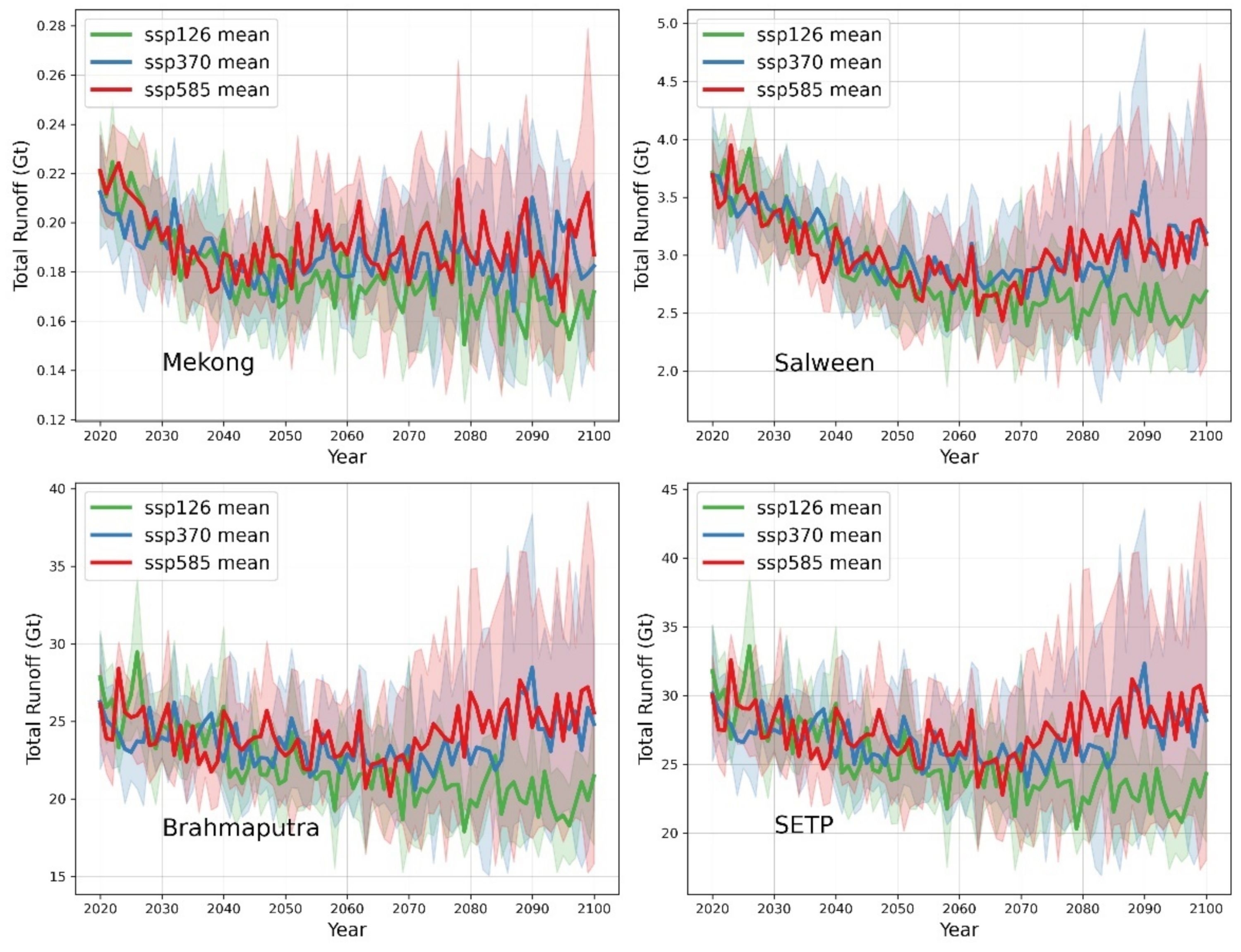
4.4. Future Glacier Runoff Components Estimation
5. Discussion
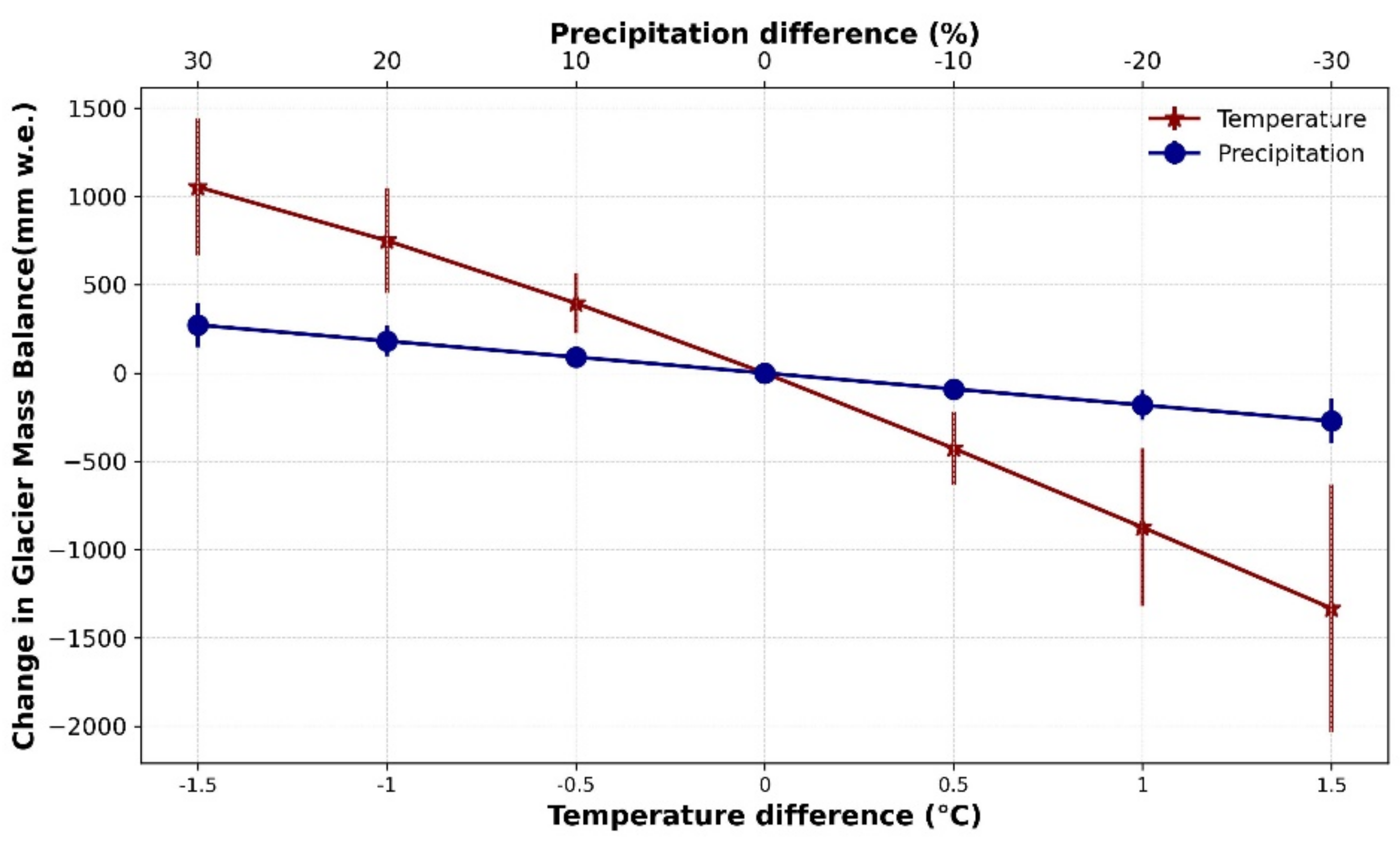
5.1. Glacier Mass Balance Sensitivity Experiments
5.2. Analysis of Climatic Considerations
5.3. Weakening Summer-Monsoon-Induced Snowfall–Rainfall Transition
5.4. Uncertainty Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rounce, D.R.; Hock, R.; Maussion, F.; Hugonnet, R.; Kochtitzky, W.; Huss, M.; Berthier, E.; Brinkerhoff, D.; Compagno, L.; Copland, L.; et al. Global Glacier Change in the 21st Century: Every Increase in Temperature Matters. Science 2023, 379, 78–83. [Google Scholar] [CrossRef]
- Farinotti, D.; Huss, M.; Fürst, J.J.; Landmann, J.; Machguth, H.; Maussion, F.; Pandit, A. A Consensus Estimate for the Ice Thickness Distribution of All Glaciers on Earth. Nat. Geosci. 2019, 12, 168–173. [Google Scholar] [CrossRef]
- Hugonnet, R.; McNabb, R.; Berthier, E.; Menounos, B.; Nuth, C.; Girod, L.; Farinotti, D.; Huss, M.; Dussaillant, I.; Brun, F.; et al. Accelerated Global Glacier Mass Loss in the Early Twenty-First Century. Nature 2021, 592, 726–731. [Google Scholar] [CrossRef]
- Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A Reconciled Estimate of Glacier Contributions to Sea Level Rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef]
- Lutz, A.; Immerzeel, W.W.; Shrestha, A.; Bierkens, M.F.P. Consistent Increase in High Asia’s Runoff Due to Increasing Glacier Melt and Precipitation. Nat. Clim. Change 2014, 4, 587–592. [Google Scholar] [CrossRef]
- Immerzeel, W.; Lutz, A.; Andrade, M.; Bahl, A.; Biemans, H.; Bolch, T.; Hyde, S.; Brumby, S.; Davies, B.; Elmore, A.; et al. Importance and Vulnerability of the World’s Water Towers. Nature 2020, 577, 364–369. [Google Scholar] [CrossRef]
- Li, S.; Zhao, H.; Yu, W.; Yao, T.; Liu, S.; Wang, N.; Yang, W.; You, C.; Wang, W.; Wu, G.; et al. Glacier anomalies and relevant disaster risks on the Tibetan Plateau and surroundings. Chin. Sci. Bull. 2019, 64, 2770–2782. [Google Scholar] [CrossRef]
- Yao, T.; Bolch, T.; Chen, D.; Gao, J.; Immerzeel, W.; Piao, S.; Su, F.; Thompson, L.; Wada, Y.; Wang, L.; et al. The Imbalance of the Asian Water Tower. Nat. Rev. Earth Environ. 2022, 3, 618–632. [Google Scholar] [CrossRef]
- Yao, T.; Xue, Y.; Chen, D.; Chen, F.; Thompson, L.; Cui, P.; Koike, T.; Lau, W.; Lettenmaier, D.; Mosbrugger, V.; et al. Recent Third Pole’s Rapid Warming Accompanies Cryospheric Melt and Water Cycle Intensification and Interactions between Monsoon and Environment: Multidisciplinary Approach with Observations, Modeling, and Analysis. Bull. Am. Meteorol. Soc. 2019, 100, 423–444. [Google Scholar] [CrossRef]
- Zhang, Q.; Shen, Z.; Pokhrel, Y.; Farinotti, D.; Singh, V.P.; Xu, C.-Y.; Wu, W.; Wang, G. Oceanic Climate Changes Threaten the Sustainability of Asia’s Water Tower. Nature 2023, 615, 87–93. [Google Scholar] [CrossRef] [PubMed]
- Shean, D.E.; Bhushan, S.; Montesano, P.; Rounce, D.R.; Arendt, A.; Osmanoglu, B. A Systematic, Regional Assessment of High Mountain Asia Glacier Mass Balance. Front. Earth Sci. 2020, 7, 363. [Google Scholar]
- Brun, F.; Berthier, E.; Wagnon, P.; Kääb, A.; Treichler, D. A Spatially Resolved Estimate of High Mountain Asia Glacier Mass Balances from 2000 to 2016. Nat. Geosci. 2017, 10, 668–673. [Google Scholar] [CrossRef]
- Wang, Q.; Yi, S.; Sun, W. Continuous Estimates of Glacier Mass Balance in High Mountain Asia Based on ICESat-1,2 and GRACE/GRACE Follow-On Data. Geophys. Res. Lett. 2021, 48, e2020GL090954. [Google Scholar] [CrossRef]
- Fan, Y.; Ke, C.-Q.; Zhou, X.; Shen, X.; Yu, X.; Lhakpa, D. Glacier Mass-Balance Estimates over High Mountain Asia from 2000 to 2021 Based on ICESat-2 and NASADEM. J. Glaciol. 2023, 69, 500–512. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different Glacier Status with Atmospheric Circulations in Tibetan Plateau and Surroundings. Nat. Clim. Change 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Wu, K.; Liu, S.; Jiang, Z.; Xu, J.; Wei, J. Glacier Mass Balance over the Central Nyainqentanglha Range during Recent Decades Derived from Remote-Sensing Data. J. Glaciol. 2019, 65, 422–439. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y.; Kääb, A. Region-Wide Glacier Mass Balances over the Pamir-Karakoram-Himalaya during 1999–2011. Cryosphere 2013, 7, 1263–1286. [Google Scholar] [CrossRef]
- Xie, F.; Liu, S.; Gao, Y.; Zhu, Y.; Bolch, T.; Kääb, A.; Duan, S.; Miao, W.; Kang, J.; Zhang, Y.; et al. Interdecadal Glacier Inventories in the Karakoram since the 1990s. Earth Syst. Sci. Data 2023, 15, 847–867. [Google Scholar] [CrossRef]
- Mölg, T.; Maussion, F.; Scherer, D. Mid-Latitude Westerlies as a Driver of Glacier Variability in Monsoonal High Asia. Nat. Clim. Change 2014, 4, 68–73. [Google Scholar] [CrossRef]
- Zhu, M.; Yao, T.; Yang, W.; Xu, B.; Wu, G.; Wang, X. Differences in Mass Balance Behavior for Three Glaciers from Different Climatic Regions on the Tibetan Plateau. Clim. Dyn. 2018, 50, 3457–3484. [Google Scholar] [CrossRef]
- Mölg, T.; Maussion, F.; Yang, W.; Scherer, D. The Footprint of Asian Monsoon Dynamics in the Mass and Energy Balance of a Tibetan Glacier. Cryosphere Discuss. 2012, 6, 1445–1461. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, B.; Zhou, X. Boreal Summer Continental Monsoon Rainfall and Hydroclimate Anomalies Associated with the Asia-Pacific Oscillation. Clim. Dyn. 2012, 39, 1197–1207. [Google Scholar] [CrossRef]
- Yang, W.; Guo, X.; Yao, T.; Zhu, M.; Wang, Y. Recent Accelerating Mass Loss of Southeast Tibetan Glaciers and the Relationship with Changes in Macroscale Atmospheric Circulations. Clim. Dyn. 2016, 47, 805–815. [Google Scholar] [CrossRef]
- Zhao, F.; Long, D.; Li, X.; Huang, Q.; Han, P. Rapid Glacier Mass Loss in the Southeastern Tibetan Plateau since the Year 2000 from Satellite Observations. Remote Sens. Environ. 2022, 270, 112853. [Google Scholar] [CrossRef]
- Zemp, M.; Huss, M.; Thibert, E.; Eckert, N.; McNabb, R.; Huber, J.; Barandun, M.; Machguth, H.; Nussbaumer, S.U.; Gärtner-Roer, I.; et al. Global Glacier Mass Changes and Their Contributions to Sea-Level Rise from 1961 to 2016. Nature 2019, 568, 382–386. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.; Ke, C.-Q.; Fan, Y.; Wang, Z. Accelerated Glacier Mass Loss in the Southeastern Tibetan Plateau since the 1970s. Adv. Clim. Change Res. 2023, 14, 372–386. [Google Scholar] [CrossRef]
- Yang, W.; Yao, T.; Guo, X.; Zhu, M.; Li, S.; Kattel, D.B. Mass Balance of a Maritime Glacier on the Southeast Tibetan Plateau and Its Climatic Sensitivity. J. Geophys. Res. Atmos. 2013, 118, 9579–9594. [Google Scholar] [CrossRef]
- Ding, B.; Yang, K.; Yang, W.; Xiaobo, H.; Chen, Y.; Zhu, L.; Guo, X.; Wang, L.; Wu, H.; Yao, T. Development of a Water and Enthalpy Budget-Based Glacier Mass Balance Model (WEB-GM) and Its Preliminary Validation. Water Resour. Res. 2017, 53, 3146–3178. [Google Scholar] [CrossRef]
- Huss, M.; Hock, R. Global-Scale Hydrological Response to Future Glacier Mass Loss. Nat. Clim. Change 2018, 8, 135–140. [Google Scholar] [CrossRef]
- Hock, R. Temperature Index Melt Modelling in Mountain Areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Hock, R.; Bliss, A.; Marzeion, B.; Giesen, R.H.; Hirabayashi, Y.; Huss, M.; Radić, V.; Slangen, A.B.A. GlacierMIP—A Model Intercomparison of Global-Scale Glacier Mass-Balance Models and Projections. J. Glaciol. 2019, 65, 453–467. [Google Scholar] [CrossRef]
- Maussion, F.; Butenko, A.; Champollion, N.; Dusch, M.; Eis, J.; Fourteau, K.; Gregor, P.; Jarosch, A.H.; Landmann, J.; Oesterle, F.; et al. The Open Global Glacier Model (OGGM) v1.1. Geosci. Model Dev. 2019, 12, 909–931. [Google Scholar] [CrossRef]
- Zhao, H.; Su, B.; Lei, H.; Zhang, T.; Xiao, C. A New Projection for Glacier Mass and Runoff Changes over High Mountain Asia. Sci. Bull. 2023, 68, 43–47. [Google Scholar] [CrossRef]
- Mannan Afzal, M.; Wang, X.; Sun, L.; Jiang, T.; Kong, Q.; Luo, Y. Hydrological and Dynamical Response of Glaciers to Climate Change Based on Their Dimensions in the Hunza Basin, Karakoram. J. Hydrol. 2023, 617, 128948. [Google Scholar] [CrossRef]
- Tang, S.; Vlug, A.; Piao, S.; Li, F.; Wang, T.; Krinner, G.; Li, L.Z.X.; Wang, X.; Wu, G.; Li, Y.; et al. Regional and Tele-Connected Impacts of the Tibetan Plateau Surface Darkening. Nat. Commun. 2023, 14, 32. [Google Scholar] [CrossRef] [PubMed]
- Schuster, L.; Rounce, D. Fabien Maussion Glacier Projections Sensitivity to Temperature-Index Model Choices and Calibration Strategies. Ann. Glaciol. 2023, 1–16. [Google Scholar] [CrossRef]
- Eis, J.; Maussion, F.; Marzeion, B. Initialization of a Global Glacier Model Based on Present-Day Glacier Geometry and Past Climate Information: An Ensemble Approach. Cryosphere 2019, 13, 3317–3335. [Google Scholar] [CrossRef]
- Eis, J.; van der Laan, L.; Maussion, F.; Marzeion, B. Reconstruction of Past Glacier Changes with an Ice-Flow Glacier Model: Proof of Concept and Validation. Front. Earth Sci. 2021, 9, 595755. [Google Scholar] [CrossRef]
- Pfeffer, W.T.; Arendt, A.A.; Bliss, A.; Bolch, T.; Cogley, J.G.; Gardner, A.S.; Hagen, J.-O.; Hock, R.; Kaser, G.; Kienholz, C.; et al. The Randolph Glacier Inventory: A Globally Complete Inventory of Glaciers. J. Glaciol. 2014, 60, 537–552. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, S. Estimation on the Response of Glaciers in China to the Global Warming in the 21st Century. Chin. Sci. Bull. 2000, 45, 668–672. [Google Scholar] [CrossRef]
- Jouberton, A.; Shaw, T.E.; Miles, E.; McCarthy, M.; Fugger, S.; Ren, S.; Dehecq, A.; Yang, W.; Pellicciotti, F. Warming-Induced Monsoon Precipitation Phase Change Intensifies Glacier Mass Loss in the Southeastern Tibetan Plateau. Proc. Natl. Acad. Sci. USA 2022, 119, e2109796119. [Google Scholar] [CrossRef]
- Zheng, G.; Mergili, M.; Emmer, A.; Allen, S.; Bao, A.; Guo, H.; Stoffel, M. The 2020 Glacial Lake Outburst Flood at Jinwuco, Tibet: Causes, Impacts, and Implications for Hazard and Risk Assessment. Cryosphere 2021, 15, 3159–3180. [Google Scholar] [CrossRef]
- Wang, X.; Tolksdorf, V.; Otto, M.; Scherer, D. WRF-based Dynamical Downscaling of ERA5 Reanalysis Data for High Mountain Asia: Towards a New Version of the High Asia Refined Analysis. Int. J. Climatol. 2020, 41, 743–762. [Google Scholar] [CrossRef]
- Huintjes, E.; Loibl, D.; Lehmkuhl, F.; Schneider, C. A Modelling Approach to Reconstruct Little Ice Age Climate from Remote-Sensing Glacier Observations in Southeastern Tibet. Ann. Glaciol. 2016, 57, 359–370. [Google Scholar] [CrossRef]
- Khadka, A.; Wagnon, P.; Brun, F.; Shrestha, D.; Lejeune, Y.; Arnaud, Y. Evaluation of ERA5-Land and HARv2 Reanalysis Data at High Elevation in the Upper Dudh Koshi Basin (Everest Region, Nepal). J. Appl. Meteorol. Climatol. 2022, 61, 931–954. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) Experimental Design and Organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, L.; Lun, Y.; Cheng, L.; Li, X.; Xu, Z. Projections of Future Precipitation and Air Temperature over the Tibetan Plateau Based on CMIP6 Multi-model Ensembles. Int. J. Climatol. 2022, 42, 9788–9822. [Google Scholar] [CrossRef]
- Tokarska, K.; Stolpe, M.; Sippel, S.; Fischer, E.; Smith, C.; Lehner, F.; Knutti, R. Past Warming Trend Constrains Future Warming in CMIP6 Models. Sci. Adv. 2020, 6, eaaz9549. [Google Scholar] [CrossRef]
- Cook, B.; Mankin, J.; Marvel, K.; Williams, A.; Smerdon, J.; Anchukaitis, K. Twenty-First Century Drought Projections in the CMIP6 Forcing Scenarios. Earth’s Future 2020, 8, e2019EF001461. [Google Scholar] [CrossRef]
- Chen, R.; Duan, K.; Shang, W.; Shi, P.; Meng, Y.; Zhang, Z. Increase in Seasonal Precipitation over the Tibetan Plateau in the 21st Century Projected Using CMIP6 Models. Atmos. Res. 2022, 277, 106306. [Google Scholar] [CrossRef]
- Crippen, R.; Buckley, S.; Agram, P.; Belz, E.; Gurrola, E.; Hensley, S.; Kobrick, M.; Lavalle, M.; Martin, J.; Neumann, M.; et al. Nasadem Global Elevation Model: Methods And Progress. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 125–128. [Google Scholar] [CrossRef]
- OGGM/Oggm: V1.6.1. Available online: https://doi.org/10.5281/zenodo.8287580 (accessed on 1 September 2023).
- Marzeion, B.; Jarosch, A.H.; Hofer, M. Past and Future Sea-Level Change from the Surface Mass Balance of Glaciers. Cryosphere 2012, 6, 1295–1322. [Google Scholar] [CrossRef]
- Huss, M.; Hock, R. A New Model for Global Glacier Change and Sea-Level Rise. Front. Earth Sci. 2015, 3, 54. [Google Scholar] [CrossRef]
- Wu, K.; Liu, S.; Jiang, Z.; Xu, J.; Wei, J.; Guo, W. Recent Glacier Mass Balance and Area Changes in the Kangri Karpo Mountains from DEMs and Glacier Inventories. Cryosphere 2018, 12, 103–121. [Google Scholar] [CrossRef]
- Sakai, A.; Fujita, K. Contrasting Glacier Responses to Recent Climate Change in High-Mountain Asia. Sci. Rep. 2017, 7, 13717. [Google Scholar] [CrossRef]
- Recinos, B.; Maussion, F.; Rothenpieler, T.; Marzeion, B. Impact of Frontal Ablation on the Ice Thickness Estimation of Marine-Terminating Glaciers in Alaska. Cryosphere 2019, 13, 2657–2672. [Google Scholar] [CrossRef]
- Rounce, D.R.; Hock, R.; Shean, D.E. Glacier Mass Change in High Mountain Asia through 2100 Using the Open-Source Python Glacier Evolution Model (PyGEM). Front. Earth Sci. 2020, 7, 331. [Google Scholar] [CrossRef]









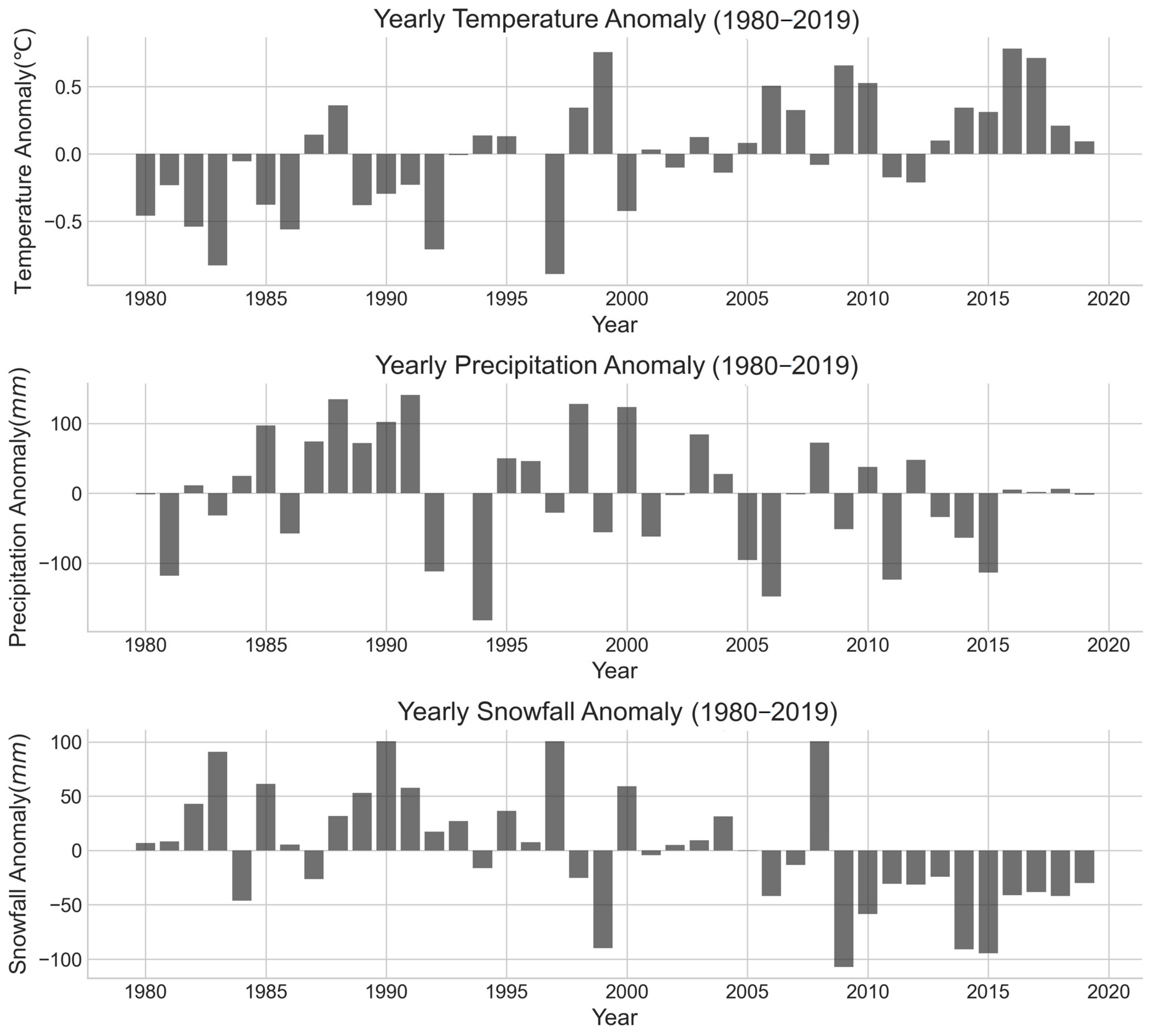

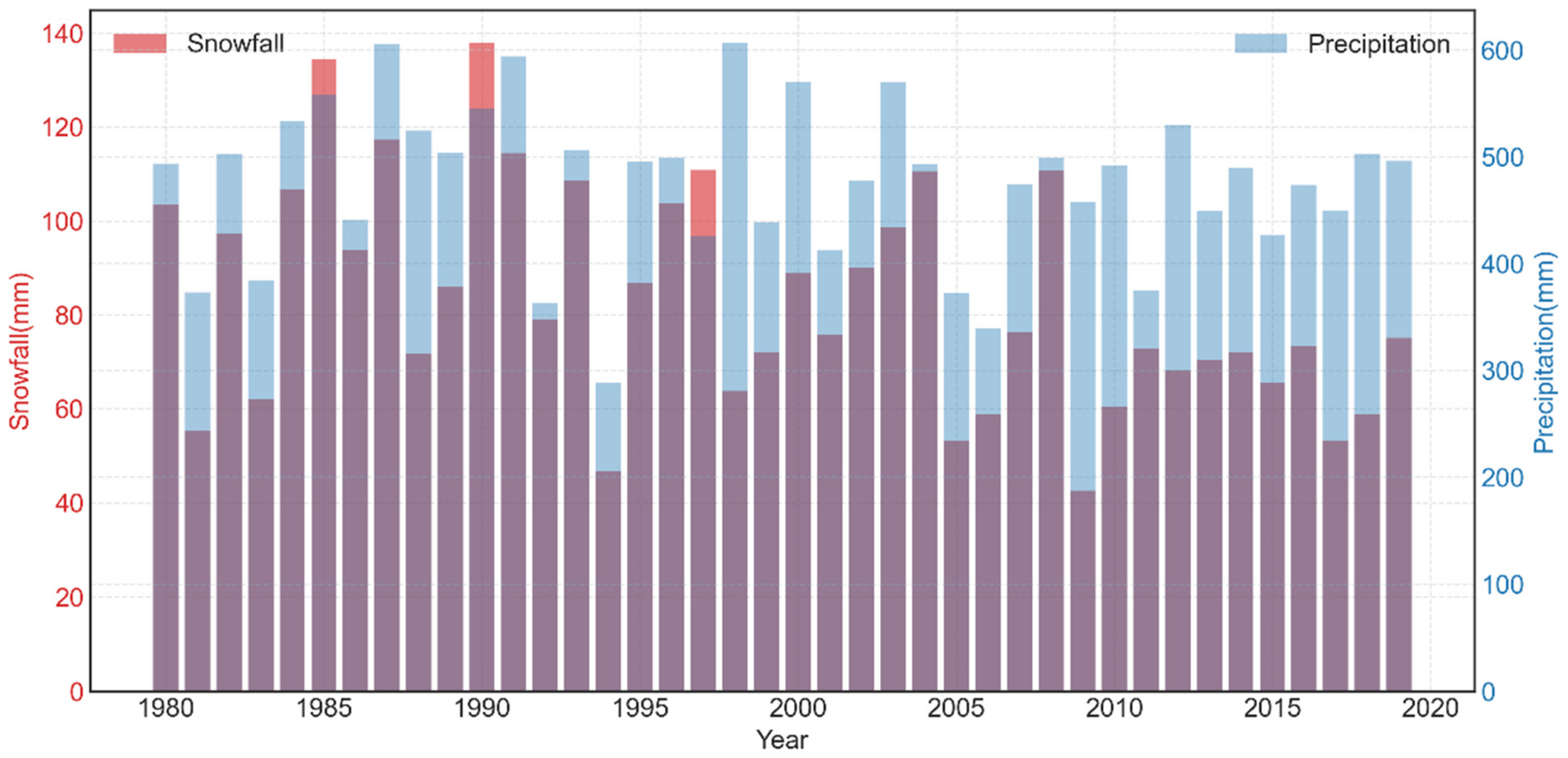
| Class | Numbers of Glaciers | Glacier Area (km2) | Glacier Area Ratio |
|---|---|---|---|
| <0.1 km2 | 1563 | 107.071 | 1.48 |
| 0.1–0.5 km2 | 3792 | 915.832 | 12.62 |
| 0.5–1 km2 | 1127 | 788.109 | 10.85 |
| 1–5 km2 | 1045 | 2132.774 | 29.37 |
| 5–10 km2 | 134 | 890.978 | 12.27 |
| >10 km2 | 95 | 2425.564 | 33.41 |
| Total | 7756 | 7260.32 | 100% |
| River Basin | Numbers of Glaciers | Glacier Area (km2) | Glacier Area Ratio |
|---|---|---|---|
| Brahmaputra | 6192 | 6285.119 | 86.6% |
| Salween | 1514 | 915.56 | 12.6% |
| Mekong | 50 | 59.648 | 0.8% |
| Total | 7756 | 7260.32 | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, L.; Li, S.; Wu, K.; Liu, S.; Zhu, Y.; Afzal, M.M.; Zhou, J.; Yi, Y.; Wei, J.; Duan, Y.; et al. A Geodetic-Data-Calibrated Ice Flow Model to Simulate Historical and Future Response of Glaciers in Southeastern Tibetan Plateau. Remote Sens. 2024, 16, 522. https://doi.org/10.3390/rs16030522
Xiao L, Li S, Wu K, Liu S, Zhu Y, Afzal MM, Zhou J, Yi Y, Wei J, Duan Y, et al. A Geodetic-Data-Calibrated Ice Flow Model to Simulate Historical and Future Response of Glaciers in Southeastern Tibetan Plateau. Remote Sensing. 2024; 16(3):522. https://doi.org/10.3390/rs16030522
Chicago/Turabian StyleXiao, Letian, Shijie Li, Kunpeng Wu, Shiyin Liu, Yu Zhu, Muhammad Mannan Afzal, Jun Zhou, Ying Yi, Jinyue Wei, Yunpeng Duan, and et al. 2024. "A Geodetic-Data-Calibrated Ice Flow Model to Simulate Historical and Future Response of Glaciers in Southeastern Tibetan Plateau" Remote Sensing 16, no. 3: 522. https://doi.org/10.3390/rs16030522
APA StyleXiao, L., Li, S., Wu, K., Liu, S., Zhu, Y., Afzal, M. M., Zhou, J., Yi, Y., Wei, J., Duan, Y., & Shen, Y. (2024). A Geodetic-Data-Calibrated Ice Flow Model to Simulate Historical and Future Response of Glaciers in Southeastern Tibetan Plateau. Remote Sensing, 16(3), 522. https://doi.org/10.3390/rs16030522








