Improved Simulated Annealing Algorithm on the Design of Satellite Orbits for Common-View Laser Time Transfer

Abstract

Laser Time Transfer (LTT) has proven to be able to improve remote time transfer accuracy compared to microwave technology. The impact of satellite clock errors and atmospheric delays during LTT will be further reduced in the common-view mode. The challenge is presented as an optimization problem that is limited by satellite trajectories. This paper introduces an improved simulated annealing algorithm designed to maximize the common-view possibility among various station pairs within regional Satellite Laser Ranging (SLR) networks by optimizing satellite orbit trajectories. The study proposes a system model that integrates LTT principles with satellite visibility considerations. The simulated annealing algorithm is improved with new annealing strategies that incorporate control strategies, and modify the cooling function. Comparative simulation analyses demonstrate the effectiveness of the algorithm, resulting in a significant reduction in computation time by over 10 times. The optimized orbits exhibit common-view windows between 3.337 and 8.955 times longer than existing orbits. Further simulations are conducted to optimize the orbits, and common-view models are established for 45 pairs among 10 stations. The optimizations result in common-view times ranging from 6.183 to 60.633 min in the Asia-Pacific region and from 5.583 to 61.75 min in the Europe-to-Asia region. This can provide valuable references for designing satellite constellations.

1. Introduction

Laser Time Transfer (LTT) is a technique based on Einstein’s clock synchronization approach that synchronizes time between two distant clocks using laser pulses in space. This technique allows for high-precision time transfer with an accuracy of tens of picoseconds [1], significantly enhancing the fields of deep space exploration, astronomy, space geodesy, and timing systems [2]. LTT has been shown to be reliable and precise when compared to previous radio technology-based time transfer methods such as GNSS co-visibility observation, microwave technology, and two-way satellite time-frequency transmission [3].

Since the 1970s and 1980s, significant advancements in laser ranging and time-frequency measurement technologies have spurred numerous international experiments for long-distance clock time comparison and prompted research on laser time comparison. In 1988, the Laser Synchronization from Stationary Orbit (LASSO) program conducted the pioneering international experiment for star-earth time transfer [4]. In 2007, China’s BeiDou navigation satellite system executed star-ground laser time difference comparison experiments at the Changchun station, involving a test star orbiting at approximately 21,000 km altitude. Subsequently, in 2013, the system successfully performed the initial laser time comparison test for 36,000 km inclined orbit synchronous navigation satellites [5]. The implementation of time transmission via laser connection, exemplified by the T2L2 payload developed collaboratively by the CNES and OCA of France, commenced with the successful launch aboard the Jason-2 satellite in 2008 [6]. T2L2, a subsequent mission to LASSO [5] and part of the experimental equipment onboard the Jason-2 mission [7,8,9], conducted 1155 time transfer experiments during the satellite’s flight at 1336 km, including 650 common-view comparison laps [10]. The current state-of-the-art for ground-to-space laser time-transfer is the Time-Transfer by Laser Link (T2L2) [11]. Extensive data processing confirmed the T2L2 approach’s accuracy of 100 picoseconds and stability of more than 1 picosecond over 1000 s [12]. Moreover, an increasing number of NEO (Near-Earth Orbit) satellites will integrate onboard clocks [13], while the establishment of LEO-MEO (Low Earth Orbit—Medium Earth Orbit) constellations will facilitate bidirectional laser connections [14].

Groundspace time transfer is a crucial process for synchronizing clocks between distant ground and satellite locations using laser time transfer links. This involves exchanging timing information between space instruments and ground-based laser stations. Each ground station utilizes multiple ground-to-space links to compare time synchronization between two laser stations. The ground-to-space transmission involves emitting laser pulses from the laser station towards the satellite, with a series of mirrors on the satellite reflecting a portion of these light pulses back to the ground station. Ground-to-ground time transmission occurs in two modes: non-common-view and common-view. The visibility of the satellite greatly impacts the success of laser time transmission [10]. In the common-view mode, ground laser stations observe satellites simultaneously. However, in non-common-view scenarios, the observation methods are different. Operating in the common-view mode involves stimulating the space oscillator solely during the laser pulse, which typically lasts a few seconds. This longer time interval under common-view mode helps to synchronize noise patterns between observatories, reducing discrepancies and eliminating errors caused by satellite clock inaccuracies and atmospheric delays, resulting in high precision and accuracy [15]. However, when a satellite is not visible, accounting for noise from the space oscillator becomes essential. In the non-common-view mode, this noise can cause significant interference.

In recent years, there has been a significant advancement in satellite technology, leading to a growing desire among people to customize satellite orbit designs for specific tasks, rather than relying on traditional, general designs [16,17]. The optimization of satellite orbits allows for simultaneous observations of the satellite by multiple ground laser stations, significantly extending the common-view observation time and reducing observation noise. The development of spacecraft trajectory optimization techniques has arisen from the need to strategically shape a spacecraft’s trajectory in order to efficiently achieve mission objectives in an optimal or near-optimal manner [18]. There are two main categories of numerical trajectory optimization methods: indirect methods (“optimize and then discretize”) and direct methods (“discretize and then optimize”) [19]. Currently, direct methods are more commonly used, involving the examination of state and input parameters to determine the minimum (or maximum) value of the objective function. This approach results in a static nonlinear optimization problem [20]. Simulated Annealing (SA) is an effective and versatile metaheuristic for searching, particularly in cases involving large discrete or continuous spaces [21]. In SA, the likelihood of considering a low-value solution decreases as the algorithm runs. This adjustment increases the probability of finding the global optimum. Algorithms in this category primarily use stochastic methods that combine local and global search techniques. Additionally, the theoretical and mathematical foundations provide strong justifications for the effectiveness of these algorithms in real-world applications [22].

This paper introduces a model for optimizing satellite orbits in order to maximize the probability of ground-based laser stations in the common view. The model uses a simulated annealing algorithm with an improved annealing strategy to achieve optimization. Two sets of experiments were conducted to validate the practicality and effectiveness of the algorithm. After modeling and optimizing the algorithm, the improved annealing strategy generates optimal satellite orbits for multiple stations within the specified model. This paper presents an optimization model and methods for adjusting satellite orbit designs to achieve observational objectives. It is specifically designed for satellite missions that involve laser retroreflector arrays and tasks that focus on laser time transfer comparisons within specific regions.

The subsequent sections of the paper are organized as follows: Section 2 explains the Ground-to-Ground laser time transfer principle, which is based on Space-to-Ground time transfer, and introduces the multi-station satellite orbit design model for the common view. Section 3 describes the methodology, including an analysis of the improved simulated annealing algorithm and the process of optimizing satellite orbits in the common view. Section 4 investigates the minimum satellite orbit altitude between two stations in the common-view mode, and presents a comprehensive analysis of the optimization of optimal satellite orbits between two and multiple Satellite Laser Ranging (SLR) stations using the improved simulated annealing algorithm. Finally, Section 5 concludes the discussion.

2. System Model for Laser Time Transfer in Common-View

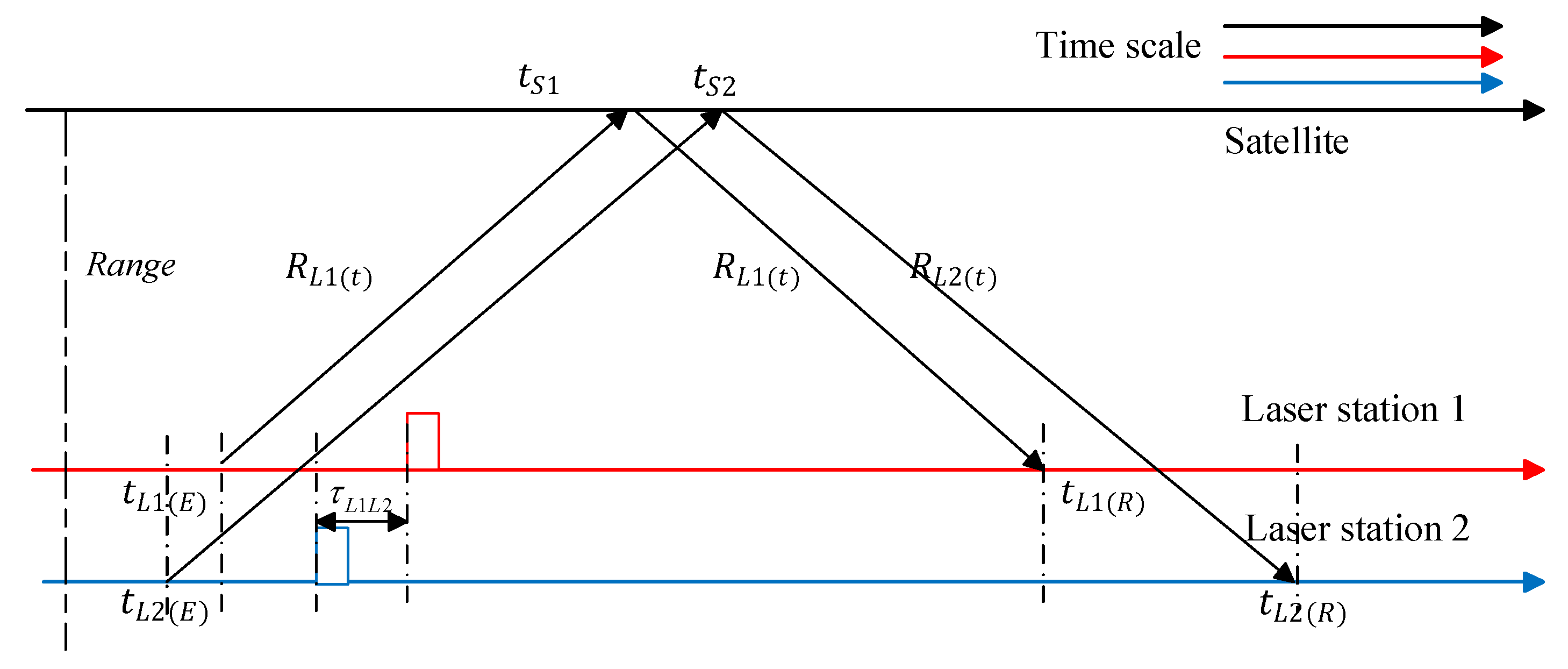
2.1. Ground-to-Ground Laser Time Transfer in Common-View

The graphic depicts the fundamental concept of the two-way laser time transfer method, in which two terminals independently generate pulses at predetermined laser emission rates. For example, in a scenario involving a link between a ground receiving station and a space probe, the ground receiving station terminal records both the arrival time ($t_{L1\left(R\right)}$) and the emission time ($t_{L1\left(E\right)}$) of the pulse it transmits, and vice versa. The satellite receiving terminal records the arrival time of pulses ($t_{S1}$). Figure 1 illustrates the common use of asynchronous answering laser time transfer to extend operational distances. In scenarios where there is a high likelihood of detection at both ends of the link and relatively short round-trip times, basic echo transponder mechanisms are sufficient for measurement purposes [23].

When two laser ranging stations, L1 and L2, are in the common-view configuration and transmit to the satellite simultaneously, the time offset ${\tau }_{L-S}$ in the ground space can be obtained by establishing the time-delay link between the ground clock and the on-board clock. By comparing the difference between ${\tau }_{L_{1}S}$ and ${\tau }_{L_{2}S}$, the time difference between the ground clocks L1 and L2 can be determined, effectively completing the synchronization of time between the ground laser stations.

The offset ${\mathsf{\tau }}_{L_{1}S}$ between the ground clock L1 and the space clock S is given by:

$${\mathsf{\tau }}_{L_{1}S}=t_{L1\left(E\right)}+\frac{t_{L1\left(R\right)}-t_{L1\left(E\right)}}{2}-t_{S1}+{\Delta }_C,$$

(1)

where $t_{L1\left(E\right)}$ denotes the moment of ground station laser pulse emission, $t_{L1\left(R\right)}$ signifies the moment of the satellite’s reflected laser pulse return, and $t_{S1}$ indicates the on-board receiving epochs for satellite laser pulse measurements. ${\Delta }_C$ stands for “correction term” and includes adjustments for instrument calibration, atmospheric conditions, velocity aberration, and relativistic effects. This correction term adjusts for relativistic effects, atmospheric phenomena, instrumental calibration, and velocity aberrations. ${\tau }_{L_{2}S}$ can be obtained in the same way. The clock offset ${\tau }_{L_1-L_2}$ between clocks at different terrestrial laser stations and the primary clock is determined by

$${\tau }_{L_1-L_2}={\mathsf{\tau }}_{L_{1}S}-{\mathsf{\tau }}_{L_{2}S}.$$

(2)

2.2. Models for Optimized Satellite Orbits Design in Multi-Station Common View

The two-body problem stands as the predominant model for analyzing spaceship dynamics. Essentially, it revolves around the dynamics of two objects, treating them as point masses and describing the gravitational force between them under the assumption that neither object experiences any external force.

The equation of motion for a satellite within the two-body problem is expressed using the gravitational formula as follows [24]:

$$\ddot{\stackrel{⃑}{r}}=-GM\frac{\stackrel{⃑}{r}}{r^3},$$

(3)

where GM denotes the Earth’s gravitational parameter, $\ddot{\stackrel{⃑}{r}}$ represents the acceleration vector of the satellite’s motion, $\stackrel{⃑}{r}$ is the position vector of the satellite in the specified coordinate system, and $r=\left|\stackrel{⃑}{r}\right|$ indicates the radius. The state vector in the two-body problem can be represented by the position and velocity vectors ($\stackrel{⃑}{r}$,$\dot{\stackrel{⃑}{r}}$) or the Keplerian orbital sextuplets: the semimajor axis ($a$), the numerical eccentricity ($e$), the inclination ($i$), the right ascension of the ascending node ($\Omega$), the argument of perigee ($\omega$), and the mean anomaly ($M$). During the orbital motion of satellites, there are various additional and complex perturbing forces at play. These include the Earth’s gravitational field, as well as gravitational influences from the Sun and Moon, Earth’s solid tides, ocean tides, and other forces that are not yet fully comprehended. While these forces are much smaller in magnitude compared to the Earth’s gravitational force, they still have an impact on the satellite’s orbit [25].

To obtain the satellite’s in-orbit state vectors, we can utilize the six known orbital parameters and convert them into the satellite’s instantaneous position vector. The unit vector in the direction of the perigee is denoted as $P$, while $Q$ represents the unit vector oriented perpendicular to the perigee within the orbital plane, aligned with the satellite’s orbital motion. $E$ is the eccentricity anomaly, $a$ and $e$ are the semimajor axis and eccentricity. The satellite’s instantaneous position vector can be expressed in terms of its orbit direction as follows:

$$R_{SCTS}=\left[\begin{array}{c}{X}_{SCTS}\\ Y_{SCTS}\\ Z_{SCTS}\end{array}\right]=a\left(\mathrm{c}\mathrm{o}\mathrm{s}E-e\right)\left[\begin{array}{c}{P}_x\\ P_y\\ P_z\end{array}\right]+a\sqrt{1-e^2}\mathrm{s}\mathrm{i}\mathrm{n}E\left[\begin{array}{c}{P}_x\\ P_y\\ P_z\end{array}\right],$$

(4)

Coordinates from the satellite’s celestial coordinate system can be translated to the instantaneous Earth coordinate system by inputting the instantaneous Greenwich accurate sidereal time ($GAST$) at a given moment. It is possible to estimate the Greenwich true sidereal time using the Greenwich mean sidereal time ($GMST$):

$$GMST=GMST0+T_r\left[UTC+\left(UT1-UTC\right)\right]=GMST0+T_{r}UT1,$$

(5)

where $GMST0$ refers to the Greenwich Mean Time at midnight of the relevant day, while $T_r$ refers to the rate of change and $UT1$ denotes the Universal Time that has been corrected for pole shift. $GMST0$ and $T_r$ are determined by the time that has elapsed in the Julian calendar element from J2000.0 to zero $UT1$ on the day when the measurement is taken, according to empirical formulas.

$$R_S=\left[\begin{array}{c}{X}_S\\ Y_S\\ Z_S\end{array}\right]=\left[\begin{array}{ccc}\cos \left(GMST\right)& \sin \left(GMST\right)& 0\\ -\sin \left(GMST\right)& \cos \left(GMST\right)& 0\\ 0& 0& 1\end{array}\right]R_{SCTS},$$

(6)

The satellite’s current Earth coordinate system undergoes a conversion process into the Earth geodetic coordinate system. This enables us to acquire the corresponding longitude $L_S$, latitude $B_S$, and height $H_S$. These coordinates can then be inverted to the Earth coordinate system coordinates of the established station, $L_r$ station-centered coordinate system accommodation, using the Earth geodetic coordinate system of the satellite.

$$R_{Sr}=\left[\begin{array}{c}{X}_{Sr}\\ Y_{Sr}\\ Z_{Sr}\end{array}\right]=\left[\begin{array}{ccc}-\mathrm{s}\mathrm{i}\mathrm{n}{B}_S\mathrm{c}\mathrm{o}\mathrm{s}{L}_S& -\mathrm{s}\mathrm{i}\mathrm{n}{B}_S\mathrm{s}\mathrm{i}\mathrm{n}{L}_S& cos{B}_S\\ -\mathrm{s}\mathrm{i}\mathrm{n}{L}_S& \mathrm{c}\mathrm{o}\mathrm{s}{L}_S& 0\\ cos{B}_{S}cos{L}_S& cos{B}_{S}sin{L}_S& \mathrm{s}\mathrm{i}\mathrm{n}{B}_S\end{array}\right]\left[\begin{array}{c}{X}_S\\ Y_S\\ Z_S\end{array}\right],$$

(7)

The conversion process for the satellite’s instant Earth coordinate system is presented in Figure 2. The IERS official website (https://www.iers.org/IERS/EN/DataProducts/data.html, accessed on 10 December 2023) provides the most recent versions of the axial precession, nutation, and polar motion that have been used.

To calculate the observation elevation angles that align with the station, the coordinates of the station and satellite relative to the centroid coordinate system of the station are needed. This aids in determining the satellite’s visibility during the station’s observable time period (${Time}_{observe}$). Technical abbreviations will be clarified upon their initial usage. The procedure for deriving the coordinates of the station coordinate system’s center for a specific satellite at a given time remains consistent across stations. It involves assessing whether the observation elevation angle ${\theta }_i$ exceeds the minimum observation angle ${\theta }_{min}$ and identifying the intersection of observation periods from various stations. This method establishes a shared observation period (referred to as ${Time}_{com}$) for a given satellite during its orbital period.

3. Algorithm for Multi-Station Satellite Orbit Optimization in Common-View

3.1. A Description of the Problem

The trajectory of satellites in their orbits determines the duration of common-view between ground SLR stations. Calculating the minimum observable satellite orbit height, which corresponds to the distance between different stations, involves using the coordinates between these stations. The visibility of satellites with varied trajectories is determined by the simultaneous observation of the same satellite at different elevation angles from each ground station. During a complete satellite orbit, if two or more ground stations can observe it simultaneously without obstruction from their lowest elevation angle, the duration is known as the common-view duration. This common-view duration is contingent on both the satellite’s orbital geometry and the distance between ground stations.

The following elements, as shown by the problem’s description above, have an impact on the multi-station satellite orbit optimization problem under the common-view mode:

• The initial precise instant in time as defined by the UTC Time system;
• The ground station coordinates, including the separation for each station;
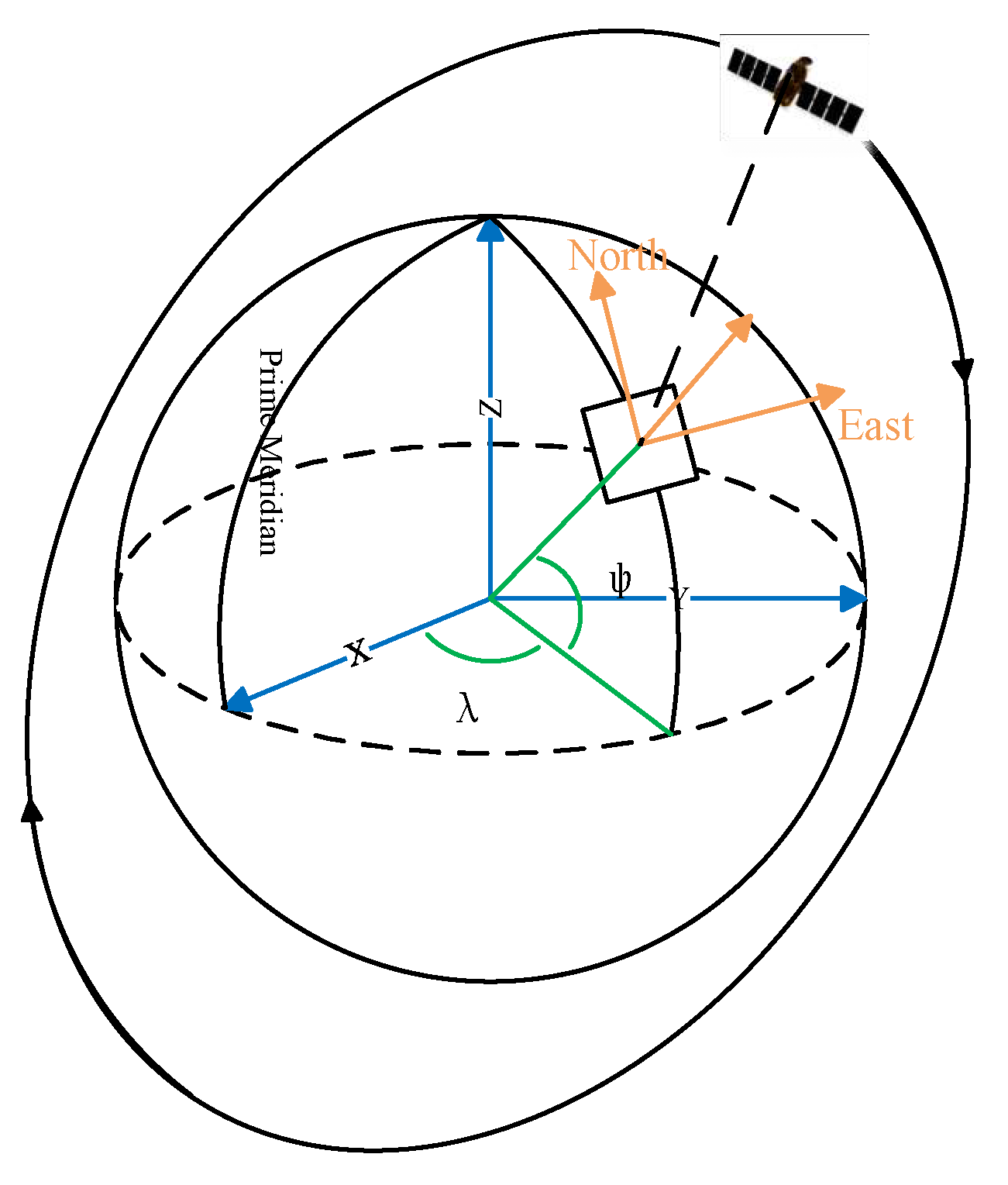
• The Keplerian orbit of the satellite is determined by six parameters: $a$, $e$, $i$, $\mathsf{\Omega }$, $\omega$, and $M$. These parameters define the satellite’s current location coordinates at any given time. For the sake of simplicity, this paper only discusses the case of circular orbits, the $e$ = 0, $\omega$ = 0, and $M$ = $E$ were selected. The mean anomaly of the circular orbits is equal to the eccentric anomaly. This type of orbit is also the choice of most satellites for scientific experiments.

3.2. The Implementation of Optimal Satellite Orbit Algorithm in Common View

3.2.1. Decision Variables

According to the system architecture and problem description above, the following decision variables in the common view affect the optimal satellite orbit design problem between numerous stations:

$$i=\left\{\begin{array}{c}{i}_{com}, \mathrm{Common} \mathrm{visible} \mathrm{orbital} \mathrm{inclination} \mathrm{of} \mathrm{a} \mathrm{ground} \mathrm{laser} \mathrm{station}.\\ i_{uncom}, \mathrm{Non-common} \mathrm{visible} \mathrm{orbital} \mathrm{inclination} \mathrm{of} \mathrm{a} \mathrm{ground} \mathrm{laster} \mathrm{station}\end{array}\right.,$$

(8)

$$\mathsf{\Omega }=\left\{\begin{array}{c}\hfill {\mathsf{\Omega }}_{com}, \mathrm{Common} \mathrm{visible} \mathrm{right} \mathrm{ascension} \mathrm{of} \mathrm{ascending} \mathrm{node}\hfill \\ {\mathsf{\Omega }}_{uncom}, \mathrm{Non-common} \mathrm{visible} \mathrm{right} \mathrm{ascension} \mathrm{of} \mathrm{ascending} \mathrm{node}\hfill \end{array}\right.,$$

(9)

The parameters $i$ and $\mathsf{\Omega }$, respectively, represent the orbital inclination of the satellite orbit and the right ascension of the ascending node. These parameters are crucial for determining the orientation of the satellite’s orbital plane. When two or more designated ground laser stations can simultaneously observe the satellite, the parameters $i$ and $\mathsf{\Omega }$ denoted as $\left(i_{com},{\mathsf{\Omega }}_{com}\right)$. In other cases, they are denoted as $i_{uncom}$ and ${\mathsf{\Omega }}_{uncom}$.

3.2.2. Constraints

In order to optimize the optimal satellite orbit design between multi-stations in the common view, the following constraints should be satisfied:

• Provide the exact moment in time: A four-dimensional space vector is required for the satellite’s instantaneous Earth coordinate system coordinates, which includes the precise UTC time used to calculate the satellite coordinates at that specific point in time. Therefore, the instant time is denoted as ${time}_{instant}=[Y,M,D,H,Min,S]$.
• Boundaries of $i_{com}$ and ${\mathsf{\Omega }}_{com}$: The shape of a satellite’s orbit is determined by its orbital inclination and the right ascension of the ascending node. Therefore, it is necessary to establish reasonable ranges for the upper and lower boundaries of these parameters. Specifically, the orbital inclination and right ascension of the ascending node should be framed within the ranges $i_{com}=[0, 180]$ and ${\mathsf{\Omega }}_{com}=[0, 360]$.
• Angular velocity constraint: If we assume that the satellite orbit is a closed circular one, then it operates at an angular rate that satisfies Kepler’s third law, which is ${\omega }_{AR}=\sqrt{\frac{GM}{r^3}}$.
• Ground laser station coordinates: Different observable time periods correspond to distinct ground laser station coordinates, that is $L_{station}=\left[\begin{array}{c}{X}_{L1 }{Y}_{L1} Z_{L1} \\ X_{L2} Y_{L2} Z_{L2} \\ ⋮\end{array}\right]$.
• Observation elevation angle constraint: The design of the satellite orbit must ensure that during observation at different stations, the elevation angle of observation is larger than the station’s lowest observation elevation angle, or ${\theta }_i\ge {\theta }_{min}$.
• Common-view time constraint: The satellite’s orbit must be designed in order to fulfill the requirement that, upon passing through several orbital planes, the satellite is visible to ground stations for the greatest possible amount of time. This is indicated by the following equation: $max:{Time}_{com}={\sum }_{i=1}^{n}f(i_{com},{\mathsf{\Omega }}_{com})$.

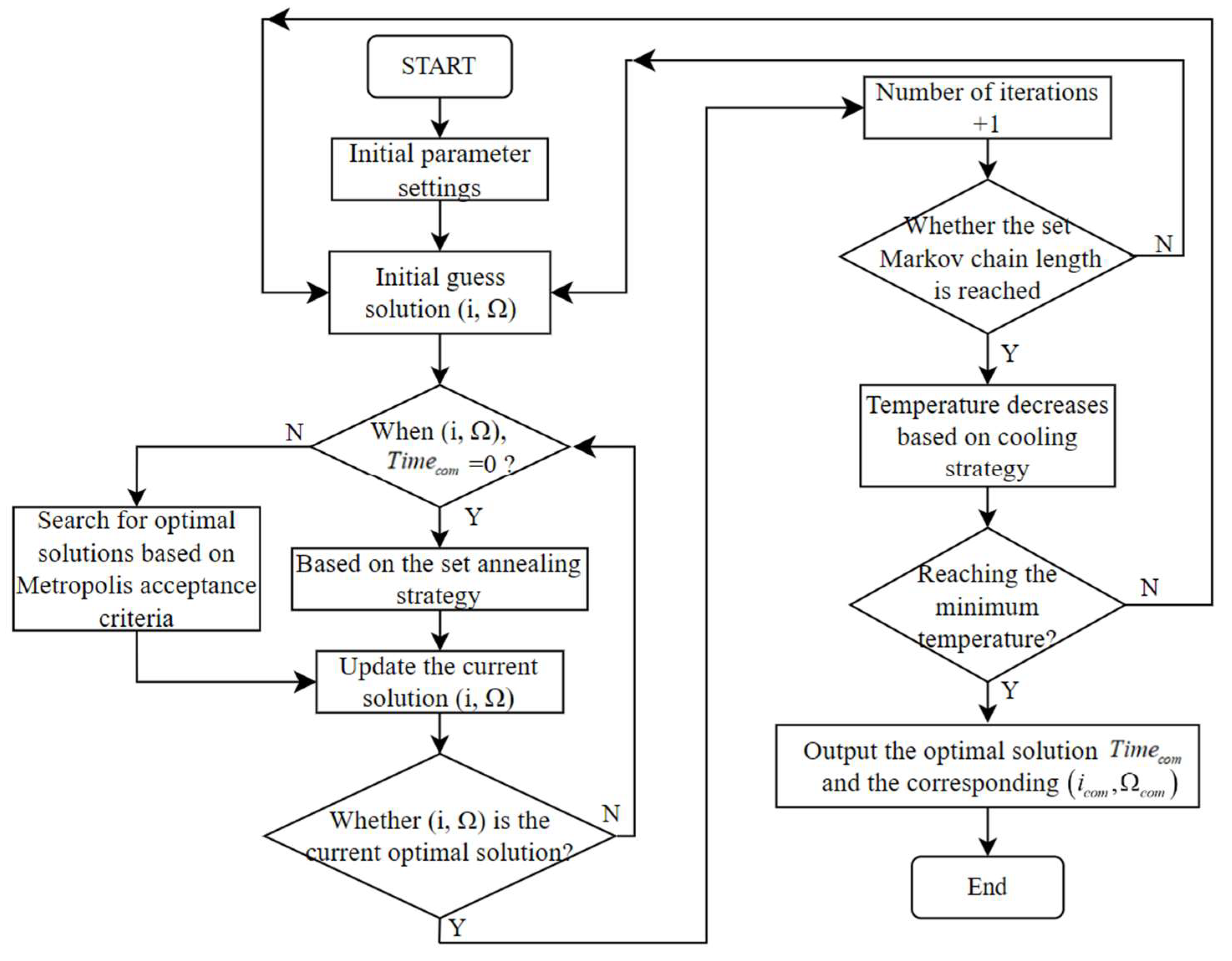
3.3. Simulation Annealing Algorithm and Optimization

The six parameters that characterize a satellite’s Keplerian orbit are important in determining the most efficient trajectory design. This design challenge can be approached as a static parametric optimization problem with a finite set of choice variables [26,27]. However, it is important to note that numerical gradient-based optimization algorithms may only converge to local optima, while heuristic methods have the potential to reach global optimal results. Therefore, there is a significant interest in utilizing specialized optimization algorithms to solve constrained trajectory optimization problems [28]. Additionally, heuristic methods can bypass computational obstacles associated with Hessian and Jacobian matrices by eliminating the need for derivative information. The general form of a constrained optimal control problem is as follows [29]:

$$\dot{x}\left(t\right)=f\left(x\left(t\right),u\left(t\right)\right) ,$$

(10)

where $x\left(t\right)\in {\mathbb{R}}^{n_x}$ and $y\left(t\right)\in {\mathbb{R}}^{n_u}$, defining the system state and control variables over the time interval $t\in [t_0,t_f]$, with $n_x$ and $n_u$ being the dimensions of the system state and control variables, respectively. The form of the boundaries and constraints are as follows:

$$\begin{array}{c}g\left(x\right(t),u(t\left)\right)\le 0\\ x\left(t_0\right)=x_0\\ x\left(t_f\right)=x_f\end{array} ,$$

(11)

The general form of the objective function is:

$$\underset{u\left(t\right)}{min }{J}_1={\int }_{t_0}^{t_f}L\left(x\right(t),u(t\left)\right)dt+\Phi \left(x\right(t_f),t_f) ,$$

(12)

where $L\left(x\right(t),u(t\left)\right)$ and $\Phi \left(x\right(t_f),t_f)$ represent the process and terminal performance indicators, respectively.

The simulated annealing algorithm is a probabilistic metaheuristic algorithm used for global optimization. It operates on the principle of gradually reducing a system’s energy to reach a low-energy state, akin to the process of cooling a solid from high temperatures [21]. This method is particularly effective in handling nonlinear, discontinuous, and stochastic objective functions. It proves advantageous in scenarios with a high-dimensional state space and substantial memory requirements [29]. The quality of the solution for combinatorial minimization problems hinges on several factors: the length of the Markov chain, the halting criterion, the temperature cooling rate, and the initial temperature. The generating principle of the domain aligns with the interference mechanism of the Metropolis algorithm, and the annealing method can be adjusted as necessary.

Given an extremely low temperature and an extremely slow decay rate, the simulated annealing algorithm can theoretically approach the global optimal solution with high precision. To ensure reasonable computation time and manage the instability of the simulated annealing algorithm caused by the probability requirement, we propose the following annealing strategy:

• Initial parameter settings: The initial guesses are selected randomly, while the upper and lower parameter boundaries are set at $i\in \left[\mathrm{0,180}\right]$ and $\mathsf{\Omega }\in \left[\mathrm{0,360}\right]$, correspondingly. The length of the Markov chain is set at 200.
• Cooling strategy: We adopt the linear annealing schedule, given by $T=T_{init}-C\ast t$, where $T_{init}$ is the initial temperature and $C$ is the cooling coefficient [30]. To expand the search space, the initial temperature is set at 500. Following this, linear cooling is performed to set the cooling coefficient to 0.8. The Metropolis criterion is a criterion for accepting new solutions [30]. This will aid in quick convergence, reducing randomness, and avoiding local optimum solutions as confirmed by the Metropolis acceptance criterion.
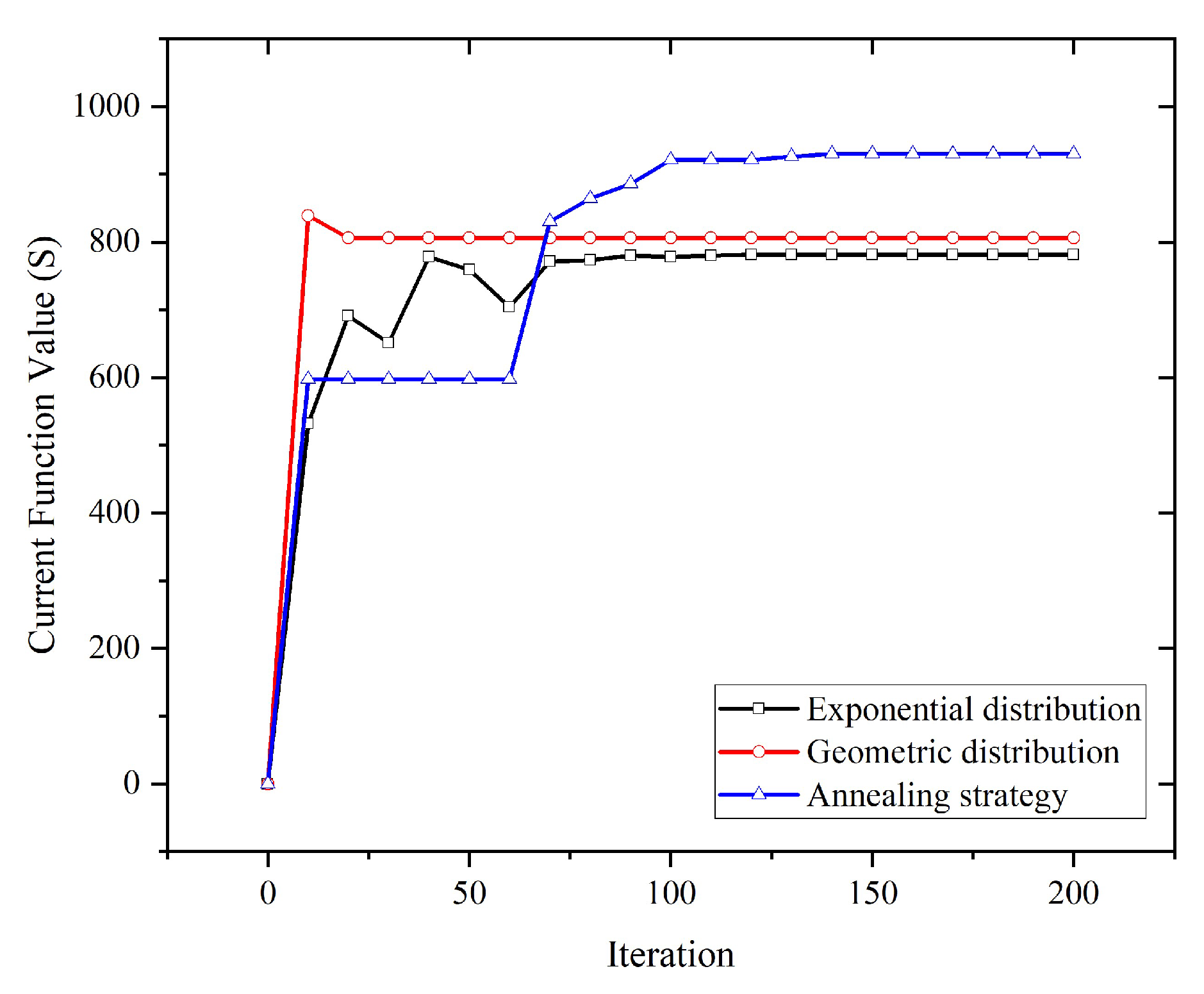
• Perturbation strategy: With the introduction of control strategies and by focusing perturbation strategies, various perturbation techniques are established, aligning with distinct Markov chain period durations. A Markov chain is a type of stochastic process in which the future state of the system is determined solely by its current state, without any influence from its past evolution [29]. For Markov chain length intervals from 0 to 60, the algorithm employs a geometric distribution perturbation strategy, using an early increase in perturbation amplitude to escape local optima. For Markov chain length intervals from 60 to 120, a uniform distribution is used, producing values ranging from −5 to 5 to expedite convergence based on the current best solution. For Markov chain length intervals from 120 to 180, the Gaussian distribution perturbation approach was applied to improve search efficiency. Inside the Markov chain length interval of 180 to 200, a uniform distribution is used to achieve a value concentration within the range of −0.1 to 0.1. This enhances the search for optimal solutions.

The initial temperature value is higher at the beginning of the optimization process, facilitating a more significant shift in the algorithm’s decay and allowing for an exhaustive exploration of the state space. As the temperature decreases, only solutions that minimize the degree of objective degradation or enhance the objective are accepted. Ultimately, the technique reaches its optimization point as the temperature approaches zero and no further decline in the objective is permitted. Figure 3 outlines the specific procedure.

4. Analysis

Before starting the simulation experiments, an investigation was conducted to determine the minimum satellite orbit altitudes for different station distances within the common-view model. Two sets of simulations were then used to confirm the efficiency and applicability of the improved simulated annealing approach in identifying ideal satellite orbits from the common-view. The first test group replicated several satellite orbits over common-view times between two stations to establish the algorithm’s ability to optimize satellite trajectories in the context of common-view. The algorithm’s viability was then evaluated by optimizing orbits for 45 station pairs among 10 SLR stations in various regions of the common-view model. The goal was to determine the best satellite orbits for several stations within the common-view model.

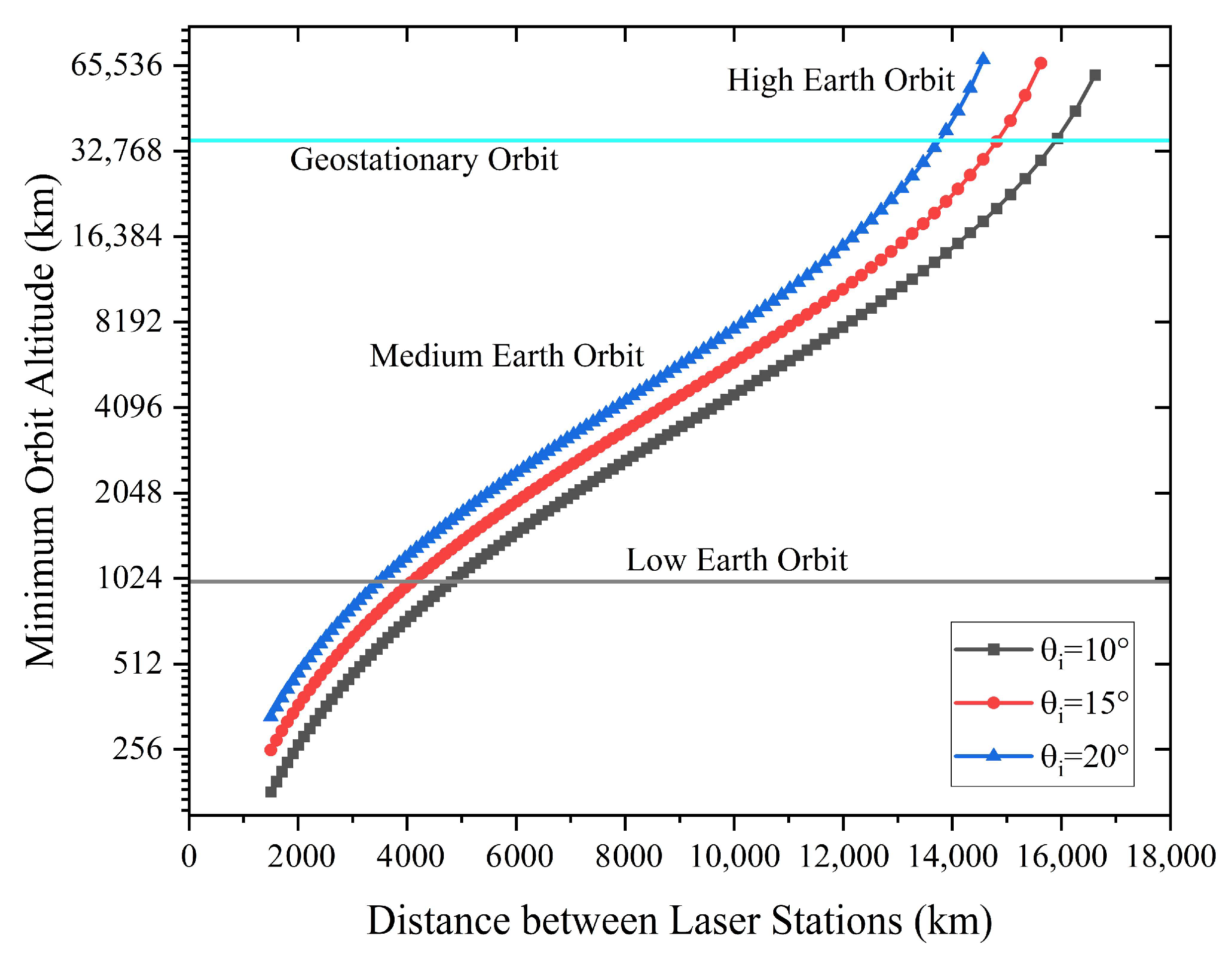
4.1. Minimum Orbit Altitude

In order to facilitate common-viewing between stations, it is imperative to predefine a minimum orbital altitude for the satellite, considering the distances between these stations. The assumption here is that the satellite can be effectively recorded by ground laser stations within a specified maximum observable elevation angle. Assuming that the average radius of the Earth is 6371 km, the minimum distance between two ground stations is set at 1500 km, while the maximum distance is approximately half the circumference of a circle with a radius of 6371 km. Therefore, when the satellite is positioned at the midpoint of the line connecting two stations, the altitude it holds corresponds to the minimum satellite orbit altitude necessary for the initiation of common-view between the two stations.

Assuming the maximum observable elevation angles of the satellite by ground laser stations are 10°, 15°, and 20°, respectively, the curve depicting the variation of the satellite’s lowest orbit altitude concerning station distance was computed. As the determination of the satellite’s observable elevation angle is established and the distance between ground laser stations increases, the achievable minimum orbit altitude for the common-view of the satellite also exponentially increases. At a 10° observation angle and an inter-station distance of 1500 km, the minimum satellite orbit altitude measures 181.52 km. When the distance falls below 4814 km, the satellite’s minimum orbit altitude is within the low Earth orbit range. Between 4814 km and 12,100 km, the satellite’s minimum orbit altitude shifts to the medium Earth orbit range. Within the range of 3540 km to 11,300 km, the minimum satellite orbit altitude falls within the medium Earth orbit range. These changing trends are shown in Figure 4. When the satellite orbit’s’ altitude increased up to 20,000 km, orbital altitudes which are common for navigation satellites, it will meet the requirements for common-view observation over continental scales directly. Therefore, considering the launch costs and the operational lifespan in orbit, meticulous satellite orbit design is essential for enhancing both the accuracy and coverage of common-view time transfer.

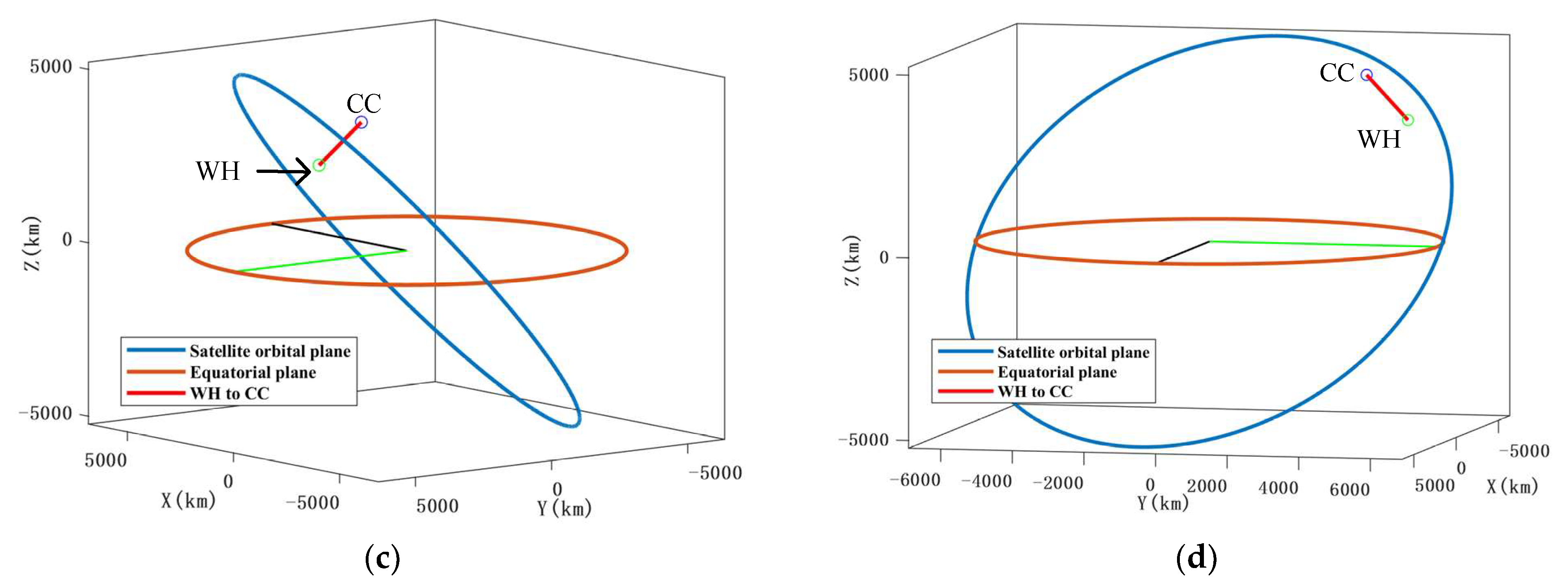
4.2. Simulation Experiments for the Optimal Satellite Orbit in the Common-View Mode between Two Stations

Based on the research conducted on the minimum satellite orbit altitude concerning various inter-station distances, designing an optimal satellite orbit to maximize the common-view time among multiple sites becomes feasible. Initially, the focus was on determining an optimal satellite trajectory to enhance mutual visibility between two ground-based laser stations, and the stations selected for common view were the Changchun and Wuhan ground laser stations. This process involves utilizing the aforementioned system model and employing conventional iterative traversal methods, particle swarm algorithms, and improved simulated annealing algorithms to determine the optimal satellite orbit between two stations in a common-view model. Comparative experiments underscore the effectiveness and advantages of the improved simulated annealing algorithm.

Parameters for the three methods were consistent across the data selection settings The Changchun(CC)[−2674.387, 3757.189, 4391.508] and Wuhan(WH)[−2279.756, 5004.737, 3219.791] SLR field stations were selected as an example to fulfill the experiment. The initial observation moment was set at UTC time on 1 August 2023, 00:00:00. The satellite’s orbit radius is established considering the minimum altitude necessary for orbits at different distances between stations, accounting for the satellite in-orbit flight life. The satellite orbit radii were set as 7000 km, 8000 km, 9000 km, and 10,000 km for different distances between the stations. Based on the experimental conditions described, the study generated outcomes that optimized the satellite orbit between two stations in the common-view model, utilizing three different methods.

The conventional iterative traverse method was performed as the following procedure:

• The optimal orbit inclination in circular orbits involving SLR stations and satellites is determined through geometric analysis. This analysis operates under the assumption that the longest common-view duration between two SLR stations takes place when the plane of the circular orbit is perpendicular to the connecting line (L1 to L2), which is regarded as the angular momentum of the circular orbit.
• Compute the common-view time of different ascending node right ascension at a specified orbital altitude and inclination angle.
• Investigate the orbital altitudes impact on the duration of common view.
• Determine the optimal orbit configuration to facilitate common view between the two stations.

Through the conventional iterative traverse method, the following results were obtained: At an orbital inclination of 48.16° for the ground stations in Changchun and Wuhan, an optimal ascending node right ascension of 27° was identified. Upon fixing the orbital inclination, adjusting the orbit altitude produced the optimal right ascension of the ascending node within an error range of ±3°, illustrated in Figure 5a. Similarly, setting the right ascension of the ascending node while varying the orbit altitude led to the optimal orbital inclination within an error range of ±1°, outlined in Figure 5b. Figure 5a indicates a common-view time curve displaying two distinctive peaks. These peaks correspond to orbital planes during the satellite trajectories: the first peak aligns with the maximum common-view time when the line connecting the ground stations is perpendicular to the satellite orbital plane (Figure 5c), while the second peak occurs when this line is nearly parallel to the satellite orbital plane (Figure 5d). The optimal satellite orbit, which corresponds to its longest common-view duration, aligns with the assumption that when the line between the two stations roughly represents the orbital plane’s angular momentum, the orbit plane coincides with the optimal satellite orbit plane within the common-view model. Additionally, the observation elevation angles of the two SLR stations observing the satellite are nearly identical.

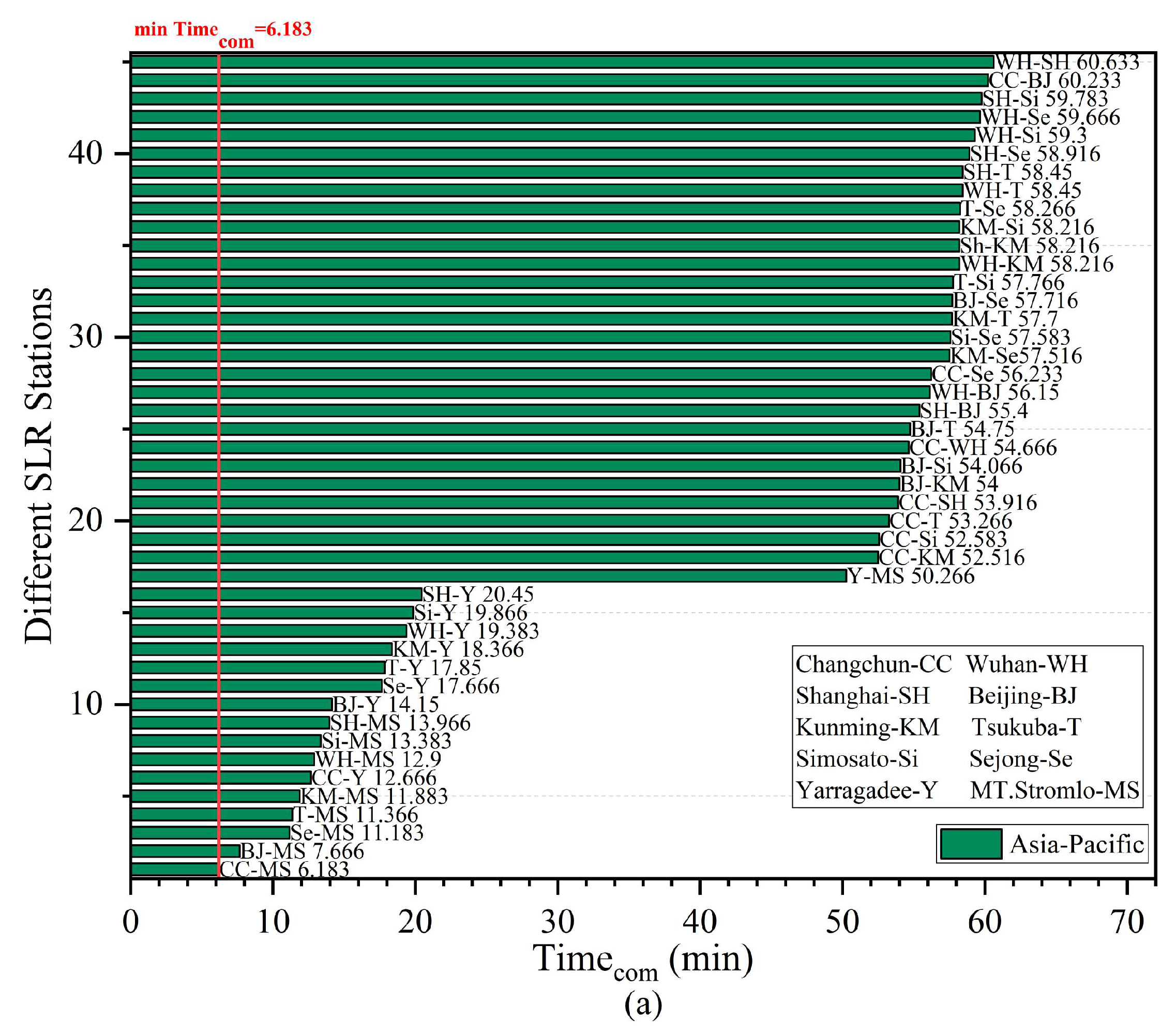
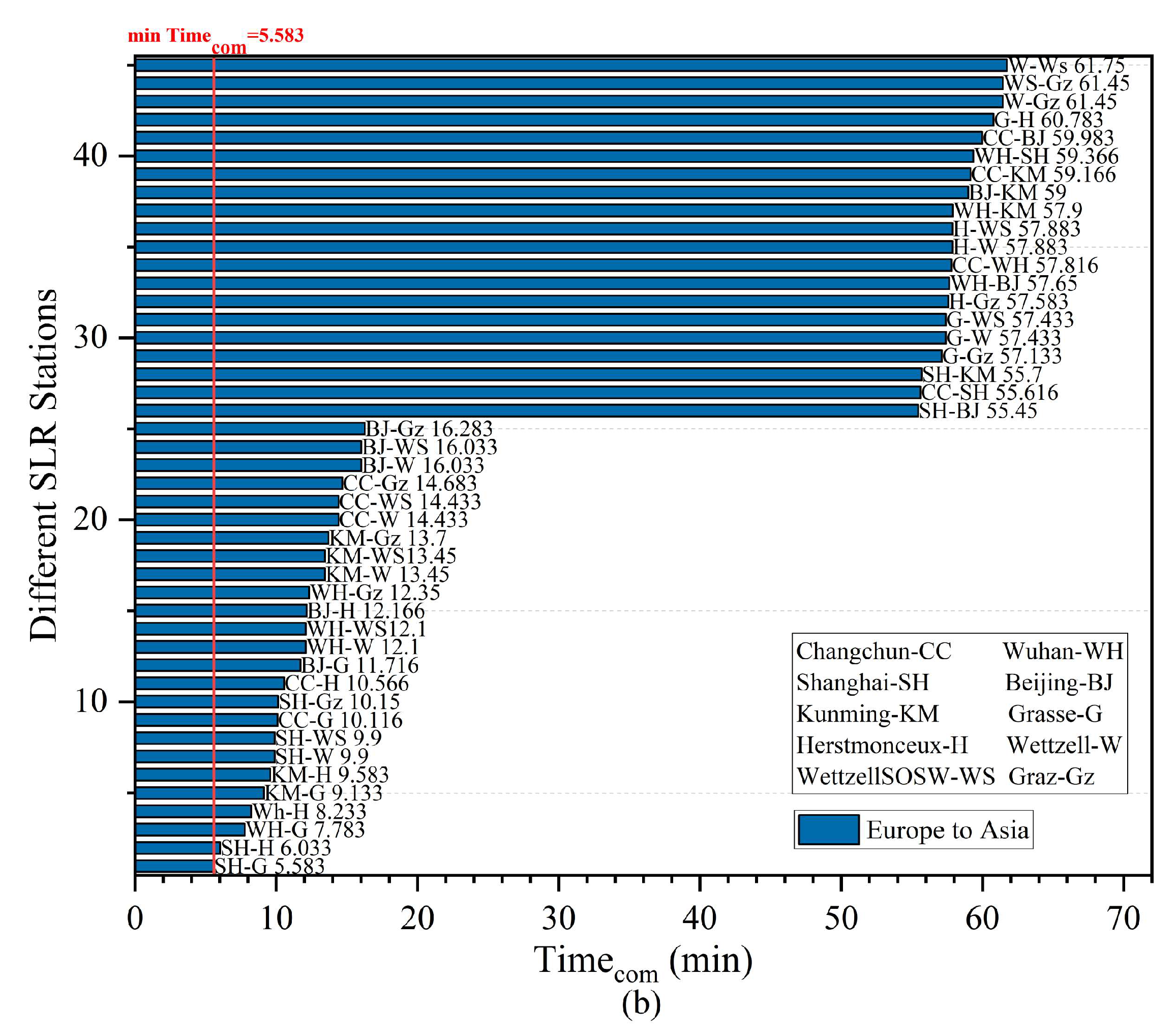
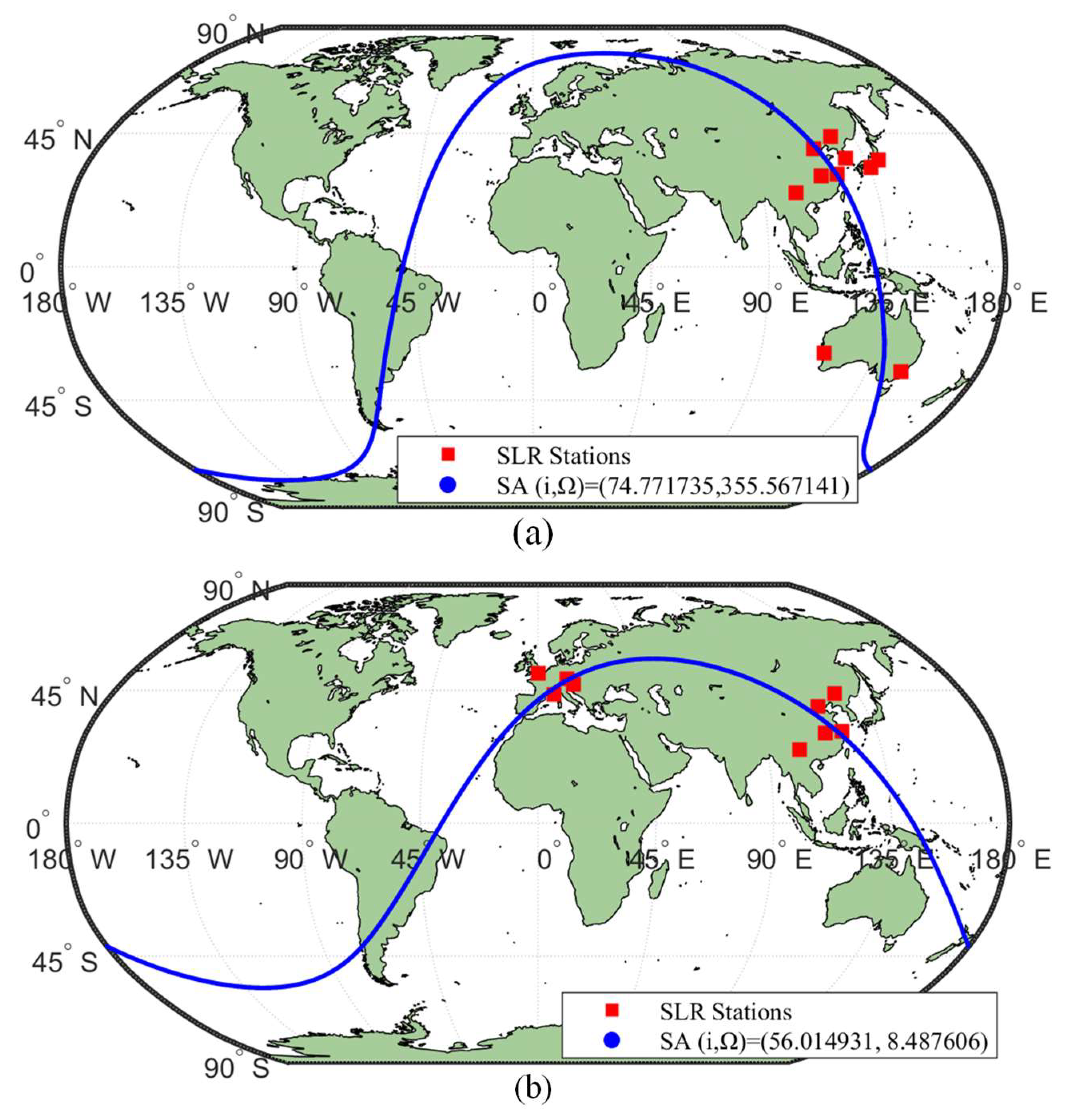
In this paper, a heuristic method that employs the simulated annealing algorithm was introduced to tackle the problem of designing optimal satellite orbits for multi-SLR stations in a common-view model. The improved simulated annealing algorithm is refined through a designed annealing strategy to break away from local optima and gradually converge towards the global optimum during the convergence process. The optimization results of the common-view time among two SLR field stations using three different annealing strategies are presented in Figure 6. Figure 6 illustrates the optimization results for the current received solution value. When employing an exponential distribution-based annealing strategy, rapid convergence is achievable, but there is a higher probability of getting trapped in local optima. Solely utilizing a geometric distribution-based annealing strategy helps diminish the likelihood of getting stuck in local optima by introducing disturbances to the optimal solution, yet it may still lead to local optima. However, with the annealing strategy outlined in Section 3.3, the simulated annealing algorithm minimizes the incidence of local optima while narrowing the search space around the current optimal solution, striving for the global optimum. This method satisfies the algorithm’s functionality.

The improved simulated annealing algorithm and particle swarm optimization algorithm were utilized to obtain results, as shown in Figure 7. The figure indicates that both algorithms achieved similar optimal satellite orbits, converging towards the global optimum. However, the computational performance of the particle swarm optimization algorithm is significantly affected by the number of iterations in the swarm. Due to the complexity of optimizing multiple-station satellite orbits in the common-view perspective, achieving comparable precision requires the particle swarm optimization algorithm to iterate 20 to 30 times more than the simulated annealing algorithm. The improved simulated annealing algorithm demonstrates reduced computational costs and shorter processing times compared to the particle swarm optimization algorithm, highlighting its superior computational efficiency.

Thirty simulations were conducted using an improved simulated annealing algorithm and particle swarm algorithm to determine the optimal satellite orbit for two SLR field stations operating under the common-view model, as shown in Figure 8. The results of the optimization process using the improved simulated annealing algorithm and particle swarm algorithm are depicted in Figure 8a, where fluctuations in outcomes can be observed. However, the common-view time’s fluctuation range is limited to only 3 s. Figure 8b displays histograms for both algorithms, illustrating the distribution of optimal solutions achieved when addressing the optimization problem of determining the best satellite orbits for multiple stations under the common-view model. These distributions are relatively concentrated and closely aligned with the global optimum. The standard deviations for the improved simulated annealing algorithm and the particle swarm algorithm are 0.45486 and 0.62972, respectively.

Under the experimental conditions outlined previously, the optimal satellite orbit between two stations was optimized using the improved simulated annealing algorithm, particle swarm optimization, and the conventional iterative traverse method. The results obtained are summarized in

Table 1. Optimization results of the improved simulated annealing, the particle swarm optimization algorithms, and the conventional iterative traverse method.

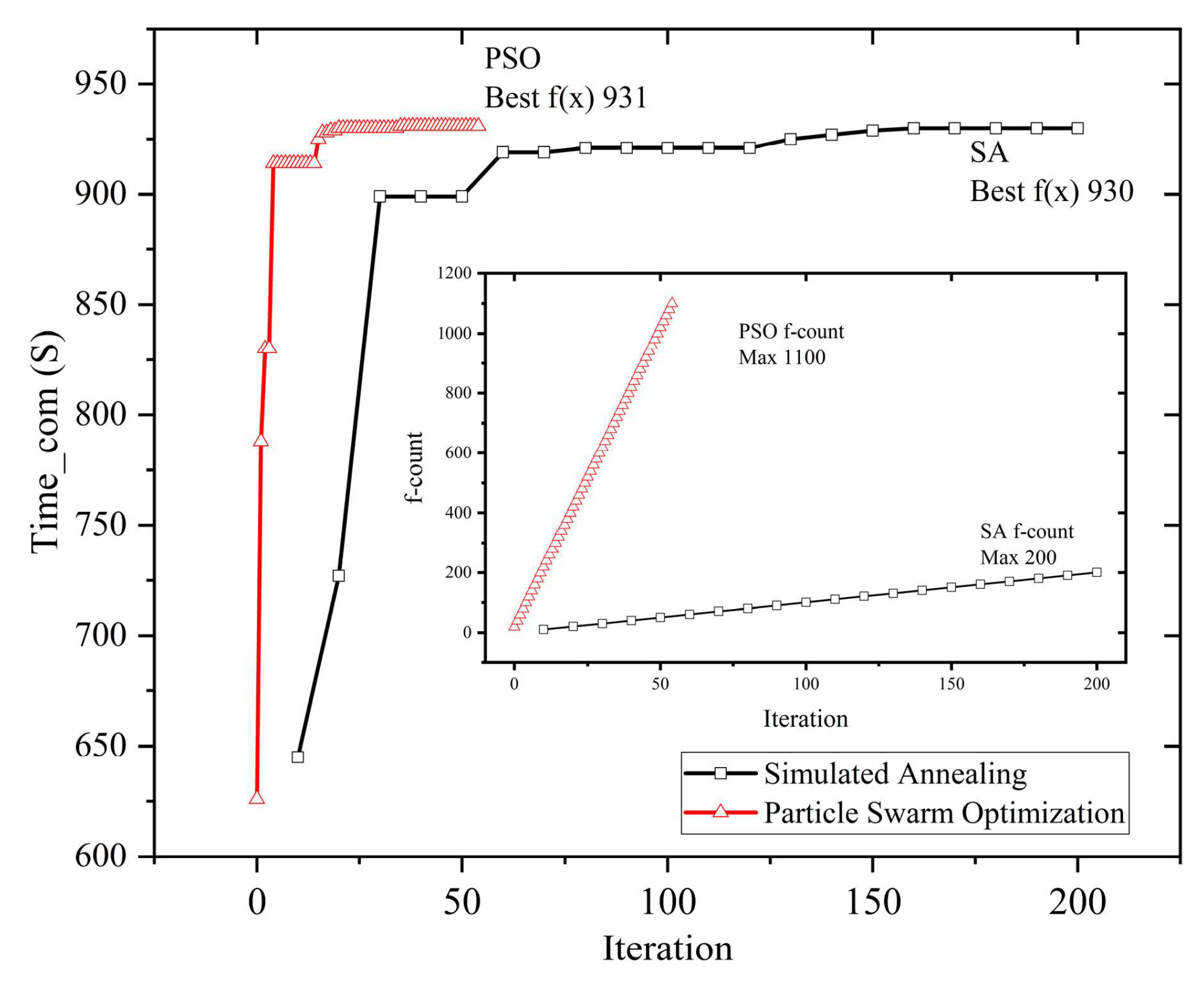
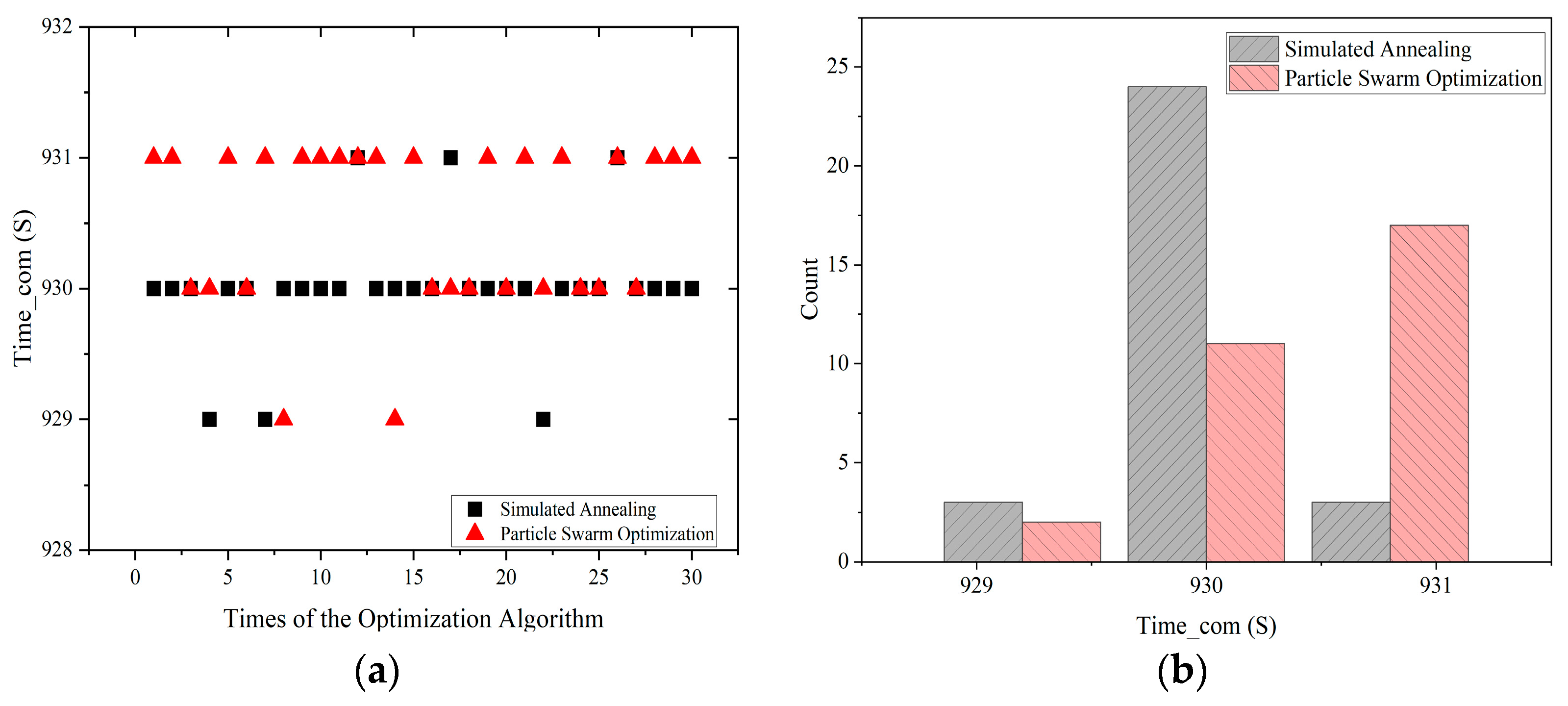
Different SLR Stations	Improved Simulated Annealing		Particle Swarm Optimization		Conventional Iterative Traverse Method
	${\mathit{T}\mathit{i}\mathit{m}\mathit{e}}_{\mathit{c}\mathit{o}\mathit{m}}\left(\mathit{S}\right)$	$({\mathit{i}}_{\mathit{c}\mathit{o}\mathit{m}},{\mathsf{\Omega }}_{\mathit{c}\mathit{o}\mathit{m}})$	${\mathit{T}\mathit{i}\mathit{m}\mathit{e}}_{\mathit{c}\mathit{o}\mathit{m}}\left(\mathit{S}\right)$	$({\mathit{i}}_{\mathit{c}\mathit{o}\mathit{m}},{\mathsf{\Omega }}_{\mathit{c}\mathit{o}\mathit{m}})$	${\mathit{T}\mathit{i}\mathit{m}\mathit{e}}_{\mathit{c}\mathit{o}\mathit{m}}\left(\mathit{S}\right)$	$({\mathit{i}}_{\mathit{c}\mathit{o}\mathit{m}},{\mathsf{\Omega }}_{\mathit{c}\mathit{o}\mathit{m}})$
CC WH (R = 7000 km)	354	(48.0322, 27.5481)	354	(47.9924, 27.6567)	353	(48.06, 27.40)
CC WH (R = 8000 km)	930	(48.0299, 27.5674)	931	(48.0157, 27.6326)	930	(48.16, 27.55)
CC WH (R = 9000 km)	1463	(48.0008, 27.6434)	1463	(48.0612, 27.7097)	1463	(48.03, 27.51)
CC WH (R = 10,000 km)	2009	(48.0461, 27.6291)	2009	(48.0852, 27.6313)	2009	(48.05, 27.57)

and

Table 2. The computation time of the improved simulated annealing, particle swarm optimization algorithms, and the conventional iterative traverse method.

Different SLR Stations	Improved Simulated Annealing		Particle Swarm Optimization		Conventional Iterative Traverse Method
	${\mathit{T}\mathit{i}\mathit{m}\mathit{e}}_{\mathit{c}\mathit{o}\mathit{m}}\left(\mathit{S}\right)$	Computation Time (min)	${\mathit{T}\mathit{i}\mathit{m}\mathit{e}}_{\mathit{c}\mathit{o}\mathit{m}}\left(\mathit{S}\right)$	Computation Time (min)	${\mathit{T}\mathit{i}\mathit{m}\mathit{e}}_{\mathit{c}\mathit{o}\mathit{m}}\left(\mathit{S}\right)$	Computation Time (min)
CC WH (R = 7000 km)	354	1.503	354	10.009	353	20.213
CC WH (R = 8000 km)	930	1.761	931	11.422	930	22.057
CC WH (R = 9000 km)	1463	2.165	1463	13.053	1463	26.895
CC WH (R = 10,000 km)	2009	2.941	2009	15.728	2009	31.804

. Table 1 shows a high level of precision between the results produced by the improved simulated annealing algorithm and those from the conventional iterative traversal method. It also achieves a similar level of accuracy compared to the particle swarm algorithm, with a discrepancy of no more than 2 s in the optimal common-view duration. Table 2 shows that increasing the orbit radius leads to longer computational times for all three methods, but the improved simulated annealing algorithm operates more than 20 times faster than the conventional iterative traverse method. Additionally, compared to the particle swarm algorithm, the improved simulated annealing algorithm significantly reduces the computation time required to reach the optimal solution, resulting in decreased computational costs, enhanced efficiency, and improved performance. Figure 9 displays the optimized satellite trajectories between two SLR stations at an orbit radius of 8000 km, obtained through the optimization process using the improved simulated annealing algorithm.

Selection of the Jason-3 and Ajisai satellites was based on existing Time Transfer by Laser Link missions and potential future LTT tasks. For the same timestamp of 1 August 2023, 00:00:00, utilizing their satellite orbit predictions (CPF), the common-view times between the Changchun and Wuhan stations within a 10-day timeframe were computed. An improved simulated annealing algorithm was employed to optimize the satellite orbits in the common-view mode at the same orbital altitude and date. The results of this optimization, compared to the existing satellite orbits, are presented in

Table 3. Comparison of common-view duration results between some existing satellite orbits and optimized satellite orbits.

Altitude (km)	Satellite	Inclination (Degrees)	10 Days ${\mathit{T}\mathit{i}\mathit{m}\mathit{e}}_{\mathit{c}\mathit{o}\mathit{m}}\left(\mathit{h}\right)$	$\mathbf{Optimized} ({\mathit{i}}_{\mathit{c}\mathit{o}\mathit{m}},{\mathsf{\Omega }}_{\mathit{c}\mathit{o}\mathit{m}})$	10 Days ${\mathit{T}\mathit{i}\mathit{m}\mathit{e}}_{\mathit{c}\mathit{o}\mathit{m}}\left(\mathit{h}\right)$	Multiplier
1336	Jason-3	66	3.05	48.101305, 27.578522	27.313	8.955
1488	Ajisai	50	8.792	48.043023, 27.651744	29.339	3.337

. Jason-3, part of the U.S.-European satellite mission series, primarily traverses the airspace of the United States and Europe, while Ajisai, a Japanese satellite, predominantly orbits over Japan. Table 3 shows that for the common-view model between the Changchun and Wuhan stations, Ajisai has a longer common-view duration compared to Jason-3. Furthermore, through optimized satellite orbit designs, the maximum continuous common-view duration over a period of 10 days was extended approximately 8.955 times for Jason-3 and 3.337 times for Ajisai.

4.3. The Improved Simulated Annealing Algorithm Optimizes Satellite Orbits in a Multi-Station Common-View Model

The simulated annealing algorithm was used to solve the optimal satellite orbit problem in the common-view mode, taking into account parameters such as minimum orbit altitude, in-orbit flight life, and orbital period. The initial UTC time was set to 1 August 2023 at 00:00:00. The orbit radius was fixed at 12,792.55 km, with a 4-h orbital period that aligns with a divisor of Earth’s rotational cycle.

Based on the quarterly global performance report provided by the International Laser Ranging Service (ILRS) website, SLR station selections were selected. Initially, ten ground stations for SLR were chosen to simulate satellite orbit optimization within the Asia-Pacific region’s common-view mode. Subsequently, ten SLR ground stations were selected to optimize satellite orbits within the shared observation model spanning Asia and Europe.

Table 4. Selected Stations within the Asia-Pacific SLR Station Network.

SLR Station	Coordinates X, Y, Z (km)	Latitude	Longitude	Height
7237 Changchun	−2674.387, 3757.189, 4391.508	43.7905°N	125.4434°E	274.900
7396 Wuhan	−2279.756, 5004.737, 3219.791	30.515667°N	114.490167°E	76.7
7821 Shanghai	−2830.744, 4676.580, 3275.072	31.0961°N	121.1866°E	99.961
7249 Beijing	−2148.760, 4426.759, 4044.509	39.6069°N	115.8920°E	82.300
7819 Kunming	−1281.301, 5640.724, 2682.905	25.0298°N	102.7977°E	1987.05
7306 Tsukuba	−3961.641, 3308.774, 3308.774	36.0675°N	140.1313°E	68.21
7838 Simosato	−3822.388, 3699.363, 3507.573	33.5777°N	135.9370°E	62.44
7394 Sejong	−3110.108, 4082.170, 3774.911	36.520991°N	127.302913°E	176.415
7090 Yarragadee	−2389.008, 5043.332, −3078.526	29.0464°S	115.3467°E	244
7825 Mt. Stromlo	−4467.064, 2683.034, −3667.007	35.3161°S	149.0099°E	805.0

displays the coordinates, latitude, longitude, and elevation information for the selected stations within the Asia-Pacific region’s SLR station network, while

Table 5. Selected Stations within the European-to-Asian SLR Station Network.

SLR Station	Coordinates X, Y, Z (km)	Latitude	Longitude	Height
7237 Changchun	−2674.387, 3757.189, 4391.508	43.7905°N	125.4434°E	274.9
7396 Wuhan	−2279.756, 5004.737, 3219.791	30.515667°N	114.490167°E	76.7
7821 Shanghai	−2830.744, 4676.580, 3275.072	31.0961°N	121.1866°E	99.9
7249 Beijing	−2148.760, 4426.759, 4044.509	39.6069°N	115.8920°E	82.3
7819 Kunming	−1281.301, 5640.724, 2682.905	25.0298°N	102.7977°E	1987.1
7845 Grasse	4581.692, 556.196, 4389.355	43.7546°N	6.9216°E	1323.1
7840 Herstmonceux	4033.463, 23.662, 4924.305	50.8674°N	0.3361°E	75.0
7827 WettzellSOSW	4075.531, 931.781, 4801.619	49.1449402°N	12.8781000°E	663.1
8834 Wettzell	4075.576, 931.785, 4801.583	49.1444°N	12.8780°E	665.0
7839 Graz	4194.426, 1162.694, 4647.246	47.0671°N	15.4933°E	539.4

presents the corresponding station details for the European-to-Asian region SLR station network.

During the optimization process, it was a requirement that any pair of the selected ten SLR stations could establish common-view, ensuring a minimum common-view duration of no less than 2 min for each pair. Additionally, the objective was to maximize the total common-view duration across all possible pairs of stations. The resulting common-view durations between pairs of SLR station networks within the Asia-Pacific region and those across Europe to Asia SLR station networks are presented in Figure 10, respectively. From Figure 10, it is evident that the minimum common-view duration between any two stations within the Asia-Pacific region is 6.183 min, and is especially longer for closer sites, reaching a maximum of 60.633 min. Between any two stations spanning Europe to Asia, the minimum common-view duration is 5.583 min, extending up to a maximum of 61.75 min. Figure 11 portrays the optimized satellite trajectories: Figure 11a displays the optimal orbits for the ten SLR stations within the Asia-Pacific region, while Figure 11b delineates the optimal orbits for the ten SLR stations spanning the Europe to Asia region. From Figure 11, it is evident that the optimized optimal satellite orbits, refined using an improved simulated annealing algorithm, traverse across various stations within the Asia-Pacific region and between Europe and Asia. This achieved the precise optimization of satellite orbits for the multi-region common-view SLR station network employed in Laser Time Transfer.

5. Conclusions

This paper focuses on optimizing satellite trajectory and designing orbits in a common-view model for networks of multiple SLR stations. The goal is to improve laser time transfer and signal transmission from ground laser stations by maximizing the longest feasible common-view time intervals. Addressing this, we introduce an improved simulated annealing algorithm designed to optimize satellite orbit trajectories. Anchored in the ground-to-ground laser time transfer principle and satellite visibility to design system model, the algorithm aims to determine optimal satellite orbits among multiple SLR station networks with a common-view perspective. Initial analysis establishes minimum satellite orbit altitudes for varying SLR station distances, based on this, conducted two sets of simulations. Comparative simulations against conventional iterative traverse and particle swarm methods reveal a substantial 10 to 20-fold reduction in computation time with an rms value of 0.45486 over 30 runs, ensuring convergence, global optimality, and stability. Selecting five satellites, including HY-2C, Sentinel-6A, LARES, Ajisai, and LAGEOS-2, their common-view times were compared with the optimized satellite orbits. Post-optimization, the common-view times at the same altitude exhibited enhancements ranging from 2.97 to 12.815 times. Further simulations optimize satellite orbits among 10 stations in the Asia-Pacific and Europe-to-Asia regions, resulting in a common-view model between all 45 station pairs in each region. Evaluation primarily focuses on common-view times among any two stations within this network, revealing intervals of 6.183 to 60.623 min in the Asia-Pacific and 5.583 to 61.75 min in the Europe-to-Asia regions. Ultimately, the refined satellite orbits foster mutual common viewing among multi-SLR station networks, significantly maximizing overall common-view durations.

To achieve longer common-view durations between stations, an ideal satellite orbit model algorithm can be created from the perspective of multiple stations. This will provide a wider range of options for selecting satellite orbit configurations during launches, simplifying time and signal transmission and improving the precision of inter-station time and signal transfer. The findings of this paper can serve as reference factors in the selection of SLR station locations, ultimately contributing to the development of a global laser ranging station network. By integrating these insights, laser time transmission and space laser communications can be achieved with higher accuracy and faster transmission rates, allowing for a more detailed design of satellite constellations.