Atmospheric Modulation Transfer Function Calculation and Error Evaluation for the Panchromatic Band of the Gaofen-2 Satellite
Abstract
1. Introduction
2. Study Area and Datasets
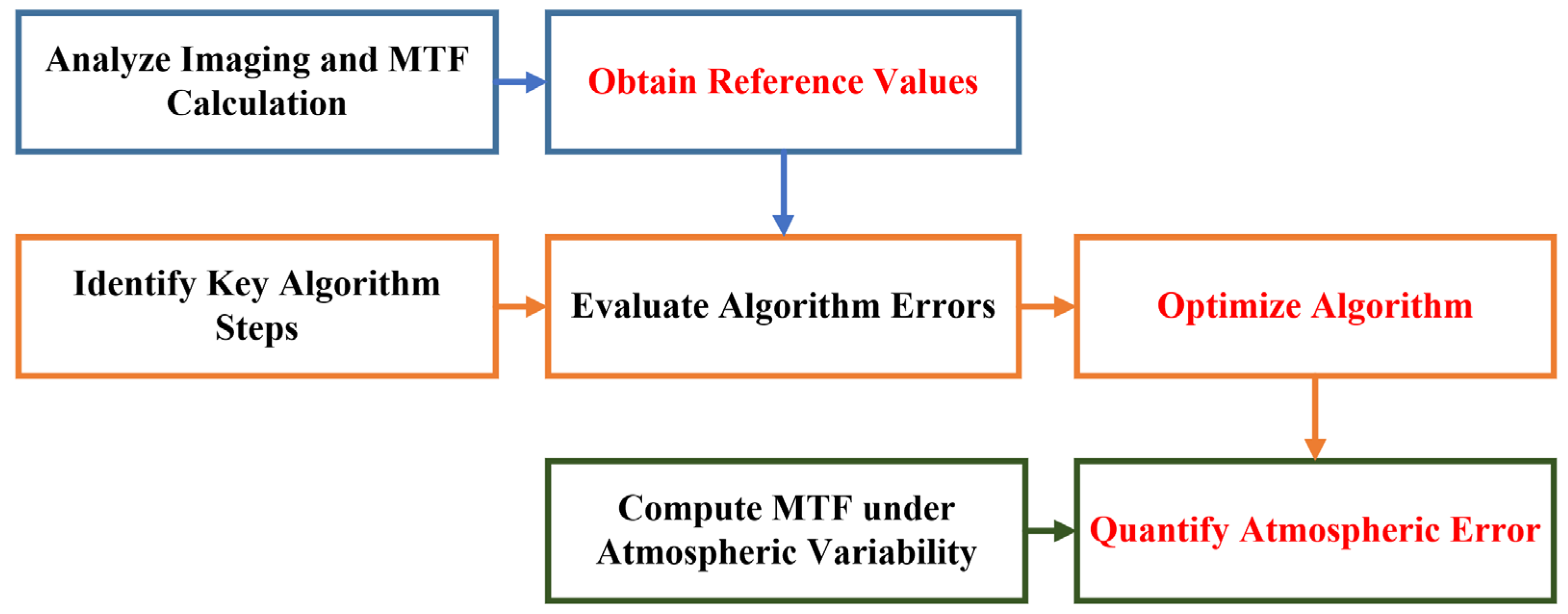
3. Algorithm
3.1. Estimation of Satellite Imaging System MTF
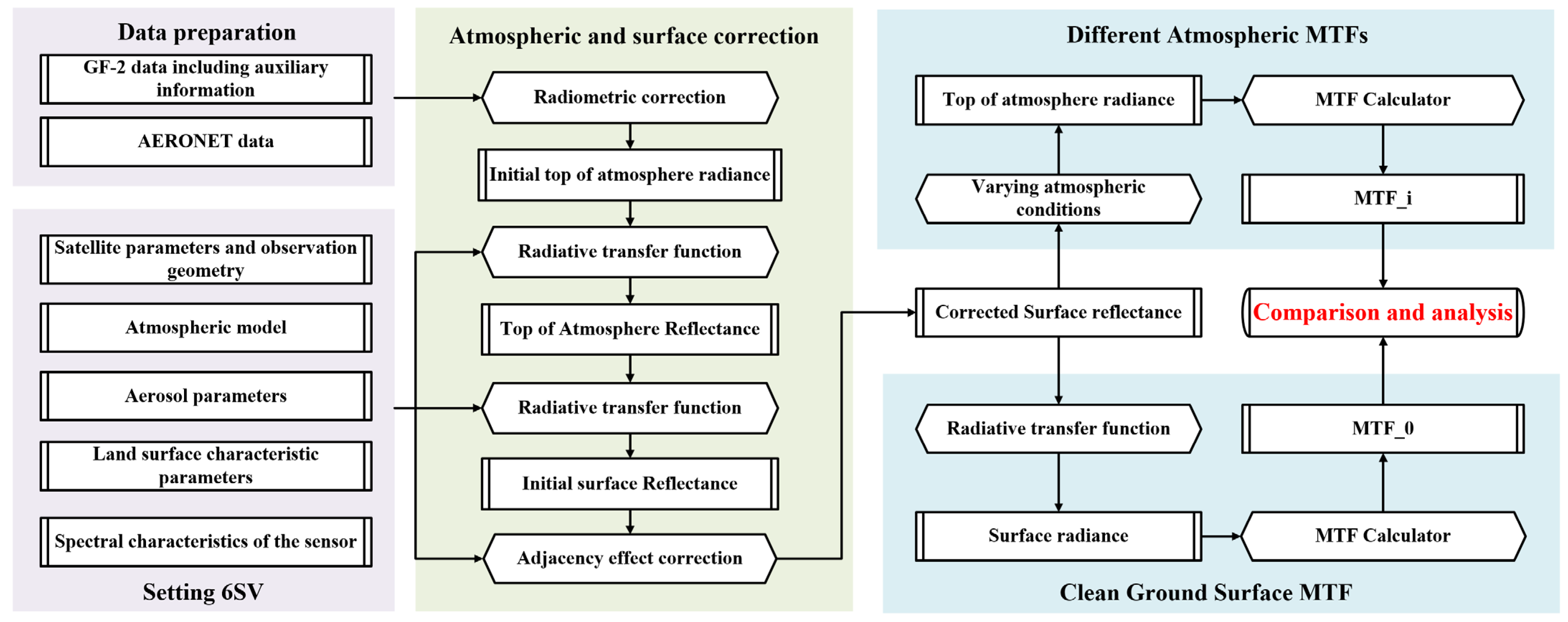
3.2. Estimation of Atmospheric Scattering and Absorption MTF
4. Results
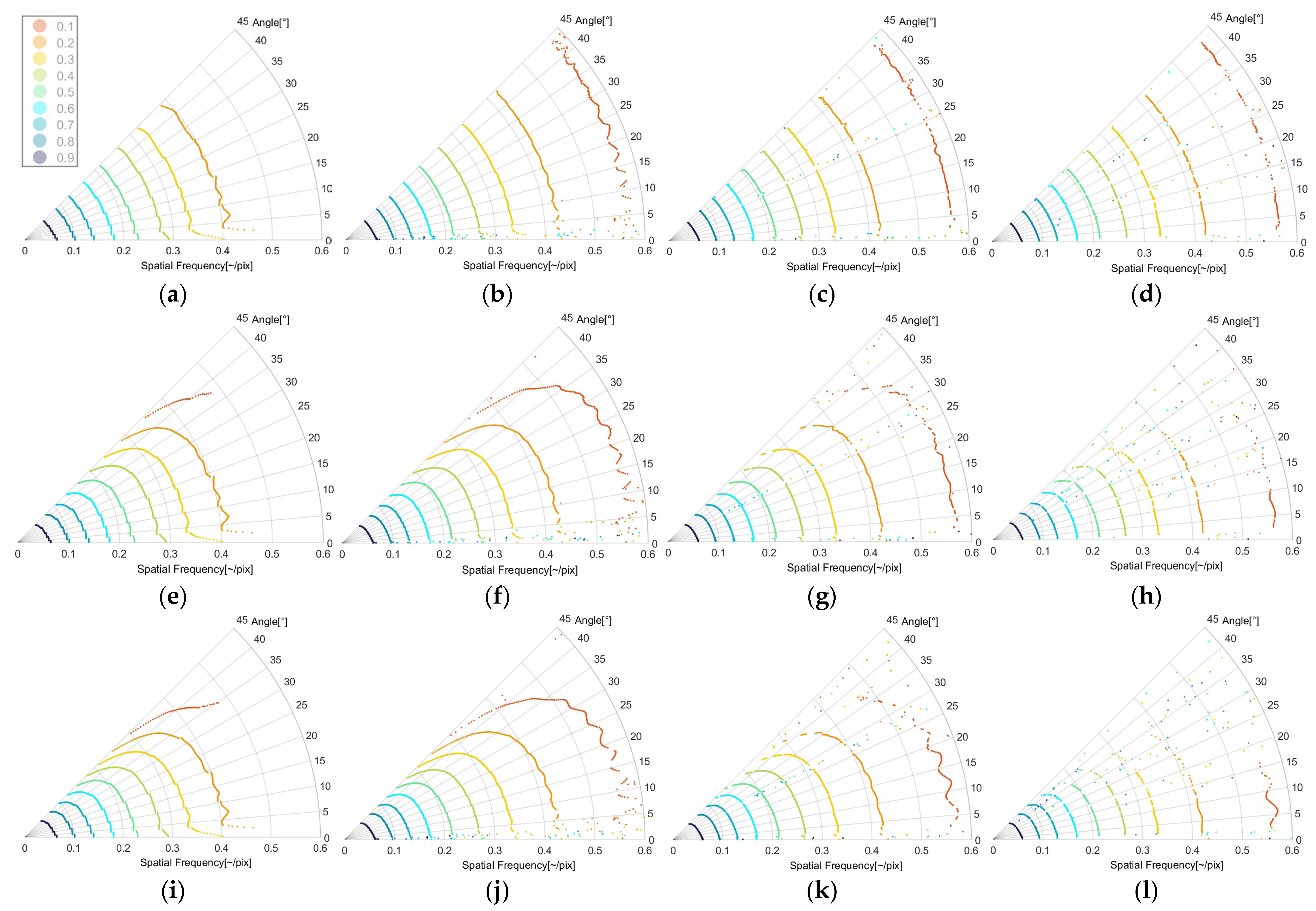
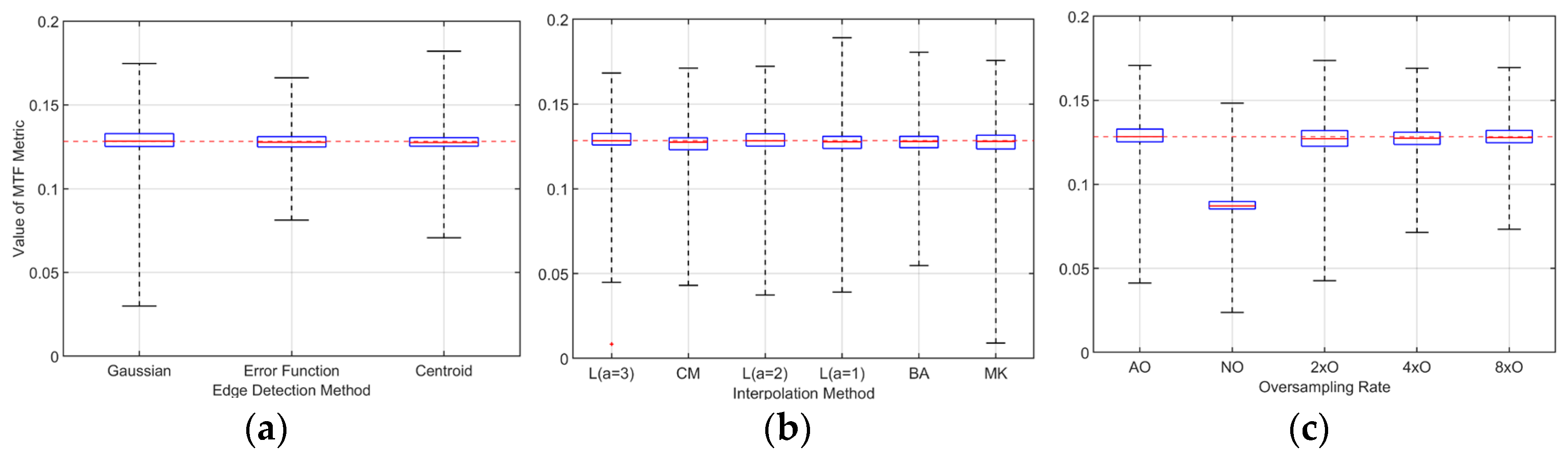
4.1. Process Analysis of Slanted-Edge Method
4.1.1. Edge Detection Method
4.1.2. Oversampling Rate
4.1.3. Interpolation Method
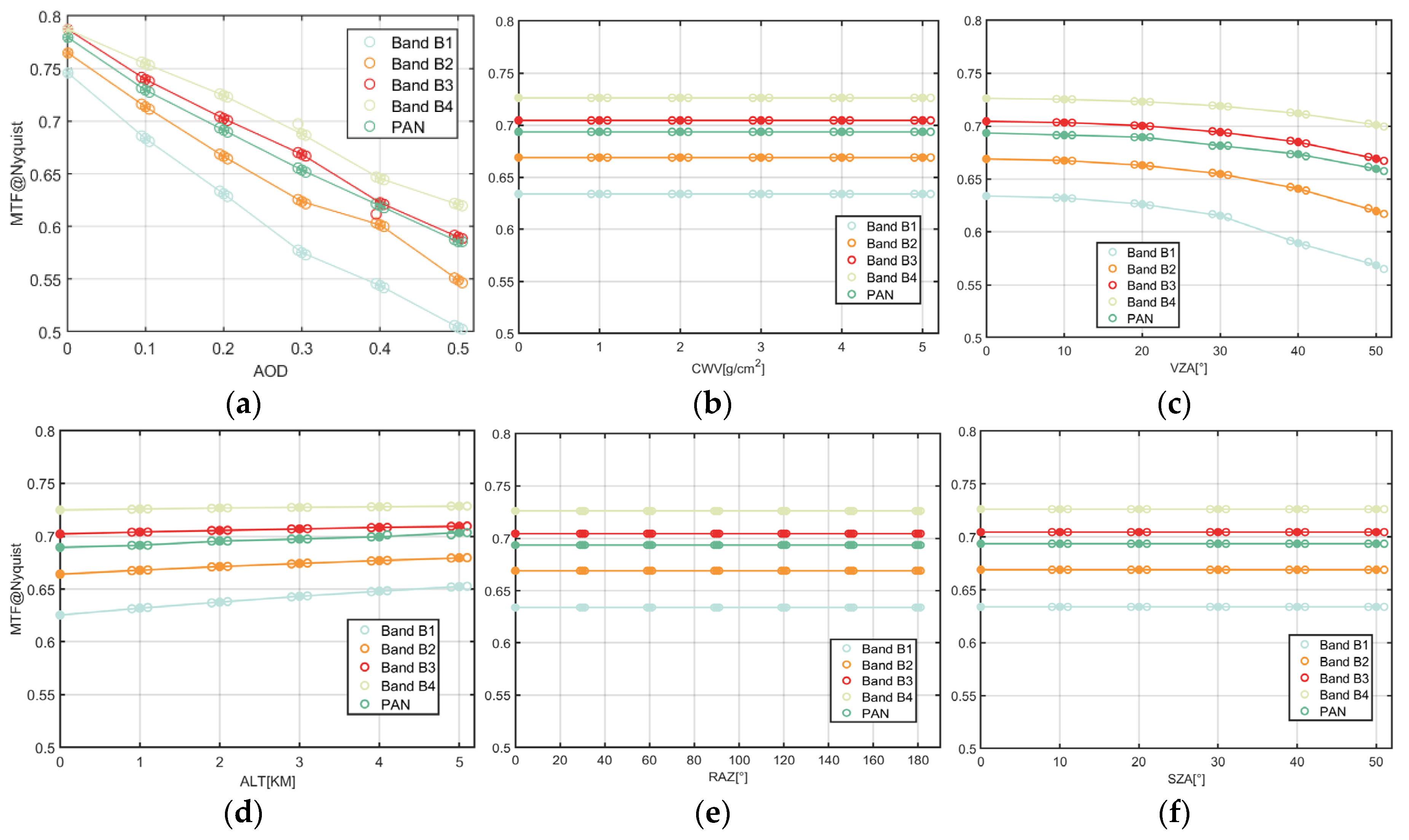
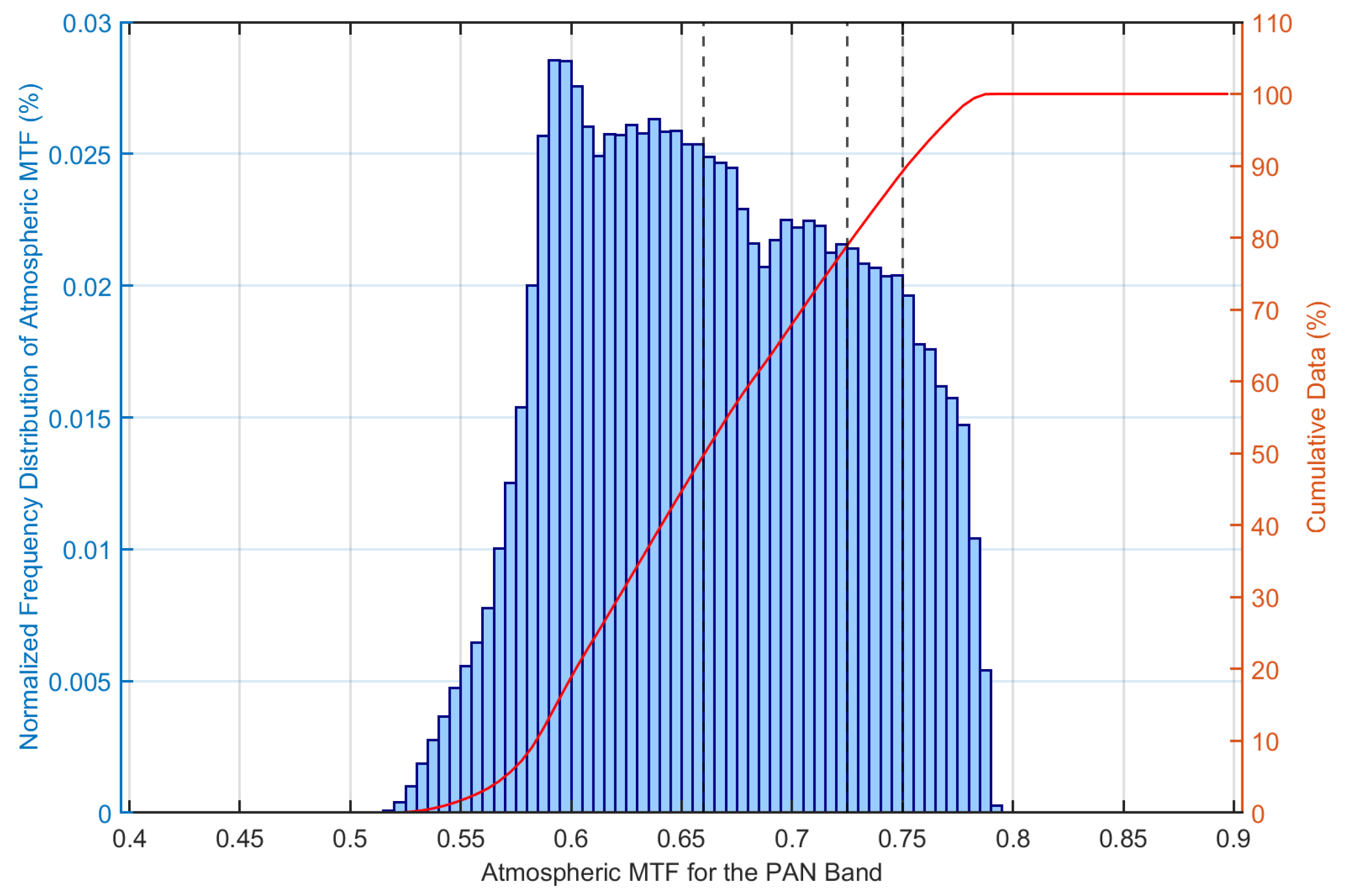
4.2. Analysis of Atmospheric Scattering and Absorption MTF
5. Discussion
5.1. Error Analysis of Slanted-Edge Method
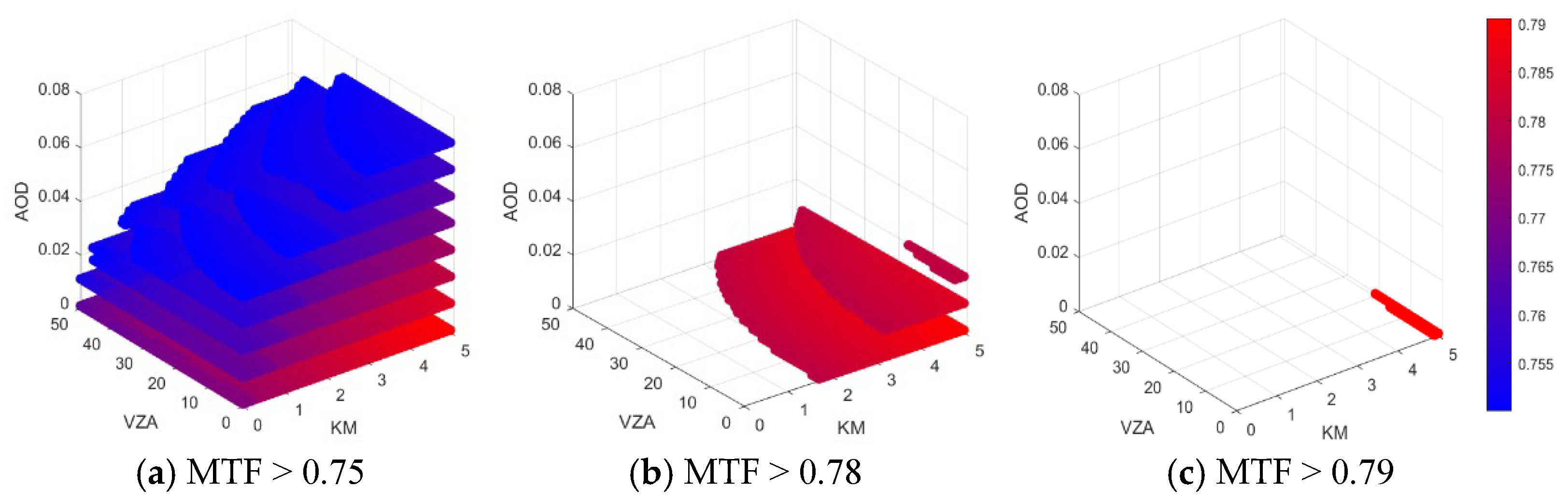
5.2. Analysis of Atmospheric Impact Factors
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liao, J.; Gao, X. Dynamic MTF analysis and calculation of aerial camera. In Proceedings of the 5th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Optoelectronic Materials and Devices for Detector, Imager, Display, and Energy Conversion Technology, Dalian, China, 26–29 April 2010; Volume 7658, pp. 288–294. [Google Scholar]
- Leger, D.; Viallefont, F.; Hillairet, E.; Meygret, A. In-flight refocusing and MTF assessment of SPOT5 HRG and HRS cameras. In Proceedings of the International Symposium on Remote Sensing: Sensors, Systems, and Next-Generation Satellites VI, Crete, Greece, 23–27 September 2002; Volume 4881, pp. 224–231. [Google Scholar] [CrossRef]
- Leger, D.; Viallefont, F.; Deliot, P.; Valorge, C. On-Orbit MTF Assessment of Satellite Cameras; Taylor & Francis Group: London, UK, 2004. [Google Scholar]
- Bensebaa, K.; Banon, G.J.F.; Fonseca, L. On orbit spatial resolution estimation of CBERS-I CCD camera. In Proceedings of the Third International Conference on Image and Graphics (ICIG’04), Hong Kong, China, 18–20 December 2004; pp. 576–579. [Google Scholar] [CrossRef]
- Bensebaa, K.; Banon, G.J.; Fonseca, L.M.; Erthal, G. On-orbit spatial resolution estimation of CBERS-2 imaging system using ideal edge target. In Signal Processing for Image Enhancement and Multimedia Processing; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; pp. 37–48. [Google Scholar] [CrossRef]
- Reulke, R.; Becker, S.; Haala, N.; Tempelmann, U. Determination and improvement of spatial resolution of the CCD-line-scanner system ADS40. ISPRS J. Photogramm. Remote Sens. 2006, 60, 81–90. [Google Scholar] [CrossRef]
- Choi, T. IKONOS Satellite on Orbit Modulation Transfer Function (MTF) Measurement Using Edge and Pulse Method. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2002. [Google Scholar]
- Rangaswamy, M.K. Quickbird II: Two-Dimensional On-Orbit Modulation Transfer Function Analysis Using Convex Mirror Array. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2003. [Google Scholar]
- Kohm, K.; Louis, S. Modulation transfer function measurement method and results for the Orbview-3 high resolution imaging satellite. Proc. ISPRS 2004, 36, 12–23. [Google Scholar]
- Tadono, T.; Shimada, M.; Watanabe, M.; Mukaida, A.; Kawamoto, S.; Imoto, N.; Yamashita, J. Initial results of calibration and validation for ALOS optical sensors. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 1643–1646. [Google Scholar] [CrossRef]
- Jeong-Heon, S.; Dong-Han, L.; Sun-Gu, L.; Du-Ceon, S.; Soo-Young, P.; Hyo-Suk, L.; Hong-Yul, P. Modulation Transfer Function (MTF) Measurement For 1 m High Resolution Satellite Images such as KOMPSAT-2 Using Edge Function. In Proceedings of the KSRS Conference, Seoul, Republic of Korea, 29 July 2005; pp. 482–484. [Google Scholar]
- Pagnutti, M.; Blonski, S.; Cramer, M.; Helder, D.; Holekamp, K.; Honkavaara, E.; Ryan, R. Targets, methods, and sites for assessing the in-flight spatial resolution of electro-optical data products. Can. J. Remote Sens. 2010, 36, 583–601. [Google Scholar] [CrossRef]
- Wahballah, W.A.; El-Tohamy, F.; Bazan, T.M. A Survey and Trade-off-Study for Optical Remote Sensing Satellite Camera Design. In Proceedings of the 2020 12th International Conference on Electrical Engineering (ICEENG), Cairo, Egypt, 7–9 July 2020; pp. 298–305. [Google Scholar] [CrossRef]
- Kameche, M.; Benmostefa, S. In-flight MTF stability assessment of ALSAT-2A satellite. Adv. Space Res. 2016, 58, 117–130. [Google Scholar] [CrossRef]
- Masaoka, K.; Yamashita, T.; Nishida, Y.; Sugawara, M. Modified slanted-edge method and multidirectional modulation transfer function estimation. Opt. Express 2014, 22, 6040–6046. [Google Scholar] [CrossRef]
- Masaoka, K. Accuracy and precision of edge-based modulation transfer function measurement for sampled imaging systems. IEEE Access 2018, 6, 41079–41086. [Google Scholar] [CrossRef]
- Masaoka, K. Edge-based modulation transfer function measurement method using a variable oversampling ratio. Opt. Express 2021, 29, 37628–37638. [Google Scholar] [CrossRef]
- Greer, P.B.; Van Doorn, T. Evaluation of an algorithm for the assessment of the MTF using an edge method. Med. Phys. 2000, 27, 2048–2059. [Google Scholar] [CrossRef]
- Viallefont-Robinet, F.; Helder, D.; Fraisse, R.; Newbury, A.; van den Bergh, F.; Lee, D.; Saunier, S. Comparison of MTF measurements using edge method: Towards reference data set. Opt. Express 2018, 26, 33625–33648. [Google Scholar] [CrossRef]
- Lutomirski, R.; Yura, H. Wave structure function and mutual coherence function of an optical wave in a turbulent atmosphere. J. Opt. Soc. Am. JOSA 1971, 61, 482–487. [Google Scholar] [CrossRef]
- Kopeika, N. Spatial-frequency dependence of scattered background light: The atmospheric modulation transfer function resulting from aerosols. J. Opt. Soc. Am. JOSA 1982, 72, 548–551. [Google Scholar] [CrossRef]
- Sadot, D.; Kopeika, N. Imaging through the atmosphere: Practical instrumentation-based theory and verification of aerosol modulation transfer function. J. Opt. Soc. Am. JOSA 1993, 10, 172–179. [Google Scholar] [CrossRef]
- LeMaster, D.A.; Eismann, M.T. Impact of atmospheric aerosols on long range image quality. In Proceedings of the Infrared Imaging Systems: Design, Analysis, Modeling, and Testing XXIII, Baltimore, MD, USA, 23–27 April 2012; Volume 8355, pp. 102–111. [Google Scholar] [CrossRef]
- Eismann, M.T.; LeMaster, D.A. Aerosol modulation transfer function model for passive long-range imaging over a nonuniform atmospheric path. Opt. Eng. 2013, 52, 046201. [Google Scholar] [CrossRef]
- Wells, W.H. Loss of Resolution in Water as a Result of Multiple Small-Angle Scattering. J. Opt. Soc. Am. 1969, 59, 686–691. [Google Scholar] [CrossRef]
- Steve, B.; Ronald, D.; Gerald, H.; Norman, S.K.; Arkadi, Z. Effects of aerosol modulation transfer function on target identification. Opt. Eng. 2020, 59, 073103. [Google Scholar]
- Norman, S.K.; Arkadi, Z.; Yitzhak, Y. Aerosol MTF revisited. In Proceedings of the Infrared Imaging Systems: Design, Analysis, Modeling, and Testing XXV, Baltimore, MD, USA, 5–9 May 2014; Volume 9071, pp. 409–422. [Google Scholar] [CrossRef]
- Li, C.; Tang, L.; Ma, L.; Zhou, Y.; Gao, C.; Wang, N.; Li, X.; Wang, X.; Zhu, X. Comprehensive calibration and validation site for information remote sensing. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Berlin, Germany, 11–15 May 2015; Volume XL-7/W3, pp. 1233–1240. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, C.; Tang, L.; Ma, L.; Wang, Q.; Liu, Q. A Permanent bar pattern distributed target for microwave image resolution analysis. IEEE Geosci. Remote Sens. Lett. 2017, 14, 164–168. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.; Slutsker, I.a.; Tanré, D.; Buis, J.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.; Nakajima, T. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Li, C.; Ma, L.; Tang, L.; Gao, C.; Qian, Y.; Wang, N.; Wang, X. A comprehensive calibration site for high resolution remote sensors dedicated to quantitative remote sensing and its applications. Natl. Remote Sens. Bull. 2021, 25, 198–219. [Google Scholar] [CrossRef]
- ISO 12233:2023; Photography–Electronic Still Picture Imaging–Resolution and Spatial Frequency Responses. International Organization for Standardization: Geneva, Switzerland, 2023.
- Abolghasemi, M.; Abbasi-Moghadam, D. Design and performance evaluation of the imaging payload for a remote sensing satellite. Opt. Laser Technol. 2012, 44, 2418–2426. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, Y.; Deng, Q.; Cheng, Z.; Zhu, B. Modeling and Simulation of Electro-Optical Imaging Systems Based on MTF. Laser Infrared 2015, 45, 549–554. [Google Scholar]
- Yang, B.; Cao, D. Technological Innovations and Insights of the “Gaofen-2” Satellite High-Resolution Camera. Aerosp. Return Remote Sens. 2015, 36, 10–15. [Google Scholar]
- Chazallet, F.; Glasser, J. Theoretical bases and measurement of the MTF of integrated image sensors. In Proceedings of the Image Quality: An Overview, Arlington, VA, USA, 10–12 April 1985; Volume 0549, pp. 131–144. [Google Scholar] [CrossRef]
- Li, X.; Jiang, X.; Zhou, C.; Gao, C.; Xi, X. An analysis of the knife-edge method for on-orbit MTF estimation of optical sensors. Int. J. Remote Sens. 2010, 31, 4995–5010. [Google Scholar] [CrossRef]
- Kotchenova, S.Y.; Vermote, E.F.; Matarrese, R.; Klemm, F.J. Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data. Part I: Path radiance. Appl. Opt. 2006, 45, 6762–6774. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcette, J.-J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Richter, R.; Bachmann, M.; Dorigo, W.; Muller, A. Influence of the Adjacency Effect on Ground Reflectance Measurements. IEEE Geosci. Remote Sens. Lett. 2006, 3, 565–569. [Google Scholar] [CrossRef]
- Pan, T. Technical characteristics of the Gaofen-2 Satellite. Aerospace China. 2015, 1, 3–9. [Google Scholar]
- Wu, Y.; Xu, W.; Piao, Y.; Yue, W. Analysis of edge method accuracy and practical multidirectional modulation transfer function measurement. Appl. Sci. 2022, 12, 12748. [Google Scholar] [CrossRef]
- Haefner, D.P. MTF measurements, identifying bias, and estimating uncertainty. In Proceedings of the Infrared Imaging Systems: Design, Analysis, Modeling, and Testing XXIX, Orlando, FL, USA, 17–18 April 2018; pp. 54–68. [Google Scholar]
- Arkadi, Z.; Ephim, G.; Shlomi, A.; Norman, S.K. Kolmogorov and non-Kolmogorov turbulence and its effects on optical communication links. In Proceedings of the Free-Space Laser Communications VII, San Diego, CA, USA, 26–30 August 2007; Volume 6709, pp. 173–184. [Google Scholar] [CrossRef]





| Data Sources | Parameters | Value |
|---|---|---|
| GF-2 satellite parameters | Solar zenith angle/SZA (°) | 54.25 |
| Solar azimuth angle (°) | 163.12 | |
| Viewing zenith angle/VZA (°) | 2.37 | |
| Viewing azimuth angle (°) | 288.13 | |
| Imaging time (UTC) | 03:29:41 | |
| AERONET ground-based observation | Aerosol optical depth/AOD | 0.1943 |
| Column water vapor/CWV (g/cm2) | 0.4071 | |
| Ozone/O3 (atm-cm) | 0.3003 | |
| Altitude of target/ALT (km) | 1.314 |
| Parameter | Value of Each Channel | ||||
|---|---|---|---|---|---|
| Diffraction wavelength/μm | PAN: 0.65 | B1: 0.49 | B2: 0.55 | B3: 0.67 | B4: 0.83 |
| Sampling pixel size/μm | 10 | 40 | |||
| WFE/λrms | 0.13 | ||||
| F-number | 15 | ||||
| Focal length of optical system/m | 7.8 | ||||
| Optical system aperture/mm | 530 | ||||
| Field of view/° | 2.1 | ||||
| Interpolation Method | MTF (Nyquist) for Gaussian Fitting Method | MTF (Nyquist) for Fitting Error Function | MTF (Nyquist) for Centroid Detection Method |
|---|---|---|---|
| Lanczos (a = 3) | 0.1283 * | 0.1277 | 0.1275 |
| Continuum magic | 0.1275 | 0.1242 | 0.1256 |
| Lanczos (a = 2) | 0.1283 | 0.1276 | 0.1274 |
| Lanczos (a = 1) | 0.1277 | 0.1262 | 0.1268 |
| Bin average | 0.1279 | 0.1274 | 0.1274 |
| Mitchell kernel | 0.1280 | 0.1261 | 0.1266 |
| Parameter Type | Value Ranges |
|---|---|
| Satellite Spectral Bands (nm) | PAN (450–900), B1 (450–520), B2 (520–600), B3 (630–690), and B4 (770–890) |
| SZA (°) | 0:10:50 with a deviation of ±1 |
| VZA (°) | 0:10:50 with a deviation of ±1 |
| RAZ (°) | 0:10:180 with a deviation of ±1 |
| AOD | 0:0.1:0.5 with a deviation of ±0.005 |
| CWV (g/cm2) | 0:1:5 with a deviation of ±0.1 |
| Altitude/ALT (km) | 0:1:5 with a deviation of ±0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Liang, M.; Ma, Y.; Zheng, Y.; Li, Z.; Chen, Z. Atmospheric Modulation Transfer Function Calculation and Error Evaluation for the Panchromatic Band of the Gaofen-2 Satellite. Remote Sens. 2024, 16, 4676. https://doi.org/10.3390/rs16244676
Li Z, Liang M, Ma Y, Zheng Y, Li Z, Chen Z. Atmospheric Modulation Transfer Function Calculation and Error Evaluation for the Panchromatic Band of the Gaofen-2 Satellite. Remote Sensing. 2024; 16(24):4676. https://doi.org/10.3390/rs16244676
Chicago/Turabian StyleLi, Zhengqiang, Mingjun Liang, Yan Ma, Yang Zheng, Zhaozhou Li, and Zhenting Chen. 2024. "Atmospheric Modulation Transfer Function Calculation and Error Evaluation for the Panchromatic Band of the Gaofen-2 Satellite" Remote Sensing 16, no. 24: 4676. https://doi.org/10.3390/rs16244676
APA StyleLi, Z., Liang, M., Ma, Y., Zheng, Y., Li, Z., & Chen, Z. (2024). Atmospheric Modulation Transfer Function Calculation and Error Evaluation for the Panchromatic Band of the Gaofen-2 Satellite. Remote Sensing, 16(24), 4676. https://doi.org/10.3390/rs16244676







