Abstract
Specific emitter identification (SEI) is a promising physical-layer authentication technique that serves as a crucial complement to upper-layer authentication mechanisms. SEI capitalizes on the inherent radio frequency fingerprints stemming from circuit discrepancies, which are intrinsic hardware properties and challenging to counterfeit. Recently, various deep learning (DL)-based SEI methods have been proposed, achieving outstanding performance. However, collecting and annotating substantial data for novel or unknown radiation sources is not only time-consuming but also cost-intensive. To address this issue, this paper proposes a few-shot (FS) metric learning-based time-frequency fusion network. To enhance the discriminative capability for radiation source signals, the model employs a convolutional block attention module (CBAM) and feature transformation to effectively fuse the raw signal’s time domain and time-frequency domain representations. Furthermore, to improve the extraction of discriminative features under FS scenarios, the proxy-anchor loss and center loss are introduced to reinforce intra-class compactness and inter-class separability. Experiments on the ADS-B and Wi-Fi datasets demonstrate that the proposed TFAF-Net consistently outperforms existing models in FS-SEI tasks. On the ADS-B dataset, TFAF-Net achieves a 9.59% higher accuracy in 30-way 1-shot classification compared to the second-best model, and reaches an accuracy of 85.02% in 10-way classification. On the Wi-Fi dataset, TFAF-Net attains 90.39% accuracy in 5-way 1-shot classification, outperforming the next best model by 6.28%, and shows a 13.18% improvement in 6-way classification.
1. Introduction
Specific emitter identification (SEI) is a technique that aims to discriminate individual transmitters by extracting radio frequency fingerprinting (RFF) features, which are the unintentional modulation characteristics beyond the signal’s main components, from the collected emitter signals [1]. Owing to the hardware discrepancies from circuit design or manufacturing processes, RFF features possess the properties of tamper-resistance and counterfeit-resilience, forming the theoretical foundation of SEI [2]. SEI has found widespread applications in military radar communication systems, interference source detection, cognitive radio, and numerous domains. However, with the increasingly complex electromagnetic environment and radar regimes, traditional SEI methods based on “hand-crafted features” heavily rely on expert knowledge, failing to adapt to the current electromagnetic landscape rapidly [3,4].
Traditional SEI methods can be categorized into transient signal-based and steady-state signal-based approaches [5]. Initially, SEI methods focused on transient signals, leveraging the emitter signals during the transition from the off to on state. These signals require a higher sampling rate due to their short duration and exhibit less reliable phase and amplitude information, being susceptible to channel noise. In contrast, steady-state signals (the modulated portion transmitted at a stable power level) are less affected by noise. Most current SEI methods employ steady-state signals, typically involving two stages: signal acquisition, followed by feature extraction and identification. The latter is considered crucial, encompassing preprocessing steps such as filtering, power normalization, synchronization, and target signal interception, before concentrating on feature extraction and identification [6].
Prior to the development of deep learning (DL), traditional SEI methodologies predominantly relied on statistical techniques for feature design, followed by the application of machine learning classifiers for signal identification. Nevertheless, these manually crafted RFF features exhibited several limitations, including suboptimal performance, limited adaptability to dynamic environments, and an inability to address the escalating complexity and proliferation of wireless transmitters. In recent years, DL has demonstrated exceptional data analysis capabilities and has gained widespread adoption in SEI. DL-based SEI techniques employ deep neural networks to autonomously extract more robust and effective RFF features from extensive transmitter signal datasets, significantly surpassing the performance of approaches based on manually engineered features [7].
Deep neural networks (DNNs) are designed to learn hidden features from data and construct decision-making classifiers automatically. Many signal emitter identification (SEI) methods leverage convolutional neural networks (CNNs) and recurrent neural networks (RNNs) to process features in the time and time-frequency domains, enabling the extraction and learning of robust radio frequency fingerprints (RFFs) [8]. For instance, Wu et al. [9] introduced a multi-scale self-attention fusion CNN to identify emitters under non-ideal channel conditions, significantly improving recognition accuracy. Similarly, Wang et al. [10] employed complex-valued CNNs to directly process complex baseband signals, improving identification performance by leveraging the inherent structure of these signals. Zhu et al. [11] utilized the short-time Fourier transform (STFT) to generate spectrograms, which were then classified by CNNs, demonstrating the effectiveness of time-frequency feature extraction. Despite the progress made by these approaches, certain limitations remain. Existing methods predominantly focus on features from either the time domain or the time-frequency domain. This narrow focus overlooks the complementary nature of these features, which, if effectively integrated, could lead to more comprehensive signal characterization. Moreover, these methods often struggle to generalize in scenarios with unseen noise patterns or signal variations. This limitation becomes especially evident in complex electromagnetic environments, where single-domain features fail to capture the diversity and intricacy of emitter signals. To address these challenges, we propose a time-frequency feature fusion module combined with a convolutional block attention module (CBAM) [12]. This configuration enhances the overall performance and robustness of SEI systems by integrating complementary features from both domains and adaptively emphasizing salient information while suppressing irrelevant features.
DL-based SEI methods rely on a large volume of historical RF signal samples and deep neural networks to extract more robust and effective RF features, demonstrating superior performance compared to methods based on handcrafted features. However, most DL-based SEI methods focus on the closed-set SEI problem, which will be elaborated upon in Section 2. In closed-set SEI, the classes of radiation sources remain consistent between the offline training and online deployment phases [13].
Nevertheless, the dynamic nature of electromagnetic environments can lead to the emergence of novel classes of radiation sources that were not encountered during training [14]. This poses a significant challenge, as traditional classification models struggle to generalize to such unseen classes. In these scenarios, the scarcity of labeled data for emerging classes further exacerbates the difficulty of accurate identification. To address this issue, few-shot learning (FSL) is particularly relevant, as it is specifically designed to perform well in scenarios where labeled data is limited. FSL aims to effectively learn from a few labeled examples, enabling generalization to novel classes with minimal supervision. Motivated by this, we propose a novel FSL strategy that incorporates proxy-anchor (PA) loss and center (CT) loss, which facilitate the extraction of discriminative features during training [15,16]. These mechanisms enhance the model’s ability to distinguish between classes, even in the presence of limited labeled data, thereby improving the recognition of emerging radiation sources.
This paper proposes a time-frequency attention fusion network with FS metric learning (TFAF-Net), which leverages an attention-based time-frequency fusion strategy to automatically fuse and extract high-dimensional representations from multiple views. Furthermore, to address the FSL scenario, the PA loss, and CT loss are introduced to extract discriminative features, enhancing the discriminative disparity among radiation sources and fortifying the network’s generalization capability and robustness. The main contributions of this paper are summarized as follows:
- A metric learning-based feature embedding scheme is proposed, aimed at extracting generalized and discriminative features, ensuring the most accurate representation of the embedding space while simultaneously maximizing inter-category distances and minimizing intra-category distances. This strategy has demonstrated superior performance, particularly in small sample tasks.
- The fusion of time-domain and frequency-domain information based on the attention mechanism is introduced, effectively exploiting the multi-view features of the signal. This method significantly enhances the quality of the extracted RF fingerprints.
- The proposed SEI method is evaluated on an open-source large-scale real ADS-B dataset and an open-source Wi-Fi dataset, and compared with multiple existing SEI methods, including FS-SEI approaches. Results demonstrate that the proposed approach achieves state-of-the-art recognition performance, thanks to its architectural design that maximizes effectiveness while maintaining reduced parameters and complexity.
2. Related Work
This section provides an overview of traditional artificial feature-based SEI methods, deep learning (DL)-based approaches, and introduces few-shot learning (FSL) as a solution to data scarcity in SEI.
2.1. Traditional SEI Methods
Early SEI approaches primarily relied on machine learning models using handcrafted RFF. These methods typically extracted features from the instantaneous, modulation, or transform domains. Techniques such as feature matching, based on inter-pulse modulation parameters like pulse width, arrival time, and carrier frequency [17], were widely adopted. However, the dependence on pre-built databases and the inability to handle unseen signals significantly limited their adaptability in complex environments. Additionally, the omission of temporal and frequency correlations further hindered their performance as modern radar systems evolved.
2.2. DL-Based SEI Methods
Deep learning has transformed SEI by enabling automatic feature extraction and classification through neural networks, including CNNs, RNNs, and LSTMs. DL-based SEI methods can be categorized into time-domain signal processing, spectrogram-based methods, and constellation diagram analysis. Time-domain methods work directly with raw IQ signals or decomposed components, while spectrogram-based approaches convert signals using transformations like Fourier and Hilbert–Huang for further analysis. For example, Pan et al. [18] employed a deep residual network to extract features from spectrograms, improving accuracy while reducing complexity. While these methods achieve superior results, they rely on large-scale labeled datasets, which are often impractical to collect.
2.3. Few-Shot Learning in SEI
DL-based SEI methods encounter significant challenges in practical applications, particularly due to the scarcity of labeled samples and category imbalance across different transmitter classes [19]. Traditional large-sample learning approaches, which rely on abundant training data, are increasingly impractical, as it is often infeasible to collect sufficient signal samples from all transmitter classes. This limitation severely impacts the ability of these methods to generalize effectively in real-world scenarios. To address these issues, a FSL strategy is required to enhance recognition performance by enabling models to learn efficiently from a limited number of labeled samples. This approach not only mitigates the data scarcity problem but also improves the robustness of SEI models in handling imbalanced class distributions, thereby making them more applicable in dynamic electromagnetic environments.
- Data Augmentation (DA): The DA-based methods aim to expand the training dataset by adding equivalent samples, thus overcoming the problem of insufficient training samples. Zhang et al. [20] proposed a DA-aided FSL method to improve the performance of SEI under limited sample conditions. This method is validated using automatic dependent surveillance–broadcast signals and introduces four DA techniques—flip, rotation, shift, and noise addition—to enhance the diversity of the training dataset and mitigate overfitting in small sample scenarios. Furthermore, the DA-based methods rely only on task-specific data, unlike other methods that leverage auxiliary data.
- Generative Model (GM): GM-based methods, such as autoencoders or GANs, are used to extract strong features from data. These features are capable of accurately representing and reconstructing the original samples. Yao et al. [21] introduced a novel approach to SEI using a FSL framework based on an Asymmetric Masked Auto-Encoder (AMAE). It addresses the challenge of identifying emitters with limited labeled samples by leveraging abundant unlabeled data for pre-training. The AMAE effectively extracts RFF features through a unique masking strategy, enhancing the model’s ability to learn meaningful representations. Compared to the Metric Model, GM may suffer from mode collapse and training instability issues common in GAN training.
- Metric Model (MM): Metric methods are grounded in the principles of “learning to compare” or “learning to measure”. These methods focus on developing representations that enable the evaluation and quantification of similarity among different samples. By learning an appropriate distance metric, these methods facilitate the classification, clustering, and retrieval of data points based on their inherent characteristics. Wu et al. [22] proposed an innovative open-set SEI method utilizing a Siamese Network. Their approach integrates unsupervised learning, clustering loss, and reconstruction loss during the training process to ensure comprehensive feature extraction. This methodology enhances the discrimination between known and unknown classes. By leveraging the Siamese Network, the method effectively measures the similarity between signal features, facilitating robust open set identification. Wang et al. [23] presented a novel FS-SEI method using interpolative metric learning (InterML). The proposed InterML method addresses these issues by eliminating the need for auxiliary data and improving generalization through interpolation and metric learning, enhancing identification accuracy and feature discriminability, particularly in FS settings.
- Meta Model (MEM): The core concept of meta methods is “learning to learn.” Meta-learning serves as an optimization approach aimed at enhancing the generalization capability of neural networks across various tasks. Yang et al. [24] proposed an SEI approach utilizing model-agnostic meta-learning, which achieved high accuracy with limited labeled samples and allowed for adaptation to new tasks without extensive retraining. Unlike MM, MeM may require careful task design and suffer from optimization challenges in meta-learning.
3. Signal Model and Problem Formulation
SEI aims to classify emitters based on the unique RFFs embedded in their transmitted signals. These RFFs arise from inherent hardware imperfections, such as oscillator instability, phase noise, and non-linear distortions. The received signal can be expressed as:
where is the received signal, represents the transmitted signal parameterized by the emitter’s unique characteristics , and is additive Gaussian noise.
The task of SEI is to classify into one of K known emitter classes. Formally, given a labeled dataset , where indicates the class label, the objective is to learn a mapping function such that:
where is the predicted class label. The mapping function can be implemented using neural networks, such as MLP, CNNs, RNNs, or hybrid models combining CNNs and RNNs to leverage spatial and temporal features.
However, in real-world scenarios, SEI often faces the challenge of limited labeled data, making it a small-sample learning problem. Traditional methods relying on large, balanced datasets fail in such cases, as they cannot effectively generalize to new or underrepresented emitter classes. This issue is compounded by variations in noise, channel effects, and the diversity of emitter characteristics, which increase the difficulty of feature extraction and classification.
To address this, FSL provides a framework to classify emitters with limited labeled data. The goal of FSL in SEI is to learn discriminative and robust feature representations from only a few labeled samples, enabling accurate classification even under challenging conditions.
4. Methodology
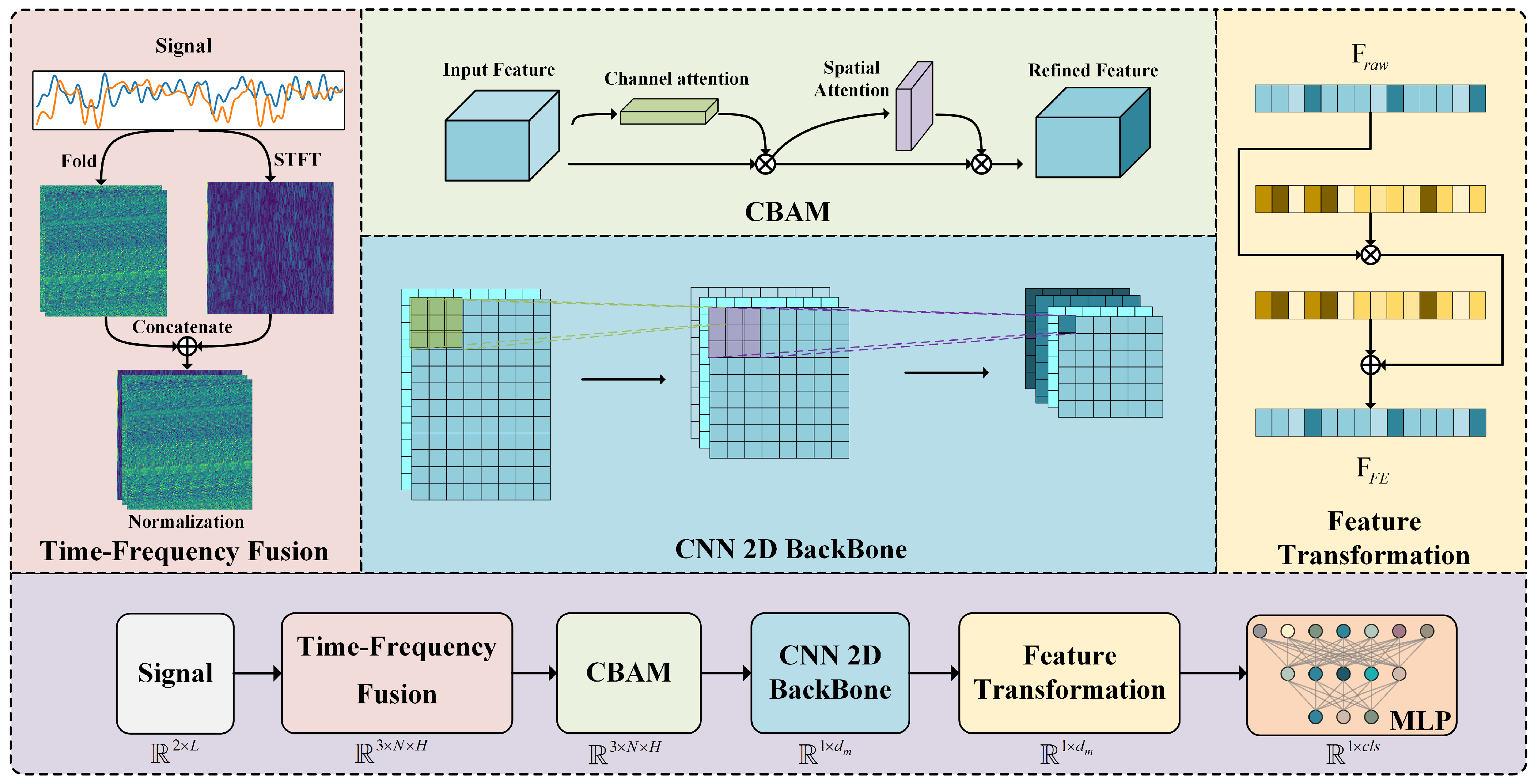
The architecture of the proposed TFAF-Net is depicted in Figure 1. The input signal first passes through a time-frequency fusion module, which extracts the time-frequency features . These features are subsequently refined via the CBAM module, producing , which is then fed into the CNN backbone for further processing.
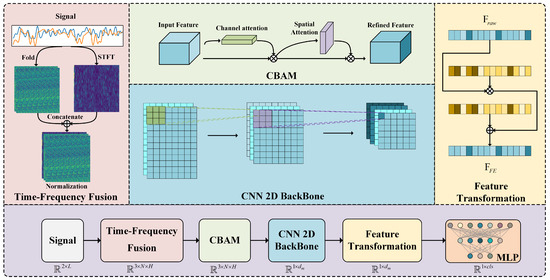
Figure 1.
Overall architecture of TFAF-Net.
As outlined in Table 1, the encoder is composed of several stages. It begins with a BatchNorm2D layer, followed by the CBAM module. The network then proceeds through a sequence of Conv2D layers with ReLU activations and BatchNorm2D layers, interspersed with MaxPool2D layers for down-sampling. As the network deepens, the number of convolutional filters increases, and an adaptive average pooling layer is applied before flattening the feature maps. The resulting flattened feature vector is transformed, and in the classifier, fully connected layers map the extracted features to a probability distribution across the C emitters. The first linear layer reduces the feature dimensionality, followed by a final linear layer that generates the classification output.

Table 1.
Neural network structure with output dimensions and parameter counts.
4.1. Time-Frequency Representations
The STFT is a widely utilized method for time-frequency analysis. It involves dividing a signal into small segments and applying a window function of specified time width to each segment. The Fourier transform is then applied to these windowed segments, providing a frequency domain representation that reveals the relationship between the time and frequency domains. The is mathematically defined as:
where is the window function, is its conjugate, is the frequency, and t is the time.
The signal spectrum is derived by squaring the magnitude of the STFT, defined as:
To obtain the amplitude spectrum of the radiated source signal , we perform an STFT transformation, yielding . The amplitude spectrum is then regularized by dividing by the L2 norm:
4.2. Time-Frequency Fusion
In the field of SEI, the extraction of fingerprint information from radio signals is pivotal for distinguishing various sources of radiation. Despite the high variability inherent in time-frequency maps, these representations serve as effective tools for identifying radio signals.
Time-frequency mapping constitutes a fundamental aspect of DL techniques that leverage information from both the time and frequency domains. Time-domain analysis enables the observation of changes in the waveform and amplitude of the radiation source’s signal, while frequency-domain analysis reveals variations in frequency and phase. By integrating insights from both domains, the accuracy and robustness of radiation source identification are significantly enhanced, primarily due to the increased variability observed among different sources.
Consider a received radio signal . Let the window function have a window size of N on the time axis and a sliding step of H. In each frame of the sliding window, the time-frequency spectrum obtained by the STFT, denoted as , represents a localized spectrum of the signal near the time . For a signal with M FFT points, the time-frequency spectrum obtained by the STFT transform has a size of , where K is computed as follows:
By applying a sliding window process to the original signal, where each window has a length of K and a sliding step of S, the original signal is transformed into a two-dimensional array. Zero-padding is performed on the original signal, where zeros are appended to the end of the signal. The padding length is defined as:
when and , the in-frame time-frequency mapping features extracted by STFT are of the same magnitude as the 2D signal arrangement obtained by the sliding window in the same frame. The fused time-frequency features are given by .
To ensure optimal performance, the concatenated features are subjected to Batch Normalization (BN). This step is crucial as it normalizes the output of the previous layer, mitigating issues related to internal covariate shift. By standardizing the inputs to each layer, BN improves the convergence speed of the training process and enhances the stability of the network. This normalization is particularly beneficial in our context, as the fusion of time-domain and frequency-domain information creates a high-dimensional feature space that may exhibit significant variability.
An innovative alignment strategy is introduced, which effectively merges time-domain and frequency-domain information, ensuring synchronization at each time step. This alignment allows for more efficient feature extraction in subsequent processing stages, enhancing the model’s ability to capture discriminative patterns. By aligning these multidimensional features, the model’s performance in identifying radio signal sources across diverse operational environments is improved. Additionally, the robustness of the feature extraction process is strengthened, resulting in enhanced overall performance and reliability of the identification framework in complex and dynamic scenarios.
4.3. Time-Frequency Feature Refine
The introduction of the attention mechanism following feature fusion is crucial for enhancing the model’s representational and generalization capabilities. Although feature fusion integrates information from multiple sources, the relative importance of these sources can vary significantly. To address this, the CBAM is employed as a lightweight yet effective mechanism that adaptively refines feature representations. CBAM consists of two complementary components: channel attention, which highlights the most informative feature channels by assigning adaptive weights, and spatial attention, which emphasizes critical spatial regions within the feature map. Together, these components enhance the model’s ability to capture salient information while maintaining a low computational cost, thereby improving both accuracy and robustness.
4.3.1. Channel Attention Module
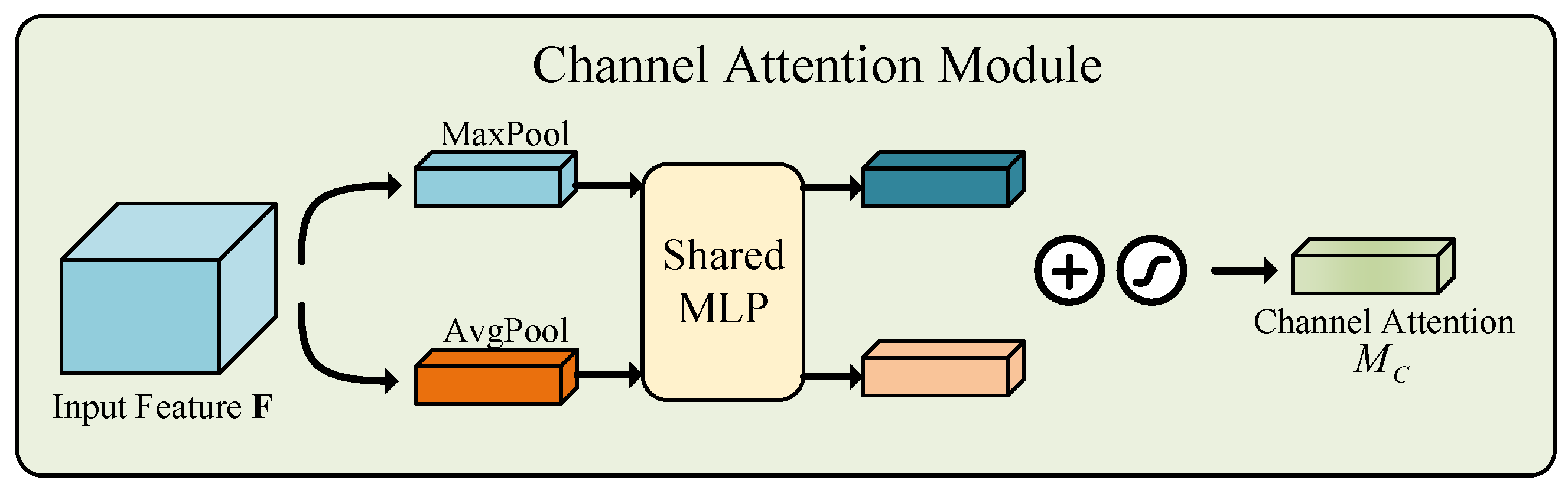
The attention module on the channel and the specific calculations are shown in Figure 2:
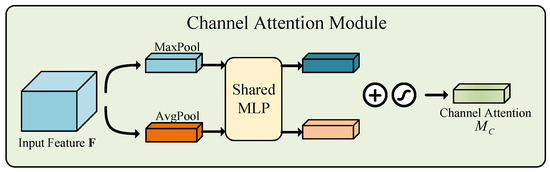
Figure 2.
Channel attention module.
The input feature map F undergoes global max pooling and average pooling along spatial dimensions, producing two feature maps. These maps are processed by a shared Multilayer Perceptron (MLP), which first reduces dimensions to (with ReLU activation), followed by a layer with C neurons. The outputs are combined via element-wise summation and passed through a sigmoid function to produce the channel attention map . Finally, is element-wise multiplied with F to generate the modulated spatial feature input for the attention module.
The process can be mathematically represented as:
where denotes the sigmoid function, , , , and . It is important to note that the MLP weights, and , are shared across both inputs, with the ReLU activation applied after .
4.3.2. Spatial Attention Module
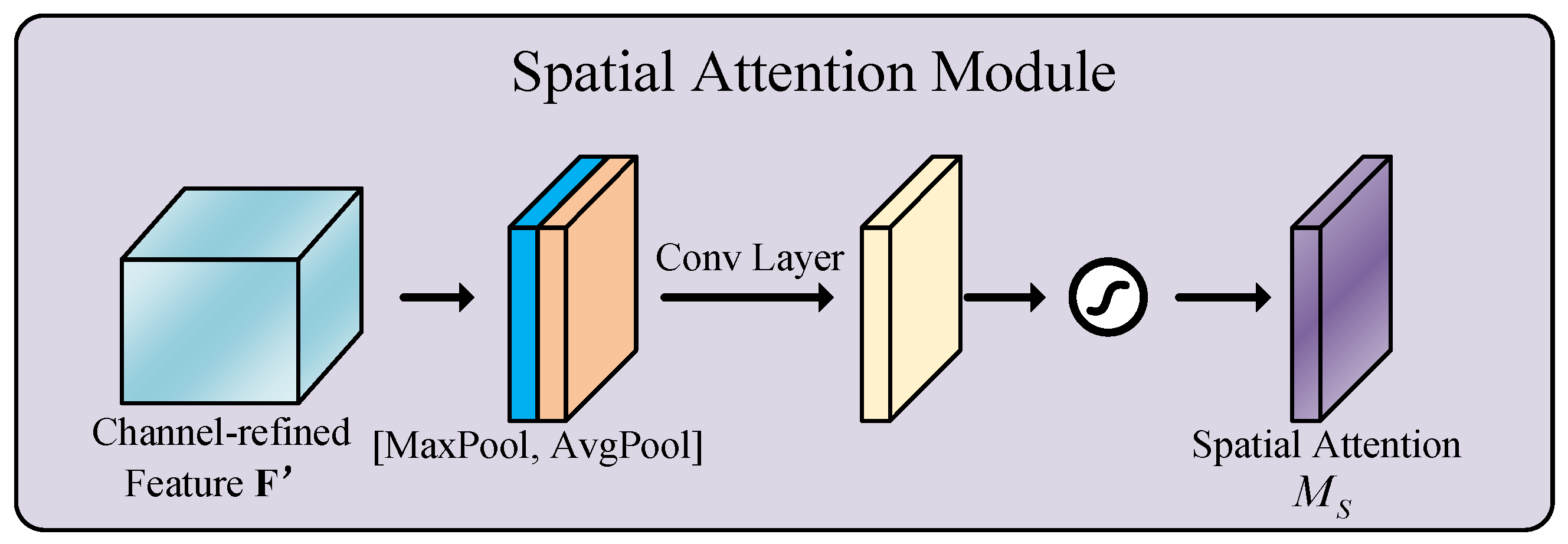
The spatial attention module and the specific calculations are shown in Figure 3.
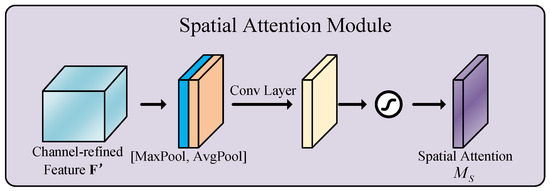
Figure 3.
Spatial attention module.
The modified feature map , generated by the channel attention module, serves as the input to the spatial attention module. Global average pooling and max pooling are applied across the channel dimension to produce two feature maps, which are concatenated along the channel axis. A convolution is then applied to reduce the feature dimension to a single channel, followed by a sigmoid activation to generate the spatial attention map . This map is element-wise multiplied with to produce the final output feature. Mathematically, the process is expressed as:
where denotes the sigmoid function and represents a convolution operation with the filter size of .
Incorporating CBAM into our framework not only optimizes feature representation but also maintains efficiency through its minimal parameter requirements. This advancement highlights the significance of attention mechanisms in modern deep learning architectures, positioning CBAM as a critical component in improving the overall efficacy of our model.
4.4. Loss Function Based on Metric Learning
Conventional radiation source identification methods are typically designed and evaluated for closed-set identification problems using a limited training dataset containing predefined categories. In closed-set recognition problems, the categories of the test samples must be present in the training dataset. Although the cross-entropy loss function performs well on the training data and achieves good classification performance, its learned features only ensure separability on the training data and do not guarantee discriminability on the unknown data. Therefore, relying only on separable features cannot meet the needs of practical deployment.
In practical deployments, the closed-set identification problem is almost infeasible because it is almost impossible to obtain radar signal samples from all possible sources for training. Therefore, the features used for identification must be discriminative and generalizable enough to be able to distinguish between signal samples in categories that have not been seen before or in categories that have only a small number of samples.
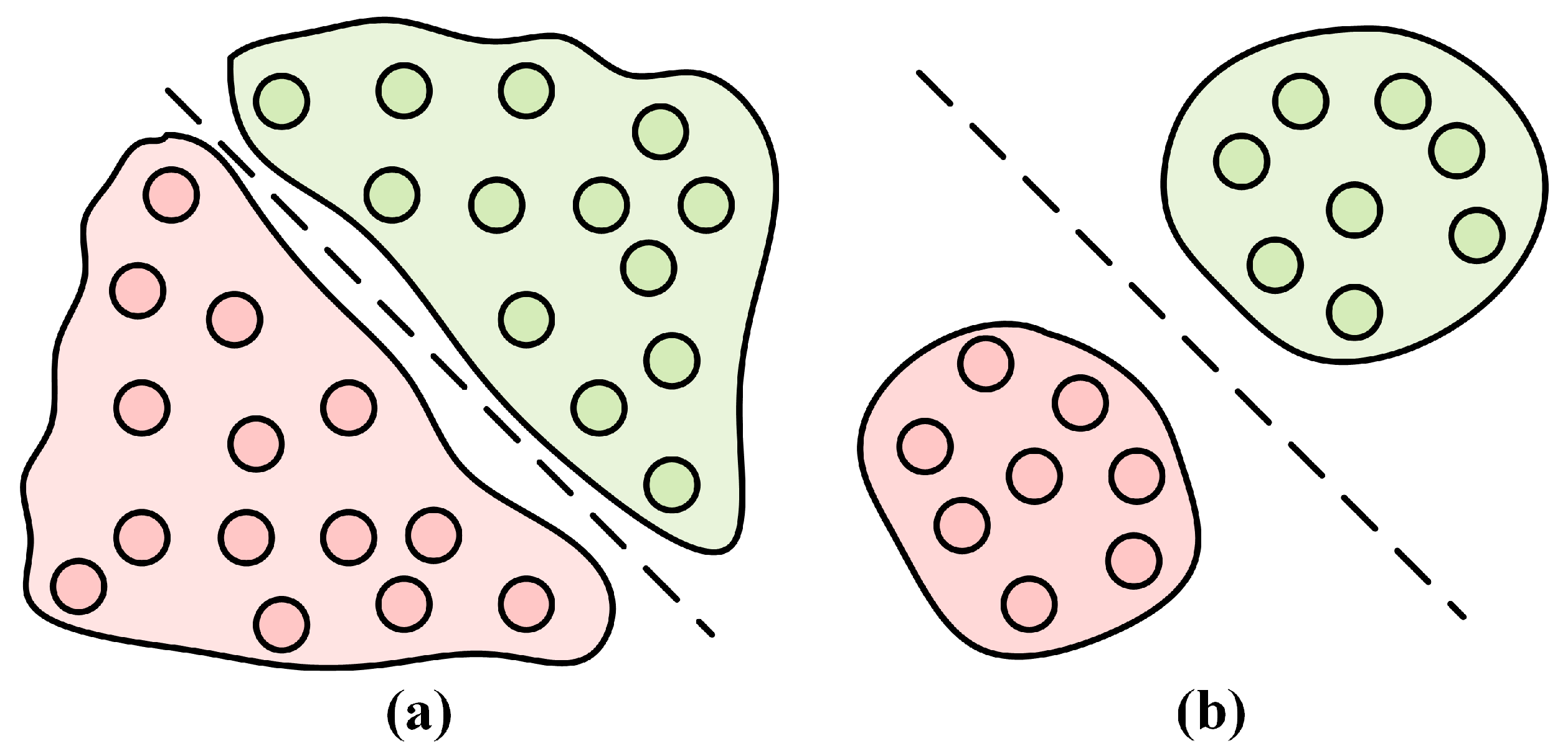
Figure 4 describes the difference between separable and discriminable features. Separable features enable classification only on the training dataset, while discriminable features enable classification on unknown data. The key to improving the performance of radiation source identification lies in extracting discriminative features, i.e., features that can effectively distinguish between different classes of signal samples. The core of discriminative features includes intra-class consistency and inter-class separability. This means that the feature distance between signal samples of the same class should be as small as possible, while the feature distance between signal samples of different classes should be as large as possible. To achieve this goal, we introduce proxy-anchor (PA) loss and Center (CT) loss.
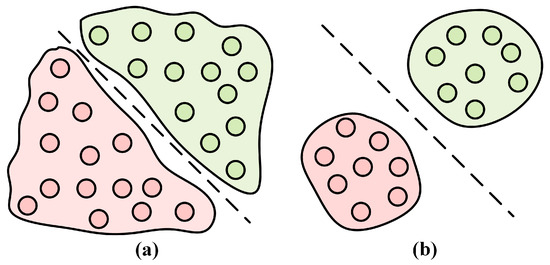
Figure 4.
Illustrate the concepts of separable features and discriminative features. The connection between these features is that while discriminative features are always separable, separable features are not necessarily discriminative. (a) Separable feature. (b) Discriminative feature. In this visualization, consistent coloration corresponds to identical categorical classifications.
4.4.1. PA Loss
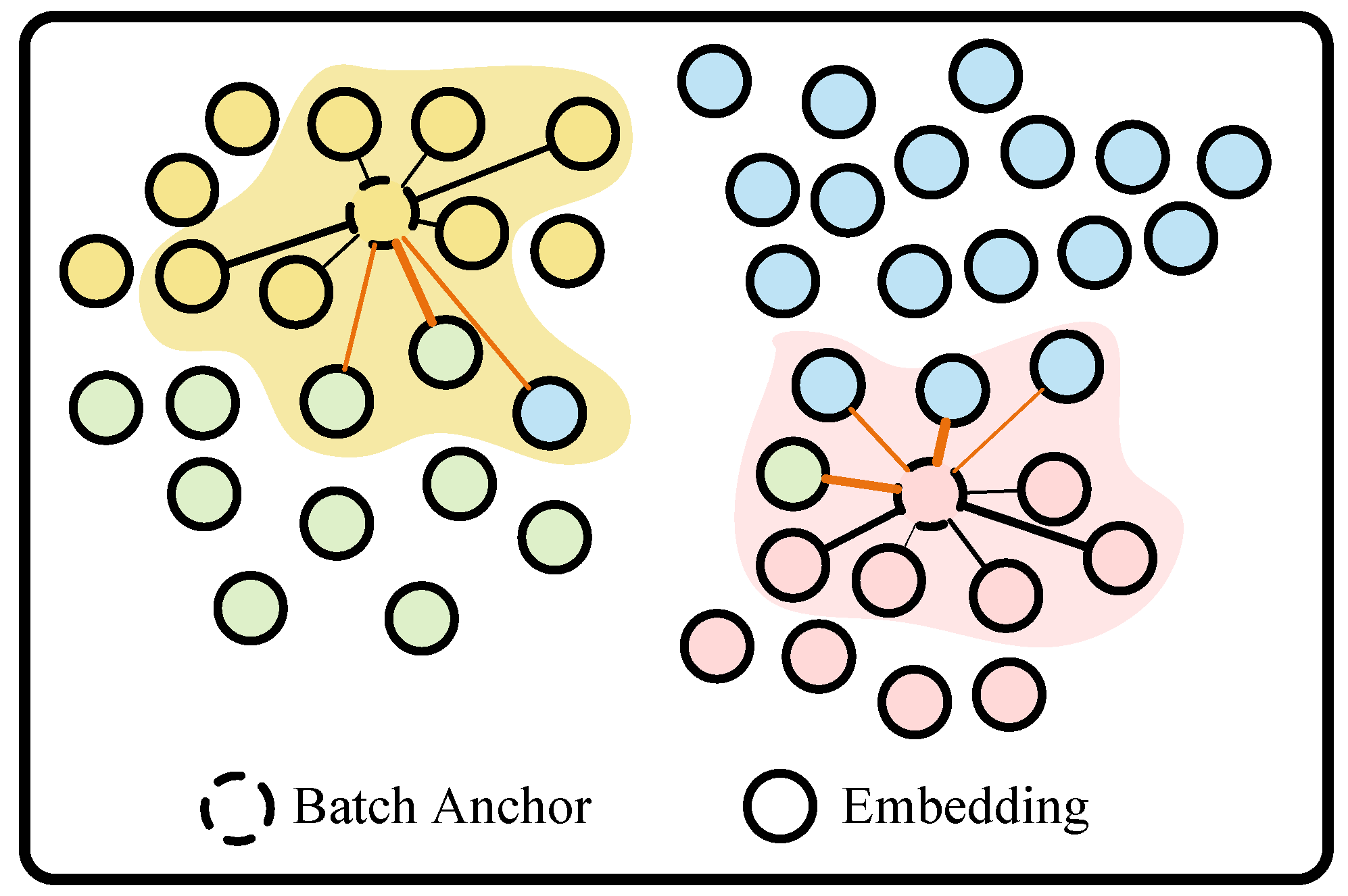
PA loss is developed to overcome the limitations of traditional face validation loss functions, particularly in managing intra- and inter-class variations, thereby improving the model’s generalization capability. As shown in Figure 5, the central idea of PA loss is to utilize each agent as an anchor to connect with the bulk data, facilitating interactions through these proxy anchors during training. The loss function is defined as follows:
where is the margin, is the scaling factor, P denotes the set of all agents, and denotes the set of positive agents in the batch. For each agent p, the batch of embedding vectors X is divided into two sets: (positive embedding vectors) and (negative embedding vectors). This loss function models the similarities and differences between embedding vectors using the Log function, aiming to bring the predicted vector p closer to the most challenging positive example and push it farther from the most challenging negative example.
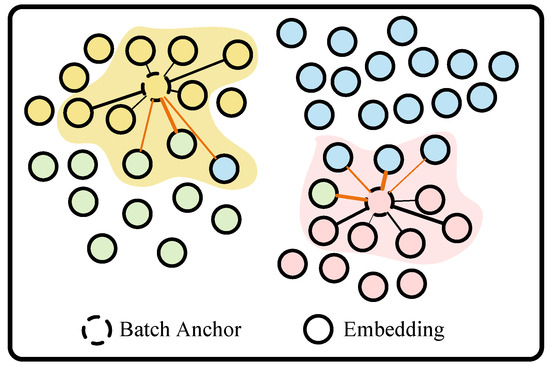
Figure 5.
PA loss schematic. In this figure, identical colors denote the same categories.
4.4.2. CT Loss
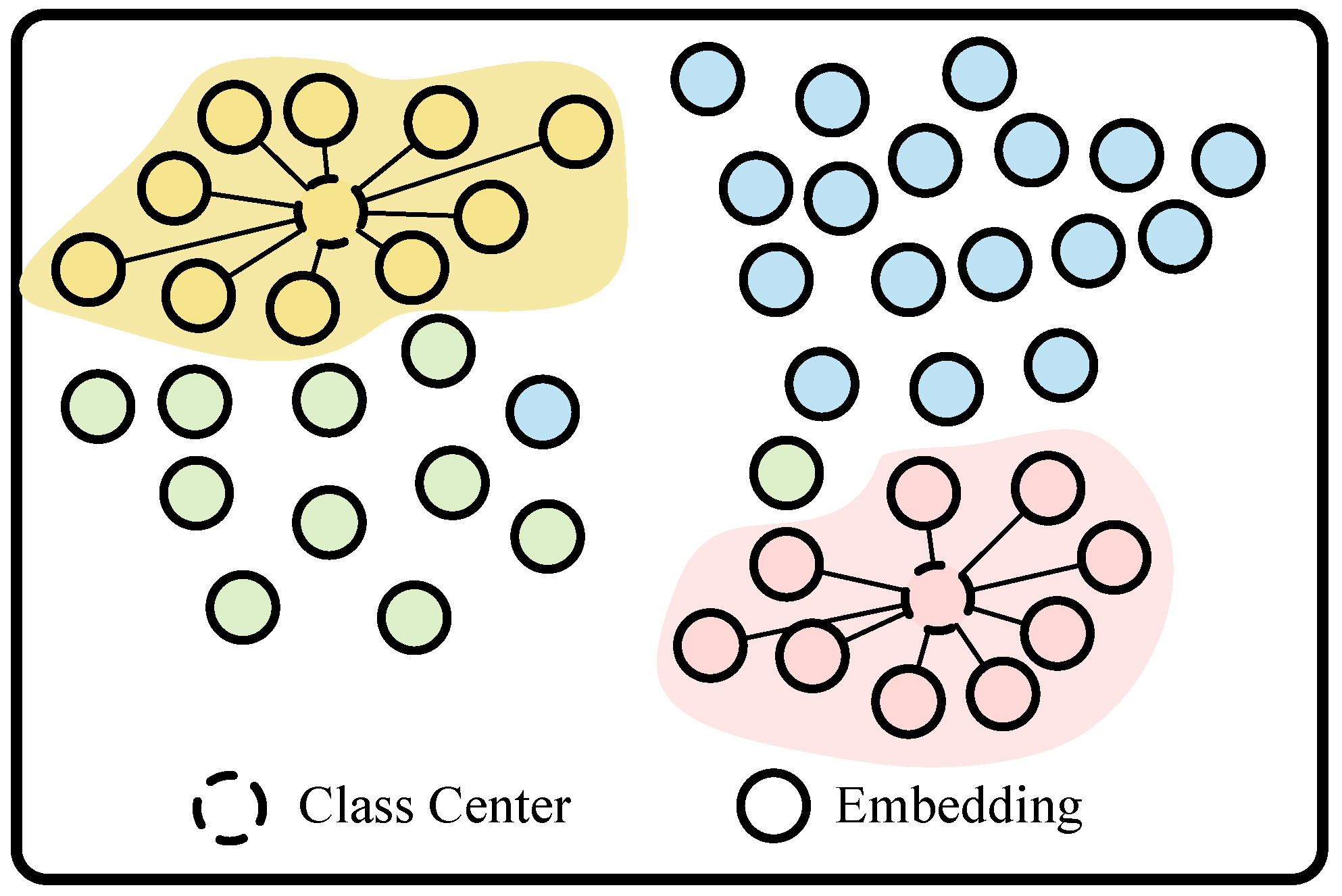
Traditional classification models typically rely on cross-entropy loss to separate features across categories; however, this does not guarantee that features within the same category are compactly clustered in the feature space, potentially leading to suboptimal performance. Center loss (CT loss) addresses this limitation by minimizing the Euclidean distance between feature vectors and their corresponding class centers, thereby enhancing intra-class compactness. Specifically, CT loss is defined as:
where represents the feature vector of the i-th sample, is the center of the corresponding class , and m is the batch size.
As illustrated in Figure 6, CT loss ensures that samples of the same class are tightly clustered by iteratively updating the class center during training, allowing it to converge towards the mean of the feature vectors for each class. This process enhances feature compactness and improves classification accuracy.
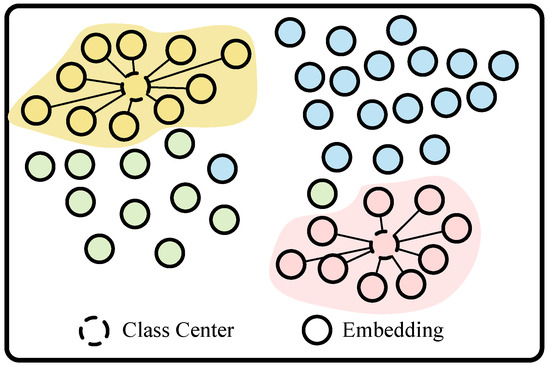
Figure 6.
CT loss schematic. In this figure, identical colors denote the same categories.
The integration of PA loss and CT loss is pivotal for enhancing the model’s discriminative capability in radiation source identification. PA loss dynamically adjusts inter-class distances, ensuring effective management of intra-class variations while maximizing separability across classes. Meanwhile, CT loss minimizes intra-class distances by clustering feature vectors around their respective class centers, addressing the limitations of traditional cross-entropy loss and promoting feature compactness. Together, these losses improve feature representation and extraction, significantly enhancing classification accuracy and robustness, particularly in complex scenarios.
4.4.3. Cross-Entropy Loss
The cross-entropy loss function after applying the softmax activation can be described as follows. For input data , the features extracted by the backbone network are denoted by :
These features are then passed through a fully connected network , resulting in the final feature vector :
The cross-entropy loss after softmax activation of is given by:
where represents the n-th element of .
The final loss function is:
where , is the constant used to balance the cross-entropy loss, PA loss, and CT loss.
4.5. Feature Transformation
In metrics-based learning algorithms, CNNs extract high-level features from input data for classification or clustering. However, the raw features output by the network may not accurately reflect true data similarities due to the limitations of similarity metrics like Euclidean distance. Euclidean distance captures only geometric relationships without considering semantic information or data distribution. Consequently, the two categories may appear dissimilar in Euclidean terms but share semantic similarities, or they may have small cosine similarities yet differ significantly in data distribution. These discrepancies can lead to inaccuracies in representing data similarities, ultimately affecting the algorithm’s performance.
To address this issue and enhance algorithm performance, it is crucial to shift and scale the network output to better capture true category similarities. This process, referred to as panning and telescoping, can be implemented using functions such as linear, exponential, or logarithmic transformations. Panning and telescoping adjust the output vectors, ensuring they have a more suitable range and distribution. For the output of CNN the transformation is performed to obtain the output features
where and are the parameters for the panning and telescoping, which can be obtained by training.
This approach offers several advantages. First, it aligns network output vectors with true similarity metrics rather than relying solely on Euclidean distance or cosine similarity. This alignment makes clustering loss more sensitive to data differences and similarities, thereby improving clustering accuracy. Second, shifting and scaling enhance the network’s robustness by preventing the gradient from vanishing or exploding due to excessively large or small output values. This improvement in stability ensures efficient training and network convergence. Third, this method increases the network’s flexibility, allowing it to adapt to diverse tasks and data distributions, thereby enhancing its generalization capability and performance during testing.
5. Experiment and Analysis
5.1. Dataset
All experiments were conducted using a PyTorch framework on an Ubuntu server equipped with an Nvidia RTX 3090 GPU. The experimental evaluation employed two distinct datasets, namely and . The dataset comprises 63,105 automatic dependent surveillance–broadcast (ADS-B) signals, recorded as raw I/Q samples from airborne transponders under open, real-world conditions. This dataset spans 198 signal classes, with each signal sampled at a rate of 50 MHz and consisting of 3000 sampling points. Conversely, the dataset, as reported in [25], includes data captured from over-the-air transmissions using 16 USRP X310 transmitters, with a fixed transmitter–receiver distance of 2 feet. Detailed attributes of these datasets are presented in Table 2.

Table 2.
Details of the dataset.
5.2. Experimental Details
The experimental setup for this study utilized a high-performance computing platform equipped with an NVIDIA GeForce RTX 3090 GPU (24 GB memory) and running the Ubuntu 20.04 operating system. The computational workflows and algorithms were executed using the PyTorch framework. Network weight optimization was facilitated through the AdamW optimizer.
During the pre-training phase, data across all categories were partitioned into training and test sets using a 7:3 split. The model demonstrating the highest accuracy in this phase was selected, and its weights were preserved for subsequent fine-tuning. To enhance model training efficiency and prevent overfitting, an early stopping mechanism was activated, which terminates training after a predetermined number of epochs without improvement in test accuracy.
In the fine-tuning phase, we copy the pre-trained weights from the Encoder part of the model to the fine-tuned model, using a fixed learning rate for different models and experimental conditions [26]. The most effective outcomes from these settings were recorded as indicative of the model’s optimal performance. This systematic approach promotes consistency and methodological rigor in evaluating the model’s efficacy. Details of these experimental conditions are documented in Table 3.

Table 3.
Experimental (pre-training, fine-tuning) parameter details.
For the time-frequency transformations, the window size and step length were determined through experimental evaluation tailored to each dataset. Specifically, for the ADS-B dataset, we set the window size to 100 and the step length to 5. For the WiFi dataset, the optimal settings were a window size of 128 and a step length of 15. These values were selected to balance computational efficiency and model performance, ensuring the extraction of key signal features while minimizing unnecessary data overlap.
5.3. Few-Shot Signal Classification Compared with the Other Methods
To evaluate the efficacy of the proposed TFAF-Net in the FS-SEI task, we conducted comparative experiments against several established SEI methods, including ResNet1D [27], ResNet2D [27], CVCNN [28], MSRI [29], CVSRN [30], MF-RESNET [31], and SFS-SEI [32]. Recognizing the critical impact of hyperparameters on model performance, we aimed to maintain experimental fairness by adhering primarily to the parameter settings recommended in their respective publications. Adjustments were made only where necessary to accommodate our data input requirements.
SFS-SEI is a resource-efficient method for SEI, utilizing an end-to-end Sparse Feature Selection (SFS) approach. It addresses challenges like large model sizes, high feature dimensionality, and slow convergence in deep learning models. By using sparse parameters and a loss function combining cross-entropy and sparse regularization, it focuses on the most relevant features, reducing redundancy. This improves SEI efficiency by speeding up convergence, lowering computational complexity, and reducing storage needs without compromising accuracy. MF-RESNET combines traditional signal features, such as power spectrum, cyclic spectrum, and bispectrum, with intrinsic features extracted by a ResNet1D network. By incorporating a channel attention mechanism, the model effectively weights and fuses the features, enhancing the identification of RFF. MSRI is based on sparse representation-based classification (SRC) and designed signal feature extractor with channel attention mechanism fused with multi-scale CNN. The extracted features include shallow features and deep features. The original AIS signals and the two levels of features are combined to create a multilevel dictionary, on which sparse representation-based recognition is performed.The algorithm can recognize transmitters with higher accuracy and requires less training time. CVSRN introduces two key innovations for SEI: the Complex-Valued Separate Residual (CVSpeRes) module, which uses complex-valued convolutions to better capture the interaction between real and imaginary components of I/Q signals, and a multiscale learning architecture that improves feature extraction and robustness in dynamic scenarios.
The computational complexity and parameter size of these models were first compared, as both FLOPs (floating-point operations) and the number of parameters serve as key indicators of model efficiency. These factors have a direct impact on the computational speed and resource consumption of the models. The FLOPs and parameter sizes of our model, in comparison to the other models, are presented in Figure 7. For classification tasks, the network’s performance is measured by overall accuracy (OA). Figure 8 and Figure 9 present the recognition performance of the proposed TFAF-Net in comparison to other methods. It is evident from the results that TFAF-Net consistently outperforms the other models across various scenarios.
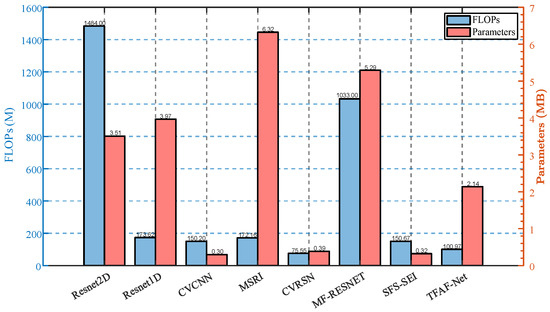
Figure 7.
Comparison of FLOPs and training parameter sizes per example for different models on the .
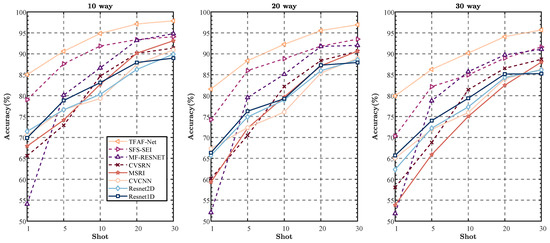
Figure 8.
Comparative results with other SEI methods on the .
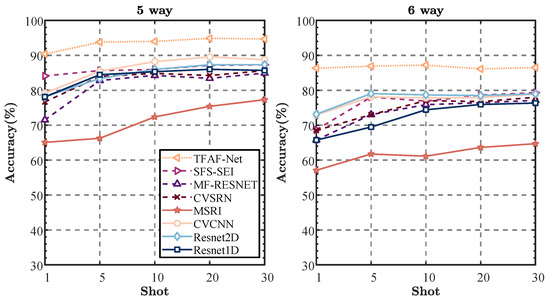
Figure 9.
Comparative results with other SEI methods on the .
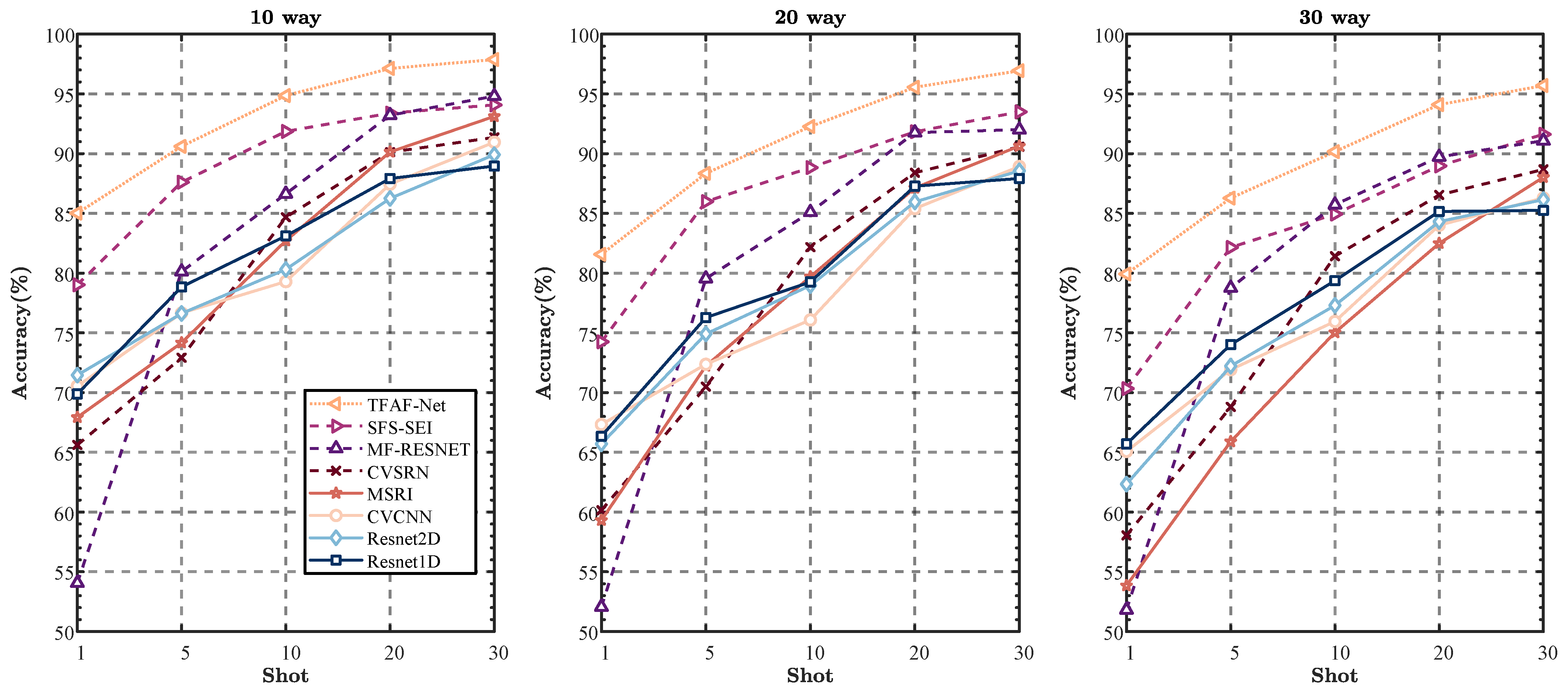
For the ADS-B dataset, experiments with 10, 20, and 30 categories show that TFAF-Net consistently outperforms other models, especially in the 1-shot classification task. In the 10-way task, TFAF-Net achieves 85.02% accuracy, surpassing SFS-SEI (79.02%) and MSRI (67.93%). Despite having lower FLOPs (100.968 M) and moderate parameters (2.139 M), TFAF-Net maintains its lead in the 20-way and 30-way tasks, achieving 81.57% and 79.93%, respectively. Even models like SFS-SEI (150.67 M FLOPs, 0.323 M params) and MSRI (172.157 M FLOPs, 6.324 M params) fall short, showing that TFAF-Net balances efficiency and high performance. Notably, in the 30-way classification, TFAF-Net outperforms the second-best model by a significant margin of 9.59%, indicating its robustness in more complex classification tasks.
Across all tested scenarios, TFAF-Net demonstrates a distinct advantage, particularly when the number of categories is small. This trend suggests that the model is highly effective in handling small-sample scenarios. For instance, while SFS-SEI and MSRI show considerable degradation in performance as the number of categories increases, particularly in the 1-shot scenario, TFAF-Net maintains its superior performance. MSRI, in particular, exhibits poor results in small-sample settings, achieving only 53.84% accuracy in the 30-way classification with 1-shot, but improves significantly as the sample size increases. In general, all models exhibit an upward trend in performance as the sample size increases. For example, in the 10-way classification, MSRI improves from 67.93% to 93.12% as the sample size increases from 1-shot to 5-shot. This shows that while MSRI struggles in low-sample scenarios, it can achieve competitive results with sufficient data. In contrast, TFAF-Net continues to outperform across all sample sizes, although the performance gap between it and other models narrows as the sample size increases. In the 20-way and 30-way tasks, a similar trend is observed. TFAF-Net continues to outperform in the 1-shot scenario with a considerable margin. However, as the sample size increases to 5-shot, models like CVCNN and ResNet2D show noticeable improvements, closing the gap in performance but still not surpassing TFAF-Net.
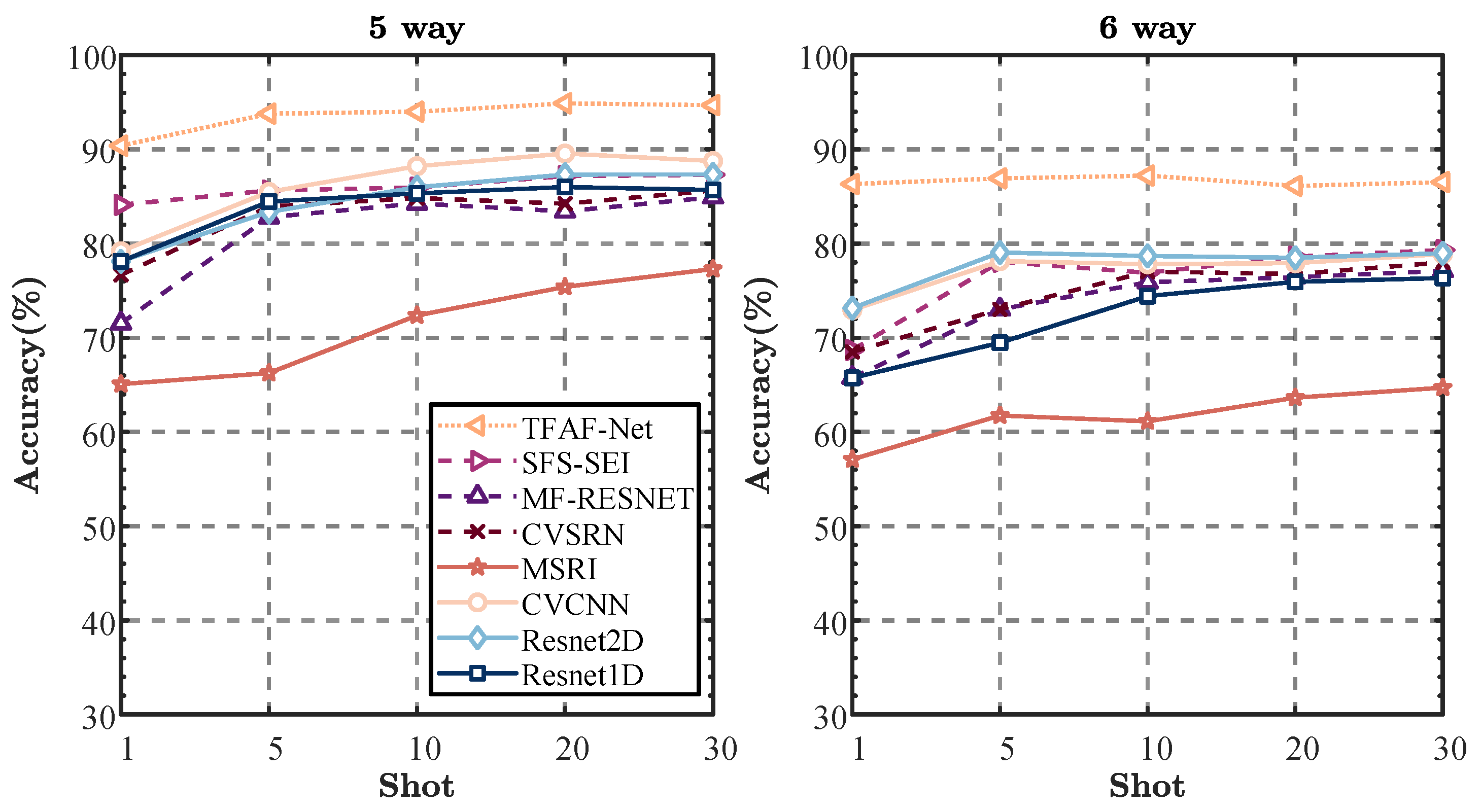
For the Wi-Fi dataset, experiments involving five and six categories reveal that TFAF-Net consistently achieves the highest recognition accuracies across all scenarios, particularly in the 1-shot classification task. In the 5-way classification, TFAF-Net achieves a recognition accuracy of 90.39%, surpassing the second-best model, SFS-SEI, by a margin of 6.28%. Similarly, in the 6-way classification, TFAF-Net achieves 86.32% accuracy, which represents a remarkable 13.18% improvement over SFS-SEI. This demonstrates TFAF-Net’s robustness in handling FSL tasks in this dataset, particularly in more complex classification tasks like 6-way classification.
As the number of samples increases, TFAF-Net continues to demonstrate superior performance. In the 5-way classification, it maintains a notable advantage over other models, with an average improvement of around 6% across different sample sizes. This trend is also observed in the 6-way classification, where TFAF-Net shows an average superiority of approximately 8% compared to the second-best model. In contrast, models like MSRI and MFRESNET show significant performance degradation with small sample sizes, indicating their inability to effectively manage FS scenarios. For instance, MSRI achieves only 57.09% accuracy in the 1-shot scenario for the 6-way classification, which is considerably lower than TFAF-Net’s 86.32%. Interestingly, increasing the sample size does not significantly enhance the performance of TFAF-Net in the Wi-Fi dataset, unlike the results observed in the ADS-B dataset. In fact, in some cases, a slight performance degradation is observed as the sample size increases, suggesting that TFAF-Net’s architecture is more robust in scenarios with fewer samples. This contrasts with models like CVCNN and ResNet2D, which show gradual improvements as the sample size increases, although they still do not surpass TFAF-Net.
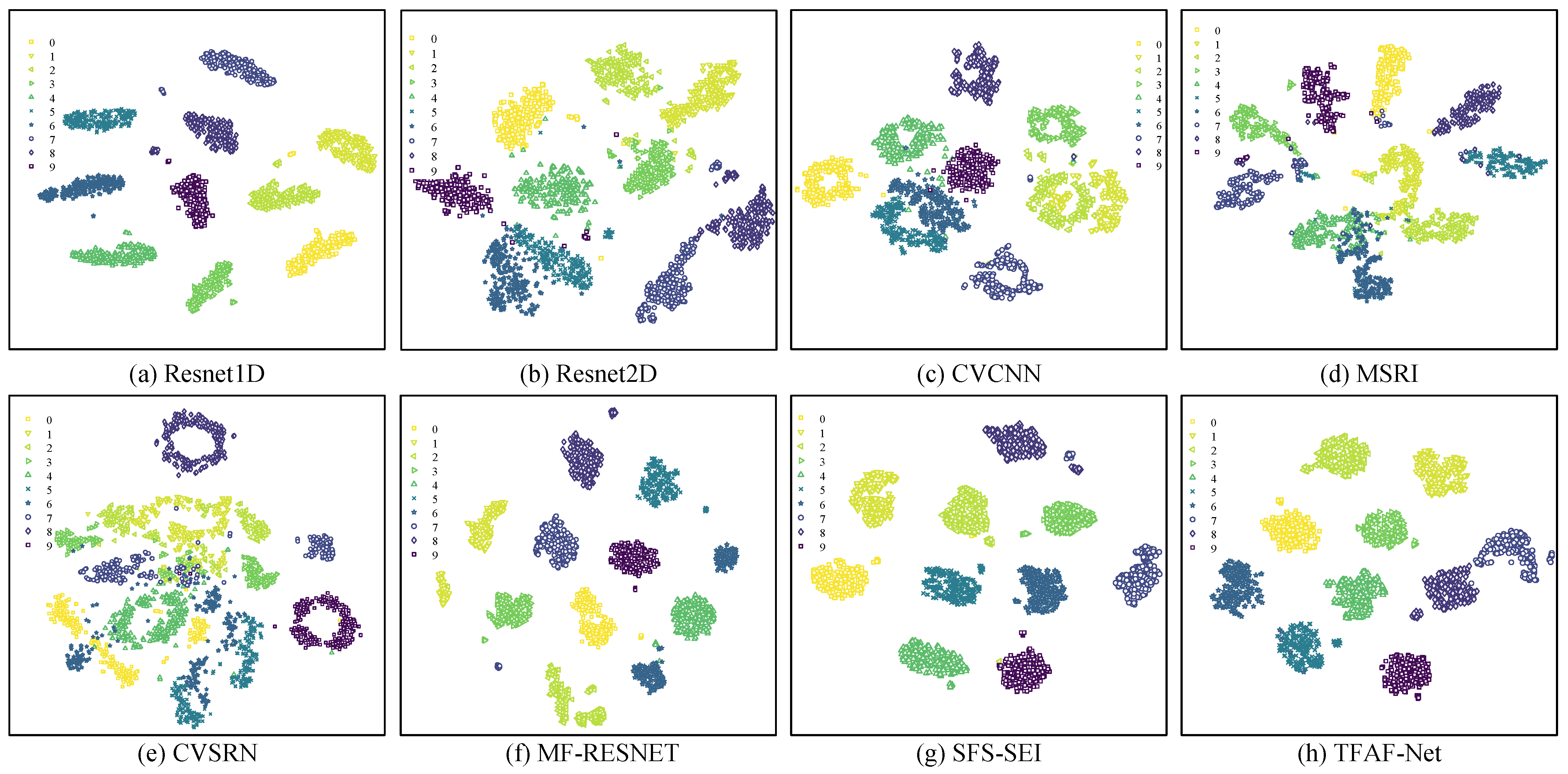
To assess the proficiency of TFAF-Net in extracting relevant features from RFFs, a rigorous comparative evaluation was undertaken, utilizing the ADS-B dataset and pitting it against established methodologies. Following the pre-training stage, the derived encoder was seamlessly integrated as RFF feature extractor. To visually illustrate the discriminative power of RFF, the dimensionality of the RFF features extracted by the encoder was condensed to two dimensions through the application of t-distributed stochastic neighbor embedding (t-SNE) [33], with the resulting visualization presented in Figure 10. The t-SNE visualizations reveal notable differences in the feature separability across models. CVCNN, MSRI, and ResNet2D exhibit substantial overlap in their extracted features, making it difficult to clearly distinguish between different categories. This indicates limitations in their ability to extract discriminative features. In contrast, models like ResNet1D, MF-RESNET, SFS-SEI, and TFAF-Net demonstrate significantly improved inter-class separability, with TFAF-Net showing superior organization of the feature space. While SFS-SEI exhibits some outlier behavior in a subset of the samples, TFAF-Net consistently maintains clear separability with minimal deviations among similar samples. This highlights TFAF-Net’s superior feature extraction capabilities and its enhanced ability to discriminate between different classes, outperforming the alternative models in terms of classification robustness and precision.
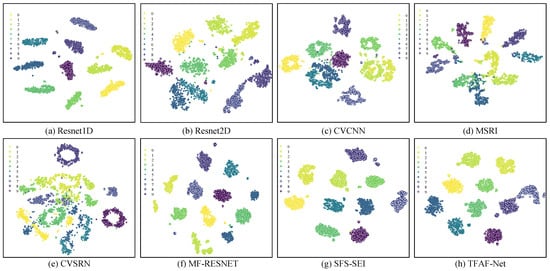
Figure 10.
Visualization of features extracted by models using t-SNE (10-way).
In conclusion, TFAF-Net demonstrates a highly effective balance between resource efficiency and classification accuracy. With relatively low FLOPs and a moderate number of parameters, it consistently outperforms other models, across various classification tasks. The t-SNE visualizations further validate its ability to extract highly discriminative features, reinforcing its effectiveness for complex classification tasks.
5.4. Ablation Studies
5.4.1. Ablation of Time-Frequency Fusion Module
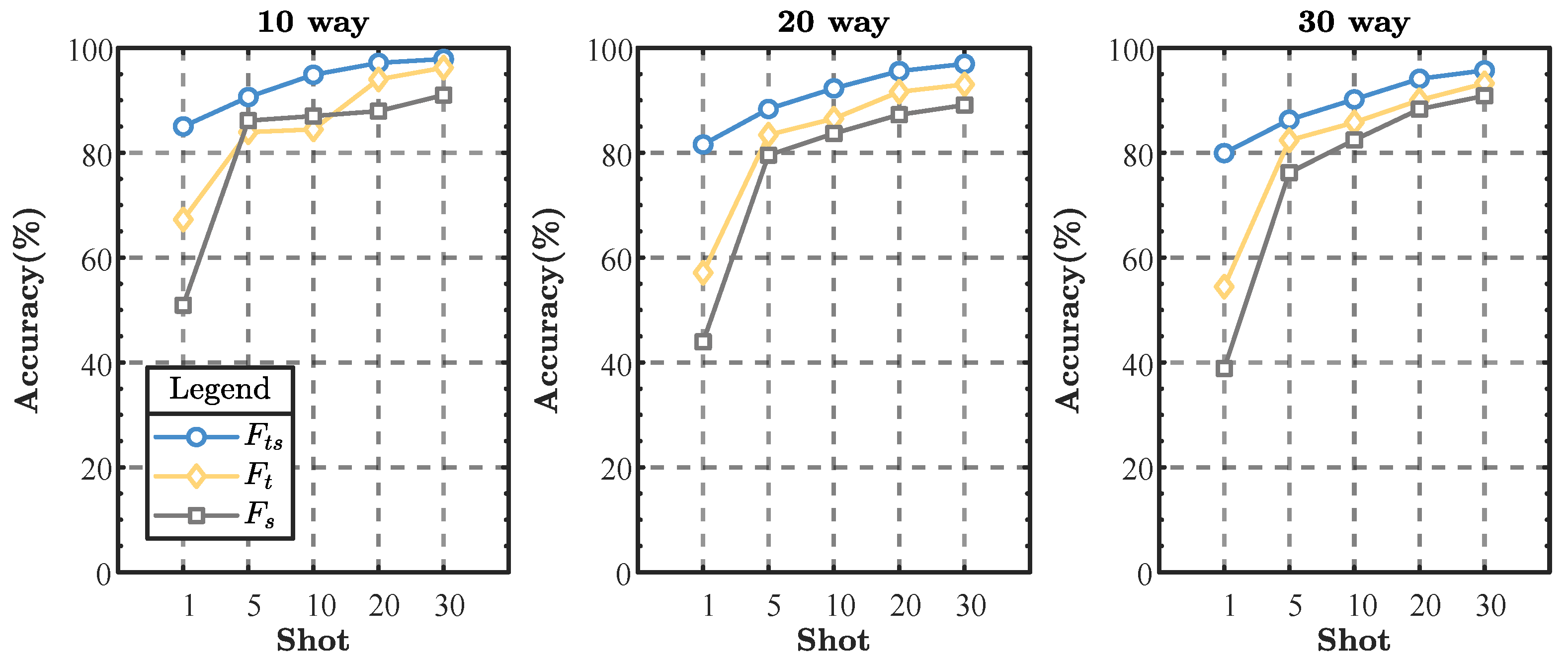
To validate the effectiveness of the time-frequency fusion module and the metric loss-based loss function, we conducted ablation studies on the ADS-B dataset. For the time-frequency fusion module, we compared the following three model configurations: (1). Models incorporating the complete time-frequency fusion module. (2). A model utilizing the original signal with sliding window processing but without the STFT-transformed time-frequency map. (3). A model excluding the original signal with sliding window processing but including the STFT-transformed time-frequency map.
From the results shown in Figure 11, it is evident that the complete time-frequency fusion module significantly outperforms the other two model configurations across all classification tasks. The complete time-frequency fusion module exhibits the highest recognition accuracy in the 10-way, 20-way, and 30-way classification tasks, verifying its superiority in capturing time-frequency features. This advantage becomes more pronounced as the number of categories increases, especially in the 30-way classification task, where the module shows significant performance improvement compared to the suboptimal model. The model using only raw signal sliding window processing outperforms the model using only STFT-transformed time-frequency maps in each classification task, suggesting that raw signal sliding window processing plays an important role in the feature extraction process. Although the model using only STFT-transformed time-frequency maps did not perform as well as the model that included the original signal with sliding window processing, its contribution was still significant in terms of increasing the richness of time-frequency features. In the complete time-frequency fusion module, the combination of STFT-transformed time-frequency maps and raw signal sliding window processing further improves model performance.
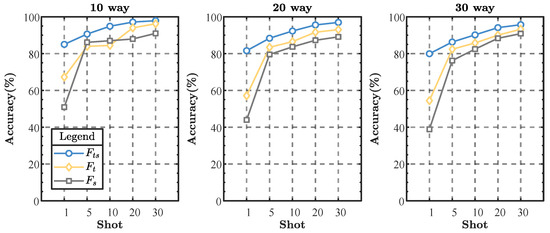
Figure 11.
The results of the ablation experiments of the time-frequency fusion module on the ADS-B dataset. denotes the time-frequency mapping using the 2D-aligned original signals and the STFT-transformed time-frequency maps, denotes the use of the 2D-aligned original signals only, and denotes the use of the STFT-transformed time-frequency maps only.
The ablation experiment results indicate that the comprehensive time-frequency fusion module substantially enhances the model’s recognition accuracy, affirming the module’s effectiveness and necessity in time-frequency feature extraction. Future research could focus on optimizing the fusion strategies of various features to further boost model performance.
5.4.2. Evaluation of Loss Function Configurations: Ablation and Comparison
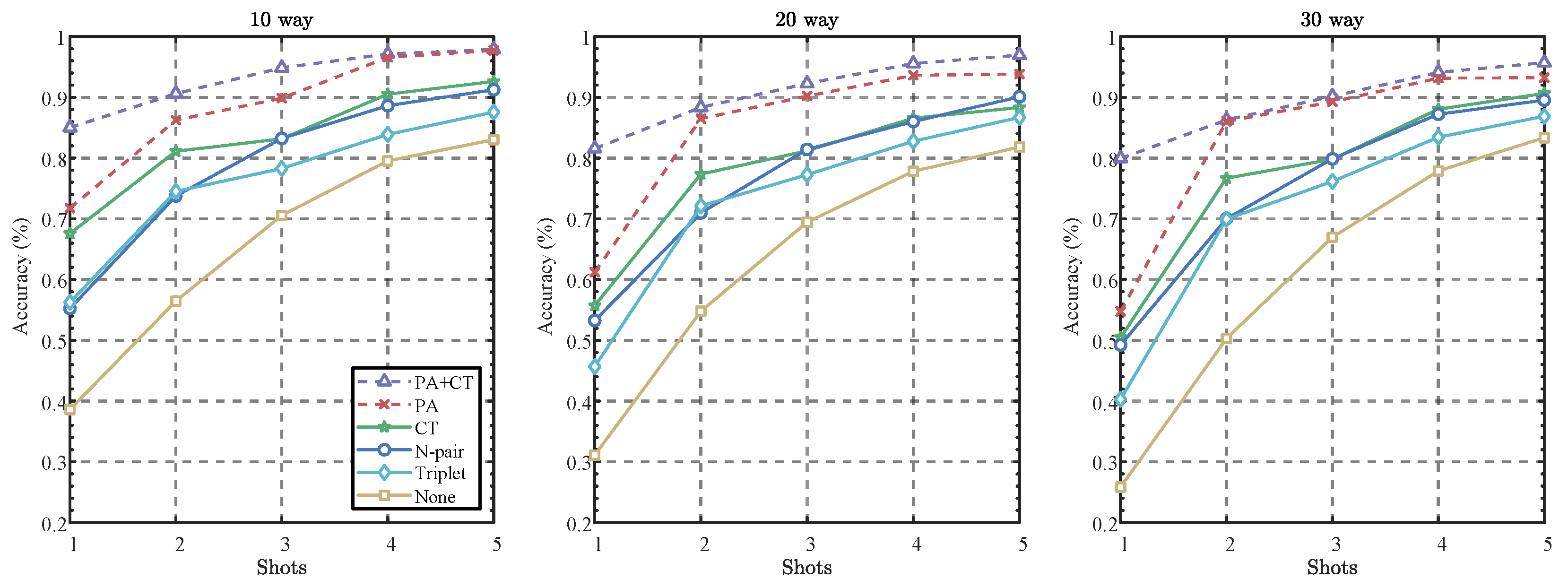
In this study, we aimed to assess the effectiveness of various loss function configurations within our model using the ADS-B dataset, as depicted in the accompanying Figure 12. Our experimental framework was anchored by a consistent baseline, specifically cross-entropy loss, which was uniformly applied across all configurations.
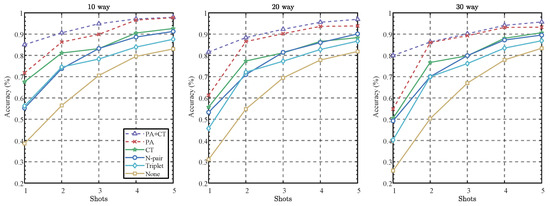
Figure 12.
Results of ablation and comparative experiments. “PA+CT” denotes the complete model configuration that integrates PA loss and CT loss in conjunction with cross-entropy loss. “PA” signifies the configuration employing only PA loss, while “CT” refers to the model utilizing only CT loss. “N-pair” and “Triplet” represent alternative loss functions for comparative analysis, as detailed in [34,35]. Lastly, “None” indicates the configuration that utilizes solely cross-entropy loss, devoid of any metric loss, serving as a baseline for performance evaluation.
We conducted a comprehensive ablation analysis of metric loss-based loss function, which integrated both PA loss and CT loss alongside cross-entropy loss. This analysis aimed to assess the impact of these losses on model performance, as illustrated in the accompanying experimental results figure. Notably, the exclusion of CT loss led to a significant decline in accuracy, decreasing from 85.02% in the 1-shot scenario to 97.71% in the 30-shot scenario for the 10-way classification task. This stark reduction underscores the critical role of CT loss in maintaining intra-class compactness, highlighting its importance in effective classification.
Similarly, the removal of PA loss led to reduced accuracy, ranging from 67.57% to 92.61% in the same classification context, highlighting its importance in enhancing inter-class separability. The most dramatic decline occurred when both PA and CT losses were omitted, yielding an accuracy as low as 25.84% in the 30-way classification with a 1-shot scenario. This stark outcome reinforces the necessity of these metric-based losses for optimal model functionality, emphasizing their essential roles in ensuring effective classification across various tasks and shot scenarios.
In addition to our ablation study, we conducted comparative experiments using N-pair and Triplet loss functions. While these methods yielded improvements over configurations that excluded either PA or CT loss, they did not achieve the accuracy levels of the complete model. Both N-pair and Triplet losses demonstrated effective inter-class separability; however, they fell short in overall performance when compared to the integrated approach of PA, CT, and cross-entropy loss.
In summary, our findings underscore the importance of integrating both PA loss and CT loss within the framework of cross-entropy loss. The results of our ablation study clearly demonstrate that these metric-based losses are essential for enhancing intra-class compactness and inter-class separability. Additionally, our comparative analysis with alternative loss functions further validates the superiority of the complete model configuration, affirming its effectiveness across various classification tasks and shot scenarios. This confirms the effectiveness and necessity of these loss functions in improving both intra-class compactness and inter-class separability across different classification tasks and shot scenarios.
6. Conclusions
In this paper, TFAF-Net is presented as an innovative approach to FS-SEI, integrating attention-driven fusion of time-frequency information, a metric-based loss module, and knowledge transfer. This method effectively addresses the challenges of SEI in data-limited scenarios. Through a two-phase process involving supervised pre-training with a labeled auxiliary dataset and subsequent fine-tuning with minimal labeled samples, TFAF-Net demonstrates significant performance improvements. On the ADS-B dataset, TFAF-Net achieves 9.59% higher accuracy in 30-way 1-shot classification compared to the second-best model. In the 10-way and 20-way settings, it shows gains of up to 6.01% and 7.32%, respectively, over the second-best model. On the Wi-Fi dataset, TFAF-Net achieves 90.39% accuracy in 5-way 1-shot classification, representing a 6.28% advantage over the next best model, and a 13.18% higher accuracy in the 6-way task.
Future directions for this research include incorporating self-supervised pre-training to maximize the utility of unlabeled data and refining the time-frequency fusion module to optimize feature extraction processes. These enhancements aim to further bolster the efficacy and applicability of FS-SEI methodologies in real-world scenarios.
Author Contributions
Conceptualization, Y.Z., S.M. and S.C.; Methodology, Y.Z. and S.C.; Software, Y.Z.; Validation, Y.Z.; Data curation, Y.Z.; Writing—original draft, Y.Z. and S.C.; Supervision, S.Y., Z.F., Y.Z. and S.C.; Funding acquisition, S.Y., Z.F. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (Nos.U22B2018, 62276205); Qin chuangyuan “Scientist + Engineer” Team Construction Project of Shaanxi Province Under No.2022KXJ-157.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Junyi Zhang was employed by the company 54th Research Institute of China Electronics Technology Group Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Liu, P.; Guo, L.; Zhao, H.; Shang, P.; Chu, Z.; Lu, X. A Long Time Span-Specific Emitter Identification Method Based on Unsupervised Domain Adaptation. Remote Sens. 2023, 15, 5214. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, C.; Feng, Y.; Bao, S. FSK Emitter Fingerprint Feature Extraction Method Based on Instantaneous Frequency. In Proceedings of the 2023 IEEE 23rd International Conference on Communication Technology (ICCT), Wuxi, China, 20–22 October 2023; pp. 397–402. [Google Scholar]
- Liu, Y.; Wang, J.; Li, J.; Niu, S.; Song, H. Machine Learning for the Detection and Identification of Internet of Things Devices: A Survey. IEEE Internet Things J. 2022, 9, 298–320. [Google Scholar] [CrossRef]
- Feng, Z.; Chen, S.; Ma, Y.; Gao, Y.; Yang, S. Learning Temporal–Spectral Feature Fusion Representation for Radio Signal Classification. IEEE Trans. Ind. Inform. 2024, 1–10. [Google Scholar] [CrossRef]
- Wiley, R. ELINT: The Interception and Analysis of Radar Signals; Artech: Norwood, MA, USA, 2006. [Google Scholar]
- Zhang, X.; Li, T. Specific Emitter Identification Based on Feature Diagram Superposition. In Proceedings of the 2022 7th International Conference on Integrated Circuits and Microsystems (ICICM), Xi’an, China, 28–31 October 2022; pp. 703–707. [Google Scholar]
- Jing, Z.; Li, P.; Wu, B.; Yan, E.; Chen, Y.; Gao, Y. Attention-Enhanced Dual-Branch Residual Network with Adaptive L-Softmax Loss for Specific Emitter Identification under Low-Signal-to-Noise Ratio Conditions. Remote Sens. 2024, 16, 1332. [Google Scholar] [CrossRef]
- Su, J.; Liu, H.; Yang, L. Specific Emitter Identification Based on CNN via Variational Mode Decomposition and Bimodal Feature Fusion. In Proceedings of the 2023 IEEE 3rd International Conference on Power, Electronics and Computer Applications (ICPECA), Shenyang, China, 29–31 January 2023; pp. 539–543. [Google Scholar]
- Wu, T.; Zhang, Y.; Ben, C.; Peng, Y.; Liu, P.; Gui, G. Specific Emitter Identification Based on Multi-Scale Attention Feature Fusion Network. In Proceedings of the 2023 IEEE 23rd International Conference on Communication Technology (ICCT), Wuxi, China, 20–22 October 2023; pp. 1390–1394. [Google Scholar]
- Wang, Y.; Gui, G.; Gacanin, H.; Ohtsuki, T.; Dobre, O.A.; Poor, H.V. An Efficient Specific Emitter Identification Method Based onComplex-Valued Neural Networks and Network Compression. IEEE J. Sel. Areas Commun. 2021, 39, 2305–2317. [Google Scholar] [CrossRef]
- Zhu, M.; Feng, Z.; Zhou, X. A novel data-driven specific emitter identification feature based on machine cognition. Electronics 2020, 9, 1308. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer: Cham, Switzerland, 2018; pp. 3–19. [Google Scholar]
- Man, P.; Ding, C.; Ren, W.; Xu, G. A Specific Emitter Identification Algorithm under Zero Sample Condition Based on Metric Learning. Remote Sens. 2021, 13, 4919. [Google Scholar] [CrossRef]
- Huang, J.; Li, X.; Wu, B.; Wu, X.; Li, P. Few-Shot Radar Emitter Signal Recognition Based on Attention-Balanced Prototypical Network. Remote Sens. 2022, 14, 6101. [Google Scholar] [CrossRef]
- Kim, S.; Kim, D.; Cho, M.; Kwak, S. Proxy Anchor Loss for Deep Metric Learning. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 3235–3244. [Google Scholar]
- Wen, Y.; Zhang, K.; Li, Z.; Qiao, Y. A Discriminative Feature Learning Approach for Deep Face Recognition. In Proceedings of the Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Zhao, Y.; Yang, R.; Wu, L.; He, S.; Niu, J.; Zhao, L. Specific Emitter Identification Using Regression Analysis between Individual Features and Physical Parameters. In Proceedings of the 2022 6th International Conference on Imaging, Signal Processing and Communications (ICISPC), Kumamoto, Japan, 22–24 July 2022; pp. 48–52. [Google Scholar]
- Pan, Y.; Yang, S.; Peng, H.; Li, T.; Wang, W. Specific emitter identification based on deep residual networks. IEEE Access 2019, 7, 54425–54434. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, X.; Lin, Z.; Huang, Z. Multi-Classifier Fusion for Open-Set Specific Emitter Identification. Remote Sens. 2022, 14, 2226. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Zhang, Y.; Lin, Y.; Gui, G.; Tomoaki, O.; Sari, H. Data Augmentation Aided Few-Shot Learning for Specific Emitter Identification. In Proceedings of the 2022 IEEE 96th Vehicular Technology Conference (VTC2022-Fall), London, UK, 26–29 September 2022; pp. 1–5. [Google Scholar]
- Yao, Z.; Fu, X.; Guo, L.; Wang, Y.; Lin, Y.; Shi, S.; Gui, G. Few-Shot Specific Emitter Identification Using Asymmetric Masked Auto-Encoder. IEEE Commun. Lett. 2023, 27, 2657–2661. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, Z.; Yue, G. Siamese Network-based Open Set Identification of Communications Emitters with Comprehensive Features. In Proceedings of the 2021 6th International Conference on Communication, Image and Signal Processing (CCISP), Chengdu, China, 19–21 November 2021; pp. 408–412. [Google Scholar]
- Wang, C.; Fu, X.; Wang, Y.; Gui, G.; Gacanin, H.; Sari, H.; Adachi, F. Interpolative Metric Learning for Few-Shot Specific Emitter Identification. IEEE Trans. Veh. Technol. 2023, 72, 16851–16855. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, B.; Ding, G.; Wei, Y.; Wei, G.; Wang, J.; Guo, D. Specific Emitter Identification with Limited Samples: A Model-Agnostic Meta-Learning Approach. IEEE Commun. Lett. 2022, 26, 345–349. [Google Scholar] [CrossRef]
- Sankhe, K.; Belgiovine, M.; Zhou, F.; Riyaz, S.; Ioannidis, S.; Chowdhury, K. ORACLE: Optimized Radio clAssification through Convolutional neuraL nEtworks. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 370–378. [Google Scholar]
- Liu, M.; Chai, Y.; Li, M.; Wang, J.; Zhao, N. Transfer Learning-Based Specific Emitter Identification for ADS-B over Satellite System. Remote Sens. 2024, 16, 2068. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Zhimian, Z.; Haipeng, W.; Xu, F.; Jin, Y.-Q. Complex-Valued Convolutional Neural Network and Its Application in Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar]
- Qian, Y.; Qi, J.; Kuai, X.; Han, G.; Sun, H.; Hong, S. Specific Emitter Identification Based on Multi-Level Sparse Representation in Automatic Identification System. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2872–2884. [Google Scholar] [CrossRef]
- Han, G.; Xu, Z.; Zhu, H.; Ge, Y.; Peng, J. A Two-Stage Model Based on a Complex-Valued Separate Residual Network for Cross-Domain IIoT Devices Identification. IEEE Trans. Ind. Inform. 2024, 20, 2589–2599. [Google Scholar] [CrossRef]
- Ying, W.; Deng, P.; Hong, S. Channel Attention Mechanism-based Multi-Feature Fusion Network for Specific Emitter Identification. In Proceedings of the 2022 IEEE 4th International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Dali, China, 12–14 October 2022; pp. 1325–1328. [Google Scholar]
- Tao, M.; Fu, X.; Lin, Y.; Wang, Y.; Yao, Z.; Shi, S.; Gui, G. Resource-Constrained Specific Emitter Identification Using End-to-End Sparse Feature Selection. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 6067–6072. [Google Scholar]
- van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Sohn, K. Improved deep metric learning with multi-class n-pair loss objective. Adv. Neural Inf. Process. Syst. 2016, 29, 1857–1865. [Google Scholar]
- Hoffer, E.; Ailon, N. Deep metric learning using triplet network. In Proceedings of the Similarity-Based Pattern Recognition: Third International Workshop, SIMBAD 2015, Copenhagen, Denmark, 12–14 October 2015; Springer: Cham, Switzerland, 2015; pp. 84–92. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).