LULC-SegNet: Enhancing Land Use and Land Cover Semantic Segmentation with Denoising Diffusion Feature Fusion
Abstract
:1. Introduction
- (1)
- Introduction of the semantic features of the DDPM architecture into LULC segmentation and injecting semantic features into the CNN feature extraction network to address information;
- (2)
- Combining machine learning clustering algorithms and spatial attention mechanisms, and efficiently extracting the DDPM semantic features for LULC segmentation;
- (3)
- Verifying the significant effect of the DDPM on improving the performance of remote sensing image LULC segmentation through detailed ablation experiments and comparative studies.
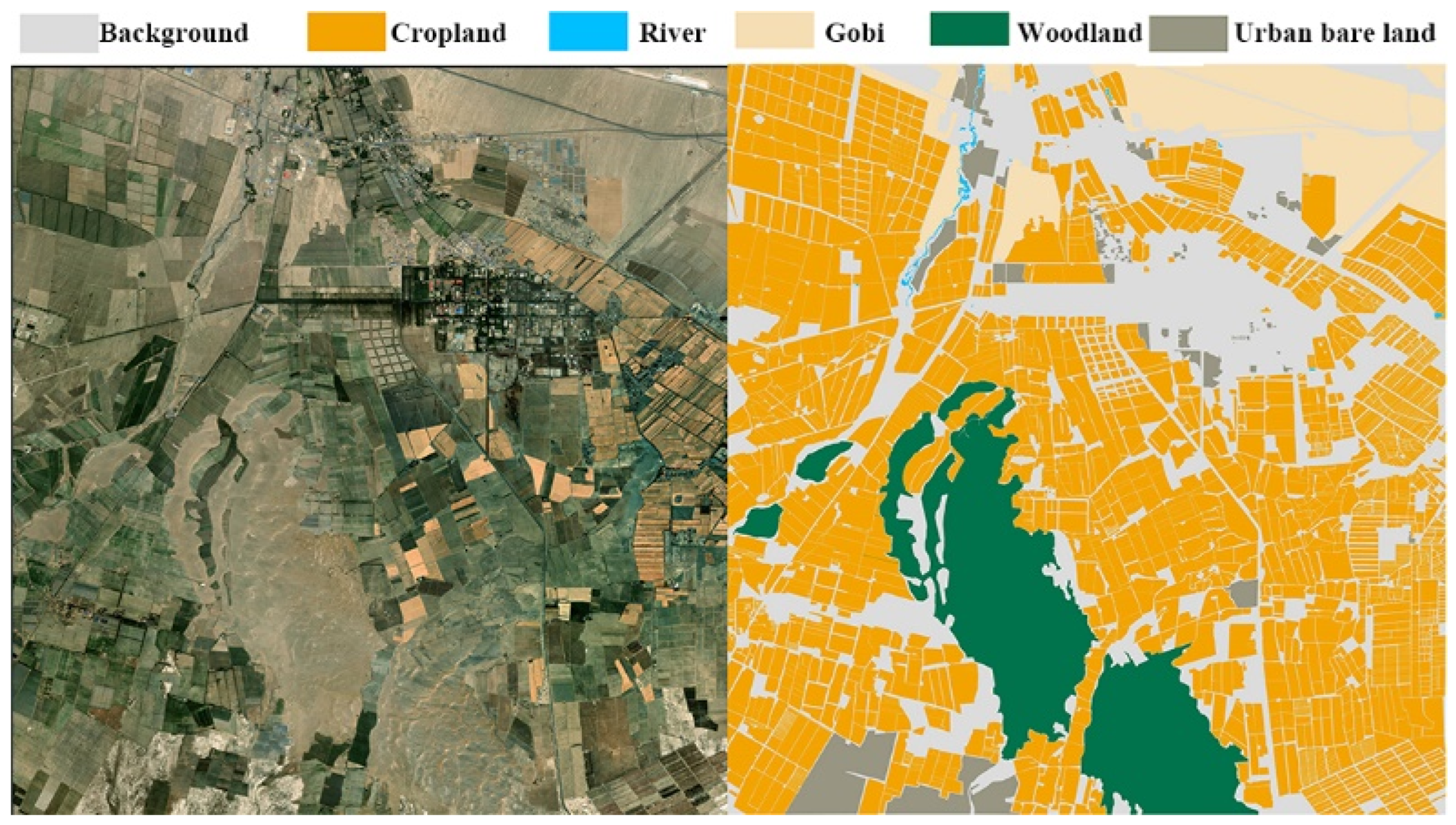
2. Study Area and Dataset
3. Materials and Methods
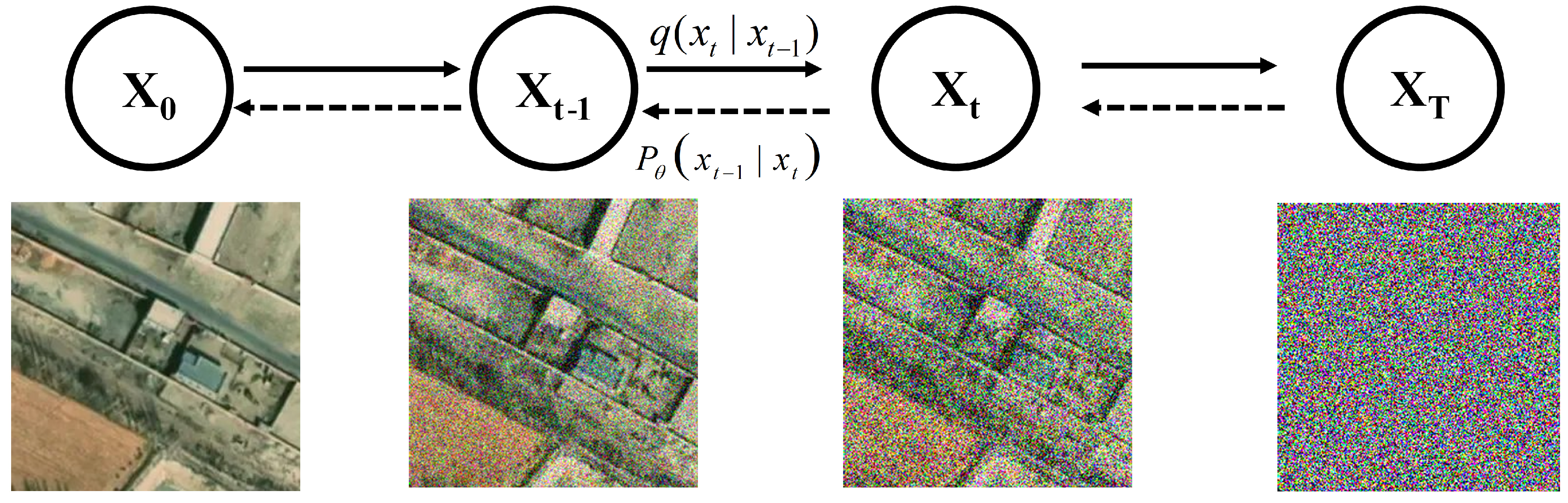
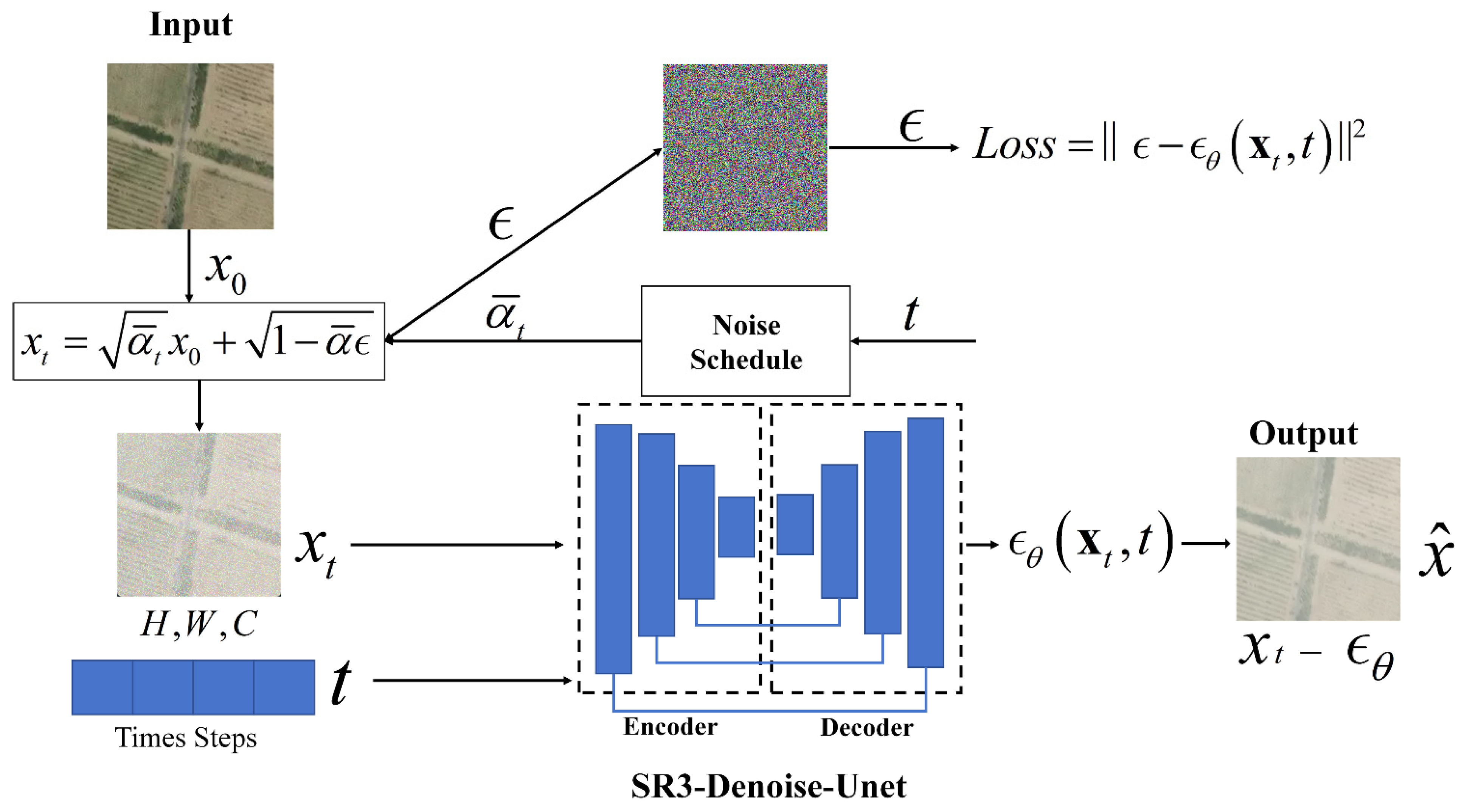
3.1. Denoise Diffusion Probabilistic Model
3.2. Unsupervised Image Generation Based on DDPM
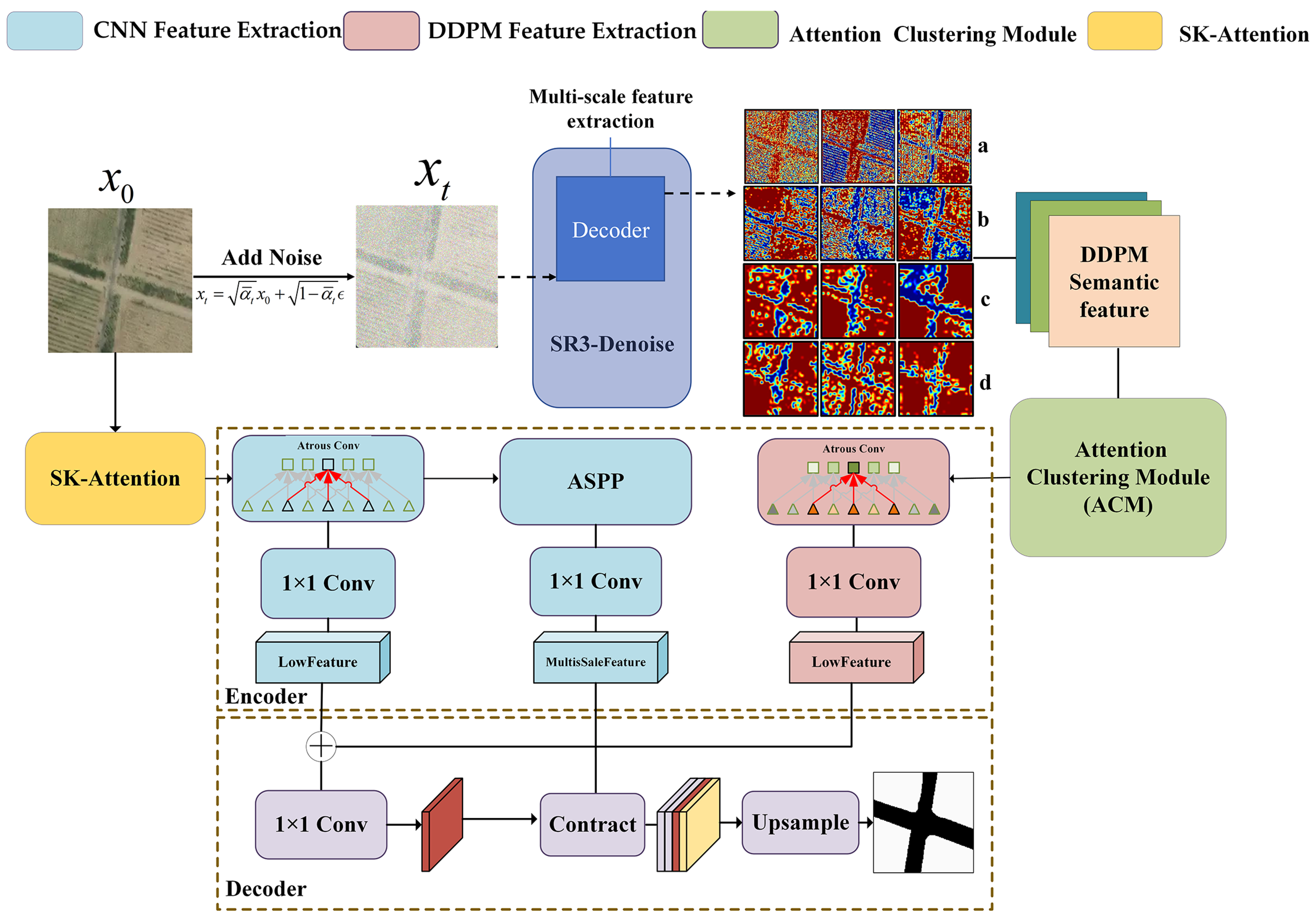
3.3. LULC Semantic Segmentation Network
3.4. Hybridization Loss Function
3.5. Evaluation Metric
4. Result
4.1. Experimental Details
4.2. ACM in the DDPM Ablation Study
4.3. LULC Segmentation Network Ablation Study
4.4. LULC Segmentation Network Quantitative Comparison Experimental Results
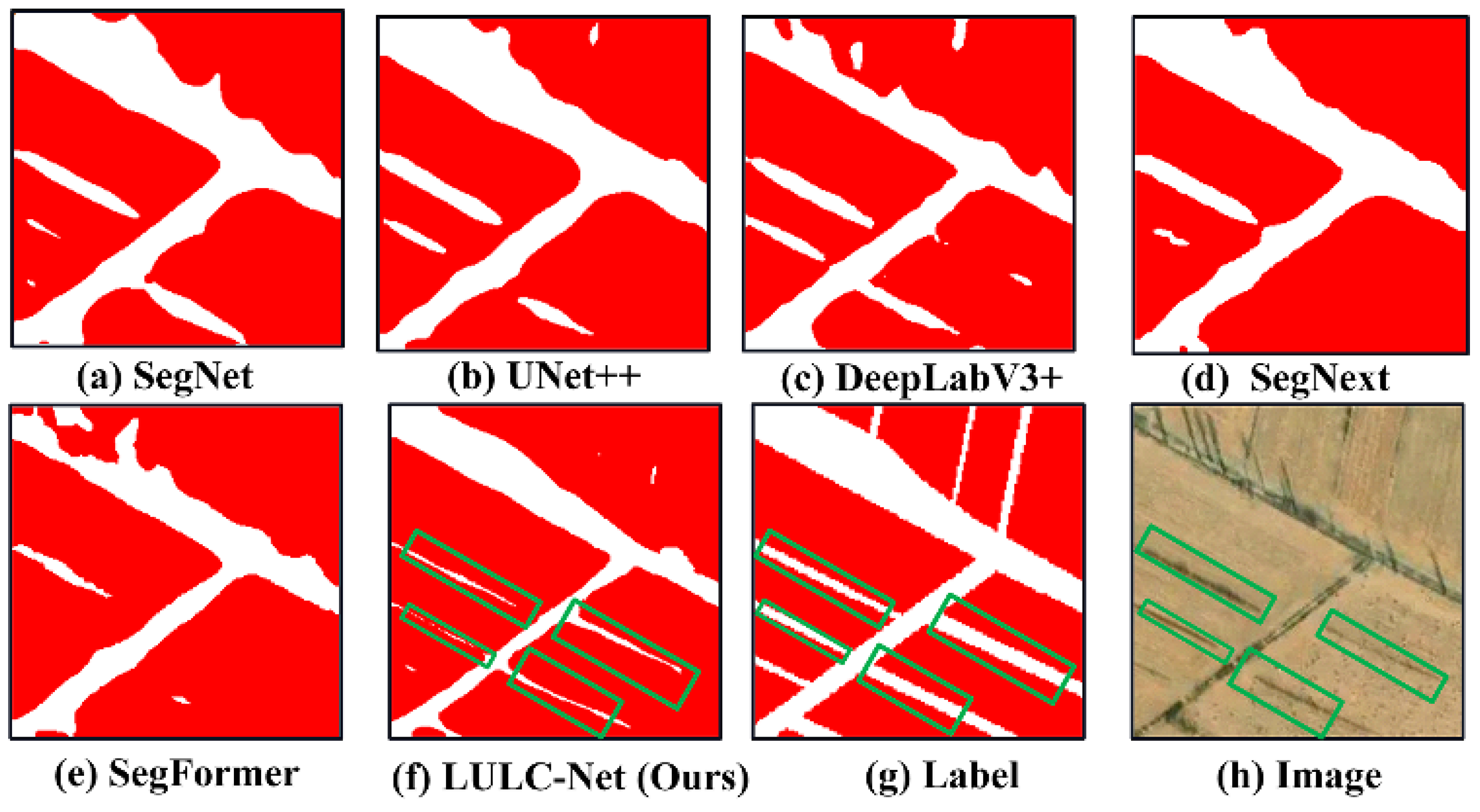
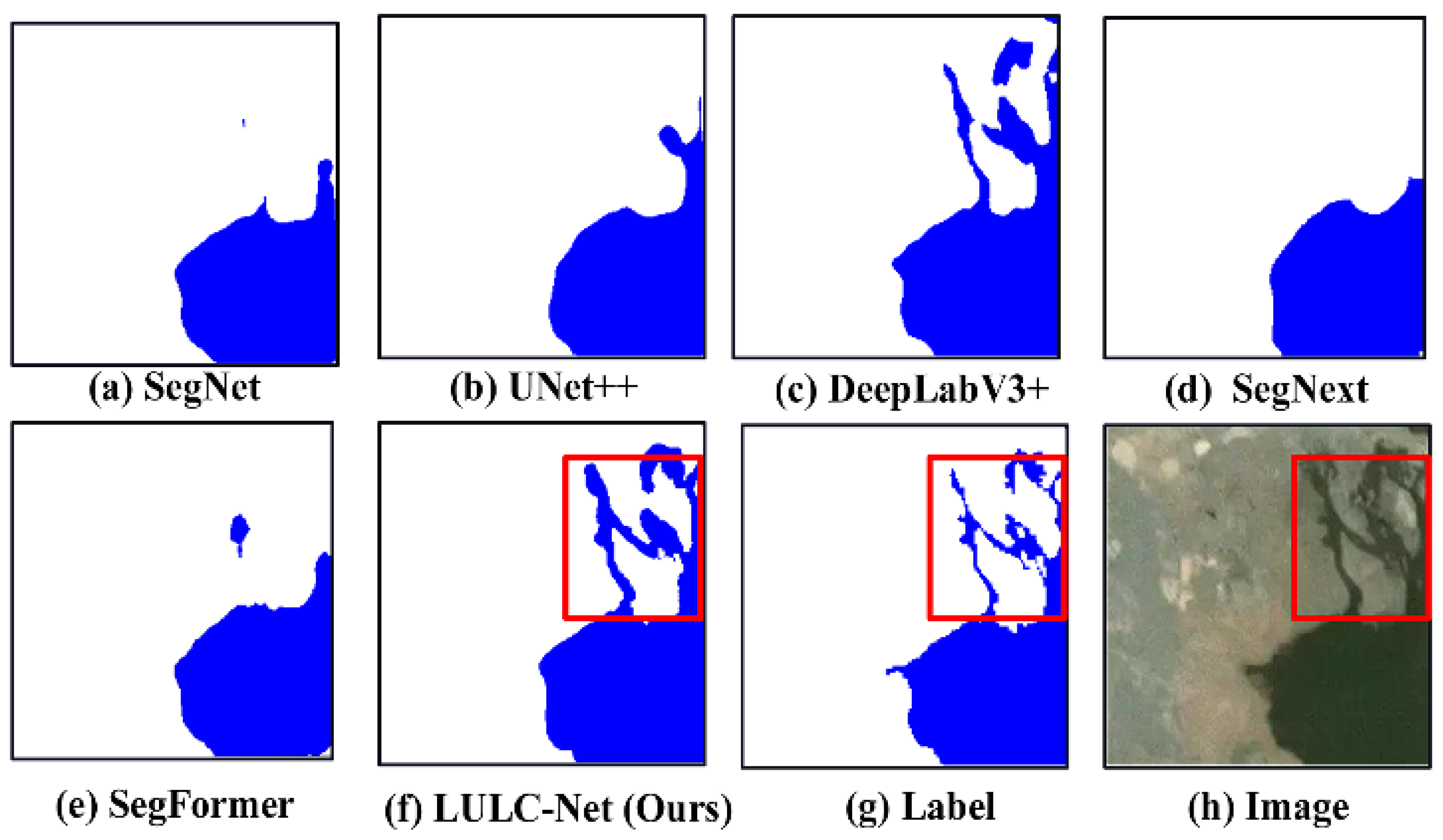
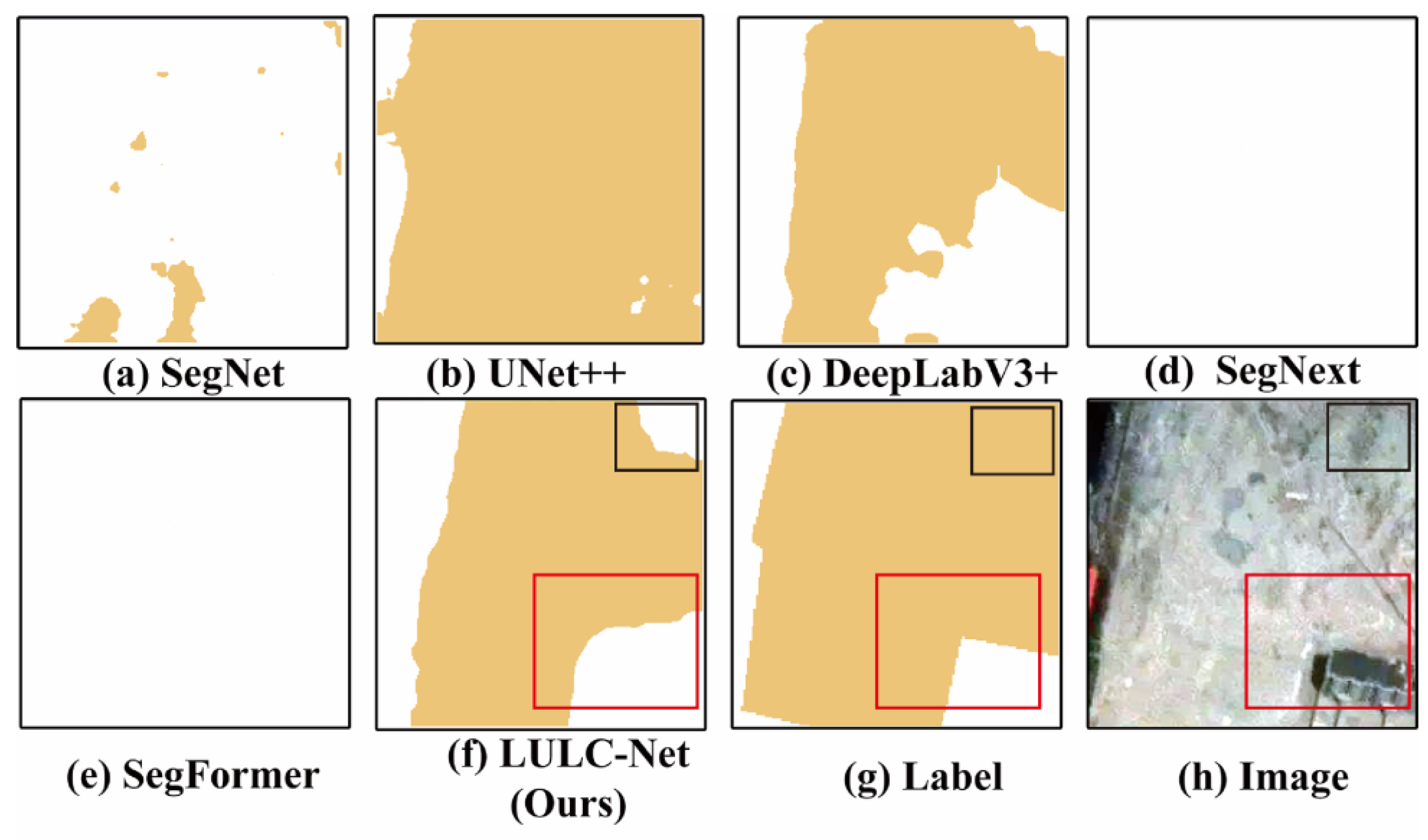
4.5. LULC Segmentation Network Visualization Results
5. Discussion
6. Conclusions
- (1)
- In this study, we designed and implemented the LULC semantic segmentation network integrated with the semantic features of the DDPM decoder, alleviating the information bottleneck of deep networks and enhancing the segmentation performance of LULC. The experimental results indicate that (1) the LULC segmentation performance improved. Compared with the mainstream semantic segmentation models, the LULC-SegNet achieved an 80.25% MIOU on the test set, surpassing other models. The network performs well with training samples that have highly imbalanced classes. Visual quality analysis demonstrates that, because of the integration of DDPM’s semantic features, the proposed network can more accurately delineate feature contours and detailed characteristics, significantly improving segmentation accuracy and effectively alleviating the information bottleneck of deep networks.
- (2)
- The advantages of independent feature extractors are as follows: We demonstrated that the DDPM can function as an independent feature extractor trained using unsupervised methods. This training mechanism avoids dependence on labeled data, making it especially suitable for handling large volumes of remote sensing data. Furthermore, the weights of the upstream diffusion model feature extractor are frozen, and the parameters of the downstream lightweight LULC segmentation model are adjusted, facilitating feature transfer for various types of remote sensing image segmentation.
- (3)
- We constructed a high-resolution remote sensing image dataset with a class imbalance to meet the requirements of the LULC segmentation tasks, particularly addressing the class imbalance characteristics of the sample categories in the Circum-Tarim region.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, Y.; Sha, Z.; Yu, M. Remote Sensing Imagery in Vegetation Mapping: A Review. J. Plant Ecol. 2008, 1, 9–23. [Google Scholar] [CrossRef]
- Vemuri, R.K.; Reddy, P.C.S.; Puneeth Kumar, B.S.; Ravi, J.; Sharma, S.; Ponnusamy, S. Deep Learning Based Remote Sensing Technique for Environmental Parameter Retrieval and Data Fusion from Physical Models. Arab. J. Geosci. 2021, 14, 1230. [Google Scholar] [CrossRef]
- Qi, W. Object Detection in High Resolution Optical Image Based on Deep Learning Technique. Nat. Hazards Res. 2022, 2, 384–392. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Yang, K.; Wang, L.; Su, F.; Chen, X. Semantic Segmentation of High-Resolution Remote Sensing Images Based on a Class Feature Attention Mechanism Fused with Deeplabv3+. Comput. Geosci. 2022, 158, 104969. [Google Scholar] [CrossRef]
- Wang, M.; Du, H.; Xu, S.; Surname, G.N. Remote Sensing Image Segmentation of Ground Objects Based on Improved Deeplabv3+. In Proceedings of the 2022 IEEE International Conference on Industrial Technology (ICIT), Shanghai, China, 22–25 August 2022; pp. 1–6. [Google Scholar]
- Li, X.; Li, Y.; Ai, J.; Shu, Z.; Xia, J.; Xia, Y. Semantic Segmentation of UAV Remote Sensing Images Based on Edge Feature Fusing and Multi-Level Upsampling Integrated with Deeplabv3. PLoS ONE 2023, 18, e0279097. [Google Scholar] [CrossRef]
- Shun, Z.; Li, D.; Jiang, H.; Li, J.; Peng, R.; Lin, B.; Liu, Q.; Gong, X.; Zheng, X.; Liu, T. Research on Remote Sensing Image Extraction Based on Deep Learning. PeerJ Comput. Sci. 2022, 8, e847. [Google Scholar] [CrossRef]
- Adegun, A.A.; Fonou Dombeu, J.V.; Viriri, S.; Odindi, J. State-of-the-Art Deep Learning Methods for Objects Detection in Remote Sensing Satellite Images. Sensors 2023, 23, 5849. [Google Scholar] [CrossRef]
- Zheng, X.; Huan, L.; Xia, G.-S.; Gong, J. Parsing Very High-Resolution Urban Scene Images by Learning Deep ConvNets with Edge-Aware Loss. ISPRS J. Photogramm. Remote Sens. 2020, 170, 15–28. [Google Scholar] [CrossRef]
- Huang, B.; Zhao, B.; Song, Y. Urban Land-Use Mapping Using a Deep Convolutional Neural Network with High Spatial Resolution Multispectral Remote Sensing Imagery. Remote Sens. Environ. 2018, 214, 73–86. [Google Scholar] [CrossRef]
- Sertel, E.; Ekim, B.; Ettehadi Osgouei, P.; Kabadayi, M.E. Land Use and Land Cover Mapping Using Deep Learning Based Segmentation Approaches and VHR Worldview-3 Images. Remote Sens. 2022, 14, 4558. [Google Scholar] [CrossRef]
- Usmani, M.; Napolitano, M.; Bovolo, F. Towards Global Scale Segmentation with OpenStreetMap and Remote Sensing. ISPRS Open J. Photogramm. Remote Sens. 2023, 8, 100031. [Google Scholar] [CrossRef]
- Rousset, G.; Despinoy, M.; Schindler, K.; Mangeas, M. Assessment of Deep Learning Techniques for Land Use Land Cover Classification in Southern New Caledonia. Remote Sens. 2021, 13, 2257. [Google Scholar] [CrossRef]
- Zhang, P.; Ke, Y.; Zhang, Z.; Wang, M.; Li, P.; Zhang, S. Urban Land Use and Land Cover Classification Using Novel Deep Learning Models Based on High Spatial Resolution Satellite Imagery. Sensors 2018, 18, 3717. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Proceedings of the 18th International Conference, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Clark, A.; Phinn, S.; Scarth, P. Optimised U-Net for Land Use–Land Cover Classification Using Aerial Photography. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2023, 91, 125–147. [Google Scholar] [CrossRef]
- Wang, J.; Yang, M.; Chen, Z.; Lu, J.; Zhang, L. An MLC and U-Net Integrated Method for Land Use/Land Cover Change Detection Based on Time Series NDVI-Composed Image from PlanetScope Satellite. Water 2022, 14, 3363. [Google Scholar] [CrossRef]
- Ding, M.; Xiao, B.; Codella, N.; Luo, P.; Wang, J.; Yuan, L. DaViT: Dual Attention Vision Transformers. In Proceedings of the 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer Nature Switzerland: Cham, Switzerland, 2022; pp. 74–92. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Zheng, W.; Feng, J.; Gu, Z.; Zeng, M. A Stage-Adaptive Selective Network with Position Awareness for Semantic Segmentation of LULC Remote Sensing Images. Remote Sens. 2023, 15, 2811. [Google Scholar] [CrossRef]
- Scheibenreif, L.; Hanna, J.; Mommert, M.; Borth, D. Self-Supervised Vision Transformers for Land-Cover Segmentation and Classification. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 18–24 June 2022; pp. 1421–1430. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep Learning and the Information Bottleneck Principle. In Proceedings of the 2015 IEEE Information Theory Workshop (ITW), Jerusalem, Israel, 26 April–1 May 2015; pp. 1–5. [Google Scholar]
- Saharia, C.; Chan, W.; Chang, H.; Lee, C.A.; Ho, J.; Salimans, T.; Fleet, D.J.; Norouzi, M. Palette: Image-to-Image Diffusion Models. In Proceedings of the SIGGRAPH‘22: Special Interest Group on Computer Graphics and Interactive Techniques Conference, Vancouver, BC, Canada, 7–11 August 2022. [Google Scholar]
- Saharia, C.; Ho, J.; Chan, W.; Salimans, T.; Fleet, D.J.; Norouzi, M. Image Super-Resolution via Iterative Refinement. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 4713–4726. [Google Scholar] [CrossRef]
- Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. Progressive Growing of GANs for Improved Quality, Stability, and Variation. arXiv 2017, arXiv:1710.10196. [Google Scholar]
- Menick, J.; Kalchbrenner, N. Generating High Fidelity Images with Subscale Pixel Networks and Multidimensional Upscaling. arXiv 2018, arXiv:1812.01608. [Google Scholar]
- Lin, C.-H.; Yumer, E.; Wang, O.; Shechtman, E.; Lucey, S. ST-GAN: Spatial Transformer Generative Adversarial Networks for Image Compositing. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9455–9464. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Advances in Neural Information Processing Systems 27, Proceedings of the Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; pp. 2672–2680. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Kingma, D.P.; Welling, M. An Introduction to Variational Autoencoders. FNT Mach. Learn. 2019, 12, 307–392. [Google Scholar] [CrossRef]
- Souly, N.; Spampinato, C.; Shah, M. Semi Supervised Semantic Segmentation Using Generative Adversarial Network. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 5689–5697. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. In Advances in Neural Information Processing Systems 33, Proceedings of the Annual Conference on Neural Information Processing Systems (NeurIPS 2020), Virtual, 6–12 December 2020; MIT Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Gedara Chaminda Bandara, W.; Gopalakrishnan Nair, N.; Patel, V.M. DDPM-CD: Denoising Diffusion Probabilistic Models as Feature Extractors for Change Detection. arXiv 2022, arXiv:2206.11892. [Google Scholar]
- Yao, J.; Chen, Y.; Guan, X.; Zhao, Y.; Chen, J.; Mao, W. Recent Climate and Hydrological Changes in a Mountain–Basin System in Xinjiang, China. Earth-Sci. Rev. 2022, 226, 103957. [Google Scholar] [CrossRef]
- Hong, Z.; Jian-Wei, W.; Qiu-Hong, Z.; Yun-Jiang, Y. A Preliminary Study of Oasis Evolution in the Tarim Basin, Xinjiang, China. J. Arid Environ. 2003, 55, 545–553. [Google Scholar] [CrossRef]
- Karras, T.; Aittala, M.; Aila, T.; Laine, S. Elucidating the Design Space of Diffusion-Based Generative Models. arXiv 2022, arXiv:2206.00364. [Google Scholar]
- Fan, J.; Shi, Z.; Ren, Z.; Zhou, Y.; Ji, M. DDPM-SegFormer: Highly Refined Feature Land Use and Land Cover Segmentation with a Fused Denoising Diffusion Probabilistic Model and Transformer. Int. J. Appl. Earth Obs. Geoinf. 2024, 133, 104093. [Google Scholar] [CrossRef]
- Saharia, C.; Ho, J.; Chan, W.; Salimans, T.; Fleet, D.J.; Norouzi, M. Image Super-Resolution via Iterative Refinement. arXiv 2021, arXiv:2104.07636. [Google Scholar]
- Baranchuk, D.; Rubachev, I.; Voynov, A.; Khrulkov, V.; Babenko, A. Label-Efficient Semantic Segmentation with Diffusion Models. arXiv 2021, arXiv:2112.03126. [Google Scholar]
- Li, H.; Yang, Y.; Chang, M.; Chen, S.; Feng, H.; Xu, Z.; Li, Q.; Chen, Y. SRDiff: Single Image Super-Resolution with Diffusion Probabilistic Models. Neurocomputing 2022, 479, 47–59. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Hu, X.; Yang, J. Selective Kernel Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 510–519. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y. Dual Attention Network for Scene Segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar] [CrossRef]
- Guo, H.; Jin, X.; Jiang, Q.; Wozniak, M.; Wang, P.; Yao, S. DMF-Net: A Dual Remote Sensing Image Fusion Network Based on Multiscale Convolutional Dense Connectivity with Performance Measure. IEEE Trans. Instrum. Meas. 2024, 73, 1–15. [Google Scholar] [CrossRef]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV 2018), Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 833–851. [Google Scholar]
- Roy, A.G.; Navab, N.; Wachinger, C. Concurrent Spatial and Channel ‘Squeeze & Excitation’ in Fully Convolutional Networks. In Medical Image Computing and Computer Assisted Intervention (MICCAI 2018), Proceedings of the 21st International Conference, Granada, Spain, 16–20 September 2018; Frangi, A.F., Schnabel, J.A., Davatzikos, C., Alberola-López, C., Fichtinger, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 11070, pp. 421–429. [Google Scholar]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the Number of Clusters in a Data Set Via the Gap Statistic. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2999–3007. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.-A. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Zhang, Y.; Fan, J.; Zhang, M.; Shi, Z.; Liu, R.; Guo, B. A Recurrent Adaptive Network: Balanced Learning for Road Crack Segmentation with High-Resolution Images. Remote Sens. 2022, 14, 3275. [Google Scholar] [CrossRef]
- Zhang, Z.; Sabuncu, M.R. Generalized Cross Entropy Loss for Training Deep Neural Networks with Noisy Labels. In Advances in Neural Information Processing Systems 31, Proceedings of the Annual Conference on Neural Information Processing Systems 2018 (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018; Curran Associates Inc.: Red Hook, NY, USA, 2018; pp. 8792–8802. [Google Scholar]
- Dickson, M.C.; Bosman, A.S.; Malan, K.M. Hybridised Loss Functions for Improved Neural Network Generalisation. In Pan-African Artificial Intelligence and Smart Systems, Procceedings of the First International Conference (PAAISS 2021), Windhoek, Namibia, 6–8 September 2021; Ngatched, T.M.N., Woungang, I., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 169–181. [Google Scholar]
- Jadon, S. A Survey of Loss Functions for Semantic Segmentation. In Proceedings of the 2020 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Via del Mar, Chile, 27–29 October 2020; pp. 1–7. [Google Scholar]
- Kalsotra, R.; Arora, S. Performance Analysis of U-Net with Hybrid Loss for Foreground Detection. Multimed. Syst. 2023, 29, 771–786. [Google Scholar] [CrossRef]
- Cheng, Q.; Li, H.; Wu, Q.; Ngi Ngan, K. Hybrid-Loss Supervision for Deep Neural Network. Neurocomputing 2020, 388, 78–89. [Google Scholar] [CrossRef]
- Yeung, M.; Sala, E.; Schönlieb, C.-B.; Rundo, L. Unified Focal Loss: Generalising Dice and Cross Entropy-Based Losses to Handle Class Imbalanced Medical Image Segmentation. Comput. Med. Imaging Graph. 2022, 95, 102026. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; ISBN 978-0-262-33737-3. [Google Scholar]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning Long-Term Dependencies with Gradient Descent Is Difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems 25, Proceedings of the 26th Annual Conference on Neural Information Processing Systems 2012, Lake Tahoe, NV, USA, 3–6 December 2012; Curran Associates, Inc.: Red Hook, NY, USA, 2012; Volume 25. [Google Scholar]
- Li, X.; Wang, W.; Wu, L.; Chen, S.; Hu, X.; Li, J.; Tang, J.; Yang, J. Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection. In Advances in Neural Information Processing Systems 33, Proceedings of the Annual Conference on Neural Information Processing Systems 2020 (NeurIPS 2020), Virtual, 6–12 December 2020; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 21002–21012. [Google Scholar]
- Qiu, S.; Cheng, X.; Lu, H.; Zhang, H.; Wan, R.; Xue, X.; Pu, J. Subclassified Loss: Rethinking Data Imbalance from Subclass Perspective for Semantic Segmentation. IEEE Trans. Intell. Veh. 2024, 9, 1547–1558. [Google Scholar] [CrossRef]
- Sudre, C.H.; Li, W.; Vercauteren, T.; Ourselin, S.; Jorge Cardoso, M. Generalised Dice Overlap as a Deep Learning Loss Function for Highly Unbalanced Segmentations. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Cardoso, M.J., Arbel, T., Carneiro, G., Syeda-Mahmood, T., Tavares, J.M.R.S., Moradi, M., Bradley, A., Greenspan, H., Papa, J.P., Madabhushi, A., et al., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2017; Volume 10553, pp. 240–248. ISBN 978-3-319-67557-2. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2016, arXiv:1511.07122. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. Unet++: A Nested u-Net Architecture for Medical Image Segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Proceedings of the 4th International Workshop, DLMIA 2018, and 8th International Workshop, ML-CDS 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, 20 September 2018; Springer: Cham, Switzerland, 2018; pp. 3–11. [Google Scholar]
- Guo, M.-H.; Lu, C.-Z.; Hou, Q.; Liu, Z.; Cheng, M.-M.; Hu, S.-M. Segnext: Rethinking Convolutional Attention Design for Semantic Segmentation. Adv. Neural Inf. Process. Syst. 2022, 35, 1140–1156. [Google Scholar]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 12077–12090. [Google Scholar] [CrossRef]
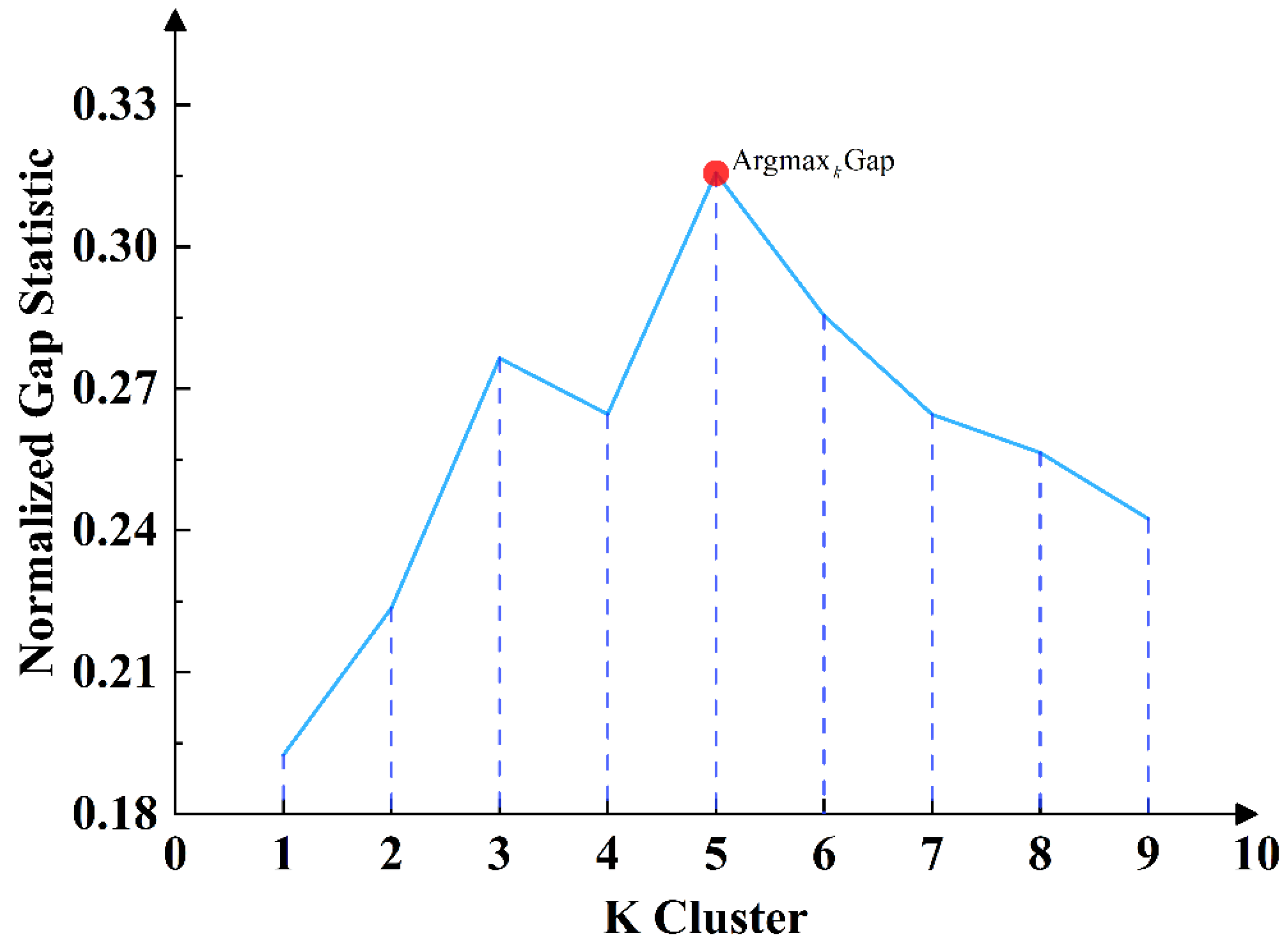
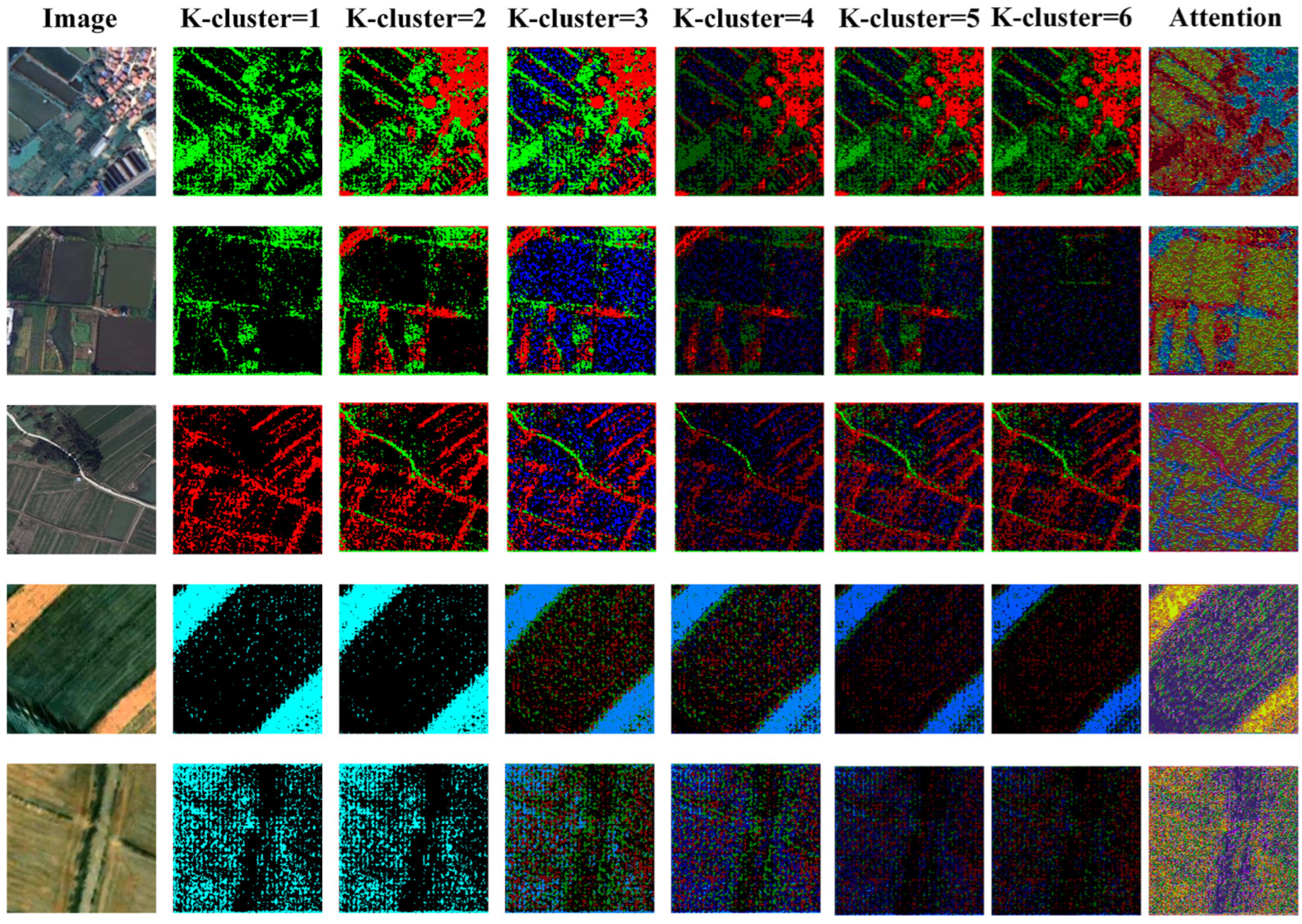

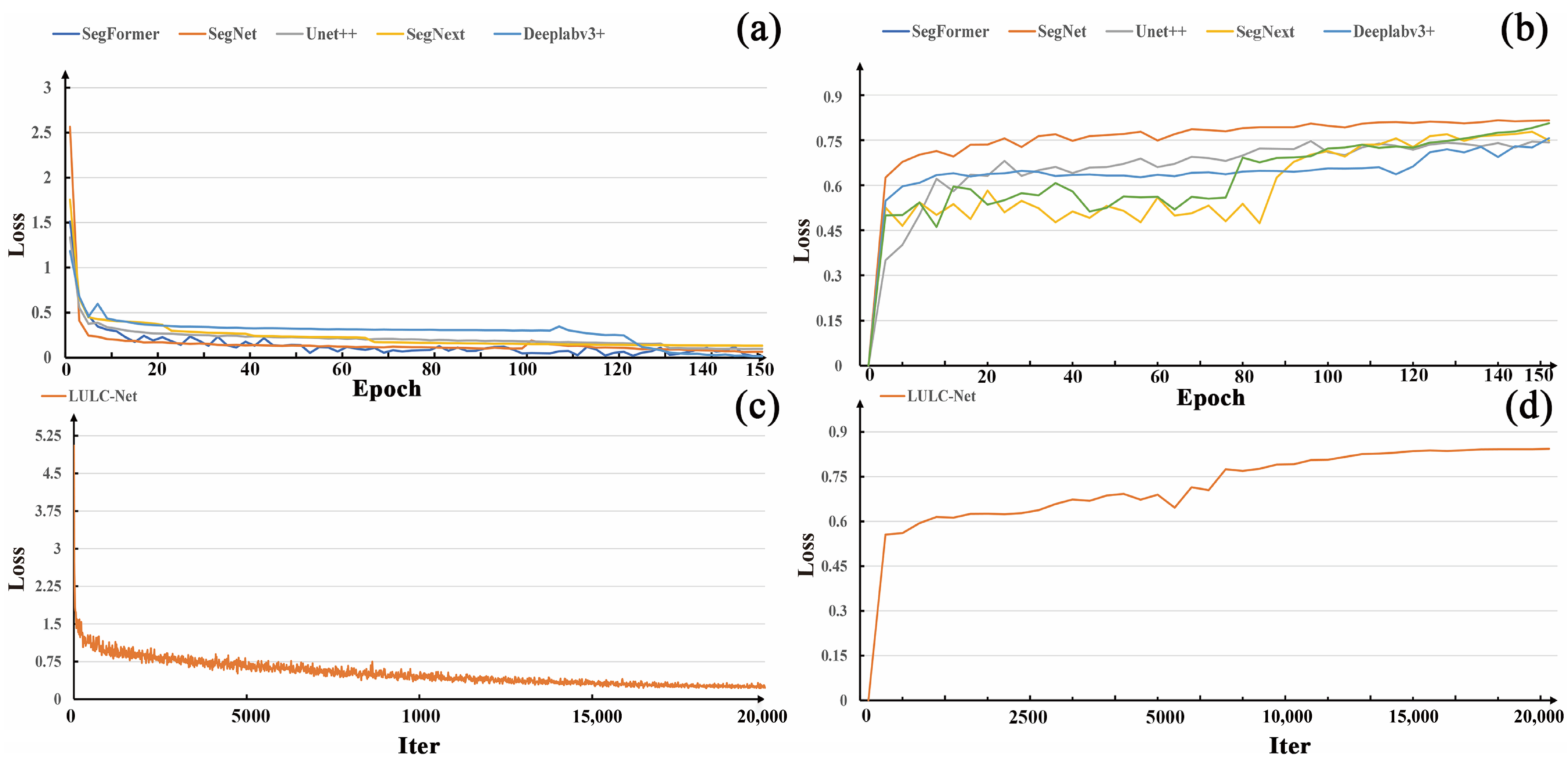
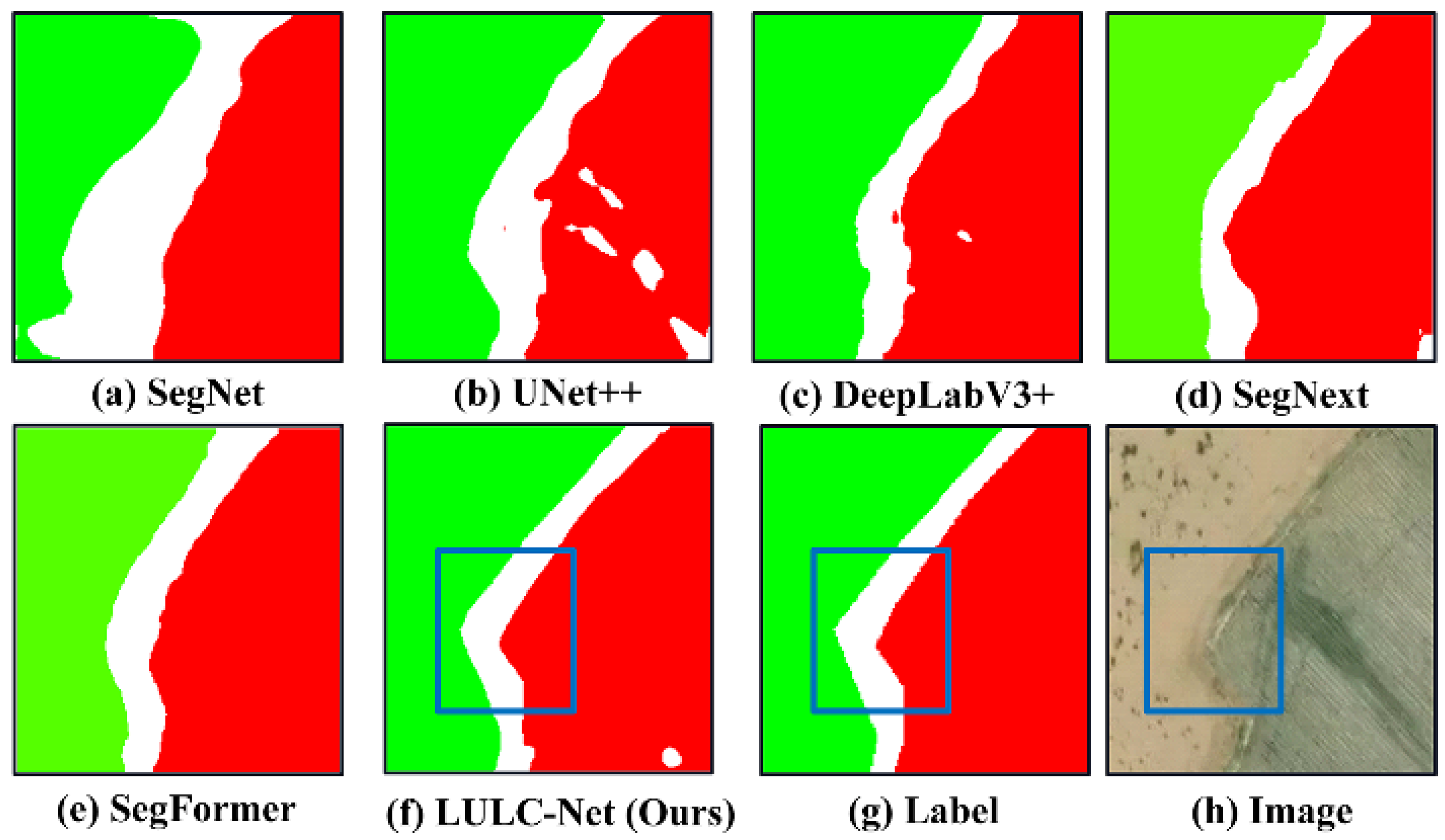

| Land Cover Category | Number of Pixels |
|---|---|
| River | 1,409,772 |
| Urban bare land | 37,132,400 |
| Gobi | 81,839,600 |
| Woodland | 125,038,000 |
| Background | 360,187,000 |
| Cropland | 605,957,000 |
| Total | 1,211,563,772 |
| Ablation Experiment | Clustering Module | Clustering Module + SK-Attention | ||||
|---|---|---|---|---|---|---|
| MIOU | PA | F1 Score | MIOU | PA | F1 Score | |
| No K-means Clustering | 60.25 | 78.87 | 78.26 | 64.22 | 79.25 | 79.03 |
| K-means Clustering (K-cluster = 1) | 60.02 | 79.46 | 79.36 | 63.56 | 79.66 | 79.65 |
| K-means Clustering (K-cluster = 2) | 61.38 | 80.63 | 79.01 | 62.65 | 80.56 | 79.96 |
| K-means Clustering (K-cluster = 3) | 65.23 | 80.06 | 78.92 | 68.78 | 80.63 | 78.65 |
| K-means Clustering (K-cluster = 4) | 69.56 | 84.78 | 83.56 | 75.65 | 88.78 | 86.56 |
| K-means Clustering (K-cluster = 5) | 76.56 | 89.56 | 88.22 | 80.25 | 93.92 | 91.92 |
| K-means Clustering (K-cluster = 6) | 72.56 | 89.06 | 87.96 | 74.56 | 90.05 | 87.06 |
| K-means Clustering (K-cluster = 7) | 71.65 | 89.28 | 86.65 | 77.65 | 89.03 | 88.36 |
| K-means Clustering (K-cluster = 8) | 72.88 | 82.78 | 80.56 | 76.56 | 84.65 | 83.39 |
| K-means Clustering (K-cluster = 9) | 69.56 | 81.35 | 80.01 | 70.65 | 80.65 | 79.65 |
| Ablation Study | MIOU | PA | F1 Score |
|---|---|---|---|
| CNN Feature Extraction | 72.65 | 90.25 | 89.63 |
| CNN Feature Extraction + Attention Module (SK-Attention) | 72.22 | 92.63 | 92.87 |
| ACM (K-cluster = 5) + CNN Feature Extraction | 79.25 | 92.22 | 91.64 |
| ACM (K-cluster = 5) + CNN Feature Extraction + Attention Module (SK-Attention) | 80.25 | 93.92 | 92.92 |
| Urban Bare Land | Woodland | Gobi | River | Cropland | Background | MIOU | F1 Score | FPS | |
|---|---|---|---|---|---|---|---|---|---|
| SegNet [65] | 49.03 * | 78.37 * | 70.15 * | 45.22 * | 83.68 * | 71.77 * | 66.37 * | 90.26 * | 29.85 * |
| UNet++ [66] | 53.06 * | 81.11 * | 72.63 * | 51.89 * | 88.45 | 74.26 | 70.23 * | 91.56 | 39.27 * |
| DeepLabV3+ [44] | 50.06 * | 84.22 * | 70.29 * | 63.32 * | 85.55 | 73.46 | 71.15 * | 93.39 | 32.65 * |
| SegNext [67] | 53.91 * | 91.52 | 83.04 | 59.14 * | 87.29 * | 73.5 | 74.73 * | 93.01 | 13.25 |
| SegFormer [68] | 54.14 * | 92.32 | 87.13 | 63.01 * | 88.04 | 75.24 | 76.81 * | 93.45 | 7.32 * |
| LULC-SegNet (Ours) | 59.14 | 93.26 | 85.68 | 73.67 | 91.32 | 78.41 | 80.25 | 93.92 | 14.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Fan, J.; Du, Y.; Zhou, Y.; Zhang, Y. LULC-SegNet: Enhancing Land Use and Land Cover Semantic Segmentation with Denoising Diffusion Feature Fusion. Remote Sens. 2024, 16, 4573. https://doi.org/10.3390/rs16234573
Shi Z, Fan J, Du Y, Zhou Y, Zhang Y. LULC-SegNet: Enhancing Land Use and Land Cover Semantic Segmentation with Denoising Diffusion Feature Fusion. Remote Sensing. 2024; 16(23):4573. https://doi.org/10.3390/rs16234573
Chicago/Turabian StyleShi, Zongwen, Junfu Fan, Yujie Du, Yuke Zhou, and Yi Zhang. 2024. "LULC-SegNet: Enhancing Land Use and Land Cover Semantic Segmentation with Denoising Diffusion Feature Fusion" Remote Sensing 16, no. 23: 4573. https://doi.org/10.3390/rs16234573
APA StyleShi, Z., Fan, J., Du, Y., Zhou, Y., & Zhang, Y. (2024). LULC-SegNet: Enhancing Land Use and Land Cover Semantic Segmentation with Denoising Diffusion Feature Fusion. Remote Sensing, 16(23), 4573. https://doi.org/10.3390/rs16234573








