Two-Dimensional Directions Determination for GNSS Spoofing Source Based on MEMS-Based Dual-GNSS/INS Integration
Abstract
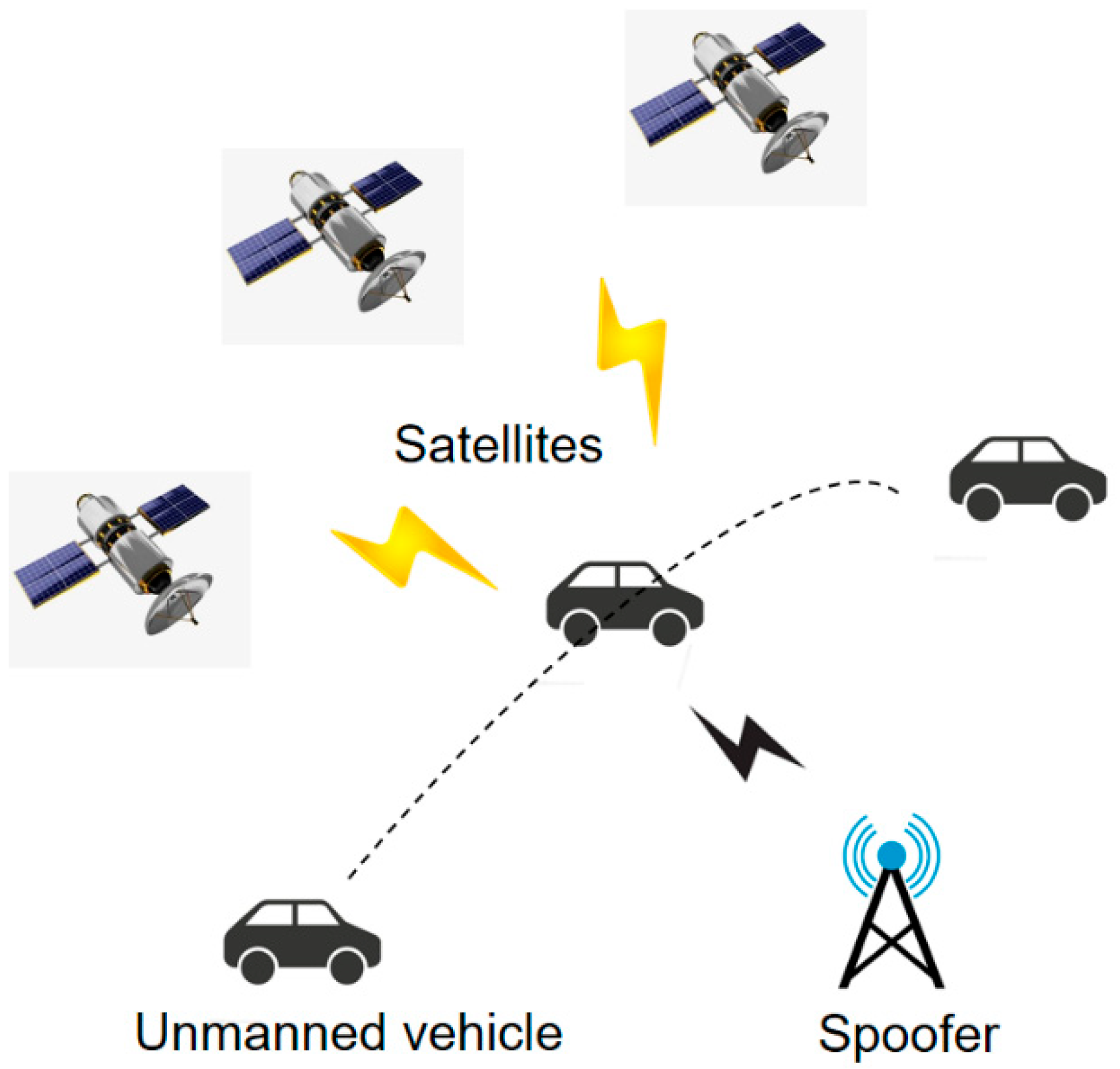
1. Introduction
2. System Model and Signal Processing Methods
2.1. Integrated Navigation Model
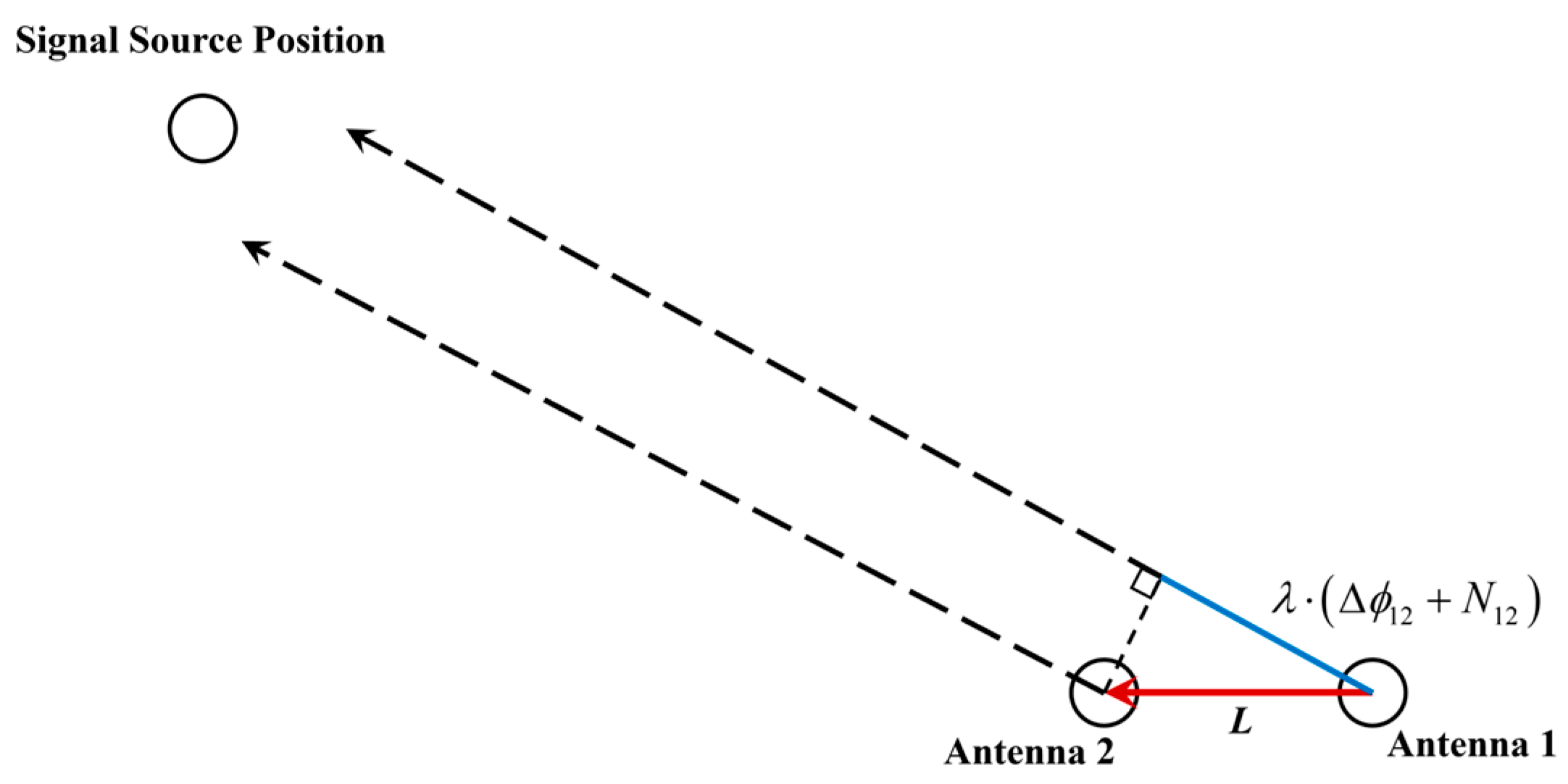
2.2. Observation Model for Real Signals
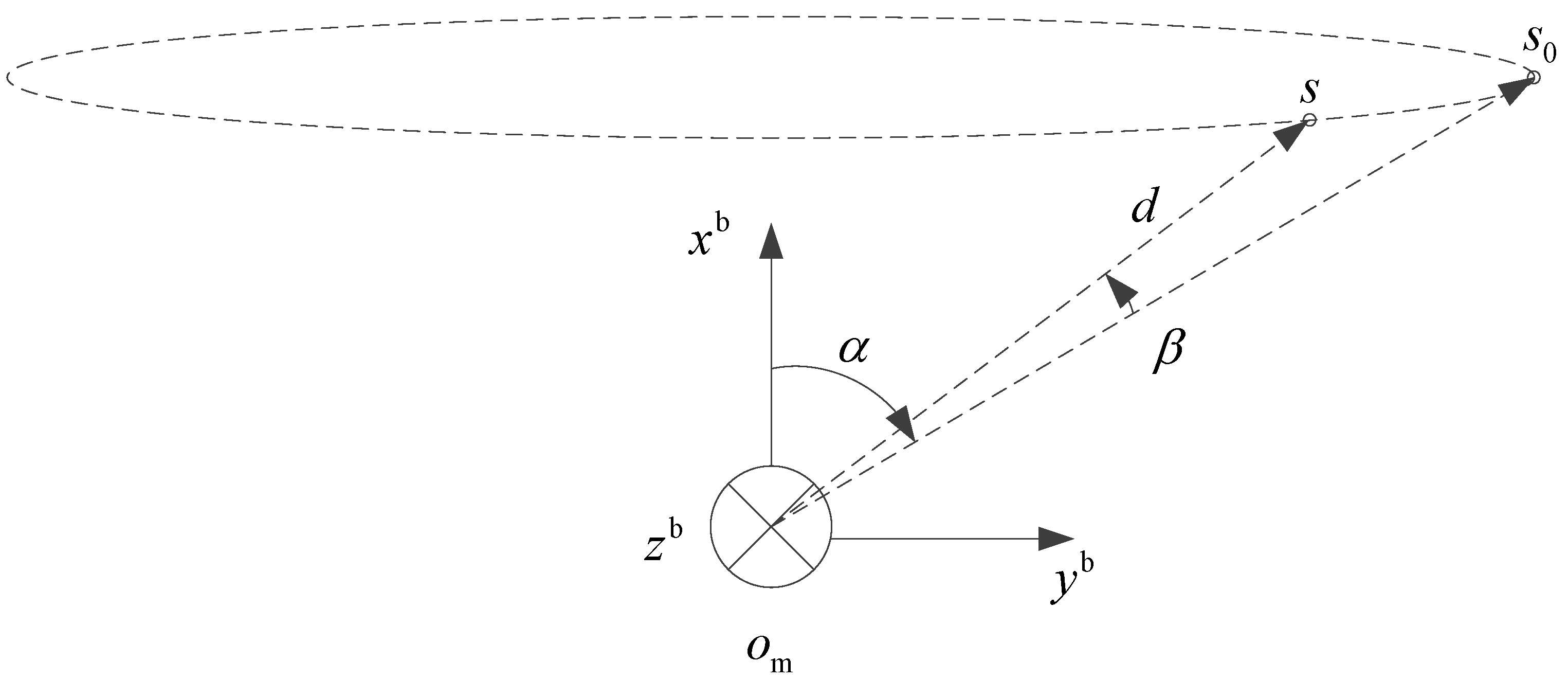
2.3. Two-Dimensional Direction Observation Model for Spoofing Signal Sources
3. Proposed Methods
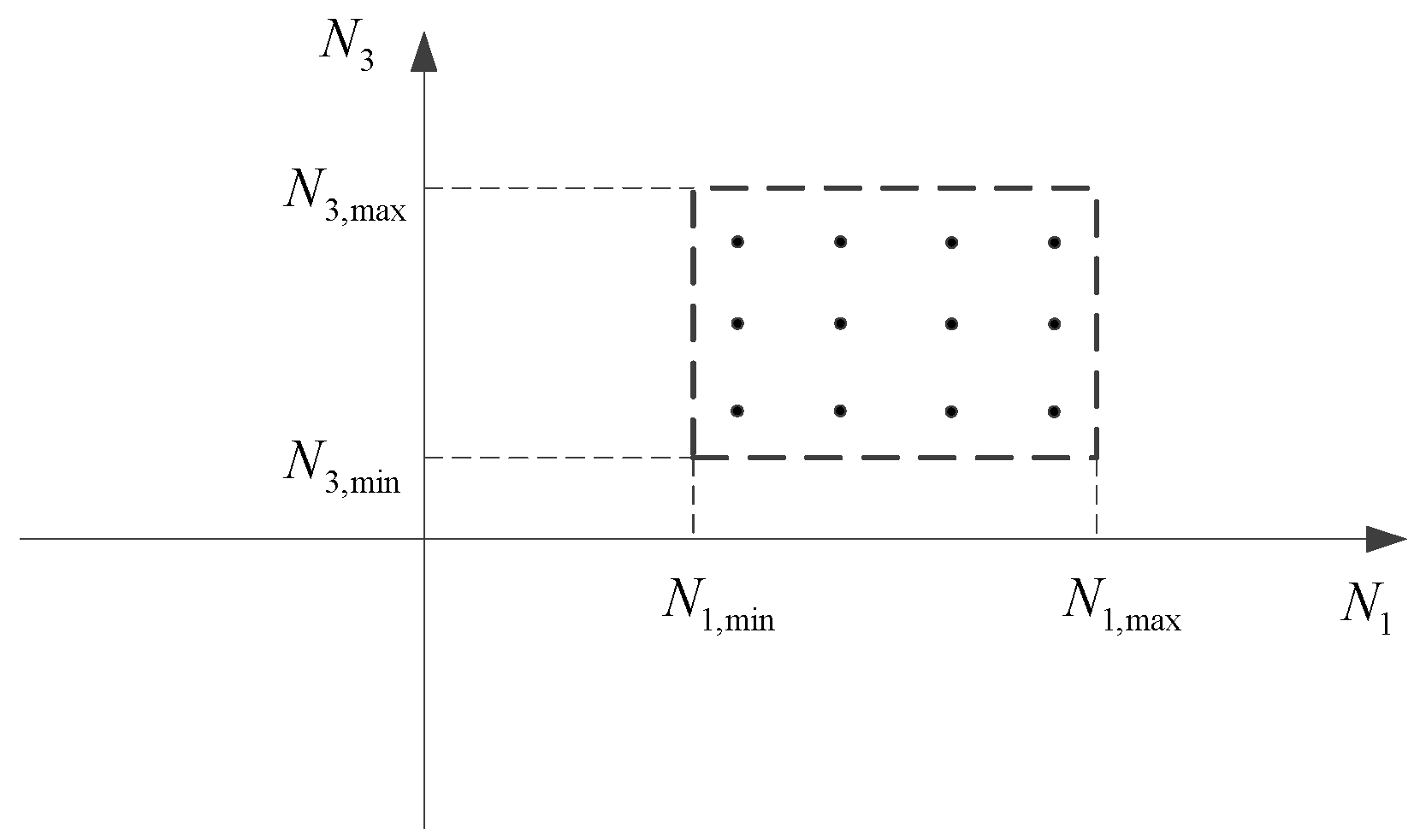
3.1. Method for Determining the AFM Carrier-Phase Ambiguity at Dual Frequencies
3.2. Method for Determining Spoofed Signals
3.3. Multi-Epoch Method for Determining the Two-Dimensional Directions of Spoofing Signal Source
4. Test Validation
4.1. Setup of Experimental Scenarios
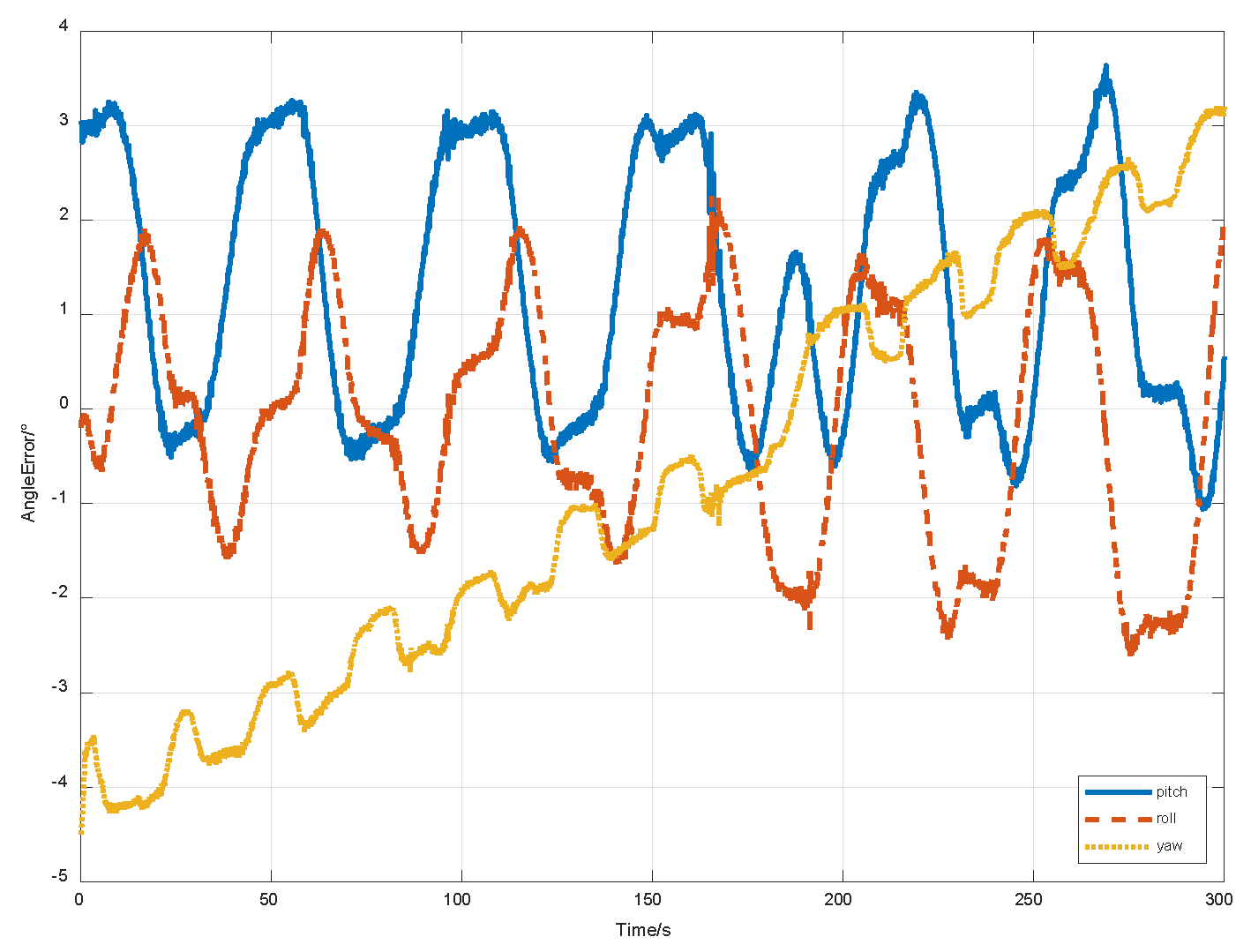
4.2. Test for BeiDou Satellites in Synchronous Orbits
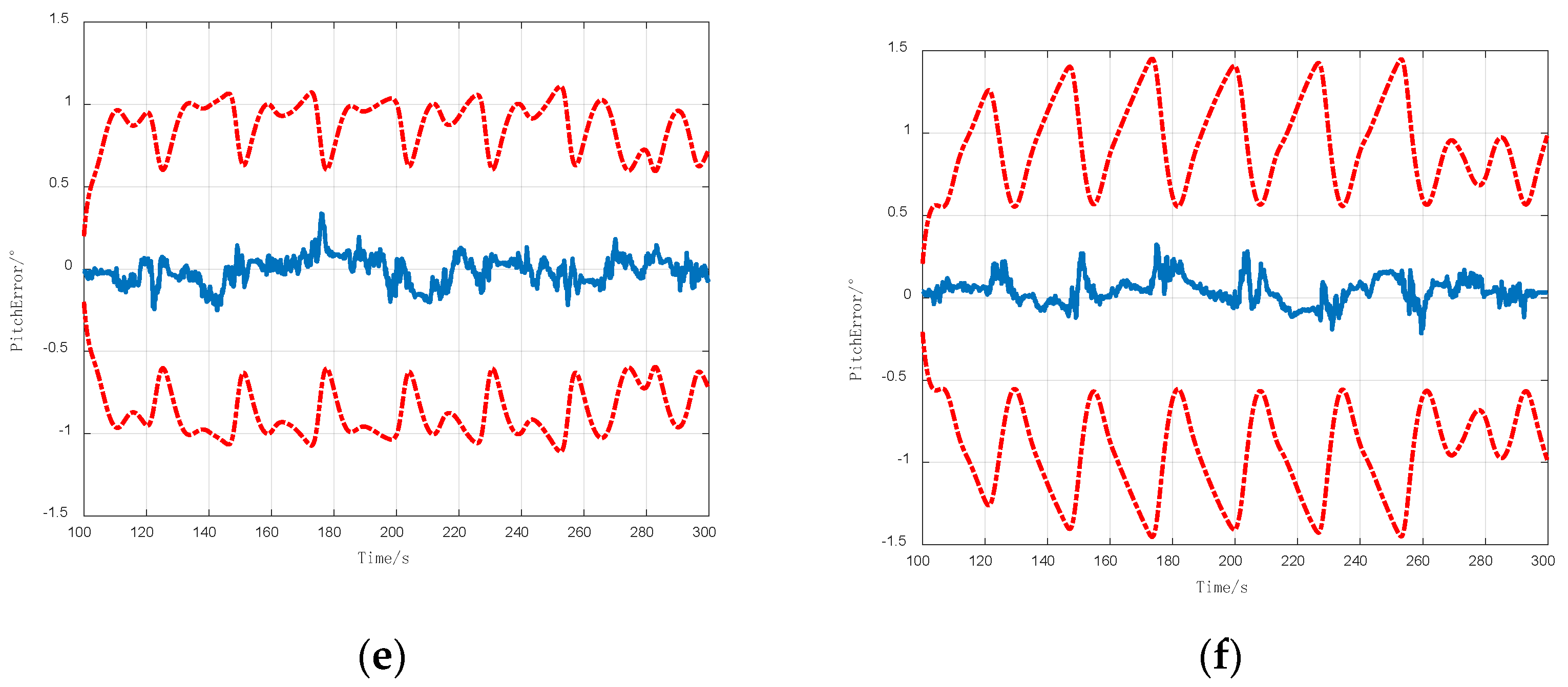
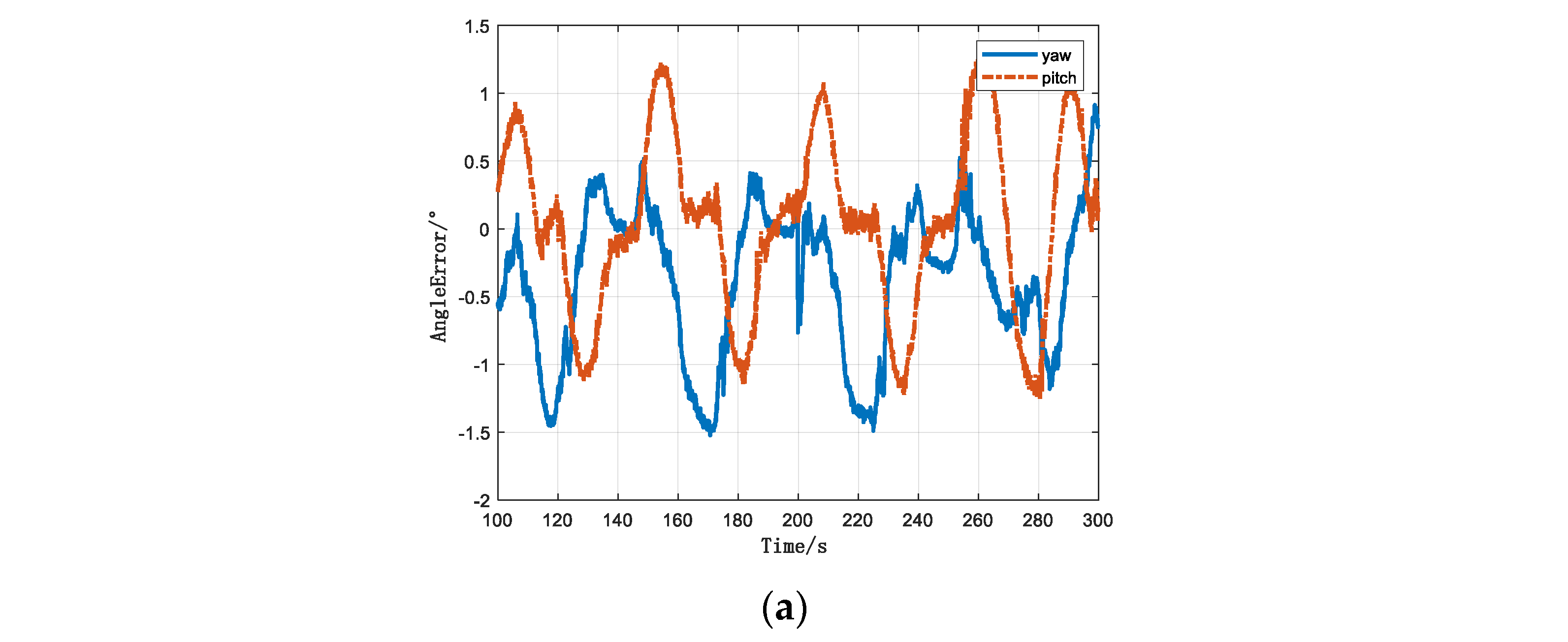
4.3. Test for a Short-Distance Spoofing Signal Source
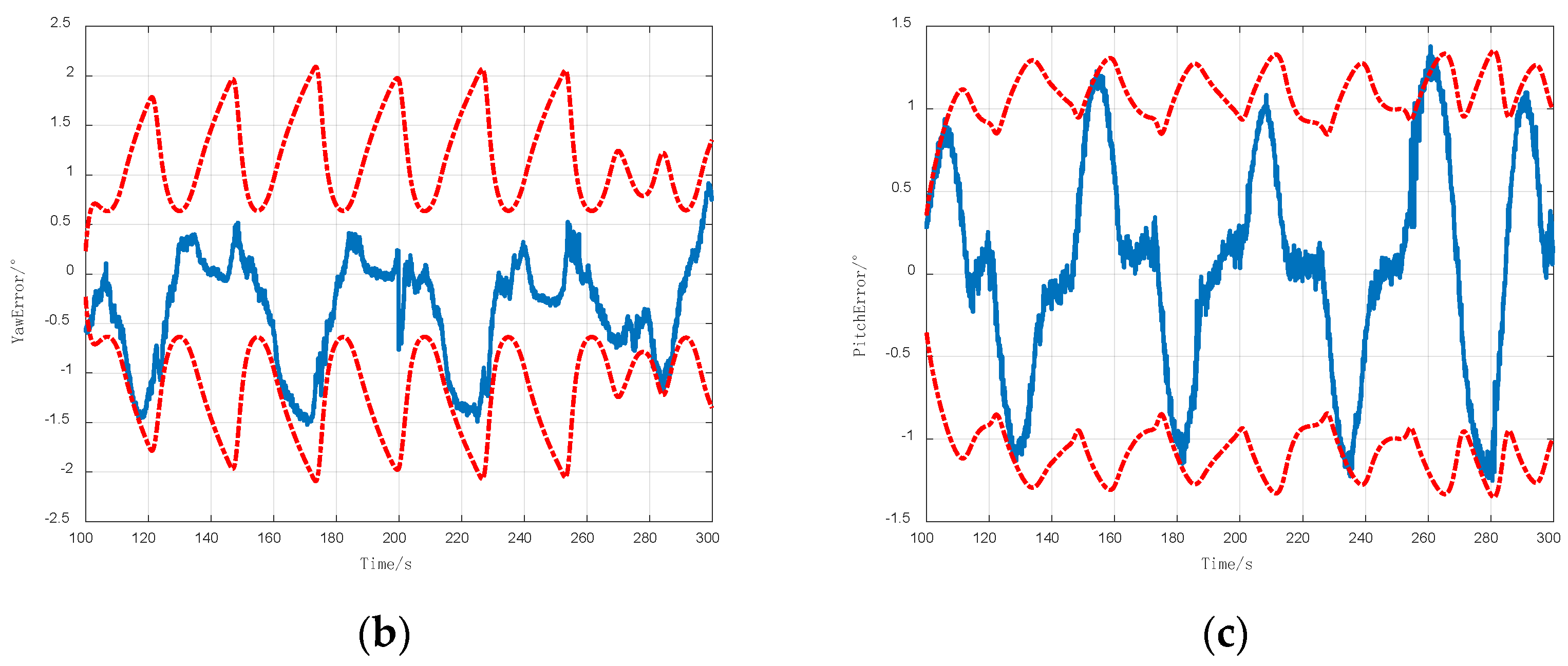
4.4. Test for the Spoofing Signal Source in the General Environment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meng, L.; Yang, L.; Yang, W.; Zhang, L. A survey of GNSS spoofing and anti-spoofing technology. Remote Sens. 2022, 14, 4826. [Google Scholar] [CrossRef]
- Feng, H.; Wengen, G.; Yunfei, L.; XinXin, G.; Pengfei, H. Joint detection and state estimation based on GPS spoofing attack in smart grids. Int. J. Electr. Power Energy Syst. 2024, 161, 110151. [Google Scholar]
- Salman, L.; Muhammad, F.; Jawwad, N.C.; Faran, A.B.; Nor, M.M.; Ijaz, H.N. A framework for preventing unauthorized drone intrusions through radar detection and GPS spoofing. Ain Shams Eng. J. 2024, 15, 102707. [Google Scholar]
- Omid, S.-T.; Mohamad, F.S.; Danaee, M.R. Null broadened-deepened array antenna beamforming for GNSS jamming mitigation in moving platforms. ICT Express 2022, 8, 161–165. [Google Scholar]
- Xie, M.; Xia, W.; Wei, S.; Li, H.; Li, P. A Robust GNSS Interference Suppression Method Based on Null Broadening of Dual-polarized Antenna Arrays. In Proceedings of the 14th IEEE International Conference on Signal Processing (ICSP), Beijing, China, 12–16 August 2018. [Google Scholar]
- Chang, J.; Huang, F.; Zhang, L.; Xu, D.; Hsu, L.T. Selection of Areas for Effective GNSS Spoofing Attacks to a Vehicle-Mounted MSF System Based on Scenario Classification Models. IEEE Trans. Veh. Technol. 2023, 72, 14645–14655. [Google Scholar] [CrossRef]
- Zhijun, W.; Cheng, L.; Yun, Z.; Rusen, L.; Meng, Y. Anti-spoofing: Integrated information authentication of BeiDou-II civil navigation message. China Commun. 2024, 21, 242–261. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Yang, Y.; Wang, P.; Yue, M. BDSec: Security authentication protocol for BeiDou-II civil navigation message. China Commun. 2024, 21, 206–218. [Google Scholar] [CrossRef]
- Liao, M.; Lyu, X.; Meng, Z.; You, Z. GNSS spoofing detection for single antenna receivers via CNR variation monitoring. J. Syst. Eng. Electron. 2024, 35, 1276–1286. [Google Scholar] [CrossRef]
- Liu, Y.; Li, S.H.; Xiao, X.; Fu, Q.W. INS-aided GNSS spoofing detection based on two antenna raw measurements. Gyroscopy Navig. 2016, 7, 178–188. [Google Scholar] [CrossRef]
- Shang, X.; Sun, F.; Wang, D.; Xiao, K.; Dou, S.; Lu, X.; Sun, J. GNSS spoofing detection based on multicorrelator distortion monitoring. GPS Solut. 2023, 27, 94. [Google Scholar] [CrossRef]
- Wang, Y.; Kou, Y.; Huang, Z.; Zhao, Y. GNSS spoofing maximum-likelihood estimation switching between MEDLL and CADLL. GPS Solut. 2023, 27, 148. [Google Scholar] [CrossRef]
- Fang, J.; Yue, J.; Xu, B.; Hsu, L.-T. A post-correlation graphical way for continuous GNSS spoofing detection. Measurement 2023, 216, 112974. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Yang, C.; Lu, M. Signal quality monitoring-based spoofing detection method for Global Navigation Satellite System vector tracking structure. IET Radar SonarNavig. 2020, 14, 944–953. [Google Scholar] [CrossRef]
- Li, J.; Li, W.; Fu, Q.; Liu, B. Research Progress of GNSS Spoofing and Spoofing Detection Technology; Institute of Electrical and Electronics Engineers Inc.: Xi’an, China, 2019. [Google Scholar]
- Li, J.; Zhu, X.; Ouyang, M.; Li, W.; Chen, Z.; Fu, Q. GNSS spoofing jamming detection based on generative adversarial network. IEEE Sens. J. 2021, 21, 22823–22832. [Google Scholar] [CrossRef]
- Xu, H.; Lian, B. Fault Detection for Multi-Source Integrated Navigation System Using Fully Convolutional Neural Network. IET Radar Sonar Navig. 2018, 12, 774–782. [Google Scholar] [CrossRef]
- Chen, S.; Ni, S.; Cheng, L.; Lei, T.; Song, X. GNSS spoofing detection method based on the intersection angle between two directions of arrival (IA-DOA) for single-antenna receivers. GPS Solut. 2024, 28, 101. [Google Scholar] [CrossRef]
- Rui, L.; Zhiwei, Y.; Qidong, C.; Guisheng, L.; Qinglin, Z. Localization of GNSS spoofing interference source based on a moving array antenna. Remote Sens. 2023, 15, 5497. [Google Scholar] [CrossRef]
- Qian, W.; Yuwei, Y. Vehicle mounted single-antenna GNSS spoofing detection method based on motion trajectory. GPS Solut. 2024, 28, 155. [Google Scholar]
- Cellmer, S.; Wielgosz, P.; Rzepecka, Z. Modified ambiguity function approach for GPS carrier phase positioning. J. Geod. 2010, 84, 267–275. [Google Scholar] [CrossRef]
- Jia, C.; Zhao, L.; Li, L.; Gao, Y.; Gao, Y.T. Pivot single-difference ambiguity resolution for multi-GNSS positioning with non-overlapping frequencies. GPS Solut. 2019, 23, 97. [Google Scholar] [CrossRef]
- Xiao, L.; Si, C.Z.; Ye, X.; Zhang, B.; Qin, G.; Bai, Y. A TCAR method for common clock source single difference carrier phase observation ambiguity fixing. J. Phys. Conf. Ser. 2022, 2253, 012008. [Google Scholar] [CrossRef]
- Forssell, B.; Martin-Neira, M.; Harris, R.A. Carrier phase ambiguity resolution in GNSS-2. In Proceedings of the 1997 10th International Technical Proceedings of the 1997 10th International Technical Meeting of the Satellite Division of the Institute of Navigation, ION GPS-97, Kansas City, MO, USA, 16–19 September 1997. Part 2 (of 2). [Google Scholar]
- Enge, P.; Jung, J.; Pervan, B. High integrity carrier phase navigation for future LAAS using multiple civilian GPS signals. In Proceedings of the 1999 American Control Conference (Cat. No. 99CH36251), San Diego, CA, USA, 2–4 June 1999. [Google Scholar]





| Gyroscope | Accelerometer | |
|---|---|---|
| Range | ±300°/s | ±10 g |
| Bias | 0.02°/h | 0.01 mg |
| Bias Stability | 0.02°/h | 0.01 mg |
| Position Accuracy | Horizontal | 0.02 m |
| Vertical | 0.03 m | |
| Attitude Accuracy | Heading | 0.01° |
| Levelling | 0.01° | |
| Velocity Accuracy | Horizontal | 0.02 m/s |
| Gyroscope | Accelerometer | |
|---|---|---|
| Range | ±500°/s | ±30 g |
| Bias | 1°/h | 200 μg |
| Bias Stability | 1°/h | 400 μg |
| Signal Frequency | BDS | BDS-2:B1I, B2I, B3I BDS-3: B1I, B3I |
|---|---|---|
| First Fix Time | Cold Start | <30 s |
| Hot Start | <10 s | |
| Signal Reacquisition | Loss of Lock Reacquisition | <1 s |
| Signal Acquisition Sensitivity | −138 dBm | |
| Measurement Accuracy | Pseudo-range | ≤10 cm |
| Carrier Phase | ≤0.005 cycle |
| Angles Error | 100 m | 10 km | 36,000 km |
|---|---|---|---|
| Yaw | ≤9° | ≤2° | ≤0.6° |
| Pitch | ≤11° | ≤2° | ≤0.6° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Wang, D.; Wu, J. Two-Dimensional Directions Determination for GNSS Spoofing Source Based on MEMS-Based Dual-GNSS/INS Integration. Remote Sens. 2024, 16, 4568. https://doi.org/10.3390/rs16234568
Zhang C, Wang D, Wu J. Two-Dimensional Directions Determination for GNSS Spoofing Source Based on MEMS-Based Dual-GNSS/INS Integration. Remote Sensing. 2024; 16(23):4568. https://doi.org/10.3390/rs16234568
Chicago/Turabian StyleZhang, Chengzhong, Dingjie Wang, and Jie Wu. 2024. "Two-Dimensional Directions Determination for GNSS Spoofing Source Based on MEMS-Based Dual-GNSS/INS Integration" Remote Sensing 16, no. 23: 4568. https://doi.org/10.3390/rs16234568
APA StyleZhang, C., Wang, D., & Wu, J. (2024). Two-Dimensional Directions Determination for GNSS Spoofing Source Based on MEMS-Based Dual-GNSS/INS Integration. Remote Sensing, 16(23), 4568. https://doi.org/10.3390/rs16234568






