This section outlines the system model and key definitions, introducing the problem addressed in this paper, along with the proposed solution and essential methods used.
2.1. System Model
The investigated system consists of a team comprising
communicating UAVs, denoted as
. Each UAV is outfitted with a camera and assigned the task of tracking and sensing a single target covertly as it moves along a known route over uneven terrains [
13,
23]. All UAVs maintain a fixed altitude, denoted as
, within the permissible deployment range, and operate within a plane
parallel to the ground plane
. The horizontal coordinates for any UAV
at any given time
within the time frame
are denoted as
. Here, the interval
encompasses the entire duration of the UAVs’ covert video sensing mission [
13,
23]. The dynamics of any UAV
are modeled using the kinematic model, neglecting wind disturbances, as follows [
24]:
In (1), the variable
indicates the orientation of UAV
relative to the
x-axis, with values ranging between 0 and 2
π, measured counterclockwise [
1,
13,
23]. We use
to represent the linear speed of UAV
, restricted to the range
, and
for its angular speed, which falls within
. These speed variables are limited by constants
and
, reflecting the maximum achievable linear and angular speeds based on the UAVs’ mobility characteristics in practice [
1,
13,
23]. During maneuvers involving a non-zero angular velocity
, the turning radius
of UAV
is computed by the formula
[
1,
13,
23].
To prevent collisions between any two UAVs, it is crucial to adhere to the following constraint at any time:
where a consistent minimum safe separation distance, denoted as
between any pair of UAVs
and
(where
), which move according to the kinematic model described in (1), must be satisfied. Failure to meet the condition in (2) during movement requires implementing measures to avoid potential collisions, such as those described in [
13,
23]. Note that
and other safety constraints must be carefully chosen to align with the specifications and design requirements of the UAVs, as detailed in [
25,
26].
All UAVs share a common mission, which is conducting covert video sensing on a single moving target in uneven terrains. These complex terrains are particularly prevalent in urban environments, characterized by numerous tall buildings, walls, and narrow roads [
27,
28]. Such obstacles can occlude the LoS between the UAV and the target, impeding effective monitoring or recording [
9,
10,
11].
The monitored target travels along a specified road within an urban environment. The target’s position at any time
is denoted by
[
1,
13,
23]. The angle of the target’s movement, measured counterclockwise from the
x-axis, is denoted as
[
1,
13,
23]. Estimation and prediction algorithms can be employed to assess and predict target positions [
29]. For practical considerations, it is assumed that when a target is recorded and seen by a UAV, its position and velocity can be determined using image processing techniques through its camera [
29]. Whenever the target is not viewed, its current position can be predicted from previously available measurements [
29]. Here, the stability of the UAVs’ cameras is assumed to be guaranteed through the use of a gimbal [
1,
13,
23].
Consequently, by continuously tracking the target’s movement along a specified path, it becomes possible to predict its trajectory into the future for a designated duration, denoted as
[
1,
13,
23]. Thus, starting from any initial time
, a prediction of the target’s position,
, is assumed to be available for the time interval
within
[
1,
13,
23]. With the known information of the route and the current target position, determining its movement direction
at any given moment becomes straightforward [
1,
13,
23].
Let us construct an approximated model of the uneven terrain region and its elevated structures, which collectively form the operational environment of our target. This study is specifically focused on a category of highly uneven terrains, as detailed in [
10]. Let us define the subset
as a polygon with
vertices, serving as our bounded area of interest for target monitoring [
10]. Within
, there exist
smaller, non-overlapping, and distinct polygons denoted as
, where
, each defined by its unique vertices
[
10]. Additionally, within each of these polygons, there are corresponding polygons denoted as
, possessing an equivalent number of vertices to their respective
counterparts [
10]. We assume that all these polygons are convex in shape. Every
and its corresponding
together form a polytope [
10]. In this configuration, each
forms the foundational base of its associated polytope, while
represents its upper surface [
10]. Furthermore, each polytope is presumed to consist of
side faces, denoted as
, where
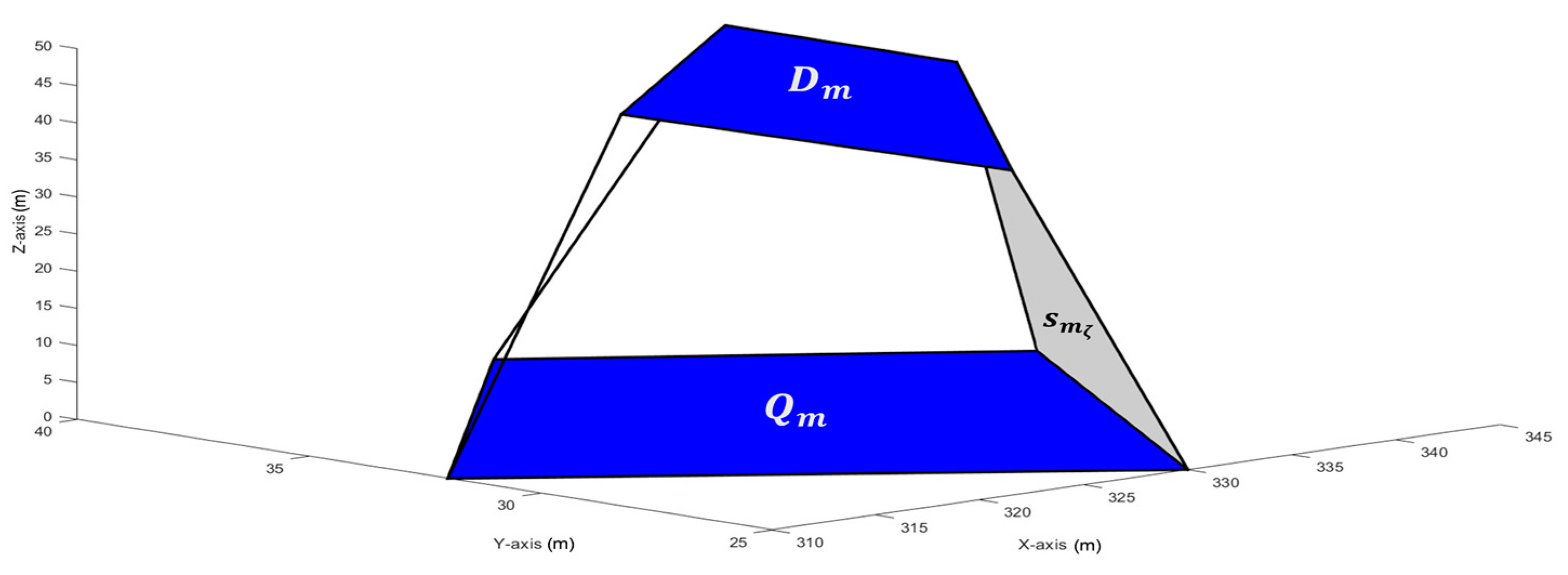
. Each of these side faces forms a convex quadrilateral with one side originating from
and the opposite side from
[see
Figure 2] [
10]. It is worth mentioning that
may not necessarily align parallel to the ground plane
, as depicted in
Figure 2. Additionally, we assume they are not perpendicular to it [
10].
Any
and
and their corresponding
collectively constitute
, referring to polytope
, representing a distinct tall terrain or structure from a diverse array such as buildings or walls [
10]. The 3D coordinates of the edges and corners of each
are available and provided as
, where
denotes a distinct index for each point in the sequence. It is important to note that, in order to prevent UAVs from colliding with the terrain, a safety constraint must be adhered to. This constraint is defined as follows:
where
denotes the minimum distance between UAV
and the highest point of the terrain,
, and
is a given positive constant [
10]. Furthermore, it is presumed that the remaining areas of polygon
, excluding the regions
, maintain a relatively flat terrain [
10].
This paper assumes that comprehensive environmental data, including ground terrain positions, structures configurations, and altitude variations, are readily available [
22]. This assumption is regarded as reasonable, as databases typically include data on significant regional terrains within operational areas [
22].
The core of the mission involves covert video sensing, requiring all UAVs to operate within a designated area, known as the feasible flight zone at any given time
, as depicted in
Figure 3. The design of this feasible zone was initially proposed in [
1]. This zone is crucial for ensuring UAVs can maneuver in an undetected way by the target while keeping the target within the UAVs’ field of view [
1]. Positioned directly behind the target, it lies between the distances
and
from the target’s horizontal position
in the operational plane
at height
.
indicates the minimum distance UAVs can approach without being detected by the target, while
represents the maximum distance from which UAVs can observe the target with satisfactory quality [
1]. Moreover, this zone is entirely encompassed within the corresponding annulus specified by an angle
, which is then used in conjunction with the target’s heading to derive two additional angles,
and
. These angles delineate the boundaries of the feasible flight zone, forming arcs that completely enclose it, as illustrated in
Figure 3 [
1].
Given the predictions of the target position for every
and parameters
,
,
,
, and
, determining the feasible flight zone for any instant is currently straightforward. Hence, for any UAV
i, it is required to adhere to the following constraint [
1]:
where
is the feasible flight zone with the target located at
[
1].
In various situations, accurately estimating the future location of a target can be challenging, potentially impacting the feasible flight zone for UAVs. We propose the reasonable assumption that prediction uncertainty is bounded at each time slot [
1]. This assumption is justified by the realistic limitations on the target’s speed. Consequently, adjusting the design of the feasible flight zone becomes crucial to accommodate uncertainties in target prediction [
1].
In (5), the process of determining the feasible flight zone transitions from relying on precise predictions to utilizing approximate ones is completed, employing estimated regions instead of exact coordinates [
1]. At any given time
, the region
is employed to compute the feasible flight zone
for any point within it
[
1]. Consequently, for the effective monitoring of any point within the
region, it is essential to calculate the feasible flight zone by intersecting the zones associated with all points within
. This revised feasible flight area is denoted as
, and each UAV
is required to operate within this zone consistently [
1,
13,
23].
Since the mission emphasizes covertness, selecting the right colors for the employed UAVs enhances their visual camouflage. Appropriate colors allow objects to blend into their surroundings, reducing the likelihood of detection [
30,
31]. By carefully matching the UAVs’ colors to specific environments, their chances of avoiding detection improve, increasing their ability to stay concealed during covert video sensing and boosting overall mission performance. In this paper, the UAVs are equipped with colors that blend seamlessly into uneven terrains, further assessing and improving their camouflage effectiveness.
2.2. Shadow Design and LoS Occlusion Avoidance
As previously explained, the purpose of establishing the feasible flight zone is to maintain an optimal distance between the UAVs and the target, ensuring they are neither too close nor too far [
1,
13,
23]. Within this zone, the UAVs maintain the target within their field of view and can record it with acceptable quality, while remaining concealed [
1]. This designated flight zone serves as the state space encompassing all potential UAV positions at any given time [
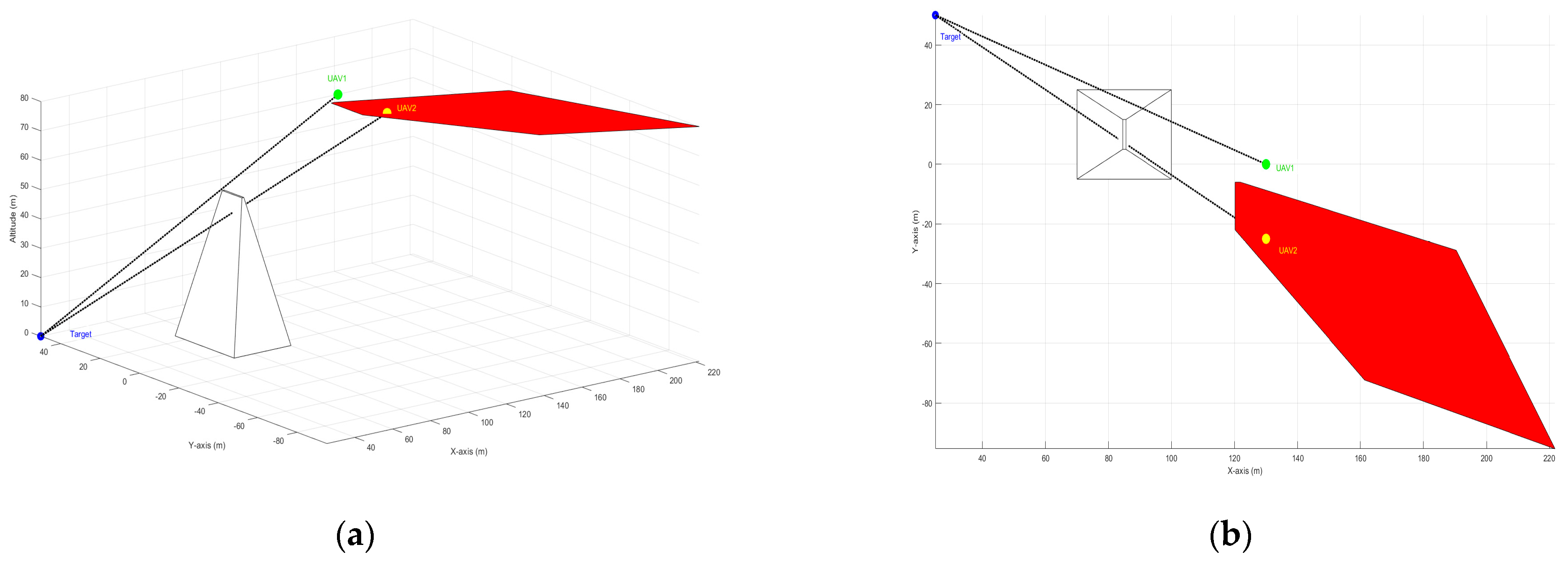
1]. Each UAV can select an optimal position within this feasible flight zone to achieve the main objective of the mission and plan a covert, collision-free trajectory. However, high structures such as buildings, mountains, hills, and other terrain features in uneven environments can block the LoS to the target, potentially resulting in the loss of the target of interest, as illustrated in
Figure 1 [
9,
10,
11].
Before we delve into the shadow design, let us examine whether any UAV
, at any given instant and any position within the feasible flight zone in (5), maintains an unobstructed LoS to the target in the presence of high structures or terrain. To achieve this, we analyze the straight-line segment connecting any position of the UAV
, where
, within the feasible flight zone, to the 3D predicted target position
at that particular instant [
11]. This relationship can be expressed as follows [
11]:
where
, and
is a free number. Assessing whether the UAV and the target maintain an unobstructed LoS at a specific moment involves identifying intersections between the line segment connecting their positions and obstacles that could potentially occlude the LoS, such as tall buildings or mountains [
11]. If any intersections are found, it indicates that there is a blocked LoS to the target. Conversely, if no intersections are identified, we can confirm that there is a clear LoS to the target. With the necessary environmental data on hand, confirming a clear LoS between any position within the feasible flight zone and the target is straightforward in real-world applications [
11].
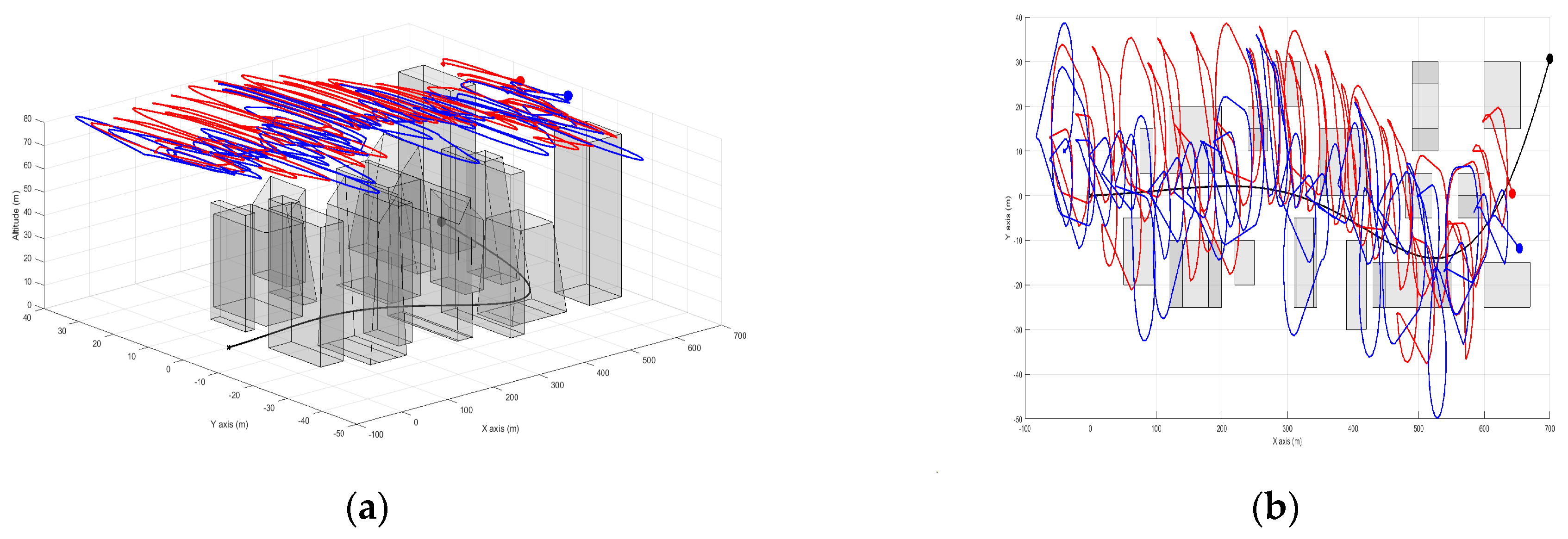
Figure 4 illustrates that despite selecting UAVs’ positions within the feasible flight zone in (5) based on an objective function aimed at creating covert paths, all UAVs experience a blocked LoS to the target. This situation could result in losing track of the target, potentially leading to mission failure [
9,
10,
11]. Thus, it is clear that not all states or positions within the feasible flight zone in (5) are viable. While some positions offer better concealment, they may still suffer from an occluded LoS. Addressing this challenge forms the core focus of this paper, aiming to exclude non-viable positions with the occluded LoS from the feasible flight zone. This ensures that the objective function can generate optimal UAV paths from the remaining positions with a clear LoS to the target.
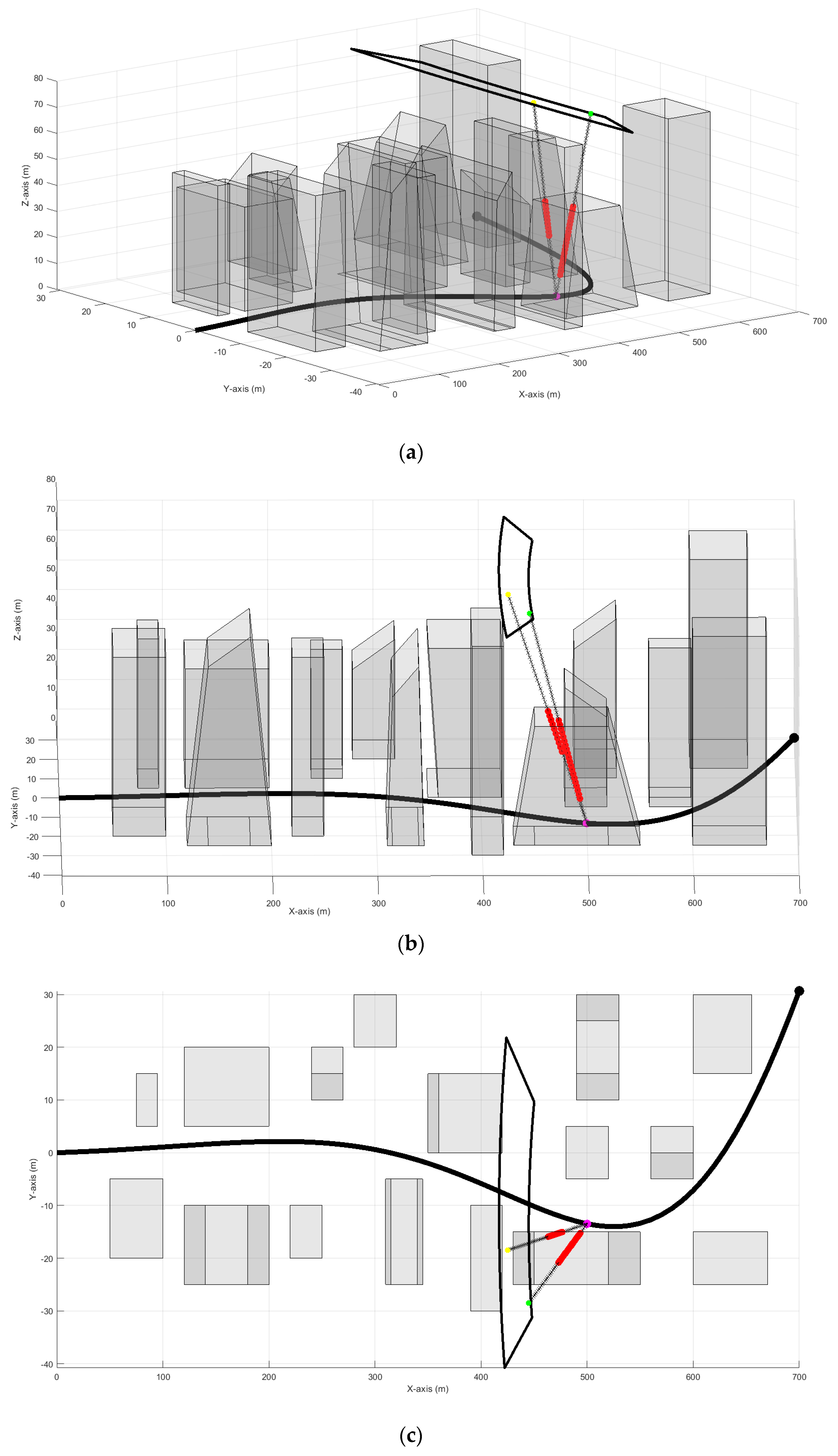
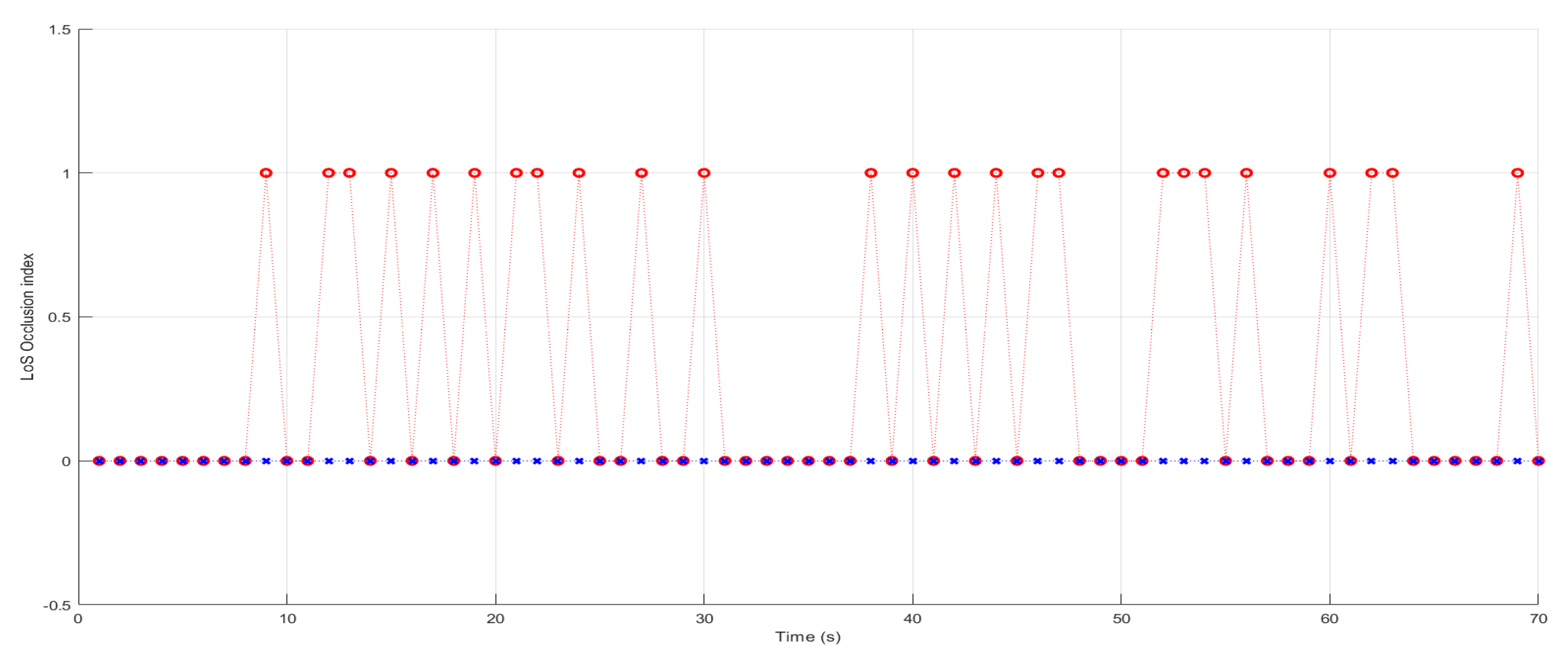
To exclude non-viable positions with an occluded LoS to the target from the feasible flight zone, adjustments must be made to the calculation process of the feasible flight zone. This involves accounting for regions within the UAVs’ operational plane where the LoS is occluded, thereby excluding them from the feasible flight zone. These regions correspond to realistic projections of tall structures or terrain within the operational region, termed as shadows. Within these areas, UAVs lack a LoS to the target [
12]. These shadows constantly change with each time step due to the target’s movement relative to surrounding tall structures and terrain [
12]. Consequently, these terrain-induced shadows are dynamic, evolving with the target’s motion (refer to
Figure 5). Moreover, these shadows may overlap, forming complex and interconnected shapes [
12].
To begin, it is crucial to note that in this paper, the trajectories of the UAVs are periodically planned and computed over multiple time steps within a designated future time frame
[
1,
13,
23]. This time frame represents the period in the future when the target position is predictable. It is discretized into intervals with a sampling interval
. The time period
is segmented into
slots of equal duration, where
[
1]. At each time slot
(where
), the continuous-time variables of UAV
—
,
,
, and
—as well as the target’s variables
and
, are discretized. They are represented discretely as
,
,
,
,
, and
, respectively [
1,
13,
23]. Subsequently, the system model (1) for UAV
is now represented in its discretized form as follows [
1,
13,
23]:
Since we are working in discrete time, we will compute the shadows of all existing terrains and integrate them into the calculation of the new feasible flight zone at the start of each time slot.
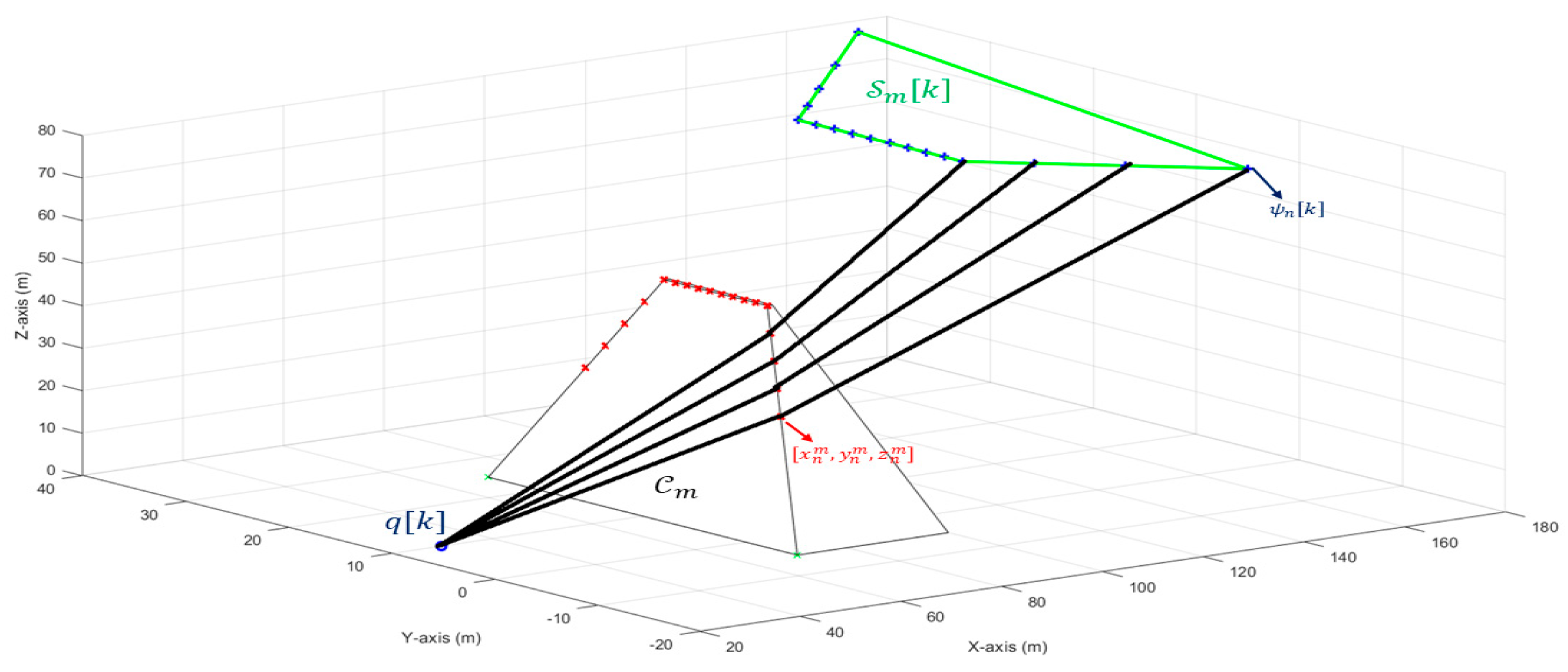
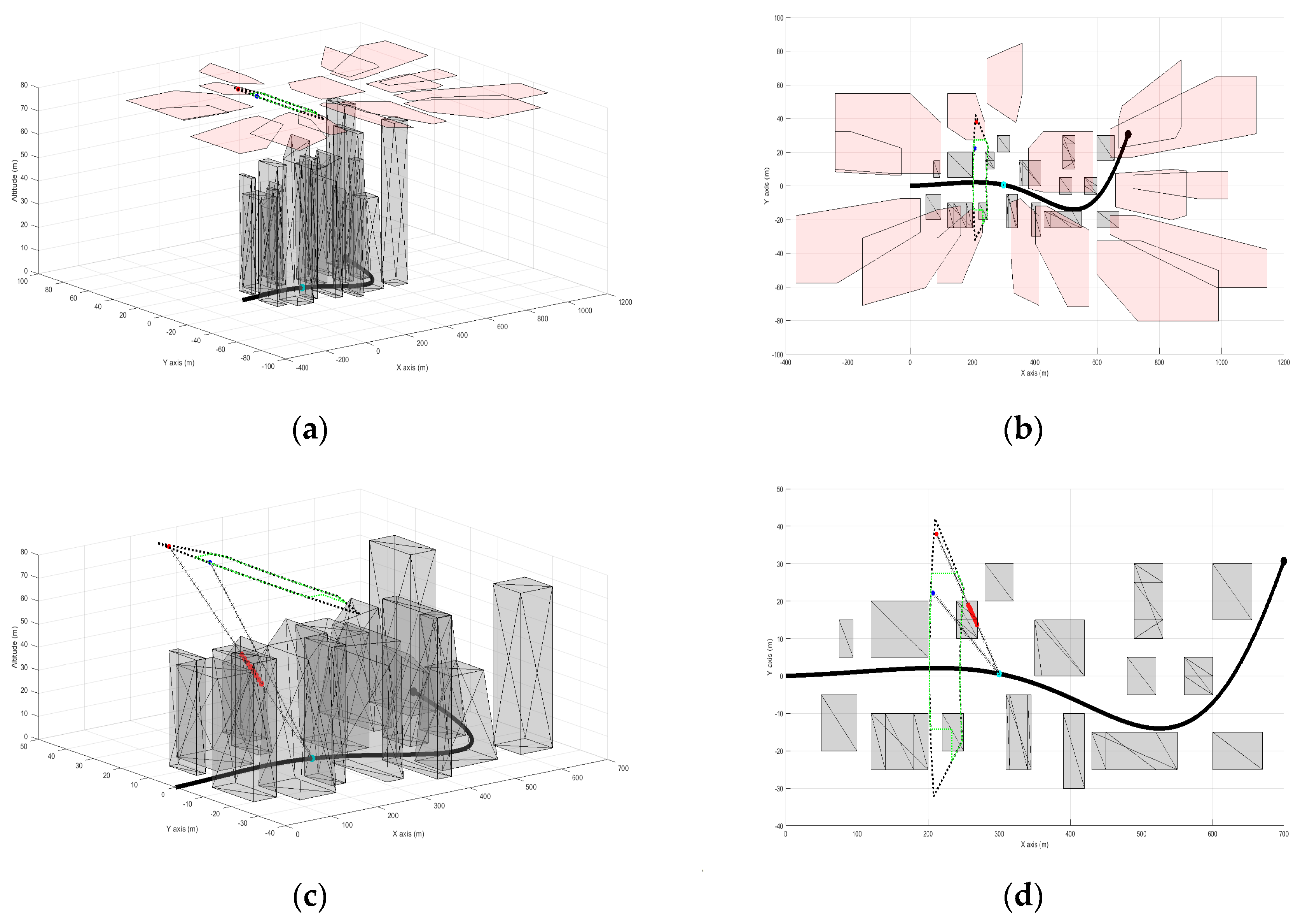
Understanding the design of shadows entails recognizing that convex objects, such as those proposed to represent the uneven terrains in this paper, maintain their convexity through perspective projection [
12,
32]. This approach is practical and can be applied when a 3D map of an uneven area is available [
12]. At any time slot
, the calculation of the shadow cast by a single structure or terrain
onto the operational plane
at height
, with the target
positioned at coordinates
[see
Figure 6], begins by establishing the vector connecting the target
with the points
as follows [
12]:
Consequently, the vector
intersects the plane
at the point [
12]:
Given that terrain points near the ground correspond to very distant points in the
plane, we selectively consider terrain points above a defined minimum height, denoted as
, ensuring that
for all
[
12]. This consideration enhances the method’s scalability to the number of terrains and their varying heights. After computing
for all
pertaining to
, we identify the convex hull of the points
to depict its shadow, as depicted in
Figure 6 [
12]. Subsequently, we construct another set comprising subsets
, each delineating the shadow of
for
.
Everything is now in place to modify the feasible flight zone defined in (5) to account for the shadows
within the UAVs’ operational plain
. These shadows are excluded from the feasible flight zone at each time slot. Let
denote the feasible flight zone defined by
at time slot
. The new feasible flight zone at instant
can be represented as the set difference between
and the union of all the other shadow regions
,
. Hence, the new feasible flight zone that any UAV
must fly within at any slot
is represented as follows:
Equation (10) defines a new feasible flight zone comprising only positions that maintain a clear LoS to the target throughout every time slot.
2.3. Objective Function
The primary issue addressed in this paper involves planning visually camouflaged trajectories for multiple UAVs. The proposed approach employs a method involving random flight patterns within the feasible flight zone to obscure the UAVs’ video sensing intentions towards the target [
1,
13,
23]. Additionally, the energy efficiency of the UAVs’ batteries is crucial, as high energy consumption can significantly reduce their lifespan [
1]. Therefore, the objective function formulated for this problem incorporates two key factors: the disguising performance of the UAVs and the energy efficiency of the resulting trajectories.
To achieve the first factor, it is essential to adopt a measure that quantifies the UAV’s concealment or disguising performance effectively. This measure assesses how much the UAV changes its direction and distance from the target over time, combining derivatives of both the UAV-target angle and distance [
1]. This quantification is crucial for evaluating the effectiveness of the disguise [
1]. Given the involvement of multiple UAVs in this study, the disguising measure for UAV
is described as follows [
1,
13,
23]:
Here,
is a given positive constant (
).
represents the angle between UAV
and the target (UAV
-target angle), measuring the angular difference between the direction of the line connecting UAV
and the target and the target’s horizontal direction angle
[
1,
13,
23]. Similarly,
represents the distance between UAV
and the target (UAV
-target distance), defined as the Euclidean distance in the horizontal plane between UAV
and the target [
1,
13,
23]. The following equations are used for UAV
to calculate
and
[
1,
13,
23]:
Given the positions of the UAVs and the target, measurements for (12) and (13) related to metric (11) can be performed in the field at each time step, ensuring effective observation and validation in practical scenarios. Maximizing the disguising measure described in (11) is crucial for effectively concealing each UAV, such as UAV
in this scenario [
1,
13,
23].
This involves each UAV making frequent and significant adjustments to its distance and angle relative to the target at each time step, thereby reducing its exposure to the target view [
1].
Having set out to quantify the visual camouflage challenge for each UAV initially, the subsequent objective is to optimize the energy efficiency of their flight paths. In practice, each UAV’s battery capacity is limited, so minimizing energy consumption is crucial to extending their operational lifespan [
1]. In this study, the length of each UAV’s trajectory is seen as a measure of its energy consumption [
1,
13,
23]. Therefore, each UAV is responsible for achieving the following objective in planning its flight trajectory [
1,
13,
23]:
By combining these two objectives in (14) and (15), we can form the main objective function to be solved as follows:
where
is a weighting factor [
1,
13,
23]. The discretized form of Equation (16) is as follows:
2.5. Proposed Solution
The problem is addressed with a decentralized approach, where each UAV independently employs an online trajectory planning method to generate optimal trajectories based on (16). We utilize the Dynamic Programming (DP) method to solve this optimization problem, subject to constraints (1), (2), and (10). DP is chosen for its ability to handle the complexities of the problem, such as nondifferentiability and nonconvexity issues in the second part of the objective function (16). Predicting the target’s motion for the complete video sensing period adds difficulty; hence, we suggest an online DP-based approach that periodically updates each UAV’s trajectory based on short-term predictions over a future time horizon
. Each UAV plans its trajectory for the next
slots, where
[
1,
13,
23].
The process initiates by designating the current time slot as the outset, referred to as stage zero [
1,
13,
23]. At this outset, UAV
calculates
control inputs, denoted as
and
, where
varies from
to
. These inputs are selected to minimize Equation (17), ensuring the subsequent position
remains within
[
1,
13,
23]. Utilizing model (7) and the computed control inputs, in conjunction with the initial position and heading at stage
for each UAV, enables the determination of their position and heading throughout each successive time step across the next
slots [
1,
13,
23]. This process delineates the optimal flight paths for each UAV throughout the duration
.
At stage zero, using the predicted target’s position and heading for the next
slots, the feasible flight zones (10) for each slot are established. These zones are determined based on the position and heading of a single target, as well as considering the terrain’s shadow on the operational plane. These values are consistent for all UAVs at each stage; thus, all UAVs share identical feasible flight zones [
13,
23]. This zone represents the state space of our system, and at stage
for all UAVs, it is denoted as
, where
. This state space is discretized into a grid, and each UAV’s position at any time slot is represented by a grid point within
. This discretization ensures that the state space remains finite at each stage [
1,
13,
23].
Now, each UAV
has a cost function:
where this function quantifies the cost incurred when transitioning from any state
in
to any state
in
[
1,
13,
23]. The values of
and
are obtained by using
and
in Equations (12) and (13), respectively, substituting
with
[
1,
13,
23]. The values of the control inputs
and
that facilitate this transition and are used in (18) will be explained later in this section.
We rewrite (18) as
to represent the cost of transitioning from the
th candidate
within
to the
th candidate
within
[
1,
13,
23]. Here,
and
are the control inputs
and
, respectively, required to make this transition [
1,
13,
23]. For simplicity, let
. With these definitions in place, we now have all the necessary components to introduce the DP framework that each UAV employs [
1,
13,
23].
Using the DP method, each UAV computes a local path starting from its initial state and spanning
subsequent states. It is important to note that not every state in one stage can transition smoothly to every state in the next stage [
1,
13,
23]. This restriction is based on the maximum distance allowed for UAV movement between states within a single time slot [
1,
13,
23]. Consequently, certain combinations of control inputs
and
may not be achievable, leading to an infinite transition cost indicated by
[
1,
13,
23]. Moreover, as finding the final location of each UAV is unnecessary, we introduce a virtual final state
at stage
with zero cost
[
1,
13,
23].
The minimum cost needed for a segment of UAV
’s local path, from initial state
to state
in stage
, is represented as
[
1,
13,
23]. The DP method is used in this manner as in [
1,
13,
23]:
Following the computation of
, the final optimal cost can be obtained by the following [
1,
13,
23]:
Initially, this DP algorithm computes the cost of transitioning from the starting states to any state in the next stage. At each subsequent stage, the algorithm updates the minimum subtrajectory cost from the previous stage by adding the cost of moving to the next state [
1,
13,
23]. This iterative process continues until all states in the penultimate stage
are processed. At the final stage, the cost is set to 0 for all states, thereby simplifying the calculation in (21)
[
1,
13,
23]. In this manner, the algorithm identifies the minimum cost of the optimal trajectory. Subsequently, to form the trajectory, an additional backtracking algorithm is necessary [
1,
13,
23].
After obtaining waypoints for their local paths, each UAV shares these data with the others. When conflicts arise between two or more UAVs, such as overlapping waypoints or insufficient separation, the involved UAVs negotiate to determine which UAV will use the conflicted waypoint and which will need to find a new one [
13,
23]. The UAVs that must find new waypoints resolve these conflicts by eliminating the conflicted waypoints from their state spaces and using the DP algorithm to find alternative waypoints that optimize the main objective [
13,
23]. This process continues iteratively until all UAVs have final, unconflicted trajectories that are ready for execution. The negotiation process employs methods similar to those described in references [
33,
34,
35].
Now, to move any UAV
from its current position
to its new position
, we must first find
and
. These parameters are also essential for computing
in (18), which is used to implement the DP method [
1,
13,
23]. One approach to determining
and
involves initiating the UAV’s rotation, if necessary, from its current position
at the start of the time slot. The UAV rotates using either
or
while traveling at a constant linear speed
[
1,
13,
23]. This rotation and linear speed continue until the UAV’s heading is directed towards
, a position referred to as the tangent point and denoted by
[
1,
13,
23]. Once at the tangent point, the UAV stops rotating and travels in a straight line towards
with the same constant linear speed
[
1,
13,
23]. This design adheres to UAV kinematics by avoiding sudden movements and sharp turns.
To choose between
or
for any UAV
, we need to determine the turn’s orientation at
. The UAV decides to turn left or right based on whether
is positioned to the left or right of its current heading angle
. This decision is made by calculating the angle
, which is measured from the
x-axis to the vector
in the counterclockwise direction [
1,
13,
23]. The UAV then determines the turning direction by evaluating the angle
, which represents the angle between the UAV’s current heading and the direction of
, measured counterclockwise [
1,
13,
23]. The turning direction is then determined based on this angle as follows [
1,
13,
23]:
The next step is to find the tangent point
and the UAV’s linear speed
. The linear speed
is used to calculate the turning radius
(
), while the tangent point
is where the UAV’s angular speed
becomes zero [
1,
13,
23]. The process begins by introducing a unit vector
, oriented perpendicular to the UAV’s heading direction
. The center of the UAV’s circular turning path,
, is then identified. This center is situated
away from the UAV’s position
, in the direction indicated by
[
1,
13,
23]. We now introduce two vectors: one from the center to
(denoted as
) and another from the center to the tangent point
(denoted as
) [
1,
11,
21]. Let
be the angle between these vectors. The method for calculating
is outlined as follows [
1,
13,
23]:
It is important to note that the dot product of the tangent line vector
and the vector
is zero because these vectors are perpendicular [
1,
11,
21]. Since
,
,
, we can derive the following equation as shown in [
1] using (23):
In (24),
denotes the angle between the vectors
and
[
1]. This angle
varies as a function of
[
1,
13,
23]. With
, you can rotate the unit vector of
counterclockwise to find the unit vector of
[
1,
13,
23].
Since
,
for any UAV
can be derived using (23) as follows:
Note that, according to (26),
is a function of
[
1,
13,
23].
For any UAV
, the function below is proposed to determine
:
Here,
represents the arc length between
and
. Equation (27) requires UAV
to reach
at speed
by the end of the
-th time slot [
1,
13,
23]. With
being perpendicular to the UAV’s heading,
can be written as
. Hence,
is represented as follows [
1,
13,
23]:
Based on
and
, (27) can be expressed as follows [
1,
13,
23]:
With all variables depending on
, (29) is simplified to solve only for
, which gives the linear speed [
1,
13,
23].
After
is calculated,
is computed. The feasibility of
must then be tested. This involves comparing the direction from
to
with the UAV’s departure direction at
. If these directions are similar,
is deemed feasible. If they are not similar,
should be replaced with
to find an alternative tangent point [
1,
13,
23].