Abstract
Coastal environments, which are crucial for economic and strategic reasons, heavily rely on accurate bathymetry for safe navigation and resource monitoring. Recent advancements in through-water photogrammetry have shown promise in mapping shallow waters efficiently. However, robust uncertainty modeling methods for these techniques, especially in challenging coastal environments, are lacking. This study introduces a novel likelihood-based approach for through-water photogrammetry, focusing on uncertainties associated with camera pose—a key factor affecting depth mapping accuracy. Our methodology incorporates probabilistic modeling and stereo-photogrammetric triangulation to provide realistic estimates of uncertainty in Water Column Depth (WCD) and Water–Air Interface (WAI) height. Using simulated scenarios for both drone and airborne surveys, we demonstrate that viewing geometry and camera pose quality significantly influence resulting uncertainties, often overshadowing the impact of depth itself. Our results reveal the superior performance of the likelihood ratio statistic in scenarios involving high attitude noise, high flight altitude, and complex viewing geometries. Notably, drone-based applications show particular promise, achieving decimeter-level WCD precision and WAI height estimations comparable to high-quality GNSS measurements when using large samples. These findings highlight the potential of drone-based surveys in producing more accurate bathymetric charts for shallow coastal waters. This research contributes to the refinement of uncertainty quantification in bathymetric charting and sets a foundation for future advancements in through-water surveying methodologies.
1. Introduction
The coastal environment is of major interest to a broad spectrum of institutional structures as well as scientific communities and industrial entities. This is largely due to the economic and social stakes (e.g., harbor, urban areas), strategic issues, and the commercial activities (ex.aquaculture) concentrated in these areas [1,2]. Bathymetry is vital for coastal engineering studies, as it provides information on the morphology of the seabed. Indeed, bathymetry-derived products are crucial for most maritime applications: navigation safety (navigation chart compilation), harbor development (pre/post-dredging surveys), and monitoring of aquatic resources. On the technological side, various innovationshave emerged in the last decades, leading to the development of sensors dedicated to bathymetric mapping [3]. Innovations in bathymetry include optical alternatives for shallower waters, as traditional acoustic solutions are less efficient and require greater investments.
Technological innovations over the last few decades have led to the development of various cameras dedicated to bathymetric mapping. A significant amount of research involving spectral imagery (hyperspectral and multispectral) has demonstrated the ability to retrieve water biophysical properties such as chlorophyll-A concentration, suspended particulate matter, and benthic habitats, in addition to the WCD. There are two major approaches for retrieving WCD from spectral imagery: radiometric and geometric. Radiometric approaches require spectral measurements as input for providing an estimation of WCD at a pixel level [4,5,6,7]. They have been mostly applied to satellite imagery, where they contributed to the establishment of Satellite-Derived Bathymetry (SDB). On the other hand, geometric approaches allow users to obtain 3D reconstructions from images by triangulating a set of pixels that are located on more than one image (homologous feature points). Recent studies have demonstrated the potential of various photogrammetric (i.e., geometric) techniques for mapping shallow water depths from satellite imagery [8,9,10] and airborne imagery [11,12]. Ref. [10] reported similar accuracy to established SDB methods and argues that through water photogrammetry is a useful option in circumstances where radiometric methods are not applicable due to heterogeneous environments, inaccurate atmospheric correction, or unavailable in situ depth measurements.
As the navigation safety of vessels relies on WCD accuracy, it is of utmost importance to quantify the uncertainty associated with the derived product. Studies on bathymetry estimation using geometric approaches tend to focus on the estimation accuracy rather than the assessment of uncertainty, despite the fact that there are many sources of uncertainty. Extending the principles involved in land photogrammetry to through-water photogrammetry presents the challenge imposed by integrating the refraction into the collinearity equations. Furthermore, it relies on the assumption of negligible local errors that is suitable for applying uncertainty propagation, as recommended in [13]. As a result, there is a knowledge gap in the literature in terms of methods for estimating the uncertainty of WCD calculated using geometric approaches in shallow coastal areas.
In this work, we introduce a novel methodology for assessing WCD uncertainty computed using stereo-photogrammetric airborne imagery. Our approach differs significantly from collinearity-based triangulation methods, particularly in its suitability for coastal area surveys. Coastal environments present unique challenges, including limited access, dynamic landscapes, safety concerns, and environmental sensitivities, which complicate the establishment of Ground Control Points (GCP). These points are crucial for aligning imagery and refining the exterior orientation parameters. In coastal areas where GCP are scarce, relying on direct georeferencing with onboard Inertial Navigation Systems INS may offer limited accuracy compared to GCP-assisted land photogrammetry. This reduces its ability to correct exterior orientation parameters, potentially compromising the precision of the WCD estimate. Our methodology, therefore, focuses on determining the true object coordinates based on the observed camera pose, assuming that the interior orientation parameters are fixed and well-characterized. Additionally, the likelihood-based framework broadens the scope of traditional variance–covariance approaches by offering a more extensive uncertainty analysis, especially in complex scenarios such as small sample sizes where traditional approaches might underperform. Moreover, the use of controlled simulations instead of real datasets allows for a more objective assessment of our methodology’s robustness under various conditions, ensuring its validity and practical applicability in real-world scenarios.
The remaining structure of this paper is organized as follows: The next section provides an overview of existing approaches for uncertainty characterization in stereo-photogrammetry and highlights their limitations in airborne marine applications. Section 3 discusses the probabilistic framework employed for evaluating stereo-triangulated WCD uncertainties. Section 4 presents the experimental results and discusses the performance of our proposed methodology under the simulated scenarios. For clarity, Table 1 provides a comprehensive list of the parameters and symbols used throughout this paper. Finally, the conclusion summarizes the key findings, underscores the contributions and the potential of our likelihood-based triangulation approach, and discusses future research directions in this rapidly evolving field.

Table 1.
Parameter symbols and descriptions.
2. Related Works
This section synthesizes current methodologies for geometric WCD inference with a focus on uncertainty evaluation in through-water photogrammetry—an emergent field with a lack in comprehensive studies on uncertainty despite its importance alongside empirical validations.
Rational Polynomial Coefficients (RPC) are typically used in satellite pushbroom datasets for triangulating feature points and deriving bathymetric estimations in shallow waters [8,10]. Dolloff et al. have demonstrated the use of the variance–covariance framework to derive triangulation uncertainties using RPC data in land contexts [14,15]. However, in through-water contexts, the uncertainty inherent in RPC-based methods presents significant challenges. In principle, data on RPC uncertainty are essential to apply the variance–covariance framework for deriving triangulation uncertainties. In practice, most procedures for quantifying RPC uncertainties rely on GCP field measurements, which are challenging to obtain in coastal areas [16]. Furthermore, the need for refraction correction when using RPC-based triangulation introduces additional complexities. Although it is conceptually possible to implement the variance–covariance framework on top of RPC-based triangulation including refraction adjustments, this process adds a layer of complication to the uncertainty analysis in these settings. This lack of direct applicability complicates the uncertainty analysis for through-water photogrammetry, emphasizing the need for tailored methodologies that can accurately incorporate these refraction adjustments.
Structure from Motion (SfM) and Multi-View Stereo (MVS) methods, while well-established in land photogrammetry, have been adapted for through-water use to account for the unique challenges posed by the aquatic environment [17,18,19]. In the terrestrial context, these methods essentially employ the variance–covariance propagation with the associated LS estimator to derive uncertainties [20]. However, when adapted to aquatic contexts, these methods deploy adaptations of the collinearity equations to accommodate the refraction effect. These required adaptations often involve adjustments either in the image space [12,21] or the object space [11,22], aiming to estimate refraction effects accurately. Such adjustments are crucial because adapting the variance–covariance approaches to these modified settings is not straightforward. Although no studies were found detailing a direct application of variance–covariance to these adaptations, the required iterative processes go beyond classical least squares methods, complicating the evaluation of the uncertainties. Furthermore, implicitly compensating for refraction in these approaches renders the physical interpretability of the results more challenging, as the refraction effect is not explicitly accounted for. In addition to the assumption of a flat water surface, these methods are conceived for scenarios where the camera is vertically oriented to the surface [23,24]. This suggests their sub-optimality when drone imagery, usually characterized by low stability, is being used to create a 3D model of the seabed.
Ref. [23] contrasts corrective methods, i.e., adaptations of RPC and SfM-MVS for through-water use with ray tracing approaches, highlighting their limitations in handling complex optical paths effectively. This comparison emphasizes the need for tailored methodologies that can more effectively incorporate complex refraction adjustments while maintaining robust uncertainty analysis in through-water photogrammetry. Ray tracing methods, explicitly modeling refraction, offer a rigorous alternative for through-water triangulation and geometric uncertainty evaluation. Significantly, the explicit modeling employed by these methods enables a segmented analysis of the uncertainty budget, which in turn allows for the extraction of meaningful insights regarding the quality of measurements. Furthermore, advancements indicate that optimizing the cost function in the object space enhances geometric accuracy compared to traditional methods that primarily focus on the image space [23,25]. Despite these advancements, it is important to note that coastal through-water photogrammetry studies have not yet fully incorporated these techniques, largely due to the predominance of corrective methods dictated by common software and dataset conventions in practice.
The discussed methods underscore the need for novel inferential approaches that integrate both triangulation and uncertainty evaluation, specifically tailored for the unique challenges of coastal environments. Our proposed likelihood-based triangulation method addresses these challenges by offering an inclusive and extensible framework for evaluating uncertainties in WCD inferences, leveraging advancements in both theoretical and practical aspects of photogrammetry.
3. Methodology
This section delineates our approach for triangulating the positions of feature points in through-water stereo-photogrammetry and quantifying the uncertainties associated with WCD measurements. Our methodology mainly adopts the MLE framework, which is theoretically equivalent to the commonly used least squares under specific assumptions and thus is inclusive of traditional methods. Unlike the decoupled procedures of least squares followed by the variance–covariance framework for uncertainty evaluation, the MLE framework integrates estimation and uncertainty quantification into a cohesive process. Its statistical properties, robust in large samples supported by first-order theory, make it a comprehensive joint framework for both estimation and uncertainty analysis. Following this, the first Section 3.1 addresses the proposed likelihood triangulation and the associated statistical modeling assumptions. This allows for establishing the likelihood function for through-water triangulation as well as the different geometric modeling aspects of the proposed approach. The second section addresses the statistical evaluation of the uncertainties, employing first-order statistical tests for parameter uncertainty.
3.1. Proposed Likelihood Triangulation
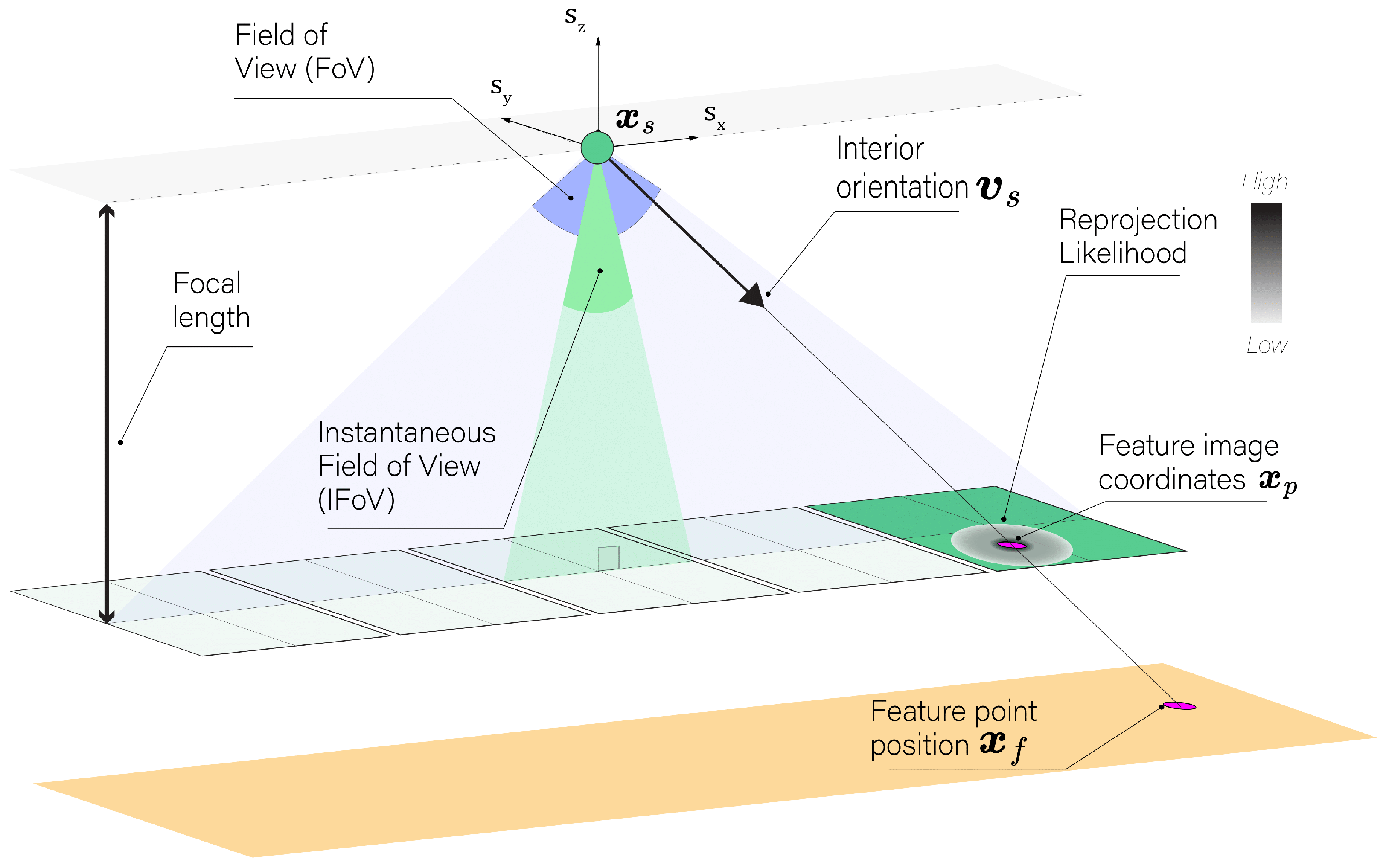
Classical triangulation in photogrammetry typically utilizes collinearity equations to relate the object coordinates of a feature point to its image coordinates , as well as the camera’s interior and exterior orientations, whose parameters can be denoted as and , respectively. As depicted in Figure 1, the primary goal in this context is to minimize reprojection error between the observed and modeled feature image coordinates, denoted as . This is formally achieved through the following LS minimization:
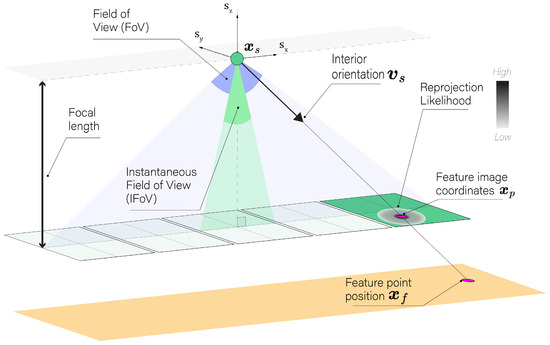
Figure 1.
Illustration of the process of minimizing reprojection error in stereo-photogrammetry. Diagram of camera setup showing the Field Of View (FoV), focal length, and the Instantaneous Field Of View (IFoV). The internal vector and feature image coordinates are highlighted, with a color bar gradient indicating the reprojection likelihood magnitude.
Here, denotes the observed image coordinates of the feature point. As a consequence of the equivalence between the least squares and the MLE when assuming additive Gaussian errors, this optimization effectively seeks to maximize the likelihood:
This reprojection likelihood function describes the probability of observing the feature point image coordinates given the parameters , , . To achieve accurate triangulation, calibration is critical to optimize interior orientation parameters such as the focal length across surveys, while exterior orientations are often refined through spatial resection using GCP to enhance accuracy. Triangulation methods often rely on optimal values of and , disregarding the integration of the uncertainty of interior and exterior orientations into the estimation of the triangulated position of the feature points. This limitation is particularly critical in coastal surveys, where access to GCP is often restricted. It becomes even more crucial for pushbroom cameras, which must resolve or refine exterior orientation per swath rather than per image. Additionally, the minimal texture and feature distinctiveness of seabeds in coastal waters may complicate pairing of features across overlapping images, further reducing confidence in the exterior orientation.
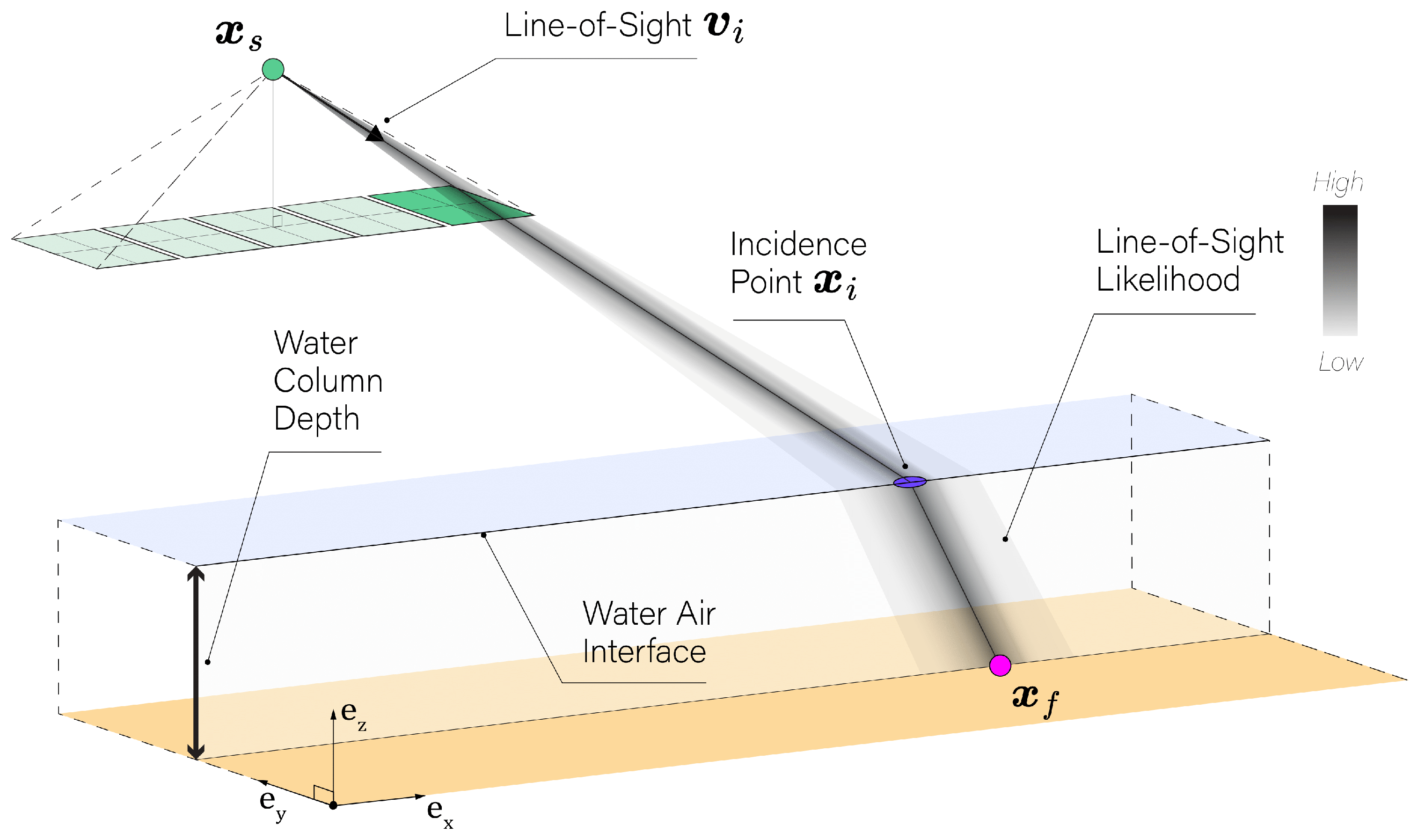
To address these challenges, our methodology emphasizes probabilistic modeling of camera pose, focusing particularly on its impact on the spatial uncertainty of the line-of-sight from the camera to the incidence point . Figure 2 illustrates this likelihood function, which can be employed in order to estimate the feature point position from camera pose data:
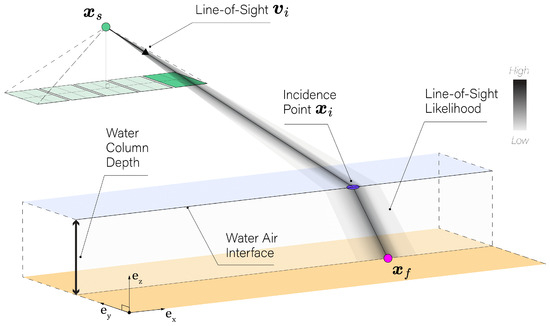
Figure 2.
Line-of-sight representation in through-water photogrammetry. Representation of the camera’s line-of-sight , demonstrating its path through the water column to the seabed feature position . Color bar gradient illustrates the magnitude of the line-of-sight likelihood.
Here, represents the measured camera pose data, is a unit vector representing the feature image coordinates in the sensor frame, h is the Water–Air Interface (WAI) height, and is the modeled camera source position. Since the influence of interior orientation is disregarded in the proposed approach, the internal vector , which describes the feature coordinates in the sensor frame, is considered fixed and known posterior to feature detection and pairing. This allows it to isolate the influence of the camera pose noise on the line-of-sight and establish its spatial likelihood, as illustrated in Figure 2.
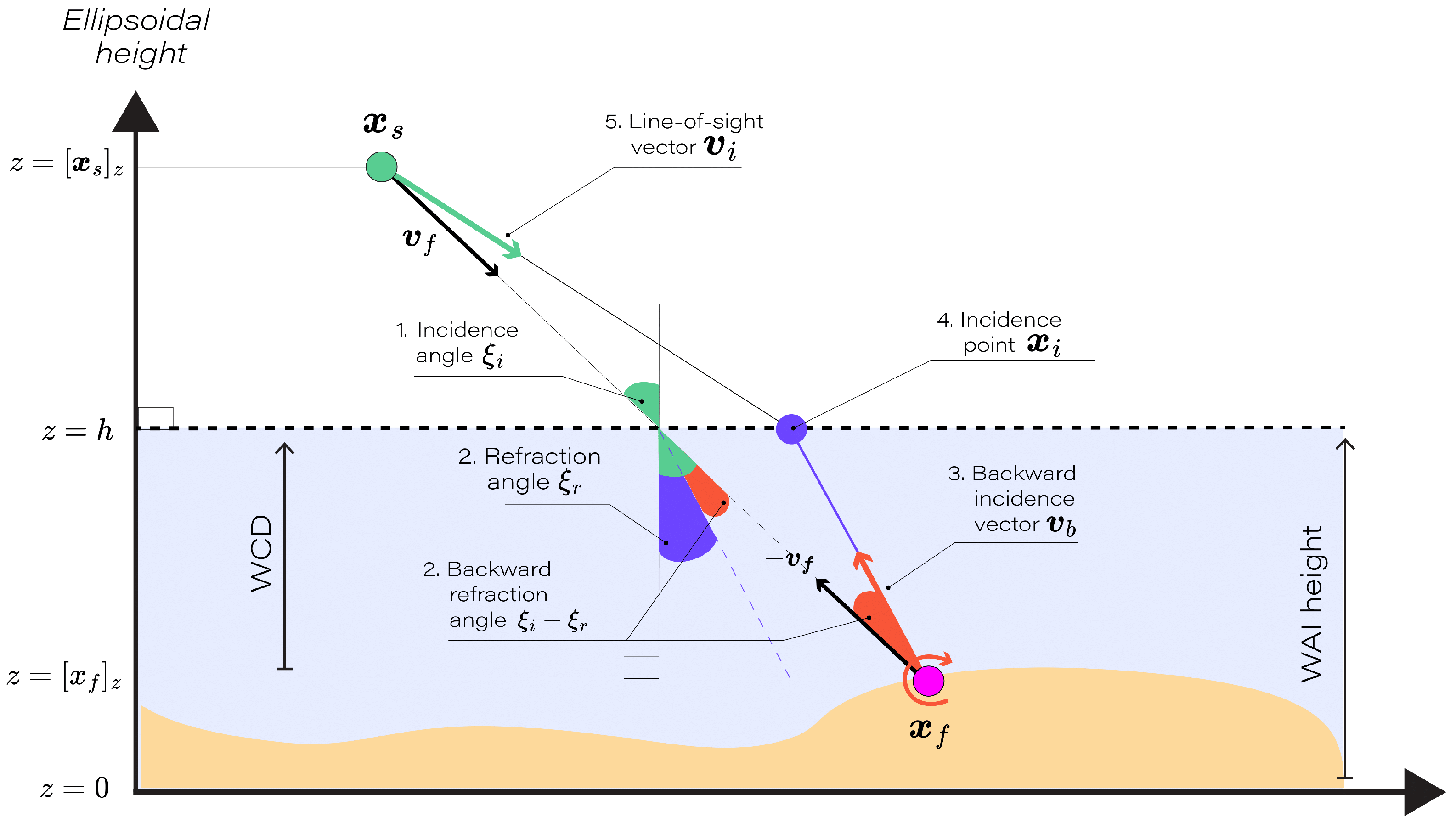
In this study, we focus on bathymetric measurements, particularly examining both the WCD and WAI height presented in Figure 3. The WCD describes the geometry of underwater environments, while the WAI marks the boundary between water and air, and its ellipsoidal height h is used for surface refraction modeling.
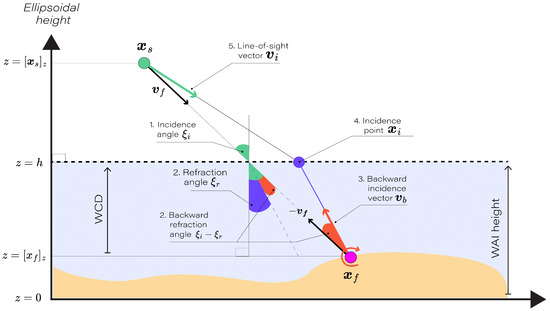
Figure 3.
Geometric representation of refraction for a feature point and one incident ray at a planar surface determined by the WAI height h.
3.1.1. Line-of-Sight Modeling
For each environmental geometric configuration consisting of the feature position and WAI height h, the objective is to model the line-of-sight vector using the parameters of the feature object coordinate , the camera source position , the horizontal water–air interface height h, and the nadir . This allows us to account for the refraction effect at the WAI through a strict geometric representation.
The steps involved in modeling the line of sight in the presence of a horizontal WAI are as follows:
- The incidence angle , the angle between the feature vector and the nadir , is calculated as follows:
- Using Snell’s Law, the refraction angle when transitioning from water to air is as follows:where n is the refractive index ratio, fixed at 1.33, representing the ratio of the speed of light in air to that in water. The incidence and refraction angles calculated in steps 1 and 2 are computed as if there was no refraction. These angles do not represent the actual incidence and refraction angles in the presence of refraction, but rather serve as proxies to determine the backward rotation necessary to model the refraction effect in the subsequent steps.
- The adjusted vector to refraction, a function of , , and the refractive index n, is computed by applying a rotation in the plane , with angle :
- The incidence point on the interface, where intercepts the water–air interface, is calculated as follows:where and are the vertical components of and , respectively.
- Finally, the line-of-sight vector , the normalized vector from to , is defined as follows:
Figure 3 illustrates the flow of Equations (4)–(8), which collectively define the model for the line-of-sight vector . This provides a direct relationship between the optical path and the geometric parameters h, , and , and it ensures a strict modeling of through-water refractive geometry. This model will now be used to address the influence of the camera’s position and orientation on the spatial uncertainty of the line-of-sight vector.
3.1.2. Camera Pose Statistical Model
Given the geometric model for the line-of-sight vector , we can directly connect these calculations to the triangulation process, which is pivotal for accurate underwater reconstructions. Considering a known interior orientation, the line-of-sight vector depends only on the camera pose.
Camera Pose Data
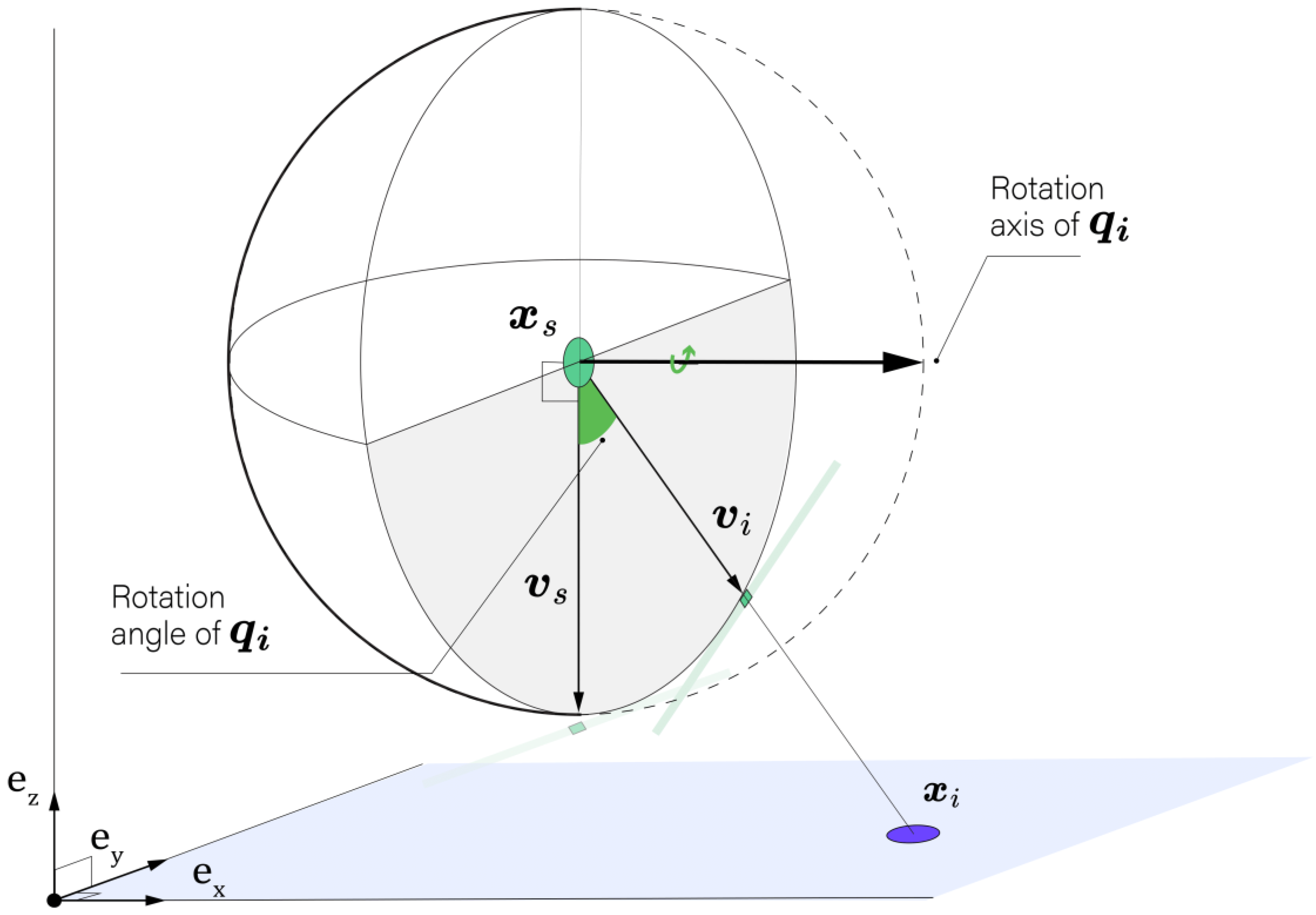
The position of the camera’s optical center is denoted as , and its orientation is modeled using the unit quaternion representing the minimum rotation between the internal vector and the line-of-sight pointing towards the incidence point, as illustrated in Figure 4. Unit quaternions are selected for representing the camera’s orientation to avoid the limitations associated with Euler angles, such as gimbal lock and the complexity of interpolation. Unit quaternions also provide a compact, non-singular representation for rotations and are particularly effective for continuous orientation tracking in three-dimensional space.
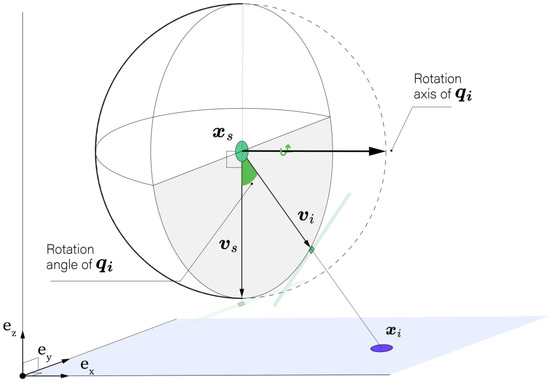
Figure 4.
Representation of the unit quaternion and the line-of-sight vector . The quaternion rotates the camera’s internal vector to align with the incidence point . The rotation axis and angle of are indicated, illustrating the geometric transformation involved.
The correspondence between the minimum rotation unit quaternions and the line-of-sights is unique up to sign, meaning that both and represent the same orientation. The unit quaternion defining the minimal rotation from to can be defined as follows:
and are the magnitudes of the internal vector and the line-of-sight, respectively, and is the dot product of both vectors. is the cross product yielding a vector that is perpendicular to both input vectors, which represents quaternion components , , and as the axis rotation component. is normalized to have unit magnitude.
Statistical Model
The position of the camera is modeled using a Gaussian distribution due to its properties in reflecting Euclidean space errors:
Here, is the measured position vector of the sensor, and and are parameters of the sensor position and its variance–covariance matrix, respectively.
The camera orientation determined by a unit quaternion is modeled using the Bingham distribution, which is specifically designed for data constrained to the surface of a hypersphere, like unit quaternions. This distribution is parameterized by an orientation matrix and a concentration matrix , which adjust the distribution’s shape based on the degree of certainty in the camera’s orientation:
Here, is the random attitude measurement of the quaternion that represents the observed orientation of the sensor. In the Bingham distribution, is an orthogonal matrix and is a diagonal matrix of size representing the orientation and concentration parameters, respectively.
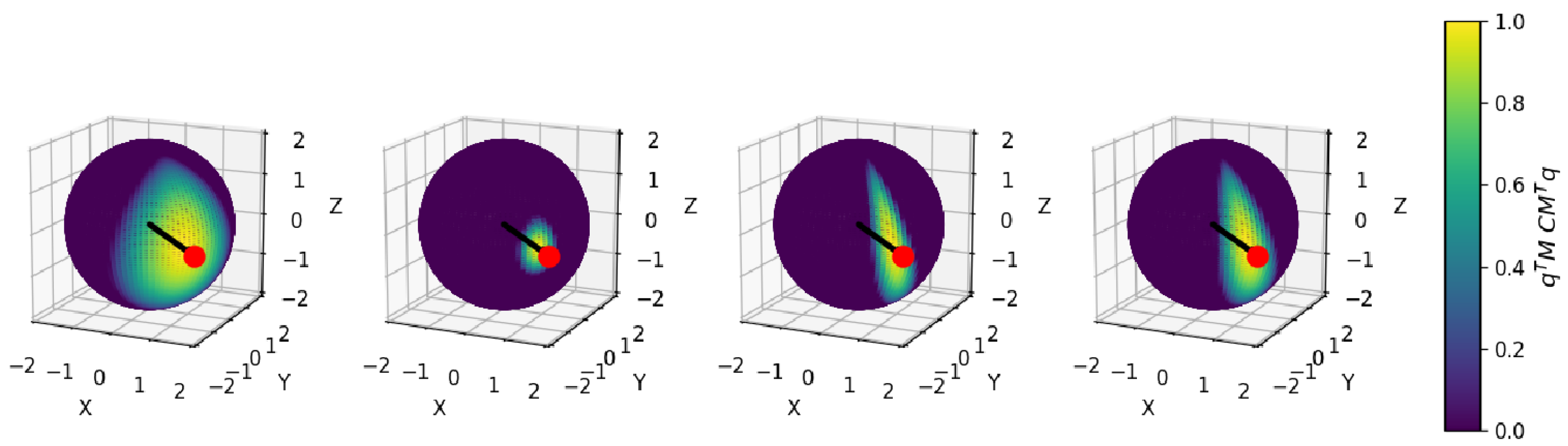
The concentration parameter determines the spread or the shape of the distribution, whereas the orientation parameter represents the location of the distribution, also called the orientation. The diagonal elements of the concentration matrix control the degree of anisotropy of the distribution. Due to the constraint of unit norm on the quaternions, one of the diagonal concentration values must be zero. The fourth diagonal element is chosen, while other conventions may use the first element. An isotropic distribution has equal concentrations along all three axes of rotation, resulting in a uniform distribution of orientations (see Figure 5). In an anisotropic distribution, the diagonal elements of are not equal, and the distribution is stretched along one or more axes of rotation. is a normalization constant that depends on the concentration of the density.
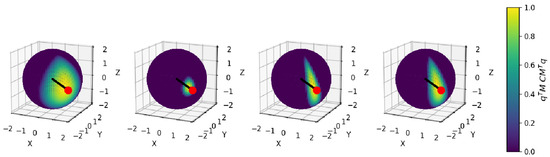
Figure 5.
Illustration of the Bingham concentration parameter influence. The right, middle, and left spherical plots correspond to , , , and , respectively. The black vector represents the line-of-sight used to arbitrarly define an orientation matrix for the Bingham distribution. The red dot represent the incidence point . The spherical heatmap represents the non-normalized Bingham log-density: mapped to the interval for the three concentration cases.
At this stage, it is critical to link the line-of-sight to the Bingham distribution parameters to accurately formulate its likelihood. The orientation matrix , where its last column is defined by the quaternion , plays a pivotal role. This quaternion aligns the sensor’s internal frame, described by vector , with the line-of-sight vector . The remaining columns of in isotropic conditions can be filled with an arbitrary orthogonal complement using methods such as the Gram–Schmidt process or singular value decomposition of . Orientation data from (INS), characterized by pronounced anisotropic uncertainties, with yaw being more variable than roll or pitch, necessitate sophisticated configuration of the Bingham distribution’s parameters, and . Such data typically arrive in Eulerian format, with mean and covariance values computed using spatial resection techniques or from outputs of a Kalman filter, and are foundational in determining these parameters.
One can consider dynamically recomputing and for each line-of-sight by directly sampling from the Eulerian noise associated with that specific orientation on the sphere. Although this approach is capable of capturing the true variability in sensor orientation, ensuring fidelity, it also requires sampling quaternion data points from the Eulerian data distribution. However, its computational intensity limits scalability across large datasets, particularly when considering optimization tasks. For practicality in extensive datasets, we use this simpler approach. and are predetermined from a representative average of the orientation data by resampling from the Eulerian attitude noise. Additionally, this static setup efficiently approximates the dynamic method under conditions of minimal attitude noise. The orientation density approximation can be formulated as follows:
The matrices , , and the normalization factor are derived from the camera orientation data realization and a fixed Euler attitude covariance using the maximum likelihood estimation method described in [26] with 10,000 randomly sampled quaternions. This ensures that the fixed parameters effectively model the orientation uncertainties, streamlining computation while maintaining analytical rigor in the evaluation of WCD uncertainties in through-water triangulation.
Having rigorously defined the statistical models for the camera’s position and orientation using Gaussian and Bingham distributions, we have established a robust framework to represent the stochastic nature of the camera’s pose. The line-of-sight vector , as modeled in Section 3.1.1, depends on the horizontal water–air interface height h, the camera source position , and the feature point coordinates . Hence, the position and the orientation distributions combine into a joint probability density function for the camera pose, parameterized as follows:
where encapsulates the statistical model of the camera’s position and orientation as a function of the line-of-sight parameters since the internal vector is fixed. This joint density function provides a quantitative measure of uncertainty and forms the link to the line-of-sight vectors employed for through-water triangulation.
3.1.3. MLE-Based Triangulation
Leveraging the presented camera pose statistical model, we construct the likelihood function that accounts for both positional and rotational uncertainties in the camera setup. The likelihood function L for a single feature point observed from a single camera can be expressed as follows:
Assuming independent camera poses, the likelihood function L for a single feature point observed from a multiple cameras can be expressed as follows:
Disregarding the constant terms that do not involve the parameters, mainly the normalization constants and , we can write the following:
The logarithm of this likelihood function, denoted as ℓ, can be written, ignoring the constant terms, as a single index m summation with two quadratic forms:
For multiple feature points observed from multiple sensors, the logarithm of this likelihood function can be expressed as a double summation over k and m, where K represents the number of feature points and M represents the number of sensors:
In a typical case, with two camera views observing a single feature point, the number of parameters to estimate is 9, including 3 for , 1 for h, and 6 for both camera positions . The MLE is then obtained by maximizing this function with respect to the parameters h, , and . For problems where we estimate the WAI height h, we utilize multi-feature multi-view likelihood to leverage more statistical information and investigate accuracy improvements.
3.2. Uncertainty Evaluation
Understanding the uncertainties associated with our estimations is crucial for robust decision-making and inference. We begin by exploring the concept of profile likelihood, which allows us to focus on parameters of interest while accounting for nuisance parameters. This leads to first-order statistical tests, where we introduce the signed likelihood ratio statistic and the Wald test statistic hypothesis testing and confidence interval (CI) computation. Subsequently, we describe the procedure of assessing the performance of the CI in terms of coverage probability, shedding light on the reliability of the first-order statistical tests. Our investigation aims to provide insights into the uncertainty quantification process, essential for interpreting and utilizing the results of our triangulation approach effectively.
3.2.1. Profile Likelihood
The likelihood function for through-water triangulation depends on the parameters , which can be decomposed into two components depending on the investigated parameter. The concept of profile likelihood plays a critical role in statistical inference, particularly when focusing on a parameter of interest while accounting for nuisance parameters:
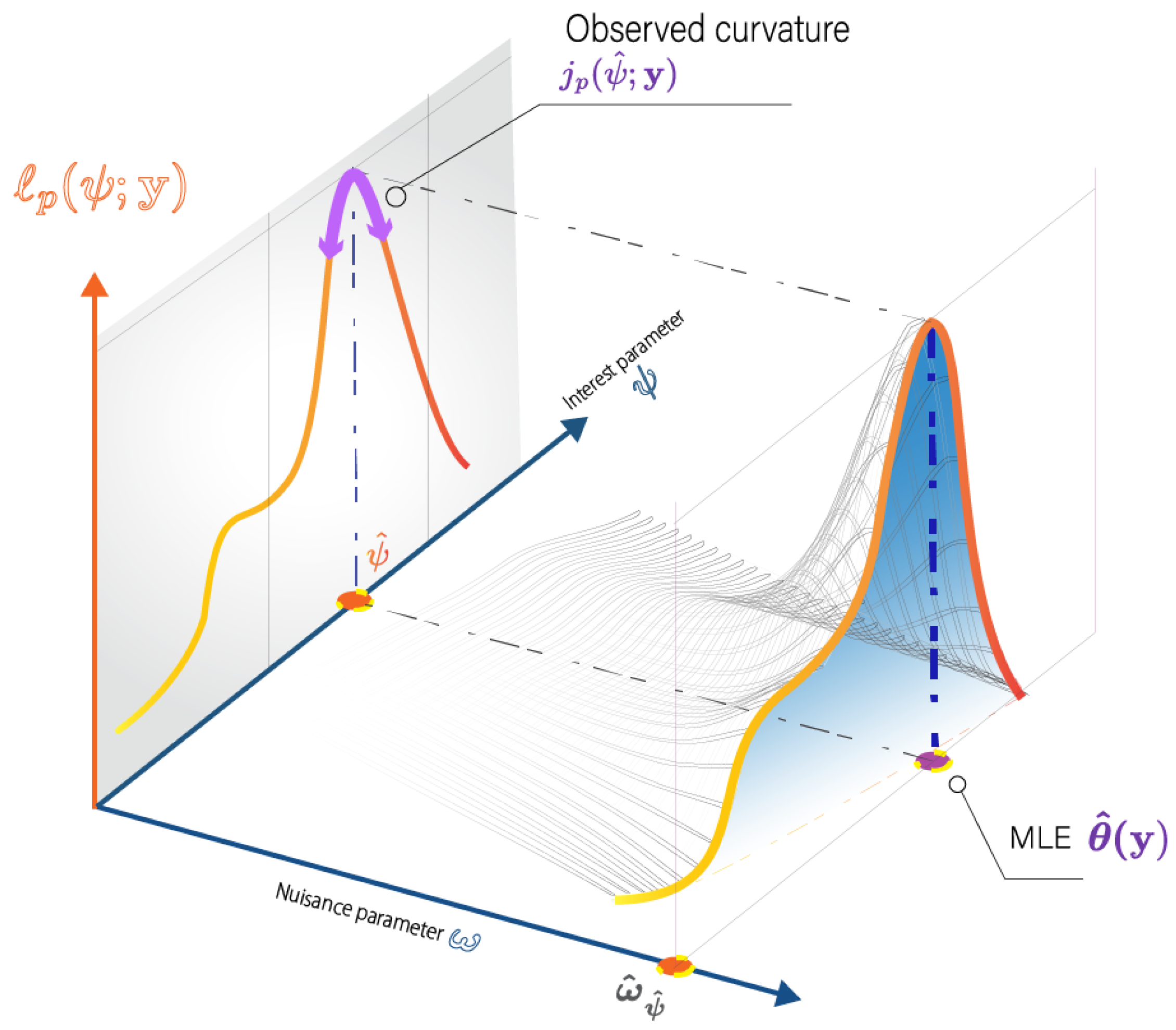
In essence, the profile likelihood simplifies the likelihood function by focusing on and adjusting the nuisance parameters accordingly. This is achieved by maximizing the likelihood with respect to the nuisance parameter, resulting in the constrained maximum likelihood for each value of (see Figure 6).
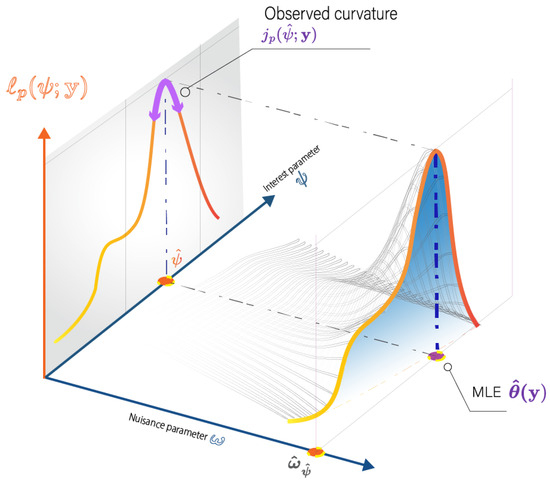
Figure 6.
Geometrical illustration of profile likelihood for a two-dimensional parameter space.
Notably, maximizing the profile likelihood is in accordance with the overall MLE of :
3.2.2. First-Order Statistical Tests
For scalar parameter , first-order inference uses test statistics like the signed likelihood ratio statistic r and the Wald test statistic [27]:
where is the partial observed information. Under certain regularity conditions, these test statistics asymptotically follow a standard normal distribution under the null hypothesis:
It should be emphasized that scalar test statistics are in harmony with multidimensional inference. In those broader contexts, the test statistics converge to a chi-squared distribution, where the degrees of freedom match the dimensionality of the interest parameter. This ensures that focusing on a scalar parameter does not deviate from the traditional multidimensional inference context. Furthermore, the first-order arsenal includes the score and the Wald test based on the expected Fisher information, in addition to the test statistics investigated in this study. In particular, it is noteworthy to emphasize the equivalence between the Wald test based on the expected Fisher information and variance–covariance/LS under additive Gaussian errors (see Appendix A). This underscores the profile likelihood framework as an encompassing approach that integrates traditional variance–covariance practices. While this study excludes the use of this test statistic, as an analytical expression of the expected Fisher information matrix cannot be readily obtained due to the use of the Bingham distribution, it is essential to highlight that the expected and observed information Wald tests often behave similarly in large samples.
3.2.3. Evaluation of Confidence Interval Performance
The performance of the CI for the parameter of interest is evaluated based on coverage probability. Coverage probability is defined as the frequency with which the true value of the parameter of interest, denoted as , falls within the estimated CI . Mathematically, coverage probability is expressed as follows:
Here, represents the significance level, set at 0.05 for a 95% confidence level (CL) in this study. To construct the CI, the following first-order test statistics are employed:
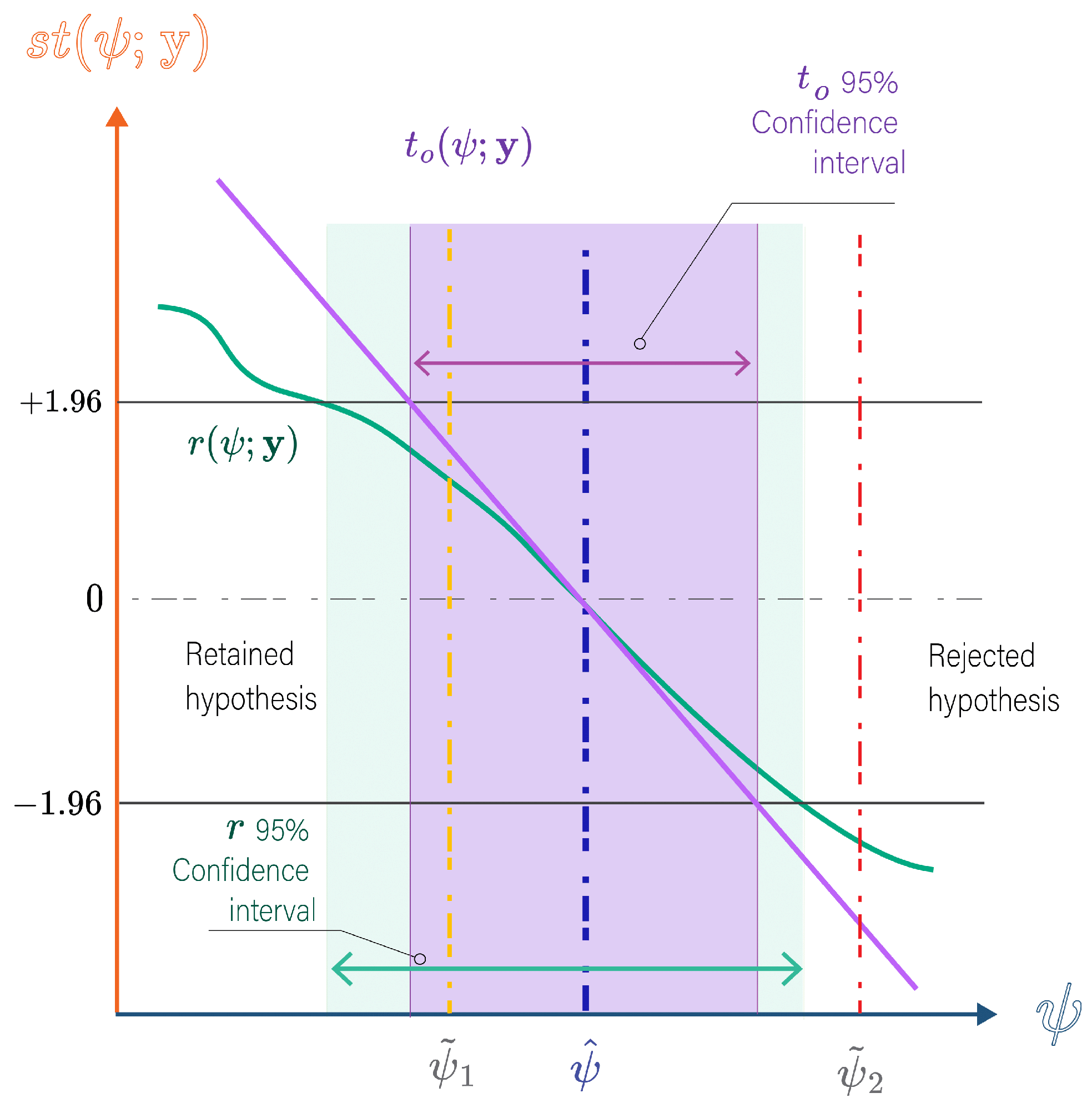
is the critical value corresponding to the tail of a standard normal distribution, generally approximated as 1.96 for the 95% CL. Figure 7 demonstrates how hypothesis testing and CI estimation are performed based on the profile likelihood for the 95% CL. In order to empirically validate the coverage probability of CI, we use Monte Carlo simulations to generate sample data from the actual parameter values . Specifically, we calculate the observed test statistic for each camera pose sample at the true value under the null hypothesis. An observed test statistic’s absolute value greater than would indicate that the null hypothesis can be rejected at the CL. The ideal performance under simulation would be rejecting the true hypothesis 5% of the time, indicating that the confidence intervals derived from the investigated test statistic align with their expected theoretical coverage.
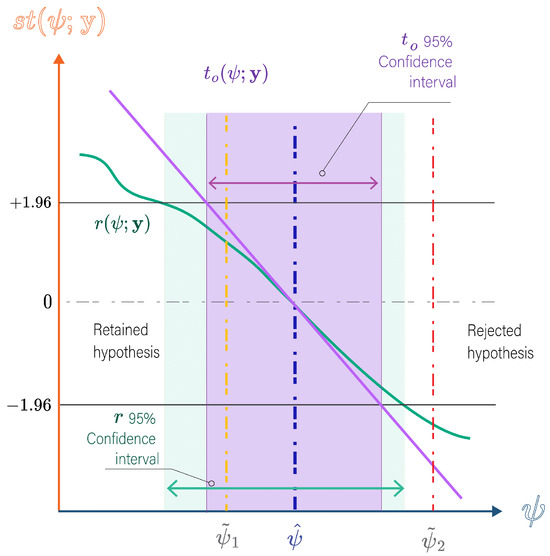
Figure 7.
First-order statistical tests and hypothesis testing: The red line indicates rejection of the null hypothesis (type I error), which should theoretically occur 5% of the time for a 95% CL, depending on the statistical test performance. The r curve, depicted for a small sample scenario, is expected to exhibit a linearly decreasing trend analogous to Wald tests with increasing sample sizes.
Unlike variance–covariance approaches, profiling can reveal the asymmetric behavior of CI in nonlinear setups, crucial for accurate uncertainty quantification. As highlighted in Figure 7, Wald tests result from construction of a linear slope, yielding a symmetric CI around the MLE . On the other hand, r effectively captures the asymmetric behavior that can arise in non-linear setups.
For the WCD uncertainty evaluation, we consider the constrained triangulation problem where h is fixed and known, whereas the primary parameter of interest is the WCD, i.e., . Additionally, we consider the case where the interest parameter is a systematic WAI height h that is inferred from multiple features observations.
4. Results
In the this section, we present an overview of the main results obtained from our probabilistic modeling and likelihood-based inference approach. We first begin by describing the simulated experiments, consisting of realistic pushbroom geometric configurations in coastal areas, used to validate the proposed methodology. The results are partitioned into two main sections, WCD inference and WAI height inference, focusing on the uncertainties of these parameters.
4.1. Simulated Experiments
The experimental setup for this study is designed to evaluate the performance of the proposed method for pushbroom camera acquisition under various flight scenarios, encompassing both airborne and drone operations. The airborne scenario simulates an altitude of 2000 m, reflecting typical conditions for aircraft-based remote sensing missions, while the drone scenario simulates a lower altitude of 120 m, indicative of low-altitude drone surveys.
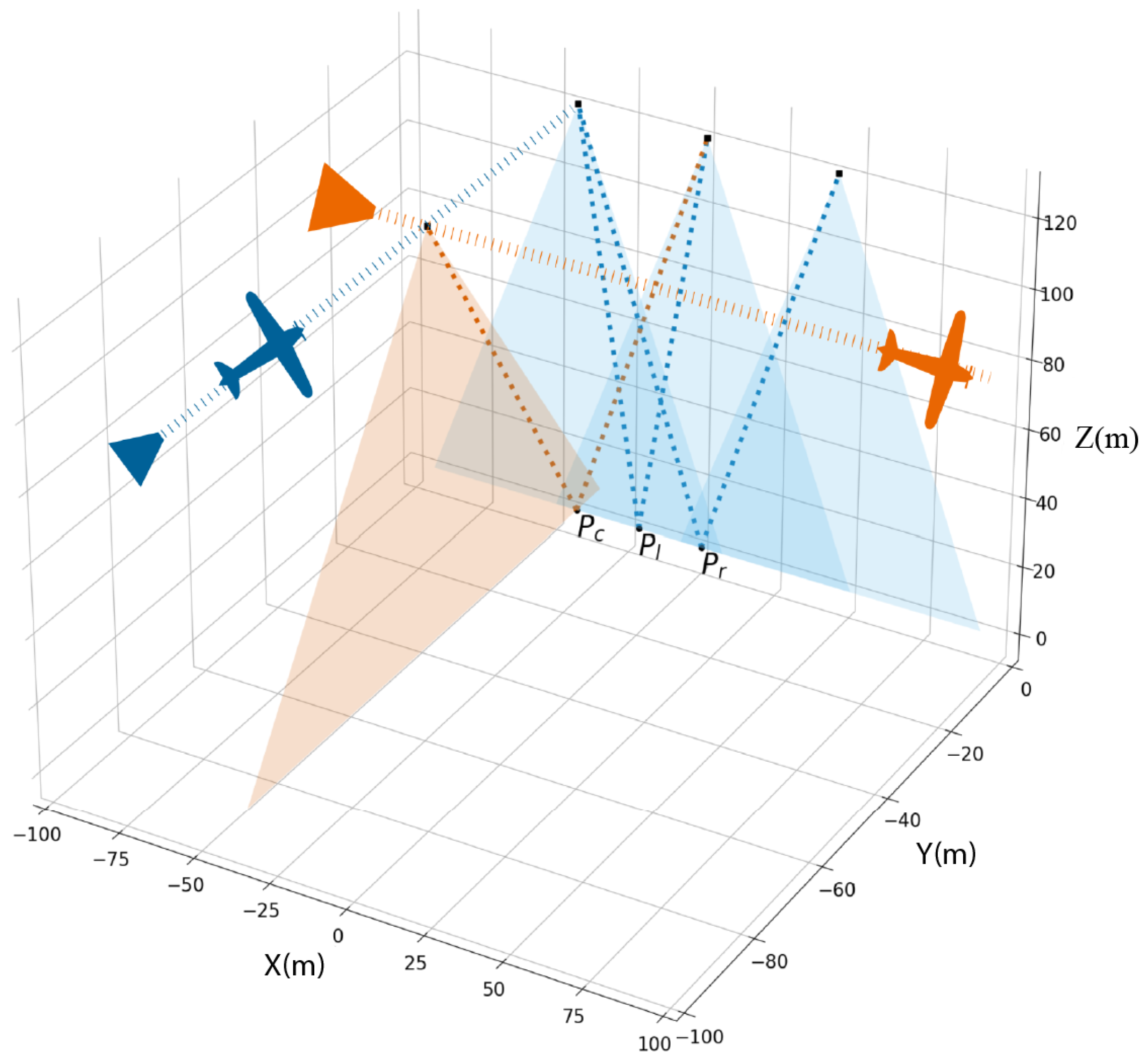
Figure 8 illustrates the camera positions (black squares) and their respective scanned FoV (blue and orange triangles) for the drone scenario. We use aFoV of 48°; a relatively extreme value to challenge our approach. To ensure comparability and consistency, the same base–height ratio determined for along-flight directions (determined by the 60% overlap constraint) is transposed to the single across-flight trajectory used for the scenario. This setup maintains a consistent geometric configuration across different orientations.
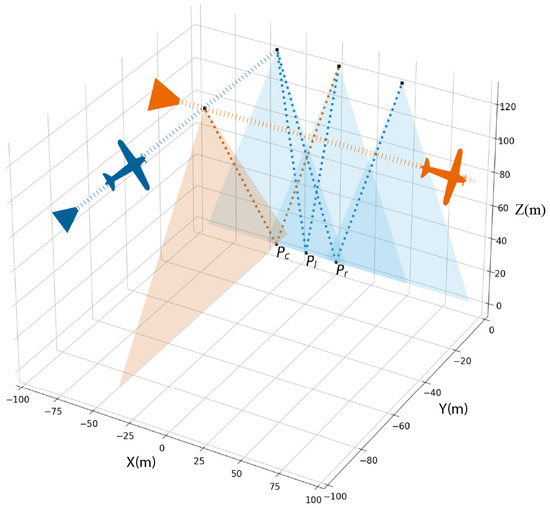
Figure 8.
Geometric configurations for drone scenario for aFoV of 48° and an overlap of 60%.
In the experimental setup, various viewing geometries were simulated to evaluate the performance of the proposed method. Table 2 presents these viewing geometries, which are determined by feature points , , and . Table 3 presents the simulated INS classes defining sensor pose quality metrics in terms of standard deviation.

Table 2.
Base–height ratios for feature points for both drone and airborne scenarios.

Table 3.
Experimental setup classes with camera pose noise metrics in terms of standard deviation.
For both the drone and the airborne experiments, three levels of camera pose quality were considered: “fair”, “good”, and “excellent”. The positional accuracy ranges from 0.5 m for the fair class to 0.05 m for the good and excellent classes. In our simulations, the precision of the camera’s attitude is modeled with distinct values for roll/pitch and heading. Specifically, for the fair class, we use 0.1 degrees for roll/pitch precision and 1 degree for heading precision. For the good class, the precision is set at 0.01 degrees for roll/pitch and 0.1 degrees for heading. Lastly, the excellent class is characterized by a uniform precision of 0.01 degrees for both roll/pitch and heading.
To assess the robustness and reliability of the proposed methodology, we perform Monte Carlo simulations by generating synthetic datasets around a true parameter value. A true attitude value of and a fixed covariance matrix were considered for the attitude, while the true camera positions were simply set to the simulated locations. These simulations involve generating a large number of synthetic datasets represented by random orientation and concentration matrices , , as well as random camera positions , each with different levels of noise. The results of the simulations are used to evaluate the performance of the methodology and to analyze the uncertainties of WCD and the WAI height in terms of the 95% CI under different conditions. Concerning the numerical computation of the MLE, the Adam optimizer is used for the WAI height inference, since the dimension of the parameter space is relatively large in this problem. The trust region optimizer available in the SciPy library is employed for the inference of WCD, chosen for its efficiency in handling problems of relatively small scales.
4.2. Water Column Depth Inference
In this section, we consider the WCD inference in the through-water context, assuming that the water–air interface height is known and fixed at .
4.2.1. WCD Uncertainties
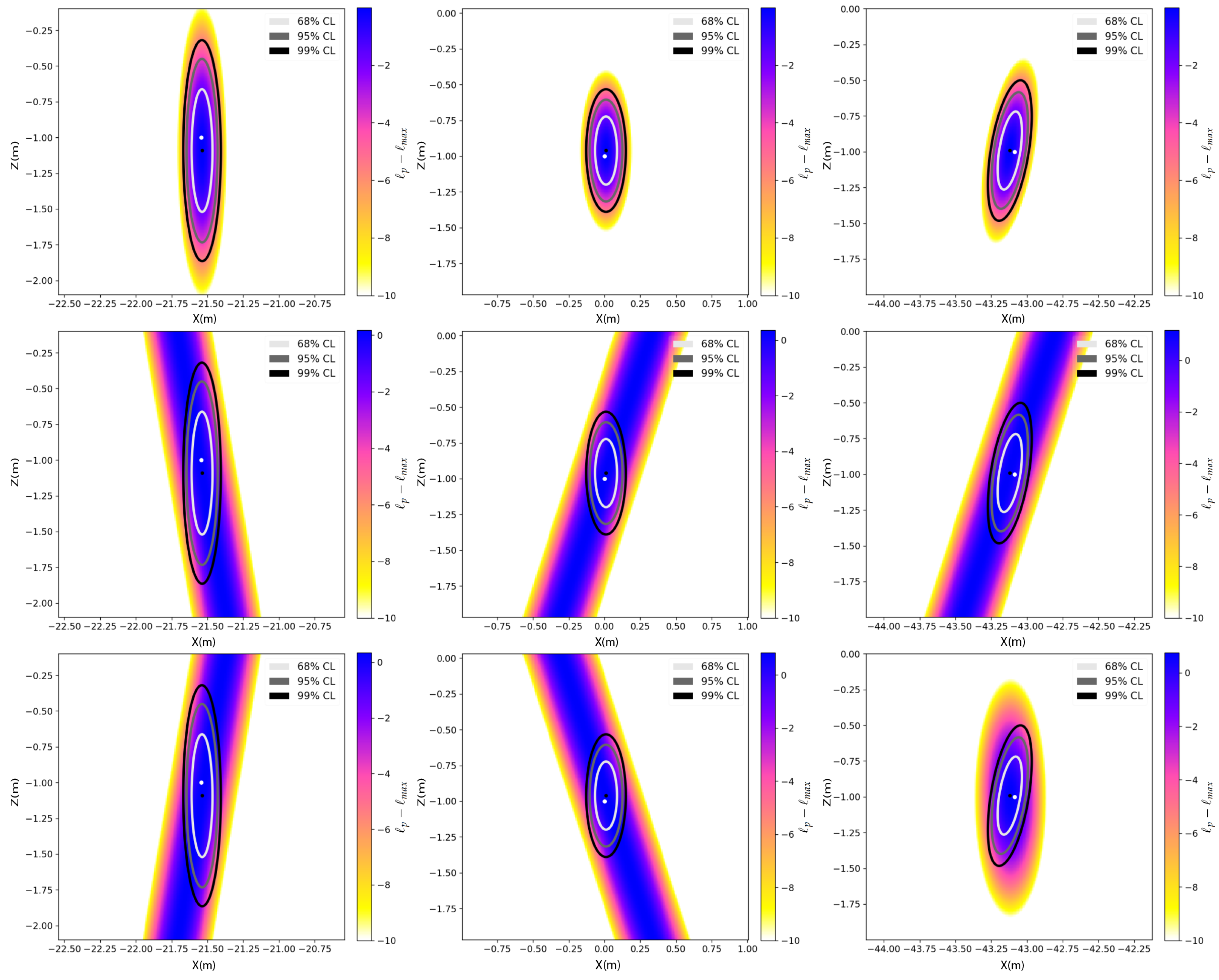
Figure 9 provides a graphical representation of the normalized profile likelihood surfaces for three points, , , and , specifically for the drone case. Each plot corresponds to a planar cut along the yz-plane of the 3D multi-view likelihood profiled along the interest parameter , displaying the confidence regions obtained using the likelihood ratio with three degrees of freedom. We observe that the uncertainties for are generally higher compared to and , with a factor of 2 between and uncertainties. In the one-medium photogrammetry, it is known that the vertical uncertainty is proportional to the base height ratio. Additionally, the point , which is viewed by perpendicular lines, exhibits non-vertical uncertainty ellipses mainly because the line-of-sights are not co-planar as suggested by the difference in camera contribution to the 3D likelihood in the yz-plane, as highlighted by Figure 9 for point . Analyzing the uncertainty ellipses within the experiment classes present in Table 3, our results indicate that the WCD uncertainty shape is not heavily influenced by the depth factor.
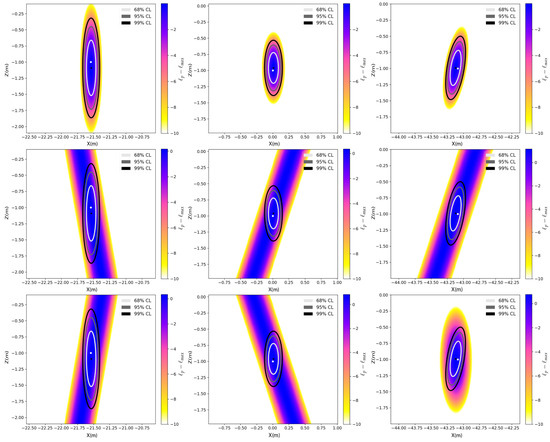
Figure 9.
Normalized profile likelihood (noted with as a shortcut) surfaces for the drone case and an excellent INS with confidence regions using the multidimentional likelihood ratio statistic for the parameter . The first row displays the combined profile likelihood, representing the sum of the likelihoods from both the left (second row) and right camera (third row) perspectives. The left, middle, and right columns are for points , , and , respectively. The white dot represents the true feature position , while the black dot represents the maximum likelihood estimate .
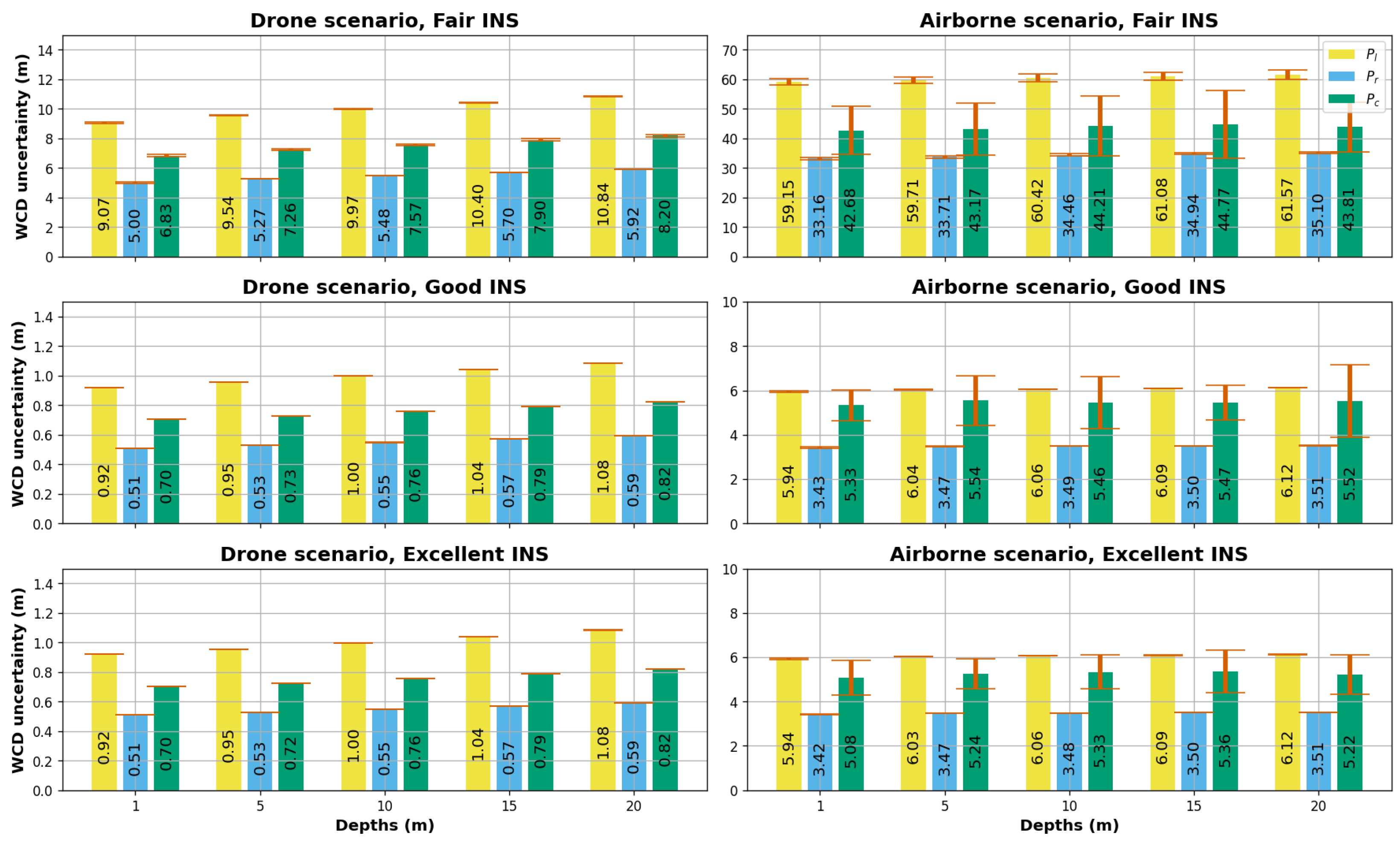
Focusing on the WCD as a parameter of interest, we can further examine its uncertainties based on the statistic using Monte Carlo simulations (as shown in Figure 10). The plot in Figure 10 provides a comparative analysis of the WCD uncertainty in terms of 95% confidence interval widths along with error bars representing the standard deviation of these intervals.
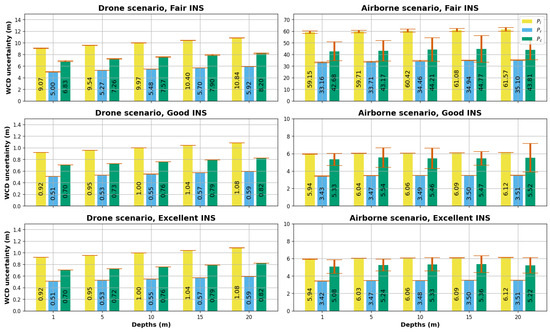
Figure 10.
WCD uncertainties based on 95% confidence intervals, (), reported by the observed Fisher information test statistic for different scenarios.
Overall, the impact of depth on the uncertainty of WCD is less significant than other viewing geometries. However, there is a slight increase in uncertainty as the depth increases, especially in the drone scenario, with a 15% uncertainty increase from 1 m to 20 m depth vs 3% uncertainty increase in the airborne scenarios. This is mainly due to the fact that base height ratio decreases as the depth of the simulated feature point increases, which generates an elongation of uncertainty ellipses. In terms of camera pose quality, both the excellent INS and good INS scenarios demonstrate relatively low and similar uncertainty values (50 cm to 1 m in the drone case and 3 m to 6m in the airborne case), with similar trends observed across different points. This indicates that increasing yaw precision does not necessarily lead to a more precise WCD estimation given the defined viewing geometries. Yaw rotation has a minimal effect on vectors that are close to the nadir, suggesting that the internal vectors are not influenced by yaw precision even with a highFoV and for large base–height ratio points. On the other hand, the fair INS class exhibits larger WCD uncertainties (factor of 10) with higher variability in the obtained WCD uncertainty. The airborne observations generally result in larger confidence regions and higher WCD uncertainties compared to the drone scenario. An increased distance for the feature rays results in an increased dilution of the attitude uncertainty; therefore, larger uncertainties are to be expected for higher flight altitudes.
Our results suggest that uncertainties in the airborne scenario are approximately six times greater than those in the drone scenario, despite a flight altitude ratio of 16:1 (2000 m for airborne versus 120 m for drone). Crucially, our study maintains consistent key parameters such as base–height ratio, FoV, and image overlap across both scenarios. In a purely geometric interpretation without probabilistic modeling, one might expect uncertainties to scale proportionally with flight altitude. In this regard, our findings indicate a statistical reduction in vertical uncertainty due to the intersection of two lines of sight, which is indicated in Figure 9 by the intersection likelihood compared to the single line-of-sight likelihood. We hypothesize that this effect increases with the altitude, elucidating why increased distances in the airborne scenario do not linearly translate into increased uncertainty, highlighting the influence of probabilistic modeling in the variability of vertical uncertainties between different flight altitudes.
Regarding the viewing geometry influence, WCD uncertainties for both drone and plane scenarios follow a similar order (increasing from to to ) and show comparable patterns of variability.
Interestingly, the uncertainties for point (viewed by cross lines) exhibit high variability, especially in the airborne flight and the fair INS case. In such a scenario, this increased variability of the uncertainty estimates for point can be attributed to the unique interplay between its viewing geometry and the anisotropic attitude noise, with a low concentration in the fair INS case. The viewing geometry of inherently results in intersecting lines-of-sight, but the sampled lines-of-sight in the fair INS class and high altitude airborne flight result in greater variability in the positional likelihood near the MLE. This, coupled with the effect of refraction, can account for this pronounced variability in the WCD uncertainty estimates for viewing geometry.
4.2.2. Evaluation of Uncertainty Metrics
In this section, we present the results of our likelihood-based inference approach for estimating the WCD uncertainty using the and r test statistics. The rejection rates of the null hypothesis (true parameter value) were calculated through Monte Carlo simulations, employing a significance threshold of .
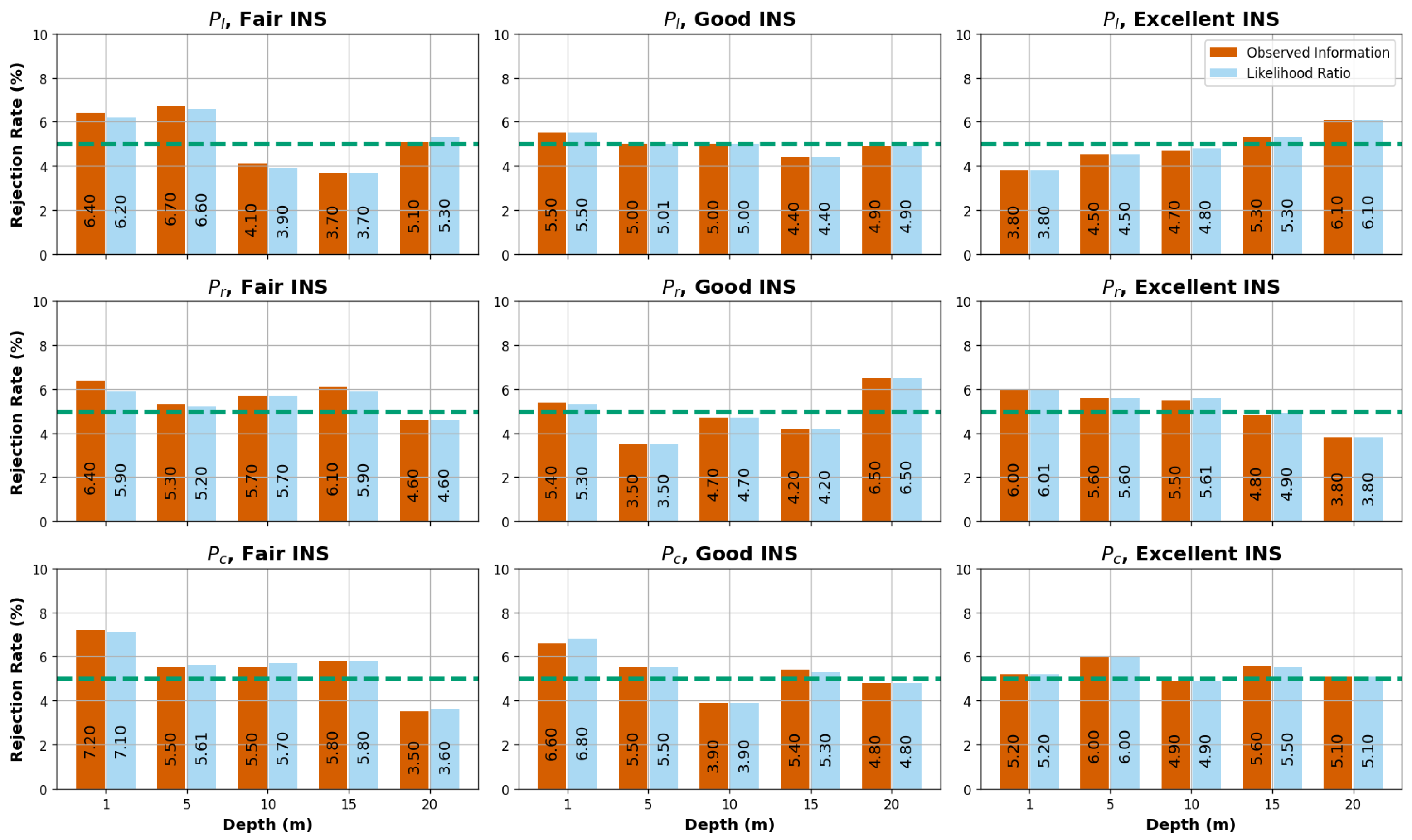
Figure 11 displays the rejection rates for various combinations of INS performances, depths, and viewing geometries in the drone scenarios. The statistical tests revealed a strong correlation among the samples, with rejection rates consistently aligning closely with the theoretical rejection rate of 5%, ranging from 3.5% to 7.0%. These findings indicate that both the and r test statistics are appropriate for estimating the 95% CI for the WCD parameter. The observed correlation suggests that the WCD uncertainties are symmetric in the drone scenarios. Although the expected Fisher information was not investigated in this study, the low variability of the uncertainties in most cases (orange error bars in Figure 10) indicates that it would have yielded similar results and performance to the observed Fisher information.
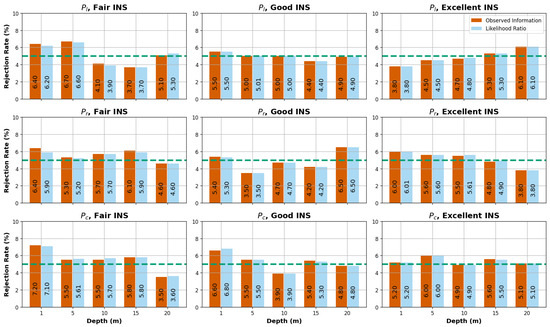
Figure 11.
Drone scenarios: rejection rates of the Wald statistic (observed Fisher information) and the signed likelihood ratio statistic r. The x-axis represents different simulated depths, while the y-axis represents the rejection rate percentage based on a CL of 95%. The green dashed horizontal line indicates the 5% rejection rate threshold.
For the airborne scenarios, we observed a similar performance to the test statistics, except for point , which showed distinct rejection rates, as illustrated in Figure 12.

Figure 12.
Airborne scenarios: rejection rates of the Wald statistic (observed Fisher information) and the signed likelihood ratio statistic r. The x-axis represents different cases, while the y-axis represents the rejection rate percentage based on a confidence level of 95%. The green dashed horizontal line indicates the 5% rejection rate threshold.
Specifically, for the fair INS scenario, the rejection rates for the test statistic exceeded 15% at point , while the r statistic demonstrated relatively consistent rejection rates across different points (3.5–7%). Given the WCD uncertainty results of , highlighted in the previous section, we can infer that the higher variability in the WCD uncertainty estimates for in the previous subsection is consistent with the observed rejection rates. These findings suggest that the -based CI may overestimate the WCD uncertainty in high-altitude scenarios. This is particularly the case for viewing geometries similar to , with a 19% rejection rate for the most noisy attitude scenario. On the other hand, the r statistic showed greater effectiveness in estimating the WCD uncertainties in this particular case ( and airborne fair INS).
In summary, the evaluation of uncertainty metrics through rejection rate analysis provides valuable insights into the reliability of uncertainty estimation methods for both the drone and airborne cases. Both scenarios exhibit reasonably consistent performance, except under extreme attitude noise and non-parallel line viewing geometries.
4.3. Water–Air Interface Height Inference
In our experimental setup, we sought to present the profile likelihood of h under multi-point and multi-view likelihood scenarios. To begin with, we need to clarify the conditions under which the WAI height is inferable from camera poses. Primarily, when the lines-of-sight are derived from parallel lines (i.e., or viewing geometry) or have equal incidence angles (i.e., viewing geometry), the lines-of-sight having the maximum likelihood will always intersect, irrespective of the WAI height. In these cases, the parameter h cannot be inferred because it has no influence on the likelihood. In contrast, when the lines-of-sight are non-coplanar with the baseline [28], then the lines-of-sight having the maximum likelihood will not intersect unless they are refracted under an optimal value of the WAI height parameter. This distinct viewing geometry can be readily obtained by introducing different incidence angles in the simulated lines-of-sight, allowing for the inference of the parameter h through the profile likelihood analysis. Either translating the same points (, and ) or introducing different flight altitudes provide viewing geometries with different incidence angles. In our setup, points , , and are translated in both the x and y dimensions, with different offsets of and , respectively. For drone simulations, and , whereas for the airborne scenarios, these offsets are scaled by the altitude ratio. Applying these adjustments, we use the likelihood (20) for the WAI height parameter h inference, with a WAI height true value of , for varying sample sizes, namely . Each sample refers to two measured camera poses for a single feature point given the refraction at . This means that for n samples, the parameter is of dimension (1 for h, for , and for ).
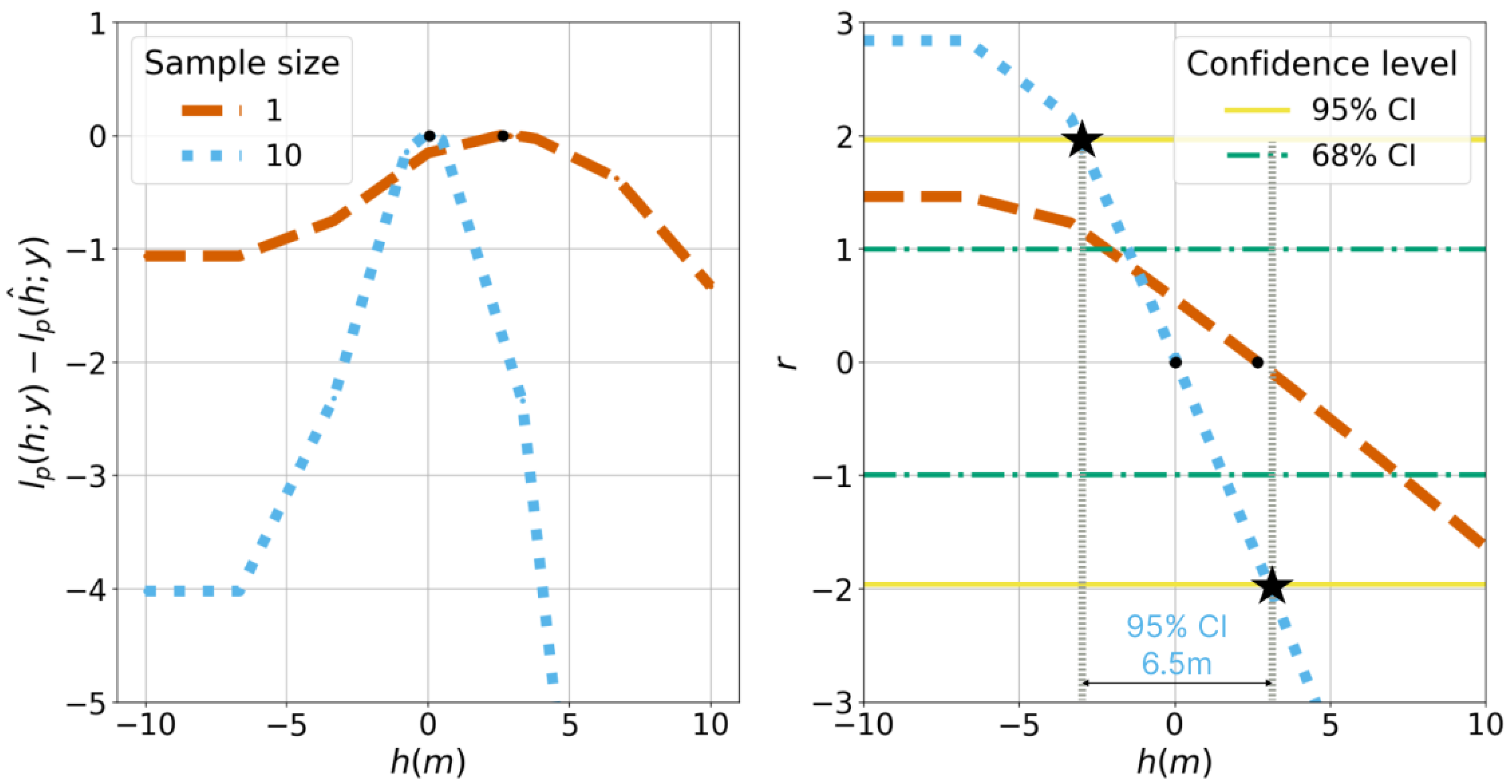
Figure 13 shows on the left side WAI height-normalized profile likelihood obtained for the translated point at a depth of 5 m and for two sample sizes: 1 and 10. The associated r statistic is presented on the right side of the figure with the CI for two levels, namely 95% and 68%. According to the profile involving only one sample (orange profile), two non-intersecting lines-of-sight can provide an optimal value for the WAI height parameter h. For both 1-sample and 10-sample profiles, we observe a typical asymmetry in the profile, which is characterized by a flatness on the left side (below 5 m depth). This pattern can be mainly attributed to the fact that when the WAI is relatively below the WCD for a given feature point, the positional likelihood should not decrease with the WAI height, since there is no refraction above the WAI. The r statistic, affected by this flatness, successfully captures this asymmetry, which results in a non-identifiable 95% CI lower bound for the 1-sample inference, although we could delineate 68% CI. On the other hand, 10 samples provides sufficient statistical information for delineating both 95% bounds for the WAI height h. However, based on the r 95% CI, the achieved precision of approximately 6.5 m for 10 samples is notably high. Therefore, it would be valuable to explore the possible improvement in WAI uncertainty when larger sample sizes are taken into account.
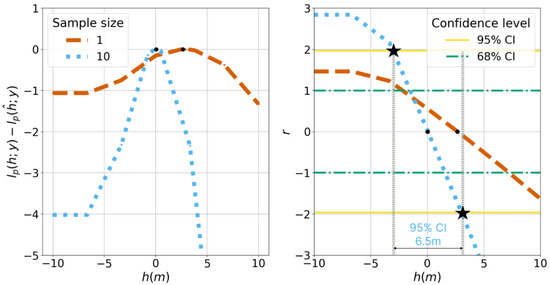
Figure 13.
Drone and excellent INS scenario: WAI height inference based on likelihood profiling for 1 and 10 samples. The graphic on the left represents the normalized profile likelihood on the y-axis according to the WAI height on the x-axis. The graphic on the right represents the r statistic on the y-axis according to the WAI height on the x-axis. The black points correspond to the WAI height MLE . Additionally, on the right side, the 95% CI for 10 samples are indicated as the width between the intersections (marked by black stars) of the r statistic curve and the 95% confidence critical values .
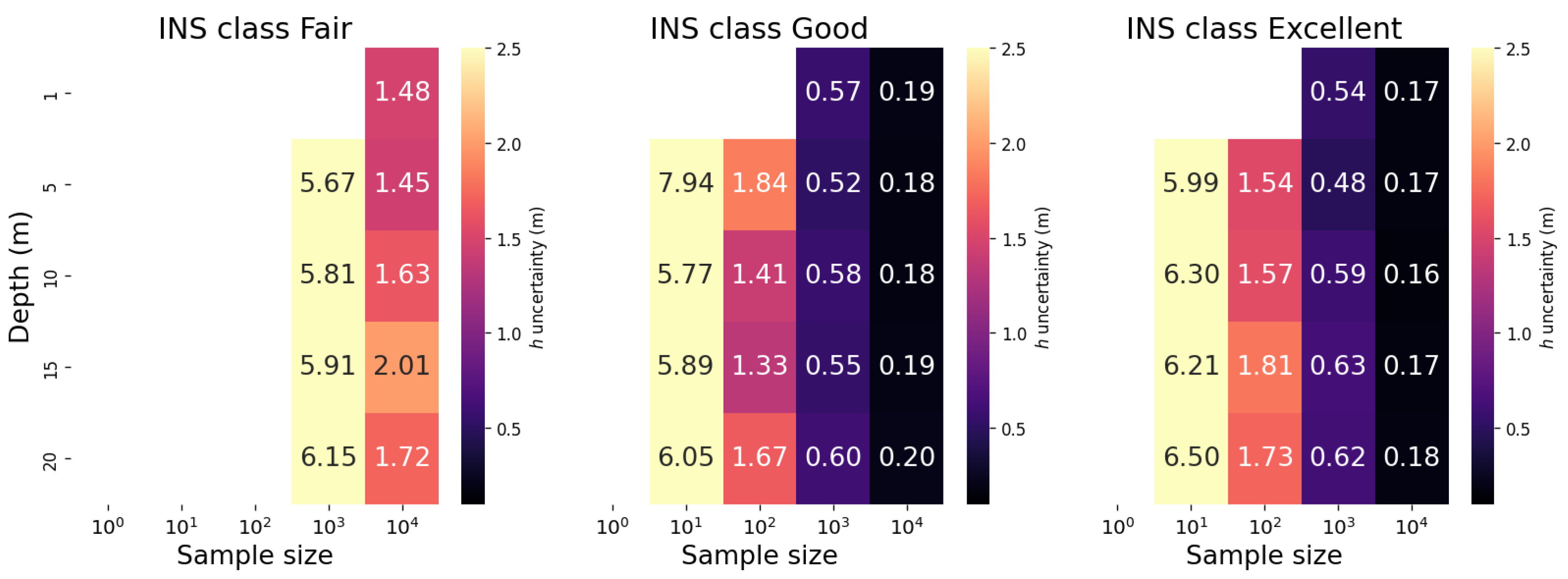
Figure 14 presents heatmaps of WAI height uncertainties, determined by the r CI for point across different INS classes for the drone scenario. These heatmaps account for a variety of depths and sample sizes. As the sample sizes increased, so did the statistical information, leading to more precise profile likelihoods and subsequently smaller uncertainties in the WAI height. Interestingly, a trend of uncertainty decreasing by a factor between 3 and was noted. This pattern, where uncertainty contracts in relation to the square root of the sample size (), echoes the square root law common in Gaussian errors and is linked to the central limit theorem’s principle of sample averages approaching a normal distribution as the sample size expands, leading to decreased uncertainty. Analogously to the WCD inference, the good and excellent INS demonstrated similar performances. Intriguingly, the depth has no major impact on the WAI uncertainties except for the observed lag of the 1 m depth scenario with sample size compared to other depths. This insinuates that the task of WAI inference tends to be more difficult when it relies on observations taken at depths near the WAI surface.
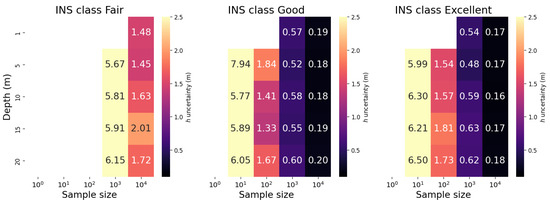
Figure 14.
Drone, scenarios, WAI height uncertainty across different INS classes reported as r statistic confidence intervals. Missing bins indicate non-identifiable 95% confidence intervals.
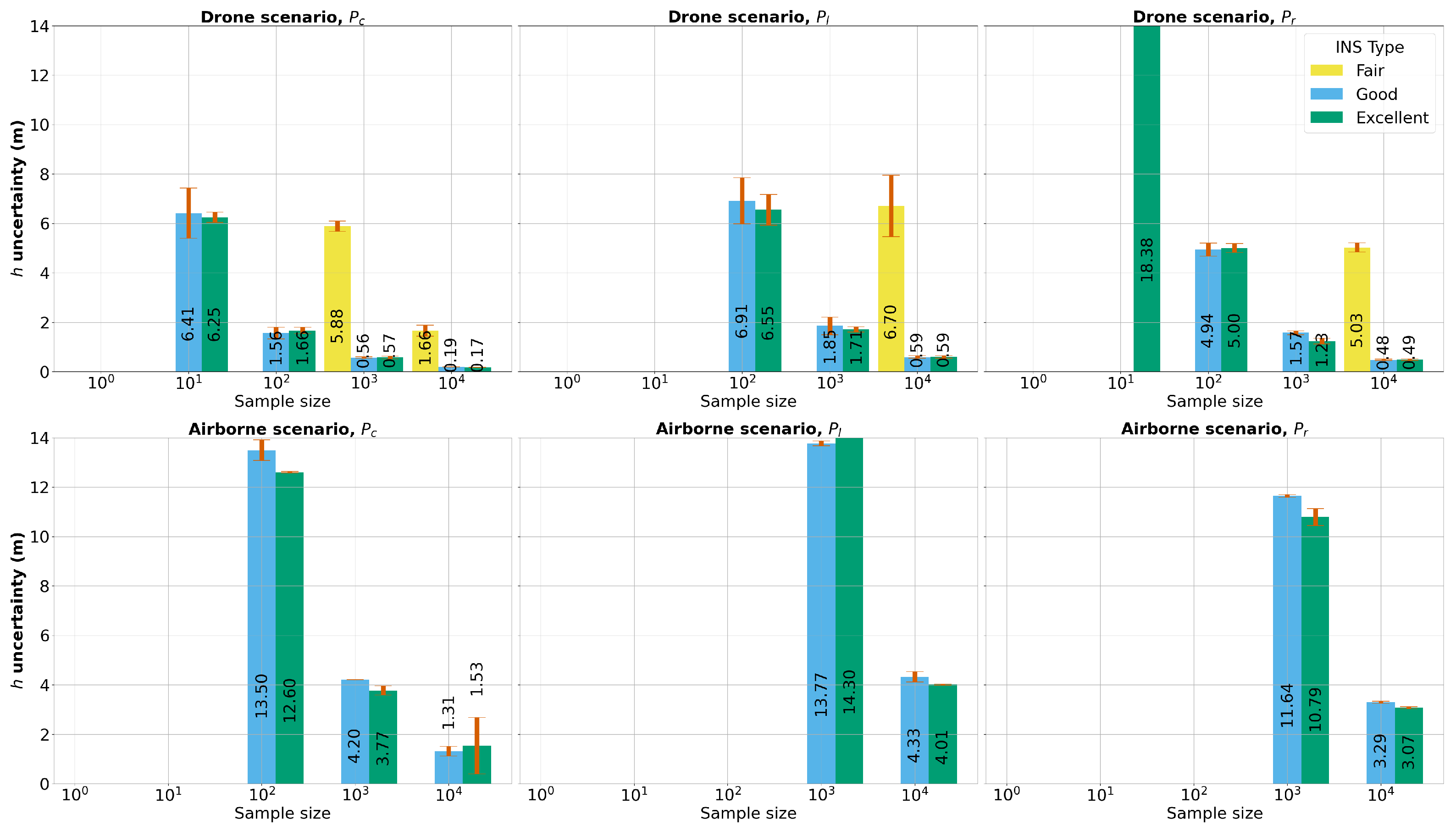
In Figure 15, we display the depth-averaged WAI uncertainties, together with their corresponding standard deviations, spanning viewing geometries, INS classes, and sample sizes for both drone and airborne settings. It is often the case that the variability of WAI uncertainty with depth, as indicated by error bars, is more pronounced in difficult scenarios (10 samples). For the WAI height inference, the viewing geometry showed the best performance overall, suggesting that cross lines are strongly relevant in pushbroom acquisitions if one is interested in inferring the WAI height. It is particularly noteworthy that the achieved WAI height 95% CI of 17 cm and 19 cm for the excellent and good INS, respectively, closely aligns with the Global Navigation Satellite System (GNSS) precision of 5 cm when considering a substantial sample size of . This suggests that with relatively small high resolution datasets, drone-based acquisitions can provide significantly accurate estimations of the WAI height in optically clear shallow waters with a textured seabed. Furthermore, considering the decline in uncertainties by a factor of with increasing sample size, even with the fair INS quality, we extrapolate that drone flights could achieve a WAI height precision of 16 cm given a sample size of about 1 million. Although 1 million matched feature points may seem substantial for a single survey of pushbroom imagery in coastal areas, given constraints like water clarity and a textured seabed, this number of points is easily attainable with high-resolution frame video imagery under optimal conditions. This emphasizes the efficiency of drone-based acquisitions even with less-than-ideal INS quality, given an adequately large dataset of paired feature points.
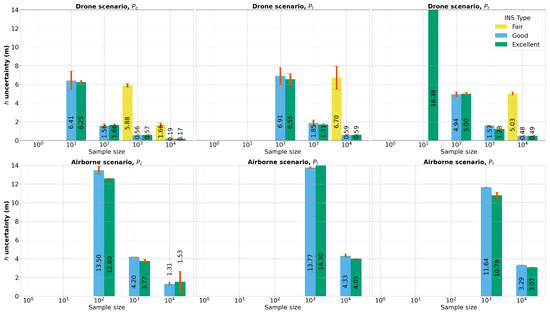
Figure 15.
Depth-averaged WAI height uncertainty across different INS types and sample sizes for each point, as reported by the r statistic confidence intervals. Missing bars correspond to non-identifiable 95% confidence intervals for all the averaged depths. The numerical values displayed on each bar correspond to the depth-averaged WAI height visually represented. The error bars represent the standard deviation of WAI height uncertainty across the different depths.
In contrast, airborne measurements yield a higher degree of uncertainty in WAI estimation, with no successful inference for the fair INS. Similarly to the WCD inference results, this is largely attributed to the increased operational altitude that intensifies optical distortion and viewing geometry variability due to a more distant and extensive footprint. Despite these challenges, airborne measurements with high-quality INS achieve a metric precision for a 10,000 sample size, allowing us to extrapolate a centimeter precision level for a sample size of 1 million.
5. Discussion
This study highlights the significant role of the camera pose quality on WCD uncertainty. The excellent INS class, typically deemed a high standard in hydrography, did not achieve satisfactory WCD precision (around 2 m) for airborne flights. This discrepancy underlines the advantages of drone-based surveys operating at lower altitudes with high-quality camera pose measurements, which provided high WCD precisions, specifically around 50 cm for high base–height ratios like . According to International Hydrographic Organization (IHO) standards [29], this precision level falls within the ‘Order 1a’ requirements without taking the influence of depth into account. However, the inherent limitations of higher base–height ratios and low flight altitudes, such as reduced and inefficient coverage, need to be considered. In contrast, for points and , the uncertainty ranged between 0.7 and 1 m, meeting the requirements of the ‘Order 2’. Furthermore, we state that combining frame and pushbroom imagery could further improve camera pose quality for high-altitude flights. Indeed, our geometric likelihood approach enables through-water photogrammetry bundle adjustment, presenting the opportunity to utilize frame imagery in order to improve camera pose accuracy. While our study provides key insights into camera pose uncertainties in through-water photogrammetry, it is important to note a limitation in our experimental design concerning multi-view geometry principles. Specifically, our experiments did not accommodate the principle of utilizing overlaps both across and along flight directions; a common approach in multi-view geometry to augment camera pose samples and reduce uncertainty in triangulation. Our focus was on maintaining uniform analysis across two camera poses in order to directly compare the effects of stereo-geometry. This approach is also appropriate given that pushbroom studies often rely on stereo-pair configurations, where extensive cross-line datasets are very limited.
As we focused on pushbroom geometric scenarios in our study, we only investigated two camera poses for triangulation, and we hypothesize that having an adequate number of feature points for each camera pose can refine the pose and eliminate the reliance on challenging-to-obtain GCP in coastal areas. Such advancements in camera pose quality have the potential to significantly enhance the precision levels of drone observations, potentially meeting stringent standards like the special order in clear shallow waters with textured seabeds.
Furthermore, based on the WCD uncertainty results, the observed Fisher information performance and its low sensitivity to sampling suggest that classical variance–covariance propagation approaches are reliable except for certain challenging scenarios. These include high flight altitudes, low-quality camera pose measurements, and viewing geometries with non co-planar FoVs ( case). These viewing geometries are more prevalent in frame imagery since the spatial footprint in frame imagery is rectangular, thus establishing the likelihood ratio statistic as a potential tool for robust uncertainty estimation in such scenarios.
Beyond the evaluated uncertainties, it is worth emphasizing that our results contribute to a deeper understanding of photogrammetric techniques for coastal photogrammetric surveying. The ability to accurately infer the water surface position from imagery alone reduces the reliance on additional tide data or separate WAI height observations. Although our initial assumptions considered a horizontal water surface, not accounting for surface fluctuations, the results showed a satisfactory precision of around 17 cm when using large samples and non-intersecting viewing geometries. This precision level is particularly impressive considering calm sea conditions and light weather situations, which can be encountered in sheltered area with low significant wave heights. Nonetheless, it is important to consider that in a real-world scenario, coastal water fluctuations could occur due to a range of factors such as changes in tide and weather, which may influence the temporal coherence of the imagery dataset. This consideration indicates that our approach can be further improved by taking into account these potential fluctuations. For instance, simulations of wave spectra and sea state conditions can be used to create more realistic scenarios, offering a comprehensive perspective on the influence of surface fluctuations on WAI height uncertainties and their subsequent impact on the derived bathymetric estimations. The noted viewing geometry condition for WAI height inference might favor in-track stereo pairs more then across-track satellite stereo pairs, which are often acquired with the same incidence angles. Therefore, a continuation of this study would be extending the investigation of the effect of viewing geometry and proposing appropriate flight acquisition modes for WAI height inference. Also, the performance of r confidence intervals that we utilized to estimate uncertainties in WAI height were not assessed through hypothesis testing, in contrast to what we performed for the WCD. This examination was out of the scope of this study and therefore could serve as a potential area for further investigation and research. Moreover, our approach for WAI inference can be effectively adapted with stationary high-quality stereo camera observations as a technique for tide monitoring.
The results also invite a deeper examination of innovative uncertainty modeling methods. Such methods can be beneficial in harmonizing the geometric inference of WCD with other forms of inference like radiometric estimation with analytical radiative transfer models within a unified theoretical likelihood framework, as explored by Jay et al. [30], Sicot et al. [31]. Interestingly, the relative insensitivity of the geometric inference to depth variations, which contrasts with its radiometric counterpart, as suggested by these studies, indicates potential complementarity between the geometric and radiometric inference. However, it is important to recognize that both approaches, geometric and radiometric, require a degree of optical water clarity. Therefore, the impact of depth can introduce inherent constraints on both types of inferences, especially in environments with turbid waters.
Our study is a robust step forward in uncertainty modeling for bathymetric photogrammetry in coastal shallow waters and has unveiled several insights. The main focus of our study is the investigation of camera pose uncertainties in through-water photogrammetry. However, it is important to acknowledge that uncertainties may arise from additional sources, such as matching errors, camera imperfections, and wave dynamics, which are significant factors in coastal water imagery.
6. Conclusions
This study represents a detailed exploration of the potential and accuracy of through-water photogrammetry, with a specific emphasis on the WCD and the WAI height inferences. Our observations reveal the profound influence of viewing geometry and camera pose quality on the resulting uncertainties, overshadowing the impact of depth.
Our approach bridges the gap between advanced probabilistic modeling and stereo-photogrammetric triangulation. This innovative integration provides a comprehensive understanding of the complexities associated with through-water 3D reconstruction methods. The utility of drone technology, complemented by high-quality camera pose measurement and spectral imagery, proves to be a compelling tool for high-precision through-water photogrammetry. Importantly, these advancements contribute to the provision of a framework for stereo-photogrammetry predictive uncertainties in bathymetric charting. Additionally, we demonstrate that inferring the water surface elevation is achievable from camera pose measurements, reducing the dependence on auxiliary data sources such as tide level measurements or WAI height observations.
Notwithstanding the success of our investigations, we acknowledge the limitations of our current study. Specifically, questions related to providing compelling recommendations for viewing geometries and hypothesis testing for WAI height require further exploration and elucidation. To enhance the robustness and reliability of our methodology under a variety of conditions, we encourage future research to incorporate surface fluctuations and camera optical imperfections.
In conclusion, our study sets a robust foundation for future investigations in the field of through-water photogrammetry. It contributes significantly towards refining photogrammetric techniques and is shaping the future of through-water surveying and data collection methodologies in coastal areas. Although this study marks only the initial steps in this evolving field, we are confident that our efforts have established an essential milestone, paving the way for further advancements in through-water photogrammetry.
Author Contributions
Conceptualization, M.A.G. and G.S.; methodology, M.A.G., S.D., G.S. and I.Q.; software, M.A.G.; validation, S.D., G.S. and I.Q.; formal analysis, M.A.G., S.D., G.S. and I.Q.; investigation, M.A.G., G.S., S.D. and I.Q.; resources, M.A.G., S.D., G.S. and I.Q.; data curation, M.A.G.; writing—original draft preparation, M.A.G.; writing—review and editing, M.A.G., S.D., G.S. and I.Q.; visualization, M.A.G.; supervision, S.D., G.S. and I.Q.; project administration, S.D. and I.Q.; funding acquisition, S.D. and G.S. and I.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Institut France-Québec pour la Coopération Scientifique en appui au Secteur Maritime (IFQM) and the Région Bretagne under the ARED program “Drones marins”.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
We would like to express our gratitude to Université Laval and ENSTA Bretagne for providing access to the necessary equipment and laboratories that were crucial for conducting this research. We also thank Michel Legris for providing valuable technical information regarding industrial INS typical performances. Additionally, we acknowledge the authors of the Deep Orientation Uncertainty Learning project for making their software available under the MIT License, which we utilized for sampling from the Bingham distribution. Finally, we extend our thanks to the Python open-source community for the optimization tools that significantly contributed to the success of this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| WCD | Water Column Depth |
| WAI | Water Air Interface |
| GCP | Ground Control Points |
| SfM | Structure from Motion |
| MVS | Multi-View Stereo |
| RPC | Rational Polynomial Coefficients |
| FoV | Field of View |
| IFoV | Instantaneous Field of View |
| SDB | Satellite-Derived Bathymetry |
| GNSS | Global Navigation Satellite System |
| INS | Inertial Navigation System |
| MLE | Maximum Likelihood Estimation |
| LS | Least Square |
| CI | Confidence Intervals |
| CL | Confidence Level |
Appendix A. Equivalence Between the Wald Test Based on the Expected Fisher Information and the Variance–Covariance Propagation Under Gaussian Errors
Under the assumption of Gaussian errors, Maximum Likelihood Estimation (MLE) for the parameter vector and the Least Square (LS) estimator are equivalent. The log-likelihood function for a model with centered additive Gaussian errors is as follows:
where is the vector of observations, and is the covariance matrix of the errors. The variance–covariance matrix associated with the LS estimator can be propagated through a first-order Taylor series expansion of around the MLE , as shown in the following formula:
where is the Jacobian matrix of partial derivatives of with respect to the parameters evaluated at . This expression for the variance–covariance matrix is equivalent to the inverse of the expected Fisher information matrix at the MLE, known from the theory of Gaussian errors [32]:
Therefore, the inverse of the expected Fisher information provides the same estimation of precision for the parameter estimates as the variance–covariance matrix derived from the LS estimator.
Consider the inference of a parameter and the following partitioning of :
According to Section 4.6 of [33], the estimator is asymptotically unbiased with the following variance:
is the partial expected Fisher information of , which is simply the diagonal value of at the block . (A3) proves that is also the diagonal value of the variance–covariance matrix (A2) under additive centered Gaussian errors. Furthermore, it can be shown that:
where is the profile likelihood and is the observed Fisher information for . This establishes the equivalence between classical variance–covariance inference and the Wald test for evaluating the CI of .
References
- Singh, G.; Cottrell, R.; Eddy, T.; Cisneros-Montemayor, A. Governing the Land-Sea Interface to Achieve Sustainable Coastal Development. Front. Mar. Sci. 2021, 8, 709947. [Google Scholar] [CrossRef]
- Martínez, M.; Intralawan, A.; Vázquez, G.; Pérez-Maqueo, O.; Sutton, P.; Landgrave, R. The coasts of our world: Ecological, economic and social importance. Ecol. Econ. 2007, 63, 254–272. [Google Scholar] [CrossRef]
- Pasquale, D.; Giovanni, B.R.; Vincenzo, P. Measurement for the Sea; Springer Series in Measurement Science and Technology Series Editors; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Lyzenga, D. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 379, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Stumpf, R.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnolology Oceanogr. 2003, 48, 547–557. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters: 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef]
- Hedley, J.; Roelfsemab, C.; Koetzc, B.; Phinn, S. Capability of the Sentinel 2 mission for tropical coral reef mapping and coral bleaching detection. Remote Sens. Environ. 2012, 120, 145–155. [Google Scholar] [CrossRef]
- Cao, B.; Fang, Y.; Jiang, Z.; Gao, L.; Hu, H. Shallow water bathymetry from WorldView-2 stereo imagery using two-media photogrammetry. Eur. J. Remote Sens. 2019, 52, 506–521. [Google Scholar] [CrossRef]
- Mandlburger, G. Through-water dense image matching for shallow water bathymetry. Photogramm. Eng. Remote Sens. 2019, 85, 445–454. [Google Scholar] [CrossRef]
- Hodúl, M.; Bird, S.; Knudby, A.; Chénier, R. Satellite derived photogrammetric bathymetry. Isprs J. Photogramm. Remote Sens. 2018, 142, 268–277. [Google Scholar] [CrossRef]
- Murase, T.; Tanaka, M.; Tani, T.; Miyashita, Y.; Ohkawa, N.; Ishiguro, S.; Suzuki, Y.; Kayanne, H.; Yamano, H. A Photogrammetric Correction Procedure for Light Refraction Effects at a Two-Medium Boundary. Photogramm. Eng. Remote Sens. 2008, 74, 1129–1136. [Google Scholar] [CrossRef]
- Agrafiotis, P.; Georgopoulos, A. Camera Constant in the Case of Two Media Photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W5, 1–6. [Google Scholar] [CrossRef]
- JCGM. Evaluation of measurement data—Guide to the expression of uncertainty in measurement. Int. Organ. Stand. 2008, 50, 134. [Google Scholar]
- Dolloff, J.T. RPC uncertainty parameters: Generation, application, and effects. In Proceedings of the ASPRS Annual Convention, Sacramento, CA, USA, 19–23 March 2012; pp. 19–23. [Google Scholar]
- Dolloff, J.; Theiss, H. The Specification and Validation of Predicted Accuracy Capabilities for Commercial Satellite Imagery. In Proceedings of the ASPRS Annual Convention, Louisville, KY, USA, 23–28 March 2014. [Google Scholar]
- Slocum, R.K.; Wright, W.; Parrish, C.; Costa, B.; Sharr, M.; Battista, T.A. Guidelines for Bathymetric Mapping and Orthoisubsectionmage Generation Using sUAS and SfM, An Approach for Conducting Nearshore Coastal Mapping; NOAA technical memorandum NOS NCCOS 265, United States, National Ocean Service; National Centers for Coastal Ocean Science (U.S.); United States, National Oceanic and Atmospheric Administration; Coral Reef Conservation Program (U.S.): Silver Spring, MD, USA, 2019. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, A.; Hassan, M.A.; Qin, C. Assessing Through-Water Structure-from-Motion Photogrammetry in Gravel-Bed Rivers under Controlled Conditions. Remote Sens. 2022, 14, 5351. [Google Scholar] [CrossRef]
- Sims-Waterhouse, D.; Isa, M.; Piano, S.; Leach, R. Uncertainty model for a traceable stereo-photogrammetry system. Precis. Eng. 2020, 63, 1–9. [Google Scholar] [CrossRef]
- Kalacska, M.; Lucanus, O.; Sousa, L.; Vieira, T.; Arroyo-Mora, J.P. Freshwater Fish Habitat Complexity Mapping Using Above and Underwater Structure-From-Motion Photogrammetry. Remote Sens. 2018, 10, 1912. [Google Scholar] [CrossRef]
- Kiraci, A.C.; Toz, G. Theoretical analysis of positional uncertainty in direct georeferencing. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B1, 1221–1226. [Google Scholar] [CrossRef]
- Skarlatos, D.; Agrafiotis, P. A novel iterative water refraction correction algorithm for use in structure from motion photogrammetric pipeline. J. Mar. Sci. Eng. 2018, 6, 77. [Google Scholar] [CrossRef]
- Tewinkel, G.C. Water Depths from Aerial Photographs. Photogramm. Eng. 1963, 29, 1037–1042. [Google Scholar]
- Rofallski, R.; Luhmann, T. An Efficient Solution to Ray Tracing Problems in Multimedia Photogrammetry for Flat Refractive Interfaces. J. Photogramm. Remote Sens. Geoinf. Sci. 2022, 90, 37–54. [Google Scholar] [CrossRef]
- Mulsow, C. A Flexible Multi-media Bundle Approach. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Newcastle upon Tyne, UK, 21–24 June 2010; Volume XXXVIII, pp. 472–477. [Google Scholar]
- Nasiri, S.M.; Hosseini, R.; Moradi, H. The optimal triangulation method is not really optimal. Iet Image Process. 2023, 17, 2855–2865. [Google Scholar] [CrossRef]
- Bingham, C. An Antipodally Symmetric Distribution on the Sphere. Ann. Stat. 1974, 2, 1201–1225. [Google Scholar] [CrossRef]
- Brazzale, A.; Davison, A.; Reid, N. Applied Asymptotics: Case Studies in Small-Sample Statistics; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Rinner, K. Problems of Two-Medium Photogrammetry. Photogramm. Eng. 1969, 35, 275–282. [Google Scholar]
- International Hydrographic Organization. International Hydrographic Organization Standards for Hydrographic Surveys S-44 Edition 6.0.0. Online Resource. Available online: https://iho.int/uploads/user/pubs/standards/s-44/S-44_Edition_6.1.0.pdf.pdf (accessed on 28 October 2024).
- Jay, S.; Guillaume, M.; Chami, M.; Audrey Minghelli, Y.D.; Lafrance, B.; Serfaty, V. Predicting minimum uncertainties in the inversion of ocean color geophysical parameters based on Cramer-Rao bounds. Opt. Express 2018, 26, A1–A18. [Google Scholar] [CrossRef] [PubMed]
- Sicot, G.; Ghannami, M.A.; Lennon, M.; Loyer, S.; Thomas, N. Likelihood Ratio statistic for inferring the uncertainty of satellite derived bathymetry. In IEEE WHISPER; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Kay, L.S.M. Fundamentals of Statistical Signal Processing: Estimation Theory. In Prentice Hall Signal Processing Series; Taylor & Francis: Oxfordshire, UK, 1993. [Google Scholar]
- Severini, T.A. Likelihood Methods in Statistics. In Oxford Statistical Series; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).